A Solution to the Non-Cooperative Equilibrium Problem for Two and Three Players Using the Fixed-Point Technique
Abstract
1. Introduction and Preliminaries
- (i)
- The topological spaces and are regarded as the strategies for the first player and second player, respectively;
- (ii)
- A topological subspace of the product space represents valid strategy pairs;
- (iii)
- We define a bi-loss operator as follows: , where represents the loss acquired by player j when strategies and are employed. A pair is stated as a NCE ifHence,Assume that the following maps exist:such that the following equations hold:The mappings and satisfying the above properties are called optimal decision rules. Any solution to the systemis a NCE. Let represent the function
- (i)
- (ii)
- (iii)
- (iv)
- where , and
- (i)
- Let and be two players, each choosing strategies from their respective strategy set and
- (ii)
- The strategy space is equipped with -space by defining the distance function m as follows:This space models the closedness of the strategies.
- (iii)
- The payoff functions are for player and for player
- (iv)
- A Nash equilibrium occurs at the strategy pair such that no player can improve their payoff by unilaterally changing their strategy:
- 1
- for player
- 2
- for player
- ・
- If both players choose , they both obtain a payoff of which is a mutually beneficial outcome.
- ・
- If chooses and chooses B, , gets 0 and gets
- ・
- The other combinations yield lower payoffs for at least one player.
- ・
- Best Response of Player :
- ・
- Given , the best response of is (since ).
- ・
- Given , the best response of is (since ).
- ・
- Best Response of Player
- ・
- Given , the best response of player is (since ).
- ・
- Given , the best response of player is (since ).
- (i)
- A sequence in -space converges with respect to to k if and only if
- (ii)
- A sequence in -space is called m-Cauchy ifexist (and are finite).
- (iii)
- A space is said to be complete if every m-Cauchy in ξ is m-convergent with respect to to k in ξ such that
- (iv)
- A sequence is a Cauchy sequence in if and only if it is a Cauchy sequence in the metric space
- (v)
- A space is complete if and only if is complete.
- (ii)
- A sequence in is called 0-Cauchy sequence if
- (iii)
- A space is said to be 0-complete if every 0-Cauchy sequence in ξ is convergent with respect to to k in ξ such that
- (i)
- A self-mapping on a -space is called a m-Caristi mapping if there is a function ξ with lower semicontinuity in the setup of , and it satisfies the inequality
- (ii)
- Self-mapping on an -space is called a m-Caristi mapping if there is a function ξ with lower semicontinuity in , and it satisfies the inequality
- () F is strictly increasing and continuous.
- () For any sequence ,
2. Main Results
- (i)
- , for all
- (ii)
- ∀, for all
3. Coupled Fixed-Point Results in M-Metric Spaces
- (i)
- (a)
- If a is a nondecreasing sequence in ξ such that for all , and , then
- (b)
- If a is a nonincreasing sequence in ξ such that for all and , then
- (i)
- (i)
4. Solution of Some Non-Cooperative Equilibrium Problems of Two Persons
- (i)
- and represent strategies for the first and second players, respectively;
- (ii)
- The denotes the set of allowed strategy pairs;
- (iii)
- The biloss operator is as follows:,where represents the loss acquired by player j when strategies and are employed, assuming that there exist maps and , which are optimal decision rules.As mentioned before, any solution to the system
- (i)
- for all and for any and ,
- (i)
- for all and for any and ;
5. Tripled Fixed-Points in M-Metric Spaces
- (i)
- for all
6. Certain Non-Cooperative Equilibrium Problems Involving Three Players
- (i)
- , , represent strategies for the first, second, and third players, respectively;
- (ii)
- The denotes the set of allowed strategy pairs;
- (iii)
- We define a triloss operator as follows:where represents the loss acquired by player j when strategies , and are employed. A pair is stated as a NCE ifThis implies thatTo determine the strategy pairs that succeed as non-cooperative equilibria, we examine the optimal decision rules and , defined as follows:Consider the any fixed-point mappingis a NCE.
- (i)
- for all and , for some and
- (i)
7. Solution of an Integral Equation
- (i)
- The unknown function k is real-valued,
- (ii)
- are increasing and decreasing functions, respectively, where:
- (iii)
- is a continuous function,
- (iv)
- , where , and and for all such that
- (v)
- there exists such thatand
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Banach, S. Sur les operations dans les ensembles abstraits et leurs applications aux equations integrales. Fund. Math. 1922, 3, 133–181. [Google Scholar]
- Alsulami, H.H.; Karapınar, E.; Piri, H. Fixed points of generalized F-Suzuki type contraction in complete metric-like spaces. Discret. Dyn. Nat. Soc. 2015, 2015, 969726. [Google Scholar]
- Beg, I.; Butt, A.R. Common fixed point for generalized set valued contractions satisfying an implicit relation in partially ordered metric spaces. Math. Commun. 2010, 15, 65–76. [Google Scholar]
- Christian, E.O. Games, Fixed Points and Mathematical Economics; School of Economics and Finance University of St Andrews: St Andrews, UK, 2007. [Google Scholar]
- Gulyaz, S.; Karapınar, E. Coupled fixed point result in partially ordered partial metric spaces through implicit function. Hacet. J. Math. Stat. 2013, 42, 347–357. [Google Scholar]
- Hancer, H.A.; Minak, G.; Altun, I. On a broad category of multivalued weakly picard operators. Fixed Point Theory 2017, 18, 229–236. [Google Scholar]
- Valero, O. On Banach fixed point theorems for partial metric spaces. Appl. Gen. Topol. 2005, 6, 229–240. [Google Scholar]
- Border, K.C. Fixed Point Theorems with Applications to Economics and Game Theory; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Thanh, T.D.; Hobiny, A.; Karapınar, E. A solution for the non-cooperative equilibrium problem of two person via fixed point theory. J. Ineq. Appl. 2015, 2015, 158. [Google Scholar]
- Matthews, S.G. Partial metric topology. Proc. 8th summer conference on general topology and applications. N. Y. Acad. Sci. 1994, 728, 183–197. [Google Scholar]
- Asadi, M.; Karapinar, E.; Salimi, P. New extension of p-metric spaces with fixed points results on M-metric spaces. J. Inequal. Appl. 2014, 18, 1–18. [Google Scholar]
- Monfared, H.; Azhini, M.; Asadi, M. Fixed point results on m-metric spaces. J. Math. Anal. 2016, 7, 85–101. [Google Scholar]
- Patle, P.R.; Patel, D.K.; Aydi, H.; Gopal, D.; Mlaiki, N. Nadler and Kannan type set valued mappings in M-metric spaces and an application. Mathematics 2019, 7, 373. [Google Scholar] [CrossRef]
- Tariq, M.; Arshad, M.; Abbas, M.; Ameer, E.; Mansour, S.; Aydi, H. A relation theoretic m-metric fixed point algorithm and related applications. AIMS Math. 2023, 8, 19504–19525. [Google Scholar]
- Tariq, M.; Arshad, M.; Ameer, E.; Aloqaily, A.; Aiadi, S.S.; Mlai, N. On Relational Weak -Contractive Mappings and Their Application. Symmetry 2023, 15, 922. [Google Scholar] [CrossRef]
- Tariq, M.; Abbas, M.; Hussain, A.; Arshad, M.; Ali, A.; Al-Sulami, H. Fixed points of non-linear set-valued (α∗,ϕM) contraction mappings and related applications. Aims Math. 2022, 7, 8861–8878. [Google Scholar]
- Mohanta, S.K.; Biswas, D. Characterization of completeness for m-metric spaces and a related fixed point theorem. J. Anal. 2020, 29, 701–711. [Google Scholar]
- Ran, A.C.M.; Reurings, M.C.B. A fixed point theorem in partially ordered sets and some applications to matrix equations. Proc. Am. Math. Soc. 2004, 132, 1435–1443. [Google Scholar]
- Nieto, J.; Rodriguez-Lopez, R. Contractive mapping theorems in partially ordered sets and applications to ordinary differential equations. Order 2005, 22, 223–239. [Google Scholar]
- Nieto, J.; Rodriguez-Lopez, R. Existence and uniqueness of fixed point in partially ordered sets and applications to ordinary differential equations. Acta Math. Sin. 2007, 23, 2205–2212. [Google Scholar]
- Guo, D.; Lakshmikantham, V. Coupled fixed points of nonlinear operators with applications. Nonlinear Anal. TMA 1987, 11, 623–632. [Google Scholar]
- Bhaskar, T.G.; Lakshmikantham, V. Fixed point theorems in partially ordered metric spaces and application. Nonlinear Anal. 2006, 65, 1379–1393. [Google Scholar]
- Lakshmikantham, V.; Ciric, L. Coupled fixed point theorems for nonlinear contractions in partially ordered metric spaces. Nonlinear Anal. 2009, 70, 4341–4349. [Google Scholar]
- Rad, G.S.; Shukla, S.; Rahimi, H. Some relations between n-tuple fixed point and fixed point results. Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Mat. 2014, 109, 471–481. [Google Scholar]
- Samet, B.; Karapınar, E.; Aydi, H.; Rajic, V. Discussion on some coupled fixed point theorems. Fixed Point Theory Appl. 2013, 2013, 50. [Google Scholar]
- Wardowski, Fixed points of a new type of contractive mappings in complete metric spaces. Fixed Point Theory Appl. 2012, 2012, 94. [CrossRef]
- Asim, M.; Mujahid, S.; Uddin, I. Fixed point theorems for F-contraction mapping in complete rectangular M-metric space. Appl. Gen. Topol. 2022, 23, 363–376. [Google Scholar]
- Cosentino, M.; Vetro, P. Fixed point results for F-contractive mappings of Hardy-Rogers-type. Filomat 2014, 28, 715–722. [Google Scholar]
- Nadler, S.B. Multivalued contraction mappings. Pac. J. Math. 1969, 30, 475–488. [Google Scholar]
- Sahin, H.; Altun, I.; Turkoglu, D. Two fixed point results for multivalued F-contractions on M-metric spaces. Rev. Real Acad. Cienc. Exactas Fis. Nat. Ser. A Mat. 2018, 113, 1839–1849. [Google Scholar] [CrossRef]
- Paesano, D.; Vetro, C. Multi-valued F-contractions in 0-complete partial metric spaces with application to Volterra type integral equation. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. 2014, 108, 1005–1020. [Google Scholar]
- Romaguera, S. A Kirk Type Characterization of Completeness for Partial Metric Spaces. Fixed Point Theory Appl. 2010, 6, 493298. [Google Scholar]
- Roldan, A.; Martinez-Moreno, J.; Roldan, C.; Karapınar, E. Some remarks on multidimensional fixed point theorems. Fixed Point Theory 2014, 15, 545–558. [Google Scholar]
- Berinde, V. Generalized coupled fixed point theorems for mixed monotone mappings in partially ordered metric spaces. Nonlinear Anal. 2011, 74, 7347–7355. [Google Scholar]

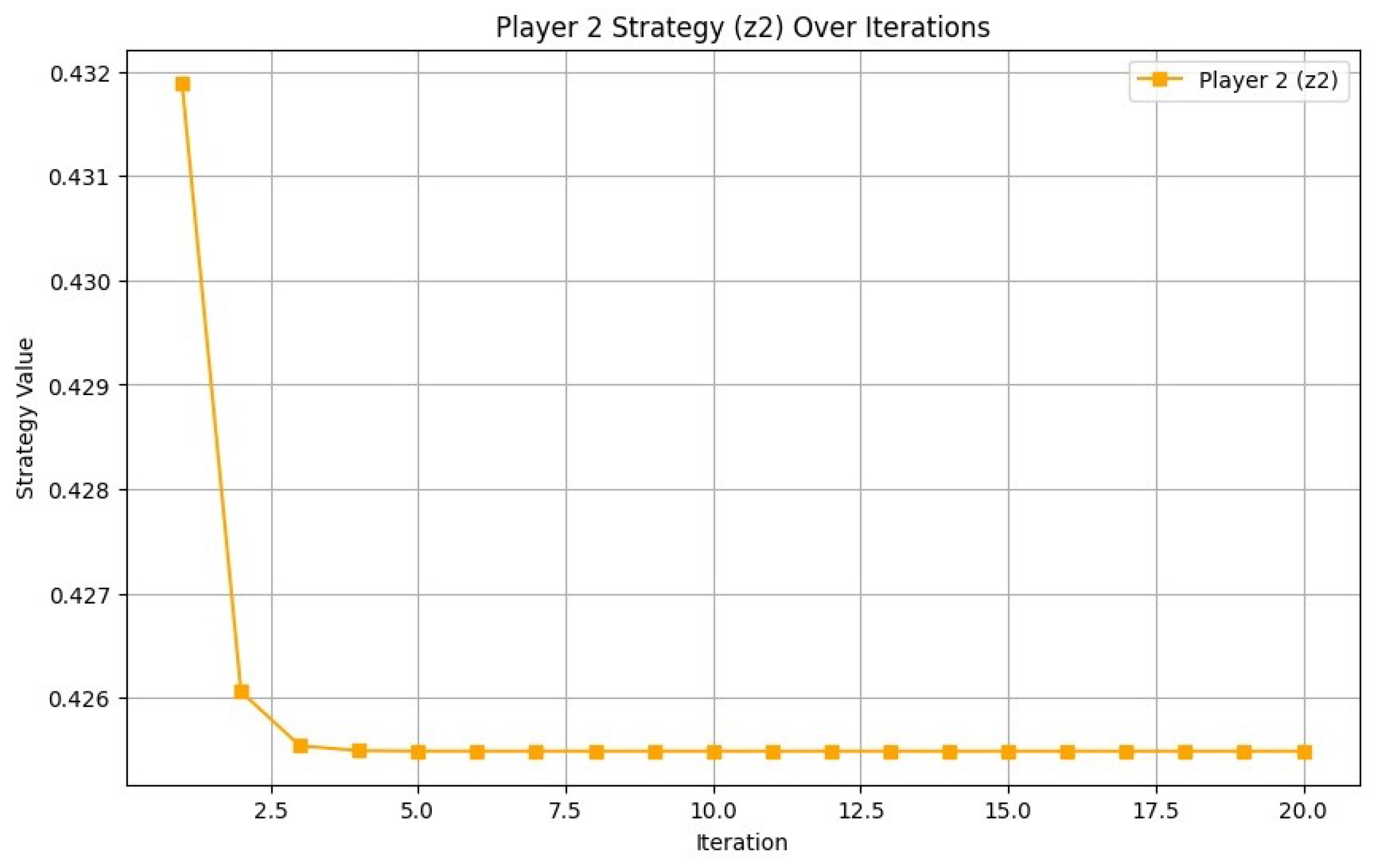
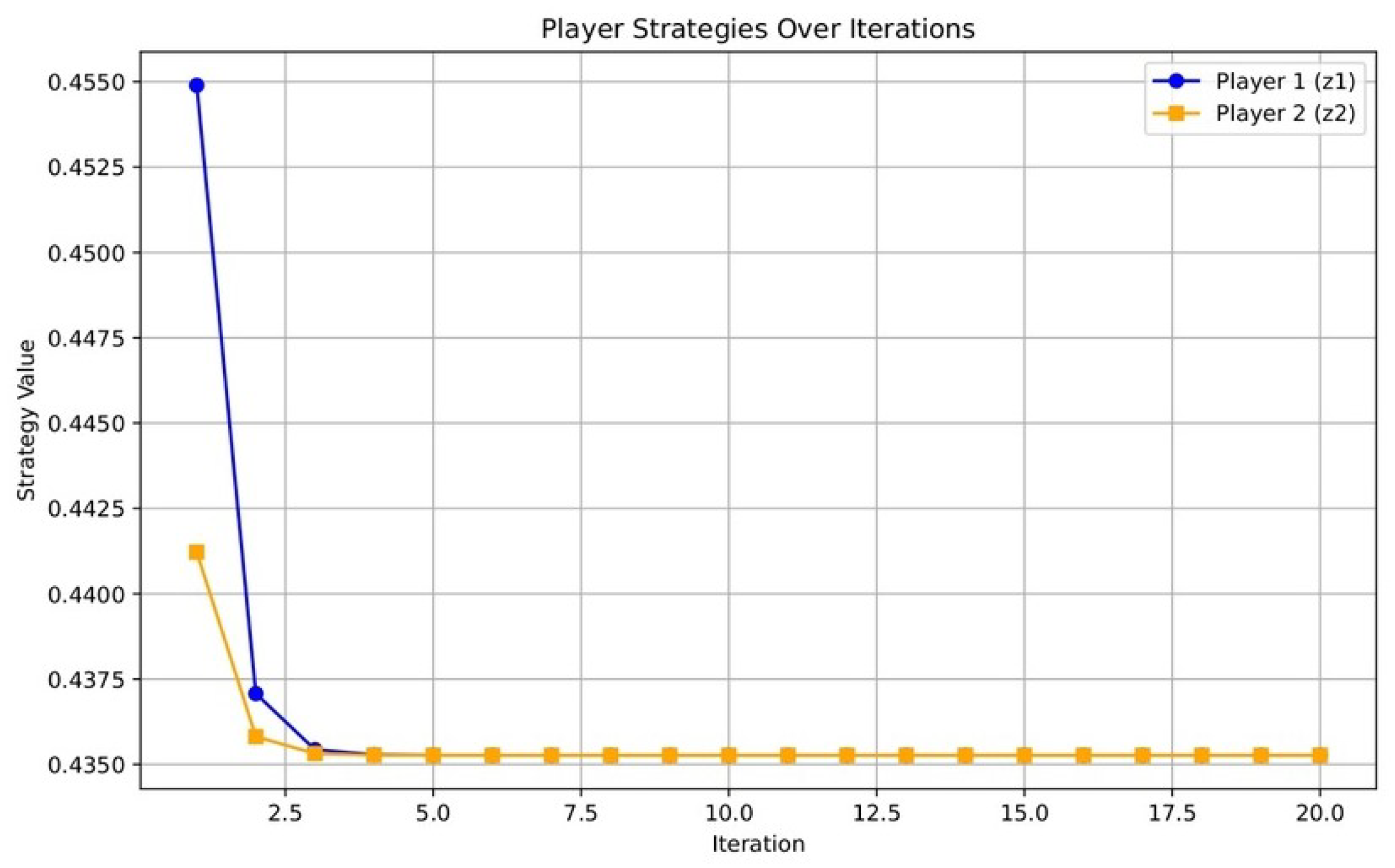
| Iteration Player | Iteration Player | Player 1 Strategy | Player 2 Strategy |
|---|---|---|---|
| 0 | 1 | ||
| 1 | 2 | ||
| 2 | 3 | ||
| 3 | 4 | ||
| 4 | 5 | ||
| 5 | 6 | ||
| 6 | 7 | ||
| …, | …, | …, | …, |
| 17 | 18 | ||
| 18 | 19 | ||
| 19 | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tariq, M.; Mansour, S.; Abbas, M.; Assiry, A. A Solution to the Non-Cooperative Equilibrium Problem for Two and Three Players Using the Fixed-Point Technique. Symmetry 2025, 17, 544. https://doi.org/10.3390/sym17040544
Tariq M, Mansour S, Abbas M, Assiry A. A Solution to the Non-Cooperative Equilibrium Problem for Two and Three Players Using the Fixed-Point Technique. Symmetry. 2025; 17(4):544. https://doi.org/10.3390/sym17040544
Chicago/Turabian StyleTariq, Muhammad, Sabeur Mansour, Mujahid Abbas, and Abdullah Assiry. 2025. "A Solution to the Non-Cooperative Equilibrium Problem for Two and Three Players Using the Fixed-Point Technique" Symmetry 17, no. 4: 544. https://doi.org/10.3390/sym17040544
APA StyleTariq, M., Mansour, S., Abbas, M., & Assiry, A. (2025). A Solution to the Non-Cooperative Equilibrium Problem for Two and Three Players Using the Fixed-Point Technique. Symmetry, 17(4), 544. https://doi.org/10.3390/sym17040544





