IM-GNN: Microservice Orchestration Recommendation via Interface-Matched Dependency Graphs and Graph Neural Networks
Abstract
1. Introduction
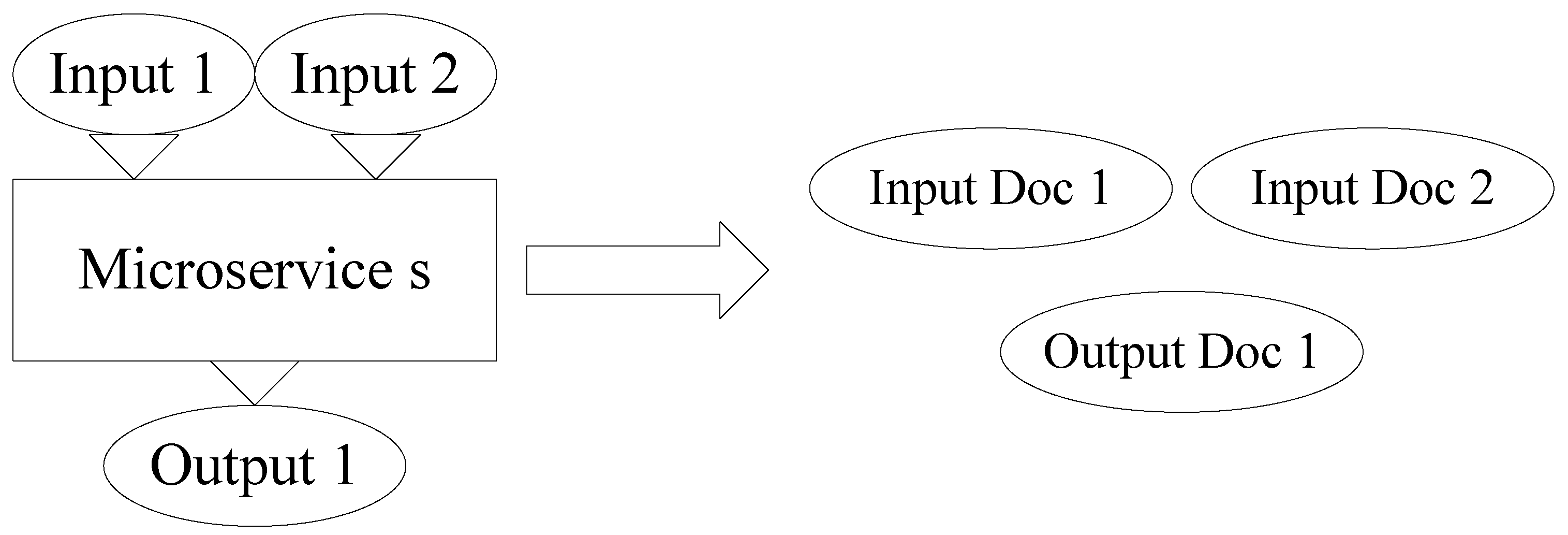
- Symmetry-Aware Dependency Graph Construction: We propose a novel method for constructing microservice dependency graphs based on interface matching, explicitly capturing the structural symmetry in microservice interactions. Initially, we introduce the TF-WF-IDF algorithm, an enhancement of the traditional TF-IDF approach [3], to extract keywords from microservice documentation. Next, we employ a language model to generate input–output representations for each microservice. Finally, we utilize an interface matching algorithm to analyze these representations and establish reciprocal call dependencies, ensuring a balanced and structured dependency graph that aligns with the execution-order constraints of orchestration.
- IM-GNN Model: We present the Interface Matching-Graph Neural Networks (IM-GNN) model for microservice workflow orchestration recommendation. This model leverages the constructed microservice dependency graph and applies graph neural networks to generate vector representations for each microservice node. By computing the similarities between these vectors, the model identifies and recommends a candidate set of microservices, ensuring that the orchestration process maintains structural coherence and functional symmetry.
- Experimental Evaluation: The proposed model undergoes extensive empirical evaluation on Amazon’s SageMaker and Comprehend datasets. These experiments validate the effectiveness of IM-GNN, demonstrating its superior recommendation accuracy compared to traditional approaches. Additionally, we analyze the impact of various hyperparameters, highlighting the role of symmetry-aware graph construction in improving model performance.
2. Materials and Methods
2.1. Preliminaries
2.2. Proposed Method
2.2.1. IM-GNN
2.2.2. Text Processing
2.2.3. Construction of the Microservice Dependency Graph
2.2.4. Construction of Graph Neural Network
| Algorithm 1 IM-GNN |
|
2.2.5. Microservice Orchestration Recommendation
2.3. Experimental Materials
2.3.1. Experimental Environments
2.3.2. Experimental Data
2.3.3. Experimental Metrics
3. Results
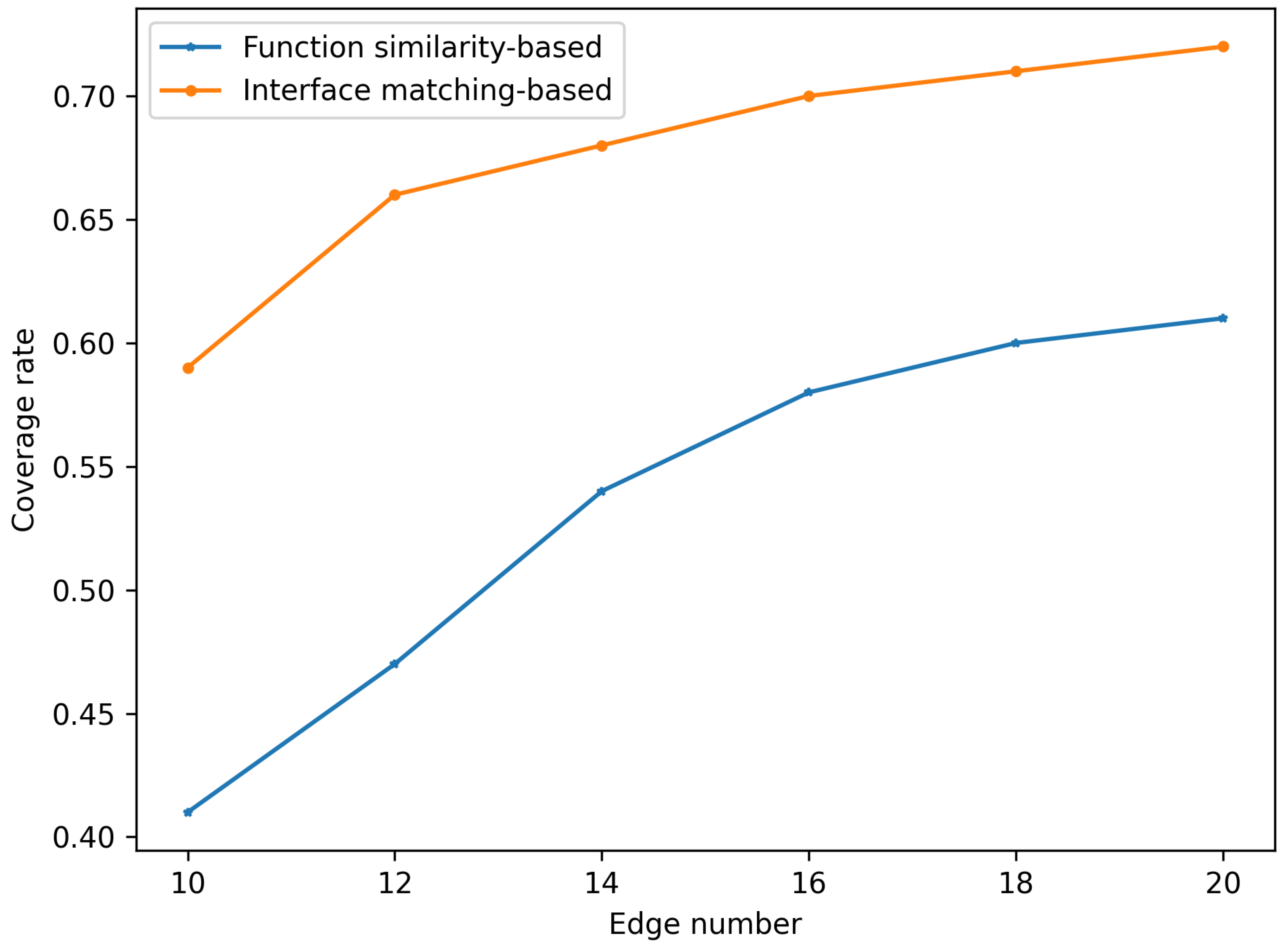
3.1. Experiments on Constructing the Microservice Dependency Graph
3.2. Ablation Study
3.3. Performance Comparison
4. Discussion
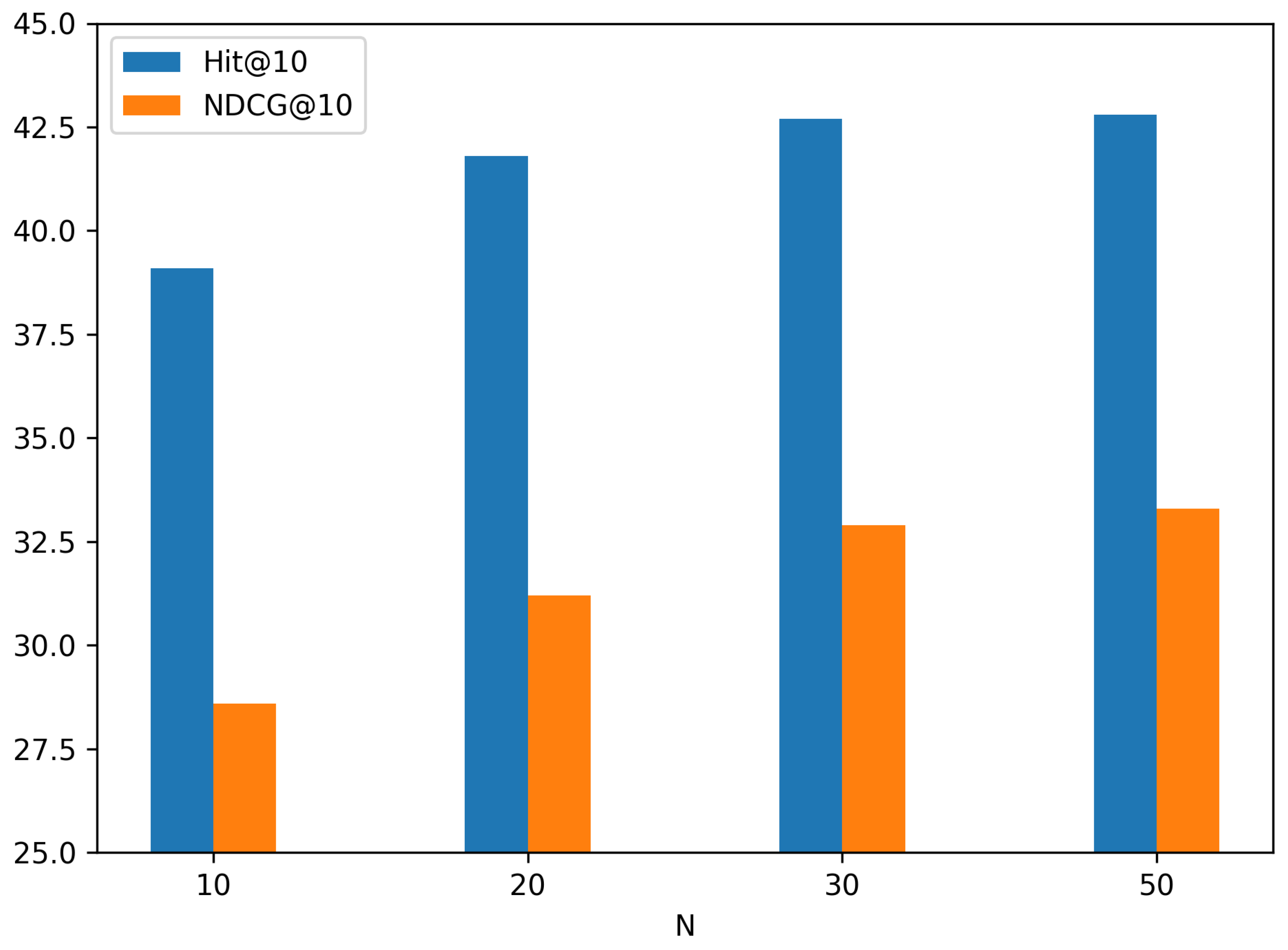
4.1. The Impact of the Number of Neighbors
4.2. The Impact of the GNN Layer
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ko, H.; Lee, S.; Park, Y.; Choi, A. A Survey of Recommendation Systems: Recommendation Models, Techniques, and Application Fields. Electronics 2022, 11, 141. [Google Scholar] [CrossRef]
- Li, Z.; Shen, X.; Jiao, Y.; Pan, X.; Zou, P.; Meng, X.; Yao, C.; Bu, J. Hierarchical Bipartite Graph Neural Networks: Towards Large-Scale E-commerce Applications. In Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), Dallas, TX, USA, 20–24 April 2020; pp. 1677–1688. [Google Scholar] [CrossRef]
- McAuley, J. Personalized Machine Learning; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Qian, F.; Pan, S.; Zhang, G. Tensor Computation for Seismic Data Processing: Linking Theory and Practice; Earth Systems Data and Models Series; Springer: Cham, Switzerland, 2025. [Google Scholar]
- Fan, W. Recommender Systems in the Era of Large Language Models (LLMs). IEEE Trans. Knowl. Data Eng. 2024, 36, 6889–6907. [Google Scholar] [CrossRef]
- Saboor, A.; Hassan, M.F.; Akbar, R.; Shah, S.N.M.; Hassan, F.; Magsi, S.A.; Siddiqui, M.A. Containerized Microservices Orchestration and Provisioning in Cloud Computing: A Conceptual Framework and Future Perspectives. Appl. Sci. 2022, 12, 5793. [Google Scholar] [CrossRef]
- Luo, S.; Xu, H.; Lu, C.; Ye, K.; Xu, G.; Zhang, L.; He, J.; Xu, C. An In-Depth Study of Microservice Call Graph and Runtime Performance. IEEE Trans. Parallel Distrib. Syst. 2022, 33, 3901–3914. [Google Scholar] [CrossRef]
- Su, Y.; Li, Y.; Zhang, Z. Two-Tower Structure Recommendation Method Fusing Multi-Source Data. Electronics 2025, 14, 1003. [Google Scholar] [CrossRef]
- Li, Y.; Liu, K.; Satapathy, R.; Wang, S.; Cambria, E. Recent Developments in Recommender Systems: A Survey [Review Article]. IEEE Comput. Intell. Mag. 2024, 19, 78–95. [Google Scholar] [CrossRef]
- Huang, S.; Wang, C.; Bian, W. A Hybrid Food Recommendation System Based on MOEA/D Focusing on the Problem of Food Nutritional Balance and Symmetry. Symmetry 2024, 16, 1698. [Google Scholar] [CrossRef]
- Vaidhyanathan, K.; Caporuscio, M.; Florio, S.; Muccini, H. ML-enabled Service Discovery for Microservice Architecture: A QoS Approach. In Proceedings of the 39th ACM/SIGAPP Symposium on Applied Computing, New York, NY, USA, 8–12 April 2024; SAC ’24. pp. 1193–1200. [Google Scholar] [CrossRef]
- Dang, Q.; Li, N.; Dong, H.; Li, X.; Guo, M. Improved Microservice Fault Prediction Model of Informer Network. In Proceedings of the 2024 IEEE 7th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 20–22 September 2024; Volume 7, pp. 1116–1120. [Google Scholar] [CrossRef]
- Kaushik, N. Improving QoS of Microservices Architecture Using Machine Learning Techniques. In Proceedings of the Software Architecture. ECSA 2024 Tracks and Workshops; Ampatzoglou, A., Pérez, J., Buhnova, B., Lenarduzzi, V., Venters, C.C., Zdun, U., Drira, K., Rebelo, L., Di Pompeo, D., Tucci, M., et al., Eds.; Springer: Cham, Switzerland, 2024; pp. 72–79. [Google Scholar]
- Niu, B.; Ma, J.; Yang, Z. A Comparative Study of CF and NCF in Children’s Book Recommender System. In Proceedings of the 2021 3rd International Workshop on Artificial Intelligence and Education (WAIE), Xi’an, China, 19–21 November 2021; pp. 43–47. [Google Scholar] [CrossRef]
- Mao, C.; Wu, Z.; Liu, Y.; Shi, Z. Matrix Factorization Recommendation Algorithm Based on Attention Interaction. Symmetry 2024, 16, 267. [Google Scholar] [CrossRef]
- Rendle, S. Factorization Machines. In Proceedings of the 2010 IEEE International Conference on Data Mining, Sydney, NSW, Australia, 20 January 2011; pp. 995–1000. [Google Scholar] [CrossRef]
- Qian, F.; He, Y.; Yue, Y.; Zhou, Y.; Wu, B.; Hu, G. Improved Low-Rank Tensor Approximation for Seismic Random Plus Footprint Noise Suppression. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–19. [Google Scholar] [CrossRef]
- Juan, Y.; Zhuang, Y.; Chin, W.S.; Lin, C.J. Field-aware Factorization Machines for CTR Prediction. In Proceedings of the 10th ACM Conference on Recommender Systems, New York, NY, USA, 15–19 September 2016; RecSys ’16. pp. 43–50. [Google Scholar] [CrossRef]
- Guo, H.; Tang, R.; Ye, Y.; Li, Z.; He, X. DeepFM: A factorization-machine based neural network for CTR prediction. arXiv 2017, arXiv:1703.04247. [Google Scholar]
- Alhwayzee, A.; Araban, S.; Zabihzadeh, D. A Robust Recommender System Against Adversarial and Shilling Attacks Using Diffusion Networks and Self-Adaptive Learning. Symmetry 2025, 17, 233. [Google Scholar] [CrossRef]
- Qian, F.; Liu, Z.; Wang, Y.; Zhou, Y.; Hu, G. Ground Truth-Free 3-D Seismic Random Noise Attenuation via Deep Tensor Convolutional Neural Networks in the Time-Frequency Domain. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Sammut, C.; Webb, G.I. (Eds.) TF–IDF. In Encyclopedia of Machine Learning; Springer: Boston, MA, USA, 2010; pp. 986–987. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. arXiv 2019, arXiv:1810.04805. [Google Scholar]
- Wittig, A. Amazon Web Services in Action, 3rd ed.; Simon and Schuster: New York, NY, USA, 2023. [Google Scholar]
- Rashed, A.; Grabocka, J.; Schmidt-Thieme, L. A Guided Learning Approach for Item Recommendation via Surrogate Loss Learning. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, New York, NY, USA, 11–15 July 2021; SIGIR ’21. pp. 605–613. [Google Scholar] [CrossRef]
- Hidasi, B.; Karatzoglou, A.; Baltrunas, L.; Tikk, D. Session-based recommendations with recurrent neural networks. arXiv 2015, arXiv:1511.06939. [Google Scholar]
- Kang, W.C.; McAuley, J. Self-Attentive Sequential Recommendation. In Proceedings of the 2018 IEEE International Conference on Data Mining (ICDM), Los Alamitos, CA, USA, 17–20 November 2018; pp. 197–206. [Google Scholar] [CrossRef]
- Ma, C.; Ma, L.; Zhang, Y.; Sun, J.; Liu, X.; Coates, M. Memory augmented graph neural networks for sequential recommendation. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 5045–5052. [Google Scholar]



| Name | Version |
|---|---|
| CPU | Intel(R) Xeon(R) Gold 6248R CPU @ 3.00 GHz |
| Memory | 128 GB |
| GPU | Nvidia Tesla T4 |
| CUDA | CUDA Toolkit 11.2 |
| OS | Ubuntu 22.04.3 |
| Programming Language | Python 3.8.0 |
| Framework | TensorFlow 2.0-gpu |
| IDE | PyCharm 2022.3.3 |
| Environment Management Tool | Anaconda 3 |
| Results | SageMaker | |
|---|---|---|
| W/O Interface Match | 36.23 | 28.44 |
| IM-GNN (ours) | 41.45 | 31.23 |
| Results | SageMaker | Comprehend | ||
|---|---|---|---|---|
| GRU4Rec | 28.65 | 25.85 | 27.81 | 26.29 |
| SASRec | 32.02 | 26.34 | 33.09 | 28.57 |
| MA-GNN | 40.44 | 30.05 | 36.74 | 35.31 |
| IM-GNN (ours) | 41.45 | 31.23 | 35.13 | 36.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, T.; Chen, T.; Sun, Y.; Xu, Y. IM-GNN: Microservice Orchestration Recommendation via Interface-Matched Dependency Graphs and Graph Neural Networks. Symmetry 2025, 17, 525. https://doi.org/10.3390/sym17040525
Zhao T, Chen T, Sun Y, Xu Y. IM-GNN: Microservice Orchestration Recommendation via Interface-Matched Dependency Graphs and Graph Neural Networks. Symmetry. 2025; 17(4):525. https://doi.org/10.3390/sym17040525
Chicago/Turabian StyleZhao, Taiyin, Tian Chen, Yudong Sun, and Yi Xu. 2025. "IM-GNN: Microservice Orchestration Recommendation via Interface-Matched Dependency Graphs and Graph Neural Networks" Symmetry 17, no. 4: 525. https://doi.org/10.3390/sym17040525
APA StyleZhao, T., Chen, T., Sun, Y., & Xu, Y. (2025). IM-GNN: Microservice Orchestration Recommendation via Interface-Matched Dependency Graphs and Graph Neural Networks. Symmetry, 17(4), 525. https://doi.org/10.3390/sym17040525





