Enhancing Quantum Key Distribution Security Through Hybrid Protocol Integration

Abstract

With the increasing complexity of cyber threats and the emergence of quantum computing, enhancing secure communication is essential. This study explores an effective hybrid quantum key distribution (QKD) protocol that integrates photonic and atomic systems to leverage their respective strengths. The concept of symmetry plays a crucial role in this context, as it underpins the principles of entanglement and the balance between key generation and error correction. The photonic system is used for the initial key generation, while the atomic system facilitates entanglement swapping, error correction, and privacy amplification. The comprehensive theoretical framework encompasses key components, detailed security proofs, performance metrics, and an analysis of system vulnerabilities, illustrating the resilience of the hybrid protocol against potential threats. Extensive experimental studies demonstrate that the hybrid QKD protocol seamlessly integrates photonic and atomic systems, enabling secure key distribution with minimal errors and loss rates over long distances. This combination of the two systems reveals exceptional resilience against eavesdropping, significantly improving both security and robustness compared with traditional QKD protocols. Consequently, this makes it a compelling solution for secure communication in the increasingly digital world.

1. Introduction

1.1. Motivation

As the amount of information continues to grow and computing technology advances rapidly, cyber threats have become increasingly complex and frequent. Consequently, the need to enhance secure communication has become critical for protecting sensitive data and ensuring the integrity of digital interaction. Furthermore, the rise in quantum computing presents a significant challenge to traditional security techniques and numerous systems that depend on them [1]. In response, innovative cryptographic solutions are being actively developed to address these emerging challenges. Among these advancements, quantum key distribution (QKD) is a leading approach for near-term implementation and commercial application. QKD can offer exceptional security, paving the way for a new era of cryptographic techniques that can withstand advanced security threats. The symmetry inherent in quantum systems involved in QKD enhances its robustness, providing a balanced approach to secure communication.

1.2. Problem Background

QKD leverages the unique properties of quantum mechanics to facilitate a secure random key exchange between two communicating parties, often referred to as Alice and Bob. Quantum random key generation (QRKG) is a fundamental component of QKD that ensures that generated keys are secure and unpredictable. The randomness generated by quantum mechanics, particularly through superposition and entanglement, produces keys that are unpredictably and uniformly distributed across the key space. This symmetry ensures that an eavesdropper cannot predict or guess the key based on the patterns or biases [2]. In addition, QKD provides a mechanism for detecting eavesdropping threats. When an intrusion occurs, it results in changes in quantum states, indicating that the key exchange may have been intercepted and alerted the parties to a potential security breach. Owing to these capabilities, QKD represents a significant advance in the field of cryptography, allowing secure communication and the detection of eavesdroppers [3]. This represents a game changer compared to traditional encryption techniques, which are fundamentally built on the complexity of mathematical problems, and are thus vulnerable to rapid advancements in computational capabilities. Furthermore, traditional techniques depend on pre-distributed keys or key exchange protocols that can be intercepted by eavesdroppers, allowing unauthorized decryption [2].

In QKD, information is encoded using quantum bits (qubits), enabling the representation of data in a manner that is not possible with classical bits. Qubits can be realized using various physical systems, and QKD can be divided into atomic and photonic systems, according to the physical system utilized. The implementation of QKD is versatile, owing to the distinct advantages and challenges presented by each category. In photonic protocols, such as BB84 [4,5], E91 [6], and E92 [7], qubits are represented by photons. These protocols encode and transmit secure cryptographic keys by taking advantage of quantum properties such as photon polarization and entanglement [8]. Photonic particles are transmitted over fiber-optic communication networks, which facilitates high-speed transmission over long distances. In addition, photons can be transmitted through free space, enabling applications such as satellite communications. These protocols have been extensively studied and widely implemented in real-world applications, establishing them as the cornerstone of quantum communication. On the other hand, atomic protocols harness the quantum states of atoms, such as energy levels, entangled atom pairs, or spin states, to facilitate secure key distribution. While individual atoms cannot be transmitted like photons, they can be manipulated within systems such as atomic ensembles or trapped ions. In these setups, information is stored in the quantum states of the multiple atoms. Atomic systems provide high precision in controlling quantum states, allowing the careful management of encoded information. These protocols are beneficial in non-ideal environments such as poor atmospheric conditions or solid materials. Although atomic QKD is less widely adopted than photonic protocols, it offers distinct benefits in scenarios with significant noise and decoherence challenges [9,10].

1.3. Problem Statement

Despite significant advances in QKD technologies, most existing protocols focus primarily on photonic or atomic systems. Although photonic systems are effective for long-distance quantum communication, they are prone to loss and noise, which can compromise the security of the QRKG process [11]. In contrast, atomic systems excel at maintaining coherence and performing sophisticated error correction and privacy amplification.

The motivation to combine photons and atoms in a QKD process addresses the inherent limitations of using photons alone, such as their susceptibility to decoherence and distance constraints, thereby leveraging the stability and robustness of atomic systems to enhance the security, reliability, and efficiency of quantum key distribution. This study aims to address these challenges by proposing an effective hybrid QKD protocol that utilizes photonic systems for initial key generation and atomic systems for subsequent error correction and privacy amplification. By integrating the strengths of both technologies, this study seeks to enhance the overall security and robustness of QKD systems. The symmetry between the photonic and atomic components of the proposed framework not only optimizes performance but also reinforces the security aspects of the communication process. This study develops a comprehensive theoretical framework for the hybrid protocol and performs performance evaluations. Through this integration, this study contributes significantly to the advancement of secure quantum communication.

1.4. Contributions

The contributions of this study are as follows:

• A theoretical framework is developed for the proposed hybrid QKD protocol that integrates photonic systems for initial key generation with atomic systems for subsequent entanglement swapping, error correction, and privacy amplification. Using these technologies, a hybrid protocol is designed to significantly enhance the security and robustness of key generation and distribution.
• Comprehensive security proofs and performance metrics are incorporated, establishing a foundation for evaluating the protocol’s resilience against potential threats, as well as the efficiency of entanglement swapping, error correction, and privacy amplification. This analysis improves our understanding of the strengths of the protocol and ensures that it meets security and performance standards in practical applications.
• Comprehensive experimental investigations are conducted to validate the proposed protocol. This includes the utilization of both photonic and atomic systems as benchmarks to assess the performance of the proposed hybrid protocol. The experiments focus on critical parameters, such as the generated key rate, successful key bits, error rate, loss rates, and detection rates of eavesdropping.

1.5. Organization

Section 2 provides an overview of traditional QKD, followed by a review of related work, and establishes the context of the current research. Section 3 introduces the proposed hybrid protocol and outlines its key components and processes. Section 4 presents detailed security proofs along with rigorous performance metrics. Section 5 presents the simulation results and analysis. Finally, Section 6 presents the conclusions and provides directions for future research.

2. Literature Review

2.1. Overview of QKD

Transmission in QKD occurs through both quantum and classical channels, each of which plays a distinct role in the secure communication process. Quantum channels are responsible for transmitting qubits between Alice and Bob, enabling the secure establishment of a shared key. These channels often utilize optical fibers that facilitate long-distance communication with minimal signal loss [12]. In contrast, classical channels support non-quantum communication, allowing Alice and Bob to exchange the necessary information for basis reconciliation, error correction, and privacy amplification. Once the text message is encrypted, it is sent over classical channels, such as email or secure file transfers. The integration of both quantum and classical channels is crucial for ensuring secure and efficient key distribution in QKD applications [12,13,14,15].

The QKD process involves several critical steps to ensure secure communication [12]:

• Encoding agreement: This initial step establishes a mutual understanding between Alice and Bob about the representation of the qubits. This ensures that both parties agree on a reliable encoding scheme.
• State encoding: In this step, Alice encodes her information into qubits, which are then transformed into quantum states suitable for secure transmission. This encoding typically utilizes various polarization states of photons and the quantum states of atoms. Alice encodes these qubits and transmits them to Bob in a controlled environment via a quantum channel.
• Measurement: The success of this step depends on whether Bob measures the qubits using the same basis as Alice uses to encode them. After receiving the qubits, Bob randomly selects the measurement bases. If he chooses the same basis as Alice, he can retrieve transmitted information successfully. Next, Alice and Bob communicate over a classical channel to discuss the bases they use for both encoding and measurement, clarifying which qubits were measured using the same basis.
• Key sharing: After the encoding and measurement processes, Alice and Bob are positioned to share their keys securely. This step involves compiling the successfully retrieved bits into a shared key.
• Error correction: Alice and Bob use error correction protocols to address discrepancies in their raw keys, which can result from noise in the quantum channel or eavesdropping attempts. By applying these techniques, they ensure that both parties have the same key, thereby improving the reliability of their communication.
• Privacy amplification: To further improve security, Alice and Bob employ privacy amplification techniques. This process reduces the amount of information that any potential eavesdropper may have acquired during transmission. Finally, this results in a key that is robust against external threats and secure.

2.2. Related Work

Recent advancements in quantum communication have increasingly focused on the use of photons and atoms to transmit quantum information. This review begins by examining photonic and atomic protocols and concludes with their potential integration. QKD has traditionally relied on well-characterized devices. However, device-independent QKD presents a promising avenue for security without this dependency, despite the implementation challenges, particularly in photonic systems. In [14], the authors verified device-independent QKD using a photonic setup that enhanced loss tolerance. They developed a polarization-entangled photon source with a heralded detection efficiency of 87.5%, achieving a positive key rate over 220 m in the fiber. Additionally, the authors in [16] demonstrated a modified Ekert QKD protocol using a coherently driven quantum dot over 250 m of single-mode fiber and free space, successfully connecting two buildings at Sapienza University in Rome. This study indicates that quantum dot-entangled photon sources are well suited for practical quantum communication applications. Despite significant advances in photonic systems, relying on well-characterized devices remains a challenge. Although advances in device-independent QKD are promising, more research is needed to enhance its practical implementation. Atomic protocols are particularly compelling because of their potential for high-fidelity entangled photon generation.

A notable study on cavity-based quantum networks [10] emphasized the importance of efficient interfaces between stationary quantum nodes, such as single atoms, and flying carriers, such as optical photons. This research proposes various protocols for generating entangled photons and reversibly mapping quantum states between photons and atoms, underscoring their significance in scalable quantum networks. Another significant contribution involved the experimental realization of heralded atom–photon quantum correlations. Research on single- and entangled-photon pair generation using atomic vapors [9] has demonstrated that atomic vapors can effectively generate both single-photon and entangled-photon pairs, which is crucial for secure quantum communication. This study highlighted the potential for enhanced photon production rates and improved entanglement fidelity, thereby strengthening quantum networks. Furthermore, the study in [17] introduced a new protocol for controlled secure direct quantum communication, which allows simultaneous authentication between Alice and Bob with the help of a third party, Charlie, through entanglement swapping. This protocol exhibited resilience against various attacks, including impersonation and intercept-and-resend attacks, and was favorable compared to existing protocols. The study in [18] showcased multiplexing-enhanced atom–photon quantum correlations over a fiber length of 12 km, indicating that integrating atom–photon systems could significantly improve the efficiency of the entanglement distribution over long distances, which is essential for large-scale quantum networks. Furthermore, [19] introduced dual field QKD over optical fibers as a promising method for secure long-distance communication. By leveraging atomic clock technologies, including narrow-linewidth lasers and phase-coherent optical pulse distribution, this study details the integration of these technologies into a dual field QKD setup on an extended metropolitan fiber network and reports the anticipated performance outcomes of the QKD system.

These studies illustrate the complementary roles of photons and atoms in quantum channels, highlighting the potential of hybrid systems to leverage the strengths of both modalities. As research grows, integrating these approaches is expected to result in more robust and efficient quantum communication protocols. In this context, a new hybrid protocol is proposed that harnesses the unique advantages of both photons and atoms, enhances security while improving key distribution efficiency, and strengthens the defense against eavesdropping. This integration not only improves security through entanglement swapping but also increases the robustness of QKD through error correction and privacy amplification.

3. The Proposed Hybrid QKD Protocol

3.1. Overview of the Proposed Hybrid Protocol

The proposed QKD protocol integrates both photonic and atomic systems to leverage their respective advantages, thus enhancing the overall security and robustness of the key generation and distribution. The framework consists of two main components: a photonic subsystem for key generation with high-speed transmission, and an atomic subsystem for enhanced security and robustness.

3.1.1. Photonic Subsystem for Key Generation

The photonic subsystem utilizes the unique polarization states of the photons to encode information to generate and distribute secure cryptographic keys. Using the inherent properties of light, this method achieves exceptionally high transmission rates over long distances, which makes it compatible with the existing fiber-optic infrastructure [20]. In addition, the use of entangled photons is crucial in this hybrid protocol. Any attempt by an eavesdropper to measure or intercept photons will inevitably disturb the system, revealing their presence because of the quantum no-cloning theorem [21]. This theorem states that it is impossible to create an exact copy of an unknown quantum state, thus ensuring that unauthorized access can be detected [22].

3.1.2. Atomic Subsystem for Entanglement Swapping, Error Correction, and Privacy Amplification

The atomic subsystem enables precise manipulation of the quantum state, facilitates local measurements, and significantly improves overall security and robustness. This is achieved through advanced techniques such as quantum entanglement, error correction, and privacy amplification [23]. Through entanglement swapping, entangled states can be created between two pairs of entangled photons, enabling the establishment of entanglement between particles that were not previously entangled. This technique offers a key advantage in eavesdropping detection. When an eavesdropper attempts to intercept entangled photons, the quantum state is disturbed, which immediately alerts the communicating parties of potential security breaches. Furthermore, this process improves the capabilities of quantum repeaters, allows the development of scalable quantum networks, and extends the range of quantum communications [24].

Error correction mitigates noise effects by employing sophisticated error correction codes within an atomic subsystem. Low-density parity check (LDPC) codes [25,26] are adopted for error correction to identify and correct errors using a sparse parity check matrix, which allows efficient decoding and improved error resilience. In addition, privacy amplification further strengthens the security of the generated key by reducing any partial information that potential eavesdroppers may have obtained. Specific mathematical functions, including BLAKE2 [27,28], are applied to the raw key to amplify privacy, which makes it extremely difficult for unauthorized parties to extract meaningful information.

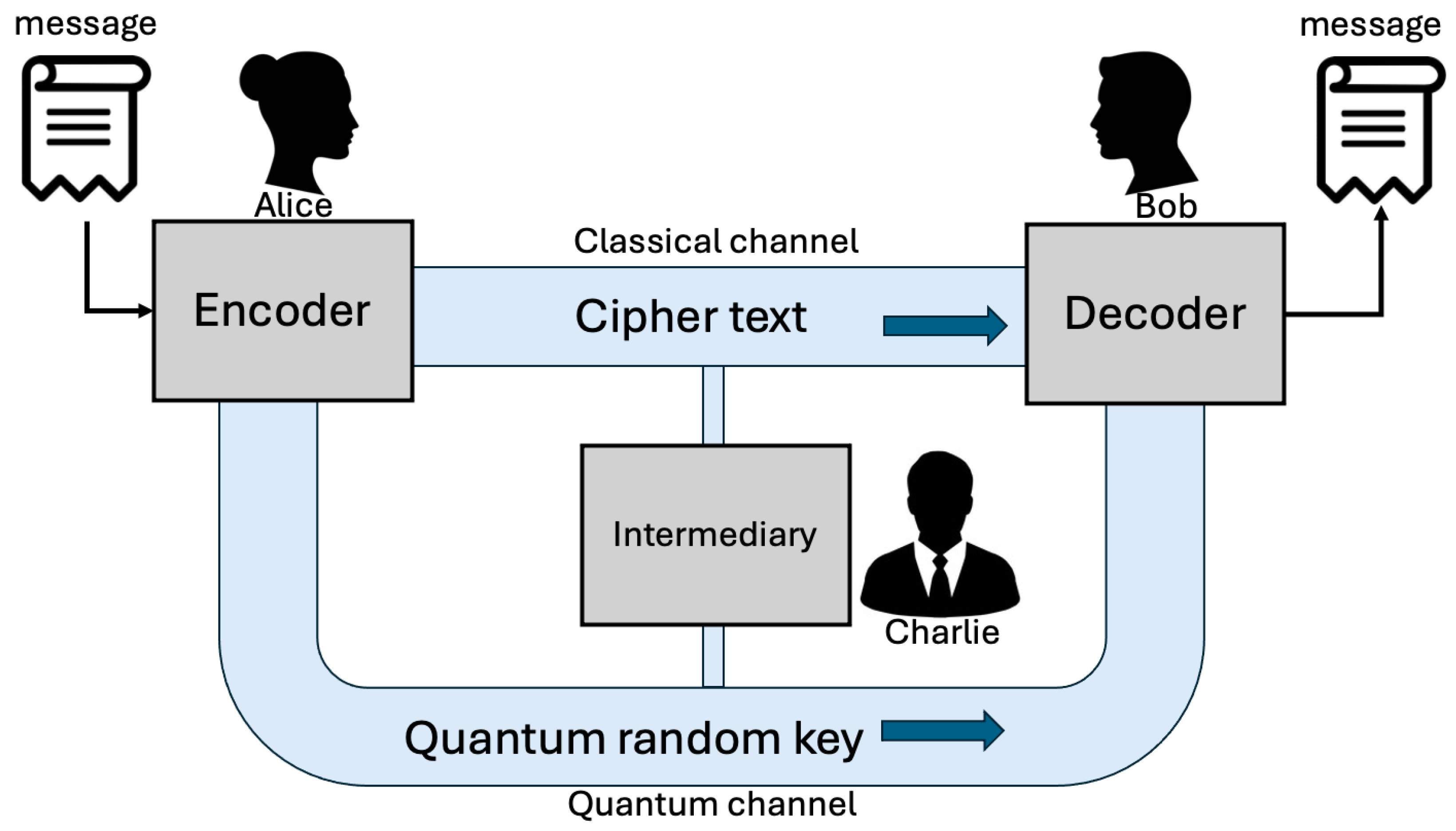
As illustrated in Figure 1, quantum and classical channels collaborate to maintain security in QKD process. In this hybrid protocol, Alice encodes information into photons using a predetermined set of polarization states. After preparing entangled pairs of photons, she sends one photon from her pair to a third party, Charlie, over a secure quantum channel, whereas Bob sends another photon from his pair to the same location. Once the photons arrive, Charlie performs the necessary measurements to facilitate entanglement swapping, thereby establishing a secure connection between Alice and Bob. With the entanglement established, Alice and Bob are now connected through entangled states, and can generate a shared key by performing local measurements on their respective entangled particles.

After generating the shared key, Alice uses it for message encryption. She encodes her original message into a codeword using LDPC code. The codeword is then encrypted with a quantum key to generate the cipher text that ensures confidentiality against eavesdropping [25,26]. After encryption, Alice sends the cipher text along with an integrity tag generated by the BLAKE2 cryptographic hash function. This tag allows Bob to verify the authenticity of the message received. If the tag matches the expected value, Bob can be confident that the message is intact and has not been altered [27,28]. To further enhance the robustness, both Alice and Bob implement error correction protocols. If Charlie detects discrepancies in the measurements or the transmitted photons, he communicates this information to Alice and Bob. They then use error-correction codes to identify and correct any errors in the received data, ensuring that the final key is consistent and secure.

Involving a third party significantly enhances security by enabling Charlie to verify the correct preparation of entangled states and accuracy of measurements. His involvement allows for the detection of eavesdropping by identifying anomalies that may arise from unauthorized interception, thereby helping Alice and Bob to confirm the integrity of their shared key. Charlie also facilitates the distribution of quantum keys, ensuring that both parties possess identical keys without the need to directly share quantum states. This decoupling minimizes the risk of compromised interactions and improves the robustness of QKD systems. Charlie’s role introduces greater flexibility in protocol design, allowing it to accommodate various configurations and more complex protocols involving multiple parties. This adaptability not only strengthens the security but also enhances the overall efficiency and scalability of quantum communication systems.

3.2. Proposed Hybrid Protocol Framework

The essential components and processes of the proposed hybrid QKD protocol are detailed in the following steps:

• Encoding agreement:
  Alice and Bob agree on a hybrid encoding scheme utilizing both photonic and atomic systems. For photonic states [29], if they decide to use a rectilinear basis, horizontal polarization represents binary 0 and vertical polarization represents binary 1, which is denoted as

  $$|0\rangle \equiv |H\rangle ,|1\rangle \equiv |V\rangle ,$$

  (1)

  where $|H\rangle$ is the horizontal polarization, and $|V\rangle$ is the vertical polarization. If they choose a diagonal basis, the states are represented as

  $$|+\rangle \equiv {\displaystyle \frac{1}{\sqrt{2}}}\left(\right|H\rangle +|V\rangle ),|-\rangle \equiv {\displaystyle \frac{1}{\sqrt{2}}}\left(\right|H\rangle -|V\rangle ),$$

  (2)

  where $|+\rangle$ and $|-\rangle$ correspond to photons polarized at ${45}^{\circ }$ and $-{45}^{\circ }$, respectively.
  For atomic states, if they agree to use the spin states of the atoms, it is expressed as

  $$|0\rangle \equiv |\uparrow \rangle ,|1\rangle \equiv |\downarrow \rangle ,$$

  (3)

  where $|\uparrow \rangle$ represents the spin-up state and $|\downarrow \rangle$ represents the spin-down states, respectively.
  This agreement ensures synchronization of how quantum states represent binary bits. Alice and Bob agree on the types of measurement bases to be used prior to the key exchange. This agreement is essential to ensure that both parties can accurately interpret the results of their measurements and establish a secure key. Similar to the BB84 protocol [4,5], Alice and Bob share the specific measurement bases utilized during the exchange.
• State encoding:
  • Photonic state preparation: Alice prepares a sequence of single photons in the desired state. The quantum state of the photon can be represented as

    $$|\psi \rangle =\sum _{i=0}^1{\alpha }_i|i\rangle ,$$

    (4)

    where ${\alpha }_0$ and ${\alpha }_1$ are the amplitudes of states $|0\rangle$ and $|1\rangle$ (or $|+\rangle$ and $|-\rangle$).
  • Entanglement generation: Alice generates entangled photon pairs. The quantum state of the entangled pair can be represented as

    $$|{\psi }_{AB}\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left({|H\rangle }_A{|V\rangle }_B+{|V\rangle }_A{|H\rangle }_B\right),$$

    (5)

    where A and B denote two photons in the entangled pair. Bob also generates his entangled photon pairs, represented as $|{\psi }_{CD}\rangle$.
• Transmission of photonic states:
  After preparing the entangled pairs of photons, Alice sends photon A to Charlie over a secure quantum channel. During the same time, Bob sends the photon C to the same location. This establishes a connection between Alice and Bob through Charlie, who performs the necessary measurements to facilitate entanglement swapping.
  The combined state of the photons that is sent to Charlie can be represented as

  $$\begin{array}{cc}\hfill {|\Psi \rangle }_{AB}\otimes {|\Psi \rangle }_{CD}& =\left({\displaystyle \frac{1}{\sqrt{2}}}\left({|H\rangle }_A{|V\rangle }_B+{|V\rangle }_A{|H\rangle }_B\right)\right)\hfill \\ \hfill & \otimes \left({\displaystyle \frac{1}{\sqrt{2}}}\left({|H\rangle }_C{|V\rangle }_D+{|V\rangle }_C{|H\rangle }_D\right)\right).\hfill \end{array}$$

  (6)
  After Charlie performs a Bell state measurement [29] on photons A and C, the state collapses into one of the Bell states, resulting in entanglement between the other two photons B and D, which is denoted as

  $$|{\Psi }^{+}{\rangle }_{BD}={\displaystyle \frac{1}{\sqrt{2}}}\left({|HH\rangle }_{BD}+{|VV\rangle }_{BD}\right).$$

  (7)
  This process enables Alice and Bob to utilize photons for secure communication, thereby forming the foundation for their key exchange protocol.
  This entanglement means that the measurement outcomes of photons B and D are correlated regardless of the distance between them. In the context of atomic states, specific measurement results can be influenced by the initial states of the atomic systems involved, which can affect the entanglement process.
• Key establishment:
  • Measurement: After performing the joint measurement on photons A and C, Charlie sends the remaining entangled photons B and D to Bob. This step involves understanding how the atomic states relate to the measurement outcomes of photons B and D.
    Bob measures these photons in the desired bases (rectilinear or diagonal) to determine their states [29]. The measurement outcomes can be represented as follows:

    $$M_B=\left\{\begin{array}{cc}0\hfill & \mathrm{if}|H\rangle \mathrm{is}\mathrm{measured},\hfill \\ 1\hfill & \mathrm{if}|V\rangle \mathrm{is}\mathrm{measured},\hfill \\ +1\hfill & \mathrm{if}|+\rangle \mathrm{is}\mathrm{measured},\hfill \\ -1\hfill & \mathrm{if}|-\rangle \mathrm{is}\mathrm{measured},\hfill \end{array}\right.$$

    (8)
    This measurement establishes the shared key by defining the information transmitted over the classical channel, specifically the basis information and the measurement outcomes. Photonic states can represent the logical bits of the message, such as using horizontal and vertical polarizations for the atomic states $|0\rangle$ and $|1\rangle$. This integration bridges classical information encoding with quantum communication.
  • Measurement sifting: After measuring the states of photons B and D, Alice and Bob engage in classical communication to compare their measurement bases. They discard results where their bases are not aligned. The number of bits retained can be expressed as follows:

    $$K_{final}=K_{initial}-K_{discarded},$$

    (9)

    where $K_{initial}$ represents the total number of bits sent and $K_{discarded}$ indicates the number of bits in which the bases do not align. Atomic states serve as a reference for how the measurement outcomes relate to the shared key, ensuring that only consistent measurements contribute to the final key. This sifting process is important to maintain the integrity and security of the key between Alice and Bob.
• Message verification and encryption:
  LDPC codes are adopted for message verification through encoding, transmission, and decoding. The original message M is transformed into a codeword using a generator matrix that adds parity bits for error detection. If the transmitted codeword is corrupted, the receiver calculates a syndrome using a parity check matrix; a zero syndrome indicates no errors, and a non-zero syndrome signals errors. If errors are detected, decoding algorithms correct the codeword by refining the estimates of the original bits [25,26].
  A sparse bipartite graph of LDPC codes consists of variable nodes (representing codeword bits) and check nodes (representing parity checks) [25,26]. The parity check matrix H is pivotal to LDPC code functionality and must satisfy the following:

  $$H\times C^T=0.$$

  (10)
  Alice encodes the original message M, which is represented as a binary vector of length k, using LDPC codes. She defines a generator matrix G of size $n\times k$ (where $n>k$), to transform the message into a codeword. The codeword C is generated by:

  $$C=M\times G.$$

  (11)
  The resulting codeword C includes both the original message bits and the additional parity bits that are essential for error detection and correction, thereby ensuring that the message is reliably prepared for transmission. Next, Alice combines her secret quantum key K with codeword C for encryption using an encryption function E, as follows:

  $$\mathrm{cipherText}=E(K,C).$$

  (12)
  This ensures that even if an eavesdropper intercepts the transmission, they cannot decipher the original message without knowing the quantum key K, thus improving the security of the message.
  In conjunction with LDPC codes, atomic states can help define the nature of errors detected during transmission. If a measured state does not match the expected atomic state, the protocol can identify discrepancies and correct the errors in message [25,26].
• Privacy amplification:
  To implement privacy amplification, Alice uses the BLAKE2 hashing function to generate integrity tags. These tags ensure that the cipher text remains unaltered during transmission, thereby allowing the receiver to verify the authenticity of the received message [27,28].
  The BLAKE2 function creates a unique integrity tag for the transmitted messages, ensuring that eavesdroppers cannot reverse the original content. Hashing the message into a fixed size output obfuscates the information, making it difficult for eavesdroppers to access sensitive data. The integrity tag allows the recipient to verify that the message has not been tampered with, thereby ensuring both authenticity and integrity [27,28].
  Alice combines her secret key K with the cipher text using concatenation. The concatenated value $K\left|\right|\mathrm{cipherText}$ forms a unique input for the BLAKE2 hash function as follows:

  $$\mathrm{tag}=\mathrm{BLAKE}2(K\Vert \mathrm{cipherText}).$$

  (13)
  This tag effectively creates a fingerprint of the cipher text combined with the secret key, ensuring that even a small change in the input produces a significantly different tag. If an eavesdropper intercepts the cipher text and attempts to modify it, they cannot produce a valid tag without knowing the secret key K, providing assurance that the message remains unchanged.
• Message transmission:
  After computing the integrity tag, Alice sends both the cipher text and computed tag over a classical channel. This allows Bob to verify the authenticity of the message upon its reception. If the tag matches the expected tag computed on the receiver’s side, Bob is confident that the message is intact.
• Message reception and verification:
  Upon receiving the cipher text, Bob follows a systematic process to verify its integrity and decode the message. In LDPC decoding, Bob begins by decoding the received cipher text using LDPC techniques that are effective for reliable data transmission [25,26]. Syndrome S is calculated using the parity check matrix H of size $m\times n$, where m is the number of parity checks, and n is the length of the codeword. The syndrome is calculated as follows:

  $$S=H·C^{\prime T},$$

  (14)

  where $C^{\prime }$ is the potentially corrupted codeword received by Bob.
  The value of syndrome S indicates the integrity of the received codeword. If $S=0$, it signifies that no errors have been detected, indicating that the received message is accurate and reliable. Otherwise, if $S\ne 0$, it indicates that errors have been detected, prompting Bob to initiate the error correction process. He employs a decoding algorithm based on belief propagation, which iteratively refines the estimates of the original bits to restore the integrity of the message [25,26].
  The LDPC decoding process includes systematic checks that enhance the integrity of the received message.
  The use of multiple parity checks allows Bob to determine the validity of the received data effectively. If an eavesdropper attempts to modify the cipher text, parity checks will likely fail, alerting Bob to potential tampering. In addition, Bob decodes the received cipher text using iterative algorithms to refine the estimates of the original message. This iterative process not only helps recover the correct message but also increases the likelihood of detecting any alterations made by an eavesdropper.
  LDPC codes provide resistance to certain attack strategies.
• Hashing for expected tag:
  Bob computes the expected tag as follows:

  $${\mathrm{tag}}_{expected}=\mathrm{BLAKE}2(K\Vert C^{\prime }).$$

  (15)
  He compares the received tag with the expected tag. If they match, the message is considered authentic; otherwise, the message is discarded and a retransmission is requested.

4. Mathematical Proof

The hybrid protocol combines high-speed photonic communication with robust atomic-state encoding, ensuring effective error correction and enhanced eavesdropping detection. Furthermore, it supports authenticity and privacy amplification, significantly strengthening the overall security framework. This section provides mathematical proof to support claims about the efficacy of this protocol.

4.1. Security of Entanglement Swapping in QKD

Statement: Entanglement swapping offers superior security for QKD protocols compared to traditional entanglement.

Proof. 

In traditional entangled photon systems, Alice and Bob share an entangled state established using a Bell state, which is represented as

$$|{\Psi }^{+}{\rangle }_{AB}={\displaystyle \frac{1}{\sqrt{2}}}{\left(\right|HH\rangle }_{AB}+{|VV\rangle }_{AB}).$$

(16)

□

In quantum security, if an eavesdropper, often referred to as Eve, intercepts photon A and measures it, she alters the state of the entire system. Although photon A is collapsed by this measurement, photon B is not directly revealed to Eve. This causes uncertainty in the correlation between Alice and Bob, increasing the quantum bit error rate (QBER), which is defined as

$$QBER={\displaystyle \frac{E}{N}},$$

(17)

where E is the number of erroneous bits introduced by Eve’s measurement, and N is the total number of measurements compared during key distribution.

In contrast, in entanglement swapping QKD, Alice and Bob each possess one photon from their respective entangled pairs. Specifically, Alice holds photon A from her pair, while Bob holds photon B from his pair. Charlie then performs a Bell state measurement on the other two photons, C and D, in which the initial state can be expressed as

$${|\Psi \rangle }_{ABCD}=|{\Psi }^{+}{\rangle }_{AC}\otimes {|{\Psi }^{+}\rangle }_{BD}.$$

(18)

If Eve intercepts photons C or D and measures them, her interference significantly impacts the entangled state of photons A and B after Charlie’s measurement. Charlie’s measurement outcome determines the resulting entangled state, and any unexpected results indicate the possibility of eavesdropping. The QBER in this scenario is defined as

$$QBER={\displaystyle \frac{E^{\prime }}{N^{\prime }}},$$

(19)

where $E^{\prime }$ accounts for the errors introduced by Eve, and $N^{\prime }$ is the total number of bits following Charlie’s measurement.

The enhanced sensitivity to eavesdropping in entanglement swapping QKD leads to a more robust security framework. Any attempt by Eve to measure photons C or D will introduce detectable errors in the correlation between photons A and B. This illustrates that entanglement swapping provides superior security for QKD protocols compared to traditional entanglement, enabling the more effective detection of eavesdropping attempts.

4.2. Authenticity and Integrity in Privacy Amplification

Statement: The privacy amplification process reduces any partial information that an eavesdropper may have about the key, ensuring that the final key is secure. Specifically, the use of a secret key K in conjunction with the BLAKE2 hash function to generate an integrity tag ensures that even if Eve has access to the cipher text, she cannot produce a valid tag without knowing K.

Definition 1.

The BLAKE2 hash function used in privacy amplification has several characteristics [27,28,30]:

• Pre-image resistance: Given a hash output h, it is computationally infeasible to find any input x such that $\mathit{BLAKE}2\left(\mathit{x}\right)=\mathit{h}$.
• Second pre-image resistance: Given an input $x_1$, it is computationally infeasible to find a different input $x_2$ such that $\mathit{BLAKE}2\left(x_1\right)=\mathit{BLAKE}2\left(x_2\right)$.
• Collision resistance: It is computationally infeasible to find two distinct inputs $x_1$ and $x_2$ such that $\mathit{BLAKE}2\left(x_1\right)=\mathit{BLAKE}2\left(x_2\right)$.

Assumption 1.

Assume Eve intercepts the cipher text C but does not know the secret key K. She has access to the cipher text and the corresponding integrity tag tag. Furthermore, assume Eve modifies the cipher text to $C^{\prime }$. In this case, Eve attempts to generate a new tag, denoted as ${\mathit{tag}}^{\prime }$ such that

$${\mathit{tag}}^{\prime }=\mathit{BLAKE}2\left(K\right||C^{\prime }).$$

(20)

To produce a valid tag that matches the original tag, Eve must find K or create a collision.

Proof. 

By the pre-image resistance property of BLAKE2, Eve cannot feasibly compute K from tag since

$$\mathrm{tag}\ne \mathrm{BLAKE}2\left(K\right||C^{\prime })\mathrm{for}\mathrm{all}{C}^{\prime }\ne C$$

(21)

If Eve tries to find a $K^{\prime }$ such that

$$\mathrm{BLAKE}2\left(K\right|\left|C\right)=\mathrm{BLAKE}2(K^{\prime }\left|\right|C^{\prime })$$

(22)

then this is infeasible due to the second pre-image resistance property of BLAKE2. □

As Eve cannot generate a valid tag ${\mathrm{tag}}^{\prime }$ for the modified cipher text $C^{\prime }$ without knowing K, it can be concluded that the integrity tag effectively amplifies privacy. Integrity tags guarantee that any modifications made to the cipher text can be identified, giving the recipient confidence in the authenticity of the message they have received. The use of BLAKE2 in conjunction with a secret key K in the integrity tag generation process guarantees that an eavesdropper, even with access to the cipher text, is prevented from forging a valid tag. This mechanism reinforces data integrity and enhances privacy through strong cryptographic principles.

4.3. Reliable Message Transmission and Integrity Verification Provided by Error Correction Codes

Statement: LDPC codes provide resistance to certain attack strategies. In quantum communication, passive eavesdropping involves an eavesdropper, who listens to the quantum transmission without altering the data. However, due to fundamental principles of quantum mechanics, such as the no-cloning theorem, any attempt by Eve to measure the quantum states will inevitably disturb them. This disturbance alerts the communicating parties to the presence of an eavesdropper and ensues the security of their communication. In the classical context, passive listening allows Eve to analyze the transmitted cipher text without making any alterations. Nevertheless, the robust error correction capabilities of LDPC codes provide a safeguard for Bob. Upon receiving the cipher text, Bob decodes the received vector $C^{\prime }$ (which may contain noise) using LDPC techniques, which rely on the integrity of the parity check matrix H of size $m\times n$, where m is the number of parity checks, and n is the length of the codeword. The relationship is defined as

$$C^{\prime }=M·G$$

(23)

where M represents the original message, and G is the generator matrix. The error correction capability of LDPC codes ensures that even if some bits are flipped due to noise or interference, Bob can still reliably recover the original message. This resilience makes LDPC codes particularly effective in environments where passive eavesdropping may occur.

In classical security, active attacks involve an attacker who attempts to modify the cipher text during transmission. This could include injecting false data, altering existing messages, or impersonating one of the communicating parties. Such actions can compromise the integrity and authenticity of the transmitted information. In quantum communication, active attacks take on a different form. Here, Eve may try to manipulate the quantum states being transmitted, potentially intercepting and resending qubits in a manner that alters the information communicated between Alice and Bob. This type of interference can often be detected due to the inherent disturbances it introduces to the quantum states. The resulting errors from such active interference are identified through syndrome calculations and parity checks. The syndrome S is mathematically represented as shown in Equation (14).

Proof. 

Assume C is the transmitted codeword and $C^{\prime }$ is the received vector after potential modification by Eve. The relationship can be expressed as follows:

$$C^{\prime }=C+\mathbf{e},$$

(24)

where $\mathbf{e}$ is the error vector introduced by noise or active tampering. The syndrome can then be expressed as

$$S=H·C^{\prime T}=H·{(C+\mathbf{e})}^T=H·C^T+H·{\mathbf{e}}^T,$$

(25)

Since $H·C^T=\mathbf{0}$ by the definition of the code, then

$$S=H·{\mathbf{e}}^T,$$

(26)

If $S\ne \mathbf{0}$, it implies that $H·{\mathbf{e}}^T\ne \mathbf{0}$, indicating that errors have occurred. Consequently, Bob can conclude that the integrity of the message has been compromised, prompting him to initiate error correction procedures to recover the original codeword C. This mathematical framework illustrates how LDPC codes play a crucial role in ensuring both reliable message transmission and integrity verification against potential attacks, whether passive or active. □

Both classical and quantum security measures are analyzed to protect against eavesdropping. LDPC codes are highlighted for their effectiveness in reliable message transmission and integrity verification. Cryptographic techniques, including hash functions and integrity tags, such as BLAKE2, help prevent unauthorized modifications and ensure authenticity. On the quantum side, QKD methods, such as entanglement swapping, enhance security by detecting eavesdropping through changes in particle correlations. Privacy amplification is also crucial for mitigating any information that an eavesdropper might gain, ensuring the final key’s security. These measures create a robust framework for safeguarding communication against various attacks.

5. Results Analysis

In QKD simulation, MATLAB R2024a (24.1) serves as the primary tool due to its robust capabilities and flexibility. It effectively models various QKD protocols, including photonic, atomic, and hybrid systems, using advanced matrices and vectors to represent quantum states and operations. The photonic and atomic protocols are employed as benchmarks to evaluate the performance of the proposed hybrid protocol. Comprehensive algorithms simulate key generation processes, incorporating critical parameters such as successful key rate, QBER, loss rates, and error rates for a thorough analysis. In addition, MATLAB’s intuitive visualization features facilitate comparisons and allow a clearer understanding of performance differences between QKD protocols. In practice, hardware limitations can impact hybrid QKD system performance, including lower efficiency, higher error rates, and sensitivity to environmental factors. Increased demand for QKD may necessitate additional resources, such as quantum repeaters and entangled photon sources, which may not be readily available or economically feasible. Real-world noise and interference can reduce the quality of quantum signals. The simulation may overestimate protocol robustness by not taking into account all relevant factors.

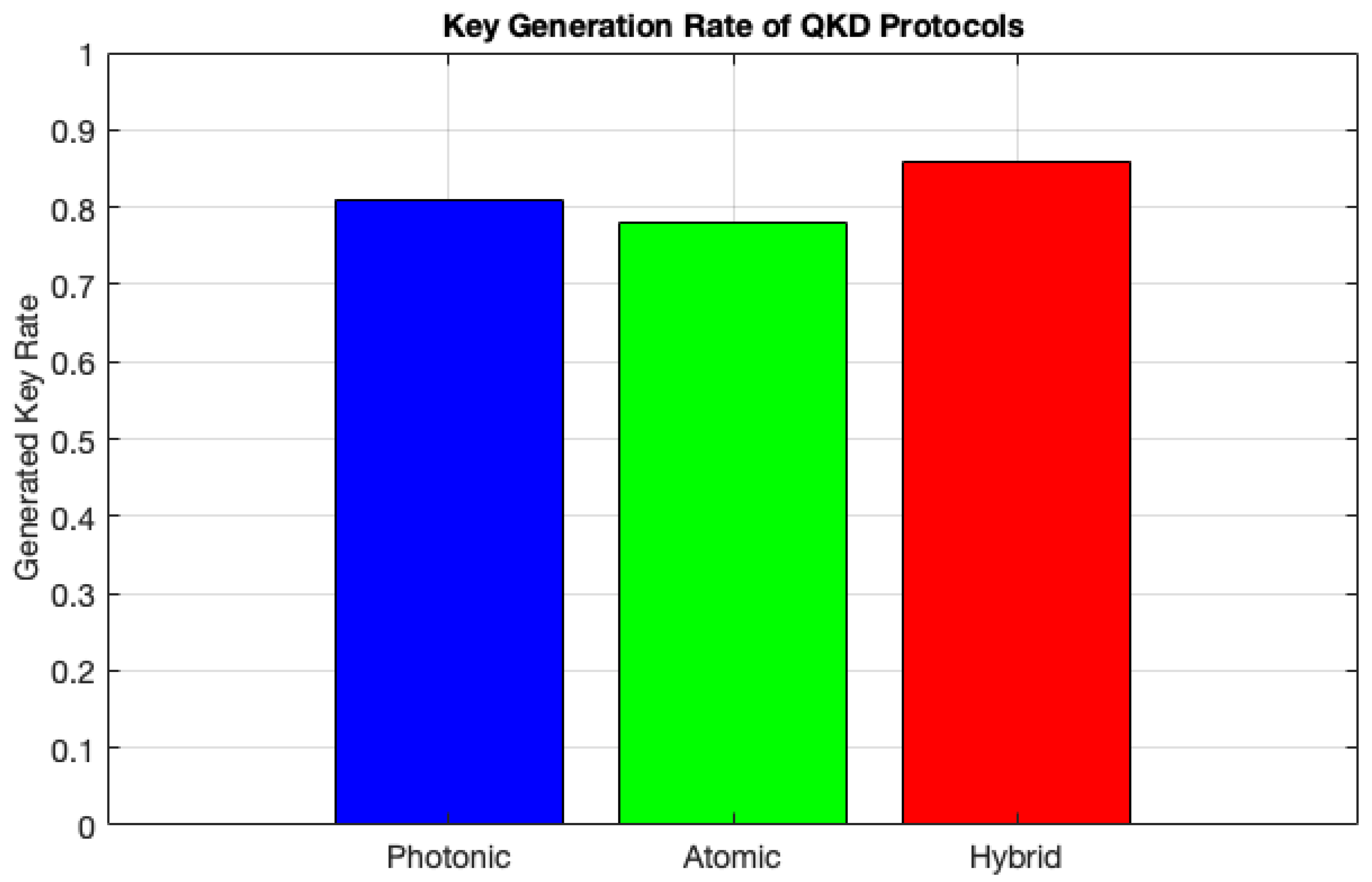
Figure 2 illustrates the key rates generated by the three QKD protocols, revealing notable performance differences. The hybrid QKD protocol demonstrates the highest key rate, indicating that integrating both photonic and atomic states enhances the overall key generation efficiency. This hybrid approach effectively harnesses the advantages of both quantum systems by utilizing a photonic subsystem for rapid transmission and an atomic subsystem to improve security and robustness. Specifically, the hybrid protocol benefits from the transmission capabilities of photons and the robust security features inherent in atomic states, supplemented by privacy amplification using BLAKE2, and error correction through LDPC codes. Privacy amplification with BLAKE2 transforms the raw key material generated during the QKD process into a shorter secure key, thus reducing the likelihood of information leakage that could be exploited by potential eavesdroppers. LDPC codes further enhance the key rate by minimizing the overhead associated with error correction, thereby allowing a greater proportion of bits to contribute directly to the final key.

In addition, the transmission speed is a very important factor because photonic QKD uses high-speed photon transmission through optical fibers, allowing for faster key establishment than atomic systems. Moreover, photonic systems usually have lower noise levels and error rates in real-world applications, leading to higher key rates. In contrast, the atomic QKD protocol has the lowest key rate, mainly because of the difficulty in manipulating atomic states. One major issue is that atomic QKD often relies on transferring information through atomic ensembles or matter-based systems, which generally operate at speeds lower than those of photonic channels. In general, these findings suggest that hybrid QKD protocols are a promising step forward in secure communications, whereas improving photonic and atomic systems could make them more effective in practice.

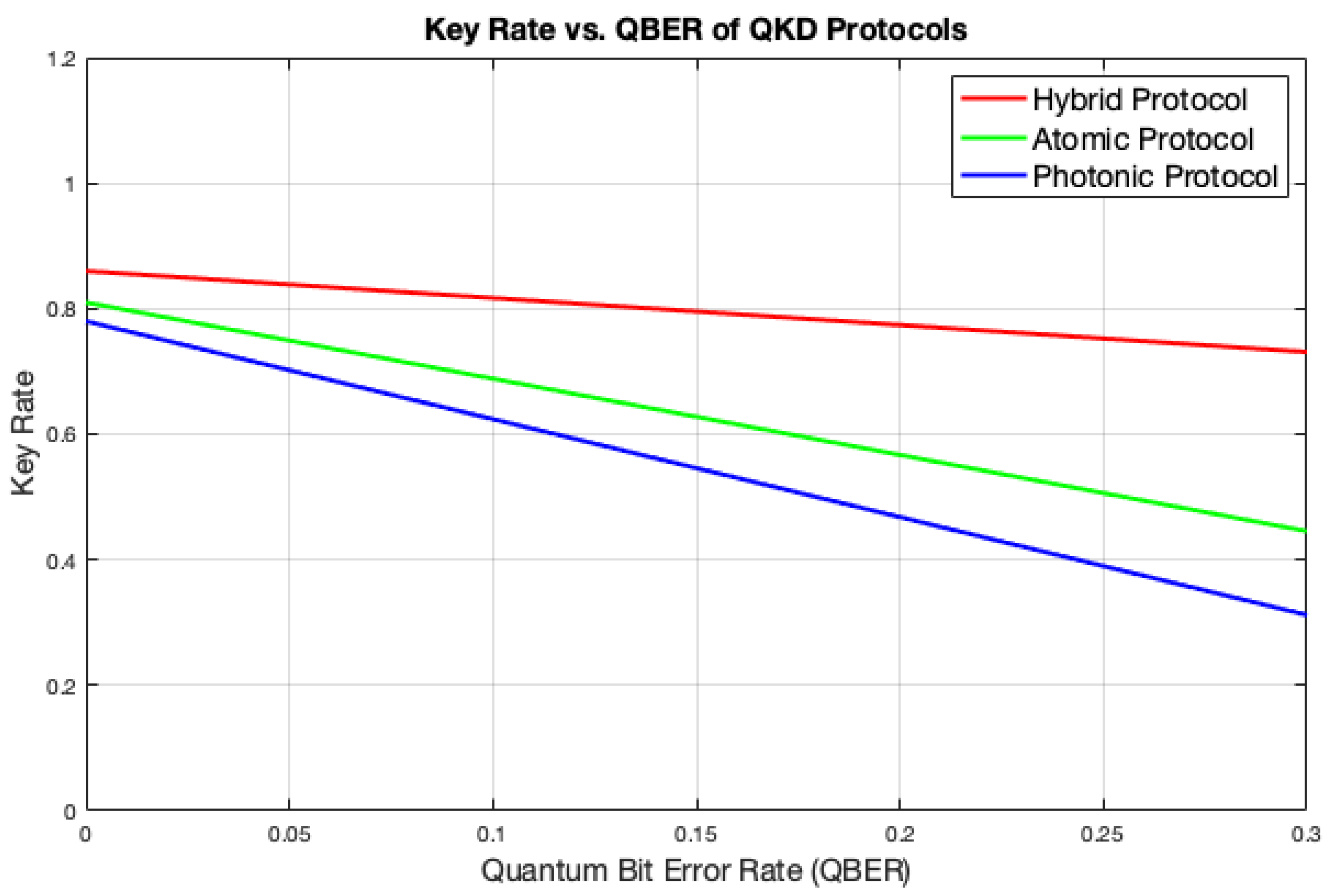
Figure 3 shows the generated key rates versus QBER for the three QKD protocols. All protocols exhibit a decrease in key generation rate as QBER increases, indicating that higher error rates negatively impact secure key generation. The hybrid protocol consistently achieves the highest key rate, suggesting greater resilience to errors and making it a strong candidate for practical quantum communication. In contrast, the atomic protocol, while showing a decrease in comparison to the hybrid, still outperforms the photonic protocol at lower QBER levels. Although it performs reasonably well, it is less effective than the hybrid as error rates increase. The photonic protocol records the lowest key rate as QBER increases, highlighting its greater susceptibility to errors and reduced reliability under high noise or interference conditions.

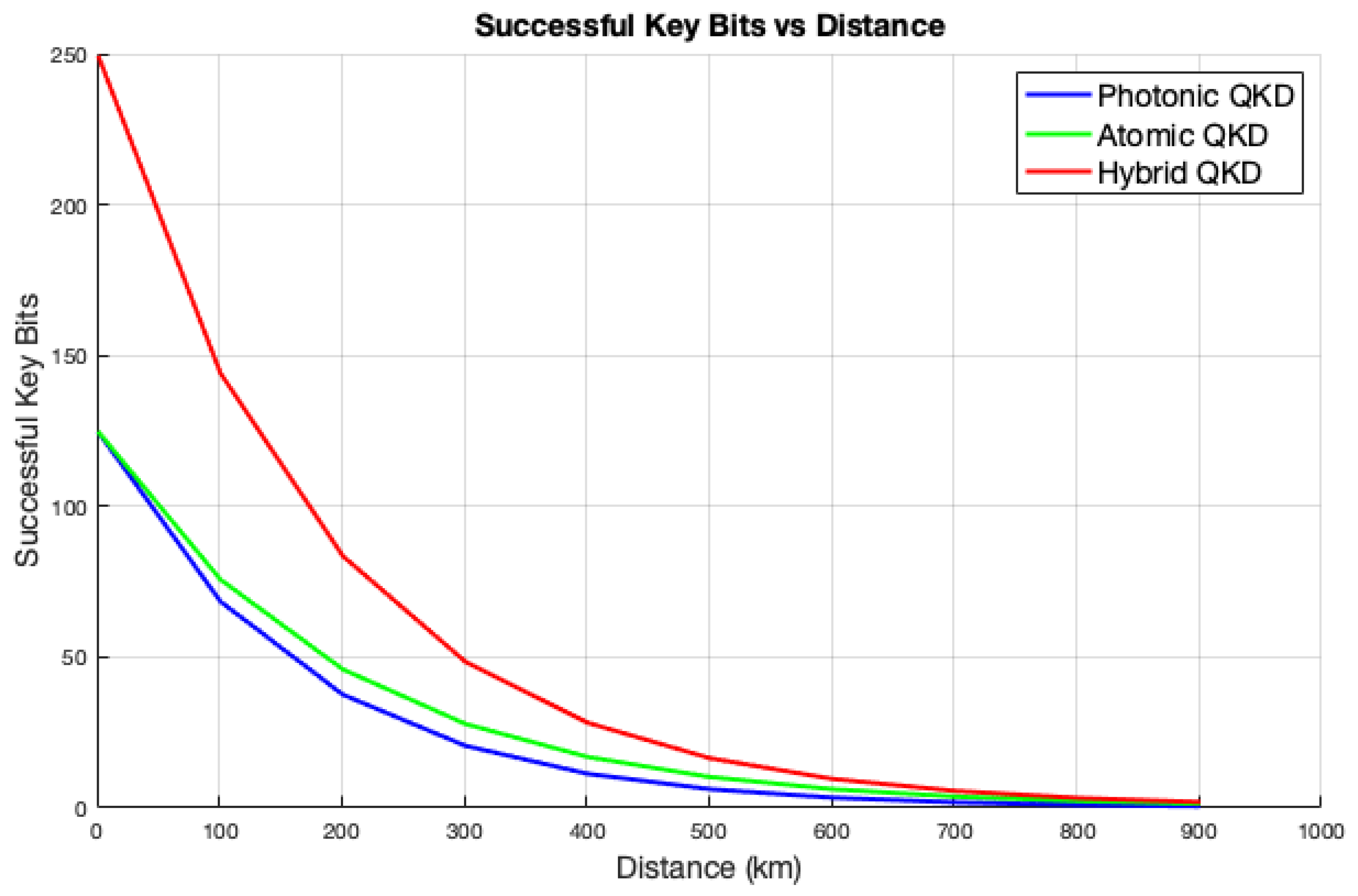
Figure 4 illustrates the successful key bits achieved by photonic, atomic, and hybrid QKD protocols versus distance, which reveals distinct performance characteristics. Successful key bits refer to bits that have been securely transmitted and verified. The hybrid protocol consistently achieves the highest number of successful key bits. Its capabilities are enhanced by the incorporation of entanglement swapping along with the application of LDPC code error correction and BLAKE2 privacy amplification. This combination not only maintains security but also enables greater distances and improves key generation efficiency. However, the number of successful key bits decreases as the distance increases across all protocols. This highlights the exceptional performance of the hybrid protocol and its robustness to errors, which makes it particularly suitable for long-distance quantum communications. In contrast, the atomic and photonic protocols exhibit a moderate decline in successful key bits, performing better at shorter distances but significantly diminishing as the distance increases. Their comparability to losses and errors highlights the limitations of secure key generation over longer distances, emphasizing the challenges in maintaining key integrity.

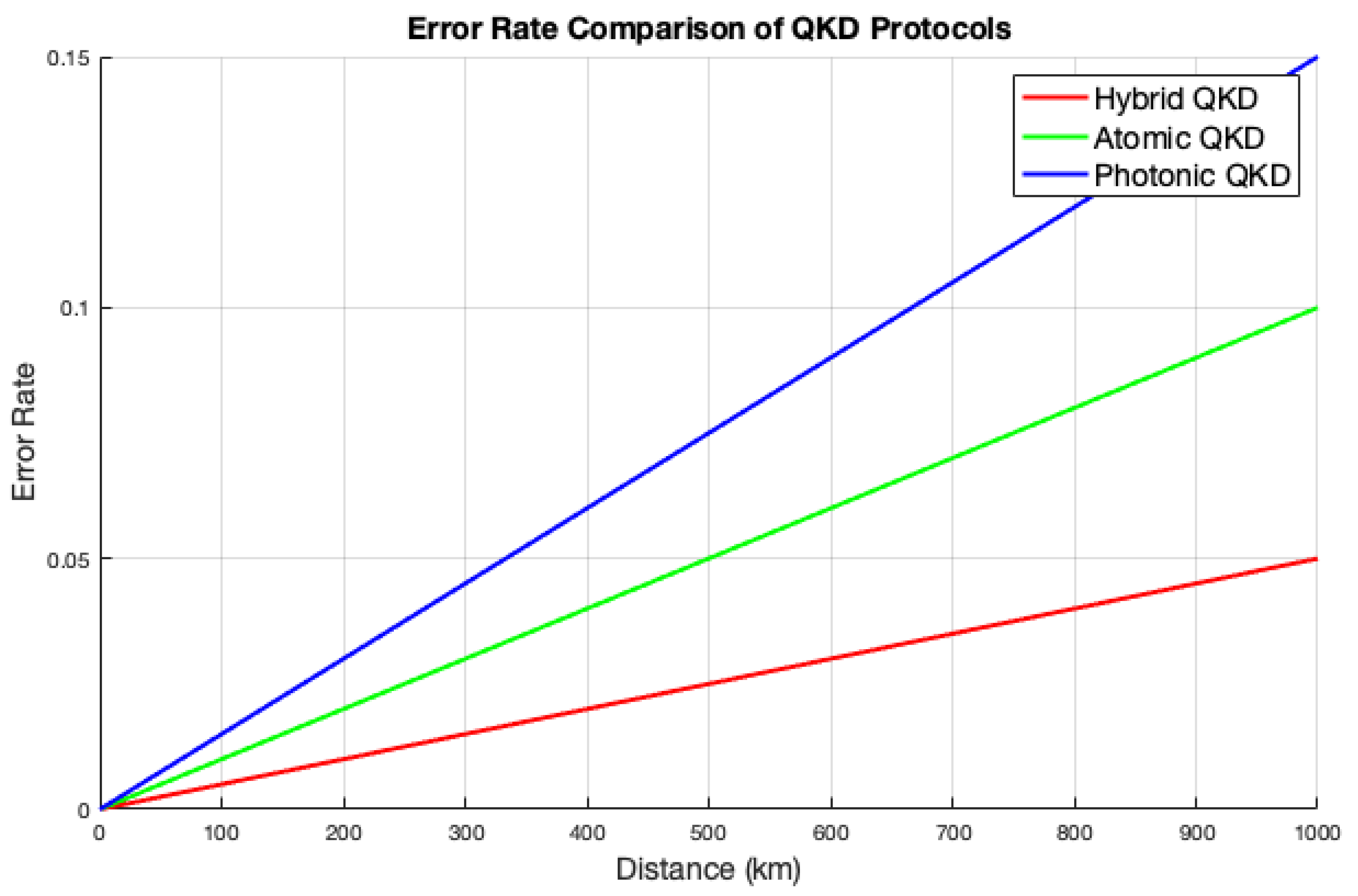
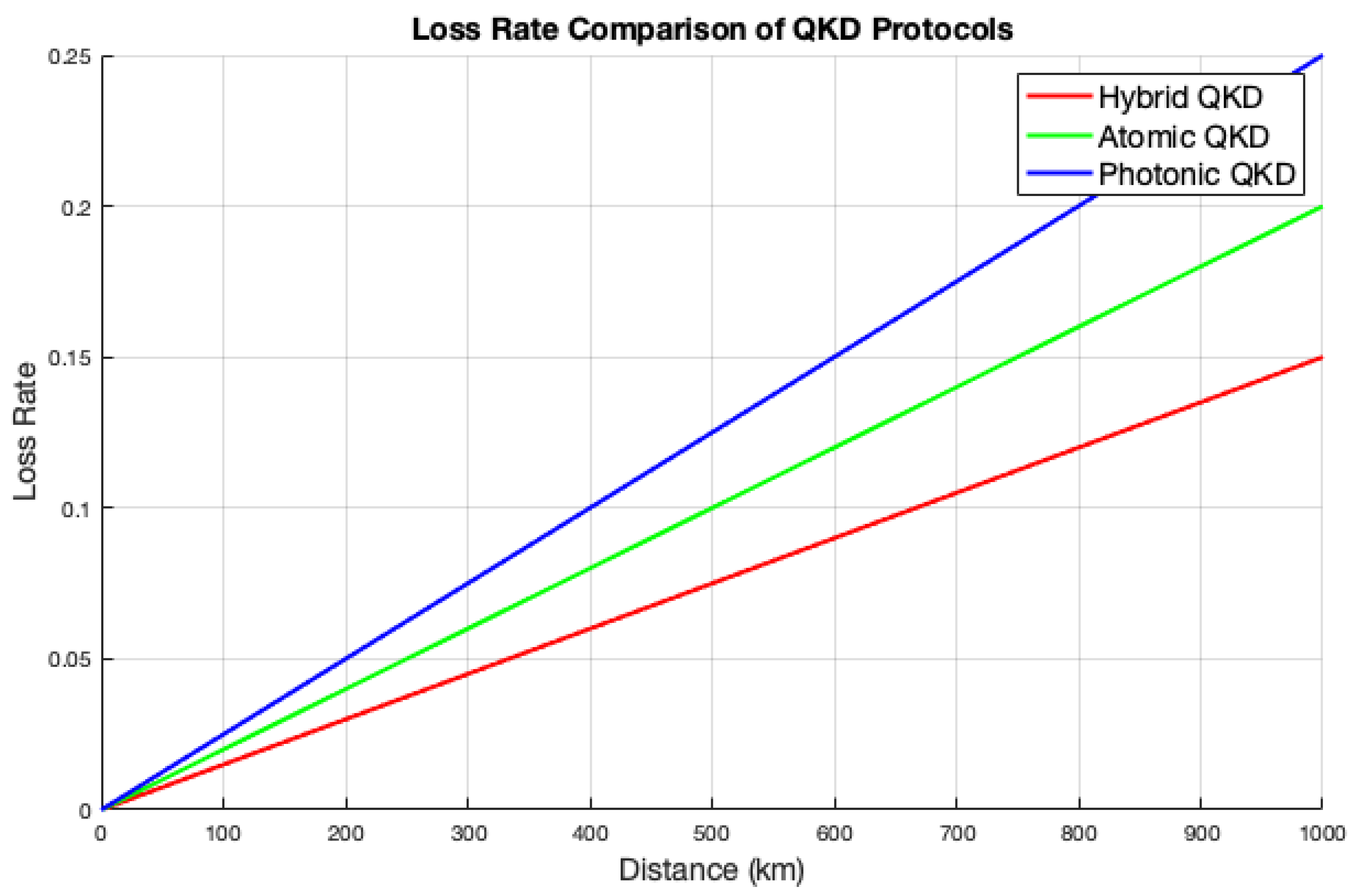
Figure 5 and Figure 6 show comparisons of error and loss rates for the three QKD protocols based on distance. All three protocols exhibit negligible error and loss rates at short distances, thereby demonstrating their effectiveness for direct communication. However, as the distance increases, the photonic protocol shows the highest error and loss rates, indicating performance degradation. The atomic protocol outperforms the photonic protocol with increasing distance, demonstrating greater robustness against errors and losses. Meanwhile, the hybrid protocol consistently maintains the lowest error and loss rates at longer distances, underscoring its superior resilience in QKD compared to the other two protocols. Additionally, there is a notable trade-off between the error and loss rates with distance in QKD protocols, where longer distances generally lead to higher error and loss rates, impacting the overall key generation efficiency.

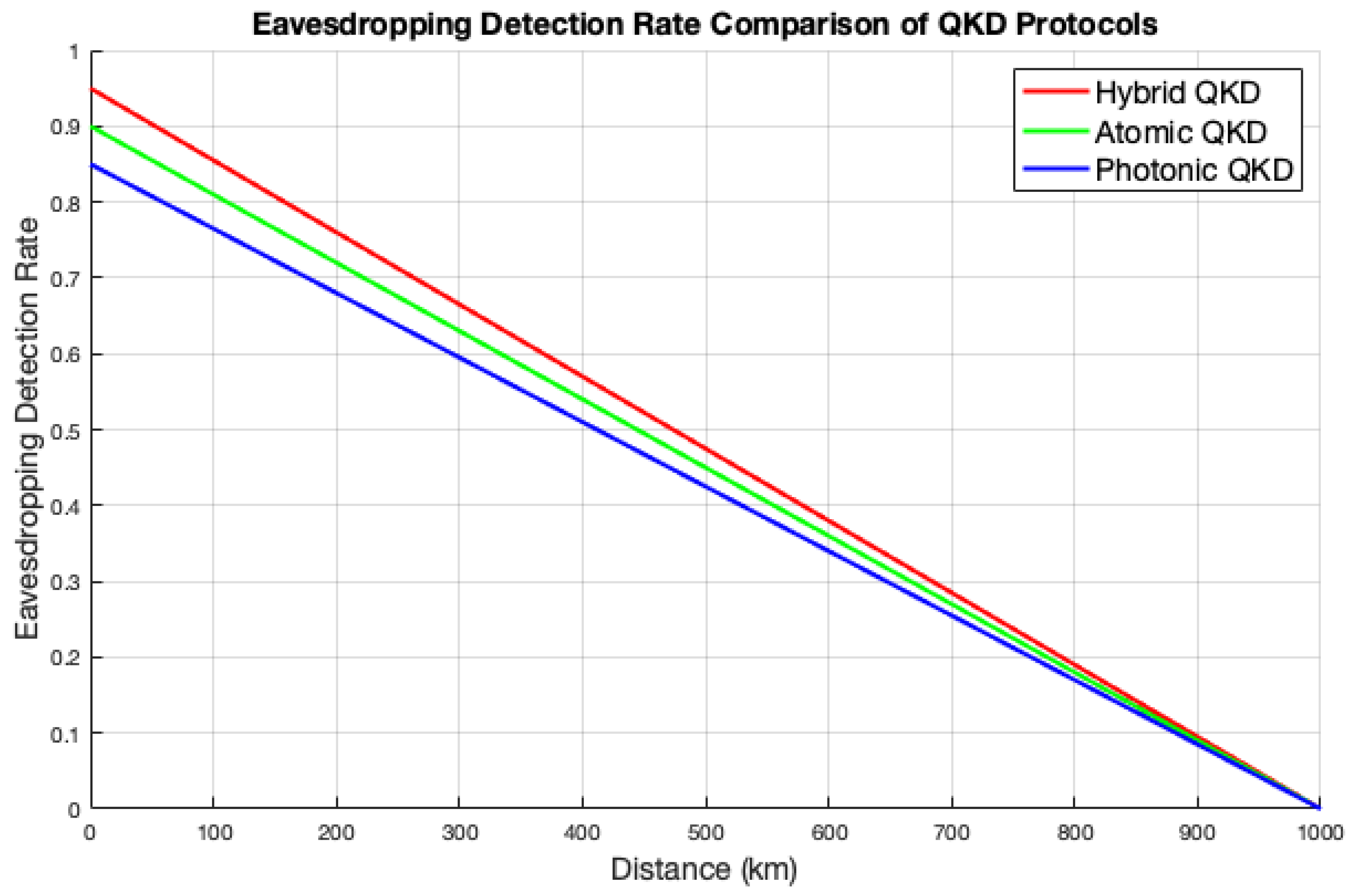
Figure 7 illustrates a comparison of the eavesdropping detection rates among the three QKD protocols versus distance. The hybrid QKD protocol achieves the highest eavesdropping detection rates by integrating the strengths of atomic and photonic systems. Generally, it exhibits higher eavesdropping detection rates due to the use of entangled states, LDPC error correction, and BLAKE2 privacy amplification. This method identifies disturbances caused by eavesdropping attempts by utilizing accurate measurements and strong security features to reduce the likelihood of interception. The atomic QKD protocol has moderate detection capabilities because of its use of collective measurements on atomic ensembles. Moreover, photonic QKD relies on the detection of individual photons, rendering it inherently more vulnerable to eavesdropping. This dependence on single-photon detection results in lower overall detection rates, exacerbated by higher error rates caused by environmental factors that can mask indicators of eavesdropping activity. Furthermore, eavesdropping detection rates for QKD protocols decrease with increasing distance, highlighting the challenges faced in maintaining security over longer transmission distances. In general, these findings illustrate the trade-off between distance and security in QKD protocols, highlighting the difficulties in maintaining high eavesdropping detection rates as distance increases.

6. Conclusions and Future Work

This paper introduces a hybrid QKD protocol that integrates photonic and atomic systems to improve security and reliability. The framework outlines key components, such as encoding agreement, state preparation, and secure message transmission, focusing on an encoding scheme for robust eavesdropping detection and efficient error correction. LDPC codes play an important role in offering effective error correction to protect the integrity of the message. Using entanglement swapping and the BLAKE2 hash for privacy amplification, the protocol ensures that intercepted information remains inaccessible without the secret key. The integration of photonic and atomic systems allows for a symmetrical approach to key generation and error correction. Photons are used for rapid key generation due to their low decoherence rates, while atomic systems contribute stability, enhancing error correction and privacy amplification. This balance ensures that the strengths of one system compensate for the weaknesses of the other, creating a more robust overall protocol.

Mathematical proofs show the effectiveness of entanglement swapping, privacy amplification, and error correction in preserving communication integrity. A comparative analysis of various QKD protocols shows that the hybrid approach integrates the strengths of the photonic and atomic states, ensuring a secure key distribution with minimal error and loss rates over long distances. Although atomic QKD excels in eavesdropping detection, photonic QKD, despite its simplicity, is more vulnerable to interception. Understanding these nuances is essential as quantum communication technology evolves, particularly for long-distance key distribution and secure communication systems.

Future work should prioritize scalability studies of QKD protocols to assess their effectiveness over longer distances and under a variety of conditions, ensuring practical deployment in real-world situations. Improving error correction techniques is critical for lowering error rates, especially in challenging transmission environments. Furthermore, more comprehensive security analyses are needed to assess the resilience of QKD protocols against advanced eavesdropping tactics and potential quantum attacks, ensuring robust security in an evolving technology landscape. Efforts will also be made to improve the trustworthiness of the third party, Charlie, by developing trust models that characterize his reliability across various operational contexts, ranging from fully trusted to untrusted.