Algebraic and Spectral Analysis of a Novel Hermitian Spin Basis

Abstract

This work aims to explore the algebraic and spectral properties of a novel parametric Hermitian non-Pauli spin basis. The primary motivation for this work is to introduce an alternative to the Pauli spin basis for investigating systems where conventional quantum statistics no longer apply. This study explores the symmetries, commutation relations, Lie algebra structures, and ladder operators of the proposed spin matrices. Additionally, it provides discussions on key findings, potential applications, and concludes with some final remarks. An example for modeling the spectrum of a quantum system is provided.

1. Introduction

In quantum mechanics, the Pauli spin matrices are a set of $2\times 2$ Hermitian matrices that play a fundamental role in describing the spin of spin $-1/2$ particles (fermions). These matrices are closely related to the angular momentum operator and serve as a basis for the vector space of $2\times 2$ Hermitian matrices over the real numbers. Specifically, any $2\times 2$ Hermitian matrix can be uniquely expressed as a linear combination of the Pauli matrices with real coefficients. The non-Pauli spin basis introduced in this work serves as an analogue to the Pauli spin basis, offering an alternative framework where any $2\times 2$ Hermitian matrix can similarly be constructed through a linear combination of the proposed basis elements.

In recent years, Hermitian matrices have been widely studied and applied across various fields, including quantum mechanics, control engineering, graph theory, signal processing, machine learning, and communication system design [1,2,3,4]. Ascertaining the algebraic and spectral properties of these matrices is key to their effective implementation. Tian (2024) [5] introduced an additional characterization of Hermitian matrices through matrix equalities. The findings provide valuable insights into techniques for constructing and classifying complex matrix equalities, thereby enhancing the understanding of challenging problems involving Hermitian and skew-Hermitian matrices. Another key application of Hermitian matrices lies in graph theory, where they play a crucial role in fields such as network systems, molecular and atomic structures, quantum computing, and neural networks. Some studies on novel Hermitian matrices in graph theory can be found in the works of Guo and Mohar (2017) [6] and Mohar (2020) [7]. In Guo and Mohar (2017) [6] and Mohar (2020) [7], a set of novel Hermitian matrices for digraphs were introduced. In addition to the proposed Hermitian adjacency matrix of directed and partially directed graphs, the work of Mohar (2020) [7] shows the existence of a more natural Hermitian matrix for utilization in research works related to algebraic graph theory. The study of Mohar (2020) [7] was extended in the research work of Li and Yu (2022) [8]. In that work, the spectra of mixed graphs via its Hermitian adjacency matrix of the second kind was extensively studied. A similar investigation was conducted for k-generalized Hermitian adjacency matrices for mixed graphs in the work of Yu et al. (2023) [9].

This work explores the spectral properties of a novel Hermitian spin basis, which plays a critical role in its application to various problems, particularly in quantum systems. A recent study on the spectral properties of Hermitian matrices was presented by Qi and Cui (2024) [10]. In that study, the authors proposed a supplementary matrix method for computing the eigenvalues of a dual Hermitian matrix and explored its application in multi-agent formation control. The authors introduced a cross-disciplinary approach to address the relative configuration problem by examining the eigenvalue problem of dual Hermitian matrices and its connection to unit gain graph theory. The spectrum of Hermitian matrices was studied from a computational perspective in the work of Drmač (2021) [11]. In that work, the author provides an overview of numerical approaches to compute the spectrum of Hermitian matrices, even in cases which are too ill-defined to be tackled by standard techniques—e.g., Cauchy, Vandermonde, and Hankel matrices. The key ingredient for the accuracy of the algorithms mentioned in Drmač (2021) [11] is the utility of the intrinsic parameters that define these matrices to obtain a non-orthogonal factorization. A similar work on spectral analysis is given in Barbarino and Serra-Capizzano (2020) [12]. In that research, the authors performed spectral analysis on the matrix sequences which are non-Hermitian perturbations of a specific Hermitian matrix–sequence. The results of that work add to the available spectral analysis tools—enabling analysis on preconditioned matrix–sequences as well as linear partial differential equations with unbounded variable coefficients. Another interesting work on the spectrum of Hermitian matrices is presented in Massey et al. (2021) [13]. In that research, the authors investigated the spectral spread of Hermitian matrices and obtained inequalities and extremal properties of complex Hermitian matrices. Additionally, they also determined the generalized commutators and distances between matrices in the unitary orbit of a Hermitian matrix. An in-depth investigation on Hermitian matrices with respect to operator norms and its associated Lie algebras is presented in [14,15,16].

In Ganesan (2023) [17], a novel spin basis was employed to investigate exotic fermionic particles. In that study, a fermionic quantum Heisenberg model was constructed, and its behavior was compared to that of a model based on the conventional Pauli spin basis. In this work, the Hermitian spin basis introduced in Ganesan (2023) [17] is further examined from both algebraic and spectral perspectives to expand its applicability in solving problems related to quantum systems. The primary motivation for this work is to introduce an alternative to the Pauli spin basis for investigating systems where conventional quantum statistics no longer apply.

This paper is organized as follows. Section 2 describes the properties of the parametrized non-Pauli spin matrices, the derived ladder operators, and the associated quantum numbers. In Section 3, analysis, potential applications, and the conclusions are presented.

2. Parametric Non-Pauli Spin Basis

A set of novel Hermitian spin matrices, along with their symmetry relations, was introduced in Ganesan (2023) [17]. With the exception of the involuntary property, the basis in the form of a parametrized spin matrix representation is:

$$\begin{array}{c}{{\mathsf{\Sigma }}^{\prime }}_1=\left[\begin{array}{cc}0& \left(m-i\right)\\ \left(m+i\right)& 0\end{array}\right], {{\mathsf{\Sigma }}^{\prime }}_2=\left[\begin{array}{cc}0& \left(m+i\right)\\ \left(m-i\right)& 0\end{array}\right] , \\ {{\mathsf{\Sigma }}^{\prime }}_3=\left[\begin{array}{cc}\sqrt{m^2+1}& 0\\ 0& -\sqrt{m^2+1}\end{array}\right] \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} m\in \mathbb{Z}.\end{array}$$

(1)

where ${{\mathsf{\Sigma }}^{\prime }}_1=\stackrel{‾}{{{\mathsf{\Sigma }}^{\prime }}_2}$ and the spin matrices given in Equation (1) contain the following symmetry:

$${{\displaystyle \frac{1}{m^2+1}}\left({{\mathsf{\Sigma }}^{\prime }}_1\right)}^2={\displaystyle \frac{1}{m^2+1}}{\left({{\mathsf{\Sigma }}^{\prime }}_2\right)}^2={{\displaystyle \frac{1}{m^2+1}}\left({{\mathsf{\Sigma }}^{\prime }}_3\right)}^2={ I}_2.$$

(2)

The matrices in the spin basis are Hermitian where ${\left(\overline{{\mathsf{\Sigma }}_k^{\prime }}\right)}^{\mathrm{T}}={{\mathsf{\Sigma }}^{\prime }}_k$ for $k=\mathrm{1,2},3$. The symmetry property of each spin matrix is symmetrically weighted in all directions by the factor ${\displaystyle \frac{1}{m^2+1}}$, e.g., ${\displaystyle \frac{1}{m^2+1}}={\displaystyle \frac{1}{2}}, {\displaystyle \frac{1}{5}} ,{\displaystyle \frac{1}{10}}\dots \in \mathbb{R}$. Similar to Ganesan (2023) [17], the Hermitian spin matrices in this work were constructed from the Pauli spin matrices as follows:

$${{\mathsf{\Sigma }}^{\prime }}_1=m{\sigma }_1-{\sigma }_2; {{\mathsf{\Sigma }}^{\prime }}_2=m{\sigma }_1+{\sigma }_2; {{\mathsf{\Sigma }}^{\prime }}_3={\sigma }_3\sqrt{m^2+1} .$$

(3)

where the Pauli spin matrices, as operators corresponding to observables for the fermionic spin at each spatial direction, are ${\sigma }_1=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right], {\sigma }_2=\left[\begin{array}{cc}0& -i\\ i& 0\end{array}\right], {\sigma }_3=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$. The spin matrices were then defined within another 16-element cyclic group structure: $G^{-1}\left(n\right)=\{\pm I_2 ,\pm {iI}_2,\pm {{\mathsf{\Sigma }}^{\prime }}_1 , \pm {{\mathsf{\Sigma }}^{\prime }}_2 , \pm {{\mathsf{\Sigma }}^{\prime }}_3, \pm i{{\mathsf{\Sigma }}^{\prime }}_1 , \pm {{i\mathsf{\Sigma }}^{\prime }}_2 , \pm {{i\mathsf{\Sigma }}^{\prime }}_3\}$. The inverse of the spin matrices, ${{\sigma }^{\prime }}_k={\left({{\mathsf{\Sigma }}^{\prime }}_k\right)}^{-1}$ is:

$$\begin{array}{c}{{\sigma }^{\prime }}_1=\left[\begin{array}{cc}0& {\displaystyle \frac{1}{\left(m+i\right)}}\\ {\displaystyle \frac{1}{\left(m-i\right)}}& 0\end{array}\right]{{ , \sigma }^{\prime }}_2=\left[\begin{array}{cc}0& {\displaystyle \frac{1}{\left(m-i\right)}}\\ {\displaystyle \frac{1}{\left(m+i\right)}}& 0\end{array}\right] , \\ {{\sigma }^{\prime }}_3=\left[\begin{array}{cc}{\displaystyle \frac{1}{\sqrt{m^2+1}}}& 0\\ 0& {\displaystyle \frac{-1}{\sqrt{m^2+1}}}\end{array}\right] \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} m\in \mathbb{Z}.\end{array}$$

(4)

where ${{\sigma }^{\prime }}_{1 }=\overline{{{\sigma }^{\prime }}_{2 }}$ and the spin matrices given in Equation (1) contain the following symmetry:

$${{(m}^2+1)\left({{\sigma }^{\prime }}_1\right)}^2={(m}^2+1){\left({{\sigma }^{\prime }}_2\right)}^2={(m}^2+1){\left({{\sigma }^{\prime }}_3\right)}^2=I_2=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right].$$

(5)

The parameter $m^2+1$ introduces equivalent weights in the spin matrices for each direction, e.g., $m^2+1=2, 5, 10,\dots \in \mathbb{Z}$. This property is key, in a physical sense, to ensure that the non-Pauli spin basis is isotropic in all directions—similar to the Pauli matrices. It is important to note that the choice of the parameter $m$ directly influences the eigenvalues of the matrices: ${{\sigma }^{\prime }}_i$ and ${{\mathsf{\Sigma }}^{\prime }}_i$. In the study of quantum systems, this parameter determines the symmetry weights (or the spin) of the particle(s) being analyzed. Similar to the Pauli group, the non-Pauli spin matrices could also be defined within a 16-element cyclic group structure: $G\left(n\right)=\{\pm I_2 ,\pm {iI}_2,\pm {{\sigma }^{\prime }}_1 , \pm {{\sigma }^{\prime }}_2 , \pm {{\sigma }^{\prime }}_3, \pm i{{\sigma }^{\prime }}_1 , \pm {{i\sigma }^{\prime }}_2 , \pm {{i\sigma }^{\prime }}_3\}$. Although the consequent analysis could be generalized for $m\in \mathbb{Z}$, the non-Pauli spin matrices given in Equations (1) and (4) were fixed at $m=1$ to simplify the analysis. The following commutation relations hold for the non-Pauli spin matrices:

$$\left[{{\sigma }^{\prime }}_1 , {{\sigma }^{\prime }}_2\right]={\displaystyle \frac{i}{\sqrt{2}}}{{\sigma }^{\prime }}_3 ; \left[{{\sigma }^{\prime }}_1 , {{\sigma }^{\prime }}_3\right]=-{\displaystyle \frac{i}{\sqrt{2}}} {{\sigma }^{\prime }}_2 ; \left[{{\sigma }^{\prime }}_2 , {{\sigma }^{\prime }}_3\right]={\displaystyle \frac{i}{\sqrt{2}}} i{{\sigma }^{\prime }}_1$$

where $\left[{{\sigma }^{\prime }}_i,{{\sigma }^{\prime }}_j\right]=-\left[{{\sigma }^{\prime }}_j,{{\sigma }^{\prime }}_i\right]$ and $\left[{{\sigma }^{\prime }}_j,{{\sigma }^{\prime }}_j\right]=O$.

The generalized commutation relation for the non-Pauli spin matrices is:

$$\left[{{\sigma }^{\prime }}_i , {{\sigma }^{\prime }}_j\right]={\displaystyle \frac{i}{\sqrt{2}}}{ \epsilon }_{ijk}{{\sigma }^{\prime }}_k.$$

(6)

where ${ \epsilon }_{ijk}$ is the Levi–Civita symbol in three dimensions used to assign $-1$, $+1$, or $0$ based on the order and repetition of indices. For the inverse non-Pauli spin matrices, the commutation relations are:

$$\left[{{\mathsf{\Sigma }}^{\prime }}_1 , {{\mathsf{\Sigma }}^{\prime }}_2\right]={\displaystyle \frac{i}{2\sqrt{2}}}{{\mathsf{\Sigma }}^{\prime }}_3; \left[{{\mathsf{\Sigma }}^{\prime }}_1 , {{\mathsf{\Sigma }}^{\prime }}_3\right]=-{\displaystyle \frac{i}{2\sqrt{2}}} {{\mathsf{\Sigma }}^{\prime }}_2 ; \left[{{\mathsf{\Sigma }}^{\prime }}_2 , {{\mathsf{\Sigma }}^{\prime }}_3\right]={\displaystyle \frac{i}{2\sqrt{2}}} {{\mathsf{\Sigma }}^{\prime }}_1$$

where $\left[{{\mathsf{\Sigma }}^{\prime }}_i,{{\mathsf{\Sigma }}^{\prime }}_j\right]=-\left[{{\mathsf{\Sigma }}^{\prime }}_j,{{\mathsf{\Sigma }}^{\prime }}_i\right]$ and $\left[{{\mathsf{\Sigma }}^{\prime }}_j,{{\mathsf{\Sigma }}^{\prime }}_j\right]=O$.

The generalized commutation relation for the non-Pauli spin matrices is:

$$\left[{{\mathsf{\Sigma }}^{\prime }}_i , {{\mathsf{\Sigma }}^{\prime }}_j\right]={\displaystyle \frac{i}{2\sqrt{2}}}{ \epsilon }_{ijk}{{\mathsf{\Sigma }}^{\prime }}_k.$$

(7)

where ${ \epsilon }_{ijk}$ is the Levi–Civita symbol in three dimensions. The non-Pauli spin matrices in Equation (4) were transformed to obtain the real Lie algebra SU(2) for systems with non-integer spins which describes the combination and interaction of small transformations.

$$\begin{array}{c}{v}_1=i{{\sigma }^{\prime }}_2=\left[\begin{array}{cc}0& {\displaystyle \frac{1}{2}}(i-1)\\ {\displaystyle \frac{1}{2}}(i+1)& 0\end{array}\right], v_2=i{{\sigma }^{\prime }}_1=\left[\begin{array}{cc}0& {\displaystyle \frac{1}{2}}(i+1)\\ {\displaystyle \frac{1}{2}}(i-1)& 0\end{array}\right],\\ v_3=-i{{\sigma }^{\prime }}_3=\left[\begin{array}{cc}{\displaystyle \frac{-i}{\sqrt{2}}}& 0\\ 0& {\displaystyle \frac{i}{\sqrt{2}}}\end{array}\right].\hfill \end{array}$$

(8)

where the symmetry holds: ${2v}_1^2={2v}_2^2={2v}_3^2=\sqrt{8}{v}_1{v}_2{v}_3=-I_2.$ The related commutator relationships are $\left[v_1,v_2\right]={\displaystyle \frac{1}{\sqrt{2}}}{v}_3$, $\left[v_1,v_3\right]=-{\displaystyle \frac{1}{\sqrt{2}}}{v}_2$ and $\left[v_2,v_3\right]={\displaystyle \frac{1}{\sqrt{2}}}{v}_1$. The generalized form of the commutator relationships with ${\epsilon }_{ijk}$ being the Levi–Civita symbol is as follows:

$$\left[v_i,v_j\right]={\displaystyle \frac{1}{\sqrt{2}}}{\epsilon }_{ijk}{v}_j \mathrm{where} \left[v_i,v_j\right]=-\left[v_j,v_i\right]$$

(9)

The complexified Lie algebra was then ascertained using the following transformation:

$$\begin{array}{c}X={\displaystyle \frac{1}{2(i+1)}}{(v}_2-i{v}_1)=\left[\begin{array}{cc}0& {\displaystyle \frac{1}{2}}\\ 0& 0\end{array}\right] ,\\ Y={\displaystyle \frac{1}{2\left(i-1\right)}}{(v}_2+i{v}_1)=\left[\begin{array}{cc}0& 0\\ {\displaystyle \frac{1}{2}}& 0\end{array}\right] ,\\ H={\displaystyle \frac{1}{i\sqrt{2}}}{v}_3=\left[\begin{array}{cc}-{\displaystyle \frac{1}{2}}& 0\\ 0& {\displaystyle \frac{1}{2}}\end{array}\right]. \end{array}$$

(10)

where $X$ is the lowering operator and $Y$ is the raising operator. Similarly, their associated commutation relations are $\left[X,Y\right]=-{\displaystyle \frac{1}{2}}H$, $\left[X,H\right]=X$ and $\left[Y,H\right]=-Y$. It can be easily demonstrated that the following Hermitian adjoint holds: $X=Y^{†}.$ Since $X$ and $Y$ may be treated as creation and annihilation operators, the fractional Hermitian particle number operator, $N$, can be defined in terms of these operators:

$$N=X^{†}X={YY}^{†} \mathrm{where} \left[N,X\right]=-{\displaystyle \frac{1}{4}}X=-{\displaystyle \frac{1}{4}}{Y}^{†}\mathrm{and} \left[N,Y\right]={\displaystyle \frac{1}{4}}Y={{\displaystyle \frac{1}{4}}X}^{†}$$

(11)

The following lemmas prove the relations for the raising and lowering operators with respect to the eigenstates, $|n⟩$:

Lemma 1 (raising operator).

The operator $NY\left|n⟩=\left({\displaystyle \frac{n}{4}}+4\right)Y\right|n⟩$, where $|n⟩$, is the eigenstate of $N$ ($N|n⟩=\left({\displaystyle \frac{n}{4}}+4\right)|n⟩)$.

Proof. 

Since the commutator $\left[N,Y\right]=NY-YN$, thus $NY=\left[N,Y\right]+YN.$

$$NY|n⟩=(\left[N,Y\right]+YN\left)\right|n⟩=\left[N,Y\right]|n⟩+YN|n⟩.$$

$YN|n⟩=Y{\displaystyle \frac{n}{4}}|n⟩$, and, from Equation (11), it is known that $\left[N,Y\right]=4Y$.

$$NY\left|n⟩=4Y\right|n⟩+Y{\displaystyle \frac{n}{4}}\left|n⟩=\left({\displaystyle \frac{n}{4}}+4\right)Y\right|n⟩.$$

□

Lemma 2 (lowering operator).

The operator $NX\left|n⟩=\left({\displaystyle \frac{n}{4}}-4\right)X\right|n⟩$, where $|n⟩,$ is the eigenstate of $N$ ($N|n⟩=\left({\displaystyle \frac{n}{4}}-4\right)|n⟩$).

Proof. 

Since the commutator $\left[N,X\right]=NX-XN$, thus $NX=\left[N,X\right]+XN.$

$$NX|n⟩=(\left[N,X\right]+XN\left)\right|n⟩=\left[N,X\right]\left|n⟩+XN\right|n⟩.$$

$XN\left|n⟩=Xn\right|n⟩,$ and, from Equation (11), it is known that $\left[N,X\right]=-4X.$

$$NX\left|n⟩=-4X\right|n⟩+X{\displaystyle \frac{n}{4}}\left|n⟩=\left({\displaystyle \frac{n}{4}}-4\right)X\right|n⟩.$$

□

The Casimir element is then determined as follows:

$$C=-\left(v_1^2+v_2^2+v_3^2\right)={\displaystyle \frac{3}{2}}{I}_2.$$

(12)

Since the Casimir element is the factored identity matrix, the Casimir element commutes with the matrices $v_i$: $\left[C,v_i\right]=0$ for $i\in \left[\mathrm{1,3}\right]$. The Casimir operator in terms of the basis given in Equation (10) is as follows:

$$C=8YX+2H^2-2H.$$

(13)

The complexified Lie algebra matrices were utilized to define the matrix operators (i.e., angular momentum operators) and the associated Casimir operator, $L^2$:

$$\begin{array}{c}{L}_{+}=\hslash X=\hslash \left[\begin{array}{cc}0& {\displaystyle \frac{1}{2}}\\ 0& 0\end{array}\right], L_{-}=\hslash Y=\hslash \left[\begin{array}{cc}0& 0\\ {\displaystyle \frac{1}{2}}& 0\end{array}\right], L_3={\displaystyle \frac{\hslash }{2}}H={\displaystyle \frac{\hslash }{2}}\left[\begin{array}{cc}-{\displaystyle \frac{1}{2}}& 0\\ 0& {\displaystyle \frac{1}{2}}\end{array}\right]. \\ L_1={\displaystyle \frac{1}{2}}\left(L_{+}+L_{-}\right)= {\displaystyle \frac{\hslash }{4}}\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right] ,\\ L_2={\displaystyle \frac{-i}{2}}\left(L_{+}-L_{-}\right)= {\displaystyle \frac{\hslash }{4}}\left[\begin{array}{cc}0& i\\ -i& 0\end{array}\right] ,\\ L^2=L_1^2+L_2^2{+L}_3^2={\displaystyle \frac{3{\hslash }^2}{16}}{I}_2. \end{array}$$

(14)

The commutation relation for the associated matrix operators is as follows:

$$\left[L_i,L_j\right]={\displaystyle \frac{1}{2}}{\epsilon }_{ijk}i\hslash L_k.$$

(15)

The following lemmas describe the commutator properties of the matrix operators.

Lemma 3. 

The commutator is $\left[L^2,L_i\right]=\left[{L_i, L}^2\right]=0$ for any $i=1,2,3$.

Proof. 

$$\left[L^2,L_i\right]=L^2{L}_i-L_i{L}^2=\left(L_1^2+L_2^2{+L}_3^2\right)L_i-L_i\left(L_1^2+L_2^2{+L}_3^2\right).$$

Since $L_i^2{L}_j=L_j^2{L}_i$ $⟹\left[L^2,L_i\right]=L_1^2{L}_i+L_2^2{L}_i{+L}_3^2{L}_i-L_1^2{L}_i+L_2^2{L}_i{+L}_3^2{L}_i=0.$

Similarly, $\left[{L_i,L}^2\right]=L_i{L}^2-{L^{2}L}_i=L_i\left(L_1^2+L_2^2{+L}_3^2\right)-\left(L_1^2+L_2^2{+L}_3^2\right)L_i.$

Since $L_i^2{L}_j=L_j^2{L}_i$ $⟹$ $\left[L^2,L_i\right]={L_1^2{L}_i+L_2^2{L}_i{+L}_3^2{L}_i-L}_1^2{L}_i+L_2^2{L}_i{+L}_3^2{L}_i=0,$

$\therefore \left[L^2,L_i\right]=\left[{L_i,L}^2\right]=0.$ □

Lemma 4. 

The commutator is $\left[L_3,L_{\pm }\right]=\mp {\displaystyle \frac{{\hslash }^2}{2}}{L}_{\pm }$.

Proof. 

The commutator relation is $\left[L_3,L_{\pm }\right]=L_3{L}_{\pm }-L_{\pm },L_3$. Since $L_{\pm }{L}_3=\pm {\displaystyle \frac{{\hslash }^2}{4}}{L}_{\pm }$ and $L_{\pm }{L}_3=-{L_{3}L}_{\pm },$ then the commutator is as follows:

$$\left[L_3,L_{\pm }\right]=L_3{L}_{\pm }-L_{\pm },L_3=-L_{\pm }{L}_3-L_{\pm }{L}_3=-2{L_{\pm }L}_3=-2\left(\pm {\displaystyle \frac{{\hslash }^2}{4}}{L}_{\pm }\right)=\mp {\displaystyle \frac{{\hslash }^2}{2}}{L}_{\pm } .$$

□

To further explore the utility of the non-Pauli spin basis in a quantum context, the eigenvalue series of the orbital quantum number $l$ and the magnetic quantum number $m_l$ for an arbitrary particle are explored in Theorems 1 and 2, respectively.

Theorem 1. 

The Casimir operator is $L^2={\hslash }^2{\displaystyle \frac{l\left(l+1\right)}{4}},$ where $l\in \mathbb{Z}$ is the orbital quantum number and $\hslash$is the Planck’s constant.

Proof. 

Using separation of variables on the spherical wave function $\psi \left(r,\theta ,\varphi \right)=\psi \left(r\right)\psi \left(\theta ,\varphi \right)$ and applying it to the Schrödinger equation, the Casimir operator is represented as follows:

$$\begin{array}{c}{\left(2L\right)}^2\psi \left(\theta ,\varphi \right)=-{\hslash }^2\left[{\displaystyle \frac{1}{\sin \theta }}{\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }\theta }}\left(\sin \theta {\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }\theta }}\right)+{\displaystyle \frac{1}{{\sin }^2\varphi }}{\displaystyle \frac{{\mathsf{\partial }}^2}{\mathsf{\partial }{\varphi }^2}}\right]\psi \left(\theta ,\varphi \right),\\ 4L^2\psi \left(\theta ,\varphi \right)={-\hslash }^2\left[{\displaystyle \frac{1}{\sin \theta }}{\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }\theta }}\left(\sin \theta {\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }\theta }}\right)+{\displaystyle \frac{1}{{\sin }^2\varphi }}{\displaystyle \frac{{\mathsf{\partial }}^2}{\mathsf{\partial }{\varphi }^2}}\right]\psi \left(\theta ,\varphi \right)={\hslash }^{2}l(l+1) \psi \left(\theta ,\varphi \right)\\ 4L^2\psi \left(\theta ,\varphi \right)={\hslash }^{2}l\left(l+1\right)\psi \left(\theta ,\varphi \right).\end{array}$$

The quantum state representation would then be as follows:

$$L^2|l,m_l⟩={\hslash }^2{\displaystyle \frac{l\left(l+1\right)}{4}}|l,m_l⟩\mathrm{with} \mathrm{integers}, l\in \mathbb{Z}.$$

□

Theorem 2. 

$L_3=m_l\hslash ,$ where $m_l\in \mathbb{Z}$ is the magnetic quantum number and $\hslash$ is the Planck’s constant.

Proof. 

In the spherical representation of the Schrödinger equation, the proposed orbital angular momentum operator is given as:

$$L_3=-{\displaystyle \frac{i\hslash }{2}}{\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }\varphi }} \mathrm{where} L_3\psi =-{\displaystyle \frac{i\hslash }{2}}{\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }\varphi }}\psi .$$

The solution form of $\psi$ is then:

$\psi =A\exp \left({\displaystyle \frac{2i{L}_3\varphi }{\hslash }}\right)$. As $A$ is independent of $\varphi$, the angle $\varphi$ could be phased by $2\pi$ while maintaining the equivalence:

$$A\exp \left({\displaystyle \frac{2i{L}_3\varphi }{\hslash }}\right)=A\exp \left({\displaystyle \frac{2i{L}_3(\varphi +2\pi )}{\hslash }}\right)⟹ \exp \left({\displaystyle \frac{-4\pi i{L}_3}{\hslash }}\right)=1.$$

In light of the identity $e^{-4\mathit{i\pi }}={\left(e^{i\pi }\right)}^{-4}={\left(-1\right)}^{-4}=1$, the orbital angular momentum is then represented as $\exp \left({\displaystyle \frac{-4\pi i{L}_3}{\hslash }}\right)={{(e}^{-4i\pi })}^{{\displaystyle \frac{L_3}{\hslash }}}.$

Since $1^{{\displaystyle \frac{L_3}{\mathrm{\hslash }}}}=1^1=1^2=\dots =1^{m_l}$ $⟹L_3=m_l\mathrm{\hslash }.$

The eigenvalues of $L_3$ would be integer multiples of $\hslash$.

$\therefore L_3=m_l\hslash$, where $m_l\in \mathbb{Z}$ is the magnetic quantum number.

□

3. Analysis and Conclusions

In the previous section, some key algebraic and spectral properties of the novel Hermitian non-Pauli spin basis were obtained. Using the mentioned spin basis, it is shown that the spin of an arbitrary particle can be obtained by fixing the parameter, $m$. In Lemmas 1 and 2, the raising and lowering operators were obtained: $NY|n⟩={\displaystyle \frac{n}{4}}+4|n⟩$ and $NX|n⟩={\displaystyle \frac{n}{4}}-4|n⟩$. For some integer $n$, the operator exacts a fractional transition between the eigenstates. For an arbitrary particle endowed with the non-Pauli spin states, the associated orbital and magnetic quantum numbers are also given in Theorems 1 and 2.

With the exception of the involuntary property of the Pauli spin matrices, the non-Pauli spin basis shares similar matrix properties to those of the Pauli spin matrices. This exception enables the non-Pauli spin basis to be represented in the inverse form—where the spin matrix representation is defined as follows:

$$\begin{array}{c}{\left({{\sigma }^{\prime }}_i\right)}^{-1}={{\mathsf{\Sigma }}^{\prime }}_i \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}:\\ {{\mathsf{\Sigma }}^{\prime }}_1=\left[\begin{array}{cc}0& 1-i\\ 1+i& 0\end{array}\right] , {{\mathsf{\Sigma }}^{\prime }}_2=\left[\begin{array}{cc}0& 1+i\\ 1-i& 0\end{array}\right], {{\mathsf{\Sigma }}^{\prime }}_3=\left[\begin{array}{cc}\sqrt{2}& 0\\ 0& -\sqrt{2}\end{array}\right].\end{array}$$

(16)

where ${{\mathsf{\Sigma }}^{\prime }}_1=\stackrel{‾}{{{\mathsf{\Sigma }}^{\prime }}_2}$ and the spin matrices given in Equation (1) contain the following symmetry:

$${{\displaystyle \frac{1}{2}}\left({{\mathsf{\Sigma }}^{\prime }}_1\right)}^2={\displaystyle \frac{1}{2}}{\left({{\mathsf{\Sigma }}^{\prime }}_2\right)}^2={{\displaystyle \frac{1}{2}}\left({{\mathsf{\Sigma }}^{\prime }}_3\right)}^2={\displaystyle \frac{i}{2\sqrt{2}}} {{\mathsf{\Sigma }}^{\prime }}_1{{\mathsf{\Sigma }}^{\prime }}_2{{\mathsf{\Sigma }}^{\prime }}_3=I_2.$$

(17)

The inverse matrices are also Hermitian where ${\left(\stackrel{‾}{{{\mathsf{\Sigma }}^{\prime }}_k}\right)}^T={{\mathsf{\Sigma }}^{\prime }}_k$ for $k=1,2,3$. Similar to its counterpart ${{\sigma }^{\prime }}_k$, the symmetry property of each spin matrix is equally weighted in all directions by the factor ${\displaystyle \frac{1}{2}}$. The spin quantum number, in this case, is the eigenvalues of $S_k={\displaystyle \frac{\hslash }{2}}{{\mathsf{\Sigma }}^{\prime }}_k$, that is, ${\displaystyle \frac{1}{\sqrt{2}}}$. This results in a fractional spin state of $\pm {\displaystyle \frac{1}{\sqrt{2}}}$ in each direction. For each state defined as $|0⟩=+{\displaystyle \frac{1}{\sqrt{2}}}$ and $|1⟩=-{\displaystyle \frac{1}{\sqrt{2}}}$ , the sum of the probability of possible spin states is $P=\sum _{k\in N}{\left|{\psi }_k\right|}^2=1$. The spin projection operators (based on the non-Pauli spin matrices) for non-integer spin states are defined as $S_k={\displaystyle \frac{\hslash }{2}}{{\sigma }^{\prime }}_k$, where $k\in \left[\mathrm{1,3}\right]$. The spin operator and its eigenvectors $z$-direction are $S_3={\displaystyle \frac{\hslash }{\sqrt{2}}}\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$, where the eigenvectors are $v_1=\left(\mathrm{0,1}\right)$ and $v_2=\left(\mathrm{1,0}\right)$.

The original form of the non-Pauli spin matrices introduced in this work is parametric (given in Equations (1)–(5)). The spin states correspond to the spin projection operator. The generalized spin of non-Pauli matrices, ${{\sigma }^{\prime }}_k$, could be determined by obtaining the eigenvalue of the spin operator $S_k={\displaystyle \frac{\hslash }{2}}{{\sigma }^{\prime }}_k$, for the spin operator in the $z$-direction is $S_3={\displaystyle \frac{\hslash }{2}}\left[\begin{array}{cc}{\displaystyle \frac{1}{\sqrt{m^2+1}}}& 0\\ 0& {\displaystyle \frac{-1}{\sqrt{m^2+1}}}\end{array}\right]$, where $m\in \mathbb{Z}$. The eigenvalue of $S_3$ will then yield the parametric spin quantum number $\pm {\displaystyle \frac{\hslash }{2\sqrt{m^2+1}}}$ for any $m\in \mathbb{Z}$. At $m=\pm 1,\pm 2, \pm 3,\dots$, the spin state would be $\pm {\displaystyle \frac{\hslash }{2\sqrt{2}}}, \pm {\displaystyle \frac{\hslash }{2\sqrt{5}}}, \pm {\displaystyle \frac{\hslash }{2\sqrt{10}}},\dots$ A similar analysis could also be carried out for the inverted set of matrices: $S_k={\displaystyle \frac{\hslash }{2}}{{\mathsf{\Sigma }}^{\prime }}_k$, where $S_3={\displaystyle \frac{\hslash }{2}}\left[\begin{array}{cc}\sqrt{m^2+1}& 0\\ 0& -\sqrt{m^2+1}\end{array}\right]$ for $m\in \mathbb{Z}$. In this case, the parametric spin quantum number would be $\pm {\displaystyle \frac{\hslash }{2}}\sqrt{m^2+1}$ for any $m\in \mathbb{Z}$. For $m=\pm 1,\pm 2, \pm 3,\dots$, the spin state would be $\pm {\displaystyle \frac{\hslash }{\sqrt{2}}}, \pm {\displaystyle \frac{\hslash \sqrt{5}}{2}}, \pm {\displaystyle \frac{\hslash \sqrt{10}}{2}},\dots$

Based on the eigenvalue of the spin projection operator, the inverse form of the non-Pauli spin basis corresponds to the spin state ${\displaystyle \frac{1}{\sqrt{2}}}$ at $m=1$. Future works may be directed toward more in-depth analysis on systems consisting of spin states $\pm {\displaystyle \frac{1}{2\sqrt{m^2+1}}}$ and $\pm {\displaystyle \frac{1}{2}}\sqrt{m^2+1}$.

One key application of the Hermitian matrices presented in this work is in scenarios where conventional quantum statistics are nonexistent, e.g., near black holes, neutron stars, and quasars. For particle trajectories beneath the Schwarzschild surface and photon sphere, the homotopy of these trajectories prevents the application of braid group-based quantum statistics [18]. Consequently, the Pauli exclusion principle ceases to apply in these regions, though this does not violate the Pauli theorem [16].

The absence of braid group statistics in such extreme environments parallels observations in the fractional quantum Hall effect, where collective particle behavior results in anyonic statistics [18,19,20]. Anyons are quasiparticles that follow intermediate statistics between fermions and bosons. When identical anyons exchange positions or undergo braiding, their wave functions retain a record of the braiding history. This intrinsic memory property is valuable for quantum computing. Given that the proposed Hermitian spin basis has the potential to accommodate anyonic statistics, it may offer applications in topological quantum computing.

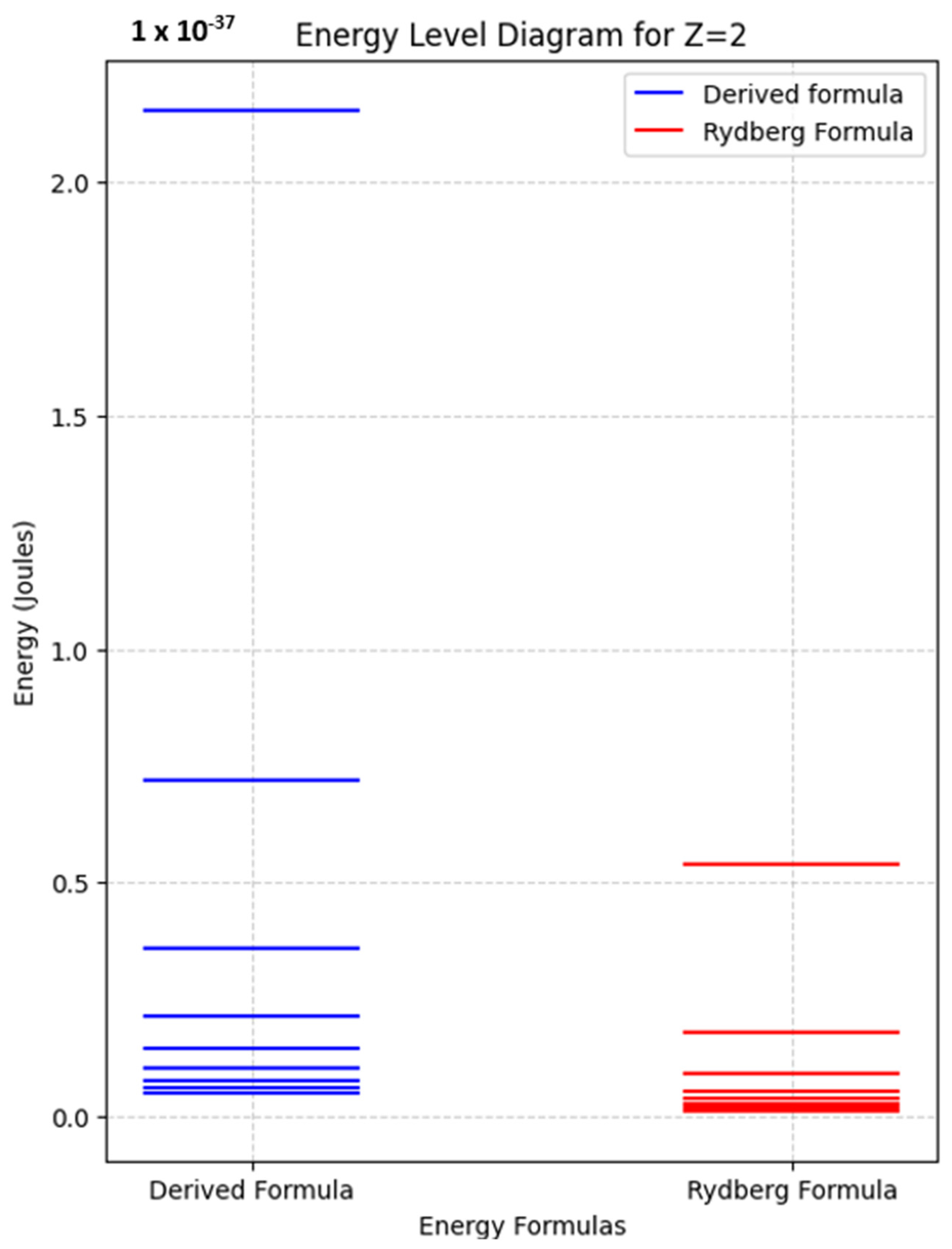
An interesting path for future research would be to study the implications of the proposed utility of non-Pauli spin matrices when applied for modeling quantum systems. In Theorem 1, the Casimir operator was derived using the proposed non-Pauli spin representation for arbitrary particles at $m=1$. Using this operator, it is then possible to construct the Hamiltonian for a quantum system. A simplified example for modeling the spectra of an anyonic hydrogen-like atom using the proposed non-Pauli spin basis is given in Appendix A.

The system of Pauli matrices can also be used to construct Minkowski spacetime. Building on this concept, an intriguing direction for future research is to explore the feasibility of constructing a spacetime metric using the proposed parametrized spin matrices in Equations (1)–(5). This investigation could involve analyzing how relativistic phenomena manifest within such a framework, including potential modifications to spacetime symmetries, causal structures, and Lorentz transformations. Additionally, studying the interplay between these novel spin-based metrics and fundamental quantum field theories may provide new insights into the geometric foundations of relativistic quantum mechanics.