An Improved Set-Valued Observer and Probability Density Function-Based Self-Organizing Neural Networks for Early Fault Diagnosis in Wind Energy Conversion Systems
Abstract
1. Introduction
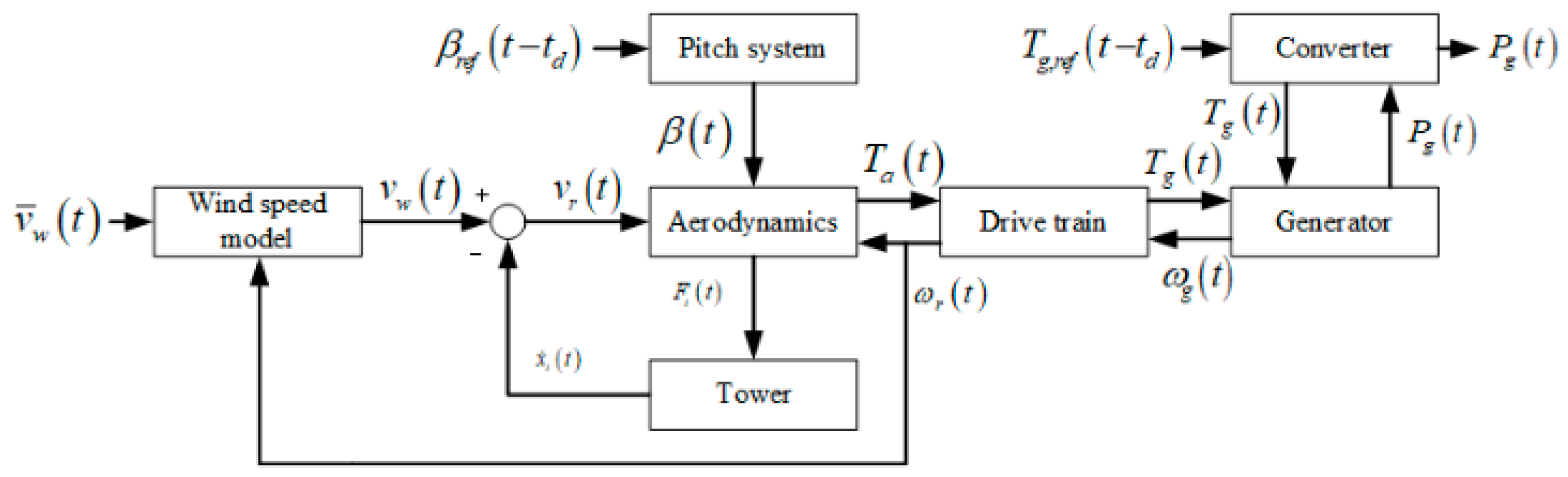
2. Model of a WECS with Delayed Inputs and an Unknown Part
2.1. The Pitch System Model
2.2. The Aerodynamics Model
2.3. The Drivetrain Model
2.4. The Converter Model
3. Observer Design, Faults Setting, and SONN Construction
3.1. Design of Improved SVO
3.2. Modelling of Pitch Angle Actuators Faults
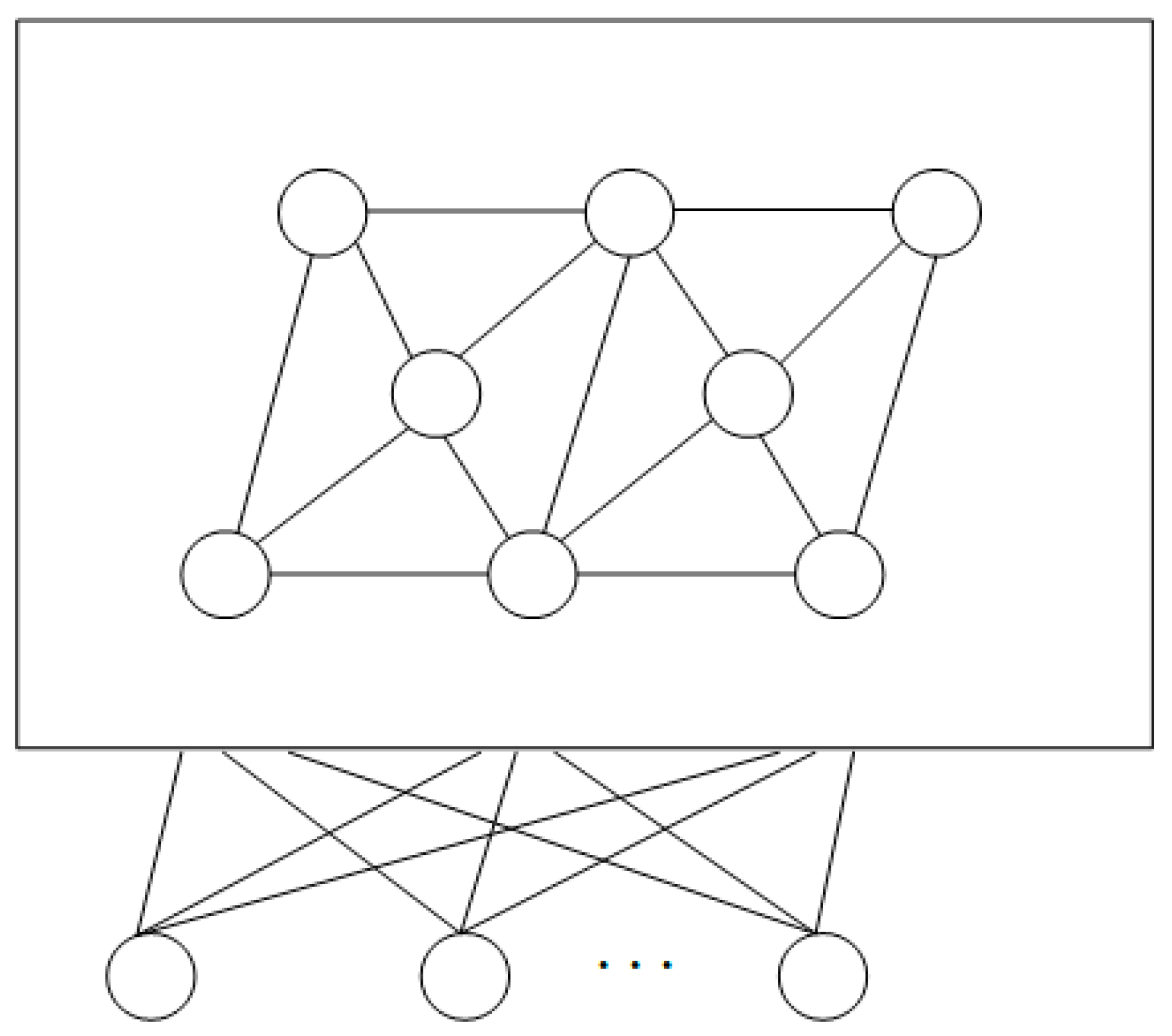
3.3. Design of SOCNN
- Initialize the runtime environment;
- Build the network. Assume that the sample data is divided into two categories, initializing weights to random values and tentatively set the learning rate ;
- Normalize the samples and feed them serially into the network;
- Identify the winning neuron. Calculate network output . Find the neuron with the maximum value in the output neuron and designated it as the winning neuron;
- Adjust weights. For the winning neuron , adjust the corresponding weights according to , while the weights of the remaining neurons are not adjusted;
- Determine whether there is convergence. Repeat steps 4 to 5. Set the maximum number of iterations. The program will automatically stop after reaching this certain number of iterations;
- Test and label. After the weights stop updating, feed the original training samples into the network for category labeling.
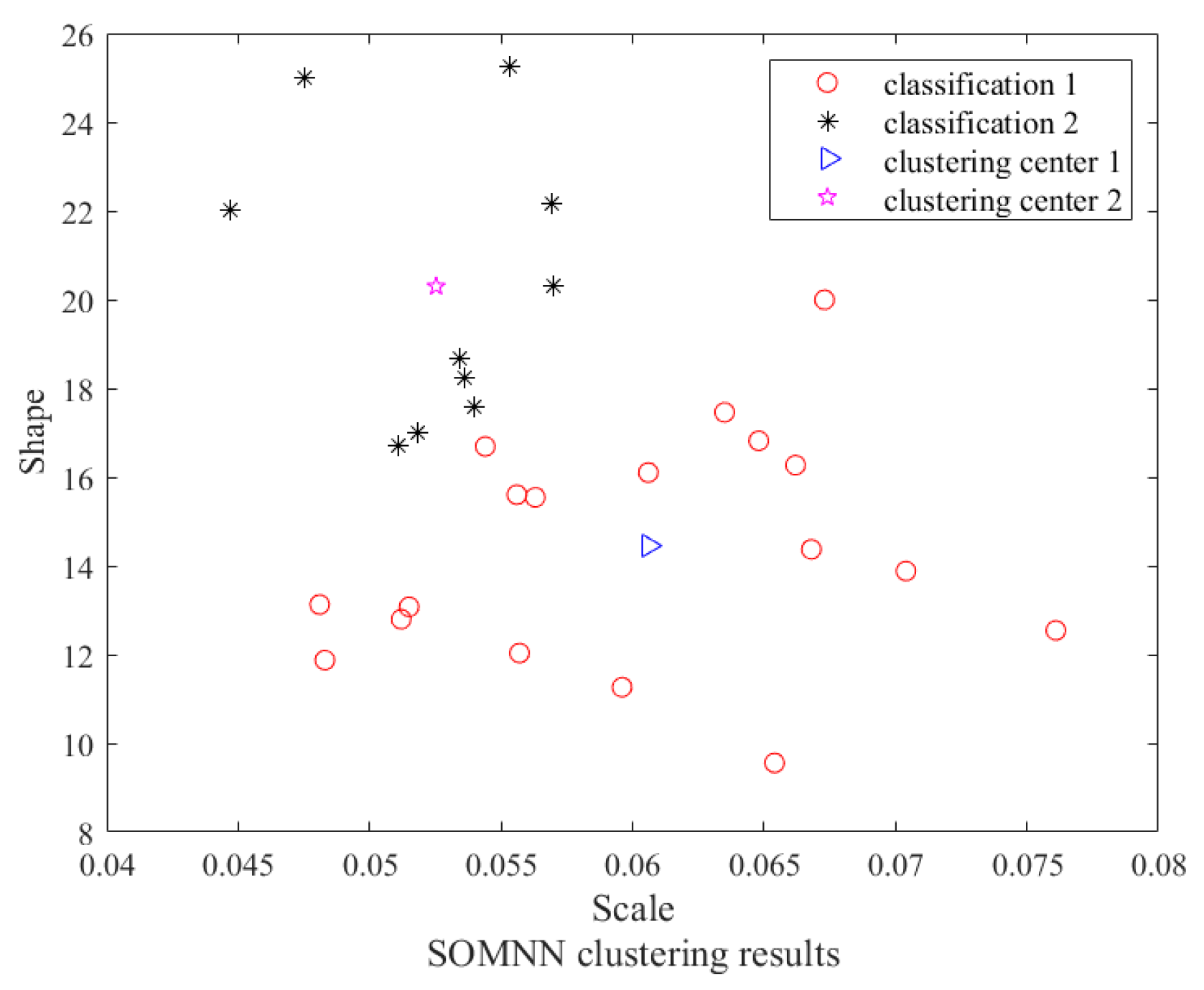
3.4. Design of SOMNN
- Initialize the runtime environment;
- Input training samples and normalize them;
- Build the network. Determine the dimension of the weight matrix based on the dimensions of the input and output vectors. Set the learning rate of change formula as follows:where represents the current iteration number, represents the total number of iterations, represents the maximum value of the learning rate, and represents the minimum value of the learning rate. The radius of the neighborhood of the optimal node is calculated as follows:where represents the maximum value of the radius of the neighborhood, and represents the minimum value of the radius of the neighborhood;
- Iterative updating. Randomly draw a vector from the sample set and feed it into the network. Calculate the Euclidean distance between the weights and the input vector using the following function:Find the minimum value of and mark as ; the neuron corresponding to is the winning neuron. Then, the learning rate for the current number of iterations and the neighborhood size parameter are calculated to determine the neighborhood domain. The weights are updated for the neurons within the neighborhood;
- Determine whether the maximum number of iterations has been reached. If not, return to step 4 until the end of training;
- Obtain the trained network, feed the training samples into the network, and obtain the clustering results.
4. Design of Fault Diagnosis Strategies
5. Simulation Studies and Discussion
5.1. Parameters Setting of the WECS and the ISVO
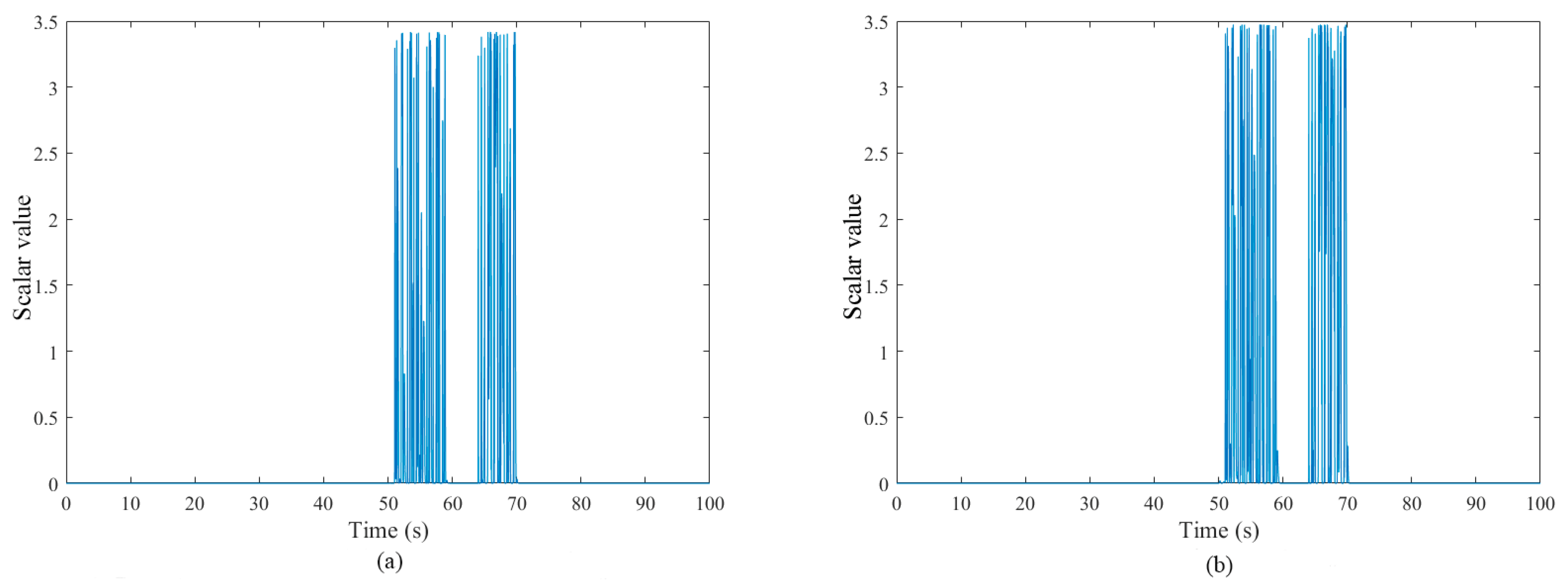
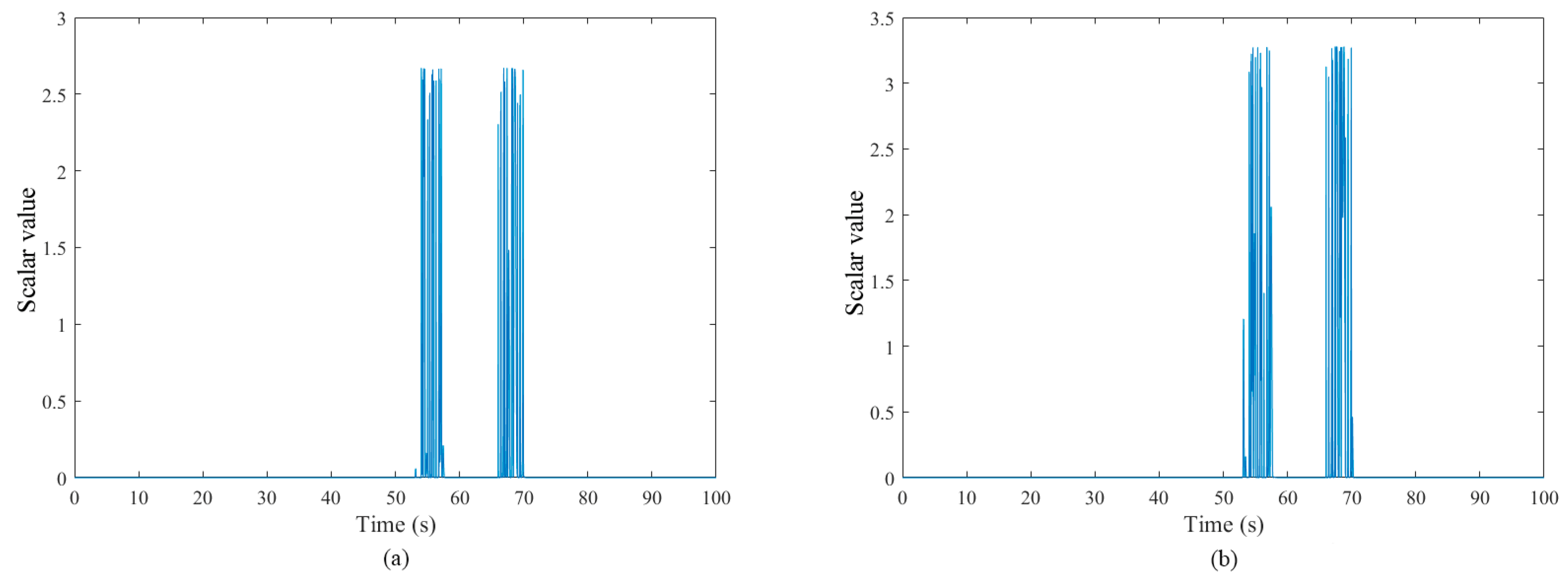
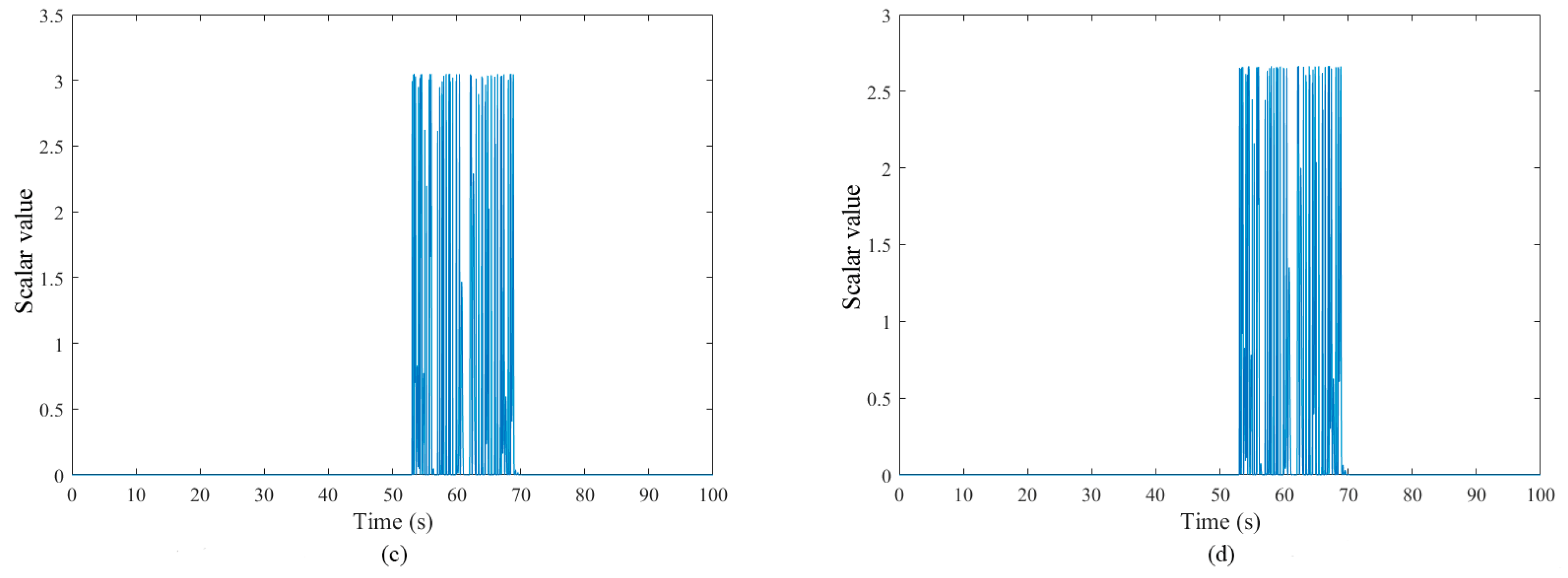
5.2. Fault Diagnosis Simulations and Analysis of Three Fault Cases
5.2.1. Fault Case I: Hydraulic Pump Wear
5.2.2. Fault Case II: Hydraulic Leak
5.2.3. Fault Case III: Hydraulic Oil Has a High Air Content
5.3. Comparative Studies for Different Fault Diagnosis Performance
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Morshedizadeh, M.; Kordestani, M.; Carriveau, R.; Ting, D.S.; Saif, M. Improved power curve monitoring of wind turbines. Wind Eng. 2017, 41, 260–271. [Google Scholar] [CrossRef]
- Gao, Z.; Liu, X. An overview on fault diagnosis, prognosis and resilient control for wind turbine systems. Processes 2021, 9, 300. [Google Scholar] [CrossRef]
- Rezamand, M.; Kordestani, M.; Carriveau, R.; Ting, D.S.; Saif, M. A new hybrid fault detection method for wind turbine blades using recursive PCA and wavelet-based PDF. IEEE Sens. J. 2020, 20, 2023–2033. [Google Scholar] [CrossRef]
- Zhao, R.N. Fault detection of WECSs based on improved SVO and Fourier transformation. IEEE Access 2024, 12, 65341–65351. [Google Scholar] [CrossRef]
- Ebrahim, M.A.; Ramadan, H.S.; Soliman, M. Robust nonfragile approach to resilient design of PID-based blade pitch control for wind energy conversion system. Asian J. Control 2019, 21, 1952–1965. [Google Scholar] [CrossRef]
- Tir, Z.; Malik, O.P.; Hashemnia, M.N. Intelligent control of a brushless doubly-fed induction generator. Int. J. Syst. Assurance Eng. Manag. 2019, 10, 326–338. [Google Scholar] [CrossRef]
- Karakasis, N.E.; Mademlis, C.A. High efficiency control strategy in a wind energy conversion system with doubly fed induction generator. Renew. Energy 2018, 125, 974–984. [Google Scholar] [CrossRef]
- Omar, A.; Khater, F.; Shaltout, A. Per unit modeling of wind energy conversion system based on PMSG. In Proceedings of the International Conference on Advanced Control Circuits and Systems (ACCS), International Conference on New Paradigms in Electronics & Information Technology (PEIT), Alexandria, Egypt, 5–8 November 2017; pp. 117–126. [Google Scholar]
- Mansouri, M.; Fezai, R.; Trabelsi, M.; Mansour, H.; Nounou, H.; Nounou, M. Fault diagnosis of wind energy conversion systems using gaussian process regression-based multi-class random forest. IFAC-PapersOnLine 2022, 55, 127–132. [Google Scholar] [CrossRef]
- Fezai, R.; Dhibi, K.; Mansouri, M.; Trabelsi, M.; Mansour, H.; Bouzrara, K.; Nounou, H.; Nounou, M. Effective random forest-based fault detection and diagnosis for wind energy conversion systems. IEEE Sens. J. 2021, 21, 6914–6921. [Google Scholar] [CrossRef]
- Fezai, R.; Bouzrara, K.; Mansouri, M.; Nounou, H.; Nounou, M.; Trabelsi, M. Reduced GPR based RF approach for fault diagnosis of wind energy conversion systems. In Proceedings of the 2021 18th International Multi-Conference on Systems, Signals & Devices (SSD), Monastir, Tunisia, 22–25 March 2021; pp. 595–600. [Google Scholar]
- Mansouri, M.; Fezai, R.; Trabelsi, M.; Hajji, M.; Harkat, M.; Nounou, H. A novel fault diagnosis of uncertain systems based on interval gaussian process regression: Application to wind energy conversion systems. IEEE Access 2020, 8, 219672–219679. [Google Scholar] [CrossRef]
- Hussain, M.; Hussain, N.M.; Shaikh, F.; Dhirani, L.L.; Kumar, L.; Sleiti, A.K. Condition Monitoring and Fault Diagnosis of Wind Turbine: A Systematic Literature Review. IEEE Access 2024, 12, 190220–190239. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Hao, L.Y.; Guo, M.J. Fault detection for uncertain nonlinear systems via recursive observer and tight threshold. Appl. Math. Comput. 2022, 414, 126665. [Google Scholar] [CrossRef]
- Pujol-Vazquez, G.; Acho, L.; Gibergans-Báguena, J. Fault detection algorithm for wind turbines’ pitch actuator systems. Energies 2020, 13, 2861. [Google Scholar] [CrossRef]
- Tolouei, H.; Shoorehdeli, M.A. Nonlinear parity approach to fault detection in nonlinear systems using unknown input observer. Iran J. Sci. Technol. Trans. Electr. Eng. 2021, 45, 321–333. [Google Scholar] [CrossRef]
- Borja-Jaimes, V.; Adam-Medina, M.; García-Morales, J.; Guerrero-Ramírez, G.V.; López-Zapata, B.Y.; Sánchez-Coronado, E.M. Actuator FDI Scheme for a Wind Turbine Benchmark Using Sliding Mode Observers. Processes 2023, 11, 1690. [Google Scholar] [CrossRef]
- Bakhshi, A.; Afi, A. Observer-based adaptive guaranteed control of wind turbine system subject to pitch angle sensor fault. Int. J. Dynam. Control 2024, 12, 1987–1999. [Google Scholar] [CrossRef]
- Eissa, M.A.; Sali, A.; Ahmad, F.A.; Darwish, R.R. Observer-based fault detection approach using fuzzy adaptive poles placement system with real-time implementation. IEEE Access 2021, 9, 83272–83284. [Google Scholar] [CrossRef]
- Wang, H. Control of Nonlinear Stochastic Systems. In Bounded Dynamic Stochastic Systems: Modelling and Control; Springer: London, UK, 2000; pp. 107–121. [Google Scholar]
- Li, T.; Guo, L.; Wu, L. Observer-based optimal fault detection using PDFs for time-delay stochastic systems. Nonlinear Anal. Real World Appl. 2008, 9, 2337–2349. [Google Scholar] [CrossRef]
- Li, T.; Guo, L. Optimal fault-detection filtering for non-gaussian systems via output PDFs. IEEE Trans. Syst. Man Cybern.—Part A Syst. Hum. 2009, 39, 476–481. [Google Scholar]
- Li, T.; Zhang, Y. Fault detection and diagnosis for stochastic systems via output PDFs. J. Frankl. Inst. 2011, 348, 1140–1152. [Google Scholar] [CrossRef]
- Zhuang, Z.; Li, F.; Wei, C. A probability density estimation for fault detection. Adv. Mater. Res. 2012, 562–564, 1113–1116. [Google Scholar] [CrossRef]
- Zarch, M.G.; Alipouri, Y.; Poshtan, J. Fault detection based on online probability density function estimation. Asian J. Control 2017, 19, 1–10. [Google Scholar]
- Aviña-Corral, V.; Rangel-Magdaleno, J.J.; Barron-Zambrano, J.H.; Rosales-Nuñez, S. Review of fault detection techniques in power converters: Fault analysis and diagnostic methodologies. Measurement 2024, 234, 114864. [Google Scholar] [CrossRef]
- Esvan-Jesús, P.P.; Vicenç, P.; Francisco-Ronay, L.E.; Guillermo, V.P.; Ildeberto, S.R.; Sergio, E.S. Fault detection and isolation in wind turbines based on neuro-fuzzy qLPV zonotopic observers. Mech. Syst. Signal Process. 2023, 191, 110183. [Google Scholar]
- Mansouri, M.; Dhibi, K.; Nounou, H.; Nounou, M. Interval-valued SVM based ABO for fault detection and diagnosis of wind energy conversion systems. IEEE Access 2022, 10, 130406–130414. [Google Scholar] [CrossRef]
- Tong, R.; Li, P.; Gao, L.; Lang, X.; Miao, A.; Shen, X. A novel ellipsoidal semisupervised extreme learning machine algorithm and its application in wind turbine blade icing fault detection. IEEE Trans. Instrum. Meas. 2022, 71, 1–16. [Google Scholar] [CrossRef]
- Zemali, Z.; Cherroun, L.; Hadroug, N.; Hafaifa, A.; Iratni, A.; Alshammari, O.S.; Colak, I. Robust intelligent fault diagnosis strategy using Kalman observers and neuro-fuzzy systems for a wind turbine benchmark. Renew. Energy 2023, 205, 873–898. [Google Scholar]
- Zhang, Y.; Huang, Y. Research on turnout fault classification diagnosis based on SOM algorithm. In Proceedings of the 2021 7th International Symposium on Mechatronics and Industrial Informatics (ISMII), Zhuhai, China, 22–24 January 2021; pp. 296–299. [Google Scholar]
- Mahar, A.A.; Mirjat, N.H.; Chowdhry, B.S.; Kumar, L.; Tran, Q.T.; Zizzo, G. Condition Assessment and Analysis of Bearing of Doubly Fed Wind Turbines Using Machine Learning Technique. Energies 2023, 16, 2367. [Google Scholar] [CrossRef]
- Qu, N.; Chen, J.; Zuo, J. PSO–SOM neural network algorithm for series arc fault detection. Adv. Math. Phys. 2020, 2020, 6721909. [Google Scholar] [CrossRef]
- Cui, W.; Xue, W.; Li, L.; Shi, J. A method for intermittent fault diagnosis of electronic equipment based on labeled SOM. In Proceedings of the 2020 International Conference on Sensing, Diagnostics, Prognostics, and Control (SDPC), Beijing, China, 5–7 August 2020; pp. 149–154. [Google Scholar]
- Zhang, Y.; Jia, Y.; Guo, C. Intelligent fault diagnosis of engine based on PCA-SOM. J. Phys. Conf. Ser. 2020, 1453, 012022. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, J.; Zou, Y. An intelligent fault diagnosis method of marine seawater cooling system based on SOM neural network. In Proceedings of the 2021 International Symposium on Computer Science and Intelligent Controls (ISCSIC), Rome, Italy, 12–14 November 2021; pp. 233–236. [Google Scholar]
- Zhao, R.N.; Shen, Y.X. Fault detection of WECSs with a delayed input and an unknown part based on SVO. IEEE Access 2020, 8, 121050–121058. [Google Scholar] [CrossRef]
- Hu, Z.K.; Chen, B.Q.; Chen, W.L.; Tan, D.B.; Shen, D.T. Review of model-based and data-driven approaches for leak detection and location in water distribution systems. Water Supply 2021, 21, 3282–3306. [Google Scholar] [CrossRef]
- Song, H.D.; Liu, X.J.; Song, M.Q. Comparative study of data-driven and model-driven approaches in prediction of nuclear power plants operating parameters. Applied Energy 2023, 341, 121077. [Google Scholar] [CrossRef]
- Mushabi, P.; Matsebe, O.; Samikannu, R. Application of PCA and SVM in fault detection and diagnosis of bearings with varying speed. Math. Probl. Eng. 2022, 1, 5266054. [Google Scholar]



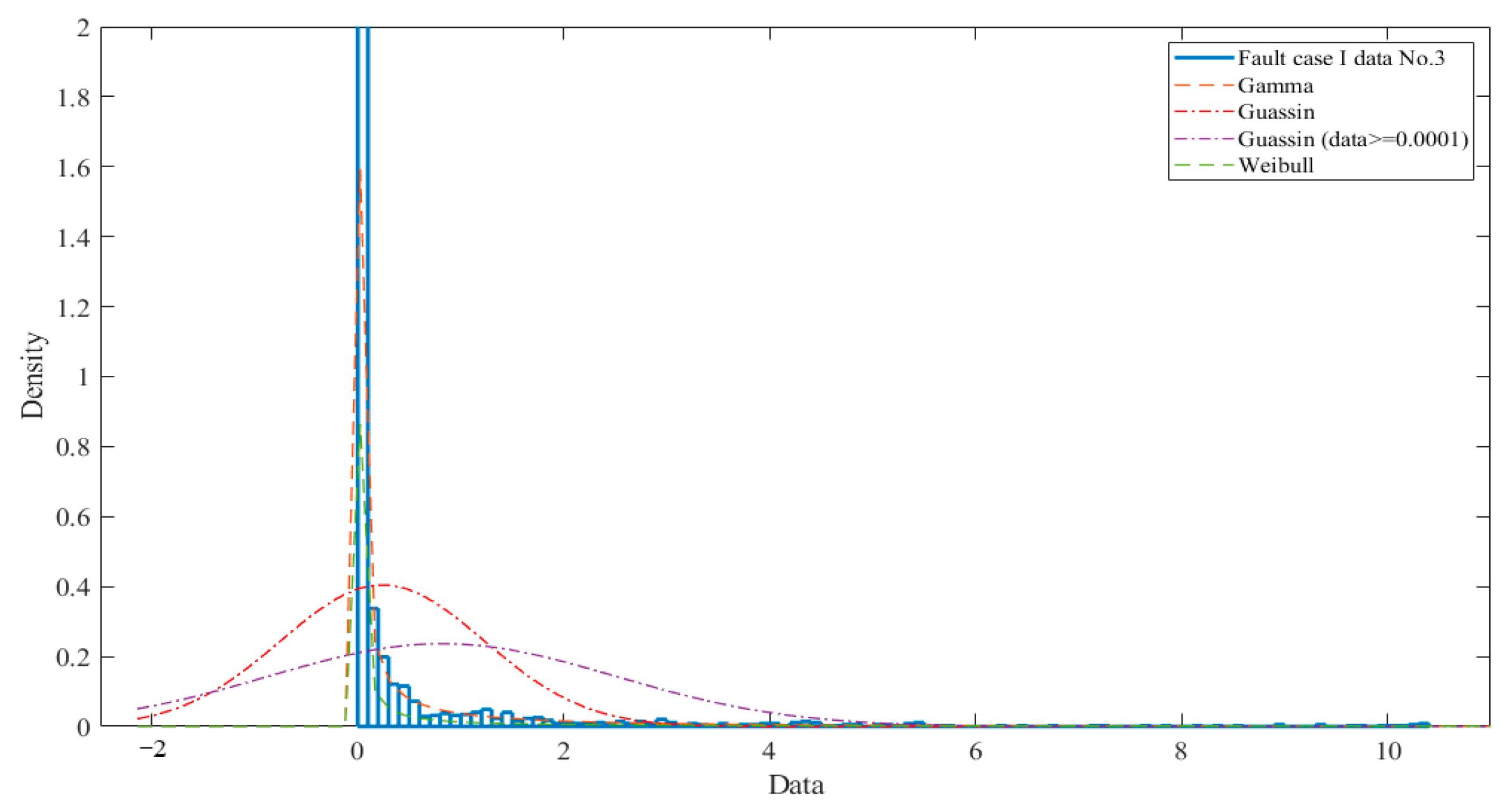

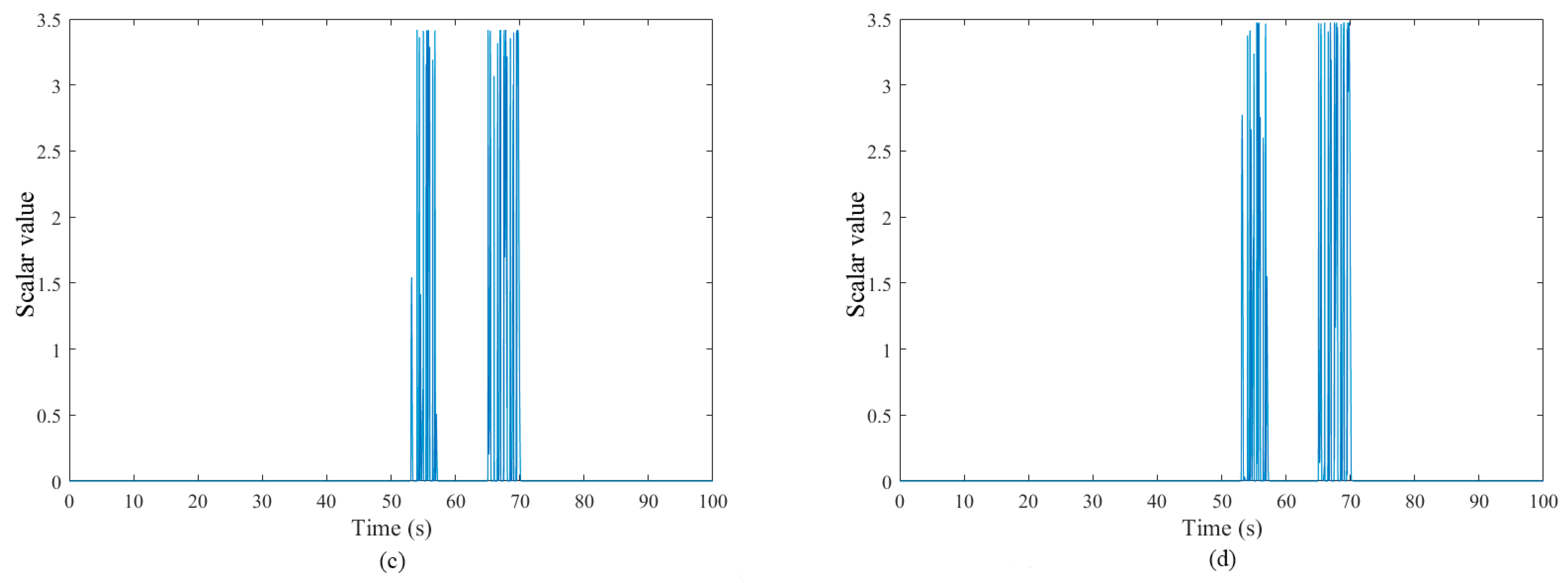

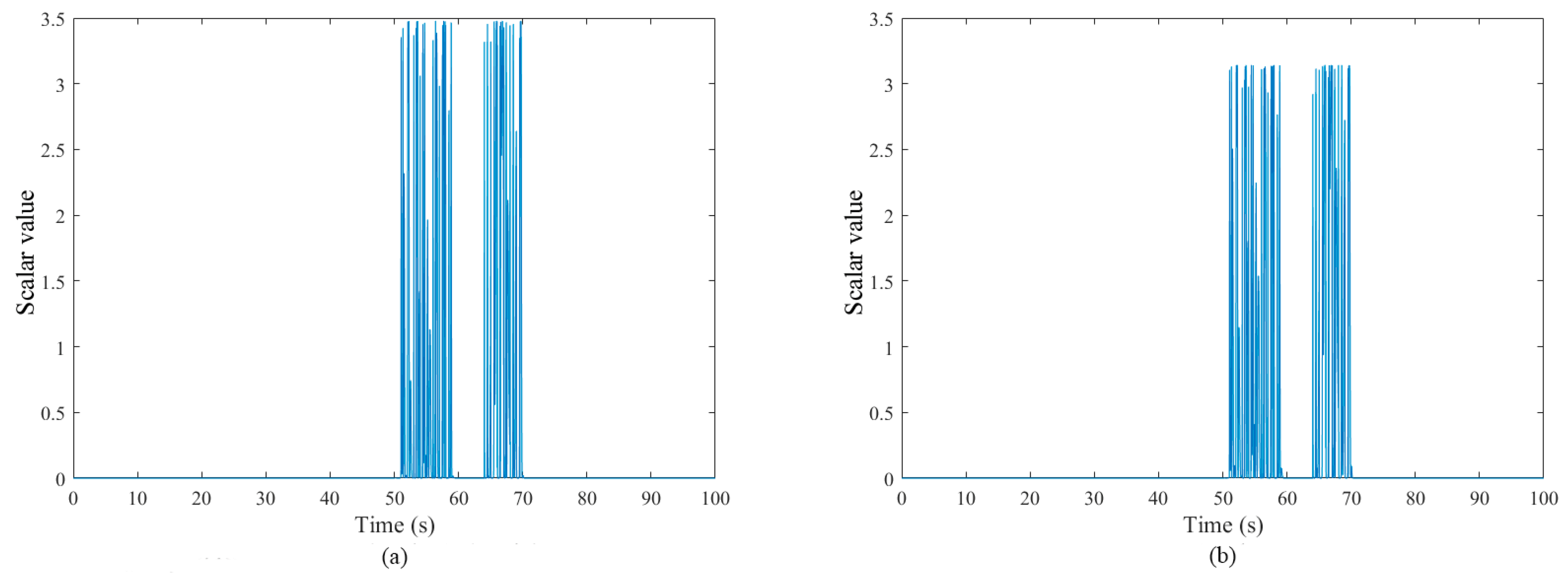
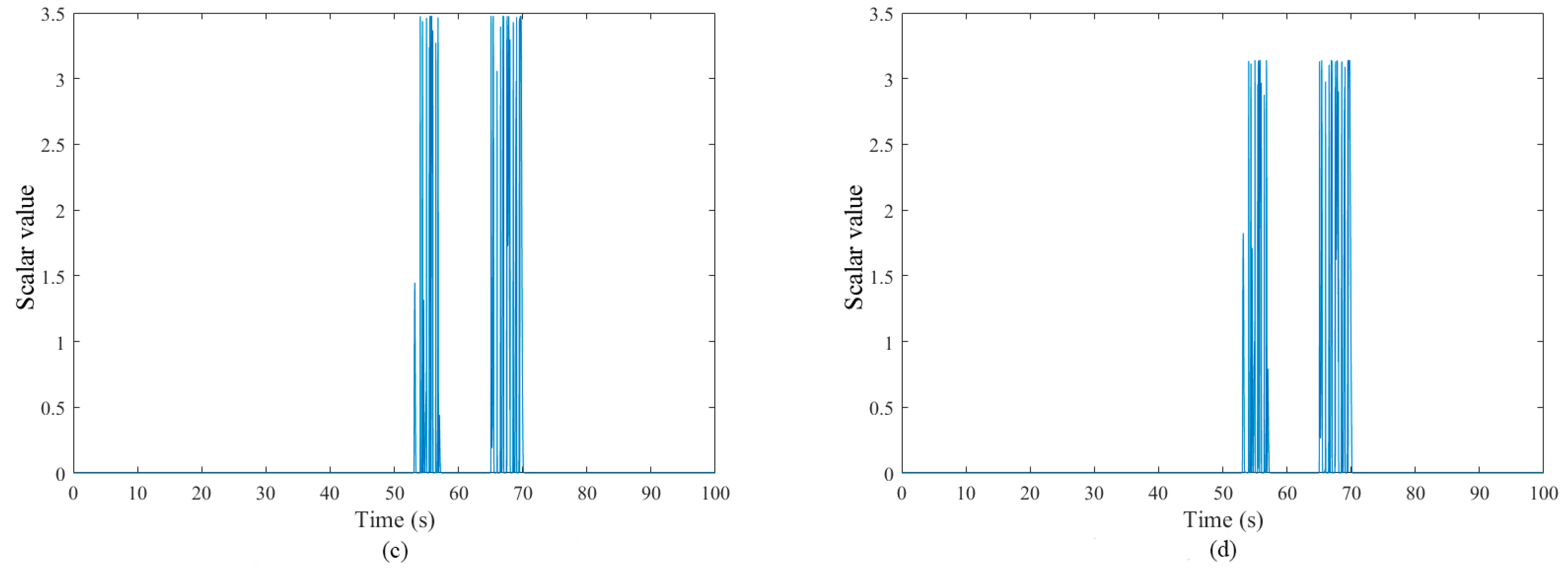

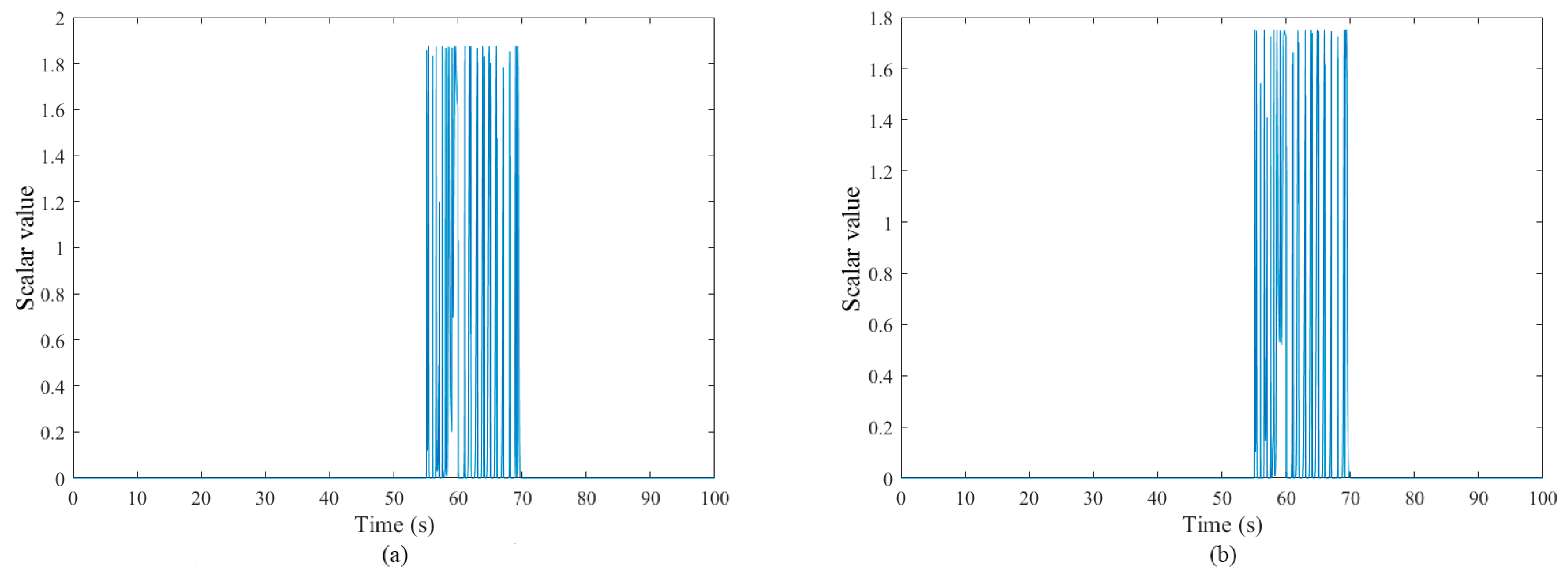
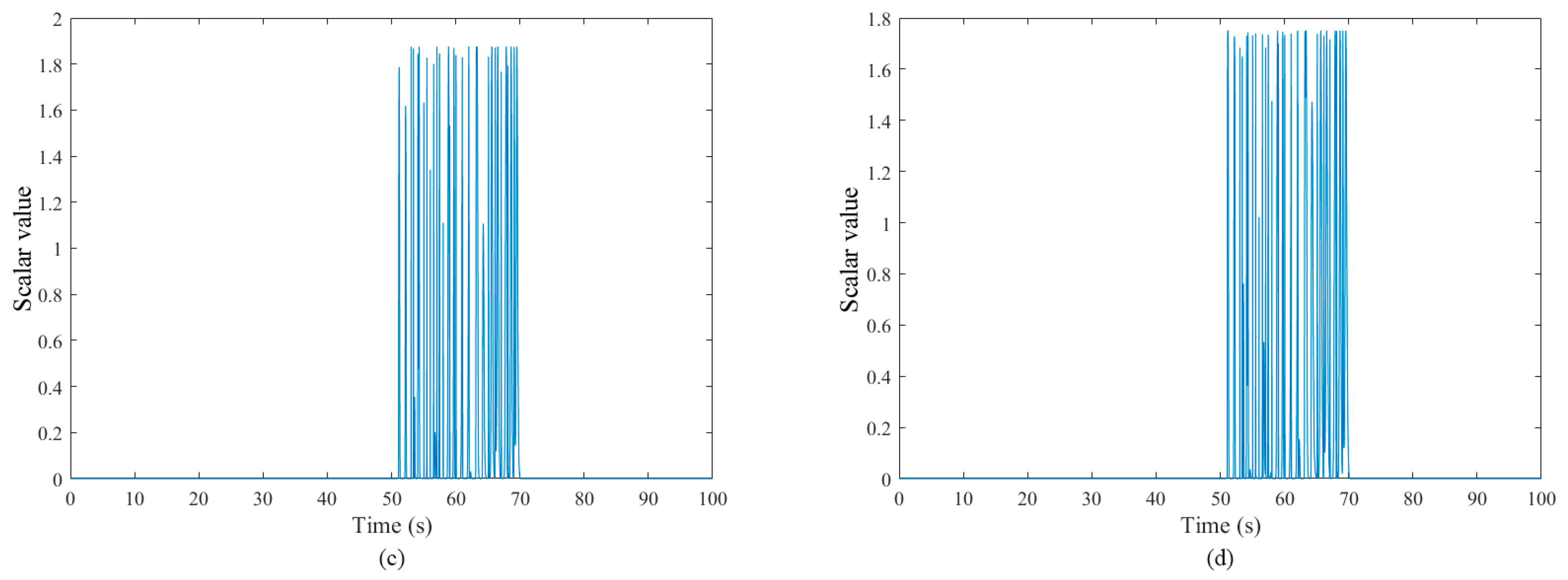
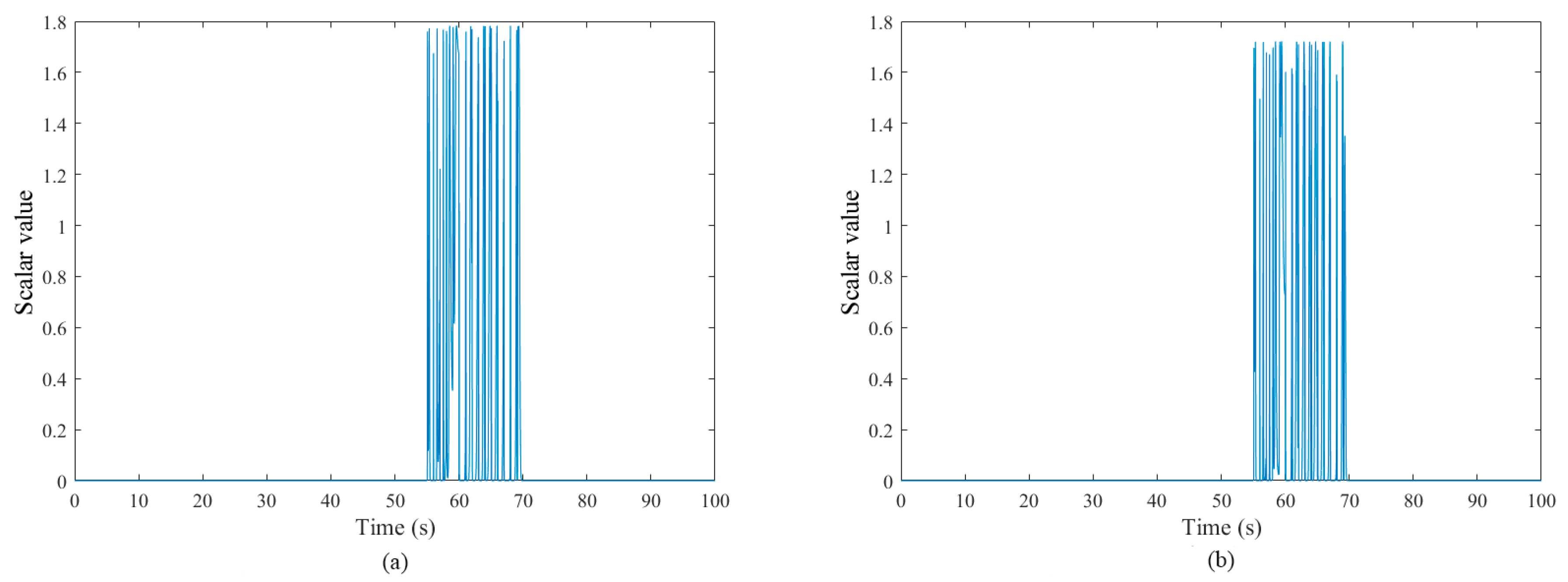
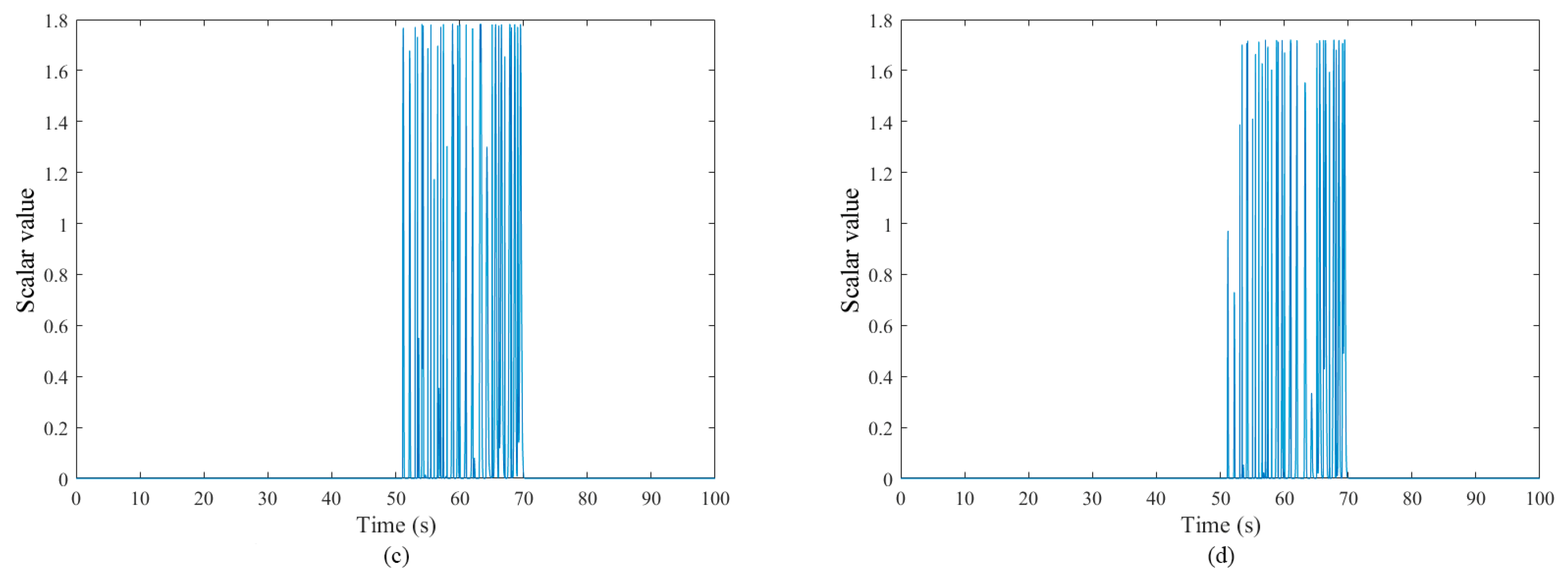
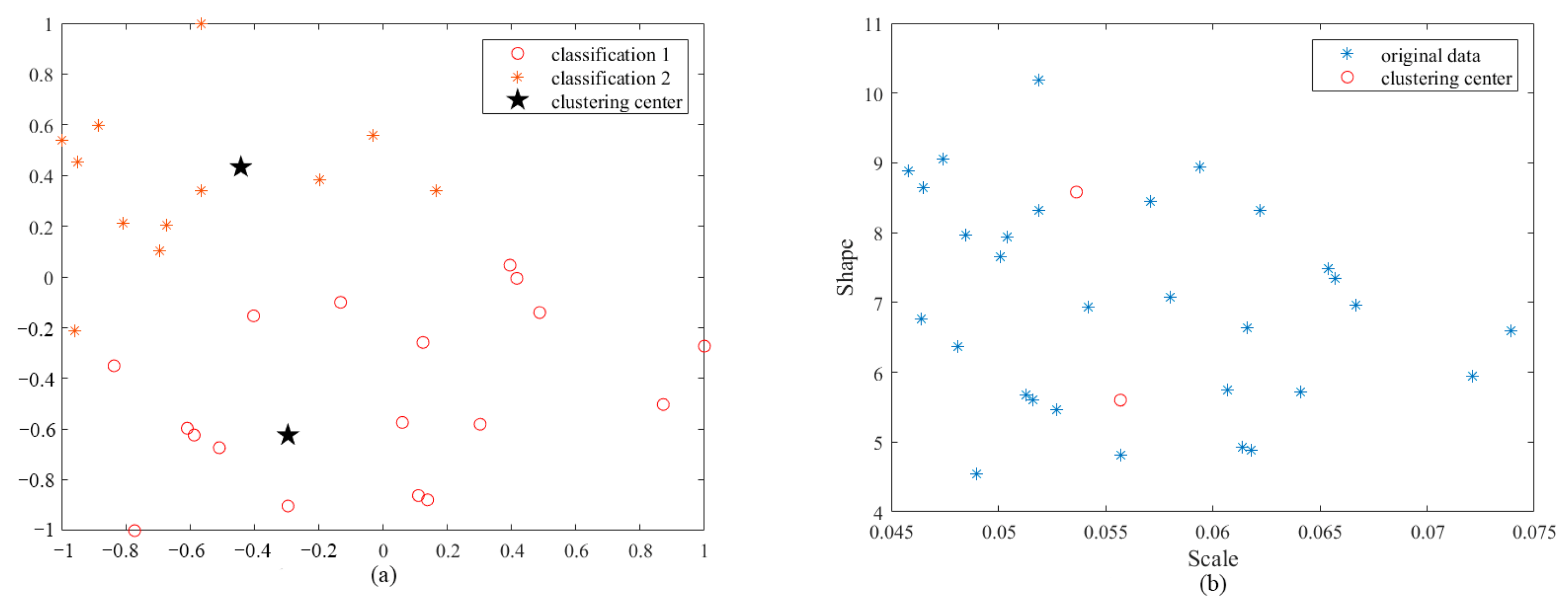



| Distribution Algorithm | Test | Log-Likelihood Value Test |
|---|---|---|
| Gaussian distribution | ||
| Gamma distribution | ||
| Weibull distribution |
| Symbol | Quantity | Value (Unit) |
|---|---|---|
| Viscous friction coefficient of the low-speed shaft | ||
| Viscous friction coefficient of the high-speed shaft | ||
| Moment of inertia of the low-speed shaft | ||
| Moment of inertia of the high-speed shaft | ||
| Torsional damping coefficient of the drive train | ||
| Torsional stiffness of the drive train | ||
| Ratio of the drive train | 95 | |
| Time constant of the first-order system | 0.02 | |
| Pitch actuator model natural frequency | ||
| Pitch actuator model damping ratio | 0.6 | |
| Air density | ||
| Radius of the cross-section of the pitch sweep |
| No. | SOCNN1 | SOCNN2 | SOMNN1 | SOMNN2 | K-mean1 | K-mean2 |
|---|---|---|---|---|---|---|
| 31 | 0.15 s | 1.02 s | 1.04 s | 1.03 s | 1.03 s | 0.16 s |
| 32 | 1.05 s | 1.04 s | 1.06 s | 1.05 s | 1.05 s | 1.04 s |
| 33 | 1.04 s | 0.19 s | 1.04 s | 1.03 s | 1.04 s | 0.21 s |
| 34 | 3.03 s | 3.03 s | 3.02 s | 3.03 s | 3.03 s | 3.02 s |
| 35 | 1.04 s | 0.15 s | 1.04 s | 0.16 s | 1.03 s | 0.16 s |
| 36 | 0.15 s | 0.13 s | 0.17 s | 0.16 s | 0.19 s | 0.14 s |
| 37 | 4.04 s | 4.03 s | 4.04 s | 4.03 s | 4.04 s | 4.03 s |
| 38 | 1.04 s | 0.12 s | 1.04 s | 0.15 s | 1.04 s | 0.21 s |
| 39 | 1.08 s | 0.12 s | 1.08 s | 0.17 s | 1.12 s | 1.09 s |
| 40 | 0.12 s | 0.11 s | 0.14 s | 0.11 s | 0.19 s | 0.16 s |
| 41 | 3.04 s | 3.03 s | 3.04 s | 3.03 s | 3.05 s | 3.05 s |
| 42 | 1.10 s | 1.09 s | 1.16 s | 1.10 s | 1.17 s | 1.12 s |
| 43 | 2.04 s | 2.03 s | 2.04 s | 2.04 s | 2.05 s | 2.04 s |
| 44 | 1.03 s | 0.97 s | 1.03 s | 1.03 s | 1.04 s | 1.02 s |
| 45 | 0.14 s | 0.11 s | 0.14 s | 0.11 s | 0.18 s | 0.16 s |
| 46 | 1.03 s | 1.02 s | 1.02 s | 1.02 s | 1.04 s | 1.03 s |
| 47 | 2.04 s | 2.03 s | 2.04 s | 2.04 s | 2.05 s | 2.04 s |
| 48 | 7.02 s | 7.02 s | 7.02 s | 7.02 s | 7.02 s | 7.02 s |
| 49 | 0.16 s | 0.13 s | 0.15 s | 0.16 s | 0.20 s | 0.17 s |
| 50 | 5.02 s | 5.02 s | 5.01 s | 5.02 s | 5.02 s | 5.03 s |
| FDS Class | Simulation Object | Average FDT (s) |
|---|---|---|
| SOCNN1 | WECS under Fault Case I | 1.30 |
| SOCNN2 | 1.13 | |
| SOMNN1 | 1.35 | |
| SOMNN2 | 1.19 | |
| K-mean1 | 1.36 | |
| K-mean2 | 1.16 | |
| FFT-ISVO * | 2.65 | |
| SVO-DIs * | 3.82 (threshold = 1) | |
| SVO | 4.18 (threshold = 1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, R. An Improved Set-Valued Observer and Probability Density Function-Based Self-Organizing Neural Networks for Early Fault Diagnosis in Wind Energy Conversion Systems. Symmetry 2025, 17, 448. https://doi.org/10.3390/sym17030448
Zhao R. An Improved Set-Valued Observer and Probability Density Function-Based Self-Organizing Neural Networks for Early Fault Diagnosis in Wind Energy Conversion Systems. Symmetry. 2025; 17(3):448. https://doi.org/10.3390/sym17030448
Chicago/Turabian StyleZhao, Ruinan. 2025. "An Improved Set-Valued Observer and Probability Density Function-Based Self-Organizing Neural Networks for Early Fault Diagnosis in Wind Energy Conversion Systems" Symmetry 17, no. 3: 448. https://doi.org/10.3390/sym17030448
APA StyleZhao, R. (2025). An Improved Set-Valued Observer and Probability Density Function-Based Self-Organizing Neural Networks for Early Fault Diagnosis in Wind Energy Conversion Systems. Symmetry, 17(3), 448. https://doi.org/10.3390/sym17030448





