A Hybrid Tree Convolutional Neural Network with Leader-Guided Spiral Optimization for Detecting Symmetric Patterns in Network Anomalies
Abstract
1. Introduction
- We introduced a hierarchical T-CNN architecture that extracts multi-scale features from network traffic. It allows for the detection of slight anomalies that other models may miss. This architecture improves the granularity of features for better detection accuracy.
- We used a deep autoencoder to learn compact, noise-free latent representations of high-dimensional network data, thereby reducing data noise while keeping important patterns for classification and highly boosting the quality of feature representation towards anomaly detection.
- A hybrid optimization technique was developed, which combined the strengths of exploration by the Pelican Optimization Algorithm and exploitation by Particle Swarm Optimization. It enhanced the fine-tuning of system parameters and improved model efficiency. Optimization enhances adaptability across various network scenarios.
- We integrated an ensemble metaclassifier to aggregate predictions from multiple models, which improved robustness. It reduced overfitting and enhanced generalizability, especially in imbalanced datasets. It ensured consistent performance across different anomaly detection tasks.
- We validated the framework on the UNSW-NB15, CIC-IDS 2017, and CIC-IDS 2018 datasets. The comparison analysis indicated better accuracy, precision, recall, and F1-score. This validated the robustness and scalability of the framework in multiple network environments.
2. Related Work
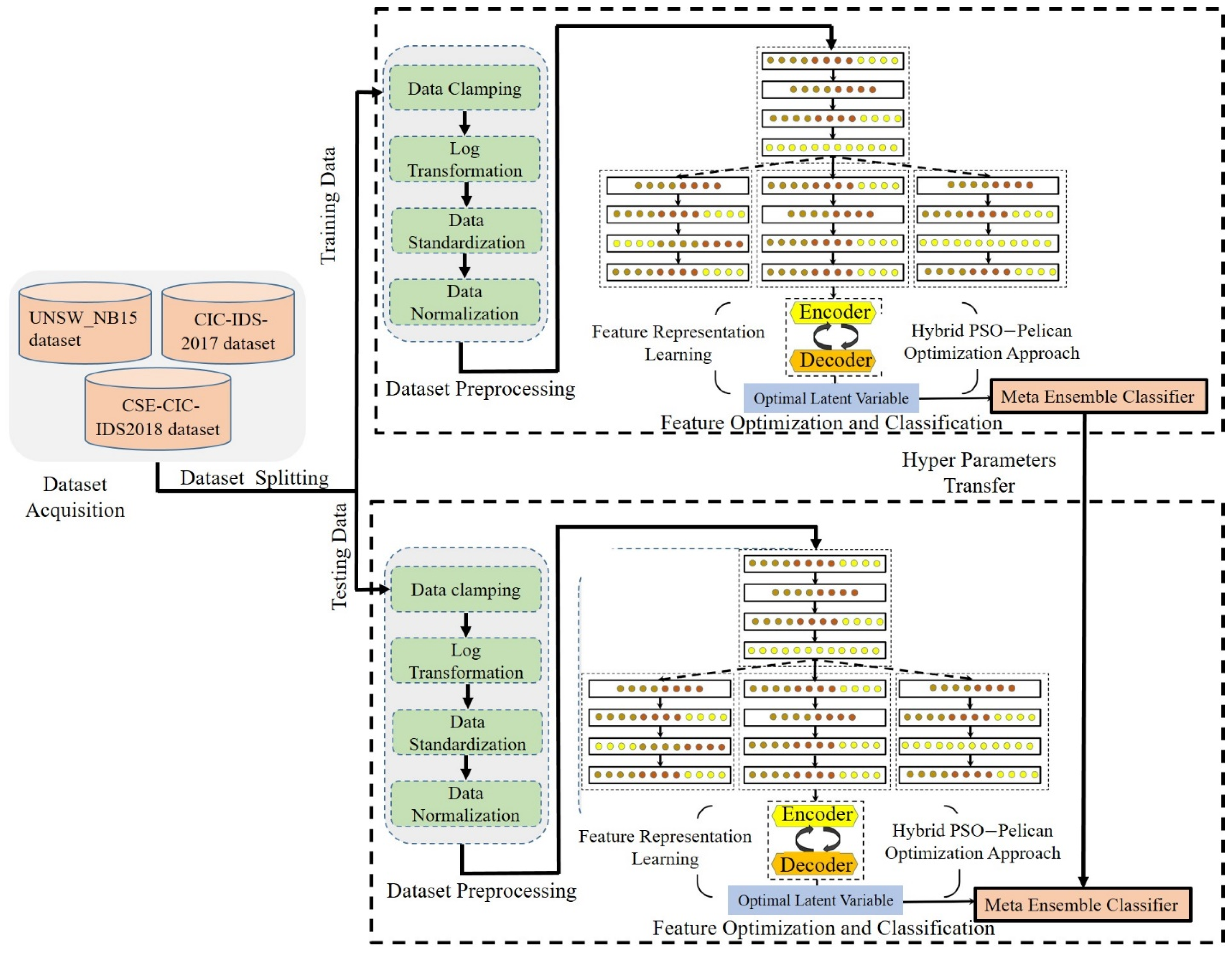
3. Proposed Methodology
3.1. Data Collection
3.1.1. UNSW_NB15 Dataset
3.1.2. CIC-IDS-2017 Dataset
3.2. Data Preprocessing
3.2.1. Data Clamping
- is the maximum value of the feature;
- is the median value of the feature;
- is the 95th percentile value of the feature.
- Check Conditions:
- Condition 1:
- Condition 2:
- 2.
- Clamping Rule:
3.2.2. Log Transformation
3.2.3. Data Standardization
3.2.4. Data Normalization
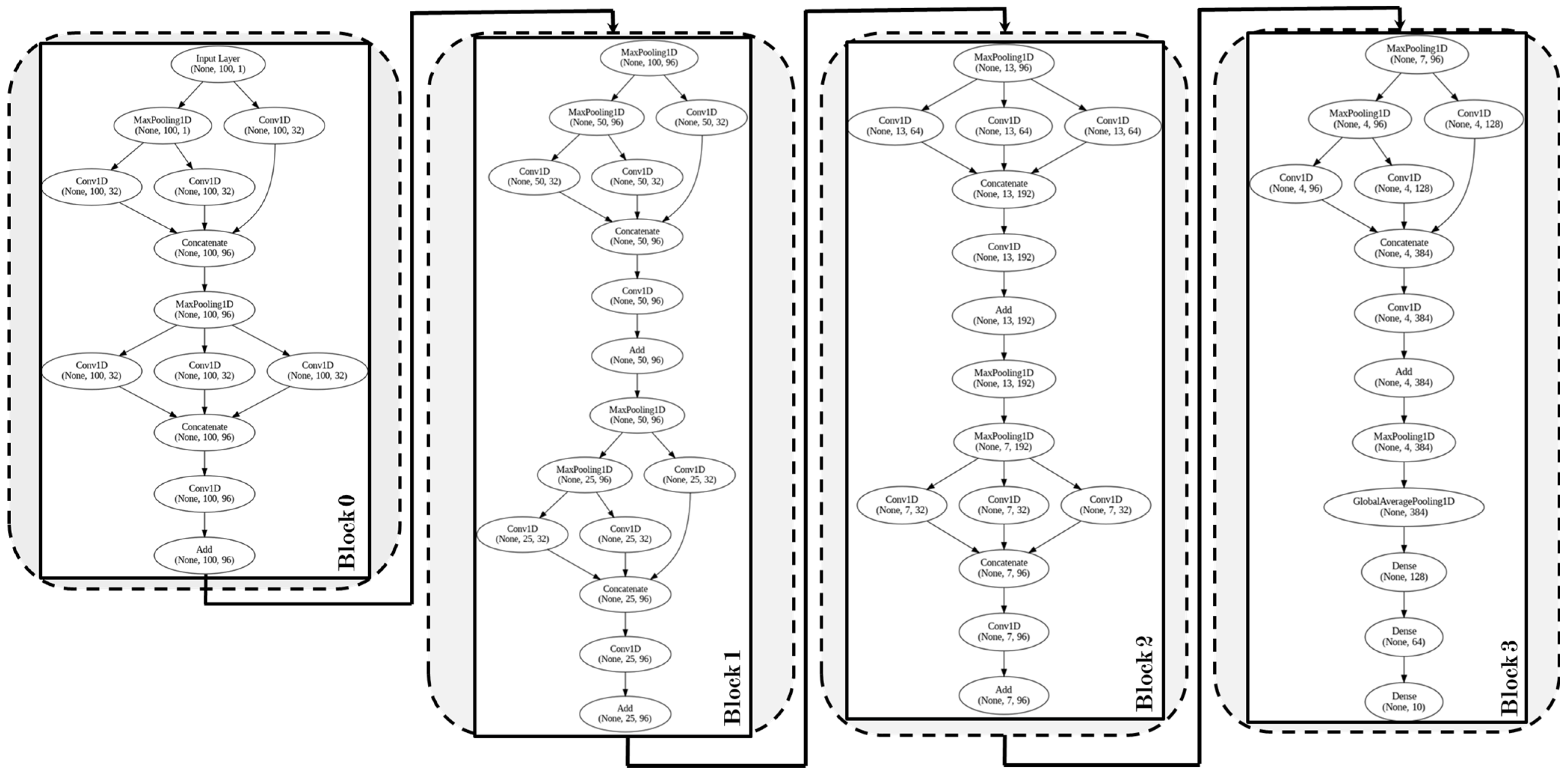
3.3. Hybrid Tree Convolutional Neural Network
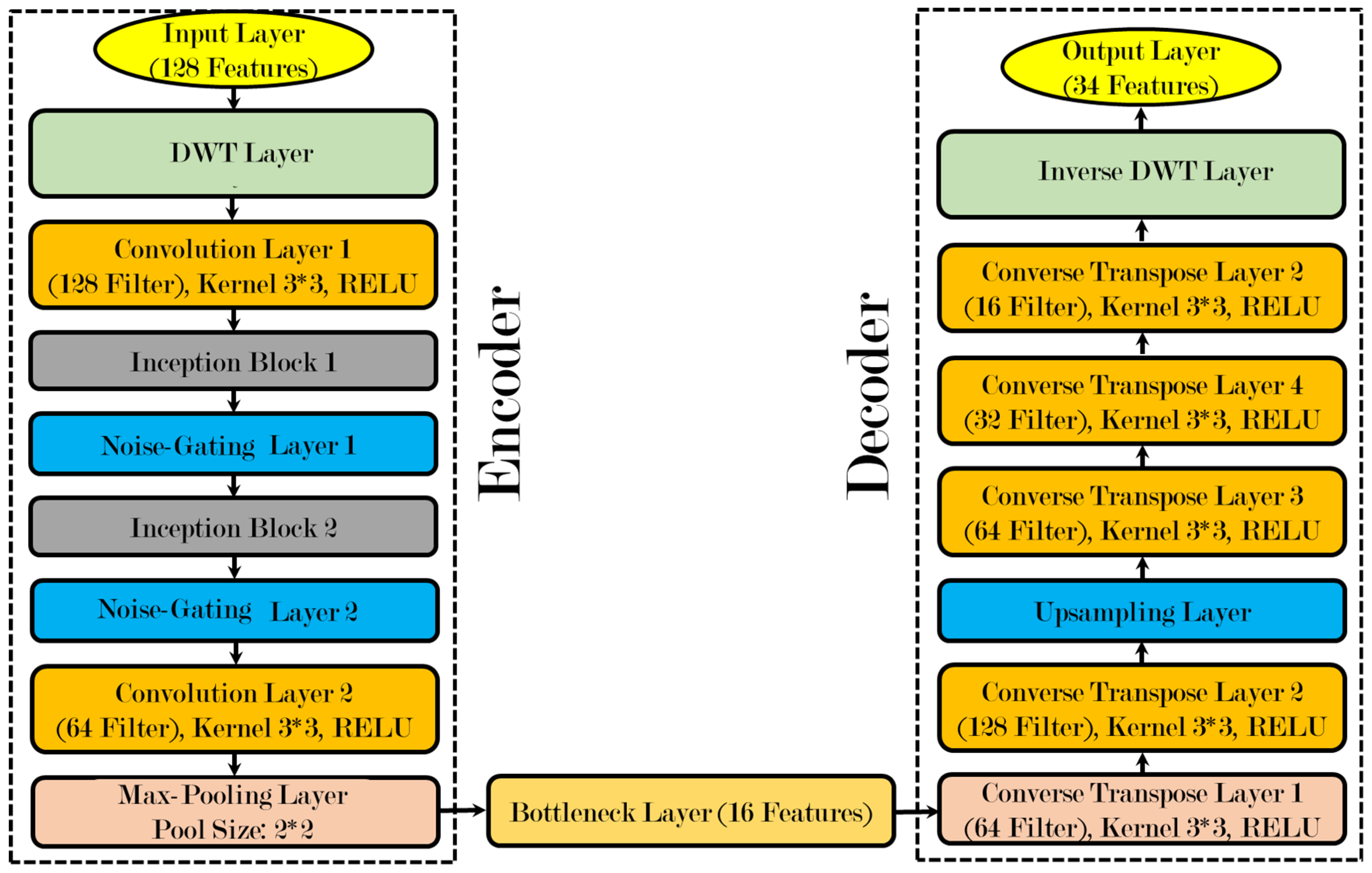
3.4. Variational Wavelet Denoising Autoencoder
3.5. Hyperparameter Tuning Using Leader-Guided Spiral Optimization Scheme
3.5.1. Mathematical Details of PSO
3.5.2. Mathematical Details of POA
Leader-Guided Velocity-Based Spiral Optimization
Fitness Function
| Algorithm 1: Leader-Guided Velocity-Based Spiral Optimization Algorithm |
| Input: population size; maximum number of iterations; , : search space boundaries; ω, c1, c2, γ: PSO and spiral parameters; α, β, θ: spiral movement parameters; k, : sigmoid weight adjustment parameters F(X): Objective function |
| Output: XLeader: Optimal solution (XLeader): Optimal fitness value |
| 1. Initialization: 1.1. Initialize the population positions Xᵢ ∼ U(, X_max), i = 1, 2, …, N. 1.2. Initialize the velocities ∼ U(, ), = 1, 2, …, . 1.3. Evaluate the fitness for all particles. 1.4. Set personal bests = and initialize the leader = . 2. Iterative Optimization: For = 1 to 2.1. Update Weights: and 2.2. For Each Particle i: 2.2.1. Update Velocity: + where 2.2.2. Update Position: 2.2.3. Apply boundary constraints: clip (, , X_max) 2.2.4. Evaluate fitness: F() 2.2.5. Update personal best: F() < F(), then = 2.3. Update Leader: If F() < F(), then = 3. End Iteration 4. Return: , F(X_Leader) |
3.6. Classification Using Meta-Ensemble Classifier
3.6.1. Support Vector Machine
3.6.2. Naïve Bayes
3.6.3. Random Forest
4. Results and Discussion
4.1. Experimental Setup
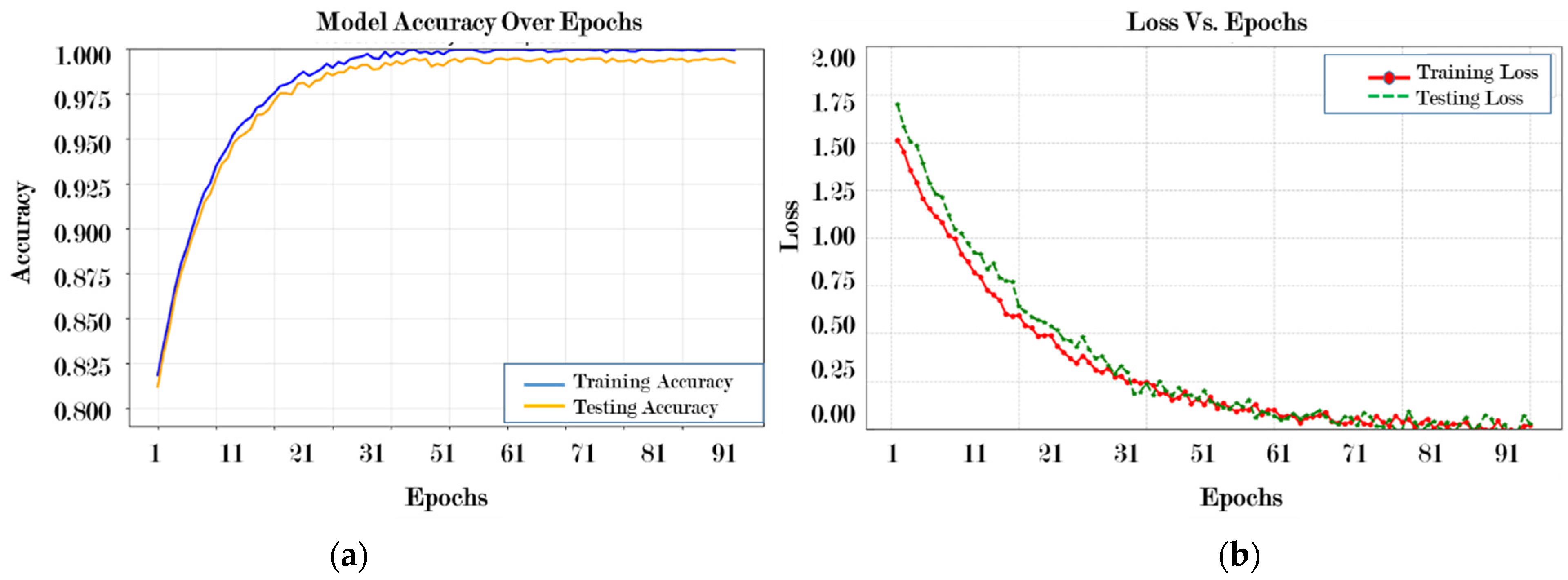
4.2. Model Validation Using Five-Fold Cross-Validation
4.3. Evaluation Matrices
- Classification Accuracy
- 2.
- Precision
- 3.
- Recall sensitivity or true-positive rate
- 4.
- F1-score
- 5.
- Confusion Matrix
4.4. Experimental Results
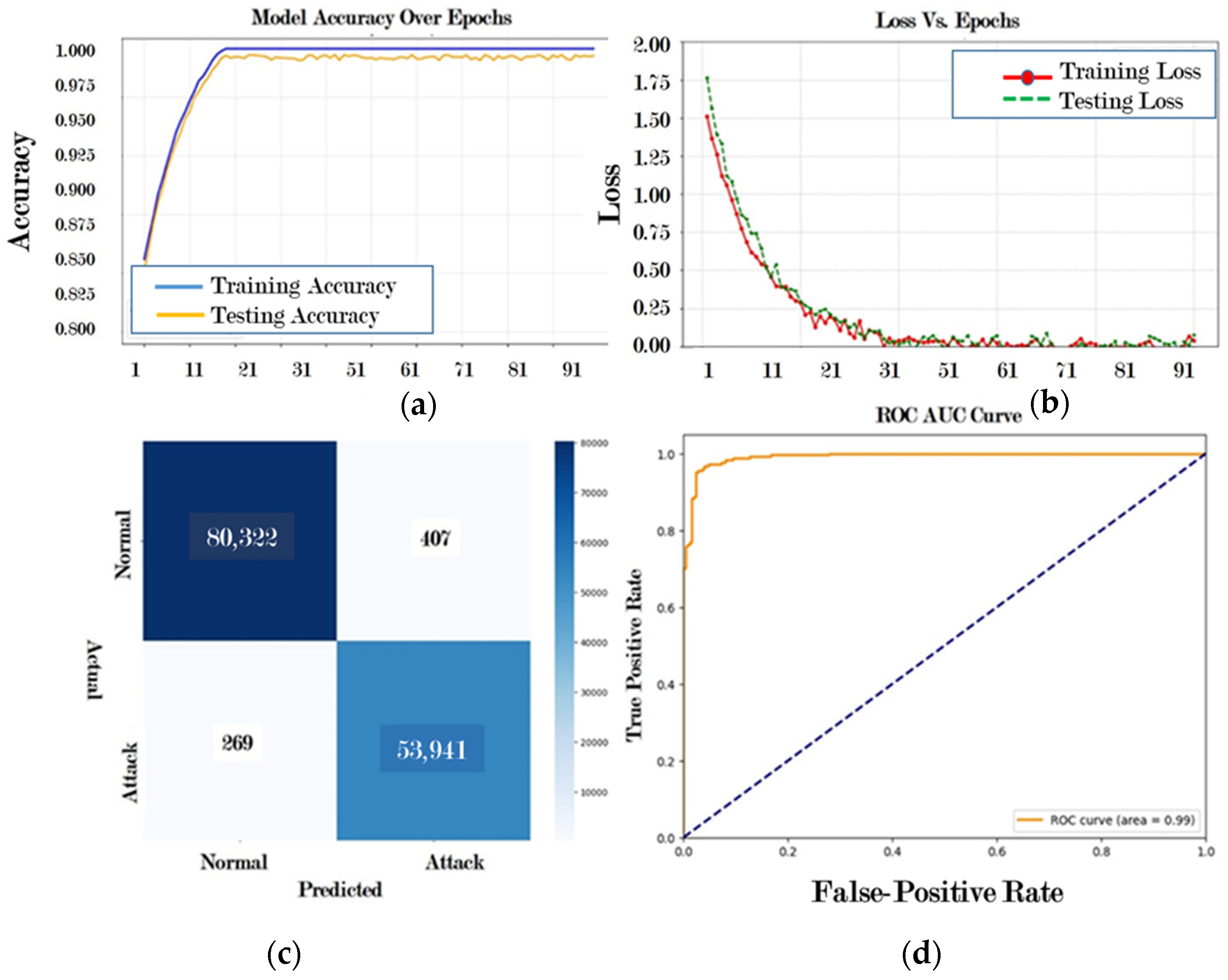
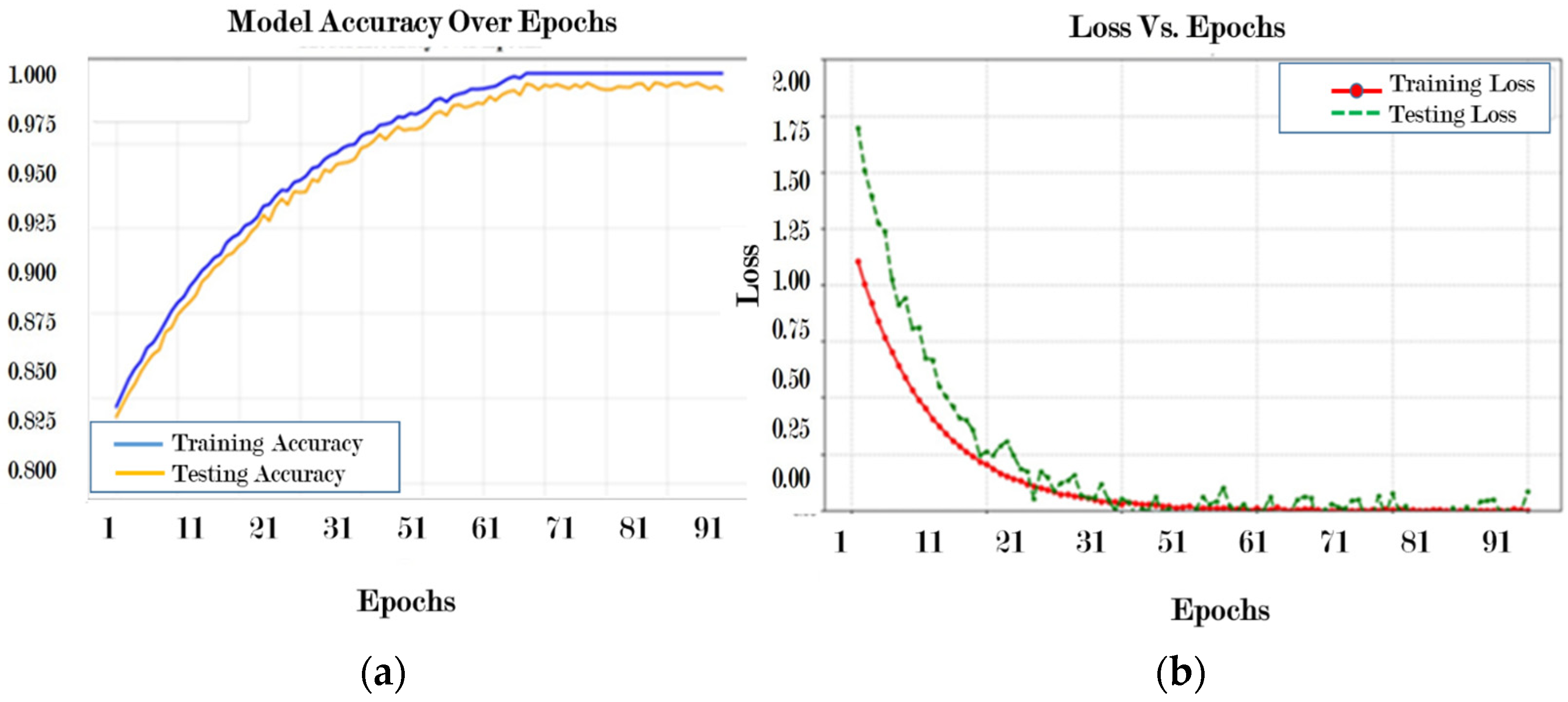
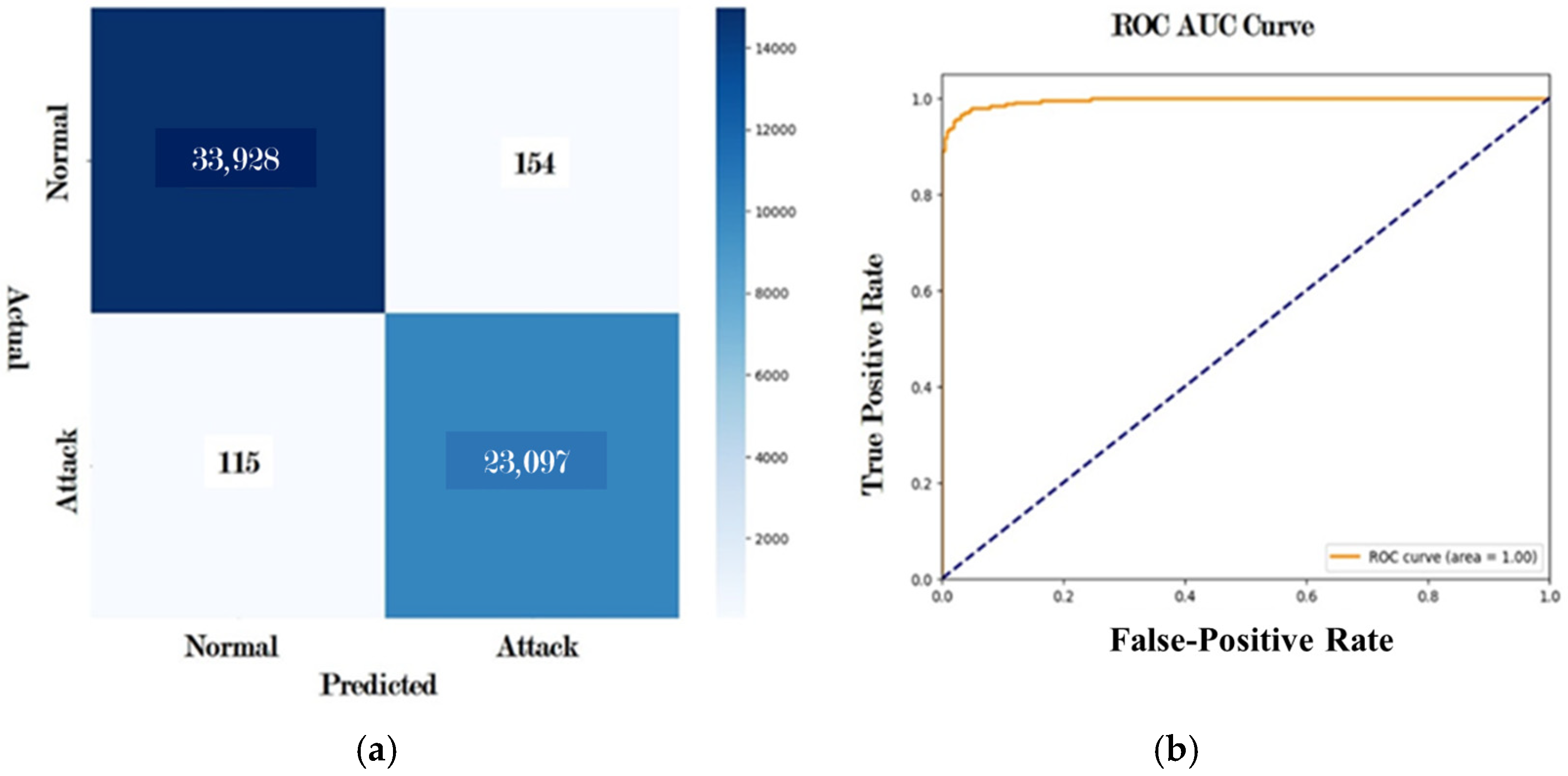
4.4.1. Results for Dataset 1 (UNSW-NB15 Dataset)
4.4.2. Results for Dataset 2 (CIC-IDS -2017 Dataset)
4.4.3. Results for Dataset 3 (CICIDS-2018 Dataset)
4.5. Results Comparison with State-of-the-Art Models
4.5.1. Performance Metrics Comparison
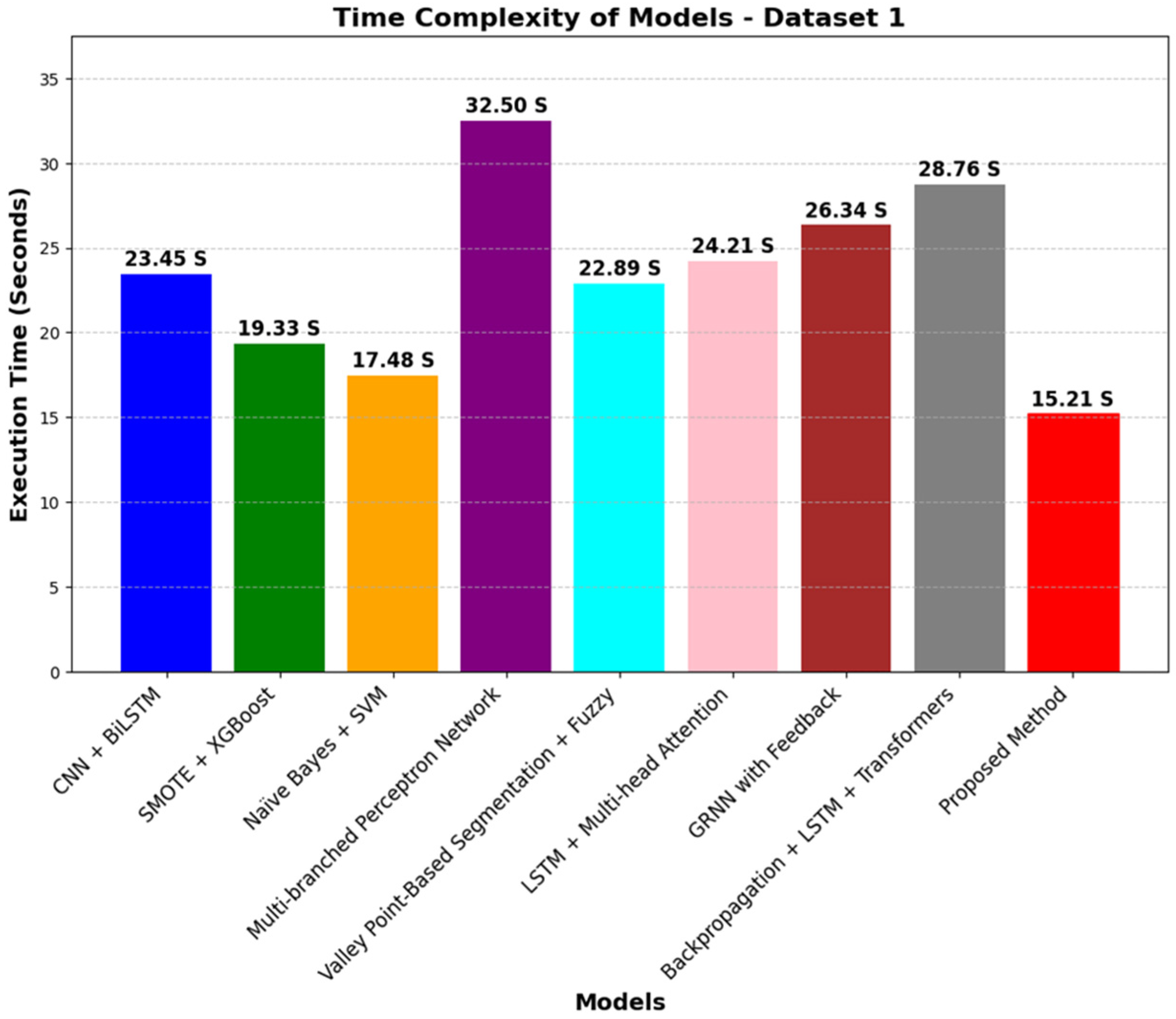
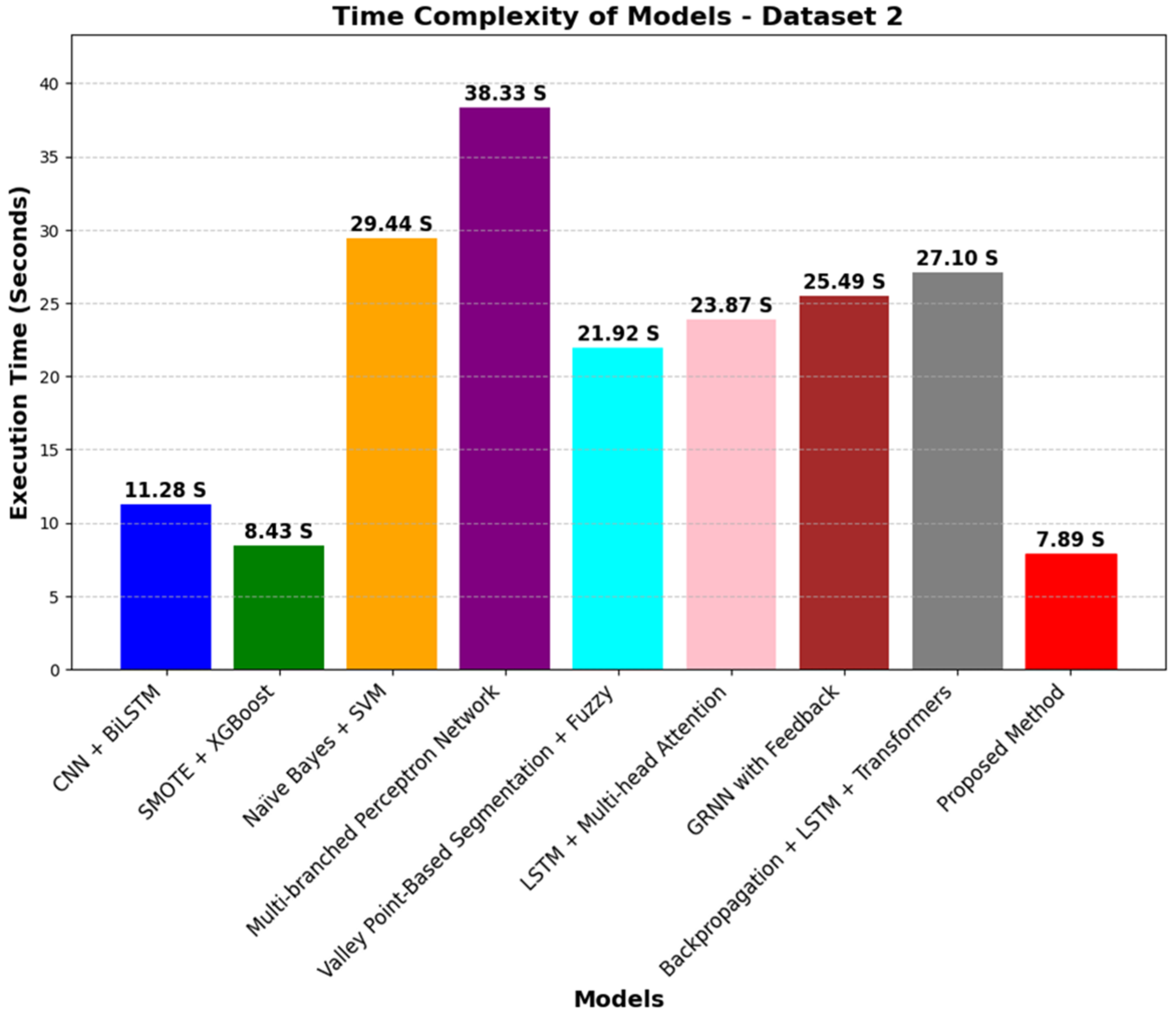
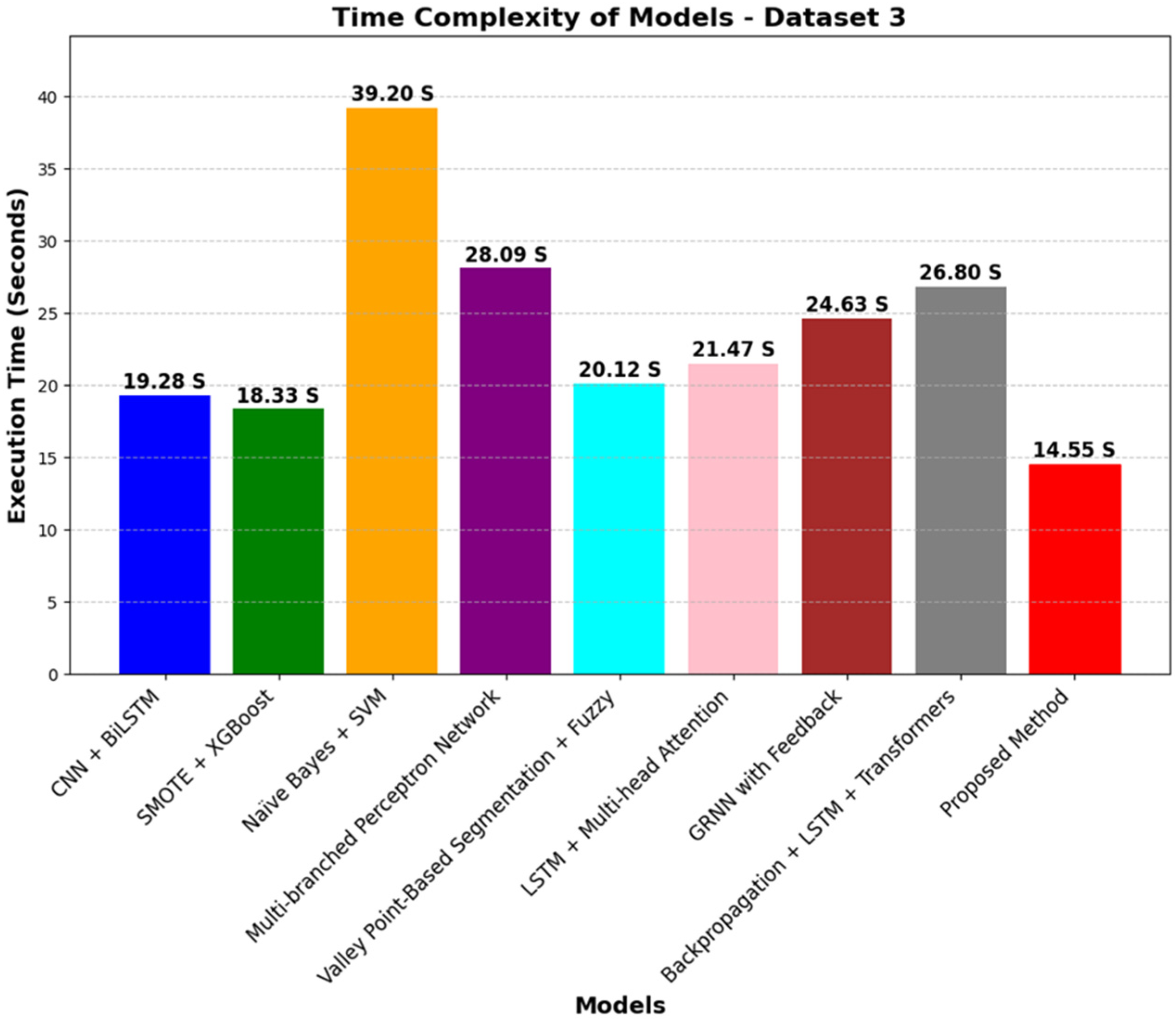
4.5.2. Time Complexity Comparison
4.6. Research Limitations
- The computational demands of the proposed method, though moderate in comparison to the Multibranched Perceptron Network, are still more demanding than simple models such as the Smote + XGBoost and CNN + BiLSTM. Thus, the method requires optimization in terms of reducing execution time without the loss of performance, especially in real-time or resource-constrained applications.
- The performance of the proposed method was tested only on three datasets. Although the used datasets were heterogeneous, wider generalization can be achieved if more datasets are considered with various class imbalances, feature dimensions, and noise levels. This could confirm the robustness of the proposed method under even more challenging and diverse settings.
- This work mainly investigates execution time in terms of time complexity. Execution time analysis gives insight into the efficiency of computation but cannot account for memory consumption, energy consumption, and even scalability to larger datasets. Maybe it would be worthwhile to consider these as well, and thus broaden the understanding of whether the method has any computational feasibility.
- One of the main limitations of the proposed approach is its heavy dependence on hyperparameters. Performance depends on the appropriate tuning of many hyperparameters related to learning rates, optimization algorithms, and even architectural configurations. These hyperparameters do improve a model’s capability to adapt better to different datasets; however, at the same time, they raise the complexity associated with training this process and would possibly demand large computing resources for hyperparameter fine-tuning. It also limits the ease of deployment for the method since suboptimal hyperparameter settings can lead to significant performance degradation.
- Although the proposed method performs well, the architecture may still need further innovations, such as lightweight components, pruning techniques, or adaptive mechanisms that dynamically adjust the computational effort depending on the complexity of the dataset. These will help improve its applicability in dynamic and real-world environments.
4.7. Research Implications
5. Conclusions and Future Scope
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Djenna, A.; Harous, S.; Saidouni, D.E. Internet of things meet internet of threats: New concern cyber security issues of critical cyber infrastructure. Appl. Sci. 2021, 11, 4580. [Google Scholar] [CrossRef]
- Ani, U.P.D.; He, H.; Tiwari, A. Review of cybersecurity issues in industrial critical infrastructure: Manufacturing in perspective. J. Cyber Secur. Technol. 2017, 1, 32–74. [Google Scholar] [CrossRef]
- Shroff, J.; Walambe, R.; Singh, S.K.; Kotecha, K. Enhanced security against volumetric DDoS attacks using adversarial machine learning. Wirel. Commun. Mob. Comput. 2022, 2022, 5757164. [Google Scholar] [CrossRef]
- Hassan, A.I.; El Reheem, E.A.; Guirguis, S.K. An entropy and machine learning based approach for DDoS attacks detection in software defined networks. Sci. Rep. 2024, 14, 18159. [Google Scholar] [CrossRef]
- Tang, K.H.; Ghanem, M.C.; Vassilev, V.; Ouazzane, K.; Gasiorowski, P. Synchronization, Optimization, and Adaptation of Machine Learning Techniques for Computer Vision in Cyber-Physical Systems: A Comprehensive Analysis. Preprints 2025, 2025010521. [Google Scholar] [CrossRef]
- Al-Khayyat, A.T.K.; Ucan, O.N. A Multi-Branched Hybrid Perceptron Network for DDoS Attack Detection Using Dynamic Feature Adaptation and Multi-Instance Learning. IEEE Access 2024, 12, 192618–192638. [Google Scholar] [CrossRef]
- Malliga, S.; Nandhini, P.S.; Kogilavani, S.V. A comprehensive review of deep learning techniques for the detection of (distributed) denial of service attacks. Inf. Technol. Control 2022, 51, 180–215. [Google Scholar] [CrossRef]
- Gwassi, O.A.H.; Uçan, O.N.; Navarro, E.A. Cyber-XAI-Block: An end-to-end cyber threat detection & fl-based risk assessment framework for iot enabled smart organization using xai and blockchain technologies. Multimed. Tools Appl. 2024, 1–42. [Google Scholar] [CrossRef]
- Alotaibi, A.; Rassam, M.A. Adversarial machine learning attacks against intrusion detection systems: A survey on strategies and defense. Future Internet 2023, 15, 62. [Google Scholar] [CrossRef]
- Yin, D.; Zhang, L.; Yang, K. A DDoS attack detection and mitigation with software-defined Internet of Things framework. IEEE Access 2018, 6, 24694–24705. [Google Scholar] [CrossRef]
- Khatri, A.; Khatri, R. DDoS Attack Detection Using Artificial Neural Network on IoT Devices in a Simulated Environment. In International Conference on IoT, Intelligent Computing and Security: Select Proceedings of IICS 2021; Springer Nature: Singapore, 2023; pp. 221–233. [Google Scholar]
- Parmar, A.; Lamkuche, H. Distributed Denial of Service Attack Detection Using Sequence-To-Sequence LSTM. In Proceedings of the International Conference on Global Economic Revolutions, Sharjah, United Arab Emirates, 27–28 February 2023; Springer Nature: Cham, Switzerland, 2023; pp. 39–53. [Google Scholar]
- Wang, J.; Wang, L.; Wang, R. A Method of DDoS Attack Detection and Mitigation for the Comprehensive Coordinated Protection of SDN Controllers. Entropy 2023, 25, 1210. [Google Scholar] [CrossRef]
- Bala, B.; Behal, S. AI techniques for IoT-based DDoS attack detection: Taxonomies, comprehensive review and research challenges. Comput. Sci. Rev. 2024, 52, 100631. [Google Scholar] [CrossRef]
- Hnamte, V.; Najar, A.A.; Nhung-Nguyen, H.; Hussain, J.; Sugali, M.N. DDoS attack detection and mitigation using deep neural network in SDN environment. Comput. Secur. 2024, 138, 103661. [Google Scholar] [CrossRef]
- Anley, M.B.; Genovese, A.; Agostinello, D.; Piuri, V. Robust DDoS attack detection with adaptive transfer learning. Comput. Secur. 2024, 144, 103962. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Y.; Zhang, Q.; Zheng, X. CNN-AttBiLSTM Mechanism: A DDoS Attack Detection Method Based on Attention Mechanism and CNN-BiLSTM. IEEE Access 2023, 11, 136308–136317. [Google Scholar] [CrossRef]
- Presekal, A.; Ştefanov, A.; Semertzis, I.; Palensky, P. Spatio-Temporal Advanced Persistent Threat Detection and Correlation for Cyber-Physical Power Systems using Enhanced GC-LSTM. IEEE Trans. Smart Grid 2024, 16, 1654–1666. [Google Scholar] [CrossRef]
- Aktar, S.; Nur, A.Y. Robust Anomaly Detection in IoT Networks using Deep SVDD and Contractive Autoencoder. In Proceedings of the 2024 IEEE International Systems Conference (SysCon), Montreal, QC, Canada, 15–18 April 2024; IEEE: New York, NY, USA, 2024; pp. 1–8. [Google Scholar]
- Jiyad, Z.M.; Al Maruf, A.; Haque, M.M.; Gupta, M.S.; Ahad, A.; Aung, Z. DDoS Attack Classification Leveraging Data Balancing and Hyperparameter Tuning Approach Using Ensemble Machine Learning with XAI. In Proceedings of the 2024 Third International Conference on Power, Control and Computing Technologies (ICPC2T), Raipur, India, 18–20 January 2024; IEEE: New York, NY, USA, 2024; pp. 569–575. [Google Scholar]
- Qaddos, A.; Yaseen, M.U.; Al-Shamayleh, A.S.; Imran, M.; Akhunzada, A.; Alharthi, S.Z. A novel intrusion detection framework for optimizing IoT security. Sci. Rep. 2024, 14, 21789. [Google Scholar] [CrossRef]
- Sajid, M.; Malik, K.R.; Almogren, A.; Malik, T.S.; Khan, A.H.; Tanveer, J.; Rehman, A.U. Enhancing intrusion detection: A hybrid machine and deep learning approach. J. Cloud Comput. 2024, 13, 123. [Google Scholar] [CrossRef]
- Ye, Z.; Luo, J.; Zhou, W.; Wang, M.; He, Q. An ensemble framework with improved hybrid breeding optimization-based feature selection for intrusion detection. Future Gener. Comput. Syst. 2024, 151, 124–136. [Google Scholar] [CrossRef]
- Kumar, G.S.C.; Kumar, R.K.; Kumar, K.P.V.; Sai, N.R.; Brahmaiah, M. Deep residual convolutional neural network: An efficient technique for intrusion detection system. Expert Syst. Appl. 2024, 238, 121912. [Google Scholar] [CrossRef]
- Moustafa, N.; Slay, J. UNSW-NB15: A comprehensive data set for network intrusion detection systems (UNSW-NB15 network data set). In Proceedings of the 2015 Military Communications and Information Systems Conference (MilCIS), Canberra, ACT, Australia, 10–12 November 2015; IEEE: New York, NY, USA, 2015; pp. 1–6. [Google Scholar]
- Sharafaldin, I.; Lashkari, A.H.; Ghorbani, A.A. Toward generating a new intrusion detection dataset and intrusion traffic characterization. ICISSp 2018, 1, 108–116. [Google Scholar]
- Leevy, J.L.; Khoshgoftaar, T.M. A survey and analysis of intrusion detection models based on CSE-CIC-IDS2018 big data. J. Big Data 2020, 7, 104. [Google Scholar] [CrossRef]
- Duan, B. The Robustness of Trimming and Winsorization When the Population Distribution Is Skewed. Ph.D. Dissertation, Tulane University, New Orleans, LA, USA, 1998. [Google Scholar]
- Feng, C.; Wang, H.; Lu, N.; Chen, T.; He, H.; Lu, Y.; Tu, X.M. Log-transformation and its implications for data analysis. Shanghai Arch. Psychiatry 2014, 26, 105. [Google Scholar] [PubMed]
- Shanker, M.; Hu, M.Y.; Hung, M.S. Effect of data standardization on neural network training. Omega 1996, 24, 385–397. [Google Scholar] [CrossRef]
- Patro, S.G.; Sahu, K.K. Normalization: A preprocessing stage. arXiv 2015, arXiv:1503.06462. [Google Scholar] [CrossRef]
- Biswas, B.; Ghosh, S.K.; Ghosh, A. DVAE: Deep variational auto-encoders for denoising retinal fundus image. In Hybrid Machine Intelligence for Medical Image Analysis; Springer Nature: Cham, Switzerland, 2020; pp. 257–273. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; IEEE: New York, NY, USA, 1999; Volume 3, pp. 1945–1950. [Google Scholar]
- Trojovský, P.; Dehghani, M. Pelican optimization algorithm: A novel nature-inspired algorithm for engineering applications. Sensors 2022, 22, 855. [Google Scholar] [CrossRef]
- Taşcı, E. A meta-ensemble classifier approach: Random rotation forest. Balkan J. Electr. Comput. Eng. 2019, 7, 182–187. [Google Scholar] [CrossRef]
- Joachims, T. SVMlight: Support vector machine. SVM-Light Support Vector Mach. 1999, 19, 25. [Google Scholar]
- Wickramasinghe, I.; Kalutarage, H. Naive Bayes: Applications, variations and vulnerabilities: A review of literature with code snippets for implementation. Soft Comput. 2021, 25, 2277–2293. [Google Scholar] [CrossRef]
- Salman, H.A.; Kalakech, A.; Steiti, A. Random forest algorithm overview. Babylonian J. Mach. Learn. 2024, 2024, 69–79. [Google Scholar] [CrossRef]
- Yadav, S.; Shukla, S. Analysis of k-fold cross-validation over hold-out validation on colossal datasets for quality classification. In Proceedings of the 2016 IEEE 6th International Conference on Advanced Computing (IACC), Bhimavaram, India, 27–28 February 2016; IEEE: New York, NY, USA, 2016; pp. 78–83. [Google Scholar]
- Susmaga, R. Confusion Matrix Visualization. In Intelligent Information Processing and Web Mining: Proceedings of the International IIS: IIPWM ‘04 Conference Held in Zakopane, Poland, 17–20 May 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 107–116. [Google Scholar]
- Buckland, M.; Gey, F. The relationship between recall and precision. J. Am. Soc. Inf. Sci. 1994, 45, 12–19. [Google Scholar] [CrossRef]
- Zhang, R.; Zhan, J.; Ding, W.; Pedrycz, W. Time series fore casting based on improved multi-linear trend fuzzy information granules for convolutional neural networks. IEEE Trans. Fuzzy Syst. 2024, 33, 1009–1023. [Google Scholar] [CrossRef]
- Gu, J.; Lu, S. An effective intrusion detection approach using SVM with naïve Bayes feature embedding. Comput. Secur. 2021, 103, 102158. [Google Scholar] [CrossRef]
- Wu, X.; Zhan, J.; Ding, W.; Pedrycz, W. GRNN Model with Feedback Mechanism Incorporating kkk-Nearest Neighbor and Modified Gray Wolf Optimization Algorithm in Intelligent Transportation. IEEE Trans. Intell. Transp. Syst. 2024, 26, 3855–3872. [Google Scholar] [CrossRef]
- Talukder, M.A.; Islam, M.M.; Uddin, M.A.; Hasan, K.F.; Sharmin, S.; Alyami, S.A.; Moni, M.A. Machine learning-based network intrusion detection for big and imbalanced data using oversampling, stacking feature embedding and feature extraction. J. Big Data 2024, 11, 33. [Google Scholar] [CrossRef]
- Cai, M.; Zhan, J.; Zhang, C.; Liu, Q. Fusion k-means clustering and multi-head self-attention mechanism for a multivariate time prediction model with feature selection. Int. J. Mach. Learn. Cybern. 2024, 1–19. [Google Scholar] [CrossRef]
- Zhu, C.; Ma, X.; D’Urso, P.; Qian, Y.; Ding, W.; Zhan, J. Long-term multivariate time series forecasting model based on Gaussian fuzzy information granules. IEEE Trans. Fuzzy Syst. 2024, 263, 125705. [Google Scholar] [CrossRef]
- Zhan, J.; Cai, M. A cost-minimized two-stage three-way dynamic consensus mechanism for social network-large scale group decision-making: Utilizing K-nearest neighbors for incomplete fuzzy preference relations. Expert Syst. Appl. 2025, 263, 125705. [Google Scholar] [CrossRef]


| Index | Reference | Limitations Addressed | Proposed Methodology | Limitation |
|---|---|---|---|---|
| 1 | Yin et al. (2018) [10] | Lack of scalability in low-resource environments | DDoS detection in IoT using cosine similarity | Unsuitable for low-resource environments |
| 2 | Khatri et al. (2023) [11] | Poor performance on real cloud traffic | ANN-based DDoS detection in cloud environments | Struggles with dynamic cloud traffic |
| 3 | Parmar et al. (2023) [12] | Complexity of metric used for anomaly classification | Sequential autoencoder for anomaly detection | Complex metric limits distinction between benign and DDoS traffic |
| 4 | Wang et al. (2023) [13] | Limited to specific attack types, lacking generalizability to new patterns | Multi-scale CNN for multilevel DDoS detection | Limited novelty |
| 5 | Bala and Bahal (2024) [14] | Analysis of multiclass DDoS classification in IoT | Systematic review of AI-based IoT DDoS approaches | Limited studies involved |
| 6 | Hnamte et al. (2024) [15] | Applicability and scalability of DDoS detection on real-world datasets | Scalable DNN framework for analyzing network traffic | High applicability but needs testing in other real-world datasets |
| 7 | Anley et al. (2024) [16] | Limited to binary and multi-label DDoS classification | Customized CNN and pre-trained architectures for DDoS detection | Limited to specific types of classification tasks |
| 8 | Zhao et al. (2023) [17] | Struggles with scaling data size and learning novel attack patterns | CNN–Bidirectional LSTM to preserve spatial and temporal data characteristics | Issues with large data sizes and new attack paradigms |
| 9 | Presekal et al. (2023) [18] | Limited performance comparison across other architectures | Hybrid GC-LSTM and deep CNN for time-series-based anomaly detection | Lacked robustness across diverse datasets |
| 10 | Aktar and Nur (2024) [19] | No dynamic adaptation to evolving attack patterns | Contractive autoencoder-based anomaly detection | Performance limited to specific datasets |
| 11 | Jiyad et al. (2024) [20] | Limited generalization for unknown attack categories | Synthetic oversampling with ensemble learning | Poor performance to unknown attacks |
| 12 | Qaddos et al. (2024) [21] | Hybrid CNN-GRU model combined with FW-SMOTE to address imbalanced datasets. | IoTID20 and UNSW-NB15 | Achieved 99.60% accuracy on IoTID20 and 99.16% accuracy on UNSW-NB15. |
| 13 | Sajid et al. (2024) [22] | Integrated XGBoost and CNN for feature extraction, combined with LSTM for classification. | CIC IDS 2017, UNSW-NB15, NSL KDD, and WSN-DS | Achieved binary and multiclass classification with optimized feature spaces |
| 14 | Ye et al. (2024) [23] | Enhanced HBO-based feature selection with Levy flight and Elite (LE) opposition-based learning strategies. | CEC2021, UCI, NSL-KDD, WUSTL-IIOT, and HAI | Improved feature selection for intrusion detection |
| 15 | Kumar et al. (2024) [24] | Authors implemented Deep Residual Convolutional Neural Network and Improved Gazelle Optimization Algorithm to improve local search ability of anomaly detection process and improve accuracy. | UNSW-NB-15, Cicddos2019, and CIC-IDS-2017 datasets | Parameter-sensitive model; scope of maximizing accuracy levels on both datasets. |
| Dataset | Label | Training Set | Validation Set |
|---|---|---|---|
| UNSW_NB15 dataset | Normal Attack | 175,341 | 82,332 |
| CIC-IDS-2017 dataset | Normal Attack | 248,073 | 62,018 |
| CSE-CIC-IDS2018 dataset | Normal Attack | 2,117,553 | 529,388 |
| Component | Parameters | Search Space | Optimal Value |
|---|---|---|---|
| Block 0 | Number of Conv1D Layers | 1–3 | 2 |
| Filter Sizes | 16, 32, 64 | 32 | |
| Kernel Size | 3, 5, 7 | 5 | |
| Stride | 1, 2 | 1 | |
| Padding | Valid, Same | Same | |
| Pooling Size | 2, 3 | 2 | |
| Activation Function | ReLU, Sigmoid, Tanh | ReLU | |
| Concatenation Layer | Enabled/Disabled | Enabled | |
| Dropout Rate | 0.1, 0.2, 0.3 | 0.2 | |
| Block 1 | Number of Conv1D Layers | 2–4 | 3 |
| Filter Sizes | 32, 64, 128 | 64 | |
| Kernel Size | 3, 5, 7 | 5 | |
| Stride | 1, 2 | 1 | |
| Residual Connections | Enabled/Disabled | Enabled | |
| Pooling Size | 2, 3 | 2 | |
| Batch Normalization | Enabled/Disabled | Enabled | |
| Dropout Rate | 0.2, 0.3, 0.4 | 0.3 | |
| General Settings | Learning Rate | 0.001, 0.01, 0.1 | 0.001 |
| Optimizer | SGD, Adam, RMSprop | Adam | |
| Batch Size | 64, 128, 256 | 64 | |
| Epochs | 50, 100, 150 | 100 | |
| Weight Initialization | Random, Xavier, He | Xavier |
| Layer Type | Hyperparameters | Values |
|---|---|---|
| Input Layer | Number of Features | 128 |
| DWT Wavelet Transformation Layer | Transformation Type | Discrete Wavelet Transform (DWT) |
| Convolution Layer 1 | Number of Filters | 128 |
| Kernel Size | 3 × 3 | |
| Activation Function | ReLU | |
| Inception Block 1 and 2 | Number of Filters (Per Branch) | Various (e.g., 16, 32, 64) |
| Kernel Sizes | 1 × 1, 3 × 3, 5 × 5 | |
| Pooling Layer | Type | Max Pooling |
| Noise-Gating Layers 1 and 2 | Gating Mechanism | Threshold-Based Gating or Learned Gating |
| Convolution Layer 2 | Number of Filters | 64 |
| Kernel Size | 3 × 3 | |
| Activation Function | ReLU | |
| Max-Pooling Layer | Pool Size | 2 × 2 |
| Bottleneck Layer | Number of Features | 16 |
| Converse Transpose Layer 1–4 | Number of Filters | 16, 32, 64, 128 |
| Kernel Size | 3 × 3 | |
| Activation Function | ReLU | |
| Upsampling Layer | Upsampling Factor | 2 × 2 |
| Inverse DWT Wavelet Layer | Transformation Type | Inverse Discrete Wavelet Transform (IDWT) |
| Output Layer | Number of Features | 34 |
| Experiment | Precision | Recall | F-Score | Accuracy |
|---|---|---|---|---|
| Ali and Osman (2024) [6] (Multibranched Hybrid Perceptron architecture with Dynamic Feature Adaption) | 0.9549 | 0.8541 | 0.9021 | 95.49 |
| Hnamte and Hussian (2024) [15] (CNN and LSTM approach) | 0.8491 | 0.7809 | 0.8136 | 82.19% |
| Gu and Lu (2021) [43] (Naïve Bayes features with SVM) | 0.8170 | 0.8023 | 0.8096 | 79.04 |
| Wu et al. (2024) [44] Regression Neural Network (GRNN) with a Feedback Mechanism | 0.8802 | 0.8644 | 0.8722 | 90.28% |
| Talukder et al. (2024) [45] (SMOTE with XGBoost) | 0.8821 | 0.8153 | 0.8473 | 87.70 |
| Cai et al. (2024) [46] LSTM with a multi-head attention mechanism | 0.8818 | 0.9204 | 0.9007 | 96.18% |
| Zhu et al. (2024) [47] Backpropagation, LSTM, and Transformer networks | 0.9254 | 0.8246 | 0.8721 | 87.42% |
| Proposed Approach | 0.9768 | 0.9853 | 0.9785 | 99.88% |
| Algorithm | Precision | Recall | F-Score | Accuracy |
|---|---|---|---|---|
| Ali and Osman (2024) [6] (Multibranched Hybrid Perceptron architecture with Dynamic Feature Adaption) | 0.9021 | 0.9274 | 0.9154 | 95.49 |
| Hnamte and Hussian (2024) [15] (CNN and LSTM approach) | 0.8821 | 0.9249 | 0.9029 | 82.19% |
| Gu and Lu (2021) [43] (Naïve Bayes features with SVM) | 0.8978 | 0.8273 | 0.8610 | 79.04 |
| Wu et al. (2024) [44] Regression Neural Network (GRNN) with Feedback Mechanism | 0.8344 | 0.8676 | 0.8507 | 88.28% |
| Talukder et al. (2024) [45] (SMOTE with XgBoost) | 0.8341 | 0.8853 | 0.8589 | 87.70 |
| Cai et al. (2024) [46] LSTM with multi-head attention mechanism | 0.8156 | 0.7892 | 0.8022 | 78.34% |
| Zhu et al. (2024) [47] Backpropagation, LSTM, and Transformer networks | 0.8733 | 0.9242 | 0.8980 | 97.14% |
| Proposed approach | 0.9843 | 0.9811 | 0.9828 | 98.70% |
| Algorithm | Precision | Recall | F-Score | Accuracy |
|---|---|---|---|---|
| Ali and Osman (2024) [6] (Multibranched Hybrid Perceptron architecture with Dynamic Feature Adaption) | 0.9472 | 0.9024 | 0.9238 | 95.49% |
| Hnamte and Hussian (2024) [15] (CNN and LSTM approach) | 0.9804 | 0.9429 | 0.9614 | 92.49% |
| Zhang et al. (2024) [42] Valley Point-Based Time Series Segmentation Algorithm with fuzzy information granules | 0.8362 | 0.8922 | 0.8633 | 88.23% |
| Gu and Lu (2021) [43] (Naïve Bayes features with SVM) | 0.8608 | 0.8970 | 0.8736 | 79.04% |
| Wu et al. (2024) [44] Regression Neural Network (GRNN) with Feedback Mechanism | 0.8824 | 0.8246 | 0.8525 | 90.48% |
| Talukder et al. (2024) [45] (SMOTE with XgBoost) | 0.8848 | 0.9043 | 0.8939 | 93.42% |
| Cai et al. (2024) [46] LSTM with multi-head attention mechanism | 0.8564 | 0.7902 | 0.8220 | 81.38% |
| Zhu et al. (2024) [47] Backpropagation, LSTM, and Transformer networks | 0.8333 | 0.9402 | 0.8835 | 92.14% |
| Proposed Approach | 0.9889 | 0.9874 | 0.9909 | 98.74% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Dulaimi, R.T.A.; Türkben, A.K. A Hybrid Tree Convolutional Neural Network with Leader-Guided Spiral Optimization for Detecting Symmetric Patterns in Network Anomalies. Symmetry 2025, 17, 421. https://doi.org/10.3390/sym17030421
Al-Dulaimi RTA, Türkben AK. A Hybrid Tree Convolutional Neural Network with Leader-Guided Spiral Optimization for Detecting Symmetric Patterns in Network Anomalies. Symmetry. 2025; 17(3):421. https://doi.org/10.3390/sym17030421
Chicago/Turabian StyleAl-Dulaimi, Reem Talal Abdulhameed, and Ayça Kurnaz Türkben. 2025. "A Hybrid Tree Convolutional Neural Network with Leader-Guided Spiral Optimization for Detecting Symmetric Patterns in Network Anomalies" Symmetry 17, no. 3: 421. https://doi.org/10.3390/sym17030421
APA StyleAl-Dulaimi, R. T. A., & Türkben, A. K. (2025). A Hybrid Tree Convolutional Neural Network with Leader-Guided Spiral Optimization for Detecting Symmetric Patterns in Network Anomalies. Symmetry, 17(3), 421. https://doi.org/10.3390/sym17030421




