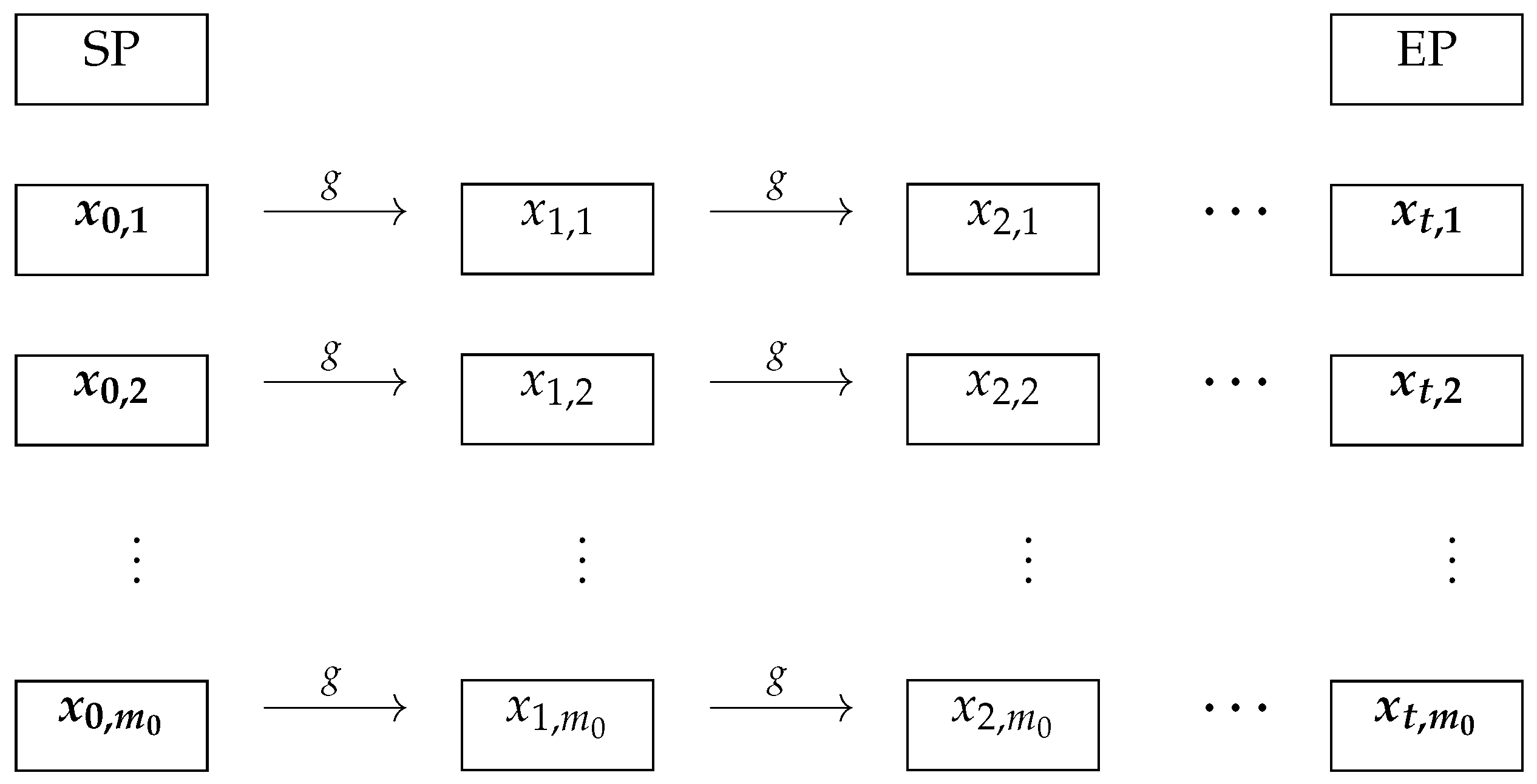Brauer Analysis of Some Time–Memory Trade-Off Attacks and Its Application to the Solution of the Yang–Baxter Equation

Abstract

This paper is focused on some algebraic and combinatorial properties of a TMTO (Time–Memory Trade-Off) for a chosen plaintext attack against a cryptosystem with a perfect secrecy property. TMTO attacks aim to retrieve the preimage of a given one-way function more efficiently than an exhaustive search and with less memory than a dictionary attack. TMTOs for chosen plaintext attacks against cryptosystems with a perfect secrecy property are associated with some directed graphs, which can be defined by suitable collections of multisets called Brauer configurations. Such configurations induce so-called Brauer configuration algebras, the algebraic and combinatorial invariant analysis of which is said to be a Brauer analysis. In this line, this paper proposes formulas for dimensions of Brauer configuration algebras (and their centers) induced by directed graphs defined by TMTO attacks. These results are used to provide some set-theoretical solutions for the Yang–Baxter equation.

1. Introduction

Hellman [1] introduced the TMTO (Time–Memory Trade-Off) attack to carry out brute-force attacks against DES. It consists of a precomputation phase whose results are stored in tables to reduce the time a brute-force attack requires. It is worth noting that if a search problem has K possible solutions, then the time–memory trade-off allows the solution to be found with high probability in T operations (time) with M words of memory, given that the time–memory product ($T\times M$) is larger than K.

After the introduction of TMTO attacks, several improvements were defined and applied to different cryptographic systems; for example, Oechslin [2] introduced rainbow tables (RTs), which aim to retrieve an element (x) in a domain (A) from its image ($y=h\left(x\right)$) of a one-way function ($h:A\to B$). Dictionary attacks are faster, but they require too much memory for practical uses.

Denning [3] attributed to Rivest the idea of using some points satisfying some appropriate criteria to minimize the frequency of accesses to the memory. According to her, Rivest suggested reducing the number of disk accesses to $\sqrt{T}$. This approach was intensively studied as the Distinguished Method (DM) by Standaert et al. [4] and Quisquater et al. [5]. Biryukov and Shamir [6] compared Hellman’s attack with the DM and applied TMTOs to stream ciphers.

Saran applied TMTO attacks to symmetric ciphers [7] and password hashing algorithms [8], and Avoine et al. introduced descending [9] and ascending [10] stepped rainbow tables.

Stinson and Paterson [11] investigated TMTO attacks for a chosen plaintext attack on a specific cipher type with the perfect secret property. Instead of distinguished points or rainbow tables, in the pre-computation phase, they used some appropriated directed graphs to retrieve a key (K) in a $o\left(N\right)$ time-memory trade-off, where N is the size of the associated plaintext, ciphertext, and key sets.

Green and Schroll [12] introduced Brauer configuration algebras to study the representation theory of a special type of path algebra called algebras of the wild representation type. Soon afterward, several applications of Brauer configuration algebras arose in the form of Brauer analyses of their algebraic and combinatorial invariants [13]. Such an analysis allows formulas to be found for the dimensions of such algebras, their centers, and the shape of some undirected graphs called covering graphs induced by the Brauer quivers defining these algebras. An extended Brauer analysis of these data studied some graph entropies based on the degree sequence of the associated covering graphs [14].

Since the combinatorial and algebraic properties of the directed graphs involved in Stinson and Paterson’s TMTO attack [11] have not been investigated, the main problem in this paper is applying Brauer analysis to them to fill this gap. In particular, it is proven that the dimensions of the induced Brauer configuration algebras and their centers depend on the size of the corresponding plaintext sets. In this fashion, this paper provides a new viewpoint of Brauer configuration algebras and their applications.

The Yang–Baxter equation was introduced first by Yang [15] in two short papers in 1967 and by Baxter in 1971 [16]; since then, Yang–Baxter equation research has dealt with advances in several fields of mathematics and sciences, such as quantum computing, quantum group theory, statistical mechanics, Hopf algebras, Lie algebras, braces theory, etc. The authors refer interested readers to [17] for a survey regarding the Yang–Baxter equation [18] and for a description of some computational solutions of such equations and their relationships with non-associative algebras, as well as to [19], where a set-theoretical solution of the Yang–Baxter equation is proposed via some braces and the Cayley graph of a permutation group.

In this paper, the application of Brauer analysis to Stinson and Paterson’s TMTO attack allows us to find set-theoretical solutions of the Yang0-Baxter equation in the following form:

$$(r\times id)\circ (id\times r)\circ (r\times id)=(id\times r)\circ (r\times id)\circ (id\times r).$$

(1)

where $r:X\times X\to X\times X$ is a suitable map from the Cartesian product of a set (X) to itself and $id:X\to X$ is the identity map. Set-theoretical solutions are among the multiple approaches to classifying solutions of the Yang–Baxter equation, which is still an open problem.

Contributions

This paper investigates algebraic properties of time–memory trade-off attacks for chosen plaintext attacks against cryptosystems with a perfect secrecy property. Its main results are Theorems 2–4 and Corollary 1.

Theorem 2 proves that directed graphs associated with TMTOs for chosen plaintext attacks induce integer partitions of numbers with in form of $N(N-1)$, where N is the size of the plaintext, ciphertext, and key sets.

Theorem 3 applies a Brauer analysis to the Brauer configuration algebras induced by TMTOs attacks. Such an analysis proves that the corresponding covering graphs are complete.

Corollary 1 analyzes the topological content information or graph entropy of the covering graphs induced by the TMTO attacks.

Theorem 4 provides set-theoretical solutions of the Yang–Baxter equation based on Latin square cryptosystems.

The organization of this paper is outlined as follows: Background, main definitions, and notations are provided in Section 2; we recall definitions of a time–memory trade-off for a chosen plaintext attack against cryptosystems that achieve perfect secrecy (Section 2.2), multisets and their induced Brauer configuration algebras (Section 2.3), and the Yang–Baxter equation (Section 2.4). We present the main results in Section 2.6. This section provides examples of the main definitions and results presented in this paper. Concluding remarks are presented in Section 3.

2. Preliminaries

This section provides basic definitions and notation regarding time–memory trade-off attacks (Section 2.2), Brauer configuration algebras (Section 2.3), and the Yang–Baxter equation Section 2.4.

2.1. Background

Green and Schroll introduced Brauer configuration algebras [12] and Brauer graph algebras [20] between 2017 and 2018 to investigate algebras of wild and tame representation types. Soon afterward, Espinosa [21] introduced the notion of specialized Brauer messages to study snake graphs and their perfect matchings, as well as indecomposable Kronecker modules [22] and the energy of $\{0,1\}$-matrices arising from some suitable graphs [23].

Brauer analysis was introduced by Cañadas et al. [13] to study quantum entanglement states based on Brauer messages and perfect matchings of the graphs associated with such states. In this work, the authors studied algebraic invariants associated with Brauer configuration algebras (${\Lambda }_{GH{Z}_n^2}$) induced by quantum entangled states of type $GHZ$ (Greenberger–Horne–Zeilinger) defined by the following identities:

$$\begin{array}{cc}\hfill |GH{Z}_n^d\rangle & ={\displaystyle \frac{1}{\sqrt{d}}}\underset{i=0}{\sum ^{d-1}}{|i\rangle }^{\otimes n}.\hfill \end{array}$$

(2)

where n is the number of particles and d is the dimension for every particle. In [13], it was proven that the dimensions of ${\Lambda }_{GH{Z}_n^2}$ and its center (${\dim }_{k}Z\left({\Lambda }_{GH{Z}_n^2}\right)$) are given by the following identities:

$$\begin{array}{cc}\hfill {\dim }_k{\Lambda }_{GH{Z}_n^2}& =4\#Crystals,\mathrm{where}k\mathrm{is}\mathrm{an}\mathrm{algebraically}\mathrm{closed}\mathrm{field}.\hfill \\ \hfill {\dim }_{k}Z\left({\Lambda }_{GH{Z}_n^2}\right)& =1+\#Crystals.\hfill \end{array}$$

(3)

Brauer analysis has also been applied to analyze several topics in cybersecurity [24]—in particular, the Advanced Encryption Standard (AES) [25].

Extended Brauer analysis, which embraces the study of some degree-based entropies, has been applied to analyze Dynkin and Euclidean diagrams [14]. Such analysis was used in [26] to define realizable branch data associated with some branched covering over some closed, connected surfaces.

Along with the works proposed by Hellman et al. [1,2,3,4,5,6,7,8,9,10,11] mentioned in the Introduction of this paper, regarding the use of TMTOs to attack several cryptosystems, we also remember that van den Broek and Poll [27] devised a TMTO attack for the A5/1 cipher used in GSM, which combines both distinguished points and rainbow tables.

Drinfeld et al. [28] proposed the study of set-theoretical solutions of the YBE (see (1)). In particular, non-degenerate, involutive set-theoretical solutions of the YBE were presented by Etingof et al. [29] and Gateva-Ivanova and Van den Bergh [30] by associating a suitable group ($G(X,r)$) with the solution $(X,r)$ of the Yang–Baxter equation.

This paper proposes set-theoretical solutions of the Yang–Baxter equation based on the Brauer analysis realized for the directed graphs defined by Stinson and Paterson [11] in their TMTO attack.

Rump [31] introduced another line of investigation to tackle the problem of classifying the non-degenerate involutive set-theoretical solutions of the YBE. It is worth noting that braces constitute one of the most important investigation lines of such an equation. For instance, Ballester et al. [19] found set-theoretical solutions based on braces and Brauer configuration algebras [32].

2.2. TMTO Attacks

This section describes a TMTO for a chosen plaintext attack proposed by Stinson and Paterson in [11].

Figure 1 shows a standard diagram of a rainbow table or rainbow matrix for a TMTO. Elements in the first column ($x_{0,j}$ with $1\le j\le m_0$) are chosen arbitrarily but must differ. They are called start points (SPs). The elements in the last column of the matrix are called end points (EPs). The combination of SPs and EPs is called a table [8].

A chain depicts the collection of elements of the same row. Functions (g) with $g:A\to A$ from the search spaceA to themselves are composition functions of the following form:

$$r_i\left(h\left(x_{i,j}\right)\right)=x_{i+1,j}=g\left(x_{i,j}\right),$$

(4)

where $r_i$ is a suitable reduction function and h is the function that the algorithm aims to invert. Functions (g) are called hash-reduction functions.

Let $\mathcal{S}=(\mathcal{P},\mathcal{C},\mathcal{K},\mathcal{E},\mathcal{D})$ be a cryptosystem or cryptographic system that possesses the perfect secrecy property, where $\mathcal{P}=\mathcal{C}=\mathcal{K}$ denotes the set of plaintexts, ciphertexts and keys, respectively. It should be noted that cryptosystems that achieve perfect secrecy are considered unbreakable.

The following result for cryptosystems with the perfect secrecy property is proven in [11].

Theorem 1 

([11], Theorem 3.4). Suppose $(\mathcal{P},\mathcal{C},\mathcal{K},\mathcal{E},\mathcal{D})$ is a cryptosystem where $\left|\mathcal{K}\right|=\left|\mathcal{C}\right|=\left|\mathcal{P}\right|$. Then, the cryptosystem provides perfect secrecy if and only if every key is used with equal probability (${\displaystyle \frac{1}{\mathcal{K}}}$), and for every $x\in \mathcal{P}$ and every $y\in \mathcal{C}$, there is a unique key (K) such that $e_K\left(x\right)=y$.

Since $\mathcal{S}$ achieves perfect secrecy, it holds that $P_{\mathcal{P}}(x/y)=P_{\mathcal{P}}\left(x\right)$ for any $x\in \mathcal{P}$ and $y\in \mathcal{C}$, where $P_{\mathcal{P}}\left(x\right)$ denotes the probability that the probability distribution associated with the set of plaintexts attains a value of x and $P_{\mathcal{P}}(x/y)$ denotes the conditional probability of attaining a plaintext value of x given a ciphertext (y). In such a case, for a given encryption function ($e_K:\mathcal{P}\to \mathcal{C}$) associated with a key ($K\in \mathcal{K}$), it holds that $e_K\left(x\right)=e_{K_1}\left(x\right)$, provided that $K=K_1$. Furthermore, $\mathcal{P}=\mathcal{Y}=\mathcal{K}=\{y_1,y_2,\cdots ,y_N\}$.

In the sequel, we describe the TMTO introduced by Stinson and Paterson [11] to conduct a chosen plaintext attack against a cryptosystem with the perfect secrecy property. We recall that in these types of attacks, the opponent obtains temporary access to the encryption machinery [11]. Hence, the opponentcan choose a plaintext string (x) and construct the corresponding ciphertext string (y).

Let x be a fixed plaintext and define a function ($g:\mathcal{Y}\to \mathcal{Y}$) such that $g\left(y\right)=e_y\left(x\right)$. We define a directed graph or quiver ($Q_{TMTO}=(Q_0,Q_1,s,t)$) whose sets of vertices ($Q_0$) and arrows ($Q_1$) are defined in such a way that

$$\begin{array}{cc}\hfill Q_0& =\mathcal{Y},\hfill \\ \hfill Q_1& =\{\alpha \in Q_1\mid s\left(\alpha \right)=y_i,t\left(\alpha \right)=g\left(y_i\right),1\le i\le N\}=\{(y_i,g\left(y_i\right))\mid 1\le i\le N\}.\hfill \end{array}$$

(5)

According to Stinson and Paterson [11], $Q_{TMTO}$ and g have the following properties:

• $Q_{TMTO}$ consists of the union of disjoint directed cycles.
• T is a desired time parameter.
  Suppose we have a set of elements ($Z=\{z_1,z_2,\cdots ,z_m\}\subset \mathcal{Y}$) such that, for every element ($y_i\in \mathcal{Y}$), either $y_i$ is contained in a cycle of a length of, at most, T or there exists an element ($z_j\ne y_i$) such that the distance from $y_i$ to $z_j$ in $Q_{TMTO}$ is, at most, T; then, there exists a set (Z) satisfying the following properties:
  • $\left|Z\right|\le {\displaystyle \frac{2N}{T}}$,
  • $\left|Z\right|$ is $o(N/T)$.

Stinson and Paterson [11] introduced the pseudo-code of an algorithm (Algorithm  1) to find a key (K), given $y=e_k\left(x\right)$. It finds K in, at most, T steps, with the time–memory trade-off represented by $o\left(N\right)$, which means that in the worst case, the algorithm recovers a key in N steps (see Example 1 in Section 2.6 of this paper).

This paper introduces Brauer configuration algebras (${\Lambda }_{TMTO}$) induced by quivers of the form of $Q_{TMTO}$.

Algorithm 1: Time–memory trade-off(y)

$y_0\leftarrow y$

$backup\leftarrow \mathbf{false}$

$\mathbf{while}g\left(y\right)\ne y_0$

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathbf{do}\left\{\begin{array}{c}\mathrm{if}y=z_j\mathrm{for}\mathrm{some}j\mathbf{and}\mathbf{not}backup\hfill \\ \mathbf{then}\left\{\begin{array}{c}y\leftarrow g^{-T}\left(z_j\right)\hfill \\ backup\leftarrow \mathbf{True}\hfill \end{array}\right.\hfill \\ \mathbf{else}\left\{\begin{array}{c}y\leftarrow g\left(y\right)\hfill \\ K\leftarrow y\hfill \end{array}\right.\hfill \end{array}\right.$$

2.3. Multisets and Brauer Configuration Algebras

This section recalls some definitions and notations dealing with multisets, Brauer configurations, and Brauer configuration algebras. Examples are presented in Example 1 in Section 2.6. The authors refer the interested reader to [12,14,26,33,34] for more information on these topics.

A multiset is a pair $(M,\mathfrak{f})$ consisting of a set (M) and a map ($\mathfrak{f}:M\to \mathbb{N}$) from M to a non-negative integers set ($\mathbb{N}$) such that $\left|M\right|={\displaystyle \sum _{m\in M}}\mathfrak{f}\left(m\right)<\infty$ [33,34]. $\mathfrak{f}$ is said to be a multiplicity function in the sense that $\mathfrak{f}\left(m\right)$ provides the number of times or occurrences of an element m in M. Roughly speaking, multisets allow for element repetition.

If $(M,\mathfrak{f})$ is a multiset and $M=\{m_1,m_2,\cdots ,m_t\}$, then $(M,\mathfrak{f})$ is determined by a fixed word in the form of $w\left(M\right)=m_{i_1}^{\mathfrak{f}\left(m_{i_1}\right)}{m}_{i_2}^{\mathfrak{f}\left(m_{i_2}\right)}\cdots m_{i_t}^{\mathfrak{f}\left(m_{i_t}\right)}$, where $\{i_1,i_2,\cdots ,i_t\}$ is a permutation of $\{1,2,\cdots ,t\}$.

In [14,26], Cañadas et al. defined multisets of type M. In such a case, if $M={\displaystyle \bigcup _{i=1}^n}{M}_i$ and $\mathfrak{M}=\{(M_1,{\mathfrak{f}}_1),(M_1,{\mathfrak{f}}_2),\cdots ,(M_n,{\mathfrak{f}}_n)\}$ is a collection of $n=\left|\mathfrak{M}\right|$ multisets with $|M_i|>1$ for $1\le i\le n$, then the collection of multisets ($\mathfrak{M}$) is said to be of type M if it satisfies the following conditions.

• If $m\in M$ and ${\mathfrak{I}}_m=\{M_{j_1,m},M_{j_2,m},\cdots ,M_{j_h,m}\}$ is the collection of all sets ($M_i$) that contain m, then ${\mathfrak{I}}_m$ is endowed with a well-order or linear-order (<)with the form of ${\mathfrak{E}}_{M_{j_1}}<{\mathfrak{E}}_{M_{j_2}}<\cdots <{\mathfrak{E}}_{M_{j_h}}$, where ${\mathfrak{E}}_{M_{j_s}}$ is an expansion of set $M_{j_s}$ with the of form $M_{j_s}^{\left(1\right)}<M_{j_s}^{\left(2\right)}<\cdots <M_{j_s}^{\left({\mathfrak{f}}_{j_s}\left(m\right)\right)}$, $f_{j_s}\left(m\right)$ is the multiplicity of m in $M_{j_s}$, and $1\le s\le h$. Henceforth, we assume the notation of $M_i$ instead of $M_{i,m}$ if no confusion arises.
• If $Succ\left(M\right)$ denotes the successor of $M_{j_i}^{\left(r\right)}$ in ${\mathfrak{I}}_m$, then it holds that

  $$\begin{array}{cc}\hfill Suc\left(M_{j_i}^{\left(r\right)}\right)& =M_{j_i}^{(r+1)},\mathrm{if}r<{\mathfrak{f}}_{j_i}\left(y\right),\hfill \\ \hfill Suc\left(M_{j_s}^{\left({\mathfrak{f}}_{j_s}\left(y\right)\right)}\right)& =M_{j_s+1}^{\left(1\right)},\mathrm{if}{j}_s<h.\hfill \end{array}$$

  (6)
• The valency ($val\left(m\right)$) of an element ($m\in M$) is expressed by the following sum:

  $$val\left(m\right)=\sum _{M_{j_i}\in {\mathfrak{I}}_m}{\mathfrak{f}}_{j_i}\left(m\right).$$

  (7)
  $\mathfrak{M}$ is endowed with a map ($\nu :M\to {\mathbb{N}}^{+}\times {\mathbb{N}}^{+}$) such that $\nu \left(m\right)=(j_m,val\left(m\right))$, where ${\mathbb{N}}^{+}$ is the set of positive integers.

  $$j_m=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}val\left(m\right)>1,\hfill \\ 2,\hfill & \mathrm{if}val\left(m\right)=1.\hfill \end{array}\right.$$
• Chains in the form of ${\mathfrak{I}}_m=S_m={\mathfrak{E}}_{M_{j_1}}<{\mathfrak{E}}_{M_{j_2}}<\cdots <{\mathfrak{E}}_{M_{j_h}}$ are said to be successor sequences. Each successor sequence ($S_m$) defined by an element ($m\in M$) gives rise to a family of equivalent circular orderings by adding a new relation in the form of $M_{j_h}^{\left(f_{j_h}\left(m\right)\right)}<M_{j_1}^{\left(1\right)}$ ($Suc(M_{j_h}^{\left(f_{j_h}\left(m\right)\right)})=M_{j_1}^{\left(1\right)}$). Note that $S_m=M_i$ is the successor sequence of an element ($m\in M_i$) with $val\left(m\right)=1$.

Remark 1. 

In [14,26] multiset collections of type M assume that $j_1<j_2<\cdots <j_h$ in successor sequences (${\mathfrak{I}}_m$). This paper does not assume such an order for them.

Collections of multisets ($\mathfrak{M}$) of type M give rise to so-called Brauer quivers [12] ($Q_{\mathfrak{M}}=(Q_0,Q_1,s,t)$) whose set of vertices ($Q_0$) is in bijective correspondence with multisets ($(M_i,{\mathfrak{f}}_i)\in \mathfrak{M}$) (Green and Schroll [12] called polygons, the elements of $\mathfrak{M}$ and vertices, the elements of M). Arrows in $Q_1$ are represented by subsets in the form of $\{M_i,Suc\left(M_i\right)\}$, i.e., these subsets define arrows in the form of $M_i\stackrel{\alpha }{\to }Suc\left(M_i\right)\in Q_1$. In particular, circular orderings defined by successor sequences induce cycles (special cycles in the sense of Green and Schroll [12]) in $Q_{\mathfrak{M}}$. If $val\left(m\right)=1$, then the special cycle defined by $m\in M_i$ is in the form of ${\left(M_i\stackrel{{\alpha }_1}{\to }{M}_i\right)}^2$ or $C_m^2$ if $C_m=M_i\stackrel{{\alpha }_1}{\to }{M}_i$.

Collections of multisets of type M are Brauer configurations as defined by Green and Schroll in [12]. According to them, these are quadruples in the form of $\mathcal{M}=(M,\mathfrak{M},\mu ,\mathcal{O})$, where M is a set of vertices, $\mathfrak{M}$ is a collection or set of polygons, $\mu$ is multiplicity function (defined as $j_m$), and $\mathcal{O}$ is an orientation defined by the successor sequences.

According to Green and Schroll [12] a vertex ($m\in M$) is truncated (non-truncated), provided that $\mu \left(m\right)val\left(m\right)=1$ ($\mu \left(m\right)val\left(m\right)>1$). Thus, a collection of multisets of type M, also called Brauer configurations of type M, has no truncated vertices. In such a case, they are said to be reduced. Moreover, a Brauer configuration is connected if its induced Brauer quiver is connected.

This paper restricts the general definitions of Brauer configuration algebras given by Green and Schroll in [12] to those induced by Brauer configurations (or collections of multisets) of type M.

Given an algebraically closed field (k), a Brauer configuration algebra of type M is a bound quiver algebra ($k{Q}_{\mathcal{m}}/I_{\mathcal{M}}$) defined by a Brauer quiver ($Q_{\mathcal{M}}$) induced by a Brauer configuration ($\mathcal{M}$) of type M and bounded by an admissible ideal ($I_{\mathcal{M}}$) generated by relations of the following types:

• $C_m-C_{m^{\prime }}$ if m and $m^{\prime }$ belong to the same multiset; $M_i\in \mathfrak{M}$; and $C_m$ and $C_{m^{\prime }}$ are special cycles at m and $m^{\prime }$, respectively. These relations are said to be of type ${\rho }_1$.
• $C_{m}f$ if $C_m$ is a special cycle at vertex $m\in M$ and f is the first arrow of $C_m$. In particular, $C_m^3\in I_{\mathcal{M}}$ if $val\left(m\right)=1$. These are relations of type ${\rho }_2$.
• Relations of type ${\rho }_3$ have the form of ${\alpha }_i^m{\alpha }_j^{m^{\prime }}$, if ${\alpha }_i^m{\alpha }_j^{m^{\prime }}\in k{Q}_{\mathcal{M}}$; $m\in C_m$; $m^{\prime }\in C_{m^{\prime }}$; $m\ne m^{\prime }$; and $C_m$ and $C_{m^{\prime }}$ are special cycles at m and $m^{\prime }$, respectively.

Cañadas et al. [14] introduced the covering graph ($\mathfrak{c}\left(Q_{\mathfrak{M}}\right)=(V_{\mathfrak{c}\left(Q_{\mathfrak{M}}\right)},E_{\mathfrak{c}\left(Q_{\mathfrak{M}}\right)})$) induced by a Brauer configuration ($\mathfrak{M}$) with a set of polygons ($\mathcal{M}$) as the set of vertices ($V_{\mathfrak{c}\left(Q_{\mathfrak{M}}\right)}$) and an edge ($e_{M_i,M_j}$) connecting two polygons if, for some $m\in M$, there exists a successor sequence ($S_m$) for which either $Succ\left(M_i\right)=M_j$ or $Succ\left(M_j\right)=M_i$ (in other words, $\{M_i,M_j\}\in E_{\mathfrak{c}\left(Q_{\mathfrak{M}}\right)}$, provided that, for some $m\in M$, ${\mathfrak{E}}_{M_i}<{\mathfrak{E}}_{M_j}$ is a covering in the corresponding successor sequence ($S_m$)). We note that covering graphs not not have multiple edges or loops.

Given a subset ($A=\{a_1,a_2,\cdots ,a_m\}$) of the set of vertices ($V_{\mathcal{G}}$) of a graph $\mathcal{G}$, a hair graph ($\mathcal{G}[(a_1,a_2,\cdots ,a_m);(n_1,n_2,\cdots ,n_m)]$) with respect to A is obtained from $\mathcal{G}$ by attaching to each point ($a_i$, $1\le i\le m$) a linear path with $n_i$ vertices.

Remark 2. 

The following properties of Brauer configuration algebras were introduced by Green and Schroll [12], Sierra [35], and Cañadas et al. [14] (see [12] Theorem B, Proposition 2.7, Theorem 3.10, Corollary 3.12, [35] Theorem 4.9, and [14] Theorem 8).

• Any Brauer configuration algebra (${\Lambda }_{\mathcal{M}}$) induced by a Brauer configuration ($\mathcal{M}=(M,\mathfrak{M},\mu ,\mathcal{O})$) is multiserial, and there exists a bijective correspondence between the set of indecomposable projective ${\Lambda }_{\mathcal{M}}$ modules and the set of multisets or polygons ($\mathfrak{M}$).
• The number of summands in the heart ($ht\left(P\right)=\mathrm{Rad}P/\mathrm{Soc}P$) of an indecomposable projective ${\Lambda }_{\mathcal{M}}$ module equals the number of non-truncated vertices in the corresponding polygon, where $\mathrm{Soc}P$ denotes the socle of the indecomposable projective ${\Lambda }_{\mathcal{M}}$ module (P), which is generated by its corresponding simple submodules.
• Green and Schroll [12] proposed the following Formula (8) for the dimension (${\dim }_k{\Lambda }_{\mathcal{M}}$) of a Brauer configuration algebra (${\Lambda }_{\mathcal{M}}$) induced by a Brauer configuration ($\mathcal{M}$).

  $${\dim }_k{\Lambda }_{\mathcal{M}}=2\left|\mathfrak{M}\right|+\sum _{m\in M}val\left(m\right)(\mu \left(m\right)val\left(m\right)-1).$$

  (8)
• Sierra [35] proposed the following Formula (9) for the dimension (${\dim }_{k}Z\left({\Lambda }_{\mathcal{M}}\right)$) of the center ($Z\left({\Lambda }_{\mathcal{M}}\right)$) of a Brauer configuration algebra (${\Lambda }_{\mathcal{M}}$) induced by a reduced and connected Brauer configuration ($\mathcal{M}$) (Brauer configurations of type M are reduced).

  $${\dim }_{k}Z\left({\Lambda }_{\mathcal{M}}\right)=1+\left|\mathfrak{M}\right|+\sum _{m\in M}\mu \left(m\right)-\left|M\right|+\#\mathrm{Loops}\left(Q_{\mathfrak{M}}\right)-\left|\{m\in M\mid val\left(m\right)=1\}\right|.$$

  (9)
• We note that any graph ($\mathcal{G}=(V_{\mathcal{G}},E_{\mathcal{G}})$) gives rise to a Brauer configuration (${\mathcal{M}}_{\mathcal{G}}$) of type M, where $M=V_{\mathcal{G}}$ and $\mathfrak{M}=E_{\mathcal{G}}$. Cañadas et al. [14] proved that the covering graph ($\mathfrak{c}\left(Q_{{\mathcal{M}}_{\mathcal{G}}}\right)$) induced by a Brauer configuration (${\mathcal{M}}_{\mathcal{G}}$) defined by a graph ($\mathcal{G}$) is isomorphic to $\mathcal{G}$ if and only if $\mathcal{G}$ is a disjoint union of copies of connected hair graphs of type $C_n[(v_1,v_2,\cdots ,v_n);(s_1,s_2,\cdots ,s_n)]$, where $C_n$ is an n-point cycle and $n\ge 3$.

2.4. Yang–Baxter Equation

As described before, the Yang–Baxter equation was introduced by Yang [15] in 1967 and Baxter [16] in 1972. Recall that if k is an algebraically closed field of characteristic zero and V is a k-vector space, then a linear automorphism ($R:V\otimes V\to V\otimes V$) is a solution of the Yang–Baxter equation, provided that it satisfies the following braided relation [22]:

$$(R\otimes id)\circ (id\otimes R)\circ (R\otimes id)=(id\otimes R)\circ (R\otimes id)\circ (id\otimes R).$$

(10)

R is a solution of the quantum Yang–Baxter equation if and only if

$$R_{12}\circ R_{13}\circ R_{23}=R_{23}\circ R_{13}\circ R_{12}$$

(11)

where $R_{ij}$ indicates R acting on the ith and jth tensor factors and the identity on the remaining factor [17].

Since a complete classification of the Yang–Baxter equation is an open problem, several approaches have been introduced to tackle it. For instance, Drinfeld et al. [28] introduced the notion of a set-theoretical solution of the Yang–Baxter equation (see (1)). In such a case, for a given set (X) and a map ($r:X\times X\to X\times X$), the identity (1) has the following form [19]:

$$r_{12}{r}_{23}{r}_{12}=r_{23}{r}_{12}{r}_{23},$$

(12)

where maps $r_{12},r_{23}:X\times X\times X\to X\times X\times X$ are defined as $r_{12}=r\times i{d}_X$ and $r_{23}=i{d}_X\times r$, respectively.

Note that if $\tau :X^2\to X^2$ is defined in such a way that $\tau (x,y)=(y,x)$, then a map ($S:X^2\to X^2$) is a set-theoretical solution of the YBE if and only if $\tau \circ S$ and $S\circ \tau$ satisfy the quantum Yang–Baxter equation (11) [18,29].

A bijective map ($r:X\times X\to X\times X$) such that $r(x,y)=({\sigma }_x\left(y\right),{\gamma }_y\left(x\right))$ is involutive if $r^2=i{d}_{X^2}$. r is said to be left non-degenerate (right non-degenerate) if each map (${\gamma }_x$) (${\sigma }_x$) is bijective.

Rump [31] introduced the notion of a brace to provide set-theoretical solutions of the Yang–Baxter equation, and Cañadas et al. proposed set-theoretical solutions of the Yang–Baxter equation based on braces and Brauer configuration algebras [32].

This paper uses Brauer quivers arising from TMTO attacks as described by Stinson and Paterson [11] to provide set-theoretical solutions of the Yang–Baxter equation.

2.5. Entropy of a Graph

The entropy of a graph or network is a measure of its complexity, as introduced by Rashevsky [36] and Trucco [37]. Cañadas et al. [14] studied based-degree graph entropies denoted as $H_{{\delta }_v}\left(\mathcal{G}\right)$, $H_{\mathfrak{d}}\left(\mathcal{G}\right)$, and $H\left({\mathfrak{M}}_{\mathcal{G}}\right)$ to apply extended Brauer analysis to some Dynkin and Euclidean diagrams. Such entropies are defined as follows for a graph ($\mathcal{G}$) and a Brauer configuration ($\mathcal{M}$) of type M.

$$\begin{array}{cc}\hfill H_{{\delta }_v}\left(\mathcal{G}\right)& ={\displaystyle \frac{1}{2|E_{\mathcal{G}}|}}\sum _{v\in V_{\mathcal{G}}}{\delta }_{v}lo{g}_2\left({\delta }_v\right).\hfill \\ \hfill H_{\mathfrak{d}}\left(\mathcal{G}\right)& =-\underset{i=1}{\sum ^{\overline{{\delta }_v}}}{\displaystyle \frac{|N_i^{{\delta }_v}|}{|V_{\mathcal{G}}|}}lo{g}_2({\displaystyle \frac{|N_i^{{\delta }_v}|}{|V_{\mathcal{G}}|}}).\hfill \\ \hfill H\left(\mathcal{M}\right)& =-\sum _{\alpha \in M}{\displaystyle \frac{\mu \left(\alpha \right)val\left(\alpha \right)}{\mathfrak{v}}}lo{g}_2({\displaystyle \frac{\mu \left(\alpha \right)val\left(\alpha \right)}{\mathfrak{v}}}).\hfill \end{array}$$

(13)

where $V_{\mathcal{G}}$ ($E_{\mathcal{G}}$) denotes the set of vertices (edges) of a graph ($\mathcal{G}$), $|N_i^{{\delta }_v}|$ denotes the number of vertices with a degree equal to i, and $\overline{{\delta }_v}=\underset{v\in V_{\mathcal{G}}}{\max }{\delta }_v$, ${\delta }_v$ is the degree of $v\in V_{\mathcal{G}}$. Furthermore, $\mathfrak{v}={\displaystyle \sum _{\alpha \in M}}\mu \left(\alpha \right)val\left(\alpha \right)$.

2.6. Main Results

This section provides the main results presented in this paper; we start by providing an illustrative example of the definitions described in previous sections.

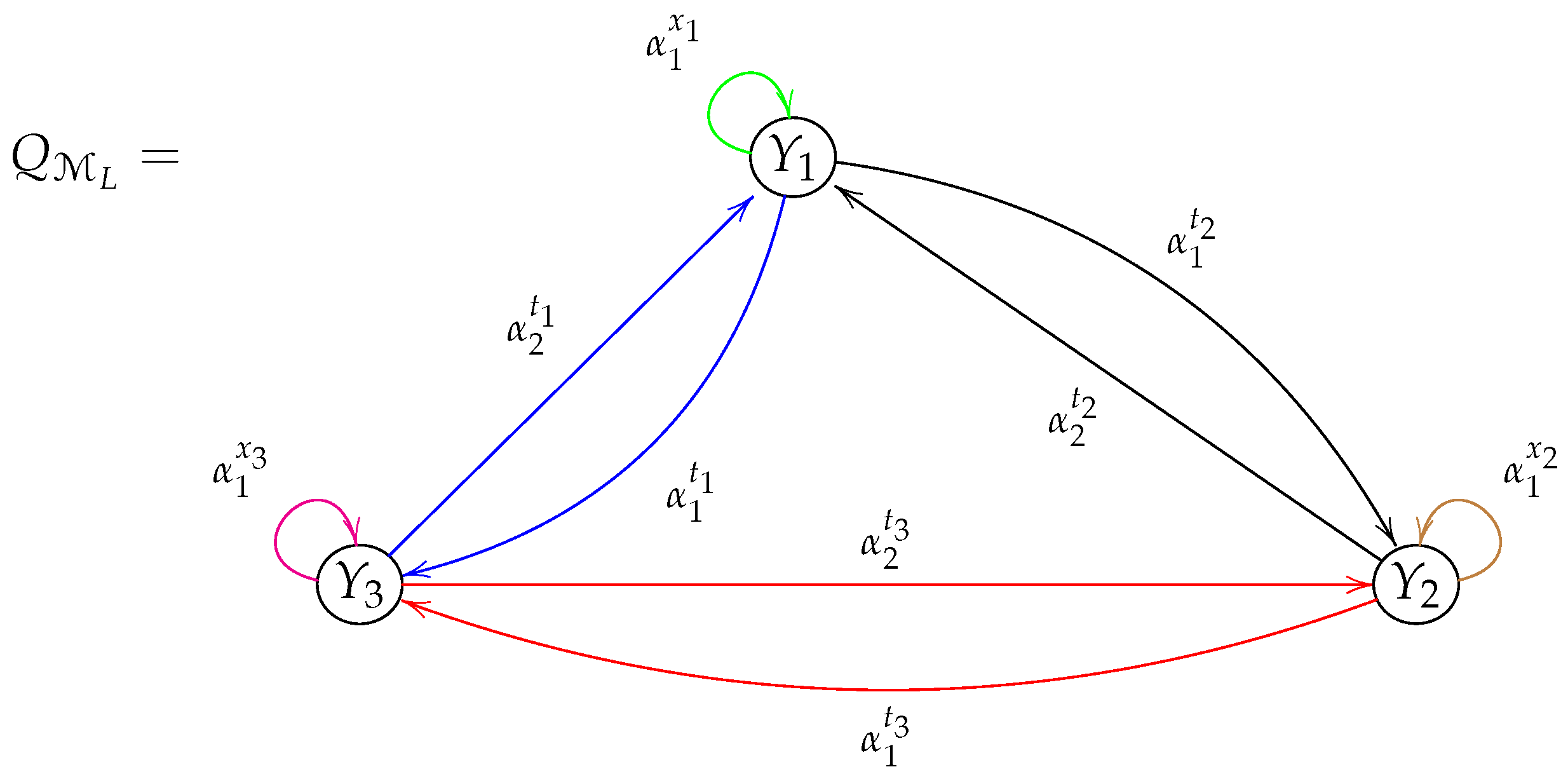
Example 1. 

Let us consider a Latin square cryptosystem ($\mathcal{S}=(\mathcal{P},\mathcal{C},\mathcal{K},\mathcal{E},\mathcal{D})$) such that $\mathcal{P}=\mathcal{C}=\mathcal{K}=\{1,2,3\}$, whose rules of encryption and decryption are represented by rows of the $3\times 3$ Latin square (L) shown in

Table 1. Example of a $3\times 3$ Latin square.

	1	3	2
L =	3	2	1
	2	1	3

, that is, $e_i\left(j\right)=L_{ij}$.

It is well known that $\mathcal{S}$ achieves perfect secrecy, provided that every key is used with equal properties [11].

We define a Brauer configuration (${\mathcal{M}}_L=(M,\mathfrak{M}=\{Y_1,Y_2,Y_3\},\mu ,\mathcal{O})$)| of type M such that

$$\begin{array}{cc}\hfill M& =\{t_1,t_2,t_3,x_1,x_2,x_3\},\hfill \\ \hfill Y_1& =\{t_1,t_2,x_1\},\hfill \\ \hfill Y_2& =\{t_2,t_3,x_2\},\hfill \\ \hfill Y_3& =\{t_1,t_3,x_3\}.\hfill \end{array}$$

(14)

Then, $val\left(x_i\right)=1$, $val\left(t_j\right)=2$, $i,j\in \{1,2,3\}$. The successor sequences are defined as follows:

$$\begin{array}{cc}\hfill S_{t_1}& =Y_1<Y_3,\hfill \\ \hfill S_{t_2}& =Y_1<Y_2,\hfill \\ \hfill S_{t_3}& =Y_2<Y_3,\hfill \\ \hfill S_{x_1}& =Y_1,\hfill \\ \hfill S_{x_2}& =Y_2,\hfill \\ \hfill S_{x_3}& =Y_3.\hfill \end{array}$$

(15)

Figure 2 shows the Brauer quiver induced by Brauer configuration ${\mathcal{M}}_L$.

The Brauer configuration algebra (${\Lambda }_{{\mathcal{M}}_L}$) induced by Brauer configuration ${\mathcal{M}}_L$ is a bound quiver algebra in the form of ${\Lambda }_{{\mathcal{M}}_L}=k{Q}_{{\mathcal{M}}_L}/I_{{\mathcal{M}}_L}$, where the admissible ideal ($I_{\mathcal{M}}$) is generated by relations of three types. The following are examples of relations in $I_{{\mathcal{M}}_L}$.

• ${\alpha }_1^{t_1}{\alpha }_2^{t_1}-{\alpha }_1^{t_2}{\alpha }_2^{t_2}$; ${\alpha }_2^{t_2}{\alpha }_1^{t_2}-{\alpha }_1^{t_3}{\alpha }_2^{t_3}$; ${\alpha }_2^{t_1}{\alpha }_1^{t_1}-{\alpha }_2^{t_3}{\alpha }_1^{t_3}$.
• ${\alpha }_i^{t_r}{\alpha }_j^{t_r}-{\left({\alpha }_1^{x_r}\right)}^2$, $i\ne j$; $i,j\in \{1,2\}$, $r\in \{1,2,3\}$.
• ${\alpha }_i^{t_r}{\alpha }_j^{t_r}{\alpha }_i^{t_r}$, $i\ne j$; $i,j\in \{1,2\}$, $r\in \{1,2,3\}$. ${\left({\alpha }_1^{x_r}\right)}^3$, $r\in \{1,2,3\}$.
• ${\alpha }_i^{t_r}{\alpha }_j^{t_s}$, if ${\alpha }_i^{t_r}{\alpha }_j^{t_s}\in k{Q}_{{\mathcal{M}}_L}$ and $r\ne s$.
• ${\alpha }_i^{t_r}{\alpha }_j^{x_s}$, if ${\alpha }_i^{t_r}{\alpha }_j^{x_s}\in k{Q}_{{\mathcal{M}}_L}$ and $r,s\in \{1,2,3\}$.

The Brauer configuration algebra (${\Lambda }_{{\mathcal{M}}_L}$) has the following properties:

• ${\Lambda }_{{\mathcal{M}}_L}$ is indecomposable as an algebra, provided that the Brauer quiver ($Q_{{\mathcal{M}}_L}$) is connected.
• ${\dim }_k{\Lambda }_{{\mathcal{M}}_L}=2\left(3\right)+3\left(2\left(1\right)\right)+3\left(1\right)=15$.
• ${\dim }_{k}Z\left({\Lambda }_{{\mathcal{M}}_L}\right)=1+3+9-6+3-3=7$.
• The covering graph ($G=\mathfrak{c}\left(Q_{{\mathcal{M}}_L}\right)$) induced by the Brauer configuration (${\mathcal{M}}_L$) is isomorphic to the three-point cycle.

The following are entropies associated with the Brauer configuration (${\mathcal{M}}_L$) and the corresponding covering graph (G).

• $H_{{\delta }_v}\left(\mathcal{G}\right)={\displaystyle \frac{1}{6}}\left(6lo{g}_2\left(2\right)\right)=1$.
• $H_{\mathfrak{d}}\left(\mathcal{G}\right)=0$, provided that G is 2-regular.
• $H\left({\mathcal{M}}_L\right)=-6\left({\displaystyle \frac{2}{12}}lo{g}_2\left({\displaystyle \frac{2}{12}}\right)\right)=lo{g}_2\left(6\right)$. Note that $2^{H\left({\mathcal{M}}_L\right)+1}$ is an approximation of the dimension of the Brauer configuration algebra (${\Lambda }_{{\mathcal{M}}_L^{\prime }}$), where ${\mathcal{M}}_L^{\prime }$ is a reduction of ${\mathcal{M}}_L$ obtained by deleting vertices in M ($x\in M$) with $val\left(x\right)=1$.

The quiver ($Q_{TMTO}$) induced by the time–memory trade-off for a chosen plaintext attack against the Latin square cryptosystem is isomorphic to the Brauer quiver ($Q_{{\mathcal{M}}_L}$). The isomorphism can be realized by the following map between the corresponding sets of arrows (${\left(Q_{TMTO}\right)}_1$ and ${\left(Q_{{\mathcal{M}}_L}\right)}_1$).

$${\mathfrak{m}}_Q:{\left(Q_{TMTO}\right)}_1\to {\left(Q_{{\mathcal{M}}_L}\right)}_1$$

(16)

$$\begin{array}{cc}\hfill {\mathfrak{m}}_Q(i,g_i\left(i\right))& ={\mathfrak{m}}_Q(i,L(i,i))={\alpha }_1^{x_i},i\in \{1,2,3\},\hfill \\ \hfill {\mathfrak{m}}_Q(h,g_h\left(1\right))& ={\mathfrak{m}}_Q(h,L(h,1))={\alpha }_{f\left(h\right)}^{t_3},h\in \{2,3\},f\left(h\right)\in \{1,2\},f\left(2\right)<f\left(3\right),\hfill \\ \hfill {\mathfrak{m}}_Q(h,g_h\left(2\right))& ={\mathfrak{m}}_Q(h,L(h,2))={\alpha }_{f\left(h\right)}^{t_3},h\in \{1,3\},f\left(h\right)\in \{1,2\},f\left(1\right)<f\left(3\right),\hfill \\ \hfill {\mathfrak{m}}_Q(h,g_h\left(3\right))& ={\mathfrak{m}}_Q(h,L(h,3))={\alpha }_{f\left(h\right)}^{t_3},h\in \{1,2\},f\left(h\right)\in \{1,2\},f\left(1\right)<f\left(2\right).\hfill \end{array}$$

(17)

In this paper, it is assumed that ${\Lambda }_{TMTO}={\Lambda }_{{\mathcal{M}}_L}$. Thus, a Brauer analysis of the Brauer configuration (${\mathcal{M}}_L$) is also a Brauer analysis for the TMTO of a known plaintext attack against the Latin square cryptosystem.

Table 2. Examples of using Algorithm 1 to recover keys with the help of a TMTO for a chosen plaintext attack against a Latin square cryptosystem.

N	x	y	Z	$\mathit{g}\left(\mathit{y}\right)$	${\mathit{g}}^{\mathbf{-}\mathbf{1}}\mathbf{\left(}\mathit{y}\mathbf{\right)}$	${\mathit{g}}^{\mathbf{-}\mathbf{2}}\mathbf{\left(}\mathit{y}\mathbf{\right)}$	${\mathit{g}}^{\mathbf{-}\mathbf{3}}\mathbf{\left(}\mathit{y}\mathbf{\right)}$	K
3	1	2	{2, 3}	{2}	{3}			3
4	3	2	{1, 2, 4}	{2}	{4}			4
5	2	3	{3, 4, 5}	{5, 3}		{3}		5
6	2	6	{2, 4, 5, 6}	{4, 5, 2, 6}		{5}		4
7	2	4	{2, 4, 5, 6, 7}	{5, 2, 7, 6, 4}		{2}		5
8	2	5	{2, 4, 5, 6}	{2, 6, 4, 5}		{6}		2
9	1	1	{1, 4, 6, 7}	{6, 1}			{7}	4
10	4	10	{1, 2, 4, 6, 7, 9, 10}	{9, 1, 7, 6, 10}			{6}	7

provides examples of the use of Algorithm 1 to recover a key from a plaintext in a Latin square cryptosystem of order $N\in \{3,4,5,6,7,8,9,10\}$; columns x and y provide a plaintext and corresponding ciphertext. Column Z shows the set (Z) defined for a TMTO, and column $g\left(y\right)$ provides all possible encryption values associated with the ciphertext (y). Column $g^{-T}\left(y\right)$ provides such a value after applying the first step of the algorithm, and column K shows the recovered key. The Latin squares used to apply the algorithm are presented in Appendix A (the corresponding $3\times 3$ Latin square is shown in Table 1).

The following result allows us to define Brauer configuration algebras from quivers of type $Q_{TMTO}$ (see (5)).

Theorem 2. 

A quiver ($Q_{TMTO}$) (see (5)) defined by a TMTO for a chosen plaintext attack against a cryptosystem ($\mathcal{S}=(\mathcal{P},\mathcal{C},\mathcal{K},\mathcal{E},\mathcal{D})$) that achieves perfect secrecy induces an integer partition (${\mathfrak{P}}_{TMTO}=l_2^{{\alpha }_2}{l}_3^{{\alpha }_3}\cdots l_N^{{\alpha }_N}$ of $N(N-1)$), where $\mathcal{P}=\mathcal{C}=\mathcal{K}=\{y_1,y_2,\cdots ,y_N\}$, ${\alpha }_j\ge 0$, $l_j^{{\alpha }_j}$ is the number of all cycles in $Q_{TMTO}$ of size j, and $l_N^{{\alpha }_N}\le N-2$.

Proof. 

Firstly, note that $Q_{TMTO}$ contains, at most, $N-2$ cycles of size N and, at most, ${\displaystyle \frac{N(N-1)}{2}}$ cycles of size 2. In particular, if x is a fixed plaintext ($x\in \mathcal{P}$), then the set of arrows $(y_j,g_{y_j}\left(x\right))$ defines a permutation (${\pi }_x\in S_N$), where $S_N$ denotes the symmetric group consisting of all N-element permutations, ${\pi }_x$ is a product of, at most, and ${\alpha }_j\left(x\right)=\lfloor {\displaystyle \frac{N}{j}}\rfloor$ cycles of size j; then, if all the encryption rules are chosen in such a way that the corresponding quiver ($Q_{TMTO}$) consists only of two cycles, it holds that $N(N-1)={\displaystyle \sum _{x\in \mathcal{P}}}{l}_2^{{\alpha }_2\left(x\right)}$ (note that in this case, there exits $z\in \mathcal{P}$ such that $(y_j,g_{y_j}\left(z\right))=(y_j,y_j)$ for all j). Thus, for any other choice of the encryption rule, it holds that $N(N-1)={\displaystyle \sum _{j=2}^N}{l}_j^{{\alpha }_j}$, provided that any permutation is a product of two cycles. This completes the proof.   □

Next, Theorem 3 provides the properties of a Brauer configuration algebra induced by a quiver of type $Q_{TMTO}$.

Theorem 3. 

Let $Q_{TMTO}$ be a quiver defined by a TMTO for a chosen plaintext attack against a cryptosystem ($\mathfrak{S}=(\mathcal{P},\mathcal{C},\mathcal{K},\mathcal{E},\mathcal{D})$) that achieves perfect secrecy; then, if $Q_{TMTO}$ has an associated integer partition (${\mathfrak{P}}_{TMTO}=l_{i_1}^{{\alpha }_{i_1}}{l}_{i_2}^{{\alpha }_{i_2}}\cdots l_{i_m}^{{\alpha }_{i_m}}$) with ${\alpha }_{i_j}>0$ and $1\le j\le m$, it holds that $Q_{TMTO}$ induces a Brauer configuration algebra (${\Lambda }_{TMTO}$) with the following properties:

• ${\Lambda }_{TMTO}$ is indecomposable as an algebra.
• Each indecomposable projective ${\Lambda }_{TMTO}$ module ($y_i$) has $d{g}^{+}\left(y_i\right)+1$ summands, where $d{g}^{+}\left(x\right)$ is the out-degree of the vertex (x) in $Q_{TMTO}$.
• $${\dim }_k{\Lambda }_{TMTO}=3N+\underset{j=1}{\sum ^m}{\alpha }_{i_j}{t}_{i_j-1}.$$

  (18)

  In particular, $3N+2\lfloor {\displaystyle \frac{N}{2}}\rfloor \le {\dim }_k{\Lambda }_{TMTO}\le N(N^2-3N+5)$, where $t_i$ denotes the ith triangular number.
• ${\dim }_{k}Z\left({\Lambda }_{TMTO}\right)=2N+1$.
• The covering graph ($\mathfrak{c}\left(Q_{TMTO}\right)$) induced by the Brauer quiver ($Q_{TMTO}$) is isomorphic to the N-vertex complete graph ($K_N$).

Proof. 

Note that $Q_{TMTO}$ defines a Brauer configuration (${\mathcal{M}}_{\mathfrak{S}}=(M,\mathfrak{M},\mu ,\mathcal{O})$) of type M such that $M=\{x_1,x_2,\cdots ,x_{\Delta },z_1,z_2,\cdots ,z_N\mid \Delta ={\alpha }_{i_1}+{\alpha }_{i_2}+\cdots +{\alpha }_{i_m}\}$, $\mathfrak{M}=\{(y_1,{\mathfrak{f}}_1),(y_2,{\mathfrak{f}}_2),\cdots ,(y_N,{\mathfrak{f}}_N)\}$, ${\mathfrak{f}}_h\left(z_h\right)=1$, ${\mathfrak{f}}_h\left(z_i\right)=0$ if $i\ne h$, $1\le h\le N$. If $r\in y_i$, then ${\mathfrak{f}}_i\left(r\right)=1$, $val\left(x_i\right)\in \{i_1,i_2,\cdots ,i_m\}$, and $1\le i\le \Delta$. The orientation ($\mathcal{O}$) is represented by arrows and cycles of $Q_{TMTO}$ defined by pairs in the form of $(y_j,e_{y_j}\left(x\right))$, with $x\in \mathcal{P}$ fixed. Under these circumstances, $Q_{TMTO}$ is the Brauer quiver induced by ${\mathcal{M}}_{\mathfrak{S}}$ whose disjoint cycles are special cycles. It induces the Brauer configuration algebra (${\Lambda }_{TMTO}=k{Q}_{TMTO}/I_{TMTO}$, where k is an algebraically closed field and $I_{TMTO}$ is an admissible ideal generated by relations of type ${\rho }_1,{\rho }_2$, and ${\rho }_3$).

In the sequel, we prove the different items proposed in the theorem.

• Note that for $x\in \mathcal{P}$ fixed, the pairs $(y_j,e_{y_j}\left(x\right))$ define a permutation (${\pi }_x\in S_N$), since the TMTO is applied to the complete set ($\mathcal{P}$) and the Brauer configuration (${\mathcal{M}}_{\mathfrak{S}}$) is connected; therefore, the Brauer quiver ($Q_{TMTO}$) is connected.
• Any element ($x\in M$) is non-truncated and defines a unique cycle in $Q_{TMTO}$ up to equivalence. Thus, the out-degree of a vertex ($y_i$) in $Q_{TMTO}$ equals the number of its elements (x) for which $val\left(x\right)>1$. The result holds, provided that each polygon ($y_i$) contains a unique element ($z_i$) such that $val\left(z_i\right)=1$.
• By definition, there are ${\alpha }_{i_j}$ vertices with valency of $i_j$ for $1\le j\le m$. Thus, ${\dim }_k{\Lambda }_{TMTO}=2N+2{\displaystyle \sum _{j=1}^m}{\alpha }_{i_j}\left(i_j(i_j-1)\right)+\left|\{z\in \mathcal{P}\mid val\left(z\right)=1\}\right|$. Moreover, the function expressed as $\mathcal{D}:{\mathfrak{L}}_{\mathfrak{S}}\to {\mathbb{N}}^{+}$ from the set of algebras of type ${\Lambda }_{TMTO}$ (induced by a TMTO for a chosen plaintext attack against the fixed cryptosystem ($\mathfrak{S}$)) to the set of positive integers attains the minimum value ($d_{\mathfrak{S}}$) if $val\left(x_i\right)=2$ for any $x_i\in M$. The maximum value ($m_{\mathfrak{S}}$) of $\mathcal{D}$ is attained if $N-2$ elements in M have a valency of N. The result holds, taking into account that $d_{\mathfrak{S}}=2N+2\Delta +\left|\{z\in M\mid val\left(z\right)=1\}\right|=3N+2\lfloor {\displaystyle \frac{N}{2}}\rfloor$ and $m_{\mathfrak{S}}=2N+(N-2)(N-1)N+\left|\{z\in M\mid val\left(z\right)=1\}\right|=3N+(N-2)(N-1)N$.
• We note that $Q_{TMTO}$ has $N=\left|\mathcal{P}\right|$ vertices and N loops; then, ${\dim }_{k}Z\left({\Lambda }_{TMTO}\right)=1+\#Loops\left(Q_{TMTO}\right)+\left|\mathcal{P}\right|=2N+1$.
• Note that for a fixed key ($y_i$) and $x\in \mathcal{P}$, $E_i=\{y_j\in \mathcal{P}\mid y_j=e_{y_i}\left(x\right)\}=\mathcal{P}$. Thus, any pair ($(y_i,y_j)\in \mathcal{P}\times \mathcal{P}$) with $i\ne j$ can be obtained from an arrow in the form of $(y_i,e_{y_i}\left(x\right))$ for some $x\in \mathcal{P}$. Such an arrow defines the edge ($(y_i,y_j)\in E\left(\mathfrak{c}\left(Q_{TMTO}\right)\right)$).

□

Corollary 1 provides the entropy values associated with the Brauer configuration (${\mathcal{M}}_{\mathfrak{S}}$) defined in Theorem 3.

Corollary 1. 

Let $G=\mathfrak{c}\left(Q_{TMTO}\right)$ be the covering graph induced by the Brauer configuration of type M (${\mathcal{M}}_{\mathfrak{S}}$); then, the following results hold:

• $H_{{\delta }_v}\left(G\right)={\displaystyle \frac{N-1}{N(N+1)}}lo{g}_2(N-1)$.
• $H_{\mathfrak{d}}\left(G\right)=0$.
• $H\left({\mathcal{M}}_{\mathfrak{S}}\right)=-({\displaystyle \frac{{\displaystyle \sum _{j=1}^m}{i}_j{\alpha }_{i_j}lo{g}_2\left(\frac{i_j}{\mathfrak{v}}\right)}{\mathfrak{v}}}+{\displaystyle \frac{2N}{\mathfrak{v}}}lo{g}_2\left({\displaystyle \frac{2}{\mathfrak{v}}}\right))$, where $\mathfrak{v}={\displaystyle \sum _{j=1}^m}{i}_j{\alpha }_{i_j}+2N$.

Proof. 

Since G is $N-1$ regular, it holds that the number of edges in G is $t_N={\displaystyle \frac{N(N+1)}{2}}$. Thus, $H_{{\delta }_v}\left(G\right)={\displaystyle \frac{N-1}{2t_N}}lo{g}_2(N-1)$ and $H_{\mathfrak{d}}\left(G\right)=-\left({\displaystyle \frac{N}{N}}lo{g}_2\left(1\right)\right)=0$.

Since ${\mathcal{M}}_{\mathfrak{S}}$ has N vertices with a valency of 1 and, for each j, there are ${\alpha }_{i_j}$ vertices with a valency of $i_j$, then $H\left({\mathcal{M}}_{\mathfrak{S}}\right)$ has the proposed values by definition. This completes the proof.  □

Theorem 4 provides set-theoretical solutions to the Yang–Baxter equation (see identity (12)).

Theorem 4. 

Let ${\mathfrak{S}}_1$ and ${\mathfrak{S}}_2$ be a pair of Latin square cryptosystems such that ${\mathfrak{S}}_1=(\mathcal{P},\mathcal{C},\mathcal{K},{\mathcal{E}}_1,{\mathcal{D}}_1)$ and ${\mathfrak{S}}_2=(\mathcal{P},\mathcal{C},\mathcal{K},{\mathcal{E}}_2,{\mathcal{D}}_2)$ with $\mathcal{P}=\mathcal{C}=\mathcal{K}=\{1,2,\cdots ,n\}$ and encryption rules ${\mathcal{E}}_1$ and ${\mathcal{E}}_2$ represented by Latin squares $L_1$ and $L_2$, respectively, where $L_2$ is obtained from $L_1$ by applying a permutation ($\pi \in S_n$) to the columns of $L_1$ and $L_2(L_2(t,L_1(t,u)),L_1(L_2(t,L_1(t,u)),$$L_2(t,L_1(t,v))\left)\right)=L_2(t,L_1(t,L_2(u,L_1(u,v))))$ for any $t,u,v\in \{1,2,\cdots ,n\}$; then, the map ($\delta :\mathcal{P}\times \mathcal{P}\to \mathcal{P}\times \mathcal{P}$) such that $\delta =\tau \circ \sigma$, where $\tau (x,y)=(y,x)$ and $\sigma ={\mathfrak{h}}_2\circ {\mathfrak{h}}_1$ with ${\mathfrak{h}}_1(i,j)=(i,L_1(i,j))$ and ${\mathfrak{h}}_2(i,L_1(i,j))=(i,L_2(i,j))$, is a set-theoretical solution of the Yang–Baxter equation.

Proof. 

Note that for $(t,u)\in {\mathcal{P}}^2$, it holds that $\delta (t,u)=(L_2(t,L_1(t,u)),t)$. Thus, if $(t,u,v)\in {\mathcal{P}}^3$, then the following identities hold:

$$\begin{array}{cc}\hfill (\delta \times id)(t,u,v)& =(\delta (t,u),v)=(L_2(t,L_1(t,u)),t)=a_1,\hfill \\ \hfill (id\times \delta )\left(a_1\right)& =(L_2(t,L_1(t,u)),L_2(t,L_1(t,v)),t)=a_2,\hfill \\ \hfill (\delta \times id)\left(a_2\right)& =(L_2(L_2(t,L_1(t,u)),L_1(L_2(t,L_1(t,u)),L_2(t,L_1(t,v)))),L_2(t,L_1(t,u)),t)),\hfill \\ \hfill (\delta \times id)\left(a_2\right)& =a_3=(a_{3,1},a_{3,2},a_{3,3}).\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill (id\times \delta )(t,u,v)& =(t,\delta (u,v))=(t,L_2(u,L_1(u,v)),u)=b_1,\hfill \\ \hfill (\delta \times id)\left(b_1\right)& =(L_2(t,L_1(t,L_2(u,L_1(u,v)))),t,u)=b_2,\hfill \\ \hfill (id\times \delta )\left(b_2\right)& =(L_2(t,L_1(t,L_2(u,L_1(u,v)))),L_2(t,L_1(t,v)),t)=b_3,\hfill \\ \hfill b_3& =(b_{3,1},b_{3,2},b_{3,3}).\hfill \end{array}$$

(20)

Therefore,

$$\begin{array}{cc}\hfill a_{3,1}& =L_2(L_2(t,L_1(t,u)),L_1(L_2(t,L_1(t,u)),L_2(t,L_1(t,v)))),\hfill \\ \hfill b_{3,1}& =L_2(t,L_1(t,L_2(u,L_1(u,v))))=a_{3,1},\hfill \\ \hfill a_{3,2}& =b_{3,2}=L_2(t,L_1(t,u))=b_{3,2},\hfill \\ \hfill a_{3,3}& =b_{3,3}=t.\hfill \end{array}$$

(21)

Thus, $a_3=b_3$ and $\delta$ satisfy the set-theoretical Yang–Baxter equation. This completes the proof.  □

3. Conclusions

Time–memory trade-off (TMTO) allows chosen plaintext attacks to be conducted against cryptosystems with a perfect secrecy property. Such TMTOs give rise to some directed graphs or quivers associated with appropriate Brauer configurations and their induced Brauer configuration algebras. The analysis of algebraic and combinatorial invariants as their dimensions, the composition series of their indecomposable projective modules, and their covering graphs is a Brauer analysis; some of these invariants can be obtained in terms of the size of the corresponding plaintexts and the length of the cycles contained in the quivers. Brauer analysis includes the topological content information analysis of the covering graphs induced by the investigated TMTOs. The analysis can also be applied to Latin square cryptosystems, which achieve perfect secrecy. As a consequence of this study, it is possible to provide set-theoretical solutions to the Yang–Baxter equation based on the structure of the Latin squares, which provide the encryption rules of such cryptosystems.

FutureWork

• TMTOs for chosen plaintext attacks against cryptosystems that achieve perfect secrecy induce appropriate integer partitions. Their Brauer analysis includes studying their defects, which allows for classification of partitions as realizable data over closed connected surfaces such as the projective plane or the sphere. An open problem consists of answering the following question:
  What kinds of directed graphs associated with TMTOs for chosen plaintext attacks induce integer partitions realizable as branch data over the projective plane or another closed, connected surface?