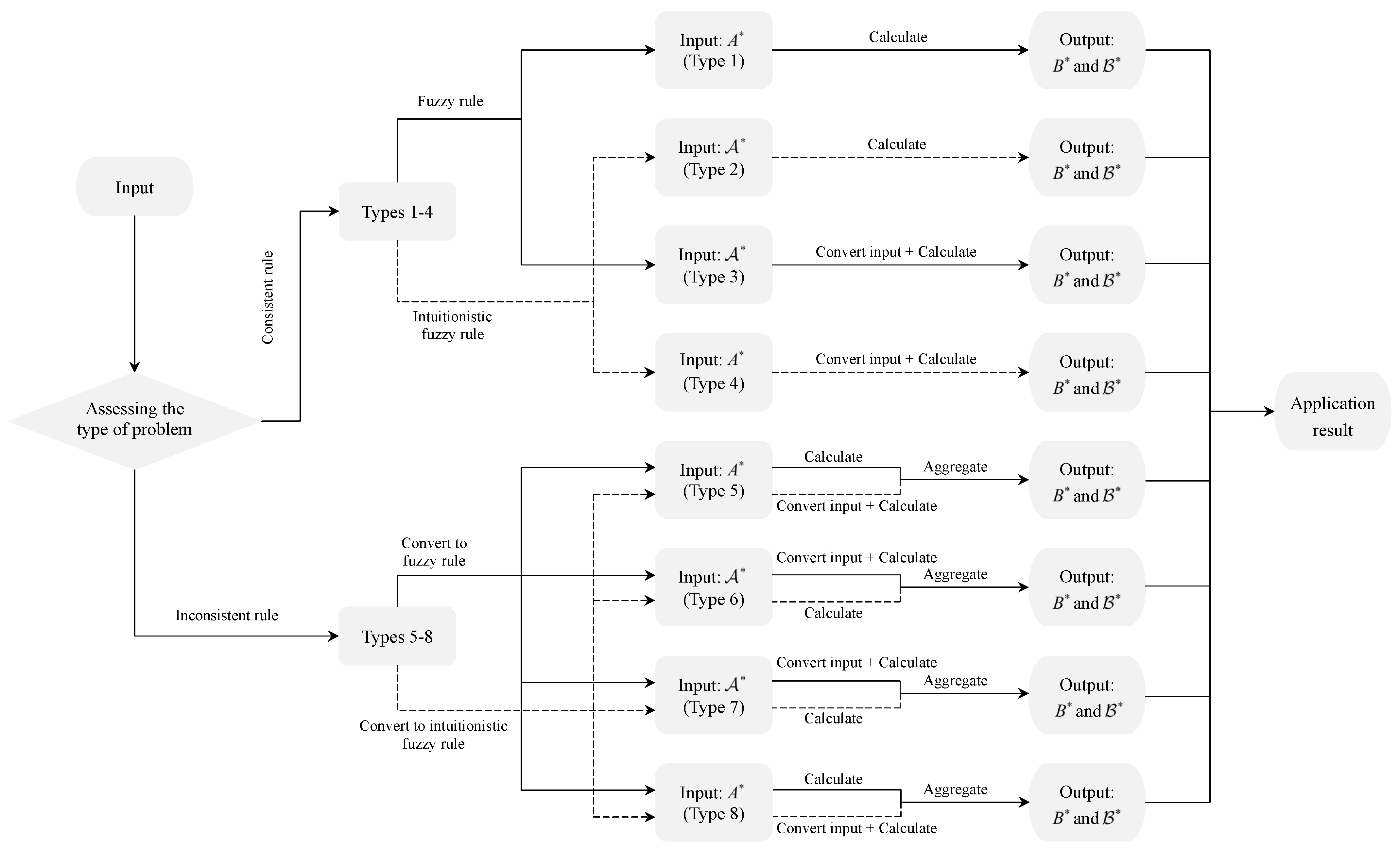
For reasoning with given if–then rules of mixed information, since there may exist the mismatch between the representation of the input and that of the given rules of the knowledge base in real life, the ability of a quintuple-implication reasoning method based on single information is limited. From
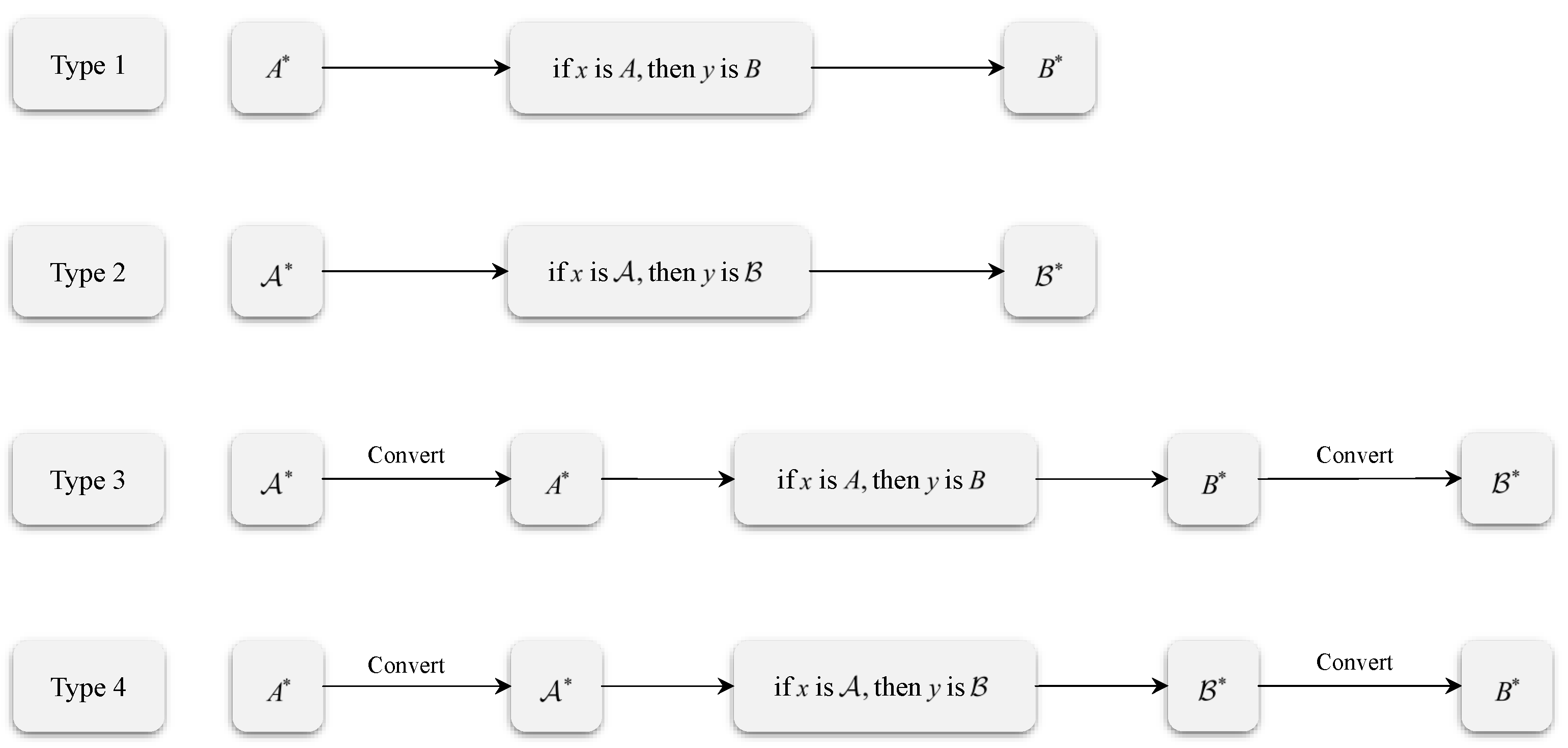
Table 1, it is easy to find that the information types in both rule antecedent and rule consequent are consistent in Types 1–4, whereas they exhibit inconsistency in Types 5–8. Considering this analysis, in this section, we will delve into the quintuple-implication principle for reasoning with mixed information from these two distinct perspectives of the given if–then rules.
As for the inference models with consistent given if–then rules (Types 1–4), the input information first needs to be consistent with the information representation in the given rules. For example, as for Type 3, the input
has the priority to be converted into the same information type
as the given rule “if
x is
A, then
y is
B”; as for Type 4, the input
has the priority to be converted into an intuitionistic fuzzy set
, same as the representation of the given rule “if
x is
, then
y is
”. Then, the subsequent inference steps can be performed to obtain the output with the same representation as the rule, together with the inference result consistent with the representation of the input by employing the reciprocal conversion formula between fuzzy sets and intuitionistic fuzzy sets.
Figure 1 shows the processing framework of the first four types of inference models.
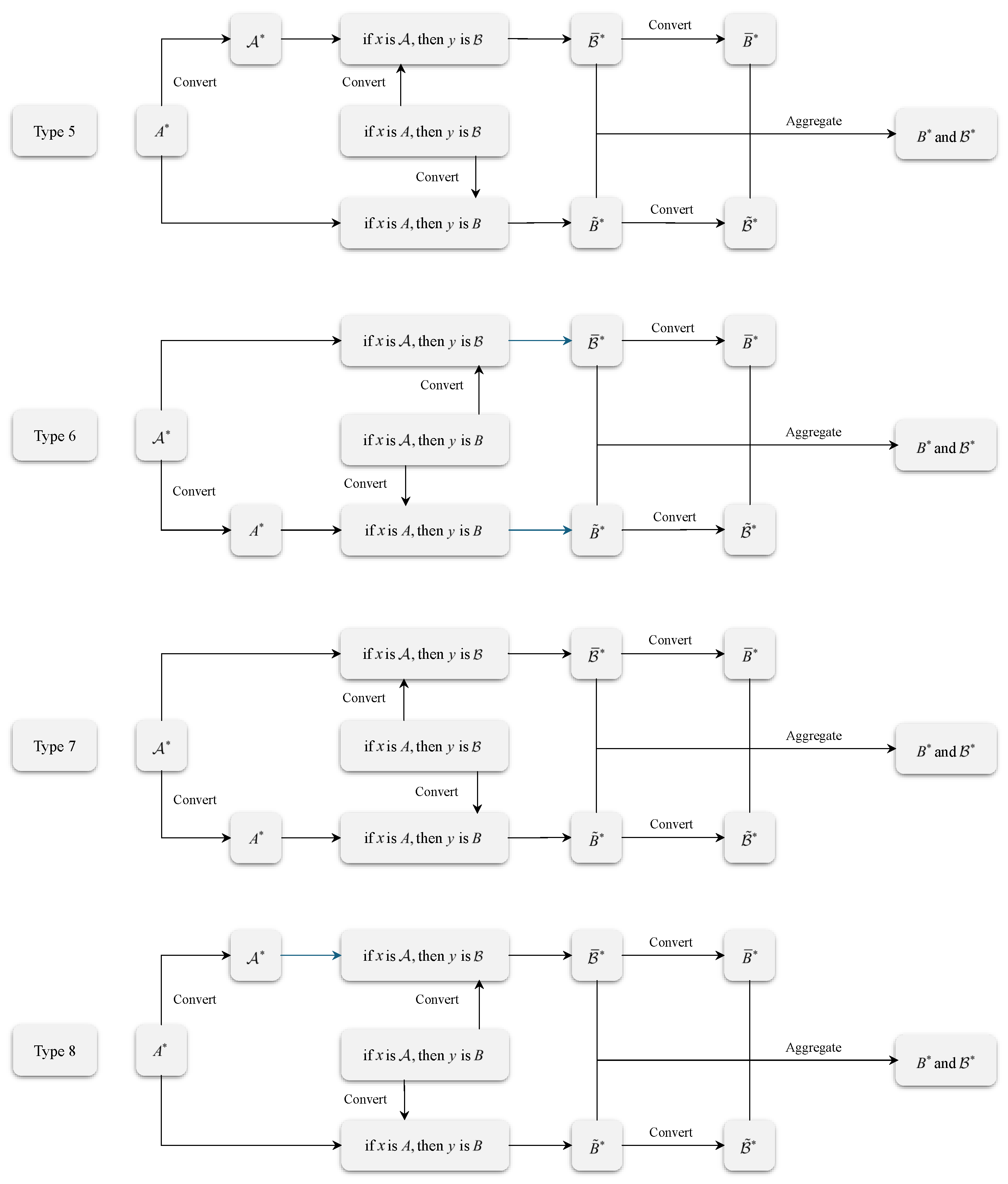
Regarding the inference model Types 5–8 with an inconsistency in the representation of rule antecedent and rule consequent, a given rule containing mixed information needs to be initially converted into a set of two distinct given rules, each having different single information representation through the corresponding conversion operations. For example, as for Types 5 and 7, the inconsistent given rule “if
x is
A, then
y is
” is considered to consist of two consistent given rules “if
x is
A, then
y is
B” with
B converted from
and “if
x is
, then
y is
” with
converted from
A; as for Types 6 and 8, the inconsistent given rule “if
x is
, then
y is
B” is viewed as being composed of two consistent given rules “if
x is
A, then
y is
B” with
A converted from
and “if
x is
, then
y is
” with
converted from
B. Next, the input is combined with each of these two given rules, respectively, to carry out the subsequent inference process. At this stage, the two directions will yield their own outputs and the processing in both directions will be found to be partially similar to the reasoning scheme based on consistent given if–then rules. Ultimately, these outputs are aggregated to produce a final inference result that can be expressed in a form consistent with the rule consequent or in alignment with the input. The processing scheme for reasoning under inconsistent given if–then rules is exhibited in
Figure 2.
3.1. The Quintuple-Implication Fuzzy Reasoning Method with Mixed Information of Consistent Rules
To address the problems in reasoning under consistent rules, we first discuss the mixed information inference problem of Type 4, described as follows:
where
is an intuitionistic fuzzy set on the universe
X,
is an intuitionistic fuzzy set on the universe
Y and
is a fuzzy set on the universe
X. We aim to derive an output based on the referential rule “if
x is
, then
y is
” and the given input “
x is
” by utilizing the quintuple-implication principle.
The method to reasoning with Type 4 mixed information
Step 1: Convert the fuzzy set
into the intuitionistic fuzzy set
via Proposition 1 in [
2], which hence leads to the following problem:
where
and
are intuitionistic fuzzy sets defined on the universe
X, and
and
are intuitionistic fuzzy sets on the universe
Y.
Step 2: Solve the inference problem in Step 1 and obtain the solution
by applying Theorem 2 in [
14] (i.e., quintuple-implication method for Type 2):
where
is an intuitionistic R-implication derived from a left-continuous intuitionistic t-norm
, → is an R-implication derived from a left-continuous t-norm ⊗ and ⊕ is the dual of ⊗.
Step 3: The solution of the Type 4 inference problem is given, as presented in
Table 2.
According to the rule “if
x is
, then
y is
”, the output can be obtained in the form of intuitionistic fuzzy sets, denoted as
. Furthermore, to ensure consistency with the information type of the input “
x is
”, we also present via Definition 3 in [
2] the solution in the form of fuzzy sets, i.e.,
.
Analogously, the inference problem of Type 3 can also be addressed:
where
A and
B represent two fuzzy sets on
X and
Y, respectively, and
is an intuitionistic fuzzy set on
X.
The method to reasoning with Type 3 mixed information
Step 1: Convert the intuitionistic fuzzy sets
into fuzzy set
by using the possibility and necessity operators stated in Definition 3 in [
2], where
. Since the fuzzy set
converted from the input
is determined by two fuzzy sets
and
, to solve the Type 3 inference problem, the following two FMP problems need to be addressed in advance:
where
are fuzzy sets transformed from intuitionistic fuzzy set
on
X, and
A and
B represent two fuzzy sets on
X and
Y, respectively.
Step 2: Obtain the solutions to the above two inference problems. According to Theorem 1 in [
7] (i.e., quintuple-implication method for Type 1),
where → is an R-implication derived from a left-continuous t-norm ⊗.
Step 3: The solution of the Type 3 inference problem is derived, as presented in
Table 3.
The fuzzy output
will be acquired via Equations (
6) and (
7) with the same information representation as the rule “if
x is
A, then
y is
B”, where
. By combining Equations (
6) and (
7) with Definition 3 in [
2], the intuitionistic fuzzy output
of the same type as the input ”
x is
” can likewise be provided, where
.
According to Equations (4)–(
7), the following proposition is presented when the t-norm is Łukasiewicz t-norm
.
Proposition 2. (1) For the Type 4 inference problem, (2) For the Type 3 inference problem, 3.2. The Quintuple-Implication Fuzzy Reasoning Method with Mixed Information of Inconsistent Rules
To reason with inconsistent if–then rules (Types 5–8 mixed information inference problems), it is essential to first gain a precise and comprehensive understanding of the inconsistent rules, conceptualizing one inconsistent rule as comprising two distinct consistent rules, each containing unique information representation.
By this analysis, for each of the Types 5–8 inference problems, the input will be combined with the two consistent rules to conduct the inference process in their respective directions. Further, the conclusions in these two directions will be aggregated to obtain the final inference result for each type, as depicted in
Figure 2. The final inference result will be expressed according to the representation of the input and rule consequent. When the representation of the input and rule consequent is the same, the final inference result will also be written with full consideration in the form that is different from the representation of the two, in addition to giving the final result with the same representation as the two.
Consider the Type 6 inference problem:
where
and
represent two intuitionistic fuzzy sets, respectively, defined on the universe
X, and
B is a fuzzy set on the universe
Y.
The method to reasoning with Type 6 mixed information
Step 1: Determine the output given the intuitionistic fuzzy if–then rule and the input.
The following IFMP problem (i.e., Type 2 inference problem) needs to be addressed:
where
is an intuitionistic fuzzy set on the universe
Y converted from fuzzy set
, and
A and
represent two intuitionistic fuzzy sets, respectively, defined on the universe
X.
Theorem 2 in [
14] is utilized to obtain the intuitionistic fuzzy output
:
where
is an intuitionistic R-implication derived from a left-continuous intuitionistic t-norm
, and further,
where → is an R-implication derived from a left-continuous t-norm ⊗ and ⊕ is the dual t-conorm of ⊗. In order to obtain the final inference result (Step 3), here, the fuzzy output
is also given, where
.
Step 2: Determine the output given the fuzzy if–then rule and the input .
Having considered that this inference issue overlaps with the Type 3 inference problem, the following two FMP problems will be addressed:
where
and
are fuzzy sets on
X converted from intuitionistic fuzzy set
;
and
are fuzzy sets on
X converted from intuitionistic fuzzy set
; and
B represents a fuzzy set on
Y. The above reasoning problems are solved according to Theorem 1 in [
7]:
where → is an R-implication derived from a left-continuous t-norm ⊗.
Thus, from Equations (
15) and (16), we can obtain the fuzzy output
,
and the intuitionistic fuzzy output
,
,
.
Step 3: Obtain the final result of the Type 6 inference problem by consolidating the outcomes of Steps 1 and 2, as presented in
Table 4.
It is easy to prove the following: by combining and , we obtain the fuzzy ; from and , we obtain the intuitionistic fuzzy ; moreover, there exists by referring to Equations (14) and (16).
Similar to the Type 6 inference problem, the solutions of Types 5, 7 and 8 are shown in
Table 5.
Proposition 3. For the Type 6 inference problem, if the t-norm is Łukasiewicz t-norm , Equations (13)–(16) can be rewritten as