1. Introduction
Bivariate distribution is a foundational concept in statistics, offering powerful tools for the simultaneous comparison of two variables. The bivariate conditional approach provides insight into the relationship between the variables and their dependencies. The conditional approach is extensively employed across a wide range of distributions, including various types of generalized distributions. Initially, ref. [
1] proposed a conditional approach for the development and adjustments of a bivariate gamma distribution. Subsequently, ref. [
2,
3,
4,
5,
6,
7] lead the way of the conditional approach for the construction of bivariate distributions. Among the various methods for construction of bivariate distribution explained by [
8], a conditional approach is an effective and robust technique due to its flexibility in integrating baseline distributions with additional functions. The authors of [
9,
10] introduced the bivariate gamma distribution by incorporating a scale parameter function and employing two identical baseline gamma distributions with a conditional approach. The authors of [
11] developed the bivariate distribution through the conditional approach to generate two parametric gamma distribution. In addition, ref. [
12] introduced the bivariate Poisson distribution with univariate conditionals. The authors of [
13] explained a semi-parametric model for the conditional joint distribution of bivariate estimations on the basis of the distribution regression and factorization methods, and ref. [
14] applied the conditional approach to estimate weakly correlated lifetime data in a bivariate model.
The bivariate Lindley distribution is an extension of the conventionally employed Lindley distribution with two dimensions. The bivariate Lindley distribution encounters numerous ways to analyze dependent random variables. The authors of [
15,
16] proposed one scale parameter Lindley distribution as an extended version of traditional exponential distribution. Recently, refs. [
17,
18,
19,
20,
21,
22,
23,
24] made valuable contributions to the construction of the bivariate Lindley distributions and explored the distributions’ potential applications across various fields. The power function (PF) distribution is an incredibly compatible model and fits well for failure rates and remains versatile for evaluating lifetime models. The authors of [
25] discussed the PF distribution due to its flexibility and preferred it over the other distributions. Although trustworthy work on power function distribution has been extensively produced, bivariate power function distributions have been rarely developed.
In the existing literature, bivariate distributions have been primarily constructed by incorporating scale parameter functions with identical baseline distributions, typically employing the conditional approach. However, real-world data sometimes exhibit a mixture of diverse asymmetric distributions, particularly whenever employing extreme and complex nature data. The conditional approach method is preferred over other construction methods due to its capability to mix identical or non-identical asymmetric distributions with incorporating functional parameters. In this research, we propose a bivariate mixture Lindley power function (BMLPF) model by incorporating a shape parameter function with a mixture of two non-identical asymmetric baseline distributions: power function distribution and Lindley distribution. The aim of this study is to explore the potential of this approach to effectively model dependencies while maintaining all the fundamental mathematical properties. This research provides a more generalized and flexible modeling approach for bivariate distributions, extending their applicability across various statistical and real-world domains.
2. The Proposed Mixture Lindley Power Function (MLPF) Distribution
A new bivariate mixture Lindley power function (BMLPF) distribution is developed using functional shape parameter with conditional approach, where conditional distribution is power function (PF) distribution, and marginal distribution is Lindley distribution.
Let a random variable
be characterized by a Lindley distribution.
where
is a scale parameter.
Let another random variable
have a power function distribution with a functional shape parameter
. The conditional distribution of
given
is defined as
By combining the above two Equations (1) and (2), the compound density function is expressed as
Adjusting allows to derive different bivariate distributions with distinct characteristics.
By letting
and incorporating it into Equation (3), the new bivariate distribution is formed with the following pdf:
The CDF of the newly proposed BMLPF distribution is obtained by integrating Equation (4) over the range,
,
where
.
The
Figure 1 provides a visualization of 3D plots for the BMLPF distribution, utilizing different combinations of parameters. These plots depict the asymmetric nature of the proposed distribution.
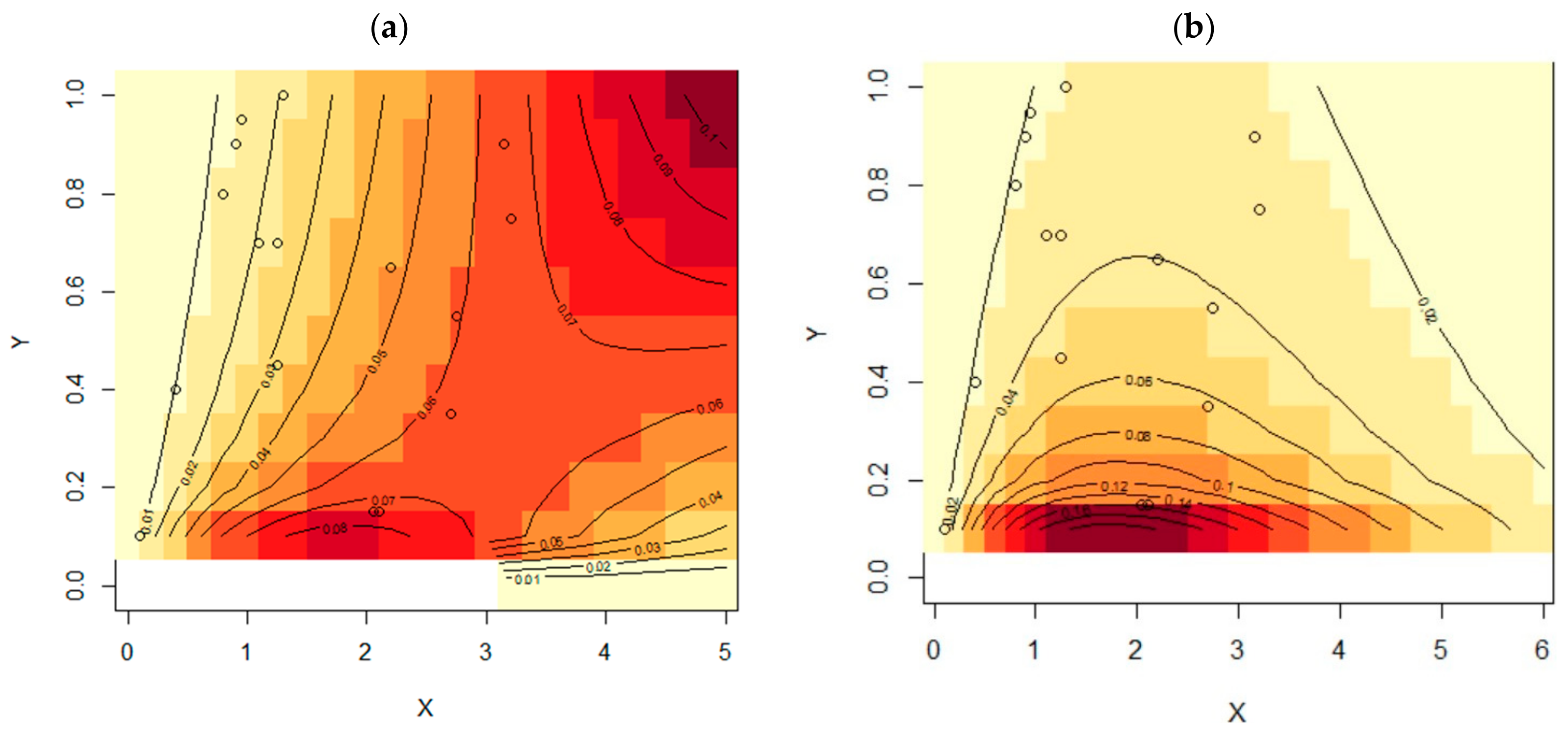
Figure 2 depicts the contour plots of BMLPF distribution for different parametric values. The proposed model exhibits an asymmetric behavior.
2.1. Mathematical Properties of BMLPF Distribution
The mathematical properties for the newly generated BMLPF distribution are explained briefly in this section.
2.1.1. Product Moments
The
product moment for two random variables
and
for the bivariate distribution is
Thus, the expression of
product moment for the joint BMLPF distribution utilizing Equation (6) is
The ratio moment between the random variables
and
are represented by two methods; one of these methods is described as
After simplification, the ratio moment for BMLPF is
Likewise, the other ratio moment for the variable
and
is
After simplification, the expression reduces to the following form:
2.1.2. Conditional Moments and Variances
The conditional density of the BMLPF distribution for
given
is observed as
The
conditional moment for
given
is
The conditional variance for
given
is provided in the
Appendix A. The conditional density for
given
is stated as
The
conditional moment for
given
is
The conditional variance for
given
is provided in the
Appendix A. The variances of
and
are found as
Let
; after simplification
The covariance of two random variables
is
The Pearson product moment correlation between two random variables is as follows:
Incorporating the findings from Equations (9)–(11) in Equation (12), the resultant Pearson correlation coefficient is given below as:
The corresponding marginal density function of
from above CDF is obtained as:
The univariate mixture Lindley power function (MLPF) distribution is derived by integrating BMLPF distribution. The univariate MLPF distribution has an enormous multipurpose structure which will incorporate the effect of mixed data characteristics. The univariate MLPF model will acquire the impact of new added parameters in the model analysis as well as in real life.
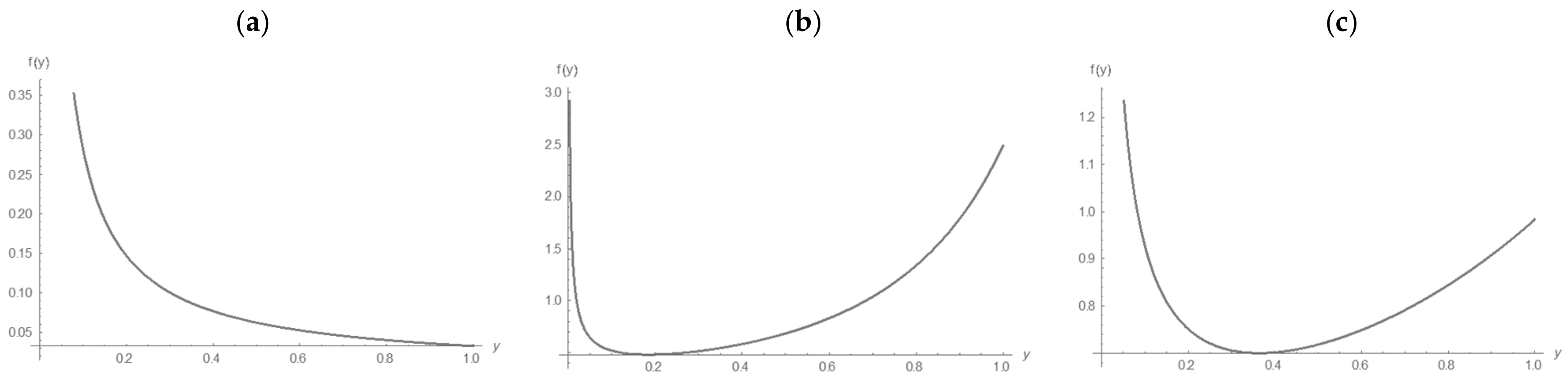
In
Figure 3, it is observed that the marginal MLPF distribution exhibits characteristics of both exponential and bathtub families, depending on parametric values. In
Figure 3a, it aligns with the exponential family. In
Figure 3b,c, the marginal distribution of
reflects the bathtub shape, characterized by a decreasing failure rate, followed by a steady phase and a later increase.
The CDF of MLPF distribution is expressed as
2.2. Properties of MLPF Distribution
The marginal probability function of mixture Lindley power function (MLPF) distribution attained from BMLPF distribution is
where,
and
are scale parameters.
The
moment of MLPF distribution is derived in Equation (16):
Median
The median of MLPF as derived from Equation (14) is presented by the following expression:
Mode
The location of mode is derived from Equation (15), and when
, the mode is positioned at
The survival and hazard rate function of the corresponding MLPF distribution is
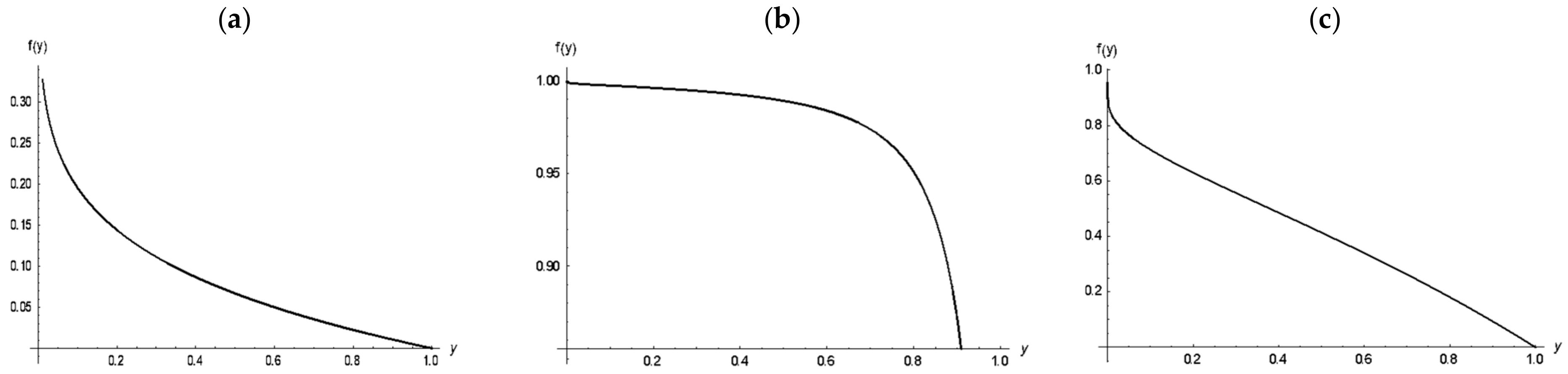
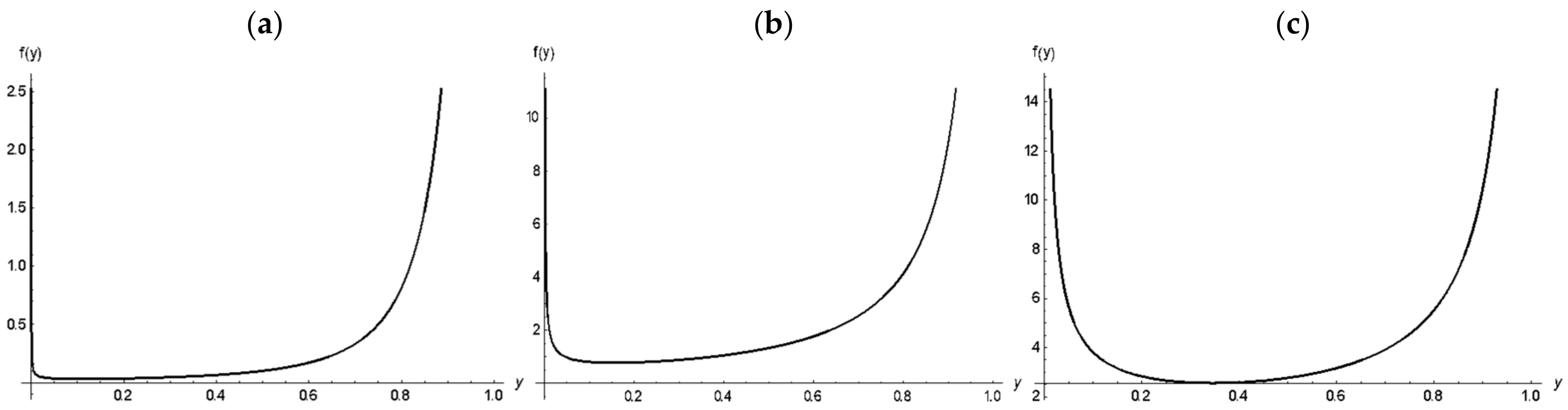
Figure 4 and
Figure 5 illustrate the survival and hazard rate function of MLPF distribution; the survival function exhibits different patterns based on parameter variations. Hazard rate function depicts the bathtub shape.
3. Reliability and Hazard Gradient Function of BMLPF Model
In this section, the evaluation of the joint behavior of the variables of bivariate distribution is effectively conducted through reliability like stress–strength model, survival, and hazard gradient functions.
3.1. Stress–Strength Model
The stress–strength model in reliability studies is utilized to evaluate the lifespan of a module described by stochastic durability
under variable stress conditions
. The model assumes that a component experiences failure when the exerted stress exceeds its durability. It is evident that the component operates effectively when its strength level
exceeds the stress level
. Consequently, the reliability of the component, denoted as R, is measured by the probability
; hence,
. This model is applied in various domains including engineering, biology, and medicine. The authors of [
26] applied the stress–strength model to numerous bivariate distributions. For our distribution, it is calculated as
Since the integral in the reliability component cannot be evaluated analytically, numerical methods can be employed to approximate its value.
3.2. Hazard Gradient Function
The mathematical expression for the hazard rate function for two-dimensional distribution explained by [
27] utilized both combined density function
and the survival function, further applied by [
28], subsequently.
By combining the results from Equations (14) and (19) in Equation (18), the resultant survival function is
The authors of [
29] explained the hazard gradient function for bivariate distribution as
where
denotes the rate of failure of
, satisfying the condition that
given the insights into exposure of
given certain information about
. Correspondingly,
represents the failure occurrence rate in
under the condition
, proposing a perspective on the reliability of
under some specified conditions of
.
The vector
indicates the hazard gradient of BMLPF distribution as
4. Dependency Structure
This section provides an overview of some well-known dependency measures for BMLPF distribution.
4.1. Clayton–Oakes’s Measure of Association
The local dependence function on the basis of survival analysis defined by [
30,
31] is designated as
where
and
By incorporating Equations (4), (20), (23) and (24) into Equation (22), we derived the result as follows:
4.2. Conditional Probability Measure
The authors of [
32] described the measure of association based on conditional probabilities to examine the relationship between two variables in a random vector
This measure is based on survival function of the joint distribution for
and
as well as their marginal survival functions.
For BMLPF distribution, the conditional probability measure calculation is as follows:
Thus, the conditional probability measure is
4.3. Correlation Measure
The Pearson product moment correlation coefficient between
and
, as determined from prior results, is
Due to the non-linearity between
and
, the Pearson correlation coefficient is limited in its effectiveness as observed in
Table 1. Therefore, to assess dependency in the proposed bivariate model, alternative dependency measures such as Kendall’s Tau and Spearman’s rho are more reliable.
5. Parameter Estimation
Numerous studies utilized the parameter estimation by different techniques, among which maximum likelihood estimation (MLE) is the most extensively applied technique. The authors of [
33] utilized this method for the underdetermined parameters of their distribution; ref. [
34] described it for estimating all the parameters jointly, as a one-step parametric method; and ref. [
35] described the mathematical structure for solving non-differential linear equations and partial differential equations.
This section describes MLE for the proposed BMLPF distribution by considering the assumption that the distribution parameters are known. Let
be the random sample of size n from any family of bivariate transmuted distributions. The likelihood function based on MLE for the BMLPF distribution is
The log likelihood functional form of the above equation is
The partial deviations with respect to different parameters are given as
The MLE for the vector of parameter are generated numerically by solving the above equations, which are derived through utilizing the likelihood function for the BMLPF distribution.
6. Generation of Random Sample
The conditional distribution approach is applied for generating random samples from BMLPF distribution. The process proceeds with the following steps:
- (a)
The initial step involves generating random observation by utilizing the CDF of marginal distribution of
- (b)
Moving towards the next step, the CDF of
is derived:
By letting
in Equation (19),
7. Real Data Application
The proposed BMLPF distribution is compared with some existing models. Although models of the same characteristics as those of the proposed model are not available in the literature, certain comparable models are used. This evaluation is performed by means of comparative analysis utilizing two real-world datasets. The following bivariate densities are utilized for real datasets.
Bivariate distribution with Rayleigh and Lindley distributions [
20]:
The authors of [
36] presented bivariate Poisson generalized Lindley distributions as
Bivariate Weibull distributions generated by [
37]:
The authors of [
38] introduced the Bivariate exponential distribution:
The two datasets are selected for their distinct characteristics: one featuring variables with different units, indicative of mixture nature, and the other representing non-mixture distribution. Using both the datasets, the model’s flexibility and effectiveness is accessed across different types of bivariate data structures. The first real dataset includes the bivariate measurement of bone mineral density (BMD) for the dominant ulna and ulna bones recorded in gram per square centimeter (gm/cm
2) from 24 children at the age of one, collected by [
39] and further utilized by [
40]. For comparison purposes, four other distributions are considered alongside the new proposed BMLPF distribution. The maximum likelihood estimates along with their standard errors are computed and the Akaike information criteria (AIC), and Bayesian information Criteria (BIC) are utilized to further evaluate the BMLPF model performance using the maxLik package in R (v: 4.3.2).
| X | 0.87 | 0.60 | 0.77 | 0.76 | 0.55 | 0.75 | 0.71 | 0.69 | 0.84 | 0.87 | 0.65 | 0.69 |
| Y | 0.97 | 0.69 | 0.74 | 0.70 | 0.62 | 0.52 | 0.79 | 0.72 | 0.66 | 0.79 | 0.73 | 0.53 |
| X | 0.67 | 0.82 | 0.75 | 0.66 | 0.69 | 0.88 | 0.58 | 0.80 | 0.54 | 0.80 | 0.57 | 0.59 |
| Y | 0.58 | 0.77 | 0.73 | 0.51 | 0.74 | 0.79 | 0.63 | 0.77 | 0.50 | 0.78 | 0.63 | 0.64 |
Table 2.
Maximum likelihood estimates for different distributions on Data 1.
Table 2.
Maximum likelihood estimates for different distributions on Data 1.
| Data 1 |
|---|
| Distribution | Parameters | Estimate | SE | Log Likelihood | AIC | BIC |
|---|
New Bivariate Mixture
Lindley Power Function Distribution (BMLPF) | | 2.9388 | 5.9841 | | | |
| 0.9296 | 1.8991 | −7.5773 | 21.1546 | 24.6887 |
| 1.8893 | 0.3076 | | | |
| Bivariate Distribution with Rayleigh and Lindley Distributions | | 1.7635 | 0.2896 | | | |
| 0.5184 | 0.0564 | −14.3791 | 32.7581 | 35.1142 |
| Bivariate Poisson Generalized Lindley Distribution | | 4.5444 | 0.0631 | | | |
| 49.0902 | 0.7476 | −41.4652 | 90.9303 | 95.6425 |
| 0.0671 | 0.7476 | | | |
| 0.0631 | 0.0237 | | | |
| Bivariate Weibull Distribution | | 2.0719 | 0.3674 | −21.7882 | 47.5764 | 49.9326 |
| 2.4118 | 0.4620 | | | |
| Bivariate Exponential Distribution | | 1.4035 | 0.2865 | −35.9723 | 73.9446 | 75.1226 |
The second dataset comprises of bivariate data obtained from 51 USA cities, where X is represented as the average precipitation measured in millimeters, and Y is denoted as the average max temperature measured in degree Celsius, originally generated by USA National Clinic Data Center (NCDC) and utilized by [
20].
| X | 99 | 61 | 86 | 113 | 96 | 83 | 57 | 80 | 79 | 75 | 70 | 15 | 62 | 95 | 81 |
| Y | 12 | 17 | 7 | 13 | 5 | 2 | 12 | 2 | 6 | 4 | 5 | 14 | 6 | 2 | 4 |
| X | 71 | 44 | 13 | 52 | 97 | 146 | 52 | 52 | 29 | 108 | 135 | 102 | 48 | 66 | 90 |
| Y | 18 | 4 | 19 | 5 | 14 | 20 | 8 | 11 | 26 | 1 | 3 | 10 | 18 | 6 | 10 |
| X | 22 | 72 | 176 | 107 | 84 | 83 | 37 | 67 | 83 | 36 | 49 | 39 | 102 | 66 | 154 |
| Y | 23 | 7 | 20 | 4 | 7 | 6 | 12 | 10 | 20 | 3 | 12 | 3 | 18 | 14 | 8 |
| X | 72 | 63 | 83 | 77 | | | | | | | | | | | |
| Y | 6 | 22 | 11 | 8 | | | | | | | | | | | |
Table 3.
Maximum likelihood estimates for different distributions on Data 2.
Table 3.
Maximum likelihood estimates for different distributions on Data 2.
| Data 2 |
|---|
| Distribution | Parameters | Estimates | SE | Log Likelihood | AIC | BIC |
|---|
New Bivariate Mixture
Lindley Power Function Distribution (BLMPF) | | 0.3739 | 3.8975 | | | |
| 0.7170 | 7.4745 | −10.6927 | 27.3854 | 33.1809 |
| 1.7725 | 0.1968 | | | |
| Bivariate Distribution with Rayleigh and Lindley Distributions | α | 19.243 | 2.097 | | | |
| φ | 173.842 | 4.689 | −473.153 | 950.3069 | 954.1705 |
| Bivariate Poisson Generalized Lindley Distribution | | 0.3375 | 2.2495 | | | |
| 27.0658 | 7.1301 | −63.0167 | 134.0335 | 141.7608 |
| 0.00966 | 0.0678 | | | |
| 0.00131 | 0.0092 | | | |
| Bivariate Weibull Distribution | | 1.5087 | 0.18386 | −36.9440 | 77.8880 | 81.7517 |
| 0.4999 | 0.06128 | | | |
| Bivariate Exponential Distribution | | 1.3027 | 0.1824 | −60.5942 | 123.1885 | 125.1203 |
To access the adequacy of the new BLMPF distribution, it is compared with the four existing distributions: two mixture distributions and two non-mixture distributions (
Table 2 and
Table 3). Through statistical assessment using AIC (Akaike information criteria), BIC (Bayesian information criteria), log likelihood, and SE, the proposed model shows enhanced alignment in reflecting data patterns. In
Table 2, the evaluation of AIC = 21.1546 and BIC = 24.6887 values suggests that the proposed distribution Is the most appropriate model for Data 1. Likewise,
Table 3 reflects the BLMPF distribution as a best fit for Data 2, as supported by its minimal AIC = 27.3854 and BIC = 33.1809 values. The significantly lower values of AIC and BIC show the optimal balance between generalizability and complexity. This exhibits efficacy of BLMPF distribution to accommodate diverse data structures with reliability and precision. Comparative analysis reveals that, for both real-life datasets, the proposed BLMPF distribution achieved the minimum AIC and BIC values, making it the most suitable model for the analyzed data.
8. Simulation Study
The simulation algorithm is also generated for the estimation of parametric values for the sample sizes n = 50, 100, 200, 500, 1000 based on 10000 replications using R package. A set of varying parameters is taken to evaluate the potential of model to remain consistent across different magnitudes. The analysis included root mean squared errors (RMSE), mean estimates, standard errors (SE), and bias and confidence intervals for each sample size. The resulting data are outlined as follows.
The
Table 4 provides the estimated values for the parameters corresponding to
1.00
. The results indicate that the parameter estimates closely align with the initial values. It is observed that, with the increase in sample size, both the bias and SE show a decreasing trend. However, the LCL and UCL remain nearly consistent across different sample sizes.
In
Table 5, the second combination of parameters set at
are detailed. The outcomes reinforce that the estimation procedure reliably generates the parameter values close to their initial settings. The Bias, SE, and RMSE decline with increasing sample size, supporting the model’s strength.
The
Table 6 displays the estimated values for the parameters for
for the sample sizes of n = 50, 100, 200, 500, and 1000. The results indicate that increasing sample size leads to more accurate estimates of the BMLPF distribution. The reduction in bias, SE, and RMSE across large sample sizes underscores the robustness of the maximum likelihood estimation procedure. These findings indicate BMLPF distribution achieved the minimum AIC and BIC values, making it the most suitable model for the analyzed data.
9. Conclusions
In this article, the new BMLPF distribution is generated by combining the power function distribution and Lindley distribution as non-identical asymmetric baselines by the incorporation of a functional shape parameter via a conditional approach. This study covers various properties, including product moments, conditional densities, correlations, conditional means, and variances. This study also assesses reliability, hazard functions, dependency structure, and parameter estimation through maximum likelihood estimation. Practical application of the model is presented through real-world data analysis and simulation experiments. The comparative evaluation with four alternative models depicts considerably lower values for AIC and BIC of the proposed BMLPF distribution. The results validate the adaptability of proposed distribution to model various data structures, including distributions of both mixture and non-mixture nature while maintaining reliability and consistency. The simulation study with varying sets of parameters shows parameter estimates are consistent with the baseline values. Moreover, the analysis indicates a decreasing trend of bias and SE with the increase in sample size. Further research can explore the impact of adjusting shape parameter functions to derive distinct bivariate distributions, each characterized by specific dependency structures. Future studies can expand on these findings to extend the bivariate framework into multivariate distribution models.
Author Contributions
A.A.: Conceptualization, methodology, software, formal analysis, investigation, validation, writing—original draft; M.I.: resources, supervision, project administration, formal analysis; M.F.: supervision, validation, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All the data are available within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| BMLPF | Bivariate mixture Lindley power function |
| MLPF | Mixture Lindley power function |
| RMSE | Root mean square error |
| SE | Standard error |
| UCL | Upper control limit |
| LCL | Lower control limit |
| Nomenclature |
| First random variable |
| Second random variable |
| Joint probability density function |
| Joint cumulative distribution Function |
| CDF | Joint cumulative distribution Function |
| Scale parameter |
| Shape parameter |
| Shape parameter |
| Shape parameter function |
| 3D | Three Dimensional |
| product moment |
| Conditional probability density function of given y |
| conditional moment for given |
| conditional moment for given |
| conditional variance for given |
| conditional density for given |
| conditional moment for given |
| conditional variance for given |
| Variance of |
| Variance of |
| Presumed term for ease of computation |
| Upper Incomplete Gamma function |
| Pearson Correlation measure |
| Covariance between and |
| Marginal distribution of |
| Distribution Function of Y |
| moment of MLPF distribution |
| Survival function of MLPF distribution |
| Hazard rate function |
| Reliability of a component |
| Hazard rate function of two-dimensional distribution |
| Survival function of two-dimensional distribution |
| rate of failure of X satisfying the condition that |
| rate of failures of under circumstances, where |
| Clayton–Oakes’s measure of association |
| Conditional probability measure |
| Partial derivative |
| Lambert W function |
| Uniform random number |
| Uniform random numbers from X using respective CDF |
| n | Sample size |
| AIC | Akaike information criteria |
| BIC | Bayesian information criteria |
| gm/cm2 | gram per square centimeter |
Appendix A
The conditional moment for
given
is:
The conditional moment for
given
is:
The conditional variance for
given
is as:
The conditional moment for
given
is:
The conditional moment for
given
is:
The conditional Variance of
given
is:
References
- McKay, A. Sampling from batches. Suppl. J. R. Stat. Soc. 1934, 1, 207–216. [Google Scholar] [CrossRef]
- Patil, G.P. On a Characterization of Multivariate Distribution by a Set of Its Conditional Distributions. Bull. Int. Stat. Inst. 1965, 41, 768–769. [Google Scholar]
- Besag, J. Spatial interaction and the statistical analysis of lattice systems. J. R. Stat. Soc. Ser. B (Methodol.) 1974, 36, 192–225. [Google Scholar] [CrossRef]
- Abrahams, J.; Thomas, J.B. A note on the characterization of bivariate densities by conditional densities. Commun. Stat.-Theory Methods 1984, 13, 395–400. [Google Scholar] [CrossRef]
- Castillo, E.; Galambos, J. Bivariate distributions with normal conditionals. Proc. Int. Assoc. Sci. Technol. Dev. 1987, 2, 59–62. [Google Scholar]
- Arnold, B.C.; Strauss, D. Pseudolikelihood estimation: Some examples. Sankhyā Indian J. Stat. Ser. B 1991, 53, 233–243. [Google Scholar]
- Wong, A.C. Shorter Communication: Inferences on the Shape Parameter of a Gamma Distribution: A Conditional Approach. Technometrics 1992, 34, 348–351. [Google Scholar] [CrossRef]
- Lai, C.D.; Balakrishnan, N. Continuous Bivariate Distributions; Springer: New York, NJ, USA, 2009. [Google Scholar]
- Mohsin, M.; Spöck, G.; Pilz, J. On the performance of a new bivariate pseudo Pareto distribution with application to drought data. Stoch. Environ. Res. Risk Assess. 2012, 26, 925–945. [Google Scholar] [CrossRef]
- Mohsin, M.; Pilz, J.; Spöck, G.; Ahsanullah, M. On some new bivariate pseudo-Gamma distribution. J. Appl. Stat. Sci. 2010, 18, 239. [Google Scholar]
- Amarasekara, S. A New Bivariate Distribution with Applications; The University of Texas at El Paso: El Paso, TX, USA, 2014. [Google Scholar]
- Ghosh, I.; Marques, F.; Chakraborty, S. A new bivariate Poisson distribution via conditional specification: Properties and applications. J. Appl. Stat. 2021, 48, 3025–3047. [Google Scholar] [CrossRef]
- Wang, Y.; Oka, T.; Zhu, D. Bivariate distribution regression with application to insurance data. Insur. Math. Econ. 2023, 113, 215–232. [Google Scholar] [CrossRef]
- Tendijck, S.; Eastoe, E.; Tawn, J.; Randell, D.; Jonathan, P. Modeling the extremes of bivariate mixture distributions with application to oceanographic data. J. Am. Stat. Assoc. 2023, 118, 1373–1384. [Google Scholar] [CrossRef]
- Lindley, D.V. Fiducial distributions and Bayes’ theorem. J. R. Stat. Society. Ser. B (Methodol.) 1958, 20, 102–107. [Google Scholar] [CrossRef]
- Lindley, D. Introduction to Probability and Statistics from a Bayesian Viewpoint, Part 1: Probability; Cambridge University Press: Cambridge, UK, 1965; pp. 134–136. [Google Scholar]
- Zamani, H.; Faroughi, P.; Ismail, N. Bivariate Poisson-Lindley distribution with application. J. Math. Stat. 2015, 11, 1. [Google Scholar] [CrossRef][Green Version]
- Vaidyanathan, V.; Sharon Varghese, A. Morgenstern type bivariate Lindley distribution. Stat. Optim. Inf. Comput. 2016, 4, 132–146. [Google Scholar] [CrossRef]
- Irshad, M.R.; Maya, R.; Ds, S. Estimation of Parameters of morgenstern type bivariate lindley distribution by ranked set sampling. Istat. J. Turk. Stat. Assoc. 2019, 12, 25–34. [Google Scholar]
- Thomas, P.Y.; Jose, J. A new bivariate distribution with Rayleigh and Lindley distributions as marginals. J. Stat. Theory Pract. 2020, 14, 1–38. [Google Scholar] [CrossRef]
- Oliveira, R.P.; Achcar, J.A.; Mazucheli, J.; Bertoli, W. A new class of bivariate Lindley distributions based on stress and shock models and some of their reliability properties. Reliab. Eng. Syst. Saf. 2021, 211, 107528. [Google Scholar] [CrossRef]
- Papageorgiou, H.; Vardaki, M. Bivariate Discrete Poisson–Lindley Distributions. J. Stat. Theory Pract. 2022, 16, 30. [Google Scholar] [CrossRef]
- Elhassanein, A. On statistical properties of a new bivariate modified Lindley distribution with an application to financial data. Complexity 2022, 2022, 2328831. [Google Scholar] [CrossRef]
- Ghorbel, M.A.; Mecene, R. On the Bivariate Generalized Gamma-Lindley Distribution. Math. Slovaca 2023, 73, 511–528. [Google Scholar] [CrossRef]
- Meniconi, M.; Barry, D. The power function distribution: A useful and simple distribution to assess electrical component reliability. Microelectron. Reliab. 1996, 36, 1207–1212. [Google Scholar] [CrossRef]
- Nadarajah, S.; Kotz, S. Reliability for some bivariate exponential distributions. Math. Probl. Eng. 2006, 2006, 041652. [Google Scholar] [CrossRef]
- Basu, A. Bivariate failure rate. J. Am. Stat. Assoc. 1971, 66, 103–104. [Google Scholar] [CrossRef]
- Mohsin, M.; Kazianka, H.; Pilz, J.; Gebhardt, A. A new bivariate exponential distribution for modeling moderately negative dependence. Stat. Methods Appl. 2014, 23, 123–148. [Google Scholar] [CrossRef]
- Johnson, N.L.; Kotz, S. A vector multivariate hazard rate. J. Multivar. Anal. 1975, 5, 53–66. [Google Scholar] [CrossRef]
- Clayton, D.G. A model for association in bivariate life tables and its application in epidemiological studies of familial tendency in chronic disease incidence. Biometrika 1978, 65, 141–151. [Google Scholar] [CrossRef]
- Oakes, D. Bivariate survival models induced by frailties. J. Am. Stat. Assoc. 1989, 84, 487–493. [Google Scholar] [CrossRef]
- Anderson, J.E.; Louis, T.A.; Holm, N.V.; Harvald, B. Time-dependent association measures for bivariate survival distributions. J. Am. Stat. Assoc. 1992, 87, 641–650. [Google Scholar] [CrossRef]
- Kundu, D.; Gupta, A.K. On bivariate Weibull-geometric distribution. J. Multivar. Anal. 2014, 123, 19–29. [Google Scholar] [CrossRef]
- Abd Elaal, M.K.; Jarwan, R.S. Inference of bivariate generalized exponential distribution based on copula functions. Appl. Math. Sci. 2017, 11, 1155–1186. [Google Scholar]
- Nave, O. Modification of semi-analytical method applied system of ODE. Mod. Appl. Sci 2020, 14, 75. [Google Scholar] [CrossRef]
- Rasheed, I.M.; Dcruz, V.; Radhakumari, M.; Devi, S.A.; Khan, N.M. Bivariate Poisson Generalized Lindley Distributions and the Associated BINAR (1) Processes. Austrian J. Stat. 2024, 53, 1–28. [Google Scholar] [CrossRef]
- Shahbaz, S.H.; Al-Sobhi, M.; Shahbaz, M.Q.; Al-Zahrani, B. A new multivariate Weibull distribution. Pak. J. Stat. Oper. Res. 2018, 14, 75–88. [Google Scholar] [CrossRef]
- Mohsin, M.; Pilz, J.; Gunter, S.; Shahbaz, S.; Shahbaz, M.Q. Some distributional properties of the concomitants of record statistics for bivariate pseudo-exponential distribution and characterization. J. Prime Res. Math. 2010, 6, 32–37. [Google Scholar]
- Johnson, R.A.; Wichern, D. Applied Multivariate Statistical Analysis. Biometrics 1998, 54, 1203. [Google Scholar] [CrossRef]
- Mohammed, B.; Hossain, M.M.; Aldallal, R.; Mohamed, M.S. Bivariate Kumaraswamy distribution based on conditional hazard functions: Properties and application. Math. Probl. Eng. 2022, 2022, 2609042. [Google Scholar] [CrossRef]
Figure 1.
The Bivariate mixture Lindley power function (BMLPF) distribution 3D plots.
Figure 1.
The Bivariate mixture Lindley power function (BMLPF) distribution 3D plots.
Figure 2.
Contour plots of BMLPF distribution. (a) k = 0.18, θ = 0.25, β = 0.08 and (b) k = 0.8, θ = 1.25, β = 0.08.
Figure 2.
Contour plots of BMLPF distribution. (a) k = 0.18, θ = 0.25, β = 0.08 and (b) k = 0.8, θ = 1.25, β = 0.08.
Figure 3.
MLPF Model. (a) MLPF with ; (b) MLPF with ; (c) MLPF with .
Figure 3.
MLPF Model. (a) MLPF with ; (b) MLPF with ; (c) MLPF with .
Figure 4.
Survival function plot of MLPF Model. (a) Survival function plots of MLPF with β = 0.14, θ = 3, k = 0.72; (b) Survival function plots of MLPF with β = 2.85, θ = 0.1, k = 1.48; (c) Survival function plots of MLPF with β = 0.32, θ = 3, k = 0.33.
Figure 4.
Survival function plot of MLPF Model. (a) Survival function plots of MLPF with β = 0.14, θ = 3, k = 0.72; (b) Survival function plots of MLPF with β = 2.85, θ = 0.1, k = 1.48; (c) Survival function plots of MLPF with β = 0.32, θ = 3, k = 0.33.
Figure 5.
Hazard rate function plot of MLPF model. (a) Hazard rate function plots of MLPF with β = 2.02, θ = 0.17, k = 1.06; (b) Hazard rate function plots of MLPF with β = 0.61, θ = 0.89, k = 0.61; (c) Hazard rate function plots of MLPF with β = 0.31, θ = 2.67, k = 2.37.
Figure 5.
Hazard rate function plot of MLPF model. (a) Hazard rate function plots of MLPF with β = 2.02, θ = 0.17, k = 1.06; (b) Hazard rate function plots of MLPF with β = 0.61, θ = 0.89, k = 0.61; (c) Hazard rate function plots of MLPF with β = 0.31, θ = 2.67, k = 2.37.
Table 1.
Pearson correlation for BMLPF distribution.
Table 1.
Pearson correlation for BMLPF distribution.
| | | | | | | | | | | |
|---|
| 0.5 | 0.5 | | 0.5531 | 1 | 0.5 | | 0.5426 | 2 | 0.5 | | 0.4917 |
| 0.5435 | | 0.5140 | | 0.4478 |
| 0.5303 | | 0.4880 | | 0.4136 |
| 0.5164 | | 0.4651 | | 0.3860 |
| 0.5029 | | 0.4451 | | 0.3672 |
| 1.5 | | 0.5303 | 1.5 | | 0.5657 | 1.5 | | 0.5663 |
| 0.5461 | | 0.5664 | | 0.5477 |
| 0.5523 | | 0.5604 | | 0.5279 |
| 0.5539 | | 0.5519 | | 0.5091 |
| 0.5531 | | 0.5426 | | 0.4917 |
| 2.5 | | 0.5010 | 2.5 | | 0.5514 | 2.5 | | 0.5738 |
| 0.5250 | | 0.5639 | | 0.5693 |
| 0.5383 | | 0.5673 | | 0.5594 |
| 0.5461 | | 0.5664 | | 0.5477 |
| 0.5505 | | 0.5633 | | 0.5358 |
| 3.5 | | 0.4775 | 3.5 | | 0.5351 | 3.5 | | 0.5697 |
| 0.5055 | | 0.5541 | | 0.5738 |
| 0.5224 | | 0.5628 | | 0.5704 |
| 0.5335 | | 0.5665 | | 0.5639 |
| 0.5409 | | 0.5673 | | 0.5561 |
Table 4.
Simulation-1 study of BMLPF distribution with combination of parameters.
Table 4.
Simulation-1 study of BMLPF distribution with combination of parameters.
|
|---|
| | Parameters | 50 | 100 | 200 | 500 | 1000 |
|---|
| ESTIMATES | | 3.00019 | 3.00018 | 3.00021 | 3.00020 | 3.00019 |
| 1.00029 | 1.00029 | 1.00033 | 1.00029 | 1.00031 |
| 1.25036 | 1.25040 | 1.25041 | 1.25045 | 1.25038 |
| RMSE | | 0.00271 | 0.00194 | 0.00388 | 0.00279 | 0.00296 |
| 0.00491 | 0.00357 | 0.00497 | 0.00358 | 0.00551 |
| 0.00359 | 0.00566 | 0.00597 | 0.00848 | 0.00480 |
| SE | | 0.00038 | 0.00019 | 0.00027 | 0.00012 | 0.00009 |
| 0.00069 | 0.00036 | 0.00035 | 0.00016 | 0.00017 |
| 0.00051 | 0.00056 | 0.00042 | 0.00038 | 0.00015 |
| BIAS | | 0.03324 | 0.01807 | 0.00957 | 0.00386 | 0.00165 |
| 0.05222 | 0.02571 | 0.01470 | 0.0054 | 0.00305 |
| 0.06719 | 0.04021 | 0.02025 | 0.00854 | 0.00377 |
| LCL | | 2.99944 | 2.99981 | 2.99967 | 2.99996 | 3.00001 |
| 0.99893 | 0.99959 | 0.99965 | 0.99998 | 0.99996 |
| 1.24936 | 1.24929 | 1.24958 | 1.24971 | 1.25008 |
| UCL | | 3.00094 | 3.00057 | 3.00075 | 3.00045 | 3.00037 |
| 1.00165 | 1.00099 | 1.00102 | 1.00061 | 1.00065 |
| 1.25136 | 1.25151 | 1.251243 | 1.25119 | 1.25068 |
Table 5.
Simulation-2 study of BMLPF distribution with combination of parameters.
Table 5.
Simulation-2 study of BMLPF distribution with combination of parameters.
|
|---|
| | | 50 | 100 | 200 | 500 | 1000 |
|---|
| ESTIMATES | k | 3.50020 | 3.50021 | 3.50020 | 3.50018 | 3.50019 |
| 1.25028 | 1.25033 | 1.25027 | 1.25029 | 1.25033 |
| 2.50038 | 2.50044 | 2.50045 | 2.50042 | 2.50042 |
| RMSE | k | 0.00300 | 0.00328 | 0.00353 | 0.00188 | 0.00297 |
| 0.00368 | 0.00644 | 0.00284 | 0.00337 | 0.00643 |
| 0.00614 | 0.00849 | 0.00849 | 0.00729 | 0.00727 |
| BIAS | k | 0.03800 | 0.01933 | 0.00945 | 0.00303 | 0.00193 |
| 0.05406 | 0.02933 | 0.01078 | 0.00557 | 0.00319 |
| 0.06861 | 0.04078 | 0.02164 | 0.00814 | 0.00415 |
| SE | k | 0.00042 | 0.00033 | 0.00025 | 0.00008 | 0.00009 |
| 0.00052 | 0.00064 | 0.00020 | 0.00015 | 0.00020 |
| 0.00087 | 0.00085 | 0.00060 | 0.00033 | 0.00023 |
| LCL | k | 3.49937 | 3.49956 | 3.49971 | 3.50002 | 3.50001 |
| 1.24926 | 1.24907 | 1.24988 | 1.24999 | 1.24993 |
| 2.49868 | 2.49877 | 2.49927 | 2.49978 | 2.49997 |
| UCL | k | 3.50103 | 3.50085 | 3.50068 | 3.50035 | 3.50038 |
| 1.25131 | 1.25159 | 1.25066 | 1.25058 | 1.25073 |
| 2.50208 | 2.50211 | 2.50162 | 2.50106 | 2.50087 |
Table 6.
Simulation-3 study of BMLPF distribution with combination of parameters.
Table 6.
Simulation-3 study of BMLPF distribution with combination of parameters.
|
|---|
| | Parameters | 50 | 100 | 200 | 500 | 1000 |
|---|
| ESTIMATES | | 2.00019 | 2.00017 | 2.00019 | 2.00017 | 2.00019 |
| 3.55033 | 3.55029 | 3.55027 | 3.55029 | 3.55029 |
| 1.05042 | 1.05045 | 1.05036 | 1.05035 | 1.05042 |
| RMSE | | 0.00287 | 0.00140 | 0.00255 | 0.00165 | 0.00219 |
| 0.00531 | 0.00345 | 0.00305 | 0.00413 | 0.00351 |
| 0.00701 | 0.00691 | 0.00449 | 0.00297 | 0.00786 |
| SE | | 0.00041 | 0.00014 | 0.00018 | 0.00007 | 0.000069 |
| 0.00075 | 0.00035 | 0.00022 | 0.00018 | 0.00011 |
| 0.00099 | 0.00069 | 0.00032 | 0.00013 | 0.00025 |
| BIAS | | 0.03128 | 0.01350 | 0.00796 | 0.00343 | 0.00157 |
| 0.06616 | 0.02835 | 0.01206 | 0.00545 | 0.00271 |
| 0.07772 | 0.04445 | 0.01732 | 0.00658 | 0.00357 |
| LCL | | 1.99939 | 1.99989 | 1.99984 | 2.00002 | 2.00006 |
| 3.54886 | 3.54961 | 3.54985 | 3.5499 | 3.55007 |
| 1.04847 | 1.04909 | 1.04974 | 1.05008 | 1.04993 |
| UCL | | 2.00099 | 2.00045 | 2.00055 | 2.00032 | 2.00033 |
| 3.55181 | 3.55096 | 3.55070 | 3.55065 | 3.55051 |
| 1.05236 | 1.05180 | 1.05098 | 1.05061 | 1.05091 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).