Research on the Quality Improvement of the Segmented Interferometric Array Integrated Optical Imaging Based on Hierarchical Non-Uniform Sampling Lens Array
Abstract
1. Introduction
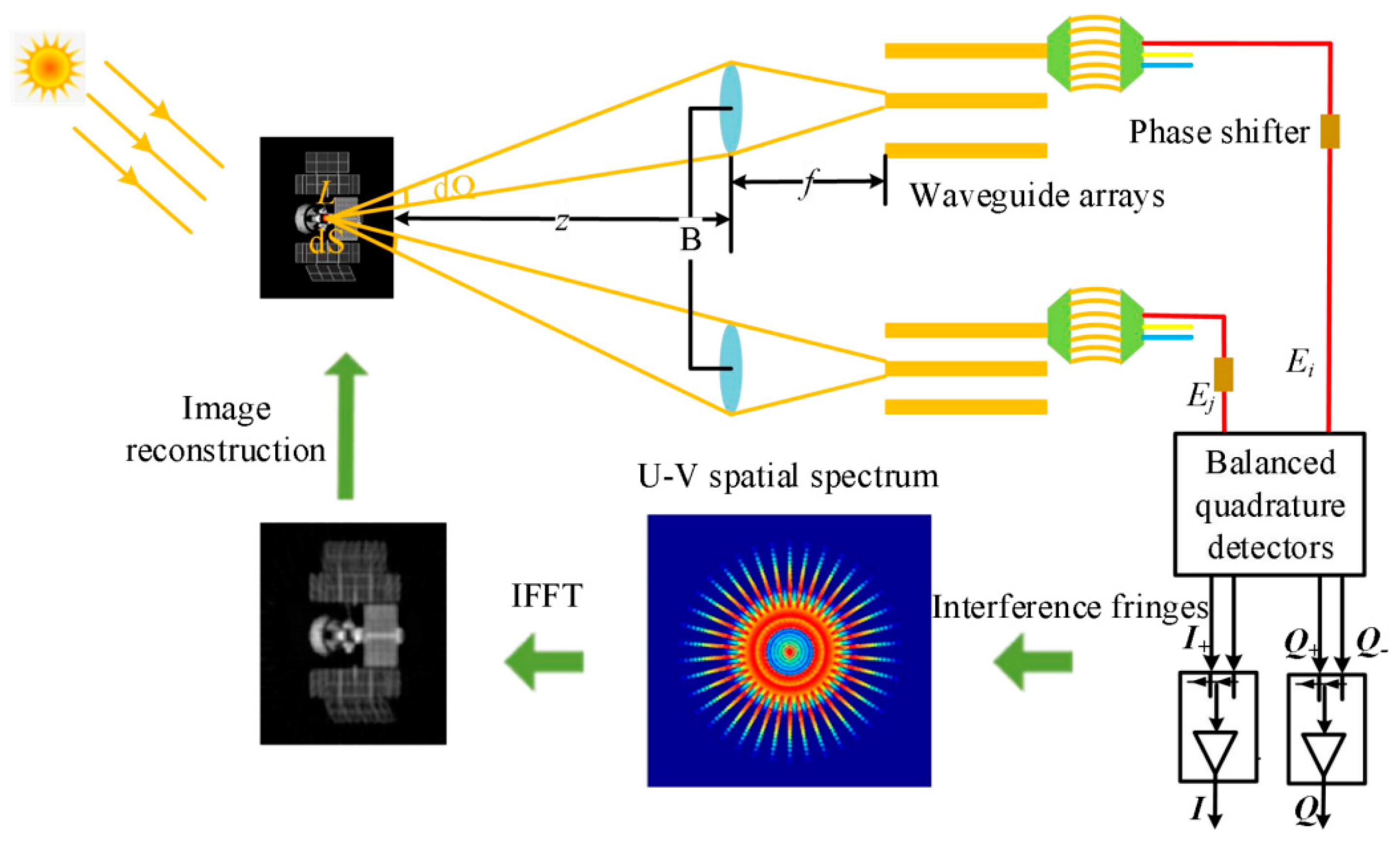
2. Segmented Interference Array Integrated Optical Imaging System
2.1. Structure and Principle of the Imaging System
2.2. Scene Radiation Field Transformation Model of the Imaging System
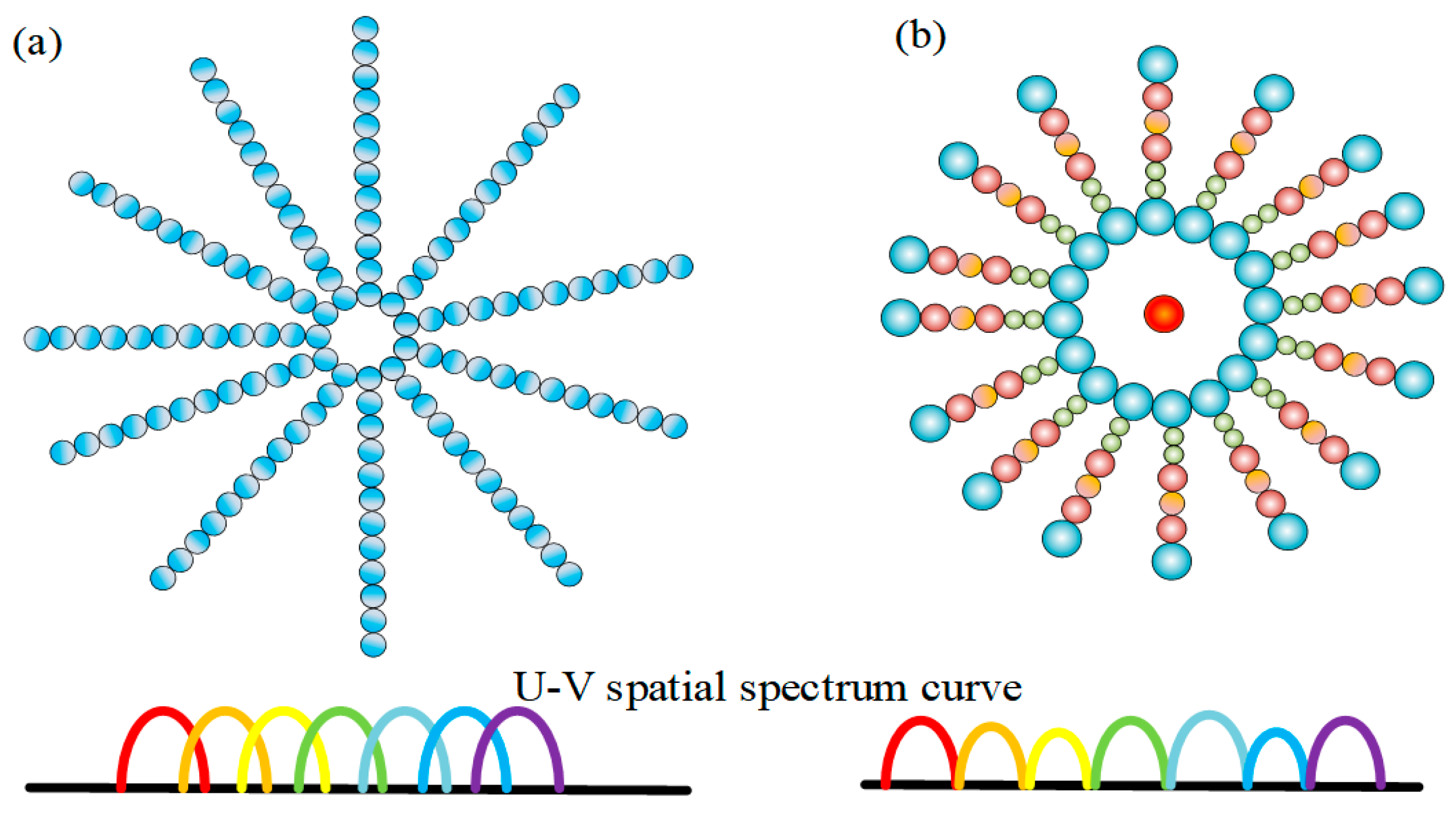
3. Optimized Design of the Lens Array
3.1. Design Principles of Hierarchical Non-Uniform Sampling Lens Array
3.2. Design Method of the Hierarchical Non-Uniform Sampling Lens Array
3.3. Baseline Pairing Method of Hierarchical Non-Uniform Sampling Lens Array
4. Research of Imaging Characteristics
4.1. Spatial Spectral Imaging Characteristics
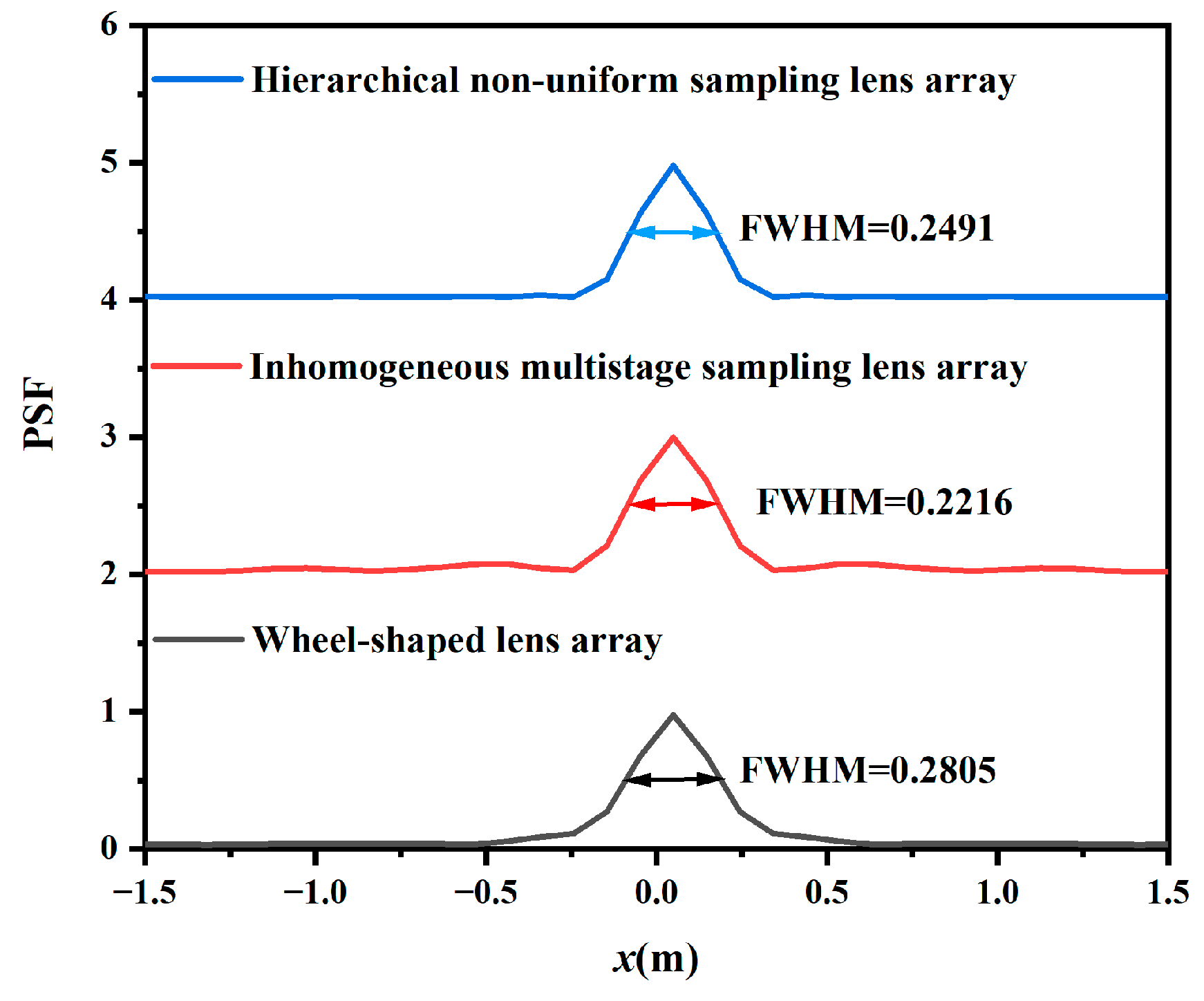
4.2. Point Spread Function (PSF) Characteristics
4.3. System Imaging Characteristics
5. Analysis of Lens Array Parameters
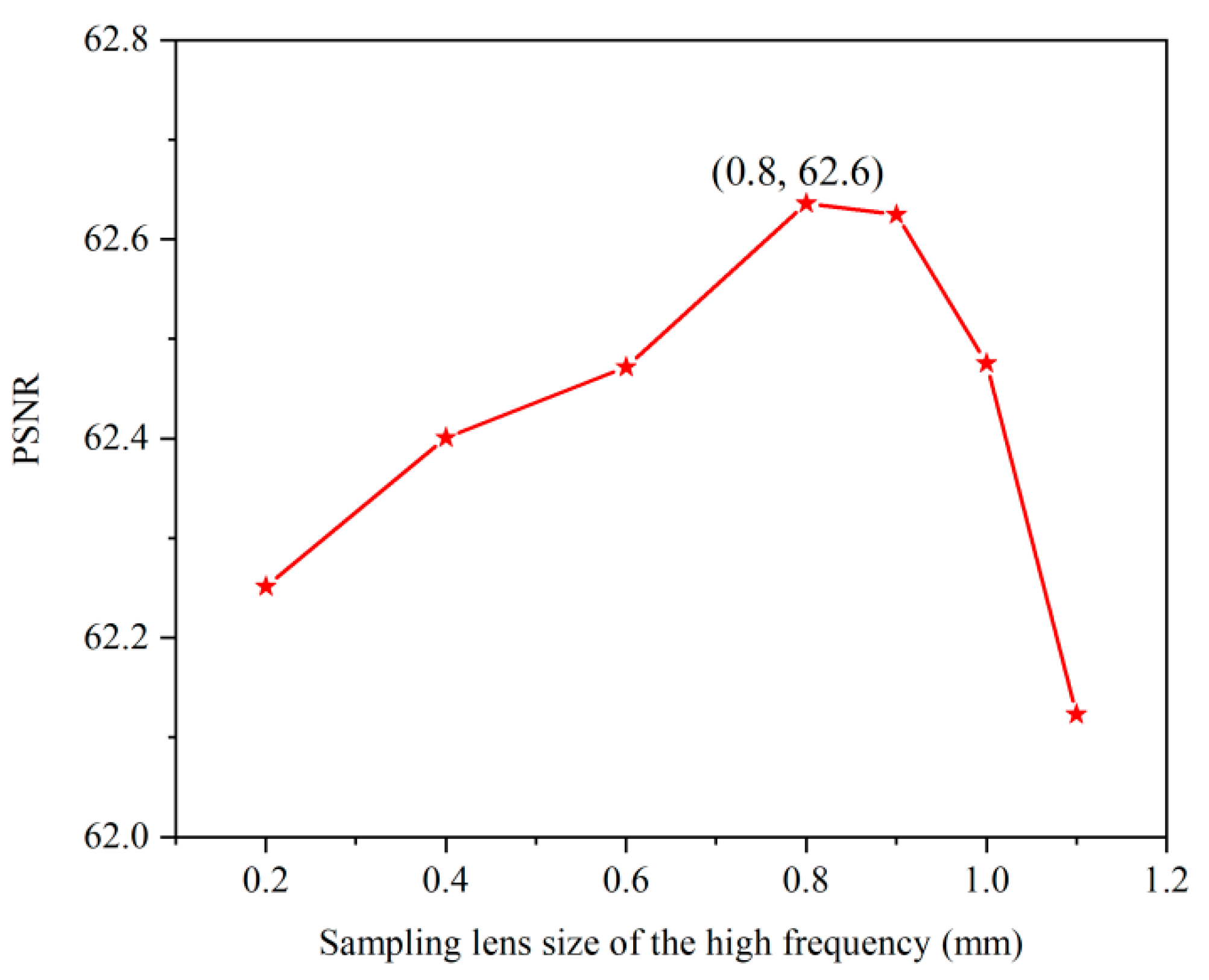
5.1. Analysis of Lenslet Size
5.2. Analysis of Lens Array Fill Factor
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pedrotti, F.L.; Leno, M.P.; Leno, S.P. Introduction to Optics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Michael, B. Handbook of Optics; McGraw-Hill: New York, NY, USA, 1995. [Google Scholar]
- Wang, H.; Kang, F.Z.; Zhao, W.; Xie, Y.J. Optical design of infrared diffractive telescope. J. Infrared Millim. Waves 2016, 35, 425–429. [Google Scholar]
- Zhang, Y.; Qin, F.; Li, X. Advances in the Sub-diffraction Limited Light Modulation by Supercritical Lens(Invited). Acta Photonica Sin. 2023, 51, 0551310. [Google Scholar]
- Radhika, D.; Padmakar, P.; Annu, J. Building a large affordable optical-NIR telescope (I): An alternate way to handle segmented primary mirror. Exp. Astron. 2023, 56, 1–36. [Google Scholar]
- Tang, H.; Liao, Z.; Jiang, J.; Chen, M.; Xian, H.; Li, H.; Liao, S. Simulation method for multichromatic light spots in mosaic aperture telescopes with large image planes during deployment. Appl. Opt. 2024, 63, 3770–3778. [Google Scholar] [CrossRef]
- Trumper, I.; Hallibert, P.; Arenberg, J.W.; Kunieda, H.; Guyon, O.; Stahl, H.P.; Kim, D.W. Optics technology for large-aperture space telescopes: From fabrication to final acceptance tests. Adv. Opt. Photonics 2018, 10, 644–702. [Google Scholar] [CrossRef]
- Zhang, X.J.; Fan, Y.C.; Bao, H.; Xue, D. Applications and development of ultra large aperture space optical remote sensors. Opt. Precis. Eng. 2016, 24, 2613–2626. [Google Scholar] [CrossRef]
- Blind, N.; Coarer, E.L.; Kern, P.; Gousset, S. Spectrographs for astrophotonics. Opt. Express 2017, 25, 27341–27369. [Google Scholar] [CrossRef] [PubMed]
- Meinel, B.A. Cost relationships for nonconventional telescope structural configurations. J. Opt. Soc. Am. 1982, 72, 14–20. [Google Scholar] [CrossRef]
- Whiteaker, K.; Marshalek, R.; Domber, J.; Kaliski, R. Large Aperture Diffractive Receiver for Deep Space Optical Communications. In Applications of Lasers for Sensing and Free Space Communications; Optica Publishing Group: Washington, DC, USA, 2015. [Google Scholar]
- An, Q.; Wang, K.; Liu, X.; Li, H.; Zhu, J. Integrated Test System for Large-aperture Telescopes Based on Astrophotonics Interconnections. Jinst 2024, 11, 1–9. [Google Scholar]
- Kendrick, R.L.; Duncan, A.; Ogden, C.; Wilm, J.; Stubb, D.M. Flat-Panel space-based spacesurveillance sensor. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 10–13 September 2013. [Google Scholar]
- Kendrick, R.; Thurman, S.T.; Duncan, A.; Ogden, C.; Wilm, J. Segmented planar imaging detector for EO reconnaissance. In Proceedings of the Imaging and Applied Optics, Arlington, VI, USA, 23–27 June 2013. [Google Scholar]
- Liu, G.; Wen, D.; Song, Z.; Jiang, T. System design of an optical interferometer based on compressive sensing: An update. Opt. Express 2020, 28, 19349–19361. [Google Scholar] [CrossRef] [PubMed]
- Cao, K.; Ye, Z.; Jiang, C.; Zhu, J.; Qiao, Z.; Jiang, Y. Lenslets combination optimal design of the segmented planar image detector for electro-optical reconnaissance. Opt. Eng. 2020, 59, 1–9. [Google Scholar] [CrossRef]
- Deng, X.; Tao, W.; Diao, Y.; Sang, B.; Sha, W. Imaging Analysis of Photonic Integrated Interference Imaging System Based on Compact Sampling Lenslet Array Considering On-Chip Optical Loss. Photonics 2023, 10, 797. [Google Scholar] [CrossRef]
- Chen, T.; Zeng, X.; Bai, Y.; Zhang, Z.; Wang, Y.; Zhang, F.; Zhang, X. Sparse-aperture photonics-integrated interferometer (SPIN) imaging system: Structural design and imaging quality analysis. Opt. Express 2021, 29, 39256–39270. [Google Scholar] [CrossRef] [PubMed]
- Pan, X.; Yang, Z.; Jia, R.; Ren, G.; Peng, Q. Photonic integrated interference imaging system based on front-end S-shaped microlens array and Con-DDPM. Opt. Express 2024, 32, 29112–29124. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Lü, G.; Feng, H.; Xu, Z.; Chen, Y. Analysis of Signal Energy and Noise in Photonic Integrated Interferometric Imaging System. Acta Opt. Sin. 2022, 42, 1311001. [Google Scholar]
- Chen, T.; Zeng, X.; Bai, Y.; Tian, M.; Zhang, X. Image Reconstruction of Photonics Integrated Interference Imaging: Entropy Prior. Acta Opt. Sin. 2021, 41, 2311002. [Google Scholar]
- Chu, Q.; Shen, Y.; Yuan, M.; Gong, M. Numerical simulation and optimal design of Segmented Planar Imaging Detector for Electro-Optical Reconnaissance. Opt. Commun. 2017, 405, 288–296. [Google Scholar] [CrossRef]
- Gao, W.; Wang, X.; Ma, L.; Guo, D.F. Quantitative analysis of segmented planar imaging quality based on hierarchical multistage sampling lens array. Opt. Express 2019, 27, 7955–7967. [Google Scholar] [CrossRef]
- Ding, C.; Zhang, X.; Liu, X.; Meng, H.; Xu, M. Structure design and image reconstruction of hexagonal-array photonics integrated interference imaging system. IEEE Access 2020, 8, 139396–139403. [Google Scholar] [CrossRef]
- Zhao, Z.; Yuan, Y.; Zhang, C.; Wang, X.; Gao, W. Imaging quality characterization and optimization of segmented planar imaging system based on honeycomb dense azimuth sampling lens array. Opt. Express 2023, 31, 35670–35684. [Google Scholar] [CrossRef]
- Yu, Q.; Wu, D.; Chen, F.; Sun, S. Design of a wide-field target detection and tracking system using the segmented planar imaging detector for electro-optical reconnaissance. Chin. Opt. Lett. 2018, 16, 071101. [Google Scholar]
- Gao, W.; Yuan, Y.; Wang, X.; Ma, L.; Zhao, Z.; Yuan, H. Quantitative analysis and optimization design of the segmented planar integrated optical imaging system based on an inhomogeneous multistage sampling lens array. Opt. Express 2021, 29, 11869–11884. [Google Scholar] [CrossRef] [PubMed]





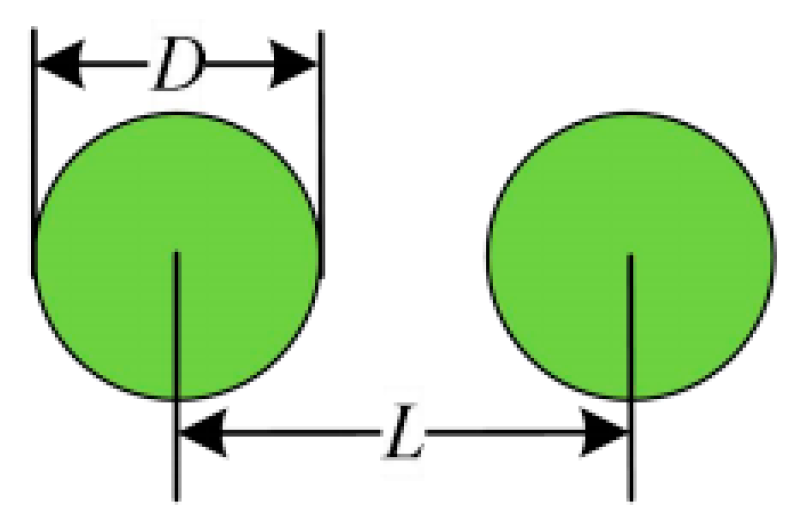
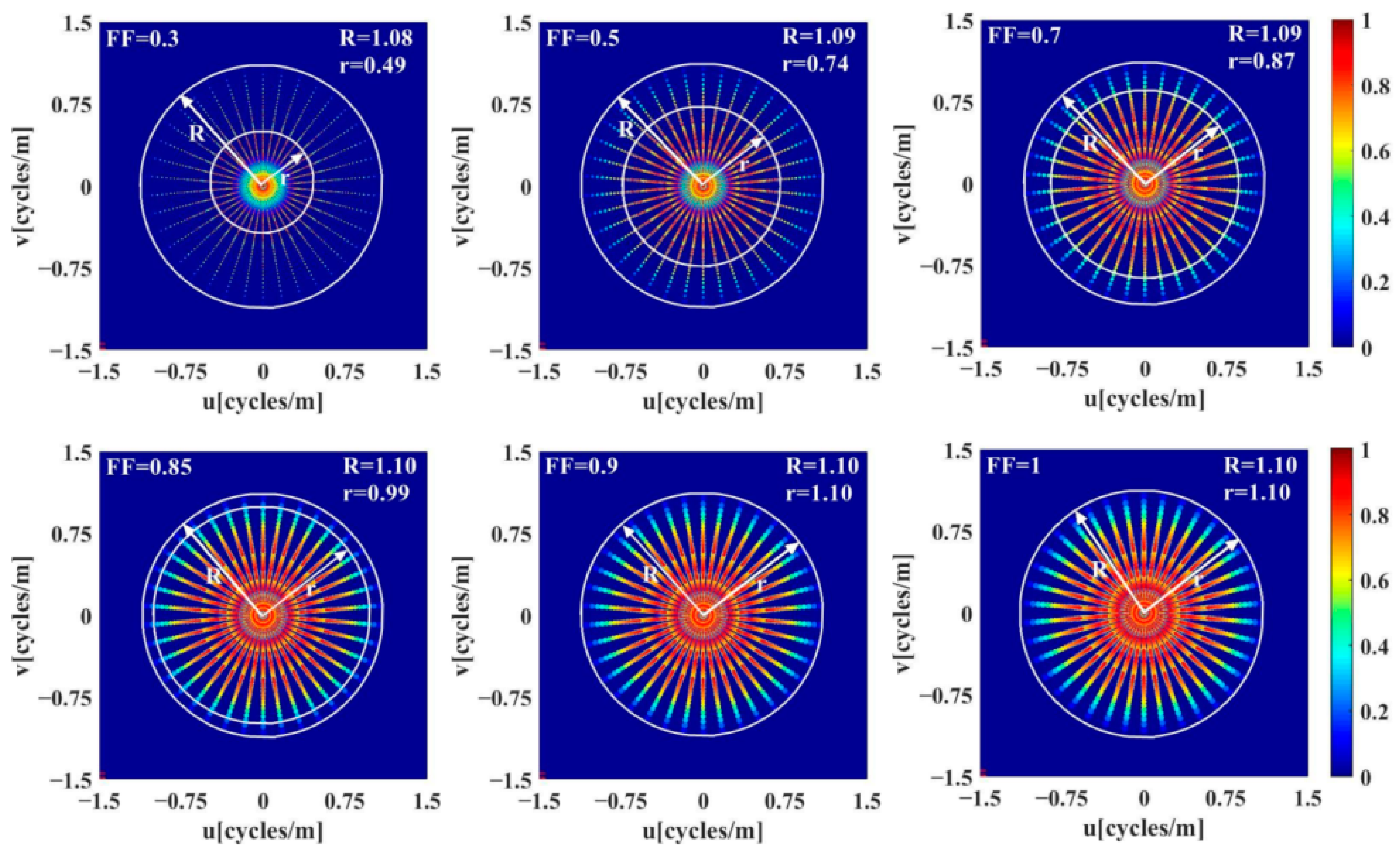
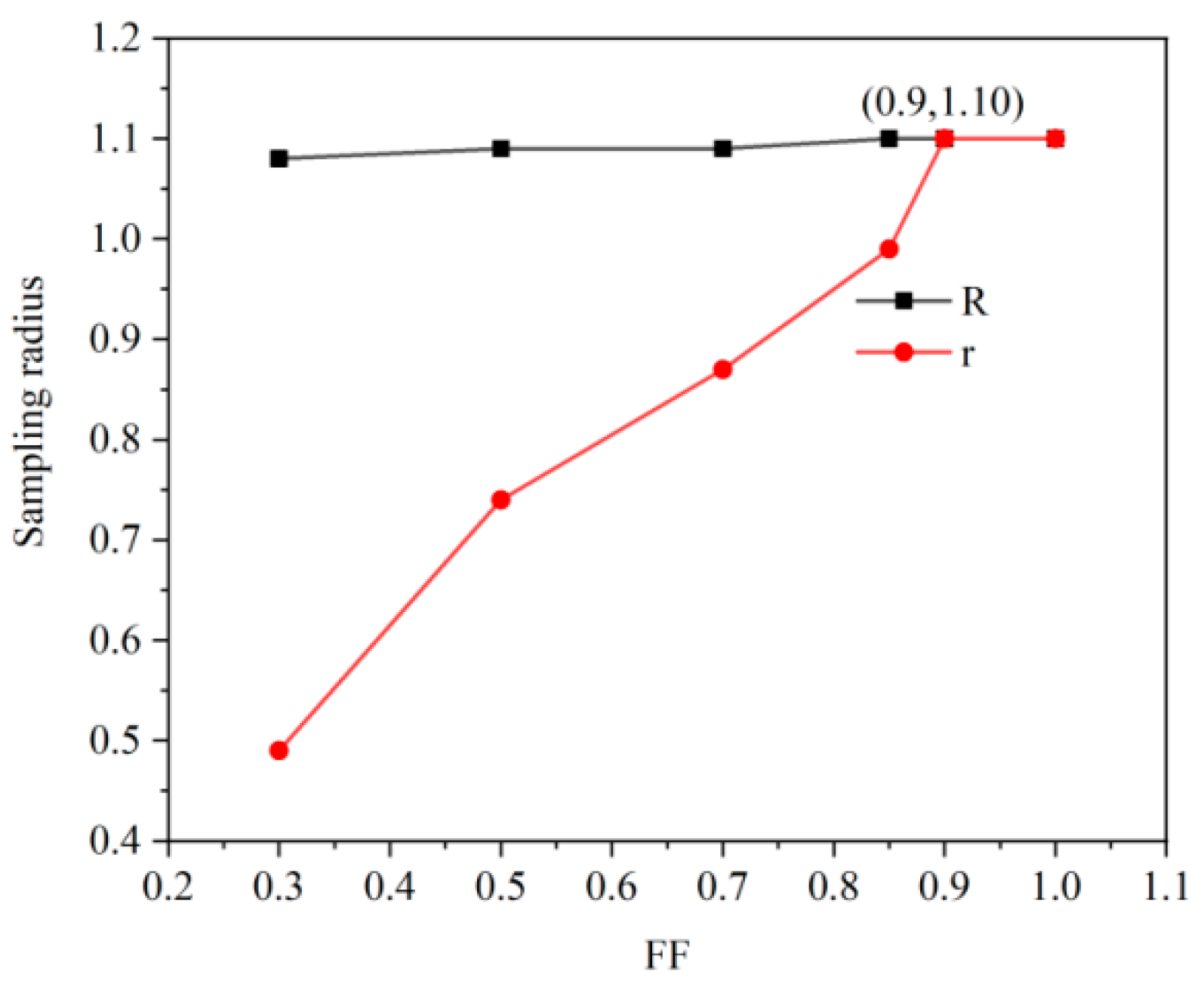
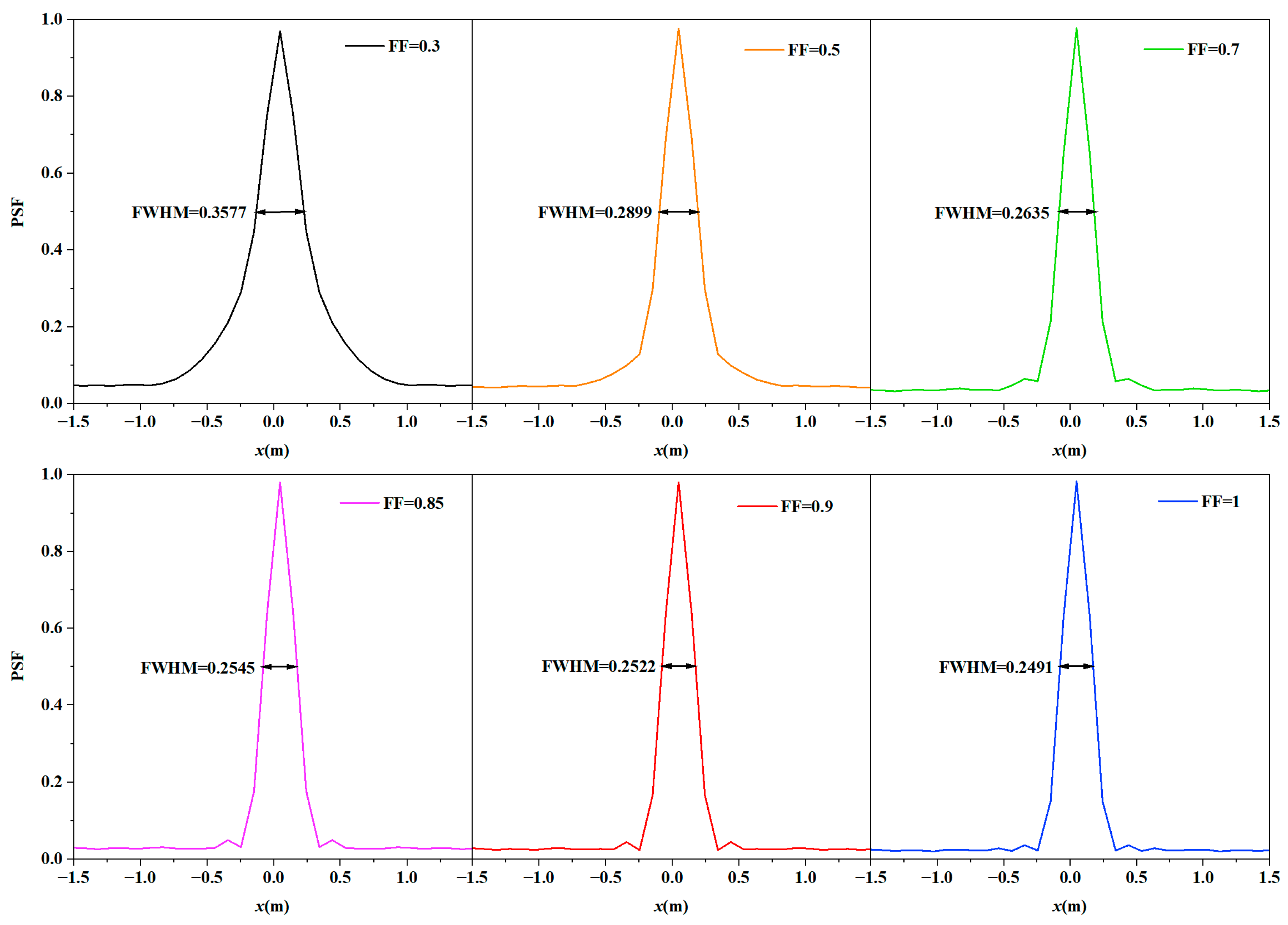

| System Parameter | Symbol | Numerical Value |
|---|---|---|
| Wavelength range | λ | 380~700 nm |
| Object distance | z | 250 km |
| The longest interference baseline length Bmax | Bmax | 104.4 mm |
| Number of lenslets on an interference arm | N | 30 |
| Number of interference arms | p | 19 |
| AWG channel number | SC | 16 |
| Wavelength distance | Δλ | 20 nm |
| Optical path difference | Δ | 7.2 μm |
| Lens array fill factor | FF | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, W.; Wang, X.; He, Y.; Zang, J.; Li, P.; Wang, F. Research on the Quality Improvement of the Segmented Interferometric Array Integrated Optical Imaging Based on Hierarchical Non-Uniform Sampling Lens Array. Symmetry 2025, 17, 336. https://doi.org/10.3390/sym17030336
Gao W, Wang X, He Y, Zang J, Li P, Wang F. Research on the Quality Improvement of the Segmented Interferometric Array Integrated Optical Imaging Based on Hierarchical Non-Uniform Sampling Lens Array. Symmetry. 2025; 17(3):336. https://doi.org/10.3390/sym17030336
Chicago/Turabian StyleGao, Weiping, Xiaorui Wang, Yanghui He, Junbin Zang, Pengwei Li, and Feipeng Wang. 2025. "Research on the Quality Improvement of the Segmented Interferometric Array Integrated Optical Imaging Based on Hierarchical Non-Uniform Sampling Lens Array" Symmetry 17, no. 3: 336. https://doi.org/10.3390/sym17030336
APA StyleGao, W., Wang, X., He, Y., Zang, J., Li, P., & Wang, F. (2025). Research on the Quality Improvement of the Segmented Interferometric Array Integrated Optical Imaging Based on Hierarchical Non-Uniform Sampling Lens Array. Symmetry, 17(3), 336. https://doi.org/10.3390/sym17030336





