Abstract
Existing methods have problems such as loss of details and insufficient reconstruction effect when processing complex images. To improve the quality and efficiency of image super-resolution reconstruction, this study proposes an improved algorithm based on super-resolution generative adversarial network and Swin Transformer. Firstly, on the ground of the traditional super-resolution generative adversarial network, combined with the global feature extraction capability of Swin Transformer, the model’s capacity to capture multi-scale features and restore details is enhanced. Subsequently, by utilizing adversarial loss and perceptual loss to further optimize the training process, the image’s visual quality is improved. The results show that the optimization algorithm had high PSNR and structural similarity index values in multiple benchmark test datasets, with the highest reaching 43.81 and 0.94, respectively, which are significantly better than the comparison algorithm. In practical applications, this algorithm demonstrated higher reconstruction accuracy and efficiency when reconstructing images with complex textures and rich edge details. The highest reconstruction accuracy could reach 98.03%, and the reconstruction time was as low as 0.2 s or less. In summary, this model can greatly improve the visual quality of image super-resolution reconstruction, better restore details, reduce detail loss, and provide an efficient and reliable solution for image super-resolution reconstruction tasks.
1. Introduction
With the rapid development of digital Image processing technology, image Super-Resolution (ISR) has become an important research direction in the field of computer vision, and its core goal is to reconstruct low-resolution images into high-resolution images. To meet the demand for high-quality images in fields such as medical imaging, remote sensing monitoring, and video enhancement [1]. However, traditional interpolation methods (such as bilinear interpolation and bicubic interpolation) are insufficient in the reconstruction of complex textures and detail-rich images, which easily lead to image blurring and detail loss [2]. In recent years, ISR algorithms based on deep learning have attracted widespread attention. The generative adversarial network (GAN) can generate super-resolution images with high visual quality through adversarial training of generators and discriminators. As a deformable structure, the super-resolution generative adversarial network (SRGAN) has achieved excellent performance in detail recovery and texture reconstruction. However, it may still have ambiguity or distortion when dealing with complex scenes and long-distance dependence, and the instability of the counter-training process also limits the performance of the model [3,4]. With the successful application of the Transformer model in the field of natural language processing, researchers have begun to introduce the Transformer model into computer vision tasks to capture global features through the self-attention mechanism, which has unique advantages in complex scenes and large-scale data processing [5]. Among them, the Swin Transformer, as an important variant of the Vision Transformer, not only achieves the efficient integration of global and local features at a low computing cost through the local window attention mechanism and the window shifting mechanism, but it also shows significant performance advantages in image feature modeling [6,7]. However, there are still few research studies on the combination of the GAN and Transformer in the existing literature, and there is still a lack of effective solutions for image super-resolution tasks with complex textures and multi-scale features. Given the above background, the paper designs a Super-Resolution Reconstruction (SRR) model that combines the SRGAN and Swin Transformer. SRGAN can recover image details by generating adversarial training, but it has shortcomings in dealing with complex scenes and long-distance dependencies. The Swin Transformer effectively captures global and local features through its self-attention mechanism, which is excellent in complex textures and multi-scale features. Introducing the Swin Transformer into the SRGAN framework can improve the image detail recovery ability and make up for the shortcomings of the SRGAN. Moreover, compared with traditional convolutional neural network combinations, the Swin Transformer has more advantages in processing complex scenes and can ultimately improve the quality of image reconstruction.
The innovation of this research lies in the introduction of the Swin Transformer into the SRGAN framework for the first time, which realizes the efficient integration of global and local features through the local window attention mechanism and the shifting window mechanism. At the same time, a new loss function is designed to optimize both perception loss and counter loss, which enhances the training stability and detail reconstruction ability of the model.
The contribution of this study lies in the realization of high-quality image reconstruction in multiple complex scenes through the proposed super-resolution reconstruction model, which improves the application effect of super-resolution tasks in detail recovery and visual quality. Through verification, the proposed model shows good adaptability in practical scenarios, and provides reliable theoretical support and practical reference for the promotion of super-resolution technology in practical engineering applications.
2. Related Work
Most existing ISR algorithms suffer from the problem of insufficient feature extraction and the loss of high-frequency details. To address these issues, many experts have proposed various optimization models. H. Lei et al. designed an improved SRGAN super-resolution reconstruction algorithm. The residual dense network is used in the generative network to extract the features of each layer of the image, and the super-resolution reconstruction effect at a large magnification is improved by a progressive upsampling method. The experimental results show that the performance of the reconstruction algorithm is good [8]. R. Abi-Rizk et al. proposed an original method to reconstruct high-resolution hyperspectral images from heterogeneous 2-D measurements degraded by the integral field spectrometer instrument for the problem of high-resolution hyperspectral image reconstruction. The majorize–minimize memory gradient optimization algorithm and low-rank approximation are used to handle high-dimensional problems, thereby achieving resolution enhancement and image quality optimization [9]. S. Ahmadi, L et al. proposed Photothermal-SR-Net for the problem of super-resolution reconstruction in photothermal imaging. The method uses the sparsity of defects in the material and includes a well-trained block sparse threshold processing in each convolutional layer to achieve faster reconstruction speed and higher image quality [10]. A. Esmaeilzehi et al. proposed a novel residual block to address the problem of feature generation in image super-resolution networks. By generating and processing morphological features and fusing them with traditional spatial features, the super-resolution performance of deep networks was significantly improved, and the existing low-complexity image super-resolution networks were surpassed on multiple benchmark datasets [11]. To address the problem of the low resolution of infrared images, D. Mishra et al. proposed a contrastive learning method for remote sensing image super-resolution in a semi-supervised setting, considering the difference between actual degradation and ideal degradation and the dependence of traditional unsupervised learning techniques on a large number of diverse training samples when reconstructing low-resolution images. The performance of visual tasks was improved by comparing two samples to discover shared features and attributes [12]. X. Chen et al. proposed a generative adversarial network model for single-image super-resolution reconstruction tasks. The model directly converts low-resolution images into high-resolution images through end-to-end mapping. By introducing spectral normalization and attention mechanisms and using a lightweight external attention method to accelerate global structure reconstruction, a good balance between performance and speed was achieved, and the performance was comparable to the latest supervised models [13]. L. Fu et al. proposed an image super-resolution method based on the instance space feature modulation and feedback mechanism. By introducing instance space features, the super-resolution reconstruction features of low-resolution images are modulated, and the features are iteratively optimized based on the feedback mechanism to improve the instance-level reconstruction capability of the model. Experiments show that this method outperforms traditional methods on the COCO-2017 dataset, and the reconstructed images have more realistic instance textures [14]. A. Khmag proposed a hybrid noise removal method that combines the pulse-coupled neural network (PCNN) and Perona–Malik equation regularization to address the high computational complexity, halo artifacts, and oversaturation problems of existing hybrid noise removal methods. PCNN locates noise, wavelet filters suppress noise, and P–M equation regularization denoising effectively improves the preservation of image details and edges [15]. In addition, A. Khmag proposed a noise removal method combined with adaptive GAN to address the contradiction between noise suppression and detail preservation in digital image processing. A semi-soft threshold model is used to avoid over-suppression, and GAN is used to extract subtle edges of noisy images to prevent accidental deletion of clean pixels. This method combines adaptive learning and scoring mechanisms to optimize image restoration performance and suppress over-smoothing [16]. In order to solve the common problems of blurred edges, inflexible convolution kernel selection, and slow training convergence in image super-resolution algorithms, Y. Chen et al. proposed a lightweight single-image super-resolution network that integrates multi-layer features. The network adopts a two-level nested residual block, uses an asymmetric structure to extract features, reduces the number of parameters, and fuses feature information from different channels through an autocorrelation-weighted unit. The experimental results show that this method outperforms existing methods in both subjective perception and objective evaluation indicators [17]. In response to the problem of visual quality degradation of BM3D under high noise density, W. Kshem et al. proposed a denoising method based on discrete wavelet transformations and improved block matching. This method breaks through the limitations of traditional BM3D by processing the LL layer of wavelet decomposition and finding correlations between similar and dissimilar blocks. The experiments show that this method outperforms existing technologies under various noise levels, as evaluated by indicators such as PSNR, SSIM, and FOM, and significantly shortens the running time, improving the denoising effect and efficiency [18].
In summary, the existing ISR reconstruction algorithms have good performance in feature extraction, edge detail preservation, and HRI generation. However, there are still many models that are prone to feature loss and blurry details when dealing with high magnification, complex textures, and edge information. In addition, the inflexibility of convolutional kernel selection and poor training stability are also urgent challenges that need to be addressed. Based on this, this study proposes an ISR reconstruction algorithm that combines SRGAN and Swin Transformer. The research aims to integrate the efficient feature extraction capability of GAN with the global modeling advantage of Transformer to better address the shortcomings of existing algorithms in feature extraction and detail restoration.
3. Image Reconstruction Algorithm Combining HO-SRGAN and SWIN Transformer
In order to further improve the effect of image super-resolution reconstruction, an image reconstruction algorithm combining the improved SRGAN and Swin Transformer is proposed. Firstly, the classical SRGAN model is improved to enhance its processing ability for high-frequency details and complex textures. The residuals and Swin Transformer are further combined to extract features, and high-resolution images are generated by upsampling. In order to adapt to noisy images, an adaptive denoising strategy is introduced, the weight of the convolution kernel is adjusted dynamically, and the noise sensing attention mechanism is used to suppress noise interference.
3.1. Construction of an Improved SRGAN Model
GAN was proposed by Ian Goodfellow et al. in 2014 and is mainly used to generate high-quality synthetic data. It is currently widely used in image generation, data augmentation, and style transformation. GAN includes two parts: generator and discriminator. The task of the former is to generate realistic data samples from random noise. The latter is responsible for distinguishing these generated samples from real data. The general structure of GAN is shown in Figure 1.
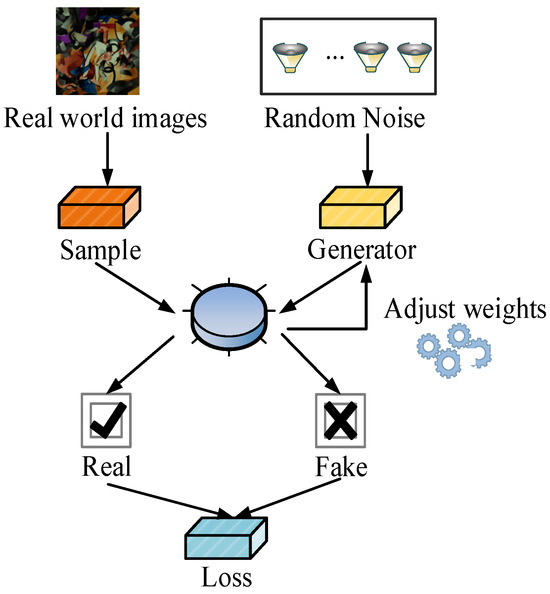
Figure 1.
GAN structure diagram.
The GAN in Figure 1 includes a generator and a discriminator, which mutually enhance each other through adversarial training. The generator receives random noise input and adjusts weights to generate realistic synthetic data, and the discriminator distinguishes whether the sample is real data or generated data. Based on the discrimination results, LF calculates the difference between the two and adjusts their respective weights. Throughout the process, the generator continuously attempts to deceive the discriminator, while the discriminator improves its discriminative ability, ultimately leading to the generator gradually generating realistic data. SRGAN is a model specifically designed for ISR reconstruction, further expanding GAN’s image processing capabilities to generate higher-resolution images [19]. The core of SRGAN is to use adversarial training between the generator and discriminator to make the generated HRIs visually more realistic. Figure 2 shows the generative and discriminative network structures of SRGAN.
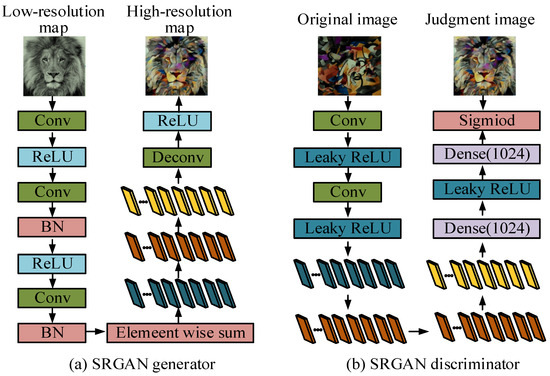
Figure 2.
Structure diagram of the generative and discriminative networks of SRGAN.
In Figure 2a, the generator of SRGAN converts LRIs into HRIs through ConvLs and residual blocks. Firstly, LRIs are subjected to ConvLs and ReLU to extract initial features, followed by feature learning through multiple residual blocks containing convolution, batch normalization, and ReLU, and fusion of input and output features through element wise summation. Next, the network performs upsampling through sub-pixel ConvLs and ReLU, ultimately outputting an HRI. In Figure 2b, the discriminator of SRGAN is utilized to distinguish whether the input image is real or generated. The input image is sequentially processed through ConvLs and Leaky ReLU to extract local features, while the batch normalization layer standardizes the output for stable training. Finally, by processing the features through a fully connected layer (FCL) and using the Sigmoid function to output binary classification results, it can be determined whether the image is a true HRI.
The traditional SRR method usually uses the mean square error (MSE) as LF. This LF optimizes the network by calculating the pixel distinctions between the generated HRI and the real image [20,21]. However, this method can easily result in HRIs appearing blurry in high-frequency details, and the final image may appear too smooth, leading to poor reconstruction results. To address this issue, SRGAN introduces perceptual LF to make the reconstructed HRIs more visually realistic. In SRGAN, assuming and are content loss and adversarial loss, thus obtaining the expression of perceived LF as shown in Equation (1) [22,23].
In Equation (1), is perceptual LF. The specific calculation method of is Equation (2).
In Equation (2), and are the number of pooling layers and ConvLs. is the initial HRI. is the HRI generated by the generator. and are two feature map sizes of different specifications. is the feature map. and are the pixel coordinates in the feature map. The specific formula for is shown in Equation (3).
In Equation (3), is the total sample size. is the quantity of samples. is a discriminator network. is the possibility that the image produced by the generator is the initial HRI. Due to the insufficient high-frequency detail performance of traditional SRGANs in processing super-resolution images, it is necessary to improve their generation network, discrimination network, and LF. The improved SRGAN is referred to as Hybrid Optimized SRGAN (HO-SRGAN). The operation process of HO-SRGAN is shown in Figure 3.
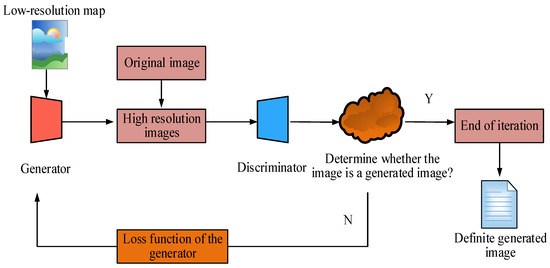
Figure 3.
Flowchart of the HO-SRGAN algorithm.
In Figure 3, the HO-SRGAN algorithm first inputs LRIs into the generative network, which generates corresponding HRIs through training. Secondly, the network distinguishes between the received HRI and the original HRI, and determines whether the generated image is analogous to the real image through comparative analysis. Then, based on the feedback from the discriminative network, if the generated image is judged to be insufficiently realistic, the system will update the LF of the generative network and adjust its parameters to minimize losses and regenerate a more realistic HRI. This process is repeated until the generated image can deceive the discriminative network. Finally, when the generated image is deemed sufficiently realistic by the discrimination network, the final output image of the generation network is outputted as a high-resolution result. The improved generation network and discrimination network structure of HO-SRGAN are shown in Figure 4.
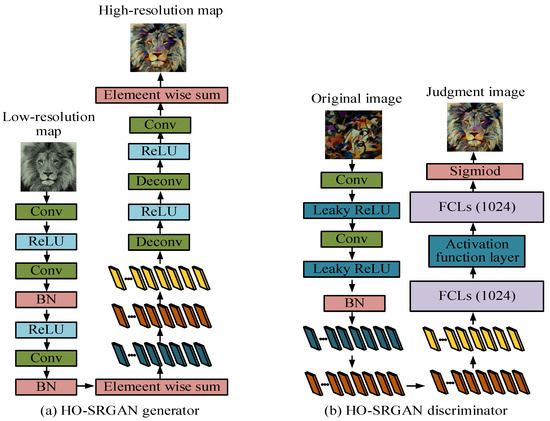
Figure 4.
Structural diagram of the generated and discriminant networks of HO-SRGAN.
Figure 4a,b shows the generative and discriminative networks of HO-SRGAN. Compared to SRGAN, HO-SRGAN’s generative network combines bicubic interpolation algorithm to better preserve image information in low-frequency regions. Secondly, the discriminative network uses a relative discriminative network instead of a standard discriminative network to ensure that the generated image details are more complete. Finally, MSE loss is added to the perception LF to balance visual effects and improve the ability to restore image details. The generation network mainly extracts image features through residual networks. The expression formula of residual network is shown in Equation (4) [24,25].
In Equation (4), is the input image. and are the weights of the first and second ConvLs. is the residual learned by the network. is the non-linear activation function ReLU. The output image after passing through the residual network is denoted as , and its expression is shown in Equation (5).
In Equation (5), the value of can be obtained by adding the input image and the residual. In the discriminative network section, the mathematical expression for the relative discriminative network is shown in Equation (6).
In Equation (6), and are the original HRI and the generated HRI. is the expected operator. is Sigmoid. is a relative discriminative network, and is the feature extracted from the image through a convolutional network. When the standard discrimination network is altered to a relative discrimination network, the LF of the discrimination network is shown in Equation (7).
In Equation (7), is the LF value of the discriminative network. At this point, the LF of the generated network is shown in Equation (8).
In Equation (8), is the LF value of the generative network. By adding MSE loss on the basis of content and adversarial losses, the overall objective LF of HO-SRGAN can be obtained as shown in Equation (9).
In Equation (9), is the overall target LF, and the meanings of and are the same as above. is the MSE loss, and its specific expansion formula is Equation (10).
In Equation (10), and are HRIs and LRIs. is the network parameter of generator , and is the total sample size.
3.2. Design of ISR Reconstruction Algorithm Combining HO-SRGAN and SWIN Tansformer
Although HO-SRGAN can improve the visual quality of images to some extent by optimizing the training process of GAN, there are still problems such as insufficient feature detail extraction and slow feature extraction speed for more complex image scenes and high-frequency details. Therefore, to further improve the detail restoration ability and feature extraction speed of the super-resolution image reconstruction model, this study also introduces the Swin Transformer as the core module of the generator. The transformer is a DL model built on SAM, which has achieved good performance in NLP tasks [26,27]. This structure can perform parallel processing on all elements in the sequence through global SAM, and effectively capture the dependency relationships between distant elements in the input sequence. Figure 5 shows the framework of the transformer.
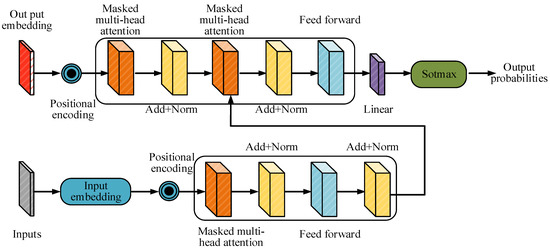
Figure 5.
Transformer frame structure diagram.
The structure of the transformer in Figure 5 mainly includes two parts: an encoder and a decoder. In the encoder section, the input data will go through embedding layers and positional encoding, and then pass through multiple identical encoder layers. Each layer includes a multi-head SAM and a Feedforward Neural Network (FFNN), and residual connections and normalization operations are used between the two [28,29]. The output of the encoder will serve as the input of the decoder. The decoder structure is similar to that of the encoder, but it adds a masking multi-head SAM to avoid the leakage of future position information. During the decoding process, the input data also go through embedding layers and positional encoding to gradually generate the target output. Due to the powerful feature capture capability of the transformer, this model has gradually been introduced into the field of CV for processing complex image tasks. The Swin Transformer, as a transformer variant designed specifically for visual tasks, further optimizes the computational efficiency and feature extraction capabilities of traditional transformers. The standard Transformer layer and optimized Swin Transformer layer structures are shown in Figure 6.
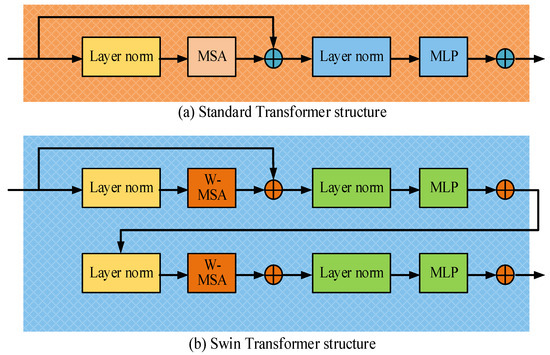
Figure 6.
Standard transformer-layer structure and the Swin Transformer-layer structure.
Figure 6a shows the standard transformer layer structure, which mainly consists of two main parts: multi-head SAM and FFNN. There is a layer normalization operation between the input and output of each module to ensure that the input data are normalized after passing through each sub layer, thereby achieving the goal of stable training process. At the same time, each module uses residual connections to add the input to the output of the sub layers, thereby alleviating the gradient vanishing problem in deep networks and allowing information to flow better. Figure 6b shows the layer structure of the Swin Transformer. Unlike the standard transformer, the Swin Transformer uses window multi-head SAM and moving window multi-head SAM, respectively, for processing self-attention calculations in local regions. Each module also includes layer normalization, FFNN, and residual connection operations. Window multi-head SAM and moving window multi-head SAM operate by dividing the image into fixed sized windows, enabling the Swin Transformer to capture local and global features of the image more efficiently. In the Swin Transformer, the calculation formula for multi-head SAM in the window is similar to traditional SAM, with the difference being that the former calculates within the window rather than globally. The mathematical formula for multi-head SAM in the window is shown in Equation (11) [30,31].
In Equation (11), , , and are the matrix of query, key, and value. denotes the dimension of the , used to scale attention scores and prevent gradient vanishing caused by excessively large dimensions. is the dot product of the and the , utilized to measure the similarity between features at different positions. is a normalization operation used to calculate the attention weight for each position. To enhance feature interaction, the Swin Transformer also introduces a moving window mechanism, where windows move between layers to ensure that cross-window features can influence each other [32,33]. The formula for moving the window multi-head SAM is the same as that for the window multi-head SAM, but the position of the window will move at different levels, forming different feature aggregation methods. The formula for the variation in feature dimensions in the hierarchical structure of the Swin Transformer is shown in Equation (12).
In Equation (12), and are the channels in the input and output feature maps. / and / are the heights and widths of the input and output feature maps. The calculation of FFNN is Equation (13).
In Equation (13), is FFNN and is the input feature vector. and are the weight matrices of the first and second FCLs. is the ReLU function. The combination of the HO-SRGAN and Swin Transformer is used to construct the final ISR reconstruction model, which is referred to as HO-SRGAN-ST. Its structure is shown in Figure 7.
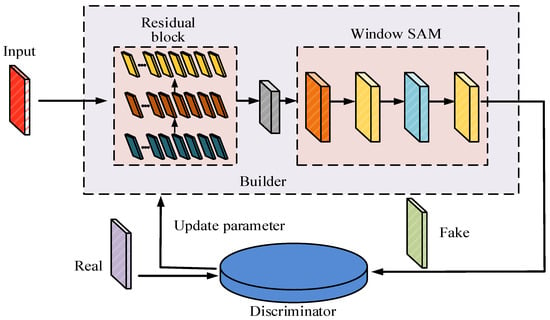
Figure 7.
Structural diagram of the HO-SRGAN-ST construct.
HO-SRGAN-ST in Figure 7 is mainly composed of a generator network and a discriminator network. The overall architecture includes input preprocessing, feature extraction, reconstruction, and adversary-discriminant modules, forming a complete super-resolution reconstruction process. The generator network extracts the basic features of the low-resolution image through the initial convolutional layer and then combines the residual block of HO-SRGAN and the window attention mechanism of the Swin Transformer for feature extraction. The residuals are used to enhance local detail, while the Swin Transformer utilizes the window attention and moving window mechanisms to improve global feature capture and optimize the recovery of complex textures. After feature extraction, the network gradually improves the resolution through the upper sampling layer, and finally outputs the super-resolution image.
The task of the discriminator network is to distinguish the generated high-resolution image from the real image and optimize the generator performance through adversarial training. In this part, multi-layer convolution is used for feature extraction and the Leaky ReLU activation function is combined to enhance the non-linear modeling ability. In addition, the relative discrimination mechanism is introduced, which not only pays attention to the pixel-level difference, but also combines the overall quality of the image to discriminate, which makes the training more stable and the generated image more authentic. In the training process, the model is optimized by combining countermeasure loss, perception loss, and mean square error loss. Countermeasure loss enhances image authenticity, perception loss guides the model to focus on high-level features, and mean square error loss maintains pixel-level consistency. Through continuous feedback from the discriminator, the generator is continuously optimized to achieve higher-quality super-resolution reconstruction.
After completing the construction of HO-SRGAN-ST, in order to enhance the robustness of the model to noisy images, the adaptive denoising strategy is further introduced into the generator network. Firstly, the local variance of the image is calculated to estimate the noise level in the input stage, and the convolutional kernel weights of the generator are dynamically adjusted by using the noise estimation results, so as to adapt to the noise of different intensities. Secondly, a noise-sensing attention mechanism is added to the Swin Transformer module. By calculating the feature mean and standard deviation of the window area, the attention weight can be focused on the low-noise area to reduce noise interference. In addition, in the reconstruction stage, adaptive residual learning is introduced to adjust the denoising intensity adaptively by comparing the noise distribution of input and feature mapping, so as to suppress noise artifacts while maintaining image details.
4. Analysis of Benchmark Performance and Application Effectiveness of HO-SRGAN-ST Model
To verify the performance of the HO-SRGAN-STISR, this study performed multiple experimental evaluations on a standard test set. Firstly, ablation tests were conducted on each module of the model to explore the impact of various components on overall performance. Secondly, benchmark performance comparisons were made with several mainstream ISR algorithms. Finally, this study applied the algorithm to practical image reconstruction tasks and evaluated its performance in processing different types of images.
4.1. Ablation Testing and Benchmark Performance Testing
PyTorch framework was used for training in the experiment. The initial learning rate was set to 0.0001, the weight attenuation was set to 0.001, and Adam was selected as the optimizer. Set the batch size to 64 and the training rounds to 100. The training data came from Set5, Set14, BSD100, and Urban100 datasets, with 80% used for training and 20% for testing. To enhance the generalization ability of the model, a series of data enhancement techniques were used during training, including random rotation (0°, 90°, 180°, 270°), random horizontal and vertical flips, and color dithering (brightness, contrast, saturation variation range of ±10%). In addition, all input images are downsampled to a quarter of the original resolution using double cubic interpolation to simulate low-resolution inputs. The entire training process is conducted on the NVIDIA RTX 3080 GPU, with each round of training taking about 0.8 h, and the total training time is about 80 h. Table 1 lists the parameters of experimental equipment and models.

Table 1.
Configuration of experimental environment and network parameter settings.
To fully evaluate the performance of HO-SRGAN-ST, the study adopts the Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index Measure (SSIM) as key evaluation indicators. These two indexes can effectively measure the improvement of image quality in the process of image super-resolution reconstruction. PSNR mainly reflects the accuracy of image restoration quality, while SSIM is used to evaluate the structural fidelity of the image. Firstly, the ablation experiment was conducted, and the results are shown in Table 2.

Table 2.
The results of the ablation experiment.
As can be seen from Table 2, the ablation experiments show that the SRGAN and Swin Transformer each contribute to improving model performance. After removing the Swin Transformer, PSNR and SSIM decreased significantly. On the Urban100 dataset, PSNR decreases by 3.15 dB, and SSIM decreases by 0.08, indicating that the Swin Transformer plays a key role in complex scenes and detail-rich image processing. The local window and moving window attention mechanism enhance the feature extraction ability. After the removal of SRGAN, although PSNR and SSIM are improved, the overall performance is lower than that of the complete model, and the reconstruction time is shortened, indicating that the adversarial training of SRGAN is crucial for high-quality image generation and can effectively recover the global structure and details. The complete model combines the high-quality image generation capability of SRGAN and the global feature modeling capability of the Swin Transformer to achieve the best super-resolution reconstruction effect, and the synergy of each module significantly improves the overall performance of the model.
The RGAN, Enhanced Deep Super Resolution Network (EDSR), and Residual Channel Attention Network (RCAN) are selected as comparison algorithms. Figure 8 shows the loss values of four algorithms tested on two datasets.
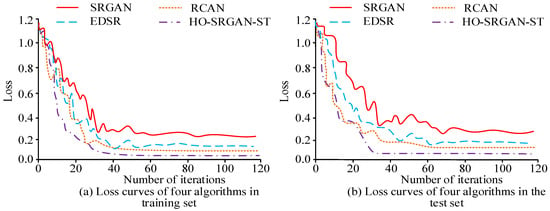
Figure 8.
Loss values of the different algorithms in both datasets.
Figure 8a,b shows the loss curve changes in SRGAN, EDSR, RCAN, and HO-SRGAN-ST in two datasets. HO-SRGAN-ST can reach a stable state after 44 and 32 iterations, respectively, with loss values of 0.03 and 0.05 in the stable state. Compared to SRGAN, EDSR, and RCAN, HO-SRGAN-ST has better stability during training and testing, and its convergence speed is also faster. Table 3 shows the benchmark performance test results of four algorithms.

Table 3.
Benchmark performance of the different algorithms.
In the test of Table 3, HO-SRGAN-ST performs the best with precision, recall, and F1 values as high as 0.96, 0.98, and 0.97, while SRGAN performs poorly with values of only 0.85, 0.83, and 0.84. In terms of reconstruction error, the error values of SRGAN, EDSR, RCAN, and HO-SRGAN-ST are 0.045, 0.038, 0.029, and 0.011, indicating that HO-SRGAN-ST has less image feature loss during the reconstruction process and can better restore the image. Comparing the reconstruction time of each image using four algorithms, it is found that the reconstruction time of HO-SRGAN-ST and RCAN are both controlled within 0.1 s, with HO-SRGAN-ST taking as little as 0.02 s. Four images with different styles are selected from the Set5, Set14, BSD100, and Urban100 datasets to compare the SRR effects of the algorithm on the four types of images. Figure 9 shows the confusion matrices obtained for each.
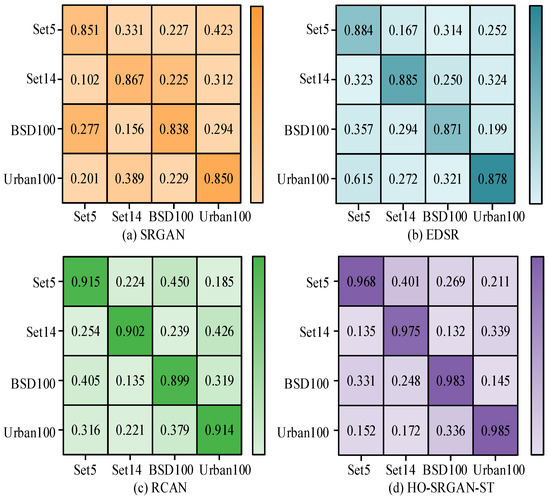
Figure 9.
Reconstruction quality confusion matrix for the four algorithms.
Figure 9a–d show the confusion matrices of reconstruction quality for SRGAN, EDSR, RCAN, and HO-SRGAN-ST. In Figure 9a, SRGAN performs relatively well on Set5 with a reconstruction quality score of 0.851, but performs poorly on BSD100 and Urban100 with reconstruction scores of 0.156 and 0.229, indicating that SRGAN has weak reconstruction ability in complex scenes. In Figure 9b, EDSR performs relatively well on all datasets, especially with high reconstruction scores of 0.885 and 0.878 on Set14 and Urban100, indicating its strong ability to reconstruct complex image details. Figure 9c,d show that RCAN performs the best on the BSD100 dataset, with a reconstruction score of 0.899. HO-SRGAN-ST performs well on all datasets, with the best reconstruction quality on BSD100 and Urban100, scoring 0.983 and 0.985, respectively. The PSNR and SSIM performance of the four algorithms are exhibited in Figure 10.
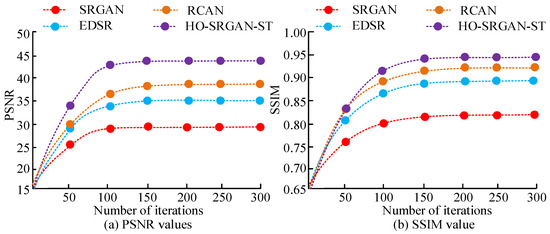
Figure 10.
PSNR and SSIM for the four algorithms.
Figure 10a,b show the PSNR and SSIM of four algorithms. The PSNR (43.81) and SSIM (0.94) values of HO-SRGAN-ST are the highest when reaching a steady state, while the PSNR (28.52) and SSIM (0.82) of SRGAN are lower. The values of EDSR and RCAN are between the other two models.
4.2. Analysis of Model Application Effectiveness
To verify the performance of the HO-SRGAN-ST in actual image reconstruction tasks, this study first collects and preprocesses image data from different practical application scenarios. Subsequently, these image data are divided into four categories: natural landscape images, urban building images, complex texture images, and portrait images. Each type of image contains different details and structural features. The performance of the HO-SRGAN-ST model and comparative algorithms in actual image reconstruction tasks is tested using the processed image dataset. Table 4 shows the reconstruction accuracy and PSNR values of various algorithms on various types of images.

Table 4.
Reconstruction accuracy of the four algorithms in a real task.
In Table 4, HO-SRGAN-ST performs well in all four image tasks. For instances, in the reconstruction of natural landscape images, the reconstruction accuracy of HO-SRGAN-ST reaches 97.58%, with a PSNR value of 40.03 dB, significantly better than other algorithms. In urban building images, the reconstruction accuracy of HO-SRGAN-ST is 96.95%, with a PSNR value of 41.57 dB, demonstrating equally excellent performance. In addition, in tasks involving complex texture images and portrait images, HO-SRGAN-ST has the highest reconstruction accuracy and PSNR value. Overall, HO-SRGAN-ST outperforms other comparison algorithms in terms of reconstruction precision and image quality across all tasks. Natural landscape images, urban architectural images, complex texture images, and portrait images are, respectively, referred to as Images 1 to 4. Figure 11 compares the average time consumption of four algorithms for reconstructing four types of images.
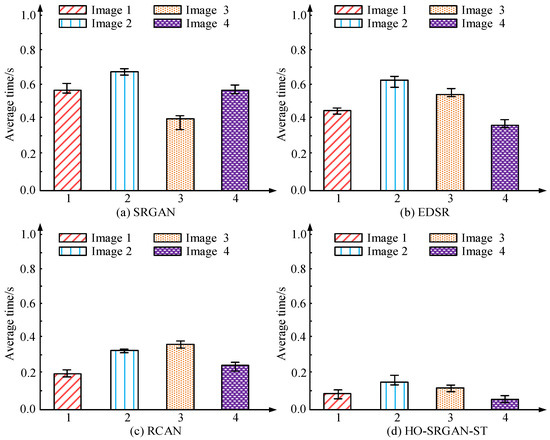
Figure 11.
Average reconstruction time for the different algorithms.
Figure 11a–d show the average time consumption for reconstructing four types of images: SRGAN, EDSR, RCAN, and HO-SRGAN-ST. HO-SRGAN-ST exhibits the shortest average reconstruction time among all image reconstruction tasks, with reconstruction times of less than 0.2 s for all images, demonstrating extremely high efficiency. In contrast, SRGAN has a longer average reconstruction time, especially on Image 2 where the reconstruction time is close to 0.7 s. The reconstruction time of EDSR and RCAN is between SRGAN and HO-SRGAN-ST, with moderate performance. Overall, HO-SRGAN-ST not only has advantages in reconstruction precision, but also significantly outperforms other algorithms in reconstruction speed, with higher practical application value. The performance of the four algorithms in actual reconstruction tasks is exhibited in Figure 12.

Figure 12.
Reconstruction results under the different algorithms.
Figure 12 shows the results of reconstructing four types of images using SRGAN, EDSR, RCAN, and HO-SRGAN-ST. HO-SRGAN-ST preserves the clearest details when reconstructing images, and the structure and text of buildings are well restored with clear and distinguishable edges. In contrast, the reconstruction effect of SRGAN is relatively blurry and can hardly restore architectural and textual details. The reconstruction effects of EDSR and RCAN are between the two, with improved detail representation, but compared to HO-SRGAN-ST, the images are still slightly blurry. In summary, HO-SRGAN-ST performs the best in image reconstruction tasks, as it can better restore details and image structures. Finally, the study compares HO-SRGAN-ST with existing research methods including majorize–minimize low-rank hyperspectral super-resolution (MM-LRHSR), residual dense super-resolution generative adversarial network (RD-SRGAN), contrastive learning for semi-supervised super-resolution (CL-SSR), and external attention generative adversarial network (EA-GAN). The comparison methods are from references [8,9,10,11] in the literature review. The comparison results are shown in Table 5.

Table 5.
Compare the results with existing methods.
As can be seen from Table 5, HO-SRGAN-ST performs better than other existing comparison methods, and its PSNR value is 29.58 dB and SSIM value is 0.89, both of which reach the highest level, indicating that the model has obvious advantages in overall reconstruction quality and visual fidelity. MAE is 0.0978, indicating that its pixel-level error is small, and its high-frequency detail recovery rate is 92.8%, which is 2.5 percentage points higher than EA-GAN, indicating that its ability in detail reconstruction is more prominent. Although the EA-GAN is slightly faster in terms of reconstruction time, the overall performance of the HO-SRGAN-ST is more balanced, especially in terms of visual quality and detail retention. Therefore, HO-SRGAN-ST shows comprehensive advantages in super-resolution reconstruction tasks in complex scenes.
5. Conclusions
To enhance the quality and speed of ISR reconstruction, this study combined the SRGAN and Swin Transformer to construct a novel SRR model, namely HO-SRGAN-ST. In the experiment, HO-SRGAN-ST was able to iterate to a stable state faster than the other three algorithms, and its loss value after reaching a stable state was as low as 0.03. In the benchmark performance tests, the precision, recall, and F1 values of HO-SRGAN-ST were as high as 0.96, 0.98, and 0.97, far higher than SRGAN’s 0.85, 0.83, and 0.84. In addition, the reconstruction error and reconstruction time per image of HO-SRGAN-ST were also lower, at 0.011 and 0.02. In the confusion matrix, HO-SRGAN-ST had the best reconstruction quality on the Urban100 dataset, with a score of up to 0.985. In the PSNR and SSIM tests, the HO-SRGAN-ST had the highest PSNR and SSIM values at 43.81 and 0.94 when it reached a steady state. In addition to testing the benchmark performance, this study also selected four different image types to test the reconstruction performance of HO-SRGAN-ST. Finally, it was found that the reconstruction accuracy of HO-SRGAN-ST was as high as 98.03%, and the reconstruction time was less than 0.2 s. HO-SRGAN-ST increases the computational complexity compared to SRGAN, but does not bring a doubling of the computational overhead because the Swin Transformer’s window attention mechanism optimizes the computational efficiency. Compared with Swin Transformer alone, the reasoning time of HO-SRGAN-ST is shorter, indicating that its computational efficiency has been optimized and it is suitable for practical application scenarios. In general, HO-SRGAN-ST not only ensures the improvement of super-resolution reconstruction quality, but also maintains better computing efficiency, and is suitable for application scenarios that require computing time.
The proposed super-resolution reconstruction algorithm is also of great value in practical application scenarios. For example, the algorithm can be widely used in medical image processing to improve the resolution of MRI and CT images, enhance the accuracy of lesion detection, and assist in accurate diagnosis. In remote sensing monitoring, the algorithm can enhance the details of satellite images and improve the accuracy of environmental monitoring and disaster assessment. In the field of video surveillance, the algorithm can optimize low-quality surveillance video, improve face recognition, and target detection capabilities. In the restoration of cultural heritage, the algorithm can be used to reconstruct blurred or damaged historical images and recover detailed information. In addition, in terms of smartphone image enhancement, the algorithm is able to improve the quality of low-pixel photos and enhance the user experience. Compared with traditional methods, this algorithm has more advantages in complex texture and high-frequency detail processing, and has a wide range of practical application values. In order to enhance the adaptability of the model to unseen images, future research can adopt adaptive feature extraction, multi-scale training, data enhancement, and optimization of loss function. Among them, multi-scale training can enhance the adaptability of the model to images with different resolutions, data enhancement can improve the generalization ability, and optimized perceptual loss and counter loss can ensure the detail recovery effect. In addition, transfer learning and self-supervised fine-tuning can further improve the applicability of the model in different scenarios such as medical images, remote sensing images, and surveillance videos.
Although HO-SRGAN-ST performs well in super-resolution tasks, it still has certain limitations in high-noise environments or complex texture images, such as detail blurring or artifact enhancement. In addition, the computational complexity of the Swin Transformer is high, which is not conducive to real-time reasoning of low computing power devices. Future studies can explore more efficient denoising mechanisms, multi-scale feature fusion strategies, and lightweight model optimization to improve model robustness and computational efficiency.
Author Contributions
Investigation, C.S., C.W. and C.H.; writing-original draft preparation, C.S.; writing-review and editing, C.H.; supervision, C.H. All authors have read and agreed to the published version of the manuscript.
Funding
Science and Technology Development Plan Project of Weifang City (Grant No. 2023GX009). Major Project of Natural Science Fundamental Research of the Jiangsu Higher Education Institutions of China (No. 23KJA520006).
Data Availability Statement
The data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yu, M.; Shi, J.; Xue, C.; Hao, X.; Yan, G. A review of single image super-resolution reconstruction based on deep learning. Multimed. Tools Appl. 2024, 83, 55921–55962. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Nan, F.; Liu, F.; Li, H.; Wang, H.; Qian, Y. Image super-resolution reconstruction based on generative adversarial network model with feedback and attention mechanisms. Multimed. Tools Appl. 2022, 81, 6633–6652. [Google Scholar] [CrossRef]
- Tao, P.; Yang, D. RSC-WSRGAN super-resolution reconstruction based on improved generative adversarial network. Signal Image Video Process. 2024, 18, 7833–7845. [Google Scholar] [CrossRef]
- Li, X.; Dong, W.; Wu, J.; Li, L.; Shi, G. Superresolution image reconstruction: Selective milestones and open problems. IEEE Signal Process. Mag. 2023, 40, 54–66. [Google Scholar] [CrossRef]
- Hu, Y.; Shang, Q. Performance enhancement of BOTDA based on the image super-resolution reconstruction. IEEE Sens. J. 2021, 22, 3397–3404. [Google Scholar] [CrossRef]
- Sharma, A.; Shrivastava, B.P. Different techniques of image SR using deep learning: A review. IEEE Sens. J. 2022, 23, 1724–1733. [Google Scholar] [CrossRef]
- Daihong, J.; Sai, Z.; Lei, D.; Yueming, D. Multi-scale generative adversarial network for image super-resolution. Soft Comput. 2022, 26, 3631–3641. [Google Scholar] [CrossRef]
- Lei, H.; Wang, Z.; Tian, C.; Zhang, Y. An improved SRGAN infrared image super-resolution reconstruction algorithm. J. Syst. Simul. 2021, 33, 2109–2118. [Google Scholar] [CrossRef]
- Abi-Rizk, R.; Orieux, F.; Abergel, A. Super-Resolution Hyperspectral Reconstruction with Majorization-Minimization Algorithm and Low-Rank Approximation. IEEE Trans. Comput. Imaging 2022, 8, 260–272. [Google Scholar] [CrossRef]
- Ahmadi, S.; Kästner, L.; Hauffen, J.C.; Jung, P.; Ziegler, M. Photothermal-SR-Net: A Customized Deep Unfolding Neural Network for Photothermal Super Resolution Imaging. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Esmaeilzehi, A.; Ahmad, M.O.; Swamy, M.N.S. SRNMSM: A Deep Light-Weight Image Super Resolution Network Using Multi-Scale Spatial and Morphological Feature Generating Residual Blocks. IEEE Trans. Broadcast. 2022, 68, 58–68. [Google Scholar] [CrossRef]
- Mishra, D.; Hadar, O. CLSR: Contrastive Learning for Semi-Supervised Remote Sensing Image Super-Resolution. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, H. A novel fast reconstruction method for single image super resolution task. Neural Process. Lett. 2023, 55, 9995–10010. [Google Scholar] [CrossRef]
- Fu, L.; Jiang, H.; Wu, H.; Yan, S.; Wang, J.; Wang, D. Image super-resolution reconstruction based on instance spatial feature modulation and feedback mechanism. Appl. Intell. 2023, 53, 601–615. [Google Scholar] [CrossRef]
- Khmag, A. Natural digital image mixed noise removal using regularization Perona–Malik model and pulse coupled neural networks. Soft Comput. 2023, 27, 15523–15532. [Google Scholar] [CrossRef]
- Khmag, A. Additive Gaussian noise removal based on generative adversarial network model and semi-soft thresholding approach. Multimed. Tools Appl. 2023, 82, 7757–7777. [Google Scholar] [CrossRef]
- Chen, Y.; Xia, R.; Yang, K.; Zou, K. MFFN: Image super-resolution via multi-level features fusion network. Vis. Comput. 2024, 40, 489–504. [Google Scholar] [CrossRef]
- Kshem, W.; Khmag, A. Improving Block Matching and 3 Dimensions (BM3D) Filtering for Image Noise Removal Using Discrete Wavelet Transformation (DWT). In Proceedings of the 2024 IEEE 4th International Maghreb Meeting of the Conference on Sciences and Techniques of Automatic Control and Computer Engineering (MI-STA), Tripoli, Libya, 19–21 May 2024; pp. 375–380. [Google Scholar] [CrossRef]
- Guo, J.; Lv, F.; Shen, J.; Liu, J.; Wang, M. An improved generative adversarial network for remote sensing image super-resolution. IET Image Process. 2023, 17, 1852–1863. [Google Scholar] [CrossRef]
- Abbas, R.; Gu, N. Improving deep learning-based image super-resolution with residual learning and perceptual loss using SRGAN model. Soft Comput. 2023, 27, 16041–16057. [Google Scholar] [CrossRef]
- Ma, C.; Rao, Y.; Lu, J.; Zhou, J. Structure-preserving image super-resolution. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 7898–7911. [Google Scholar] [CrossRef]
- Huang, S.; Liu, X.; Tan, T.; Hu, M.; Wei, X.; Chen, T.; Sheng, B. TransMRSR: Transformer-based self-distilled generative prior for brain MRI super-resolution. Vis. Comput. 2023, 39, 3647–3659. [Google Scholar] [CrossRef]
- Guo, X.; Tu, Z.; Zhang, H.; Dong, H. Super-resolution reconstruction based on generative adversarial networks with dual branch half instance normalization. IET Image Process. 2024, 18, 1434–1446. [Google Scholar] [CrossRef]
- Hou, Y.; Canul-Ku, M.; Cui, X.; Zhu, M. Super-resolution reconstruction of vertebrate microfossil computed tomography images based on deep learning. X-Ray Spectrom. 2024, 53, 405–414. [Google Scholar] [CrossRef]
- Liu, X.; Su, S.; Gu, W.; Yao, T.; Shen, J.; Mo, Y. Super-resolution reconstruction of CT images based on multi-scale information fused generative adversarial networks. Ann. Biomed. Eng. 2024, 52, 57–70. [Google Scholar] [CrossRef]
- Wang, G.; Wang, K.C.; Yang, G. Reconstruction of sub-mm 3D pavement images using recursive generative adversarial network for faster texture measurement. Comput. Aided Civ. Infrastruct. Eng. 2023, 38, 2206–2224. [Google Scholar] [CrossRef]
- Hu, Y.; Li, J.; Huang, Y.; Gao, X. Image super-resolution with self-similarity prior guided network and sample-discriminating learning. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 1966–1985. [Google Scholar] [CrossRef]
- Zhang, T.; Hu, G.; Yang, Y.; Du, Y. A super-resolution reconstruction method for shale based on generative adversarial network. Transp. Porous Media 2023, 150, 383–426. [Google Scholar] [CrossRef]
- Liu, H.; Shao, M.; Wang, C.; Cao, F. Image super-resolution using a simple transformer without pretraining. Neural Process. Lett. 2023, 55, 1479–1497. [Google Scholar] [CrossRef]
- Ju, R.Y.; Chen, C.C.; Chiang, J.S.; Lin, Y.S.; Chen, W.H. Resolution enhancement processing on low quality images using swin transformer based on interval dense connection strategy. Multimed. Tools Appl. 2024, 83, 14839–14855. [Google Scholar] [CrossRef]
- Wang, J.; Zou, Y.; Alfarraj, O.; Sharma, P.K.; Said, W.; Wang, J. Image super-resolution method based on the interactive fusion of transformer and CNN features. Vis. Comput. 2024, 40, 5827–5839. [Google Scholar] [CrossRef]
- Gao, X.; Wu, S.; Zhou, Y.; Wu, X.; Wang, F.; Hu, X. Lightweight image super-resolution via multi-branch aware CNN and efficient transformer. Neural Comput. Appl. 2024, 36, 5285–5303. [Google Scholar] [CrossRef]
- Bhosle, K.; Musande, V. Evaluation of deep learning CNN model for recognition of devanagari digit. Artif. Intell. Appl. 2023, 1, 114–118. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).