Reliable Transmission of Energy Harvesting Full-Duplex Relay Systems with Short-Packet Communications
Abstract
1. Introduction
- (1)
- We investigate short-packet communications in an energy-constrained FD relay system with hardware impairments, where both antennas at the relay are employed for energy harvesting. We further explore independent and identical channels for energy harvesting.
- (2)
- We derive closed-form approximations for the overall average BLER and effective throughput under both scenarios, which characterize the impact of key system parameters on the reliable performance of the FD relay system.
- (3)
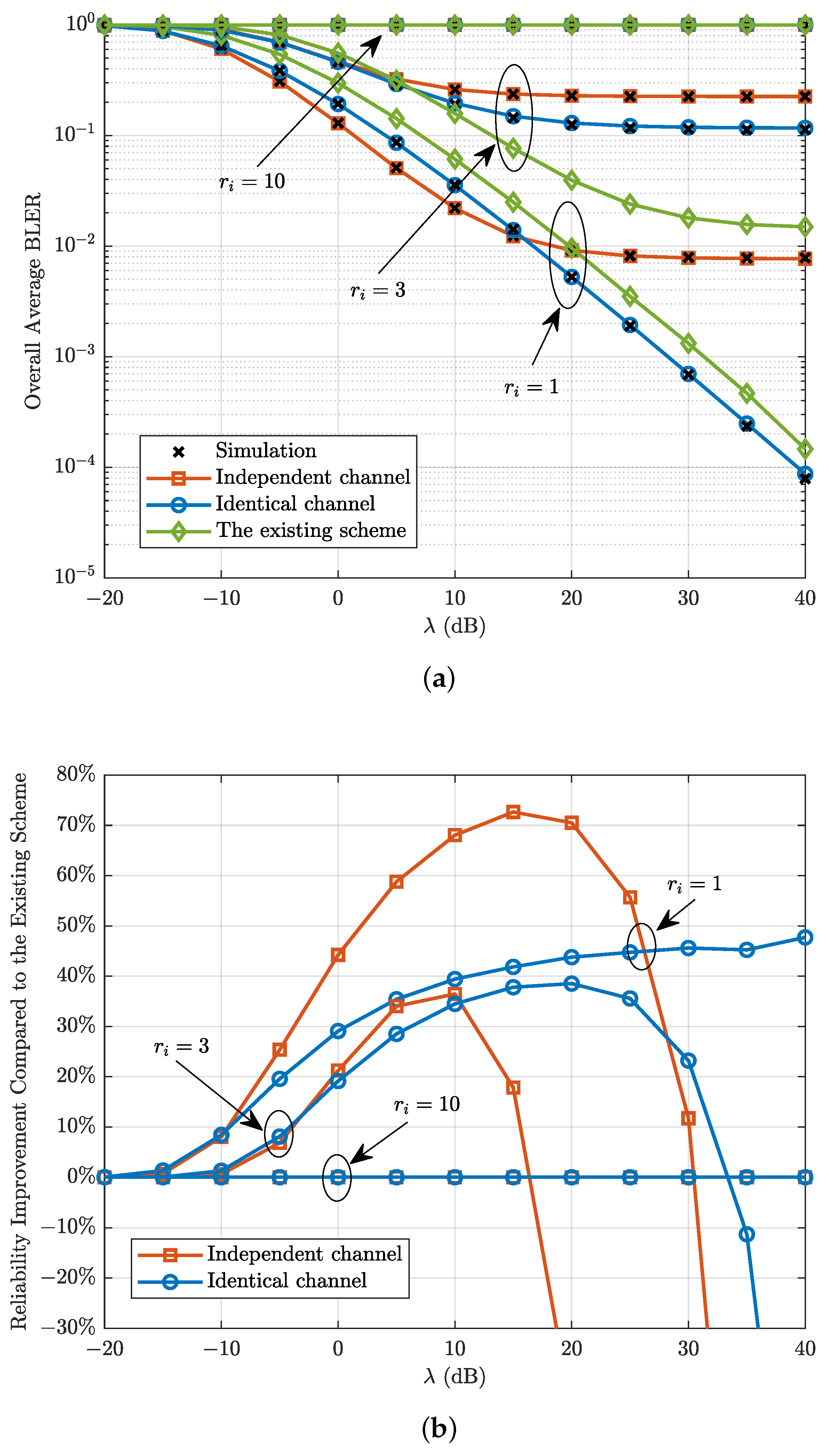
- We validate our analysis through computer simulations, which demonstrate that the proposed scheme improves the reliability and throughput of the system compared with the existing scheme in the literature at low transmission rates and transmit SNRs.
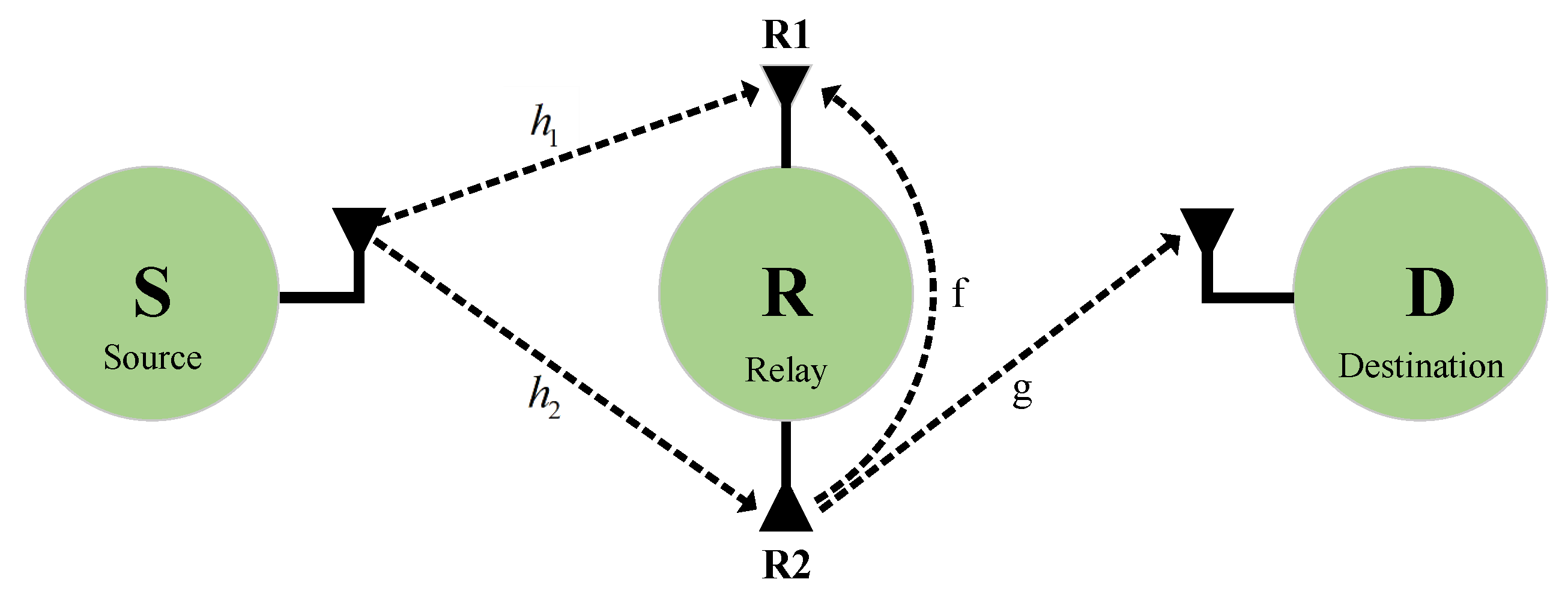
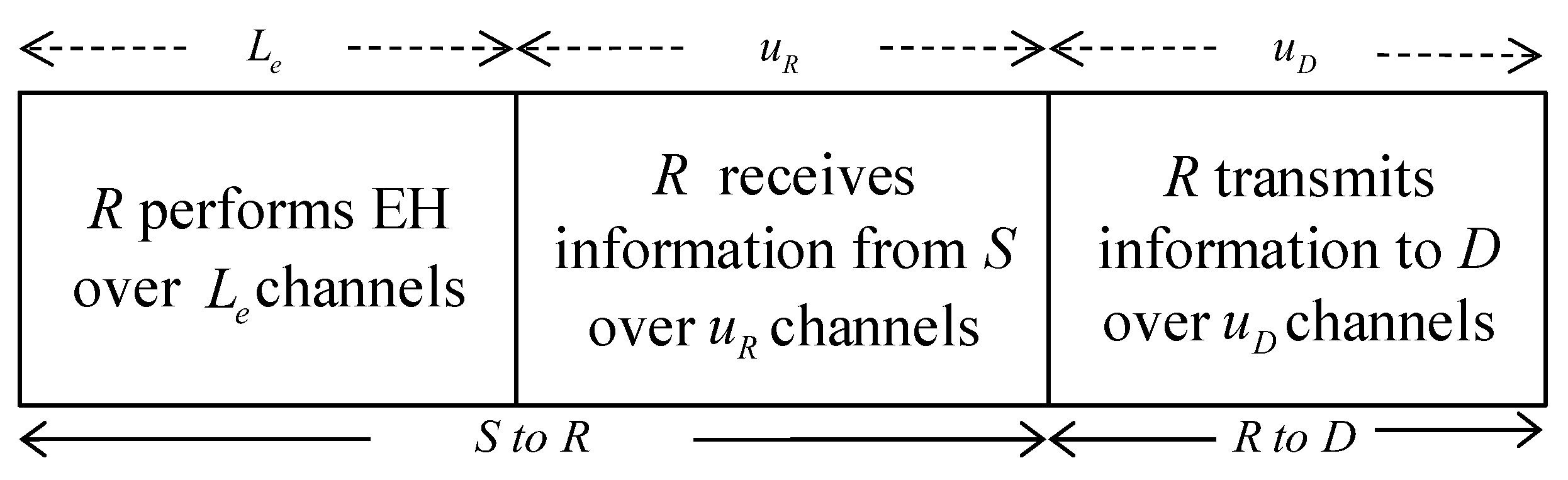
2. System Model
3. Performance Analysis
3.1. Preliminaries
3.2. Statistical Characterization of the SNRs
3.3. Overall Average BLER Under the Independent Channel
3.4. Overall Average BLER Under the Identical Channel
3.5. Effective Throughput
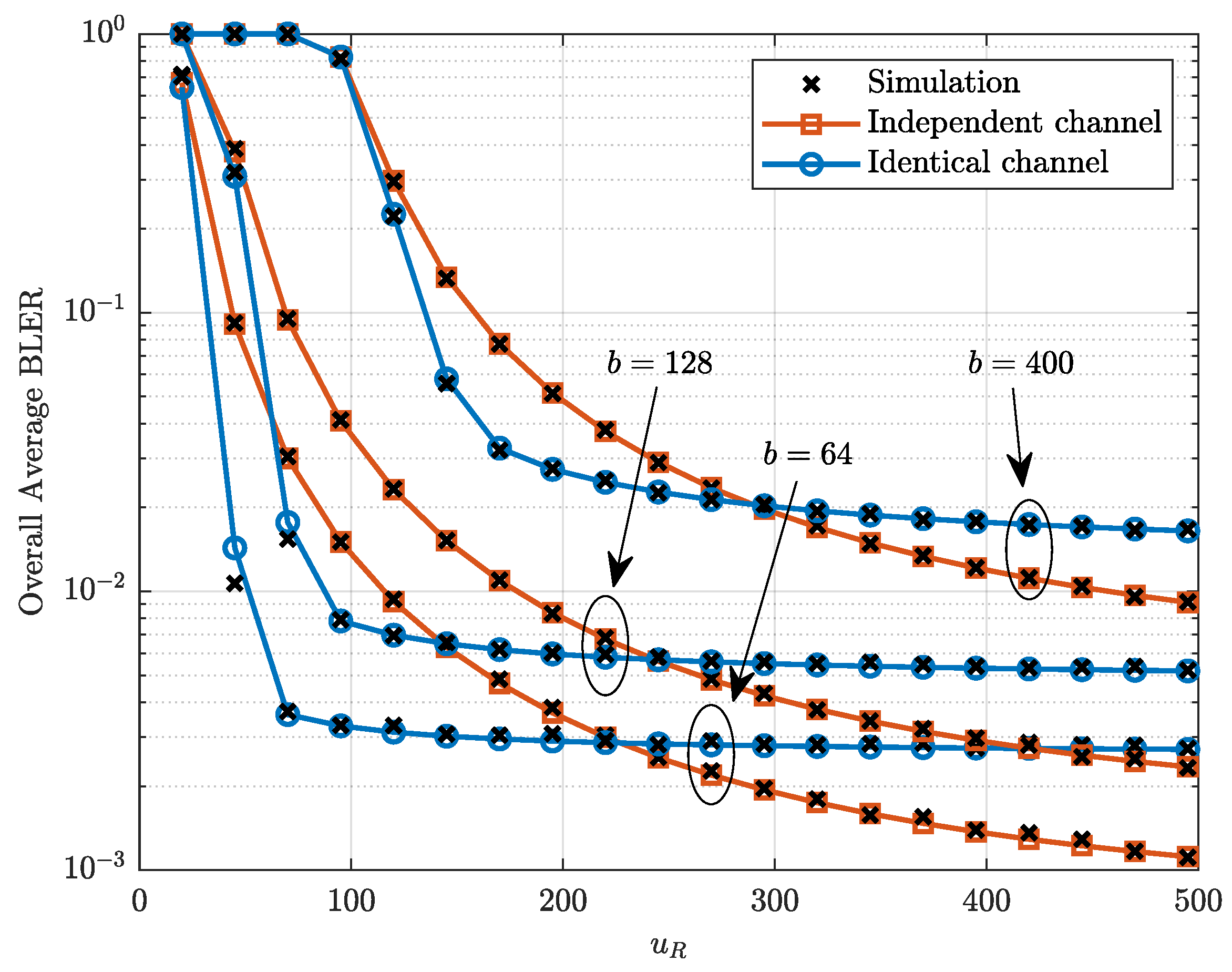
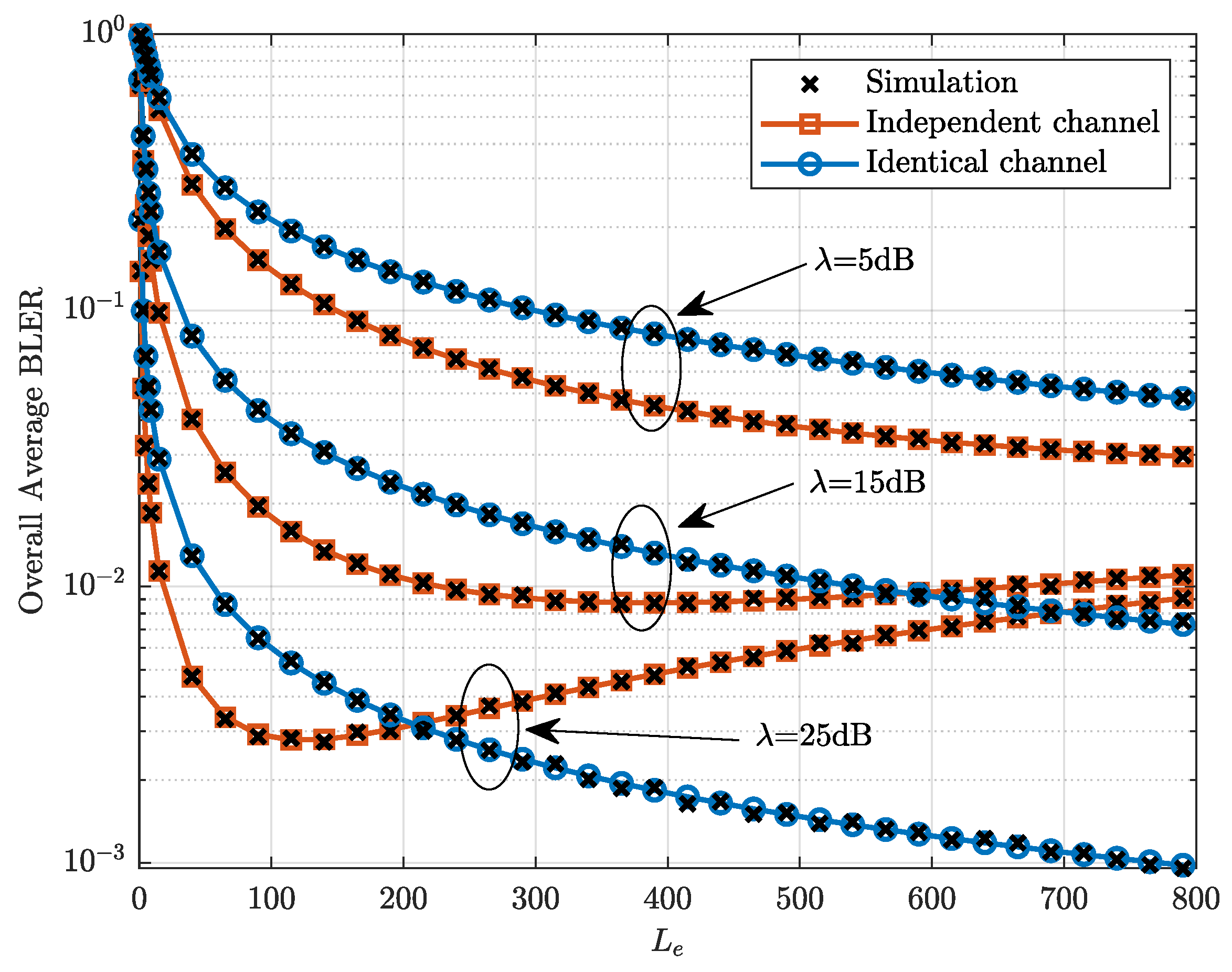
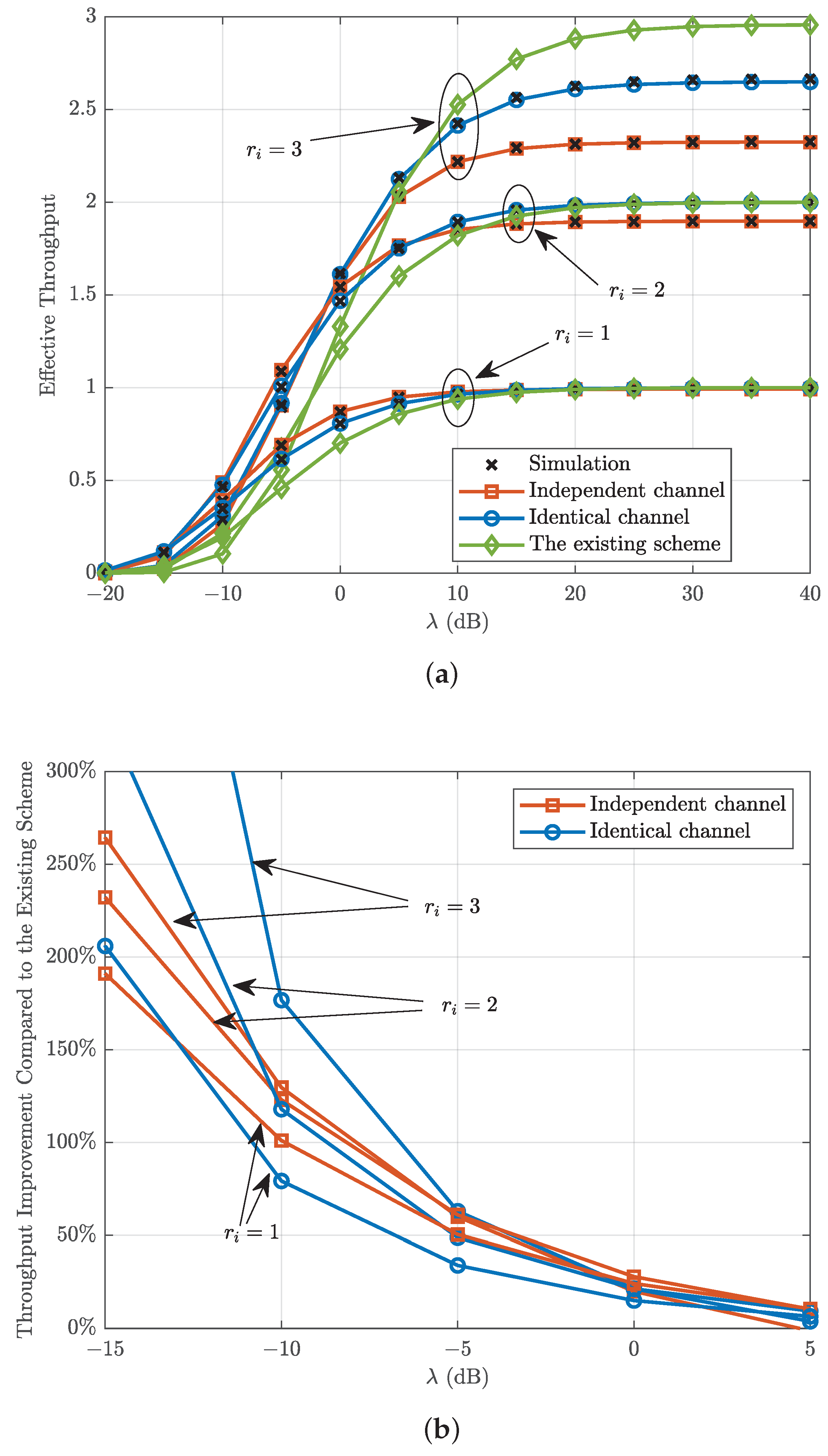
4. Numerical Results and Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FD | full-duplex |
| RF | radio frequency |
| BLER | block error rate |
| SNRs | signal-to-noise-ratios |
| IoT | Internet of Things |
| QoS | quality-of-service |
| 5G | fifth-generation |
| URLLC | ultra-reliable low-latency communications |
| EH | energy harvesting |
| RIS | reconfigurable intelligent surface |
| NOMA | nonorthogonal multiple access |
| SWIPT | simultaneous wireless information and power transfer |
| IQ | in-phase/quadrature |
| CSI | channel state information |
| DF | decode-and-forward |
| AWGN | additive white Gaussian noise |
| probability density function | |
| CDF | cumulative density function |
| D-2-D | Device-to-Device |
| DDPG | deep deterministic policy gradi-ent |
| UAV | unmanned aerial vehicles |
| AF | amplify-and-forward |
| MIMO | multiple-input multiple-output |
| EVMs | error vector magnitudes |
| LTE | Long-Term Evolution |
Appendix A
Appendix B
Appendix C
Appendix D
Appendix E
References
- Guo, F.; Yu, F.R.; Zhang, H.; Li, X.; Ji, H.; Leung, V.C.M. Enabling Massive IoT Toward 6G: A Comprehensive Survey. IEEE Internet Things J. 2021, 8, 11891–11915. [Google Scholar] [CrossRef]
- López, O.L.A.; Mahmood, N.H.; Shehab, M.; Alves, H.; Rosabal, O.M.; Marata, L. Statistical Tools and Methodologies for Ultrareliable Low-Latency Communication—A Tutorial. Proc. IEEE 2023, 111, 1502–1543. [Google Scholar] [CrossRef]
- Popovski, P.; Stefanović, Č.; Nielsen, J.J.; de Carvalho, E.; Angjelichinoski, M.; Trillingsgaard, K.F. Wireless Access in Ultra-Reliable Low-Latency Communication (URLLC). IEEE Trans. Commun. 2019, 67, 5783–5801. [Google Scholar] [CrossRef]
- You, X.; Sheng, B.; Huang, Y.; Xu, W.; Zhang, C.; Wang, D. Closed-Form Approximation for Performance Bound of Finite Blocklength Massive MIMO Transmission. IEEE Trans. Commun. 2023, 71, 6939–6951. [Google Scholar] [CrossRef]
- Polyanskiy, Y.; Poor, H.V.; Verdu, S. Channel Coding Rate in the Finite Blocklength Regime. IEEE Trans. Inf. Theory 2010, 56, 2307–2359. [Google Scholar] [CrossRef]
- Tu, N.H.; Lee, K. Performance Analysis and Optimization of Multihop MIMO Relay Networks in Short-Packet Communications. IEEE Trans. Wirel. Commun. 2022, 21, 4549–4562. [Google Scholar] [CrossRef]
- Hu, Y.; Ozmen, M.; Gursoy, M.C.; Schmeink, A. Optimal Power Allocation for QoS-Constrained Downlink Multi-User Networks in the Finite Blocklength Regime. IEEE Trans. Wirel. Commun. 2018, 17, 5827–5840. [Google Scholar] [CrossRef]
- Benbuk, A.A.; Kouzayha, N.; Costantine, J.; Dawy, Z. Charging and Wake-Up of IoT Devices using Harvested RF Energy with Near-Zero Power Consumption. IEEE Internet Things Mag. 2023, 6, 162–167. [Google Scholar] [CrossRef]
- Hu, Y.; Yuan, X.; Zhang, G.; Schmeink, A. Sustainable Wireless Sensor Networks with UAV-Enabled Wireless Power Transfer. IEEE Trans. Veh. Technol. 2021, 70, 8050–8064. [Google Scholar] [CrossRef]
- Sun, X.; Yang, W.; Cai, Y.; Wang, M. Secure mmWave UAV-Enabled SWIPT Networks Based on Random Frequency Diverse Arrays. IEEE Internet Things J. 2021, 8, 528–540. [Google Scholar] [CrossRef]
- Sun, X.; Yang, W.; Cai, Y.; Xiang, Z.; Tang, X. Secure Transmissions in Millimeter Wave SWIPT UAV-Based Relay Networks. IEEE Wirel. Commun. Lett. 2019, 8, 785–788. [Google Scholar] [CrossRef]
- Tao, L.; Yang, W.; Lu, X.; Wang, M.; Song, Y. Achieving Covert Communication in Uplink NOMA Systems via Energy Harvesting Jammer. IEEE Commun. Lett. 2021, 25, 3785–3789. [Google Scholar] [CrossRef]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kennedy, R.A. Relaying Protocols for Wireless Energy Harvesting and Information Processing. IEEE Trans. Wirel. Commun. 2013, 12, 3622–3636. [Google Scholar] [CrossRef]
- Kalamkar, S.S.; Banerjee, A. Secure Communication via a Wireless Energy Harvesting Untrusted Relay. IEEE Trans. Veh. Technol. 2017, 66, 2199–2213. [Google Scholar] [CrossRef]
- Agrawal, K.; Jee, A.; Prakriya, S. Performance of SWIPT in Cooperative Networks with Direct Link and Nonlinear Energy Harvesting at the Battery-Assisted Relay. IEEE Trans. Green Commun. Netw. 2022, 6, 1198–1215. [Google Scholar] [CrossRef]
- Ouamri, M.A.; Barb, G.; Singh, D.; Adam, A.B.M.; Muthanna, M.S.A.; Li, X. Nonlinear Energy-Harvesting for D2D Networks Underlaying UAV with SWIPT Using MADQN. IEEE Commun. Lett. 2023, 27, 1804–1808. [Google Scholar] [CrossRef]
- Ouamri, M.A.; Machter, Y.; Singh, D.; Alkama, D.; Li, X. Joint Energy Efficiency and Throughput Optimization for UAV-WPT Integrated Ground Network Using DDPG. IEEE Commun. Lett. 2023, 27, 3295–3299. [Google Scholar] [CrossRef]
- Chen, D.; Cheng, Y.; Wang, X.; Yang, W.; Hu, J.; Cai, Y. Energy-efficient secure multiuser scheduling in energy harvesting untrusted relay networks. J. Commun. Netw. 2019, 21, 365–375. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Li, L. Performance Analysis of Impaired SWIPT NOMA Relaying Networks Over Imperfect Weibull Channels. IEEE Syst. J. 2020, 14, 669–672. [Google Scholar] [CrossRef]
- Chen, D.; Li, J.; Hu, J.; Zhang, X.; Zhang, S.; Wang, D. Secrecy Performance Analysis of Energy Harvesting Untrusted Relay Networks with Hardware Impairments. Int. J. Distrib. Sens. Netw. 2024, 2024, 4806603. [Google Scholar] [CrossRef]
- Kurma, S.; Sharma, P.K.; Dhok, S.; Singh, K.; Li, C.-P. Adaptive AF/DF Two-Way Relaying in FD Multiuser URLLC System with User Mobility. IEEE Trans. Wirel. Commun. 2022, 21, 10224–10241. [Google Scholar] [CrossRef]
- Yuan, L.; Du, Q.; Fang, F. Performance Analysis of Full-Duplex Cooperative NOMA Short-Packet Communications. IEEE Trans. Veh. Technol. 2022, 71, 13409–13414. [Google Scholar] [CrossRef]
- Tu, N.H.; Lee, K. Multihop MIMO Full-Duplex Relay Networks with Short-Packet URLLCs. IEEE Syst. J. 2024, 18, 1975–1986. [Google Scholar] [CrossRef]
- Nguyen, T.-V.; Huynh-The, T.; Bao, V.-N.Q. Short-Packet Communications in Wireless Energy Transfer Full-Duplex IoT Networks with Deep Learning Design. J. Commun. Netw. 2024, 26, 297–307. [Google Scholar] [CrossRef]
- Raut, P.; Sharma, P.K.; Tsiftsis, T.A.; Zou, Y. Power-Time Splitting-Based Non-Linear Energy Harvesting in FD Short-Packet Communications. IEEE Trans. Veh. Technol. 2020, 69, 9146–9151. [Google Scholar] [CrossRef]
- Nguyen, T.-V.; Huynh-The, T.; An, B. A Deep CNN-based Relay Selection in EH Full-Duplex IoT Networks with Short-Packet Communications. In Proceedings of the ICC 2021—IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021. [Google Scholar]
- Nguyen, T.-V.; Huynh-The, T.; Quoc Bao, V.N. Performance Analysis and Deep Learning Evaluation of URLLC Full-Duplex Energy Harvesting IoT Networks over Nakagami-m Fading Channels. In Proceedings of the 2023 IEEE Statistical Signal Processing Workshop (SSP), Hanoi, Vietnam, 2–5 July 2023. [Google Scholar]
- Sharma, P.K.; Sharma, N.; Dhok, S.; Singh, A. RIS-Assisted FD Short Packet Communication with Non-Linear EH. IEEE Commun. Lett. 2023, 27, 522–526. [Google Scholar] [CrossRef]
- Kaboyo, S.; Abd El-Malek, A.H.; Muta, O.; Abo-Zahhad, M.; Elsabrouty, M. Age of Information Analysis for Full Duplex Cooperative SWIPT NOMA System. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024. [Google Scholar]
- Li, X.; Wang, Q.; Liu, M.; Li, J.; Peng, H.; Piran, M.; Li, L. Cooperative Wireless-Powered NOMA Relaying for B5G IoT Networks with Hardware Impairments and Channel Estimation Errors. IEEE Internet Things J. 2021, 8, 5453–5467. [Google Scholar] [CrossRef]
- Liu, Z.; Ye, Y.; Lu, G.; Hu, R.Q. System Outage Performance of SWIPT Enabled Full-Duplex Two-Way Relaying with Residual Hardware Impairments and Self-Interference. IEEE Syst. J. 2023, 17, 337–348. [Google Scholar] [CrossRef]
- Kumar, D.; Singya, P.K.; Nebhen, J.; Bhatia, V. Performance of SWIPT-Enabled FD TWR Network with Hardware Impairments and Imperfect CSI. IEEE Syst. J. 2023, 17, 1224–1234. [Google Scholar] [CrossRef]
- Kumar, D.; Singya, P.K.; Krejcar, O.; Bhatia, V. On Performance of a SWIPT Enabled FD CRN with HIs and Imperfect SIC Over α–μ Fading Channel. IEEE Trans. Cogn. Commun. Netw. 2023, 9, 99–113. [Google Scholar] [CrossRef]
- Kumar, D.; Singya, P.K.; Bhatia, V. On Performance of Wireless-Powered FD Relaying Network with Imperfect SIC and Hardware Impairments. In Proceedings of the 2023 National Conference on Communications (NCC), Guwahati, India, 23–26 February 2023. [Google Scholar]
- Kam, S.; Kim, D.; Lee, H.; Hong, D. Bidirectional full-duplex systems in a multispectrum environment. IEEE Trans. Veh. Technol. 2015, 64, 3812–3817. [Google Scholar] [CrossRef]
- Chen, D.; Li, J.; Hu, J.; Zhang, X.; Zhang, S.; Wang, D. Interference-Assisted Energy Harvesting Short Packet Communications with Hardware Impairments. Int. J. Intell. Netw. 2024, 5, 231–240. [Google Scholar] [CrossRef]
- Zheng, D.; Yang, Y.; Wei, L.; Jiao, B. Decode-and-Forward Short-Packet Relaying in the Internet of Things: Timely Status Updates. IEEE Trans. Wirel. Commun. 2021, 20, 8423–8437. [Google Scholar] [CrossRef]
- Solanki, S.; Singh, V.; Upadhyay, P.K. RF energy harvesting in hybrid two-way relaying systems with hardware impairments. IEEE Trans. Veh. Technol. 2019, 68, 11792–11805. [Google Scholar] [CrossRef]
- Holma, H.; Toskala, A. LTE for UMTS: Evolution to LTE-Advanced, 2nd ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Gu, Y.; Chen, H.; Li, Y.; Vucetic, B. Ultra-Reliable Short-Packet Communications: Half-Duplex or Full-Duplex Relaying? IEEE Wirel. Commun. Lett. 2018, 7, 348–351. [Google Scholar] [CrossRef]
- Xia, C.; Xiang, Z.; Meng, J.; Liu, H.; Pan, G. Reliable Transmission of Short Packets in Cognitive Radio Inspired NOMA Network. IEEE Syst. J. 2023, 17, 6148–6158. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products, 7th ed.; Academic Press: New York, NY, USA, 2007. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th ed.; US Govt. Print: Washington, DC, USA, 1972.


| [20] | [22] | [24] | [25] | [28] | [30] | [31] | This Work | |
|---|---|---|---|---|---|---|---|---|
| FD | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| EH: | ||||||||
| - EH with one antenna | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| - EH with two antennas | ✓ | |||||||
| Short-packet communications | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| Hardware impairments | ✓ | ✓ | ✓ | ✓ | ||||
| BLER | ✓ | ✓ | ✓ | ✓ | ✓ |
| Symbol | Description |
|---|---|
| The energy conversion efficiency | |
| The transmit power of S | |
| The transmit power of R | |
| The transmission duration of each channel | |
| and | The channel coefficients from S to R |
| The variances of and | |
| g | The channel coefficient from R to D |
| The variance of g | |
| f | The self-interference channel at R |
| The variance of f | |
| The number of channels used for EH | |
| The number of channels utilized for information transmission from S to R | |
| The number of channels utilized for information transmission from R to D | |
| The level of imperfections in the hardware of transmitter | |
| The level of imperfections in the hardware of receiver | |
| b | The number information bits transmitted from S to D |
| The variance of AWGN at node i, | |
| The transmission rate | |
| The instantaneous BLER | |
| The average BLER | |
| The overall average BLER | |
| G | The effective throughput |
| Parameter | Value |
|---|---|
| Energy conversion efficiency | 0.7 |
| Level of hardware impairments | |
| Channel variances | dB, dB, dB |
| Number of channels | , |
| Noise variance | |
| Complexity accuracy tradeoff parameter |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Yu, M.; Huang, J.; Chen, D.; Li, J.; Jiang, P. Reliable Transmission of Energy Harvesting Full-Duplex Relay Systems with Short-Packet Communications. Symmetry 2025, 17, 281. https://doi.org/10.3390/sym17020281
Yang C, Yu M, Huang J, Chen D, Li J, Jiang P. Reliable Transmission of Energy Harvesting Full-Duplex Relay Systems with Short-Packet Communications. Symmetry. 2025; 17(2):281. https://doi.org/10.3390/sym17020281
Chicago/Turabian StyleYang, Chenxi, Mingkang Yu, Jinshu Huang, Dechuan Chen, Jin Li, and Pei Jiang. 2025. "Reliable Transmission of Energy Harvesting Full-Duplex Relay Systems with Short-Packet Communications" Symmetry 17, no. 2: 281. https://doi.org/10.3390/sym17020281
APA StyleYang, C., Yu, M., Huang, J., Chen, D., Li, J., & Jiang, P. (2025). Reliable Transmission of Energy Harvesting Full-Duplex Relay Systems with Short-Packet Communications. Symmetry, 17(2), 281. https://doi.org/10.3390/sym17020281







