Quantum-Resistant Lattice-Based Proxy Signature

Abstract

With the advancement of quantum computing, the utilization of quantum algorithms such as Shor’s algorithm enables the efficient resolution of problems that are intractable in classical computing paradigms, posing a significant threat to traditional signature schemes. Lattice-based cryptography is considered one of the most promising post-quantum cryptographic algorithms due to its computational advantages and potential resistance to quantum attacks. Proxy signature is an authorization mechanism that allows the original signer to delegate the signing power to a proxy. The security of existing proxy signature schemes is mostly based on classical hard problems, which cannot guarantee security under quantum attacks. Therefore, this paper combines lattice-based cryptography with proxy signatures to propose a new lattice-based proxy signature scheme (NLBPS). NLBPS constructs signatures using lattice-based trapdoor sampling algorithms and preimage sampling algorithms. Comparative analysis shows that the proposed scheme has relatively smaller key and signature sizes compared to some existing lattice-based proxy signature schemes, and it also offers a certain improvement in computational efficiency.

1. Introduction

The concept of proxy signatures was introduced by Mambo, Usuda and Okamoto [1] in 1996. In this signature scheme, the original signer is allowed to delegate the signing authority to the proxy signer. By running an interactive proxy delegation protocol, the proxy signer can obtain a proxy signing key to sign messages on behalf of the original signer. In 2003, Bodyreva et al. [2] formally defined the security model for proxy signature schemes, and proposed a provably secure strong proxy signature scheme. To optimize the key management mechanism in public key cryptosystems, Shamir et al. [3] pioneeringly introduced identity-based signature schemes, where a user’s public key can be directly derived from their identity information. Subsequently, Xu et al. [4] combined identity information with proxy signature technology to design an identity-based proxy signature scheme; however, the security model of this scheme only defined unforgeability and did not consider scenarios involving adaptive chosen messages and adaptive chosen identity attacks. In 2024, Bannore et al. [5] developed a role-based proxy signature scheme on elliptic curve groups, combining role authorization mechanisms with proxy signature technology, which is suitable for the field of e-government.

With the rapid development of quantum computing technology, malicious attackers can efficiently solve classically difficult problems in polynomial time using Shor’s quantum algorithm [6], which poses a serious security threat to traditional schemes. Among the many quantum-resistant cryptographic schemes, lattice-based cryptography has garnered widespread attention due to its strong security proof in terms of its worst-case hardness [7] and efficient implementation. In 2008, Gentry et al. [8] designed a preimage sampling function using the Gaussian sampling algorithm and constructed a provably secure lattice signature scheme based on this technology, known as the GPV scheme. In 2010, Agrawal et al. [9] proposed a lattice basis delegation in a fixed dimension and presented two hierarchical identity-based encryption schemes. These schemes achieved fixed-dimensional delegation authorization, but the computational complexity of the public key generation process was relatively high. In 2013, Kim et al. [10] combined preimage sampling and fixed dimensional basis delegation technology to propose an identity-based proxy signature, and the scheme is proxy-protected in an adaptive security model, but only considered unforgeability in the security analysis of the scheme. In 2019, Wu et al. [11] proposed a proxy signature scheme on the NTRU lattice, which shortened the signature and key length. In 2021, Luo et al. [12] gave a formal concept of attribute-based proxy re-signature and discussed the potential applications of the scheme, whose public key and signature are relatively long. In 2022, Wang et al. [13] proposed a lattice proxy signature scheme suitable for cloud storage scenarios, but the complexity of the proxy authorization and proxy signing processes was relatively high. In 2023, Yu et al. [14] applied the lattice proxy signature scheme to the network coding environment, reducing the computational complexity and improving computational efficiency by reducing the dimension of the proxy key.

In this paper, we propose a new lattice-based proxy signature scheme called NLBPS. NLBPS uses a trapdoor sampling algorithm [15] to generate the public and private key matrices for the original signer and the proxy signer. It utilizes the preimage sampling function for proxy authorization and signature integrity. NLBPS is based on the hard assumption of the small integer solution problem and is provably secure in the random oracle model. Compared to some existing lattice-based proxy signature schemes, NLBPS achieves fixed-dimensional lattice-based proxy signatures with fewer original algorithms, and the required signature and public key sizes are shorter.

2. Preliminaries

2.1. Lattice and Lattice Problems

Definition 1. 

Let $B=\left[b_1,b_2,\cdots ,b_m\right]\subset R^n$ consist of $m$ linearly independent vectors, and the lattice $\Lambda$ is defined as follows:

$$\mathsf{\Lambda }=\mathsf{\Lambda }(B)=\{Bc:c\in Z^m\}=\left\{{\sum }_{i=1}^m{c}_i{b}_i,c_i\in Z\right\}.$$

$B$ is the basis of the lattice $\Lambda$. $n$ is the dimension of the lattice, $m$ is the dimension of the vector and the rank of the lattice. If $m=n$, the lattice $\Lambda$ is classified as a full-rank lattice. Unless stated otherwise, all lattices discussed in this paper are assumed to be full-rank lattices.

Typically, there are two kinds of special full-rank integer lattices established on $Z_q$. For a matrix $B\in Z_q^{n\times m}$, the orthogonal lattice and the q-ary integer lattice are defined as follows:

$$\begin{array}{c}{\mathsf{\Lambda }}_q^{\perp }\left(B\right)=\left\{e\in Z_q^m:Be=0\mathit{mod}q\right\}\hfill \\ {\mathsf{\Lambda }}_q^u\left(B\right)=\{e\in Z_q^m:u=Be\mathit{mod}q,u\in Z_q^n\}\hfill \end{array}.$$

Definition 2. 

Let $B$ is a basis of $\Lambda \left(B\right)$. The dual lattice of $\Lambda \left(B\right)$, denoted ${\Lambda }^{*}$, is defined to be ${\Lambda }^{*}={\Lambda }^{*}\left(B^{*}\right)=\left\{y\in span\left(B\right)|\forall x\in \Lambda \left(B\right),⟨x,y⟩\in Z\right\}$, while the dual basis $B^{*}=(B^{-1}{)}^T$ is a basis of ${\Lambda }^{*}$.

Definition 3. 

Given a basis $B\in Z^{m\times n}$ of a lattice $\Lambda$, a rational $r>0$, output a set $S=\{a_1,a_2,\cdots ,a_n\}$ of $n$ linearly independent lattice vectors where $‖S‖\le r{\lambda }_n$. Let this problem be denoted as ${SIVP}_{n,m,r}$.

Definition 4. 

Given $n,m,q\in N$, a real $\beta >0$ and a random matrix $B\in Z_q^{n\times m}$, find a non-zero integer vector $e\in Z^m$ such that $Be=0\mathit{mod}q$ and $‖e‖\le \beta$. Let this problem be denoted as ${SIS}_{n,m,q,\beta }$.

Lemma 1 

([8]). For any $\beta =poly\left(n\right)$ and any prime $q\ge \beta \omega \left(\sqrt{n\mathit{log}n}\right)$, given $n,m\in N^{+}$, the average-case problem $SI{S}_{n,m,q,\beta }$ is as hard as approximating the ${SIVP}_{n,m,r}$ problem in the worst case with certain $r=\beta \cdot \tilde{O}\left(\sqrt{n}\right)$ factors.

Definition 5. 

([8]). For any real $s>0$, define the Gaussian function on $R^n$ with vector $c\in R^n$ as the center and $s>0$ as the parameter as

$$\forall x\in R^n,{\rho }_{s,c}\left(x\right)=\mathit{exp}\left(-\pi {‖x-c‖}^2/s^2\right).$$

For any real $s>0$ and vector $c\in R^n$, define the discrete Gaussian distribution over $\Lambda$ centered at vector $c$ with parameter $s$ as

$$\forall x\in \mathsf{\Lambda },D_{\mathsf{\Lambda },s,c}(x)={\displaystyle \frac{{\rho }_{s,c}\left(x\right)}{{\rho }_{s,c}\left(\mathsf{\Lambda }\right)}}.$$

When the subscripts $s$ and $c$ are taken to 1 and 0, respectively, they can be omitted.

Definition 6. 

([8]). For any full-rank n-dimensional lattice $\Lambda$, real $\epsilon >0$ and $s>0$, the smoothing parameter ${\eta }_{\epsilon }\left(\Lambda \right)$ is the smallest real $s$ such that ${\rho }_{1/s}({\Lambda }^{*}\backslash \{0\left\}\right)\le \epsilon$.

Lemma 2. 

([8]). For any full-rank n-dimensional lattice $\Lambda$, Gaussian center $c\in R^n$, real $\epsilon >0$, $s\ge 2{\eta }_{\epsilon }\left(\Lambda \right)$, and for every $x\in \Lambda$, we have $D_{\Lambda ,s,c}(x)\le {\displaystyle \frac{1+\epsilon }{1-\epsilon }}\cdot 2^{-n}$. In particular, for $\epsilon < {\displaystyle \frac{1}{3}}$, the min-entropy of $D_{\Lambda ,s,c}\left(x\right)$ is at least $n-1$.

2.2. Lattice Trapdoor Algorithms

Lemma 3. 

([15]). For any prime $q=poly\left(n\right)$ and $m=O\left(n\mathit{log}q\right)$, there is a probabilistic polynomial-time algorithm $TrapGen(1^n,1^m,q)$ that outputs a matrix $B\in Z_q^{n\times m}$ and a full-rank set $S\in {\Lambda }_q^{\perp }\left(B\right)$, where the distribution of $B$ is statistically close to uniform over $Z_q^{n\times m}$ and the length $‖S‖\le L=m^{2.5}$.

In particular, the set $S$ can be converted efficiently to a basis $T\in Z_q^{m\times m}$ of ${\Lambda }_q^{\perp }\left(B\right)$ such that $‖\tilde{T}‖\le ‖\tilde{S}‖\le L$, $\tilde{S}$ and $\tilde{T}$ denote the Gram–Schmidt orthogonalization of $S$ and $T$.

Lemma 4. 

([8]). For any prime $q=poly\left(n\right)$, $m\ge 5n\mathit{log}q$ and a matrix $B\in Z_q^{n\times m}$, let $T\in Z_q^{m\times m}$ be a basis for a full-rank n-dimensional lattice ${\Lambda }_q^{\perp }\left(B\right)$. Then, for a parameter $s>‖\tilde{T}‖\cdot \omega \left(\sqrt{\mathit{log}m}\right)$ and a center $c\in R^m$:

(1)

There is a probabilistic polynomial-time algorithm $SampleD(T,s,c)$ that outputs a sample from a distribution that is statistically close to $D_{{\mathsf{\Lambda }}_q^{\perp },s,c}$.

(2)

There is a probabilistic polynomial-time algorithm $Sampre(B,T,s,u)$ that, on input of a random vector $u\in Z_q^n$, a matrix $B\in Z_q^{n\times m}$ and a basis $T\in Z_q^{m\times m}$, outputs $e\in {\mathsf{\Lambda }}_q^u\left(B\right)$ sampled from a distribution that is statistically close to $D_{{\mathsf{\Lambda }}_q^u,s,c}$.

Lemma 5. 

(8). There is a collection of collision-resistant $Sampre(B,T,s,u)$ if the average-case problem $SI{S}_{n,m,q,\beta }$ is hard.

Lemma 6. 

([8]). For any matrix $B\in Z_q^{n\times m}$, an efficiently computable function $h_B\left(x\right)=Bx\mathit{mod}q$ with domain $D_n=\left\{x\in Z^m|‖x‖\le s\sqrt{m}\right\}$, and range $R_n=Z_q^n$, there is a probabilistic polynomial-time algorithm $SampreDom\left(1^m\right)$ that outputs an $x$ sampled from some distribution over $D_n$, for which the distribution of $h_B\left(x\right)$ is uniform over $R_n$.

3. Lattice-Based Proxy Signature and System Model

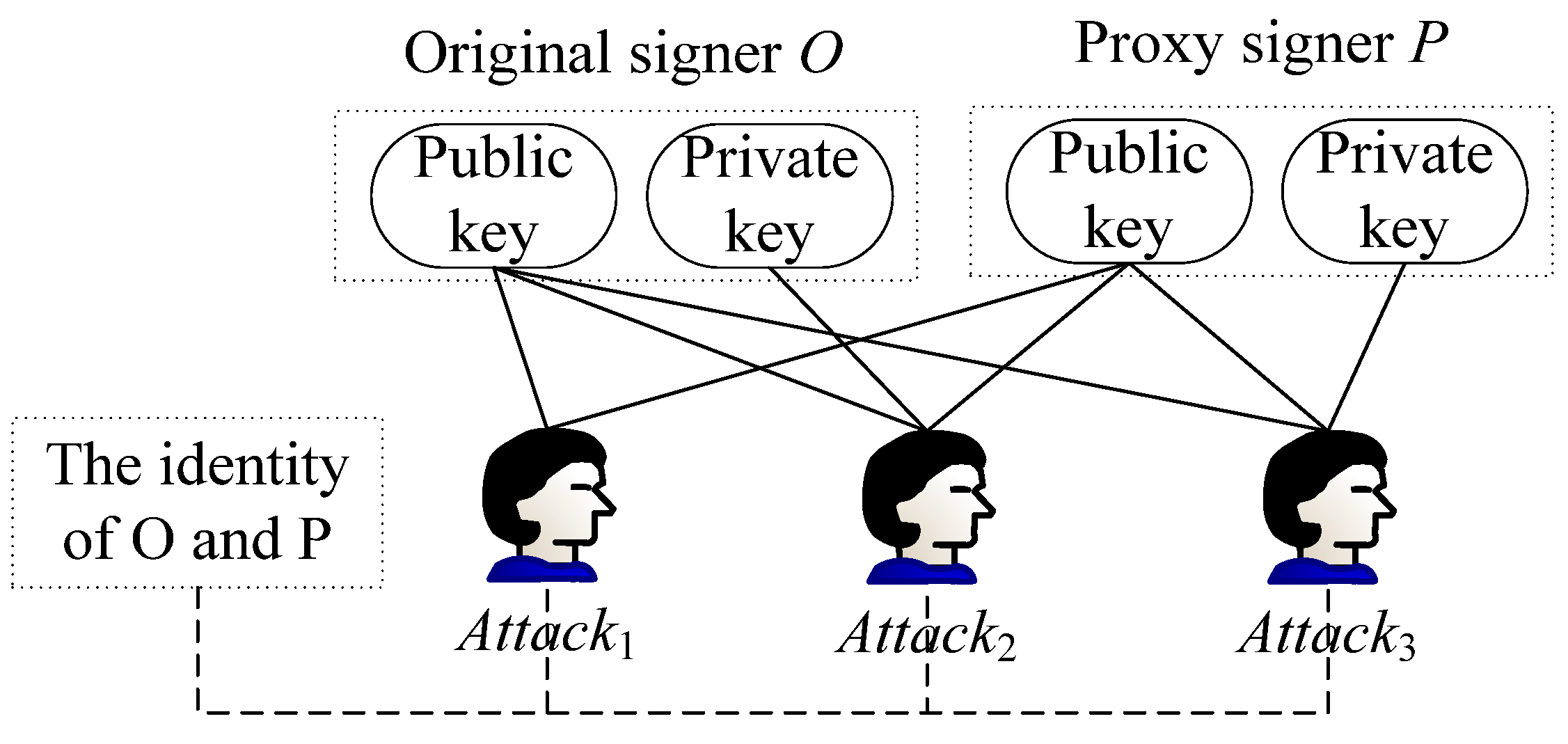
3.1. Formal Definition

In a lattice-based proxy signature scheme, there are four different entities: a trusted key generation center (KGC), an original signer $O$ with ${ID}_O$, a proxy signer $P$ with ${ID}_P$ and a verifier. The scheme consists of the following seven algorithms:

(1) $Setup$: KGC inputs the system security parameter $n$, outputs the system master key pair $(A,T)$ and the system public parameters $params$, keeps the system secret master key $T$, and publishes $params$ to all system users.

(2) $KeyExtract$: Given a user’s identity $ID$, KGC generates the key pair $(A_{ID},T_{ID})$ for a user’s identity $ID$, and returns $(A_{ID},T_{ID})$ to the corresponding user through a security channel.

(3) $Delegate$: The original signer $O$ generates the warrant $w$, where $w$ describes the delegation relationship, scope and valid period of delegation, and the identities of $O$ and $P$. The original signer $O$ inputs the warrant $w$, their key pair, the delegation secret and identity information, and outputs the delegation $W_{O\to P}$.

(4) $DVerify$: For the proxy signer $P$, they verify the legality of the delegation information $W_{O\to P}$. If it is legal, the output is 1 and the delegation is accepted. Otherwise, the output is 0 and the delegation is rejected.

(5) $PKGen$: The proxy signer $P$ generates the delegation secret whether the delegation is accepted. He inputs his key pair, his delegation secret and $W_{O\to P}$, and outputs the delegation secret key pair $(A_{OP},T_{OP})$.

(6) $PSign$: The proxy signer $P$ inputs the message $\mu$, the delegation $W_{O\to P}$, the delegation secret key pair $(A_{OP},T_{OP})$ and his delegation secret, and outputs the proxy signature $e_{OP}$ of the message $\mu$.

(7) $PVerify$: For arbitrary users, they verify the delegated signature $e_{OP}$ of the message $\mu$ with regard to the delegation $W_{O\to P}$. If it is legal, the output is 1 and the proxy signature is accepted. Otherwise, the output is 0 and the proxy signature is rejected.

3.2. System Model

There are three types of adversary models in the lattice-based proxy signature scheme. Let $O$ be the original signer and $P$ be the proxy signer, as shown in Figure 1.

Figure 1. Capabilities of three types of adversaries.

(1) Type I: The adversary $Attac{k}_1$ knows the public keys of $O$ and $P$, and their identity information.

(2) Type II: The adversary $Attac{k}_2$ knows the key pair of $O$, the public key of $P$, and their identity information.

(3) Type III: The adversary $Attac{k}_3$ knows the key pair of $P$, the public key of $O$, and their identity information.

It is clear that, for the above three types of adversary models mentioned, if the lattice-based proxy signature scheme is secure against type II (or type III) adversaries, it will also be secure against type I adversaries. Consequently, the security evaluation of the lattice-based proxy signature scheme presented in this paper primarily focuses on whether the signature scheme demonstrates unforgeability under the type II and type III adversary models. The game interaction process between the challenger and the type II and type III adversaries is shown in Figure 2 and Figure 3.

Figure 2. The game between $Attac{k}_2$ and $C$.

Figure 3. The game between $Attac{k}_3$ and $C$.

Game 1: Game 1, that is interactive between the adversary $Attac{k}_2$ and the challenger $C$, is shown in Figure 2.

Game 2: Game 2, that is interactive between the adversary $Attac{k}_3$ and the challenger $C$, is shown in Figure 3.

4. Our Scheme

Let $O$ be the original signer and $P$ be the proxy signer. Now, we propose a new lattice-based proxy signature scheme (NLBPS) as follows:

• $\mathit{S}\mathit{e}\mathit{t}\mathit{u}\mathit{p}$: On inputting the system security parameter $n$, set $q=poly\left(n\right)$. Set $m=O\left(n\mathit{log}q\right)$ is the dimension of the lattices and $s=\tilde{L}\omega \left(\sqrt{n\mathit{log}m}\right)$ is the Gaussian parameter. KGC works as follows:
  • Choose two secure cryptographic hash functions: $H_1$: $Z_q^n\times Z_q^n\times \{\mathrm{0,1}{\}}^{\mathrm{*}}\to Z_q^n$ and $H_2$: $Z_q^n\times Z_q^n\times \{\mathrm{0,1}{\}}^{\mathrm{*}}\to Z_q^n$.
  • Invoke $TrapGen(1^n,1^m,q)$ to generate a random matrix $A\in Z_q^{n\times m}$ and a short basis $T\in Z_q^{m\times m}$ for ${\mathsf{\Lambda }}_q^{\perp }\left(A\right)$ such that $‖\tilde{T}‖\le \tilde{L}$.
  • Output the master key pair $(A,T)$ and the system public parameters $params=⟨n,m,q,\tilde{L},s,A,H_1,H_2⟩$.

• $\mathit{K}\mathit{e}\mathit{y}\mathit{E}\mathit{x}\mathit{t}\mathit{r}\mathit{a}\mathit{c}\mathit{t}$: Given a user’s identity $ID$, KGC invokes $TrapGen(1^n,1^m,q)$ to generate the key pair $(A_{ID},T_{ID})$ for a user’s identity $ID$, where $A_{ID}\in Z_q^{n\times m}$ is the public key and $T_{ID}\in Z_q^{m\times m}$ is the private key. The original signer $O$ and the proxy signer $P$ both obtain the public–private key pair through this procedure. $O$ and $P$ hold $(A_O,T_O)$ and $(A_P,T_P)$, respectively.
• $\mathit{D}\mathit{e}\mathit{l}\mathit{e}\mathit{g}\mathit{a}\mathit{t}\mathit{e}$: The original signer $O$ generates the warrant $w=\{\mathrm{0,1}{\}}^{\mathrm{*}}$, where $w$ describes the delegation relationship, scope and valid period of delegation, and the identities of $O$ and $P$. Then, the original signer $O$ works as follows:
  • Choose $k_O\in Z_q^n$ at random as the authorization token and publish it.
  • Evaluate $d_O\leftarrow Sampre(A_O,T_O,s,k_O)$ to obtain $d_O\in Z_q^m$ as his delegation secret.
  • Compute $h_O=H_1(I{D}_O\parallel I{D}_P\parallel w)\in Z_q^n$ and $u_O=A_O{d}_O+h_O\in Z_q^n$.
  • Set $e_O\leftarrow Sampre(A_O,T_O,s,u_O)$. Note that $A_O{e}_O=u_{O}modq$ in $Z_q^n$.

Finally, the original signer $O$ outputs the delegation $W_{O\to P}=(w,e_O,k_O)$.

• $\mathit{D}\mathit{V}\mathit{e}\mathit{r}\mathit{i}\mathit{f}\mathit{y}$: For the proxy signer $P$, they verify the legality of the delegation $W_{O\to P}=(w,e_O,k_O)$ as follows:
  • Compute $h_O=H_1(I{D}_O\parallel I{D}_P\parallel w)\in Z_q^n$.
  • If $A_O{e}_O=k_O+h_O$ and $‖e_O‖\le s\sqrt{m}$, output 1 and accept the delegation $W_{O\to P}$. Otherwise, output 0 and reject it.
• $\mathit{P}\mathit{K}\mathit{G}\mathit{e}\mathit{n}$: The proxy signer $P$ inputs their key pair $(A_O,T_O)$, their delegation secret $k_O$ and $W_{O\to P}=(w,e_O,k_O)$; if the delegation $W_{O\to P}=(w,e_O,k_O)$ is accepted, they follow the next steps:
  • Choose $k_P\in Z_q^n$ at random and compute $u_P=k_P+A_O{e}_O\in Z_q^n$.
  • Evaluate $d_P\leftarrow Sampre(A_P,T_P,s,u_P)$ to obtain $d_P\in Z_q^m$ as their delegation secret.

Finally, the proxy signer $P$ outputs the delegated private key $T_{OP}=(T_P,d_P)$ and the delegated public key $A_{OP}=(A_P,A_O,k_P,k_O)$. For arbitrary users, they can determine the legitimacy of the delegation through the delegated public key $A_{OP}$.

• $\mathit{P}\mathit{S}\mathit{i}\mathit{g}\mathit{n}$: The proxy signer $P$ inputs the message $\mu$, the delegation $W_{O\to P}$ and the delegated public–private key pair $(A_{OP},T_{OP})$, and taking the following steps:
  • Compute $u_{OP}=H_2(k_O\parallel k_P\parallel \mu )+A_P{d}_P\in Z_q^n$.
  • Evaluate $e_{OP}\leftarrow Sampre(A_P,T_P,s,u_{OP})$ to obtain the delegated signature of $e_{OP}\in Z_q^m$ of the message $\mu$.
• $\mathit{P}\mathit{V}\mathit{e}\mathit{r}\mathit{i}\mathit{f}\mathit{y}$: For arbitrary users, they verify the delegated signature $e_{OP}\in Z_q^m$ of the message $\mu$ as follows:
  • Compute $h_O=H_1(I{D}_O\parallel I{D}_P\parallel w)$.
  • If $A_P{e}_{OP}=H_2(k_O\parallel k_P\parallel \mu )+k_O+k_P+h_O$ and $‖e_{OP}‖\le s\sqrt{m}$, accept the signature and output 1. Otherwise, output 0 and reject the signature.

5. Scheme Analysis

5.1. The Correctness of NLBPS

• For the $\mathit{D}\mathit{V}\mathit{e}\mathit{r}\mathit{i}\mathit{f}\mathit{y}$ algorithm, the correctness of the verification equation is elaborated as follows:

  $$A_O{e}_O=u_O=A_O{d}_O+h_O=k_O+h_O.$$
• For the $\mathit{P}\mathit{V}\mathit{e}\mathit{r}\mathit{i}\mathit{f}\mathit{y}$ algorithm, the correctness of the verification equation is elaborated as follows:

  $$\begin{array}{cc}\hfill A_P{e}_{OP}& =u_{OP}\hfill \\ \hfill & =H_2\left(k_O\parallel k_P\parallel \mu \right)+u_P\hfill \\ \hfill & =H_2\left(k_O\parallel k_P\parallel \mu \right)+k_P+A_O{e}_O\hfill \\ \hfill & =H_2\left(k_O\parallel k_P\parallel \mu \right)+k_P+u_O\hfill \\ \hfill & =H_2\left(k_O\parallel k_P\parallel \mu \right)+k_P+A_O{d}_O+h_O\hfill \\ \hfill & =H_2\left(k_O\parallel k_P\parallel \mu \right)+k_P+k_O+h_O\hfill \end{array}.$$

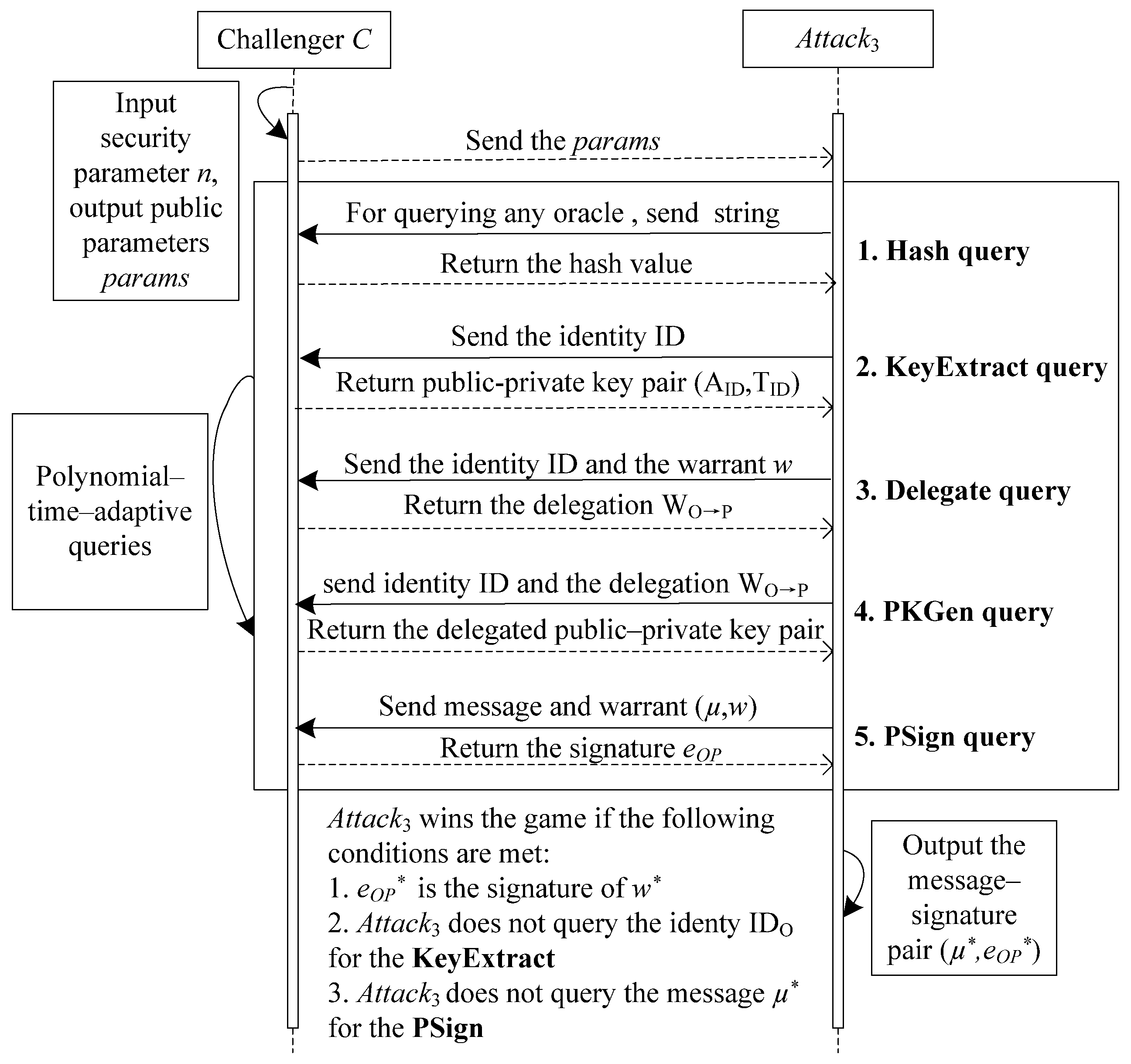
5.2. The Security Analysis of NLBPS

Our scheme security consists of three types of adversaries; if NLBPS has existential unforgeability against type II and type III adversaries, it will also have existential unforgeability against type I adversaries. Therefore, we only take two types of adversaries into consideration.

Theorem 1. 

If the ${SIS}_{n,m,q,2\sqrt{m}}$ problem is hard, the proposed lattice-based proxy signature scheme NLBPS is existential unforgeable against an adaptive chosen message and identity attacks in the random oracle model.

Proof of Theorem 1. 

We prove this theorem by contradiction. Assuming that an adversary breaks the existential unforgeability of the signature scheme with a non-negligible probability, then we can construct a challenger to solve the problem ${SIS}_{n,m,q,2\sqrt{m}}$ by running the adversary as a subroutine. □

Corollary 1. 

Let $Q_{H_i}$ be the maximum number of queries that $Attac{k}_2$ makes to the random oracle $H_i$ at a single query time for $i=1, 2$. Define $Q_k$, $Q_p$, $Q_{pk}$ and $Q_s$ as the maximum number of $\mathit{K}\mathit{e}\mathit{y}\mathit{E}\mathit{x}\mathit{t}\mathit{r}\mathit{a}\mathit{c}\mathit{t}$ queries, $\mathit{D}\mathit{e}\mathit{l}\mathit{e}\mathit{g}\mathit{a}\mathit{t}\mathit{e}$ queries, $\mathit{P}\mathit{K}\mathit{G}\mathit{e}\mathit{n}$ queries, and $\mathit{P}\mathit{S}\mathit{i}\mathit{g}\mathit{n}$ queries, respectively. $t_k$, $t_p$, $t_{pk}$ and $t_s$ correspond to the time for each $\mathit{K}\mathit{e}\mathit{y}\mathit{E}\mathit{x}\mathit{t}\mathit{r}\mathit{a}\mathit{c}\mathit{t}$ query, $\mathit{D}\mathit{e}\mathit{l}\mathit{e}\mathit{g}\mathit{a}\mathit{t}\mathit{e}$ query, $\mathit{P}\mathit{K}\mathit{G}\mathit{e}\mathit{n}$ query, and $\mathit{P}\mathit{S}\mathit{i}\mathit{g}\mathit{n}$ query, respectively. If there is a type II adversary $Attac{k}_2$ that can break the existential unforgeability of NLBPS in the random oracle model with a non-negligible probability $\epsilon$ within a time bound $t$, then there exists a polynomial-time challenger $C$ that solves the problem ${SIS}_{n,m,q,2\sqrt{m}}$ with a non-negligible probability:

$${\epsilon }^{\prime }\ge {\displaystyle \frac{\epsilon }{Q_{H_2}}}\left(1-{\displaystyle \frac{1}{2^m}}\right)\left(1-{\displaystyle \frac{1}{Q_k}}\right){\left(1-{\displaystyle \frac{1}{Q_{pk}{Q}_{H_2}}}\right)}^{Q_s}.$$

This solution is achievable within a time constraint of

$$t^{\prime }<t+(Q_k{t}_k+Q_p{t}_p+Q_{pk}{t}_{pk}+Q_s{t}_s+Q_{H_1}{t}_{H_1}+Q_{H_2}{t}_{H_2})$$

Proof of Corollary 1. 

The type II adversary $Attac{k}_2$ knows the key pair of $O$, the public key of $P$, and the identity information of both agents. First of all, $Attac{k}_2$ announces to $C$ the identity ${ID}_P^{*}$ and the message ${\mu }^{*}$ that will be challenged.

The challenger $C$ receives an instance of the problem ${SIS}_{n,m,q,2\sqrt{m}}$. Given $q\in N^{+}$ and a uniformly random matrix $A_P^{*}\in Z_q^{n\times m}$, $C$ tries to find small non-zero vector $e\in Z^m$ such that $A_P^{*}e=0\mathit{mod}q$ and $‖e‖\le 2s\sqrt{m}$.

$\mathit{S}\mathit{e}\mathit{t}\mathit{u}\mathit{p}$: On inputting the system security parameter $n$, set $q=poly\left(n\right)$. Set $m=O\left(n\mathit{log}q\right)$ as the dimension of the lattices and $s=\tilde{L}\omega \left(\sqrt{n\mathit{log}m}\right)$ as the Gaussian parameter. $C$ invokes $TrapGen(1^n,1^m,q)$ to generate a random matrix $A\in Z_q^{n\times m}$ and a basis $T\in Z_q^{m\times m}$ for ${\mathsf{\Lambda }}_q^{\perp }\left(A\right)$ such that $‖\tilde{T}‖\le \tilde{L}$. $C$ maintains five lists$—L_1$, $L_2$, $LD$, $LP$, $LS$—that are initially empty. $C$ sets the master key pair $(A,T)$ and system public parameters $params=⟨n,m,q,\tilde{L},s,A,H_1,H_2⟩$, and sends $params$ to $Attac{k}_2$.

Random oracle hash queries: We assume that the $Attac{k}_2$’s queries are distinct; otherwise, the simulator will consistently produce the same output for identical inputs without increasing the query counter. Then, $Attac{k}_2$ performs the following queries:

• $H_1$ query: $C$ maintains a list $L_1$ of tuples $(I{D}_O,I{D}_P,w,h_1)$. For the query to $L_1$, if $(I{D}_O,I{D}_P,w)$ is in the list $L_1$, then $C$ returns $h_1$ to $Attac{k}_2$. Otherwise, $C$ chooses $h_1\in Z_q^n$ at random, adds it to list $L_1$ and then returns it to $Attac{k}_2$.
• $H_2$ query: $C$ maintains a list of tuples $(k_1,h_1,\mu ,A_P,d_2,k_2,h_2,e_{OP})$ which is called the $L_2$ list. For the query on $(k_1,h_1,\mu ,A_P)$, $C$ searches $(k_1,h_1,\mu ,A_P,d_2,k_2,h_2,e_{OP})$ in the list $L_2$. If it exists, $C$ returns $(k_2,h_2,d_2,e_{OP})$ to $Attac{k}_2$. Otherwise,

  (a)

  If $I{D}_P=I{D}_P^{\mathrm{*}}$, $C$ invokes $d_2\leftarrow SampreD\mathrm{o}\mathrm{m}\left(1^m\right)$ and $e_{OP}\leftarrow SampreDom\left(1^m\right)$, then computes $h_2=A_P{e}_{OP}-A_P{d}_2$ and $k_2=A_p{d}_2-k_1-h_1$.

  (b)

  If $I{D}_P\ne I{D}_P^{\mathrm{*}}$, $C$ chooses $k_2\in Z_q^n$ at random, computes $u_P=k_2+A_O{e}_1\in Z_q^n$ and runs $Sampre(A_P,T_P,s,u_P)$ to generate $d_2\in Z_q^m$. Then, $C$ chooses $h_2\in Z_q^n$ at random, computes $u_{OP}=h_2+A_P{d}_2\in Z_q^n$ and runs $Sampre(A_P,T_P,s,u_{OP})$ to generate $e_{OP}\in Z_q^m$.

Finally, $C$ returns $(k_2,h_2,d_2,e_{OP})$ to $Attac{k}_2$ and adds $(k_1,h_1,\mu ,A_P,d_2,k_2,h_2,e_{OP})$ to list $L_2$.

$\mathit{K}\mathit{e}\mathit{y}\mathit{E}\mathit{x}\mathit{t}\mathit{r}\mathit{a}\mathit{c}\mathit{t}$ query: For the query on the identity $ID$, if $ID=I{D}_P^{*}$, $C$ returns $\perp$ to $Attac{k}_2$, then declares failure and halts. This event is recorded as $Even{t}_1$. Otherwise, if $ID\ne {ID}_P^{*}$, $C$ invokes $TrapGen(1^n,1^m,q)$ to return the corresponding key pair $(A_{ID},T_{ID})$ to $Attac{k}_2$.

$\mathit{D}\mathit{e}\mathit{l}\mathit{e}\mathit{g}\mathit{a}\mathit{t}\mathit{e}$–query: $C$ maintains a list $LD$ of tuples $({ID}_O,{ID}_P,w,e_1,k_1,h_1)$. $Attac{k}_2$ submits $(I{D}_O,I{D}_P,w)$ to $C$ for querying the delegation. $C$ firstly calls $H_1$ query to obtain $(I{D}_O,I{D}_P,w,h_1)$. Then, $C$ looks into list $LD$; if it can find the corresponding $(I{D}_O,I{D}_P,w,e_1,k_1,h_1)$ in $LD$, $C$ returns $(w,e_1,k_1,h_1)$ to $Attac{k}_2$. Otherwise, $C$ chooses $k_1\in Z_q^n$ at random, and runs algorithm $Sampre(A_O,T_O,s,k_1)$ to generate $d_1\in Z_q^m$. Then, $C$ returns $(w,e_1,k_1,h_1)$ to $Attac{k}_2$ and adds $({ID}_O,{ID}_P,w,e_1,k_1,h_1)$ to list $LD$.

$\mathit{P}\mathit{K}\mathit{G}\mathit{e}\mathit{n}$ query: $C$ maintains a list $LP$ of tuples $({ID}_O,{ID}_P,e_1,k_2,T_P^{*},d_2)$. For the query on $({ID}_O,{ID}_P,e_1)$, $C$ searches $({ID}_O,{ID}_P,e_1,k_2,T_P^{*},d_2)$ in the list $LP$. If it exists, $C$ returns $T_{OP}=(T_P^{*},d_2)$ to $Attac{k}_2$. Otherwise, $C$ calls $\mathit{D}\mathit{e}\mathit{l}\mathit{e}\mathit{g}\mathit{a}\mathit{t}\mathit{e}$ query to obtain $(w,e_1,k_1,h_1)$ and calls $H_2$ query to obtain $(k_2,h_2,d_2,e_{OP})$.

• If ${ID}_P={ID}_P^{\mathrm{*}}$, let $T_P^{\mathrm{*}}=T_O$; the delegated private key and the $Attac{k}_2$ corresponding public key are $T_{OP}=(T_P^{\mathrm{*}},d_2)$ and $A_{OP}=(A_P,A_O,k_1,k_2)$, respectively.
• If ${ID}_P\ne {ID}_P^{\mathrm{*}}$, let $T_P^{\mathrm{*}}=T_P$; the delegated private key and the corresponding public key are $T_{OP}=(T_P^{\mathrm{*}},d_2)$ and $A_{OP}=(A_P,A_O,k_1,k_2)$, respectively.

Finally, $C$ publishes the delegated public key $A_{OP}=(A_P,A_O,k_1,k_2)$, and returns $T_{OP}=(T_P^{\mathrm{*}},d_2)$ to ${\mathit{Attack}}_2$. Then, $C$ adds $({ID}_O,{ID}_P,e_1,k_2,T_P^{\mathrm{*}},d_2)$ to list $LP$.

$\mathit{P}\mathit{S}\mathit{i}\mathit{g}\mathit{n}$ query: $C$ maintains a list $LS$ of tuples $({ID}_O,{ID}_P,\mu ,w,e_{OP})$. $Attac{k}_2$ submits $({ID}_O,{ID}_P,\mu ,w)$ to $C$ for querying the signature.

• If ${ID}_P={ID}_P^{\mathrm{*}}$ and $\mu ={\mu }^{\mathrm{*}}$, $C$ returns $\perp$ to $Attac{k}_2$, then declares failure and halts. This event is recorded as $Even{t}_2$.
• If ${ID}_P={ID}_P^{\mathrm{*}}$ and $\mu \ne {\mu }^{\mathrm{*}}$, $C$ searches $({ID}_O,{ID}_P,\mu ,w,e_{OP})$ in the list $LS$. If it exists, $C$ returns $(\mu ,e_{OP})$ to $Attac{k}_2$. Otherwise, $C$ calls $\mathit{D}\mathit{e}\mathit{l}\mathit{e}\mathit{g}\mathit{a}\mathit{t}\mathit{e}$ query to obtain $(w,e_1,k_1,h_1)$, calls $\mathit{P}\mathit{K}\mathit{G}\mathit{e}\mathit{n}$ query to obtain $(k_2,T_P^{\mathrm{*}},d_2)$ and calls $H_2$ query to obtain $(k_2,h_2,d_2,e_{OP})$. Then, $C$ returns $(\mu ,e_{OP})$ to $Attac{k}_2$ and adds $(I{D}_O,I{D}_P,e_1,T_P^{\mathrm{*}},d_2)$ to list $LS$.
• If ${ID}_P\ne {ID}_P^{\mathrm{*}}$, $C$ searches $({ID}_O,{ID}_P,\mu ,w,e_{OP})$ in the list $LS$. If it exists, $C$ returns $(\mu ,e_{OP})$ to $Attac{k}_2$. Otherwise, $C$ calls $\mathit{D}\mathit{e}\mathit{l}\mathit{e}\mathit{g}\mathit{a}\mathit{t}\mathit{e}$ query to obtain $(w,e_1,k_1,h_1)$, calls $\mathit{P}\mathit{K}\mathit{G}\mathit{e}\mathit{n}$ query to obtain $(k_2,T_P^{\mathrm{*}},d_2)$ and calls $H_2$ query to obtain $(k_2,h_2,d_2,e_{OP})$. Then, $C$ returns $(\mu ,e_{OP})$ to $Attac{k}_2$ and adds $({ID}_O,{ID}_P,e_1,T_P^{\mathrm{*}},d_2)$ to list $LS$.

If $Even{t}_1$ and $Even{t}_2$ do not occur, then $C$’s simulation is perfect. The adversary $Attac{k}_2$ forges a valid signature pair $({\mu }^{*},e_{OP}^{*})$ of the tuple $(I{D}_O,I{D}_P,{\mu }^{*},w)$ with a non-negligible probability $\epsilon$. This forgery satisfies the condition $‖e_{OP}^{*}‖\le s\sqrt{m}$, and the equation $A_P{e}_{OP}^{*}=H_2(k_1\parallel k_2\parallel {\mu }^{*})+k_1+k_2+h_1$. Thus, the following equation holds:

$$\begin{array}{cc}\hfill A_P{e}_{OP}^{*}& =H_2\left(k_O\parallel k_P\parallel {\mu }^{*}\right)+k_1+k_2+h_1\hfill \\ \hfill & =A_P{e}_{OP}-A_P{d}_2+k_1+k_2+h_1\hfill \\ \hfill & =A_P{e}_{OP}-A_P{d}_2+k_1+(A_P{d}_2-k_1-h_1)+h_1\hfill \\ \hfill & =A_P{e}_{OP}\hfill \end{array}.$$

Therefore, we obtain that $A_P{e}_{OP}-A_P{e}_{OP}^{*}=A_P(e_{OP}-e_{OP}^{*})=0\mathit{mod}q$. According to Lemma 2, the minimum entropy of the preimage of the $Sampre$ algorithm is at least $n-1$. Consequently, the probability that the equation $e_{OP}=e_{OP}^{*}$ is negligible. Furthermore, given that $‖e_{OP}‖\le s\sqrt{m}$ and $‖e_{OP}^{*}‖\le s\sqrt{m}$, it follows that $‖e_{OP}-e_{OP}^{*}‖\le ‖e_{OP}‖+‖e_{OP}^{*}‖\le 2s\sqrt{m}$. Let $A_P^{*}=A_P$, then the challenger $C$ can output $e_{OP}-e_{OP}^{*}$ as a solution to the instance of the problem $SI{S}_{n,m,q,2\sqrt{m}}$.

If $Even{t}_1$ and $Even{t}_2$ do not occur, Game 1 proceeds normally. The probability of Game 1 running without these events is as follows:

$$\mathit{Pr}(\neg Even{t}_1\wedge \neg Even{t}_2)\ge \left(1-{\displaystyle \frac{1}{Q_k}}\right){\left(1-{\displaystyle \frac{1}{Q_{pk}{Q}_{H_2}}}\right)}^{Q_s}.$$

In the event that the adversary $Attac{k}_2$ forges a valid signature without performing adaptive queries, the probability of such an occurrence is ${\displaystyle \frac{1}{2^m}}$. Consequently, if $Attac{k}_2$ forges the signature with a non-negligible probability $\epsilon$ in time $t$ through adaptive queries, then there exists a challenger $C$ who, within a polynomial time $t^{\prime }<t+(Q_k{t}_k+Q_p{t}_p+Q_{pk}{t}_{pk}+Q_s{t}_s+Q_{H_1}{t}_{H_1}+Q_{H_2}{t}_{H_2})$, can solve the problem ${SIS}_{n,m,q,2\sqrt{m}}$ with a non-negligible probability ${\epsilon }^{\prime }$ given by

$${\epsilon }^{\prime }\ge {\displaystyle \frac{\epsilon }{Q_{H_2}}}\left(1-{\displaystyle \frac{1}{2^m}}\right)\left(1-{\displaystyle \frac{1}{Q_k}}\right){\left(1-{\displaystyle \frac{1}{Q_{pk}{Q}_{H_2}}}\right)}^{Q_s}.$$

Corollary 2. 

Let $Q_{H_i}$ be the maximum number of queries that $Attac{k}_3$ makes to the random oracle $H_i$ at a single query time for $i=\mathrm{1,2}$. Define $Q_k$, $Q_p$, $Q_{pk}$ and $Q_s$ as the maximum number of $\mathit{K}\mathit{e}\mathit{y}\mathit{E}\mathit{x}\mathit{t}\mathit{r}\mathit{a}\mathit{c}\mathit{t}$ queries, $\mathit{D}\mathit{e}\mathit{l}\mathit{e}\mathit{g}\mathit{a}\mathit{t}\mathit{e}$ queries, $\mathit{P}\mathit{K}\mathit{G}\mathit{e}\mathit{n}$ queries, and $\mathit{P}\mathit{S}\mathit{i}\mathit{g}\mathit{n}$ queries, respectively. $t_k$, $t_p$, $t_{pk}$ and $t_s$ correspond to the time for each $\mathit{K}\mathit{e}\mathit{y}\mathit{E}\mathit{x}\mathit{t}\mathit{r}\mathit{a}\mathit{c}\mathit{t}$ query, $\mathit{D}\mathit{e}\mathit{l}\mathit{e}\mathit{g}\mathit{a}\mathit{t}\mathit{e}$ query, $\mathit{P}\mathit{K}\mathit{G}\mathit{e}\mathit{n}$ query, and $\mathit{P}\mathit{S}\mathit{i}\mathit{g}\mathit{n}$ query, respectively. If there is a type III adversary $Attac{k}_3$ that can break the existential unforgeability of NLBPS in the random oracle model with a non-negligible probability $\epsilon$ within a time bound $t$, then there exists a polynomial-time challenger $C$ that solves the problem ${SIS}_{n,m,q,2\sqrt{m}}$ with a non-negligible probability

$${\epsilon }^{\prime }\ge {\displaystyle \frac{\epsilon }{Q_{Q_{H_2}}}}\left(1-{\displaystyle \frac{1}{2^m}}\right)\left(1-{\displaystyle \frac{1}{Q_k}}\right){\left(1-{\displaystyle \frac{1}{Q_p{Q}_{H_1}}}\right)}^{Q_s+Q_{H_2}}.$$

This solution is achievable within a time constraint of

$$t^{\prime }<t+\left(Q_k{t}_k+Q_p{t}_p+Q_s{t}_s+Q_{H_1}{t}_{H_1}+Q_{H_2}{t}_{H_2}\right).\square$$

Proof of Corollary 2. 

The type III adversary $Attac{k}_3$ knows the key pair of $O$, the public key of $P$, and the identity information of both agents. First of all, $Attac{k}_3$ announces to $C$ the identity $I{D}_O^{*}$ and the message ${\mu }^{*}$ that will be challenged.

The challenger $C$ receives an instance of the problem ${SIS}_{n,m,q,2\sqrt{m}}$. Given $q\in N^{+}$ and a random matrix $A_P^{*}\in Z_q^{n\times m}$, $C$ tries to find a small non-zero vector $e\in Z^m$ such that $A_P^{*}e=0\mathit{mod}q$ and $‖e‖\le 2s\sqrt{m}$.

$\mathit{S}\mathit{e}\mathit{t}\mathit{u}\mathit{p}$: On inputting the system security parameter $n$, set $q=poly\left(n\right)$. Set $m=O\left(n\mathit{log}q\right)$ as the dimension of the lattices and $s=\tilde{L}\omega \left(\sqrt{n\mathit{log}m}\right)$ as the Gaussian parameter. $C$ invokes $TrapGen(1^n,1^m,q)$ to generate a random matrix $A\in Z_q^{n\times m}$ and a basis $T\in Z_q^{m\times m}$ for ${\mathsf{\Lambda }}_q^{\perp }\left(A\right)$ such that $‖\tilde{T}‖\le \tilde{L}$. $C$ maintains five lists$—L_1$, $L_2$, $LD$, $LP$, $LS$—that are initially empty. $C$ sets the master key pair $(A,T)$ and system public parameters $params=⟨n,m,q,\tilde{L},s,A,H_1,H_2⟩$ and sends $params$ to $Attac{k}_3$.

Random oracle hash queries: We assume that the $Attac{k}_3$’s queries are distinct; otherwise, the simulator will consistently produce the same output for identical inputs without increasing the query counter. Then, $Attac{k}_2$ performs the following queries:

• $H_1$ query: $C$ maintains a list $L_1$ of tuples $({ID}_O,{ID}_P,w,A_O,k_1,e_1,h_1)$. For the query to $L_1$, if $({ID}_O,{ID}_P,w,A_O,k_1,e_1)$ is in the list $L_1$, then $C$ returns $h_1$ to $Attac{k}_3$. Otherwise,

  (a)

  If ${ID}_O={ID}_O^{\mathrm{*}}$, $C$ computes $h_1=A_O{e}_1-k_1\in Z_q^n$.

  (b)

  If ${ID}_O\ne {ID}_O^{\mathrm{*}}$, $C$ randomly chooses $h_1\in Z_q^n$.

Finally, $C$ returns $h_1$ to $Attac{k}_3$ and adds $({ID}_O,{ID}_P,w,A_O,k_1,e_1,h_1)$ to list $L_2$.

2.

$H_2$ query: $C$ maintains a list of tuples $(k_1,k_2,\mu ,h_2)$ which is called the $L_2$ list. For the query on $(k_1,k_2,\mu )$, $C$ searches $(k_1,k_2,\mu ,h_2)$ in the list $L_2$. If it exists, $C$ returns $h_2$ to $Attac{k}_3$. Otherwise, $C$ chooses $h_2\in Z_q^n$ at random, returns $h_2$ to $Attac{k}_3$ and adds $(k_1,k_2,\mu ,h_2)$ to list $L_2$.

$\mathit{K}\mathit{e}\mathit{y}\mathit{E}\mathit{x}\mathit{t}\mathit{r}\mathit{a}\mathit{c}\mathit{t}$ query: For the query on the identity $ID$, if $ID={ID}_O^{*}$, $C$ returns $\perp$ to $Attac{k}_3$, then declares failure and halts. This event is recorded as $Even{t}_1$. Otherwise, if $ID\ne {ID}_O^{*}$, $C$ invokes $TrapGen(1^n,1^m,q)$ to return the corresponding key pair $(A_{ID},T_{ID})$ to $Attac{k}_3$.

$\mathit{D}\mathit{e}\mathit{l}\mathit{e}\mathit{g}\mathit{a}\mathit{t}\mathit{e}$ query: $C$ maintains a list $LD$ of tuples $({ID}_O,{ID}_P,w,e_1,k_1)$. $Attac{k}_3$ submits $({ID}_O,{ID}_P,w)$ to $C$ for querying the delegation. Then, $C$ looks into list $LD$; if it can find the corresponding $({ID}_O,{ID}_P,w,e_1,k_1)$ in $LD$, $C$ returns $(w,e_1,k_1)$ to $Attac{k}_3$. Otherwise,

• If ${ID}_O={ID}_O^{\mathrm{*}}$, $C$ invokes $e_1\leftarrow SampreDom\left(1^m\right)$ and chooses $k_1\in Z_q^n$ at random. Then, $C$ calls $H_1$ query to obtain $h_1\in Z_q^n$.
• If ${ID}_O\ne {ID}_O^{\mathrm{*}}$, $C$ randomly chooses $k_1\in Z_q^n$, and runs algorithm $Sampre(A_O,T_O,s,k_1)$ to generate $d_1\in Z_q^m$ as the delegated secret. Then, $C$ calls $H_1$ query to obtain $h_1\in Z_q^n$, computes $u_O=A_O{d}_O+h_1\in Z_q^n$ and invokes $e_1\leftarrow Sampre(A_O,T_O,s,u_O)$.

Finally, $C$ returns $(w,d_1,e_1,k_1)$ to $Attac{k}_3$ and adds $({ID}_O,{ID}_P,w,e_1,k_1)$ to list $LD$.

$\mathit{P}\mathit{K}\mathit{G}\mathit{e}\mathit{n}$ query: $C$ maintains a list $LP$ of tuples $({ID}_O,{ID}_P,e_1,T_P,d_2)$. For the query on $({ID}_O,{ID}_P,e_1)$, $C$ searches $({ID}_O,{ID}_P,e_1,T_P,d_2)$ in the list $LP$. If it exists, $C$ returns $T_{OP}^{\mathrm{*}}=(T_P,d_2)$ to $Attac{k}_3$. Otherwise, $C$ randomly chooses a matrix $k_2\in Z_q^n$, computes $u_2=k_2+A_O{e}_1\in Z_q^n$ and invokes $d_2\leftarrow Sampre(A_P,T_P,s,u_2)$. Finally, $C$ publishes the delegated public key $A_{OP}^{\mathrm{*}}=(A_P,A_O,k_1,k_2)$ and returns $T_{OP}^{\mathrm{*}}=(T_P,d_2)$ to $Attac{k}_3$. Then, $C$ adds $({ID}_O,{ID}_P,e_1,k_2,T_P^{\mathrm{*}},d_2)$ to list $LP$.

$\mathit{P}\mathit{S}\mathit{i}\mathit{g}\mathit{n}$ query: $C$ maintains a list $LS$ of tuples $({ID}_O,{ID}_P,\mu ,w,e_{OP})$. $Attac{k}_3$ submits $({ID}_O,{ID}_P,\mu ,w)$ to $C$ for querying the signature.

• If ${ID}_O={ID}_O^{\mathrm{*}}$ and $\mu ={\mu }^{\mathrm{*}}$, $C$ returns $\perp$ to $Attac{k}_3$, then declares failure and halts. This event is recorded as $Even{t}_2$.
• If ${ID}_O={ID}_O^{\mathrm{*}}$ and $\mu \ne {\mu }^{\mathrm{*}}$, $C$ searches $({ID}_O,{ID}_P,\mu ,w,e_{OP})$ in the list $LS$. If it exists, $C$ returns $(\mu ,e_{OP})$ to $Attac{k}_3$. Otherwise, $C$ calls $\mathit{D}\mathit{e}\mathit{l}\mathit{e}\mathit{g}\mathit{a}\mathit{t}\mathit{e}$ query to obtain $(w,e_1,k_1)$, calls $\mathit{P}\mathit{K}\mathit{G}\mathit{e}\mathit{n}$ query to obtain $(e_1,T_P,d_2)$ and calls $H_2$ query to obtain $(k_1,k_2,\mu ,h_2)$. Then, $C$ computes $u_{OP}=h_2+A_P{d}_2\in Z_q^n$ and invokes $e_{OP}\leftarrow Sampre(A_P,T_P,s,u_{OP})$. Finally, $C$ returns $(\mu ,e_{OP})$ to $Attac{k}_3$ and adds $({ID}_O,{ID}_P,\mu ,w,e_{OP})$ to list $LS$.
• If ${ID}_O\ne {ID}_O^{\mathrm{*}}$, $C$ searches $({ID}_O,{ID}_P,\mu ,w,e_{OP})$ in the list $LS$. If it exists, $C$ returns $(\mu ,e_{OP})$ to $Attac{k}_3$. Otherwise, $C$ calls $\mathit{D}\mathit{e}\mathit{l}\mathit{e}\mathit{g}\mathit{a}\mathit{t}\mathit{e}$ query to obtain $(w,e_1,k_1)$, calls $\mathit{P}\mathit{K}\mathit{G}\mathit{e}\mathit{n}$ query to obtain $(e_1,T_P,d_2)$, and calls $H_2$ query to obtain $(k_1,k_2,\mu ,h_2)$. Then, $C$ computes $u_{OP}=h_2+A_P{d}_2\in Z_q^n$ and invokes $e_{OP}\leftarrow Sampre(A_P,T_P,s,u_{OP})$. Then, $C$ returns $(\mu ,e_{OP})$ to $Attac{k}_3$ and adds $({ID}_O,{ID}_P,\mu ,w,e_{OP})$ to list $LS$.

If $Even{t}_1$ and $Even{t}_2$ do not occur, then $C$’s simulation is perfect. The adversary $Attac{k}_3$ forges a valid signature pair $({\mu }^{*},e_{OP}^{*})$ of the tuple $({ID}_O,{ID}_P,{\mu }^{*},w)$ with a non-negligible probability $\epsilon$. This forgery satisfies the condition $\left|\right|e_{OP}^{*}\left|\right|\le s\sqrt{m}$, and the equation $A_P{e}_{OP}^{*}=H_2\left(k_O\parallel k_P\parallel {\mu }^{*}\right)+k_1+k_2+h_1$. Thus, the following equation holds:

$$\begin{array}{cc}\hfill A_P{e}_{OP}^{*}& =H_2\left(k_O\parallel k_P\parallel {\mu }^{*}\right)+k_1+k_2+h_1\hfill \\ \hfill & =H_2\left(k_O\parallel k_P\parallel {\mu }^{*}\right)+k_1+k_2+(A_O{e}_1-k_1)\hfill \\ \hfill & =H_2\left(k_O\parallel k_P\parallel {\mu }^{*}\right)+k_2+A_O{e}_1\hfill \\ \hfill & =H_2\left(k_O\parallel k_P\parallel {\mu }^{*}\right)+A_O{d}_2\hfill \\ \hfill & =A_P{e}_{OP}\hfill \end{array}.$$

Therefore, we obtain $A_P{e}_{OP}-A_P{e}_{OP}^{*}=A_P(e_{OP}-e_{OP}^{*})=0\mathit{mod}q$. According to Lemma 2, the minimum entropy of the preimage of the $Sampre$ algorithm is at least $n-1$. The probability that $e_{OP}=e_{OP}^{*}$ is negligible. Furthermore, given that $‖e_{OP}‖\le s\sqrt{m}$ and $‖e_{OP}^{*}‖\le s\sqrt{m}$, it follows that $‖e_{OP}-e_{OP}^{*}‖\le ‖e_{OP}‖+‖e_{OP}^{*}‖\le 2s\sqrt{m}$. Let $A_P^{*}=A_P$; then, the challenger $C$ can output $e_{OP}-e_{OP}^{*}$ as a solution to the instance of the problem $SI{S}_{n,m,q,2\sqrt{m}}$.

If $Even{t}_1$ and $Even{t}_2$ do not occur, Game 2 proceeds normally. The probability of Game 2 running without these events is as follows:

$$\mathit{Pr}(\neg Even{t}_1\wedge \neg Even{t}_2)\ge (1-{\displaystyle \frac{1}{Q_k}}){\left(1-{\displaystyle \frac{1}{Q_p{Q}_{H_1}}}\right)}^{Q_s+Q_{H_2}}.$$

In the event that the adversary $Attac{k}_3$ forges a valid signature without performing adaptive queries, the probability of such an occurrence is ${\displaystyle \frac{1}{2^m}}$. Consequently, if $Attac{k}_3$ forges the signature with a non-negligible probability $\epsilon$ in time $t$ through adaptive queries, then there exists a challenger $C$ who, within a polynomial time $t^{\prime }<t+(Q_k{t}_k+Q_p{t}_p+Q_s{t}_s+Q_{H_1}{t}_{H_1}+Q_{H_2}{t}_{H_2})$, can solve the problem $SI{S}_{n,m,q,2\sqrt{m}}$ with a non-negligible probability ${\epsilon }^{\prime }$ given by

$${\epsilon }^{\prime }\ge {\displaystyle \frac{\epsilon }{Q_{H_2}}}\left(1-{\displaystyle \frac{1}{2^m}}\right)\left(1-{\displaystyle \frac{1}{Q_k}}\right){\left(1-{\displaystyle \frac{1}{Q_p{Q}_{H_1}}}\right)}^{Q_s+Q_{H_2}}.\square$$

Furthermore, Boneh et al. [16] introduced the concept of a history-free reduction, and prove that such reductions imply security in the quantum model. They showed that the GPV scheme has a history-free reduction, thereby establishing its post-quantum security. Specifically, the GPV scheme is secure in the quantum random oracle model (QROM), where a quantum adversary can issue a query to the random oracle that represents a superposition of an exponentially large number of states. Our proposed NLBPS is a variant of the GPV scheme, built upon the same foundational principles. This ensures that NLBPS maintains its security in the presence of quantum attacks. The detailed proof process is not reiterated here.

5.3. The Performance Comparison of NLBPS

In this section, our scheme is compared with other proxy signature schemes in terms of computation costs and storage size. Specifically, the scheme presented in [10] is a lattice-based proxy signature scheme, the scheme in [13] describes a lattice-based proxy signature scheme in cloud storage, and the scheme in [17] constructs an attribute-based proxy signing scheme. All three schemes involve the delegation of signing authority to a proxy. The comparison results are summarized in Table 1 and define some notations as follows: $T_{Ha}$ denotes the execution time of a generic hash function operation, while $T_{Sam}$ denotes the execution time of $Sampre$ algorithm operation. Additionally, $V_T$, $V_S$, $V_B$, and $V_O$ represent the $TrapGen$ algorithm, the $Sampre$ algorithm, the basis delegation without dimension increase algorithm [9], and other algorithms, respectively.

Table 1. Performance comparison among Refs. [10,13,17] and ours.

Scheme	[10]	[13]	[17]	Our Scheme
Signing cost	$2T_{Ha}+2T_{Sam}$	$T_{Ha}+T_{Sam}$	$T_{Ha}+T_{Sam}$	$T_{Ha}+T_{Sam}$
Verification cost	$2T_{Ha}$	$(n+k+2)T_{Ha}$	$3T_{Ha}$	$2T_{Ha}$
The size of signature	$2m\log q$	$\left(2m+n\right)\log q$	$2m\log q$	$m\log q$
The size of delegated key	$2m^2\log q$	$2m^2\log q$	$2m^2\log q$	$m^2\log q$
The number of algorithms	$V_T+V_S+V_B$	$V_T+V_S+2V_O$	$V_T+V_S+V_B$	$V_T+V_S$

The comparison of computation costs and storage size are listed in Table 1. The computation costs include signing cost and verification cost. Our scheme offers computational improvements over the methods presented in [10]. Specifically, our proxy signing process requires less time by omitting one execution of the hash function and the $Sampre$ algorithm, thus saving $T_{Ha}+T_{Sam}$. The signature verification also saves time by eliminating one hash function execution, saving $T_{Ha}$. The storage size includes the size of signature and the delegated secret key. Compared with the schemes in [10], our scheme has the shortest storage size. The size of signature and the delegated secret key of our scheme are $m\log q$ and $m^2\log q$, respectively. Furthermore, our scheme requires fewer algorithms, including only the $TrapGen$ and $Sampre$ algorithms, which makes it more suitable for resource-limited applications such as the Internet of Things (IOT).

6. Conclusions

In this paper, we present a new lattice-based proxy signature scheme (NLBPS) that combines trapdoor sampling algorithms with preimage sampling algorithms. Utilizing a trapdoor sampling algorithm [15], we generate public–private key pairs for both the original signer and the proxy signer. Subsequently, proxy authorization and signature messages are carried out through the application of preimage sampling algorithms. Based on the hardness of the small integer solution (SIS) problem, we present the security analysis of NLBPS in the random oracle model. The performance comparison shows that our scheme has some advantages in computation costs and storage size. In the future, this section would be followed by a detailed discussion of the security proof and a comparative analysis with existing schemes, including a description of the computational complexity and potential areas for future research. The preimage sampling algorithms employed in the proxy signature process depend on the trapdoor basis to obtain the preimage, which consequently incurs high computational costs. In the future, we will consider using proxy signature without trapdoor as a basis for implementing a lattice-based proxy signature scheme.