Abstract
With the advancement of quantum computing, the utilization of quantum algorithms such as Shor’s algorithm enables the efficient resolution of problems that are intractable in classical computing paradigms, posing a significant threat to traditional signature schemes. Lattice-based cryptography is considered one of the most promising post-quantum cryptographic algorithms due to its computational advantages and potential resistance to quantum attacks. Proxy signature is an authorization mechanism that allows the original signer to delegate the signing power to a proxy. The security of existing proxy signature schemes is mostly based on classical hard problems, which cannot guarantee security under quantum attacks. Therefore, this paper combines lattice-based cryptography with proxy signatures to propose a new lattice-based proxy signature scheme (NLBPS). NLBPS constructs signatures using lattice-based trapdoor sampling algorithms and preimage sampling algorithms. Comparative analysis shows that the proposed scheme has relatively smaller key and signature sizes compared to some existing lattice-based proxy signature schemes, and it also offers a certain improvement in computational efficiency.
1. Introduction
The concept of proxy signatures was introduced by Mambo, Usuda and Okamoto [1] in 1996. In this signature scheme, the original signer is allowed to delegate the signing authority to the proxy signer. By running an interactive proxy delegation protocol, the proxy signer can obtain a proxy signing key to sign messages on behalf of the original signer. In 2003, Bodyreva et al. [2] formally defined the security model for proxy signature schemes, and proposed a provably secure strong proxy signature scheme. To optimize the key management mechanism in public key cryptosystems, Shamir et al. [3] pioneeringly introduced identity-based signature schemes, where a user’s public key can be directly derived from their identity information. Subsequently, Xu et al. [4] combined identity information with proxy signature technology to design an identity-based proxy signature scheme; however, the security model of this scheme only defined unforgeability and did not consider scenarios involving adaptive chosen messages and adaptive chosen identity attacks. In 2024, Bannore et al. [5] developed a role-based proxy signature scheme on elliptic curve groups, combining role authorization mechanisms with proxy signature technology, which is suitable for the field of e-government.
With the rapid development of quantum computing technology, malicious attackers can efficiently solve classically difficult problems in polynomial time using Shor’s quantum algorithm [6], which poses a serious security threat to traditional schemes. Among the many quantum-resistant cryptographic schemes, lattice-based cryptography has garnered widespread attention due to its strong security proof in terms of its worst-case hardness [7] and efficient implementation. In 2008, Gentry et al. [8] designed a preimage sampling function using the Gaussian sampling algorithm and constructed a provably secure lattice signature scheme based on this technology, known as the GPV scheme. In 2010, Agrawal et al. [9] proposed a lattice basis delegation in a fixed dimension and presented two hierarchical identity-based encryption schemes. These schemes achieved fixed-dimensional delegation authorization, but the computational complexity of the public key generation process was relatively high. In 2013, Kim et al. [10] combined preimage sampling and fixed dimensional basis delegation technology to propose an identity-based proxy signature, and the scheme is proxy-protected in an adaptive security model, but only considered unforgeability in the security analysis of the scheme. In 2019, Wu et al. [11] proposed a proxy signature scheme on the NTRU lattice, which shortened the signature and key length. In 2021, Luo et al. [12] gave a formal concept of attribute-based proxy re-signature and discussed the potential applications of the scheme, whose public key and signature are relatively long. In 2022, Wang et al. [13] proposed a lattice proxy signature scheme suitable for cloud storage scenarios, but the complexity of the proxy authorization and proxy signing processes was relatively high. In 2023, Yu et al. [14] applied the lattice proxy signature scheme to the network coding environment, reducing the computational complexity and improving computational efficiency by reducing the dimension of the proxy key.
In this paper, we propose a new lattice-based proxy signature scheme called NLBPS. NLBPS uses a trapdoor sampling algorithm [15] to generate the public and private key matrices for the original signer and the proxy signer. It utilizes the preimage sampling function for proxy authorization and signature integrity. NLBPS is based on the hard assumption of the small integer solution problem and is provably secure in the random oracle model. Compared to some existing lattice-based proxy signature schemes, NLBPS achieves fixed-dimensional lattice-based proxy signatures with fewer original algorithms, and the required signature and public key sizes are shorter.
2. Preliminaries
2.1. Lattice and Lattice Problems
Definition 1.
Let consist of linearly independent vectors, and the lattice is defined as follows:
is the basis of the lattice . is the dimension of the lattice, is the dimension of the vector and the rank of the lattice. If , the lattice is classified as a full-rank lattice. Unless stated otherwise, all lattices discussed in this paper are assumed to be full-rank lattices.
Typically, there are two kinds of special full-rank integer lattices established on . For a matrix , the orthogonal lattice and the q-ary integer lattice are defined as follows:
Definition 2.
Let is a basis of . The dual lattice of , denoted , is defined to be , while the dual basis is a basis of .
Definition 3.
Given a basis of a lattice , a rational , output a set of linearly independent lattice vectors where . Let this problem be denoted as .
Definition 4.
Given , a real and a random matrix , find a non-zero integer vector such that and . Let this problem be denoted as .
Lemma 1
([8]). For any and any prime , given , the average-case problem is as hard as approximating the problem in the worst case with certain factors.
Definition 5.
([8]). For any real , define the Gaussian function on with vector as the center and as the parameter as
For any real and vector , define the discrete Gaussian distribution over centered at vector with parameter as
When the subscripts and are taken to 1 and 0, respectively, they can be omitted.
Definition 6.
([8]). For any full-rank n-dimensional lattice , real and , the smoothing parameter is the smallest real such that .
Lemma 2.
([8]). For any full-rank n-dimensional lattice , Gaussian center , real , , and for every , we have . In particular, for , the min-entropy of is at least .
2.2. Lattice Trapdoor Algorithms
Lemma 3.
([15]). For any prime and , there is a probabilistic polynomial-time algorithm that outputs a matrix and a full-rank set , where the distribution of is statistically close to uniform over and the length .
In particular, the set can be converted efficiently to a basis of such that , and denote the Gram–Schmidt orthogonalization of and .
Lemma 4.
([8]). For any prime , and a matrix , let be a basis for a full-rank n-dimensional lattice . Then, for a parameter and a center :
- (1)
- There is a probabilistic polynomial-time algorithm that outputs a sample from a distribution that is statistically close to .
- (2)
- There is a probabilistic polynomial-time algorithm that, on input of a random vector , a matrix and a basis , outputs sampled from a distribution that is statistically close to .
Lemma 5.
(8). There is a collection of collision-resistant if the average-case problem is hard.
Lemma 6.
([8]). For any matrix , an efficiently computable function with domain , and range , there is a probabilistic polynomial-time algorithm that outputs an sampled from some distribution over , for which the distribution of is uniform over .
3. Lattice-Based Proxy Signature and System Model
3.1. Formal Definition
In a lattice-based proxy signature scheme, there are four different entities: a trusted key generation center (KGC), an original signer with , a proxy signer with and a verifier. The scheme consists of the following seven algorithms:
(1) : KGC inputs the system security parameter , outputs the system master key pair and the system public parameters , keeps the system secret master key , and publishes to all system users.
(2) : Given a user’s identity , KGC generates the key pair for a user’s identity , and returns to the corresponding user through a security channel.
(3) : The original signer generates the warrant , where describes the delegation relationship, scope and valid period of delegation, and the identities of and . The original signer inputs the warrant , their key pair, the delegation secret and identity information, and outputs the delegation .
(4) : For the proxy signer , they verify the legality of the delegation information . If it is legal, the output is 1 and the delegation is accepted. Otherwise, the output is 0 and the delegation is rejected.
(5) : The proxy signer generates the delegation secret whether the delegation is accepted. He inputs his key pair, his delegation secret and , and outputs the delegation secret key pair .
(6) : The proxy signer inputs the message , the delegation , the delegation secret key pair and his delegation secret, and outputs the proxy signature of the message .
(7) : For arbitrary users, they verify the delegated signature of the message with regard to the delegation . If it is legal, the output is 1 and the proxy signature is accepted. Otherwise, the output is 0 and the proxy signature is rejected.
3.2. System Model
There are three types of adversary models in the lattice-based proxy signature scheme. Let be the original signer and be the proxy signer, as shown in Figure 1.
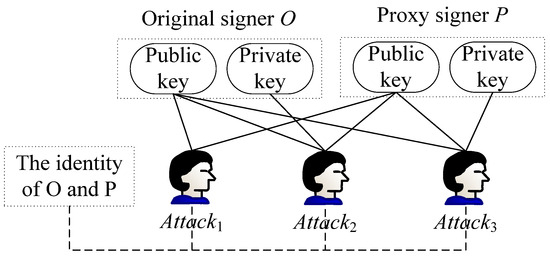
Figure 1.
Capabilities of three types of adversaries.
(1) Type I: The adversary knows the public keys of and , and their identity information.
(2) Type II: The adversary knows the key pair of , the public key of , and their identity information.
(3) Type III: The adversary knows the key pair of , the public key of , and their identity information.
It is clear that, for the above three types of adversary models mentioned, if the lattice-based proxy signature scheme is secure against type II (or type III) adversaries, it will also be secure against type I adversaries. Consequently, the security evaluation of the lattice-based proxy signature scheme presented in this paper primarily focuses on whether the signature scheme demonstrates unforgeability under the type II and type III adversary models. The game interaction process between the challenger and the type II and type III adversaries is shown in Figure 2 and Figure 3.
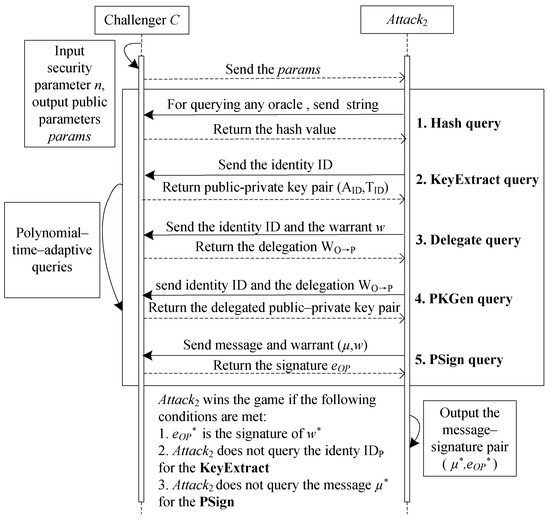
Figure 2.
The game between and .
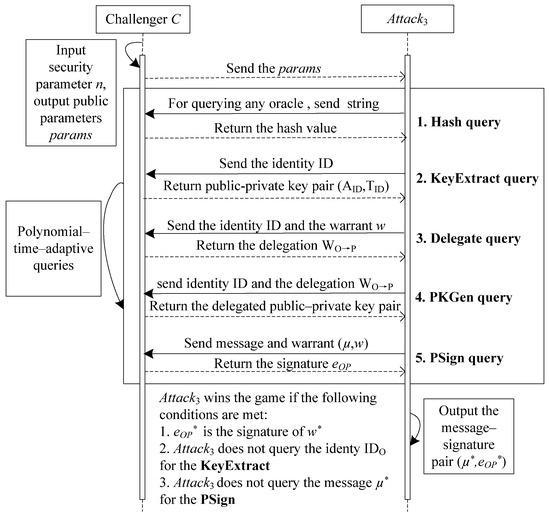
Figure 3.
The game between and .
Game 1: Game 1, that is interactive between the adversary and the challenger , is shown in Figure 2.
Game 2: Game 2, that is interactive between the adversary and the challenger , is shown in Figure 3.
4. Our Scheme
Let be the original signer and be the proxy signer. Now, we propose a new lattice-based proxy signature scheme (NLBPS) as follows:
- : On inputting the system security parameter , set . Set is the dimension of the lattices and is the Gaussian parameter. KGC works as follows:
- Choose two secure cryptographic hash functions: : and : .
- Invoke to generate a random matrix and a short basis for such that .
- Output the master key pair and the system public parameters .
- : Given a user’s identity , KGC invokes to generate the key pair for a user’s identity , where is the public key and is the private key. The original signer and the proxy signer both obtain the public–private key pair through this procedure. and hold and , respectively.
- : The original signer generates the warrant , where describes the delegation relationship, scope and valid period of delegation, and the identities of and . Then, the original signer works as follows:
- Choose at random as the authorization token and publish it.
- Evaluate to obtain as his delegation secret.
- Compute and .
- Set . Note that in .
Finally, the original signer outputs the delegation .
- : For the proxy signer , they verify the legality of the delegation as follows:
- Compute .
- If and , output 1 and accept the delegation . Otherwise, output 0 and reject it.
- : The proxy signer inputs their key pair , their delegation secret and ; if the delegation is accepted, they follow the next steps:
- Choose at random and compute .
- Evaluate to obtain as their delegation secret.
Finally, the proxy signer outputs the delegated private key and the delegated public key . For arbitrary users, they can determine the legitimacy of the delegation through the delegated public key .
- : The proxy signer inputs the message , the delegation and the delegated public–private key pair , and taking the following steps:
- Compute .
- Evaluate to obtain the delegated signature of of the message .
- : For arbitrary users, they verify the delegated signature of the message as follows:
- Compute .
- If and , accept the signature and output 1. Otherwise, output 0 and reject the signature.
5. Scheme Analysis
5.1. The Correctness of NLBPS
- For the algorithm, the correctness of the verification equation is elaborated as follows:
- For the algorithm, the correctness of the verification equation is elaborated as follows:
5.2. The Security Analysis of NLBPS
Our scheme security consists of three types of adversaries; if NLBPS has existential unforgeability against type II and type III adversaries, it will also have existential unforgeability against type I adversaries. Therefore, we only take two types of adversaries into consideration.
Theorem 1.
If the problem is hard, the proposed lattice-based proxy signature scheme NLBPS is existential unforgeable against an adaptive chosen message and identity attacks in the random oracle model.
Proof of Theorem 1.
We prove this theorem by contradiction. Assuming that an adversary breaks the existential unforgeability of the signature scheme with a non-negligible probability, then we can construct a challenger to solve the problem by running the adversary as a subroutine. □
Corollary 1.
Let be the maximum number of queries that makes to the random oracle at a single query time for . Define , , and as the maximum number of queries, queries, queries, and queries, respectively. , , and correspond to the time for each query, query, query, and query, respectively. If there is a type II adversary that can break the existential unforgeability of NLBPS in the random oracle model with a non-negligible probability within a time bound , then there exists a polynomial-time challenger that solves the problem with a non-negligible probability:
This solution is achievable within a time constraint of
Proof of Corollary 1.
The type II adversary knows the key pair of , the public key of , and the identity information of both agents. First of all, announces to the identity and the message that will be challenged.
The challenger receives an instance of the problem . Given and a uniformly random matrix , tries to find small non-zero vector such that and .
: On inputting the system security parameter , set . Set as the dimension of the lattices and as the Gaussian parameter. invokes to generate a random matrix and a basis for such that . maintains five lists, , , , —that are initially empty. sets the master key pair and system public parameters , and sends to .
Random oracle hash queries: We assume that the ’s queries are distinct; otherwise, the simulator will consistently produce the same output for identical inputs without increasing the query counter. Then, performs the following queries:
- query: maintains a list of tuples . For the query to , if is in the list , then returns to . Otherwise, chooses at random, adds it to list and then returns it to .
- query: maintains a list of tuples which is called the list. For the query on , searches in the list . If it exists, returns to . Otherwise,
- (a)
- If , invokes and , then computes and .
- (b)
- If , chooses at random, computes and runs to generate . Then, chooses at random, computes and runs to generate .
Finally, returns to and adds to list .
query: For the query on the identity , if , returns to , then declares failure and halts. This event is recorded as . Otherwise, if , invokes to return the corresponding key pair to .
–query: maintains a list of tuples . submits to for querying the delegation. firstly calls query to obtain . Then, looks into list ; if it can find the corresponding in , returns to . Otherwise, chooses at random, and runs algorithm to generate . Then, returns to and adds to list .
query: maintains a list of tuples . For the query on , searches in the list . If it exists, returns to . Otherwise, calls query to obtain and calls query to obtain .
- If , let ; the delegated private key and the corresponding public key are and , respectively.
- If , let ; the delegated private key and the corresponding public key are and , respectively.
Finally, publishes the delegated public key , and returns to . Then, adds to list .
query: maintains a list of tuples . submits to for querying the signature.
- If and , returns to , then declares failure and halts. This event is recorded as .
- If and , searches in the list . If it exists, returns to . Otherwise, calls query to obtain , calls query to obtain and calls query to obtain . Then, returns to and adds to list .
- If , searches in the list . If it exists, returns to . Otherwise, calls query to obtain , calls query to obtain and calls query to obtain . Then, returns to and adds to list .
If and do not occur, then ’s simulation is perfect. The adversary forges a valid signature pair of the tuple with a non-negligible probability . This forgery satisfies the condition , and the equation . Thus, the following equation holds:
Therefore, we obtain that . According to Lemma 2, the minimum entropy of the preimage of the algorithm is at least . Consequently, the probability that the equation is negligible. Furthermore, given that and , it follows that . Let , then the challenger can output as a solution to the instance of the problem .
If and do not occur, Game 1 proceeds normally. The probability of Game 1 running without these events is as follows:
In the event that the adversary forges a valid signature without performing adaptive queries, the probability of such an occurrence is . Consequently, if forges the signature with a non-negligible probability in time through adaptive queries, then there exists a challenger who, within a polynomial time , can solve the problem with a non-negligible probability given by
Corollary 2.
Let be the maximum number of queries that makes to the random oracle at a single query time for . Define , , and as the maximum number of queries, queries, queries, and queries, respectively. , , and correspond to the time for each query, query, query, and query, respectively. If there is a type III adversary that can break the existential unforgeability of NLBPS in the random oracle model with a non-negligible probability within a time bound , then there exists a polynomial-time challenger that solves the problem with a non-negligible probability
This solution is achievable within a time constraint of
Proof of Corollary 2.
The type III adversary knows the key pair of , the public key of , and the identity information of both agents. First of all, announces to the identity and the message that will be challenged.
The challenger receives an instance of the problem . Given and a random matrix , tries to find a small non-zero vector such that and .
: On inputting the system security parameter , set . Set as the dimension of the lattices and as the Gaussian parameter. invokes to generate a random matrix and a basis for such that . maintains five lists, , , , —that are initially empty. sets the master key pair and system public parameters and sends to .
Random oracle hash queries: We assume that the ’s queries are distinct; otherwise, the simulator will consistently produce the same output for identical inputs without increasing the query counter. Then, performs the following queries:
- query: maintains a list of tuples . For the query to , if is in the list , then returns to . Otherwise,
- (a)
- If , computes .
- (b)
- If , randomly chooses .
Finally, returns to and adds to list .
- 2.
- query: maintains a list of tuples which is called the list. For the query on , searches in the list . If it exists, returns to . Otherwise, chooses at random, returns to and adds to list .
query: For the query on the identity , if , returns to , then declares failure and halts. This event is recorded as . Otherwise, if , invokes to return the corresponding key pair to .
query: maintains a list of tuples . submits to for querying the delegation. Then, looks into list ; if it can find the corresponding in , returns to . Otherwise,
- If , invokes and chooses at random. Then, calls query to obtain .
- If , randomly chooses , and runs algorithm to generate as the delegated secret. Then, calls query to obtain , computes and invokes .
Finally, returns to and adds to list .
query: maintains a list of tuples . For the query on , searches in the list . If it exists, returns to . Otherwise, randomly chooses a matrix , computes and invokes . Finally, publishes the delegated public key and returns to . Then, adds to list .
query: maintains a list of tuples . submits to for querying the signature.
- If and , returns to , then declares failure and halts. This event is recorded as .
- If and , searches in the list . If it exists, returns to . Otherwise, calls query to obtain , calls query to obtain and calls query to obtain . Then, computes and invokes . Finally, returns to and adds to list .
- If , searches in the list . If it exists, returns to . Otherwise, calls query to obtain , calls query to obtain , and calls query to obtain . Then, computes and invokes . Then, returns to and adds to list .
If and do not occur, then ’s simulation is perfect. The adversary forges a valid signature pair of the tuple with a non-negligible probability . This forgery satisfies the condition , and the equation . Thus, the following equation holds:
Therefore, we obtain . According to Lemma 2, the minimum entropy of the preimage of the algorithm is at least . The probability that is negligible. Furthermore, given that and , it follows that . Let ; then, the challenger can output as a solution to the instance of the problem .
If and do not occur, Game 2 proceeds normally. The probability of Game 2 running without these events is as follows:
In the event that the adversary forges a valid signature without performing adaptive queries, the probability of such an occurrence is . Consequently, if forges the signature with a non-negligible probability in time through adaptive queries, then there exists a challenger who, within a polynomial time , can solve the problem with a non-negligible probability given by
Furthermore, Boneh et al. [16] introduced the concept of a history-free reduction, and prove that such reductions imply security in the quantum model. They showed that the GPV scheme has a history-free reduction, thereby establishing its post-quantum security. Specifically, the GPV scheme is secure in the quantum random oracle model (QROM), where a quantum adversary can issue a query to the random oracle that represents a superposition of an exponentially large number of states. Our proposed NLBPS is a variant of the GPV scheme, built upon the same foundational principles. This ensures that NLBPS maintains its security in the presence of quantum attacks. The detailed proof process is not reiterated here.
5.3. The Performance Comparison of NLBPS
In this section, our scheme is compared with other proxy signature schemes in terms of computation costs and storage size. Specifically, the scheme presented in [10] is a lattice-based proxy signature scheme, the scheme in [13] describes a lattice-based proxy signature scheme in cloud storage, and the scheme in [17] constructs an attribute-based proxy signing scheme. All three schemes involve the delegation of signing authority to a proxy. The comparison results are summarized in Table 1 and define some notations as follows: denotes the execution time of a generic hash function operation, while denotes the execution time of algorithm operation. Additionally, , , , and represent the algorithm, the algorithm, the basis delegation without dimension increase algorithm [9], and other algorithms, respectively.

Table 1.
Performance comparison among Refs. [10,13,17] and ours.
The comparison of computation costs and storage size are listed in Table 1. The computation costs include signing cost and verification cost. Our scheme offers computational improvements over the methods presented in [10]. Specifically, our proxy signing process requires less time by omitting one execution of the hash function and the algorithm, thus saving . The signature verification also saves time by eliminating one hash function execution, saving . The storage size includes the size of signature and the delegated secret key. Compared with the schemes in [10], our scheme has the shortest storage size. The size of signature and the delegated secret key of our scheme are and , respectively. Furthermore, our scheme requires fewer algorithms, including only the and algorithms, which makes it more suitable for resource-limited applications such as the Internet of Things (IOT).
6. Conclusions
In this paper, we present a new lattice-based proxy signature scheme (NLBPS) that combines trapdoor sampling algorithms with preimage sampling algorithms. Utilizing a trapdoor sampling algorithm [15], we generate public–private key pairs for both the original signer and the proxy signer. Subsequently, proxy authorization and signature messages are carried out through the application of preimage sampling algorithms. Based on the hardness of the small integer solution (SIS) problem, we present the security analysis of NLBPS in the random oracle model. The performance comparison shows that our scheme has some advantages in computation costs and storage size. In the future, this section would be followed by a detailed discussion of the security proof and a comparative analysis with existing schemes, including a description of the computational complexity and potential areas for future research. The preimage sampling algorithms employed in the proxy signature process depend on the trapdoor basis to obtain the preimage, which consequently incurs high computational costs. In the future, we will consider using proxy signature without trapdoor as a basis for implementing a lattice-based proxy signature scheme.
Author Contributions
Conceptualization, L.Z. and J.L.; data curation, J.L.; formal analysis, H.L.; investigation, J.L.; methodology, L.Z. and J.L.; project administration, L.Z. and J.L.; software: J.L. and H.L.; supervision, L.Z.; validation, J.L. and H.L.; visualization, J.L. and H.L.; writing—original draft, J.L.; writing—review and editing, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created.
Acknowledgments
The authors of this paper would like to express their sincere gratitude to the editors and reviewers for their hard work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mambo, M.; Usuda, K.; Okamoto, E. Proxy Signatures for Delegating Signing Operation. In Proceedings of the Proceedings of the 3rd ACM Conference on Computer and Communications Security, New Delhi, India, 14–15 March 1996; Association for Computing Machinery: New York, NY, USA, 1996; pp. 48–57. [Google Scholar]
- Boldyreva, A.; Palacio, A.; Warinschi, B. Secure Proxy Signature Schemes for Delegation of Signing Rights. J. Cryptol. 2012, 25, 57–115. [Google Scholar] [CrossRef]
- Shamir, A. Identity-Based Cryptosystems and Signature Schemes. In Proceedings of the Advances in Cryptology: Proceedings of CRYPTO 84 4; Springer: Berlin/Heidelberg, Germany, 1985; pp. 47–53. [Google Scholar]
- Chen, G. Parallel and Distributed Processing and Applications-ISPA 2005 Workshops: ISPA 2005 International Workshops, AEPP, ASTD, BIOS, GCIC, IADS, MASN, SGCA, and WISA, Nanjing, China, 2–5 November 2005, Proceedings; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005; Volume 3759. [Google Scholar]
- Bannore, A.; Patil, R.Y.; Patil, Y.H.; Deshpande, H. Proxy Signature-Based Role Delegation Scheme: Formal Analysis and Simulation. Int. J. Inf. Technol. 2024, 16, 4027–4038. [Google Scholar] [CrossRef]
- Shor, P.W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Bernstein, D.J.; Lange, T. Post-Quantum Cryptography. Nature 2017, 549, 188–194. [Google Scholar] [CrossRef]
- Gentry, C.; Peikert, C.; Vaikuntanathan, V. Trapdoors for Hard Lattices and New Cryptographic Constructions. In Proceedings of the Fortieth Annual ACM Symposium on Theory of Computing, Victoria, BC, Canada, 17–20 May 2008; ACM: New York, NY, USA, 2008; pp. 197–206. [Google Scholar]
- Agrawal, S.; Boneh, D.; Boyen, X. Lattice Basis Delegation in Fixed Dimension and Shorter-Ciphertext Hierarchical IBE. In Advances in Cryptology—CRYPTO 2010; Rabin, T., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6223, pp. 98–115. ISBN 978-3-642-14622-0. [Google Scholar]
- Kim, K.S.; Hong, D.; Jeong, I.R. Identity-Based Proxy Signature from Lattices. J. Commun. Netw. 2013, 15, 1–7. [Google Scholar] [CrossRef]
- Wu, F.; Yao, W.; Zhang, X.; Wang, W.; Zheng, Z. Identity-based Proxy Signature over NTRU Lattice. Int. J. Commun. Syst. 2019, 32, e3867. [Google Scholar] [CrossRef]
- Luo, F.; Al-Kuwari, S.; Susilo, W.; Duong, D.H. Attribute-Based Proxy Re-Signature from Standard Lattices and Its Applications. Comput. Stand. Interfaces 2021, 75, 103499. [Google Scholar] [CrossRef]
- Wang, Q.; Cheng, C.; Xu, R.; Ding, J.; Liu, Z. Analysis and Enhancement of a Lattice-Based Data Outsourcing Scheme With Public Integrity Verification. IEEE Trans. Serv. Comput. 2022, 15, 2226–2231. [Google Scholar] [CrossRef]
- Yu, H.; Wang, N. Certificateless Network Coding Proxy Signatures from Lattice. Front. Comput. Sci. 2023, 17, 175810. [Google Scholar] [CrossRef]
- Alwen, J.; Peikert, C. Generating Shorter Bases for Hard Random Lattices. Theory Comput. Syst. 2011, 48, 535–553. [Google Scholar] [CrossRef]
- Boneh, D.; Dagdelen, Ö.; Fischlin, M.; Lehmann, A.; Schaffner, C.; Zhandry, M. Random Oracles in a Quantum World. In Proceedings of the Advances in Cryptology–ASIACRYPT 2011: 17th International Conference on the Theory and Application of Cryptology and Information Security, Seoul, South Korea, 4–8 December 2011; Proceedings 17. Springer: Berlin/Heidelberg, Germany, 2011; pp. 41–69. [Google Scholar]
- Wei, L.; Li, D.; Liu, Z. Provable Secure Attribute-Based Proxy Signature Over Lattice Small Integer Solution Problem in Random Oracle Model. Electronics 2023, 12, 1619. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).