Spectral Polynomials and Spectra of Graphs Beyond Cubic and Icosahedral Symmetries: n-Octahedra, n-Cubes, Symmetric and Semi-Symmetric Graphs, Giant Fullerene Cages and Generalized Petersen Graphs

Abstract

We report the results of our computations of the spectral polynomials and spectra of a number of graphs possessing automorphism symmetries beyond cubic and icosahedral symmetries. The spectral (characteristic) polynomials are computed in fully expanded forms. The coefficients of these polynomials contain a wealth of combinatorial information that finds a number of applications in many areas including nanomaterials, genetic networks, dynamic stereochemistry, chirality, and so forth. This study focuses on a number of symmetric and semi-symmetric graphs with automorphism groups of high order. In particular, Heawood, Coxeter, Pappus, Möbius–Kantor, Tutte–Coxeter, Desargues, Meringer, Dyck, n-octahedra, n-cubes, icosahedral fullerenes such as C₈₀(I_h), golden supergiant C₂₄₀(I_h), Archimedean (I_h), and generalized Petersen graphs up to 720 vertices, among others, have been studied. The spectral polynomials are computed in fully expanded forms as opposed to factored forms. Several applications of these polynomials are briefly discussed.

1. Introduction

Spectral polynomials, also called the characteristic polynomials of graphs, have been of considerable interest over several decades [1,2,3,4,5,6,7,8,9,10,11]. One of the reasons for this active interest is the graph isomorphism disease [1,2,3,4], which was originally thought to be solved through characteristic polynomials, although it has been since known that there are non-isomorphic graphs with the same spectral polynomials [4]. In addition to the graph isomorphism disease reason [1], the spectral polynomials are extremely interesting because their coefficients contain a plethora of structural information pertinent to graphs, solids, molecules, fullerenes, nanomaterials, and so forth [12,13,14,15]. The related matching polynomials, Laplacians, and other polynomials are of interest as they provide the first and quick structural insights into a number of structural, spectroscopic, and electronic features for systems containing π-electrons such as the HOMO-LUMO gaps, aromaticity, delocalization energies, especially for larger networks such as giant fullerenes, carbon nanotubes, two-dimensional graphene sheets, and so forth [16,17,18,19,20,21,22,23,24,25,26,27,28,29]. The coefficients of the spectral polynomial also contain combinatorially rich information, such as the various circuits present in the structures, dimers, and, consequently, they facilitate the combinatorial enumeration of resonance structures and related phenomena of aromaticity and superaromaticity [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43].

More recent interest in spectral polynomials has been fueled by the advent of novel fullerene cages [44,45,46,47,48,49,50,51,52], supergiant fullerenes, etc., which are defined by cages that typically contain 12 pentagons and a varied number of hexagons. Their properties and a compelling need to gain quick insights into their electronic and vibrational spectroscopic properties have catalyzed a reviving, growing interest in these polynomials and in enhancing our understanding of the concept of aromaticity. As a result of the discovery of such fascinating materials, the number of graph theoretical studies on these systems has increased over the decades. The magnetic and electronic properties of these systems combined with their NMR, Raman, and IR spectra have all catalyzed the need to understand and quantify the fundamental underlying connectivity related features and automorphisms of these large cages. Furthermore, the exponential growth of machine learning and artificial intelligence techniques as they pertain to large networks and molecular structures have kindled further interest in the development of graph theoretical and combinatorial methods for application in large molecular networks, cages, and materials [53,54]. Several developments of QSAR analysis, including shape characterizations [55,56], aim to develop invariants for molecular characterizations.

The spectra of graphs possessing high symmetries, that is, those with large orders of automorphism groups, have been of interest over the years due to their intriguing nature; some high-symmetry structures exhibit integral spectra with high degeneracies, while others exhibit integral to semi-integral spectra with remaining eigenvalues that can be expressed in the form of simple radicals or compound surds. Hence, graphs exhibiting integral spectra and applications of graph spectra to computer science and other areas have received attention from several researchers over the years [57,58]. This is a clear consequence of the high orders of the automorphism groups of such graphs, which facilitate facile factoring of their secular determinants, resulting in the factorization of their spectral polynomials. A clear contrast between the computation of spectra and the computing of explicitly expanded spectral polynomials must be pointed out. While the factored forms of spectral polynomials can be readily generated from their spectra, the expanded polynomials that yield the explicit coefficients of each term in the spectral polynomial are much more challenging to compute as they involve computations of all possible symmetric functions of the spectral values. Although for graphs with totally integral spectra containing a few vertices the task of expanding the factored polynomials to construct the spectral polynomials is less challenging, this is not the case for larger systems with mixed spectra that involve compound surds or totally irrational spectra. For larger systems like these, expanding the factored polynomial terms by computing all possible S-functions of the roots is a combinatorially and computationally daunting task. Yet, many applications need the explicit coefficients in the spectral polynomials, as they contain structurally rich information, as pointed out above. The related matching polynomials have several applications, as their coefficients enumerate the number of disjoint dimers in graphs, for example, the lattice statistics and the dimers in chemisorptions with adjacent neighbor exclusions, Kekulé resonance structures, and partial dimer covers of giant fullerenes [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]. Furthermore, recently, the delta polynomials [16] have been formulated for new insights into aromaticity, and these polynomials require both spectral and matching polynomials for their constructions, and hence the computations of aromaticity index.

Carbon nanospheres and giant golden fullerenes possessing icosahedral symmetries have opened up the doors for computational and combinatorial studies on such systems. As high-level ab initio quantum chemical studies on such large systems are very difficult and computationally intensive, other viable techniques such as the computations of spectral polynomials can aid with the initial understanding of the structures, electronic properties, relative stabilities of isomers, and their Raman and IR spectra. Many of the high symmetry graphs that we have considered in the present study are also important to the enumeration of chemical isomerization or rearrangement pathways [59,60,61,62,63,64]. Furthermore, the Stones–Wales rearrangement graphs and isomerization graphs of nonrigid molecules, water clusters, and so forth are graphs with large automorphism groups, as dynamic symmetries in these systems result in the wreath product groups of large orders.

Stimulated by several experimental and theoretical studies, we undertake systematic computations of spectral polynomials of graphs possessing high symmetries, semi-symmetric graphs, and graphs with integral spectra as well as twisted topologies such as Mobius–Kantor graphs. The current study also considers graphs arising from n-cubes and n-octahedra from the standpoints of their spectral polynomials and explorations into graphs with integral spectra. We have also included generalized Petersen graphs and giant fullerenes exhibiting icosahedral symmetries for the computations of spectral polynomials. In this study, new results are reported for the spectral polynomials of a number of such large structures and cages, which are of considerable interest in nanomaterial chemistry and other disciplines. Hence, the present study addresses the computational challenges associated with the computations of spectral polynomials of large systems and giant fullerenes.

2. Mathematical and Computational Methods Pertinent to Spectral Polynomials

The spectral polynomial, which is also referred to as the characteristic polynomial of a graph G, is defined as the secular determinant of the adjacency matrix, which is, in turn, defined as follows:

$$A_{ij}=\left\{\begin{array}{c}1ifverticesiandjareconnected\\ 0otherwise\end{array}\right.$$

The spectral (characteristic) polynomial of the graph G, denoted by P_G, is then obtained as follows:

$$P_G\left(x\right)=\left|\begin{array}{c}A-xI\end{array}\right|=C_0{x}^n+C_1{x}^{n-1}+\cdots +C_{n-1}x+C_n,$$

C_k, is the kth coefficient in spectral polynomial. The coefficient contains combinatorially rich structural information, as provided by Sach’s theorem as follows:

$$C_k={\sum }_{g\in G_i}{(-1)}^{c\left(g\right)}{2}^{r\left(g\right)},$$

where G_is are Sach’s subgraphs of G containing k vertices, c(g) is the disjoint components in the subgraph g, and r(g) is the number of cycles in the subgraph g. The related acyclic polynomial or the matching polynomial of G is defined using the parameters p(G, k)s, which enumerate the number of k disjoint dimers or k-matchings on the graph G by the following expression:

$$M_G\left(x\right)={\sum }_{k\text{'}=0}^{\left[\frac{n}{2}\right]}{\left(-1\right)}^k\text{'}p\left(G,k\text{'}\right)x^{n-2k\text{'}}={\sum }_{k=0;even}^{\left[\frac{n}{2}\right]}{\left(-1\right)}^k{M}_k{x}^{n-k},$$

p(G, k’) are the number of ways to place k’ disjoint dimers on the graph, n is the cardinality of the vertex set of the graph, and [n/2] is the greatest integer contained in n/2. Let k = 2k’, as only even terms survive in the matching polynomial; hence, the polynomial can be cast in terms of k in a more convenient form, as shown above. The matching polynomials coincide with the spectral polynomials for trees, and hence the term acyclic polynomials is coined for the matching polynomials. The spectral polynomials contain very rich combinatorial information pertinent to the structure of the graph such as the number of various disjoint circuits present in the graph in addition to the disjoint dimers or a combination of both.

The computations of spectral polynomials are more efficiently accomplished through matrix multiplication methods than by computing them from the spectra of the graphs through S-functions. We note that the spectra of the highly symmetrical graphs considered here can be computed by harnessing their symmetries through factorization of the secular determinant. However, the spectra yield factorized forms of the spectral polynomials at best, which need to be expanded, and the coefficients of the corresponding terms need to be collected. These processes become a computationally daunting problem as the process of computing all S-functions of the spectra is an NP problem. On the other hand, it has been established that the spectral polynomials can be directly computed through iterative n matrix multiplications, which provide an O(n⁴) polynomial algorithm for the direct computations of spectral polynomials. As these computational techniques are adequately described in previous papers [10,16], we shall not repeat the same here. A unique advantage of the present technique is that it can be applied to any graph irrespective of its symmetry or regularity, as it is not symmetry-based. As the technique computes the powers of adjacency matrix, it can be used for any graph, including highly irregular graphs.

As computations of spectral polynomials for the graphs considered here contain up to 720 vertices, the coefficients in the polynomials grow astronomically, culminating in a combinatorial explosion. Consequently, we have uniformly employed REAL*16 quadruple precision arithmetic to compute the coefficients, which are the traces of the matrices generated iteratively through matrix multiplication algorithms. The quadruple precision arithmetic yields an accuracy of up to 33–35 digits for the coefficients in the spectral polynomials. More importantly, large coefficients up to 1.1897314953572317650857593266280070162 × 10⁴⁹³² can be computed. The other limitation is simply that the O(n³) matrix multiplications n times iteratively to compute the coefficients in quadruple precision, which could be CPU-intensive for larger graphs. We did not invoke symmetry factoring as it only leads to polynomials in factored form, whereas we need the expanded polynomials with explicit coefficients, computed for several applications that need them. We also use other debugging aids to validate the algorithm by computing the constant coefficient of the spectral polynomial from the spectra, as the constant coefficient is given by the product of the spectral eigenvalues.

The definition of n-polyhedra considered here follows that of the n-cube definition through the Cartesian product of two graphs introduced by Harary [65]. Let Q_n be any an n-dimensional polyhedral, given its three-dimensional counterpart as Q₃. Then, Q_n is defined recursively by the Cartesian product:

Q_n = Q_n−1 × K₂ for n ≥ 4,

with Q₃ defined as the corresponding 3D polyhedral graph,

K₂ is a graph on two vertices connected by an edge. Hence, the adjacency matrix of the next polyhedra, Q_n+1, denoted by A_Qn+1, is given as follows:

$$A_{Q_{n+1}}=\left[\begin{array}{cc}{A}_{Q_n}& I\\ I& A_{Q_n}\end{array}\right],$$

where I is simply an identity matrix of the same order as Q_n. The order of $A_{Q_{n+1}}$ is twice that of $A_{Q_n}$, and hence for every iteration the order of the adjancy matrix doubles. For hypercubes or n-cubes, the order of the matrix grows as 2ⁿ × 2ⁿ. For example, the order of the adjacency matrix of an 8-cube is 256 × 256, while the order of the adjacency matrix of a 6-octahedron is 48 × 48, noting that the 3-octahedon has a 6 × 6 adjacency matrix owing to the 6 vertices of an octahedron. Hence, the recursive relation defined above facilitates the computational generation of n-polyhedra for any n and the computations of their properties such as spectra, and so forth. Several other graphs and their symmetry groups considered here including the nd-hypercubes, Möbius graphs, etc., have many applications in chemistry, physics and material science [66,67,68,69,70,71,72,73,74].

The generalized Petersen graphs, G(n,k), for any n and k contain 2n vertices and comprise an outer n-sided polygon and an n-gon star within. The outer polygon and the inner star are connected by the corresponding vertices by a single edge for each such pair. It can be formulated symbolically as follows. Suppose {v₀, v₁, v₂,……v_n−1,} is the set of successive (not necessarily adjacent) vertices of the inner star. Let {u₀, u₁, u₂,……u_n−1} be the set of vertices of the outer polygon with n sides. The generalized Petersen graph, G(n,k), is obtained by joining vertices v₀ and v_k, v₁ and v_1+k,.. v₂ and v_2+k, ….v_i and v_{i+k(mod n)},……v_n−1 and v_{n+k−1 (mod n)}. All the subscripts of the vertices are integer modulo n. Once the inner star is formed as determined by the parameter k, the outer n-gon and the inner star are joined by the corresponding folds, that is, connecting u₀ to v_o, u₁ to v₁…… u_n−1 to v_n−1. Hence, the generalized Petersen graph G(n,k) for k ≤ n/2 is defined by the edge set:

{u_iu_i+1, u_iv_i, v_iv_{i+k(mod n)} | 0 ≤ i ≤ n − 1, k ≤ n/2}

The concept of the generalized Petersen graph was pioneered by Coxeter [75] and has been studied by many researchers [76]. There are many generalized Petersen graphs that have been well studied, for example, the Dűrer graph, Desargues–Levi graph, Nauru graph, Mobius–Kantor graph, and so forth.

In the current study, we compute the spectral polynomials and spectra of several simple but highly symmetric to very complex clustered graphs, such as n-octahedra, n-cubes, giant icosahedral fullerenes such as C₂₄₀(I_h), Archimedean, and a few large generalized Petersen graphs up to 720 vertices, together with semi-symmetric, Möbius, and isomerization graphs. Some of the simpler and highly symmetric graphs that we include in our study are a Heawood graph, Folkman’s graph, Desargues–Levi graph, Möbius–Kantor graph, Coxeter graph, Meringer graph, Dyck graph, and so forth. Many of these graphs have integral or partially integral spectra and all are regular graphs. Folkman’s graph is a semi-symmetric graph with an automorphism group of the wreath product, S₅[S₂], containing 3840 symmetry elements. They all exhibit integral graph spectra. All these graphs have several applications to fullerene chemistry, fullerene nanospheres, dynamic stereochemistry, dynamic chirality, water clusters, aromaticity, chemisorption, and so forth.

3. Results and Discussions

A.

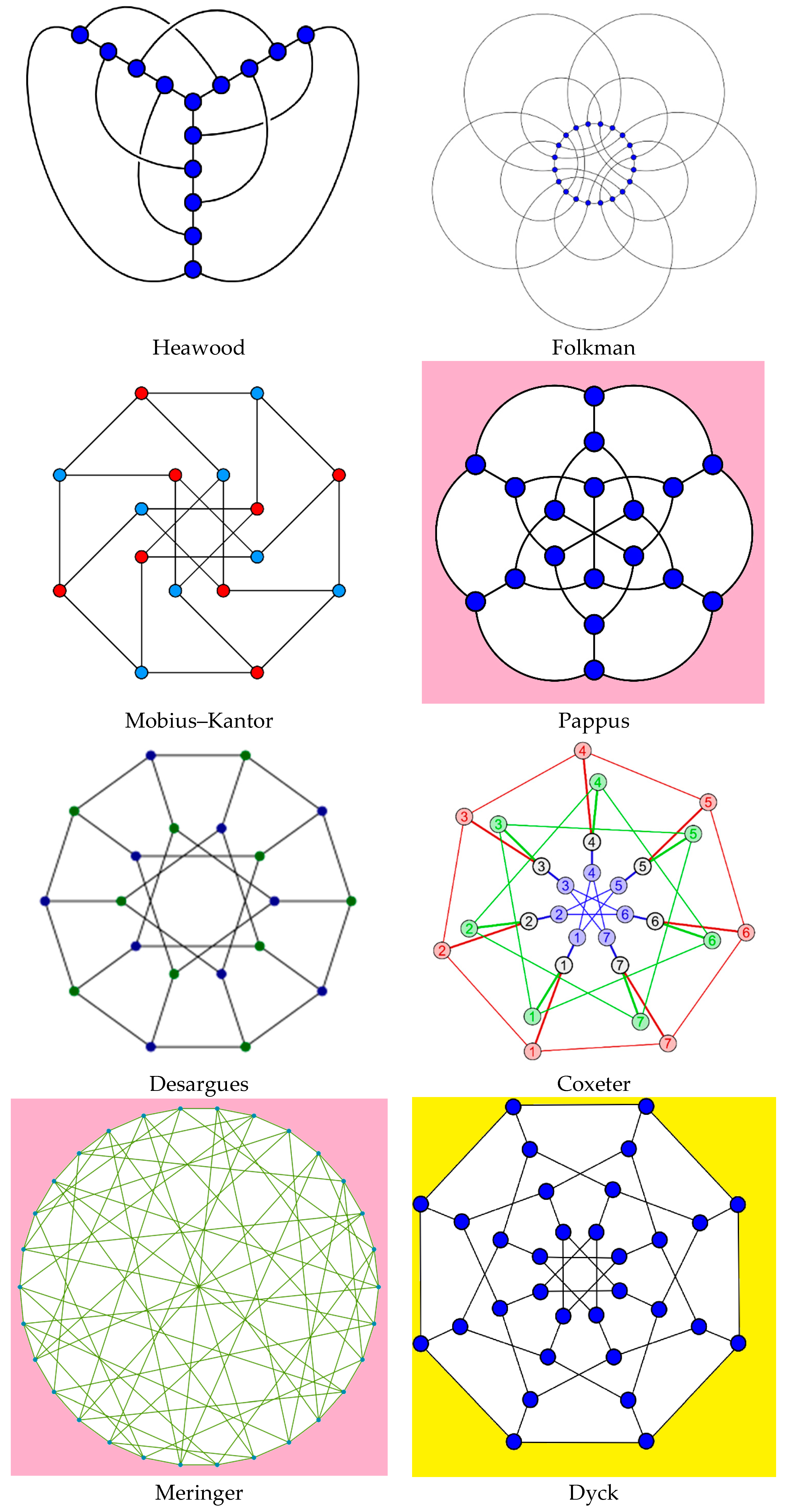
Spectral polynomials of small graphs with high automorphism groups: Heawood graph, Folkman’s graph, Möbius–Kantor, and Pappus, Desargues–Levi, Coxeter, Meringer, Coxeter–Tutte, and Dyck graphs.

In this section, we obtain the fully expanded spectral polynomials of graphs with fewer than 30 vertices, as shown in Figure 1, that possess high-order automorphism groups beyond the cubic symmetries. Many of these graphs exhibit well-known integral spectra, and thus their spectral polynomials are readily obtained in factored forms. Yet, the expanded spectral polynomials contain useful structural information, and thus in

Table 1. Spectral (characteristic) polynomial and spectra of (a) Heawood graph with PGL₂(7) group of 336 operations; (b) Folkman’s graph S₅[S₂] automorphism group; (c) Mobius–Kantor graph O_h² with 48 symmetry operations; (d) Coxeter–Tutte graph with automorphism group 1440; (e) Pappus graph with automorphism group of 216 operations; (f) Desargues graph with S5 × S2 group of 240 operations; (g) Coxeter graph with PGL₂(7) group of 336 operations; (h) Meringer graph with automorphism group of 96 operations; (i) Dyck graph with a group of 192 symmetry operations.

Heawood		Mobius– Kantor		Pappus		Desargues		Coxeter		Meringer		Dyck
k	C14−k	k	C16−k	k	C18−k	k	C20−k	k	C28−k	k	C30−k	k	C32−k
14	1	16	1	18	1	20	1	28	1	30	1	32	1
13	0	15	0	17	0	19	0	27	0	29	0	31	0
12	−21	14	−24	16	−27	18	−30	26	−42	28	−75	30	−48
11	0	13	−0	15	0	17	0	25	−0	27	0	29	0
10	168	12	228	14	297	16	375	24	777	26	2475	28	1032
9	0	11	−0	13	0	15	0	23	−0	25	−384	27	0
8	−700	10	−1144	12	−1755	14	−2580	22	−8344	24	−48,401	26	−13,168
7	0	9	−0	11	0	13	0	21	−48	23	19,104	25	0
6	1680	8	3342	10	6075	12	10,815	20	57,666	22	628,056	24	111,372
5	0	7	−0	9	0	11	0	19	1232	21	−430,848	23	0
4	−2352	6	−5832	8	−12,393	10	−28,830	18	−268,716	20	−5,679,240	22	−660,720
3	0	5	−0	7	0	9	0	17	−13,104	19	5,785,632	21	0
2	1792	4	5940	6	13,851	8	49,545	16	860,314	18	36,262,896	20	2,839,768
1	0	3	−0	5	0	7	0	15	74,256	17	−51,046,080	19	0
0	−576	2	−3240	4	−6561	6	−54,480	14	−1,893,960	16	−160,269,840	18	−9,014,832
Folkman		1	−0	3	0	5	0	13	−239,568	15	307,544,960	17	0
20	1	0	729	2	0	4	36,960	12	2,827,965	14	452,708,352	16	21,377,718
19	0	Cox–Tutte		1	0	3	0	11	433,776	13	−1,269,818,112	15	0
18	−40	30	1	0	0	2	−14,080	10	−2,790,970	12	−584,794,368	14	−38,077,072
17	0	29	0			1	0	9	−396,816	11	3,482,735,616	13	0
16	600	28	−45			0	2304	8	1,772,925	10	−840,302,592	12	50,932,344
15	0	27	0					7	118,192	9	−5,777,448,960	11	0
14	−4320	26	900					6	−719,376	8	4,925,411,328	10	−50,813,520
13	0	25	0					5	44,352	7	4,173,987,840	9	0
12	15,120	24	−10,560					4	170,464	6	−793,758,9248	8	37,211,500
11	0	23	0					3	−37,632	5	1,877,016,576	7	0
10	−20,736	22	80,640					2	−16,128	4	3,963,420,672	6	−19,410,000
9	0	21	0					1	7168	3	−3,784,048,640	5	0
8	0	20	−419,328					0	−768	2	1,374,683,136	4	6,825,000
7	0	19	0							1	−188,743,680	3	0
6	0	18	1,505,280							0	0	2	−1,450,000
5	0	17	0									1	0
4	0	16	−3,686,400									0	140,625
		15	0
		14	5,898,240
		13	0
		12	−5,570,560
		11	0
		10	2,359,296
Spectra of Heawood graph
−3.0		−1.414214		−1.414214		−1.414214		−1.414214		−1.414214
−1.414214		1.414214		1.414214		1.414214		1.414214		1.414214
1.414214		3.0
Spectra of Folkman’s graph
−4.0		−2.449490		−2.449490		−2.449490		−2.449490		0.0
0.0		0.0		0.0		0.0		0.0		0.0
0.0		0.0		0.0		2.449490		2.449490		2.449490
2.449490		4.0
Spectra of Mobius–Kantor graph
−3.0		−1.732051		−1.732051		−1.732051		−1.732051		−1.0
−1.0		−1.0		1.0		1.0		1.0		1.732051
1.732051		1.732051		1.732051		3.0
Spectra of Coxeter–Tutte graph
−3.0		−2.0		−2.0		−2.0		−2.0		−2.0
−2.0		−2.0		−2.0		−2.0		−0.0		−0.0
−0.0		−0.0		−0.0		−0.0		0.0		0.0
0.0		0.0		2.0		2.0		2.0		2.0
2.0		2.0		2.0		2.0		2.0		3.0
Spectra of Pappus graph
−3.0		−1.732051		−1.732051		−1.732051		−1.732051		−1.732051
−1.732051		−0.0		−0.0		0.0		0.0		1.732051
1.732051		1.732051		1.732051		1.732051		1.732051		3.0
Spectra of Desargues–Levi graph
−3.0		−2.0		−2.0		−2.0		−2.0		−1.0
−1.0		−1.0		−1.0		−1.0		1.0		1.0
1.0		1.0		1.0		2.0		2.0		2.0
2.0		3.0
Spectra of Coxeter graph
−2.414214		−2.414214		−2.414214		−2.414214		−2.414214		−2.414214
−1.0		−1.0		−1.0		−1.0		−1.0		−1.0
−1.0		0.414214		0.414214		0.414214		0.414214		0.414214
0.414214		2.0		2.0		2.0		2.0		2.0
2.0		2.0		2.0		3.0
Spectra of Meringer graph
−3.0		−3.0		−2.732051		−2.732051		−2.732051		−2.732051
−2.561553		−2.561553		−2.561553		−2.0		−2.0		−2.0
0.0		0.732051		0.732051		0.732051		0.732051		1.561553
1.561553		1.561553		2.0		2.0		2.0		2.0
2.0		2.0		2.0		2.0		2.0		5.0
Spectra of Dyck graph
−3.0		−2.236068		−2.236068		−2.236068		−2.236068		−2.236068
−2.236068		−1.0		−1.0		−1.0		−1.0		−1.0
−1.0		−1.0		−1.0		−1.0		1.0		1.0
1.0		1.0		1.0		1.0		1.0		1.0
1.0		2.236068		2.236068		2.236068		2.236068		2.236068
2.236068		3.0

we uniformly show the expanded spectral polynomials of these graphs (Figure 1).

We start with the Heawood graph (Figure 1), which is an extremely interesting small graph that nonetheless has a relatively large automorphism group of PGL₂(7) group that contains 336 operations. The graph contains 14 vertices and 21 edges and it is both edge- and vertex-transitive. The graph also exhibits many interesting properties by virtue of it being toroidal, that is, its embedding on a torus contains no crossing. The graph is Hamiltonian and it is a totally symmetric graph. It appears to be the only cubic, symmetrical graph with 14 vertices and, moreover, its odd number of edges makes it quite interesting. As seen from Table 1, the high-order automorphism symmetry of such a small graph results in a highly degenerate spectrum. This is consistent with the character table of the PGL₂(7) group, which contains one 7-dimensional, four 6-dimensional, and two 1-dimensional irreducible representations. Hence, the spectra of the Heawood graph contain a 6-fold degenerate ±$\sqrt{2}$ eigenvalue and integral ±3 eigenvalues. As the Heawood graph is bipartite, its spectra exhibit a mirror symmetry relative to 0. In this case, the factored spectral polynomial can be expanded and one can verify our computed spectral polynomial for the graph shown in Table 1. For example, the constant term of the computed spectral polynomial is 576, which is the product of the eigenvalues or 2⁶3². Likewise, all computed coefficients in Table 1 can be analytically verified for this graph due to its highly degenerate spectra and small number of vertices. The coefficients of all odd terms are zeroes in the spectral polynomial, consistent with the bipartite nature of the Heawood graph. Moreover, for this particular graph, the square root of the constant coefficient or $\sqrt{2^6{3}^2}$ = 24 yields the number of perfect matchings of the Heawood graph, although this property is not valid for all graphs, especially those containing zero eigenvalues in the spectra. The coefficient of x¹² yields the number of edges, which is 21, as can be seen from Table 1. This is the only odd coefficient in the spectral polynomial of the Heawood graph (Table 1).

The next graph in Figure 1 is Folkman’s graph, which exhibits a wreath product S₅[S₂] automorphism group containing 3840 symmetry elements. The automorphism group is isomorphic with the automorphism group of the 5-cube. The graph is edge symmetric but not vertex-transitive, and thus it is an interesting case of a semi-symmetric graph. Like the previous graph, due to its high symmetry, its spectra exhibit 4-fold degeneracy of ±$\sqrt{6}$ eigenvalues and a 10-fold degenerate 0 eigenvalue. The remaining ±4 eigenvalues match with the quadratic nature of this graph. As the graph is bipartite, its spectra exhibit mirror symmetry with respect to 0. Due to the 10-fold degenerate zero eigenvalues of this graph, the product of the eigenvalues is zero; hence, as seen from Table 1, the constant coefficient is zero. As seen from Table 1, not only is this coefficient zero but several trailing coefficients of the spectral polynomial of Folkman’s graph are also all zero. Consequently, the zero constant coefficient for the spectral polynomial of this graph does not yield the number of perfect matchings which, in fact, turns out to be 768 for Folkman’s graph. The graph contains 40 edges, as inferred from the second leading nonzero coefficient. There are several geometrical interpretations for the coefficients of the spectral polynomials. For example, the fourth coefficient of the Folkman’s graph contains contributions from cycles of length 4 and two disjoint dimers (2-matchings). As there are 660 disjoint ways that two dimers (2-matchings) can be generated on Folkman’s graph, we obtain the number of four-cycles in Folkman’s graph from Sach’s theorem as follows:

−2n₄ + 660 = C₄ = 600 or n₄ = 30

Thus, it can be deduced that there are 30 cycles of length 4 contained in the Folkman graph. Alternatively, if the number of four-cycles is known, we can deduce the number of 2-matchings from the coefficient.

One of the motivations for the study of the Möbius–Kantor graph is that it plays an important role in the stereochemistry of Möbius strips, twisted molecules, and Möbius ladders, and thus finds a number of applications in such areas. These graphs, in general, have played important roles in aiding the synthesis of twisted molecules and in shedding light on their stereochemistry [66,67,68]. The Möbius–Kantor graph contains 16 vertices and 24 edges (Figure 1). The automorphism group of the Möbius–Kantor graph is the double group of the octahedral group (O_h²), which comprises 96 symmetry operations. We also note that the Möbius–Kantor graph finds important applications in relativistic spinor representations [69,70,71,72], as the Cayley graph of the Pauli group is the Möbius–Kantor graph. Moreover, it is a subgraph of the 4D-hypercube, which has an automorphism group of the wreath product S₄[S₂] spanning 384 automorphisms. Hence, the Möbius–Kantor graph makes an interesting case for the study of spectral polynomials. As seen from Table 1, its spectra are highly degenerate, with (±$\sqrt{3}$)⁴ (±1)³ ±3. As the graph is bipartite, its spectra exhibit a mirror symmetry relative to 0. This is also reflected in the spectral polynomial as the coefficients of all odd terms are zeroes (Table 1). As seen from Figure 1, there are no cycles of length 4 in the Möbius–Kantor graph, and thus the coefficient C₁₂ enumerates the number of 2-matchings that can be seen to be 228 (Table 1). On the other hand, there are several 6-cycles in the Möbius–Kantor graph, and thus the coefficient C₁₀ contains both 6-cycles as well as three disjoint dimers (3-matchings). As there are 12 6-cycles in the Möbius–Kantor graph, by Sach’s theorem, it can then be inferred that the number of 3-matchings in the Möbius–Kantor graph is 1096.

Next, we consider the Desargues–Levi graph, which has played an important role in the dynamic stereochemistry of complexes exhibiting pseudorotations, especially with trigonal bipyramidal geometries as well as nucleophilic displacement reactions [60]. The isomerization pathways in these dynamical processes can be represented by the Desargues–Levi graph when chirality is explicitly included in the representations. The Desargues–Levi graph is considered the double twin of the Petersen graph, as it contains twice the vertices and it can be readily derived from the Petersen graph. The Desargues–Levi graph, which is also the generalized Petersen graph G(10,3), contains 20 vertices and 30 edges (Figure 1). It can be shown that the automorphism group of this graph is S₅ x S₂ compared to the S₅ automorphism group of the Petersen graph. As the Desargues–Levi graph is bipartite, its spectra exhibit mirror symmetry, as seen in Table 1. The graph is of special interest as it exhibits integral spectra with the pattern (±2)⁴ (±1)⁵ ±3. (Table 1). The computed coefficients in the spectral polynomial of the Desargues–Levi graph can thus be readily verified from the spectral pattern. For example, the constant coefficient in the spectral polynomial is given by 2⁸3² = 2304 (Table 1). We have computed the spectral polynomial of the Desargues–Levi graph, and it is included in Table 1. As seen from Table 1, the C₁₈ coefficient in the spectral polynomial of the Desargues–Levi graph is the number of edges, while the C₁₆ coefficient is the number of 2-matchings, as there are no 4-cycles in the Desargues–Levi graph (Figure 1). Hence, we infer from Table 1 that the number of 2-matchings of the Desargues–Levi graph is 375. As there are only 20 hexagons in the Desargues–Levi graph, the number of 3-matchings in the Desargues–Levi graph can be inferred as 2540 from the C₁₄ coefficient of the spectral polynomial for the Desargues–Levi graph in Table 1.

The Pappus graph, with 18 vertices, makes an interesting case as its automorphism group contains 216 operations. Moreover, it is a completely symmetric graph with a partial integral spectrum (Table 1). Its spectra are characterized by the following paired pattern: (±$\sqrt{3}$)⁶ (0)⁴ ± 3. The presence of four zero eigenvalues in the spectra renders several of the trailing coefficients to be zeroes in the spectral polynomial, as seen from Table 1. As the Pappus graph is bipartite, the coefficients of the odd terms in the spectral polynomial vanish. The second leading coefficient of 27 yields the number of edges in the graph, while the fourth coefficient of 297 suggests that there are 297 2-matchings in the graph, as there are no 4-cycles in the Pappus graph, as seen from Figure 1. As there are 18 6-cycles in the Pappus graph, the number of 3-matchings in the graph is 1719, as inferred from the coefficient of C₁₂ in the spectral polynomial, which is 1755 (Table 1).

Three more high-symmetry graphs that we will simultaneously discuss are the Coxeter graph, Meringer graph, and the Tutte–Coxeter graph. The Meringer graph and Tutte–Coxeter graph contain 30 vertices each, and hence their spectra and polynomials can be compared. On the other hand, the Coxeter graph is a fully symmetric cubic graph containing 28 vertices and 42 edges. The automorphism group of the Coxeter graph is PGL₂(7), with 338 symmetry operations. Hence, the automorphism group of the Coxeter graph is isomorphic with that of the Heawood graph considered at the start of this section. As seen from Table 1, the spectra of the Coxeter graph exhibit the pattern—(2 + $\sqrt{2}$)⁶(1)⁷ (2 − $\sqrt{2}$)⁶ (2)⁸3¹. Evidently, the graph is not bipartite but its high symmetry is reflected in the 6-fold, 7-fold and 8-fold degeneracies of the eigenvalues. The coefficient of C₂₆ in Table 1 yields the number of edges, while the C₂₄ coefficient of 777 directly provides the number of 3-matchings in the Coxeter graph as it contains no hexagons (Figure 1). On the other hand, the C₂₁ coefficient of 48 indicates that there are 24 heptagons in the Coxeter graph. The Coxeter graph exhibits 84 perfect matchings, although the constant coefficient in the spectral polynomial of 768 is a mixture of perfect matchings, two 7-cycles, 14-cycles, and so forth. Although the Meringer and Tutte–Coxeter graphs contain the same number of vertices, the former is a 5-regular graph with 75 edges, while the Tutte–Coxeter graph is a cubic graph with 45 edges. Hence, they exhibit very different spectra and spectral polynomials (Table 1). The Tutte–Coxeter graph exhibits 1440 automorphic symmetry operations constituting a symmetry group isomorphic with the direct product S₆ × S₂. The Meringer graph’s automorphism group contains 96 operations. The spectral polynomials of both graphs are juxtaposed in Table 1. As seen from Table 1, the spectral polynomial and spectra of the Meringer graph are considerably more complex compared to those of the Tutte–Coxeter graph. For example, the fourth leading coefficients of the two graphs are 900 and 2475, respectively, suggesting that there are 900 2-matchings in the Tutte–Coxeter graph while there are 2475 2-matchings in the Meringer graph, as both graphs do not possess cycles of length 4. Evidently, the Meringer graph is much more complex by virtue of it being a (5,5) cage, while the Tutte–Coxeter graph with higher symmetry is considerably simpler. We note that the Tutte–Coxeter graph exhibits 288 perfect matchings and that they are related to the Stirling numbers of the first kind.

Next, we consider the Dyck graph as a last example of a graph with high symmetry. Its automorphism group is the fourth cover of the octahedral group and it thus contains 192 symmetry operations, which makes it an interesting case for our study. In addition, the graph contains 32 vertices and 48 edges. Moreover, the Dyck graph exhibits a highly degenerate spectral pattern of (±$\sqrt{5}$)⁶ (±1)⁹ ±3. Hence, it is a bipartite graph, as echoed by the mirror symmetry inherent in its spectra. The spectra polynomials of the Dyck graph are consistent with 48 edges and they also suggest that there are 1032 2-matchings in the Dyck graph, as they do not contain cycles of length 4. It can be deduced that there are 13,136 3-matchings in the Dyck graph from the C₂₆ coefficient of the spectral polynomial, which is 13,168. This follows from the fact that there exist 16 hexagonal circuits in the Dyck graph (Figure 1). The other subsequent terms of the Dyck graph are far more complex due to contributions from several Sach’s subgraphs to those terms, and hence the graph is combinatorially and structurally more complex among the graphs considered in this section.

B.

Spectral Polynomials and Spectra of n-polyhedra: n-octahedra and n-cubes

Figure 2 displays two sets of n-polyhedra generated from the cube and octahedron as building blocks. The evolution of n-polyhedra recursively from the lower polyhedra was defined in the previous section, and hence we shall not repeat it. Moreover, we previously obtained the spectra of n-cubes using the Hadamard transform technique [73], but the spectral polynomials of n-cubes have not been computed before. Thus, all the results for the n-octahedra and all spectral polynomials of n-cubes are newly reported here.

Table 2. Characteristic polynomials and integral spectra of n-octahedron and n-cube (n = 4–6).

4-Octa		5-Octa		6-Octa		4-Cube		5-Cube		6-Cube
k	C12-k	k	Cn-k	k	Cn-k	k	C16-k	k	C32-k	k	C64-k
12	1	24	1	48	1	16	1	32	1	64	1
11	−0	23	0	47	0	15	0	31	0	63	0
10	−30	22	−72	46	−168	14	−32	30	−80	62	−192
9	−32	21	−64	45	−128	13	0	29	0	61	0
8	231	20	1968	44	12,420	12	352	28	2680	60	16,896
7	384	19	3072	43	17,664	11	0	27	0	59	0
6	−388	18	−25,856	42	−532,280	10	−1792	26	−50,160	58	−908,800
5	−960	17	−55,296	41	−1,072,512	9	0	25	0	57	0
4	63	16	169,728	40	14,672,178	8	4352	24	586,140	56	33,592,320
3	896	15	475,136	39	37,926,400	7	0	23	0	55	0
2	258	14	−509,952	38	−272,681,208	6	−4096	22	−4,516,176	54	−909,139,968
1	−288	13	−2,113,536	37	−872,304,000	5	0	21	0	53	0
0	−135	12	249,856	36	3,470,385,364	4	0	20	23,674,440	52	18,737,135,616
		11	4,718,592	35	13,809,256,704	3	0	19	0	51	0
		10	1,966,080	34	−29,739,824,040	2	0	18	−86,417,520	50	−301,908,492,288
		9	−4,194,304	33	−155,328,255,104	1	0	17	0	49	0
		8	−3,145,728	32	157,058,583,615	0	0	16	224,447,430	48	3,873,651,425,280
		7	0	31	1,263,649,277,952			15	0	47	0
		6	0	30	−301,066,597,648			14	−421,986,160	46	−40,094,935,285,760
		5	0	29	−7,502,268,038,400			13	0	45	0
		4	0	28	−2,440,891,321,464			12	580,113,224	44	337,843,889,111,040
		3	0	27	32,604,315,138,560			11	0	43	0
		2	0	26	25,318,817,961,552			10	−583,700,560	42	−2,331,017,163,571,200
		1	0	25	−103,524,258,893,568			9	0	41	0
		0	0	24	−123,311,080,690,180			8	425,462,940	40	13,209,766,838,927,360
				23	237,736,933,180,416			7	0	39	0
				22	394,216,798,254,480			6	−218,887,920	38	−61,503,043,157,360,640
				21	−382,142,821,520,128			5	0	37	0
				20	−900,143,474,860,728			4	75,436,920	36	234,656,483,109,765,120
				19	384,459,573,742,080			3	0	35	0
				18	1,518,867,106,899,248			2	−15,641,424	34	−72,938,303,710,769,9712
				17	−111,013,896,556,800			1	0	33	0
				16	−1,919,452,896,925,809			0	1,476,225	32	1,828,695,408,465,936,384
				15	−355,750,689,224,704					31	0
				14	1,815,718,389,293,880					30	−3,641,408,101,162,156,032
				13	719,896,206,628,224					29	0
				12	−1,266,265,410,678,540					28	5,624,722,156,190,433,280
				11	−753,880,362,630,912					27	0
				10	626,650,172,863,848					26	−6,496,794,306,202,828,800
				9	517,774,476,424,320					25	0
				8	−200,757,797,644,302					24	5,280,189,088,115,195,904
				7	−241,587,920,079,360					23	0
				6	30,076,757,583,336					22	−2,693,152,577,167,556,608
				5	74,358,227,028,096					21	0
				4	3,814,694,126,820					20	648,518,346,341,351,424
				3	−13,696,722,604,800
				2	−2,434,531,221,000
				1	1,147,912,560,000
				0	313,882,340,625
Spectra of 4-Octahedron
−3.0	−3.0	−1.0	−1.0	−1.0	−1.0
−1.0	1.0	1.0	1.0	3.0	5.0
Spectra of 5-Octahedron
−4.0	−4.0	−2.0	−2.0	−2.0	−2.0
−2.0	−2.0	−2.0	0.0	0.0	0.0
0.0	0.0	0.0	0.0	0.0	2.0
2.0	2.0	2.0	4.0	4.0	6.0
Spectra of 6-Octahedron
−5.0	−5.0	−3.0	−3.0	−3.0	−3.0
−3.0	−3.0	−3.0	−3.0	−3.0	−1.0
−1.0	−1.0	−1.0	−1.0	−1.0	−1.0
−1.0	−1.0	−1.0	−1.0	−1.0	−1.0
−1.0	−1.0	1.0	1.0	1.0	1.0
1.0	1.0	1.0	1.0	1.0	1.0
1.0	1.0	3.0	3.0	3.0	3.0
3.0	3.0	5.0	5.0	5.0	7.0
Spectra of 4-Cube
−4.0	−2.0	−2.0	−2.0	−2.0	−0.0
0.0	0.0	0.0	0.0	0.0	2.0
2.0	2.0	2.0	4.0
Spectra of 5-Cube
−5.0	−3.0	−3.0	−3.0	−3.0	−3.0
−1.0	−1.0	−1.0	−1.0	−1.0	−1.0
−1.0	−1.0	−1.0	−1.0	1.0	1.0
1.0	1.0	1.0	1.0	1.0	1.0
1.0	1.0	3.0	3.0	3.0	3.0
3.0	5.0
Spectra of 6-Cube
−6.0	−4.0	−4.0	−4.0	−4.0	−4.0
−4.0	−2.0	−2.0	−2.0	−2.0	−2.0
−2.0	−2.0	−2.0	−2.0	−2.0	−2.0
−2.0	−2.0	−2.0	−2.0	−0.0	−0.0
−0.0	−0.0	−0.0	−0.0	−0.0	−0.0
−0.0	−0.0	0.0	0.0	0.0	0.0
0.0	0.0	0.0	0.0	0.0	0.0
2.0	2.0	2.0	2.0	2.0	2.0
2.0	2.0	2.0	2.0	2.0	2.0
2.0	2.0	2.0	4.0	4.0	4.0
4.0	4.0	4.0	6.0

shows our computed spectral polynomials of n-cube and n-octahedra for n = 4, 5, 6.

As seen from Table 2, all spectra for the n-octahedra and n-cube are integral-consistent with their symmetry and the regular nature of these n-polyhedra. Furthermore, a few general trends are observed in the spectra. For the n-octahedra, the spectra form an interesting pattern. The 4-octahedron and 5-octhedron exhibit spectral patterns of {−3(2), −1(5), 1(3), 3(1), 5(1)}, and {−4(2), −2(7), 0(8), 2(4),4(2), 6}, suggesting that n-octahedra exhibit even spectra when n is odd, and odd spectra when n is even. Thus, the 6-octahedrom exhibits the spectral pattern {−5(2), −3(9), −1(15), 1(12), 3(6), 5(3), 7(1)}, and so forth. The corresponding spectral pattern of the n-cube follows a binomial distribution that has been discussed in depth before [72].

The spectral polynomials increase in their combinatorial complexity as a function of n for both n-polyhedra, as evidenced from Table 2. The spectral polynomials of n-octahedra exhibit an odd–even alternation (Table 2), as several of the trailing coefficients are zero for the odd n-octahedra, while all coefficients are nonzero for the even n-octahedra. As the starting octahedron contains triangles, the third coefficients of all spectral polynomials of n-octahedra are nonzero. For example, there are 15 triangles in the 4-octahedra, 36 triangles in the 5-octaheron, and 84 triangles in the 6-octahedron, thus they form a sequence {8, 15, 36, 84,…}. Likewise, the next coefficient in the n-octahedra corresponds to the 4-cycles and two disjoint dimers. For example, the 4-octahedron exhibits 42 4-cycles and it can thus be inferred from the coefficient of C₈ = 231 in the spectral polynomial that there are 315 disjoint matchings with four vertices, chosen from the 4-octahedron or 315 disjoint ways to place two disjoint match sticks on the edges of the 4-octahedron.

The spectral polynomials of the n-cubes are also considerably more complex, although their integral spectra form simple binomial distributions. Only the odd n-cubes contain nonzero coefficients, as all of the even n-cubes contain zeroes in their spectra, while the odd n-cubes do not have 0 spectral values. Hence, several trailing coefficients in the spectral polynomials of the even n-cubes are zeroes. As n-cubes contain several square faces, it is evident that the coefficient of the fourth term contains contributions from both the square faces and two disjoint matchings. For example, for the 4-cube, as there are 24 faces which can be deduced from the Coxeter configuration of n-cubes, we obtain the number of ways to place two disjoint dimers on the 4-cube as 400, as inferred from the fourth coefficient in the characteristic polynomial of the 4-cube (352). In general, the number of faces contained in the n-cube is n(n − 1) × 2^{n − 3}. Consequently, we can deduce the numbers of 2-matchings for the 5-cube and 6-cube to be 2840 and 16896 + 6 × 5 × 2⁴ = 17,376, respectively. As seen from Table 2, none of the n-cubes contain cycles of odd lengths, in contrast to the n-octahedra which contain both odd and even cycles as the parent octahedron contains 8 triangles. The coefficients of the constant term in the spectral polynomial of all odd cubes are perfect squares, for example, the constant coefficient of the 5-cube can be expressed as 1215². Thus, the coefficients shown in Table 2 contain combinatorially rich information pertinent to the structural features of the graphs.

Graphs with integral spectra have received particular attention in the mathematical literature, and a few studies have specifically focused on the search for such graphs and the construction of graphs possessing integral or semi-integral spectra [57,83,84]. As such graphs often tend to have high symmetries, especially if they occur with high symmetry, and they can be harnessed in applications that seek high-symmetry structures. There are also other interesting applications of graph spectra to the construction and analysis of the energy spectrum of a non-ideal Bose gas, achieved by introducing graphs comprising rectangles and continuous lines [85]. Although graphs with integral spectra have not found significant application in materials or chemical science, by virtue of many of them being highly symmetric, we expect these graphs to have potential applications in the search of high-symmetry entities.

C.

Spectral Polynomials of Supergiant Fullerenes and Generalized Petersen Graphs

The advent of buckminsterfullerene [44], C₆₀, with an icosahedral symmetry and a closed cage form, has resulted in the further discovery of a plethora of fullerenes, giant and supergiant fullerenes, carbon nanotubes [45], and nanospheres of high symmetry. These structures are actively being investigated by experimental and theoretical researchers for their intriguing material and chemical properties [42,43,44,45,46,47,48,49,50,51,52]. There are several combinatorial and graph theoretical techniques that can make very valuable contributions to enhancing our understanding of these molecular structures. Stimulated by such studies, we devote this section to the spectra and spectral polynomials of these structures, as well as to the generalized Petersen graphs, which have been the subject matter of numerous graph–theoretical studies [75,76].

Figure 3 shows two fullerenes, both with icosahedral symmetry; one belongs to the class of golden giant fullerenes of the formula C_60n², with C₆₀ buckminsterfullerene [44] being the first member of the series. The second one is C₈₀, also with the icosahedral symmetry. The spectral polynomials of these two structures have not been previously obtained; furthermore, their spherical structure types, both with 12 pentagons, make them perfect candidates for the present study.

Table 3. Spectral (characteristic) polynomials and spectra of C₂₄₀, golden fullerene, and C₈₀, both with I_h symmetry.

Supergiant Fullerene C240: Ih Symmetry			Fullerene C80: Ih Symmetry
k	C240-k		k	C80-k
240	1		80	1
239	0		79	−0
238	−360		78	−120
237	0		77	−0
236	63,900		76	6,900
235	−24		75	−24
234	−7,455,700		74	−253,220
233	8,400		73	2,640
232	643,238,070		72	6,665,250
231	−1,449,240		71	−138,840
230	−43,765,604,316		70	−134,074,668
229	164,318,400		69	4,649,280
228	2445,983,522,150		68	2,144,400,610
227	−13,772,791,440		67	−111,390,840
226	−115,483,543,870,380		66	−28,014,828,600
225	910,181,939,872		65	2,034,173,640
224	4,701,527,059,529,265		64	304,771,472,295
223	−49,395,215,227,920		63	−29,454,679,080
222	−167,648,707,691,087,420		62	−2,800,871,913,120
221	2,264,002,673,490,240		61	347,355,807,000
220	5,300,892,235,419,864,426		60	21,982,913,536,506
219	−89,455,905,039,333,480		59	−3,400,629,844,080
218	−150,106,442,753,314,932,360		58	−148,597,115,610,060
217	3,095,063,861,360,503,920		57	28,032,598,630,800
216	3,837,990,865,403,514,684,635		56	870,782,603,143,245
215	−94,929,696,941,052,350,832		55	−196,675,986,598,104
214	−89,214,815,606,936,913,307,740		54	−4,446,095,763,848,880
213	2,606,866,654,781,819,504,840		53	1,184,149,280,392,400
212	1,896,368,878,405,224,684,770,400		52	19,855,655,662,646,790
211	−64,620,553,360,631,460,336,960		51	−6,157,335,886,362,960
210	−37,044,948,371,954,529,056,063,656		50	−77,775,412,124,784,276
209	1,455,895,045,330,922,474,674,320		49	27,786,279,810,761,760
208	667,936,566,937,916,468,417,641,050		48	267,713,181,302,978,565
207	−29,986,069,149,330,479,067,914,440		47	−109,222,881,940,156,720
206	−11,157,980,465,768,328,477,435,561,180		46	−810,610,645,577,880,600
205	567,420,196,254,073,164,997,202,232		45	374,966,869,205,421,336
204	173,272,188,234,359,680,778,390,285,010		44	2,159,504,514,172,334,900
203	−9,907,490,766,609,936,176,882,434,560		43	−1,126,235,220,601,566,120
202	−2,508,706,834,146,599,915,120,612,739,600		42	−5,058,329,868,205,795,680
201	160,228,001,555,018,310,378,540,341,040		41	2,962,294,863,144,099,920
200	33,954,306,934,029,341,067,084,013,161,996		40	10,401,040,837,191,228,618
199	−2,408,107,366,425,017,858,165,622,286,560		39	−6,824,327,055,789,596,280
198	−430,617,032,155,529,976,402,418,565,888,418		38	−18,723,827,983,032,022,240
197	33,733,309,861,467,028,170,339,491,094,360		37	13,761,319,627,538,589,720
196	5,128,190,205,096,393,871,427,396,075,601,794		36	29,389,984,702,098,348,120
195	−441,602,915,472,953,441,053,236,800,435,968		35	−24,256,112,112,485,663,584
194	−57,457,939,438,911,746,894,371,388,726,145,160		34	−39,987,774,847,141,119,240
193	5,415,272,424,948,212,577,371,671,947,088,195		33	37,287,514,249,778,822,040
192	606,747,145,859,062,755,972,596,777,547,121,216		32	46,754,900,712,550,670,195
191	−62,337,209,301,203,951,387,803,680,398,611,184		31	−49,829,511,883,061,754,120
190	−6.048221186670528995008469688407721 × 1036		30	−46,365,386,945,168,044,056
189	6.74912600115078522823923911813332 × 1035		29	57,635,855,484,766,164,320
188	5.699540039759760361514507167613912 × 1037		28	38,163,065,106,847,280,460
187	−6.884583524982830022301898752320899 × 1036		27	−57,367,377,814,733,742,720
186	−5841734623839887376439698725423304 × 1038		26	−25,028,715,850,369,172,460
185	6.627142032028232385508691182230046 × 1037		25	48,761,446,947,388,280,472
184	4.2983064355992869496309485626364736 × 1039		24	11,836,058,202,682,257,720
183	−628668554149521028367699179934285 × 1038		23	−35,032,832,823,083,608,120
182	−3.44790786602597840263375583644471 × 1040		22	−2,546,201,709,135,643,740
181	5.1896410873880857187239934664719776 × 1039		21	20,976,283,634,720,851,080
180	2.626884237337310961834946860618086 × 1041		20	−1,729,379,075,500,688,166
179	−4.232531280244278624723071801119075 × 1040		19	−10,255,337,938,895,367,360
178	−1.9026703048880961127625771343127042 × 1042		18	2,388,847,093,968,947,640
177	3.274107113301917807776400399677189 × 1041		17	3,963,782,111,401,409,320
176	1.3112983988222523472609017774452832 × 1043		16	−1,568,049,183,041,116,425
175	−2.4046912924293780571314609164157965 × 1042		15	−1,141,429,955,133,602,688
174	−8.606042251846876681048515170294774 × 1043		14	696,942,492,398,230,080
173	1.6784484961723877612599983253829556 × 1043		13	211,387,203,870,296,880
172	5.3825845751316303370481341944343536 × 1044		12	−219,949,319,166,357,690
171	−1.114333623087190923789821800463615 × 1044		11	−9,893,398,173,518,960
170	−3.2104081045968696155099365191591615 × 1045		10	47,809,319,577,549,300
…	…		9	−7,196,177,291,756,040
…	…		8	−6,355,394,133,712,305
0	4.7272376508569497895171096411125664 × 1030		7	2,265,666,348,699,840
			6	307,052,294,351,520
			5	−293,140,993,064,048
			4	36,331,138,153,170
			3	11,793,686,090,760
			2	−4,491,814,487,580
			1	581,319,267,480
			0	−28,012,848,759
Spectra of Supergiant Golden Fullerene C240 (Ih)
−2.883504	−2.883504	−2.883504	−2.867285	−2.867285	−2.867285
−2.867285	−2.703937	−2.703937	−2.703937	−2.703937	−2.592337
−2.592337	−2.592337	−2.592337	−2.592337	−2.444550	−2.444550
−2.444550	−2.420027	−2.420027	−2.420027	−2.420027	−2.420027
−2.306530	−2.306530	−2.306530	−2.149180	−2.149180	−2.149180
−2.149180	−2.149180	−2.067984	−2.067984	−2.067984	−2.067984
−2.025797	−2.025797	−2.025797	−2.000000	−1.810855	−1.810855
−1.810855	−1.810855	−1.784087	−1.784087	−1.784087	−1.784087
−1.784087	−1.740291	−1.740291	−1.740291	−1.687162	−1.687162
−1.687162	−1.621105	−1.621105	−1.621105	−1.433222	−1.433222
−1.433222	−1.433222	−1.373319	−1.373319	−1.373319	−1.373319
−1.373319	−1.356691	−1.356691	−1.356691	−1.356691	−1.356691
−1.257513	−1.257513	−1.257513	−1.257513	−1.207321	−1.207321
−1.207321	−1.207321	−1.207321	−1.062685	−1.062685	−1.062685
−1.041813	−1.041813	−1.041813	−1.000000	−1.000000	−1.000000
−1.000000	−1.000000	−1.000000	−1.000000	−1.000000	−1.000000
−1.000000	−0.924454	−0.924454	−0.924454	−0.812907	−0.812907
−0.812907	−0.812907	−0.673649	−0.673649	−0.673649	−0.673649
−0.673649	−0.583190	−0.583190	−0.583190	−0.583190	−0.583190
−0.120318	−0.120318	−0.120318	−0.059657	−0.059657	−0.059657
0.436773	0.436773	0.436773	0.436773	0.436773	0.535260
0.535260	0.535260	0.535260	0.535260	0.634142	0.634142
0.634142	0.634142	0.795960	0.795960	0.795960	0.795960
0.807945	0.807945	0.807945	0.881840	0.881840	0.881840
0.908763	0.908763	0.908763	0.908763	0.908763	1.000000
1.000000	1.000000	1.000000	1.000000	1.000000	1.000000
1.000000	1.000000	1.000000	1.178291	1.178291	1.178291
1.178291	1.178291	1.187699	1.187699	1.187699	1.187699
1.239628	1.239628	1.239628	1.298090	1.298090	1.298090
1.298090	1.298090	1.503117	1.503117	1.503117	1.503117
1.521385	1.521385	1.521385	1.521385	1.521385	1.556133
1.556133	1.556133	1.611066	1.611066	1.611066	1.815577
1.815577	1.815577	1.815577	1.850203	1.850203	1.850203
1.866030	1.866030	1.866030	1.866030	1.866030	2.000000
2.128884	2.128884	2.128884	2.128884	2.128884	2.142063
2.142063	2.142063	2.215507	2.215507	2.215507	2.392017
2.392017	2.392017	2.392017	2.445125	2.445125	2.445125
2.445125	2.445125	2.625191	2.625191	2.625191	2.625191
2.673879	2.673879	2.673879	2.821200	2.821200	2.821200
2.821200	2.821200	2.939600	2.939600	2.939600	3.000000
Spectra of Icosahedral Fullerene C80 (Ih)
−2.699315	−2.699315	−2.699315	−2.651093	−2.651093	−2.651093
−2.651093	−2.198691	−2.198691	−2.198691	−2.198691	−1.935432
−1.935432	−1.935432	−1.935432	−1.935432	−1.618034	−1.618034
−1.618034	−1.618034	−1.618034	−1.618034	−1.618034	−1.618034
−1.200081	−1.200081	−1.200081	−1.0	−1.0	−1.0
−1.0	−1.0	−1.0	−0.713538	−0.713538	−0.713538
−0.713538	0.273891	0.273891	0.273891	0.273891	0.618034
0.618034	0.618034	0.618034	0.618034	0.618034	0.618034
0.618034	1.0	1.0	1.0	1.0	1.0
1.0	1.377203	1.377203	1.377203	1.377203	1.462598
1.462598	1.462598	1.462598	1.462598	1.912229	1.912229
1.912229	1.912229	281281	281281	281281	2.472834
2.472834	2.472834	2.472834	2.472834	2.818115	2.818115
2.818115	3.0

shows the spectral polynomials and spectra of the two icosahedral fullerenes shown in Figure 3. As a result of the large number of coefficients that grow in astronomical proportions, we show only the first few coefficients for the spectral polynomial of C₂₄₀, while all coefficients of the spectral polynomial of C₈₀ are explicitly shown in Table 3. As both graphs are not bipartite and as they contain 12 isolated pentagons, the spectral polynomials contain nonzero odd coefficients. The coefficients of the third term yield the number of edges, while the fifth term corresponds to contributions from the 4-cycles and 2-matchings (two disjoint dimers) in the graph. As there are no 4-cycles in either of the structures, the number of 2-matchings of C₂₄₀ and C₈₀ are 63,900 and 6900, respectively. The next coefficient yields twice the number of pentagons present in the structures, and as both structures have 12 pentagons, these coefficients are 24 in both the spectral polynomials. Subsequent coefficients become more complex, for example, the 7th term is composed of hexagons and 3-matchings as there are no 4-cycles. The number of hexagons in any fullerene (which always has 12 pentagons) can be deduced by Euler’s rule as (n-20)/2, where n is the number of vertices. Thus, we have 110 hexagons in C₂₄₀ and 30 hexagons in C_80. Consequently, the number of 3-matchings in C₈₀ can be deduced from the coefficient, with the C₇₄ of the C₈₀ fullerene being 253,160. Likewise, as there are 110 hexagons in C₂₄₀, we infer from the coefficient C₂₃₄ of the spectral polynomial that the number of 3-matchings in C₂₄₀ is 7,455,480, a result not known until now. The constant coefficient is independently corroborated by computing the product of the spectral values shown in Table 3 for the two structures. The degeneracy of the various spectral values in Table 3 is consistent with the I_h symmetry, and as both graphs are trivalent, we have 3.0 as the highest eigenvalue in the spectra.

As a final set of graphs, we consider those of Archimedean (C₁₂₀) with I_h symmetry, as shown in Figure 4. Unlike fullerenes, the C₁₂₀ Archimedean cage structure does not contain pentagons; instead, we have hexagons, squares, and decagons. The presence of 4-membered rings in the structure lends less stability compared to the corresponding fullerenes or the dimer of C₆₀. Yet, there has been interest in the pursuit of the structure shown in Figure 4.

We have included a generalized Petersen graph G(60,3) for comparison, with the same number of vertices as Archimedean C₁₂₀. The G(60,3) graph is bipartite as k = 3 is odd, and the C₁₂₀ cage with I_h symmetry is also bipartite. Both are cubic graphs and hence they present good comparative structures for the spectral polynomials, even though there are many differences between the two graphs. In Figure 5, we show the computer-generated adjacency matrix of the G(60,3) generalized Petersen graph. We note that the Archimedean structure deviates from fullerenes in not only in the absence of pentagons but also by virtue of being bipartite.

Table 4. Spectral polynomial and spectra of G(60,3) and Archimedean C₁₂₀; both are cubic and contain n = 120 vertices.

G(60,3)—All Odd Coefs Are Zero Only Even Coefs Are Shown			Archimedene C120 Ih
k	Cb-k		Cn-k
120	1		1
118	−180		−180
116	15,750		15,690
114	−892,860		−882,460
112	36,876,345		36,002,715
110	−1,183,071,096		−1,135,676,880
108	30,697,459,620		28,830,540,620
106	−662,294,994,720		605,370,867,120
104	12,122,712,447,420		10,724,090,893,725
102	−191,146,403,259,680		−162,682,223,973,660
100	2,627,342,156,012,562		2,137,824,997,367,262
98	−31,781,816,819,028,000		−24,559,722,045,606,780
96	340,965,242,569,443,770		248,476,237,317,489,919
94	−3,264,986,310,221,207,160		−2,227,172,552,007,275,639
92	28,054,594,391,644,991,610		17,773,081,766,605,412,040
90	−217,281,600,535,414,573,160		−126,785,990,833,562,201,901
88	1,522,597,140,765,638,802,780		811,214,030,007,340,751,802
86	−9,684,792,477,464,440,484,880		−4,668,308,290,447,788,760,611
84	56,070,178,428,467,218,064,830		24,217,880,944,735,623,869,286
82	−296,160,109,890,416,361,428,760		−11,346,917,356,303,897,063,139
80	1,430,008,713,073,408,819,374,015		480,886,446,025,397,096,756,536
78	−6,322,658,765,178,971,561,833,460		−1,845,667,128,265,467,014,180,368
76	25,634,415,237,650,811,338,783,790		6,421,197,446,225,090,384,763,177
74	−95,415,256,746,818,787,811,819,500		−20,264,333,185,513,523,340,033,948
72	326,358,788,644,990,105,475,935,560		58,037,942,867,756,242,524,535,748
70	−1,026,550,222,361,385,631,900,698,756		−150,897,704,088,219,599,214,664,480
68	2,971,083,522,023,498,075,620,793,850		356,203,198,431,727,918,898,852,579
66	−7,915,244,885,046,631,268,351,837,700		−763,386,163,922,575,136,997,166,481
64	19,414,214,933,695,045,040,860,422,315		1,485,072,345,968,873,883,971,819,917
62	−43,843,051,820,752,972,910,346,678,720		−2,621,662,455,033,825,652,650,138,049
60	91,149,903,160,281,097,618,182,429,904		4,198,049,320,217,010,824,338,368,942
58	−174,407,398,329,673,957,422,500,193,480		−6,094,310,658,772,104,625,950,326,473
56	306,997,303,344,994,767,604,833,350,865		8,015,348,715,315,034,977,772,825,607
54	−496,821,074,662,257,075,415,252,129,260		−9,543,437,842,639,635,315,518,318,973
52	738,618,693,971,750,466,919,056,091,500		1.027739682936630734700449256×1028
50	−1,007,800,557,988,460,823,587,457,781,068		−1.000028973818866162960590646×1028
48	1,260,540,542,432,930,681,069,386,712,300		8,781,884,478,265,548,931,050,238,250
46	−1,443,340,157,403,216,035,993,067,030,060		−6,950,813,776,786,441,008,698,586,201
44	1,510,466,448,053,717,869,780,001,900,430		4,951,169,673,130,384,907,223,135,336
42	−1,442,026,246,599,052,952,378,971,479,380		−3,168,616,508,417,229,180,219,494,941
40	1,253,196,204,279,457,770,381,146,932,305		1,818,395,639,160,030,392,431,910,492
38	−988,943,111,078,689,399,839,434,418,960		−933,722,074,986,794,748,257,541,866
36	706,626,962,932,350,094,618,120,735,490		427,936,739,631,884,433,905,609,166
34	−455,667,663,241,511,840,138,930,828,880		−174,559,200,434,963,752,237,231,269
32	264,178,558,483,371,293,785,696,421,190		63,167,679,119,015,442,272,490,183
30	−137,097,377,892,211,849,514,626,681,408		−20,202,702,500,850,294,524,063,193
28	63,360,615,577,689,007,821,823,287,330		5,685,948,285,290,922,542,550,711
26	−25,921,535,062,352,622,278,618,137,560		−1,401,137,114,127,009,299,874,253
24	9,321,131,766,342,541,097,932,696,205		300,515,209,314,416,465,229,072
22	−2,921,155,890,212,282,221,257,004,020		−55,706,952,143,363,900,167,310
20	789,674,303,777,263,666,519,980,294		8,850,309,146,844,763,155,406
18	−181,817,382,076,098,654,444,319,620		-I,192,863,242,058,215,039,057
16	35,088,808,404,272,449,157,332,545		134,700,818,861,930,470,640
14	−5,559,522,299,955,307,222,951,320		−12,545,905,215,362,926,146
12	703,240,714,219,584,001,807,760		944,752,313,686,677,771
10	−68,254,034,915,538,778,780,032		−56,038,624,208,633,088
8	4,782,522,709,793,521,720,320		2,527,779,421,175,040
6	−217,682,509,196,494,551,040		−82,532,952,345,600
4	5,118,895,223,567,585,280		1,811,566,632,960
2	−24,777,598,446,305,280		−23,581,808,640
0	33,790,875,992,064		136,048,896
Spectra of Generalized Petersen Graph G(60,3)
−3.000000	−2.946523	−2.946523	−2.801366	−2.801366	−2.602781
−2.602781	−2.391089	−2.391089	−2.302776	−2.302776	−2.230618
−2.230618	−2.198492	−2.198492	−2.188901	−2.188901	−2.000000
−2.000000	−2.000000	−2.000000	−1.924521	−1.924521	−1.820104
−1.820104	−1.657815	−1.657815	−1.644748	−1.644748	−1.509385
−1.509385	−1.471949	−1.471949	−1.302776	−1.302776	−1.286625
−1.286625	−1.141979	−1.141979	−1.000000	−1.000000	−1.000000
−1.000000	−1.000000	−1.000000	−1.000000	−0.944634	−0.944634
−0.898068	−0.898068	−0.877648	−0.877648	−0.772963	−0.772963
−0.474903	−0.474903	−0.456850	−0.456850	−0.054036	−0.054036
0.054036	0.054036	0.456850	0.456850	0.474903	0.474903
0.772963	0.772963	0.877648	0.877648	0.898068	0.898068
0.944634	0.944634	1.000000	1.000000	1.000000	1.000000
1.000000	1.000000	1.000000	1.141979	1.141979	1.286625
1.286625	1.302776	1.302776	1.471949	1.471949	1.509385
1.509385	1.644748	1.644748	1.657815	1.657815	1.820104
1.820104	1.924521	1.924521	2.000000	2.000000	2.000000
2.000000	2.188901	2.188901	2.198492	2.198492	2.230618
2.230618	2.302776	2.302776	2.391089	2.391089	2.602781
2.602781	2.801366	2.801366	2.946523	2.946523	3.000000
Spectra of Archimedene C120 (Ih)
−3.00000	−2.90210	−2.90210	−2.90210	−2.72140	−2.72140
−2.72140	−2.72140	−2.72140	−2.54502	−2.54502	−2.54502
−2.54502	−2.17561	−2.17561	−2.17561	−2.15420	−2.15420
−2.15420	−2.15420	−1.88840	−1.88840	−1.88840	−1.88840
−1.88840	−1.82800	−1.82800	−1.82800	−1.82800	−1.82800
−1.00000	−1.00000	−1.00000	−1.00000	−1.00000	−1.00000
−0.90210	−0.90210	−0.90210	−0.83021	−0.83021	−0.83021
−0.83021	−0.68460	−0.68460	−0.68460	−0.68460	−0.68460
−0.46641	−0.46641	−0.46641	−0.46641	−0.46641	−0.43940
−0.43940	−0.43940	−0.43940	−0.17561	−0.17561	−0.17561
0.17561	0.17561	0.17561	0.43940	0.43940	0.43940
0.43940	0.46641	0.46641	0.46641	0.46641	0.46641
0.68460	0.68460	0.68460	0.68460	0.68460	0.83021
0.83021	0.83021	0.83021	0.90210	0.90210	0.90210
1.00000	1.00000	1.00000	1.00000	1.00000	1.00000
1.82800	1.82800	1.82800	1.82800	1.82800	1.88840
1.88840	1.88840	1.88840	1.88840	2.15420	2.15420
2.15420	2.15420	2.17561	2.17561	2.17561	2.54502
2.54502	2.54502	2.54502	2.72140	2.72140	2.72140
2.72140	2.72140	2.90210	2.90210	2.90210	3.00000

juxtaposes the spectral polynomials of the two graphs with the same number of vertices and edges, and both with the same regular cubic connectivity. As both graphs are bipartite, we have shown only the coefficients of the even terms in Table 4, as all the odd terms are zero. As we descend through Table 4, we find that the spectral differences between the two graphs becomes more pronounced towards the tail end of the spectral polynomials. The contrast becomes extremely accentuated for the constant coefficients, which are 33,790,875,992,064 and 136,048,896, respectively, for the two structures. Thus, the overall connectivities of the two structures are dramatically contrasted at the tail end and mid points of the spectral polynomials. The spectra of the two structures (Table 4) exhibit a high degree of degeneracies, consistent with the high symmetries inherent to the automorphism groups of the two structures. The products of the spectra yield the constant coefficients in the spectral polynomials of the two structures. We can also obtain some matchings from the coefficients. For example, the 2-matchings in G(60,3) are given by the third coefficient in the spectral polynomial or 15,750, as there are no 4-cycles in G(60,3).

Table 5. Spectral polynomial and spectra of generalized Petersen graph G(360,19), n = 720 ^a.

Spectral Polynomial of Generalized Petersen Graph G(360,19)
K		Cn-k
720		1
718		−1080
716		580,500
714		−207,046,440
712		55,127,270,610
710		−11,687,473,970,856
708		2,055,192,601,955,220
706		−308,311,704,981,633,240
704		40,279,248,752,112,449,415
702		−4,655,425,300,557,056,838,960
700		481,961,518,974,263,346,274,728
698		−45,143,834,567,423,768,973,556,560
696		3,857,580,142,194,956,808,063,882,900
694		−3,028,178,938,227,920,486,720,376,156,005
692		21,966,898,016,471,960,685,886,317,562,680
690		−1,480,100,147,994,601,999,836,922,582,716,650
688		93,041,387,533,636,155,387,504,144,396,818,912
…		…
11		0
….
0		0
Spectra of Generalized Petersen Graph G(360,19)
−3.000000	−2.946841	−2.946841	−2.946841	−2.946841	−2.902113
−2.902113	−2.879385	−2.879385	−2.809498	−2.809498	−2.809498
−2.809498	−2.767294	−2.767294	−2.767294	−2.767294	−2.722888
−2.722888	−2.722888	−2.722888	−2.641498	−2.641498	−2.641498
−2.641498	−2.618034	−2.618034	−2.598258	−2.598258	−2.598258
−2.598258	−2.533123	−2.533123	−2.533123	−2.533123	−2.532089
−2.532089	−2.492879	−2.492879	−2.492879	−2.492879	−2.449490
−2.449490	−2.449490	−2.449490	−2.422441	−2.422441	−2.422441
−2.422441	−2.383369	−2.383369	−2.383369	−2.383369	−2.363567
−2.363567	−2.363567	−2.363567	−2.343352	−2.343352	−2.343352
−2.343352	−2.309275	−2.309275	−2.309275	−2.309275	−2.298068
−2.298068	−2.298068	−2.298068	−2.275827	−2.275827	−2.275827
−2.275827	−2.260958	−2.260958	−2.260958	−2.260958	−2.247589
−2.247589	−2.247589	−2.247589	−2.236068	−2.236068	−2.236068
−2.236068	−2.236068	−2.236068	−2.236068	−2.236068	−2.230746
−2.230746	−2.230746	−2.230746	−2.215479	−2.215479	−2.215479
−2.215479	−2.214072	−2.214072	−2.214072	−2.214072	−2.208933
−2.208933	−2.208933	−2.208933	−2.175571	−2.175571	−2.146832
−2.146832	−2.146832	−2.146832	−2.125697	−2.125697	−2.125697
−2.125697	−2.085383	−2.085383	−2.085383	−2.085383	−2.085285
−2.085285	−2.085285	−2.085285	−2.052962	−2.052962	−2.052962
−2.052962	−2.043421	−2.043421	−2.043421	−2.043421	−2.016105
−2.016105	−2.016105	−2.016105	−2.014904	−2.014904	−2.014904
−2.014904	−2.001464	−2.001464	−2.001464	−2.001464	−2.000000
−2.000000	−2.000000	−2.000000	−2.000000	−2.000000	−1.940970
−1.940970	−1.940970	−1.940970	−1.924015	−1.924015	−1.924015
−1.924015	−1.810771	−1.810771	−1.810771	−1.810771	−1.773754
−1.773754	−1.773754	−1.773754	−1.732051	−1.732051	−1.732051
−1.732051	−1.717941	−1.717941	−1.717941	−1.717941	−1.677111
−1.677111	−1.677111	−1.677111	−1.676487	−1.676487	−1.676487
−1.676487	−1.639862	−1.639862	−1.639862	−1.639862	−1.628712
−1.628712	−1.628712	−1.628712	−1.618034	−1.618034	−1.618034
−1.618034	−1.618034	−1.618034	−1.612687	−1.612687	−1.612687
−1.612687	−1.500960	−1.500960	−1.500960	−1.500960	−1.365312
−1.365312	−1.365312	−1.365312	−1.350714	−1.350714	−1.350714
−1.350714	−1.347296	−1.347296	−1.248834	−1.248834	−1.248834
−1.248834	−1.211574	−1.211574	−1.211574	−1.211574	−1.179453
−1.179453	−1.179453	−1.179453	−1.134582	−1.134582	−1.134582
−1.134582	−1.133704	−1.133704	−1.133704	−1.133704	−1.108549
−1.108549	−1.108549	−1.108549	−1.106079	−1.106079	−1.106079
−1.106079	−1.047801	−1.047801	−1.047801	−1.047801	−1.000000
−1.000000	−1.000000	−0.943892	−0.943892	−0.943892	−0.943892
−0.902113	−0.902113	−0.879385	−0.879385	−0.840363	−0.840363
−0.840363	−0.840363	−0.765305	−0.765305	−0.765305	−0.765305
−0.749080	−0.749080	−0.749080	−0.749080	−0.742587	−0.742587
−0.742587	−0.742587	−0.705046	−0.705046	−0.705046	−0.705046
−0.698564	−0.698564	−0.698564	−0.698564	−0.652704	−0.652704
−0.618034	−0.618034	−0.618034	−0.618034	−0.618034	−0.618034
−0.612230	−0.612230	−0.612230	−0.612230	−0.565291	−0.565291
−0.565291	−0.565291	−0.553028	−0.553028	−0.553028	−0.553028
−0.542273	−0.542273	−0.542273	−0.542273	−0.532089	−0.532089
−0.445039	−0.445039	−0.445039	−0.445039	−0.442652	−0.442652
−0.442652	−0.442652	−0.381966	−0.381966	−0.381083	−0.381083
−0.381083	−0.381083	−0.366704	−0.366704	−0.366704	−0.366704
−0.363016	−0.363016	−0.363016	−0.363016	−0.241427	−0.241427
−0.241427	−0.241427	−0.183172	−0.183172	−0.183172	−0.183172
−0.175571	−0.175571	−0.152597	−0.152597	−0.152597	−0.152597
−0.072655	−0.072655	−0.072655	−0.072655	−0.038239	−0.038239
−0.038239	−0.038239	−0.013907	−0.013907	−0.013907	−0.013907
−0.000000	−0.000000	−0.000000	−0.000000	−0.000000	−0.000000
0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
0.013907	0.013907	0.013907	0.013907	0.038239	0.038239
0.038239	0.038239	0.072655	0.072655	0.072655	0.072655
0.152597	0.152597	0.152597	0.152597	0.175571	0.175571
0.183172	0.183172	0.183172	0.183172	0.241427	0.241427
0.241427	0.241427	0.363016	0.363016	0.363016	0.363016
0.366704	0.366704	0.366704	0.366704	0.381083	0.381083
0.381083	0.381083	0.381966	0.381966	0.442652	0.442652
0.442652	0.442652	0.445039	0.445039	0.445039	0.445039
0.532089	0.532089	0.542273	0.542273	0.542273	0.542273
0.553028	0.553028	0.553028	0.553028	0.565291	0.565291
0.565291	0.565291	0.612230	0.612230	0.612230	0.612230
0.618034	0.618034	0.618034	0.618034	0.618034	0.618034
0.652704	0.652704	0.698564	0.698564	0.698564	0.698564
0.705046	0.705046	0.705046	0.705046	0.742587	0.742587
0.742587	0.742587	0.749080	0.749080	0.749080	0.749080
0.765305	0.765305	0.765305	0.765305	0.840363	0.840363
0.840363	0.840363	0.879385	0.879385	0.902113	0.902113
0.943892	0.943892	0.943892	0.943892	1.000000	1.000000
1.000000	1.047801	1.047801	1.047801	1.047801	1.106079
1.106079	1.106079	1.106079	1.108549	1.108549	1.108549
1.108549	1.133704	1.133704	1.133704	1.133704	1.134582
1.134582	1.134582	1.134582	1.179453	1.179453	1.179453
1.179453	1.211574	1.211574	1.211574	1.211574	1.248834
1.248834	1.248834	1.248834	1.347296	1.347296	1.350714
1.350714	1.350714	1.350714	1.365312	1.365312	1.365312
1.365312	1.500960	1.500960	1.500960	1.500960	1.612687
1.612687	1.612687	1.612687	1.618034	1.618034	1.618034
1.618034	1.618034	1.618034	1.628712	1.628712	1.628712
1.628712	1.639862	1.639862	1.639862	1.639862	1.676487
1.676487	1.676487	1.676487	1.677111	1.677111	1.677111
1.677111	1.717941	1.717941	1.717941	1.717941	1.732051
1.732051	1.732051	1.732051	1.773754	1.773754	1.773754
1.773754	1.810771	1.810771	1.810771	1.810771	1.924015
1.924015	1.924015	1.924015	1.940970	1.940970	1.940970
1.940970	2.000000	2.000000	2.000000	2.000000	2.000000
2.000000	2.001464	2.001464	2.001464	2.001464	2.014904
2.014904	2.014904	2.014904	2.016105	2.016105	2.016105
2.016105	2.043421	2.043421	2.043421	2.043421	2.052962
2.052962	2.052962	2.052962	2.085285	2.085285	2.085285
2.085285	2.085383	2.085383	2.085383	2.085383	2.125697
2.125697	2.125697	2.125697	2.146832	2.146832	2.146832
2.146832	2.175571	2.175571	2.208933	2.208933	2.208933
2.208933	2.214072	2.214072	2.214072	2.214072	2.215479
2.215479	2.215479	2.215479	2.230746	2.230746	2.230746
2.230746	2.236068	2.236068	2.236068	2.236068	2.236068
2.236068	2.236068	2.236068	2.247589	2.247589	2.247589
2.247589	2.260958	2.260958	2.260958	2.260958	2.275827
2.275827	2.275827	2.275827	2.298068	2.298068	2.298068
2.298068	2.309275	2.309275	2.309275	2.309275	2.343352
2.343352	2.343352	2.343352	2.363567	2.363567	2.363567
2.363567	2.383369	2.383369	2.383369	2.383369	2.422441
2.422441	2.422441	2.422441	2.449490	2.449490	2.449490
2.449490	2.492879	2.492879	2.492879	2.492879	2.532089
2.532089	2.533123	2.533123	2.533123	2.533123	2.598258
2.598258	2.598258	2.598258	2.618034	2.618034	2.641498
2.641498	2.641498	2.641498	2.722888	2.722888	2.722888
2.722888	2.767294	2.767294	2.767294	2.767294	2.809498
2.809498	2.809498	2.809498	2.879385	2.879385	2.902113
2.902113	2.946841	2.946841	2.946841	2.946841	3.000000

^a Only the first few coefficients and the constant term are shown.

shows the spectral polynomial and spectra of the generalized Petersen graph G(360,19) containing 720 vertices. The graph is interesting because 19² modulo(360) is 1 and hence the graph is both vertex-transitive and bipartite. We have shown only the first few coefficients in the spectral polynomial, although the entire computed spectra are shown in the second part of Table 5. As seen from Table 5, there are 1080 edges in the G(360,19) graph, with the next coefficient offering the number of 2-matchings as 580,500 since there are no 4-cycles in the graph. The coefficients ascend rapidly, as seen in Table 5, and for this reason only the first few coefficients are shown in Table 5. The spectra exhibit a perfect mirror symmetry as expected for a bipartite graph, with ±3 as the leading and trailing roots consistent with the cubic graph. The constant coefficient is zero for G(360,13), as there are 12 zero eigenvalues in the spectra of the graph. Moreover, as seen from Table 5, the number of 3-matchings in the generalized Petersen graph G(360,19) is 207,046,440 as there are no 4-cycles and 6-cycles in the graph. Consequently, spectral polynomials of even such large graphs contain useful information pertinent to the structure and connectivity of the graph.

It should be pointed out that the spectral polynomials of graphs are generators of several orthogonal polynomials. For example, the spectral polynomials of path graphs, P_n, and cycle graphs, Cn, generate the Chebyshev polynomials of the first and second kinds. As this topic has been visited elsewhere [86], we shall not repeat all of the nuances pertinent to orthogonal polynomials and spectral polynomials. Moreover, the spectra and spectral polynomials of many graphs of recursive nature such as fans, wheels, Bethe lattices, cactus graph, etc., form interesting patterns.

There are several applications of graph spectra to many areas besides chemistry and materials science. For example, a recent study applied spectral graph theory for the prediction of degenerative neurological diseases such as Alzheimer’s disease [87]. In this application, the authors exploited the concept of spectral graph convolutions to obtain building blocks for graph neural network models, thereby facilitating important applications to autism and neurodegenerative Alzheimer’s disease [87]. Graph spectra have also been applied to brain networks through metric learning of spectral graph convolutions [88]. Graph spectra were recently applied to spectral-based clustering [89] in order to improve the efficiency of such techniques. Consequently, spectral graph theory should have applications in the merging areas of machine learning, big data, and artificial intelligence. We expect such topics to be the subject matter of future research in this growing and promising area.

Spectral polynomials and graph spectra offer powerful structural descriptors when other techniques based on vertex degrees or distances may fail to discriminate the structures. This is especially the case for highly regular graphs possessing high orders of automorphism groups, such as the ones considered in this study. Graph energies derived from spectra and graph spectral-based entropies have been shown to be powerful structural quantifiers [90]. The related Reimann zeta functions derived from graph spectra offer yet another set of structural quantifiers [90]. Given the emerging applications of graph spectra to neural networks and brain networks, many more applications of these techniques are expected to appear in the near future. The only known disadvantage of using graph spectra as structural quantifies is that there exist two non-isomorphic graphs with the same graph spectra [91], called isospectral graphs. However, this deficiency can be overcome by the introduction of orthogonal parameters, as shown in [91].

4. Conclusions

In the current study, we computed several spectra and spectral polynomials of many symmetric, twisted, and semi-symmetric graphs, and n-polyhedra, such as n-octahedra and n-cubes. Moreover, the spectra and spectral polynomials of giant fullerene cages of icosahedral symmetries and generalized Petersen graphs up to 720 vertices were computed. We also discussed the rich combinatorial and structural information contained in the coefficients of the spectral polynomials of these graphs. It was shown that many of these graphs exhibited very interesting combinatorial patters. The spectral polynomials and their spectra would find several applications in quantitative similarity measures, aromaticity measures, and as generating functions for a number of combinatorial problems. Moreover, it is anticipated that future applications of these polynomials could be applied to several areas such as dynamic stereochemistry, twisted topologies, Möbius molecules, relativistic quantum chemistry, machine learning, neural networks, and artificial intelligence. Furthermore, spectra and spectral polynomials are fundamental to the characterization of nanospheres, nanomaterials, nanotubes, covalent organic frameworks, and metal–organic framework—all of which exhibit multiple topologies and varied complexities, thus necessitating developments in combinatorial and graph theoretical techniques.