Abstract
Background: Postural symmetry ensures balanced alignment and equal weight distribution, promoting optimal function and minimizing stress on muscles and joints. This study aimed to evaluate lower limb movement symmetry in response to mechanical perturbations. Methods: Twelve healthy young women were subjected to mechanical perturbation tests while standing on the Motek GRAIL system treadmill. Maximum values of kinematic and kinetic parameters and symmetry indices were counted to compare the responses of dominant and non-dominant limbs. Results: The study identified symmetrical and asymmetrical features in lower limb dynamics. Symmetry nearness was observed in the ankle joint angle (SI = 0.03), the hip torque (SI = 0.03), and the vertical component of the ground reaction force (SI = 0.04). However, significant asymmetries were found in the medio-lateral component of the ground reaction force (SI = 1.84), ankle torque (SI = 0.23), knee torque (SI = 0.19), hip angle (SI = 0.15), and knee angle (SI = 0.08). The anterior–posterior component of the ground reaction force (SI = 0.14) showed asymmetry but was not statistically significant. Conclusions: Perturbations impact lower limb dynamics, revealing dominance- and joint-specific asymmetries. Bilateral assessment is crucial for understanding postural control, guiding rehabilitation to restore symmetry, and reducing the risk of injuries, falls, and musculoskeletal strain, particularly in athletes and older adults. These findings emphasize the value of symmetry indices in optimizing therapy and prevention strategies.
1. Introduction
Postural control is a fundamental aspect of human movement that enables individuals to maintain balance and stability during both static and dynamic activities [1]. It involves the integration of sensory information from the visual, vestibular, and somatosensory systems, the processing of that information in the central nervous system, and the subsequent motor responses that adjust the body’s position in space. Effective postural control relies on the coordinated activity of various body segments and muscle groups, with particular emphasis on the lower limbs, which serve as the primary support structure during standing, walking, and other weight-bearing activities.
Symmetry is a key factor in maintaining effective postural control and overall stability [2]. It refers to the balanced and proportional distribution of movements, forces, or mechanical properties between corresponding parts of the body, typically the left and right sides [3]. It reflects the uniformity in joint angles, muscle activation, and force generation during activities such as walking, running, or maintaining posture. From a biomechanical perspective, symmetry is essential for efficient movement, reducing strain on the musculoskeletal system, and minimizing the risk of injury. For this reason, it is often assessed to identify motor control deficiencies, detect imbalances, or guide rehabilitation strategies [4].
Maintaining symmetry becomes increasingly challenging when destabilizing stimuli arise from internal or external sources, as these factors can disrupt the body’s balance and lead to asymmetries that require compensatory mechanisms to restore stability. Internal factors contributing to asymmetry often stem from anatomical, physiological, or neurological differences within the body. Anatomical variations, such as differences in limb length, joint alignment, or structural restrictions, can create imbalances between the left and right sides [2,4]. Neurological conditions affecting the central or peripheral nervous system may impair motor control and coordination, further contributing to asymmetry [5]. Additionally, prior injuries, such as fractures, ligament tears, or soft tissue damage, frequently result in compensatory movement patterns that lead to long-term imbalances [5]. The body also naturally exhibits directional asymmetry due to the arrangement of internal organs, such as the heart on the left, the liver on the right, and the structural differences between the lungs, with three lobes on the right and two on the left [6]. While these inherent asymmetries are a normal part of human anatomy and typically do not affect functional balance, they reflect the body’s side-dependent development.
In contrast, external factors influencing asymmetry are primarily environmental and behavioral. Uneven surfaces, unstable platforms, or other environmental conditions can force the body to adapt asymmetrically, creating imbalances in posture and movement [6,7]. Footwear, particularly poorly designed or improper types such as high-heeled shoes, can significantly contribute to asymmetry by increasing instability, altering foot mechanics, and causing greater supination and plantar flexion [8]. Mechanical perturbations, such as sudden shifts in support or unexpected forces, challenge the body’s ability to maintain symmetry and stability, particularly if postural control mechanisms are impaired [6,9]. Activity-specific demands, such as participating in sports that emphasize one side of the body, like tennis or golf, can also reinforce asymmetrical movement patterns over time [6,10]. Psychological factors, such as kinesiophobia, or fear of movement, further exacerbate these imbalances by limiting natural movement and altering motor patterns [6].
Most research on asymmetry has concentrated on assessments of musculoskeletal strength and range of motion, primarily due to the specificity of tasks performed during movement [11]. However, in static conditions such as standing, the asymmetry of stabilizing functions in the limbs can be analyzed through measurements of center of pressure (CoP) differences and load distribution. Studies have shown that increased lower limb asymmetry is directly associated with greater postural instability, emphasizing the critical role of symmetry in maintaining stability [2]. Symmetry ensures an even distribution of forces within the musculoskeletal system, which is essential for balance and efficient movement.
While research on postural control spans a variety of populations, including healthy and impaired individuals of all ages, experimental protocols like walking on a treadmill can be challenging for older adults, who may lack experience with such tasks. Studying young women specifically is particularly relevant, as research suggests they exhibit greater asymmetry in weight distribution and pelvic obliquity compared to men [12]. However, other studies have indicated that women tend to have superior balance-maintenance abilities, demonstrated by a shorter CoP path length. Additionally, women’s enhanced ability to process and integrate sensory signals allows them to effectively compensate for external disturbances [13,14], despite their increased sensitivity to certain stimuli, such as sound [15]. This combination of factors makes the study of lower limb symmetry in young women a valuable area of research for understanding postural control dynamics.
Although the literature extensively examines symmetry and asymmetry during gait, studies addressing these factors in the context of quiet standing—particularly under conditions involving external perturbations—are relatively scarce. For instance, Zhu, et al. [16] investigated the response of lower limbs to unexpected perturbations, such as sudden pulls from a harness attached at the waist. Their findings revealed that these perturbations increased postural sway and joint moment values. Interestingly, the magnitude and force of the perturbations did not significantly affect the degree of compensation. Much of the current research focuses on the trajectory of the CoP during static balance maintenance and evaluates symmetry under conditions free from destabilizing forces, relying primarily on data collected from force platforms. Despite considerable research on gait dynamics and CoP trajectory analysis, there remains a significant gap in the literature regarding the symmetry of lower limb movements in response to external forces during quiet standing. Therefore, this study aimed to investigate the impact of repetitive mechanical perturbations on lower limb symmetry, focusing on the kinematic and kinetic responses of both the dominant and non-dominant limbs. It was hypothesized that lower limb dynamics under disturbance would vary according to lower limb dominance and joint characteristics.
2. Materials and Methods
2.1. Participants
The sample size for the study was determined using G*Power 3.1.9.7 (University of Kiel, Germany), with a Wilcoxon test conducted a priori. The parameters used for the calculation included a significance level (p) of 0.05, a desired power of 0.80, and an effect size (d) of 0.8, which corresponds to a large effect size. Based on these inputs, G*Power recommended a sample size of 12 participants.
Twelve young women participated in this study (mean age: 21.38 ± 3.07 years old, body weight: 63.08 ± 13.26 kg, body height: 168.83 ± 6.87 cm). Participants were recruited voluntarily through advertisements and university announcements, with no monetary or material incentives provided. All participants met the inclusion criteria, which required them to have no prior history of muscular or neurological disorders, no lower limb injuries within the past six months, regular physical activity (at least two days per week), previous experience with treadmill walking, and a dominant right lower limb.
Leg dominance was determined using the kicking test, in which participants indicated their preferred leg for kicking a ball. All participants had a dominant right lower limb, which is more common in the general population [17,18]. In this way, the study was more representative of the majority population and allowed for protocol standardization, minimizing the variability associated with limb dominance.
Exclusion criteria included a lack of treadmill walking experience, balance impairments, or the use of medications influencing the nervous system. Each participant provided written informed consent before participation. The study was approved by the University Review Committee (no. SKE01-15/2023) and was in accordance with the ethical standards outlined in the Declaration of Helsinki.
2.2. Measurement Protocol
The kinematic and kinetic parameters of perturbed and unperturbed free standing were measured using the Gait Real-Time Analysis Interactive Laboratory (GRAIL, Motek Medical B.V., Amsterdam, The Netherlands). This advanced system integrates a dual split-belt treadmill (long: 2200 mm, wide: 2 × 500 mm) operating at 1000 Hz, a motion capture system (Vicon Metrics Ltd., Oxford, UK) equipped with ten Bonita cameras capturing at 100 Hz, three video cameras, and synchronized virtual reality environments (VR). The VR setup includes a circular screen (5 m diameter, 3 m height, and 180° field of view) supported by three projectors, enabling immersive and controlled simulations (Figure 1A). Participants’ movements were recorded using the Human Body Model 2 (HBM2), with 25 reflective markers to track motion (Figure 1B). A safety harness suspended from the ceiling ensured participant security during testing. During the study, participants wore their comfortable athletic shoes, which they commonly use for treadmill walking or gym workouts.

Figure 1.
(A) Overview of the Interactive Gait Real-Time Analysis Laboratory (GRAIL, Motek Medical B.V., Amsterdam, The Netherlands). (B) Front, side, and rear view of the marker set used in the Human Body Model. Front, side, and rear views of the marker set used in the Human Body Model. Green markers indicate anatomical landmarks used to define the skeletal structure during initialization. Key landmarks include the following: STRN (jugular notch of the sternum), XYPH (xiphoid process of the sternum), NAVE (navel), T10 (10th thoracic vertebra), LASIS and RASIS (left and right anterior superior iliac spine), LPSIS and RPSIS (left and right posterior superior iliac spine), SACR (midpoint between LPSIS and RPSIS), LGTRO and RGTRO (left and right greater trochanter), LFLTHI and RFLTHI (left and right thigh, lateral midpoint between the greater trochanter and lateral knee), LLEK and RLEK (left and right lateral epicondyle of the knee), LATI and RATI (left and right shank, lateral midpoint between the knee and ankle), LLM and RLM (left and right lateral malleolus of the ankle), LMT5 and RMT5 (left and right 5th metatarsal), LTOE and RTOE (tips of the left and right toes), and LHEE and RHEE (left and right heel) [7].
The GRAIL system, controlled by D-Flow 3.26 software (Motek Medical B.V., Amsterdam, The Netherlands), facilitated perturbation initiation, data acquisition, and model adjustments. The perturbation applied to participants consisted of a sudden movement of the treadmill belt beneath one of their lower limbs. The study protocol included two trials of quiet standing under different conditions: (1) quiet standing with eyes forward, during which the treadmill belt moved abruptly under the left lower limb; (2) quiet standing with eyes forward, during which the treadmill belt moved abruptly under the right lower limb. Additionally, participants were instructed to return to the starting position after each perturbation (Figure 2).
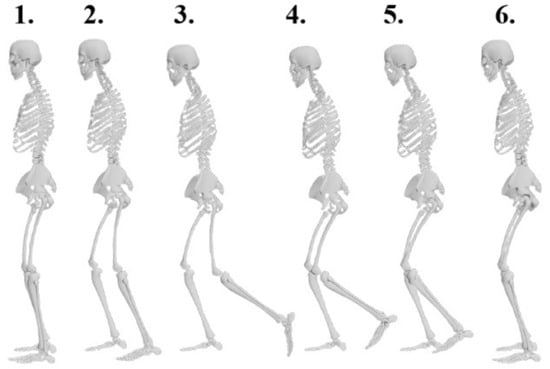
Figure 2.
Sequential representation of left lower limb response during perturbation: phases of treadmill belt acceleration (1–3) and recovery (4–6).
Each trial lasted 43 s. During each trial, the perturbation occurred four times at 10 s intervals, specifically at the 10th, 20th, 30th, and 40th second of the measurement period (Figure 3A). The treadmill was initially set to a static position in acceleration mode, and the perturbation intensity was set to level 5 on a scale of 1 to 5. This corresponded to an increase in treadmill belt speed from about 0 m/s to 0.67 m/s. The single perturbation lasted for approximately 0.92 s (Figure 3B).

Figure 3.
Plot of the left lane treadmill speed change: (A) over the entire trial duration and (B) at the first perturbation.
Kinematic parameters, such as lower limb joint angles, and kinetic parameters, including lower limb joint torques and ground reaction forces, were recorded with high precision, offering a comprehensive insight into postural control under perturbed and unperturbed conditions. Data collected using D-Flow 3.26 software were saved as *.mox files and then imported into Matlab 2021a (MathWorks, Natick, MA, USA) via a toolbox developed by Feldhege, et al. [19].
The maximum values of each kinematic and kinetic parameter were identified across the two trials involving perturbations, including measurements for the left and lower limbs and their corresponding responses on the opposite sides. For one person, there were four such peaks for a single parameter from one lower limb (Figure 4).
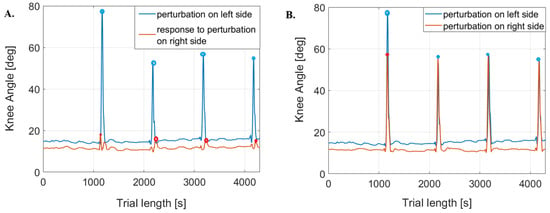
Figure 4.
Examples of knee joint angle plots. (A) is for the perturbed side and the responding side in one trial; (B) is for the left and right perturbed sides, respectively, from different trials, where points indicate maximum peaks.
Symmetry indices (SIs) were then calculated using the following formula [20]:
L and R represent the parameter values for the left and right lower limbs, respectively (Figure 4). An SI value of 0 indicates perfect symmetry, while SI ≥ 100% reflects asymmetry. The difference between the left and right lower limbs was calculated because the left leg was designated as the supporting leg, while the right leg was defined as the dominant leg. Therefore, it was assumed that parameter values for the left lower limb would be higher.
2.3. Statistical Analysis
Statistical analysis was performed using Statistica v.12 software (StatSoft, Cracow, Poland), with a significance level set at p < 0.05. The Shapiro–Wilk test was employed to assess the normality of data distribution. The Wilcoxon test was applied to identify statistically significant differences in the following comparisons: (1) maximum peak values achieved during perturbation of the right and left lower limbs separately; (2) maximum peak values during perturbation of the left lower limb compared to the corresponding values for the right lower limb; (3) maximum peak values during perturbation of the right lower limb compared to the corresponding values for the left lower limb.
The effect size (r) for the Wilcoxon test was calculated for each comparison according to the following formula [21,22]:
Z is the Z-score for the Wilcoxon test, which reflects the test statistic from the comparison of ranks; N is the number of non-zero differences (i.e., the number of pairs that show a difference between the two measurements) [22]. According to Prajzner [23], the proposed interpretation is as follows: a small effect size is between 0 and 0.30, a medium effect size is between 0.31 and 0.50, a strong effect size is between 0.51 and 0.70, and a large effect size is between 0.71 and 1.
3. Results
3.1. Comparison of Kinematic and Kinetic Parameters for Perturbed Dominant and Non-Dominant Lower Limbs
Among the parameters with statistically significant differences, the largest asymmetry was observed in the medio-lateral (ML) component of the ground reaction force (GRF) (SI = 1.84, large effect size, p < 0.0001). Significant asymmetries were also identified in the ankle torque (SI = 0.23, strong effect size, p = 0.0005), knee torque (SI = 0.19, medium effect size, p = 0.0224), hip angle (SI = 0.15, large effect size, p = 0.0016), and knee angle (SI = 0.08, large effect size, p = 0.0001). Although a substantial asymmetry was noted in the anterior–posterior (AP) component of the GRF (SI = 0.14, small effect size), it was not statistically significant (p = 0.0755) (Table 1).

Table 1.
Median (lower; upper quartile) for kinematic and kinetic parameters of the non-dominant (left) and dominant (right) lower limb during perturbation. The penultimate column shows the values of the symmetry index (SI), and the last one presents the p-value for the Wilcoxon test, where * indicates statistically significant differences.
Among the parameters with no statistically significant differences, the ankle joint angle showed the highest symmetry among the kinematic parameters (SI = 0.03, medium effect size, p = 0.2637). Similarly, the hip joint demonstrated the greatest symmetry among muscle torque values (SI = 0.03, small effect size, p = 0.4840). The vertical component of the ground reaction force (GRF) also exhibited moderate symmetry, but the difference was not statistically significant (SI = 0.04, medium effect size, p = 0.560).
3.2. Comparison of Kinematic and Kinetic Parameters of the Perturbed and Responding Limb
3.2.1. Perturbation of the Non-Dominant (Left) Limb
Significant asymmetries (p < 0.0001) were observed for eight of the nine parameters when comparing the impaired non-dominant limb (left) with the responsive dominant limb (right). The largest statistically significant (p < 0.0001) asymmetries were recorded in knee torque (SI = 1.23, large effect size) and the medio-lateral (ML) component of the GRF (SI = 1.49, large effect size). Negative SI values, indicating greater activation or response in the responding limb, were found for the ankle joint angle (SI = −0.28, large effect size) and hip torque (SI = −0.26, large effect size). The vertical (PD) component of the GRF showed minor asymmetry (SI = −0.20, small effect size). These findings highlight the substantial impact of perturbation responses, particularly in the ankle and hip joints of the dominant limb (Table 2).

Table 2.
Median (lower; upper quartile) for kinematic and kinetic parameters of the non-dominant (left) lower limb during perturbation and the responding dominant (right) lower limb. The penultimate column shows the values of the symmetry index (SI), and the last one presents the p-value for the Wilcoxon test, where * indicates statistically significant differences.
3.2.2. Perturbation of the Dominant (Right) Limb
When the dominant limb (right) was perturbed, statistically significant negative asymmetries were observed for the knee torque (SI = −2, large effect size, p < 0.0001), knee angle (SI = −0.83, large effect size, p < 0.0001), ankle torque (SI = −0.32, medium effect size, p < 0.0001), and hip angle (SI = −0.13, medium effect size, p = 0.0004) (Table 3).

Table 3.
Median (lower; upper quartile) for kinematic and kinetic parameters of the dominant (right) lower limb during perturbation and the responding non-dominant (left) lower limb. The penultimate column shows the values of the symmetry index (SI), and the last one presents the p-value for the Wilcoxon test, where * indicates statistically significant differences.
Significant positive asymmetries were noted for the medio-lateral (ML) component of the GRF (SI = 1.80, large effect size, p < 0.0001), ankle angle (SI = 0.27, large effect size, p < 0.0001), vertical (PD) component of the GRF (SI = 0.23, large effect size, p < 0.0001), and hip torque (SI = 0.11, medium effect size, p = 0.0178).
Minimal asymmetry was observed for the anterior–posterior (AP) component of the GRF (SI = −0.01, small effect size, p = 0.4003), which was not statistically significant. These findings demonstrate distinct asymmetry patterns, with knee and ankle parameters exhibiting the most pronounced differences.
4. Discussion
This study focused on understanding how external repetitive mechanical perturbations impact the dynamic interplay between the dominant and non-dominant lower limbs during quiet standing. The study used a proprietary perturbation protocol using GRIAL (Motek Medical B.V., Amsterdam, The Netherlands), which allowed precise perturbation inputs. This accuracy allowed the creation of safe and reproducible perturbations. The results indicated that, while some parameters tended to be symmetrical, significant asymmetries were evident in others. This suggests that postural control mechanisms adapt differently based on limb dominance and joint-specific factors.
Symmetry indexes (SIs) indicated that, overall, there was considerable symmetry in some parameters, particularly in ankle joint angles (SI = 0.03), hip torque (SI = 0.03), and the vertical component of the ground reaction force (SI = 0.04). These findings align with previous research emphasizing the importance of ankle and hip stability in maintaining postural control during standing tasks [24]. However, significant asymmetries were observed in other parameters, such as the medio-lateral (ML) component of the ground reaction force (SI = 1.84), knee torque (SI = 0.19), and ankle torque (SI = 0.23). These findings suggest that different joints and planes of motion exhibit varying capacities to maintain symmetry under perturbation. The pronounced asymmetry in the ML component of the ground reaction force highlights the challenge of maintaining balance in the medio-lateral direction, as previously identified by studies investigating balance responses during standing and walking [7]. This imbalance may reflect the inherent difficulty of counteracting forces applied perpendicular to the sagittal plane, which requires more complex neuromuscular coordination. Similarly, asymmetries in torque at the ankle and knee joints likely stem from differences in load-bearing roles during perturbations, with the non-dominant limb providing greater support and the dominant limb executing compensatory responses.
4.1. Limb Dominance and Postural Control
A key finding was the differential response of dominant and non-dominant limbs during perturbations. The non-dominant limb consistently displayed higher maximum torque and angle values, as reflected in the positive SIs for most parameters. This is consistent with previous research suggesting that non-dominant limbs are better suited for stabilizing functions, while dominant limbs are optimized for dynamic, precision tasks such as kicking or stepping [17,25,26,27]. The greater engagement of the non-dominant limb in stabilizing functions during perturbation may be an adaptive mechanism to enhance balance and reduce postural sway [2,10].
Interestingly, when a perturbation was applied to the dominant limb, the non-dominant limb (as the responding limb) exhibited higher levels of asymmetry in the torque and ground reaction force. This indicates a directional dependency in postural responses, where the stabilizing capacity of the non-dominant limb is more effective during perturbations of the dominant side. Conversely, when perturbations were applied to the non-dominant limb, the dominant limb’s compensatory responses were less effective, leading to larger asymmetries in torque and joint angles. These findings underscore the importance of considering limb dominance in rehabilitation strategies and highlight the need for bilateral training to reduce such asymmetries [4,16].
4.2. Joint-Specific Responses
Joint-specific analysis revealed significant differences in how the hip, knee, and ankle joints responded to perturbations. The hip joint exhibited relatively symmetrical torque responses (SI = 0.03), suggesting its central role in global postural adjustments [11]. However, asymmetries were more prominent at the knee (SI = 0.19) and ankle (SI = 0.23) joints, which are often involved in fine-tuning balance during dynamic tasks. The knee joint’s pronounced asymmetry may reflect its role in absorbing and redistributing forces during perturbation recovery, as previously suggested by biomechanical models of joint dynamics [28].
The ankle joint’s asymmetry during perturbations, despite its high symmetry during unperturbed standing (SI = 0.03), highlights the dynamic nature of joint-specific responses. This discrepancy may result from the ankle’s dual role in stabilizing the body and initiating corrective movements. The larger torque values observed in the non-dominant ankle suggest that it plays a more active role in stabilizing the body when subjected to perturbations, particularly in the ML direction.
4.3. Implications for Rehabilitation
This study provides actionable rehabilitation strategies to address lower limb asymmetries and improve stability. Significant asymmetries in torque and ground reaction forces necessitate bilateral assessments to detect imbalances that increase injury risk or hinder performance. Rehabilitation should target sagittal and frontal plane symmetry, especially for those with impaired postural control [4,5]. Clinicians should use tools like isokinetic dynamometry for torque assessment, force plates for dynamic movement analysis (e.g., squats, jumps, and walking), and the Y-balance test for dynamic balance evaluation [29,30]. Motion capture systems and the Functional Movement Screen (FMS) can identify asymmetries in movement patterns [31].
Rehabilitation programs should address asymmetries and enhance stability using evidence-based interventions. Neuromuscular training, like single-leg stance and unstable surface exercises, improves proprioception and joint control [32,33]. Biofeedback tools, such as pressure-sensitive insoles and virtual reality systems, provide real-time feedback for correcting asymmetries [33,34,35]. Perturbation-based training, including split-belt treadmill exercises and manual perturbations, enhances dynamic stability [16]. Strengthening programs, such as unilateral exercises (e.g., single-leg deadlifts and Bulgarian split squats) and eccentric training, improve load control and stabilization [33,35]. Manual therapy, including targeted stretching and myofascial release, addresses muscle tightness contributing to asymmetry [36,37].
Clinicians should conduct regular bilateral assessments, personalize rehabilitation plans, and use biofeedback tools to correct imbalances. Progression from static exercises to dynamic, task-specific drills can improve balance and proprioception. Educating patients on recognizing asymmetries and incorporating corrective exercises into daily routines will ensure long-term benefits. Collaboration with specialists can further enhance outcomes. These strategies can reduce asymmetries, improve postural control, and optimize functional performance.
4.4. Study Limitations and Future Directions
Although this study provides valuable insights, it is not without limitations. The small sample size (n = 12) restricts the generalizability of the findings. Future research should include a larger and more diverse sample incorporating both older individuals and young adults with varying levels of physical and functional ability to capture better the broader spectrum of changes.
Moreover, the study included only healthy young women with right-limb dominance, thus excluding other populations with differing limb dominance patterns or postural control deficits. This limited scope does not account for the variability in postural control in the wider population. Future research should expand to include men, individuals with left-limb dominance, and those with neurological or other functional impairments to determine whether similar patterns exist across diverse demographic groups. Moreover, the exclusion of clinical populations limits the applicability of the findings to individuals with conditions such as stroke or neuromuscular diseases. Examining these groups in future studies would help clarify how such conditions influence lower limb symmetry.
Another limitation lies in the study’s focus on maximum values of kinematic and kinetic parameters during perturbations. While this highlights peak responses, it overlooks temporal changes in symmetry indices and the strategies employed to regain stability over time. Future studies should investigate the dynamic progression of postural adjustments to provide a deeper understanding of the mechanisms driving symmetry and asymmetry during perturbations.
5. Conclusions
Repetitive mechanical perturbations significantly influence lower limb symmetry, with notable differences between dominant and non-dominant limbs. While some parameters, such as ankle joint angles and vertical ground reaction forces, exhibited high symmetry, others, including knee torque and the medio-lateral ground reaction force component, displayed significant asymmetries. These findings emphasize the importance of bilateral assessments in postural control research and rehabilitation. Tailored interventions addressing both limb dominance and joint-specific asymmetries could enhance balance and stability, reduce the risk of injury, and improve functional performance.
These findings have significant implications for both future research and clinical practice. Firstly, they may contribute to the development of more advanced methods for assessing lower limb asymmetry. Future studies could incorporate detailed biomechanical analyses, such as evaluating dynamic joint loading during daily physical activities, to gain a deeper understanding of limb imbalances. In clinical practice, these results highlight the importance of personalized rehabilitation approaches. Addressing joint-specific asymmetries could lead to the design of targeted exercise protocols. For instance, individuals with asymmetry in knee torque may benefit from exercises that strengthen the muscles around the knee, such as eccentric, isometric, or resistance training under controlled conditions. For those with asymmetries in medio-lateral ground reaction forces, exercises focused on improving frontal plane stability, such as balance training on unstable surfaces or proprioception exercises, could be essential.
Additionally, these findings could inform the development of injury prevention programs. Integrating bilateral postural assessments as a routine screening tool for athletes or individuals exposed to repetitive mechanical strain may help identify those at risk of injury.
In conclusion, the results suggest the potential for more complex, individualized interventions in both research and clinical settings, which could significantly enhance balance, stability, and functional performance in both patients and athletes.
Author Contributions
Conceptualization, M.G. and M.B.; methodology, M.G. and M.B.; software, M.G. and M.B.; validation, M.G. and M.B.; formal analysis, M.G. and M.B.; investigation, M.G. and M.B.; resources, M.B.; data curation, M.G. and M.B.; writing—original draft preparation, M.G; writing—review and editing, M.B.; visualization, M.G. and M.B.; supervision, M.B.; project administration, M.B.; funding acquisition, M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Józef Piłsudski University of Physical Education in Warsaw, grant number UPB No. 2 (114/12/PRO/2023).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study. The study was approved by the University Review Committee (no. SKE01-15/2023) and was in accordance with the ethical standards outlined in the Declaration of Helsinki.
Data Availability Statement
The measurement data used to support the findings of this study are available from the corresponding author upon request.
Acknowledgments
Special thanks to Karol Kowieski and Martyna Jarocka for their invaluable help with data collection and participant recruitment.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kędziorek, J.; Błażkiewicz, M. Nonlinear Measures to Evaluate Upright Postural Stability: A Systematic Review. Entropy 2020, 22, 1357. [Google Scholar] [CrossRef] [PubMed]
- Kašček Bučinel, A.; Supej, M.; Petrone, N.; Čuk, I. How does body symmetry influence standing balance? Kinesiology 2019, 51, 52–59. [Google Scholar] [CrossRef]
- Kumar, S.N.; Omar, B.; Joseph, L.H.; Htwe, O.; Jagannathan, K.; Hamdan, N.M.; Rajalakshmi, D. Evaluation of limb load asymmetry using two new mathematical models. Glob. J. Health Sci. 2014, 7, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Blanchet, M.; Guertin, P.; Pilon, F.; Gorce, P.; Prince, F. From Neural Command to Robotic Use: The Role of Symmetry/Asymmetry in Postural and Locomotor Activities. Symmetry 2021, 13, 1773. [Google Scholar] [CrossRef]
- Ogihara, H.; Tsushima, E.; Kamo, T.; Sato, T.; Matsushima, A.; Niioka, Y.; Asahi, R.; Azami, M. Kinematic gait asymmetry assessment using joint angle data in patients with chronic stroke-A normalized cross-correlation approach. Gait Posture 2020, 80, 168–173. [Google Scholar] [CrossRef]
- Keogh, J.A.J.; Waddington, E.E.; Masood, Z.; Mahmood, S.; Palanisamy, A.C.; Ruder, M.C.; Karsan, S.; Bishop, C.; Jordan, M.J.; Heisz, J.J.; et al. Monitoring lower limb biomechanical asymmetry and psychological measures in athletic populations-A scoping review. Scand. J. Med. Sci. Sports 2023, 33, 2125–2148. [Google Scholar] [CrossRef]
- Ciunelis, K.; Borkowski, R.; Błażkiewicz, M. The Impact of Induced Acceleration Perturbations in Selected Phases of the Gait Cycle on Kinematic and Kinetic Parameters. Appl. Sci. 2024, 14, 4849. [Google Scholar] [CrossRef]
- Błażkiewicz, M.; Hadamus, A. Effect of wearing high-heeled shoes on postural control and foot loading symmetry. Acta Bioeng. Biomech. 2023, 25, 49–57. [Google Scholar] [CrossRef]
- Błażkiewicz, M.; Hadamus, A.; Borkowski, R. Recurrence Quantification Analysis as a Form of Postural Control Assessment: A Systematic Review. Appl. Sci. 2023, 13, 5587. [Google Scholar] [CrossRef]
- Kadri, M.A.; Noé, F.; Maitre, J.; Maffulli, N.; Paillard, T. Effects of Limb Dominance on Postural Balance in Sportsmen Practicing Symmetric and Asymmetric Sports: A Pilot Study. Symmetry 2021, 13, 2199. [Google Scholar] [CrossRef]
- Arsenault, D.; Ivanova, T.D.; Garland, S.J. Postural control in response to unilateral and bilateral external perturbations in older adults. Gait Posture 2022, 94, 26–31. [Google Scholar] [CrossRef] [PubMed]
- Prado-Rico, J.M.; Duarte, M. Asymmetry of Body Weight Distribution During Quiet and Relaxed Standing Tasks. Mot. Control 2019, 23, 553–565. [Google Scholar] [CrossRef]
- Nolff, M.R.; Conner, N.O.; Haworth, J.L.; Goble, D.J. Lower Limb Asymmetry Evaluation Using the Balance Tracking System (BTrackS) Single Leg Stance Protocol. J. Mot. Behav. 2023, 55, 493–498. [Google Scholar] [CrossRef] [PubMed]
- Hadamus, A.; Gulatowska, M.; Ferenc, A.; Shahnazaryan, K.; Brzuszkiewicz-Kuźmicka, G.; Błażkiewicz, M. Influence of leg dominance on the symmetry in body balance measurements. Phys. Act. Rev. 2025, 13, 88–96. [Google Scholar] [CrossRef]
- Błażkiewicz, M.; Gulatowska, M.; Hadamus, A.; Kędziorek, J.; Brzuszkiewicz-Kuźmicka, G. Effect of Annoying Sounds on Postural Control. J. Clin. Med. 2024, 13, 2638. [Google Scholar] [CrossRef]
- Zhu, R.T.; Lyu, P.-Z.; Li, S.; Tong, C.Y.; Ling, Y.T.; Ma, C.Z. How Does Lower Limb Respond to Unexpected Balance Perturbations? New Insights from Synchronized Human Kinetics, Kinematics, Muscle Electromyography (EMG) and Mechanomyography (MMG) Data. Biosensors 2022, 12, 430. [Google Scholar] [CrossRef]
- Promsri, A.; Haid, T.; Federolf, P. How does lower limb dominance influence postural control movements during single leg stance? Hum. Mov. Sci. 2018, 58, 165–174. [Google Scholar] [CrossRef]
- Barut, C.; Ozer, C.M.; Sevinc, O.; Gumus, M.; Yunten, Z. Relationships between hand and foot preferences. Int. J. Neurosci. 2007, 117, 177–185. [Google Scholar] [CrossRef]
- Feldhege, F.; Richter, K.; Bruhn, S.; Fischer, D.C.; Mittlmeier, T. MATLAB-based tools for automated processing of motion tracking data provided by the GRAIL. Gait Posture 2021, 90, 422–426. [Google Scholar] [CrossRef]
- Blazkiewicz, M.; Wiszomirska, I.; Wit, A. Comparison of four methods of calculating the symmetry of spatial-temporal parameters of gait. Acta Bioeng. Biomech. 2014, 16, 29–35. [Google Scholar]
- Rosenthal, R. Parametric measures of effect size. In The Handbook of Research Synthesis; Russell Sage Foundation: New York, NY, USA, 1994; pp. 231–244. [Google Scholar]
- Rosnow, R.L. Effect sizes for experimenting psychologists. Can. J. Exp. Psychol. 2003, 57, 221–237. [Google Scholar] [CrossRef] [PubMed]
- Prajzner, A. Selected Indicators of Effect Size in Psychological Research. Ann. Univ. Mariae Curie-Skłodowska Sect. J. Paedagog.-Psychol. 2023, 35, 139–157. [Google Scholar] [CrossRef]
- Gribble, P.A.; Hertel, J.; Plisky, P. Using the Star Excursion Balance Test to assess dynamic postural-control deficits and outcomes in lower extremity injury: A literature and systematic review. J. Athl. Train. 2012, 47, 339–357. [Google Scholar] [CrossRef]
- Promsri, A.; Bangkomdet, K.; Jindatham, I.; Jenchang, T. Leg Dominance—Surface Stability Interaction: Effects on Postural Control Assessed by Smartphone-Based Accelerometry. Sports 2023, 11, 75. [Google Scholar] [CrossRef]
- Promsri, A.; Haid, T.; Werner, I.; Federolf, P. Leg Dominance Effects on Postural Control When Performing Challenging Balance Exercises. Brain Sci. 2020, 10, 128. [Google Scholar] [CrossRef]
- Promsri, A.; Longo, A.; Haid, T.; Doix, A.M.; Federolf, P. Leg Dominance as a Risk Factor for Lower-Limb Injuries in Downhill Skiers-A Pilot Study into Possible Mechanisms. Int. J. Environ. Res. Public Health 2019, 16, 3399. [Google Scholar] [CrossRef]
- Blazkiewicz, M.; Kedziorek, J.; Hadamus, A. The Impact of Visual Input and Support Area Manipulation on Postural Control in Subjects after Osteoporotic Vertebral Fracture. Entropy 2021, 23, 375. [Google Scholar] [CrossRef]
- Błażkiewicz, M.; Lann Vel Lace, K.; Hadamus, A. Gait Symmetry Analysis Based on Dynamic Time Warping. Symmetry 2021, 13, 836. [Google Scholar] [CrossRef]
- Kędziorek, J.; Błażkiewicz, M. The impact of external perturbations on postural control. Acta Bioeng. Biomech. 2024, 26, 3–11. [Google Scholar] [CrossRef]
- Macmillan, C.; Olivier, B.; Benjamin-Damons, N.; Wood, W.A.; Obiora, O.L. Altered sagittal plane mechanics is associated with Functional Movement Screen deep squat score. S. Afr. J. Physiother. 2023, 79, a1865. [Google Scholar] [CrossRef]
- Escamilla-Nunez, R.; Sivasambu, H.; Andrysek, J. Exploration of Vibrotactile Biofeedback Strategies to Induce Stance Time Asymmetries. Can. Prosthet. Orthot. J. 2022, 5, 36744. [Google Scholar] [CrossRef] [PubMed]
- Matla, J.; Filar-Mierzwa, K.; Ścisłowska-Czarnecka, A.; Jankowicz-Szymańska, A.; Bac, A. The Influence of the Physiotherapeutic Program on Selected Static and Dynamic Foot Indicators and the Balance of Elderly Women Depending on the Ground Stability. Int. J. Environ. Res. Public Health 2021, 18, 4660. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Kim, H.; Shin, W.S. Effects of Vibrotactile Biofeedback Providing Real-Time Pressure Information on Static Balance Ability and Weight Distribution Symmetry Index in Patients with Chronic Stroke. Brain Sci. 2022, 12, 358. [Google Scholar] [CrossRef] [PubMed]
- Queen, R.M.; Peebles, A.T.; Miller, T.K.; Savla, J.; Ollendick, T.; Messier, S.P.; Williams, D.B., 3rd. Reduction of Risk Factors for ACL Re-injuries using an Innovative Biofeedback Approach: Rationale and Design. Contemp. Clin. Trials Commun. 2021, 22, 100769. [Google Scholar] [CrossRef]
- Nawasreh, Z.; Logerstedt, D.; Failla, M.; Snyder-Mackler, L. No difference between mechanical perturbation training with compliant surface and manual perturbation training on knee functional performance after ACL rupture. J. Orthop. Res. Off. Publ. Orthop. Res. Soc. 2018, 36, 1391–1397. [Google Scholar] [CrossRef]
- Choi, J.M.; Cho, E.Y.; Lee, B.H. Effects of Dynamic Stretching Combined with Manual Therapy on Pain, ROM, Function, and Quality of Life of Adhesive Capsulitis. Healthcare 2023, 12, 45. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).