Abstract
Quantum batteries are quantum systems designed to store energy and release it on demand. The optimization of their performance is an intensively studied topic within the realm of quantum technologies. Such optimization forces the question: how do quantum many-body systems work as quantum batteries? To address this issue, we rely on symmetry and symmetry breaking via quantum phase transitions. Specifically, we analyze a dimerized quantum XY chain in a transverse field as a prototype of an energy storage device. This model, which is characterized by ground states with different symmetries depending on the Hamiltonian parameters, can be mapped onto a spinless fermionic chain with superconducting correlations, displaying a rich quantum phase diagram. We show that the stored energy strongly depends on the quantum phase diagram of the model when large charging times are considered.
1. Introduction
Models of interacting spins have great importance in various contexts of physics [1]. Firstly, they enable quantitative predictions within the theory of magnetism [2,3,4,5]. Materials well described by spin models in various dimensions are indeed not rare [6,7,8,9,10,11]. At the same time, they are at the core of topological phases, both for thermal and the ground-state properties [12,13,14]. In this context, their relation to the fascinating field of frustrated systems is worth mentioning [15,16,17,18,19]. Moreover, they have recently played a crucial role in the determination of novel paradigms in the theory of thermalization and information spread through the general procedure called quantum quench [20,21,22,23]. A quantum quench is a sudden variation of a parameter of the Hamiltonian of a quantum system. Quantum quenches can be achieved experimentally within very diverse platforms [24,25,26].
Alongside the large range of physical applications, many effective techniques have been proposed for analysis of spin systems. These range from the celebrated spin wave theory based on the Holstein–Primakoff transformation [27] to numerical ones, based on even the Fedotov–Popov transformation [28,29]. Additionally, one-dimensional models can be analyzed by means of bosonization [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47] as long as the low-energy properties are considered. Even more remarkably, they sometimes might be exactly solved by means of the Bethe Ansatz technique [48] or more simply by the Wigner–Jordan transformation [49]. Such exact solutions, which are at the heart of the so-called theory of quantum integrable systems [50], can indeed help in understanding some general principles of quantum many-body interacting systems and are hence extremely valuable.
Indeed, the existence of such techniques has strongly favored the adoption of quantum spin chains in the context of quantum technologies [51]. Indeed, a two-level system can mathematically be described as a spin 1/2, so that one-dimensional collections of qubits are immediately described by interacting spin chains. This fact has been exploited in the fields of quantum information, quantum communication, quantum computation, and, more relevantly for the present article, quantum energy storage.
In this context, quantum spin chains have been proposed as quantum batteries (QBs) [52,53,54,55,56,57]. Conceived for the first time a decade ago [58], QBs are miniaturized device able to store and efficiently deliver energy, exploiting purely non-classical effects such as quantum superposition and entanglement [59,60,61]. The interest in such devices is not only motivated by fundamental issues in quantum thermodynamics [62,63,64,65,66], but it is also driven by the need to integrate quantum energy providers to improve the performance of quantum circuits [67,68,69,70,71] or quantum computing architectures [72,73,74] with the hope that QBs could outperform their classical counterparts [58,75].
Among all the mechanisms that can be envisioned to charge a QB, one is tightly connected to the vast literature on quantum quenches. Such protocol works in the following way [76,77]: a system is prepared in the ground state of a Hamiltonian , called the battery Hamiltonian. Then, the Hamiltonian suddenly changes, say at , to a different operator —the charging Hamiltonian—that implements the time evolution. Finally, after a time interval , the Hamiltonian is brought back to the original operator . In such a way, for fixed and values, one can evaluate the energy transferred to the quantum system as a function of the charging time . A QB working according to the mechanism just described and composed of a collection of interacting two-level systems is usually called a spin QB.
Recently, it has been shown that a dimerized XY spin chain used as a spin QB shows a rich phenomenology [56]. The energy stored as a function of is characterized by the presence of three regimes: (i) A short charging time regime, where prominent oscillations as a function of are present; (ii) A plateau regime—resembling the prethermalization plateau of the quantum quench theory—where no oscillations as a function of are present; (iii) a recurrence time where oscillations are restored for times large enough to probe the level spacing. This last regime is pushed to in the thermodynamic limit. Among the three regimes, the second one shows an interesting behavior: the energy stored strongly depends on the quantum phase diagram of the charging Hamiltonian, and in particular, it is sensitive to a quantum phase transition (QPT) induced in the model by the dimerization strength [56]. In other words, in a specific case, it has been shown that the dependence of the stored energy on the parameters of the Hamiltonian when the battery Hamiltonian and the charging Hamiltonian are kept within the same quantum phase are strikingly different with respect to the case in which and are in different quantum phases. In a sense, the QPTs of the charging Hamiltonian appear to be manifest in the behavior of the stored energy.
In this article, we extend the analysis to a richer model, that is the dimerized XY chain in an external transverse field [78], to prove that, even within this larger model, the energy stored in the plateau regime strongly depends on the quantum phase diagram of the charging Hamiltonian.
2. Model
The model under investigation is the so-called dimerized XY quantum chain in a transverse field [78]. The Hamiltonian is given by where the subscript B indicates the fact that this system will be considered as a QB.
In the above expression, N is the number of unit cells, considered here to be even for simplicity, and (with ) are Pauli matrices, in the usual representation, corresponding to the j-th site spin. The parameter J is the energy scale of the system, , , and h characterize the strength of the anisotropy, the dimerization, and the external field, respectively.
By focusing for simplicity on the even-parity sector of the model [23], and considering the periodic boundary conditions , it is possible to diagonalize the above Hamiltonian by means of a standard Wigner–Jordan transformation mapping spins into free spinless fermions [49]. Notice that the obtained fermionic Hamiltonian corresponds to the dimerized Kitaev chain and is characterized by interesting topological features [79], due to the competition between fractional solitons [80,81,82,83,84,85] and Majorana fermions [86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104]. In terms of two species of auxiliary fermionic annihilation operators and , and assuming from now on as reference scale for the energies, we obtain (from now one we will consider ).
Here, and
where the following definitions have been used:
and , with the number of dimers. For , the gap closes at
while for , the gap closes at
These equations represent the phase boundaries of the model, whose plots are reported in Figure 1. In [56], it has been shown that the charging process at zero external field shows signatures of the presence of the QPT lines of the model. Those lines can be obtained by setting in Equations (4) and (5), as shown by the blue and red dashed lines in Figure 2, respectively. The Figure also shows a very interesting and intricated phase diagram at finite h.
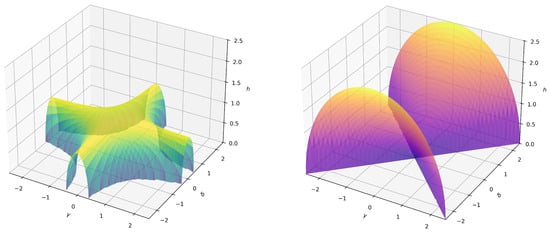
Figure 1.
Three-dimensional plot of the phase boundaries (left panel) and (right panel).

The goal of this work is to explore the charging process of a QB described by the Hamiltonian in Equation (1): the presence of a non-zero field enriches the previously studied quantum phase diagram, opening up the possibility of investigating different QPT scenarios.
3. Study of QPT Effects
The general approach of our analysis is as follows: we first select a plane in the (, , h)-space by imposing a constraint on the model parameters. The QPT lines are then identified as the intersections of the phase boundaries, defined by Equations (4) and (5), with the chosen plane. Next, we perform a sudden quench of one or more model parameters, focusing on the asymptotic limit where the charging time approaches infinity, and finally, we plot the energy stored per dimer in the battery as a function of the pre-quench parameter. In the asymptotic regime we are studying, the energy stored in the QB assumes the form [56].
Here, represents the -th element of the matrix , defined as . In particular, and are both 4 × 4 matrices: the columns of correspond to the eigenvectors of the QB Hamiltonian, which depends on the pre-quench parameters, and similarly, the columns of correspond to the eigenvectors of the charging Hamiltonian, which depends on the post-quench parameters. Equation (6) provides the value of the stored energy given a generic sudden quench of the parameters. As mentioned, our aim here is to explore the effects of QPTs. In the following, we will provide paradigmatic examples in this direction which represent the whole phase space.
3.1. Quench of at Given h and
In this scenario, we perform a quench of the anisotropy parameter from an initial value to a final value , with and positive constants, along the line given by the intersection of the plane and the one. The situation is sketched in Figure 3.
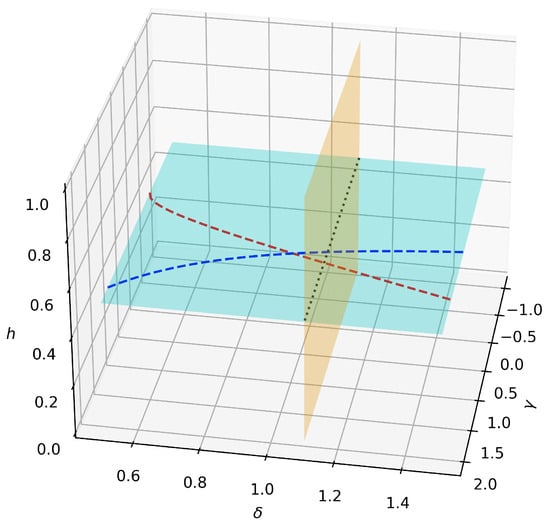
Figure 3.
Section of the phase diagram of the model. The cyan and orange planes have equations and , respectively, while the black dotted line is given by the intersection of the aforementioned planes and it is the line where the quench takes place. The blue and red dashed lines are the QPT lines given by the intersection of the boundaries reported in Equations (4) and (5) with the plane.
Figure 4 shows the energy stored per dimer (in units of ) as a function of , with fixed at for both the zero-field scenario (black curve) and the non-zero constant external field one (, green curve). The impact of the phase diagram is evident from the behavior of both curves: for the green curve, we can see that the energy initially rapidly increases until reaches the dashed red QPT line in Figure 3, while in the region between the two QPT lines, the curve rises more gradually and finally, after crossing the second QPT line, the curve begins to decrease. For the black curve, we observe analogous behavior, but other than gaining slightly more energy, the QPT lines are shifted with respect to the previous case since the intersections between the 3D phase diagram and the plane are different.
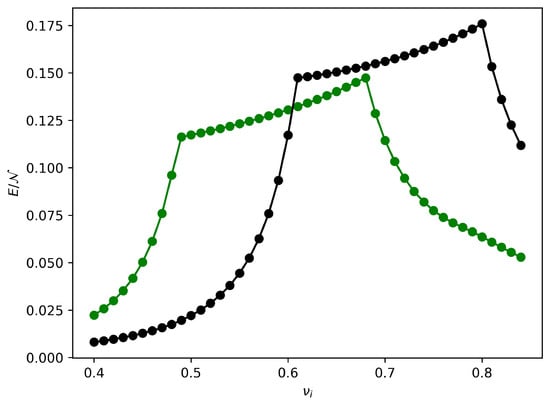
Figure 4.
Energy stored per dimer as a function of after a quench of the anisotropy parameter at fixed and in the asymptotic regime, i.e., , for (green curve) and (black curve). In both curves, the first peak appears when crosses the dashed red QPT line in Figure 3, while the second peak appears when it crosses the dashed blue QPT line.
3.2. Quench of h at Given and
Now, we perform a quench of the external field, once again from an initial value to a final value , along the line given by the intersection of the and the planes, as shown in Figure 5.
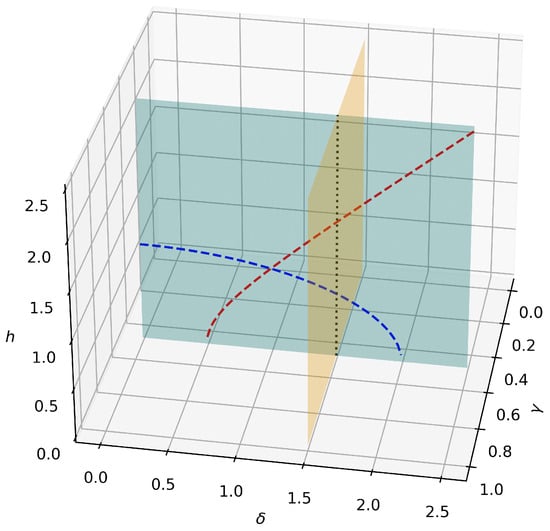
Figure 5.
Section of the phase diagram of the model. The cyan and orange planes have equations and , respectively, while the black dotted line is given by the intersection of the aforementioned planes; this is the line where the quench takes place. The blue and red dashed lines are the QPT lines given by the intersection of the boundaries reported in Equations (4) and (5) with the plane.
As in the previous case, Figure 6 shows the energy stored per dimer as a function of , with fixed at . The observed trend is very similar to the one shown in Figure 4, with an initial rising until the first QPT line, an almost-linear rise until the second one, and then a decrease.
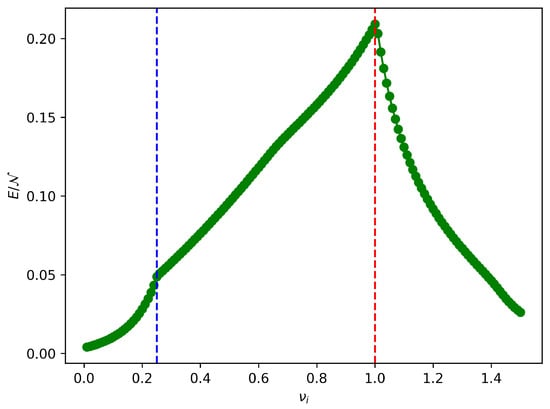
Figure 6.
Energy stored per dimer as a function of after a quench of the external field at fixed , and in the asymptotic regime, i.e., . The two dashed red and blue lines represent the values of such that the charging Hamiltonian depending on is critical.
3.3. Quench of h and at Given
Lastly, we vary both the anisotropy and the external field. The plane on which we perform the time evolution has the equation and the dotted black line has the following parametric equation
so that the quench of has an impact on both and h. The QPT lines are represented in Figure 7.
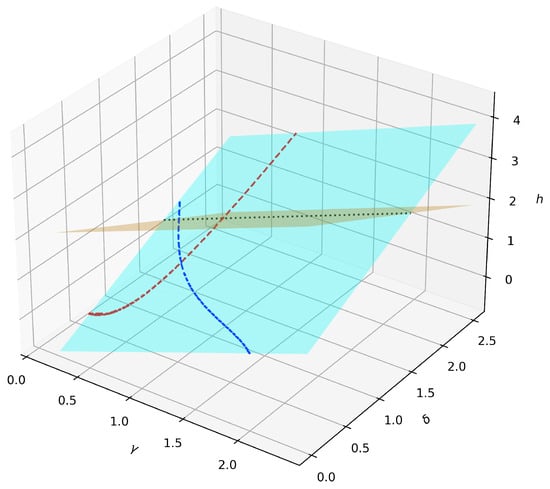
Figure 7.
Section of the phase diagram of the model. The cyan and orange planes have equations and , respectively, while the black dotted line is given by the intersection of the aforementioned planes and it is the line where the quench takes place. The blue and red dashed lines are the QPT lines given by the intersection of the boundaries reported in Equations (4) and (5) with the plane.
After fixing , we obtain the plot reported in Figure 8: even in this more complex scenario, we can observe the same features also presented in the previous two cases.
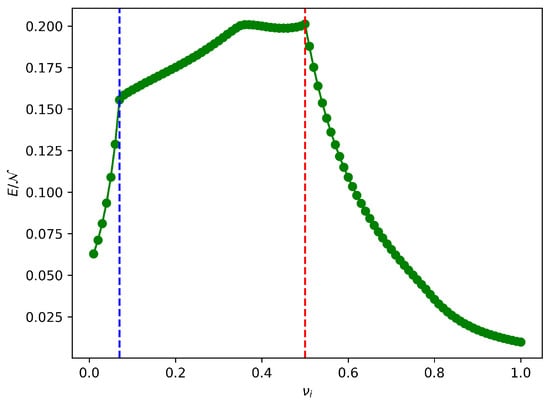
Figure 8.
Energy stored per dimer as a function of after a quench of both the anisotropy parameter and the external field at fixed and in the asymptotic regime, i.e., . The two dashed red and blue lines represent the values of such that the charging Hamiltonian depending on is critical.
4. Conclusions
In this work, we have investigated the interplay between QPTs and the energy storage properties of a dimerized XY spin chain subjected to an external transverse field used as a QB. By extending previous analyses carried out in the absence of an external field, we have demonstrated that the introduction of a non-zero field enriches the quantum phase diagram and significantly influences the charging process. We considered three different scenarios: a quench of the anisotropy parameter , a quench of the external field h and a simultaneous quench of both and h. In all cases, we focused on the asymptotic regime of long charging times (), where the energy stored per dimer was analyzed as a function of the pre-quench parameter.
Our results reveal common patterns across all scenarios: first, the stored energy initially rises sharply until the first QPT line is crossed. In the region between two QPT lines, where a plateau was observed in the zero-field case () quenching the dimerization parameter [56], the energy now increases: this change reflects the role of both the type of quench and the external field in modifying the phenomenology of the plateau regime and suggests that QPT signatures at the level of the stored energy persist even for more complex models. Finally, after crossing the second QPT line, the stored energy begins to decrease. This behavior highlights the sensitivity of the system to the quantum phase diagram of the charging Hamiltonian. As an extension of this work, in order to have a more general understanding of the role of QPTs on quantum batteries based on integrable systems, it would be interesting to analyze scenarios in which the matrix used to compute the energy stored in Equation (6) can be accessed analytically. For instance, by analyzing the so-called cluster Ising model [105,106], one could assess the role of multi-spin interactions, while considering free fermions on generic lattices the effects related to dimensionality and topology might be unveiled [107,108]. Additionally, the role of non-sudden quenches, initial thermal states, noise, and dissipation needs to be addressed to translate our analysis to real-world quantum batteries [109,110,111,112,113,114,115,116,117,118].
Author Contributions
Conceptualization, R.G., N.T.Z. and D.F.; methodology, R.G., N.T.Z. and D.F.; investigation, R.G.; software, R.G.; formal analysis, R.G., N.T.Z. and D.F.; visualization, R.G.; supervision, F.C.; writing—original draft preparation, R.G., F.C., N.T.Z. and D.F.; writing—review and editing, R.G., F.C., N.T.Z. and D.F.; funding acquisition, N.T.Z. and D.F. All authors have read and agreed to the published version of the manuscript.
Funding
N.T.Z. acknowledges funding through the NextGenerationEu Curiosity Driven Project “Understanding even-odd criticality”. N.T.Z. acknowledges funding through the “Non-reciprocal supercurrent and topological transitions in hybrid Nb- InSb nanoflags” project (Prot. 2022PH852L) in the framework of PRIN 2022 initiative of the Italian Ministry of University (MUR) for the National Research Program (PNR). This project has been funded within the programme “PNRR Missione 4—Componente 2—Investimento 1.1 Fondo per il Programma Nazionale di Ricerca e Progetti di Rilevante Interesse Nazionale (PRIN)”. D.F. acknowledges funding from the European Union-NextGenerationEU through the “Quantum Busses for Coherent Energy Transfer” (QUBERT) project, in the framework of the Curiosity Driven 2021 initiative of the University of Genova and through the “Solid State Quantum Batteries: Characterization and Optimization” (SoS-QuBa) project (Prot. 2022XK5CPX), in the framework of the PRIN 2022 initiative of the Italian Ministry of University (MUR) for the National Research Program (PNR). This project has been funded within the program “PNRR Missione 4—Componente 2—Investimento 1.1 Fondo per il Programma Nazionale di Ricerca e Progetti di Rilevante Interesse Nazionale (PRIN)”.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- De las Cuevas, G.; Cubitt, T.S. Simple universal models capture all classical spin physics. Science 2016, 351, 1180–1183. [Google Scholar] [CrossRef]
- Auerbach, A. Interacting Electrons and Quantum Magnetism; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Wysin, G.M. Magnetism theory: Spin models. In Magnetic Excitations and Geometric Confinement; 2053–2563; IOP Publishing: Bristol, UK, 2015; pp. 1–47. [Google Scholar] [CrossRef]
- Cialone, M.; Celegato, F.; Coïsson, M.; Barrera, G.; Fiore, G.; Shvab, R.; Klement, U.; Rizzi, P.; Tiberto, P. Tailoring magnetic properties of multicomponent layered structure via current annealing in FePd thin films. Sci. Rep. 2017, 7, 16691. [Google Scholar] [CrossRef] [PubMed]
- Cialone, M.; Fernandez-Barcia, M.; Celegato, F.; Coisson, M.; Barrera, G.; Uhlemann, M.; Gebert, A.; Sort, J.; Pellicer, E.; Rizzi, P.; et al. A comparative study of the influence of the deposition technique (electrodeposition versus sputtering) on the properties of nanostructured Fe70Pd30 films. Sci. Technol. Adv. Mater. 2020, 21, 424–434. [Google Scholar] [CrossRef] [PubMed]
- Manousakis, E. The spin-½ Heisenberg antiferromagnet on a square lattice and its application to the cuprous oxides. Rev. Mod. Phys. 1991, 63, 1–62. [Google Scholar] [CrossRef]
- Bramwell, S.; Harris, M. Frustration in Ising-type spin models on the pyrochlore lattice. J. Phys. Condens. Matter 1998, 10, L215. [Google Scholar] [CrossRef]
- Mydosh, J.A. Spin glasses: Redux: An updated experimental/materials survey. Rep. Prog. Phys. 2015, 78, 052501. [Google Scholar] [CrossRef]
- Pan, F.; Chico, J.; Delin, A.; Bergman, A.; Bergqvist, L. Extended spin model in atomistic simulations of alloys. Phys. Rev. B 2017, 95, 184432. [Google Scholar] [CrossRef]
- Cavaliere, F.; Razzoli, L.; Carrega, M.; Benenti, G.; Sassetti, M. Hybrid quantum thermal machines with dynamical couplings. iScience 2023, 26, 106235. [Google Scholar] [CrossRef]
- Eckhardt, C.J.; Passetti, G.; Othman, M.; Karrasch, C.; Cavaliere, F.; Sentef, M.A.; Kennes, D.M. Quantum Floquet engineering with an exactly solvable tight-binding chain in a cavity. Commun. Phys. 2022, 5, 122. [Google Scholar] [CrossRef]
- Feng, X.Y.; Zhang, G.M.; Xiang, T. Topological Characterization of Quantum Phase Transitions in a Spin-1/2 Model. Phys. Rev. Lett. 2007, 98, 087204. [Google Scholar] [CrossRef]
- Duivenvoorden, K.; Quella, T. Topological phases of spin chains. Phys. Rev. B 2013, 87, 125145. [Google Scholar] [CrossRef]
- Dubinkin, O.; Hughes, T.L. Higher-order bosonic topological phases in spin models. Phys. Rev. B 2019, 99, 235132. [Google Scholar] [CrossRef]
- Balents, L. Spin liquids in frustrated magnets. Nature 2010, 464, 199–208. [Google Scholar] [CrossRef] [PubMed]
- Diep, H.T. Frustrated Spin Systems; World Scientific: Singapore, 2013. [Google Scholar]
- Sacco Shaikh, D.; Catalano, A.G.; Cavaliere, F.; Franchini, F.; Sassetti, M.; Traverso Ziani, N. Phase diagram of the topologically frustrated XY chain. Eur. Phys. J. Plus 2024, 139, 1–14. [Google Scholar] [CrossRef]
- Marić, V.; Giampaolo, S.M.; Franchini, F. Quantum phase transition induced by topological frustration. Commun. Phys. 2020, 3, 220. [Google Scholar] [CrossRef]
- Lacroix, C.; Mendels, P.; Mila, F. Introduction to Frustrated Magnetism: Materials, Experiments, Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 164. [Google Scholar]
- Mitra, A. Quantum quench dynamics. Annu. Rev. Condens. Matter Phys. 2018, 9, 245–259. [Google Scholar] [CrossRef]
- Essler, F.H.; Fagotti, M. Quench dynamics and relaxation in isolated integrable quantum spin chains. J. Stat. Mech. Theory Exp. 2016, 2016, 064002. [Google Scholar] [CrossRef]
- Porta, S.; Gambetta, F.M.; Traverso Ziani, N.; Kennes, D.M.; Sassetti, M.; Cavaliere, F. Nonmonotonic response and light-cone freezing in fermionic systems under quantum quenches from gapless to gapped or partially gapped states. Phys. Rev. B 2018, 97, 035433. [Google Scholar] [CrossRef]
- Porta, S.; Cavaliere, F.; Sassetti, M.; Traverso Ziani, N. Topological classification of dynamical quantum phase transitions in the xy chain. Sci. Rep. 2020, 10, 12766. [Google Scholar] [CrossRef]
- Faure, Q.; Takayoshi, S.; Simonet, V.; Grenier, B.; Månsson, M.; White, J.S.; Tucker, G.S.; Rüegg, C.; Lejay, P.; Giamarchi, T.; et al. Tomonaga-Luttinger Liquid Spin Dynamics in the Quasi-One-Dimensional Ising-Like Antiferromagnet BaCo2V2O8. Phys. Rev. Lett. 2019, 123, 027204. [Google Scholar] [CrossRef]
- Faure, Q.; Takayoshi, S.; Petit, S.; Simonet, V.; Raymond, S.; Regnault, L.P.; Boehm, M.; White, J.S.; Månsson, M.; Rüegg, C.; et al. Topological quantum phase transition in the Ising-like antiferromagnetic spin chain BaCo2V2O8. Nat. Phys. 2018, 14, 716–722. [Google Scholar] [CrossRef]
- Kinoshita, T.; Wenger, T.; Weiss, D.S. A quantum Newton’s cradle. Nature 2006, 440, 900–903. [Google Scholar] [CrossRef]
- Holstein, T.; Primakoff, H. Field Dependence of the Intrinsic Domain Magnetization of a Ferromagnet. Phys. Rev. 1940, 58, 1098–1113. [Google Scholar] [CrossRef]
- Popov, V.N.; Fedotov, S. The functional-integration method and diagram technique for spin systems. Zh. Eksp. Teor. Fiz 1988, 94, 183–194. [Google Scholar]
- Traverso, S.; Fleckenstein, C.; Sassetti, M.; Ziani, N.T. An exact local mapping from clock-spins to fermions. SciPost Phys. Core 2023, 6, 055. [Google Scholar] [CrossRef]
- Traverso Ziani, N.; Fleckenstein, C.; Dolcetto, G.; Trauzettel, B. Fractional charge oscillations in quantum dots with quantum spin Hall effect. Phys. Rev. B 2017, 95, 205418. [Google Scholar] [CrossRef]
- Rodriguez, R.; Parmentier, F.; Ferraro, D.; Roulleau, P.; Gennser, U.; Cavanna, A.; Sassetti, M.; Portier, F.; Mailly, D.; Roche, P. Relaxation and revival of quasiparticles injected in an interacting quantum Hall liquid. Nat. Commun. 2020, 11, 2426. [Google Scholar] [CrossRef] [PubMed]
- Gambetta, F.M.; Ziani, N.T.; Barbarino, S.; Cavaliere, F.; Sassetti, M. Anomalous Friedel oscillations in a quasihelical quantum dot. Phys. Rev. B 2015, 91, 235421. [Google Scholar] [CrossRef]
- Ziani, N.T.; Cavaliere, F.; Sassetti, M. Theory of the STM detection of Wigner molecules in spin-incoherent CNTs. Europhys. Lett. 2013, 102, 47006. [Google Scholar] [CrossRef]
- Ziani, N.T.; Cavaliere, F.; Becerra, K.G.; Sassetti, M. A Short Review of One-Dimensional Wigner Crystallization. Crystals 2021, 11, 20. [Google Scholar] [CrossRef]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 885–964. [Google Scholar] [CrossRef]
- Cazalilla, M.A.; Citro, R.; Giamarchi, T.; Orignac, E.; Rigol, M. One dimensional bosons: From condensed matter systems to ultracold gases. Rev. Mod. Phys. 2011, 83, 1405–1466. [Google Scholar] [CrossRef]
- Trotzky, S.; Chen, Y.A.; Flesch, A.; McCulloch, I.P.; Schollwöck, U.; Eisert, J.; Bloch, I. Probing the relaxation towards equilibrium in an isolated strongly correlated one-dimensional Bose gas. Nat. Phys. 2012, 8, 325–330. [Google Scholar] [CrossRef]
- Imambekov, A.; Glazman, L.I. Universal Theory of Nonlinear Luttinger Liquids. Science 2009, 323, 228–231. [Google Scholar] [CrossRef] [PubMed]
- Imambekov, A.; Schmidt, T.L.; Glazman, L.I. One-dimensional quantum liquids: Beyond the Luttinger liquid paradigm. Rev. Mod. Phys. 2012, 84, 1253–1306. [Google Scholar] [CrossRef]
- Wu, C.; Bernevig, B.A.; Zhang, S.C. Helical Liquid and the Edge of Quantum Spin Hall Systems. Phys. Rev. Lett. 2006, 96, 106401. [Google Scholar] [CrossRef]
- Fiete, G.A.; Le Hur, K.; Balents, L. Coulomb drag between two spin-incoherent Luttinger liquids. Phys. Rev. B 2006, 73, 165104. [Google Scholar] [CrossRef]
- Fiete, G.A. Colloquium: The spin-incoherent Luttinger liquid. Rev. Mod. Phys. 2007, 79, 801–820. [Google Scholar] [CrossRef]
- Matveev, K.A.; Furusaki, A.; Glazman, L.I. Bosonization of strongly interacting one-dimensional electrons. Phys. Rev. B 2007, 76, 155440. [Google Scholar] [CrossRef]
- Voit, J. One-dimensional Fermi liquids. Rep. Prog. Phys. 1995, 58, 977. [Google Scholar] [CrossRef]
- Haldane, F.D.M. Effective Harmonic-Fluid Approach to Low-Energy Properties of One-Dimensional Quantum Fluids. Phys. Rev. Lett. 1981, 47, 1840–1843. [Google Scholar] [CrossRef]
- Haldane, F.D.M. ’Luttinger liquid theory’ of one-dimensional quantum fluids. I. Properties of the Luttinger model and their extension to the general 1D interacting spinless Fermi gas. J. Phys. Solid State Phys. 1981, 14, 2585. [Google Scholar] [CrossRef]
- Giamarchi, T. Quantum Physics in One Dimension; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Bethe, H. Zur theorie der metalle: I. Eigenwerte und eigenfunktionen der linearen atomkette. Z. Phys. 1931, 71, 205–226. [Google Scholar] [CrossRef]
- Jordan, P.; Wigner, E. Über das Paulische Äquivalenzverbot. Z. Phys. 1928, 47, 631–651. [Google Scholar] [CrossRef]
- Franchini, F. An Introduction to Integrable Techniques for One-Dimensional Quantum Systems; Springer: Berlin/Heidelberg, Germany, 2017; Volume 940. [Google Scholar]
- Bayat, A.; Bose, S.; Johannesson, H. Entanglement in Spin Chains: From Theory to Quantum Technology Applications; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Le, T.P.; Levinsen, J.; Modi, K.; Parish, M.M.; Pollock, F.A. Spin-chain model of a many-body quantum battery. Phys. Rev. A 2018, 97, 022106. [Google Scholar] [CrossRef]
- Liu, J.X.; Shi, H.L.; Shi, Y.H.; Wang, X.H.; Yang, W.L. Entanglement and work extraction in the central-spin quantum battery. Phys. Rev. B 2021, 104, 245418. [Google Scholar] [CrossRef]
- Zhao, F.; Dou, F.Q.; Zhao, Q. Quantum battery of interacting spins with environmental noise. Phys. Rev. A 2021, 103, 033715. [Google Scholar] [CrossRef]
- Catalano, A.; Giampaolo, S.; Morsch, O.; Giovannetti, V.; Franchini, F. Frustrating Quantum Batteries. PRX Quantum 2024, 5, 030319. [Google Scholar] [CrossRef]
- Grazi, R.; Sacco Shaikh, D.; Sassetti, M.; Traverso Ziani, N.; Ferraro, D. Controlling Energy Storage Crossing Quantum Phase Transitions in an Integrable Spin Quantum Battery. Phys. Rev. Lett. 2024, 133, 197001. [Google Scholar] [CrossRef] [PubMed]
- Ali, A.; Elghaayda, S.; Al-Kuwari, S.; Hussain, M.I.; Rahim, M.T.; Kuniyil, H.; Seuda, C.; Allati, A.E.; Mansour, M.; Haddadi, S. Super-Extensive Scaling in 1D Spin-1/2XY − Γ(γ) Chain Quantum Battery. arXiv 2024, arXiv:2411.14074. [Google Scholar]
- Alicki, R.; Fannes, M. Entanglement boost for extractable work from ensembles of quantum batteries. Phys. Rev. E 2013, 87, 042123. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharjee, S.; Dutta, A. Quantum thermal machines and batteries. Eur. Phys. J. 2021, 94, 239. [Google Scholar] [CrossRef]
- Campaioli, F.; Gherardini, S.; Quach, J.Q.; Polini, M.; Andolina, G.M. Colloquium: Quantum batteries. Rev. Mod. Phys. 2024, 96, 031001. [Google Scholar] [CrossRef]
- Quach, J.; Cerullo, G.; Virgili, T. Quantum batteries: The future of energy storage? Joule 2023, 7, 2195–2200. [Google Scholar] [CrossRef]
- Benenti, G.; Casati, G.; Saito, K.; Whitney, R.S. Fundamental aspects of steady-state conversion of heat to work at the nanoscale. Phys. Rep. 2017, 694, 1–124. [Google Scholar] [CrossRef]
- Esposito, M.; Harbola, U.; Mukamel, S. Nonequilibrium fluctuations, fluctuation theorems, and counting statistics in quantum systems. Rev. Mod. Phys. 2009, 81, 1665–1702. [Google Scholar] [CrossRef]
- Campisi, M.; Fazio, R. Dissipation, correlation and lags in heat engines. J. Phys. Math. Theor. 2016, 49, 345002. [Google Scholar] [CrossRef]
- Vinjanampathy, S.; Anders, J. Quantum thermodynamics. Contemp. Phys. 2016, 57, 545–579. [Google Scholar] [CrossRef]
- Potts, P.P. Quantum Thermodynamics. arXiv 2024, arXiv:2406.19206. [Google Scholar]
- Hu, C.K.; Qiu, J.; Souza, P.J.P.; Yuan, J.; Zhou, Y.; Zhang, L.; Chu, J.; Pan, X.; Hu, L.; Li, J.; et al. Optimal charging of a superconducting quantum battery. Quantum Sci. Technol. 2022, 7, 045018. [Google Scholar] [CrossRef]
- Gemme, G.; Andolina, G.M.; Pellegrino, F.M.D.; Sassetti, M.; Ferraro, D. Off-Resonant Dicke Quantum Battery: Charging by Virtual Photons. Batteries 2023, 9, 197. [Google Scholar] [CrossRef]
- Dou, F.Q.; Yang, F.M. Superconducting transmon qubit-resonator quantum battery. Phys. Rev. A 2023, 107, 023725. [Google Scholar] [CrossRef]
- Razzoli, L.; Gemme, G.; Khomchenko, I.; Sassetti, M.; Ouerdane, H.; Ferraro, D.; Benenti, G. Cyclic solid-state quantum battery: Thermodynamic characterization and quantum hardware simulation. Quantum Sci. Technol. 2025, 10, 015064. [Google Scholar] [CrossRef]
- Cavaliere, F.; Gemme, G.; Benenti, G.; Ferraro, D.; Sassetti, M. Dynamical blockade of a reservoir for optimal performances of a quantum battery. arXiv 2024, arXiv:2407.16471. [Google Scholar]
- Chiribella, G.; Yang, Y.; Renner, R. Fundamental Energy Requirement of Reversible Quantum Operations. Phys. Rev. X 2021, 11, 021014. [Google Scholar] [CrossRef]
- Menta, R.; Cioni, F.; Aiudi, R.; Polini, M.; Giovannetti, V. Globally driven superconducting quantum computing architecture. arXiv 2024, arXiv:2407.01182. [Google Scholar]
- Elyasi, S.N.; Rossi, M.A.C.; Genoni, M.G. Experimental simulation of daemonic work extraction in open quantum batteries on a digital quantum computer. arXiv 2024, arXiv:2410.16567. [Google Scholar]
- Binder, F.C.; Vinjanampathy, S.; Modi, K.; Goold, J. Quantacell: Powerful charging of quantum batteries. New J. Phys. 2015, 17, 075015. [Google Scholar] [CrossRef]
- Andolina, G.M.; Farina, D.; Mari, A.; Pellegrini, V.; Giovannetti, V.; Polini, M. Charger-mediated energy transfer in exactly solvable models for quantum batteries. Phys. Rev. B 2018, 98, 205423. [Google Scholar] [CrossRef]
- Crescente, A.; Ferraro, D.; Carrega, M.; Sassetti, M. Enhancing coherent energy transfer between quantum devices via a mediator. Phys. Rev. Res. 2022, 4, 033216. [Google Scholar] [CrossRef]
- Perk, J.; Capel, H.; Zuilhof, M.; Siskens, T. On a soluble model of an antiferromagnetic chain with alternating interactions and magnetic moments. Phys. Stat. Mech. Its Appl. 1975, 81, 319–348. [Google Scholar] [CrossRef]
- Wakatsuki, R.; Ezawa, M.; Tanaka, Y.; Nagaosa, N. Fermion fractionalization to Majorana fermions in a dimerized Kitaev superconductor. Phys. Rev. B 2014, 90, 014505. [Google Scholar] [CrossRef]
- Ziani, N.T.; Fleckenstein, C.; Vigliotti, L.; Trauzettel, B.; Sassetti, M. From fractional solitons to Majorana fermions in a paradigmatic model of topological superconductivity. Phys. Rev. B 2020, 101, 195303. [Google Scholar] [CrossRef]
- Jackiw, R.; Rebbi, C. Solitons with fermion number ½. Phys. Rev. D 1976, 13, 3398–3409. [Google Scholar] [CrossRef]
- Kivelson, S.; Schrieffer, J.R. Fractional charge, a sharp quantum observable. Phys. Rev. B 1982, 25, 6447–6451. [Google Scholar] [CrossRef]
- Goldstone, J.; Wilczek, F. Fractional Quantum Numbers on Solitons. Phys. Rev. Lett. 1981, 47, 986–989. [Google Scholar] [CrossRef]
- Heeger, A.J.; Kivelson, S.; Schrieffer, J.R.; Su, W.P. Solitons in conducting polymers. Rev. Mod. Phys. 1988, 60, 781–850. [Google Scholar] [CrossRef]
- Qi, X.L.; Hughes, T.L.; Zhang, S.C. Fractional charge and quantized current in the quantum spin Hall state. Nat. Phys. 2008, 4, 273–276. [Google Scholar] [CrossRef]
- Fleckenstein, C.; Ziani, N.T.; Calzona, A.; Sassetti, M.; Trauzettel, B. Formation and detection of Majorana modes in quantum spin Hall trenches. Phys. Rev. B 2021, 103, 125303. [Google Scholar] [CrossRef]
- Traverso, S.; Sassetti, M.; Traverso Ziani, N. Emerging topological bound states in Haldane model zigzag nanoribbons. Npj Quantum Mater. 2024, 9, 9. [Google Scholar] [CrossRef]
- Traverso, S.; Traverso Ziani, N.; Sassetti, M. Effects of the Vertices on the Topological Bound States in a Quasicrystalline Topological Insulator. Symmetry 2022, 14, 1736. [Google Scholar] [CrossRef]
- Traverso, S.; Sassetti, M.; Ziani, N.T. Role of the edges in a quasicrystalline Haldane model. Phys. Rev. B 2022, 106, 125428. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Unpaired Majorana fermions in quantum wires. Physics-Uspekhi 2001, 44, 131. [Google Scholar] [CrossRef]
- Deng, M.T.; Vaitiekėnas, S.; Hansen, E.B.; Danon, J.; Leijnse, M.; Flensberg, K.; Nygård, J.; Krogstrup, P.; Marcus, C.M. Majorana bound state in a coupled quantum-dot hybrid-nanowire system. Science 2016, 354, 1557–1562. [Google Scholar] [CrossRef]
- Peñaranda, F.; Aguado, R.; San-Jose, P.; Prada, E. Quantifying wave-function overlaps in inhomogeneous Majorana nanowires. Phys. Rev. B 2018, 98, 235406. [Google Scholar] [CrossRef]
- Fleckenstein, C.; Domínguez, F.; Traverso Ziani, N.; Trauzettel, B. Decaying spectral oscillations in a Majorana wire with finite coherence length. Phys. Rev. B 2018, 97, 155425. [Google Scholar] [CrossRef]
- Roy, D.; Bondyopadhaya, N.; Tewari, S. Topologically trivial zero-bias conductance peak in semiconductor Majorana wires from boundary effects. Phys. Rev. B 2013, 88, 020502. [Google Scholar] [CrossRef]
- Flensberg, K. Tunneling characteristics of a chain of Majorana bound states. Phys. Rev. B 2010, 82, 180516. [Google Scholar] [CrossRef]
- Law, K.T.; Lee, P.A.; Ng, T.K. Majorana Fermion Induced Resonant Andreev Reflection. Phys. Rev. Lett. 2009, 103, 237001. [Google Scholar] [CrossRef] [PubMed]
- Prada, E.; San-Jose, P.; de Moor, M.W.A.; Geresdi, A.; Lee, E.J.H.; Klinovaja, J.; Loss, D.; Nygård, J.; Aguado, R.; Kouwenhoven, L.P. From Andreev to Majorana bound states in hybrid superconductor–semiconductor nanowires. Nat. Rev. Phys. 2020, 2, 575–594. [Google Scholar] [CrossRef]
- Ivanov, D.A. Non-Abelian Statistics of Half-Quantum Vortices in p-Wave Superconductors. Phys. Rev. Lett. 2001, 86, 268–271. [Google Scholar] [CrossRef]
- Marra, P. Majorana nanowires for topological quantum computation. J. Appl. Phys. 2022, 132, 231101. [Google Scholar] [CrossRef]
- Leijnse, M.; Flensberg, K. Introduction to topological superconductivity and Majorana fermions. Semicond. Sci. Technol. 2012, 27, 124003. [Google Scholar] [CrossRef]
- Nayak, C.; Simon, S.H.; Stern, A.; Freedman, M.; Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 2008, 80, 1083–1159. [Google Scholar] [CrossRef]
- Kitaev, A. Fault-tolerant quantum computation by anyons. Ann. Phys. 2003, 303, 2–30. [Google Scholar] [CrossRef]
- Oreg, Y.; Refael, G.; von Oppen, F. Helical Liquids and Majorana Bound States in Quantum Wires. Phys. Rev. Lett. 2010, 105, 177002. [Google Scholar] [CrossRef] [PubMed]
- Lutchyn, R.M.; Sau, J.D.; Das Sarma, S. Majorana Fermions and a Topological Phase Transition in Semiconductor-Superconductor Heterostructures. Phys. Rev. Lett. 2010, 105, 077001. [Google Scholar] [CrossRef] [PubMed]
- Smacchia, P.; Amico, L.; Facchi, P.; Fazio, R.; Florio, G.; Pascazio, S.; Vedral, V. Statistical mechanics of the cluster Ising model. Phys. Rev. A 2011, 84, 022304. [Google Scholar] [CrossRef]
- Ding, C. Phase transitions of a cluster Ising model. Phys. Rev. E 2019, 100, 042131. [Google Scholar] [CrossRef] [PubMed]
- Susskind, L. Lattice fermions. Phys. Rev. D 1977, 16, 3031–3039. [Google Scholar] [CrossRef]
- Shamir, Y. Chiral fermions from lattice boundaries. Nucl. Phys. 1993, 406, 90–106. [Google Scholar] [CrossRef]
- Neyenhuis, B.; Zhang, J.; Hess, P.W.; Smith, J.; Lee, A.C.; Richerme, P.; Gong, Z.X.; Gorshkov, A.V.; Monroe, C. Observation of prethermalization in long-range interacting spin chains. Sci. Adv. 2017, 3, e1700672. [Google Scholar] [CrossRef]
- Kim, M.S.; de Oliveira, F.A.M.; Knight, P.L. Properties of squeezed number states and squeezed thermal states. Phys. Rev. A 1989, 40, 2494–2503. [Google Scholar] [CrossRef] [PubMed]
- Puskarov, T.; Schuricht, D. Time evolution during and after finite-time quantum quenches in the transverse-field Ising chain. SciPost Phys. 2016, 1, 003. [Google Scholar] [CrossRef]
- Jeske, J.; Vogt, N.; Cole, J.H. Excitation and state transfer through spin chains in the presence of spatially correlated noise. Phys. Rev. A 2013, 88, 062333. [Google Scholar] [CrossRef]
- Aftergood, J.; Takei, S. Noise in tunneling spin current across coupled quantum spin chains. Phys. Rev. B 2018, 97, 014427. [Google Scholar] [CrossRef]
- Singh, M.; Gangadharaiah, S. Driven quantum spin chain in the presence of noise: Anti-Kibble-Zurek behavior. Phys. Rev. B 2021, 104, 064313. [Google Scholar] [CrossRef]
- Werner, P.; Troyer, M.; Sachdev, S. Quantum Spin Chains with Site Dissipation. J. Phys. Soc. Jpn. 2005, 74, 67–70. [Google Scholar] [CrossRef]
- Chen, C.; An, J.H.; Luo, H.G.; Sun, C.P.; Oh, C.H. Floquet control of quantum dissipation in spin chains. Phys. Rev. A 2015, 91, 052122. [Google Scholar] [CrossRef]
- Schwager, H.; Cirac, J.I.; Giedke, G. Dissipative spin chains: Implementation with cold atoms and steady-state properties. Phys. Rev. A 2013, 87, 022110. [Google Scholar] [CrossRef]
- Shibata, N.; Katsura, H. Dissipative spin chain as a non-Hermitian Kitaev ladder. Phys. Rev. B 2019, 99, 174303. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).