BCA: Besiege and Conquer Algorithm
Abstract
1. Introduction
- A methodology grounded in human behavior is proposed, and a thorough besiege and conquer strategy is conducted.
- All mechanisms are modeled mathematically, including besiege, conquer, balance, and feedback strategies. The besiege strategy contributes to exploration, while the conquer strategy is dedicated to exploitation. The balance and feedback strategies enhance the balance between exploration and exploitation capabilities.
- The BCA introduces the parameter BCB, which controls the balance mechanism to speed up convergence.
- The superiority of the BCA is verified on IEEE CEC 2017 benchmark test functions, two engineering designs, and three classification problems.
2. Related Work
2.1. Meta-Heuristic Algorithms
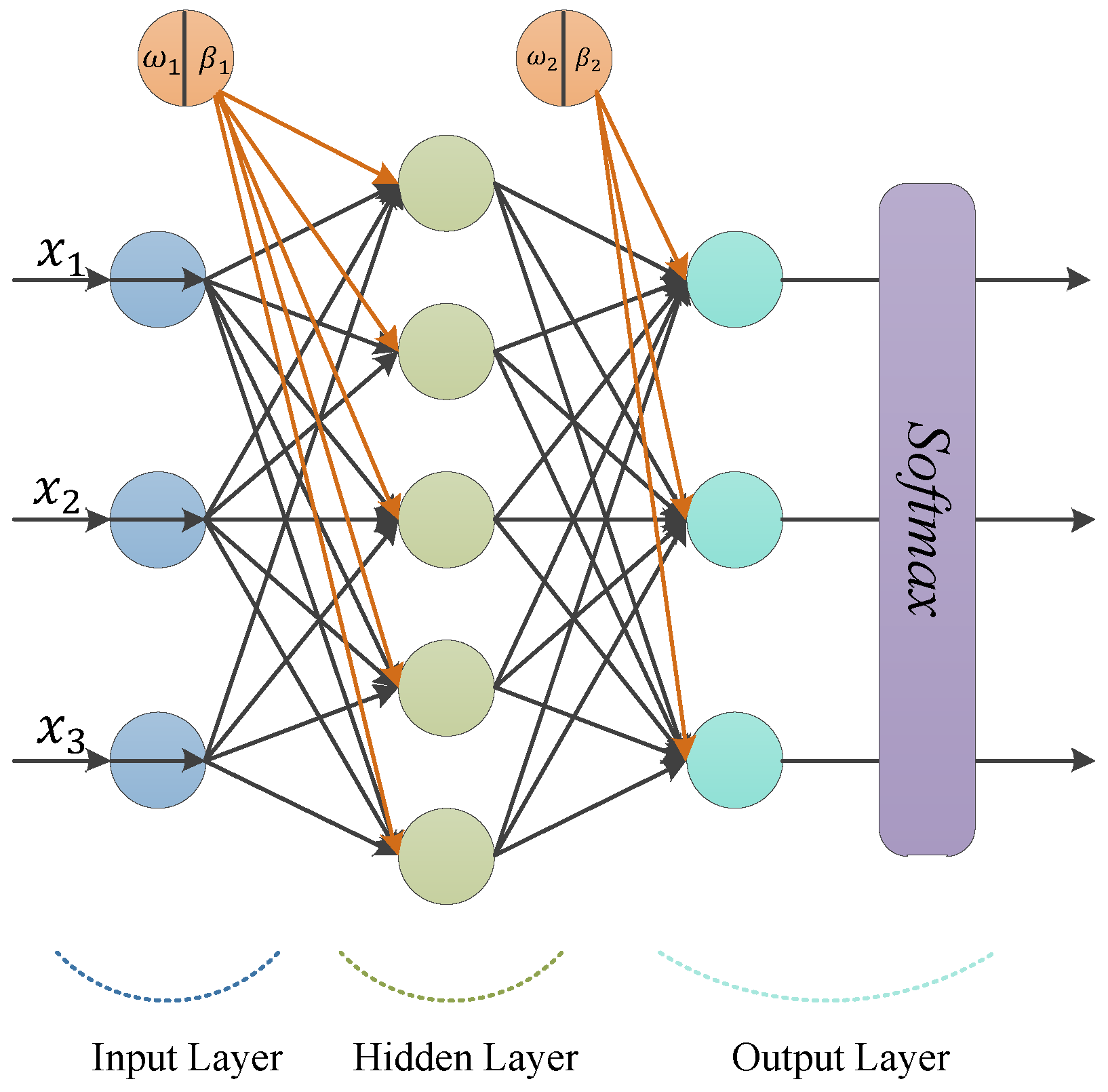
2.2. Multi-Layer Perceptron (MLP)
- Feedforward Architecture: Information flows from the input layer through the hidden layers to the output layer without any feedback connections.
- Non-linear Activation Functions: Each neuron typically employs an activation function, such as ReLU, sigmoid, or tanh, to introduce non-linearity, enabling the network to learn complex functional relationships.
- Backpropagation Training: The network is trained using the backpropagation algorithm, which calculates gradients to update weights, thereby minimizing the discrepancy between the predicted outputs and the actual target values.
2.3. Enhancing MLP Optimization Using Meta-Heuristic Optimization Methods
3. Besiege and Conquer Algorithm (BCA)
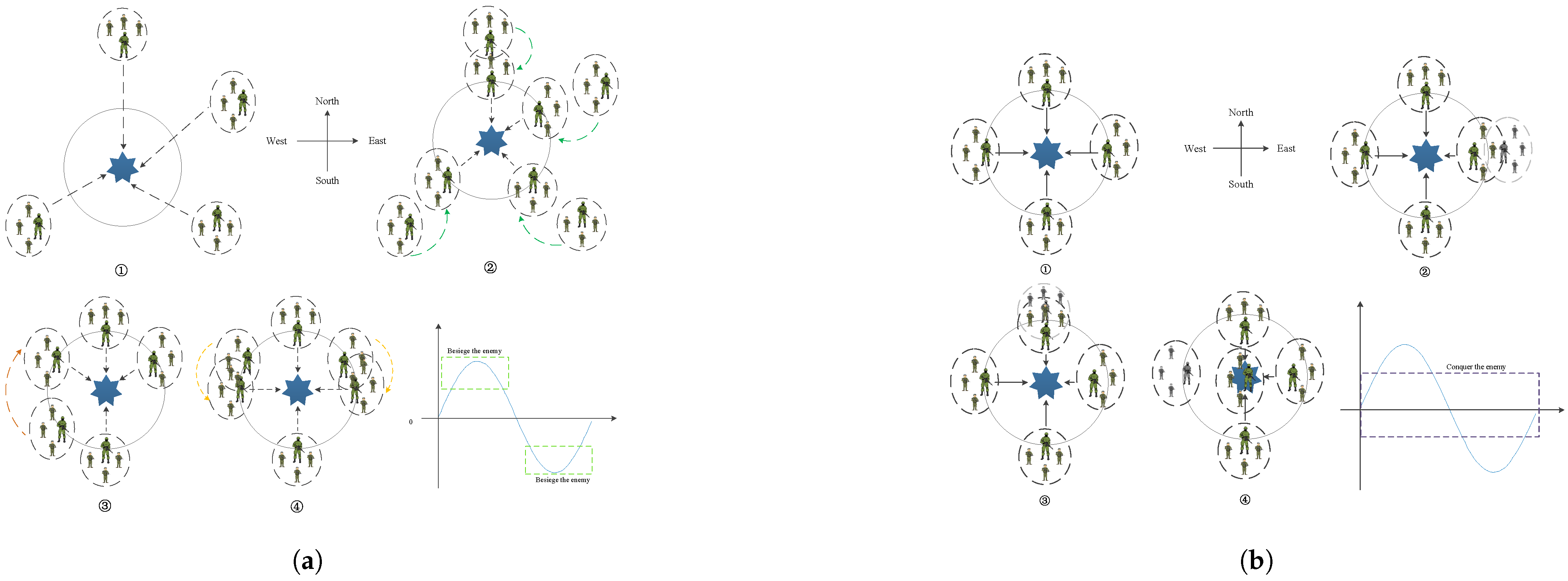
3.1. Inspiration
3.2. Initialization Phase
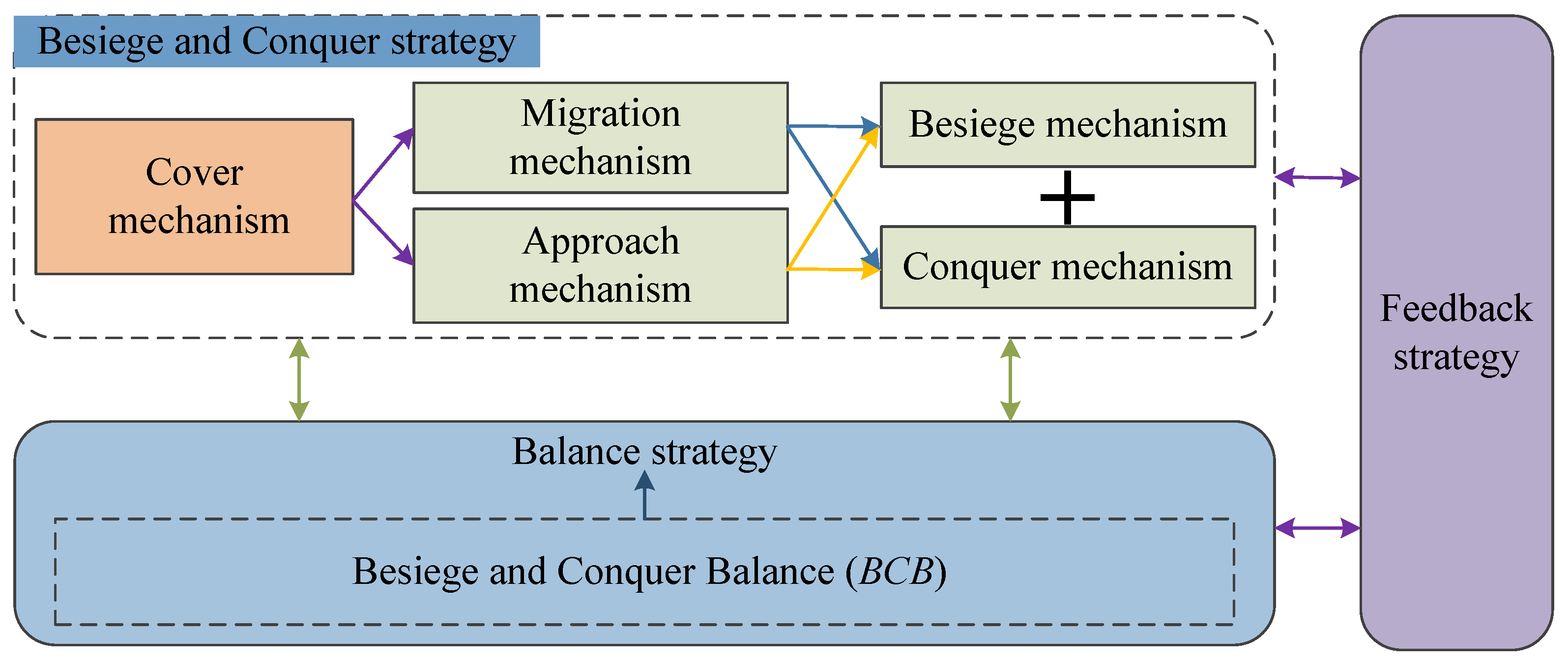
3.3. Besiege and Conquer Strategies
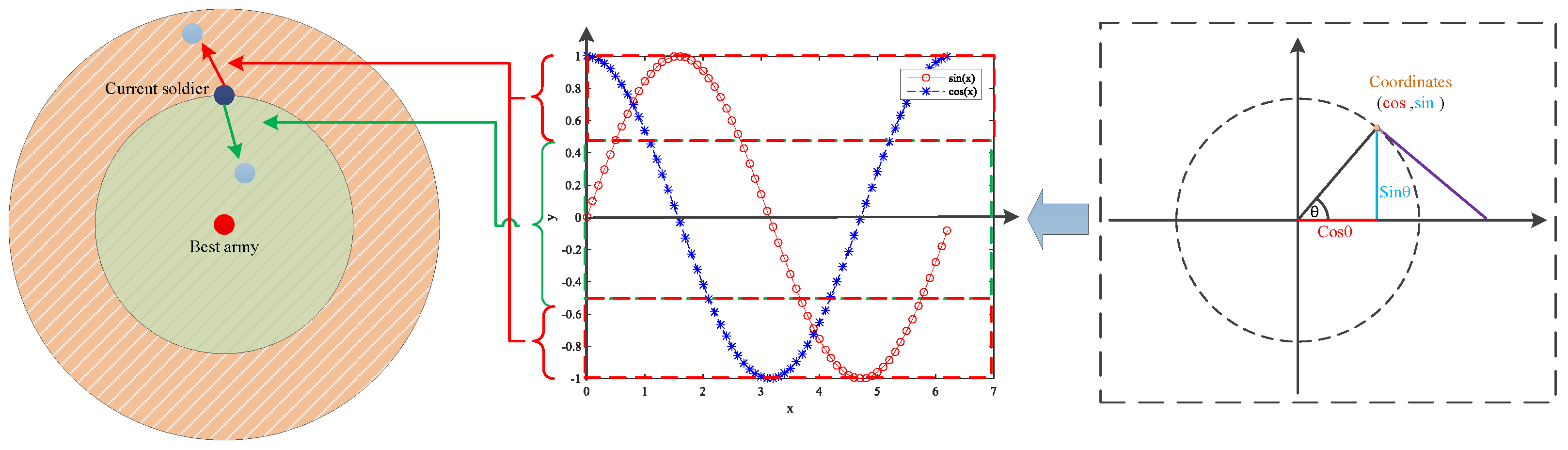
3.4. Balance Strategy
3.5. Feedback Strategy
3.6. Computational Complexity
- Problem definition is set as O(1).
- Initialization of the population demands .
- Generation of soldiers demands .
- Evaluation of solutions demands .
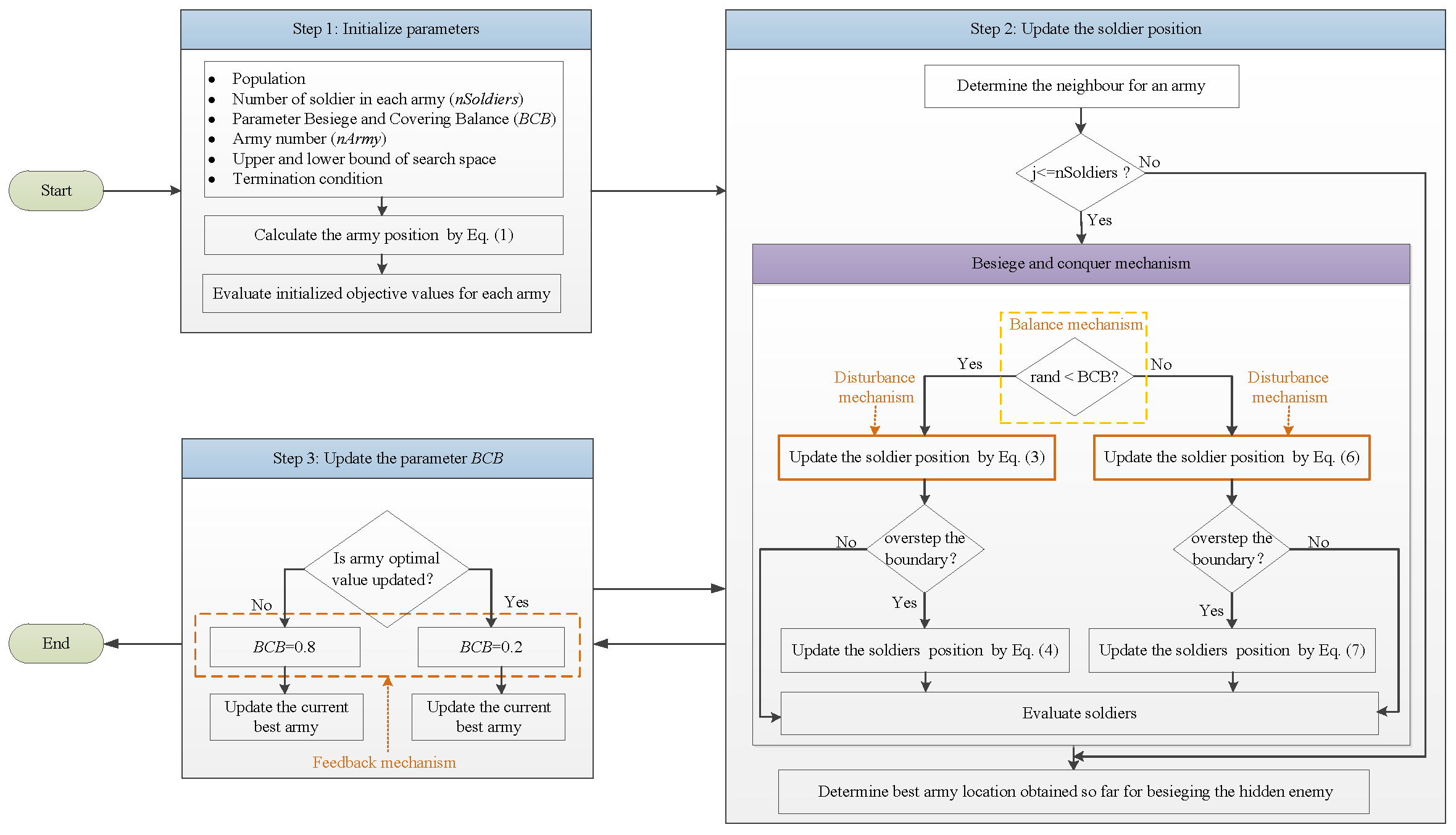
| Algorithm 1 BCA: Besiege and Conquer Algorithm |
| Step 1: Initialize parameters: 1.1 Initialize population and the number of soldiers (nSoldiers). 1.2 Put up Besiege and Conquer Balance (BCB) parameter. 1.3 Set the iteration number (MaxIteration). 1.4 Set the number of army (nArmy). 1.5 Initialize the upper bound (ub) and lower bound (lb) of the search space. 1.6 Determine the termination condition (MaxIteration). 1.7 Initialize the army position through Equation (1). 1.8 Evaluate initialized objective values for each army. Step 2: While t < MaxIter 2.1 For i: nArmy 2.1.1 Determination of the neighbor for army 2.1.2 For j: nSoldiers For d: dim If rand BCB Update the position of the soldier by Equation (3) If Update the position of the soldier by Equation (4) End If Else Update the position of the soldier by Equation (6) If () Update the position of the soldier by Equation (7) End If End For End For End For 2.1.3 Evaluate soldiers’ objectives in each army End While Step 3: 3.1 Determine the best army location obtained so far. 3.2 Judge whether the army optimal value is updated. 3.3 If army optimal value is updated ; Else ; End If Step 4: Update the best army. |
4. Experiment Setting
4.1. Experimental Test Functions
4.2. Comparative Algorithms
5. Experimental Results and Discussion
5.1. Computational Complexity Analysis
5.2. Parameters Sensitivity
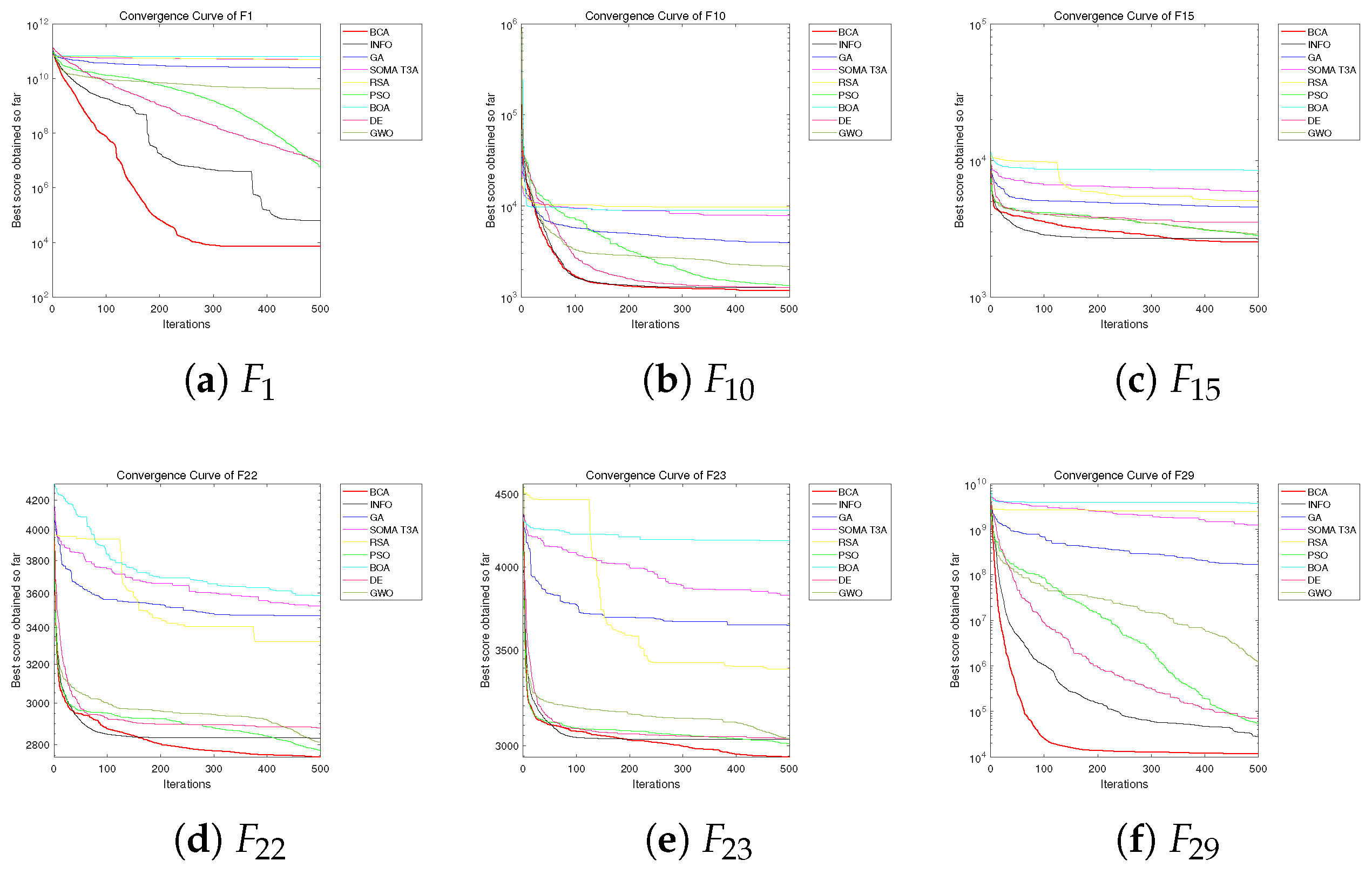
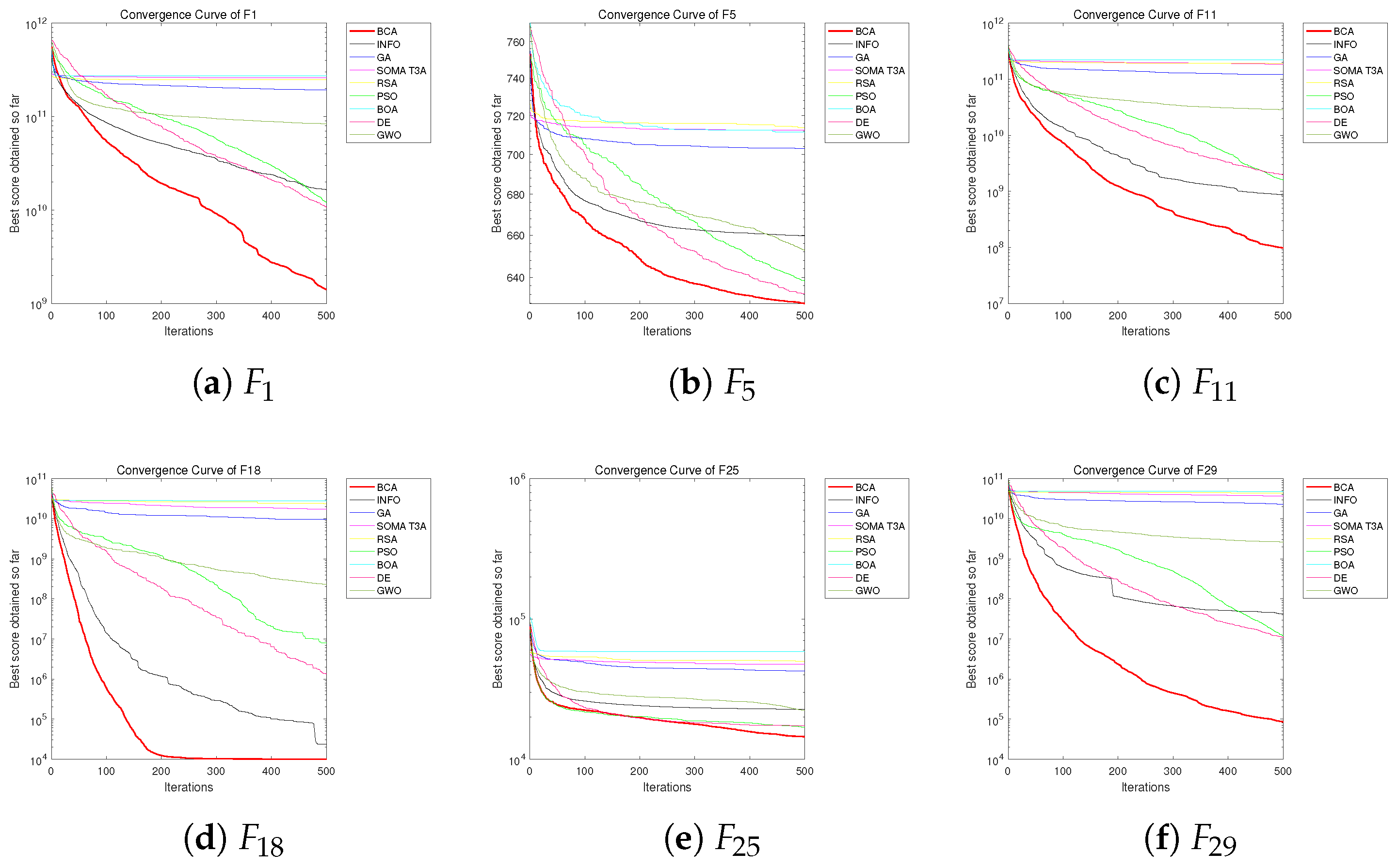
5.3. Exploitation Analysis
5.4. Exploration Analysis
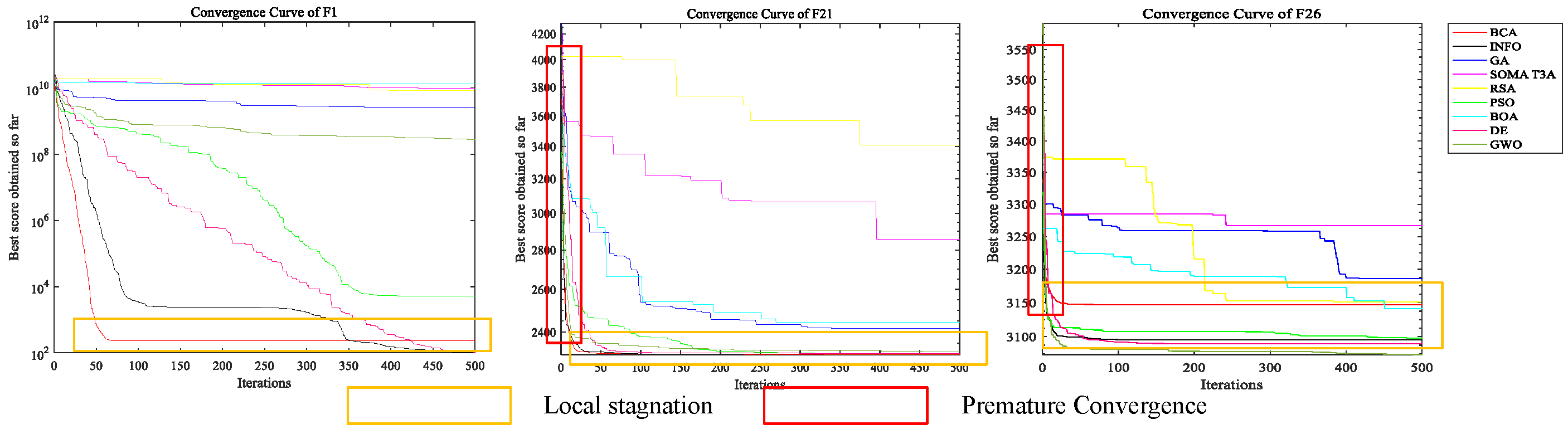
5.5. Local Minima Avoidance Analysis
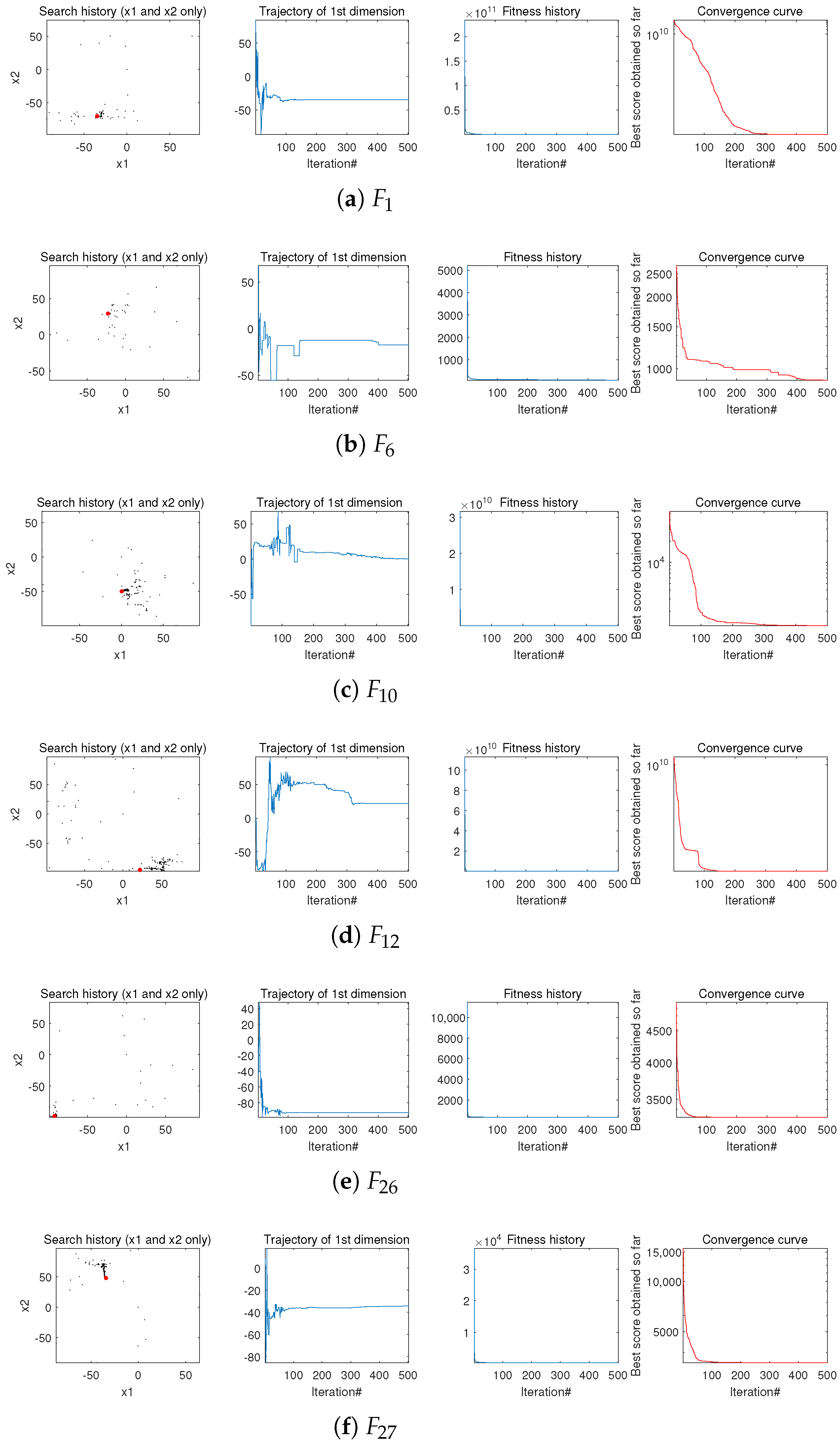
5.6. Qualitative Analysis
5.7. Quantitative Analysis
5.8. Limitation Analysis
6. Real-World Engineering Problems
6.1. Optimization Process
6.2. Tension/Compression Spring Design Problem
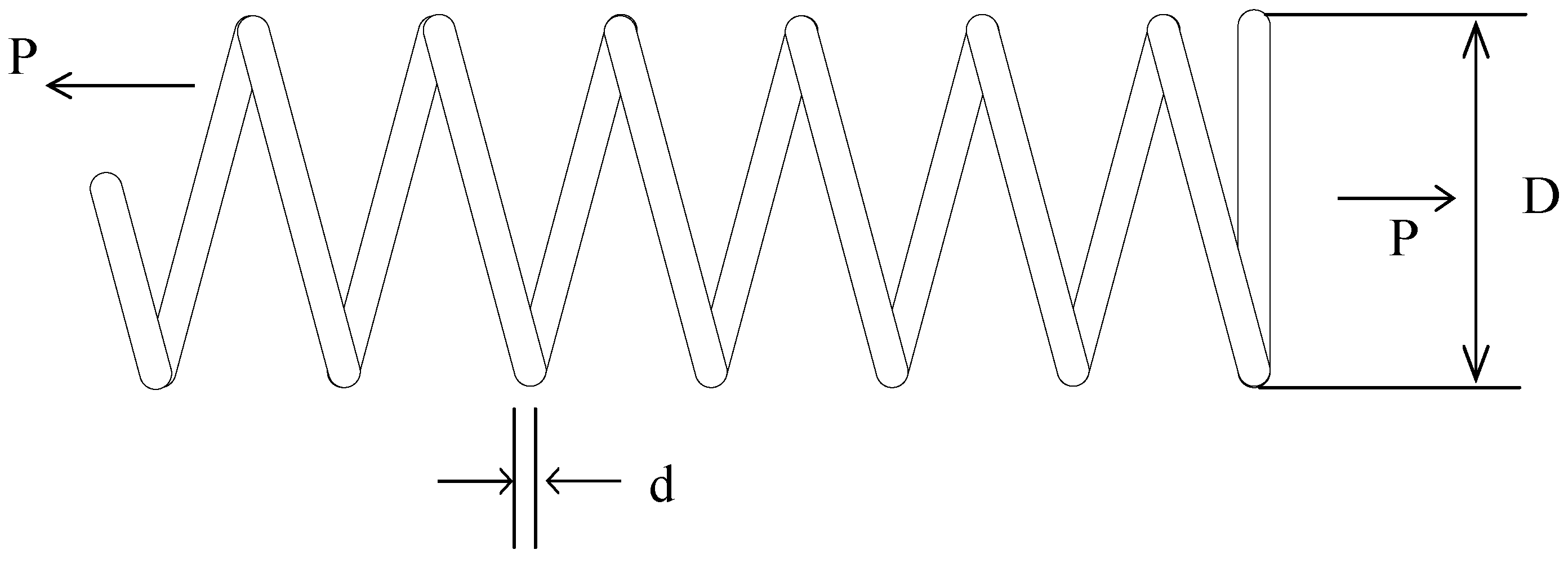
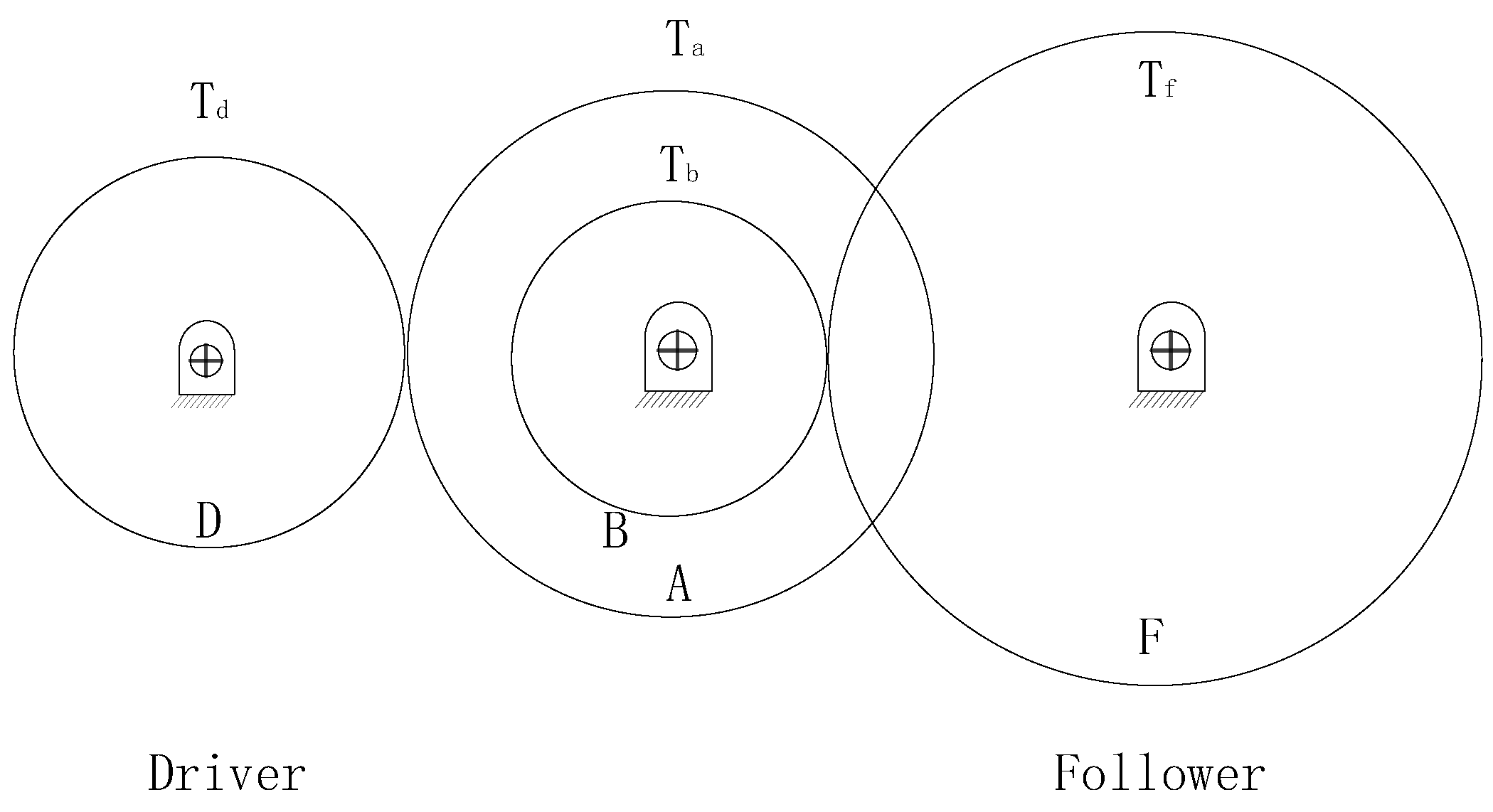
6.3. Gear Train Design Problem
7. BCA for Training MLPs
7.1. Optimization Process
7.2. Experimental Results on Three Datasets
7.2.1. Xor Dataset
7.2.2. Ballon Dataset
7.2.3. Tic-Tac-Toe Endgame Dataset
8. Conclusions and Future Work
- The besiege strategy can increase population diversity to enhance the exploration capability.
- The conquer strategy facilitates exploitation and delegates to the local search.
- The balance and feedback strategies not only enhance the balance between exploitation and exploration but also help to find the best solutions.
- The introduction of parameter BCB assists in gradually shifting its focus from exploitation to exploration, and avoiding local stagnation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bernal, C.P.; Angel, M.; Moya, C.M. Optimizing energy efficiency in unrelated parallel machine scheduling problem through reinforcement learning. Inf. Sci. 2024, 693, 121674. [Google Scholar] [CrossRef]
- Mazroua, A.A.; Bartnikas, R.; Salama, M. Neural network system using the multi-layer perceptron technique for the recognition of pd pulse shapes due to cavities and electrical trees. IEEE Trans. Power Deliv. 1995, 10, 92–96. [Google Scholar] [CrossRef]
- Chen, C.; da Silva, B.; Yang, C.; Ma, C.; Li, J.; Liu, C. Automlp: A framework for the acceleration of multi-layer perceptron models on FPGAs for real-time atrial fibrillation disease detection. IEEE Trans. Biomed. Circuits Syst. 2023, 12, 1371–1386. [Google Scholar] [CrossRef]
- Rojas, M.G.; Olivera, A.C.; Vidal, P.J. A genetic operators-based ant lion optimiser for training a medical multi-layer perceptron. Appl. Soft Comput. 2024, 151, 111192. [Google Scholar] [CrossRef]
- Erdogmus, D.; Fontenla-Romero, O.; Principe, J.C.; Alonso-Betanzos, A.; Castillo, E. Linear-least-squares initialization of multilayer perceptrons through backpropagation of the desired response. IEEE Trans. Neural Netw. 2005, 16, 325–337. [Google Scholar] [CrossRef]
- Zervoudakis, K.; Tsafarakis, S. A global optimizer inspired from the survival strategies of flying foxes. Eng. Comput. 2023, 39, 1–34. [Google Scholar] [CrossRef]
- Połap, D.; Woźniak, M. Polar bear optimization algorithm: Meta-heuristic with fast population movement and dynamic birth and death mechanism. Symmetry 2017, 9, 203. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Ali, A.; Assam, M.; Khan, F.U.; Ghadi, Y.Y.; Nurdaulet, Z.; Zhibek, A.; Shah, S.Y.; Alahmadi, T.J. An optimized multilayer perceptron-based network intrusion detection using gray wolf optimization. Comput. Electr. Eng. 2024, 120, 109838. [Google Scholar] [CrossRef]
- Li, X.-D.; Wang, J.-S.; Hao, W.-K.; Wang, M.; Zhang, M. Multi-layer perceptron classification method of medical data based on biogeography-based optimization algorithm with probability distributions. Appl. Soft Comput. 2022, 121, 108766. [Google Scholar] [CrossRef]
- Zervoudakis, K.; Tsafarakis, S. A mayfly optimization algorithm. Comput. Ind. Eng. 2020, 145, 106559. [Google Scholar] [CrossRef]
- Oyelade, O.N.; Aminu, E.F.; Wang, H.; Rafferty, K. An adaptation of hybrid binary optimization algorithms for medical image feature selection in neural network for classification of breast cancer. Neurocomputing 2024, 617, 129018. [Google Scholar] [CrossRef]
- Xue, Y.; Zhang, C. A novel importance-guided particle swarm optimization based on mlp for solving large-scale feature selection problems. Swarm Evol. Comput. 2024, 91, 101760. [Google Scholar] [CrossRef]
- Lu, Y.; Tang, Q.; Yu, S.; Cheng, L. A multi-strategy self-adaptive differential evolution algorithm for assembly hybrid flowshop lot-streaming scheduling with component sharing. Swarm Evol. Comput. 2025, 92, 101783. [Google Scholar] [CrossRef]
- Sörensen, K. Metaheuristics—The metaphor exposed. Int. Trans. Oper. Res. 2015, 22, 3–18. [Google Scholar] [CrossRef]
- Tong, M.; Peng, Z.; Wang, Q. A hybrid artificial bee colony algorithm with high robustness for the multiple traveling salesman problem with multiple depots. Expert Syst. Appl. 2025, 260, 125446. [Google Scholar] [CrossRef]
- Ansah-Narh, T.; Nortey, E.; Proven-Adzri, E.; Opoku-Sarkodie, R. Enhancing corporate bankruptcy prediction via a hybrid genetic algorithm and domain adaptation learning architecture. Expert Syst. Appl. 2024, 258, 125133. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, L.; Xie, L.; Hu, T.; Li, G.; Bai, S.; Yi, Z. Multilayer perceptron neural network with regression and ranking loss for patient-specific quality assurance. Knowl.-Based Syst. 2023, 271, 110549. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Heidari, A.A.; Noshadian, S.; Chen, H.; Gandomi, A.H. INFO: An efficient optimization algorithm based on weighted mean of vectors. Expert Syst. Appl. 2022, 195, 116516. [Google Scholar] [CrossRef]
- Abualigah, L.; Abd Elaziz, M.; Sumari, P.; Geem, Z.W.; Gandomi, A.H. Reptile search algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 2022, 191, 116158. [Google Scholar] [CrossRef]
- Diep, Q.B. Self-organizing migrating algorithm team to team adaptive–SOMA T3A. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 1182–1187. [Google Scholar]
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Belegundu, A.D.; Arora, J.S. A study of mathematical programming methods for structural optimization. Part I Theory Int. J. Numer. Methods Eng. 1985, 21, 1583–1599. [Google Scholar] [CrossRef]
- Prayoonrat, S.; Walton, D. Practical approach to optimum gear train design. Comput. Des. 1988, 20, 83–92. [Google Scholar] [CrossRef]
- McGarry, K.J.; Wermter, S.; MacIntyre, J. Knowledge extraction from radial basis function networks and multilayer perceptrons. In Proceedings of the IJCNN’99. International Joint Conference on Neural Networks. Proceedings (Cat. No. 99CH36339), Washington, DC, USA, 10–16 July 1999; Volume 4, pp. 2494–2497. [Google Scholar]
- Pazzani, M.J. Influence of prior knowledge on concept acquisition: Experimental and computational results. J. Exp. Psychol. Learn. Mem. Cogn. 1991, 17, 416–432. [Google Scholar] [CrossRef][Green Version]
- Aha, D.W. Incremental constructive induction: An instance-based approach. In Machine Learning Proceedings 1991; Morgan Kaufmann: Burlington, MA, USA, 1991; pp. 117–121. [Google Scholar]
- Renkavieski, C.; Parpinelli, R.S. Meta-heuristic algorithms to truss optimization: Literature mapping and application. Expert Syst. Appl. 2021, 182, 115197. [Google Scholar] [CrossRef]
- Jian, Z.; Zhu, G. Affine invariance of meta-heuristic algorithms. Inf. Sci. 2021, 576, 37–53. [Google Scholar] [CrossRef]
- Rechenberg, I. Evolution Strategy: Optimization of Technical Systems by Means of Biological Evolution; Fromman-Holzboog: Stuttgart, Germany, 1973; Volume 104, pp. 15–16. [Google Scholar]
- Hillis, W.D. Co-evolving parasites improve simulated evolution as an optimization procedure. Phys. D Nonlinear Phenom. 1990, 42, 228–234. [Google Scholar] [CrossRef]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialis-tic competition. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 4661–4667. [Google Scholar]
- Civicioglu, P. Transforming geocentric cartesian coordinates to geodetic coordinates by using differential search algorithm. Comput. Geosci. 2012, 46, 229–247. [Google Scholar] [CrossRef]
- Civicioglu, P. Backtracking search optimization algorithm for numerical optimization problems. Appl. Math. Comput. 2013, 219, 8121–8144. [Google Scholar] [CrossRef]
- Salimi, H. Stochastic fractal search: A powerful meta-heuristic algorithm. Knowl.-Based Syst. 2015, 75, 1–18. [Google Scholar] [CrossRef]
- Dhivyaprabha, T.; Subashini, P.; Krishnaveni, M. Synergistic fibroblast optimization: A novel nature-inspired computing algorithm. Front. Inf. Technol. Electron. Eng. 2018, 19, 815–833. [Google Scholar] [CrossRef]
- Motevali, M.M.; Shanghooshabad, A.M.; Aram, R.Z.; Keshavarz, H. Who: A new evolutionary algorithm bio-inspired by wildebeests with a case study on bank customer segmentation. Int. J. Pattern Recognit. Artif. Intell. 2019, 33, 1959017. [Google Scholar] [CrossRef]
- Rahman, M.C.; Rashid, A.T. A new evolutionary algorithm: Learner performance based behavior algorithm. Egypt. Inform. J. 2021, 22, 213–223. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- He, S.; Wu, Q.H.; Saunders, J.R. Group search optimizer: An optimization algorithm inspired by animal searching behavior. IEEE Trans. Evol. Comput. 2009, 13, 973–990. [Google Scholar] [CrossRef]
- Kaveh, A.; Mahdavi, V.R. Colliding bodies optimization: A novel meta-heuristic method. Comput. Struct. 2014, 139, 18–27. [Google Scholar] [CrossRef]
- Kashan, A.H. League championship algorithm (LCA): An algorithm for global optimization inspired by sport champi-onships. Appl. Soft Comput. 2014, 16, 171–200. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, M.; Gao, L.; Pan, Q. Queuing search algorithm: A novel metaheuristic algorithm for solving engineering optimization problems. Appl. Math. Model. 2018, 63, 464–490. [Google Scholar] [CrossRef]
- Zhang, L.M.; Dahlmann, C.; Zhang, Y. Human-inspired algorithms for continuous function optimization. In Proceedings of the 2009 IEEE International Conference on Intelligent Computing and Intelligent Systems, Shanghai, China, 20–22 November 2009; IEEE: Piscataway, NJ, USA, 2009; Volume 1, pp. 318–321. [Google Scholar]
- Shayeghi, H.; Dadashpour, J. Anarchic society optimization based pid control of an automatic voltage regulator (avr) system. Electr. Electron. Eng. 2012, 2, 199–207. [Google Scholar] [CrossRef]
- Mousavirad, S.J.; Ebrahimpour-Komleh, H. Human mental search: A new population-based meta-heuristic optimization algorithm. Appl. Intell. 2017, 47, 850–887. [Google Scholar] [CrossRef]
- Moghdani, R.; Salimifard, K. Volleyball premier league algorithm. Appl. Soft Comput. 2018, 64, 161–185. [Google Scholar] [CrossRef]
- Mohamed, A.W.; Hadi, A.A.; Mohamed, A.K. Gaining-sharing knowledge based algorithm for solving optimization problems: A novel nature-inspired algorithm. Int. J. Mach. Learn. Cybern. 2020, 11, 1501–1529. [Google Scholar] [CrossRef]
- Al-Betar, M.A.; Alyasseri, Z.A.A.; Awadallah, M.A.; Abu Doush, I. Coronavirus herd immunity optimizer (CHIO). Neural Comput. Appl. 2021, 33, 5011–5042. [Google Scholar] [CrossRef] [PubMed]
- Braik, M.; Ryalat, M.H.; Al-Zoubi, H. A novel meta-heuristic algorithm for solving numerical optimization problems: Ali baba and the forty thieves. Neural Comput. Appl. 2022, 34, 409–455. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Rashedi, E.; Rashedi, E.; Nezamabadi-Pour, H. A comprehensive survey on gravitational search algorithm. Swarm Evol. Comput. 2018, 41, 141–158. [Google Scholar] [CrossRef]
- Formato, R.A. Central force optimization. Prog Electromagn Res. 2007, 77, 425–491. [Google Scholar] [CrossRef]
- Mladenović, N.; Hansen, P. Variable neighborhood search. Comput. Oper. Res. 1997, 24, 1097–1100. [Google Scholar] [CrossRef]
- Erol, O.K.; Eksin, I. A new optimization method: Big bang–big crunch. Adv. Eng. Softw. 2006, 37, 106–111. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Hatamlou, A. Black hole: A new heuristic optimization approach for data clustering. Inf. Sci. 2013, 222, 175–184. [Google Scholar] [CrossRef]
- Shareef, H.; Ibrahim, A.A.; Mutlag, A.H. Lightning search algorithm. Appl. Soft Comput. 2015, 36, 315–333. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Kaveh, A.; Dadras, A. A novel meta-heuristic optimization algorithm: Thermal exchange optimization. Adv. Eng. Softw. 2017, 110, 69–84. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Jiang, J.; Meng, X.; Chen, Y.; Qiu, C.; Liu, Y.; Li, K. Enhancing tree-seed algorithm via feed-back mechanism for optimizing continuous problems. Appl. Soft Comput. 2020, 92, 106314. [Google Scholar] [CrossRef]
- Mavrovouniotis, M.; Li, C.; Yang, S. A survey of swarm intelligence for dynamic optimization: Algorithms and applications. Swarm Evol. Comput. 2017, 33, 1–17. [Google Scholar] [CrossRef]
- Jiang, J.; Liu, Y.; Zhao, Z. TriTSA: Triple tree-seed algorithm for dimensional continuous optimization and constrained engineering problems. Eng. Appl. Artif. Intell. 2021, 104, 104303. [Google Scholar] [CrossRef]
- Jiang, J.; Meng, X.; Qian, L.; Wang, H. Enhance tree-seed algorithm using hierarchy mechanism for constrained optimization problems. Expert Syst. Appl. 2022, 209, 118311. [Google Scholar] [CrossRef]
- Jiang, J.; Zhao, Z.; Liu, Y.; Li, W.; Wang, H. DSGWO: An improved grey wolf optimizer with diversity enhanced strategy based on group-stage competition and balance mechanisms. Knowl.-Based Syst. 2022, 250, 109100. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly algorithms for multimodal optimization. In International Symposium on Stochastic Algorithms; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. [Google Scholar]
- Pan, W.-T. A new fruit fly optimization algorithm: Taking the financial distress model as an example. Knowl.-Based Syst. 2012, 26, 69–74. [Google Scholar] [CrossRef]
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Kiran, M.S. TSA: Tree-seed algorithm for continuous optimization. Expert Syst. Appl. 2015, 42, 6686–6698. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper optimisation algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp swarm algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Alsattar, H.A.; Zaidan, A.; Zaidan, B. Novel meta-heuristic bald eagle search optimisation algorithm. Artif. Intell. Rev. 2020, 53, 2237–2264. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-Qaness, M.A.; Gandomi, A.H. Aquila optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Połap, D.; Woźniak, M. Red fox optimization algorithm. Expert Syst. Appl. 2021, 166, 114107. [Google Scholar] [CrossRef]
- Bairwa, A.K.; Joshi, S.; Singh, D. Dingo Optimizer: A nature-inspired metaheuristic approach for engineering problems. Math. Probl. Eng. 2021, 2021, 2571863. [Google Scholar] [CrossRef]
- Braik, M.S. Chameleon swarm algorithm: A bio-inspired optimizer for solving engineering design problems. Expert. Syst. Appl. 2021, 174, 114685. [Google Scholar] [CrossRef]
- Braik, M.; Hammouri, A.; Atwan, J.; Al-Betar, M.A.; Awadallah, M.A. White shark optimizer: A novel bio-inspired meta-heuristic algorithm for global optimization problems. Knowl.-Based Syst. 2022, 243, 108457. [Google Scholar] [CrossRef]
- Guan, X.; Hu, T.; Zhang, Z.; Wang, Y.; Liu, Y.; Wang, Y.; Hao, J.; Li, G. Multi-layer perceptron-particle swarm optimization: A lightweight optimization algorithm for the model predictive control local planner. Int. J. Adv. Robot. Syst. 2024, 21, 17298806241301581. [Google Scholar] [CrossRef]
- Kumari, V.; Kumar, P.R. Optimization of multi-layer perceptron neural network using genetic algorithm for arrhythmia classification. Communications 2015, 3, 150–157. [Google Scholar] [CrossRef][Green Version]
- Piotrowski, A.P. Differential evolution algorithms applied to neural network training suffer from stagnation. Appl. Soft Comput. 2014, 21, 382–406. [Google Scholar] [CrossRef]
- Stober, E.O. The hunger games: Weaponizing food. Mark. Ideas 2022, 37, 1–8. [Google Scholar]
- Madhi, W.T.; Abd, S.M. Characteristics of the hero in contemporary arabic poetry. PalArch’s J. Archaeol. Egypt/Egyptology 2021, 18, 1846–1862. [Google Scholar]
- Janson, H.W. The equestrian monument from cangrande della scala to peter the great. In Aspects of the Renaissance; University of Texas Press: Austin, TX, USA, 2021; pp. 73–86. [Google Scholar]
- Sanders, R. The pareto principle: Its use and abuse. J. Serv. Mark. 1987, 1, 37–40. [Google Scholar] [CrossRef]
- Hernández, G.; Zamora, E.; Sossa, H.; Téllez, G.; Furlán, F. Hybrid neural networks for big data classification. Neurocomputing 2020, 390, 327–340. [Google Scholar] [CrossRef]
- Meng, X.; Jiang, J.; Wang, H. AGWO: Advanced GWO in multi-layer perception optimization. Expert Syst. Appl. 2021, 173, 114676. [Google Scholar] [CrossRef]





| Algorithm | Abbreviations | Authors and Year |
|---|---|---|
| Evolution Strategy | ES | Rechenberg et al., 1973 [34] |
| Genetic Algorithm | GA | Holland et al., 1992 [10] |
| CoEvolutionary Algorithm | CEA | Hillis et al., 1990 [35] |
| Differential Evolution | DE | Storn et al., 1997 [25] |
| Imperialist Competitive Algorithm | ICA | Atashpaz-Gargari et al., 2007 [36] |
| Differential Search Algorithm | DSA | Civicioglu et al., 2012 [37] |
| Backtracking Search Optimization Algorithm | BSA | Civicioglu et al., 2013 [38] |
| Stochastic Fractal Search | SFS | Salimi et al., 2015 [39] |
| Synergistic Fibroblast Optimization | SFO | Dhivyaprabha et al., 2018 [40] |
| Wildebeests Herd Optimization | WHO | Motevali et al., 2019 [41] |
| Learner Performance based Behavior Algorithm | LPB | Rahman et al., 2021 [42] |
| Algorithms | Abbreviations | Authors and Year |
|---|---|---|
| Imperialist Competitive Algorithm | ICA | Atashpaz-Gargari et al., 2007 [36] |
| Human-Inspired Algorithm | HIA | Zhang et al., 2009 [48] |
| League Championship Algorithm | LCA | Kashan et al., 2014 [46] |
| Teaching–Learning-Based Optimization | TLBO | Rao et al., 2011 [43] |
| Anarchic Society Optimization | ASO | Shayeghi et al., 2012 [49] |
| Human Mental Search | HMS | Mousavirad et al., 2017 [50] |
| Volleyball Premier League | VPL | Moghdani et al., 2018 [51] |
| Gaining Sharing Knowledge | GSK | Mohamed et al., 2020 [52] |
| Coronavirus Herd Immunity Optimizer | CHIO | Al-Betar et al., 2021 [53] |
| Ali baba and the Forty Thieves | AFT | Braik et al., 2022 [54] |
| Algorithms | Abbreviations | Authors and Year |
|---|---|---|
| Simulated Annealing | SA | Kirkpatrick et al., 1983 [55] |
| Variable Neighborhood Search | VNS | Mladenović et al., 1997 [58] |
| Big Bang–Big Crunch | BB-BC | Erol et al., 2006 [59] |
| Central Force Optimization | CFO | Formato et al., 2007 [57] |
| Gravitational Search Algorithm | GSA | Rashedi et al., 2009 [60] |
| Black Hole Algorithm | BHA | Hatamlou et al., 2013 [61] |
| Colliding Bodies Optimization | CBO | Kaveh et al., 2014 [45] |
| Lightning Search Algorithm | LSA | Shareef et al., 2015 [62] |
| Multi-Verse Optimizer | MVO | Mirjalili et al., 2016 [63] |
| Thermal Exchange Optimization | TEO | Kaveh et al., 2017 [64] |
| Equilibrium Optimizer | EO | Faramarzi et al., 2020 [65] |
| Algorithms | Abbreviations | Authors and Year |
|---|---|---|
| Ant Colony Optimization | ACO | Dorigo et al., 1991 [9] |
| Particle Swarm Optimization | PSO | Kennedy et al., 1995 [26] |
| Firefly Algorithm | FA | Yang Xin-She, 2009 [71] |
| Fruit Fly Optimization | FOA | Pan Wen-Tsao, 2012 [72] |
| Ant Lion Optimizer | ALO | Mirjalili 2015 [73] |
| Tree-Seed Algorithm | TSA | Kiran, 2015 [74] |
| Dragonfly Algorithm | DA | Mirjalili et al., 2016 [75] |
| Whale Optimization Algorithm | WOA | Mirjalili et al., 2016 [76] |
| Grasshopper Optimization Algorithm | GOA | Saremi et al., 2017 [77] |
| Salp Swarm Algorithm | SSA | Mirjalili et al., 2017 [78] |
| Butterfly Optimization Algorithm | BOA | Arora et al., 2019 [24] |
| Bald Eagle Search Algorithm | BES | Alsattar et al., 2020 [79] |
| Harris Hawks Optimizer | HHO | Abualigah et al., 2021 [80] |
| Red Fox Optimizer | RFO | Połap et al., 2021, [81] |
| Dingo Optimization Algorithm | DOA | Bairwa et al., 2021 [82] |
| Chameleon Swarm Algorithm | CSA | Braik, 2021 [83] |
| Reptile Search Algorithm | RSA | Abualigah et al., 2022 [22] |
| White Shark Optimizer | WSO | Braik Malik et al., 2022 [84] |
| Notation | Meaning |
|---|---|
| The dimension of the army | |
| The soldier of the dimension with iteration | |
| The current best army (discovered enemy) with iteration | |
| A random army of the dimension with iteration | |
| Regularization parameter | |
| The cover coefficient | |
| lb,ub | The lower and upper bound of the given search space |
| nSoldiers | The number of soldiers |
| BCB | Besiege and Conquer Balance |
| Algorithms | Parameter | Value | Reference |
|---|---|---|---|
| BCA | BCB | 0.8 | |
| nSoldiers | 3 | ||
| INFO | No hyperparameter settings | [21] | |
| RSA | Evolutionary sense | [22] | |
| Sensitive parameter controlling the exploration accuracy | 0.005 | ||
| Sensitive parameter controlling the exploitation accuracy | 0.1 | ||
| GWO | a | Liner from 2 to 0 | [8] |
| BOA | Power exponent | 0.1 | [24] |
| Sensory modality | 0.01 | ||
| Probability switch (p) | 0.8 | ||
| SOMA T3A | Step | [23] | |
| PRT | 0.05 + 0.95 | ||
| PSO | Cognitive component | 2 | [26] |
| Social component | 2 | ||
| DE | Scale factor primary | 0.6 | [25] |
| Scale factor secondary | 0.5 | ||
| Scale factor secondary | 0.3 | ||
| Crossover rate | 0.8 | ||
| GA | CrossPercent | 70% | [10] |
| MutatPercent | 20% | ||
| ElitPercent | 10% | ||
| 10D | 30D | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Function | nSoldier = 2 | nSoldier = 3 | nSoldier = 4 | nSoldier = 5 | Function | nSoldier = 2 | nSoldier = 3 | nSoldier = 4 | nSoldier = 5 | ||
| Unimodal Functions | 3.0846 | 2.7349 | 7.7035 | 1.3394 | Unimodal Functions | 5.4825 | 5.8610 | 1.1128 | 4.2021 | ||
| 3.0949 | 3.0000 | 2.4666 | 1.0033 | 9.5782 | 9.1813 | 8.8295 | 9.6163 | ||||
| Multimodal Functions | 4.0602 | 4.0906 | 4.3333 | 4.2246 | Multimodal Functions | 4.8535 | 5.1259 | 7.6105 | 1.4731 | ||
| 5.1145 | 5.1430 | 5.2292 | 5.2810 | 6.9397 | 6.3094 | 6.3101 | 6.8227 | ||||
| 6.0000 | 6.0032 | 6.0344 | 6.1100 | 6.0028 | 6.0157 | 6.2252 | 6.3103 | ||||
| 7.3803 | 7.2268 | 7.3195 | 7.4333 | 9.6636 | 9.4231 | 1.0266 | 1.1529 | ||||
| 8.1197 | 8.1401 | 8.2305 | 8.2462 | 1.0044 | 9.1677 | 9.2094 | 9.5984 | ||||
| 9.0035 | 9.0559 | 1.0147 | 1.0088 | 9.6527 | 1.2018 | 3.4503 | 4.0112 | ||||
| 1.6642 | 1.5155 | 1.6689 | 1.7918 | 8.6455 | 8.0815 | 6.6932 | 5.7858 | ||||
| Hybrid Functions | 1.1060 | 1.1169 | 1.1516 | 1.6462 | Hybrid Functions | 1.2447 | 1.1850 | 3.3216 | 4.0884 | ||
| 1.4101 | 1.8262 | 7.6760 | 2.7037 | 5.6230 | 9.7535 | 1.2471 | 1.2526 | ||||
| 6.3975 | 1.0754 | 8.7964 | 1.2086 | 2.1185 | 2.3155 | 1.7233 | 3.0925 | ||||
| 1.4446 | 1.4436 | 1.4575 | 2.2201 | 4.5091 | 7.8492 | 1.0781 | 1.6536 | ||||
| 1.6004 | 1.5665 | 2.0493 | 6.5510 | 1.2666 | 1.1432 | 1.3389 | 3.9439 | ||||
| 1.6235 | 1.6946 | 1.8341 | 1.8097 | 3.2972 | 2.8115 | 2.6830 | 2.8585 | ||||
| 1.7339 | 1.7370 | 1.7720 | 1.7691 | 2.0290 | 2.0641 | 2.1830 | 2.3095 | ||||
| 7.6635 | 7.5756 | 9.1449 | 8.5387 | 1.8141 | 1.4815 | 3.4402 | 5.0139 | ||||
| 2.0163 | 1.9412 | 2.9480 | 3.3431 | 1.1171 | 1.4182 | 1.5584 | 6.6029 | ||||
| 2.0093 | 2.0347 | 2.1076 | 2.1114 | 2.4423 | 2.4354 | 2.5215 | 2.5333 | ||||
| Composition Functions | 2.3135 | 2.2993 | 2.3069 | 2.3106 | Composition Functions | 2.5061 | 2.4294 | 2.4247 | 2.4567 | ||
| 2.3542 | 2.2991 | 2.4485 | 2.3745 | 3.6015 | 5.3314 | 5.1472 | 5.8761 | ||||
| 2.6134 | 2.6172 | 2.6336 | 2.6467 | 2.7878 | 2.7657 | 2.8392 | 2.9193 | ||||
| 2.7260 | 2.7278 | 2.7333 | 2.7556 | 3.0183 | 2.9604 | 2.9892 | 3.0420 | ||||
| 2.9366 | 2.9315 | 2.9410 | 2.9384 | 2.8892 | 2.8986 | 3.0963 | 3.2930 | ||||
| 3.1356 | 3.3707 | 3.1790 | 3.2100 | 4.7202 | 4.3892 | 5.4223 | 6.7499 | ||||
| 3.1030 | 3.1240 | 3.1397 | 3.1405 | 3.2282 | 3.2482 | 3.3226 | 3.3470 | ||||
| 3.3097 | 3.2913 | 3.3675 | 3.4173 | 3.2279 | 3.2397 | 3.5564 | 3.9394 | ||||
| 3.2144 | 3.2056 | 3.2466 | 3.2717 | 3.7674 | 3.7521 | 4.0859 | 4.1870 | ||||
| 2.0827 | 2.8017 | 6.0841 | 1.0338 | 1.2610 | 1.0956 | 1.5343 | 2.0374 | ||||
| 50D | 100D | ||||||||||
| Function | nSoldier= 2 | nSoldier= 3 | nSoldier= 4 | nSoldier= 5 | Function | nSoldier= 2 | nSoldier= 3 | nSoldier= 4 | nSoldier= 5 | ||
| Unimodal Functions | 2.2155 | 2.0239 | 6.7977 | 2.1753 | Unimodal Functions | 4.2844 | 2.5720 | 6.2050 | 1.2140 | ||
| 2.4021 | 2.4341 | 2.3537 | 2.3822 | 6.4573 | 6.3313 | 6.5750 | 6.7979 | ||||
| Multimodal Functions | 5.8195 | 5.9412 | 1.8270 | 3.6785 | Multimodal Functions | 1.5671 | 1.1256 | 9.3277 | 2.1264 | ||
| 9.0606 | 8.1345 | 7.7596 | 8.8940 | 1.6604 | 1.4450 | 1.3806 | 1.6253 | ||||
| 6.0550 | 6.0710 | 6.3175 | 6.4129 | 6.3002 | 6.2828 | 6.4901 | 6.6447 | ||||
| 1.2670 | 1.2209 | 1.5840 | 2.0320 | 2.4678 | 2.5133 | 3.8345 | 5.0119 | ||||
| 1.2240 | 1.0672 | 1.1088 | 1.1795 | 1.9327 | 1.7600 | 1.7474 | 1.9928 | ||||
| 4.0432 | 5.3850 | 1.3424 | 1.9343 | 3.5799 | 3.8626 | 6.4847 | 7.6842 | ||||
| 1.5238 | 1.5087 | 1.2615 | 1.1332 | 3.2727 | 3.2433 | 3.1304 | 2.9131 | ||||
| Hybrid Functions | 1.8119 | 1.5757 | 5.9873 | 1.4609 | Hybrid Functions | 1.4601 | 1.4255 | 9.7561 | 1.1785 | ||
| 7.5257 | 5.7793 | 9.4934 | 3.9893 | 3.5939 | 1.1284 | 1.2216 | 2.7504 | ||||
| 9.1517 | 1.2298 | 1.1167 | 7.9810 | 1.5045 | 1.3561 | 6.7898 | 3.4474 | ||||
| 2.7398 | 5.6463 | 3.3394 | 6.5692 | 4.8115 | 2.7004 | 1.8884 | 2.8560 | ||||
| 7.7526 | 8.2671 | 4.3185 | 3.8452 | 7.3906 | 7.3133 | 8.2907 | 8.4903 | ||||
| 5.0489 | 4.2202 | 3.4537 | 3.9827 | 1.1266 | 1.0296 | 7.4809 | 8.4029 | ||||
| 3.9683 | 3.6335 | 3.3731 | 3.5296 | 7.8248 | 7.4606 | 6.8917 | 1.5298 | ||||
| 8.3843 | 4.4784 | 9.7898 | 2.2358 | 1.9926 | 1.3042 | 1.8313 | 3.738 | ||||
| 1.9051 | 1.5268 | 8.9817 | 2.3109 | 1.1467 | 9.5134 | 7.4317 | 6.1740 | ||||
| 4.0439 | 3.6484 | 3.3779 | 3.487 | 7.6536 | 7.7604 | 7.0747 | 7.2755 | ||||
| Composition Functions | 2.7426 | 2.6121 | 2.6046 | 2.6857 | Composition Functions | 3.4163 | 3.2773 | 3.3503 | 3.5862 | ||
| 1.5769 | 1.5592 | 1.3809 | 1.3377 | 3.5191 | 3.492 | 3.0837 | 2.9716 | ||||
| 3.0911 | 3.0069 | 3.2211 | 3.3350 | 3.8555 | 3.5242 | 4.0349 | 4.1911 | ||||
| 3.3510 | 3.2801 | 3.3271 | 3.4428 | 4.4885 | 4.1094 | 4.9017 | 5.3913 | ||||
| 3.0758 | 3.0885 | 4.1700 | 5.9169 | 4.3383 | 3.8788 | 1.0377 | 1.6568 | ||||
| 7.6214 | 6.0522 | 8.8032 | 1.0473 | 1.7191 | 1.4683 | 2.1762 | 2.7959 | ||||
| 3.3861 | 3.4761 | 3.8879 | 4.1217 | 3.7895 | 3.6972 | 4.3947 | 4.7517 | ||||
| 3.3468 | 3.3626 | 5.2080 | 6.6049 | 5.3290 | 4.6914 | 1.4082 | 1.9022 | ||||
| 4.6264 | 4.34027 | 5.1836 | 5.6978 | 1.0077 | 7.9907 | 1.00667 | 1.4889 | ||||
| 1.1449 | 1.1202 | 1.2465 | 6.4638 | 3.5244 | 9.0104 | 4.7855 | 3.1963 | ||||
| Function Type | 30D | |||||||
| BCA vs. INFO (w/l/e) | BCA vs. RSA (w/l/e) | BCA vs. SOMA T3A (w/l/e) | BCA vs. GWO (w/l/e) | BCA vs. BOA (w/l/e) | BCA vs. DE (w/l/e) | BCA vs. PSO (w/l/e) | BCA vs. GA (w/l/e) | |
| Uni-model Function | 1/1/0 | 1/1/0 | 2/0/0 | 1/1/0 | 2/0/0 | 2/0/0 | 2/0/0 | 1/1/0 |
| Multi-model Function | 5/2/0 | 7/0/0 | 7/0/0 | 5/2/0 | 7/0/0 | 5/2/0 | 5/2/0 | 6/1/0 |
| Hybrid Functions | 5/5/0 | 10/0/0 | 10/0/0 | 9/1/0 | 10/0/0 | 5/5/0 | 8/2/0 | 10/0/0 |
| Composition Functions | 8/2/0 | 10/0/0 | 10/0/0 | 7/3/0 | 10/0/0 | 8/2/0 | 10/0/0 | 10/0/0 |
| Total | 19/11/0 | 28/1/0 | 29/0/0 | 22/7/0 | 29/0/0 | 20/9/0 | 25/4/0 | 27/2/0 |
| Function Type | 50D | |||||||
| BCA vs. INFO (w/l/e) | BCA vs. RSA (w/l/e) | BCA vs. SOMA T3A (w/l/e) | BCA vs. GWO (w/l/e) | BCA vs. BOA (w/l/e) | BCA vs. DE (w/l/e) | BCA vs. PSO (w/l/e) | BCA vs. GA (w/l/e) | |
| Uni-model Function | 1/1/0 | 2/0/0 | 1/1/0 | 2/0/0 | 2/0/0 | 2/0/0 | 2/0/0 | 1/1/0 |
| Multi-model Function | 5/2/0 | 7/0/0 | 7/0/0 | 6/1/0 | 7/0/0 | 5/2/0 | 6/1/0 | 6/1/0 |
| Hybrid Functions | 4/6/0 | 10/0/0 | 10/0/0 | 7/3/0 | 10/0/0 | 9/1/0 | 6/4/0 | 9/1/0 |
| Composition Functions | 8/2/0 | 10/10/0 | 10/10/0 | 8/2/0 | 10/10/0 | 9/1/0 | 9/1/0 | 9/1/0 |
| Total | 19/11/0 | 29/0/0 | 28/1/0 | 23/6/0 | 29/0/0 | 25/4/0 | 23/6/0 | 25/4/0 |
| Function Type | 100D | |||||||
| BCA vs. INFO (w/l/e) | BCA vs. RSA (w/l/e) | BCA vs. SOMA T3A (w/l/e) | BCA vs. GWO (w/l/e) | BCA vs. BOA (w/l/e) | BCA vs. DE (w/l/e) | BCA vs. PSO (w/l/e) | BCA vs. GA (w/l/e) | |
| Uni-model Function | 1/1/0 | 1/1/0 | 1/1/0 | 2/0/0 | 2/0/0 | 2/0/0 | 2/0/0 | 1/1/0 |
| Multi-model Function | 2/5/0 | 6/1/0 | 6/1/0 | 3/4/0 | 7/0/0 | 5/2/0 | 6/1/0 | 6/1/0 |
| Hybrid Functions | 4/6/0 | 10/0/0 | 9/1/0 | 8/2/0 | 10/0/0 | 9/1/0 | 6/4/0 | 9/1/0 |
| Composition Functions | 9/1/0 | 9/1/0 | 9/1/0 | 7/3/0 | 9/1/0 | 9/1/0 | 9/1/0 | 9/1/0 |
| Total | 16/13/0 | 26/3/0 | 25/4/0 | 20/9/0 | 28/1/0 | 25/4/0 | 23/6/0 | 25/4/0 |
| Function | BCA | INFO | RSA | SOMA_T3A | GWO | BOA | DE | PSO | GA | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Unimodal Functions | Mean | 7.3880 | 1.4797 | 4.8720 | 4.9633 | 4.1568 | 5.9652 | 6.0843 | 3.9834 | 2.6017 | |
| Std. | 6.7454 | 8.0437 | 6.5562 | 3.4129 | 1.8381 | 6.4292 | 3.7530 | 3.9821 | 3.3396 | ||
| Mean | 8.3146 | 1.5641 | 8.2286 | 8.3233 | 7.6636 | 8.1579 | 1.8618 | 1.0133 | 6.9717 | ||
| Std. | 1.7206 | 6.5204 | 4.6242 | 5.5701 | 1.4066 | 3.6184 | 2.6071 | 2.6407 | 7.6528 | ||
| Multimodal Functions | Mean | 4.9649 | 5.0578 | 1.0047 | 1.2526 | 7.3329 | 2.1430 | 4.9515 | 6.0999 | 6.8051 | |
| Std. | 3.0714 | 2.4421 | 3.1019 | 1.2582 | 2.6180 | 3.4920 | 1.1336 | 5.0173 | 1.0775 | ||
| Mean | 6.2601 | 6.5256 | 9.3392 | 9.1887 | 6.4466 | 9.3711 | 7.2164 | 6.2390 | 8.3551 | ||
| Std. | 6.4823 | 2.9596 | 2.7766 | 1.4446 | 4.1253 | 1.9692 | 1.5936 | 5.1134 | 2.7043 | ||
| Mean | 6.0272 | 6.2577 | 6.9182 | 6.9286 | 6.1685 | 6.9796 | 6.0317 | 6.0440 | 6.7563 | ||
| Std. | 2.7117 | 1.0257 | 5.1185 | 3.0113 | 4.7764 | 5.4640 | 1.0001 | 1.8947 | 5.9692 | ||
| Mean | 8.9593 | 9.9630 | 1.3910 | 1.4453 | 9.1927 | 1.4259 | 9.8754 | 9.0824 | 1.2033 | ||
| Std. | 6.9389 | 7.8008 | 3.4784 | 3.3319 | 5.1047 | 3.1782 | 1.4285 | 4.5985 | 4.9971 | ||
| Mean | 9.3177 | 9.2555 | 1.1447 | 1.1491 | 9.1408 | 1.1366 | 1.0281 | 9.3753 | 1.0674 | ||
| Std. | 7.0344 | 3.3423 | 1.8699 | 1.3349 | 2.7180 | 1.3730 | 1.1465 | 4.9395 | 2.5073 | ||
| Mean | 1.3907 | 3.0992 | 1.1193 | 1.2359 | 3.1211 | 9.8685 | 1.2164 | 2.0726 | 7.7142 | ||
| Std. | 5.7378 | 7.1942 | 9.0623 | 8.5897 | 1.3575 | 9.1532 | 1.0076 | 1.3533 | 1.1240 | ||
| Mean | 8.1898 | 5.2763 | 8.4987 | 8.6665 | 5.7265 | 9.1584 | 8.7828 | 7.1740 | 8.1345 | ||
| Std. | 1.1729 | 6.3960 | 5.6988 | 3.1658 | 1.6905 | 3.5099 | 3.1398 | 1.2008 | 6.0967 | ||
| Hybrid Functions | Mean | 1.1835 | 1.2740 | 9.7759 | 7.4048 | 2.2520 | 6.5269 | 1.2146 | 1.3422 | 3.7805 | |
| Std. | 5.8982 | 5.6408 | 4.1619 | 7.2237 | 9.6268 | 1.6504 | 3.0307 | 7.1024 | 5.4228 | ||
| Mean | 9.5317 | 1.1902 | 1.4036 | 8.1473 | 1.1483 | 1.5110 | 5.3128 | 5.3493 | 5.2030 | ||
| Std. | 1.0400 | 1.4872 | 3.2013 | 1.1724 | 1.1814 | 3.8408 | 1.3264 | 7.0306 | 1.0609 | ||
| Mean | 2.0148 | 2.3429 | 1.1569 | 2.0260 | 1.9977 | 1.5656 | 1.0655 | 1.2126 | 3.0901 | ||
| Std. | 1.8459 | 2.3964 | 5.0479 | 3.4694 | 4.2831 | 6.9907 | 5.1243 | 5.9190 | 1.0280 | ||
| Mean | 8.1822 | 8.9611 | 7.1491 | 2.6733 | 5.1371 | 1.2091 | 1.5327 | 6.4990 | 7.8694 | ||
| Std. | 9.6417 | 8.3701 | 6.2921 | 7.9807 | 7.3396 | 3.2678 | 3.0669 | 4.7071 | 3.5142 | ||
| Mean | 1.0747 | 8.7682 | 6.2763 | 3.2771 | 1.2451 | 9.1247 | 2.0125 | 3.8490 | 4.2598 | ||
| Std. | 9.7030 | 8.2320 | 3.5718 | 8.4128 | 2.0567 | 3.2735 | 3.1098 | 9.4447 | 4.8209 | ||
| Mean | 2.9198 | 2.7770 | 5.4631 | 5.6578 | 2.9158 | 9.8574 | 3.2026 | 2.8450 | 4.6878 | ||
| Std. | 5.0390 | 3.3337 | 6.3234 | 4.8396 | 4.2457 | 1.9100 | 1.5115 | 3.5540 | 4.6143 | ||
| Mean | 2.0399 | 2.3911 | 6.6210 | 3.4163 | 2.1926 | 5.1271 | 2.6787 | 2.0744 | 2.9505 | ||
| Std. | 1.1135 | 2.9662 | 4.7490 | 1.7524 | 2.7291 | 1.9614 | 2.1667 | 2.1001 | 3.2960 | ||
| Mean | 7.7814 | 1.3282 | 4.5941 | 3.8286 | 3.4731 | 2.8351 | 5.4324 | 2.0066 | 7.3208 | ||
| Std. | 1.0304 | 9.0093 | 3.7883 | 2.0043 | 3.2317 | 7.6202 | 1.4745 | 1.7028 | 4.5066 | ||
| Mean | 1.2889 | 1.0950 | 7.4788 | 6.4076 | 3.7638 | 8.5804 | 2.1355 | 1.9417 | 1.2621 | ||
| Std. | 1.1564 | 1.1168 | 6.2283 | 2.5103 | 8.3869 | 4.7651 | 1.7647 | 1.7074 | 9.9661 | ||
| Mean | 2.4143 | 2.6088 | 3.0591 | 2.9896 | 2.5280 | 3.0625 | 2.2733 | 2.4472 | 2.7151 | ||
| Std. | 2.122 | 1.9812 | 1.5895 | 9.5183 | 1.4077 | 1.3445 | 1.6974 | 2.3705 | 1.4118 | ||
| Composition Functions | Mean | 2.4371 | 2.4318 | 2.7361 | 2.7216 | 2.4191 | 2.5979 | 2.5109 | 2.4451 | 2.6487 | |
| Std. | 6.9269 | 3.3990 | 5.4538 | 3.0677 | 2.7440 | 4.8889 | 1.3871 | 4.3882 | 4.1045 | ||
| Mean | 5.6464 | 4.6169 | 8.8274 | 8.8268 | 6.6580 | 6.5895 | 9.9666 | 5.6468 | 6.5363 | ||
| Std. | 3.5173 | 2.2771 | 1.2110 | 3.1078 | 2.3309 | 9.0012 | 3.1172 | 3.2973 | 6.1926 | ||
| Mean | 2.7655 | 2.8282 | 3.3377 | 3.5206 | 2.8358 | 3.6649 3 | 2.8781 | 2.7909 | 3.3941 | ||
| Std. | 5.7598 | 4.6297 | 7.9028 | 6.2823 | 5.2785 | 1.9079 | 1.4794 | 4.4467 | 1.0907 | ||
| Mean | 2.9328 | 2.9853 | 3.4752 | 3.8190 | 3.0511 | 4.0122 | 3.0386 | 3.0085 | 3.6716 | ||
| Std. | 6.7951 | 5.7706 | 1.8902 | 7.1766 | 7.3606 | 2.9513 | 1.2820 | 3.9095 | 7.1213 | ||
| Mean | 2.9019 | 2.9172 | 4.9411 | 4.5437 | 3.0264 | 5.4129 | 2.8896 | 2.9377 | 3.6190 | ||
| Std. | 1.9859 | 2.3514 | 6.4920 | 1.9325 | 8.3053 | 4.6183 | 2.6780 | 2.6898 | 9.7065 | ||
| Mean | 4.5451 | 5.6475 | 1.0502 | 1.0450 | 5.0378 | 1.0610 | 5.7637 | 5.1020 | 8.9843 | ||
| Std. | 8.7765 | 1.0821 | 8.5372 | 4.5798 | 7.4092 | 8.3320 | 1.2686 | 5.0098 | 4.7159 | ||
| Mean | 3.2483 | 3.2820 | 3.9878 | 4.3977 | 3.2000 | 4.7381 | 3.2120 | 3.2753 | 4.1949 | ||
| Std. | 1.9161 | 5.4519 | 4.219 | 1.7630 | 2.4229 | 3.1335 | 7.6240 | 2.8524 | 1.9942 | ||
| Mean | 3.2433 | 3.2468 | 6.5226 | 6.8475 | 3.3544 | 7.6036 | 3.2720 | 3.3028 | 5.1823 | ||
| Std. | 2.8094 | 2.5404 | 7.9387 | 3.0725 | 1.3707 | 4.9561 | 2.7703 | 4.4193 | 2.3464 | ||
| Mean | 3.7791 | 4.2619 | 6.6501 | 6.9804 | 3.6817 | 7.4031 | 4.5047 | 3.9346 | 5.8452 | ||
| Std. | 2.2075 | 2.9220 | 1.0196 | 4.8584 | 3.0165 | 9.1913 | 2.3321 | 2.3988 | 3.9740 | ||
| Mean | 1.0876 | 1.9525 | 2.9254 | 1.2403 | 2.1538 | 3.3004 | 7.1202 | 3.7456 | 2.3894 | ||
| Std. | 3.8180 | 1.3548 | 1.1521 | 3.6092 | 5.8043 | 1.2809 | 4.1259 | 3.7595 | 1.3164 | ||
| Average Ranking | 2.13 | 2.70 | 7.60 | 7.63 | 3.87 | 8.13 | 3.73 | 3.33 | 5.90 | ||
| Total Ranking | 1 | 2 | 7 | 8 | 5 | 9 | 4 | 3 | 6 | ||
| Function | BCA | INFO | RSA | SOMA_T3A | GWO | BOA | DE | PSO | GA | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Unimodal Functions | Mean | 8.0698 | 1.2081 | 1.0054 | 1.0541 | 1.9953 | 9.9579 | 4.2853 | 4.7099 | 6.7499 | |
| Std. | 2.5848 | 3.3163 | 8.7185 | 4.1479 | 6.6208 | 7.6477 | 1.0631 | 4.3556 | 3.6694 | ||
| Mean | 2.1874 | 1.0352 | 1.7072 | 1.7426 | 2.9008 | 3.0258 | 4.0362 | 2.4174 | 1.6088 | ||
| Std. | 4.4722 | 3.3469 | 1.4597 | 1.4382 | 9.6064 | 1.2568 | 6.6267 | 5.1004 | 1.4334 | ||
| Multimodal Functions | Mean | 5.8938 | 6.4763 | 2.7104 | 2.9864 | 3.0583 | 4.1718 | 6.6851 | 8.8720 | 1.7406 | |
| Std. | 7.0100 | 8.8827 | 4.5861 | 2.4337 | 1.0917 | 3.6393 | 4.1228 | 1.1478 | 2.6666 | ||
| Mean | 7.8413 | 8.0011 | 1.1750 | 1.2143 | 7.9093 | 1.2140 | 9.6133 | 8.0109 | 1.0797 | ||
| Std. | 1.2354 | 5.3138 | 2.5710 | 1.3604 | 3.4174 | 2.5134 | 2.1992 | 7.7571 | 4.2529 | ||
| Mean | 6.0651 | 6.4537 | 7.0573 | 6.9849 | 6.3233 | 7.0448 | 6.1448 | 6.1507 | 6.8897 | ||
| Std. | 3.0238 | 6.7509 | 4.3169 | 2.0565 | 6.6989 | 4.4172 | 2.0835 | 3.4453 | 5.222 | ||
| Mean | 1.2372 | 1.3888 | 1.9726 | 2.0541 | 1.1988 | 2.0184 | 1.2313 | 1.2571 | 1.7464 | ||
| Std. | 1.7023 | 1.0297 | 3.3972 | 3.3665 | 9.2951 | 3.4824 | 2.5992 | 8.0061 | 8.6661 | ||
| Mean | 1.0984 | 1.0977 | 1.5119 | 1.4972 | 1.1061 | 1.5184 | 1.2211 | 1.1243 | 1.4017 | ||
| Std. | 1.3220 | 5.3863 | 2.1038 | 1.5377 | 6.7371 | 2.8109 | 1.8749 | 8.4016 | 4.1217 | ||
| Mean | 5.5744 | 9.2101 | 3.8790 | 4.0799 | 1.6457 | 3.7342 | 3.0368 | 6.7222 | 3.0784 | ||
| Std. | 3.6592 | 2.3518 | 2.3156 | 2.4841 | 4.4410 | 2.6924 | 7.5760 | 5.4127 | 3.8685 | ||
| Mean | 1.4690 | 8.1527 | 1.5335 | 1.4691 | 1.0845 | 1.5445 | 1.5134 | 1.4055 | 1.3846 | ||
| Std. | 1.3087 | 9.1292 | 4.0800 | 3.2265 | 3.3112 | 4.7646 | 5.7015 | 1.1317 | 7.4803 | ||
| Hybrid Functions | Mean | 1.5325 | 1.4936 | 2.1183 | 1.9607 | 7.3545 | 2.7563 | 1.8245 | 2.1715 | 1.5010 | |
| Std. | 4.1856 | 3.2047 | 2.6847 | 1.5181 | 2.5495 | 1.9258 | 1.7100 | 4.2295 | 2.3156 | ||
| Mean | 6.0038 | 1.5783 | 7.4291 | 7.2731 | 5.0761 | 1.0244 | 1.7041 | 4.7613 | 4.1717 | ||
| Std. | 3.9285 | 1.1161 | 1.9085 | 5.4454 | 4.0055 | 1.2312 | 8.4455 | 2.8385 | 5.6714 | ||
| Mean | 8.8823 | 3.3263 | 4.5817 | 3.9844 | 7.8005 | 7.6975 | 1.2000 | 2.9367 | 1.7893 | ||
| Std. | 8.3569 | 4.2739 | 1.4543 | 5.9399 | 1.5196 | 1.0671 | 4.0879 | 1.5111 | 3.9607 | ||
| Mean | 7.1093 | 9.3353 | 5.9906 | 2.5106 | 3.1367 | 1.6226 | 5.8469 | 8.3739 | 2.7865 | ||
| Std. | 7.0911 | 9.7111 | 3.9631 | 8.9211 | 4.5229 | 9.3788 | 2.8929 | 1.0091 | 1.4505 | ||
| Mean | 9.5976 | 1.0522 | 6.6059 | 5.9406 | 4.1580 | 1.3721 | 1.2541 | 8.4425 | 1.5639 | ||
| Std. | 7.5456 | 6.5294 | 2.9172 | 4.6824 | 6.0041 | 3.2457 | 1.2170 | 7.5388 | 4.9284 | ||
| Mean | 4.1961 | 3.7242 | 8.4170 | 8.9178 | 3.6754 | 1.5434 | 5.6286 | 4.0180 | 7.2506 | ||
| Std. | 1.1946 | 4.4344 | 1.4172 | 5.6007 | 5.3702 | 1.7538 | 2.9782 | 7.1457 | 6.0709 | ||
| Mean | 3.6761 | 3.2831 | 1.1912 | 1.1882 4 | 3.2836 | 9.4433 | 3.8683 | 3.4948 | 4.4646 | ||
| Std. | 5.0328 | 3.3696 | 4.0412 | 1.8850 | 4.3853 | 1.2499 | 2.4086 | 5.1286 | 4.6452 | ||
| Mean | 3.7145 | 6.5369 | 2.2561 | 5.3734 | 1.8814 | 2.3829 | 7.2114 | 9.1979 | 5.1911 | ||
| Std. | 3.4216 | 5.7179 | 8.4785 | 1.0627 | 2.4697 | 1.1768 | 3.5520 | 7.7993 | 1.1650 | ||
| Mean | 1.7769 | 2.0862 | 4.2811 | 3.2215 | 2.1014 | 7.5964 | 2.4024 | 7.7060 | 5.6002 | ||
| Std. | 1.4976 | 1.2405 | 1.2925 | 6.7984 | 5.2307 | 1.5056 | 4.6330 | 3.3516 | 1.9099 | ||
| Mean | 3.9894 | 3.3028 | 4.2539 | 4.0362 | 3.2912 | 4.4428 | 4.3908 | 3.7272 | 3.6308 | ||
| Std. | 3.1532 | 3.7555 | 2.2889 | 1.5749 | 5.1545 | 1.7880 | 1.8545 | 3.8193 | 2.6442 | ||
| Composition Functions | Mean | 2.6289 | 2.6137 | 3.1229 | 3.1833 | 2.6297 | 3.1620 | 2.7704 | 2.6479 | 3.0632 | |
| Std. | 1.4251 | 5.9255 | 8.5638 | 3.2547 | 7.3004 | 7.3181 | 2.5858 | 7.9332 | 4.3429 | ||
| Mean | 1.6405 | 1.0111 | 1.7409 | 1.6761 | 1.3105 | 1.6839 | 1.6646 | 1.4385 | 1.5936 | ||
| Std. | 9.7241 | 6.4693 | 3.9289 | 3.2032 | 3.0878 | 7.4231 | 4.0475 | 2.9685 | 7.9201 | ||
| Mean | 2.9959 | 3.1934 | 4.0747 | 4.2654 | 3.0818 | 4.8310 | 3.2146 | 3.0819 | 4.3706 | ||
| Std. | 1.2535 | 1.2322 | 1.9257 | 7.5957 | 9.1497 | 1.9073 | 1.8505 | 7.3836 | 1.0892 | ||
| Mean | 3.2918 | 3.2877 | 4.4812 | 5.0063 | 3.3843 | 6.0799 | 3.3377 | 3.3251 | 4.7415 | ||
| Std. | 1.1679 | 9.0870 | 6.6486 | 9.4557 | 1.1332 | 3.4054 | 2.0458 | 4.8423 | 1.2742 | ||
| Mean | 3.0860 | 3.1876 | 1.3539 | 1.4018 | 4.3759 | 1.5817 | 3.1449 | 3.2742 | 9.3090 | ||
| Std. | 3.2256 | 4.9994 | 1.6051 | 7.1673 | 7.1319 | 8.6365 | 3.2658 | 7.0189 | 4.8423 | ||
| Mean | 6.5998 | 1.0058 | 1.6336 | 1.6454 | 7.2661 | 1.8529 | 8.4696 | 7.3589 | 1.4126 | ||
| Std. | 1.1763 | 1.7772 | 8.1251 | 4.5176 | 1.0119 | 4.6464 | 3.5477 | 8.7881 | 7.1047 | ||
| Mean | 3.4756 | 3.7370 | 5.9281 | 6.9078 | 3.2000 | 6.6606 | 3.3844 | 3.6645 | 6.4421 | ||
| Std. | 9.5517 | 1.8797 | 1.0353 | 3.6858 | 2.1386 | 5.6742 | 7.7249 | 1.0106 | 4.2455 | ||
| Mean | 3.3779 | 3.5239 | 1.1726 | 1.2045 | 3.3962 | 1.1800 | 3.5984 | 3.5421 | 8.9990 | ||
| Std. | 5.7735 | 1.0620 | 1.5292 | 5.8127 | 3.8952 | 1.1263 | 9.5782 | 1.1275 | 4.9551 | ||
| Mean | 4.3124 | 5.1213 | 5.7134 | 3.3590 | 4.6454 | 1.4499 | 5.6166 | 4.7325 | 1.4915 | ||
| Std. | 4.0225 | 5.0900 | 8.1925 | 8.3978 | 6.2813 | 3.2654 | 2.6784 | 5.0232 | 2.9872 | ||
| Mean | 1.2805 | 1.7690 | 7.3830 | 5.8149 | 5.1098 | 1.0356 | 2.1101 | 8.5554 | 1.8142 | ||
| Std. | 3.1411 | 9.3920 | 2.5616 | 8.3036 | 2.0667 | 2.3883 | 1.0839 | 5.0240 | 4.4706 | ||
| Average Ranking | 2.20 | 2.40 | 7.43 | 7.47 | 3.53 | 8.53 | 4.10 | 3.57 | 5.77 | ||
| Total Ranking | 1 | 2 | 7 | 8 | 3 | 9 | 5 | 4 | 6 | ||
| Function | BCA | INFO | RSA | SOMA_T3A | GWO | BOA | DE | PSO | GA | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Unimodal Functions | Mean | 2.4262 | 1.5827 | 2.5051 | 2.6181 | 8.1909 | 2.8481 | 1.2168 | 1.0303 | 1.9283 | |
| Std. | 2.1697 | 5.9449 | 6.8445 | 4.6747 | 1.1466 | 9.0918 | 2.3400 | 2.0291 | 8.5353 | ||
| Mean | 6.5836 | 3.7586 | 3.4850 | 3.5384 | 1.3649 | 9.5001 | 9.2191 | 7.3736 | 3.5431 | ||
| Std. | 8.5490 | 6.1650 | 1.1314 | 1.0242 | 5.1518 | 1.1966 | 1.0117 | 9.8121 | 2.4768 | ||
| Multimodal Functions | Mean | 1.1402 | 2.1230 | 8.6240 | 8.5233 | 1.1234 | 1.0456 | 1.9129 | 2.2175 | 5.5811 | |
| Std. | 1.6994 | 4.5247 | 1.1066 | 7.1279 | 2.9543 | 9.9881 | 3.6458 | 3.5647 | 4.8785 | ||
| Mean | 1.4523 | 1.3003 | 2.0685 | 2.1246 | 1.3395 | 2.1023 | 1.4984 | 1.4913 | 1.9419 | ||
| Std. | 3.0949 | 6.0707 | 4.5174 | 3.3107 | 5.4478 | 2.7335 | 4.1121 | 1.3418 | 6.3060 | ||
| Mean | 6.2673 | 6.5983 | 7.1255 | 7.1278 | 6.5269 | 7.1582 | 6.3221 | 6.4121 | 7.0139 | ||
| Std. | 7.8883 | 6.0012 | 3.7904 | 1.4522 | 4.5112 | 3.3421 | 3.8317 | 7.7823 | 3.7522 | ||
| Mean | 2.4105 | 2.8567 | 3.9083 | 4.0947 | 2.3550 | 3.9955 | 2.2631 | 2.6027 | 3.5544 | ||
| Std. | 3.2586 | 2.4278 | 9.0787 | 5.3391 | 1.3874 | 7.1554 | 8.6077 | 1.7078 | 1.5662 | ||
| Mean | 1.7870 | 1.7241 | 2.5308 | 2.5713 | 1.6996 | 2.5950 | 1.9096 | 1.7887 | 2.3853 | ||
| Std. | 2.8372 | 1.0907 | 5.9205 | 3.0255 | 8.2933 | 4.5855 | 3.500 | 1.5337 | 6.1557 | ||
| Mean | 3.3261 | 2.6853 | 8.2162 | 8.2940 | 5.4341 | 8.5244 | 2.1295 | 4.5034 | 7.2344 | ||
| Std. | 1.0941 | 3.0790 | 3.6701 | 3.2867 | 1.4229 | 3.5794 | 5.6631 | 2.4891 | 4.7622 | ||
| Mean | 3.2281 | 1.7869 | 3.2081 | 3.1765 | 2.5030 | 3.3361 | 3.3478 | 3.1371 | 3.0695 | ||
| Std. | 1.4270 | 1.7704 | 9.0578 | 5.3961 | 6.1326 | 5.5069 | 5.9817 | 1.1393 | 1.0018 | ||
| Hybrid Functions | Mean | 1.2551 | 3.2673 | 2.1884 | 1.8807 | 1.2569 | 1.1115 | 3.4259 | 1.2228 | 1.5227 | |
| Std. | 3.0498 | 7.6137 | 2.8094 | 1.7728 | 2.8048 | 2.5365 | 4.5553 | 3.0212 | 2.0980 | ||
| Mean | 1.0159 | 8.2837 | 1.7894 | 1.8373 | 2.6146 | 2.2615 | 1.2339 | 1.4037 | 1.2383 | ||
| Std. | 5.6502 | 8.3954 | 2.2378 | 7.2630 | 8.4709 | 1.2059 | 5.5010 | 6.2157 | 1.0713 | ||
| Mean | 1.1851 | 3.5256 | 4.6528 | 4.3217 | 3.7958 | 5.0376 | 1.9034 | 1.6131 | 2.5314 | ||
| Std. | 8.1518 | 1.0772 | 5.4012 | 2.4149 | 2.6778 | 3.5562 | 1.9179 | 4.6544 | 2.4457 | ||
| Mean | 2.9782 | 1.5074 | 9.3691 | 4.3262 | 9.8780 | 1.7488 | 2.3123 | 1.1788 | 1.8978 | ||
| Std. | 2.0700 | 7.3534 | 4.2511 | 9.3987 | 4.7507 | 5.3129 | 8.3497 | 7.3408 | 4.1156 | ||
| Mean | 6.1051 | 1.8254 | 2.3222 | 2.1381 | 8.4784 | 2.8782 | 1.3875 | 8.3210 | 1.0750 | ||
| Std. | 4.3314 | 2.3018 | 3.7678 | 1.9326 | 1.1504 | 3.5521 | 2.3709 | 2.6313 | 1.1435 | ||
| Mean | 9.8380 | 6.3684 | 2.0929 | 2.0376 | 9.1569 | 2.5379 | 1.1466 | 9.3651 | 1.8110 | ||
| Std. | 2.2106 | 7.4683 | 3.1865 | 1.1518 | 1.7239 | 1.8175 | 4.0190 | 1.6248 | 1.6440 | ||
| Mean | 7.3028 | 6.2763 | 1.2741 | 2.2644 | 9.0987 | 3.0086 | 8.1420 | 6.7173 | 5.6565 | ||
| Std. | 1.2345 | 9.5553 | 1.1567 | 7.8162 | 4.6655 | 1.6597 | 3.0139 | 9.0206 | 3.2081 | ||
| Mean | 9.2284 | 2.1110 | 1.5856 | 1.0757 | 1.5438 | 2.2938 | 5.3408 | 1.8286 | 3.6796 | ||
| Std. | 7.9516 | 1.2088 | 8.5792 | 2.4989 | 8.9871 | 1.3454 | 1.9901 | 1.1332 | 9.9945 | ||
| Mean | 1.6481 | 1.0110 | 2.3574 | 1.8007 | 1.0655 | 2.9969 | 4.9848 | 3.6414 | 1.0713 | ||
| Std. | 4.0296 | 2.0092 | 4.9719 | 1.5611 | 1.5996 | 3.5853 | 1.5144 | 1.2319 | 1.8233 | ||
| Mean | 7.6005 | 5.5823 | 7.7664 | 7.4699 | 6.1301 | 8.2367 | 7.1889 | 7.4633 | 7.1668 | ||
| Std. | 3.2761 | 5.2891 | 2.6622 | 2.3863 | 1.4393 | 3.1704 | 2.8736 | 5.2791 | 3.2952 | ||
| Composition Functions | Mean | 3.2061 | 3.3173 | 4.6039 | 4.7637 | 3.3123 | 4.9988 | 3.4553 | 3.3432 | 4.7138 | |
| Std. | 3.0861 | 1.5987 | 2.1284 | 5.8958 | 9.0393 | 1.8975 | 3.8367 | 1.3888 | 1.5033 | ||
| Mean | 3.4888 | 2.1203 | 3.4798 | 3.4291 | 2.9534 | 3.4654 | 3.3976 | 3.3656 | 3.3430 | ||
| Std. | 6.8231 | 2.0965 | 5.9158 | 5.0831 | 5.5320 | 5.0334 | 5.0728 | 1.4131 | 1.0478 | ||
| Mean | 3.4270 | 3.9970 | 5.7098 | 6.7390 | 3.9791 | 6.8537 | 3.9121 | 3.7042 | 6.7026 | ||
| Std. | 1.0831 | 1.8032 | 2.2234 | 1.3785 | 1.1420 | 3.2125 | 4.3860 | 1.0324 | 3.0047 | ||
| Mean | 4.1427 | 4.8633 | 9.0247 | 1.0304 | 4.9121 | 1.4845 | 4.4334 | 4.3668 | 1.1008 | ||
| Std. | 2.2216 | 3.0941 | 2.2474 | 4.1372 | 1.4091 | 1.1676 | 5.7606 | 1.1141 | 5.3080 | ||
| Mean | 3.9451 | 4.4219 | 2.5541 | 2.6442 | 9.0625 | 2.8948 | 5.2123 | 5.3468 | 1.8131 | ||
| Std. | 2.4271 | 2.7817 | 1.6708 | 1.2230 | 1.6244 | 2.0025 | 4.7429 | 6.0285 | 6.0790 | ||
| Mean | 1.4253 | 2.4819 | 5.0168 | 4.7764 | 2.2388 | 5.7504 | 1.6418 | 1.6479 | 4.3008 | ||
| Std. | 2.2698 | 3.6772 | 3.5322 | 1.7066 | 1.8713 | 2.1206 | 5.2302 | 1.1404 | 2.0140 | ||
| Mean | 3.6732 | 4.1662 | 1.2084 | 1.3883 | 3.2000 | 1.6125 | 3.7738 | 4.1689 | 1.2293 | ||
| Std. | 1.1192 | 2.4580 | 2.7715 | 5.0937 | 2.7202 | 1.1549 | 1.9439 | 1.6458 | 8.7161 | ||
| Mean | 4.4414 | 5.6510 | 2.9822 | 2.7928 | 3.5548 | 3.9325 | 1.0193 | 7.2703 | 2.5580 | ||
| Std. | 7.1057 | 1.0350 | 2.0328 | 6.0543 | 1.3957 | 1.9787 | 2.4050 | 2.0799 | 9.1464 | ||
| Mean | 7.8602 | 8.4401 | 7.6068 | 3.4879 | 7.9197 | 1.3111 | 1.0405 | 9.1411 | 5.5861 | ||
| Std. | 1.3546 | 9.1056 | 5.7523 | 9.2666 | 1.6097 | 4.3956 | 4.9541 | 9.8512 | 1.6627 | ||
| Mean | 1.0003 | 3.0133 | 4.1761 | 3.9200 | 2.8882 | 4.7457 | 8.3342 | 1.2042 | 2.2226 | ||
| Std. | 6.6358 | 2.0704 | 4.4631 | 1.7074 | 2.3192 | 4.5899 | 4.2568 | 1.9619 | 3.6108 | ||
| Average Ranking | 2.47 | 2.47 | 7.17 | 7.10 | 3.67 | 8.80 | 4.07 | 3.63 | 5.67 | ||
| Total Ranking | 1 | 1 | 8 | 7 | 4 | 9 | 5 | 3 | 6 | ||
| BCA | 30D | ||||||||
| vs. SCO | vs. INFO | vs. GA | vs. SOMA_T3A | vs. RSA | vs. PSO | vs. BOA | vs. DE | vs. GWO | |
| 1.7344 | 2.5364 | 1.4936 | 1.7344 | 5.2165 | 3.3173 | 5.7517 | 3.8723 | 5.7064 | |
| Yes | NO | Yes | Yes | Yes | Yes | Yes | Yes | Yes | |
| Yes | NO | Yes | Yes | Yes | Yes | Yes | Yes | Yes | |
| BCA | 50D | ||||||||
| vs. SCO | vs. INFO | vs. GA | vs. SOMA_T3A | vs. RSA | vs. PSO | vs. BOA | vs. DE | vs. GWO | |
| 1.7344 | 5.5774 | 7.5137 | 1.3601 | 1.2381 | 3.1618 | 1.7344 | 2.0515 | 2.7653 | |
| Yes | NO | Yes | Yes | Yes | Yes | Yes | Yes | Yes | |
| Yes | NO | Yes | Yes | Yes | Yes | Yes | Yes | Yes | |
| BCA | 100D | ||||||||
| vs. SCO | vs. INFO | vs. GA | vs. SOMA_T3A | vs. RSA | vs. PSO | vs. BOA | vs. DE | vs. GWO | |
| 1.7344 | 9.4261 | 5.3070 | 2.5967 | 1.9729 | 8.3071 | 2.1266 | 1.0570 | 2.9575 | |
| Yes | NO | Yes | Yes | Yes | Yes | Yes | Yes | Yes | |
| Yes | NO | Yes | Yes | Yes | Yes | Yes | Yes | Yes | |
| Function | N = 30 | N = 60 | N = 90 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Median | Mean | Std. | Median | Mean | Std. | Median | ||
| Unimodal Functions | 7.3880 | 6.7454 | 3.8861 | 5.4449 | 5.6765 | 3.5046 | 4.6746 | 1.4123 | 5.7977 | |
| 8.3146 | 1.7206 | 8.1638 | 7.7592 | 1.1306 | 7.5372 | 6.6083 | 6.2693 | 1.4721 | ||
| Multimodal Functions | 4.9649 | 3.0714 | 4.9252 | 4.9179 | 2.2574 | 4.8842 | 4.8495 | 4.8633 | 2.7164 | |
| 6.2601 | 6.4823 | 6.0346 | 6.7939 | 5.7299 | 7.0420 | 6.9770 | 7.0603 | 3.7821 | ||
| 6.0272 | 2.7117 | 6.0198 | 6.0004 | 9.8761 | 6.0001 | 6.0004 | 6.0003 | 2.9621 | ||
| 8.9593 | 6.9389 | 8.9541 | 9.5491 | 2.8263 | 9.6248 | 9.5526 | 9.5864 | 1.6341 | ||
| 9.3177 | 7.0344 | 9.0080 | 9.9036 | 5.1629 | 1.0037 | 1.0078 | 1.0112 | 3.0123 | ||
| 1.3907 | 5.7378 | 1.1280 | 9.0601 | 7.9865 | 9.0440 | 9.0141 | 9.0101 | 1.4670 | ||
| 8.1898 | 1.1729 | 8.4436 | 8.4277 | 3.4190 | 8.4837 | 8.2718 | 8.2482 | 3.6665 | ||
| Hybrid Functions | 1.1835 | 5.8982 | 1.1776 | 1.2044 | 5.0040 | 1.1950 | 1.2334 | 1.2427 | 3.2662 | |
| 9.5317 | 1.0400 | 6.3189 | 2.6591 | 2.8870 | 1.5407 | 2.4397 | 1.6314 | 2.1469 | ||
| 2.0148 | 1.8459 | 1.4413 | 1.3349 | 1.3905 | 8.0189 | 1.6795 | 1.1447 | 1.6274 | ||
| 8.1822 | 9.6417 | 4.7288 | 3.847 | 3.3347 | 3.6679 | 2.5751 | 1.4199 | 2.4443 | ||
| 1.0747 | 9.7030 | 7.1497 | 1.1307 | 1.0356 | 7.4763 | 1.4489 | 1.2136 | 1.1371 | ||
| 2.9198 | 5.0390 | 3.0275 | 3.1022 | 4.1633 | 3.2082 | 3.1699 | 3.2143 | 2.012 | ||
| 2.0399 | 1.1135 | 2.0585 | 1.9230 | 1.4829 | 1.9132 | 1.9150 | 1.8817 | 1.2865 | ||
| 7.7814 | 1.0304 | 4.2460 | 1.1602 | 8.7514 | 9.2794 | 1.8026 | 1.3069 | 1.6463 | ||
| 1.2889 | 1.1564 | 8.2227 | 1.4547 | 1.5462 | 8.2788 | 1.1386 | 8.5105 | 9.7387 | ||
| 2.4143 | 2.1220 | 2.4204 | 2.2592 | 1.7011 | 2.2061 | 2.2178 | 2.1996 | 2.0358 | ||
| Composition Functions | 2.4371 | 6.9269 | 2.4561 | 2.4795 | 5.1795 | 2.4966 | 2.4993 | 2.5033 | 1.7737 | |
| 5.6464 | 3.5173 | 4.3274 | 3.4979 | 2.7257 | 2.3000 | 2.5517 | 2.3000 | 1.3769 | ||
| 2.7655 | 5.7598 | 2.7475 | 2.7889 | 7.8776 | 2.8320 | 2.8359 | 2.8518 | 5.4288 | ||
| 2.9328 | 6.7951 | 2.9132 | 3.0039 | 5.7480 | 3.0292 | 3.0291 | 3.0306 | 1.4249 | ||
| 2.9019 | 1.9859 | 2.8905 | 2.8867 | 1.8345 | 2.8871 | 2.8878 | 2.8871 | 4.8380 | ||
| 4.5451 | 8.7765 | 4.6629 | 4.6645 | 9.0179 | 4.5846 | 4.9001 | 5.2268 | 8.6492 | ||
| 3.2483 | 1.9161 | 3.2453 | 3.2207 | 1.5836 | 3.2194 | 3.2151 | 3.2136 | 1.0483 | ||
| 3.2433 | 2.8094 | 3.2344 | 3.2195 | 3.8101 | 3.2183 | 3.2019 | 3.2045 | 3.5352 | ||
| 3.7791 | 2.2075 | 3.7431 | 3.6631 | 2.0532 | 3.5980 | 3.6891 | 3.6264 | 2.0704 | ||
| 1.0876 | 3.8180 | 1.0020 | 1.1098 | 5.8710 | 8.8924 | 1.3314 | 1.101 | 7.2877 | ||
| Function | N = 30 | N = 60 | N = 90 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Median | Mean | Std. | Median | Mean | Std. | Median | ||
| Unimodal Functions | 8.0698 | 2.5848 | 8.5769 | 5.6533 | 5.4529 | 3.8752 | 1.6929 | 2.5291 | 7.7395 | |
| 2.1874 | 4.4722 | 2.1759 | 2.086 | 2.5998 | 2.0824 | 1.9983 | 2.4721 | 1.9739 | ||
| Multimodal Functions | 5.8938 | 7.0100 | 5.9366 | 5.4685 | 4.6212 | 5.4588 | 5.8317 | 4.8414 | 5.7983 | |
| 7.8413 | 1.2354 | 7.7960 | 9.5733 | 2.7532 | 9.6231 | 9.4155 | 4.0125 | 9.5446 | ||
| 6.0651 | 3.0238 | 6.0599 | 6.0357 | 1.7040 | 6.0326 | 6.0443 | 1.9290 | 6.0391 | ||
| 1.2372 | 1.7023 | 1.2142 | 1.2462 | 2.7839 | 1.2492 | 1.2554 | 3.1171 | 1.2627 | ||
| 1.0984 | 1.3220 | 1.0452 | 1.2465 | 5.9646 | 1.2548 | 1.2486 | 2.7830 | 1.2516 | ||
| 5.5744 | 3.6592 | 5.0946 | 2.1500 | 9.4137 | 1.821 | 2.2068 | 7.1179 | 1.9962 | ||
| 1.4690 | 1.3087 | 1.5137 | 1.4969 | 4.2448 | 1.5050 | 1.4696 | 5.2522 | 1.4790 | ||
| Hybrid Functions | 1.5325 | 4.1856 | 1.4082 | 1.4942 | 1.2734 | 1.4626 | 1.5806 | 1.4222 | 1.5572 | |
| 6.0038 | 3.9285 | 5.2296 | 4.6185 | 2.6767 | 4.4667 | 6.7136 | 3.4054 | 6.9069 | ||
| 8.8823 | 8.3569 | 5.8793 | 8.9058 | 1.0131 | 3.3792 | 6.8728 | 5.1488 | 5.4100 | ||
| 7.1093 | 7.0911 | 4.7577 | 1.764 | 1.5576 | 1.4294 | 1.8604 | 1.5231 | 1.2970 | ||
| 9.5976 | 7.5456 | 9.4456 | 6.2588 | 4.800 | 4.5249 | 9.6673 | 5.6008 | 8.5047 | ||
| 4.1961 | 1.1946 | 4.6432 | 4.9000 | 5.0821 | 5.0144 | 5.0119 | 4.0126 | 5.0726 | ||
| 3.6761 | 5.0328 | 3.8736 | 3.7952 | 4.5891 | 3.9097 | 3.917 | 1.8772 | 3.9074 | ||
| 3.7145 | 3.4216 | 2.1930 | 6.1150 | 5.1799 | 5.0918 | 6.2919 | 3.6692 | 6.0346 | ||
| 1.7769 | 1.4976 | 1.6746 | 1.2614 | 1.0910 | 1.0209 | 1.7584 | 1.2659 | 1.5127 | ||
| 3.9894 | 3.1532 | 4.0624 | 4.0121 | 1.7131 | 4.0342 | 3.9080 | 1.6453 | 3.9554 | ||
| Composition Functions | 2.6289 | 1.4251 | 2.6798 | 2.7164 | 7.8921 | 2.7452 | 2.7498 | 2.2452 | 2.7450 | |
| 1.6405 | 9.7241 | 1.6771 | 1.5945 | 2.6014 | 1.6382 | 1.5775 | 2.5859 | 1.6241 | ||
| 2.9959 | 1.2535 | 2.9727 | 3.1145 | 1.0888 | 3.1561 | 3.1700 | 4.3416 | 3.1780 | ||
| 3.2918 | 1.1679 | 3.3428 | 3.3416 | 2.6905 | 3.3404 | 3.3468 | 1.7065 | 3.3473 | ||
| 3.0860 | 3.2256 | 3.0836 | 3.0413 | 3.4239 | 3.0383 | 3.0566 | 3.3287 | 3.0536 | ||
| 6.5998 | 1.1763 | 6.0904 | 7.6085 | 1.0757 | 7.9554 | 7.7630 | 1.2142 | 8.2386 | ||
| 3.4756 | 9.5517 | 3.4703 | 3.3717 | 7.7598 | 3.3570 | 3.3469 | 4.9444 | 3.3398 | ||
| 3.3779 | 5.7735 | 3.3638 | 3.3182 | 2.8599 | 3.3120 | 3.3166 | 2.8689 | 3.3176 | ||
| 4.3124 | 4.0225 | 4.3761 | 4.7976 | 7.7415 | 4.6373 | 4.9083 | 6.1360 | 5.1620 | ||
| 1.2805 | 3.1411 | 1.2535 | 1.1792 | 4.2818 | 1.1050 | 1.0317 | 2.3300 | 9.6863 | ||
| Function | N = 30 | N = 60 | N = 90 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Median | Mean | Std. | Median | Mean | Std. | Median | ||
| Unimodal Functions | 2.4262 | 2.1697 | 1.4349 | 2.1735 | 1.6368 | 1.9405 | 4.8626 | 2.2534 | 4.5258 | |
| 6.5836 | 8.5490 | 6.5079 | 6.0051 | 4.8053 | 5.9572 | 5.6070 | 5.0478 | 5.6712 | ||
| Multimodal Functions | 1.1402 | 1.6994 | 1.1296 | 1.0799 | 1.7728 | 1.0504 | 1.5534 | 6.5074 | 1.409 | |
| 1.4523 | 3.0949 | 1.5810 | 1.5998 | 1.3127 | 1.6277 | 1.6358 | 6.5052 | 1.6395 | ||
| 6.2673 | 7.8883 | 6.2470 | 6.2634 | 6.3532 | 6.2555 | 6.3272 | 6.1965 | 6.3235 | ||
| 2.4105 | 3.2586 | 2.3947 | 2.2629 | 1.4796 | 2.2637 | 2.3654 | 1.2481 | 2.3764 | ||
| 1.7870 | 2.8372 | 1.9033 | 1.9130 | 1.4320 | 1.9451 | 1.9346 | 6.5322 | 1.9489 | ||
| 3.3261 | 1.0941 | 3.0414 | 2.4906 | 6.5603 | 2.4154 | 2.8735 | 8.0231 | 2.9131 | ||
| 3.2281 | 1.4270 | 3.2546 | 3.2493 | 4.6601 | 3.2445 | 3.2077 | 5.5939 | 3.2266 | ||
| Hybrid Functions | 1.2551 | 3.0498 | 1.2013 | 1.2502 | 2.2621 | 1.2619 | 1.2094 | 1.9187 | 1.1893 | |
| 1.0159 | 5.6502 | 9.3947 | 1.0162 | 4.2322 | 1.0274 | 3.5831 | 1.9544 | 3.1847 | ||
| 1.1851 | 8.1518 | 9.4589 | 9.3345 | 8.3468 | 5.5971 | 9.3405 | 7.8067 | 5.2999 | ||
| 2.9782 | 2.0700 | 2.4561 | 2.8133 | 1.3232 | 2.6904 | 7.9611 | 6.1426 | 5.2904 | ||
| 6.1051 | 4.3314 | 4.9656 | 7.0866 | 5.5325 | 5.6302 | 4.8590 | 3.1298 | 3.8430 | ||
| 9.8380 | 2.2106 | 1.0919 | 1.0982 | 9.0023 | 1.1099 | 1.1047 | 3.8279 | 1.1076 | ||
| 7.3028 | 1.2345 | 7.7119 | 7.5733 | 7.8489 | 7.7642 | 7.5426 | 3.3576 | 7.6183 | ||
| 9.2284 | 7.9516 | 6.2699 | 1.5234 | 8.0396 | 1.2651 | 2.1013 | 1.3007 | 1.9431 | ||
| 1.6481 | 4.0296 | 4.9390 | 8.7120 | 9.0183 | 3.5736 | 9.2523 | 7.0218 | 6.9492 | ||
| 7.6005 | 3.2761 | 7.6956 | 7.5911 | 2.1343 | 7.5550 | 7.5043 | 1.9804 | 7.5278 | ||
| Composition Functions | 3.2061 | 3.0861 | 3.1123 | 3.451 | 8.7610 | 3.4666 | 3.4806 | 6.2116 | 3.4850 | |
| 3.4888 | 6.8231 | 3.4930 | 3.4561 | 6.0301 | 3.4606 | 3.4332 | 7.2741 | 3.4458 | ||
| 3.4270 | 1.0831 | 3.409 | 3.7837 | 2.2633 | 3.7978 | 3.906 | 1.5031 | 3.9565 | ||
| 4.1427 | 2.2216 | 4.1747 | 4.3501 | 2.5350 | 4.4379 | 4.4577 | 1.1226 | 4.4796 | ||
| 3.9451 | 2.4271 | 3.8940 | 3.8960 3 | 2.6916 | 3.8134 | 4.2877 | 2.7775 | 4.2707 | ||
| 1.4253 | 2.2698 | 1.4234 | 1.6057 | 2.3513 | 1.7050 | 1.7742 | 9.7393 | 1.7790 | ||
| 3.6732 | 1.119 | 3.6588 | 3.6297 | 9.8681 | 3.6233 | 3.8026 | 1.3702 | 3.7729 | ||
| 4.4414 | 7.1057 | 4.1383 | 4.0945 | 3.5898 | 3.9512 | 4.6269 | 6.2025 | 4.4988 | ||
| 7.8602 | 1.3546 | 7.4896 | 1.0043 | 1.179 | 1.0306 | 1.0371 | 5.4174 | 1.0520 | ||
| 1.0003 | 6.6358 | 7.9011 | 2.0147 | 2.0424 | 1.1431 | 6.3088 | 5.7825 | 4.1689 | ||
| Variables | g | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| d | D | N | Mean | Std. | Best | Worst | |||||
| BCA | 0.058 | 0.589 | 4.682 | −0.008 | −0.032 | −4.692 | −0.568 | 0.013 | 0.001 | 0.01 | 0.015 |
| GWO | 0.05 | 0.3744 | 8.5615 | −0.0013 | −1.32 | −4.8521 | −0.717 | 0.0099 | 6.77 | 0.0099 | 0.0099 |
| PSO | 0.0539 | 0.4120 | 8.6554 | −2.22 | −0.1220 | −4.1508 | −0.6894 | 0.0135 | 0.0010 | 0.0127 | 0.0175 |
| RSA | 0.050 | 0.336 | 13.077 | −0.085 | −0.100 | −3.851 | −0.742 | 0.013 | 0.001 | 0.011 | 0.013 |
| GA | 0.0506 | 0.3862 | 14.5477 | −0.7745 | −0.0082 | −2.2784 | −0.7088 | 0.0185 | 0.0037 | 0.012 | 0.0285 |
| DE | 0.0517 | 0.3567 | 11.2913 | −4.43 | −0.1343 | −4.0537 | −0.7278 | 0.0127 | 2.03 | 0.0127 | 0.0128 |
| INFO | 0.0533 | 0.4567 | 6.0900 | −9.52 | −4.25 | −4.8952 | −0.6600 | 0.0101 | 0.0003 | 0.0099 | 0.0108 |
| BOA | 0.0503 | 0.3740 | 10.7850 | −0.2279 | −0.0185 | −3.6833 | −0.7172 | 0.0118 | 0.0010 | 0.0010 | 0.0151 |
| Variables | ||||||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Best | Worst | |||||
| BCA | 49 | 19 | 18 | 49 | 2.86 | 9.63 | 1.43 | 3.85 |
| GWO | 38 | 20 | 16 | 59 | 6.56 | 8.69 | 1.02 | 3.20 |
| PSO | 57 | 27 | 14 | 47 | 4.79 | 2.07 | 0 | 1.09 |
| RSA | 37 | 14 | 16 | 42 | 6.69 | 1.53 | 1.72 | 6.08 |
| GA | 47 | 17 | 18 | 47 | 5.66 | 2.65 | 1.29 | 1.45 |
| DE | 42 | 18 | 20 | 60 | 6.64 | 8.82 | 1.13 | 2.86 |
| INFO | 44 | 25 | 15 | 58 | 1.35 | 7.42 | 0 | 4.06 |
| BOA | 56 | 17 | 24 | 55 | 4.97 | 8.10 | 2.54 | 3.75 |
| BCA-MLP | BOA-MLP | SMA-MLP | RSA-MLP | PSO-MLP | SCA-MLP | |
|---|---|---|---|---|---|---|
| Classification accuracy | 96.6667% | 20.4167% | 22.9167% | 24.1667% | 40.4167% | 51.6667% |
| 0.0004 | 0.1301 | 0.2007 | 0.1605 | 0.1333 | 0.0414 | |
| Std. | 0.0008 | 0.0437 | 0.0271 | 0.0389 | 0.0685 | 0.0324 |
| BCA-MLP | BOA-MLP | SMA-MLP | RSA-MLP | PSO-MLP | SCA-MLP | |
|---|---|---|---|---|---|---|
| Classification accuracy | 100% | 85.1667% | 98% | 51.1667% | 70.5% | 100% |
| 5.4761 | 4.7226 | 3.1037 | 1.5287 | 6.1734 | 2.8029 | |
| Std. | 2.8897 | 9.1955 | 8.5071 | 1.7109 | 6.8740 | 3.9437 |
| BCA-MLP | BOA-MLP | SMA-MLP | RSA-MLP | PSO-MLP | SCA-MLP | |
|---|---|---|---|---|---|---|
| Classification accuracy | 97.2690% | 64.4444% | 81.6822% | 73.4268% | 93.8837% | 96.2098% |
| 1.2609 | 1.4308 | 1.0694 | 1.2134 | 1.4620 | 1.3243 | |
| Std. | 2.3301 | 8.5751 | 2.3023 | 1.4956 | 1.5816 | 1.4103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, J.; Meng, X.; Wu, J.; Tian, J.; Xu, G.; Li, W. BCA: Besiege and Conquer Algorithm. Symmetry 2025, 17, 217. https://doi.org/10.3390/sym17020217
Jiang J, Meng X, Wu J, Tian J, Xu G, Li W. BCA: Besiege and Conquer Algorithm. Symmetry. 2025; 17(2):217. https://doi.org/10.3390/sym17020217
Chicago/Turabian StyleJiang, Jianhua, Xianqiu Meng, Jiaqi Wu, Jun Tian, Gaochao Xu, and Weihua Li. 2025. "BCA: Besiege and Conquer Algorithm" Symmetry 17, no. 2: 217. https://doi.org/10.3390/sym17020217
APA StyleJiang, J., Meng, X., Wu, J., Tian, J., Xu, G., & Li, W. (2025). BCA: Besiege and Conquer Algorithm. Symmetry, 17(2), 217. https://doi.org/10.3390/sym17020217







