Chaos Regulation via Complex Nonlinear Feedback and Its Implementation Based on FPAA
Abstract
1. Introduction
2. Dynamics of Chaotic Systems with Complex Nonlinear Feedback
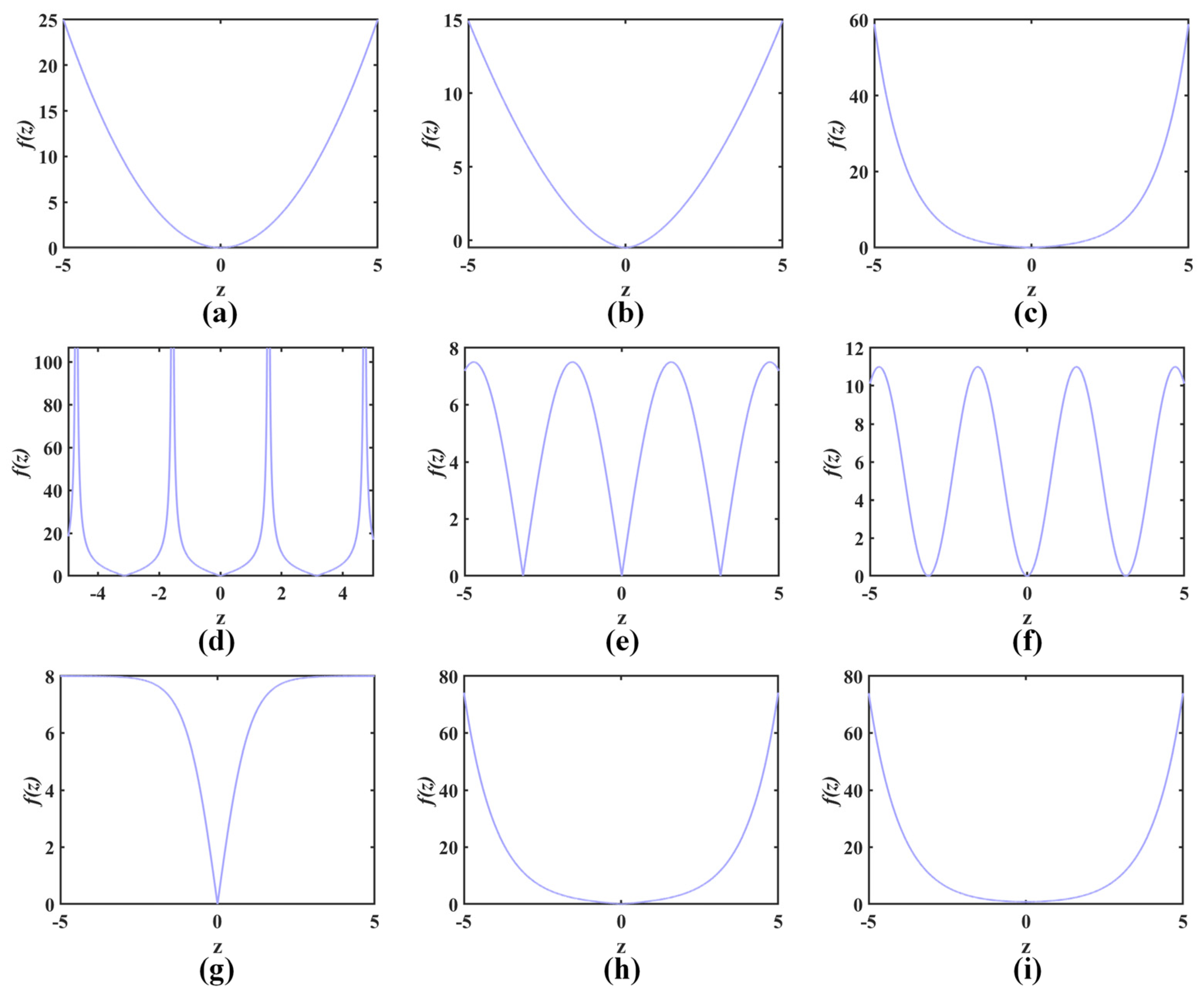
2.1. Complex Nonlinear Electromagnetic Constraint Relation in Nature
2.2. Effect of Complex Nonlinear Feedback on Strange Attractors in a Chaotic System
3. Regulation of System Dynamics by Complex Nonlinear Feedback
3.1. The Influence on the Non-Bifurcation Parameter of the System
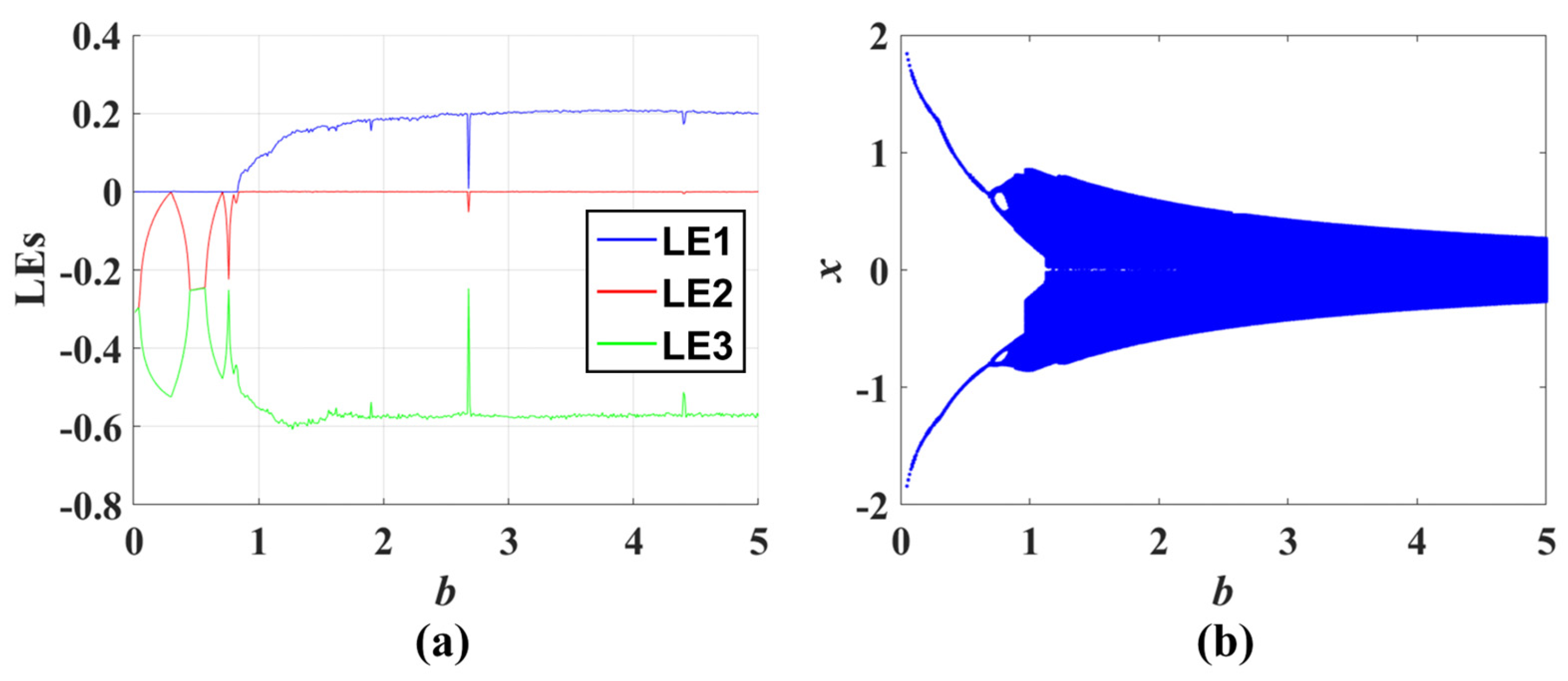
3.2. The Influence of Complex Nonlinear Feedback on Bifurcation Parameters
- (1)
- (2)
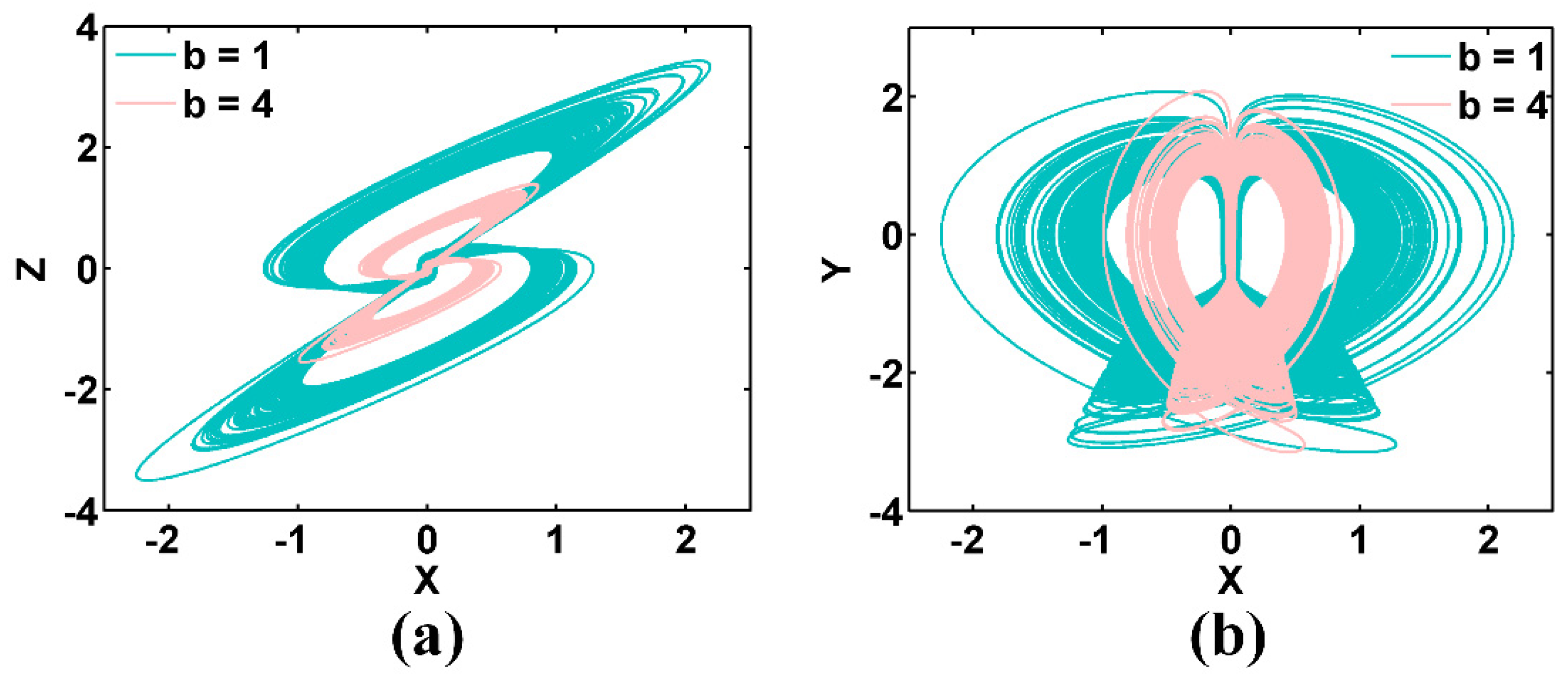
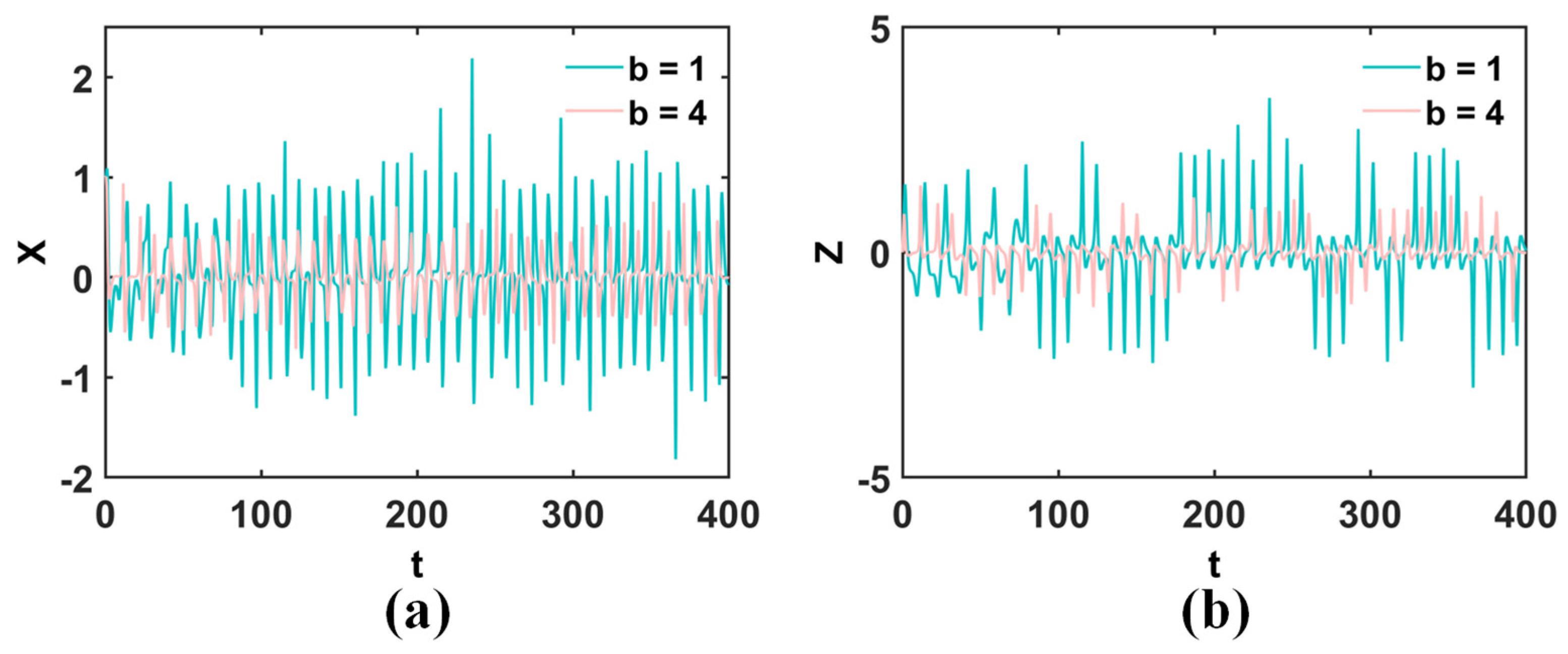
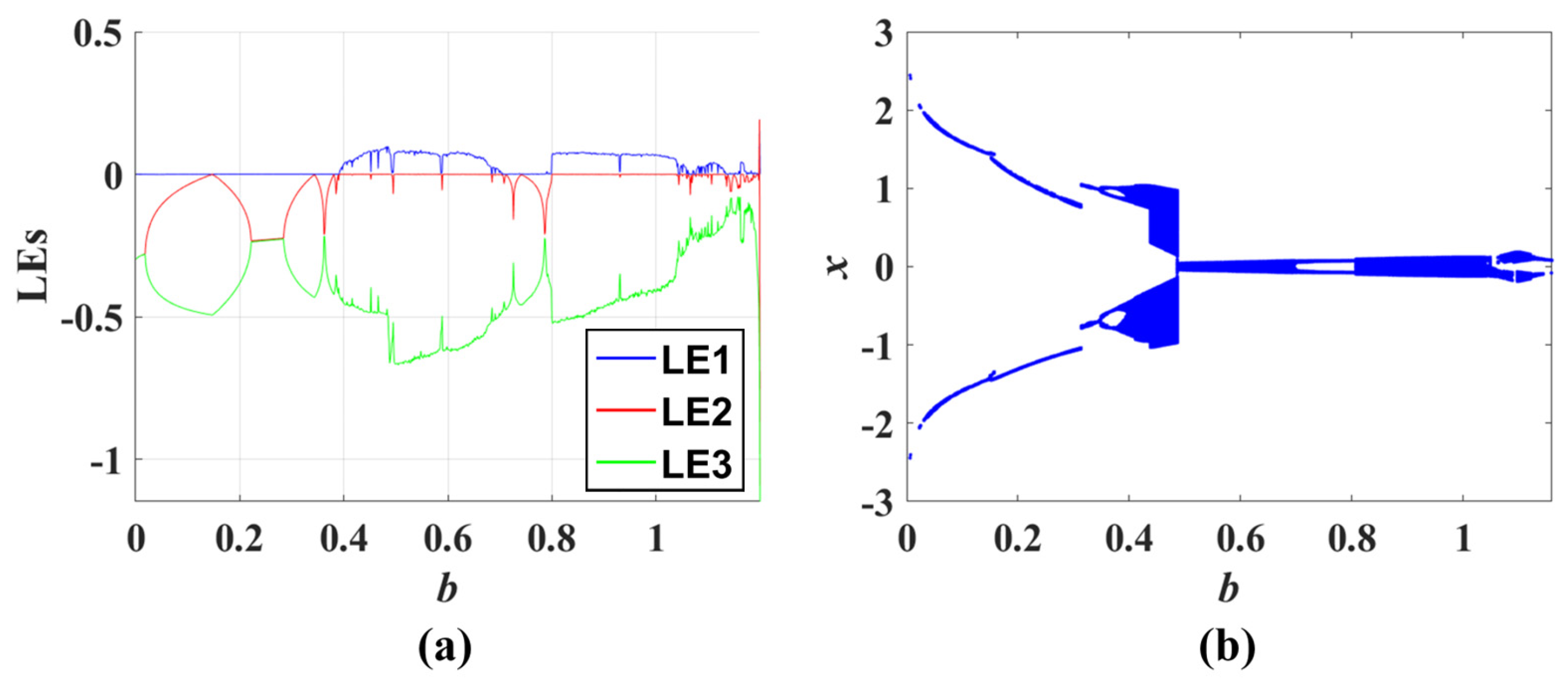
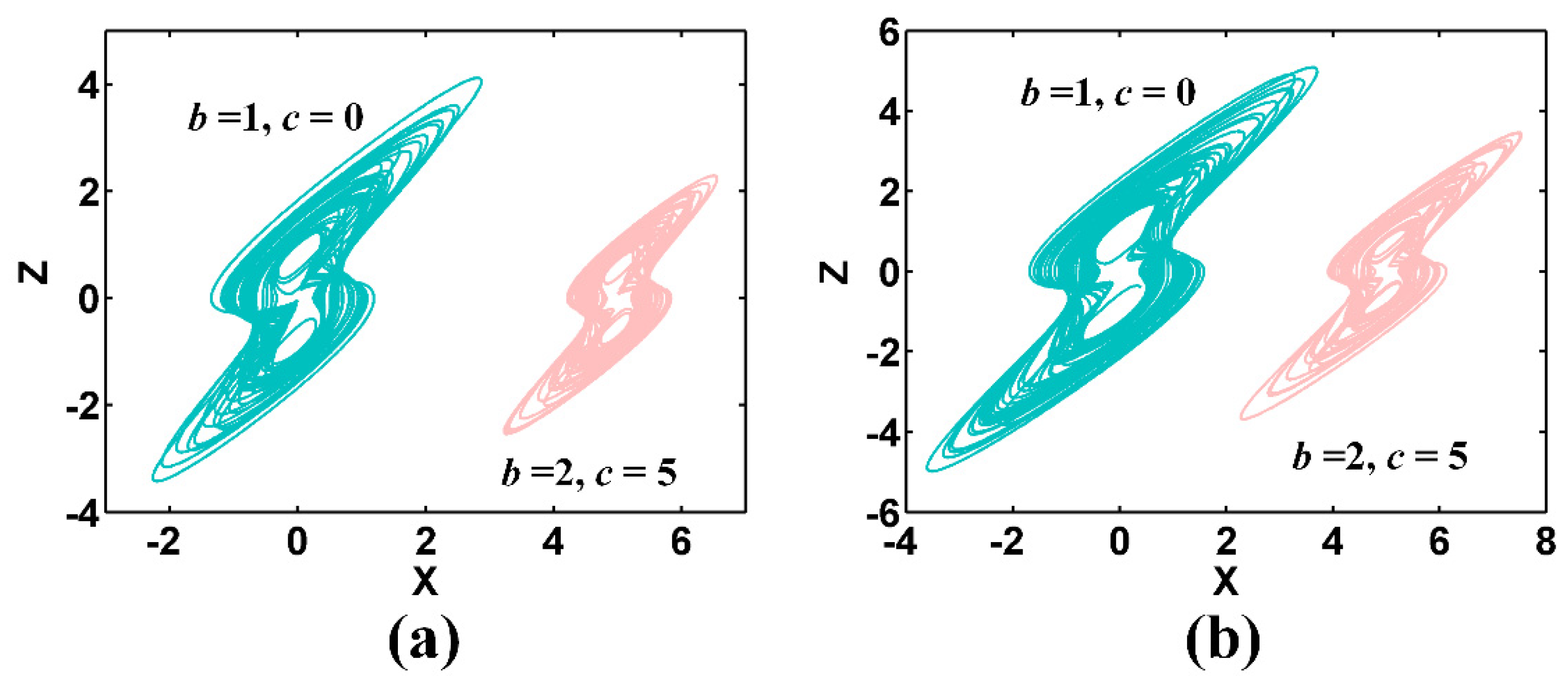
- Attractor size expansion/reduction can be realized by adjusting the parameter b in systems CSCF0 and CSCF1. The other feedback of the complex function causes the parameter b to become a bifurcation parameter, although, in some numerical range, it can modify the attractor size, such as in CSCF8.
- (3)
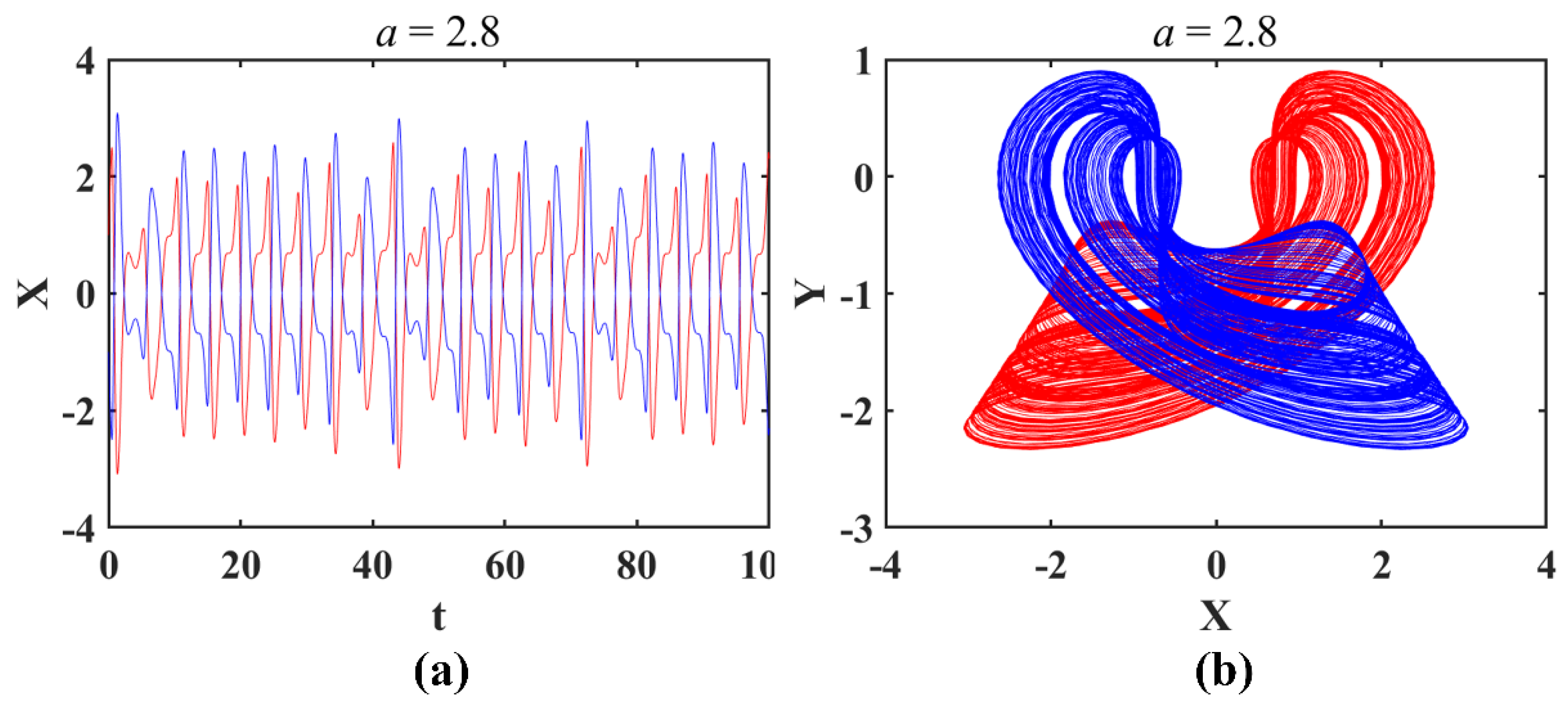
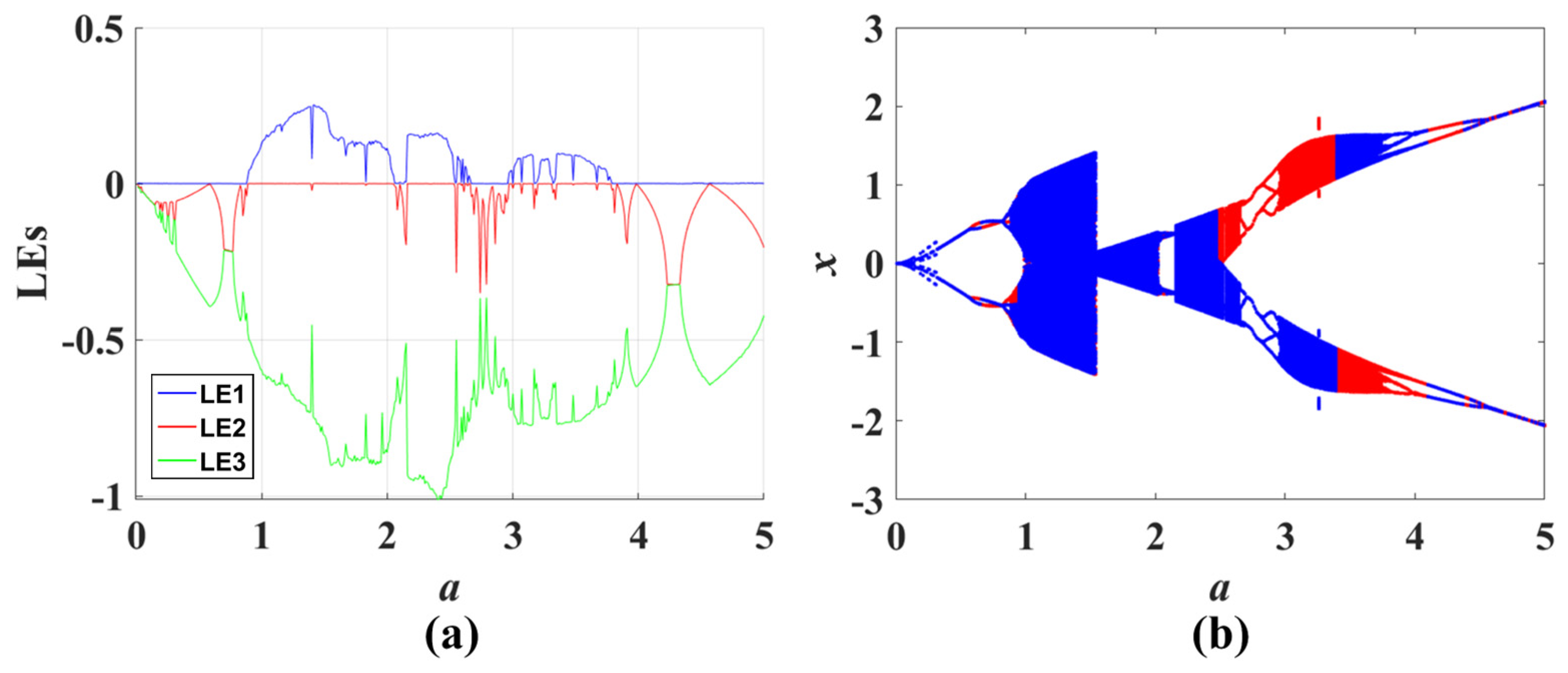
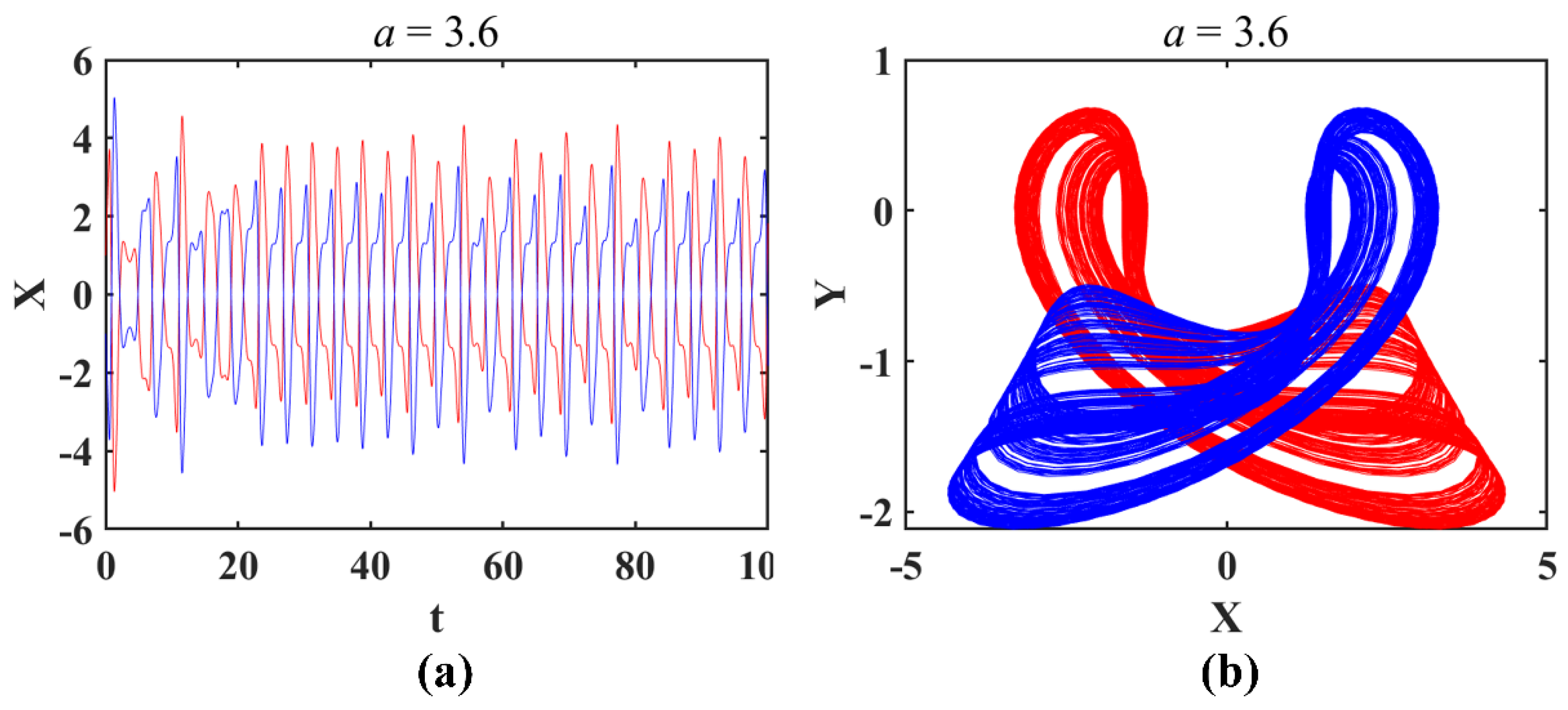
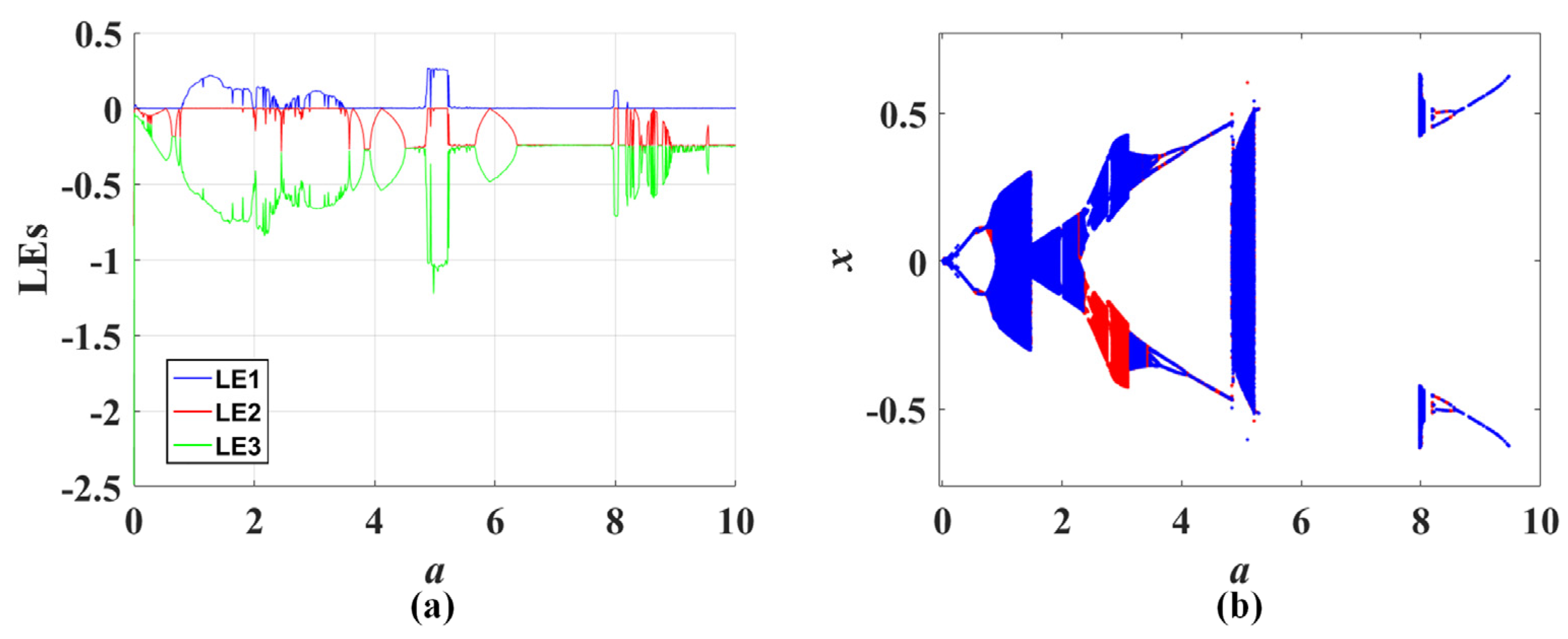
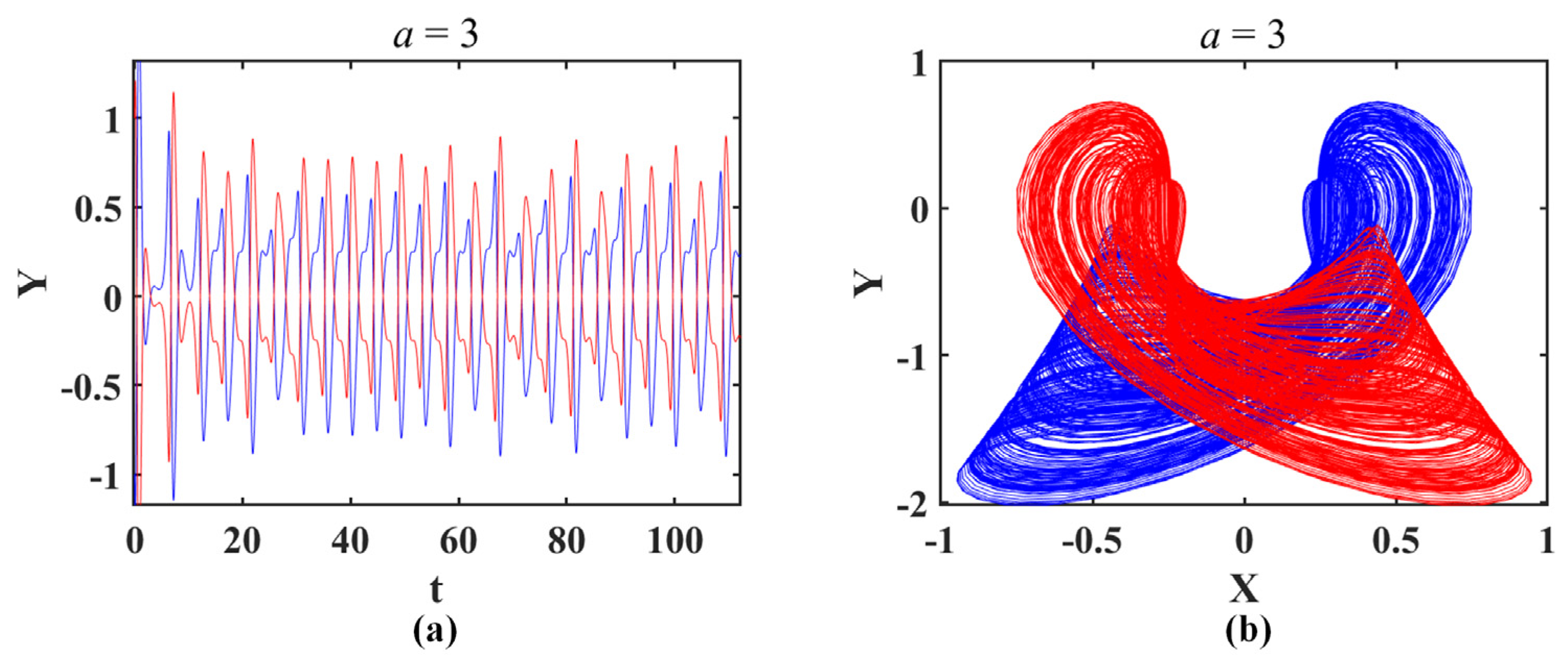
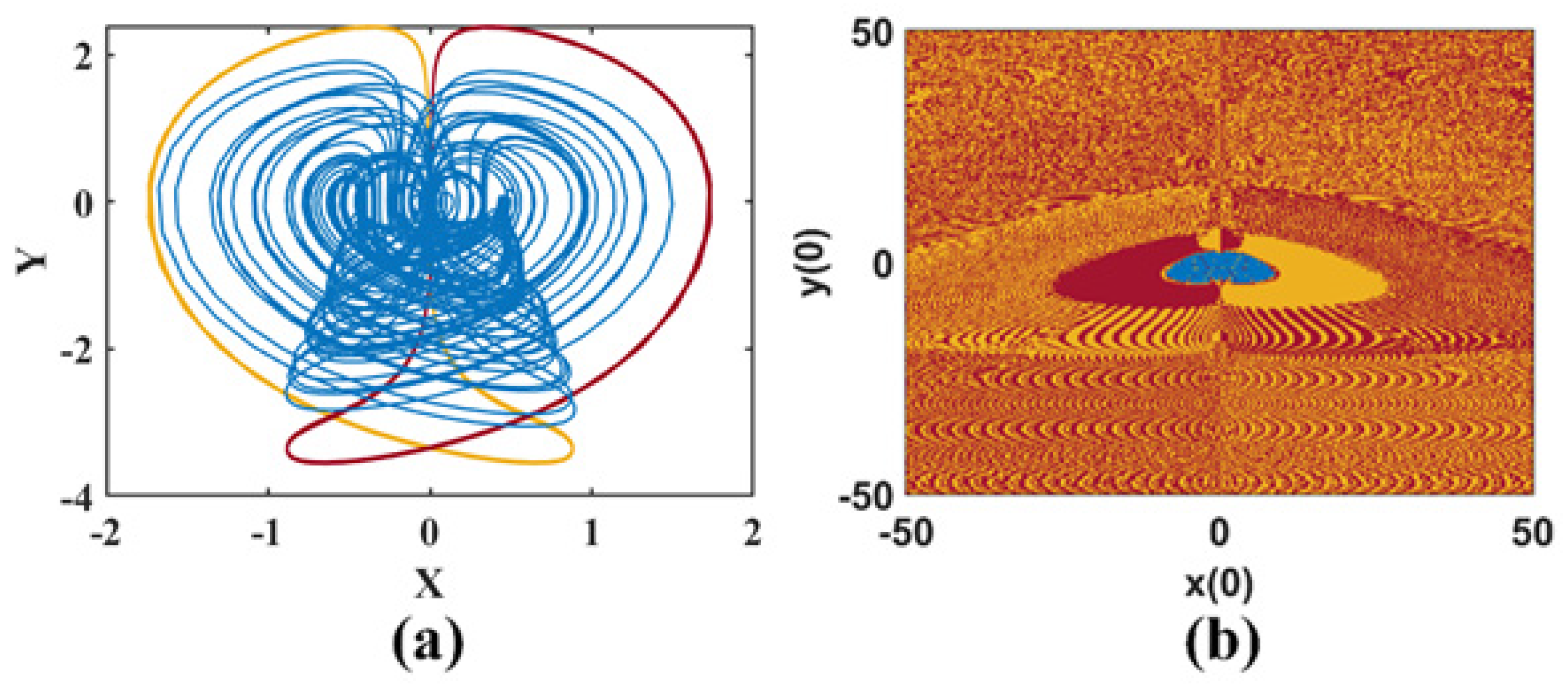
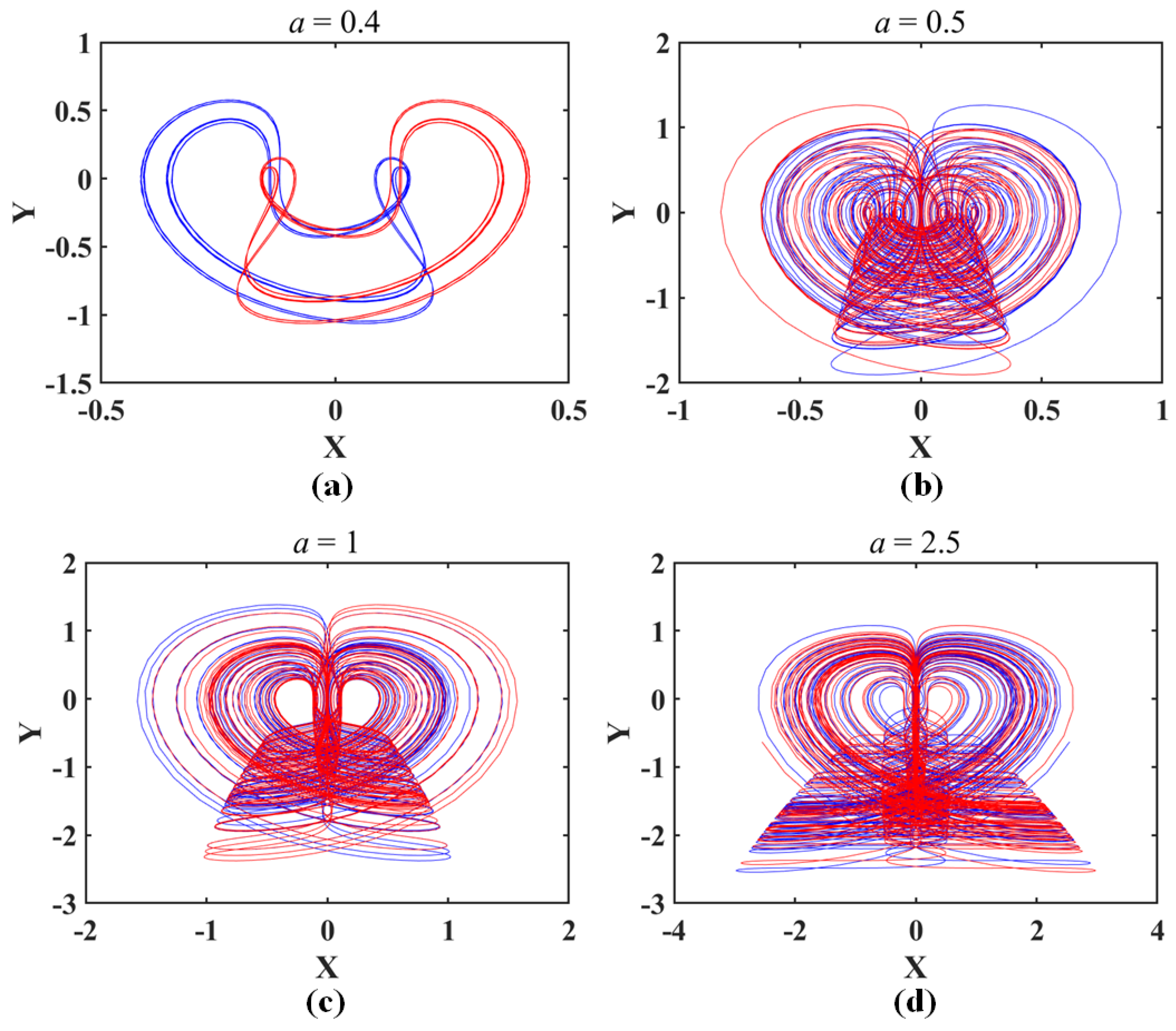
- The symmetry of complex feedback functions provides the possibility of coexisting attractors in chaotic systems with this structure (shown in Figure 9, Figure 11, Figure 13, Figure 15 and Figure 17), and wide-mouth-like feedback can even bring three or more coexisting attractors, like system CSCF8 (shown in Figure 16).
- (4)
- All the systems (CSCF0–CSCF8) have a single parameter c in the last dimension, leading to direct offset boosting of the variable x.
- (5)
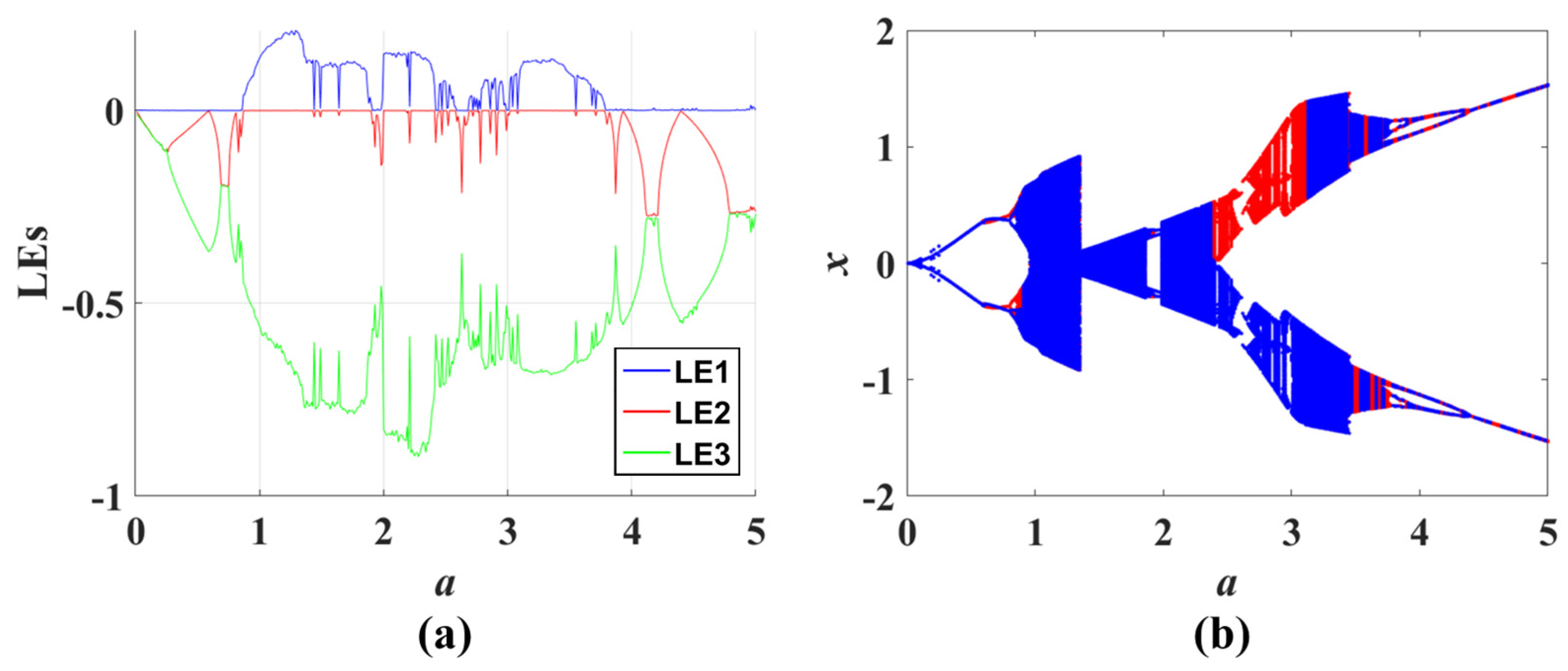
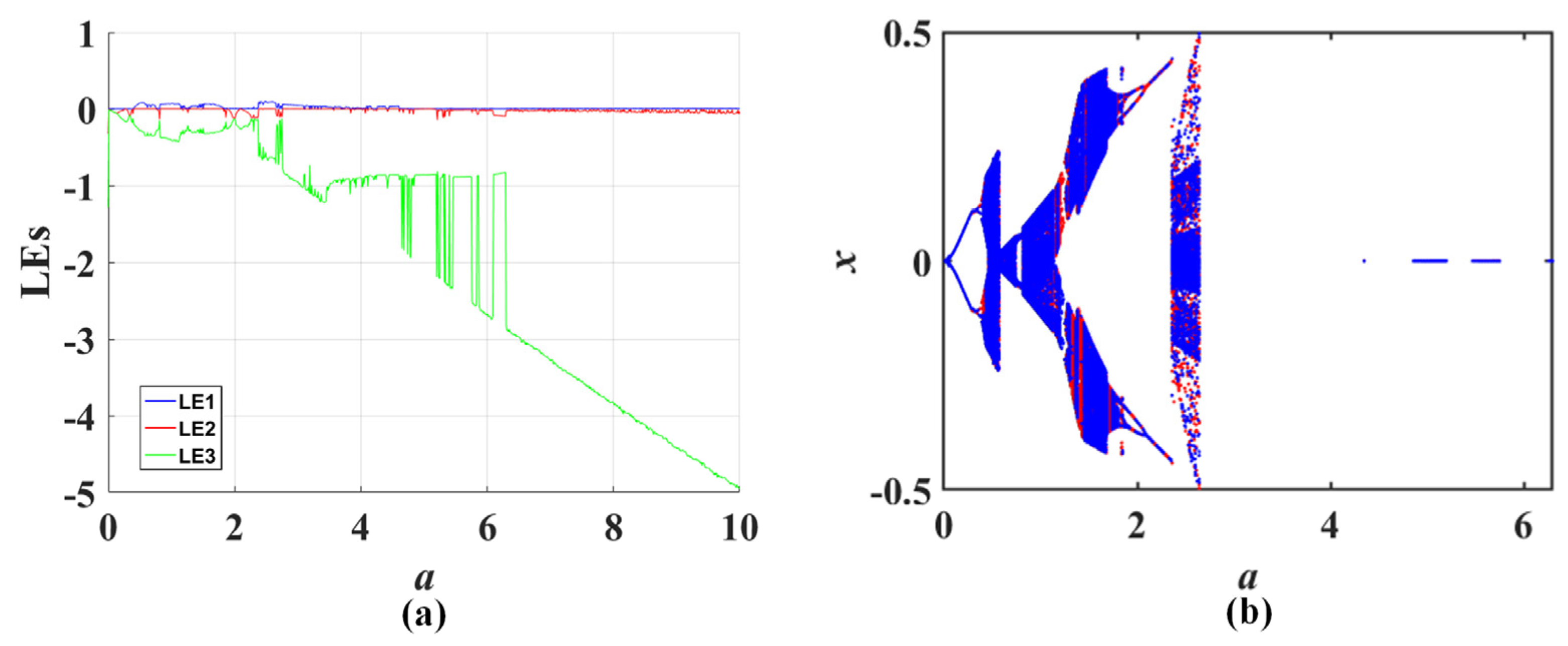
- The impact of complex nonlinear feedback on system dynamics is reflected in the transition between non-bifurcation parameters and bifurcation parameters, as well as the bifurcation dynamics. The transition from the non-bifurcation parameter to the bifurcation one when the original system is introduced to new complex feedback usually does not cause structural rupture or deformation of the attractor. Therefore, there are no coexisting attractors generated as a result (as shown in Figure 6 and Figure 7). For the bifurcation parameters, after introducing complex functions, all the derived systems retain the original basic bifurcation patterns, including the generation of coexisting attractors (shown in Figure 9, Figure 11, Figure 13, Figure 15 and Figure 17).
4. Circuit Realization Based on FPAA
4.1. FPAA Internal Resources and System Scale Transformation
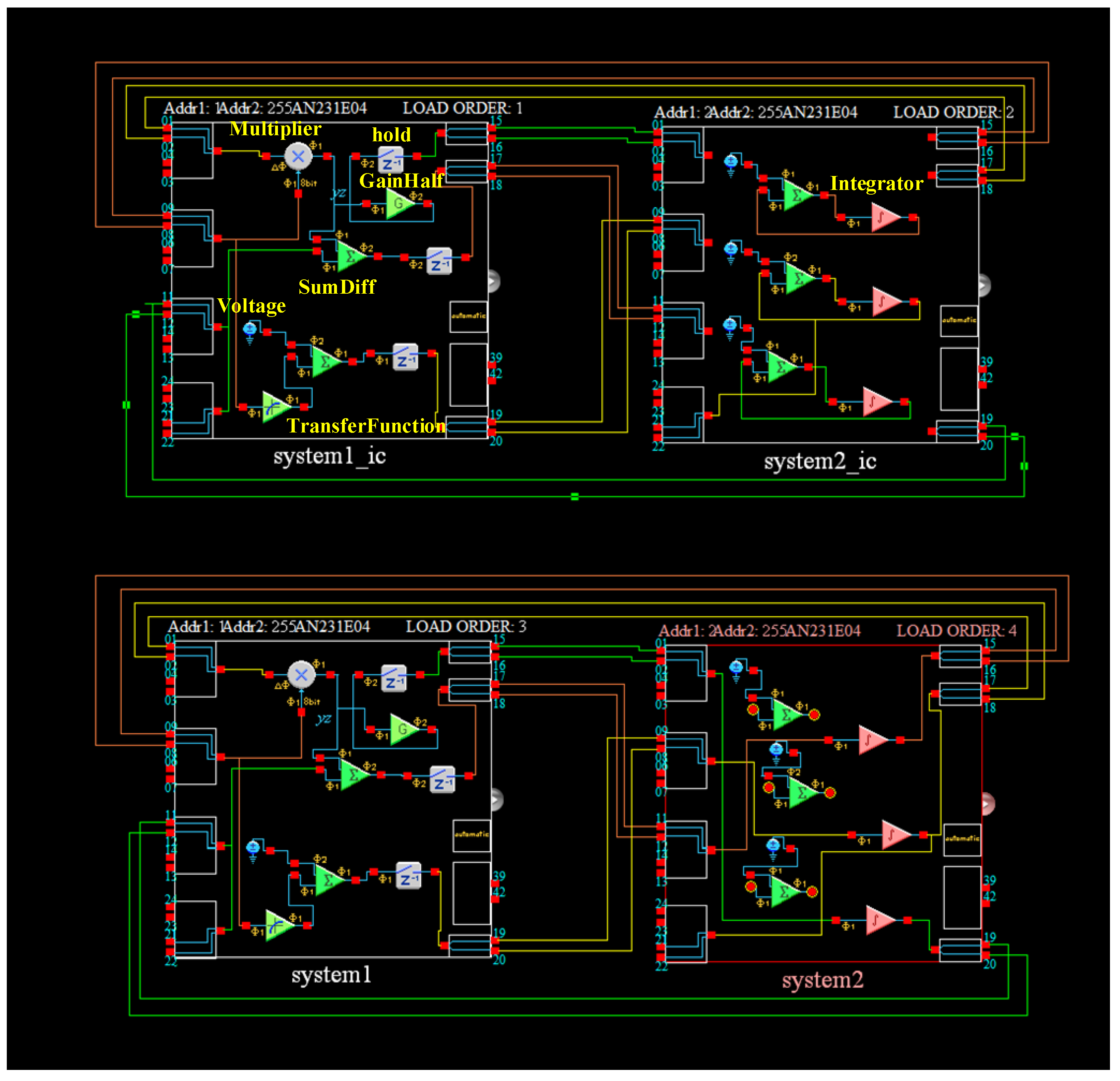
4.2. Circuit Implementation Based on FPAA
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pareek, N.K.; Patidar, V.; Sud, K.K. Image encryption using chaotic logistic map. Image Vis. Comput. 2006, 24, 926–934. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Y.; Liang, S.; Li, D. A new chaotic algorithm for image encryption. Chaos Solitons Fractals 2006, 29, 393–399. [Google Scholar] [CrossRef]
- Ma, F.; Wu, L.; Ye, Y.; Zhang, F. A secure multi-party hybrid encryption sharing scheme with a new 2D sine-cosine chaotic system and compressed sensing. Nonlinear Dyn. 2024, 112, 11523–11546. [Google Scholar] [CrossRef]
- Yao, P.; Wu, H.; Gao, B.; Tang, J.; Zhang, Q.; Zhang, W.; Yang, J.J.; Qian, H. Fully hardware-implemented memristor convolutional neural network. Nature 2020, 577, 641–646. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Shen, Y. Exponential stabilization of memristor-based chaotic neural networks with time-varying delays via intermittent control. IEEE Trans. Neural Netw. Learn. Syst. 2014, 26, 1431–1441. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Ding, X.; Chen, B.; Parastesh, F.; Iu, H.H.-C.; Wang, N. A universal configuration framework for mem-element-emulator-based bionic firing circuits. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 4120. [Google Scholar] [CrossRef]
- Xu, Q.; Fang, Y.; Wu, H.; Bao, H.; Wang, N. Firing patterns and fast–slow dynamics in an N-type LAM-based FitzHugh–Nagumo circuit. Chaos Solitons Fractals 2024, 187, 115376. [Google Scholar] [CrossRef]
- Feng, W.; Jiang, N.; Zhang, Y.; Jin, J.; Zhao, A.; Liu, S.; Qiu, K. Pulsed-chaos MIMO radar based on a single flat-spectrum and Delta-like autocorrelation optical chaos source. Opt. Express 2022, 30, 4782–4792. [Google Scholar] [CrossRef]
- Chen, J.D.; Wu, K.W.; Ho, H.L.; Lee, C.T.; Lin, F.Y. 3-D multi-input multi-output (MIMO) pulsed chaos lidar based on time-division multiplexing. IEEE J. Sel. Top. Quantum Electron. 2022, 28, 1–9. [Google Scholar] [CrossRef]
- Sheng, Z.; Li, C.; Gao, Y.; Li, Z.; Chai, L. A switchable chaotic oscillator with multiscale amplitude/frequency control. Mathematics 2023, 11, 618. [Google Scholar] [CrossRef]
- Sprott, J.C. A new class of chaotic circuit. Phys. Lett. A 2000, 266, 19–23. [Google Scholar] [CrossRef]
- de Sousa Vieira, M.; Lichtenberg, A.J. Controlling chaos using nonlinear feedback with delay. Phys. Rev. E 1996, 54, 1200. [Google Scholar] [CrossRef] [PubMed]
- Holmes, P. A nonlinear oscillator with a strange attractor. Philosophical Transactions of the Royal Society of London. Ser. A Math. Phys. Sci. 1979, 292, 419–448. [Google Scholar]
- Thomas, R. Deterministic chaos seen in terms of feedback circuits: Analysis, synthesis, “labyrinth chaos”. Int. J. Bifurc. Chaos 1999, 9, 1889–1905. [Google Scholar] [CrossRef]
- Kengne, J.; Njitacke Tabekoueng, Z.; Kamdoum Tamba, V.; Negou, A.N. Periodicity, chaos, and multiple attractors in a memristor-based Shinriki’s circuit. Chaos Interdiscip. J. Nonlinear Sci. 2015, 25, 103126. [Google Scholar] [CrossRef]
- Sprott, J.C. Some simple chaotic flows. Phys. Rev. E 1994, 50, R647. [Google Scholar] [CrossRef]
- Kamdem Kuate, P.D.; Lai, Q.; Fotsin, H. Complex behaviors in a new 4D memristive hyperchaotic system without equilibrium and its microcontroller-based implementation. Eur. Phys. J. Spec. Top. 2019, 228, 2171–2184. [Google Scholar] [CrossRef]
- Bao, B.C.; Bao, H.; Wang, N.; Chen, M.; Xu, Q. Hidden extreme multistability in memristive hyperchaotic system. Chaos Solitons Fractals 2017, 94, 102–111. [Google Scholar] [CrossRef]
- Zhang, S.; Zheng, J.; Wang, X.; Zeng, Z. A novel no-equilibrium HR neuron model with hidden homogeneous extreme multistability. Chaos Solitons Fractals 2021, 145, 110761. [Google Scholar] [CrossRef]
- Njitacke, Z.T.; Doubla, I.S.; Mabekou, S.; Kengne, J. Hidden electrical activity of two neurons connected with an asymmetric electric coupling subject to electromagnetic induction: Coexistence of patterns and its analog implementation. Chaos Solitons Fractals 2020, 137, 109785. [Google Scholar] [CrossRef]
- Li, Y.; Liu, J.; Liu, H. A complex-variable disturbed laser with application to hidden multi-scroll attractor generation. Nonlinear Dyn. 2024, 1–19. [Google Scholar] [CrossRef]
- Zhang, X.; Li, C.; Lei, T.; Fu, H.; Liu, Z. Offset boosting in a memristive hyperchaotic system. Phys. Scr. 2023, 99, 015247. [Google Scholar] [CrossRef]
- Ma, Y.; Mou, J.; Jahanshahi, H.; Alkhateeb, A.F.; Bi, X. Design and DSP implementation of a hyperchaotic map with infinite coexisting attractors and intermittent chaos based on a novel locally active memcapacitor. Chaos Solitons Fractals 2023, 173, 113708. [Google Scholar] [CrossRef]
- Ramakrishnan, B.; Tamba, V.K.; Metsebo, J.; Ngatcha, D.T.; Rajagopal, K. Control, synchronisation and antisynchronisation of chaos in two non-identical Josephson junction models via sliding mode control and its FPGA implementation. Pramana 2023, 97, 46. [Google Scholar] [CrossRef]
- Karawanich, K.; Chimnoy, J.; Khateb, F.; Marwan, M.; Prommee, P. Image cryptography communication using FPAA-based multi-scroll chaotic system. Nonlinear Dyn. 2024, 112, 4951–4976. [Google Scholar] [CrossRef]
- Marco, M.D.; Forti, M.; Pancioni, L.; Tesi, A. Drift of invariant manifolds and transient chaos in memristor Chua’s circuit. Electron. Lett. 2023, 59, e12948. [Google Scholar] [CrossRef]
- Muni, S.S.; Fatoyinbo, H.O.; Ghosh, I. Dynamical effects of electromagnetic flux on chialvo neuron map: Nodal and network behaviors. Int. J. Bifurc. Chaos 2022, 32, 2230020. [Google Scholar] [CrossRef]
- Lu, Y.M.; Wang, C.H.; Deng, Q.L.; Xu, C. The dynamics of a memristor-based Rulkov neuron with fractional-order difference. Chin. Phys. B 2022, 31, 060502. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C. Variable-boostable chaotic flows. Optik 2016, 127, 10389–10398. [Google Scholar] [CrossRef]
- Chai, L.; Liu, J.; Chen, G.; Zhang, X.; Li, Y. Amplitude control and chaotic synchronization of a complex-valued laser ring network. Fractals 2023, 31, 2350091. [Google Scholar] [CrossRef]
- Li, Y.; Liu, J.; Hao, Z.; Liu, H.; Zhang, X. Multi-scroll hidden hyperchaotic attractor and extreme multistability with offset boosting in a memristor-coupled complex-valued laser network. Eur. Phys. J. Plus 2024, 139, 1–13. [Google Scholar] [CrossRef]
- Li, C.; Thio, W.J.C.; Sprott, J.C.; Iu, H.H.-C.; Xu, Y. Constructing infinitely many attractors in a programmable chaotic circuit. IEEE Access 2018, 6, 29003–29012. [Google Scholar] [CrossRef]






| Systems | Parameters | Equilibria | Eigenvalues | x0 y0 z0 | LEs | DKY | |
|---|---|---|---|---|---|---|---|
| CSCF0 | bz2 | a = 1 b = 1 | [0, 0, 1] [0, 0, −1] | −0.7709,0.3855 ± 1.5639i −0.7709,0.3855 ± 1.5639i | −1 1 −1 | (0.1394,−0.0002,−0.5671) | 2.2454 |
| CSCF1 | b|z|1.7 − 0.5 | a = 1 b = 1 | [0, 0, 1.2693] [0, 0, −1.2693] | −0.6888,0.3444 ± 1.1856i −0.6888,0.3444 ± 1.1856i | −1 1 −1 | (0.2606,−0.2239,−0.5034) | 2.0729 |
| CSCF2 | be|z| − 0.5 | a = 1 b = 0.4 | [0, 0, 1.3217] [0, 0, −1.3217] | −0.7698,0.3849 ± 1.5579i −0.7698,0.3849 ± 1.5579i | −1 1 −1 | (0.0868,−0.0009,−0.5227) | 2.1720 |
| CSCF3 | b|tan z| | a = 3.7 b = 5 | [0, 0, 0.1399] [0, 0, −0.1399] | −1.3376,0.6688 ± 1.5345i −1.3376,0.6688 ± 1.5345i | −1 1 −1 | (0.1609,−0.0021,−0.9230) | 2.1643 |
| CSCF4 | b|sin z| | a = 3.3 b = 7.5 | −1.0967,0.5484 ± 1.2251i −1.0967,0.5484 ± 1.2251i | −1 1 −1 | (0.1698,−0.0017,−0.8433) | 2.1993 | |
| CSCF5 | bsin2 z | a = 5 b = 11 | −1.8310,0.9155 ± 2.1099i −1.8310,0.9155 ± 2.1099i | −1 1 −1 | (0.2534,−0.0007,−1.0297) | 2.2454 | |
| CSCF6 | b|tanh z| | a = 3.1 b = 8 | −0.5647,0.2823 ± 0.5569i −0.5647,0.2823 ± 0.5569i | −1 1 −1 | (0.2037,−0.1058,−0.7622) | 2.3544 | |
| CSCF7 | bcosh(z) − 0.2 | a = 1 b = 1 | −0.7854,0.3927 ± 1.6492i | −1 1 −1 | (0.5423,−0.1976,−0.6966) | 2.4948 | |
| CSCF8 | b|sinh(z)| | a = 1 b = 1 | −1.6772,0.8386 ± 2.3293i −1.6772,0.8386 ± 2.3293i | −1 1 −1 | (0.1919,−0.0870,−0.6350) | 2.1651 |
| System | System Scaling Ratio | System | System Scaling Ratio |
|---|---|---|---|
| CSCF1 | CSCF2 | ||
| CSCF3 | CSCF4 | ||
| CSCF5 | CSCF6 | ||
| CSCF7 | CSCF8 |
| Name | Options | Parameters | Clocks |
|---|---|---|---|
| Multiplier | Sample and Off: Off | Multiplication Factor: 0.333 | ClockA:250 kHz ClockB:4 MHz |
| SumDiff(1) | Output Phase: Phase 1 Input 1: Non-inverting Input 2: Non-inverting Input 3: Off Input 4: Off | Gain 1: Num1 Gain 2: Num2 | ClockA:250 kHz |
| SumDiff(2) | Output Phase: Phase 1 Input 1: Non-inverting Input 2: Inverting Input 3: Off Input 4: Off | Gain 1:Num3 Gain 2:Num4 | ClockA:250 kHz |
| Voltage | Polarity Positive (+2 V) | ||
| GainHalf | Polarity: Non-inverting Input Sampling Phase: Phase 1 | Gain: Num5 | ClockA:250 kHz |
| Hold | Input Sampling Phase: Phase 1/2 (The Phase depends on the output of the connected adder) | ClockA:250 kHz | |
| TransferFunction | Output Hold: Off | ClockA:250 kHz ClockB:4 MHz |
| Name | Options | Parameters | Clocks |
|---|---|---|---|
| Integrator(1) ~ (3) | Polarity: Non-inverting Input Sampling Phase: Phase 1 Compare Control To: No Reset | Integration Const: 0.0025 [1/us] | ClockA:250 kHz |
| SumDiff(1) | Output Phase: Phase 1 Input 1: Inverting Input 2: Inverting Input 3: Off Input 4: Off | Gain 2: 1.00 | ClockA:250 kHz |
| SumDiff(2) | Output Phase: Phase 1 Input 1: Non-inverting Input 2: Inverting Input 3: Off Input 4: Off | Gain 2: 1.00 | ClockA:250 kHz |
| SumDiff(3) | Output Phase: Phase 1 Input 1: Inverting Input 2: Inverting Input 3: Off Input 4: Off | Gain 2: 1.00 | ClockA:250 kHz |
| CSCF0 | CSCF1 | CSCF2 | |||
|---|---|---|---|---|---|
| Num 1 | 18 | Num 1 | 24 | Num 1 | 30 |
| Num 2 | 1 | Num 2 | 1.2 | Num 2 | 1 |
| Num 3 | 0.083 | Num 3 | 0.09375 | Num 3 | 0.075 |
| Num 4 | 4.167 | Num 4 | 1.25 | Num 4 | 1 |
| Num 5 | 18 | Num 5 | 20 | Num 5 | 10 |
| CSCF3 | CSCF4 | CSCF5 | |||
|---|---|---|---|---|---|
| Num 1 | 30 | Num 1 | 9 | Num 1 | 30 |
| Num 2 | 3 | Num 2 | 2 | Num 2 | 2 |
| Num 3 | 0.05 | Num 3 | 0.167 | Num 3 | 0.05 |
| Num 4 | 1 | Num 4 | 2.5 | Num 4 | 1 |
| Num 5 | 33 | Num 5 | 13.85 | Num 5 | 75 |
| CSCF6 | CSCF7 | CSCF8 | |||
|---|---|---|---|---|---|
| Num 1 | 6 | Num 1 | 9 | Num 1 | 15 |
| Num 2 | 2.5 | Num 2 | 1 | Num 2 | 1 |
| Num 3 | 0.167 | Num 3 | 0.2 | Num 3 | 0.15 |
| Num 4 | 2.667 | Num 4 | 5 | Num 4 | 2 |
| Num 5 | 7.26 | Num 5 | 9.3 | Num 5 | 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Li, C.; Cen, X.; Zhang, X.; Chai, L. Chaos Regulation via Complex Nonlinear Feedback and Its Implementation Based on FPAA. Symmetry 2025, 17, 212. https://doi.org/10.3390/sym17020212
Xu J, Li C, Cen X, Zhang X, Chai L. Chaos Regulation via Complex Nonlinear Feedback and Its Implementation Based on FPAA. Symmetry. 2025; 17(2):212. https://doi.org/10.3390/sym17020212
Chicago/Turabian StyleXu, Jitong, Chunbiao Li, Xiaoliang Cen, Xin Zhang, and Lin Chai. 2025. "Chaos Regulation via Complex Nonlinear Feedback and Its Implementation Based on FPAA" Symmetry 17, no. 2: 212. https://doi.org/10.3390/sym17020212
APA StyleXu, J., Li, C., Cen, X., Zhang, X., & Chai, L. (2025). Chaos Regulation via Complex Nonlinear Feedback and Its Implementation Based on FPAA. Symmetry, 17(2), 212. https://doi.org/10.3390/sym17020212






