Adaptive Terrain Modeling for Side-Slope Surfaces
Abstract
1. Introduction
2. Geometric Expression
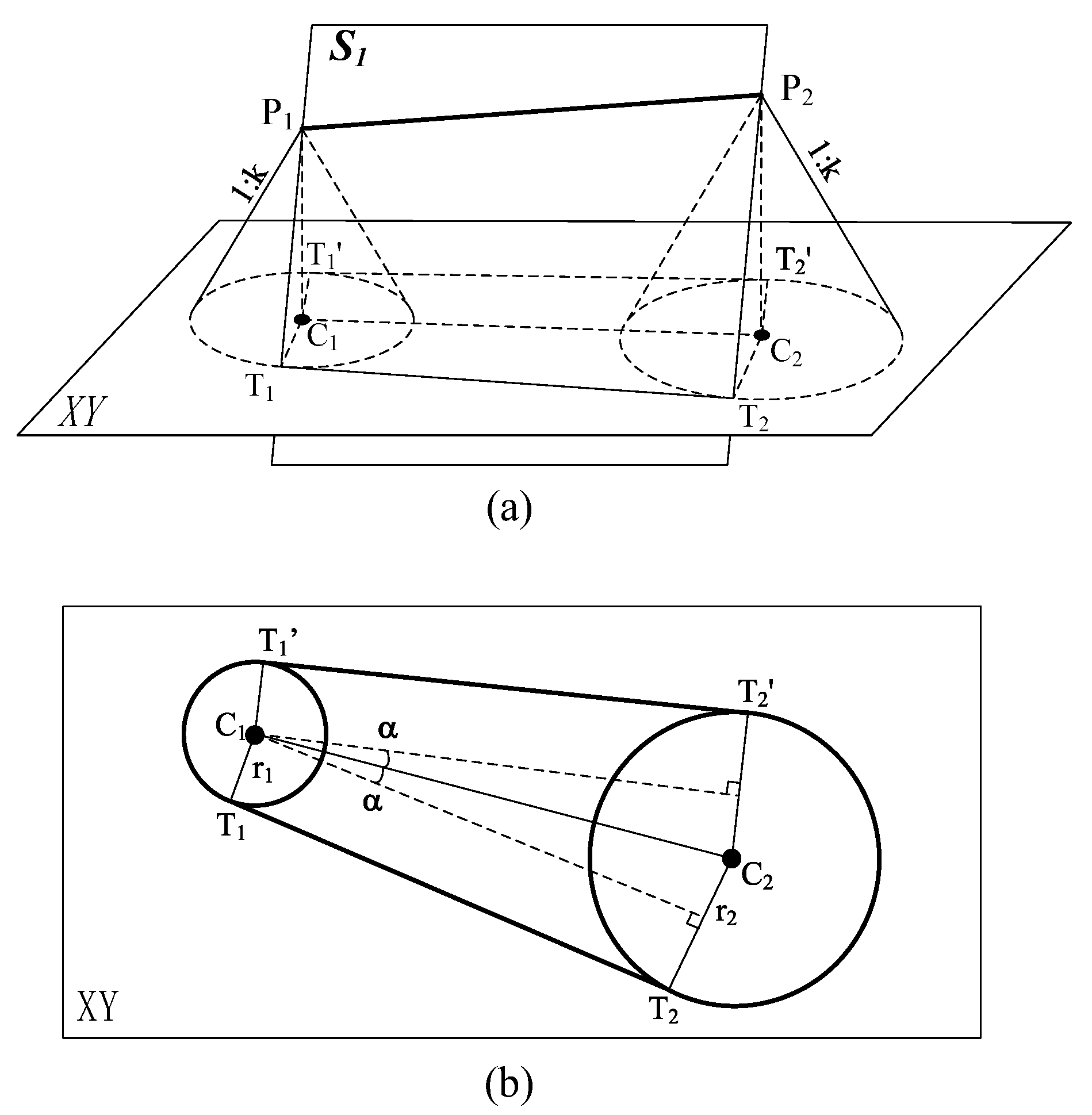
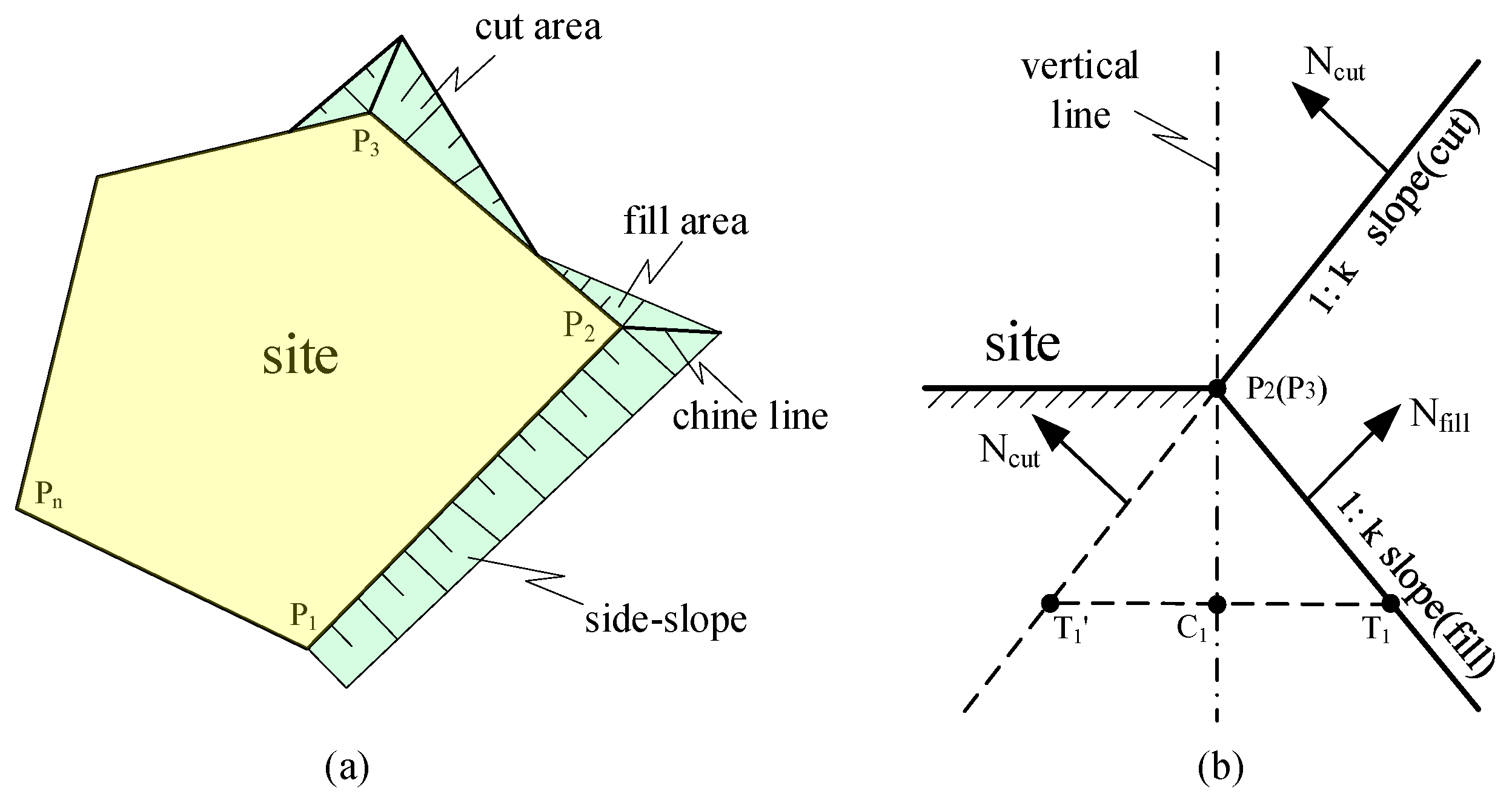
2.1. Side-Slope Plane Equation
2.2. Terrain Triangle Meshes
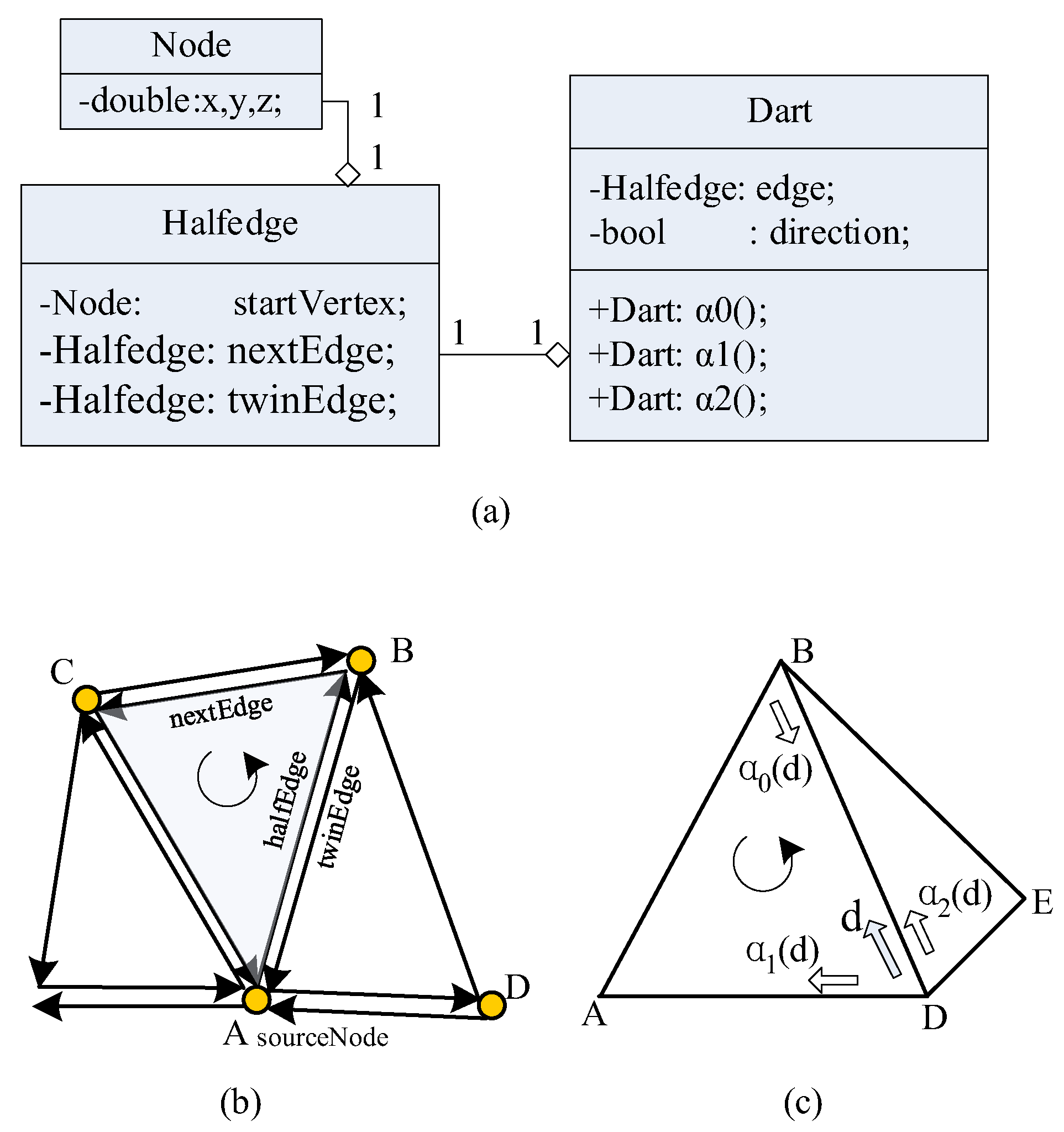
2.2.1. Half-Edge Data Structure
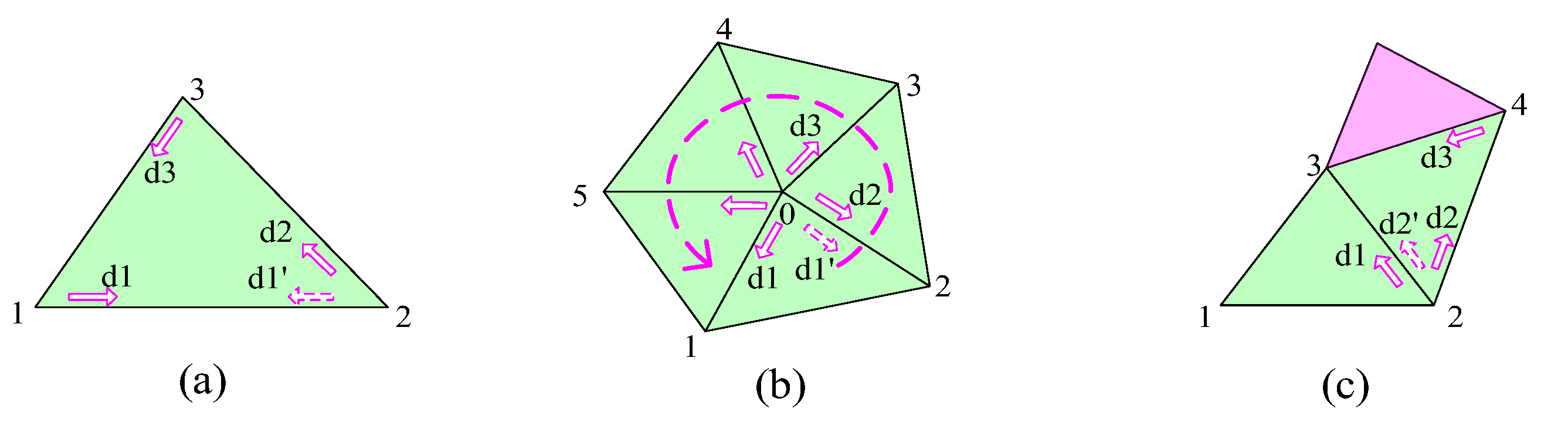
2.2.2. Topological Combination Operations
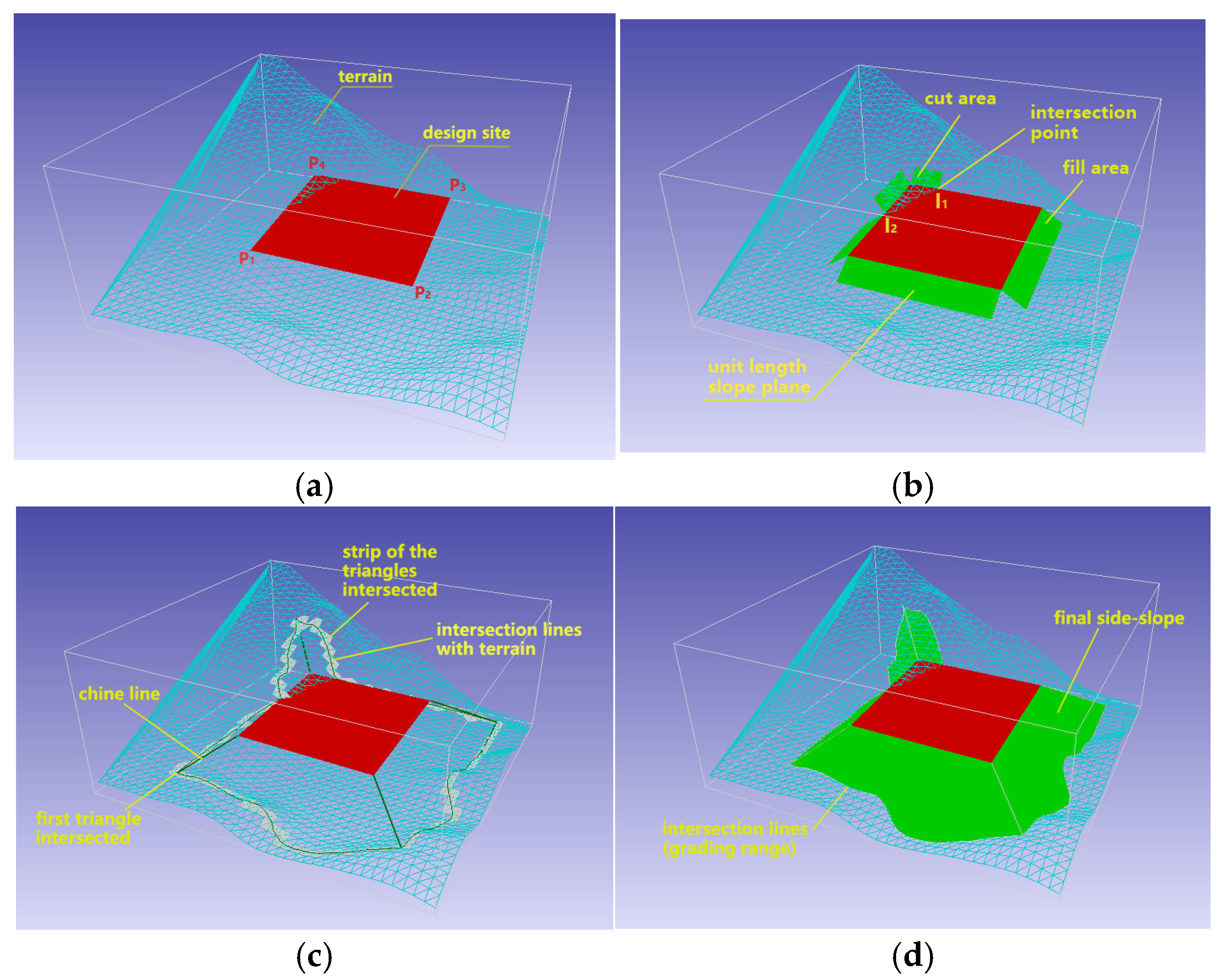
3. The First Stage
3.1. Rules for Changes in Fill/Cut Side-Slope Types
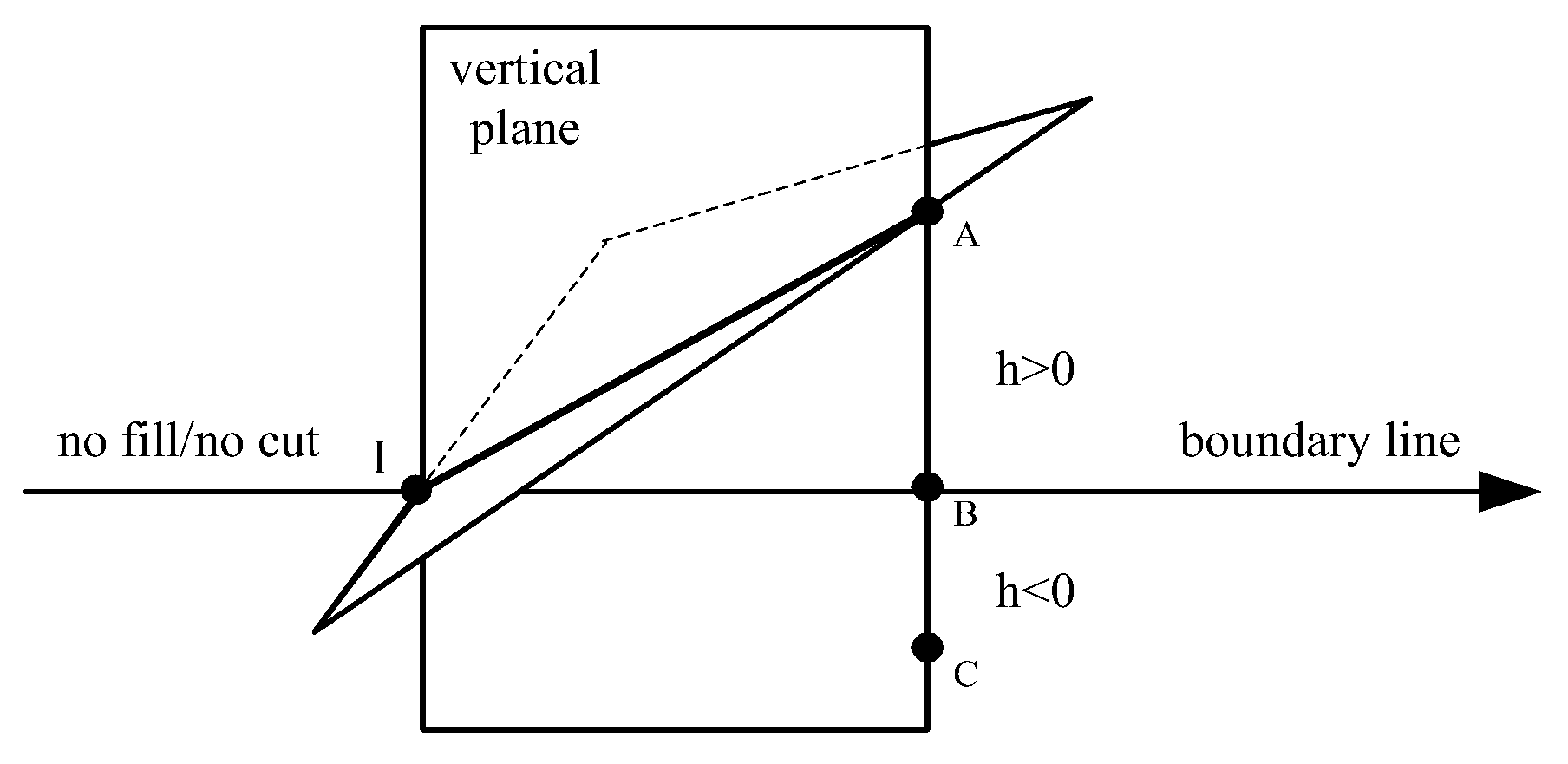
3.2. Finding the Intersecting Triangles in Mesh
3.3. Calculation of Intersection Points Between Boundary Lines and Terrain Mesh
3.4. Determine the Side-Slope Type and Its Equation Piece by Piece
| Algorithm 1. Traveling-along-lines |
| Input: Terrain mesh M, boundary lines PL, slope value kfill and kcut. Output: Side-slope equations for each segment on the boundary line, Eqs{} ordered point set (turning point + intersection point). 1. Fetch the first turning points P1 of PL 2. ∆t: = locateTriangle (P1, M) 3. IF above (P1, ∆t) THEN L: = 1 4. ELSE L: = −1 5. IF (L == 1) THEN k: = kfill 6. ELSE k: = kcut 7. FOREACH (P1,P2) IN PL segments 8. P: = P1 9. Ints: = intersect (P1P2, M) 10. FOREACH I IN Ints 11. IF L == 0 THEN continue 12. Eqs←side-slopeEq (P, I, L, k) 13. L: = −1*L 14. P: = I 15. Eqs←side-slopeEq (P, P2, L, k) |
4. The Second Stage
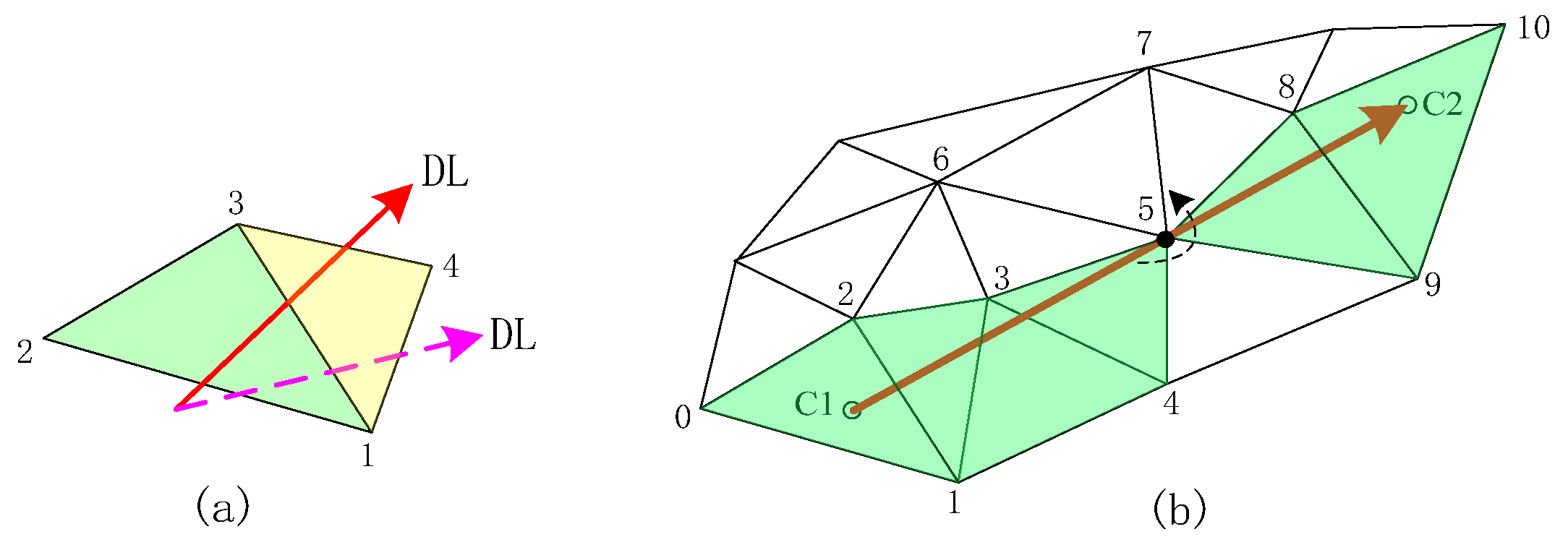
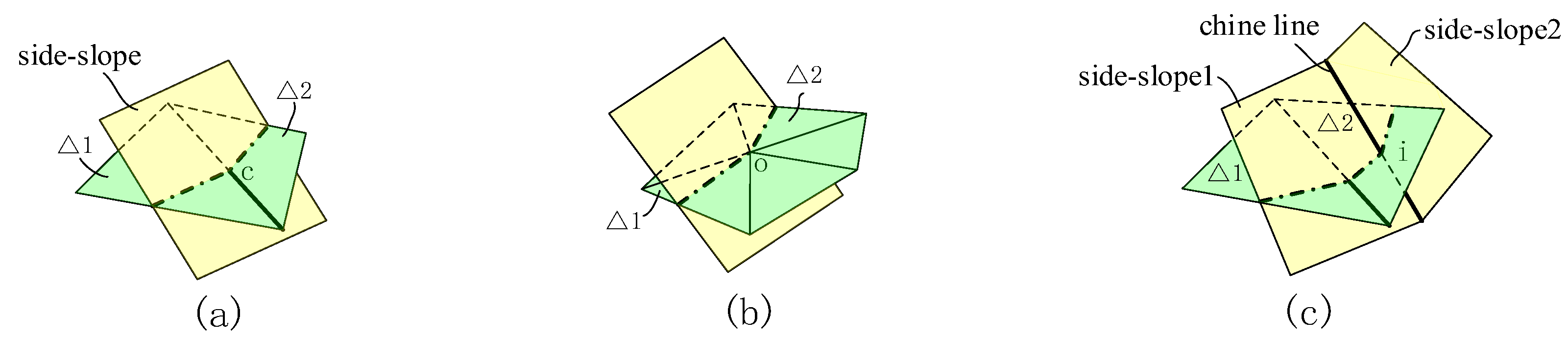
4.1. Topological Continuity of the Intersection Between the Side-Slope Plane and the Triangular Mesh
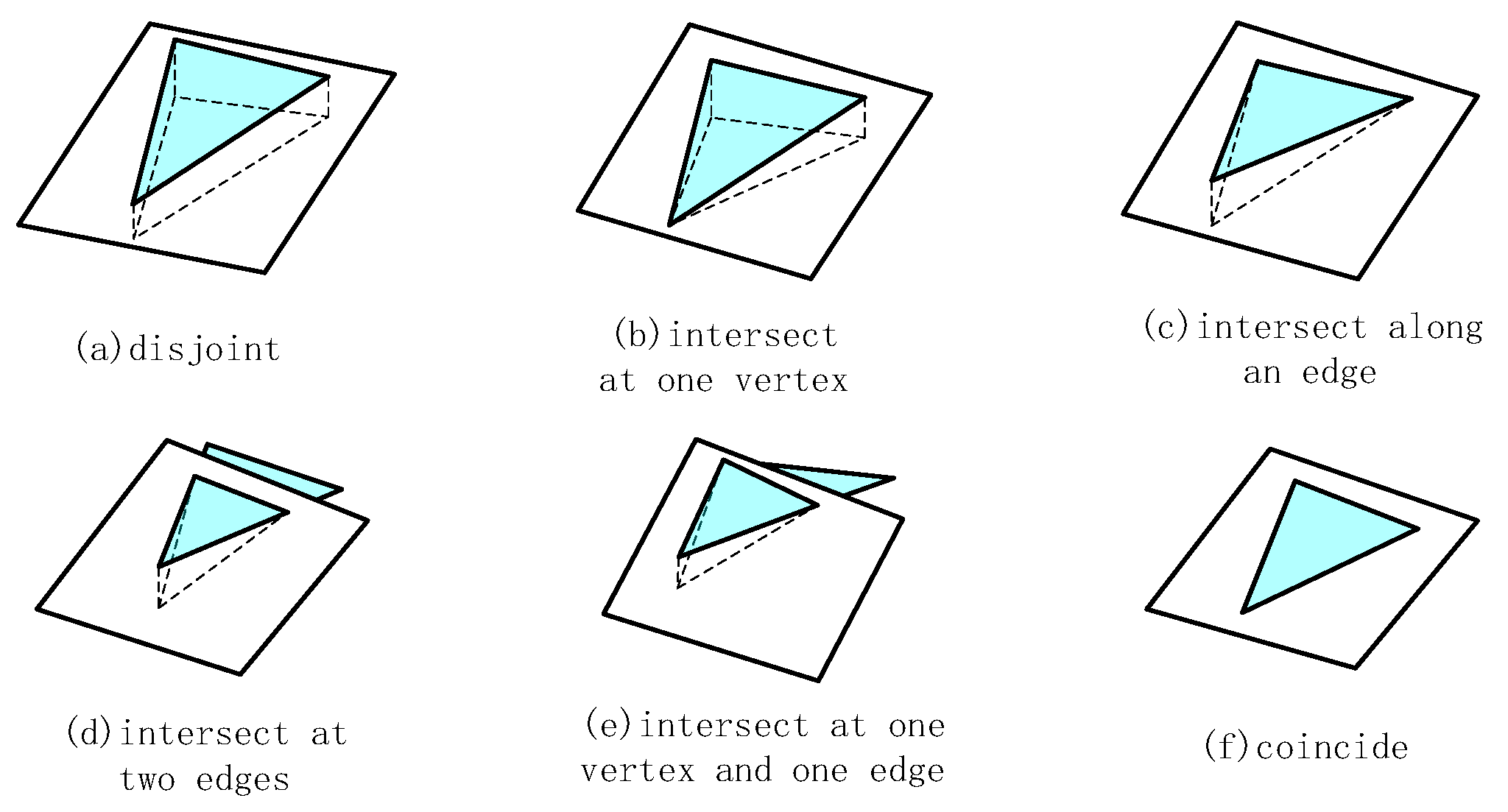
4.1.1. Spatial Relationship Between Plane and Triangle
4.1.2. Topological Continuity Analysis
4.2. Algorithm of Traveling Along Plane
4.3. Calculation of the Intersection Line Between the Side-Slope Surface and the Terrain Mesh
| Algorithm 2. Traveling-along-planes |
| Input: Boundary lines PL, equations of side-slope planes {Eqs}, terrain mesh M. Output: The intersection lines {INTs} between side-slope planes and terrain mesh. 1. Find the first triangle that intersects the side-slope 2. R(t) = P1 + (N2 × N1) · t //See Equation (13) 3. i: = intersect (R(t), M) 4. ∆t: = locateTriangle (i,M) 5. FOREACH side-slope plane sp IN Eqs: 6. ∆t2: = locateTriangle (P2, M) 7. WHILE ∆t ≠ ∆t2 DO: 8. INTs←INTs +intersect (sp, ∆t) 9. ∆t: = AdjcentTriangle (sp, ∆t) |
5. Discussion
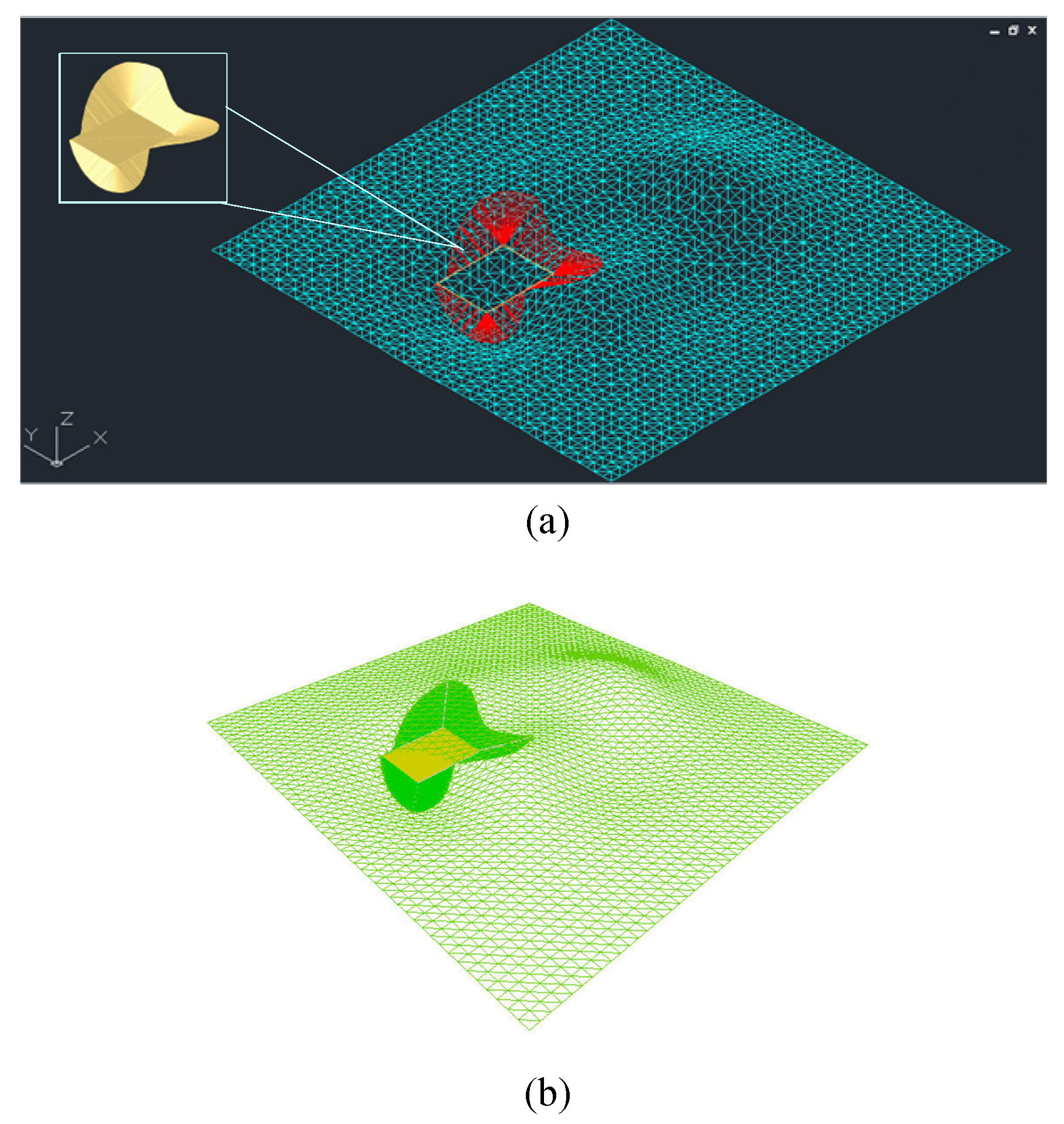
5.1. Examples
5.2. Analysis
5.3. Comparison
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Glaeser, G. Geometry and Its Applications in Arts, Nature and Technology; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 201–206. [Google Scholar]
- Hare, W.; Lucet, Y.; Rahman, F. A mixed-integer linear programming model to optimize the vertical alignment considering blocks and side-slopes in road construction. Eur. J. Oper. Res. 2015, 241, 631–641. [Google Scholar] [CrossRef]
- Momo, N.S.; Hare, W.; Lucet, Y. Modeling side slopes in vertical alignment resource road construction using convex optimization. Comput. Aided Civ. Infrastruct. Eng. 2023, 38, 211–224. [Google Scholar] [CrossRef]
- Yuan, L.; Liu, S.; Meng, L. Numerical simulation analysis of slope stability from rainwater utilizing the Civil3D+Flac3D coupling. Desalin. Water Treat. 2024, 319, 100517–100527. [Google Scholar] [CrossRef]
- OpenRoads Designer, Roadway Design Software. Available online: https://www.bentley.com/software/openroads-designer/ (accessed on 12 September 2024).
- HintCAD. Available online: https://www.hintcad.cn/product/3862.html (accessed on 15 October 2024). (In Chinese).
- Hartmann, E. Geometry and Algorithms for Computer Aided Design; Darmstadt University of Technology: Darmstadt, Germany, 2003; Volume 95. [Google Scholar]
- Koźniewski, E.; Koźniewski, M.; Orłowski, M.; Owerczuk, J. Modeling an embankment with a natural slope. J. Biul. Pol. Soc. Geom. Eng. Graph. 2013, 25, 49–56. [Google Scholar]
- Zhou, F.; Li, C.; Ding, Y. Developable iso⁃slope surface and its application to slope modeling. J. Wuhan Univ. 2019, 52, 610–615. [Google Scholar]
- Yang, P.; Qian, X. Direct boolean intersection between acquired and designed geometry. Comput. Aided Des. 2009, 41, 81–94. [Google Scholar] [CrossRef]
- Lin, H.; Qin, Y.; Liao, H.; Xiong, Y. Affine arithmetic based B-Spline surface intersection with GPU acceleration. IEEE Trans. Vis. Comput. Graph. 2013, 20, 172–181. [Google Scholar]
- Shou, H.H.; Zhou, C. Triangular grid intersection based on hierarchical enclosing box and average cell. J. Zhejiang Univ. Technol. 2018, 46, 540–543+557. [Google Scholar]
- Shi, Y.F.; Zhang, Y.H.; Cheng, T. Intersection algorithm for surface segmentation based on space polygon triangulation. J. Graph. 2019, 40, 447–451. [Google Scholar]
- Elsheikh, M. A reliable triangular mesh intersection algorithm and its application in geological modelling. Eng. Comput. 2014, 30, 143–157. [Google Scholar] [CrossRef]
- Svelander, F.; Kettil, G.; Johnson, T.; Mark, A.; Logg, A.; Edelvik, F. Robust intersection of structured hexahedral meshes and degenerate triangle meshes with volume fraction applications. Numer. Algorithms 2018, 77, 1029–1068. [Google Scholar] [CrossRef]
- Ventura, M.; Guedes Soares, C. Surface intersection in geometric modeling of ship hulls. J. Mar. Sci. Technol. 2012, 17, 114–124. [Google Scholar] [CrossRef]
- Botsch, M.; Pauly, M.; Kobbelt, L.; Alliez, P.; Lévy, B.; Bischoff, S.; Röossl, C. Geometric Modeling Based on Polygonal Meshes. In Eurographics 2008 Tutorial Notes; Eurographics: Crete, Greece, 2008; pp. 17–18. [Google Scholar]
- Bradley, P.; Paul, N. Comparing G-maps with other topological data structures. GeoInformatica 2014, 18, 595–620. [Google Scholar] [CrossRef]
- O’Rourke, J. Computational Geometry in C; China Machine Press: Beijing, China, 2005; pp. 239–245. [Google Scholar]
- Hjelle, Ø.; Dæhlen, M. Triangulations and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; pp. 25–28. [Google Scholar]
- Autodesk. AutoCAD Civil 3D. Available online: https://www.autodesk.com/products/civil-3d/ (accessed on 12 September 2024).
- Zhao, J.C.; Bai, R.C.; Liu, G.W. Research on TIN fast intersection algorithm and its application. Comput. Appl. Res. 2016, 33, 3667–3670+3695. [Google Scholar]
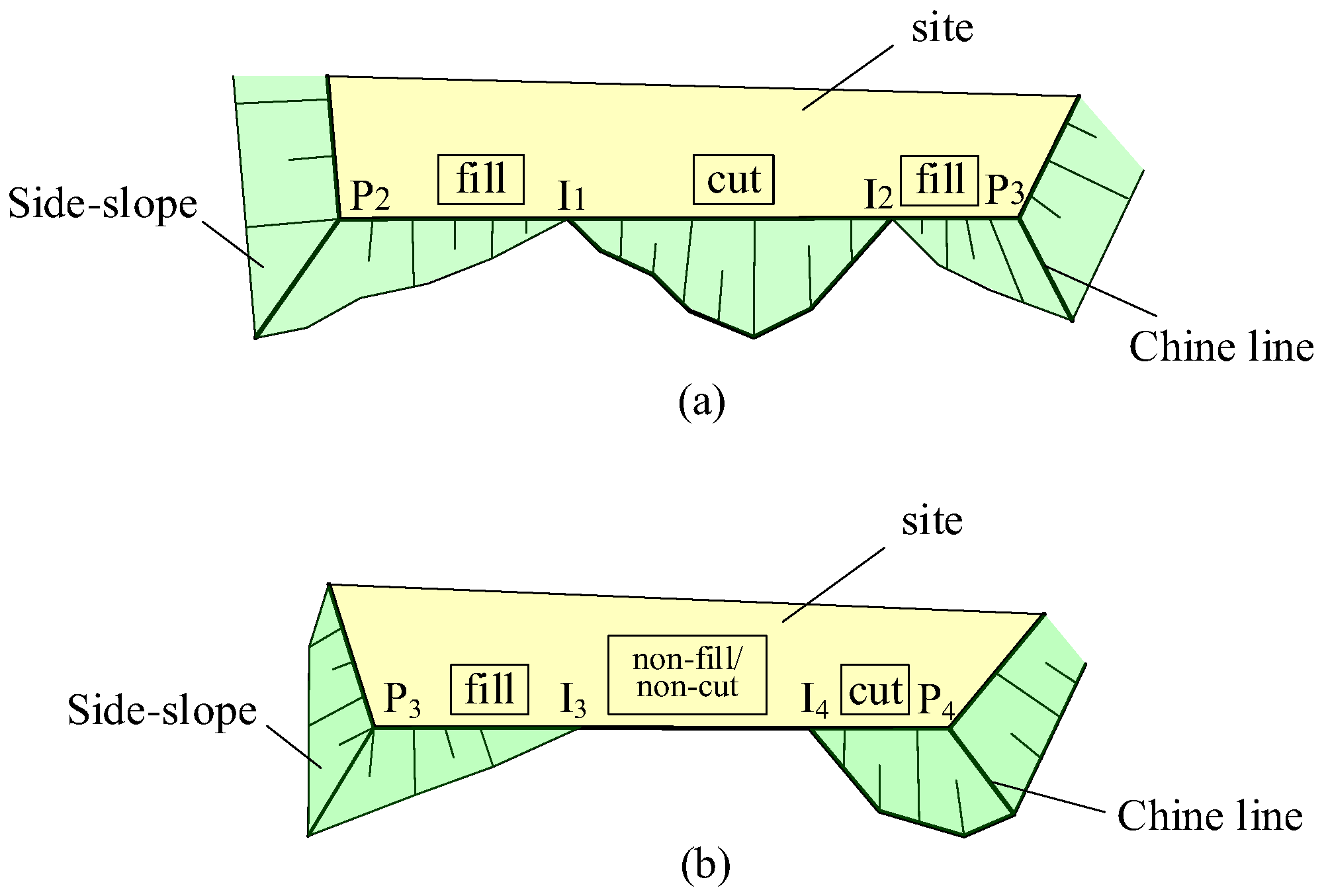



| No. | Spatial Relationship Between Boundary Line and Triangle Surface | Change in Fill/Cut Type |
|---|---|---|
| 1 | Intersecting and Intersection Point Inside the Triangle | Reversal at the intersection point, either from fill to excavation or from excavation to fill |
| 2 | Intersecting and Intersection Point on One Side of the Triangle | No change in fill/cut type |
| 3 | Coplanar (two intersection points on the triangle edge) | This segment becomes neither fill nor excavation; the type of the next segment is determined by the method in Figure 6 |
| 4 | Not Intersecting | No change in fill/cut type |
| No. | Start Point | Point Type | End Point | Inverse | Fill/Cut Type | L Sign | Slope Value |
|---|---|---|---|---|---|---|---|
| 1 | P1 | Turning Point | P2 | false | fill | 1 | 1:1.5 |
| 2 | P2 | Turning Point | P3 | false | fill | 1 | 1:1.5 |
| 3 | P3 | Turning Point | I1 | false | fill | 1 | 1:1.5 |
| 4 | I1 | Intersection Point | P4 | true | cut | −1 | 1:0.75 |
| 5 | P4 | Turning Point | I2 | false | cut | −1 | 1:0.75 |
| 6 | I2 | Intersection Point | P1 | true | fill | 1 | 1:0.75 |
| Total Number of Triangles in the Mesh | Number of Intersecting Triangles | Time (ms) |
|---|---|---|
| 2848 | 254 | 2.5682 |
| 8544 | 442 | 2.6644 |
| 14,240 | 551 | 2.9308 |
| 19,936 | 671 | 3.5895 |
| 25,632 | 750 | 4.1023 |
| 42,720 | 991 | 5.4027 |
| 59,808 | 1126 | 6.0809 |
| 71,200 | 1265 | 6.7120 |
| 76,892 | 1288 | 7.2347 |
| 99,680 | 1447 | 7.9305 |
| 128,160 | 1670 | 8.8576 |
| 139,552 | 1735 | 9.1974 |
| 213,600 | 2207 | 11.7620 |
| Total Number of Triangles in the Mesh | ZHAO [22] (ms) | The Method Proposed (ms) |
|---|---|---|
| ~19,000 | 229 | 3.59 |
| ~139,000 | 2604 | 9.20 |
| ~250,000 | 5104 | 13.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, F. Adaptive Terrain Modeling for Side-Slope Surfaces. Symmetry 2025, 17, 191. https://doi.org/10.3390/sym17020191
Zhou F. Adaptive Terrain Modeling for Side-Slope Surfaces. Symmetry. 2025; 17(2):191. https://doi.org/10.3390/sym17020191
Chicago/Turabian StyleZhou, Fangxiao. 2025. "Adaptive Terrain Modeling for Side-Slope Surfaces" Symmetry 17, no. 2: 191. https://doi.org/10.3390/sym17020191
APA StyleZhou, F. (2025). Adaptive Terrain Modeling for Side-Slope Surfaces. Symmetry, 17(2), 191. https://doi.org/10.3390/sym17020191





