Realizing Fuel Conservation and Safety for Emerging Mixed Traffic Flows: The Mechanism of Pulse and Glide Under Signal Coordination

Abstract

Pulse and glide (PnG) has limited application in urban traffic flows, particularly in emerging mixed traffic flows comprising connected and automated vehicles (CAVs) and human-driven vehicles (HDVs), as well as at signalized intersections. In light of this, green wave coordination is applied to the urban network of multiple signalized intersections. Under perception asymmetries, HDVs lack environmental perception capabilities, while CAVs are equipped with perception sensors of varying performance. CAVs could activate the PnG mode and set its average speed based on signal phase and safety status, enabling assessment of fuel savings and safety. The findings reveal that (i) excluding idling fuel consumption, when the traffic volume is low and market penetration rate (MPR) of CAVs exceeds 70%, CAVs could significantly reduce regional average fuel consumption by up to 8.8%. (ii) Compared to HDVs, CAVs could achieve a fuel saving rate (FSR) ranging from 7.1% to 50%. In low-traffic-volume conditions, CAVs with greater detection ranges could swiftly activate the PnG mode to achieve fuel savings, while in higher-traffic-volume conditions, more precise sensing aids effectiveness. (iii) the PnG mode could ensure safety for CAVs and HDVs, with CAVs equipped with highly precise sensing exhibiting particularly robust safety performance.

1. Introduction

Since the onset of the 21st century, rapid global economic growth has significantly increased the demand for goods transportation and personal mobility, leading to the rapid depletion of energy reserves, particularly fossil fuels, and an escalating greenhouse effect [1,2]. Road transportation, as a critical component of the transportation system, accounts for a substantial proportion of fuel consumption within the broader transportation sector, prompting significant expectations for energy conservation. To address the fuel consumption issues in road transportation, numerous researchers have explored strategies to reduce system-wide fuel consumption by optimizing transportation infrastructure [3,4]. Concurrently, as the primary participants in road traffic, vehicles have garnered considerable attention for fuel reduction, with proposed measures including reducing vehicle weight, enhancing engine efficiency, and optimizing aerodynamic characteristics [5,6,7]. Vehicle fuel consumption is influenced not only by the inherent properties of the vehicle but also, to a significant extent, by driver behavior [8,9]. Meanwhile, the pulse and glide (PnG) strategy, which seeks to optimize fuel consumption through speed modulation, has gained increasing attention due to its implementation simplicity [10,11,12].

The PnG strategy reduces vehicle fuel consumption through periodic acceleration and gliding deceleration, imposing no constraints on the vehicle’s inherent functionality. Natarajan et al. [13] and Sohn et al. [14] demonstrated the fuel saving potential of PnG at the individual vehicle level for manual and automatic transmission vehicles, respectively. In real-world driving scenarios, a vehicle’s operation is influenced by surrounding traffic, particularly the presence of a leading vehicle, as maintaining a safe following distance is essential to avoid crashes. To address this, Li et al. [15] investigated a car-following scenario with two vehicles, where the following vehicle employed PnG. Their simulations revealed that PnG reduced fuel consumption by 20% compared to vehicles under normal driving conditions. Furthermore, Imanishi et al. [16] conducted real-vehicle experiments, finding that at a leading vehicle speed of 40 km/h, PnG achieved a fuel saving of 43.4% compared to constant-speed (CS) driving. Beyond vehicle dynamics, the impact of road conditions, such as road gradient, on the fuel saving potential of PnG has also garnered attention [17]. Additionally, Huang et al. [18] applied PnG at intersections, demonstrating its effectiveness in reducing fuel consumption in such contexts. While existing studies have explored the fuel saving potential of PnG in single-vehicle, car-following, and traffic flow scenarios, research on traffic flow applications remains relatively underdeveloped compared to the former two. Moreover, most studies validating PnG’s fuel saving potential have been conducted on dedicated test tracks or freeways, with limited verification in urban environments, particularly under complex conditions such as those involving intersections.

On the other hand, advancements in automation and communication technologies have introduced a new participant in road transportation: connected and automated vehicles (CAVs), leading to the emerging mixed traffic flow comprising both human-driven vehicles (HDVs) and CAVs [19,20]. Unlike HDVs, CAVs equipped with perception sensors such as cameras, radar, and lidar could acquire real-time information about surrounding vehicles, environmental conditions, and their own motion dynamics [21,22]. This results in pronounced asymmetry in environmental perception within emerging mixed traffic flows. Furthermore, the communication capabilities of CAVs enable information exchange between CAVs and infrastructure, facilitating precise real-time and coordinated control [23,24]. In response to the emergence of CAVs, Li et al. [25] applied the PnG strategy to CAVs within a mixed platoon of 30 vehicles consisting of both CAVs and HDVs, finding that the overall fuel consumption of the platoon could be reduced by up to 24%. This study confirmed the feasibility of implementing PnG in CAVs coexisting with HDVs, though the operational conditions in the study diverged significantly from real-world traffic flow scenarios. Moreover, with the rapid advancement of CAV-related technologies, environmental perception capabilities among individual CAVs also exhibit a lack of symmetry, and the fuel saving potential of different CAVs under varying PnG control strategies remains underexplored.

In summary, with the continuous increase in vehicle ownership, road traffic loads have been steadily rising, particularly in urban areas, making the application of the PnG strategy to reduce vehicle fuel consumption and, consequently, regional fuel consumption increasingly imperative. To this end, this study investigates the fuel saving potential and safety of the PnG mode within the emerging mixed traffic flow in an urban road network with three consecutive signalized intersections, under asymmetric perception capabilities and specific signal coordination schemes. The research is conducted through the following three key aspects: (i) analysis of vehicle trajectory data at the relevant intersections to design signal timing and implement green wave coordinated control based on road traffic load, thereby creating conditions for CAVs to pass through intersections during green phases; (ii) characterization of traffic flow at each intersection, utilizing time to collision (TTC) to classify conflict levels, providing a basis for determining the conflict status of CAVs, and enabling the activation of the PnG mode and planning of its average speed based on the conflict level and signal phase, while accounting for variations in detection range and precision among CAVs; (iii) modeling of the target road network and adjusting the market penetration rate (MPR) of CAVs and volume, followed by simulations to evaluate the fuel saving potential and safety of the PnG mode across different CAV types, MPRs, and traffic flow conditions.

2. Methodology

2.1. Emerging Mixed Traffic Flows

The next generation simulation (NGSIM) dataset is a pivotal resource in the field of transportation, providing a wealth of authentic microscopic traffic data crucial for understanding micro-level traffic flow and car-following behavior, thereby advancing the development of traffic flow theory [26,27]. 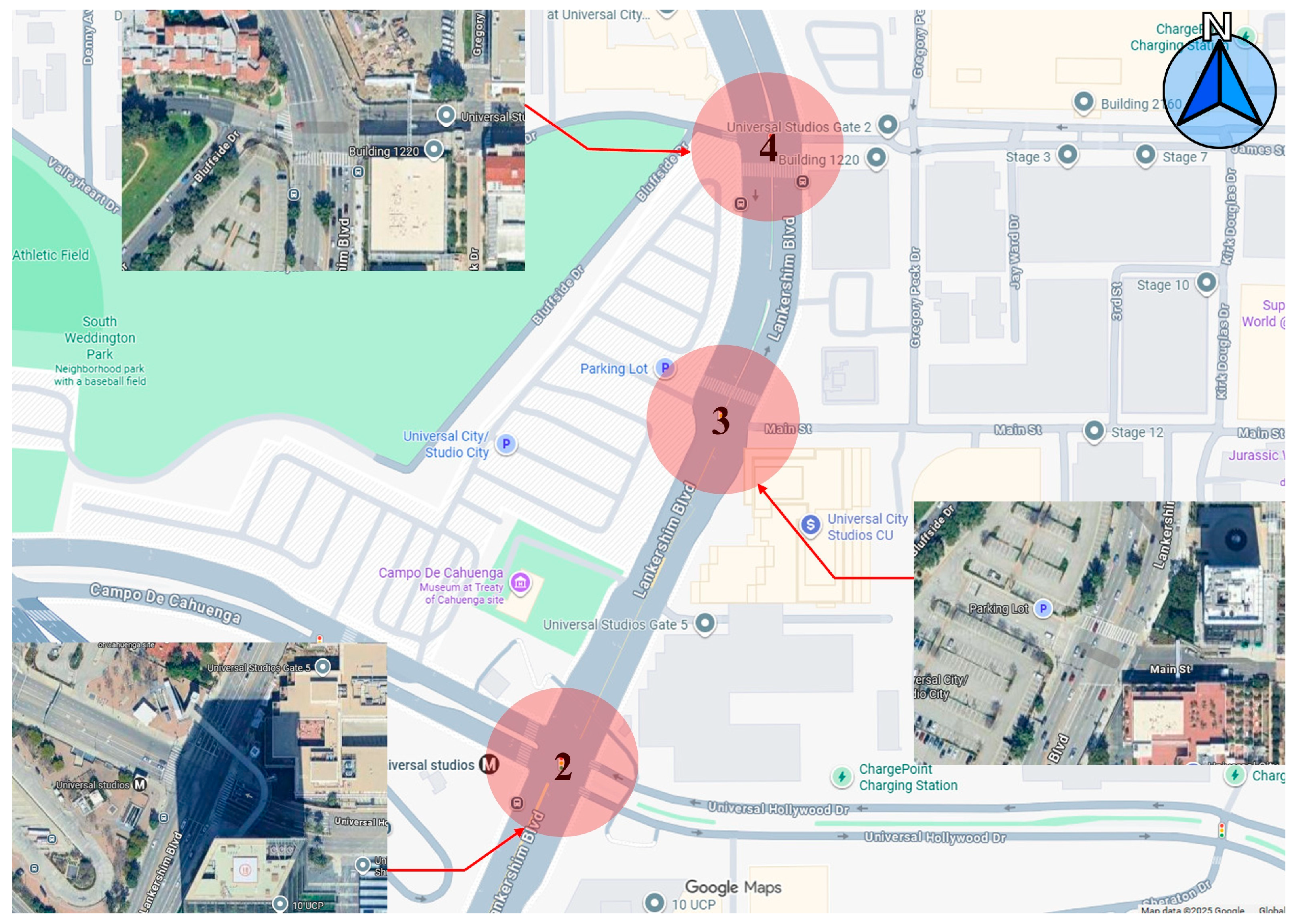Over the past decade, numerous microscopic traffic studies have leveraged NGSIM’s traffic flow data, which includes urban roadway scenarios [28]. In light of this, using the traffic flow data recorded on the Lankershim Boulevard segment from 8:30 to 8:45 as the data source, select intersections 2, 3, and 4 as the target intersections. Extract vehicle movement data within the region formed by these three intersections, and construct a road network model based on the trajectory data. The geographic location of the study area is shown in Figure 1, while the geometric design information of each intersection used in the simulation model is presented in

Table 1. Approach length of each intersection in the target area.

	EBA	WBA	SBA	NBA
Intersection 2	125 m	125 m	400 m	325 m
Intersection 3	100 m	100 m	325 m	250 m
Intersection 4	100 m	100 m	250 m	100 m

Note: NBA is the northbound approach; SBA denotes the southbound approach; EBA represents the east-bound approach; WBA signifies the westbound approach.

and

Table 2. Number of lanes on each approach at intersections in the target area.

	EBA	WBA	SBA	NBA
Intersection 2	3	3	5	6
Intersection 3	2	2	5	5
Intersection 4	3	2	5	5

.

The traffic flow on this road segment consists of four vehicle types: motorcycles, trucks, buses, and cars, with the former three constituting a small proportion, accounting for only 4.63% of the total. To more accurately represent the actual operational conditions and traffic load within the intersection, after eliminating vehicle trajectory data with spatiotemporal inconsistencies, it is necessary to convert the volumes of motorcycles, trucks, and buses into equivalent traffic volumes using cars as the standard [29]. The method for calculating equivalent traffic volumes is provided in Equation (1).

$$PC{E}_{obj}={\displaystyle \frac{h_{obj}+h_{obj}^{\prime }}{h_s+h_s^{\prime }}}$$

(1)

where ${\mathit{PCE}}_{\mathit{obj}}$ is the $\mathit{PCE}$ of the objective vehicle type; $h_{\mathit{obj}}$ denotes the average time headway of objective vehicle type, s; $h_{obj}^{\prime }$ represents the average time headway of the vehicles following the objective vehicle type, s; $h_s$ signifies the average time headway of a standard passenger car, s; and $h_s^{\prime }$ is the average time headway of the vehicles following a standard car, s.

Based on this, after obtaining the traffic volume during peak periods at the target area’s intersections, the traffic volume is scaled up by 400% to derive the peak hour traffic flow for the intersections. The traffic flow and directionality for intersection 2, intersection 3, and intersection 4 during peak hours are presented in

Table 3. Traffic flow information of the intersection 2.

	Volume (veh/h)	Left-Turning (%)	Right-Turning (%)
Eastbound	436	51.38	3.67
Westbound	352	18.18	57.95
Southbound	2504	35.62	5.59
Northbound	1920	3.54	27.71

,

Table 4. Traffic flow information of the intersection 3.

	Volume (veh/h)	Left-Turning (%)	Right-Turning (%)
Eastbound	32	50.00	37.50
Westbound	92	56.52	39.13
Southbound	2376	3.03	2.36
Northbound	1796	2.23	6.24

and

Table 5. Traffic flow information of the intersection 4.

	Volume (veh/h)	Left-Turning (%)	Right-Turning (%)
Eastbound	64	37.05	56.25
Westbound	84	52.38	42.86
Southbound	2460	6.02	0.65
Northbound	1808	0.88	11.06

, respectively.

Upon determining the directional traffic flows at each intersection approach, vehicle routes were assigned based on real-world trajectory data. The specific origin-destination routes are detailed in

Table 6. Traffic flows originating from intersection 4.

Route	1	2	3	4	5	6	7	8	9	10	11	12	13
Depart	4N	4N	4N	4N	4N	4N	4N	4W	4W	4W	4E	4E	4E
Arrive	4W	4E	3W	3E	2W	2E	2S	4N	4E	2S	4N	4W	2S

Note: 4N is the north of intersection 4; 4W denotes the west of intersection 4; 4E presents the east of intersection 4; 3W signifies the west of intersection 3; 3E is the east of intersection 3; 2W denotes the west of intersection 2; 2E presents the east of intersection 2; and 2S signifies the south of intersection 2.

,

Table 7. Traffic flows originating from intersection 3.

Route	1	2	3	4	5	6
Depart	2W	2W	2W	2E	2E	2E
Arrive	4N	2E	2S	4N	2W	2S

and

Table 8. Traffic flows originating from intersection 2.

Route	1	2	3	4	5	6	7	8	9	10	11	12	13
Depart	2S	2S	2S	2S	2S	2S	2S	2W	2W	2W	2E	2E	2E
Arrive	2W	2E	3W	3E	4W	4E	4N	2S	2E	4N	2S	2W	4N

. For all defined routes, the departure lane parameter “departlane” was set to “free,” thereby allowing each vehicle to select the fastest available lane at the moment of insertion.

The MPRs of CAVs were set at 0%, 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, and 100%, progressively integrating CAVs into the traffic flow originally composed solely of HDVs [30,31]. Based on the society of automotive engineers (SAE) classification of automation levels, current market-available CAVs predominantly operate at L1 and L2, relying primarily on onboard sensors such as cameras, radar, and lidar to acquire information about their own state and surrounding environment [32,33,34]. Accordingly, CAV sensing systems could be categorized into vision-based and lidar-based systems. Radar is an indispensable component in both vision-based and lidar-based configurations, and could be further classified into short-range radar (0.15–30 m), medium-range radar (1–100 m), and long-range radar (10–250 m) [35]. Based on these radar detection ranges, CAVs in emerging mixed traffic flows were divided into three types, CAV-S1, CAV-S2, and CAV-S3, corresponding to radar detection ranges of 30 m, 60 m, and 100 m, respectively, with the assumption that longitudinal target detection by CAVs relies on their equipped radar [36]. As previously stated, CAVs in the emerging mixed traffic flow exhibit varying levels of automation, and the performance differences of the onboard radar systems on which they rely are manifested not only in maximum detection range but also in sensing accuracy. In prior studies, longitudinal ranging errors of onboard radar systems have been reported to reach or exceed 2 m, 5 m, and even 10 m [37,38,39]. On this basis, the radar detection accuracy for CAV-S1, CAV-S2, and CAV-S3 was set with error margins of [−2, +2] m, [−5, +5] m, and [−10, +10] m, respectively, thereby achieving the perception asymmetry among different CAVs. Additionally, the proportions of CAV-S1, CAV-S2, and CAV-S3 within the CAV population were configured as 45%, 35%, and 20%, respectively, to complete the setup of the emerging mixed traffic flow [19,20]. These proportions do not represent market penetration rates, but instead reflect the practical assumption that vehicles with shorter sensing ranges correspond to lower-cost advanced driver assistance systems (ADAS) configurations and are therefore more common in the market, whereas vehicles equipped with medium- and long-range sensing capabilities rely on more expensive sensors and thus constitute smaller shares of CAVs.

On the other hand, when simulating regional traffic operations by inputting extracted traffic flow data into SUMO, the intelligent driver model (IDM) and cooperative adaptive cruise control (CACC) were employed as the car-following models for HDVs and CAVs, respectively. Specifically, key parameters in the car-following models, including maximum acceleration (acc), maximum deceleration (dec), maximum speed (spe), and the minimum gap maintained at a standstill (gap), were calibrated based on the actual operating conditions of the vehicles. More precisely, the expected values of maximum acceleration, maximum deceleration, and maximum speed at each intersection were adopted as the acc, dec, and spe parameters for both IDM and CACC [40]. For the calibration of the gap parameter, vehicle trajectory segments were extracted according to commonly accepted minimum safe TTC ranges for HDVs and CAVs. TTC values between 1.0 and 1.5 s for HDVs and between 0.9 and 1.0 s for CAVs represent typical lower-bound safe following conditions observed in previous studies, where drivers or automated systems maintain the smallest stable spacing. Therefore, trajectory data falling within these TTC intervals were used to estimate the corresponding steady-state spacing and to derive the gap parameters for IDM and CACC. The expected values for the parameters to be calibrated at each intersection are presented in

Table 9. Expectations of parameters that need to be calibrated.

Intersection	Acc (m/s2)	Dec (m/s2)	Spe (m/s)	Gap-IDM (m)	Gap-CACC (m)
2	4.83	4.83	16.03	5.62	5.63
3	4.83	4.83	17.01	5.29	4.29
4	4.83	4.83	17.02	7.08	5.17

.

Based on the actual operating conditions of vehicles in the study area, the car-following model parameters were calibrated as follows: acc and dec were set to 4.83 m/s², and spe was set to 16.69 m/s. Additionally, the gap was established at 6.0 m for IDM and 5.0 m for CACC. To account for the lateral maneuvers exhibited by both HDVs and CAVs during real-world operation, the default lane-changing model LC2013 implemented in SUMO is adopted [41]. The physical attributes and kinematic characteristics of each vehicle type are presented in

Table 10. Control models and key parameters for different type vehicles.

	Length (m)	Acc (m/s2)	Dec (m/s2)	Spe (m/s)	Gap (m)	Car-Following Model	Lane-Changing Model
HDV	5	4.83	4.83	16.69	6	IDM	LC2013
CAV-S1	5	4.83	4.83	16.69	5	CACC	LC2013
CAV-S2	5	4.83	4.83	16.69	5	CACC	LC2013
CAV-S3	5	4.83	4.83	16.69	5	CACC	LC2013

, which indicates that, apart from differences in control strategies and perception capabilities, no discrepancies exist in the inherent vehicle parameters across different vehicle types. Furthermore, all vehicles are modeled as gasoline-powered passenger cars compliant with Euro 4 emission standards, with fuel consumption derived from the emission factors provided by the handbook emission factors for road transport (HBEFA) version 3.1 [42].

2.2. Control Strategies for Intersections and Vehicles

2.2.1. Signal Timing for the Intersection

To achieve green wave coordinated control among intersections 2, 3, and 4, signal timing schemes were designed for each intersection based on the traffic flow direction, number of lanes, and lane functions at their respective approaches [43,44,45]. The resulting fixed signal timing schemes for each intersection are presented in

Table 11. Signal timing of the intersection.

Intersection	Phase 1	Phase 2	Phase 3	Phase 4
2	TR of NBA-SBA: 41g-3y-3r	TR of EBA-WBA: 21g-3y-3r	L of NBA-SBA: 43g-3y-3r	L of EBA-WBA: 21g-3y-3r
3	TLR of NBA-EBA: 42g-3y-3r	TLR of SBA-WBA: 23g-3y-3r	-	-
4	TLR of NBA-EBA: 27g-3y-3r	TLR of SBA-WBA: 16g-3y-3r	-	-

Note: L is the left-turn lane; TR denotes the shared through and right-turn lane; and TLR represents the shared through, left-turn, and right-turn lane.

.

From Table 3, Table 4 and Table 5, it could be observed that the NBAs of the intersections constitute the dominant inflow paths, with a substantial number of vehicles entering the study area from the NBA of intersection 4 and exiting mainly through the SBA of intersection 2. Given that this directional flow represents the primary movement within the network and contributes most significantly to overall traffic demand, the green-wave coordination is designed along the NBAs to improve progression efficiency for these major-stream vehicles. The phase splits at each intersection were first determined using the Webster signal timing method, in which the optimal cycle length and the green–yellow allocations for each phase were calculated based on the observed approach volumes and lane configurations derived from the NGSIM trajectory data. The average vehicle speed at the NBA of intersection 4 is 5.56 m/s, while that at the NBA of intersection 3 is 11.11 m/s. For intersection 2, the average vehicle speed at both the NBA and SBA is 8.33 m/s. Additionally, the recorded segment length of the NBA at intersection 4 is 100 m, the distance between the center points of intersection 4 and intersection 3 is 500 m, and the distance between the center points of intersection 3 and intersection 2 is 650 m. After the phase splits and cycle lengths were obtained through the Webster method, the offsets between consecutive intersections were then assigned according to these distances and the prevailing average speeds along the north–south direction. Under these physical road conditions, traffic demand characteristics, and prevailing speeds, the resulting signal timing configuration for green wave coordination targeting the north-to-south traffic flow is illustrated in Figure 2.

2.2.2. Evaluation of the Crash Risk for Vehicles

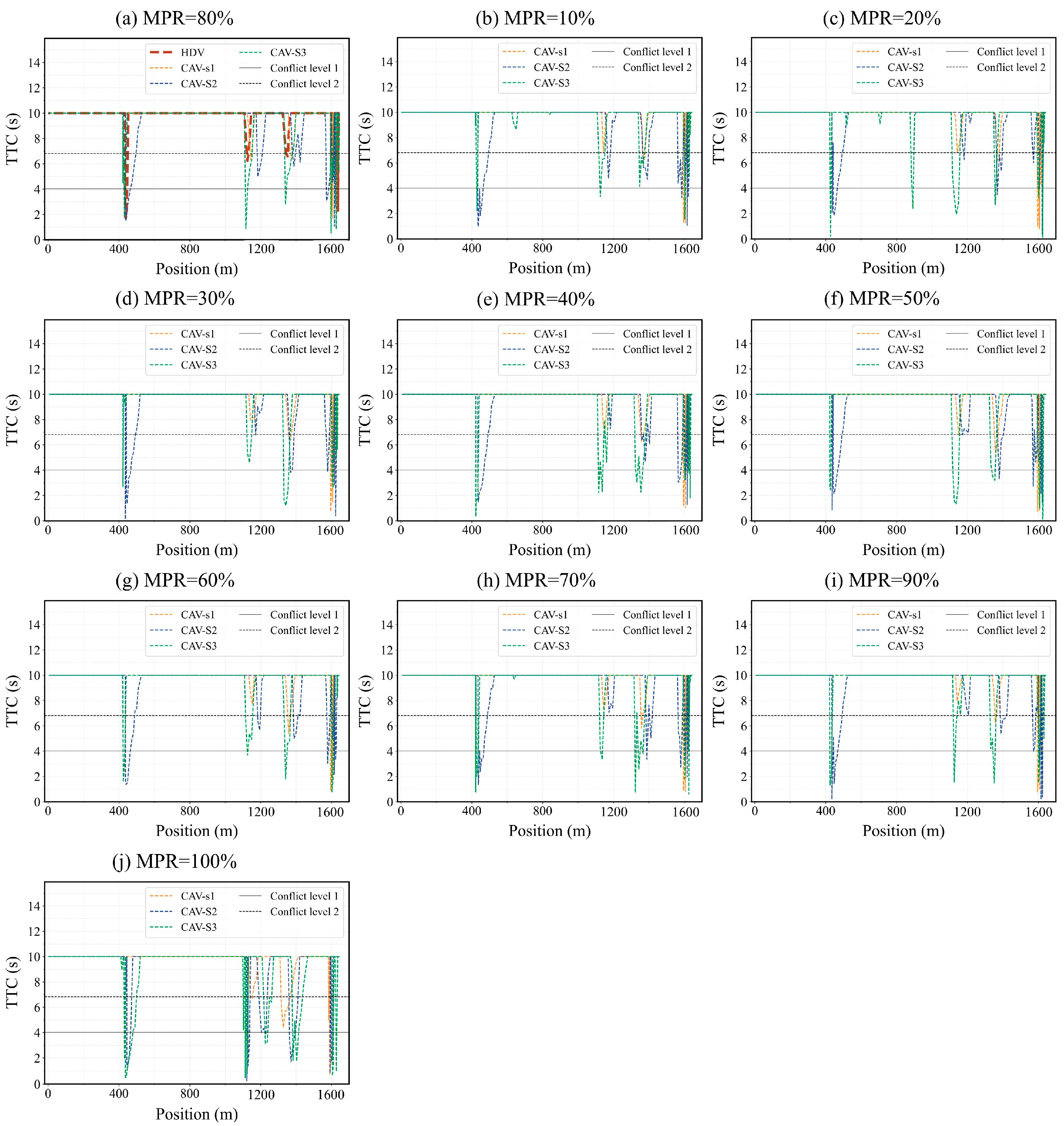
Prior to implementing control strategies for CAVs in emerging mixed traffic flows, it is essential to ascertain the current safety status of the target vehicle, determine the presence of potential conflicts, and evaluate the severity of crash risks to provide a foundation for vehicle control decisions. The application of the PnG to CAVs fundamentally involves controlling their longitudinal speed. For conflicts that may arise due to longitudinal speed variations, TTC is one of the most commonly used surrogate safety measures in such scenarios [46,47]. Furthermore, the calculation of TTC is straightforward, and the required parameters are relatively easy to obtain, making it well-suited for processing large-scale data or prolonged applications. Consequently, TTC was selected as the evaluation metric for the crash risk to characterize the safety status of vehicles within the study area, with its mathematical expression provided in Equation (2).

$$TT{C}_i\left(t\right)={\displaystyle \frac{\left(X_{i-1}\left(t\right)-X_t\left(t\right)\right)-l}{v_i\left(t\right)-v_{i-1}\left(t\right)}}$$

(2)

where $X_{i-1}$ is the position of the leading vehicle; $X_i$ denotes the position of the following vehicle; $v_{i-1}$ represents the velocity of the leading vehicle; $v_i$ signifies the velocity of the following vehicle; and $l$ is the length of the vehicle.

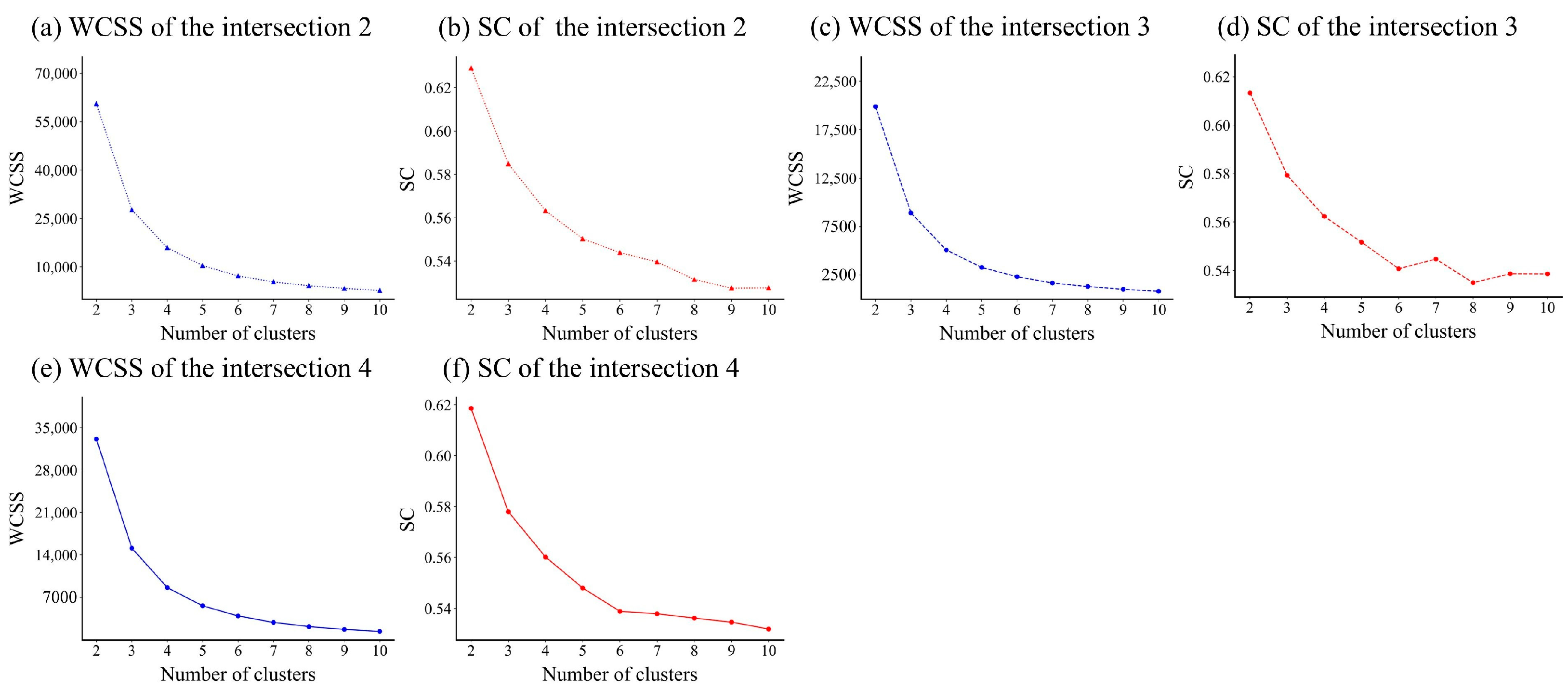
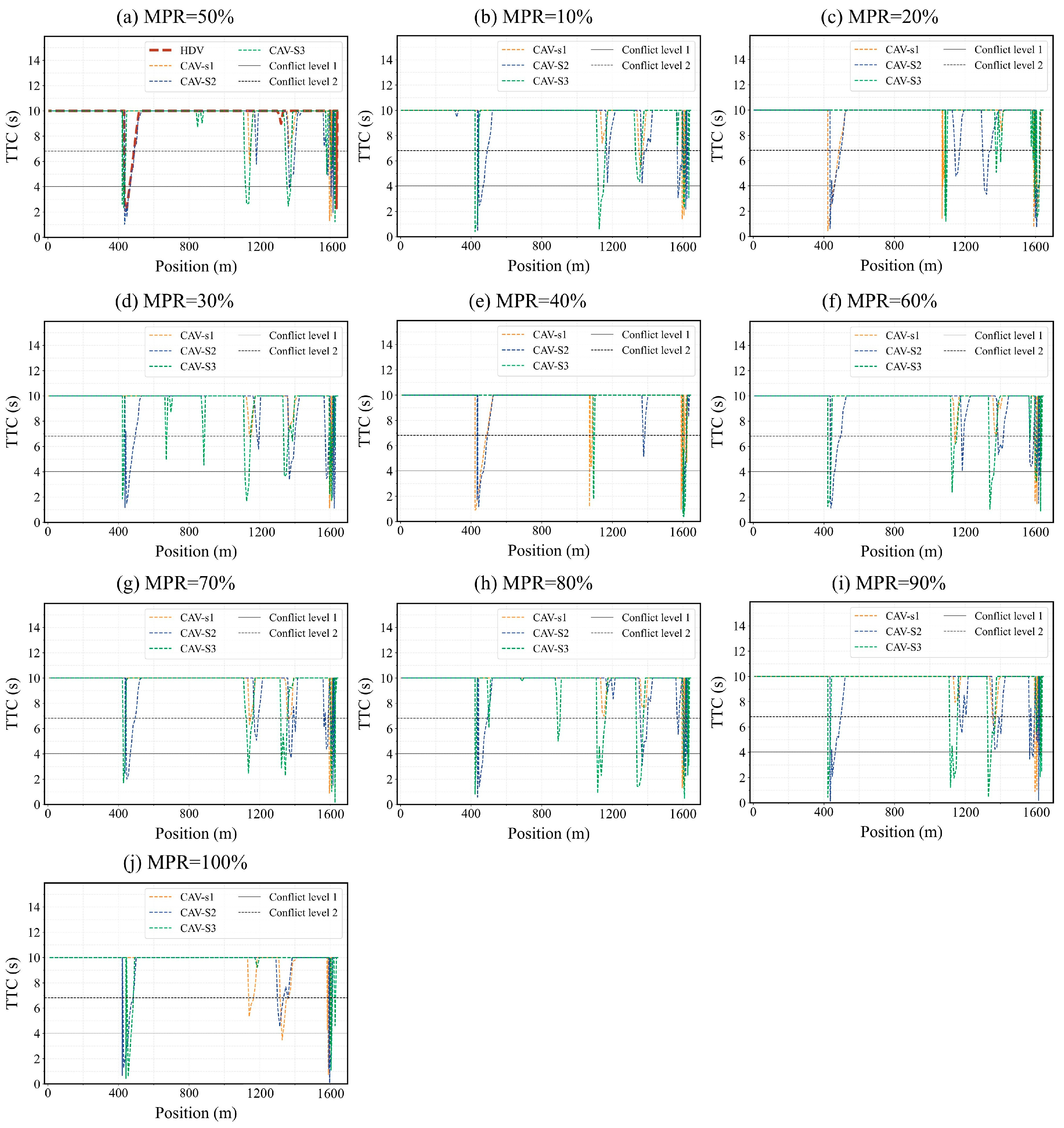
After calculating the TTC values within the regions of each intersection and filtering for data within the range of [1,10], the distribution characteristics of TTC at each intersection were analyzed using clustering methods. Specifically, the elbow method and silhouette coefficient (SC) were employed to determine the optimal number of clusters for intersections 2, 3, and 4. The elbow method identifies the optimal number of clusters by locating the inflection point (elbow) where the within-cluster sum of squares (WCSS) ceases to decrease substantially, whereas the silhouette coefficient (SC) method favors the cluster number that maximizes the average silhouette score. The search range for the number of clusters was set to [2,10].

For the TTC data collected at Intersection 2, a pronounced change in the rate of WCSS reduction was observed when the cluster number reached 3. Beyond this point, further increases in the number of clusters yielded progressively smaller reductions in WCSS, while the silhouette coefficient exhibited a consistent declining trend with increasing cluster numbers. Consequently, the optimal number of clusters for the TTC distribution at Intersection 2 was determined to be 3, as illustrated in Figure 3a,b. A similar analysis was performed for Intersection 3, with results shown in Figure 3c,d, again yielding an optimal cluster number of 3. The corresponding results for Intersection 4 are presented in Figure 3e,f, where the optimal number of clusters was likewise found to be 3.

Subsequently, a gaussian mixture model (GMM) was applied to cluster the TTC data for these intersections, with the resulting clustering outcomes presented in

Table 12. Clustering results for TTC of the intersection 2.

Cluster	Max (s)	Min (s)	Mean (s)	Weight	Standard Deviation (s)
1	3.95	1.01	2.72	0.42	0.71
2	6.69	3.96	5.19	0.34	0.78
3	9.99	6.70	8.20	0.24	0.95

,

Table 13. Clustering results of the intersection 3.

Cluster	Max (s)	Min (s)	Mean (s)	Weight	Standard Deviation (s)
1	3.98	1.01	2.62	0.37	0.83
2	6.93	3.99	5.37	0.36	0.85
3	9.99	6.94	8.40	0.27	0.87

and

Table 14. Clustering results of the intersection 4.

Cluster	Max (s)	Min (s)	Mean (s)	Weight	Standard Deviation (s)
1	4.13	1.01	2.77	0.40	0.83
2	7.00	4.14	5.48	0.35	0.83
3	9.99	7.01	8.44	0.25	0.85

.

When the TTC falls within cluster 1, it indicates a significant crash risk, designated as conflict level 1. At this level, vehicles should decelerate or, if necessary, change lanes to avoid rear-end crashes. Notably, the upper limit of conflict level 1 at intersection 2 is the lowest, at 3.95 s, primarily due to the high traffic volume, elevated traffic flow density, and reduced inter-vehicle spacing at this intersection. Cluster 2 signifies the presence of a conflict with a high likelihood of further escalation, denoted as conflict level 2, where acceleration maneuvers should be executed with caution to avoid excessive intensity. In contrast, cluster 3 corresponds to larger TTC values, indicating greater flexibility for speed adjustments, and is classified as conflict level 3. When TTC exceeds 10 s, a conflict with the leading vehicle persists, but the driver or control system has sufficient space to adjust the vehicle’s speed, allowing maintenance of the current speed or acceleration, thus designated as conflict level 4. It should be noted that TTC values exceeding 10 s are not interpreted as absolute safety; rather, they indicate that the vehicle has sufficient longitudinal spacing under normal conditions. When TTC decreases and the vehicle transitions into lower conflict levels, the corresponding control strategies are activated to ensure that safety is continuously maintained.

2.2.3. Speed Planning for Vehicles

(1)

PnG control under the green wave

For a CAV entering the study area from the NBA of intersection 4 and intending to exit via the SBA of intersection 2, when it first appears at the NBA of an intersection, assuming no leading vehicle in its lane, if it arrives at the stop line at the area’s average speed during the green indication of the corresponding signal phase, it is deemed likely to be within the green wave. Furthermore, if the vehicle is within the green wave and its initial appearance at the NBA coincides with the green indication, and there is either no leading vehicle, no conflict, or the TTC is at conflict level 2 or higher, the area’s average speed is adopted as the average speed for the vehicle’s PnG mode. The acceleration is set to the optimal value of 0.61 m/s² derived by Tian et al. [48], while the gliding deceleration is established at 0.16 m/s², thereby simulating the condition in which the engine is decoupled from the powertrain and the vehicle glides purely by inertia, achieving zero fuel consumption during this phase [17].

On the other hand, when a vehicle is within the green wave but initially appears at the NBA before the onset of the green indication, its average speed in the PnG mode should enable it to traverse the intersection within the first 30% of the green indication, provided there are no leading vehicles, no conflicts, or a conflict level of 4 [18]. The specific calculation method is presented in Equation (3).

$$V_m=\{\begin{array}{cc}{\displaystyle \frac{p_a-p_p}{t_{gs}+0.3\times l_g-t_a}}& t_a+{\displaystyle \frac{p_a-p_p}{v_d}}>t_{gs}+0.3\times l_g\\ v_d& t_a+{\displaystyle \frac{p_a-p_p}{v_d}}\le t_{gs}+0.3\times l_g\end{array}$$

(3)

where $V_m$ is the average speed of the PnG mode, m/s; $p_a$ denote the position where the vehicle first appeared at the NBA, m; $p_p$ represents the position of the stop line for the NBA, m; $t_a$ signifies the time where the vehicle first appeared at the NBA; $t_{\mathit{gs}}$ is the start time of the green light; $l_g$ denotes the length of the green light, s; and $v_d$ represents the average speed of the area where the vehicle is located, m/s.

Conversely, when a conflict exists and the conflict level exceeds 1, the vehicle could determine the average speed for the PnG mode based on its current conflict level. In contrast, if the vehicle is in conflict level 1, it should fully adhere to the control of CACC, maintaining sufficient spacing from the leading vehicle to increase the TTC and thereby improve the vehicle’s safety state. Specifically, if the vehicle is in conflict level 2, it is required to pass through the intersection within the first 90% of the green indication, with the calculation process for the average speed of its PnG mode outlined as follows:

$$V_m=\{\begin{array}{cc}{\displaystyle \frac{p_a-p_p}{t_{gs}+0.9\times l_g-t_a}}& t_a+{\displaystyle \frac{p_a-p_p}{v_d}}>t_{gs}+0.9\times l_g\\ v_d& t_a+{\displaystyle \frac{p_a-p_p}{v_d}}\le t_{gs}+0.9\times l_g\end{array}$$

(4)

For CAVs in conflict level 3, the vehicle is scheduled to traverse the intersection within the first 60% of the green indication, with the computation of its PnG mode average speed detailed in Equation (5).

$$V_m=\{\begin{array}{cc}{\displaystyle \frac{p_a-p_p}{t_{gs}+0.6\times l_g-t_a}}& t_a+{\displaystyle \frac{p_a-p_p}{v_d}}>t_{gs}+0.6\times l_g\\ v_d& t_a+{\displaystyle \frac{p_a-p_p}{v_d}}\le t_{gs}+0.6\times l_g\end{array}$$

(5)

It should be noted that the thresholds of 30%, 60%, and 90% of the green phase are not derived from existing PnG or signal-coordination literature. Instead, these values are purposely designed within the proposed control framework to reflect the perception asymmetry among different CAV types. CAVs equipped with larger detection ranges could assess traffic conditions and the leading vehicle earlier, allowing them to safely activate the PnG mode sooner. Assigning smaller green-window requirements (e.g., 30%) enables these CAVs to make fuller use of the green-wave progression and pass the intersection efficiently. In contrast, CAVs with shorter detection ranges require more time to verify safety conditions before accelerating, and thus larger thresholds (60% or 90%) ensure that the planned traversal remains feasible and safe. Therefore, the progressive thresholds serve as a graded control mechanism aligned with the sensing capabilities of each CAV type.

(2)

PnG control outside the green wave

When CAVs are not within the green wave, the activation of the PnG mode should still adhere to safety constraints. In scenarios where there is no leading vehicle, no conflict exists, or the conflict level is 2 or higher, the vehicle may adopt the average speed of the current area as the PnG mode’s average speed to perform acceleration and deceleration maneuvers. Conversely, for CAVs where the TTC does not meet safety constraints, the vehicle should operate under CACC to maintain a safe distance from the leading vehicle, prohibiting the activation of the PnG mode to avoid crashes due to acceleration.

On the other hand, for HDVs operating under the IDM, only the desired speed is specified without additional control measures. Specifically, when an HDV is traveling at the NBA of intersection 4, its desired speed is set to 5.56 m/s. When the HDV navigates the road segment between intersection 4 and intersection 3 in the southbound direction, its desired speed is set to 11.11 m/s. For all other road segments, the desired speed is uniformly set to 8.83 m/s. The desired speeds of HDVs on each segment were obtained from the empirical trajectory dataset used to construct the network. Specifically, the average observed speed of HDVs on each segment was calculated and adopted as the desired speed, allowing the simulated HDVs to more closely reflect the driving behavior patterns and traffic operation characteristics observed in the real-world data.

3. Results and Discussion

The simulated traffic volume was adjusted to 40% and 60% of the PHV, which are designated as scenario 1 and scenario 2, respectively, to model the operation of the study area during off-peak periods. The simulation duration was set to 3602 s, with the initial 2 s designated as a warm-up phase, during which no vehicle control or data collection was performed to prevent the inclusion of anomalous data. It is noteworthy that, although the perception errors of different CAVs are random within a specified error bound, SUMO produces deterministic outputs when all input parameters and computational environment remain unchanged. Consequently, repeated simulations under identical configurations yield identical fuel consumption results.

The regional fuel consumption results are presented in

Table 15. Results of fuel consumption without idle.

MPR (%)	FC (L/100 km)
	0	10	20	30	40	50	60	70	80	90	100
Scenario 1	11.57	12.17	12.46	12.53	12.41	12.04	11.85	11.67	11.46	10.83	10.69
Scenario 2	12.55	13.51	14.72	14.62	15.05	15.01	14.46	14.14	14.33	13.34	11.44

and

Table 16. Results of fuel consumption with idle.

MPR (%)	FCI (L/100 km)
	0	10	20	30	40	50	60	70	80	90	100
Scenario 1	13.69	14.84	15.55	15.56	15.52	15.57	14.68	15.18	15.45	14.39	15.21
Scenario 2	15.12	16.59	19.15	18.90	19.89	20.86	20.36	20.27	22.36	20.84	19.18

. Table 15 displays the average fuel consumption per 100 km excluding idling fuel consumption (FC), while Table 16 shows the average fuel consumption per 100 km including idling fuel consumption (FCI). The calculation processes for FC and FCI are detailed in Equations (6) and (7), respectively. For FCI, a general increase is observed across the region as the proportion of HDVs decreases. However, with an increasing MPR of CAVs, the FC in both scenario 1 and scenario 2 initially rises, then decreases, ultimately achieving a lower value than that observed at an MPR of 0%.

$$FC={\displaystyle \frac{f_t\times {10}^5}{72\times {10}^4\times d_t}}$$

(6)

$$FCI={\displaystyle \frac{\left(f_t-f_w\right)\times {10}^5}{72\times {10}^4\times d_t}}$$

(7)

where $f_t$ is total fuel consumption, mg, its density is 0.72 g/cm³; $f_w$ represents the idling fuel consumption generated when the vehicle is zero, mg; and $d_t$ denotes the total travel distance produced by all vehicles, m.

Furthermore, Figure 4 illustrates the fuel saving rate (FSR) achieved for both FC and FCI in the study area as the MPR of CAVs increases from 10% to 100%, relative to a homogeneous traffic flow composed solely of HDVs. The mathematical expression for FSR is provided in Equation (8). For FC, the maximum FSR reaches 7.61% in scenario 1 and 8.84% in scenario 2, demonstrating that the implementation of the PnG mode by CAVs under green wave coordinated control could yield significant fuel saving benefits for the region. Conversely, when accounting for idling fuel consumption, the maximum FSR values for scenario 1 and scenario 2 are −5.11% and −9.72%, respectively.

$$FSR={\displaystyle \frac{f_p-f_m}{f_p}}\times 100\%$$

(8)

where $f_p$ is the fuel consumption of the single traffic flow; and $f_m$ denotes the fuel consumption of the emerging mixed traffic flow.

The initial increase in FC at low MPRs occurs because the intermittent PnG activation of a small number of CAVs introduces speed fluctuations that HDVs respond to conservatively, thereby increasing their instantaneous fuel consumption; as the MPR becomes higher, CAVs dominate the traffic stream and the coordinated PnG operation smooths vehicle trajectories, leading to a subsequent decrease in FC.

3.1. Fuel Consumption Under Different Emerging Mixed Traffic Flows

In scenario 1, when the MPR of CAVs reaches 30%, the FC exhibits its lowest value. The per-unit-distance fuel consumption for different vehicle types, excluding idling fuel consumption, is illustrated in Figure 5a. At this point, the fuel consumption of HDVs is generally higher than that of the average per-unit-distance fuel consumption (90.65 mg/m) observed at an MPR of 0%. In contrast, the fuel consumption of different CAV types is typically concentrated around 50 mg/m, indicating that the lower FSR is primarily driven by the increased fuel consumption of HDVs. Similarly, in scenario 2, when the MPR is 40%, the fuel consumption of most HDVs exceeds the average per-unit-distance fuel consumption of 97.96 mg/m recorded at an MPR of 0%. Furthermore, the median fuel consumption values for CAV-S1, CAV-S2, and CAV-S3 are close to 97.96 mg/m, demonstrating no substantial fuel saving benefits overall, thus failing to effectively offset the increased fuel consumption of HDVs, as shown in Figure 5b.

Based on this, regarding fuel consumption during vehicle operation, compared to HDVs, CAVs could activate the PnG mode to conserve fuel while adhering to safety constraints. The FSR achieved in scenario 1 is depicted in Figure 6a. Specifically, at MPRs of 0% and 100%, the FSRs for CAV-S1, CAV-S2, and CAV-S3, relative to HDVs, are 7.1%, 7.1%, and 14.3%, respectively. The FSRs of CAV-S1 and CAV-S2 (7.1%) exceed the upper threshold of 5% reported by Xue et al. [49] and surpass the lower bound of 5% established by Natarajan et al. [13]. Both referenced studies investigate the fuel saving potential of PnG modes in passenger vehicles, which is consistent with the vehicle type and control logic examined in the present work, thereby ensuring result comparability. Additionally, Cao et al. [50] reported a maximum FSR of 9% for PnG operation relative to CS cruising under steady-state conditions. The FSRs of CAV-S1 and CAV-S2 lie within this range, as the present study adopts the same comparative baseline (PnG versus CS mode) as Cao et al. [50]. The FSR of CAV-S3 (14.3%) exceeds the maximum value reported by Cao et al. [50] but remains below the peak FSR of 22% documented by Natarajan et al. [13], and is comparable to the maximum FSR of 17% achieved by Korta et al. [51]. These variations primarily arise from differences in driving environment: Natarajan et al. [13] and Korta et al. [51] evaluated unconstrained freeway scenarios, whereas this study focuses on urban arterials with traffic signal constraints. In emerging mixed traffic flows, the FSR for CAV-S3 ranges from 25% to 50%, with the minimum value approaching the 24% reported by Li et al. [25] (for mixed CAV-HDV platoons) and the maximum value being comparable to the 45% maximum FSR reported by Xu et al. [52] (for PnG in step-gear transmission vehicles). All these studies confirm that PnG’s fuel saving potential is closely related to traffic and road conditions, and results of this study are consistent with this overall trend. Regarding the maximum FSR, CAV-S1, CAV-S2, and CAV-S3 exhibit consistency. However, the minimum FSR for CAV-S1 is 18.8%, and for CAV-S2, it is 23.5%, both of which fall within the range covered by Sohn et al. [14] (30%) and Kim et al. [17] (33%). All these works validate that PnG could avoid low-efficiency steady-speed operation, and results of this study further confirm this mechanism in urban mixed traffic with signals.

As traffic volume increases, compared to HDVs at a MPR of 0%, the FSR achieved by CAV-S1, CAV-S2, and CAV-S3 in a traffic flow composed entirely of CAVs at an MPR of 100% becomes less pronounced, with all three achieving an FSR of 13.3%. This value closely aligns with the 17% reported by Korta et al. [51], primarily due to the reduced average inter-vehicle spacing on the road. Both studies indicate that higher traffic density narrows the space available for PnG glide phases, leading to slightly lower FSR. The FSRs achieved by CAVs compared to HDVs in scenario 2 are illustrated in Figure 6b. When the MPR is neither 0% nor 100%, the maximum FSR reaches only 37.5%, with a minimum of 25%, which is consistent with the findings of Li et al. [25] (24% FSR in mixed platoons) and Sohn et al. [14] (30% FSR in PnG application). This phenomenon is largely attributed to the general increase in vehicle fuel consumption under high traffic volume, particularly for HDVs, which lack perception capabilities and are more susceptible to speed fluctuations. Notably, in scenario 2, CAV-S1 consistently exhibits a leading FSR, indicating that in challenging traffic conditions, high sensor precision enables CAVs to better grasp PnG timing and avoid unnecessary adjustments. This observation is in line with Korta et al.’s [51] conclusion that perception accuracy contributes to PnG’s fuel saving effect.

On the other hand, from the perspective of vehicles’ overall travel within the region, in scenario 1, when the MPR is 50%, the FCI achieves its lowest FSR, with the median fuel consumption of HDVs exceeding the average per-unit-distance fuel consumption of 112.15 mg/m observed at an MPR of 0%. This indicates that over 50% of HDVs experience an increase in fuel consumption. In contrast, the median fuel consumption of CAV-S1, CAV-S2, and CAV-S3 remains below 112.15 mg/m, though the difference between them is minimal, as shown in Figure 7a. As traffic volume increases in scenario 2, the FSR reaches its minimum at an MPR of 80%, where the median fuel consumption of all vehicle types surpasses the 121.83 mg/m recorded at an MPR of 0%, resulting in a significant increase in the region’s FCI, as depicted in Figure 7b.

It is worth noting that when idling fuel consumption is included, the regional FCI increases mainly due to the behavior of HDVs rather than the PnG mode itself. Although PnG reduces fuel consumption for CAVs during motion, its acceleration-deceleration pattern introduces additional speed fluctuations into the traffic stream. HDVs, lacking perception capabilities, maintain a conservative following distance to CAVs operating under PnG, which leads to longer deceleration periods and occasional stops near intersections. These behaviors increase idling duration and consequently raise the overall FCI of the region.

3.2. Operation of HDVs and CAVs with Different Perception Capabilities

At the vehicle motion level, whether in homogeneous or emerging mixed traffic flows, HDVs strive to maintain a CS in accordance with the set velocity while adhering to the safety constraints of the car-following model. At a MPR of 50%, CAVs on the road attempt to traverse the target intersection during the green indication through corresponding speed planning, avoiding stops at the approach. This indirectly facilitates the swift passage of HDVs, enabling them to potentially pass through the intersection without stopping. To some extent, this reduces the occurrence of emergency braking and idling for HDVs, thereby shortening travel time and mitigating instantaneous spikes in fuel consumption, ultimately reducing the overall fuel consumption of HDVs throughout their journey, as illustrated in Figure 8. To pass through the intersection during the green indication, CAVs should perform speed planning while ensuring safety, particularly in the presence of a leading vehicle. CAV-S3, with its longest detection range, could identify a leading vehicle at a greater distance earlier, allowing for a more timely assessment of the current safety conditions and enabling the rapid activation of the PnG mode while maintaining safety. The detection range of CAV-S1 is shorter than that of CAV-S2, though the difference is minimal, resulting in similar timing for initiating the PnG mode for these two CAV types. However, CAV-S1’s superior precision enables it to execute the planned speed with greater accuracy, minimizing deviations from the target speed. Nevertheless, under deteriorating traffic conditions ahead, a shorter detection range may lead to delayed reaction times. On the other hand, the perception capabilities of CAVs allow them to activate the PnG mode while adhering to safety constraints, where the presence of the G-phase effectively reduces fuel consumption. The alternation between acceleration and deceleration creates a speed variation range for CAVs, enhancing their adaptability to some extent and preventing abrupt speed changes. This, in turn, exerts a suppressive effect on the peak instantaneous fuel consumption during vehicle acceleration.

In scenario 2, as traffic volume increases, CAVs continue to facilitate the passage of HDVs by traversing intersections during the green indication, thereby reducing HDV travel time and fuel consumption, as depicted in Figure 9b,c. Concurrently, as the MPR rises to 80%, the majority of vehicles surrounding HDVs are CAVs. During startup acceleration, CAVs should accelerate continuously to the upper limit of the target speed before decelerating, which expedites the dispersion of traffic flow around HDVs. This enables HDVs to start more smoothly, and even when deceleration is required to ensure safety, HDVs could adopt a relatively gradual deceleration rate at sufficient spacing, thereby avoiding significant spikes in instantaneous fuel consumption, as shown in Figure 9d. On the other hand, increased traffic volume leads to higher traffic density at the intersection approach, reducing inter-vehicle spacing. Consequently, CAV-S2 and CAV-S3 exhibit minimal differences from CAV-S1 in leading vehicle detection, resulting in a high degree of overlap in the operational periods of their PnG modes. However, during vehicle startup, the high-precision advantage of CAV-S1 continues to enable effective and rapid activation of the PnG mode, facilitating corresponding acceleration and deceleration maneuvers.

For completeness, the operation of vehicles under low MPR conditions was also examined. When the MPR is 10%, the traffic flow remains predominantly HDV-driven, and the influence of CAVs on regional dynamics is limited. Although individual CAVs are still able to activate the PnG mode, their capacity to smooth traffic flow or reduce stop-go behavior for surrounding HDVs is minimal due to the sparse distribution of CAVs. HDVs largely maintain driving patterns similar to those in the homogeneous-HDV baseline, including conservative car-following, larger gaps, and occasional stops near intersections. Consequently, the benefits of PnG at low MPRs are confined to individual CAVs and do not propagate through the traffic stream, resulting in limited improvements in delay or fuel consumption at the network level.

3.3. Safety of Different Vehicles Under Emerging Mixed Traffic Flows

In scenario 1, at a MPR of 50%, the fuel consumption performance in the region is relatively suboptimal. However, in such an environment, the safety of all vehicle types is adequately ensured. The safety disturbances caused by CAV-S1, CAV-S2, and CAV-S3 to HDVs are minimal, with TTC values predominantly exceeding 10 s during conflicts, corresponding to conflict level 4. When fluctuations occur in the speed of the leading vehicle, HDVs have sufficient time and space for drivers to make appropriate maneuvering decisions, as shown in Figure 10a. Notably, in Figure 10, TTC values exceeding 10 s are recorded as 10 s. Thus, the actual TTC may be significantly greater, indicating an even safer vehicle. Conversely, Figure 9 reveals that TTC values at the NBA of intersection 4 are relatively smaller, primarily due to the limited road range considered during data collection. In the simulation, road modeling is based on the initial position of vehicles, but in reality, vehicles may decelerate before entering the data collection area to avoid severe conflicts with the leading vehicle. Overall, compared to the detection range of sensors, their precision is more critical for controlling vehicle safety states. CAV-S1, with its superior precision, rarely enters conflict levels 1 or 2 when not in conflict level 4, effectively mitigating conflict escalation. In contrast, CAV-S3, despite having the longest detection range, has relatively lower precision, which could lead to distance estimation errors. This may cause vehicles to underestimate the severity of current conflicts, resulting in continuous TTC reduction, particularly at intersections with multiple signal phases and complex right-of-way dynamics, such as intersection 2.

As traffic volume increases, vehicle safety states become more prone to fluctuations, with a higher frequency of inter-vehicle conflicts and a tendency for conflicts to escalate in severity, as illustrated in Figure 11. Based on prior fuel consumption results, at a MPR of 80% in scenario 2, the region’s fuel consumption performance is relatively poor. Nevertheless, the safety of both HDVs and CAVs remains assured. Excluding the situation at the NBA of intersection 4, when an HDV experiences a conflict with the leading vehicle, its TTC consistently exceeds 1.5 s, with only brief periods in conflict level 1 and the vast majority of time spent in conflict levels 3 and 4. For CAVs, compared to scenario 1, CAV-S2 exhibits increased TTC fluctuations, with its conflict levels aligning more closely with those of CAV-S3, while CAV-S1 continues to perform stably, maintaining conflict level 3 or higher at all times. Additionally, increased traffic volume leads to reduced average inter-vehicle spacing on the road, thereby diminishing the perceptual differences between CAV-S3 and CAV-S2 arising from their differing detection ranges.

4. Conclusions

This study aims to evaluate the fuel saving potential and safety of the pulse and glide (PnG) mode under green wave coordination control within emerging mixed traffic flows characterized by perception asymmetry. Considering the traffic characteristics during peak periods, green wave coordination control was implemented for the signal timing of three consecutive intersections. Using time to collision (TTC) as the evaluation metric, the conflict levels at each intersection were classified to establish vehicle safety constraints, thereby enabling connected and automated vehicles (CAVs) with varying perception capabilities to determine whether to activate the PnG mode and the corresponding average speed. A model of the target road network was developed, and parameters of the car-following model were calibrated based on real-world vehicle trajectory data. Through simulations, the traffic flow in the region was adjusted, and the fuel consumption and safety of human-driven vehicles (HDV) and CAVs during off-peak periods were assessed under varying market penetration rates (MPRs) of CAVs.

Simulation results suggest that, when idling fuel consumption is excluded, introducing CAVs at certain MPRs (above 50–90% depending on traffic volume) could improve regional fuel efficiency under the studied conditions. Specifically, in scenarios with lower traffic volumes, an MPR exceeding 50% (i.e., scenario 1) is required, while in the higher-traffic-volume scenario, an MPR above 90% appears necessary in simulations for PnG to yield net regional fuel savings (excluding idling). However, when idling fuel consumption is accounted for, the activation of the PnG mode may, to some extent, increase the region’s average fuel consumption, though this effect is relatively minor in scenario 1. This increase primarily contributes to elevated fuel consumption for HDVs, as CAVs exhibit noticeable speed fluctuations when operating in PnG mode. HDVs, lacking perception capabilities, should consistently maintain a larger safety distance from potential leading CAVs, resulting in strictly constrained speed variations, an effect that is particularly pronounced in scenario 1. At the vehicle motion level, the PnG mode enables CAVs to achieve significantly lower fuel consumption compared to HDVs, with a fuel saving rate (FSR) ranging from a maximum of 50% to a minimum of 7.1%. This fuel saving advantage is most evident in low-traffic conditions. Specifically, in low-traffic scenarios with larger inter-vehicle spacing, CAV-S3, with its greater detection range, could activate the PnG mode earlier. In contrast, under high-traffic conditions, CAV-S1 demonstrates superior fuel saving performance due to its high-precision sensors, which enable the accurate and rapid activation of the PnG mode within limited spacing. The proposed PnG mode, combined with TTC-based safety constraints, maintained safety (TTC generally > 1.5 s) for both CAVs and HDVs throughout all simulated scenarios. The higher sensor precision of CAV-S1 appeared to contribute to more stable conflict management compared to CAV-S2 and CAV-S3.

5. Limitations and Future Work

Several limitations should be considered when interpreting the findings of this study. Although vehicles were allowed to change lanes using the default SUMO lane-changing algorithm, lane-changing behavior was not explicitly modeled or analyzed, and the analysis focused primarily on longitudinal dynamics. Consequently, the potential influence of detailed lateral maneuvers on PnG activation, safety assessment, and fuel consumption remains unexamined. In addition, the results are derived from the specific modeling framework adopted in this work, including the PnG control logic, perception accuracy settings, and signal coordination scheme. Mitigating the adverse impacts on HDVs and increasing the upper limit of traffic flow for effective PnG implementation remain challenges that require further study. Future research may incorporate more detailed lane-changing models, explore coordinated PnG modes among CAVs, and consider uncertainties in sensing and communication to enhance the realism and generalizability of the analysis, as well as integrating additional surrogate safety indicators to provide a more comprehensive assessment of vehicle safety states beyond TTC.