Numerical Study of Symmetry in Tunneling-Induced Soil Arch

Abstract

This paper addresses the issue of stress redistribution in surrounding soil during the construction of shallow-buried, large-section loess tunnels. Using the Luochuan Tunnel as a case study, we employ the FLAC 3D numerical simulation method to investigate the effects of advanced pipe roof support on the stability of the surrounding soil. The results demonstrate that advanced pipe umbrella reduces the stress release amplitude at the vault by 50% compared to the unsupported condition, due to a “pre-support-load bearing mechanism”, while promoting orderly stress recovery. The “longitudinal beam effect” and “transverse arch effect” of soils effectively suppress the plastic zone area of the surrounding soil from 413.3 m² (unsupported) to 95.0 m², achieving a reduction exceeding 77%. Furthermore, the pipe umbrella support facilitates the formation of a more efficient “active soil arch”, which exhibits distinct symmetrical characteristics. The arch’s stress distribution and spatial structure both follow symmetrical patterns, significantly enhancing the self-stabilizing capacity of the surrounding soil. As a result, the height of the stress release zone at the tunnel excavation face and the surrounding soil stability areas is reduced by 45.9% and 63.3%, respectively, compared to the unsupported condition. This study also establishes a Pasternak elastic foundation beam model that accounts for the spatiotemporal effects of support, elucidating the mechanism of pipe umbrella support and providing a theoretical foundation for the design and construction risk control of shallow large-section loess tunnels.

1. Introduction

Tunnel engineering, as critical structures for overcoming complex terrain obstacles, are witnessing increasingly larger scales and higher construction difficulties. This trend has led to the emergence of numerous shallow, large-cross-section loess tunnels [1,2,3,4,5]. Under such geological conditions, the construction of large-cross-section tunnels can easily trigger engineering hazards, including abrupt stress release in surrounding soil, excessive surface settlement, or even collapse [6,7]. These hazards pose severe threats to construction safety and the stability of adjacent buildings. Consequently, effectively controlling surrounding soil deformation and stress redistribution during the excavation of shallow loess tunnels has become a key issue that constrains project implementation.

To address this challenge, advanced support systems, particularly pipe umbrella support, have been widely adopted in high-risk tunnel engineering practices [8,9,10,11,12]. Currently, scholars have conducted research on the effectiveness of pipe umbrella support. Extensive field observations and model tests reveal that shallow loess tunnels exhibit distinct failure characteristics: a loosening pressure zone readily forms above the vault, with its extent demonstrating deterministic relationships with burial depth, cross-sectional dimensions, and loess cohesion [13,14,15]. As a key measure for controlling stress redistribution in the surrounding soil of tunnels, advanced support techniques enhance the self-bearing capacity of the rock mass. Among these techniques, pipe umbrella support significantly optimize stress transfer paths by simultaneously achieving “longitudinal beam effect” and “transverse arch effect” [16,17]. In recent years, numerical simulation technology has emerged as an important method for studying this issue. Many researchers have employed the finite element method or finite difference method to elucidate the general principles of pipe umbrella support [18,19]. It primarily regulates the stress redistribution of the surrounding soil through the dual-path mechanism of “stress transfer + stiffness enhancement,” with its effectiveness influenced by parameters such as pipe diameter, installation density, and advance length. However, existing numerical studies still lack refined and quantitative analyses of the evolution of internal stress paths and the development patterns of plastic zones in the surrounding soil under the influence of pipe umbrella. Additionally, regarding the three-dimensional effects of large-section tunnel excavation and the “spatial effect” exerted by pipe umbrella, related simulation studies require further exploration.

This study employs numerical simulation to establish a numerical model for tunnel excavation process using FLAC3D 6.0 [20]. It compares and analyzes stress variations under two working conditions: unsupported excavation and excavation with advanced pipe umbrella support. The study reveals the influence of advanced pipe umbrella support on the stress redistribution process, the development range of the plastic zone, and the overall stability of surrounding soil in shallow large-section loess tunnels. The research aims to provide a theoretical basis and quantitative references for the optimization of design and risk control of advanced support in shallow loess tunnels. Additionally, this study investigates the symmetry inherent in the stress field, plastic zone, and soil arch structure around the tunnel. In shallow-buried, large-section loess tunnels, the symmetry of both the tunnel geometry and the load distribution typically leads to a stress redistribution that assumes distinct spatial symmetry patterns. This is evidenced not only by the symmetrical propagation of stress paths but also by the symmetric expansion of plastic zones and the symmetric morphology of the soil arch. Understanding this symmetrical behavior is crucial for predicting tunnel stability and optimizing support design.

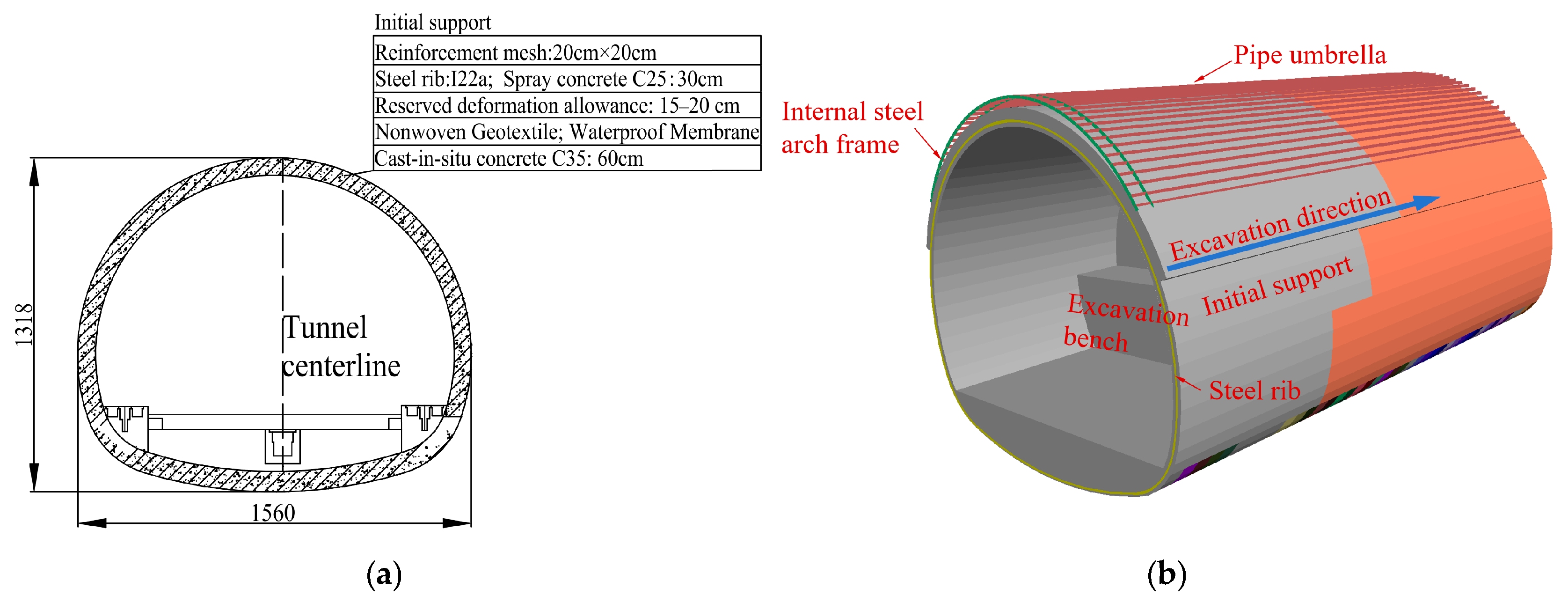
2. Engineering Background

The Luochuan Tunnel is a single-tube double-track tunnel on the newly constructed Xi’an-Yan’an High-Speed Railway, with a total length of 4140.43 m. It features an excavation span of 15.60 m, a height of 13.18 m, a cross-sectional area of 167.3 m², and a maximum burial depth of 64 m, classifying it as a large-section loess tunnel. The tunnel primarily traverses wind-deposited clayey loess from the Upper and Middle Pleistocene epochs of the Quaternary system, with the surrounding soil predominantly classified as Grade V, exhibiting poor self-stabilization capacity. The construction employs the three-bench temporary invert method, combined with systematic advanced support and a composite lining structure. The support system includes Φ108 pipe umbrella, each 30 m long with a wall thickness of 6 mm, arranged within a 140° range at the arch section, with a circumferential spacing of 40 cm. The shotcrete is 30 cm thick C25 concrete, reinforced with φ8 mm steel mesh laid in double layers at 20 × 20 cm grid spacing, and I22a steel ribs installed at 0.6m longitudinal intervals. A deformation allowance of 15–20 cm is reserved during support installation. The secondary lining consists of 60 cm thick cast-in-place C35 concrete, with a complete waterproofing system formed by non-woven fabric and waterproof board between the initial support and secondary lining. For detailed lining structure, refer to Figure 1.

3. Three-Dimensional Numerical Model

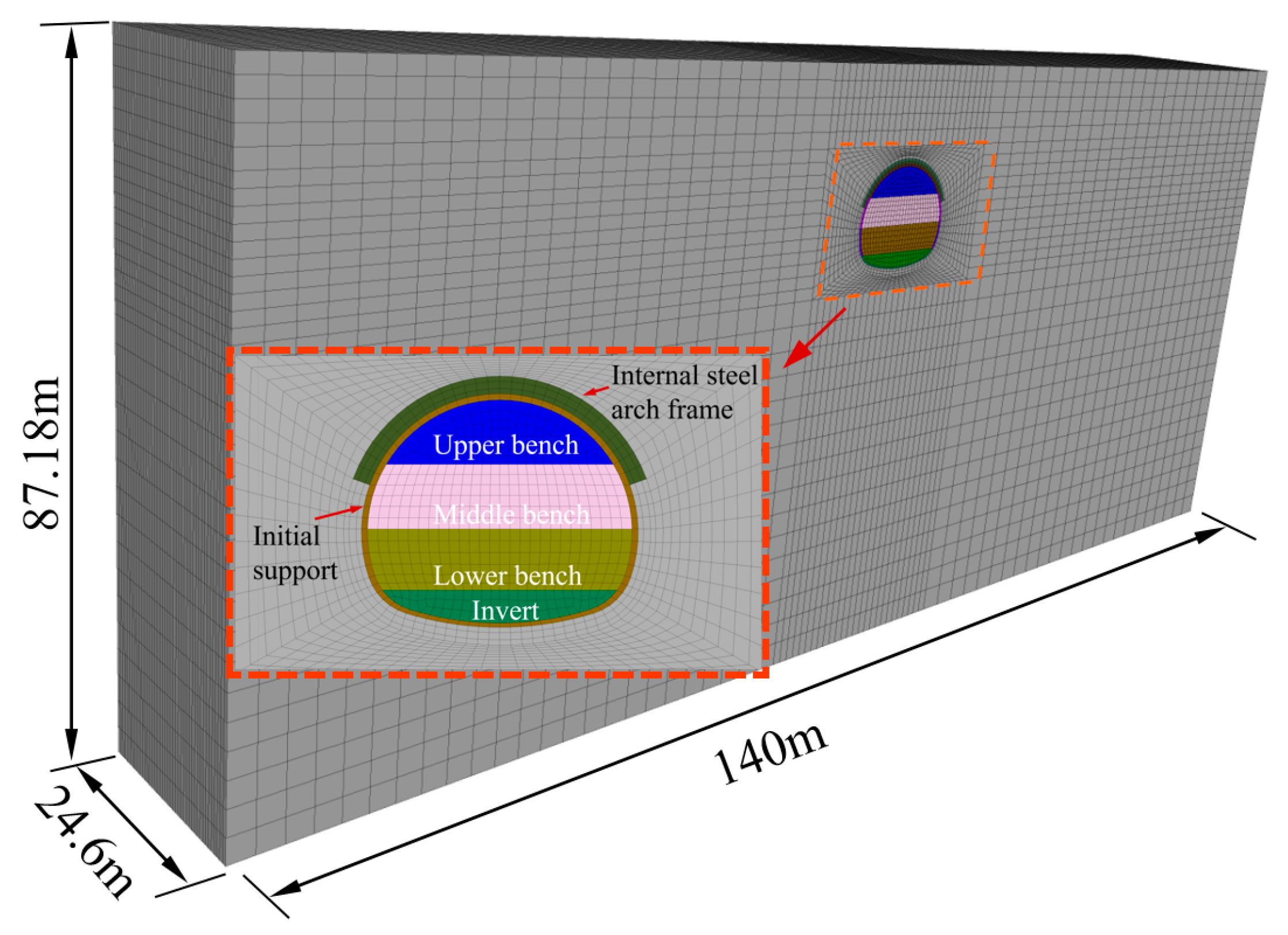
3.1. Model Establishment

This study establishes a three-dimensional numerical model based on the Luochuan Tunnel as the engineering background. The tunnel cross-section features a three-centered arch with an inverted arch, geometrically adhering strictly to a symmetrical layout, an excavation height of 13.18 m, a width of 15.6 m, and a burial depth of 24 m. The overall model dimensions are 140 m (length) × 24.6 m (width) × 87.18 m (height). To minimize boundary effects, the left and right boundaries are positioned 70 m from the tunnel center, and the bottom boundary is set at 56 m from the center, both being 3–5 times the tunnel diameter [21,22,23], thus meeting theoretical requirements. The surrounding soil is simulated using hexahedral solid elements, with refined meshing around the tunnel periphery and excavation zones, while gradually increasing the mesh size in distant areas, effectively improving computational efficiency while ensuring calculation accuracy. To ensure the reliability of numerical simulation results, mesh size must be determined with reference to both theoretical guidelines and case studies. For static analysis in stress-concentration zones, a mesh density of at least four elements per square meter is recommended [24]; this has been validated by yielding stability coefficients comparable to those from limit equilibrium methods. For dynamic analysis, a separate criterion requires the element size to be smaller than one-tenth of the wavelength corresponding to the highest significant frequency of the input motion [25]. In the present tunnel model, the mesh in critical surrounding areas was refined to satisfy both of these requirements. The boundary conditions are established as follows: normal displacement constraints are applied to the four lateral sides of the model, the upper surface is treated as a free boundary, and the lower surface is subjected to a fixed constraint. The pipe umbrella is modeled using beam elements, primarily based on its structural form and mechanical properties: as a slender structure, it primarily experiences bending and shear forces, and beam elements effectively represent its “longitudinal beam” and “lateral arch” effects. Compared to solid and shell elements, beam elements offer higher computational efficiency while maintaining accuracy. They also facilitate connection to adjacent support components via nodes, making them suitable for integrated model analysis. They are connected to the steel ribs through structural nodes. The tunnel soil is divided into four parts according to the three-bench method: upper bench, middle bench, lower bench, and invert. The tunnel model is illustrated in Figure 2.

3.2. Model Parameters

In both working conditions, the tunnel was excavated using the three-bench method, characterized by a bench length of 2.4 m and an excavation advance of 0.6 m per cycle. The advanced support system utilized Φ108 pipe umbrella, which possess an elastic modulus of 210 GPa, an individual length of 30 m, and a circumferential spacing of 0.4 m. These pipe umbrellas were installed within a 140° range of the arch section and were driven at a 0° elevation angle in soil sections. In soil tunnel analysis based on continuum mechanics, elastic-plastic constitutive models are commonly employed, with the Mohr-Coulomb criterion being widely adopted [26]. Specifically, shear strength envelope analysis of four typical loess samples indicates that their strength behavior conforms to this criterion [27]. Moreover, extensive numerical simulations demonstrate that loess tunnel excavation analyses using this model yield results closely matching field measurements, thereby validating its rationality and accuracy [28,29,30]. In the model, the surrounding soil was represented using the Mohr-Coulomb constitutive model, with mechanical parameters derived from laboratory tests conducted on non-disturbed loess. In practical engineering, the secondary lining is typically installed as a long-term safety reserve after the tunnel cross-section has stabilized. Positioned at a significant distance from the excavation face, it becomes load-bearing only after the excavation-induced stress adjustments have largely occurred [31,32]. Consequently, the secondary lining is treated as a safety reserve in this study and is excluded from the numerical calculations. The initial support primarily comprises I25a steel arches, advance support, C25 shotcrete, and steel mesh. In accordance with the principle of stiffness equivalence [33], the elastic modulus of the shotcrete is integrated into the initial support within this numerical model, Although the stiffness-equivalent method cannot precisely simulate the interaction between steel arches and concrete or the micromechanical stress redistribution following concrete cracking, and its homogenization assumption may overestimate the overall flexural capacity of the structure, this approach effectively captures the macroscopic confinement effect of composite support on the surrounding rock while significantly reducing the complexity and computational cost of three-dimensional numerical simulations [34,35,36]. Yielding a comprehensive elastic modulus E for the initial support.

$$E=E_0+E_g\times S_g/S_c$$

(1)

In the equation; E is the elastic modulus of the converted initial support; E₀ is the elastic modulus of the original shotcrete; S_g is the cross-sectional area of the steel arch; E_g is the elastic modulus of the steel arch; S_c is the cross-sectional area of the shotcrete. The specific mechanical parameters are shown in

Table 1. Model mechanical parameters.

Name	γ (kN/m3)	φ (°)	c (kPa)	ν	E
Q2 Loess	16.5	27.5	47.5	0.3	45 MPa
Initial support	24.83	-	-	0.24	28.51 GPa

.

4. Results

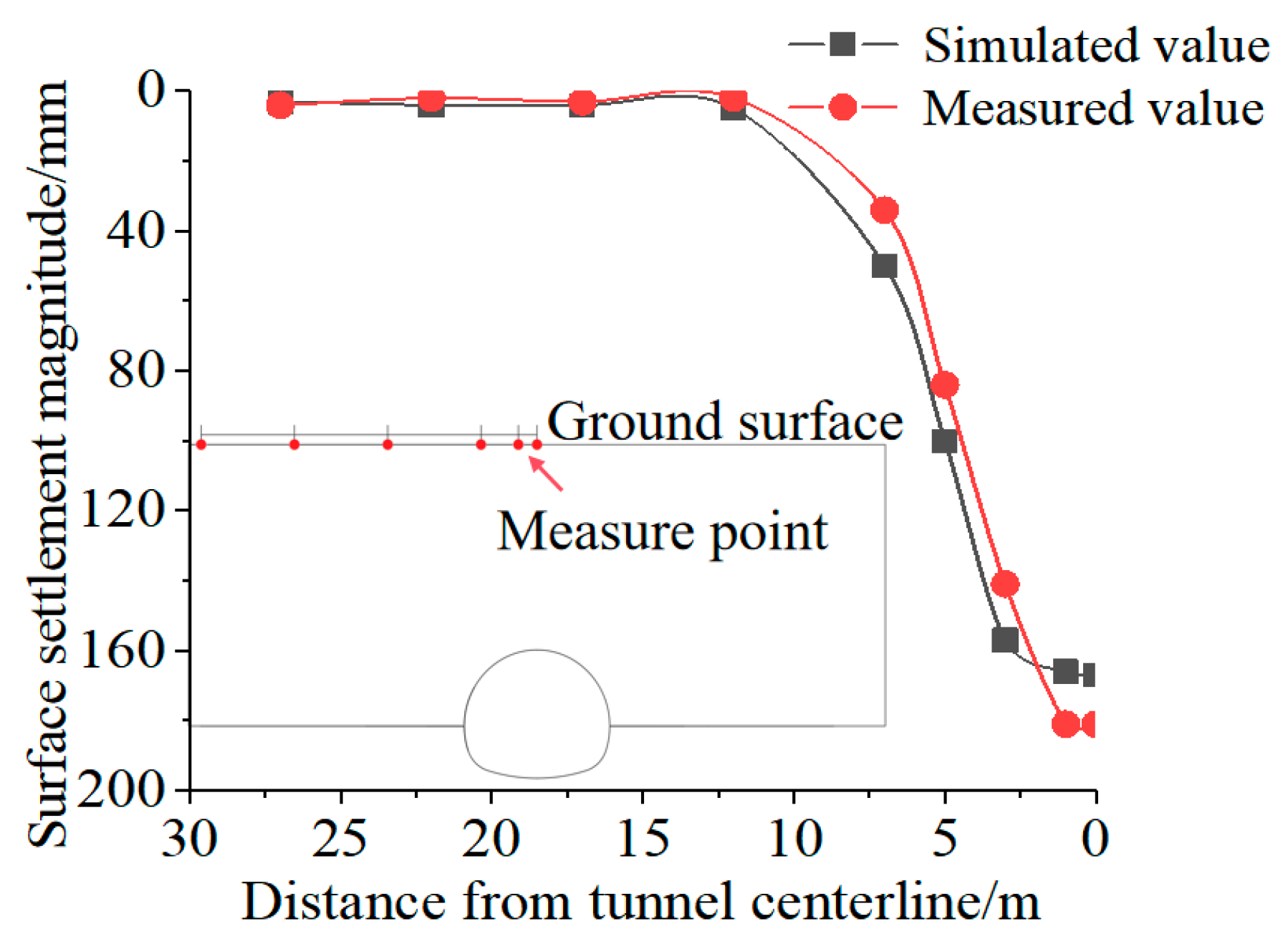
4.1. Validation of Simulation Model

To evaluate the reliability of numerical simulations, this study compares and analyzes the surface settlement curves obtained from numerical simulations with actual field monitoring data. This verification process assesses the validity of the established model, selected parameters, and constitutive relations, thereby providing a reliable basis for subsequent analyses of challenging-to-measure indicators such as stress and plastic zones. The surface settlement variations in both datasets are illustrated in Figure 3.

The surface settlement patterns and magnitudes predicted by the 3D numerical model established in this study exhibit a high degree of consistency with the actual monitoring results, maintaining an error margin of less than 10%. Consequently, it can be concluded that this model accurately represents the mechanical response associated with tunnel excavation and support. Therefore, it is suitable for subsequent in-depth analyses and research regarding internal mechanical behaviors, such as surrounding soil stress and the formation of plastic zones.

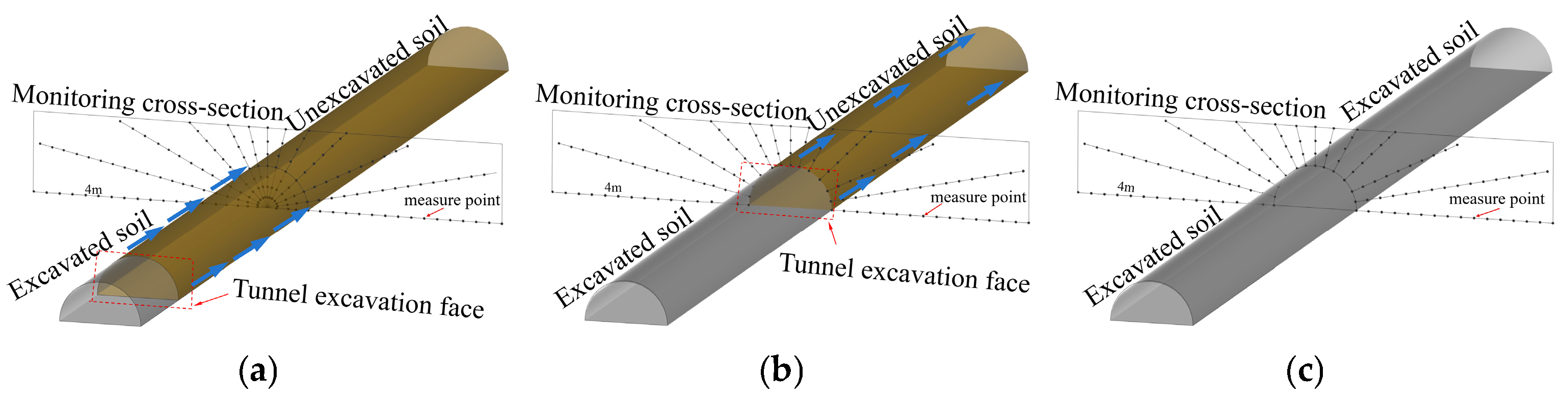
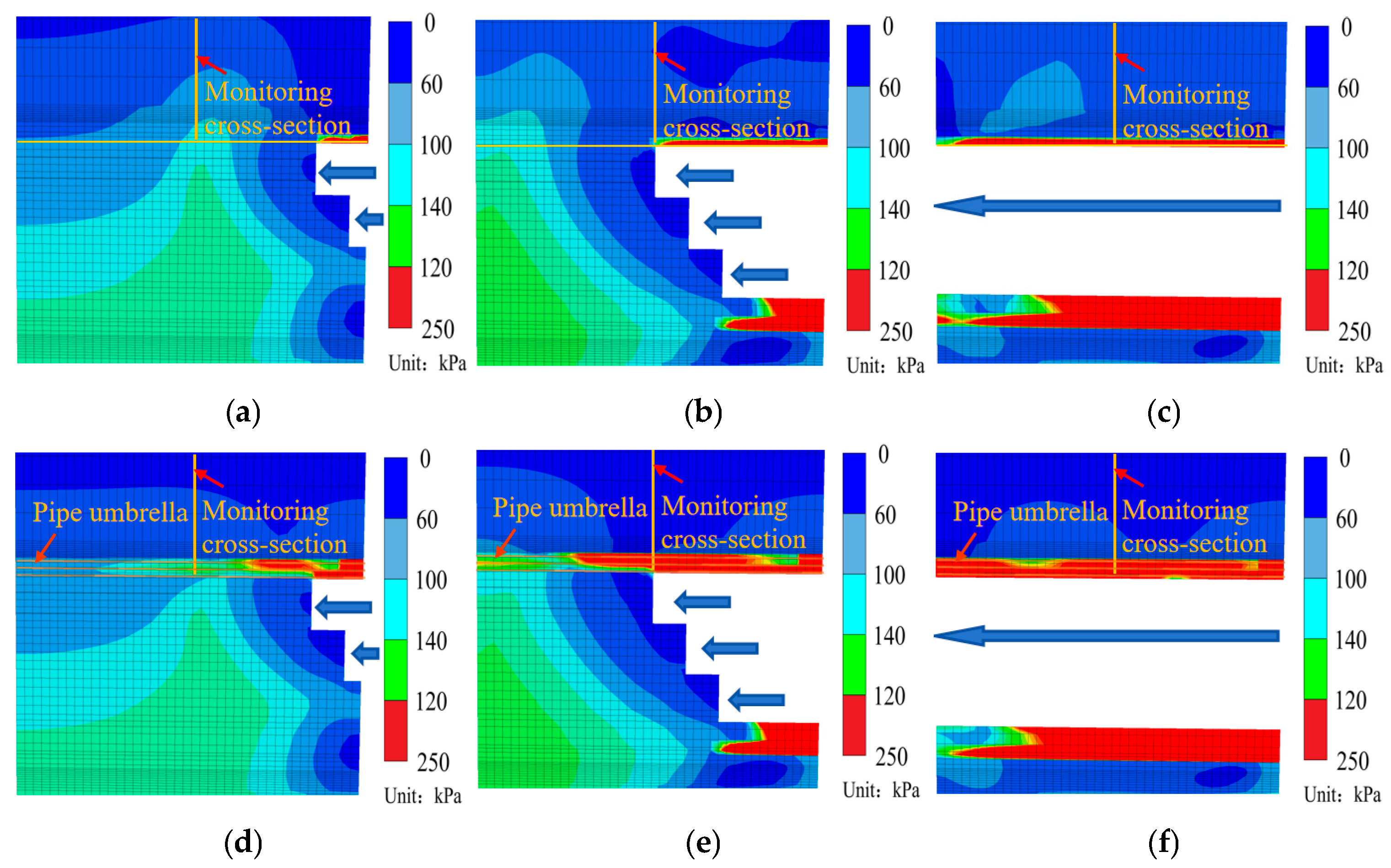
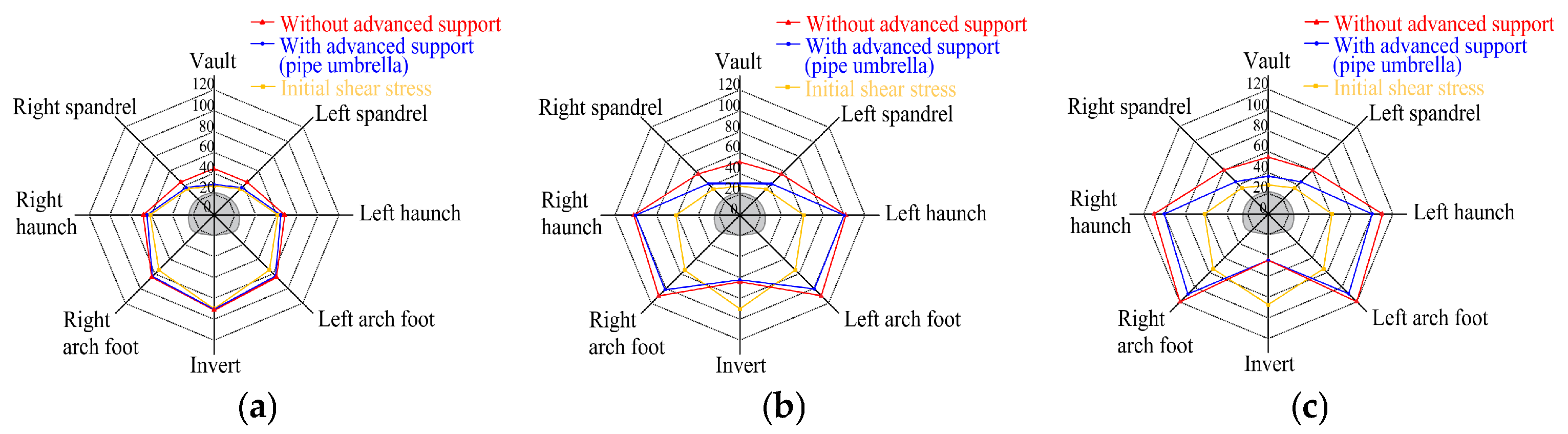
4.2. Monitoring Points Arrangement

To investigate the regulatory effect of advanced on stress redistribution in the surrounding soil during tunnel excavation, a monitoring section was established at a distance of 12.3 m along the longitudinal axis of the tunnel. Monitoring lines were arranged every 15° in the radial direction of the surrounding soil within this section. Measurement points were installed at 4 m intervals along each monitoring line, extending from the tunnel wall into the deeper surrounding soil, thereby forming a comprehensive monitoring network that encompasses the stress field around the tunnel. Stress monitoring was conducted when the tunnel excavation face advanced to positions −0.5 D, 0 D, and 0.75 D relative to the monitoring cross-section. This approach was implemented to capture the dynamic evolution of stress states during excavation, where D represents the diameter of the tunnel excavation. The layout of the monitoring points is depicted in Figure 4. The blue arrows in this figure and in subsequent ones indicate the direction of tunnel excavation.

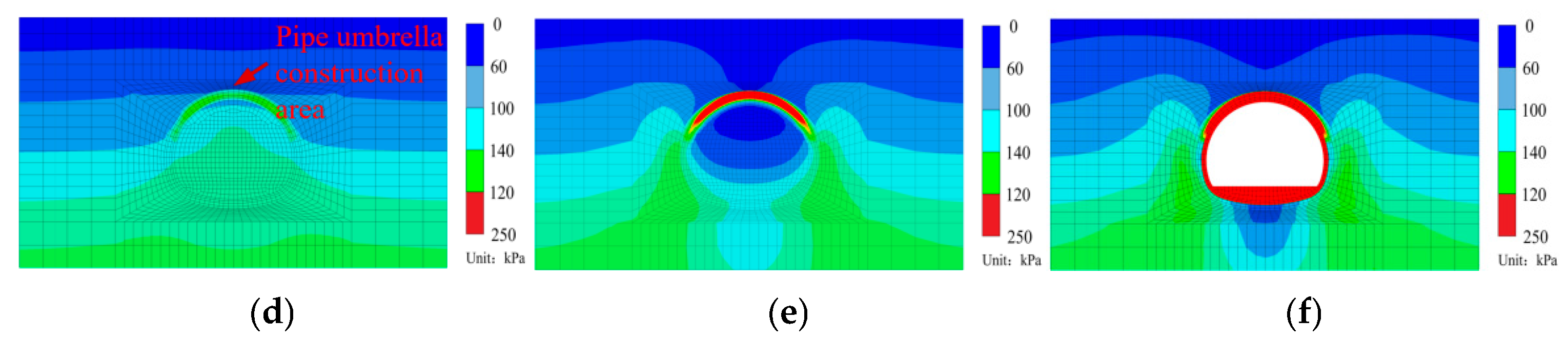
4.3. Comparative Analysis of Stress Field Evolution Under Two Working Conditions

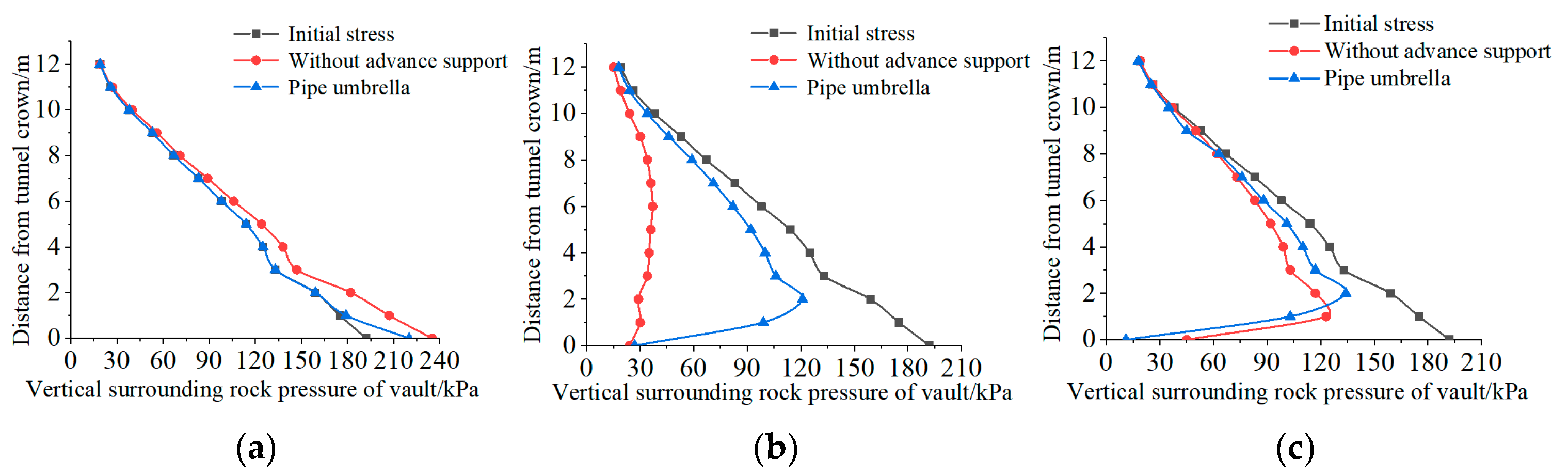
4.3.1. Vertical Stress Distribution at Different Depths Above the Vault

The variation in vertical surrounding soil pressure at the vault of monitoring sections during tunnel excavation at different depths is illustrated in Figure 5. The results indicate that in shallow large-section loess tunnels, significant stress concentration occurs in the vault surrounding soil ahead of the tunnel excavation face due to three-dimensional spatial effects. This surrounding soil autonomously balances the overlying load through the ‘wedging’ effect. When the tunnel excavation face is 0.5 D away from the monitoring section, stress concentration occurs under both conditions (without advance support and with pipe umbrella support). However, the stress increase ranges from 5% to 22% without advance support, which is significantly higher than that with pipe umbrella support. When the tunnel excavation face reaches the monitoring section (0 D), the vault stress sharply decreases by over 80% without support, ultimately forming an inefficient pressure arch. In contrast, pipe umbrella support effectively restrains stress release at the free surface and confines the disturbance range, resulting in a significantly reduced stress release magnitude. After full tunnel (0.75 D), the vault stresses under both conditions show recovery. The pipe umbrella support, due to its effective control of initial disturbances, exhibits smaller stress recovery amplitudes, with surrounding soil stresses above 10 m largely returning to their initial state. These results indicate that pipe umbrella support transforms stress redistribution into an orderly and controllable process, significantly reducing the disturbance range and enhancing tunnel stability.

The longitudinal profile of vertical stress is illustrated in Figure 6. The results indicate that, in the absence of advance support, significant stress concentration occurs at the monitoring section when the tunnel excavation face is excavated to a position 0.5 D ahead of this section. Upon reaching the monitoring section, the vertical stress at the crown experiences a drastic release due to the development of the free surface, with a reduction exceeding 80%. Following the tunnel breakthrough, the stress partially recovers but exhibits considerable fluctuations, indicating a lack of overall stability in the surrounding soil. In contrast, the advance pipe umbrella support demonstrates excellent stress regulation capabilities: it effectively alleviates stress concentration in the surrounding soil at the −0.5 D stage, significantly suppresses the magnitude of crown stress release when excavation reaches the monitoring section, and facilitates steady, uniform stress recovery after breakthrough, ultimately resulting in a stable load-bearing system.

According to the results of the numerical simulation analysis, the most unfavorable stress position of the pipe umbrella occurs near the tunnel excavation face. To accurately describe the working state of the pipe umbrella, this study comprehensively considers key factors such as stress release, time-dependent behavior of the initial support, elastoplastic characteristics of the surrounding soil, and the dynamic variation in subgrade reaction coefficients. This comprehensive approach allows for the reconstruction of the mechanical analysis framework for pipe umbrellas. Accordingly, the pipe umbrella structure is longitudinally segmented into several sections, each exhibiting distinct mechanical characteristics along the tunnel axis, as illustrated in Figure 7.

Assuming that the surrounding soil is a continuous homogeneous medium and that the bending behavior of the pipe umbrella adheres to Euler-Bernoulli beam theory, the Winkler foundation model is inadequate as it does not consider the continuity of the foundation soil. This limitation hinders a comprehensive representation of the actual stress state in the interaction between the pipe umbrella and the surrounding soil. Consequently, this paper employs the Pasternak elastic foundation beam model, derived from the two-parameter model, which accommodates deformation continuity by incorporating transverse shear interactions between foundation springs. This approach aligns more closely with the actual working conditions of pipe umbrella support. The formula for the foundation reaction force is as follows:

$$p\left(x\right)=kw(x)-G_p{d}^{2}w(x)/d{x}^2$$

(2)

In the equation; p(x) is the foundation reaction force; k is the coefficient of foundation reaction; Gp is the shear modulus of surrounding soil foundation.

According to the force equilibrium of the unit,

$$dV(x)/dx=d^{2}M(x)/d{x}^2=bq(x)-b^{\ast }p(x)$$

(3)

In the equation, V is the section shear force; M is the section bending moment; q is the external load; b is the foundation beam width, b^∗ is the equivalent foundation beam width, calculated by the equation.

Based on the Euler-Bernoulli beam theory, the static equilibrium equation governing pipe umbrella deflection can be derived;

$$EI{d}^{4}w(x)/d{x}^4+b^{\ast }kw(x)-b^{\ast }{G}_p{d}^{2}w\left(x\right)d{x}^2=bq(x)$$

(4)

To comprehensively reveal the spatial interaction between pipe umbrella support and surrounding soil, this study further extracted the vertical stresses at key vault positions along the tunnel’s longitudinal direction (excavation direction) under two working conditions. As illustrated in Figure 8, under unsupported conditions, the stresses at all measuring points in the vault exhibited a sharp attenuation during tunnel excavation, with stress values at the face decreasing to 20–43 kPa, representing a reduction of 70–90% compared to the initial stress. Meanwhile, significant fluctuations and rebounds were observed in the stress curves behind the excavation face at all locations, indicating that the surrounding soil was in an unstable state of intense adjustment. In contrast, under the pipe umbrella support condition, the maximum reduction in vault stress was maintained within the range of 23% to 28%, with a smooth stress curve throughout and no significant fluctuations or rebounds, demonstrating highly stable mechanical characteristics.

The pipe umbrella support system significantly mitigates the disturbance caused by excavation unloading on the crown stress, suppressing the fluctuation amplitude of surrounding soil stress to a relatively low level. This finding demonstrates that the pipe umbrella, through its synergistic interaction with the surrounding soil, effectively restrains the loosening of local rock blocks and facilitates the continuous, controlled redistribution of surrounding soil stress, thereby forming a stable load-bearing system.

By considering the spatiotemporal effects of pipe umbrella and stratum loads as well as numerical simulation results, the original model [19] was improved to establish a new Pasternak elastic foundation beam model as shown in Figure 9.

The control equations are established for each divided support section as follows:

(1) In the AB section, the tunnel has been constructed with initial support, utilizing steel arches to provide resistance. The pipe umbrella in this zone primarily supports the vertical load q(x), which arises from the release of surrounding soil stress, the elastic reaction force p(x) generated by the bending deformation of the pipe umbrella, and the reaction force from the foundation beam. The differential control equation governing its deflection is presented below:

$$EI{d}^{4}w(x)/d{x}^4+k_n{b}^{\ast }w(x)-G_n{b}^{\ast }{d}^{2}w(x)/d{x}^2=b{q}_0$$

(5)

In the formula, k_n and G_n represent the coefficient of subgrade reaction and the ground shear modulus of the supporting section, respectively.

(2) In the unsupported section (BC section), where the initial support has not yet been installed, the pipe umbrella is unable to obtain the supporting reaction force from the foundation beam, resulting in px = 0. The primary loads acting on the pipe umbrella consist of the vertical distributed load q(x), which is caused by the release of surrounding soil stress, and the reaction force generated by the bending deformation of the pipe umbrella itself.

$$EI{d}^{4}w(x)/d{x}^4=bq(x)$$

(6)

(3) In the disturbance segment (CD section), there exists a risk of instability and collapse in the surrounding soil of the tunnel to be excavated; however, this section also provides a certain degree of supporting reaction force. Nevertheless, the elastic resistance coefficient of its foundation requires modification. The differential governing equation for the deflection of the CD section is as follows:

$$EI{d}^{4}w\left(x\right)d{x}^4+k_r\left(x\right)b^{\ast }w(x)-G_r{b}^{\ast }{d}^{2}w\left(x\right)d{x}^2=bq(x)$$

(7)

In the equation, kr and Gr represent the coefficient of subgrade reaction and the shear modulus of the foundation for the elastic disturbance zone, respectively.

The deflection differential control equation for pipe umbrella, established based on Pasternak foundation beam theory, enables the calculation of deflection distribution patterns for tunnel advance support across various sections. This approach facilitates the analysis of the influence of parameters such as pipe umbrella overlap length, diameter, and excavation step distance on deformation. Furthermore, through parameter sensitivity analysis, key design parameters, including pipe umbrella diameter, circumferential spacing, and excavation step distance, can be optimized.

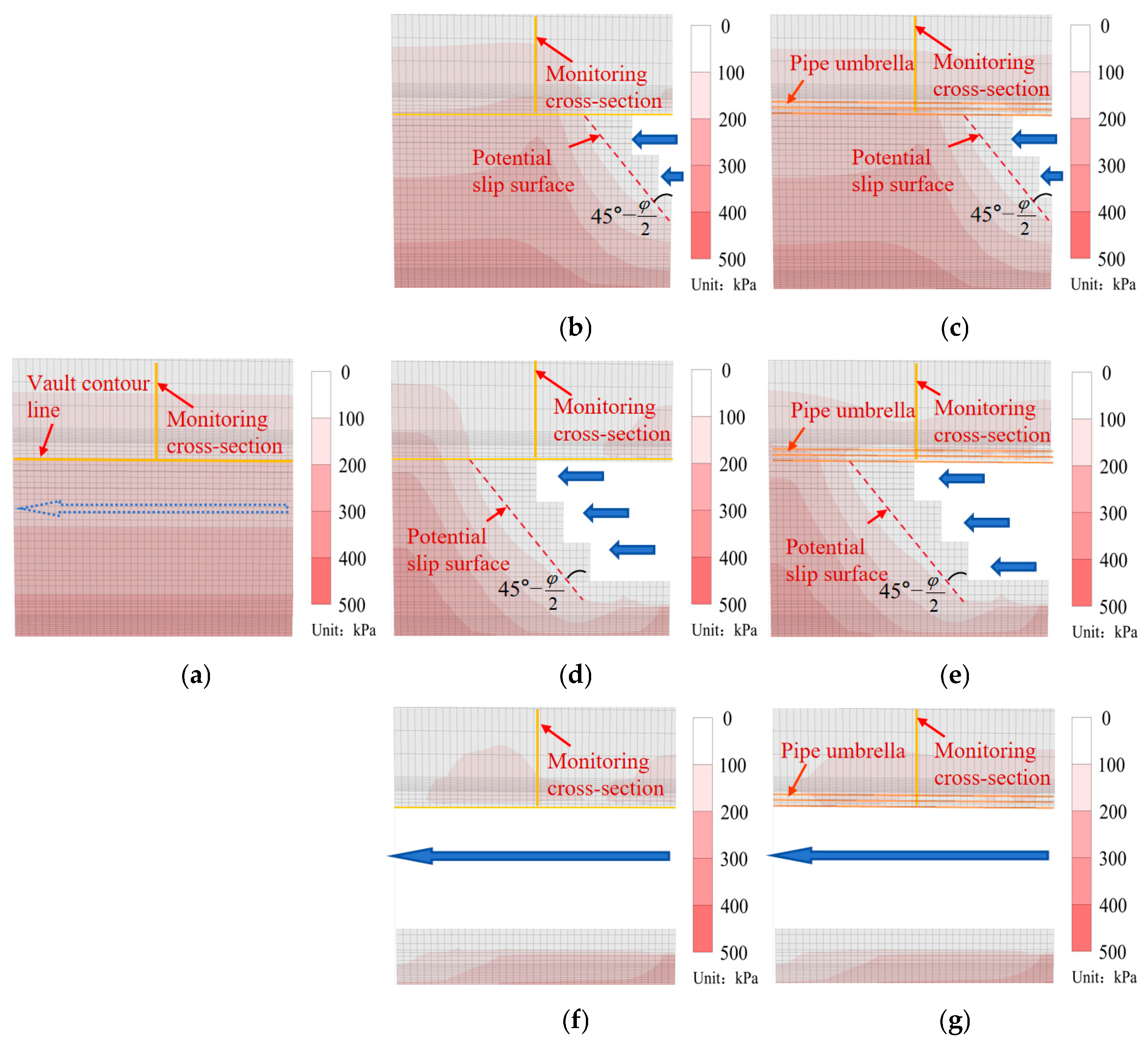
4.3.2. Maximum Shear Stress Distribution

The distribution of maximum shear stress at the monitoring cross-section under two working conditions, excavated to different depths, is illustrated in Figure 10. Throughout the excavation process, the advance pipe umbrella support significantly mitigated stress disturbances in the surrounding soil, thereby enhancing the stress state of the tunnel. When the working face advanced to the −0.5 D position, the pipe umbrella effectively obstructed advance disturbances and reduced the development of shear stress at the monitoring cross-section. Upon reaching the excavation cross-section, the pipe umbrella notably curtailed the expansion and connectivity of shear stress at the spandrel, effectively preventing the formation of potential sliding surfaces. Following the breakthrough, the pipe umbrella confined the high shear stress zone to a limited area surrounding itself, thereby enhancing the overall stability of the surrounding soil. It is important to emphasize that a significant concentration of shear stress consistently exists within the area where the pipe umbrella is constructed. This observation indicates that the pipe umbrella actively regulates stress distribution in the surrounding soil by bearing loads, which serves as a crucial mechanical manifestation of its supporting function.

The longitudinal distribution characteristics of shear stress in the surrounding soil during tunnel excavation are illustrated in Figure 11. As excavation progresses, a pronounced zone of shear stress concentration emerges within a specific range behind the working face. Under unsupported conditions, this high-shear-stress zone continues to expand both longitudinally and vertically with advancing excavation, exhibiting significant increases in both the affected scope and the magnitude of stress. In contrast, the pipe umbrella support scenario effectively mitigates shear stress concentration: the high-stress zone primarily develops along the tunnel’s longitudinal direction, while its vertical distribution is strictly confined within the height range of the pipe umbrella installation, with no evident stress redistribution observed in the overlying rock mass above the pipe umbrella.

To more precisely elucidate the regulatory effect of advanced pipe umbrella support on the shear stress distribution of surrounding tunnel rock, this study further extracted the maximum shear stress values at various locations of the monitoring cross-section under different excavation depths. The results are illustrated in Figure 12. When the tunnel excavation face was positioned 0.5 D ahead of the monitoring section, the crown shear stress decreased from 44 kPa under unsupported conditions to 29 kPa with pipe umbrella support, representing a reduction of 34%, which effectively alleviated stress concentration prior to excavation. When the tunnel excavation face reached the monitoring section, the spandrel shear stress increased to 57 kPa under unsupported conditions, whereas pipe umbrella support restrained it to 43 kPa, achieving a 25% reduction and demonstrating excellent constraint capability against spandrel deformation. However, the support effect at the arch foot was limited under the 0 D condition, with shear stress only decreasing from 111 kPa to 109 kPa (a mere 2% reduction), which is significantly lower than that observed at other locations. Additionally, when excavation reached the monitoring section in the arch bottom area, the pressure under unsupported conditions decreased from the initial 89 kPa to 65 kPa, representing a reduction of 27%, and further dropped to 41 kPa after tunnel breakthrough.

By comparing the variations in shear stress during tunnel excavation under two working conditions, it is evident that the pipe umbrella support effectively mitigates stress concentration in critical areas, such as the vault and spandrel, thereby controlling the distribution range of shear stress. This enhancement in stress distribution primarily arises from the dual mechanisms of the pipe umbrella support: first, through the “beam effect,” which transfers the overlying soil load to the unexcavated area ahead, thereby reducing stress concentration at the excavation face; second, through the “reinforcement effect,” which improves the shear strength parameters of the surrounding soil. The persistent shear stress concentration observed in the pipe umbrella installation zone serves as a key indicator of its supporting function.

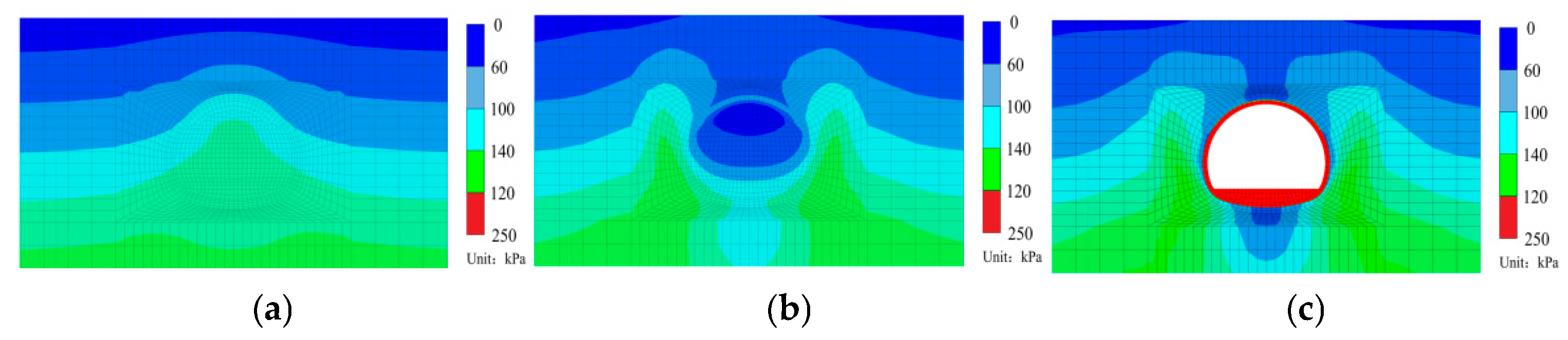
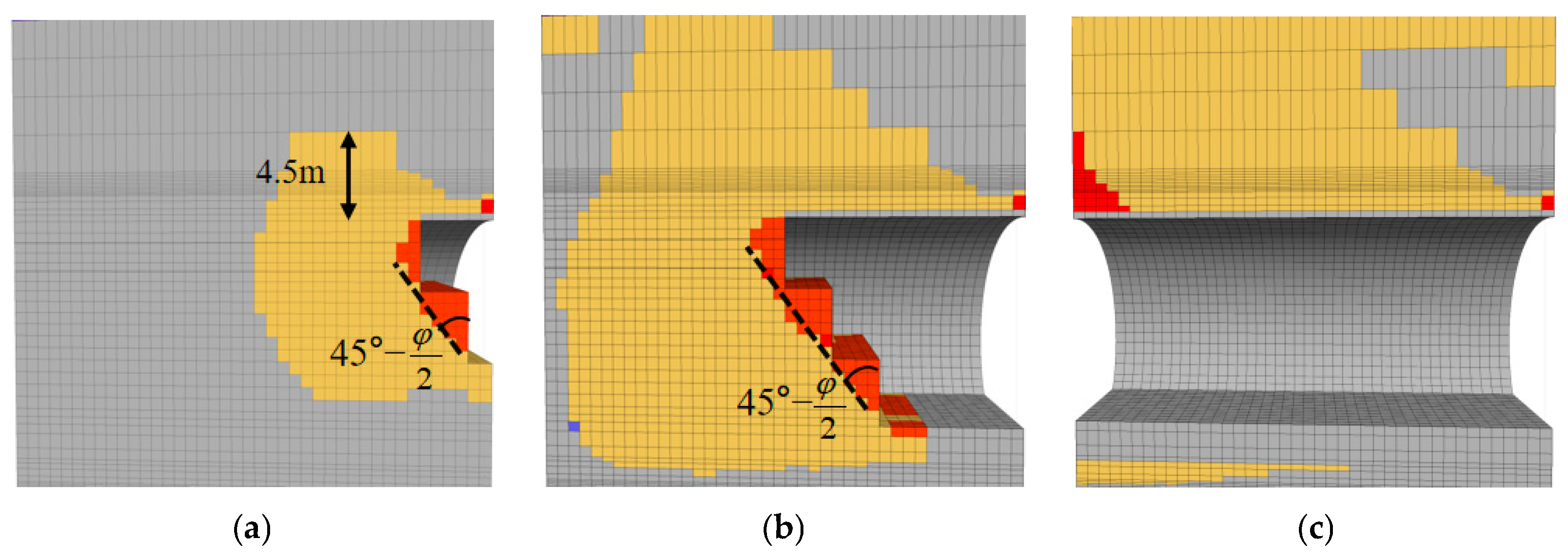
4.3.3. Plastic Zone

The distribution of plastic zones at the monitoring section during excavation at varying depths is illustrated in Figure 13. In shallow, large-section loess tunnels, the plastic zone of the surrounding soil at the monitoring section develops continuously throughout the excavation process, primarily exhibiting shear plastic failure. However, this development pattern is significantly influenced by the support conditions. In the absence of advance support, when excavation reaches the monitoring section, the plastic zone rapidly extends to the ground surface, resulting in a through-going failure. As excavation progresses, the area of the plastic zone further expands from 351.7 m² to 413.3 m², marking a 17% increase, which indicates a continuous intensification of surrounding soil instability. Conversely, pipe umbrella support effectively suppresses the expansion of the vault plastic zone throughout the entire process. With pipe umbrella support in place, the plastic zone is strictly confined within a limited range, with its area increasing only from 62.0 m² to 95.0 m², representing a reduction of over 77% in scale compared to the unsupported scenario.

The longitudinal distribution of plastic zones under two working conditions is illustrated in Figure 14. Both conditions are predominantly characterized by shear plastic failure. In unsupported conditions, the plastic zone expands rapidly as excavation progresses; when the tunnel excavation face reaches −0.5 D, the height of the plastic zone has already reached 4.5 m, and it further extends to the ground surface (11.3 m) upon reaching the monitoring section, thereby forming a continuous potential failure zone. Conversely, pipe umbrella support entirely restricts the upward development of the plastic zone, with no significant expansion observed. Notably, a tensile-shear composite plastic zone emerges near the tunnel excavation face under both conditions, exhibiting a fracture angle of approximately 45°–φ/2, which indicates high-risk stress conditions in this area. Additionally, the pipe umbrella construction zone displays a complex stress distribution, confirming its role as ‘advanced support’ and stress regulation by actively bearing loads and reconstructing stress paths.

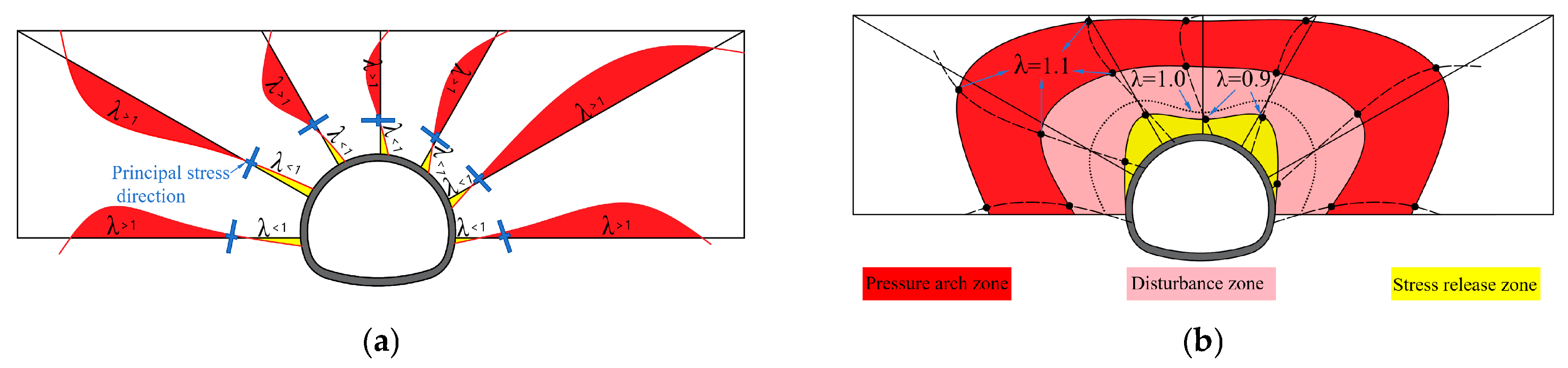
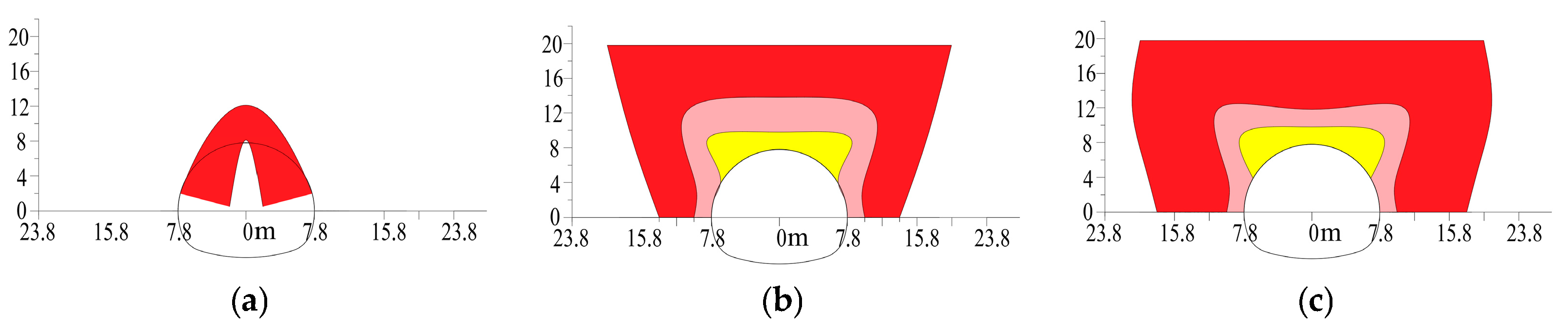
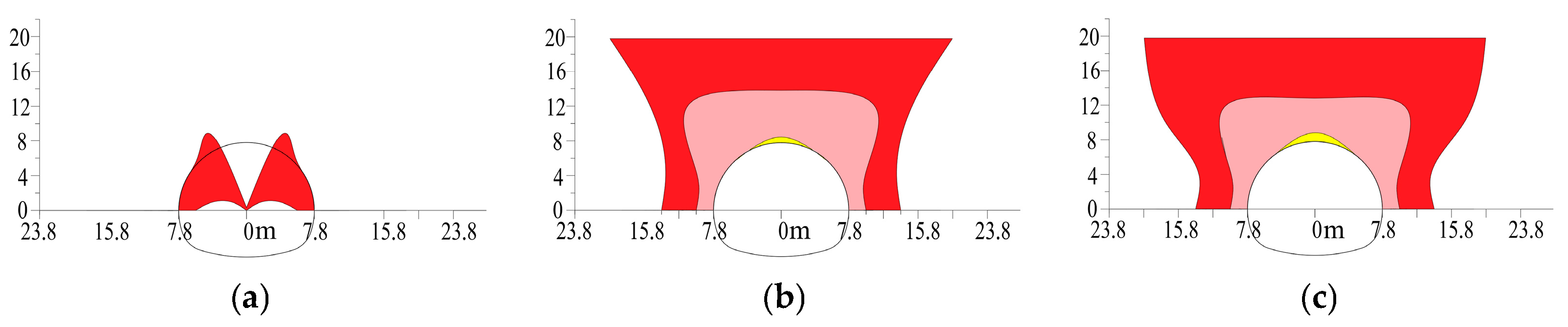
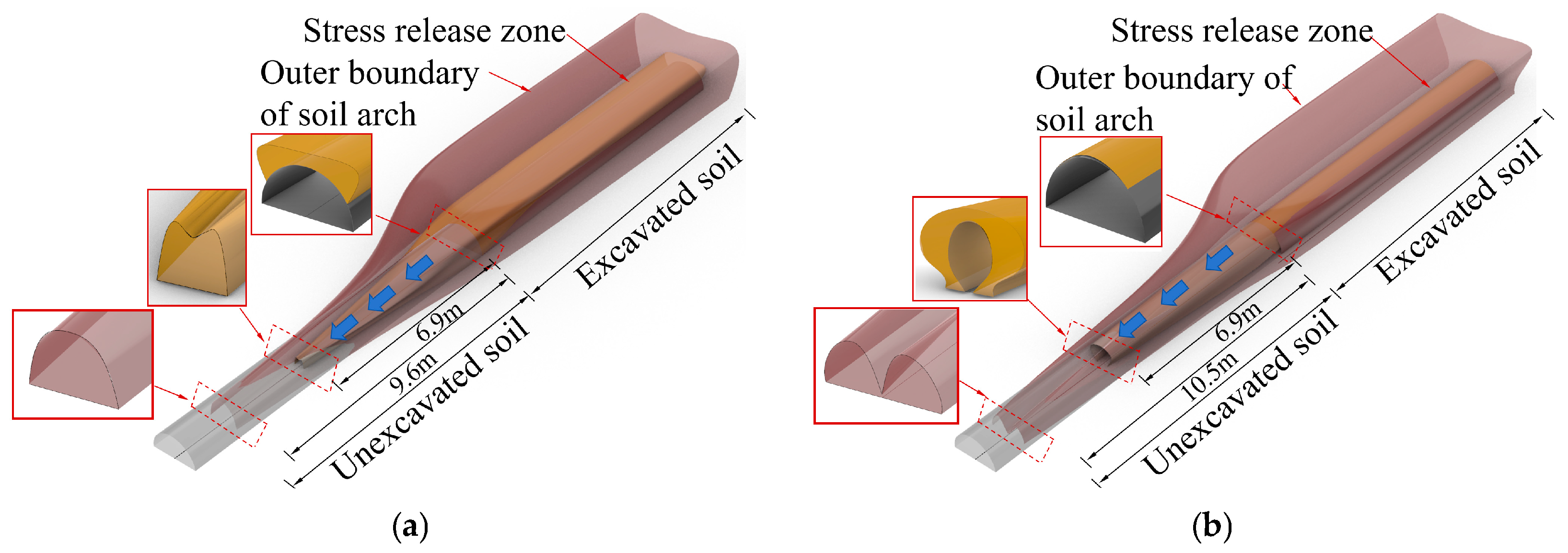
4.4. Evolution of Soil Arch

As the core mechanism of stress redistribution in the surrounding soil of tunnels, the soil arching effect is manifested through the deflection of stress paths induced by particle interactions, which transfers partial overburden loads via an arch-shaped bearing structure to the undisturbed zones on both sides of the tunnel. During this process, symmetrically distributed stress transfer paths and plastic zones form along both sides of the tunnel axis. This process creates a system that comprises coexisting low-stress relaxation zones and high-stress pressure arches above the crown. Symmetrical stress paths promote a uniform distribution of overburden pressure along the arch axis. This enhances the load-transfer efficiency of the bearing arch and mitigates localized stress concentrations. The symmetrical development of the plastic zone indicates contained shear deformation, thereby preventing arch instability due to asymmetric failure. Although both the pressure arch and relaxation zone display macroscopic symmetry under both unsupported and pipe-curtain-supported conditions, their underlying mechanisms differ fundamentally. In unsupported conditions, symmetry arises from a passive, self-adjusting response of the rock mass, resulting in a form that is inherently less stable. In contrast, the pipe curtain support actively induces symmetry by pre-establishing a high-stiffness structure. This engineered, active symmetry significantly improves the tunnel’s overall stability and resistance to disturbance. To accurately delineate the spatiotemporal distribution of soil arches, this study employs the ratio λ of tangential stress to initial geostress as a quantitative criterion based on numerical simulation results. Regions where λ > 1.1 are identified as pressure arch bearing zones, those with λ < 0.9 as relaxation zones, and transitional disturbed zones for values between 0.9 and 1.1 [37]. The specific discrimination method is illustrated in Figure 15.

Under unsupported conditions, the evolution of surrounding soil stress exhibits distinct passive bearing characteristics. As illustrated in Figure 16, approaching the monitoring cross-section at −0.5 D, the pressure arch area had already reached 96 m², indicating that the surrounding soil began self-organizing to form a load-transfer structure. As excavation progressed to the monitoring cross-section, the pressure arch area sharply increased to 392 m², while a relaxation zone covering 52 m² simultaneously formed. Upon reaching 0.75 D beyond the monitoring cross-section, the pressure arch area further expanded to 531 m², with the relaxation zone growing to 60 m². This continuous expansion trend reveals the instability of stress redistribution in unsupported surrounding soil, where the soil mass can only maintain temporary equilibrium by forming extensive, yet less efficient, passive soil arches. “Passive soil arch” refers to a load-bearing structure formed passively in tunnel excavation when, without advance support, the surrounding rock undergoes plastic deformation and stress adjustment solely through its own strength.

The pipe umbrella support effectively enhanced the stress redistribution of the surrounding soil at all stages, as illustrated in Figure 17. At the −0.5 D stage, its “longitudinal beam-forming” effect reduced the pressure arch area by 52%, decreasing it to 85 m². This advance load transfer suppressed stress concentration in the front surrounding soil. At the 0 D stage, the pressure arch area was diminished by 12% compared to the unsupported condition, while the relaxation zone area decreased by 62%, reaching 39 m². This optimization transformed the “passive soil arch” at the free face into a “thin yet efficient” active soil arch. By the 0.75 D stage, the continuous action of the pipe umbrella stabilized the relaxation zone at 42 m², significantly facilitating steady stress recovery. “Active soil arch” refers to a soil arch formed under the advance support of pipe arches, which actively intervenes and guides stress paths through its “beam-arch effect,” thereby achieving greater depth of influence and higher load-bearing efficiency.

Tunnel excavation unloading causes deflection in the stress path of the overlying soil mass, transferring part of the overburden load to the unexcavated area ahead of the tunnel and the stable soil on both sides. This creates a three-dimensional, arch-shaped high-stress bearing zone around the tunnel bore. When the tunnel excavation reaches the monitoring section, the evolution characteristics of the three-dimensional pressure arch under the conditions of advanced pipe umbrella support and unsupported scenarios exhibit significant differences. As illustrated in Figure 18, in the absence of advanced support, the soil can only form a natural load-transfer path. The soil arch develops in a typical arch shape up to 9.6 m ahead of the tunnel excavation face. Meanwhile, stress concentration at the arch foot causes the plastic zone to penetrate from top to bottom, resulting in a relaxation zone that displays an ‘M’-shaped distribution starting from 6.9 m. Under the condition of advanced pipe umbrella support, the ‘beam effect’ of the pipe umbrella actively transfers the upper load of the excavation section to the undisturbed soil ahead, extending the influence range of the soil arch to 10.5 m and reshaping it into an ‘M’-shaped distribution. As the tunnel excavation face advances, the stress on the pipe umbrella increases. When shear plastic failure occurs in the underlying soil along the periphery of the pipe umbrella, the relaxation zone begins to develop annularly along the pipe umbrella layout direction from 6.9 m. The pipe umbrella effectively confines the failure range to its surrounding area, thereby significantly enhancing the overall stability of the tunnel.

The observed phenomenon arises from the differences in stress paths and load-bearing mechanisms of the surrounding soil under two distinct working conditions. In the absence of advance support, tunnel excavation leads to stress redistribution, which causes the surrounding soil to passively enter a plastic state due to unloading. This extensive plastic zone fosters the development of a relatively thick ‘passive soil arch’ in the upper surrounding soil, characterized by low bearing efficiency and significant soil relaxation. Conversely, the pipe umbrella support pre-reinforces the surrounding soil through its ‘beam-arch effect,’ actively optimizing the load transfer path. This process facilitates the formation of a thinner yet more deeply influenced ‘active soil arch,’ effectively constraining the development of the plastic zone, substantially reducing surrounding soil relaxation, and enhancing overall tunnel stability.

5. Conclusions

This paper conducts a comparative study on the excavation response of shallow, large-section loess tunnels under unsupported conditions and those with advanced pipe umbrella support. A field-data-validated 3D model has been established, leading to the following main conclusions:

(1)

The advanced pipe umbrella support system achieves effective full-process control over stress redistribution in the surrounding soil through its “pre-support and load-bearing” mechanism. This mechanism effectively alleviates stress concentration 0.5 D ahead of the tunnel excavation face, reduces the stress release magnitude at the vault from over 80% in unsupported conditions to below 30% when excavation reaches the monitoring section, and facilitates stable and orderly stress recovery following tunnel breakthrough. Ultimately, this results in the formation of a more efficient active pressure arch system with a higher load-bearing capacity.

(2)

The longitudinal beam-forming and transverse arch-forming effects of pipe umbrella significantly enhance the mechanical stability of surrounding soil. These effects effectively mitigate the concentration and propagation of shear stress at critical locations, such as the arch shoulder and arch foot. Furthermore, they reduce the extent of the plastic zone in the surrounding soil from 413.3 m² (when fully penetrating to the ground surface without support) to 95.0 m², achieving a reduction of over 77%. This reduction prevents overall instability of the surrounding soil and ensures construction safety.

(3)

The pipe umbrella support optimizes the formation mechanism and load-bearing efficiency of the soil arch. In unsupported conditions, the surrounding soil responds passively, leading to the development of a “passive soil arch” characterized by extensive coverage and considerable thickness, albeit with significant relaxation. In contrast, the pipe umbrella actively assumes and redistributes loads, prompting the surrounding soil to form an “active soil arch” with a greater influence depth and a markedly reduced relaxation zone, thus achieving efficient reconstruction of the load transfer path.

(4)

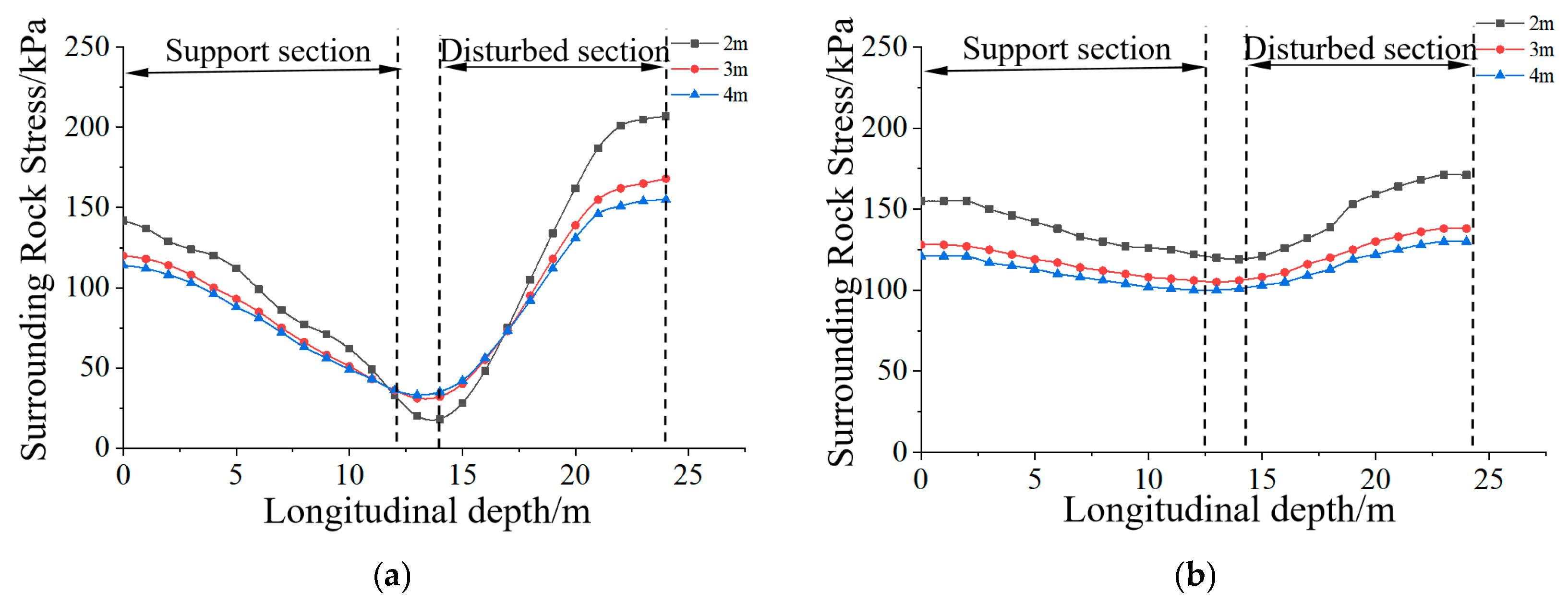
Based on the spatiotemporal distribution characteristics of loads revealed by numerical simulation, the established Pasternak elastic foundation beam model, which accounts for the spatiotemporal effects of support, describes the segmented mechanical behavior of pipe umbrella in supported, unsupported, and disturbed zones. This model identifies the most unfavorable stress location of the pipe umbrella near the tunnel excavation face, theoretically elucidates its ‘longitudinal beam-forming’ mechanism from a mechanical perspective, and provides a quantitative theoretical tool for optimizing support parameters.

6. Discussion

A limitation of this study is that the numerical simulations did not address the water sensitivity of loess or variations in moisture content. These factors are likely to affect both the development of the arching effect during excavation and the bearing capacity of advance support. Therefore, future work should develop a moisture content model incorporating the coupled effects of joint fissures and rainwater infiltration. Such a model is essential to investigate the performance of advance support in mediating stress redistribution within loess tunnel surrounding rock under extreme hydrological conditions.