Microscopic Mechanism of Fracturing Fluid Flowback Regulated by Coal Bridge-Proppant Wettability Contrast

Abstract

Fracturing is a key technology for developing deep coalbed methane, in which the wettability contrast between proppants and coal bridges significantly influences flowback efficiency. This study integrates in situ wettability measurements with phase-field simulations to analyze the mechanisms by which wettability contrast, proppant distribution, and capillary number affect microscale fracturing fluid flowback. The results indicate that: (1) Proppant spatial distribution governs displacement pathways, with the centralized aggregation pattern reducing residual saturation by 5.4% compared to the lateral aggregation pattern under the same capillary number; (2) under the centralized aggregation pattern, neutrally modified proppants lower residual saturation to 5.87%, representing a reduction of approximately 52.8% compared to the unmodified system; and (3) microscopic throat constraints and macroscopic symmetric placement work synergistically to alleviate retention heterogeneity and enhance flowback uniformity. Based on these findings, a dual-target optimization strategy of “neutral wettability modification of proppants + central symmetrical placement” is proposed, providing theoretical support for efficient flowback in deep coalbed methane wells.

1. Introduction

The development of deep coalbed methane resources is a crucial component of China’s energy security system. However, efficient extraction is fundamentally limited by the low permeability of the reservoirs [1]. Native fractures within the coal matrix typically exhibit microscale apertures, and the poor connectivity of the pore-fracture network significantly restricts gas seepage capacity [2,3,4]. Although hydraulic fracturing technology can extend coal fractures to create an artificial fracture network, the rapid closure of fractures due to in situ stress rebound after pump shutdown, combined with low flowback efficiency and substantial fracturing fluid retention during the fracturing fluid flowback stage, severely limits coalbed methane productivity [5,6]. Therefore, it is of great theoretical and engineering significance to investigate the synergistic control of proppant wettability differences and spatial distribution on the microscopic mechanisms governing fracturing fluid flowback, as this study aims to address fracturing fluid retention in deep coalbed methane wells and enhance gas recovery efficiency.

Rigid proppants, such as quartz sand and ceramic particles, are typically added to the fracturing fluid and placed into fractures to maintain effective aperture [7]. This approach not only establishes long-term stable seepage paths but also, during fracturing fluid flowback, enhances coalbed methane displacement fracturing fluid efficiency by regulating proppant wettability and spatial distribution patterns, reduces fracturing fluid retention and mitigates its obstruction to gas production, thereby ensuring stable gas productivity [8,9]. However, the wettability difference between primary hydrophilic proppants and native hydrophilic coal bridges alters gas–water interface dynamics within the fracture space, inducing non-uniform capillary force field distribution. This wettability difference not only modifies the dynamic migration behavior of the gas–water interface but also significantly restricts the expansion efficiency of gas displacement pathways by regulating local capillary resistance and viscous force competition, dominating the spatial distribution characteristics of residual liquid phase retention [10,11]. Therefore, it is a fundamental scientific basis for overcoming the seepage production efficiency bottleneck in deep coalbed methane reservoirs to quantitatively elucidate the synergistic control mechanism of wettability heterogeneity, proppant spatial distribution, and the displacement capillary number on gas–liquid two-phase flow during fracturing fluid flowback in mixed wettability environments.

In deep coalbed methane extraction, the morphology and evolution of gas–water two-phase flow within reservoir fractures directly determine the dynamics of relative permeability and the ultimate recovery efficiency. The reservoir’s in situ temperature and pressure, as crucial environmental parameters for wettability testing, directly affect the authenticity of coal rock–fluid interface characterization. Neglecting these conditions can lead to deviations between wettability analysis and actual operating conditions, thereby compromising the reliability of gas–water displacement law [12]. Wang et al. confirmed that increasing temperature promotes the desorption of free water in coal and expands seepage paths through coal rock nitrogen-water two-phase displacement experiments under varying temperatures (30–180 °C) and pressures [13]. In contrast, increasing pressure increases bound water content and reduces the two-phase seepage area. These results clearly demonstrate that temperature and pressure influence fracture gas–water flow by regulating wettability. However, this kind of research primarily focuses on the wettability of the coal rock matrix without considering the mixed wettability environment formed by proppant retention after fracturing. Proppant wettability is a key factor regulating gas–water flow in fractures. The wettability difference between proppants and coal bridges alters the fluid environment within fractures. Moreover, the wettability contrast between conventional hydrophilic proppants and coal bridges can induce a non-uniform capillary force field, suppressing gas displacement pathways and governing residual water retention [14]. To enhance recovery efficiency, studies have shown that modifying proppants from hydrophilic to neutral or weakly hydrophilic can effectively improve multiphase flow efficiency. Wang et al. conducted experimental and numerical studies on oil-water two-phase flow in fractures with strongly/weakly oil-loving proppants [15]. Experiments demonstrated that stronger oil affinity delays water breakthrough time in fractures, reduces water phase retention, effectively accelerates fracturing fluid recovery, and lowers pressure loss during multiphase flow through the proppant layer. Results confirm that proppant surface wettability significantly influences oil-water flow behavior within fractures. Dong et al. demonstrate that mixed wettability proppants outperform single oil-wet ceramic proppants in enhancing oil flow efficiency and inhibiting liquid channeling, due to the oil-connected dominant pathways formed by their surface microstructure [16]. This provides a theoretical basis for regulating gas–water interface dynamics in fractures and optimizing gas seepage paths by modifying proppants from hydrophilic to weakly hydrophilic. The spatial distribution pattern of proppants within fractures controls the pore structure and seepage paths of the fracture network, playing a crucial role in two-phase flow efficiency and recovery [17]. In rough or cross fractures, proppant transport involves a solid–liquid two-phase flow process. Fracture non-planarity and roughness hinder proppant migration, leading to settlement blockage near the leading edge and rough walls, thereby reducing the effective propped length and conductivity. Ren et al. show that coated proppants undergo aggregation and growth stages due to cementation characteristics, forming high-porosity sandbanks that enhance conductivity [18]. An uneven spatial distribution pattern can create dominant flow channels and retention areas, affecting gas–water seepage and residual water distribution. Wang et al. confirmed that geometric characteristics such as fracture aperture, roughness, and tortuosity are key factors controlling the flow pattern and stability of gas–water two-phase flow through fracture visualization experiments [19]. Reducing aperture or increasing roughness exacerbates slug flow, while higher tortuosity suppresses it, providing a basis for optimizing placement patterns and improving flow stability. In response to the complexity of gas–water two-phase flow mechanisms in mixed wettability environments and the challenges of microscopic experimental observation, numerical simulation has become a crucial approach to overcome this research bottleneck. The phase-field method (PFM) naturally handles topological variations such as interface merging and fracture without complex interface tracking, and readily incorporates interfacial effects like surface tension and wettability. By implementing contact angle boundary conditions, it accurately simulates fluid behavior over solid surfaces with different wettability, demonstrating significant adaptability [20]. Maier et al. used the Navier–Stokes Cahn–Hilliard model to simulate the convective drying process of porous media, with simulation results showing high consistency with microfluidic experiments, verifying the accuracy of the phase-field method in simulating gas–liquid interface propagation and phase transitions in porous media [21]. Chen et al. investigated gas–water flow in mixed wettability porous media using a phase-field model, analyzing the influence of heterogeneous wettability particle content on seepage characteristics [22]. Chen et al. enhanced the efficiency and stability of the phase-field method for handling the high density ratio and turbulence problems, and incorporated Physics-Informed Neural Networks (PINNs) to solve higher-order nonlinear Cahn-Hilliard equations, thereby further improving simulation accuracy [23]. In summary, the synergistic mechanisms among wettability heterogeneity between proppant and coal, proppant spatial distribution pattern, and capillary number in fractured deep coal seams remain unclear, directly limiting efficient gas displacement.

This study investigates the gas–water displacement process in a mixed wettability system involving proppant and coal bridges within coal fractures. By integrating in situ wettability tests conducted under reservoir conditions of high-temperature and high-pressure with phase-field numerical simulations, a model of gas–liquid interface evolution under heterogeneous wettability environments is established. The research systematically investigates the synergistic effects of wettability heterogeneity, proppant spatial distribution patterns, and capillary number on both fracturing fluid flowback pathways and residual fracturing fluid retention, as well as providing a theoretical foundation for addressing the crucial challenges of “low flowback efficiency and significant fracturing fluid retention” in deep coalbed methane wells. Furthermore, it establishes a multiscale theoretical framework for designing proppant surface modifications and optimizing spatial placement in deep coalbed methane fracturing, thereby supporting the development of efficient gas recovery technologies.

2. Materials and Methods

2.1. In Situ Wettability of Reservoir

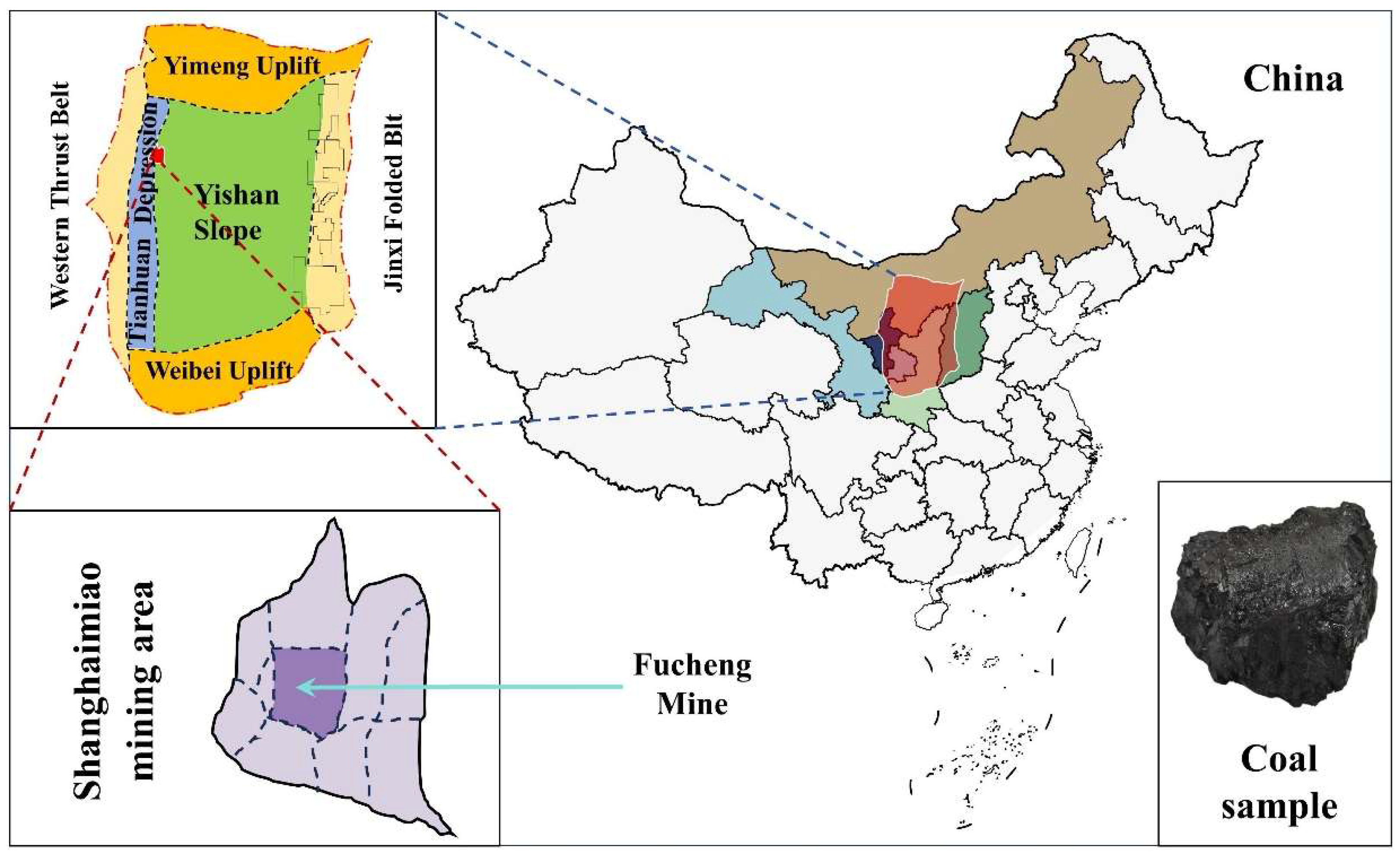
2.1.1. Coal Sample Selection

The coal samples used in this study were collected from Fucheng Mine in the Shanghaimiao mining area, Otog Front Banner, Ordos City, Inner Mongolia Autonomous Region, China, which is located in the tectonic unit of the western margin of the Ordos Basin, as shown in Figure 1. Geotectonically, this area resides on the northwestern margin of the Ordos Basin, a pivotal sedimentary basin within the North China Craton, characterized by a structural framework shaped by multi-phase tectonic movements. The regional geological structure predominantly manifests as a gentle monoclinal formation [24]. The target coal seams belong to the Permian-Carboniferous coal-bearing measures, primarily from the Lower Permian Shanxi Formation and the Upper Carboniferous Taiyuan Formation, which feature well-preserved, thick coal seams that have undergone intermediate to high-rank metamorphism, endowing them with superior gas adsorption capacity and reservoir properties [25]. Having experienced multi-stage tectonic evolution, the block exhibits a typical coupling of structural fracture control and high-pressure gas enrichment [26]. These comprehensive geological attributes collectively establish the Fucheng Mine in the Shanghaimiao Mining Area as a representative and critical geological carrier for investigating the mechanisms of deep coalbed methane extraction in China.

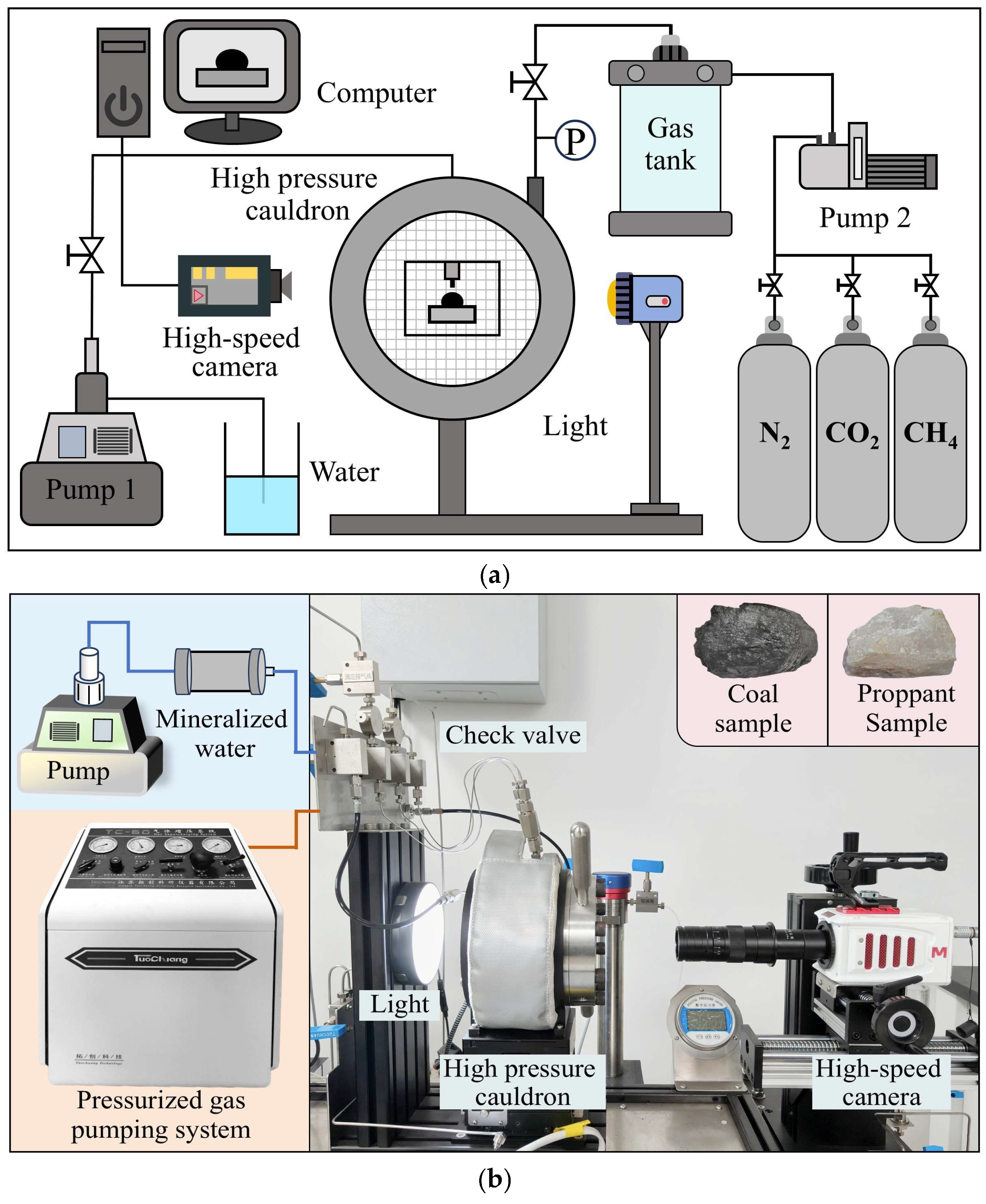
2.1.2. In Situ Wettability Equipment and Methods

To accurately determine the wettability characteristics of coal reservoirs under in situ temperature and pressure conditions, particularly to simulate the mixed wettability behavior resulting from differences between coal bridges and proppant surfaces within fracture channels after proppant injection, this study employed a self-developed high-temperature/high-pressure wettability measurement system to simultaneously measure the contact angles on both coal bridge and proppant surfaces under in situ conditions, as illustrated in Figure 2. Initially, a pre-mixed simulated coalbed methane (CH₄ 89.5%, CO₂ 7.2%, N₂ 3.3%) was injected into a high-pressure cauldron (Jiangsu Tuochuang, Scientific Research Instrument Co., Ltd., Nantong, Jiangsu, China; V = 1 L, the maximum pressure of 40 MPa) by a gas booster pump (Setok Fluid Control (Guangdong) Co., Ltd., Guangzhou, Guangdong, China; the pressure range of 0.7–40 MPa, the pressure accuracy is 0.5% FS) until the internal pressure stabilized at the target reservoir pressure of 6.18 MPa. Subsequently, a heating system (Omega Engineering (Shanghai) Co., Ltd., Shanghai, China; the temperature range is 273.15–393.15 K, the error is ±1 K) was activated to raise the temperature inside the high-pressure cauldron to the target reservoir temperature of 307.65 K. The prepared coal sample and proppant were then placed inside the cauldron and fully exposed to the simulated reservoir temperature, pressure, and gas atmosphere. This process ensures that the sample surfaces achieve adsorption equilibrium, thereby accurately reproducing their in situ properties. After the system temperature and pressure stabilized, the precision injection pump (Teledyne ISCO, Inc., Lincoln, NE, USA; the flow rate range is 0.1–30 mL/min, the accuracy of 0.3% FS) and the check valve system were employed to deposit trace mineralized water droplets (simulated fracturing fluid, 1 wt% KCl,) very slowly onto the surfaces of coal and proppant samples, respectively [27]. A high-resolution digital camera (M230, Revealer, Hefei Zhongke Junda Vision Technology Co., Ltd., Hefei, Anhui, China; the resolution is 1920 × 1080) was utilized to record the droplet morphology in real time.

The captured droplet contour images were imported into ImageJ software (Version 1.8.0), where at least five discrete points were uniformly selected along the droplet gas–liquid interface contour. A best-fitted ellipse equation was then obtained. The contact angle (θ) for both coal and proppant under in situ reservoir conditions was determined by calculating the tangent angle between the fitted ellipse at the solid–liquid–gas three-phase contact point and the baseline of the solid sample surface. To ensure data reliability, three representative sites were selected on the non-edge surface of each sample at positions >200 μm from the boundary. Each site was measured three times repeatedly, and the average value of 9 sets of data is taken as the final result.

2.2. Mixed Wettability Gradient Modeling and Numerical Implementation

2.2.1. Governing Equation

The gas–water displacement process in mixed wettability fractures is modeled using the phase-field method to capture the gas–liquid interface evolution [29]. This method treats interfacial tension and capillary forces through continuum assumptions, thereby avoiding the computational bottleneck associated with explicit interface tracking [30]. It is especially suitable for numerically characterizing both the microscale capillary force gradient and dynamic competitive behavior of the three-phase contact line induced by wettability differences [31]. Based on the laws of mass and momentum conservation, incompressible fluid motion is described by the modified Navier–Stokes equations [32]:

$$\rho \left({\displaystyle \frac{\partial u}{\partial t}}+u\times \nabla u\right)=-\nabla p+\nabla \cdot \left(\eta \left(\nabla u+{\left(\nabla u\right)}^T\right)\right)+\sigma \nabla \varphi +F_{ext}$$

(1)

$$\nabla \cdot u=0$$

(2)

where ρ is the fluid density, kg/m³, ρw = 998 kg/m³, ρg = 1.2 kg/m³; u is the velocity field, m/s; t is the time, s; p is the fluid pressure, Pa; η is fluid viscosity, Pa·s, η_w = 1.0 × 10⁻³ Pa·s, η_g = 1.8 × 10⁻⁵ Pa·s; σ is a parameter for controlling the surface tension of the interface; ϕ is the Phase field variables; F_ext is the external volume force, N/m³.

The phase field variable ϕ ϵ [−1, 1] follows the extended form of Cahn-Hilliard theory [33]:

$${\displaystyle \frac{\partial \varphi }{\partial t}}+u\cdot \nabla \varphi =\nabla \cdot \left({\displaystyle \frac{M\lambda }{{\epsilon }^2}}\nabla \mu \right)$$

(3)

$$\Psi =-\nabla \cdot \left({\epsilon }^2\nabla \varphi \right)+\varphi \left({\varphi }^2-1\right)+{\displaystyle \frac{\epsilon }{\sqrt{2}}}cos{\theta }_w\left(x\right)$$

(4)

where ᴪ is the phase field auxiliary variable; M is the mobility, set to 1; μ is the chemical potential, defined as the variational derivative of the free energy functional, J/m³; λ is the mixed energy density; ε is the interface thickness parameter, m, automatically set to half the grid width; θ_w(x) is a space-dependent contact angle distribution function.

Considering the influence of wall wettability, the solid boundary condition is applied via the contact angle θ_w:

$${\displaystyle \frac{\partial \varphi }{\partial t}}+u\cdot \nabla \varphi =\nabla \cdot \left({\displaystyle \frac{M\lambda }{{\epsilon }^2}}\nabla \mu \right)$$

(5)

$$\Psi =-\nabla \cdot \left({\epsilon }^2\nabla \varphi \right)+\varphi \left({\varphi }^2-1\right)+{\displaystyle \frac{\epsilon }{\sqrt{2}}}cos{\theta }_w\left(x\right)$$

(6)

where θ_w is the contact angle; and n is the unit normal to the solid surface.

The mixing energy density λ is related to the surface tension coefficient σ as

$$\lambda ={\displaystyle \frac{3\epsilon \cdot \sigma }{2\sqrt{2}}}$$

(7)

The interface thickness parameter ε is generally defined as

$$\epsilon =2h_c$$

(8)

where h_c is the size of the feature mesh in the region through which the interface passes.

$$M={\epsilon }^2$$

(9)

The free energy density function quantitatively characterizes the mechanical state of the system by combining the bulk free energy and the interfacial energy term [34]. In the mixed wettability system of this study, the interfacial tension σ is the dominant factor governing the gas–liquid interface dynamics, as it directly determines the capillary force difference between the proppant and coal bridge surfaces, which has been quantitatively correlated with the mixing energy density λ through Equation (5), thereby directly reflecting the modulating effect of wettability modification on interfacial energy. Thus, to simplify the computation and enhance the intuitiveness of the physical parameters, this study specifically simplifies the interfacial energy term by directly employing the interfacial tension σ to characterize its primary influence. The resulting free energy density function is expressed as follows [35]:

$$f\left(\varphi \right)={\displaystyle \frac{\epsilon }{4}}{\left({\varphi }^2-1\right)}^2+{\displaystyle \frac{\sigma }{2}}{\left|\nabla \varphi \right|}^2$$

(10)

The volume fractions V_f1 for the displacing gas phase and V_f2 for the displaced liquid phase are defined based on the phase-field variable ϕ as [36]:

$$V_{f1}={\displaystyle \frac{1-\varphi }{2}}$$

(11)

$$V_{f2}={\displaystyle \frac{1+\varphi }{2}}$$

(12)

$$V_{f1}+V_{f2}=1$$

(13)

Density and viscosity across the gas–liquid interface are calculated via the volume fraction weighted average method, expressed as:

$$\rho ={\rho }_1{V}_{f1}+{\rho }_2{V}_{f2}$$

(14)

$$\eta ={\eta }_1{V}_{f1}+{\eta }_2{V}_{f2}$$

(15)

where ρ₁ and η₁ are density and viscosity of the gas phase, respectively; ρ₂ and η₂ are the density and viscosity of the liquid phase, respectively.

2.2.2. Model Assumes That

A wettability difference exists between the coal bridge and the proppant, and the wettability of the proppant changes significantly after modification with the silane coupling agent KH-570. This creates a mixed wettability environment and produces two configurations: lateral proppant aggregation and mid-proppant aggregation [37]. This study aims to investigate the influence of the aforementioned wettability difference distribution pattern on gas–water two-phase flow. Accordingly, the reservoir microstructure is simplified as a homogeneous porous medium composed of circular particles and pores, with the following assumptions applied to the model:

• The porous medium consists of uniformly arranged circular particles with different surface wettability, ignoring the heterogeneity of particle size and geometry;
• The flow system is immiscible gas–liquid two-phase, without material exchange and chemical reaction between the two phases, corresponding to the displacement relationship between coalbed methane and fracturing fluid during fracturing fluid backflow;
• Fluid is an incompressible Newtonian fluid, and its flow follows the Navier–Stokes equations [38]. The phase field model satisfies the continuum assumption;
• The coal bridge skeleton is a rigid structure, and the pores have no stress-sensitive deformation [39]. This model does not consider the stress-sensitive effect [40].

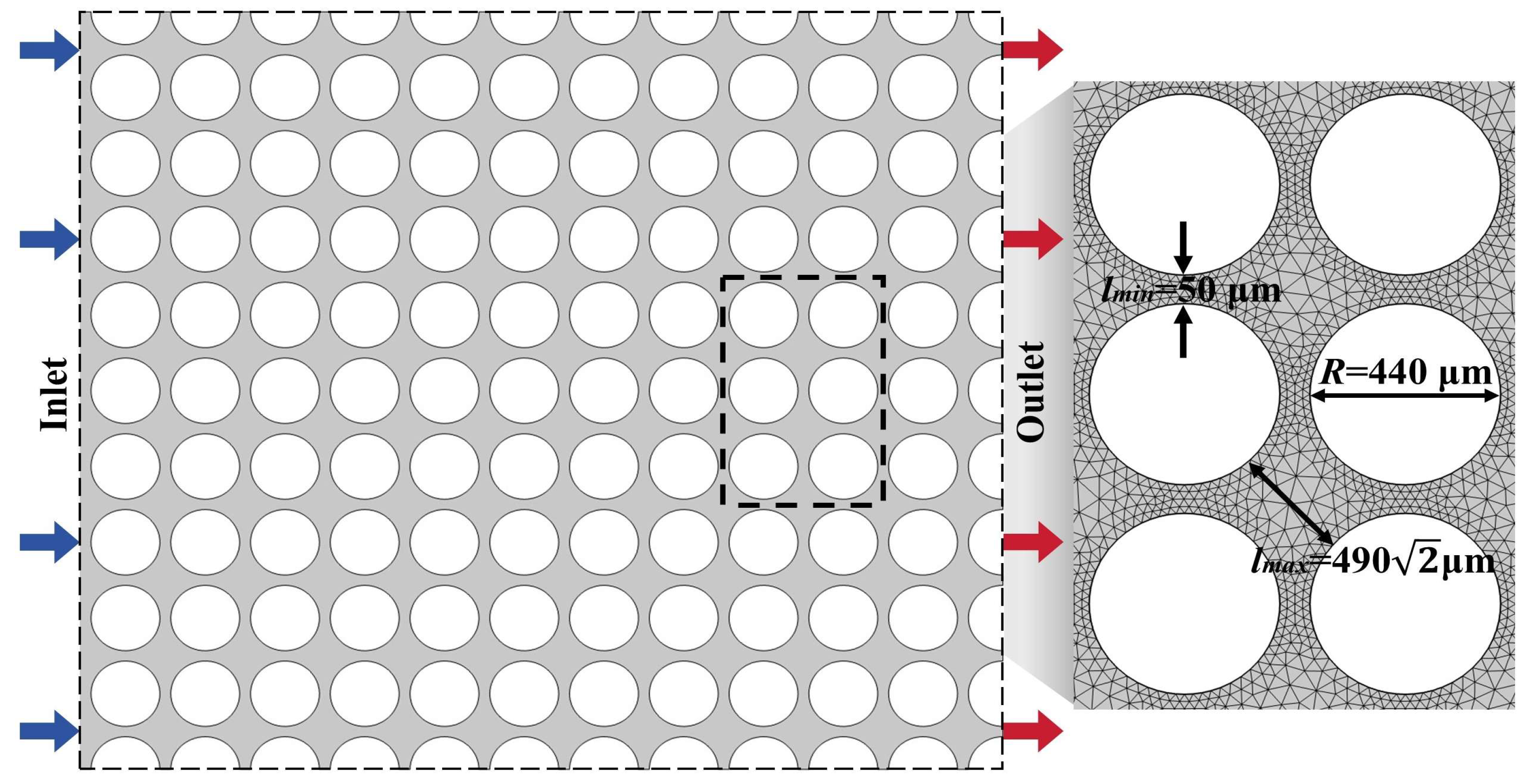
2.2.3. Wettability Modeling and Meshing

To accurately characterize the seepage environment and mixed wettability characteristics of residual proppant particles within coal fractures, this study establishes a geometric model of microscale periodic lattice porous media using the COMSOL Multiphysics platform (Version 6.2). The model calculation domain is a rectangular region measuring 5600 μm × 4900 μm, containing regularly arranged circular and semi-circular solid units with a radius of 220 μm. The minimum spacing between units is controlled at 50 μm, forming continuous pore spaces between the units. Through geometric parameter optimization, the porosity was determined to be 0.637. This model abstracts the real multi-scale fracture network topology characteristics of coal reservoirs, and enables the controllable parametric simulation of proppant retention state while preserving the natural connectivity of pore-throat structures [41].

The spatial heterogeneity of proppant distribution within fractures is achieved using the Poisson disk distribution algorithm to generate a random seed lattice satisfying a minimum spacing constraint. By controlling the areal density of the lattice plane, the proppant domain area proportion is maintained at 21.7% in both unilateral accumulation and centralized proppant aggregation patterns, thereby matching the representative scenario of local enrichment of proppant in fracturing engineering and ensuring consistency in quantitative comparison benchmarks [42]. After spatial identification, the selected solid units are assigned the wettability properties of the proppant, while the unidentified units retain the inherent wettability of the coal bridge, thereby quantifying the regulatory mechanism of wettability gradients on the gas–liquid interface dynamics. Combined with actual retention patterns, the model establishes two characteristic proppant spatial distribution patterns: The Lateral Proppant Aggregation (L-A) Pattern constrains over 60% of the identified points to the upper 1/3 width interval of the rectangular domain, forming an asymmetric proppant network near the unilateral wall. The Centralized Proppant Aggregation (C-A) Pattern constrains over 60% of the identified points to the central 40% width range, generating a band-like aggregation zone along the flow channel centerline, as shown in Figure 3 [43]. Both patterns accurately replicate the physical essence of the mixed wettability environment between coal bridges and proppants within fracturing fractures through spatially constrained random identification and differential wettability assignment.

Due to the significant scale difference in the pore structure, with a large span between the maximum characteristic size (l_max = 490$\sqrt{2}$ μm) and the minimum characteristic size (l_min = 50 μm), a COMSOL geometry adaptive algorithm was employed for mesh discretization to balance computational accuracy and efficiency, as illustrated in Figure 4. To accurately capture the evolution dynamics of the gas–liquid interface, a local mesh refinement strategy is implemented in the throat regions. Meanwhile, a moderately coarsened mesh is used in the pore regions to effectively reduce computational resource consumption. Triangular elements are chosen as the mesh elements, providing adequate adaptation to the geometric features of circular solid boundaries. A mesh independence study confirms that when the number of elements exceeds 70,000, the error in the gas–water displacement front velocity is less than 2%. The final model generates approximately 120,000 mesh elements, ensuring both interfacial tracking accuracy and computational stability requirements.

To address the micro-scale characteristics of coal seam fracture throats, local mesh refinement is prioritized in these regions during the mesh design phase. This strategy not only resolves flow dominated by capillary forces in the throat but also mitigates the critical limitation of the standard Cahn-Hilliard model, which employs a constant mobility parameter M = 1. In high-curvature zones—such as proppant gaps and narrow throats—constant mobility often induces non-physical interface shrinkage, leading to local mass loss and potentially biased estimates of residual saturation. To improve interfacial accuracy and ensure mass conservation, a curvature-dependent mobility scheme was adopted, where M(ϕ) is reduced adaptively in high-curvature regions. This approach effectively suppresses artificial shrinkage while preserving global mass conservation and energy dissipation, offering superior accuracy in capturing gas–water interface behavior in throat structures without resorting to excessive mesh refinement or complex adaptive techniques. The expression used is [44]:

$$M\left(\varphi \right)={\displaystyle \frac{{\varphi }^2}{1+{\gamma }_c\left|\nabla \cdot \left(\frac{\nabla \varphi }{\left|\nabla \varphi \right|}\right)\right|}}$$

(16)

where γ_c is the curvature sensitivity coefficient.

2.2.4. Model Boundary Setting

The left side of the model serves as the inlet for gas–liquid two-phase flow, featuring a 150 μm-wide injection buffer zone. A constant velocity boundary condition was applied at the inlet to inject fracturing fluid, with the velocity(v) set between 1.98 × 10⁻⁴ and 6.12 × 10⁻² m/s. The right side functions as the outlet, where a constant pressure boundary condition is applied, with the outlet pressure set to 6.18 MPa, corresponding to the reservoir’s static pressure gradient. The top and bottom boundaries are assigned symmetric no-slip boundary conditions to simulate the infinite extension of the fracture environment. In the phase-field model, the interface mobility parameter M is set to 1, and the interface thickness control parameter ε is defined as twice the minimum mesh size in regions traversed by the interface to accurately capture interfacial evolution dynamics [45]. Additionally, a wettability no-slip boundary condition is applied on the surfaces of the proppant particles, where the normal velocity component of the fluid at the wall surface is 0.

This model aims to simulate the coalbed methane extraction process with proppant retained in coal fractures. To achieve spatial heterogeneity in wettability, seed points following a Poisson disk distribution are randomly generated within the model domain to represent the spatial locations of proppant particles. Accordingly, the wettability characteristics of the wall boundary (∂Ω) must be defined to quantify the regulatory effect of wettability differences between the proppant and coal surfaces on gas–liquid interface behavior. This can be implemented as follows:

The surface energy density function f_w(ϕ) is introduced at the solid boundary, and the boundary conditions are defined [46]:

$$f_w\left(\varphi \right)=-{\gamma }_w\cos {\theta }_e\cdot \varphi$$

(17)

$$\sigma n\cdot \nabla \varphi -{\gamma }_w\cos {\theta }_e=0$$

(18)

where θ_e is the contact angle of the solid–liquid–gas three-phase equilibrium, which is used to define the wall wettability; γ_w is the wall energy coefficient.

2.3. Model Verification

To obtain key boundary conditions for the model and verify its reliability, this study first measured the contact angles of coal bridge, unmodified proppant, and modified proppant under in situ reservoir temperature and pressure conditions (6.18 Mpa, 307.65 K). The results indicate that the coal bridge surface exhibits weak hydrophilicity with θ = 73.3°, while the unmodified proppant shows strong hydrophilicity with θ = 46.5°. In contrast, the contact angle of the proppant modified with the silane coupling agent KH-570 significantly increased to 88.7°, indicating enhanced hydrophobicity and a transition to neutral wettability [47]. This wettability transition parameter serves as a crucial boundary condition in the mixed wettability model. The measured contact angle value (88.7° for the modified proppant) was directly assigned as an input parameter for subsequent displacement simulations, thereby characterizing the changes in interfacial behavior resulting from the transition of the proppant surface in the mixed wettability model from strong hydrophilicity to neutral wettability.

To verify the accuracy of the numerical model, this study simulated the gas–liquid interface behavior on three representative interfaces (coal bridge, unmodified proppant, and modified proppant) using the phase-field method, based on the aforementioned in situ contact angle measurements. The numerical results demonstrate high consistency with observations from high-temperature and high-pressure experiments. On the unmodified hydrophilic proppant surface, the mineralized water exhibited significant spreading morphology, whereas on the modified proppant surface, it demonstrated dynamic characteristics of retraction. The droplet on the coal bridge surface assumed a near-spherical morphology. The errors between simulated and measured contact angles were all less than 2%, as illustrated in Figure 5. This high level of agreement confirms that the phase-field method accurately captures the regulatory mechanisms of wettability differences on gas–liquid interfacial behavior under high-pressure conditions, thereby establishing a physically realistic numerical foundation for subsequent gas–water displacement simulations controlled by capillary number [48].

2.4. Numerical Simulation Experiment Design and Execution

To investigate the influence of proppant spatial distribution patterns and capillary numbers on coalbed methane-water displacement, this study established an integrated numerical workflow, as illustrated in Figure 6. Based on the microstructural characteristics of coal fractures, a porous media model was constructed incorporating two proppant distribution patterns reflective of realistic retention behavior. The model was initialized using measured contact angles, fluid properties, and boundary conditions, employing an improved phase-field method to capture gas–liquid interface dynamics and fluid migration. Systematic simulations were conducted for both unmodified hydrophilic and modified neutral-wet proppants under each distribution pattern, with the logarithmic capillary number (lgCa) varied from −5.61 to −3.12 to cover capillary- to viscous-dominated flow regimes.

The dynamic evolution of the gas phase volume fraction was monitored to analyze displacement pathways and residual fracturing fluid distribution. After the system stabilized, the gas distribution was processed using ImageJ: binarization with optimized thresholds enhanced phase contrast, and the Analyze Particles algorithm was employed to quantify the residual liquid area fraction for determining residual saturation (S_rw) as well as to analyze the geometric characteristics of residual clusters. Regions adjacent to the outlet were excluded to minimize end effects. Detailed results for each combination of conditions are presented in the Results and Analysis section.

3. Results and Analysis

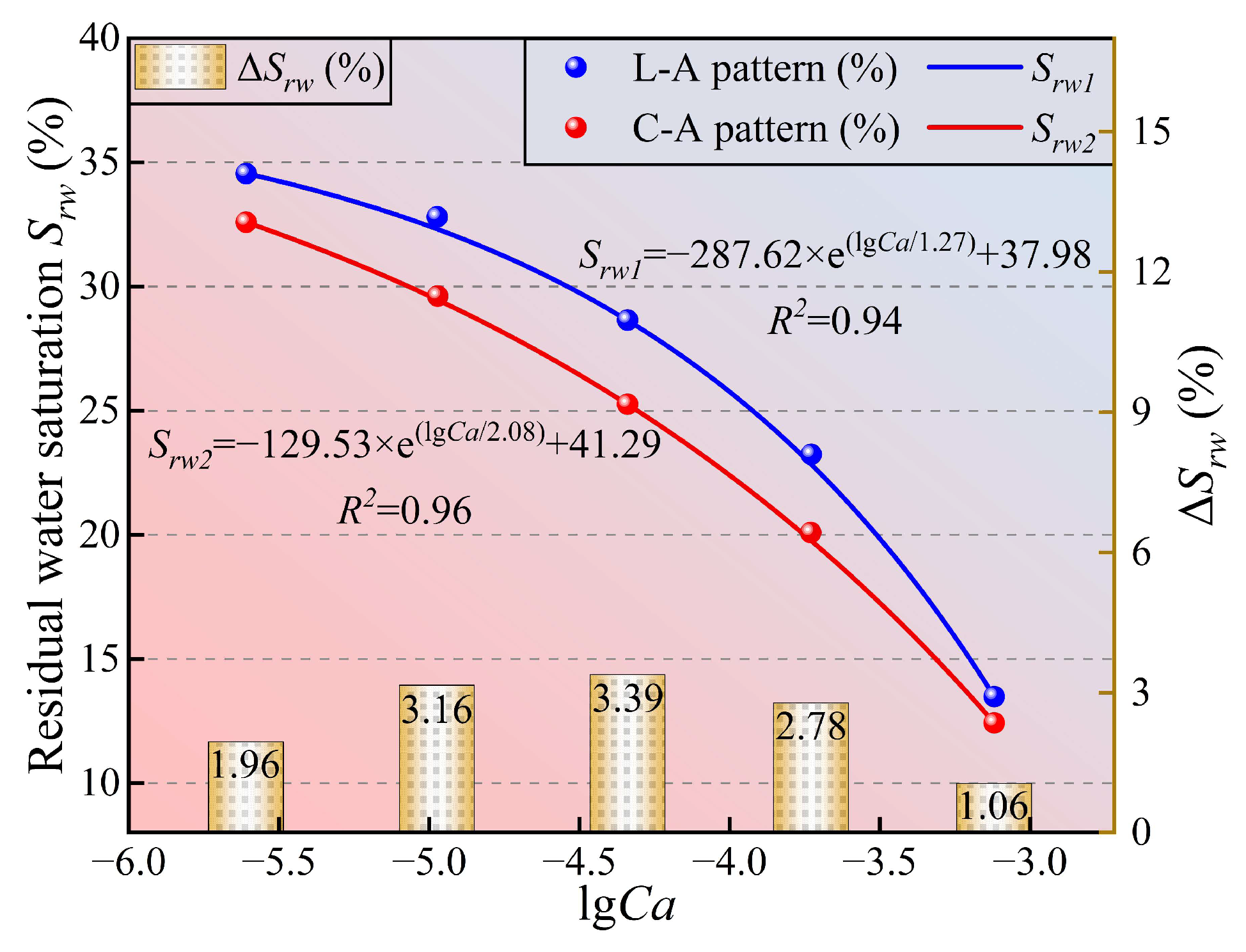
3.1. The Influencing Mechanism of Proppant Spatial Aggregation Patterns on Fracturing Fluid Flowback

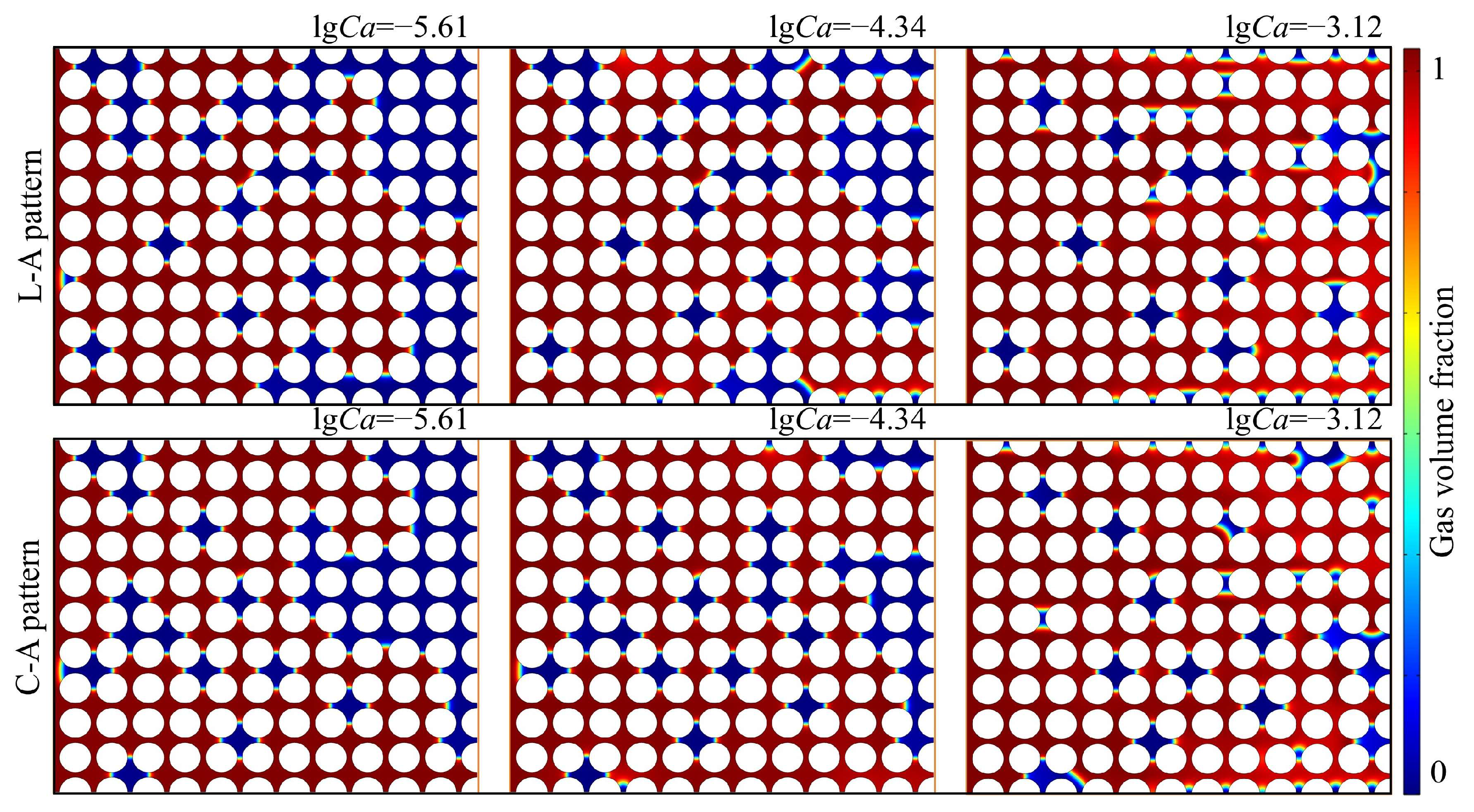
3.1.1. The Influence Law of Coal Bridge-Hydrophilic Proppant on Displacement Path

The proppant exhibits strong hydrophilicity under in situ conditions, with a measured contact angle of 46.5°. The flowback behavior of fracturing fluid at different capillary numbers is shown in Figure 7. When lgCa is −5.61, in the L-A pattern, the strongly hydrophilic proppant promotes the formation of a continuous liquid film retention zone within the particle clearance, resulting in an S_rw of 34.55%. The gas phase can only break through via a narrow central channel, demonstrating significant heterogeneous displacement characteristics. In the C-A pattern, the fracturing fluid is constrained through capillary forces to form a continuous liquid film within the central proppant accumulation zone near the outlet, forcing the gas to flow through a narrow gap along the lower side, which was unobstructed by proppant, resulting in an S_rw of 32.7%. When lgCa increases to −4.34, although the gas phase in the L-A pattern can penetrate the mid-lower flow channels, the coupling influences of hydrophilicity and gravity still maintain a wide retention zone, reducing S_rw to 28.65%. The C-A pattern demonstrated superior liquid flowback efficiency, with the gas phase rapidly breaking through both side flow channels while the liquid phase retreated to the edge regions. The S_rw decreased to 25.1%, which is 3.2 percentage points lower than that of the L-A pattern. When lgCa reached −3.12, the flowback process was dominated by viscous forces. Under this condition, the C-A pattern exhibited an almost complete fracturing fluid displacement effect, with the S_rw decreasing to as low as 12.44%, significantly outperforming the L-A pattern in flowback efficiency. The S_rw in both patterns followed an exponential decay law as lgCa increased, with the coefficient of determination (R²) reaching 0.94 and 0.96, respectively, which indicates a highly statistically significant trend, as illustrated in Figure 8.

The differences in displacement pathways primarily stem from the coupled regulatory mechanisms of proppant hydrophilicity and its spatial distribution characteristics. In the L-A pattern, the compression effect within the flow channel enhances capillary retention, leading to the formation of a continuous liquid film retention zone under low lgCa conditions. In contrast, the C-A pattern optimizes the distribution of displacement forces through its symmetrical flow channel layout, effectively reducing spatial variations in capillary forces and resulting in residual liquid remaining as dispersed patches. As lgCa increases, the dominant influence of viscous forces gradually strengthens, effectively weakening capillary trapping effects and promoting more efficient fracturing fluid flowback. By improving the spatial distribution pattern of the proppant, the C-A pattern significantly enhances the displacement efficiency of gas–liquid two-phase flow, providing an essential theoretical foundation for fracturing optimization.

3.1.2. Effect of Coal Bridge-Modified Proppant on Displacement Path

The neutral wettability-modified proppant, with a contact angle of 88.7°, exhibited distinctly different spatial displacement behaviors in the L-A and C-A patterns, with their evolution observed as lgCa increased from −5.61 to −3.12, as illustrated in Figure 9. When lgCa is −5.61, under the L-A pattern, the neutral wettability surface suppressed liquid spreading and adsorption by reducing the solid–liquid interfacial energy. The fracturing fluid was retained as discrete clusters within the gaps between proppant particles and along the edges on both sides of the model, resulting in an S_rw of 33.86%. Meanwhile, the gas phase broke through via a narrow central channel, forming a displacement front with a “convex edge flat” morphology. In the C-A pattern, the liquid distribution was more dispersed, forming isolated patches around the proppants and accumulating into large clusters at the outflow section edge, leading to an S_rw of 30.16%. When lgCa increased to −4.34, in the L-A pattern, the gas phase accelerated the penetration of the proppant aggregation side flow channel through hydrophobic repulsion, displacing the liquid into smaller clusters that retracted to the outflow end and corners, reducing the S_rw to 22.63%. In contrast, the C-A pattern demonstrated enhanced global displacement capability, with the residual liquid remaining as fragmented patches on proppant surfaces and edge pore throats, further lowering the S_rw to 15.35%—a difference of 7.28% between the two patterns. When lgCa is −3.12, the C-A pattern achieved nearly complete fracturing fluid displacement, with an S_rw as low as 5.87%, which is 20.9% lower than the 7.42% observed in the L-A pattern, demonstrating superior flowback efficiency. The S_rw in both distribution patterns follows an exponential decay with increasing lgCa, with the coefficient of determination (R²) ranging from 0.96 to 0.95, as illustrated in Figure 10.

Analysis of the displacement mechanism reveals that the modified proppant reverses the direction of capillary action through interfacial repulsion, working synergistically with the spatial distribution pattern. In the L-A pattern, the top band-like aggregation of modified particles creates a local repulsion concentration area. As lgCa increases, the local superposition of viscous and repulsive forces accelerates the retraction of the liquid phase. In contrast, the C-A pattern achieves a global coupling of repulsive and viscous forces due to its flow channel symmetry, promoting the fragmentation and detachment of the liquid phase. Notably, when lgCa is −3.12, owing to its superior uniformity of displacement force transmission, the displacement efficiency far surpasses that of the L-A pattern. Under relatively high capillary number conditions, the C-A pattern optimizes the spatial distribution of displacement forces, sharply reducing the cluster count by 66.7% and achieving a minimum S_rw of 5.87%, thereby verifying the engineering superiority of the ternary synergistic mechanism of “wettability-spatial distribution-displacement force”.

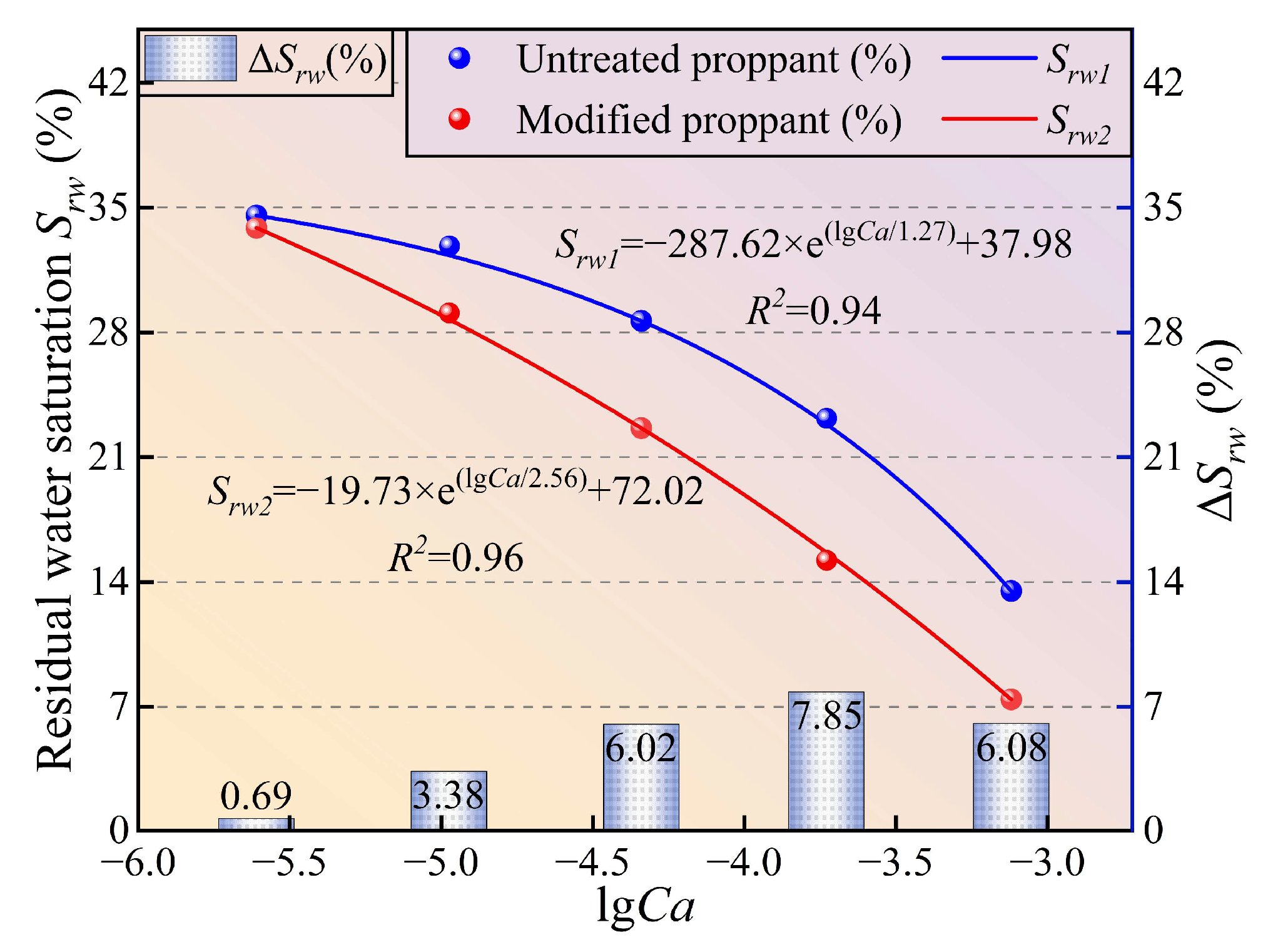
3.2. The Influence Mechanism of Proppant Modification on Fracturing Fluid Flowback

3.2.1. Distribution Characteristics of Residual Phase of Fracturing Fluid in Hydrophilic Proppant

In the L-A pattern, the wettability of the proppant and the asymmetric flow channel structure are deeply coupled, jointly determining the evolution of S_rw with the capillary number. For the strongly hydrophilic proppant, when lgCa is −5.61, the flow channel compression effect significantly enhances local capillary trapping. Synergizing with the strong hydrophilic adsorption on the proppant surface, this promotes the formation of a continuous liquid film on the aggregation side, resulting in the initial S_rw as high as 34.55%, as illustrated in Figure 11. Even when lgCa increases to −3.12 and viscous forces gradually dominate, the residual liquid trapped in particle clearances due to strong solid–liquid adhesion remains difficult to displace effectively, causing the S_rw to decrease only slowly to 13.5%. In contrast, neutral wettability proppants exhibit distinct behavior. With a contact angle of 88.7°, at the hydrophilic-hydrophobic balance point, they effectively reduce interfacial energy, disrupt liquid film continuity, and significantly weaken the capillary adsorption force. When lgCa is −5.61, this effectively inhibits the formation of a continuous retention zone, resulting in an initial S_rw of only 33.86%. As Ca continues to increase, especially after lgCa reaches −4.34, the asymmetric flow channel structure directionally guides and amplifies the synergistic effect between viscous forces and hydrophobic repulsion, significantly accelerating liquid phase retraction. The S_rw eventually decreases sharply to 7.42%, representing an overall reduction of 45.1% compared to the hydrophilic system, highlighting the significant advantage of neutral wettability. The crux of this difference lies in the fact that weak hydrophilic modification fundamentally reverses the functional role of the proppant: from promoting capillary retention to driving liquid phase detachment.

The dynamic displacement process further reveals the timeliness characteristics of wettability control. When lgCa is −4.34, corresponding to the transition stage of displacement, the S_rw in the neutral wettability system stabilizes at 22.63%, which is 21.01% lower than that in the hydrophilic system. Dynamic analysis demonstrates that the continuously applied interfacial repulsion by the neutral wettability surface effectively disrupts the retention stability of the liquid phase within particle gaps, promoting faster liquid phase detachment. Simultaneously, the asymmetric flow channel structure optimizes the force field distribution, enhancing the efficient synergy of viscous forces and interfacial repulsion in space. In the modified system, liquid clusters exhibit an accelerating contraction trend, with breakthrough occurring significantly earlier, as illustrated in Figure 12. In contrast, the hydrophilic system exhibits strong surface adsorption that delays liquid migration, resulting in prolonged residual phase retention and a higher final saturation value. The consistency between dynamic and static characteristics indicates that within the L-A pattern, neutral wettability modification operates through dual mechanisms of “interface repulsion drive” and “topological effect amplification.” This approach not only significantly reduces the ultimate S_rw by 45% but also shortens the displacement cycle, providing a crucial theoretical basis for optimizing proppant wettability design.

3.2.2. Distribution Characteristics of Residual Phase of Fracturing Fluid in Modified Proppant

The symmetrical flow channel topology of the C-A pattern is deeply coupled with wettability, governing the evolution of S_rw by promoting the equilibrium distribution of displacement forces. For the hydrophilic proppant, S_rw decreased only gradually from 32.59% to 12.44% as the capillary number increased. In contrast, the modified proppant exhibited a sharp reduction in S_rw from 30.16% to 5.87%, representing a reduction of 1.2 times that of the hydrophilic group, as illustrated in Figure 13. This disparity stems from the central function of symmetric flow channels: their uniform flow environment effectively suppresses local distortions in capillary forces, providing an ideal setting to enhance the synergistic effects of neutral wettability modification. When interfacial repulsion disrupts the liquid film continuity, symmetric topology transfers displacement forces through equalization, synergistically weakening capillary trapping and systematically reducing the risk of residual phase retention. Compared to the L-A pattern, the C-A pattern eliminates the retention enhancement effect caused by flow channel compression, thereby enhancing the optimization efficacy of neutral wettability modification on S_rw by a factor of 1.55, underscoring the global amplification effect enabled by topological symmetry.

The breakthrough moment is a crucial point in fracturing fluid flowback, marking the formal establishment of coalbed methane dominant seepage paths. At this stage, the S_rw drops sharply to 15.35%, which is 9.91 percentage points lower than that of the hydrophilic system, corresponding to a relative reduction of 39.2%. Meanwhile, no secondary retention phenomenon is observed after breakthrough, indicating that the symmetric structure combined with neutral wettability modification effectively prevents secondary fracturing fluid retention during the middle and late flowback stages, ensuring flowback process stability, as illustrated in Figure 14. This rapid and stable displacement is attributed to the spatiotemporal synergy between symmetric flow channels and interfacial repulsion. The balanced flow environment effectively suppresses local liquid accumulation, while the neutral wettability surface continuously disrupts liquid film continuity by reducing interfacial energy, jointly accelerating liquid phase migration. Notably, in the displacement crucial zone, the S_rw of the neutral wettability system has already decreased to 20.26%, outperforming the final values of other combinations and confirming its integrated advantage of “rapid breakthrough-efficient displacement”. Compared to the final S_rw in the L-A pattern, the C-A pattern avoids asymmetric retention effects through symmetric topology, fully releasing the potential of neutral wettability modification and establishing a profound synergistic mechanism of “dynamic equilibrium distribution-interface repulsion drive”.

3.3. Cross-Scale Collaboration Mechanism

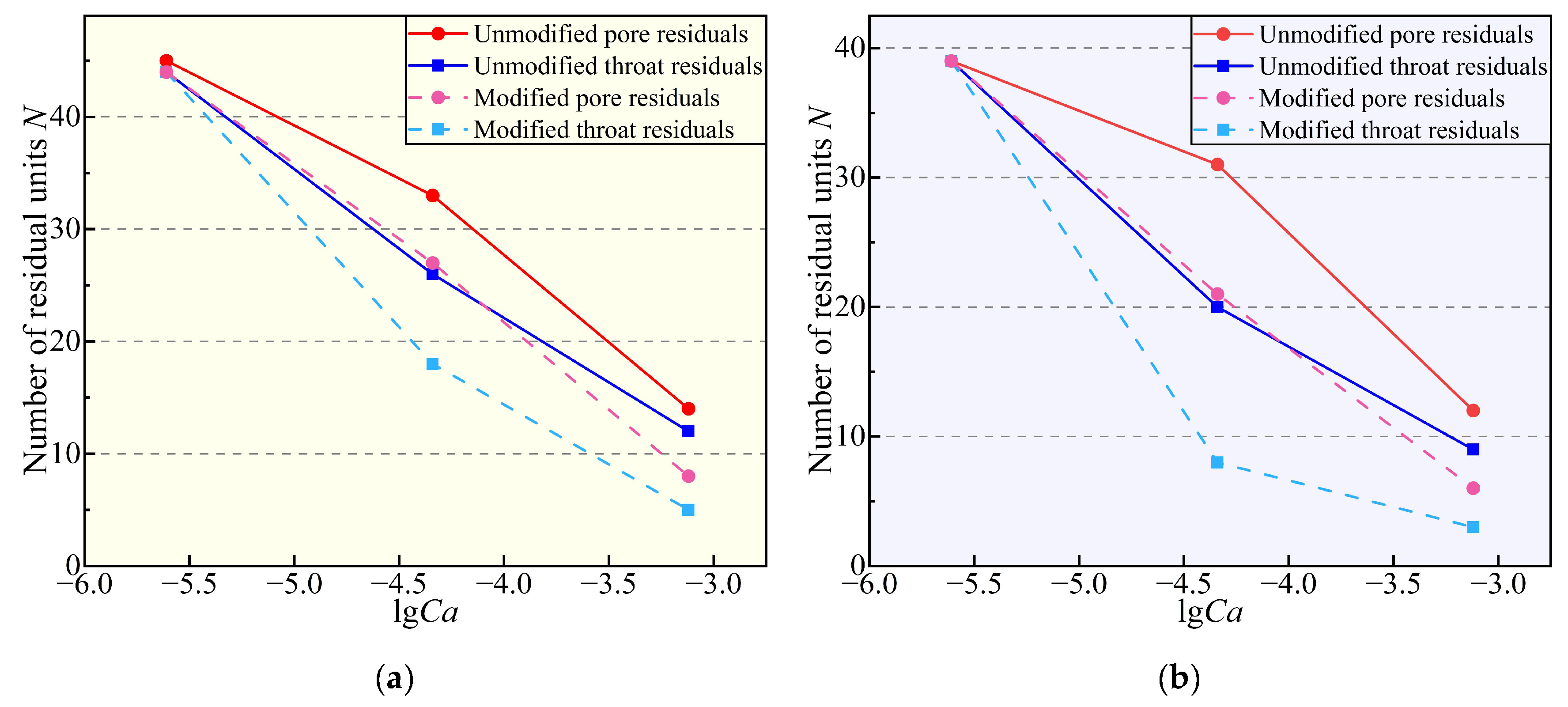
3.3.1. Local Distribution Characteristics of Pore-Throat Scale Residual Phase

This study reveals a cross-scale synergistic mechanism between proppant wettability and spatial distribution, as shown in Figure 15. Within microscale throat spaces, neutral wettability modification exhibits a significant scale-dependent effect: in the L-A pattern, the amount of residual liquid in throats decreased by 30.8% compared to the hydrophilic state, whereas in the C-A pattern, the reduction reached 60%, which is 2–3 times greater decrease than the reduction in the number of residual phases within its own pores. This difference in scale effects stems from the unique micro-nano constraint characteristics of throats—in these narrow geometric spaces, the solid–liquid interfacial energy accounts for over 70% of the total energy. When the contact angle approaches 90°, indicating neutral wettability through modification, the capillary resistance in throats exhibits nonlinear attenuation in response to changes in interfacial tension. The strong geometric constraint effect in throats amplifies wettability control through two pathways: the capillary pressure gradient increases exponentially as the curvature radius decreases, while the sensitivity of gas–liquid interface curvature variations becomes significantly enhanced in confined spaces.

The scale differentiation phenomenon of pore throat decline confirms that the key to efficient coalbed methane displacement lies in the deep coupling between microscopic interface regulation and macroscopic seepage field reconstruction. At the microscopic level, the throat constraint effect results in a multiplication effect of the reduction in capillary resistance achieved through neutral wettability modification. At the macroscopic level, the symmetric flow channel structure of the C-A pattern optimizes the spatial distribution of displacement forces, effectively suppressing local capillary force distortion. Through their synergistic effect, the interfacial energy regulation is ultimately transformed into a breakthrough 60% reduction in residual phase within throats under the C-A pattern, providing multiscale theoretical support for a dual-target optimization strategy of “neutral wettability modification + central symmetrical placement” of proppants.

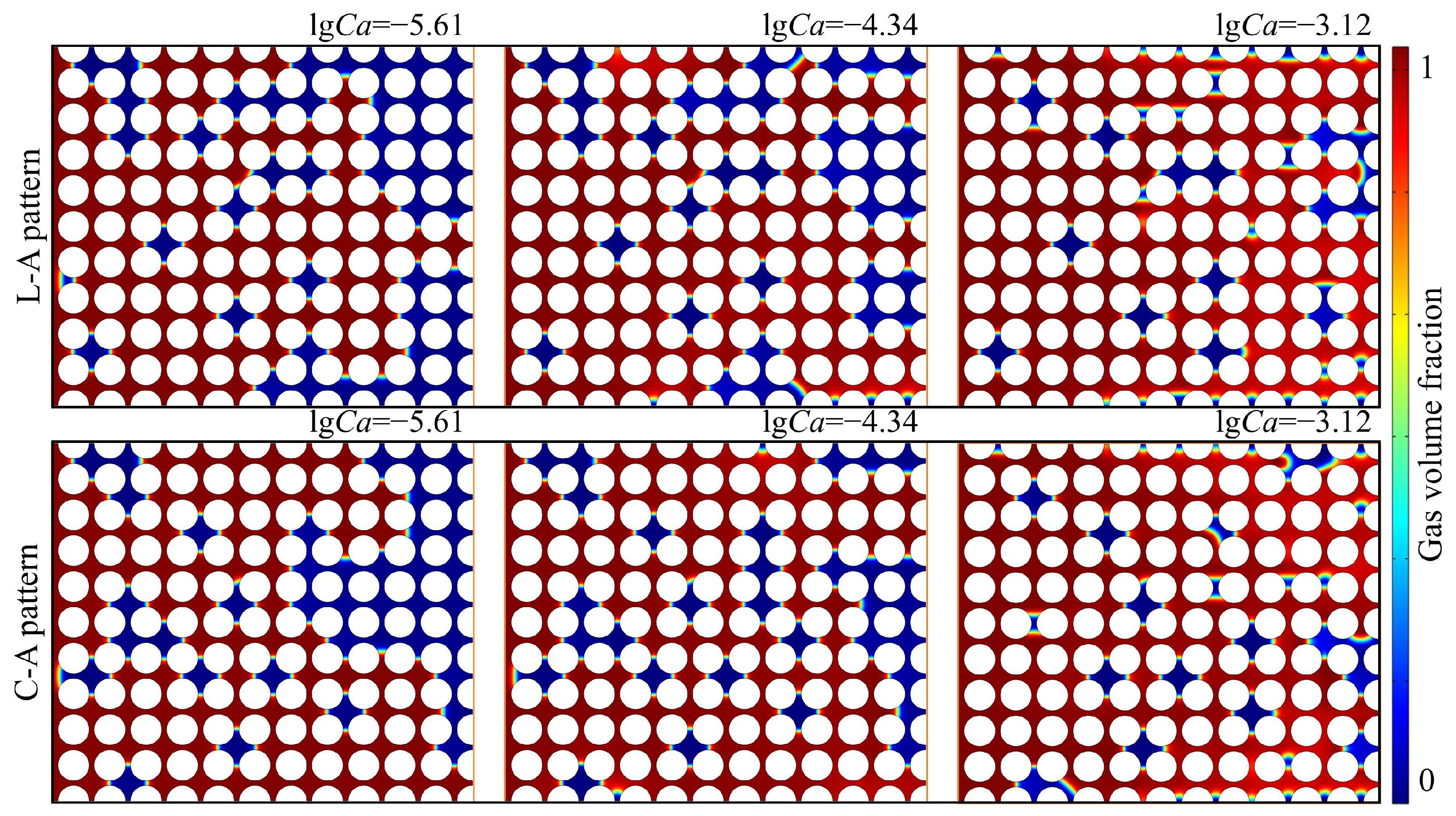
3.3.2. The Influence of Capillary Number on the Local Distribution of Residual Phase

In the L-A pattern, the spatial heterogeneity of displacement forces caused by the asymmetric flow channel structure significantly enhances local capillary trapping effects, which profoundly limits the efficacy of wettability optimization. The number and maximum characteristic radius of clusters under different operating conditions were calculated using Equations (19) and (20), as illustrated in Figure 16. When lgCa is −5.61, the strongly hydrophilic proppant, due to its high solid–liquid interfacial energy, drives the liquid phase to form a continuous, large-scale retention zone on the aggregated side, with a maximum cluster radius of 678.8 μm and a cluster count of 11, consistent with the hydrophilic-enhanced liquid film binding mechanism described in this study. Although the neutrally modified proppant effectively reduces the interfacial adsorption energy barrier, resulting in a slight reduction in the maximum radius to 653.2 μm, the asymmetric topology severely hinders the effective transmission of interfacial repulsion. Consequently, the cluster count remains at 10, and the system remains in an aggregated state. This clearly reveals the rigid constraint imposed by the spatial distribution pattern on enhancing the wettability reversal interface. When lgCa increases to −3.12, although the modified system sharply reduces the cluster count to 4 and decreases the maximum radius to 320.3 μm through interfacial repulsion, the scale of the residual clusters remains 1.94 times larger than that observed in the C-A pattern. This fully illustrates that a single-target strategy relying solely on neutral wettability modification of proppants has inherent physical limitations in asymmetric flow fields, and its synergistic effect is constrained by the rigidity of the spatial distribution pattern.

$$r_i=\sqrt{{\displaystyle \frac{A_i}{\pi }}}$$

(19)

$$r_{\max }=\max \{r_1,r_2,\cdots ,r_N\}$$

(20)

where A is the residual liquid phase cluster area, μm²; and r is the radius of the cluster, μm.

In contrast, the C-A pattern achieves a more uniform spatial distribution of displacement forces through its symmetric flow channels, providing an ideal field for cross-scale synergy between wettability and capillary number. When lgCa is −5.61, the strongly hydrophilic system forms large network clusters with a maximum radius of 873.4 μm and a count of 11, highlighting the role of hydrophilicity in promoting continuous retention. In contrast, neutral modification immediately initiates a dynamic process dominated by interfacial repulsion, reducing the maximum radius to 815.4 μm while maintaining 11 clusters, indicating an initial reversal of capillary trapping. Most importantly, when lgCa reaches −4.34, the equilibrium shear stress field of the symmetrical flow field deeply couples with interfacial repulsion. The uniform flow distribution eliminates macroscopic capillary force distortion, enabling the interfacial repulsion effect—amplified by geometric constraints within microscopic throats—to propagate throughout the entire domain. This interaction drives a sharp reduction of 28.5% in the maximum radius to 358.3 μm and increases the cluster count to 12. When lgCa is −3.12, the uniform flow environment and interface repulsion generate a synergistic chain reaction: the macroscopically symmetric distribution pattern ensures distortion-free transmission of displacement forces, while the strong constraining effect in microscopic throats multiplies the undermining effect of neutral wettability on capillary resistance. This ultimately drives the residual fracturing fluid toward miniaturized dispersion, reducing the cluster count to 6 and sharply decreasing the maximum radius to 164.6 μm. This process addresses the central challenge in fracturing fluid flowback—“large cluster retention blocking throat”—and provides continuous channels for coalbed methane seepage. Through this deep cross-scale synergy, the reduction in cluster size achieved by neutral modification is 11 times greater than that observed in the L-A pattern, directly enabling residual liquid phase chain removal and a breakthrough S_rw as low as 5.87%. These results comprehensively verify the engineering superiority of the dual-target strategy combining symmetric proppant placement with surface neutral wettability modification.

To evaluate the advancement of the research results, the residual fracturing fluid saturation (Srw = 5.87%) obtained under the optimal conditions (central aggregation, neutral modification, lgCa = −3.12) in this study was compared with the recent literature. For instance, Zhang et al. reported a residual water phase saturation of approximately 15–25% in oil-wet to water-wet mixed-wettability fractures; Chu et al. obtained a minimum residual wet phase saturation of about 12% in wettability heterogeneous porous media [48,49]. Despite the differences in experimental systems and scales, the comparison shows that the Srw value (5.87%) achieved through the “wettability-spatial distribution” coordinated regulation in this study is significantly lower. This highlights the potential and engineering application value of the proposed strategy in minimizing the retention of fracturing fluids.

4. Conclusions

Through in situ wetting property tests under high temperature and high pressure and phase field simulations, this study has revealed the synergistic regulatory mechanism of the wetting properties, spatial distribution, and capillary number of the proppant during the backflow process of deep coal seam gas fracturing fluid. The main conclusions are as follows:

(1)

The spatial distribution of the proppant determines the backflow path and retention strength. Lateral aggregation enhances capillary trapping, with the residual fluid saturation reaching up to 34.55%, while central aggregation optimizes the distribution of driving force in the symmetrical flow channels, reducing the residual fluid saturation by 5.4% and making the driving front more uniform.

(2)

The modification of proppant wetting properties reverses the direction of interfacial forces. Neutral modification drives the fracturing fluid to detach through interface repulsion, which can reduce the residual fluid saturation by up to 52.8%, significantly improving the backflow efficiency.

(3)

The capillary number controls the exponential decay law of residual fluid saturation. The combination of central aggregation and neutral modification achieves the lowest residual fluid saturation (5.87%) at lgCa = −3.12, and the number of residual clusters decreases by 66.7%.

(4)

Microscopic throat constraints and macroscopic symmetrical structures have a cross-scale synergistic effect. Geometric constraints of throat geometry amplify the weakening effect of neutral modification on capillary resistance, while the macroscopic symmetrical structure inhibits local capillary trapping. The coupling of these two factors promotes the reduction of the maximum radius of residual clusters to 164.6 μm.

This study established a ‘wetting property–spatial distribution–capillary number’ cross-scale collaborative theory and proposed a dual-target optimization strategy of ‘neutral proppant wetting property modification + central symmetrical placement’. This provides a new theoretical framework and technical approach for the efficient fracturing design of deep coal seam gas wells.