Resolving Spatial Asymmetry in China’s Data Center Layout: A Tripartite Evolutionary Game Analysis

Abstract

The rapid advancement of artificial intelligence has driven a surge in demand for computing power. As the core computing infrastructure, data centers have expanded in scale, escalating electricity consumption and magnifying a regional mismatch between computing capacity and energy resources: facilities are concentrated in the energy-constrained East, while the renewable-rich West possesses vast, untapped hosting capacity. Focusing on cross-regional data-center migration under the “Eastern Data, Western Computing” initiative, this study constructs a tripartite evolutionary game model comprising the Eastern Local Government, the Western Local Government, and data-center enterprises. The central government is modeled as an external regulator that indirectly shapes players’ strategies through policies such as energy-efficiency constraints and carbon-quota mechanisms. First, we introduce key parameters—including energy efficiency, carbon costs, green revenues, coordination subsidies, and migration losses—and analyze the system’s evolutionary stability using replicator-dynamics equations. Second, we conduct numerical simulations in MATLAB 2024a and perform sensitivity analyses with respect to energy and green constraints, central rewards and penalties, regional coordination incentives, and migration losses. The results show the following: (1) Multiple equilibria can arise, including coordinated optima, policy-failure states, and coordination-impeded outcomes. These coordinated optima do not emerge spontaneously but rather depend on a precise alignment of payoff structures across central government, local governments, and enterprises. (2) The eastern regulatory push—centered on energy efficiency and carbon emissions—is generally more effective than western fiscal subsidies or stand-alone energy advantages at reshaping firm payoffs and inducing relocation. Central penalties and coordination subsidies serve complementary and constraining roles. (3) Commercial risks associated with full migration, such as service interruption and customer attrition, remain among the key barriers to shifting from partial to full migration. These risks are closely linked to practical relocation and connectivity constraints—such as logistics and commissioning effort, and cross-regional network latency/bandwidth—thereby potentially trapping firms in a suboptimal partial-migration equilibrium. This study provides theoretical support for refining the “Eastern Data, Western Computing” policy mix and offers generalized insights for other economies facing similar spatial energy–demand asymmetries.

1. Introduction

Artificial intelligence (AI) has become a primary driver of the digital economy. As the essential underpinning of AI, the scale and energy efficiency of computing capacity directly determine the pace and prospects of technological progress in this domain [1]. Following the emergence of generative AI applications such as ChatGPT and DeepSeek, use cases have expanded rapidly. Global demand for AI-training computing is reportedly quadrupling annually, outpacing many of the fastest technology adoptions in modern history. For example, it exceeds the peak growth of mobile phone adoption—roughly a doubling per year from 1980 to 1987—and installed solar capacity—about a 1.5× annual increase from 2001 to 2010 [2]. The China Academy of Information and Communications Technology (CAICT) predicts in the “In-depth Research and Future Development Trend Forecast Report on the Computing Power Industry from 2025–2030” that by 2028 China’s intelligent-computing capacity will exceed 3000 EFlops and account for roughly 35% of global AI computing, making China the world’s largest AI computing market. The surge in demand for computing power is driving substantial electricity consumption. Because data centers are the critical infrastructure that meets this demand, their expansion has intensified the challenge of high energy use. The International Energy Agency (IEA) projects that global electricity demand from data centers will rise from 415 TWh in 2024 to 945 TWh by 2030—a level exceeding Japan’s current annual electricity consumption [3]. Goldman Sachs Research forecasts that by 2030, global data center electricity demand will have increased by about 165% relative to 2023 levels. In the United States, consumption is expected to rise by roughly 130% from 2024 levels, reaching approximately 240 TWh [4]. In China, the situation is similarly severe. CAICT estimates that data centers consumed 150 billion kWh in 2022, representing approximately 1.5% of national electricity use. An IEEE-published study projects that this figure will surge to 400 billion kWh by 2030—around 4% of national electricity use—equivalent to the annual generation of five Three Gorges Dams [5]. This level of energy use imposes a substantial economic burden and severe environmental pressure. From an operating-cost perspective, electricity is among the largest expenses for data centers. According to the Open Data “Center Committee’s Data Center White Paper (2023)” published by the Open Data Center Committee (ODCC), electricity can account for 60–70% of total cost of ownership (TCO). Beyond the high economic costs, the environmental consequences are equally significant. Recent research indicates that, despite operational improvements and greater use of renewable energy—which could reduce greenhouse-gas emissions by up to 70%—the overall carbon footprint of data centers is still projected to be about 13% higher in 2030 than in 2020. Achieving net-zero will require additional mitigation and compensation mechanisms across the value chain [6]. The IEA estimates that, by 2030, data center emissions will account for about 1% of global CO₂ emissions under its core scenario and roughly 1.4% under a rapid-growth scenario [7]. The ODCC further projects that carbon emissions from China’s data centers will exceed 200 million tonnes by 2030. These data underscore a central tension in the AI era: the imperative to alleviate “compute anxiety” requires large-scale data center expansion, whereas the “dual-carbon” goals (carbon peaking and carbon neutrality) demand strict control of energy consumption and optimization of the energy mix. Therefore, balancing an adequate supply of computing capacity with optimization of the energy mix—so as to realize green, sustainable data centers—has become a major challenge for China in the AI era.

In China, this challenge manifests as a regional mismatch between data center layout and energy-resource endowments, producing a supply–demand imbalance between the eastern and western regions [8]. Studies indicate that China’s data centers follow a “dense in the east, sparse in the west” distribution pattern, with three highly concentrated clusters in the Beijing–Tianjin–Hebei, Yangtze River Delta, and Pearl River Delta regions [9]. On the one hand, the economically developed eastern regions, which serve as the hub of the digital economy, concentrate the majority of the nation’s computing demand. However, data centers there face constraints of limited land and energy resources, high operating costs, and stringent environmental regulation [10]. Conversely, the western regions possess abundant renewable resources, favorable climates, and low land costs, conferring a natural advantage for hosting large-scale data centers. Yet underdeveloped local digital economies and lagging industrial bases mean that these regions host few data centers, often with low utilization rates [11]. This geographic mismatch between resources and demand not only exacerbates energy shortages in the East but also risks wasting green energy in the West [12]. To address the structural challenges—namely, the uneven distribution of computing resources, the energy supply–demand imbalance, and the high energy consumption and carbon emissions of eastern data centers—and to foster synergistic development between computing power and energy, China has implemented a series of national strategies and policies. In May 2021, the National Development and Reform Commission (NDRC) and other departments jointly issued the “Implementation Plan for the Coordinated Innovation System of the National Integrated Big Data Center Computing Hub,” officially proposing the “Eastern Data, Western Computing” project, laying the top-level design foundation for guiding the orderly transfer of eastern computing demand to the west. Building on this foundation, in October 2023 the Ministry of Industry and Information Technology (MIIT) and five other ministries released the Action Plan for the High-Quality Development of Computing Infrastructure, which further advanced the strategy by calling for an “optimized layout of computing facilities” and for “efficient complementarity and synergy between eastern and western regions.” Subsequently, in July 2024 an action plan issued by the NDRC and other ministries set higher implementation standards, specifying the need to “improve the data center layout” and “increase the utilization of renewable energy.” Taken together, this progressive series of policies delineates a clear strategic path for the green, intensive westward development of China’s data center industry and provides the macro-policy context for the strategic choices of the agents analyzed in this paper’s game-theoretic model.

2. Literature Review

2.1. Research on Data Center Optimization and Green Transition

Amid implementation of the “Eastern Data, Western Computing” strategy, the cross-regional configuration of data centers has become a focal concern for both government and industry. Differences in resource endowments, economic development, and strategic objectives between East and West misalign stakeholder interests and strategies, generating a complex, dynamic game. Academic research in this area has evolved along two main dimensions. The first concerns foundational work on data center optimization, spanning energy efficiency, operations, and siting. Early cost- and performance-oriented studies identified land availability, electricity prices, and climate as key determinants of site selection [13]. For example, Turek et al. showed that incorporating mesoscale climate effects into siting models can reduce cooling costs by 15–25% [14], while Lei et al. developed a Power Usage Effectiveness (PUE) prediction model to guide data center siting [15]. At the operational level, scholars have applied game theory to resource optimization: Shi et al. proposed a genetic-algorithm-based virtual-machine scheduling strategy that improves energy efficiency in cloud computing through optimized resource management [16], and Liu et al. developed a game-theoretic model for smart-grid environments to analyze optimal defense-resource allocation for data centers under network-attack scenarios [17]. The second dimension—spurred by China’s “dual-carbon” targets—focuses on green development pathways. Zhu et al. analyzed energy-saving technologies and potential decarbonization pathways for data centers, highlighting implications for global carbon-neutrality goals by comparing 20 representative cases [18]. At the macro level, Xie et al. projected that the “Eastern Data, Western Computing” initiative could reduce CO₂ emissions by 2125 million metric tonnes between 2020 and 2050, demonstrating substantial carbon-reduction potential [19]. Furthermore, studies indicate that policy instruments—such as carbon quotas, green-electricity subsidies, and carbon taxes—are pivotal in steering the industry’s green transition [20,21]. Although PUE is widely used to measure energy efficiency, its limitations become apparent when assessing green transitions [22], as early as 2013, Yuventi and Vuduc noted that PUE does not capture the cleanliness of energy sources, so a coal-fired facility with low PUE may emit more carbon than a clean-energy-powered one with higher PUE [23], and Horner et al. similarly showed that decoupling from the energy mix allows PUE-centric assessments to misrepresent environmental impacts [24]. These limitations have prompted a shift toward direct carbon assessment, revealing an inherent tension between energy efficiency and carbon reduction. For example, Mao et al. identified an inverted-U relationship between computing infrastructure and carbon intensity [25], and Ni et al. quantified total carbon emissions and the peaking pathway for China’s data centers with greater precision [26]. More critically, Zhang et al. revealed a paradox within the “Eastern Data, Western Computing” initiative, relocating a data center from Shanghai to Sichuan could cut emissions by 79.6% despite a potential increase in PUE, whereas moving from Beijing to coal-reliant Inner Mongolia could raise emissions by 24.9% [27]. This finding demonstrates that a credible green transition requires synergistic optimization of both energy efficiency and the energy mix.

2.2. Applications of Evolutionary Game Theory

However, cross-regional optimization is not merely a technical choice; it is a complex process of strategic trade-offs among multiple agents, including the central and local governments and data center enterprises. Evolutionary game theory (EGT) provides an appropriate analytical framework for modeling dynamic, multi-agent decision-making in such complex systems [28]. Unlike traditional game models that examine static competition, EGT is better suited to capturing long-term dynamic interactions among boundedly rational agents [29,30]. EGT has been widely applied to studies of government–enterprise interactions. For example, Xi et al. constructed a two-player evolutionary game to analyze the strategic choices of agricultural enterprises and the government under environmental regulation [31], and Zhou et al. employed a similar government–enterprise game to examine mechanisms for controlling environmental pollution [32]. Research has also examined how subsidy designs affect inter-enterprise technological strategy games: Liu et al. developed a three-player EGT model with high- and low-carbon enterprises and found that dynamic subsidies and taxes significantly influence corporate innovation decisions [33]. Tripartite and multi-party game models have also become increasingly prevalent. From a responsible-innovation perspective, Jia et al. constructed a three-player EGT model involving the government, waste-to-energy enterprises, and local communities to explore their strategic interactions [34]. From a social-service perspective, Wang and Yu analyzed the decision-making of individuals, data users, and the government in the value-realization process for personal data [35]. However, these studies often focus on vertical hierarchies or multi-agent interactions confined to a single region. They pay insufficient attention to horizontal “co-opetitive” (cooperative-competitive) relationships between governments during cross-regional industrial transfer and neglect how differentiated resource endowments shape strategic choices. Consequently, research on the spatial optimization of the data center industry remains scarce. For example, although Sun et al. constructed a game model of industrial transfer, they treated the origin and destination governments as homogeneous agents, overlooking how differences in resource endowments affect the strategy choices [36].

Building on this literature, this paper employs evolutionary game theory to construct a tripartite model that captures the strategic evolution among eastern local governments, western local governments, and data center enterprises during implementation of the “Eastern Data, Western Computing” initiative. Using the model, the study examines how eastern and western local governments formulate optimal regulatory and incentive strategies within the national policy framework. It also investigates how enterprises’ migration decisions are shaped by costs and policies, and whether the three agents converge to an evolutionarily stable strategy (ESS) that balances economic benefits with environmental sustainability. The findings elucidate the mechanisms of cross-regional resource allocation in the era of large AI models and provide an analytical basis for future policymaking. The remainder of the paper details the model’s structure and parameters, analyzes simulation results, and offers corresponding policy recommendations.

3. Model Construction

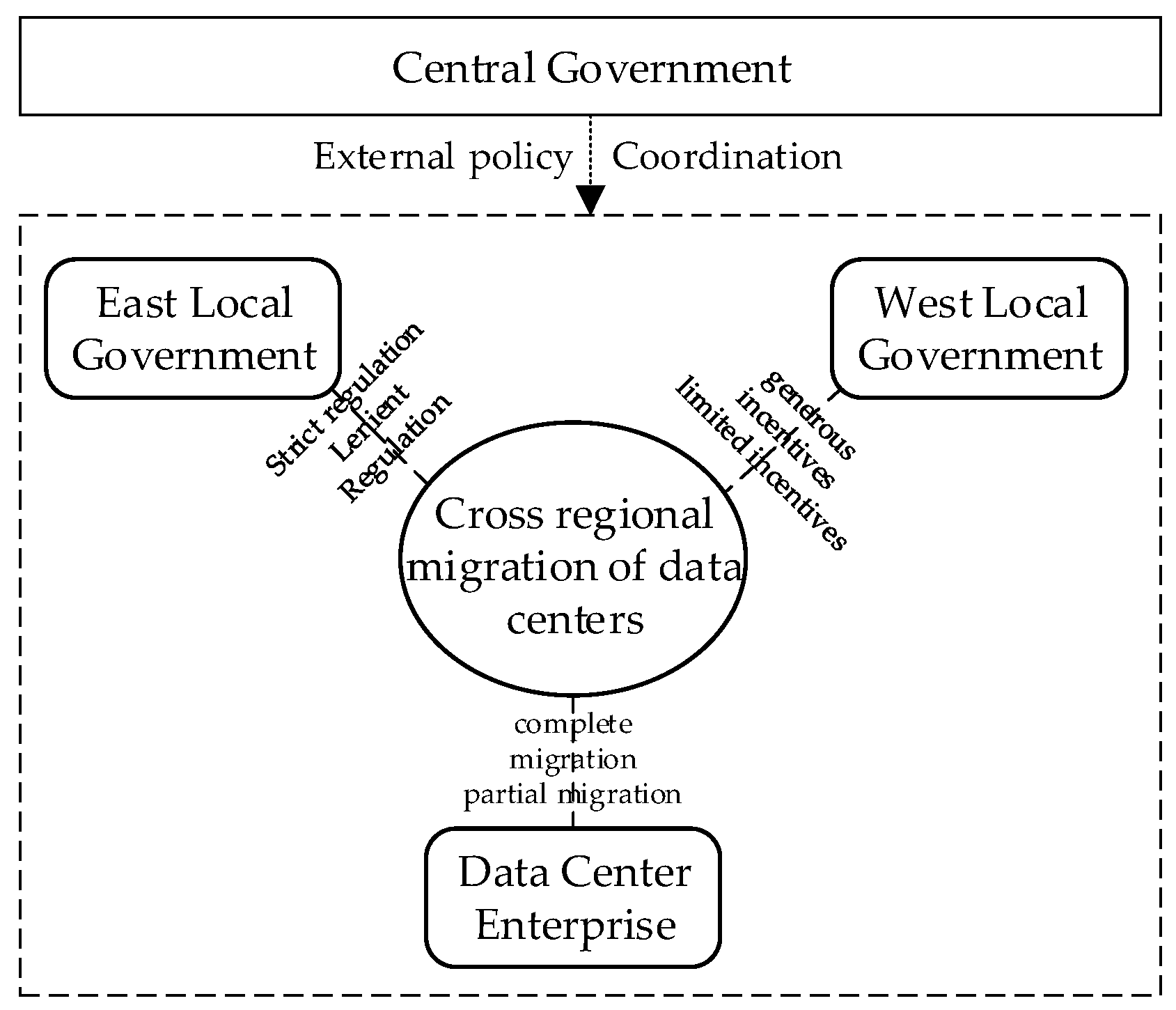
3.1. Problem Description

China’s data center deployment exhibits pronounced regional structural patterns. In the eastern region, the AI industry is vibrant, demand for computing power is strong, and supporting infrastructure is well developed; however, the region faces constraints such as limited land and high energy costs. To achieve green development of data centers, the East must tighten PUE and carbon-efficiency standards. By contrast, the western region possesses abundant renewable resources and ample land but has a weak digital-industry base and relatively lagging economic growth; thus, preferential land and tax policies are needed to attract the migration of data center activities. In cross-regional data-center migration, the East typically creates a regulatory “push” by tightening energy-efficiency and carbon-compliance requirements, whereas the West provides a developmental “pull” through hosting incentives and infrastructure improvement. Because these policy forces interact repeatedly with enterprises’ boundedly rational adjustments and may generate path-dependent outcomes, an evolutionary game framework is suitable for characterizing the dynamic strategy evolution toward (or away from) coordination.

3.2. Model Assumptions

Figure 1 depicts the strategic interactions among the Eastern Local Government (ELG), the Western Local Government (WLG), and the data-center enterprise (DCE). An extensive-form game tree is used to illustrate the sequence of moves; it consists of nodes and branches. Decision nodes mark the players’ choice points; this game contains seven such nodes. Terminal nodes correspond to complete strategy profiles (outcomes). The extensive-form game involving ELG, WLG, and DCE is presented in Figure 2.

Against this backdrop, the “Eastern Data, Western Computing” initiative encourages enterprises to adopt differentiated migration strategies—retaining latency-sensitive services in the East while shifting non-real-time computing tasks to the West—to optimize resource allocation. These decisions are shaped by enterprises’ cost structures, the generosity of policy incentives offered by western local governments, the stringency of regulatory oversight in the East, and national-level external incentives—such as PUE subsidies, carbon-quota schemes, and revenues from green power certificates. To examine data center migration decisions and the resulting interregional strategic interactions, this study develops an evolutionary game model with three players: the eastern local government, the western local government, and data center enterprises. The central government is not modeled as a direct player; instead, it influences the game through exogenous policy parameters. To reflect the East–West heterogeneity in resource endowments and policy objectives, the two local governments are modeled as asymmetric agents with different policy instruments and constraint environments. Specifically, ELG is characterized by a regulation-oriented decision (strict vs. lenient regulation) under tighter energy and environmental constraints, whereas WLG is characterized by an incentive-oriented decision (generous vs. limited incentives) given its comparative advantage in low-carbon energy and the goal of attracting industrial transfer. This asymmetric design makes explicit how regional heterogeneity is represented in the strategy sets and payoff components of the model. The specific assumptions are as follows:

Assumption 1 

(Agents and Bounded Rationality). The three agents—eastern local government (ELG), western local government (WLG), and data center enterprise (DCE)—are boundedly rational in strategy selection. Under the “Eastern Data, Western Computing” initiative, all parties face incomplete information and uncertainty about the future; hence, decisions are not achieved in a single optimal move but are updated dynamically according to expected payoffs. The strategy profile therefore tends to converge toward a stable configuration, making evolutionary game theory more suitable than traditional game models for explaining the process.

Assumption 2 

(Strategy Set of the Eastern Local Government, ELG). As the jurisdictional regulator of data centers and the executor of the “dual-carbon” strategy, the Eastern Local Government (ELG) has the strategy set {strict regulation, lenient regulation}. Strict regulation denotes rigorous enforcement of national PUE standards and carbon-emissions controls, with cost-based penalties applied to noncompliant enterprises. Lenient regulation refers to moderately relaxing regulatory standards in the short term to retain local industry, tolerating limited exceedances of energy use and carbon emissions. Let x be the probability that E chooses strict regulation and 1 − x the probability it chooses lenient regulation, where 0 ≤ x ≤ 1.

Assumption 3 

(Strategy Set of the Western Local Government, WLG). As the principal recipient of data center migration under the “Eastern Data, Western Computing” initiative, the Western Local Government (WLG) has the strategy set {generous incentives, limited incentives}. Generous incentives entail substantial fiscal support—such as land provision, electricity subsidies, and tax relief—to attract relocating enterprises, actively assisting them in meeting green-compliance requirements. Limited incentives provide only modest policy support, reflecting a cautious stance in project competition and offering merely basic assistance. Let y be the probability that WLG adopts generous incentives and 1 − y the probability that it adopts limited incentives, where 0 ≤ y ≤ 1.

Assumption 4 

(Strategy Set of the Data-Center Enterprise, DCE). As a profit-maximizing agent, the data-center enterprise (DCE) has the strategy set {complete migration, partial migration}. When making migration decisions to maximize expected returns, DCE rationally evaluates factors such as energy costs in the East and West, the generosity of policy incentives, migration and reconstruction costs, and the stringency of regulatory oversight. Partial migration denotes shifting latency-insensitive yet computing-intensive workloads—e.g., AI training, big-data analytics, and animation rendering—to the West, thereby capturing part of the energy-cost advantage and available incentives while retaining core infrastructure in the East. Complete migration entails moving most or all computing infrastructure and associated workloads to the West, fully accessing regional resource and policy benefits but incurring higher infrastructure migration and rebuilding costs; it represents a more thorough reconfiguration of the industrial footprint. It should be noted that such a reconfiguration involves physical relocation (server transportation and equipment reassembly) as well as operational cutover; accordingly, enterprises may face relocation expenditures and transition frictions that, in practice, encompass logistics costs, installation and commissioning effort, time delays, and supply-chain stability considerations, which are abstracted in the model as migration-related expenditures and transition frictions. Let z be the probability that DCE chooses complete migration, and 1 − z the probability of partial migration, where 0 ≤ z ≤ 1.

Assumption 5 

(External Environment and Coordination Mechanism). The central government is not modeled as a direct player; instead, it sets the exogenous policy environment. To incentivize policy coupling, the model introduces a regional coordination subsidy: when the Eastern Local Government adopts strict regulation and the Western Local Government adopts generous incentives, the central government grants an additional coordination subsidy to both jurisdictions to reward their joint policy alignment.

3.3. Parameter Definitions

The model’s parameters are specified to reflect China’s data-center industry conditions and to remain consistent with traceable policy and market mechanisms, thereby supporting empirical plausibility. The bases for parameter specification are as follows:

• Baseline cost parameters. The eastern regulatory cost, western incentive cost, and enterprise migration cost are anchored to benchmark ranges reported in authoritative industry studies, such as those from the China Center for Information Industry Development (CCID), and complemented by relevant policy documents issued by the National Development and Reform Commission (NDRC). In particular, the eastern regulatory cost is modeled as a largely administrative expenditure that is relatively stable in the short run and does not scale proportionally with enterprise size.
• Policy and green parameters. Policy-linked items—including the PUE-compliance subsidy, corporate carbon-quota-related costs, green-certificate-related returns, and differentiated intergovernmental transfers—are specified with reference to national “dual-carbon” policy documents, officially released market transaction indicators, and Ministry of Finance regulations. Carbon-related parameters follow the compliance-and-trading logic of China’s national Emissions Trading System (ETS) and are benchmarked to published transaction statistics for China Emission Allowances (CEA). Green attributes are aligned with the official green electricity certificate issuance and trading framework. Notably, power usage effectiveness (PUE) enters the model through the compliance concept underlying the subsidy instrument, rather than as an explicitly assigned numerical PUE value.
• Behavioral granularity parameters. To capture heterogeneous behavioral intensities, the model introduces a migration-degree coefficient and an incentive-intensity coefficient, which measure, respectively, the depth of enterprise migration and the strength of western governmental support. Although both affect incentive-related outlays, they correspond to different decision makers and operate through different payoff components.
• Societal cost parameters. Non-pecuniary costs—such as migration-related losses borne by enterprises and reputation-related losses borne by governments—are informed by established evolutionary-game studies that incorporate social and public-opinion pressures, reflecting the comprehensive considerations present in real-world decision-making.

All variables and parameters, together with their definitions, units, and source notes, are summarized in Appendix A (

Table A1. Parameter Symbols and Their Meanings.

Parameter	Symbol	Parametric Meaning and Practical Interpretation
Eastern regulatory cost	CE	The regulatory expenditure incurred by ELG to strictly supervise data-center PUE and carbon emissions.
Western incentive cost	CW	The fiscal cost borne by WLG to implement incentive policies aimed at attracting data-center enterprises.
Western incentive intensity coefficient	m	The proportional coefficient for WLG’s fiscal cost when offering incentive policies (0 < m ≤ 1).
Enterprise migration degree coefficient	k	The proportion of an enterprise’s data center capacity relocated to the West relative to its total facility scale (0 < k ≤ 1).
Enterprise migration costs	CF	The comprehensive migration expenditure required for relocating the data center to the West, encompassing logistics and transportation (server shipping), equipment reassembly, installation and commissioning, and site/facility preparation, with the realized cost varying with the migration degree k.
Baseline return of eastern enterprises	RE	The baseline profit obtained when the enterprise’s data center remains fully in the East and operates normally (varying with the migration degree).
Western energy advantage return	EW	The economic gain from using western renewable energy—relative to eastern energy costs—when the enterprise completely relocates.
Western subsidy	SG	The subsidy provided by WLG to enterprises relocating to the West (varying with the incentive intensity, with SG < CW).
Central PUE-compliance subsidy	SP	The fiscal subsidy granted by the central government to data-center enterprises that, after complete migration, meet the required PUE standard.
Central regional-coordination subsidy	SC	An additional subsidy is provided by the central government when ELG adopts strict regulation and WLG offers generous incentives simultaneously, rewarding their coordinated policy interaction.
Coordination subsidy allocation ratio	n	The share of the central coordination subsidy allocated to ELG (0 < n ≤ 1).
Enterprise carbon-quota cost	CC	The cost paid by the enterprise to ELG for purchasing additional carbon quotas when, under strict regulation, partial migration leads to excess emissions from facilities remaining in the East.
Enterprise green certificate return	RG	The revenue obtained from green certificates when the enterprise completely relocates and uses renewable electricity in the West.
Central fiscal transfer to the East	BE	The fiscal transfer provided by the central government to ELG when it strictly enforces regulatory standards.
Central fiscal transfer to the West	BW	The fiscal transfer provided by the central government to WLG when it actively undertakes data-center projects by offering incentive policies.
Eastern penalty revenue	TE	The fines collected by ELG from noncompliant facilities that remain in the East after partial migration under strict regulation.
Central penalty cost	TC	The punitive cost imposed by the central government on ELG and WLG when they relax regulation or fail to actively undertake data-center projects.
Loss of complete enterprise migration	D1	The short-term commercial losses associated with complete migration—such as service interruption risk, customer churn, and temporary service-quality degradation—potentially amplified by logistics frictions (server transportation), installation and commissioning time, and supply-chain stability during relocation.
Partial migration loss of enterprises	D2	The operating loss under partial migration caused by cross-regional coordination and data transmission, where network latency, bandwidth constraints/costs, transmission stability, and data-transmission efficiency affect service quality and performance.
Reputational loss of ELG	SE	The social cost borne by the ELG due to reputational damage arising from environmental problems caused by lax enforcement when enterprises partially migrate.
Reputational loss of WLG	SW	The social cost borne by the WLG stemming from reputational damage and the negative externalities of “race-to-the-bottom” local competition triggered by generous incentives policies when enterprises completely migrate.

).

3.4. Payoff Matrix

According to the analysis of the above parameter settings, the benefits of the three players under different strategies are shown in

Table 1. The revenue matrices of the game stakeholders under each strategy combination.

ELG	WLG	DCE
		Complete Migration	Partial Migration
Strict Regulation	Generous Incentives	$B_E-C_E+n{S}_C$	$B_E-C_E+T_E+n{S}_C+C_C$
		$B_W+(1-n)S_C-C_W-S_W-S_G$	$B_W+(1-n)S_C-C_W$
		$S_G+E_W+S_P+R_G-C_F-D_1$	$S_G+(1-k)R_E-k{C}_F-D_2-C_C-T_E$
	Limited Incentives	$B_E-C_E$	$B_E-C_E+T_E+C_C$
		$-m{C}_W-T_C-m{S}_G$	$-m{C}_W-T_C$
		$m{S}_G+E_W+S_P+R_G-C_F-D_1$	$m{S}_G+(1-k)R_E-k{C}_F-D_2-C_C-T_E$
Lenient Regulation	Generous Incentives	$-T_C$	$-T_C-S_E$
		$B_W-C_W-S_W-S_G$	$B_W-C_W$
		$S_G+E_W+S_P+R_G-C_F-D_1$	$S_G+(1-k)R_E-k{C}_F-D_2$
	Limited Incentives	$-T_C$	$-T_C-S_E$
		$-m{C}_W-T_C-m{S}_G$	$-m{C}_W-T_C$
		$m{S}_G+E_W+S_P+R_G-C_F-D_1$	$m{S}_G+(1-k)R_E-k{C}_F-D_2$

. To enhance transparency and internal consistency, the construction of the payoff matrix (Table 1) was examined for internal consistency. All cost and benefit components—such as enforcement costs, incentive expenditures, and migration-related losses—are mapped to the corresponding agents under the relevant strategy profiles to avoid omission or double counting. Each parameter is intended to represent a distinct real-world mechanism and enters the payoff of the associated stakeholder only when its activation condition is satisfied.

3.5. Expected Payoff Functions and Replicator-Dynamics Equations

Replicator dynamics and the evolutionarily stable strategy (ESS) are two core constructs of evolutionary game theory. Replicator dynamics provide a dynamic description and analysis of how boundedly rational agents adjust their strategies over time [37]. The replicator-dynamics equations for ELG, WLG, and DCE are presented below in the standard two-strategy form, where nonlinear prefactors (e.g., x(1 − x)) arise endogenously from the replicator framework. The expected payoff functions (V_E1, …, V_C2) are derived directly from Table 1 using standard probability-weighted expectations over the other two players’ mixed strategies, and the resulting expressions were cross-checked for internal consistency against the corresponding payoff entries to avoid omission of key components. As shown in Table 1, the expected payoff for ELG under strict regulation, V_E1, the expected payoff under lenient regulation, V_E2, and the average expected payoff, V_E are given as follows:

$$\begin{array}{l}{V}_{E1}=yz(B_E-C_E+n{S}_C)+y(1-z)(B_E-C_E+T_E+n{S}_C+C_C)+(1-y)z(B_E-C_E)\\ +(1-y)(1-z)(B_E-C_E+T_E+C_C)\end{array}$$

(1)

$$V_{E2}=-yz{T}_C+y(1-z)(-T_C-S_E)-(1-y)z{T}_C+(1-y)(1-z)(-T_C-S_E)$$

(2)

$$\begin{array}{l}{V}_E=x{V}_{E1}+(1-x)V_{E2}\\ =xyn{S}_C-xz{T}_E-xz(C_C+S_E)+x(B_E+C_C-C_E+S_E+T_C+T_E)+z{S}_E-T_C-S_E\end{array}$$

(3)

Replicator dynamic equation of behavioral strategy choice of ELG:

$$\begin{array}{l}F(x)={\displaystyle \frac{dx}{dt}}=x(V_{E1}-V_E)=x(1-x)(V_{E1}-V_{E2})\\ =x(1-x)\left(B_E+C_C+S_E+T_C+T_E-C_E-z(C_C+S_E+T_E)+yn{S}_C\right)\end{array}$$

(4)

Similarly, by the standard replicator dynamics formula, the replicator dynamics equations for ELG and DCE can be derived respectively. The expected payoff for WLG under generous incentives, V_W1, the expected payoff under limited incentives, V_W2, and the average expected payoff, V_W, are given by:

$$\begin{array}{l}{V}_{W1}=xz(B_W+(1-n)S_C-C_W-S_W-S_G)+x(1-z)(B_W+(1-n)S_C-C_W)\\ +(1-x)z(B_W-C_W-S_W-S_G)+(1-x)(1-z)(B_W-C_W)\end{array}$$

(5)

$$\begin{array}{l}{V}_{W2}=xz(-m{C}_W-T_C-m{S}_G)+x(1-z)(-m{C}_W-T_C)\\ +(1-x)z(-m{C}_W-T_C-m{S}_G)+(1-x)(1-z)(-m{C}_W-T_C)\end{array}$$

(6)

$$\begin{array}{l}{V}_W=y{V}_{W1}+(1-y)V_{W2}\\ =y\left(B_{W}x-C_{W}x-S_{W}xz-S_{G}xz+S_{C}xy-n{S}_{C}xy-S_{G}mz+C_{W}mx+T_{C}x-T_C-C_{W}m\right)\\ +(1-y)\left(B_{W}x-C_{W}x-S_{W}xz-S_{G}xz-C_{W}mx-T_C-S_{G}mz+T_{C}x+C_{W}m\right)\end{array}$$

(7)

Replicator dynamics equation governing WLG’s strategic choice is given by:

$$\begin{array}{l}F(y)={\displaystyle \frac{dy}{dt}}=y(V_{W1}-V_W)=y(1-y)(V_{W1}-V_{W2})\\ =y(1-y)\left(B_W - C_W + T_C+ C_{W}m+ S_{C}x - S_{G}z- S_{W}z - S_{C}nx + S_{G}mz\right)\end{array}$$

(8)

The expected payoff for DCE under complete migration, V_C1, the expected payoff under partial migration, V_C2, and the average expected payoff, V_C, are given by:

$$\begin{array}{l}{V}_{C1}=xy(S_G+E_W+S_P+R_G-C_F-D_1)+x(1-y)(m{S}_G+E_W+S_P+R_G-C_F\\ -D_1)+(1-x)y(S_G+E_W+S_P+R_G-C_F-D_1)\\ +(1-x)(1-y)(m{S}_G+E_W+S_P+R_G-C_F-D_1)\end{array}$$

(9)

$$\begin{array}{l}{V}_{C2}=xy(S_G+(1-k)R_E-k{C}_F-D_2-C_C-T_E)+x(1-y)\\ \cdot (m{S}_G+(1-k)R_E-k{C}_F-D_2-C_C-T_E)\\ +(1-x)y(S_G+(1-k)R_E-k{C}_F-D_2)\\ +(1-x)(1-y)(m{S}_G+(1-k)R_E-k{C}_F-D_2)\end{array}$$

(10)

$$\begin{array}{l}{V}_C=z{V}_{C1}+(1-z)V_{C2}\\ =R_E-D_2-k(C_F+R_E)+m{S}_G-x(C_C+T_E)+y(S_G-m{S}_G)\\ +z(-C_F-D_1+D_2+E_W-R_E+R_G+S_P+k{C}_F)+xz(C_C+T_E)+kz{R}_E\end{array}$$

(11)

Replicator dynamics equation governing DCE’s strategic choice is given by:

$$\begin{array}{l}F(z)={\displaystyle \frac{dz}{dt}}=z(V_{C1}-V_C)=z(1-z)(V_{C1}-V_{C2})\\ =z(1-z)\left(D_2-D_1-C_F+E_W-R_E+R_G+S_P+C_{F}k+C_{C}x+R_{E}k+T_{E}x\right)\end{array}$$

(12)

4. Evolutionary Game Equilibrium Analysis

4.1. Solving for Equilibrium Points

This section applies stability results from differential-equation theory to examine the evolutionary paths of the three players—ELG, WLG, and DCE. The replicator system is analyzed by solving the stationarity conditions F(x) = 0, F(y) = 0 and F(z) = 0. This yields the eight boundary points E₁–E₈ with (x, y, z)∈{0, 1}³, i.e., E₁(0, 0, 0), E₂(0, 0, 1), E₃(0, 1, 0), E₄(0, 1, 1), E₅(1, 0, 0), E₆(1, 0, 1), E₇(1, 1, 0) and E₈(1, 1, 1), which are mathematically valid pure-strategy equilibria. In particular, given the standard replicator structure (e.g., terms such as x(1 − x)), the boundary values 0 and 1 are naturally included among the stationary solutions. In addition, candidate mixed-strategy equilibria E₉–E₁₅(x*, y*, z*) may arise as interior solutions when payoff differences vanish. Following Ritzberger et al. [37], stability analysis for a three-player evolutionary game can be restricted to the eight pure-strategy equilibria listed above. Since policy implications require long-run behavioral predictions, the subsequent discussion focuses on equilibria that are locally asymptotically stable under Jacobian-based conditions; unstable candidates are not used for policy interpretation. Consistent with Friedman’s approach, evolutionarily stable strategies (ESS) are identified via a local stability analysis based on the system’s Jacobian matrix. Accordingly, the Jacobian matrix of the system is obtained as:

$$J=\left[\begin{array}{ccc}{J}_{11}& J_{12}& J_{13}\\ J_{21}& J_{22}& J_{23}\\ J_{31}& J_{32}& J_{33}\end{array}\right]$$

(13)

where

$$\begin{array}{l}{J}_{11}=(1-2x)\left(B_E+C_C-C_E+S_E+T_C+T_E-C_{C}z-S_{E}z-T_{E}z+S_{C}ny\right)\\ J_{12}=nx(1-x)S_C\\ J_{13}=x(x-1)(C_C+S_E+T_E)\\ J_{21}=y(1-y)(S_C-S_{C}n)\\ J_{22}=(1-2y)\left(B_W-C_W+T_C+C_{W}m+S_{C}x-S_{G}z-S_{W}z-S_{C}nx+S_{G}mz\right)\\ J_{23}=y(y-1)(S_G+S_W-S_{G}m)\\ J_{31}=z(1-z)(C_C+T_E)\\ J_{32}=0\\ J_{33}=(1-2z)\left(D_2-D_1-C_F+E_W-R_E+R_G+S_P+C_{F}k+C_{C}x+R_{E}k+T_{E}x\right)\end{array}$$

(14)

By examining the eigenvalues of the Jacobian matrix, the system’s local stability and near-equilibrium dynamics can be characterized [37]. According to Lyapunov’s first (indirect) method, if all eigenvalues of the Jacobian have negative real parts, the equilibrium is asymptotically stable; if at least one eigenvalue has a positive real part, the equilibrium is unstable; and if all eigenvalues have negative real parts except for one or more with zero real part, the equilibrium is in a critical state and stability cannot be determined from eigenvalue signs alone. The computed eigenvalues at each equilibrium and their implications are summarized in Appendix A (

Table A2. Stability analysis of equilibrium points in tripartite evolutionary games.

Equilibrium Point	Eigenvalues λ1, λ2, λ3	Stability Condition
E1(0, 0, 0)	$\begin{array}{l}{\lambda }_1=B_W-C_W+T_C+m{C}_W,\\ {\lambda }_2=B_E+C_C-C_E+S_E+T_C+T_E,\\ {\lambda }_3=D_2-D_1-C_F+E_W\\ -R_E+R_G+S_P+k{C}_F+k{R}_E\end{array}$	$\begin{array}{l}{B}_W+T_C+m{C}_W<C_W,\\ B_E+C_C+S_E+T_C+T_E<C_E,\\ D_2+E_W+R_G+S_P+k{C}_F\\ +k{R}_E<D_1+C_F+R_E\end{array}$
E2(0, 0, 1)	$\begin{array}{l}{\lambda }_1=B_E-C_E+T_C,\\ {\lambda }_2=B_W-C_W-S_G-S_W\\ +T_C+m{C}_W+m{S}_G,\\ {\lambda }_3=C_F+D_1-D_2-E_W\\ +R_E-R_G-S_P-k{C}_F-k{R}_E\end{array}$	$\begin{array}{l}{B}_E+T_C<C_E,\\ B_W+T_C+m{C}_W+m{S}_G\\ <C_W+S_G+S_W,\\ C_F+D_1+R_E<D_2+E_W+R_G\\ +S_P+k{C}_F+k{R}_E\end{array}$
E3(0, 1, 0)	$\begin{array}{l}{\lambda }_1=C_W-B_W-T_C-m{C}_W,\\ {\lambda }_2=B_E+C_C-C_E\\ +S_E+T_C+T_E+n{S}_C,\\ {\lambda }_3=D_2-D_1-C_F+E_W-R_E\\ +R_G+S_P+k{C}_F+k{R}_E\end{array}$	$\begin{array}{l}{C}_W<B_W+T_C+m{C}_W,\\ B_E+C_C+S_E+T_C+T_E+n{S}_C<C_E,\\ D_2+E_W+R_G+S_P+k{C}_F\\ +k{R}_E<R_E+D_1+C_F\end{array}$
E4(0, 1, 1)	$\begin{array}{l}{\lambda }_1=B_E-C_E+T_C+n{S}_C,\\ {\lambda }_2=C_W-B_W+S_G\\ +S_W-T_C-m{C}_W-m{S}_G,\\ {\lambda }_3=C_F+D_1-D_2-E_W\\ +R_E-R_G-S_P-k{C}_F-k{R}_E\end{array}$	$\begin{array}{l}{B}_E-C_E+T_C+n{S}_C,\\ C_W+S_G+S_W<B_W+T_C\\ +m{C}_W+m{S}_G,\\ C_F+D_1+R_E<D_2+E_W\\ +R_G+S_P+k{C}_F+k{R}_E\end{array}$
E5(1, 0, 0)	$\begin{array}{l}{\lambda }_1=C_E-C_C-B_E-S_E-T_C-T_E\\ {\lambda }_2=B_W-C_W+S_C+T_C+m{C}_W-n{S}_C\\ {\lambda }_3=C_C-C_F-D_1+D_2+E_W\\ -R_E+R_G+S_P+T_E+k{C}_F+k{R}_E\end{array}$	$\begin{array}{l}{C}_E<C_C+B_E+S_E+T_C+T_E,\\ B_W+S_C+T_C+m{C}_W<n{S}_C+C_W,\\ C_C+D_2+E_W+R_G+S_P\\ +T_E+k{C}_F+k{R}_E<C_F+D_1+R_E\end{array}$
E6(1, 0, 1)	$\begin{array}{l}{\lambda }_1=C_E-B_E-T_C\\ {\lambda }_2=B_W-C_W+S_C-S_G-S_W\\ +T_C+m{C}_W+m{S}_G-n{S}_C\\ {\lambda }_3=C_F-C_C+D_1-D_2-E_W\\ +R_E-R_G-S_P-T_E-k{C}_F-k{R}_E\end{array}$	$\begin{array}{l}{C}_E<B_E+T_C,\\ B_W+S_C+T_C+m{C}_W+m{S}_G\\ <C_W+S_G+S_W+n{S}_C,\\ C_F+D_1+R_E<R_G+S_P+T_E\\ +k{C}_F+k{R}_E+C_C+D_2+E_W\end{array}$
E7(1, 1, 0)	$\begin{array}{l}{\lambda }_1=C_W-B_W-S_C-T_C-m{C}_W+n{S}_C\\ {\lambda }_2=C_E-C_C-B_E-S_E-T_C-T_E-n{S}_C\\ {\lambda }_3=C_C-C_F-D_1+D_2+E_W\\ -R_E+R_G+S_P+T_E+k{C}_F+k{R}_E\end{array}$	$\begin{array}{l}{C}_W+n{S}_C<B_W+S_C+T_C+m{C}_W,\\ C_E<C_C+B_E+S_E+T_C+T_E+n{S}_C,\\ C_C+D_2+E_W+R_G+S_P+T_E\\ +k{C}_F+k{R}_E<C_F+D_1+R_E\end{array}$
E8(1, 1, 1)	$\begin{array}{l}{\lambda }_1=C_E-B_E-T_C-S_{C}n\\ {\lambda }_2=C_W-B_W-S_C+S_G+S_W\\ -T_C-m{C}_W-m{S}_G+n{S}_C\\ {\lambda }_3=C_F-C_C+D_1-D_2-E_W\\ +R_E-R_G-S_P-T_E-k{C}_F-k{R}_E\end{array}$	$\begin{array}{l}{C}_E<B_E+T_C+S_{C}n,\\ C_W+S_G+S_W+n{S}_C\\ <B_W+S_C+T_C+m{C}_W+m{S}_G,\\ C_F+D_1+R_E<R_G+S_P+T_E\\ +k{C}_F+k{R}_E+C_C+D_2+E_W\end{array}$

).

4.2. Analysis of the Four Scenarios of Equilibrium Point Stability Strategy

Given the complexity of the model parameters, the stability and evolutionary paths of each equilibrium are analyzed with reference to the conditions in Table A2. The discussion proceeds through four distinct scenarios: it begins with the ideal, policy-aligned case and then examines how the system evolves toward non-ideal states when key conditions are not satisfied. These scenarios correspond to partial or complete violations of the preceding assumptions and are used to assess how factors such as insufficient policy incentives and inadequate enterprise migration returns affect the system’s equilibrium. For readability,

Table 2. Scenario-to-equilibrium mapping and key policy levers.

Scenario	Stable Equilibrium	Qualitative Description	Key Policy Lever
Scenario 1	E8(1, 1, 1)	Coordinated optimum	Aligned net payoffs (effective push–pull + central support/discipline)
Scenario 2	E1(0, 0, 0)	Policy failure/stalemate	Weak push/pull (insufficient central incentives/discipline)
Scenario 3	E6(1, 0, 1)	Strong eastern push, weak western pull	Eastern compliance pressure dominates (migration profitable even with limited incentives)
Scenario 4	E7(1, 1, 0)	Coordination impeded: active governments, cautious firms	Enterprise-side migration risk (reduce complete-migration loss; improve networks/markets)

summarizes the mapping from the four scenarios to their corresponding stable equilibrium outcomes, provides a qualitative interpretation, and highlights the key policy lever(s) driving each scenario.

Scenario 1. 

When C_E − B_E − T_C − nS_C < 0, C_W + S_G + S_W + nS_C − B_W − S_C − T_C − mC_W − mS_G < 0, and C_F + D₁ + R_E − R_G − S_P − T_E − kC_F − kR_E − C_C − D₂ − E_W < 0, the system attains the ideal equilibrium E₈(1, 1, 1). This configuration constitutes the optimal strategy mix under the “Eastern Data, Western Computing” initiative, aligning eastern green development, western economic expansion, and the migration of the data-center industry. Achieving this equilibrium requires three conditions: (i) ELG realizes a positive net payoff from strict regulation, with intergovernmental transfers and coordination subsidies (plus sanctions) fully offsetting enforcement costs, sustaining adherence to national green standards rather than lenient regulation. (ii) WLG secures a positive net payoff from generous incentives: aggregate benefits associated with hosting industrial transfer exceed fiscal outlays and risks, creating fiscal space for a high-attractiveness policy while avoiding a race to the bottom. (iii) DCE obtains a positive net payoff from complete migration: the push from ELG’s strict regulation (costly efficiency compliance and carbon-quota charges) and the pull from WLG’s incentives (energy-cost advantages, green-certificate revenues, subsidies) together cover migration/rebuilding costs and transitional losses, inducing complete migration. When these conditions jointly hold—so that national policy design incentivizes and disciplines ELG and WLG while preserving DCE’s migration surplus—the tripartite evolutionary game converges stably to E₈(1, 1, 1).

Scenario 2. 

When B_W + T_C + mC_W − C_W < 0, B_E + C_C + S_E + T_C + T_E − C_E < 0, and D₂ − D₁ − C_F + E_W − R_E + R_G + S_P + kC_F + kR_E < 0, the system enters complete policy failure and converges to E₁(0, 0, 0): lenient regulation, limited incentives, and partial migration. Central incentives are inadequate, local governments lack initiative, and enterprises display weak migration intent, entrenching the East–West development gap, while escalating AI computing demand further aggravates the East’s energy constraints. Mechanistically: (i) ELG faces a negative net payoff from strict regulation, so to avoid tax base erosion it opts for lenient regulation, tacitly allowing energy-intensive operations. (ii) DCE perceives low regulatory pressure and compliance costs if staying in the East, whereas moving West entails uncertain incentives and high migration costs; thus status quo maintenance and risk avoidance prevail, yielding partial migration at most. (iii) WLG, despite willingness and resource endowments, would incur fiscal dissipation by offering generous incentives without inbound enterprises; given eastern permissiveness and enterprise inaction, its best response is limited incentives to avoid resource misallocation. Overall, this equilibrium embodies a vicious cycle of policy involution, in which poorly designed central incentives and reliance on spontaneous market adjustment push all parties toward conservative strategies, producing the stalemate of no regulation by ELG, no hosting by WLG, and no migration by DCE.

Scenario 3. 

C_E − B_E − T_C < 0, B_W + S_C + T_C + mC_W + mS_G − C_W − S_G − S_W − nS_C < 0, and C_F + D₁ + R_E − R_G − S_P − T_E − kC_F − kR_E − C_C − D₂ − E_W < 0, migration can occur even with insufficient western incentives, yielding a “strong eastern push, weak western pull” configuration. This more realistic intermediate state features ELG’s strict enforcement under strong national pressure, while WLG—constrained by fiscal conditions—offers only limited incentives, so the dynamics converge to E₆(1, 0, 1): strict regulation, limited incentives, complete migration. The equilibrium is an incomplete, push-dominated outcome. Specifically, (i) ELG attains a positive net payoff from strict regulation, as subsidies and penalty avoidance exceed enforcement costs, sustaining compliance with PUE and carbon standards. (ii) WLG faces a negative net payoff from generous incentives and therefore rationally adopts limited incentives to preserve fiscal sustainability. (iii) DCE finds complete migration profitable even under a strong-push/weak-pull regime: high eastern compliance costs, combined with western energy-cost advantages and green-certificate revenues, generate a surplus that more than offsets migration and rebuilding costs. Consequently, tightening eastern green regulation and cost constraints emerges as a potent policy lever: under appropriate conditions, a sufficiently strong eastern push can induce migration toward resource-advantaged regions with effects comparable to—if not greater than—large-scale western subsidies.

Scenario 4. 

When C_W − B_W − S_C − T_C − mC_W + nS_C < 0, C_E − B_E − C_C − S_E − T_C − T_E − nS_C < 0, and C_C − C_F − D₁ + D₂ + E_W − R_E + R_G + S_P + T_E + kC_F + kR_E < 0, the system enters a “coordination impeded—active governments, cautious enterprises” state. Even as ELG maintains strict regulation and WLG offers generous incentives, commercial risks at the enterprise level impede progress, so the dynamics stabilize at E₇(1, 1, 0): strict regulation, generous incentives, partial migration. Specifically, (i) ELG’s strict enforcement yields a positive net payoff even with only partial migration, sustaining a push-out stance; (ii) WLG’s generous incentives also deliver a positive net payoff—owing to sufficient central support or the catalytic value of hosting partial business—thus WLG remains an active host; and (iii) DCE chooses partial migration because the net payoff of complete migration is negative: risks such as service disruption and core-customer loss outweigh policy incentives and cost savings. This equilibrium highlights the need to shift policy focus from pure intergovernmental coordination to removing enterprise-centered frictions—e.g., improving East–West network quality and cultivating western markets for computing-intensive applications—to reduce migration risk and increase enterprises’ willingness to migrate.

4.3. Local Stability Analysis of Equilibria

To visualize how equilibrium stability varies across the four policy–environment scenarios, the signs of the Jacobian eigenvalues at the eight pure-strategy equilibria are evaluated under the conditions specified for each case; the results are summarized in

Table 3. Signs of λ₁, λ₂, λ₃ and Local Stability of Equilibrium Points (Scenarios 1, 2, 3, 4).

Equilibrium Points	Scenario 1		Scenario 2		Scenario 3		Scenario 4
	λ1, λ2, λ3	Stability	λ1, λ2, λ3	Stability	λ1, λ2, λ3	Stability	λ1, λ2, λ3	Stability
E1(0, 0, 0)	?, ?, +	unstable	−, −, −	ESS	+, ?, +	Saddle	?, +, −	unstable
E2(0, 0, 1)	?, ?, +	unstable	?, ?, +	unstable	+, ?, −	unstable	?, +, +	unstable
E3(0, 1, 0)	−, +, ?	unstable	−, +, ?	unstable	+, +, ?	unstable	−, −, ?	unstable
E4(0, 1, 1)	−, +, +	Saddle	−, +, +	Saddle	+, +, −	unstable	+, ?, +	unstable
E5(1, 0, 0)	+, −, ?	unstable	+, −, ?	unstable	−, −, ?	Saddle/ESS	−, −, −	ESS
E6(1, 0, 1)	+, −, +	Saddle	+, −, +	Saddle	−, −, −	ESS	−, −, +	Saddle
E7(1, 1, 0)	+, +, ?	unstable	+, +, ?	unstable	−, +, ?	unstable	−, −, −	ESS
E8(1, 1, 1)	−, −, −	ESS	+, +, +	Source	−, +, −	Saddle	−, −, +	Saddle

Note: (i) In Table 3, “+” and “−” indicate that the eigenvalue signs of the Jacobian at the corresponding equilibrium are positive or negative, respectively. “?” denotes indeterminacy under the scenario-specific assumptions: the sign cannot be uniquely determined and depends on other parameter values in the model. (ii) Source. An equilibrium at which all three eigenvalues are positive; it is a fully unstable repelling point, with trajectories diverging in all directions. (iii) Saddle. An equilibrium with eigenvalues of mixed sign; it is directional, locally attracting along eigen-directions with negative eigenvalues and repelling along those with positive eigenvalues, hence nonstable. (iv) Unstable point. An equilibrium where positive, negative, and undetermined eigenvalues coexist, which is likewise nonstable.

. Analysis of Table 3 reveals several salient properties of the tripartite evolutionary system. (i) The evolutionary trajectory is highly sensitive to the external policy environment: different strategies steer the system toward markedly different terminal equilibria. Under Scenario 1, the dynamics converge to the first-best E₈(1, 1, 1); however, once incentives are lacking—as in Scenario 2—the system rapidly collapses to E₁(0, 0, 0), underscoring that top-level national policy design fundamentally determines whether the data-center industry can achieve a green and orderly spatial configuration. (ii) The system exhibits pronounced path dependence, especially under market frictions, making initial strategy choices pivotal. In Scenario 4 (“migration impeded”), two stable equilibria, E₅ and E₇, emerge; when enterprises are highly cautious and migration willingness is weak, partial migration prevails regardless of whether WLG initially adopts generous or limited incentives—though if WLG chooses limited incentives and k ⟶ 0, no migration may occur. (iii) The ideal cooperative arrangement is fragile; aligning the interests of ELG, WLG, and DCE requires sustained and precisely targeted policy maintenance. Across the 32 potential states, most are unstable saddles or sources, and truly ESS stable equilibria are scarce. The first-best E₈ is stable only in Scenario 1; in all other scenarios it becomes an unstable saddle or source. Hence, realizing the desired industrial layout demands persistent, precisely matched incentives—any single “weak link” can divert the system from the optimal path toward second-best or even inferior equilibria.

5. Simulation Analysis

To further validate the proposed tripartite evolutionary game model and visualize the dynamic evolution of the strategies of ELG, WLG, and DCE under varying conditions, this section conducts numerical simulations. We first assess convergence in the ideal scenario and then examine how initial strategy probabilities and changes in key parameters shape the system’s evolutionary trajectory and equilibrium outcomes.

5.1. Parameter Settings and Initial Values

Parameter values in the numerical analysis are anchored to traceable sources rather than being assigned ad hoc: (i) authoritative industry reports and cost surveys for baseline cost ranges, (ii) officially released transaction statistics and institutional rules for market-linked carbon and green attributes, and (iii) national policy documents for the design logic of central-level instruments, supplemented by closely related peer-reviewed studies [35,36,38]. Specifically, cost parameters in the model—such as data-center migration costs and the regulatory and incentive expenditures of ELG and WLG—follow benchmark ranges reported by national-level industry institutions (e.g., CCID/CAICT). Policy-linked parameters are referenced to China’s institutionalized mechanisms: carbon-related terms follow the compliance-and-trading logic of China’s national Emissions Trading System (ETS) and are benchmarked to published transaction statistics for China Emissions Allowances (CEA), while green attributes are aligned with the official green electricity certificate issuance and trading framework. Monetary quantities are expressed in a unified unit (10⁸ CNY) to ensure computational consistency. To reflect the initiative’s ideal progression—namely, convergence to E₈(1, 1, 1)—a baseline parameter set satisfying the corresponding stability conditions is specified and reported in

Table 4. Baseline parameterization of the simulation model (Unit: 10⁸ CNY).

Parameter	Baseline Value	Parameter	Baseline Value	Parameter	Baseline Value
CE	30	BW	40	TC	15
CW	50	BE	20	TE	25
CF	100	SG	40	D1	10
CC	30	SP	20	D2	5
RG	15	SC	20	m	0.4
RE	80	SE	10	k	0.5
EW	40	SW	10	n	0.5

Note: Parameters m, k, and n are dimensionless weights.

. Baseline parameterization of the simulation model (Unit: 10⁸ CNY). Robustness is then assessed through the sensitivity experiments in Section 5.3, and detailed parameter definitions and source notes are documented in Appendix A. In this two-strategy replicator setting, the boundary equilibria E₁–E₈ are fixed corner points, whereas empirical parameterization affects which equilibrium is locally stable and therefore selected in the long run. This mechanism is illustrated in Section 5.3 by showing how parameter variations can move the system out of the stability domain of E₈(1, 1, 1) and lead to convergence to alternative stable outcomes.

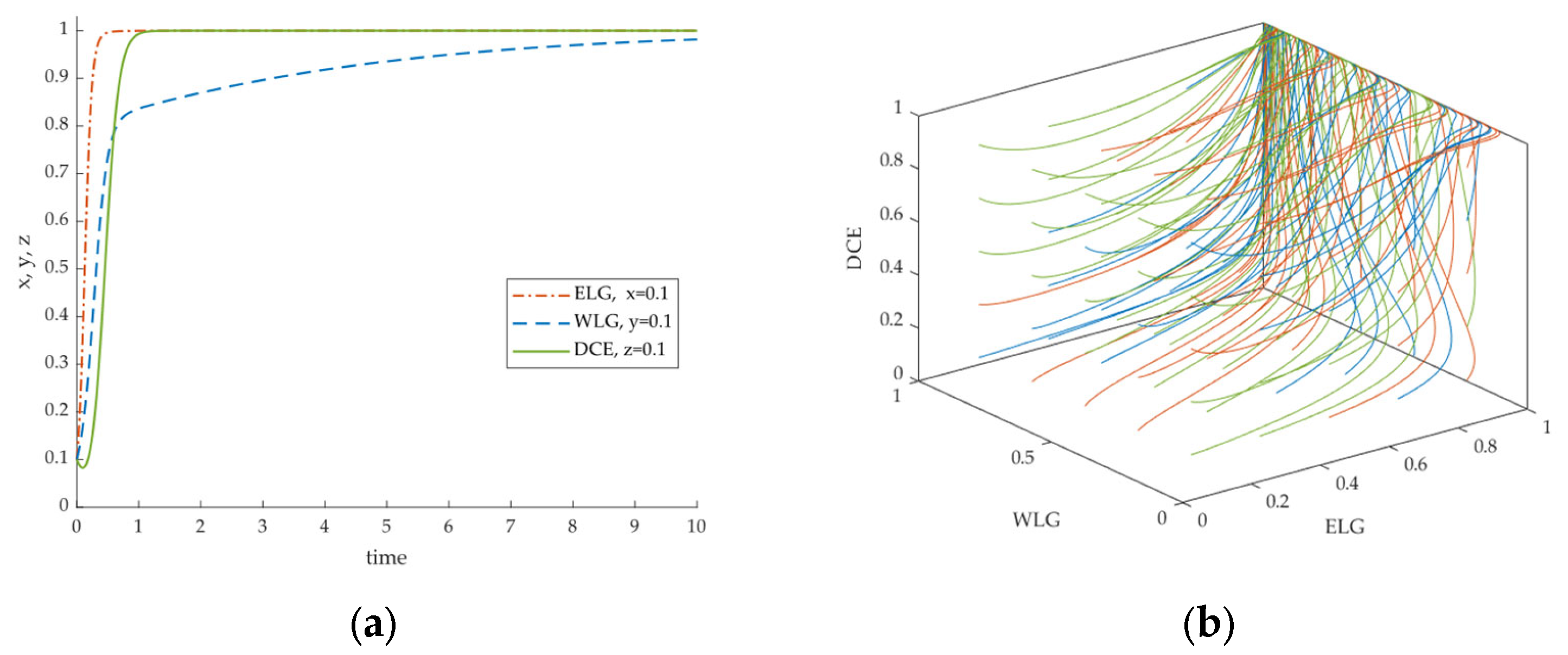
5.2. Model Stability Analysis

As a core feature of the dynamic game system, the strategy chosen by any one player exerts a significant influence on the decision-making of the other parties. Based on the baseline parameter values, a specific initial strategy profile (x₀, y₀, z₀) = (0.1, 0.1, 0.1) is selected, and numerical simulations are used to trace the time evolution of the three players’ strategies. As shown in Figure 3a, although the initial strategic propensities of all three players are low, under the baseline parameters the probabilities of ELG’s strict regulation strategy (x), WLG’s generous incentives strategy (y), and DCE’s complete migration strategy (z) all rise rapidly over time and eventually converge to 1. Among them, ELG’s strategy evolves fastest, followed by DCE, while WLG exhibits the slowest adjustment speed. This provides preliminary evidence that, under the ideal parameter configuration, the system tends to evolve toward the target equilibrium E₈(1, 1, 1). To further assess stability under different initial conditions, multiple initial strategy profiles are sampled over (0, 1) for x, y, and z at intervals of 0.2, yielding 216 initial points in total. Numerical simulations are then performed for these initial points to examine the overall evolutionary trajectories, as shown in Figure 3b. The results indicate that, despite heterogeneous initial strategies, all trajectories ultimately converge to the equilibrium E₈(1, 1, 1). This provides strong support that, under the baseline parameterization, E₈(1, 1, 1) is globally asymptotically stable, thereby corroborating the preceding theoretical derivations.

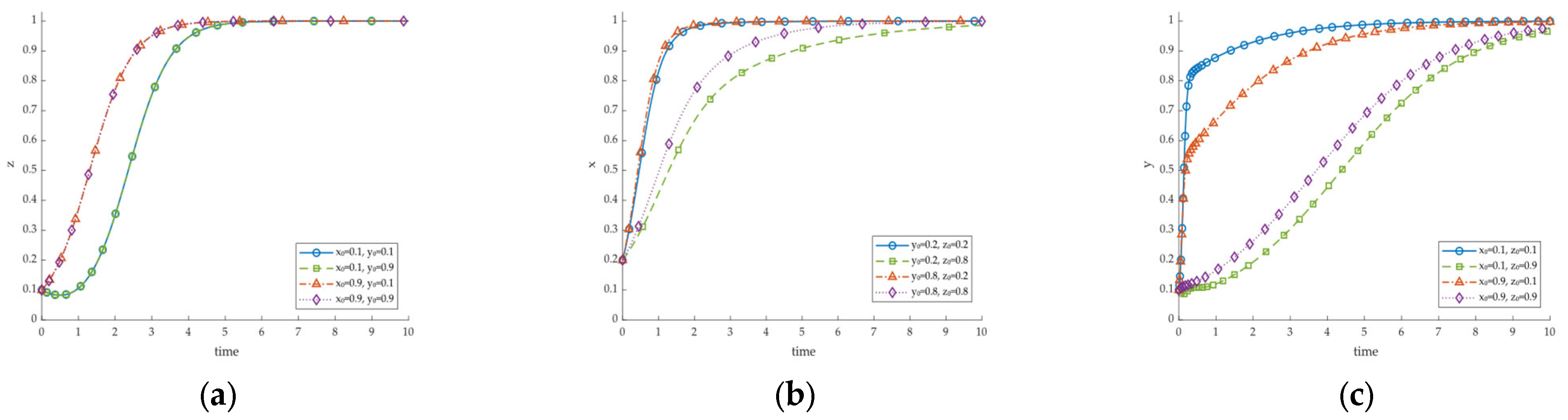
5.3. The Initial Willingness and Its Impact on the Strategy Evolution of the Three Parties

After confirming stability and convergence under the baseline parameters, the analysis turns to how the three players’ initial strategic willingness (initial probabilities) shapes the system’s early-stage dynamic evolution. By fixing one player’s initial willingness and varying that of the other two, the mutual influences and transmission mechanisms among their strategy choices can be identified.

5.3.1. Impact of ELG and WLG’s Initial Willingness on DCE’s Migration Decision

To examine how the initial willingness of the Eastern local government (ELG) and the Western local government (WLG) affects the data center enterprise’s (DCE) migration decision, the initial choice probability of DCE is fixed at z₀ = 0.1, while the initial willingness of ELG and WLG, x₀ and y₀, is set to 0.1 or 0.9 to generate four different initial willingness combinations. The evolutionary path of the enterprise’s migration probability z is then observed, as shown in Figure 4a. The simulation results show that DCE’s migration decision is sensitive to the local governments’ initial strategies. Although in all four scenarios the enterprise’s decision converges to complete migration (z = 1), the speed of convergence differs: when both ELG’s willingness to adopt strict regulation and WLG’s willingness to adopt generous incentives are high (x₀ = 0.9, y₀ = 0.9), DCE’s strategy evolves fastest, whereas low initial willingness on both sides (x₀ = 0.1, y₀ = 0.1) yields the slowest evolution. This suggests that an active and coordinated initial stance across central and local governments can significantly accelerate enterprises’ westward migration decisions, with the push generated by eastern regulation and cost pressure acting as a more fundamental driver than the pull created by western incentive policies.

5.3.2. Impact of WLG and DCE’s Initial Willingness on ELG’s Regulatory Decision

With ELG’s initial choice probability fixed at x₀ = 0.1, the analysis then examines how the initial behavior of WLG and DCE feeds back into ELG’s decision. The initial willingness probabilities y₀ and z₀ are set to 0.1 (low willingness) and 0.9 (high willingness) to form four combinations, and the evolutionary path of ELG’s strategy x is observed, as shown in Figure 4b. The evolution speed of ELG’s strategy depends primarily on DCE’s initial migration willingness z₀, when the enterprise’s initial migration willingness is low (z₀ = 0.1), ELG’s evolution toward strict regulation is very rapid regardless of WLG’s initial willingness, whereas when the enterprise already exhibits strong migration willingness (z₀ = 0.9), the urgency for ELG to adopt strict regulation declines and the evolution of its strategy slows markedly. This indicates that ELG’s regulatory behavior is highly adaptive. When the core market actor lacks migration momentum, ELG, as the main source of push, intervenes more quickly and proactively to ensure the achievement of strategic objectives.

5.3.3. Impact of ELG and DCE’s Initial Willingness on WLG’s Incentive Decision

Similarly, the initial choice probability of WLG is fixed at y₀ = 0.1, while the initial willingness of ELG and DCE, x₀ and z₀, is set to 0.1 (low willingness) or 0.9 (high willingness) to form four combinations. The evolutionary path of WLG’s incentive strategy y is then observed, as shown in Figure 4c. The simulation results show that the evolution of WLG’s strategy is significantly influenced by both ELG and DCE. DCE’s initial migration willingness z₀ is the key factor shaping WLG’s decision: when migration willingness is low, WLG’s evolution toward the generous incentives strategy accelerates markedly, whereas strong migration willingness leads to noticeably slower evolution. This reveals a form of strategic adaptiveness in WLG’s pull: when enterprises’ migration willingness is insufficient, WLG responds more actively and rapidly by offering generous incentives to enhance its attractiveness, while once enterprises display strong willingness, the urgency of providing large fiscal subsidies diminishes. ELG’s initial strategy x₀ plays a moderating role. When enterprise migration willingness is low (z₀ = 0.1) and the push from ELG is also weak (x₀ = 0.1), WLG’s evolution is the fastest, suggesting that when WLG perceives a “double-low” situation in both push and enterprise willingness, it chooses to maximize its pull to promote migration. By contrast, when enterprise migration willingness is high (z₀ = 0.9) but the push from ELG remains weak (x₀ = 0.1), WLG’s evolution is the slowest, approximating a free-riding behavior.

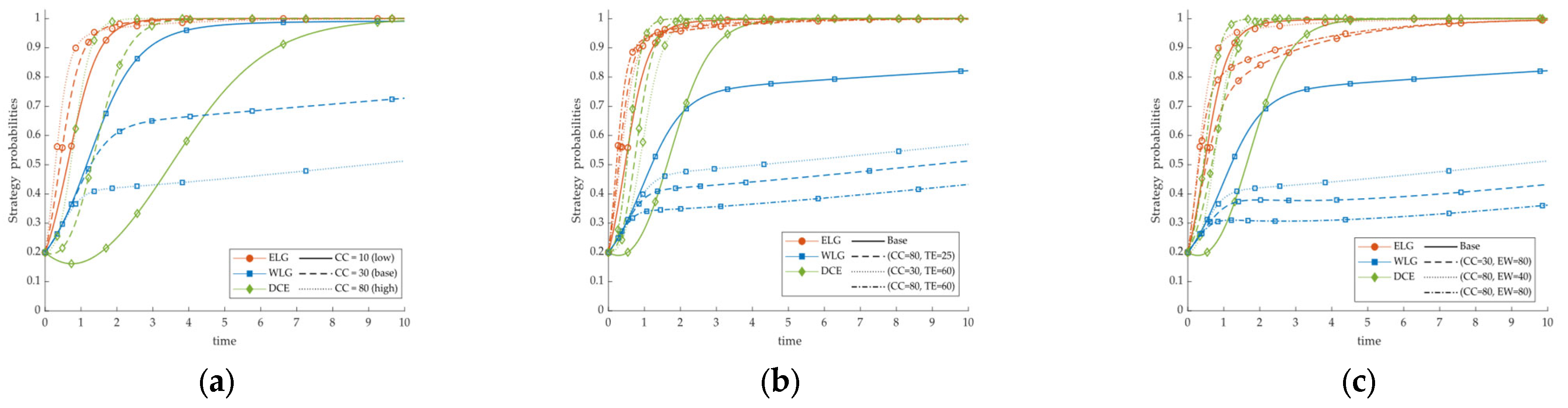
5.4. Sensitivity Analysis of Policy Parameters

Building on the preceding model, this section conducts numerical simulations to assess how changes in key parameters affect the evolutionary paths of the three players’ strategies and the long-run equilibria, and to elucidate the mechanisms of different policy instruments. To capture joint effects among ELG, WLG, and DCE and to characterize how policy portfolios shape strategic evolution, the analysis focuses on parameters that influence at least two agents’ payoffs across four dimensions, energy and green constraints, policy penalties, regional coordination incentives, and migration risk, and selects nine parameters for sensitivity testing. Specifically, the parameters are the enterprise carbon-quota cost (C_C), the eastern penalty revenue (T_E), western energy advantage return (E_W), the central PUE-compliance subsidy (S_P), the central penalty cost (T_C), the central regional-coordination subsidy (S_C), and the allocation ratio of the coordination subsidy (n), the loss from complete migration (D₁), and the loss from partial migration (D₂). Among these parameters, the carbon-quota cost (C_C) is pivotal because it directly links ELG’s regulatory return to DCE’s migration incentive. The sensitivity exercises therefore consider three settings, varying C_C alone, jointly varying C_C and T_E, and jointly varying C_C and E_W. These settings allow examination of how changes in the relative strength of the eastern carbon constraint and the western energy advantage under green regulation affect enterprise migration choices and the type of equilibrium attained. In addition, to identify the effects of central-level instruments on system trajectories, the analysis varies the central PUE-compliance subsidy (S_P) and the central penalty cost (T_C) to assess how subsidy and penalty intensities influence DCE and the stability of local strategic coordination. It also examines the central regional-coordination subsidy (S_C) and its allocation ratio (n) under the baseline setting, evaluating how the scale of coordination incentives and the distribution of benefits between the East and the West shape the long-run choices of the three agents. Finally, the analysis examines how data-center migration risk influences enterprises’ willingness to migrate.

From a mathematical perspective, the numerical sensitivity experiments in this section can be interpreted as probing the partial derivatives of the replicator dynamics with respect to key policy parameters. For instance, varying the carbon-quota cost C_C corresponds to examining how F(x), F(y), and F(z) respond locally to C_C, i.e., F(x)/∂C_C, F(y)/∂C_C, and F(z)/∂C_C (and similarly for subsidy-related parameters such as S_P). In practice, this derivative-based interpretation is implemented numerically by perturbing a parameter around its baseline value and re-integrating the system, which provides a finite-difference approximation to the corresponding local derivative effect [39]. Accordingly, the simulated changes in evolutionary trajectories, convergence patterns, and long-run outcomes offer a derivative-consistent numerical illustration of the model-implied parametric sensitivities and their implications for evolutionary adjustment and stability [40]. In interpretation, F(x)/∂C_C (and analogously for F(y) and F(z)) quantifies how a marginal change in C_C alters the instantaneous evolutionary “velocity” of the corresponding strategy probability at a given state. The simulations then aggregate these local effects over time through numerical integration, thereby linking derivative-based sensitivity to observable changes in trajectories, convergence patterns, and equilibrium outcomes.

In the simulations, the initial strategy probabilities are set to x₀ = y₀ = z₀ = 0.2. Parameter values are then varied to compare changes in evolutionary trajectories and long-run stable equilibria, with particular attention to whether the green, coordinated migration outcome, ELG strict regulation, WLG generous incentives, and DCE complete migration—emerges more readily, and to how convergence speed and path characteristics differ across policy portfolios.

5.4.1. Sensitivity Analysis of Carbon-Quota Cost Combined with Green Penalties and Energy Advantages (C_C, T_E, E_W)

Figure 5a–c depict the time paths of the strategy selection probabilities for the Eastern Local Government (ELG), the Western Local Government (WLG), and the data-center enterprise (DCE) under policy scenarios that vary the carbon-quota cost (C_C) and its combinations with other parameters. Overall, within the parameter ranges shown, whether C_C is increased alone or combined with the eastern penalty revenue (T_E) or the western energy-advantage return (E_W), all three probabilities converge to values close to 1, which corresponds to the ideal equilibrium E₈(1, 1, 1) in Scenario 1. This indicates that the net payoffs of ELG strict regulation, WLG generous incentives, and DCE complete migration remain positive in the present ranges, and the system stays in the optimal region of the “Eastern Data, Western Computing” strategy.

In Figure 5a, which varies C_C only, the trajectories of x, y, and z differ across C_C = 10, 40, and 80. As C_C rises from a low to a high level, the increase in x accelerates and, under high C_C, x converges to 1 early, reflecting higher carbon-quota revenue under partial migration that raises ELG’s net return from strict regulation and strengthens regulatory intensity. By contrast, the slope of y becomes flatter as C_C increases and its steady level within the window is slightly lower, indicating that when the carbon-cost constraint is sufficiently strong, eastern push effects dominate and the West can accept inflows without maintaining very high incentive intensity. The sensitivity of z to C_C is most pronounced, under low C_C, z climbs slowly, whereas under high C_C it approaches 1 much faster. Higher carbon-quota costs compress the scope for retaining eastern operations and accelerate convergence to complete migration, consistent with C_C entering the enterprise payoff as a cost term in Scenario 1.

Building on the single-parameter analysis, Figure 5b and Figure 5c report the combination settings (C_C, T_E) and (C_C, E_W), respectively. In Figure 5b, relative to the baseline case (C_C = 30, T_E = 25), three variants are considered: higher C_C only (C_C = 80, T_E = 25), higher T_E only (C_C = 30, T_E = 60), and both higher (C_C = 80, T_E = 60). As T_E increases, the rise of x becomes notably faster and, under high T_E, x approaches 1 almost at the outset. Penalties associated with PUE and carbon compliance directly raise the return to strict regulation, giving ELG stronger incentives to adopt a high intensity stance early. Meanwhile, y in some settings declines slightly or its increase slows, indicating that in a strong constraint environment based on carbon costs and penalties, migration is driven mainly by negative incentives on the eastern side and the West can benefit from spillovers without raising incentive intensity. For DCE, although z eventually converges to 1 in all (C_C, T_E) cases, its speed is not always the highest compared with the (C_C, E_W) cases. In the baseline and some high-penalty combinations, z exhibits a nonmonotonic path with a slight initial dip followed by a gradual rise, reflecting a reassessment phase as the enterprise weighs complete migration losses against carbon and penalty pressures. In Figure 5c, relative to the baseline (C_C = 30, E_W = 40), three variants are considered: higher C_C only (C_C = 80, E_W = 40), higher E_W only (C_C = 40, E_W = 80), and both higher (C_C = 80, E_W = 80). Increasing E_W has a milder effect on ELG behavior. Although x still converges to a high level across settings, its speed is lower than under high T_E, which suggests that strengthening the western energy advantage works mainly through the pull side by improving the long run return structure and lowering electricity costs rather than directly boosting ELG’s regulatory return. For WLG, higher E_W raises the economic value of renewable supply and allows incentives to complement energy endowments, which supports a higher long run level of y. More importantly, convergence of z under (C_C, E_W) is generally faster than under (C_C, T_E). Raising E_W, especially together with raising C_C, makes z approach 1 earlier and more smoothly. By contrast, in the baseline, z converges most slowly and shows an initial decline before rising, indicating clear hesitation about complete migration when the energy advantage and the penalty mechanism are not yet strong.

Collectively, Figure 5a–c demonstrate that within the parameter region associated with Scenario 1, the system converges to the ideal equilibrium E₈(1, 1, 1) whenever the three net payoff constraints remain positive. However, different configurations of carbon costs, penalties, and energy advantages significantly affect convergence speed and the distribution of policy pressure across the three agents. The strong constraint policy mix that layers T_E on C_C increases ELG’s regulatory return and the enterprise’s noncompliance cost, which strengthens short term push forces and partially substitutes for WLG incentives. The eastern pressure and western advantage mix that pairs C_C with E_W enhances the West’s long run comparative advantage and reduces operating costs, which promotes enterprise migration more persistently and often yields faster convergence of z. The comparison suggests that policy design should coordinate eastern cost constraints, western energy advantages, and enterprise migration risk in order to balance efficiency and stability while keeping the equilibrium type unchanged.

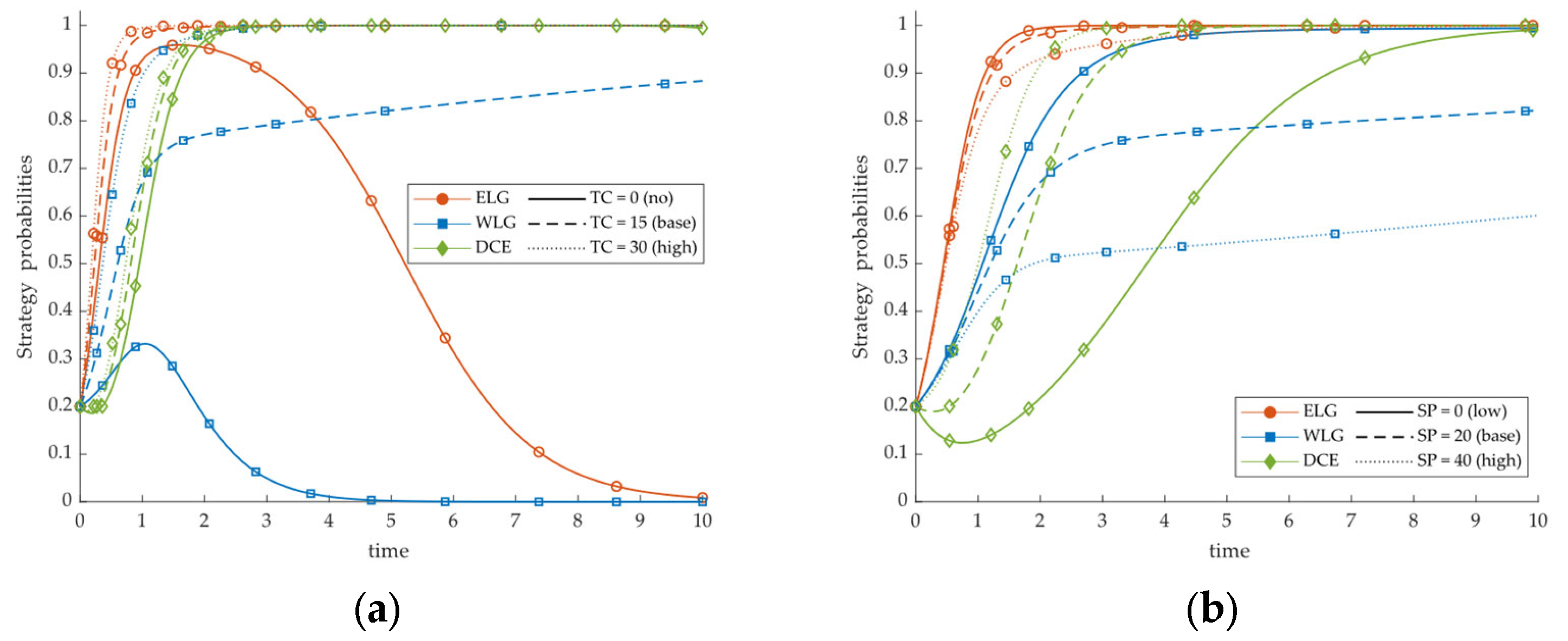
5.4.2. Sensitivity Analysis of Central Penalty Cost (T_C)

This subsection examines how the central penalty cost (T_C) shapes the strategic evolution of ELG, WLG, and DCE. Figure 6a presents the time paths of the strategy selection probabilities under three scenarios, namely no penalty (T_C = 0), baseline penalty (T_C = 15), and high penalty (T_C = 30).

When T_C = 0, which implies the absence of effective central accountability, ELG’s probability of strict regulation x rises rapidly at the outset due to carbon-cost and penalty-revenue drivers, then intersects with DCE’s probability of complete migration z. As migration proceeds and eastern energy and emissions pressures ease, the marginal return to strict regulation declines, so x falls and remains low. WLG’s probability of generous incentives y also increases initially, but with migration largely completed and diminishing marginal returns to investment attraction, the lack of central penalties leads WLG to scale back incentives, and y gradually approaches 0. Hence, without T_C, DCE still converges to complete migration under the present parameters, yet local policy execution exhibits an early effort followed by relaxation, which risks drifting from the ideal coordinated state toward intermediate states marked by a strong eastern push with weak western pull or by impeded coordination. When T_C increases to the baseline and high levels, the trajectories differ markedly. As T_C rises from 0 to 15 and then to 30, the rise of x accelerates and remains near one without a noticeable decline. The path of y shifts from rise then fall to rapid rise with a sustained high level, since central accountability for lax regulation and passive undertaking keeps both governments motivated to maintain coordinated policies even after most migration has been completed. At the same time, z is also sensitive to T_C, and stronger penalties make z approach 1 earlier and faster, which indicates that central accountability accelerates convergence from partial to complete migration by strengthening coordinated pressure on strict regulation in the East and active undertaking in the West.

5.4.3. Sensitivity Analysis of Central PUE-Compliance Subsidy (S_P)

In the central policy dimension, in addition to the accountability-based central penalty cost (T_C), the central government can directly affect enterprise migration returns by subsidizing compliant data centers. To evaluate the role of the central PUE-compliance subsidy (S_P), this section holds all other baseline parameters constant and sets S_P to no subsidy (S_P = 0), a baseline level (S_P = 20), and a high level (S_P = 40); the simulation outcomes are shown in Figure 6b.

Overall, across the three subsidy levels, the probabilities that ELG adopts strict regulation, WLG adopts generous incentives, and DCE adopts complete migration all converge close to 1, and the long-run equilibrium remains the ideal state E₈(1, 1, 1) described in Scenario 1. This indicates that, within the present parameter ranges, once key conditions such as the carbon-quota cost, local incentives, and energy advantages make the three net-payoff constraints of Scenario 1 hold, adjustments to S_P do not change the evolutionarily stable strategy (ESS) but instead affect convergence speed and the shape of the trajectories within the existing equilibrium region.

From ELG’s perspective, because S_P enters only the enterprise payoff function, its effect on ELG’s immediate payoff differential is limited; the paths of x under the three scenarios nearly overlap, each approaching one rapidly at the outset and then remaining stable. This suggests that ELG’s choice of strict regulation is driven primarily by C_C, T_E, and T_C, whereas S_P influences the eastern regulatory environment indirectly by altering enterprise migration decisions rather than directly triggering a policy switch. For WLG, the generous incentives probability y responds visibly to S_P. When S_P = 0, y rises quickly early on; as S_P increases from 0 to 20 and 40, the slope of y flattens and, within the same horizon, it has not yet converged to 1, instead showing a gradual rise toward a high plateau. This indicates that higher S_P partly reduces the need for WLG to sustain very high incentive intensity, since larger central subsidies substitute for deep local concessions once enterprises complete migration and meet PUE standards. For DCE, the impact of S_P is more direct and pronounced: as S_P rises from 0 to 40, the increase in the probability of complete migration z accelerates markedly. Under no subsidy, z converges slowly and exhibits a nonmonotonic path with a slight early dip followed by a gradual rise, whereas under high subsidy the higher long-run payoff from complete migration with PUE compliance partially offsets perceived migration risks, so z approaches 1 earlier, indicating that S_P accelerates the evolution from partial migration to complete migration.

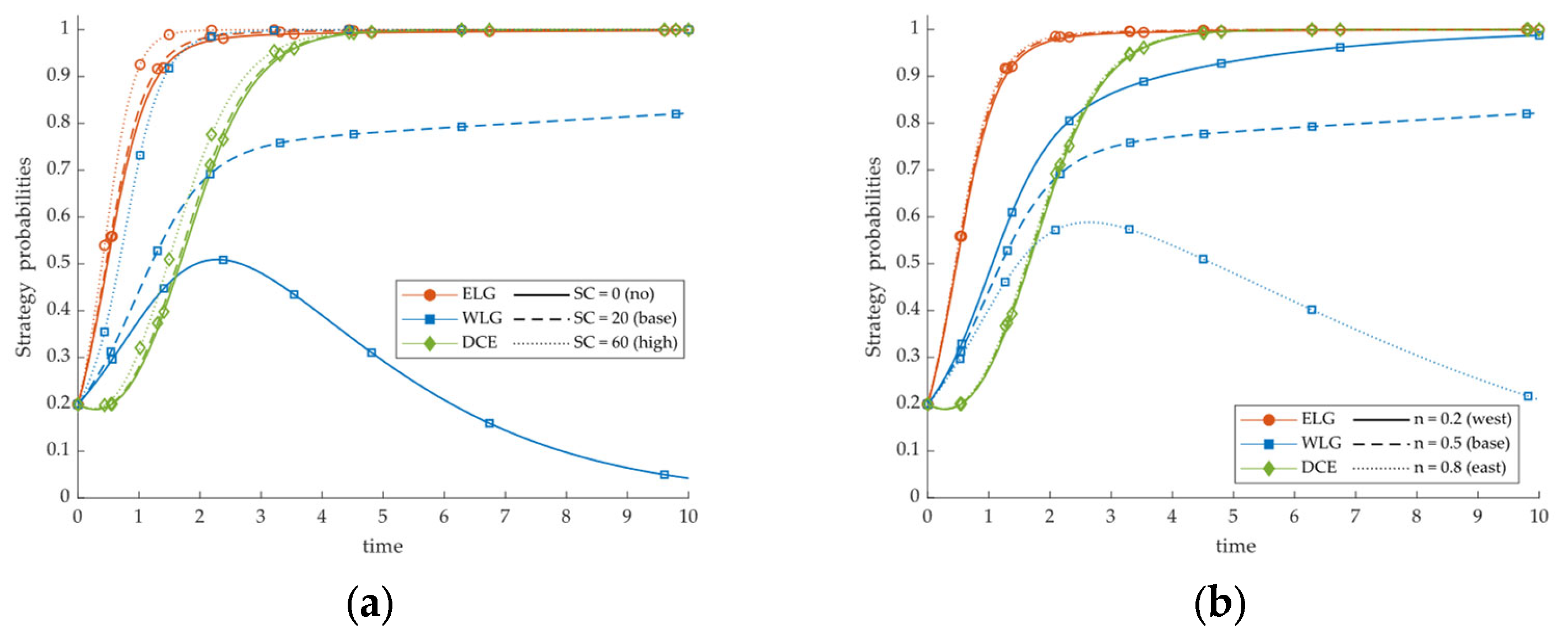
5.4.4. Sensitivity Analysis of Central Regional-Coordination Subsidy and Allocation Ratio (S_C, n)

In the regional-coordination dimension, the central regional-coordination subsidy (S_C) and its allocation ratio (n) between the East and the West are pivotal parameters that simultaneously enter the payoff functions of the Eastern Local Government (ELG) and the Western Local Government (WLG). Figure 7a shows the evolutionary paths of the three players under S_C = 0, 20 (baseline), and 60, whereas Figure 7b keeps the total subsidy at the baseline and varies the allocation ratio from West-skewed (n = 0.2) to even split (n = 0.5) and East-skewed (n = 0.8), to examine the effect of distributional structure. As Figure 7a indicates, increasing S_C from 0 to 60 continuously accelerates the rise of ELG’s strict-regulation probability x; higher SC makes x approach one earlier, implying that the central reward for the “ELG strict regulation + WLG generous incentives” combination raises ELG’s net return from strict regulation, consistent with Scenario 1. The probability of complete migration z converges to one across all cases, and convergence is faster at higher S_C, showing that stronger coordination increases the combined eastern push and western pull and accelerates the transition from partial to complete migration. Unlike ELG and DCE, WLG’s response to S_C is nonlinear: for S_C = 0 and 20, y rises and approaches one, whereas for S_C = 60 it first increases and then recedes toward zero, indicating that an overly large S_C with an unchanged allocation can reduce WLG’s relative net return under “generous incentives + coordination” and shift the system toward Scenario 3 with convergence to E₆(1,0,1). If, relative to the baseline parameters, enterprise migration costs or risk losses are further increased, the system may drift toward Scenario 4 and evolve into a partial-migration state characterized by active governments and cautious enterprises. With S_C fixed at the baseline, Figure 7b shows that x and z are nearly indistinguishable and converge rapidly to values close to one for n = 0.2, 0.5, and 0.8; hence, spatial reallocation of S_C does not alter the complete migration outcome nor ELG’s incentive to sustain strict regulation, provided the net return conditions hold in Scenarios 1 or 3. By contrast, y is highly sensitive to n, it stays highest for n = 0.2, rises to a lower plateau for n = 0.5, and peaks then declines for n = 0.8, mirroring the high-S_C pattern in Figure 7a and again pointing toward the Scenario 3 structure of strong eastern push and weak western pull.

These findings underscore the double-edged nature of central coordination. A moderate S_C coupled with a balanced allocation ratio n helps satisfy the three net-payoff constraints of Scenario 1 and supports stable convergence to the ideal equilibrium E₈(1, 1, 1). However, when S_C is excessive and strongly East-skewed, WLG’s net return to high incentives is eroded, and the system drifts toward the Scenario 3 configuration of strong push and weak pull while maintaining strict regulation and complete migration. Designing cross-regional incentives should therefore balance the total S_C with the dynamic distribution of benefits between East and West to reinforce ELG’s regulation without crowding out WLG’s willingness to sustain generous incentives.

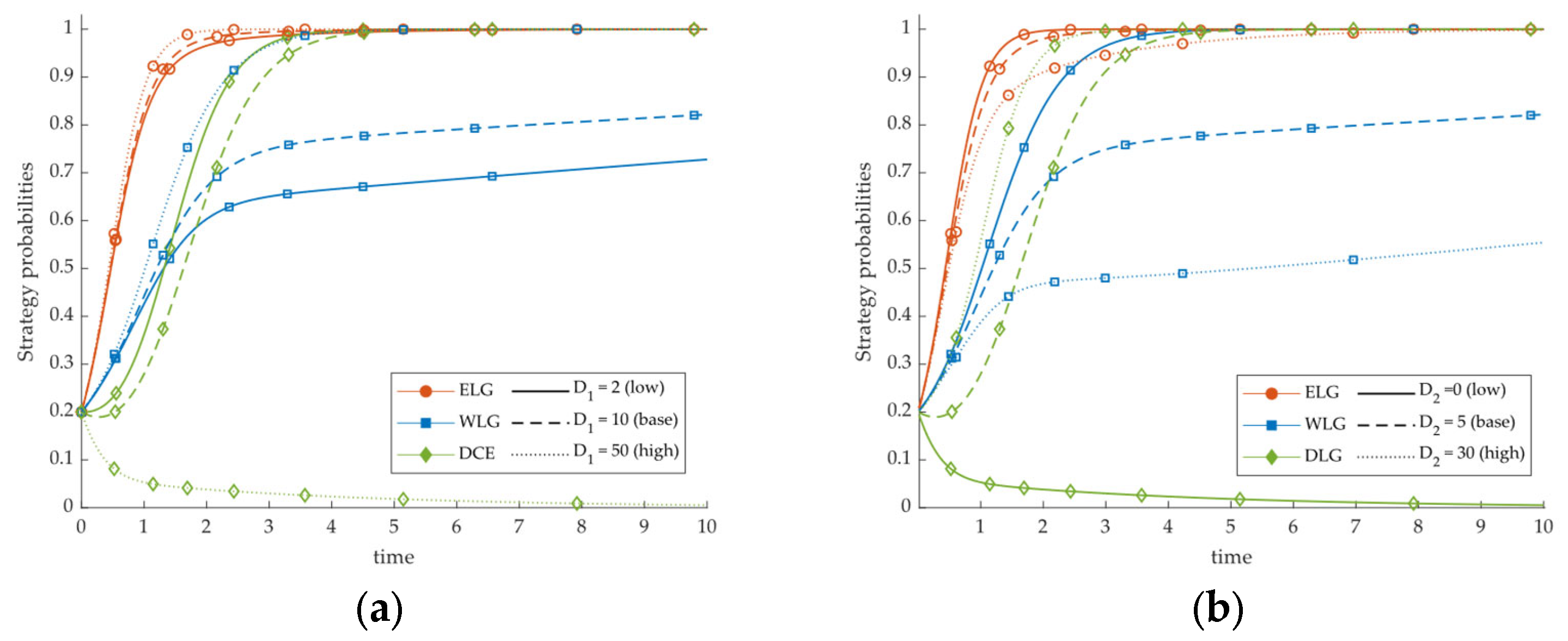
5.4.5. Sensitivity Analysis of Migration-Loss Parameters (D₁, D₂)

At the enterprise-decision level, the complete migration loss (D₁) and partial migration loss (D₂), which reflect commercial risks during migration (such as service interruption, customer churn, and service quality degradation), are key parameters that differentiate the net returns between complete and partial migration. Figure 8a and Figure 8b report the evolutionary trajectories of the three players’ strategy probabilities when varying D₁ and D₂, respectively. In Figure 8a, holding other parameters at their baseline values, the complete-migration loss is set to D₁ = 2 (low), D₁ = 10 (base), and D₁ = 50 (high). As D₁ increases from low to high, the ascent of ELG’s strict-regulation probability x and WLG’s generous incentives probability y accelerates, and both ultimately converge close to 1 across all settings. This indicates that, regardless of enterprises’ migration choices, central incentives and accountability sustain the governments’ motivation to maintain the “strict regulation plus high incentives” policy mix, consistent with the positive-government–payoff conditions in Scenarios 1 and 4. By contrast, DCE’s behavior is highly sensitive to D₁; under low-risk and baseline settings, the probability of complete migration z converges to 1. When D₁ rises to a high level (D₁ = 50), z drops rapidly at the outset and gradually converges to zero, implying a switch to partial migration. The system then shifts toward the Scenario 4 configuration: ELG maintains strict regulation and WLG high incentives, yet the firm’s net return to complete migration becomes negative due to excessive D₁, leading to a cautious, symbolic partial migration response under policy pressure.

Figure 8b fixes D₁ at its baseline and varies the partial migration loss to D₂ = 0 (low), D₂ = 5 (base), and D₂ = 30 (high). The trajectories of ELG and WLG change little across scenarios; the probabilities of strict regulation and generous incentives converge rapidly to high levels. This suggests that local-government optima are governed primarily by policy returns and central constraints and are relatively insensitive to D₂. DCE exhibits the opposite pattern. When D₂ = 30, partial migration entails sizable quality and reputational losses, so enterprises prefer to bear the risk of complete migration, and z rises rapidly toward one. Under the baseline D₂ = 5, z also converges to one but at a slower rate. When D₂ = 0, partial migration is virtually costless; z declines early and converges to 0, indicating persistent partial migration as enterprises compare high risks of complete migration to negligible costs of partial migration. The system thus again falls into the Scenario 4 equilibrium E₇(1,1,0) of active governments and cautious enterprises.

Taken together, Figure 8a,b show that the migration-loss parameters largely determine whether the system converges to the ideal coordinated equilibrium of Scenario 1 or drifts toward the partial-migration trap of Scenario 4. Low values of D₁ and moderate values of D₂ keep the net return to complete migration positive under strong eastern regulation, high western incentives, and central inducements, leading the system to evolve to E8(1, 1, 1). Conversely, when D₁ is excessive or D₂ is very low, enterprises remain in partial migration due to risk considerations even if governmental push and pull are in place, yielding Scenario 4 with active governments and cautious enterprises. This finding implies that, beyond shaping the policy environment through carbon costs, subsidies, and penalties, reducing commercial losses in networking, market access, and operations is also critical to breaking the partial migration equilibrium and advancing the implementation of the “Eastern Data, Western Computing” initiative. More specifically, a higher D₁ can be associated with the physical processes of complete migration—such as server transportation and equipment reassembly—where logistics costs, transit time, and supply-chain stability amplify service interruption risks, customer churn, and temporary service-quality degradation. By contrast, D₂ is closely related to communication-infrastructure conditions under partial migration, where cross-regional network latency, bandwidth availability/costs, transmission stability, and data-transmission efficiency shape the operational penalties of keeping workloads split across regions.

6. Conclusions

6.1. Summary and Conclusions

Against the backdrop of surging computational demand in the AI era and the resulting regional mismatch between data-center deployment and energy endowments across eastern and western China, this study addresses the optimization of migration decisions and develops a tripartite evolutionary game model involving the Eastern Local Government (ELG), the Western Local Government (WLG), and data-center enterprises (DCE). The model incorporates policy and cost parameters and examines strategic interactions and evolutionary trajectories under energy-efficiency regulation, carbon constraints, fiscal subsidies, and migration risk. Numerical simulations and sensitivity analyses reveal how alternative policy instruments and cost structures shape migration equilibria, from which the principal conclusions and policy implications are derived.

• There exist multiple attainable equilibria and the coordinated optimum does not arise spontaneously. The system can converge to a coordinated state with strict regulation, high incentives, and complete migration; to a policy-failure state with lenient regulation, low incentives, and partial migration; or to intermediate outcomes such as a strong eastern push with weak western pull or active governments with cautious enterprises. Only when the intensities and structures of eastern regulation, western incentives, and central rewards and penalties are well aligned does the system converge stably to the coordinated optimum; otherwise it tends to remain in suboptimal or failing states.
• The eastern regulatory push is the primary driver, while western incentives and central policies amplify and calibrate these driving effects. Raising eastern carbon-quota costs and environmental penalties significantly accelerates convergence to complete migration and reduces dependence on large western subsidies, indicating that strong constraints are more effective than subsidies alone in promoting complete migration. Western energy-cost advantages and local incentives display threshold effects: below the threshold, migration costs dominate and firms prefer partial migration; above the threshold, these factors primarily affect the speed of convergence. Central penalties provide a baseline constraint on local behavior, whereas PUE-compliance and regional-coordination subsidies improve return expectations and reduce policy uncertainty, thereby accelerating coordination; excessive subsidy levels or East-skewed allocations may erode WLG’s capacity to sustain high incentives and divert the system from the ideal state.
• Migration risk is pivotal for understanding persistent partial migration under otherwise favorable policy environments. When complete migration entails substantial business-interruption and customer-loss costs and partial migration is nearly costless, firms adopt a conservative partial-migration strategy; lowering the risk of complete migration and moderately raising the opportunity cost of partial migration are necessary prerequisites for converting policy push and pull into firm action and moving the system from a partial-migration equilibrium to coordinated complete migration.

6.2. Policy Recommendations

Based on the evolutionary equilibrium analysis, policy recommendations are organized by actor (ELG, WLG, the central government, and DCE) to clarify implementation priorities and responsibilities.

• Eastern Local Government (ELG): Strengthen a credible regulatory push. ELG should reinforce green regulation by strictly enforcing energy-efficiency and carbon-compliance requirements and by progressively increasing compliance costs (e.g., via carbon pricing, C_C) to discourage low-efficiency capacity. To avoid disruptive shocks, phased arrangements—such as time windows for technological upgrading and staged relocation—should accompany enforcement, thereby improving policy credibility and strengthening the regulatory “push”.
• Western Local Government (WLG): Build sustainable hosting competitiveness. WLG should shift from short-term subsidy competition (e.g., S_G) toward long-term competitiveness in total cost and business environment. Priority should be given to expanding reliable renewable-energy supply and upgrading backbone networks and supporting services, which can reduce migration frictions and operational losses (e.g., D₁, D₂) and make the “pull” fiscally sustainable beyond the subsidy period. In addition, practical “migration-enablement” measures are needed, such as providing secure and standardized logistics services for server/equipment transportation and reassembly, setting up installation and commissioning support capacity, and improving cross-regional connectivity through dedicated bandwidth/peering arrangements and stability-oriented service guarantees.
• The central government: Coordinate incentives and constraints to align regions. Central-level instruments should be designed to prevent local inaction while stabilizing expectations. Coordination subsidies (e.g., S_C) can be made conditional on the joint adoption of stringent regulation and meaningful incentives, and should be combined with enforceable penalties (e.g., T_C) and balanced interregional transfers to align incentives without crowding out western participation. To address infrastructure bottlenecks directly, central programs can prioritize interregional backbone upgrades that reduce latency and improve transmission stability, and support “green-channel” institutional arrangements for data-center relocation (e.g., streamlined permitting and standardized technical/operational requirements for secure transportation and commissioning).
• Data-center enterprises (DCE): Reduce complete-migration risks and convert policy signals into action. To lower effective losses from complete migration, a staged relocation roadmap should be supported by risk-compensation tools (e.g., migration insurance and green financing for first movers). In parallel, strengthening cross-regional high-speed interconnection and computing-scheduling platforms and cultivating western demand for computing services can improve revenue stability after relocation. Operationally, migration plans should incorporate redundancy and service-continuity arrangements (e.g., data replication and performance-oriented network service commitments) to reduce interruption risk and customer-loss pressure during relocation.

6.3. Global Generalizability

Although this study is motivated by China’s East–West mismatch between computing demand and low-carbon energy endowments, the policy logic is transferable to other economies with similar spatial asymmetries (e.g., demand concentrated in electricity-constrained load centers and clean energy potential located in resource-abundant regions). In such settings, the model’s instruments can be mapped to local institutions: C_C reflects carbon pricing or compliance costs, S_P/T_C correspond to efficiency-oriented rewards and penalties, and S_C together with n represent interregional transfer or cost-sharing rules that align incentives across jurisdictions. This mapping facilitates comparative assessments of policy portfolios under different market designs and infrastructure constraints, and suggests that effective outcomes should be pursued through a balanced mix of credible constraints, sustainable pull factors, and coordination mechanisms rather than subsidies alone.

6.4. Limitations and Further Research

The model captures East–West heterogeneity through an asymmetric specification of ELG and WLG (different policy instruments, constraints, and payoff components), but it abstracts the East and West as single representative governments and treats DCE as a representative decision-maker; hence, within-region heterogeneity across provinces and across firm types is not explicitly modeled. Future research may extend the framework to multi-region and multi-type settings (e.g., province-level governments and heterogeneous data-center firms) to examine how interregional competition–cooperation and firm heterogeneity shape migration dynamics and equilibrium selection. In addition, the central government is represented as an exogenous regulator through policy parameters; a natural extension is a four-player evolutionary game in which the central government is modeled as an explicit strategic agent with feedback and adaptation. The current analysis is deterministic; incorporating stochastic shocks (e.g., sudden policy adjustments, technology breakthroughs, renewable variability, or abrupt demand shifts) would allow robustness assessments under uncertainty. Finally, physical constraints—such as grid capacity limits, renewable intermittency, and storage/cooling technology—are not embedded in the payoff structure; integrating evolutionary-game dynamics with power-system simulation and location-optimization (and, where appropriate, agent-based modeling) would enable a more tightly coupled policy–behavior–physics assessment of long-run cross-regional data-center migration.