Multi-Threshold Art Symmetry Image Segmentation and Numerical Optimization Based on the Modified Golden Jackal Optimization
Abstract
1. Introduction
- (1).
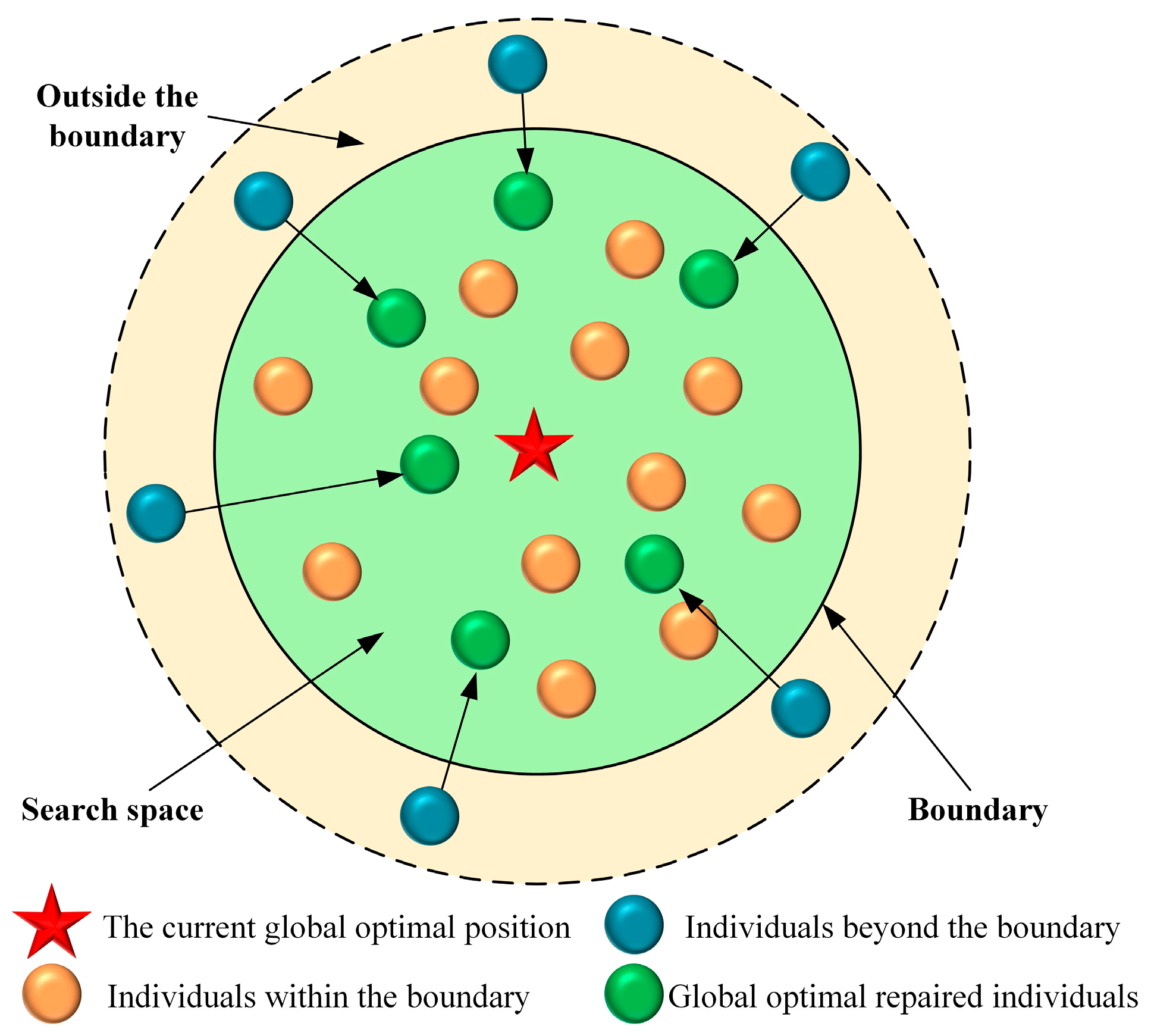
- We propose a Modified Golden Jackal Optimization (MGJO) algorithm by integrating three innovative strategies to address the inherent limitations of the standard GJO. First, the good-point set population initialization strategy replaces random initialization, ensuring the initial population is more uniformly and widely distributed in the search space, which lays a solid foundation for global exploration. Second, the dual crossover strategy—combining horizontal crossover (promoting information sharing among individuals to expand search coverage) and vertical crossover (enabling fine-grained search at the dimension level to deepen local exploitation)—effectively enhances the algorithm’s ability to balance exploration and exploitation, especially for high-dimensional complex problems. Third, the global-optimum-based boundary handling mechanism replaces the passive “reset-to-boundary” strategy, guiding out-of-bound individuals toward the global optimal region to retain valid search information and improve the utilization of boundary-area search resources. These three strategies work synergistically to overcome the shortcomings of standard GJO, including uneven initialization, insufficient information exchange, and passive boundary handling, enriching the improvement framework of swarm intelligence algorithms.
- (2).
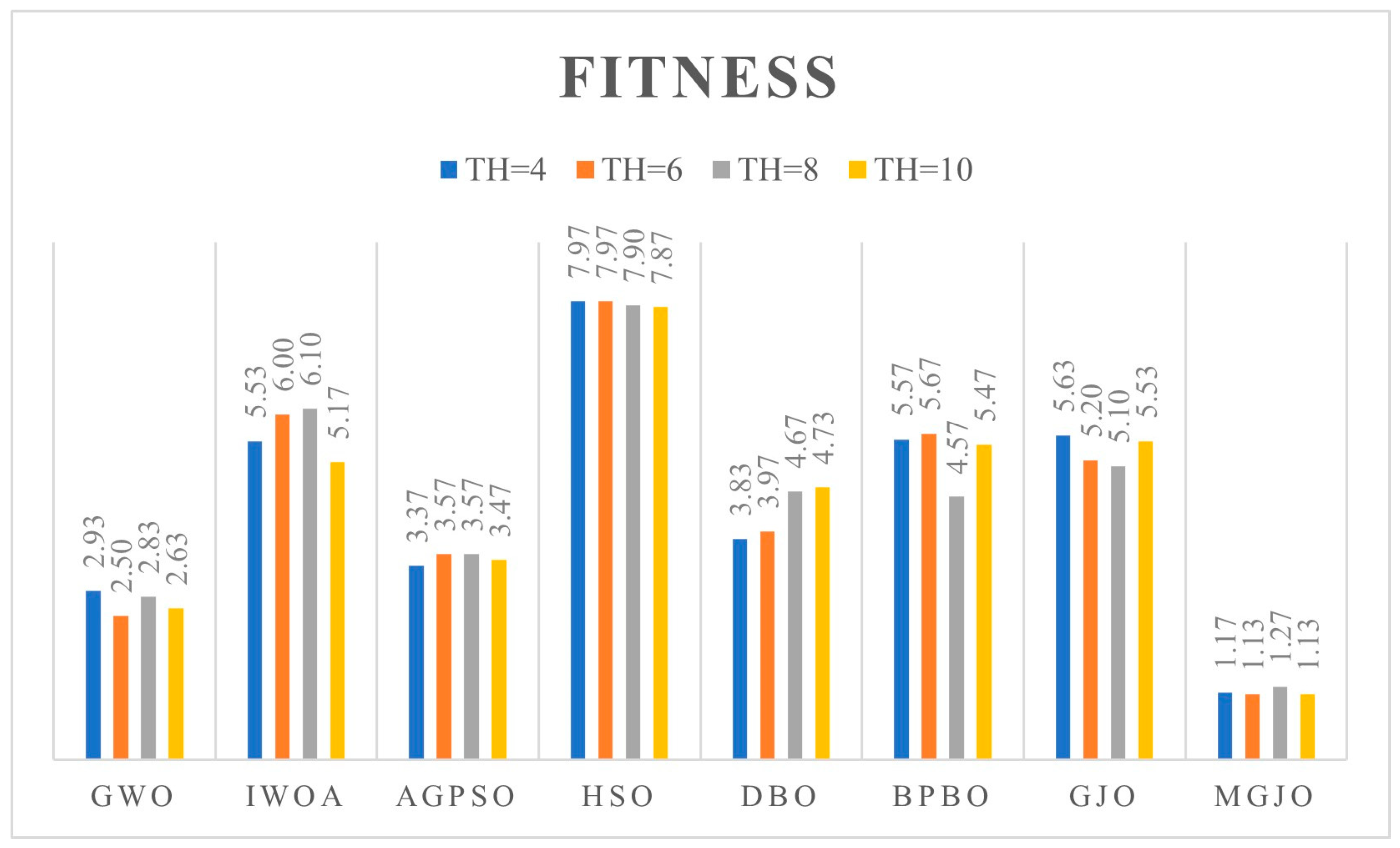
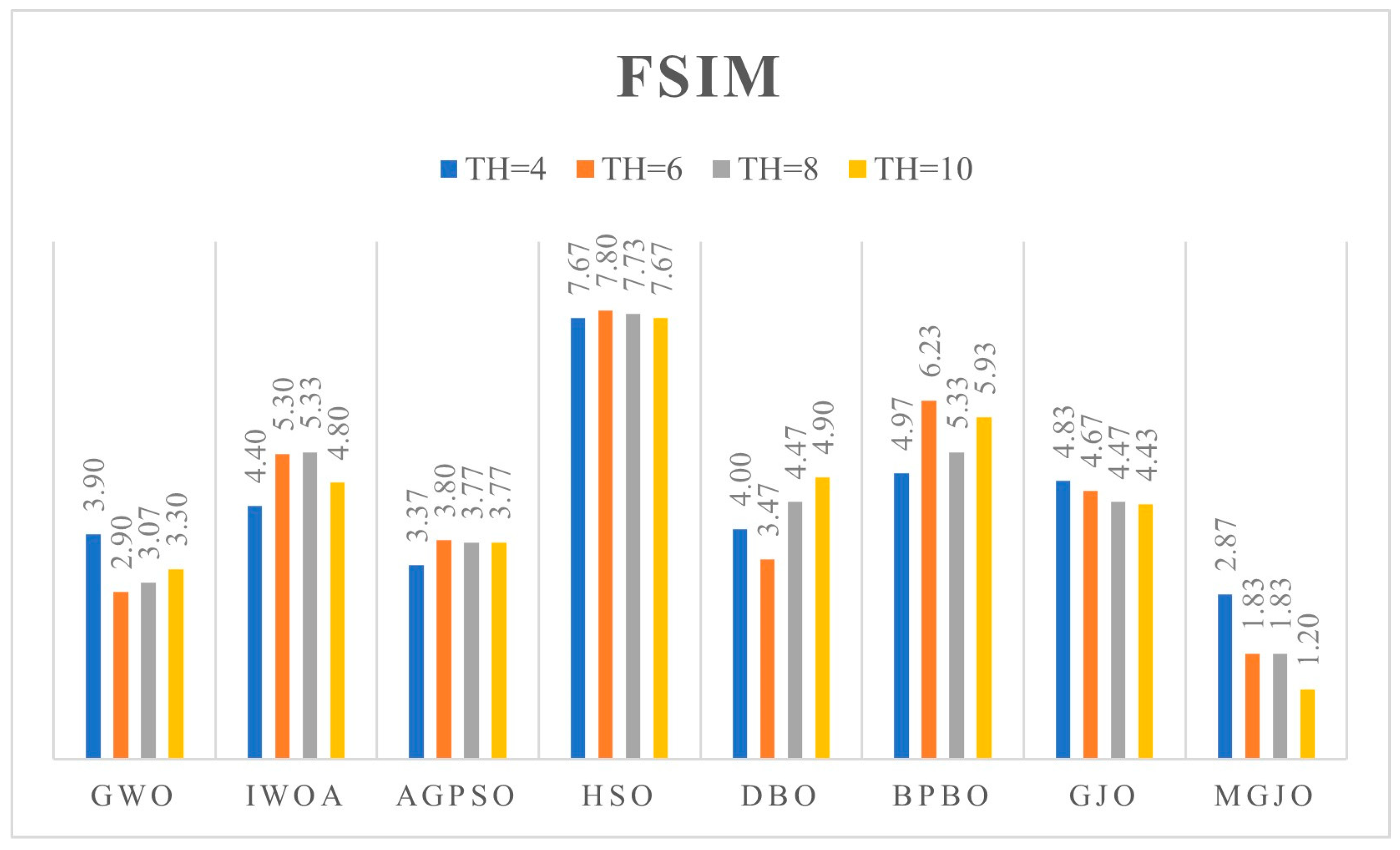
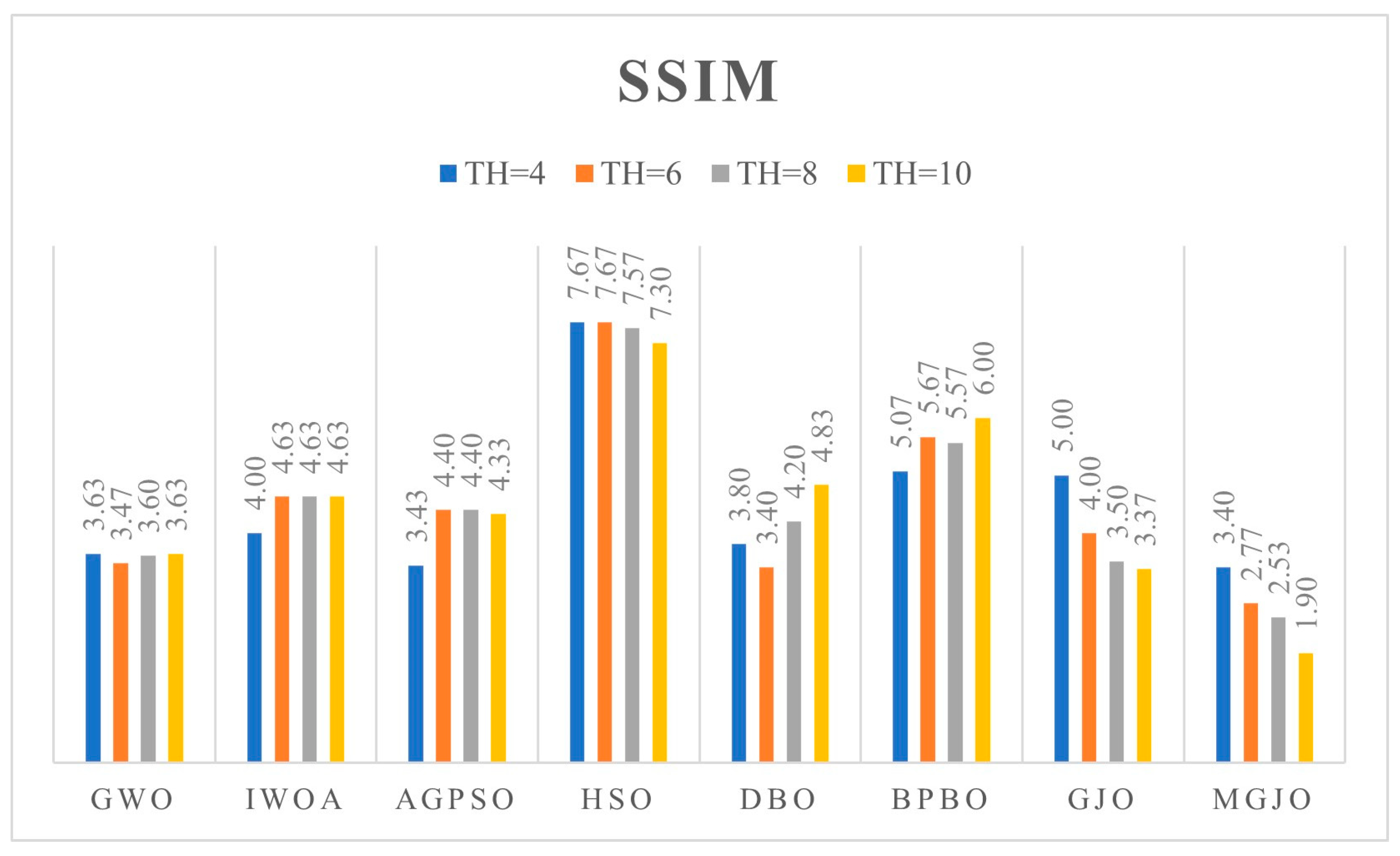
- We conduct comprehensive validation of MGJO’s performance through numerical optimization experiments and multilevel threshold image segmentation applications. On the CEC2017 (dim = 30, 100) and CEC2022 (dim = 10, 20) benchmark suites, MGJO outperforms seven mainstream algorithms (e.g., GWO, IWOA, GJO) in optimization accuracy, stability, and exploration–exploitation balance, as verified by population diversity analysis, ablation experiments, and statistical tests (Wilcoxon rank-sum test, Friedman mean-rank test). When applied to multilevel threshold segmentation of artistic images and benchmark images (e.g., Baboon, Lena) with Otsu’s between-class variance as the objective function, MGJO achieves higher fitness values (closer to Otsu’s optimal values) across 4-, 6-, 8-, and 10-level threshold tasks, and the segmented images exhibit superior peak signal-to-noise ratio (PSNR), structural similarity (SSIM), and feature similarity (FSIM), effectively preserving brushstroke details and color layers. This dual validation confirms MGJO’s effectiveness in both numerical optimization and practical image segmentation scenarios, providing an efficient solution for high-dimensional complex optimization problems and artistic image processing demands.
2. Golden Jackal Optimization and the Proposed Methodology
2.1. Golden Jackal Optimization (GJO)
2.1.1. Search Space Formulation
2.1.2. Exploration Stage (Target Prospecting and Discovery)
2.1.3. Intensification Phase (Prey Capture and Constriction)
2.1.4. Transitioning from Exploration to Exploitation
2.2. Proposed Golden Jackal Optimization
2.2.1. Good-Point-Set Population Initialization
2.2.2. Double-Crossover Strategy
2.2.3. Boundary Processing Mechanism Based on Global Optimization
| Algorithm 1. Pseudocode of the Modified Golden Jackal Optimizer (MGJO) |
| 1: Inputs: The population size , and the maximum iterations 2: Inputs: The location of prey population 3: while do 4: *Compute the objective function values for all candidate solutions. 5: the best prey (Male jackal position) 6: second best prey (Female jackal position) 7: for do 8: Update the evading energy using Equation (5) 9: Update using Equation (6) 10: if do (Exploration) 11: Update the prey position using Equations (4) and (7) 12: Using Equation (13) for boundary adjustment 13: else do (Exploitation) 14: Update the prey position using Equations (7) and (8). 15: Apply Equation (13) to perform solution-boundary correction. 16: end if 17: end for 18: Update the prey position using Equations (11) and (12) 19: end while 20: Return . |
2.3. Time Complexity Analysis
3. Numerical Experiments
3.1. Configuration of Algorithmic Parameters
3.2. Qualitative Analysis of MGJO
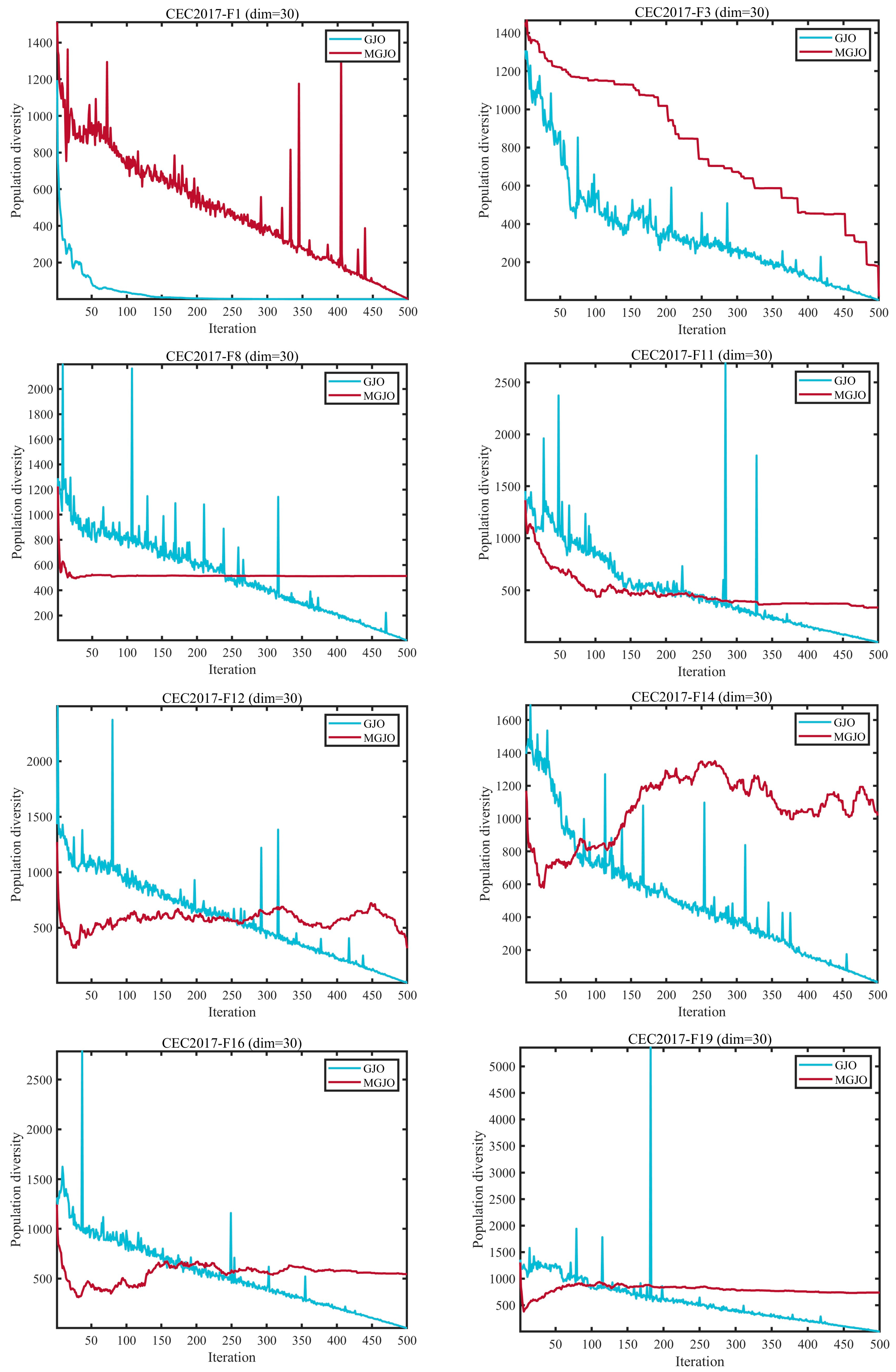
3.2.1. Analysis of the Population Diversity
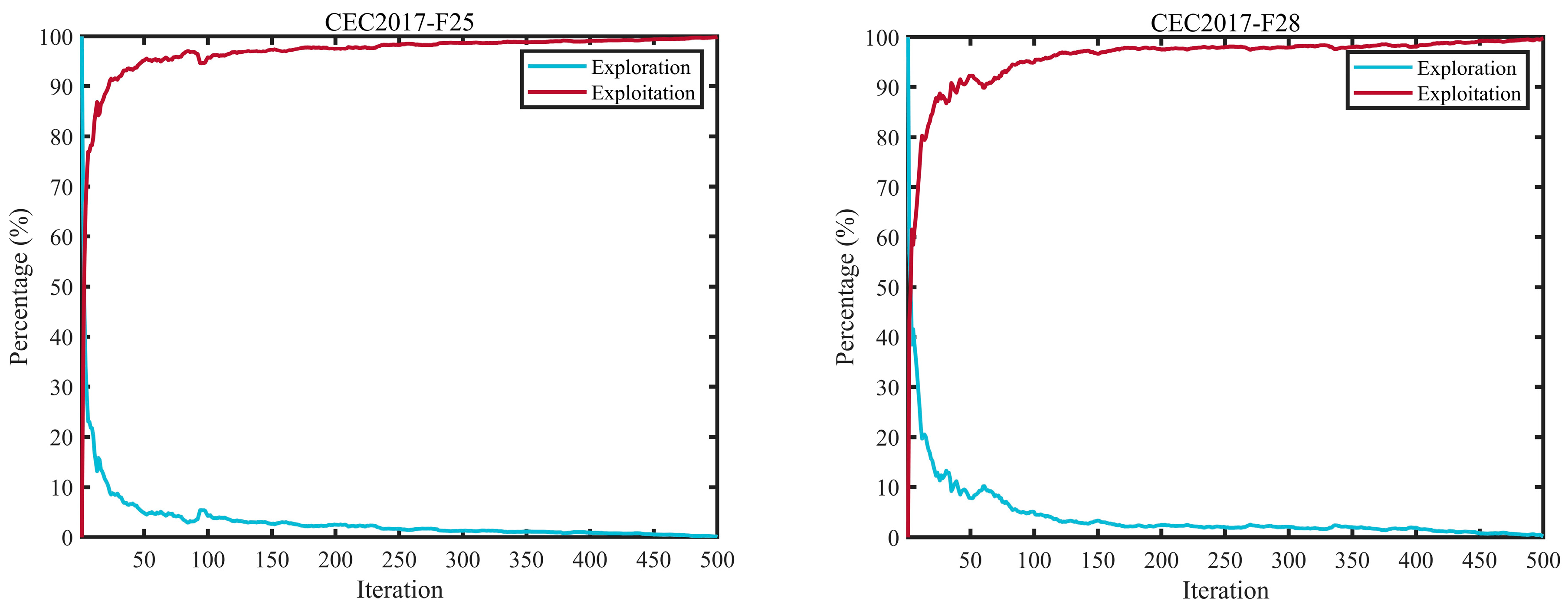
3.2.2. Examination of Global Search and Local Refinement Dynamics
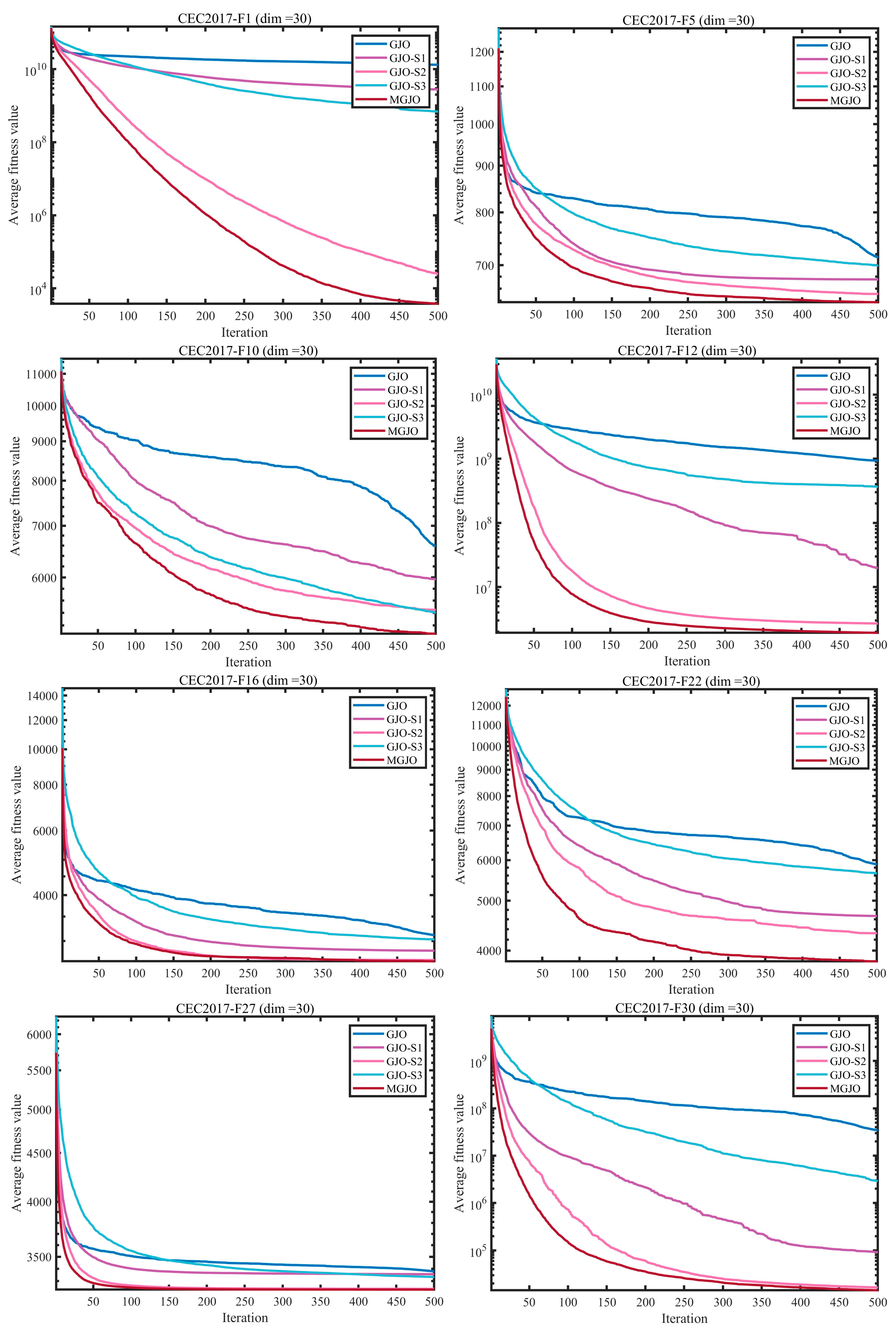
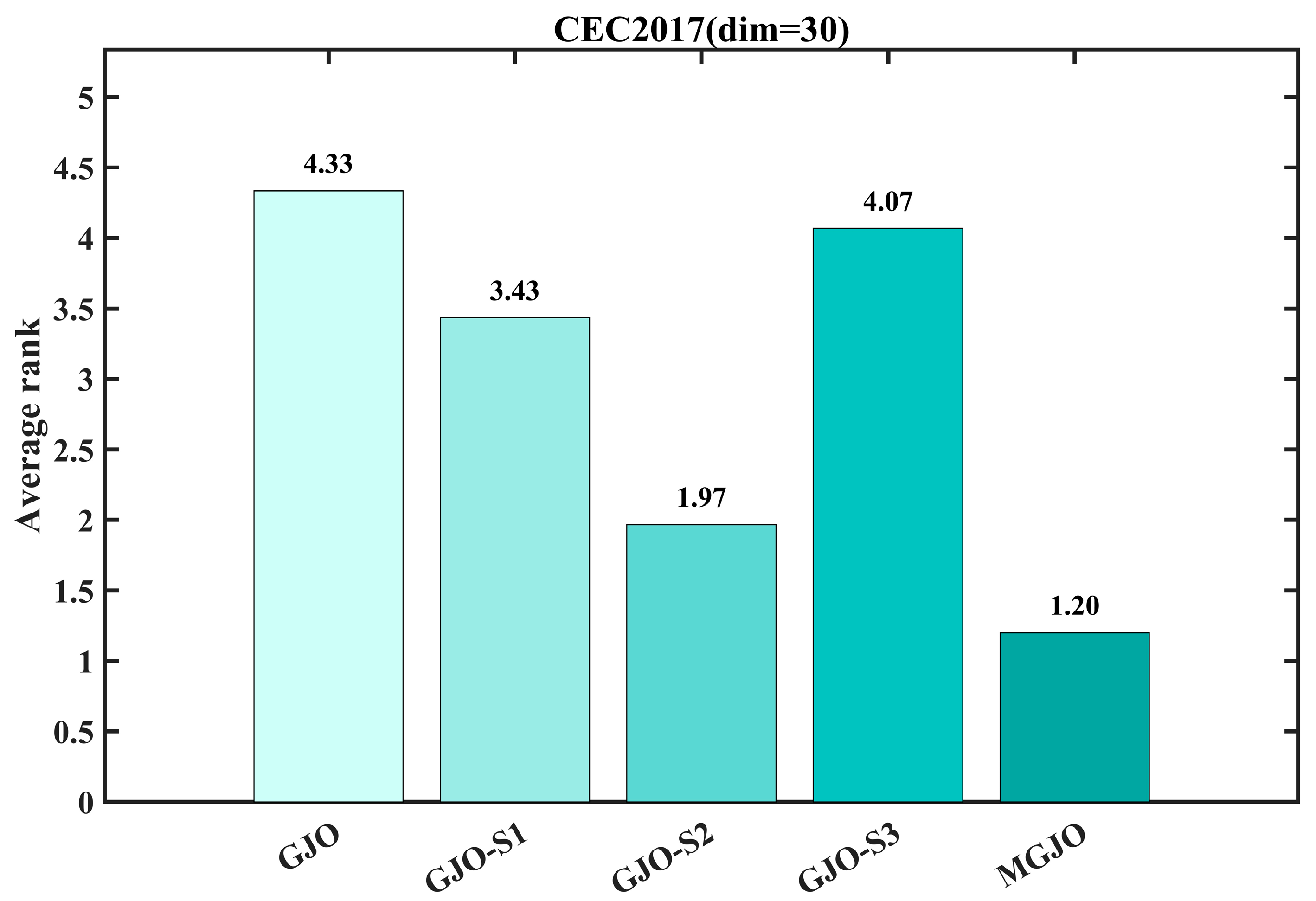
3.2.3. Impact Analysis of the Modification
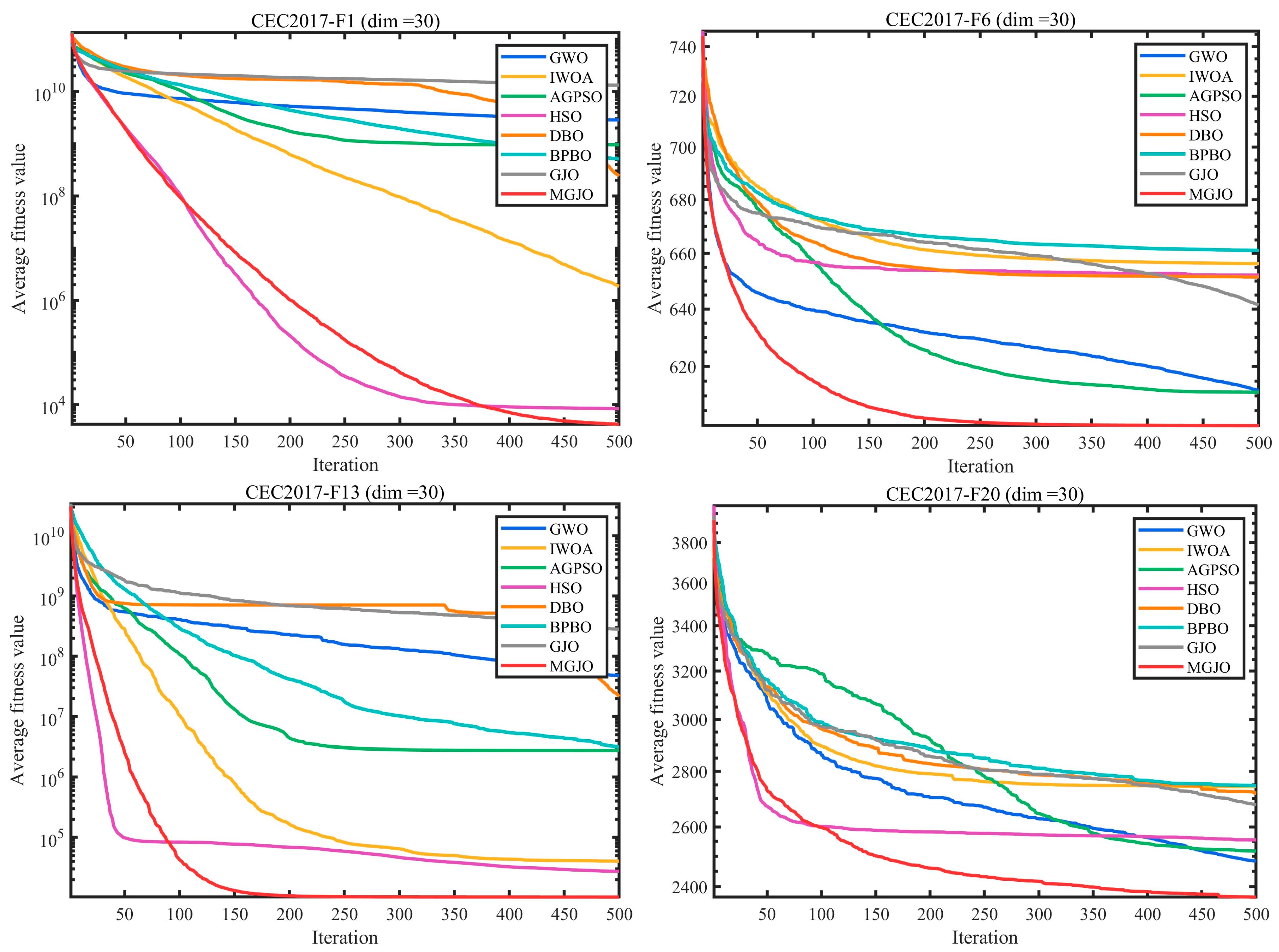
3.3. Performance Evaluation and Discussion on CEC2017 and CEC2022 Benchmark Sets
3.4. Stability Analysis
3.4.1. Statistical Analysis Using Wilcoxon Rank-Sum Test
3.4.2. Friedman Average Ranking Assessment
4. MGJO for Multilevel Thresholding Art Image Segmentation
4.1. Evaluation Index
4.2. Evaluation of Otsu Thresholding Performance Using MGJO Framework
5. Summary and Prospect
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, S.; Meng, F.; Cai, L.; Yang, R. Boomerang aerodynamic ellipse optimizer: A human game-inspired optimization technique for numerical optimization and multilevel thresholding image segmentation. Math. Comput. Simul. 2025, 238, 604–636. [Google Scholar] [CrossRef]
- Wang, X.; Snášel, V.; Mirjalili, S.; Pan, J.-S. MAAPO: An innovative membrane algorithm based on artificial protozoa optimizer for multilevel threshold image segmentation. Artif. Intell. Rev. 2025, 58, 324. [Google Scholar] [CrossRef]
- Rao, H.; Jia, H.; Zhang, X.; Abualigah, L. Hybrid Adaptive Crayfish Optimization with Differential Evolution for Color Multi-Threshold Image Segmentation. Biomimetics 2025, 10, 218. [Google Scholar] [CrossRef]
- Huo, Y.; Gang, S.; Guan, C. FCIHMRT: Feature Cross-Layer Interaction Hybrid Method Based on Res2Net and Transformer for Remote Sensing Scene Classification. Electronics 2023, 12, 4362. [Google Scholar] [CrossRef]
- Tamilarasan, A.; Rajamani, D. Towards efficient image segmentation: A fuzzy entropy-based approach using the snake optimizer algorithm. Results Eng. 2025, 26, 105335. [Google Scholar] [CrossRef]
- Ramos-Frutos, J.; Oliva, D.; Miguel-Andrés, I.; Casas-Ordaz, A.; Ramos-Soto, O.; Aranguren, I.; Zapotecas-Martínez, S. Multi-population estimation of distribution algorithm for multilevel thresholding in image segmentation. Neurocomputing 2025, 641, 130325. [Google Scholar] [CrossRef]
- Qiao, Z.; Wu, L.; Heidari, A.A.; Zhao, X.; Chen, H. An enhanced tree-seed algorithm for global optimization and neural architecture search optimization in medical image segmentation. Biomed. Signal Process. Control 2025, 104, 107457. [Google Scholar] [CrossRef]
- Guo, H.; Wang, J.G.; Liu, Y. Multi-threshold image segmentation algorithm based on Aquila optimization. Vis. Comput. 2023, 40, 2905–2932. [Google Scholar] [CrossRef]
- Zheng, J.; Gao, Y.; Zhang, H.; Lei, Y.; Zhang, J. OTSU Multi-Threshold Image Segmentation Based on Improved Particle Swarm Algorithm. Appl. Sci. 2022, 12, 11514. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M. Crested Porcupine Optimizer: A new nature-inspired metaheuristic. Knowl.-Based Syst. 2024, 284, 111257. [Google Scholar]
- Dorigo, M.; Birattari, M.; Stützle, T. Ant Colony Optimization. Comput. Intell. Mag. IEEE 2006, 1, 28–39. [Google Scholar]
- Yang, X.-S.; He, X. Bat algorithm: Literature review and applications. Int. J. Bio-Inspired Comput. 2013, 5, 141–149. [Google Scholar] [CrossRef]
- Wang, R.-B.; Hu, R.-B.; Geng, F.-D.; Xu, L.; Chu, S.-C.; Pan, J.-S.; Meng, Z.-Y.; Mirjalili, S. The Animated Oat Optimization Algorithm: A nature-inspired metaheuristic for engineering optimization and a case study on Wireless Sensor Networks. Knowl.-Based Syst. 2025, 318, 113589. [Google Scholar]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A novel meta-heuristic optimization algorithm. Knowl. Based Syst. 2022, 242, 108320. [Google Scholar]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Jia, H.; Peng, X.; Lang, C. Remora optimization algorithm. Expert Syst. Appl. 2021, 185, 115665. [Google Scholar] [CrossRef]
- Hayyolalam, V.; Kazem, A.A.P. Black widow optimization algorithm: A novel meta-heuristic approach for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2020, 87, 103249. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2022, 79, 7305–7336. [Google Scholar] [CrossRef]
- Mohammadi-Balani, A.; Nayeri, M.D.; Azar, A.; Taghizadeh-Yazdi, M. Golden eagle optimizer: A nature-inspired metaheuristic algorithm. Comput. Ind. Eng. 2021, 152, 107050. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Khishe, M.; Mosavi, M.R. Chimp optimization algorithm. Expert Syst. Appl. 2020, 149, 113338. [Google Scholar] [CrossRef]
- Wang, L.; Cao, Q.; Zhang, Z.; Mirjalili, S.; Zhao, W. Artificial rabbits optimization: A new bio-inspired meta-heuristic algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2022, 114, 105082. [Google Scholar] [CrossRef]
- Aziz, M.A.E.; Ewees, A.A.; Hassanien, A.E. Whale Optimization Algorithm and Moth-Flame Optimization for multilevel thresholding image segmentation. Expert Syst. Appl. 2017, 83, 242–256. [Google Scholar] [CrossRef]
- SMookiah; Parasuraman, K.; Chandar, S.K. Color image segmentation based on improved sine cosine optimization algorithm. Soft Comput. 2022, 26, 13193–13203. [Google Scholar] [CrossRef]
- Aranguren, I.; Valdivia, A.; Morales-Castañeda, B.; Oliva, D.; Elaziz, M.A.; Perez-Cisneros, M. Improving the segmentation of magnetic resonance brain images using the LSHADE optimization algorithm. Biomed. Signal Process. Control 2021, 64, 102259. [Google Scholar] [CrossRef]
- Dhal, K.G.; Das, A.; Ray, S.; Gálvez, J.; Das, S. Nature-Inspired Optimization Algorithms and Their Application in Multi-Thresholding Image Segmentation. Arch. Comput. Methods Eng. 2019, 27, 855–888. [Google Scholar] [CrossRef]
- Jiang, Z.; Zou, F.; Chen, D.; Cao, S.; Liu, H.; Guo, W. An ensemble multi-swarm teaching–learning-based optimization algorithm for function optimization and image segmentation. Appl. Soft Comput. 2022, 130, 109653. [Google Scholar] [CrossRef]
- Elaziz, M.A.; Al-qaness, M.A.A.; Al-Betar, M.A.; Ewees, A.A. Polyp image segmentation based on improved planet optimization algorithm using reptile search algorithm. Neural Comput. Appl. 2025, 37, 6327–6349. [Google Scholar] [CrossRef]
- Premalatha, R.; Dhanalakshmi, P. An innovative segmentation algorithm based on enhanced fuzzy optimization of skin cancer images. Multimed. Tools Appl. 2025, 84, 40425–40448. [Google Scholar] [CrossRef]
- Abdel-Salam, M.; Houssein, E.H.; Emam, M.M.; Samee, N.A.; Gharehchopogh, F.S.; Bacanin, N. EATHOA: Elite-evolved hiking algorithm for global optimization and precise multi-thresholding image segmentation in intracerebral hemorrhage images. Comput. Biol. Med. 2025, 196, 110835. [Google Scholar] [CrossRef]
- Chopra, N.; Ansari, M.M. Golden jackal optimization: A novel nature-inspired optimizer for engineering applications. Expert Syst. Appl. 2022, 198, 116924. [Google Scholar] [CrossRef]
- Yang, W.; Lai, T.; Fang, Y. Multi-Strategy Golden Jackal Optimization for engineering design. J. Supercomput. 2025, 81, 1–60. [Google Scholar] [CrossRef]
- Mohapatra, S.; Mohapatra, P. Fast random opposition-based learning Golden Jackal Optimization algorithm. Knowl. Based Syst. 2023, 275, 110679. [Google Scholar] [CrossRef]
- Hu, G.; Chen, L.; Wei, G. Enhanced golden jackal optimizer-based shape optimization of complex CSGC-Ball surfaces. Artif. Intell. Rev. 2023, 56, 2407–2475. [Google Scholar] [CrossRef]
- Devi, R.M.; Premkumar, M.; Kiruthiga, G.; Sowmya, R. IGJO: An Improved Golden Jackel Optimization Algorithm Using Local Escaping Operator for Feature Selection Problems. Neural Process. Lett. 2023, 55, 6443–6531. [Google Scholar] [CrossRef]
- Bai, J.; Khatir, S.; Abualigah, L.; Wahab, M.A. Ameliorated Golden jackal optimization (AGJO) with enhanced movement and multi-angle position updating strategy for solving engineering problems. Adv. Eng. Softw. 2024, 194, 103665. [Google Scholar] [CrossRef]
- Meng, X.; Tan, L.; Wang, Y. An efficient hybrid differential evolution-golden jackal optimization algorithm for multilevel thresholding image segmentation. PeerJ Comput. Sci. 2024, 10, e2121. [Google Scholar] [CrossRef]
- Mai, X.; Zhong, Y.; Li, L. The Crossover strategy integrated Secretary Bird Optimization Algorithm and its application in engineering design problems. Electron. Res. Arch. 2025, 33, 471–512. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, D.; Fu, S.; Chen, J. Enhanced aquila optimizer based on tent chaotic mapping and new rules. Sci. Rep. 2024, 14, 3013. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Wu, R.; Huang, H.; Wei, J.; Han, Z.; Wen, L.; Yuan, Y. Multi-strategy improved artificial rabbit optimization algorithm based on fusion centroid and elite guidance mechanisms. Comput. Methods Appl. Mech. Eng. 2024, 425, 116915. [Google Scholar] [CrossRef]
- Xie, J.; He, J.; Gao, Z.; Wang, S.; Liu, J.; Fan, H.J.H. An enhanced snow ablation optimizer for UAV swarm path planning and engineering design problems. Heliyon 2024, 10, e37819. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P. Problem Definitions and Evaluation Criteria for the CEC 2017 Competition and Special Session on Constrained Single Objective Real-Parameter Optimization. Nanyang Technol. Univ. Singap. Tech. Rep. 2016, 1–18. [Google Scholar]
- Luo, W.; Lin, X.; Li, C.; Yang, S.; Shi, Y. Benchmark functions for CEC 2022 competition on seeking multiple optima in dynamic environments. arXiv 2022, arXiv:2201.00523. [Google Scholar] [CrossRef]
- Huang, S.; Liu, D.; Fu, Y.; Chen, J.; He, L.; Yan, J.; Yang, D. Prediction of Self-Care Behaviors in Patients Using High-Density Surface Electromyography Signals and an Improved Whale Optimization Algorithm-Based LSTM Model. J. Bionic Eng. 2025, 22, 1963–1984. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A.; Sadiq, A.S. Autonomous particles groups for particle swarm optimization. Arab. J. Sci. Eng. 2014, 39, 4683–4697. [Google Scholar] [CrossRef]
- Akbari, E.; Rahimnejad, A.; Gadsden, S.A. Holistic swarm optimization: A novel metaphor-less algorithm guided by whole population information for addressing exploration-exploitation dilemma. Comput. Methods Appl. Mech. Eng. 2025, 445, 118208. [Google Scholar] [CrossRef]
- Ghasemi, M.; Akbari, M.A.; Zare, M.; Mirjalili, S.; Deriche, M.; Abualigah, L. Birds of prey-based optimization (BPBO): A metaheuristic algorithm for optimization. Evol. Intell. 2025, 18, 88. [Google Scholar] [CrossRef]
- Ou, Y.; Qin, F.; Zhou, K.-Q.; Yin, P.-F.; Mo, L.-P.; Zain, A.J.S.M. An improved grey wolf optimizer with multi-strategies coverage in wireless sensor networks. Symmetry 2024, 16, 286. [Google Scholar] [CrossRef]
- Wang, W.-C.; Tian, W.-C.; Xu, D.-M.; Zang, H.-F. Arctic puffin optimization: A bio-inspired metaheuristic algorithm for solving engineering design optimization. Adv. Eng. Softw. 2024, 195, 103694. [Google Scholar] [CrossRef]
- Mohammed, B.O.; Aghdasi, H.S.; Salehpour, P. Dhole optimization algorithm: A new metaheuristic algorithm for solving optimization problems. Clust. Comput. 2025, 28, 430. [Google Scholar] [CrossRef]
- Chai, X.; Wu, Z.; Li, W.; Fan, H.; Sun, X.; Xu, J. Image Segmentation Based on the Optimized K-Means Algorithm with the Improved Hybrid Grey Wolf Optimization: Application in Ore Particle Size Detection. Sensors 2025, 28, 2785. [Google Scholar] [CrossRef] [PubMed]
- Abualigah, L.; Al-Okbi, N.K.; Alomari, S.A.; Almomani, M.H.; Moneam, S.; Yousif, M.A.; Snasel, V.; Saleem, K.; Smerat, A. Optimized image segmentation using an improved reptile search algorithm with Gbest operator for multi-level thresholding. Sci. Rep. 2025, 15, 12713. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Zhang, X.; Wang, B. ACPOA: An Adaptive Cooperative Pelican Optimization Algorithm for Global Optimization and Multilevel Thresholding Image Segmentation. Biomimetics 2025, 15, 596. [Google Scholar] [CrossRef]
- Shi, J.; Chen, Y.; Wang, C.; Heidari, A.A.; Liu, L.; Chen, H.; Chen, X.; Sun, L. Multi-threshold image segmentation using new strategies enhanced whale optimization for lupus nephritis pathological images. Displays 2024, 84, 102799. [Google Scholar] [CrossRef]
- Abdel-salam, M.; Houssein, E.H.; Emam, M.M.; Samee, N.A.; Azam, M.T. A novel dynamic Nelder-based Electric Eel Foraging algorithm for global optimization and pathological colorectal cancer image segmentation. Comput. Biol. Med. 2025, 197, 110982. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Bei, J.; Song, H.; Zhang, H.; Zhang, P. A whale optimization algorithm with combined mutation and removing similarity for global optimization and multilevel thresholding image segmentation. Appl. Soft Comput. 2023, 137, 110130. [Google Scholar] [CrossRef]
- Jiang, Y.; Yeh, W.-C.; Hao, Z.; Yang, Z. A cooperative honey bee mating algorithm and its application in multi-threshold image segmentation. Inf. Sci. 2016, 369, 171–183. [Google Scholar] [CrossRef]






| Algorithm | Improvement Strategies | Core Novelty | Reference |
|---|---|---|---|
| IGJO | Operators in Gradient-Based Optimizers | Enhances initial population diversity via opposition sampling | [38] |
| AGJO | The enhanced movement strategy, the global search strategy, and the multi-angle position update strategy for prey. | Improves convergence speed | [39] |
| EGJO | Combined with opposition-based learning, spring vibration-based adaptive mutation and binomial-based cross-evolution strategy | Enhances local exploitation via elite information guidance | [37] |
| DE-GJO | Hybrid differential evolution (DE) crossover | Introduces DE operators to expand search range | [40] |
| MGJO | Good-point set initialization, Dual crossover (horizontal + vertical) and Global-optimum boundary handling | Synergistic strategy integration, Dimension-level fine-grained search and Boundary information retention |
| Algorithms | Name of the Parameter | Value of the Parameter |
|---|---|---|
| GWO | [0, 2] | |
| IWOA | [0, 1], [−1, 1], Linear reduction from 2 to 1 | |
| AGPSO | 0.9, 0.4, [2.55, 0.5], [1.25, 2.25] | |
| HSO | 3 | |
| DBO | ||
| BPBO | 0.7 | |
| GJO | ||
| MGJO |
| Function | Metric | GJO | GJO-S1 | GJO-S2 | GJO-S3 | MGJO |
|---|---|---|---|---|---|---|
| F1 | Ave | 1.3149 × 1010 | 2.7855 × 1009 | 2.4665 × 1004 | 6.9047 × 1008 | 3.7651 × 1003 |
| Std | 4.2973 × 1009 | 2.8560 × 1009 | 2.6383 × 1004 | 4.1807 × 1009 | 3.6750 × 1003 | |
| F2 | Ave | 3.7800 × 1036 | 3.1681 × 1033 | 2.7613 × 1016 | 2.0410 × 1037 | 2.2475 × 1014 |
| Std | 2.4403 × 1037 | 1.5166 × 1034 | 1.1158 × 1017 | 1.3717 × 1038 | 9.1683 × 1014 | |
| F3 | Ave | 6.1534 × 1004 | 1.3289 × 1005 | 9.6556 × 1004 | 1.3319 × 1005 | 8.2440 × 1004 |
| Std | 1.0117 × 1004 | 3.8009 × 1004 | 2.7842 × 1004 | 4.0889 × 1004 | 2.2117 × 1004 | |
| F4 | Ave | 1.3075 × 1003 | 8.3526 × 1002 | 5.1802 × 1002 | 9.6771 × 1002 | 5.1436 × 1002 |
| Std | 7.3982 × 1002 | 9.9451 × 1002 | 2.5429 × 1001 | 1.0191 × 1003 | 1.9166 × 1001 | |
| F5 | Ave | 7.1420 × 1002 | 6.7542 × 1002 | 6.5085 × 1002 | 6.9936 × 1002 | 6.3749 × 1002 |
| Std | 4.5854 × 1001 | 3.3407 × 1001 | 3.5259 × 1001 | 2.9212 × 1001 | 2.9944 × 1001 | |
| F6 | Ave | 6.3982 × 1002 | 6.2638 × 1002 | 6.0290 × 1002 | 6.2545 × 1002 | 6.0006 × 1002 |
| Std | 8.1038 × 1000 | 1.1338 × 1001 | 6.5810 × 1000 | 1.0352 × 1001 | 3.9619 ×10−02 | |
| F7 | Ave | 1.0474 × 1003 | 1.0361 × 1003 | 9.3598 × 1002 | 1.1160 × 1003 | 8.9236 × 1002 |
| Std | 5.9275 × 1001 | 9.9329 × 1001 | 6.1129 × 1001 | 1.0098 × 1002 | 4.1074 × 1001 | |
| F8 | Ave | 9.8532 × 1002 | 9.4049 × 1002 | 9.3302 × 1002 | 9.5380 × 1002 | 9.1312 × 1002 |
| Std | 4.1609 × 1001 | 3.2855 × 1001 | 2.4688 × 1001 | 2.1915 × 1001 | 2.9506 × 1001 | |
| F9 | Ave | 5.4780 × 1003 | 5.0697 × 1003 | 2.9440 × 1003 | 4.9617 × 1003 | 1.9042 × 1003 |
| Std | 1.7382 × 1003 | 2.2601 × 1003 | 1.0698 × 1003 | 1.0561 × 1003 | 7.5839 × 1002 | |
| F10 | Ave | 6.5879 × 1003 | 5.9690 × 1003 | 5.4494 × 1003 | 5.4013 × 1003 | 5.0730 × 1003 |
| Std | 1.3246 × 1003 | 1.4901 × 1003 | 4.7779 × 1002 | 3.4518 × 1002 | 6.4052 × 1002 | |
| F11 | Ave | 4.1974 × 1003 | 3.5650 × 1003 | 2.8659 × 1003 | 7.3527 × 1003 | 1.5479 × 1003 |
| Std | 1.5985 × 1003 | 2.5612 × 1003 | 2.2137 × 1003 | 5.2060 × 1003 | 7.1265 × 1002 | |
| F12 | Ave | 9.3605 × 1008 | 1.9871 × 1007 | 2.6930 × 1006 | 3.6412 × 1008 | 1.9249 × 1006 |
| Std | 6.8215 × 1008 | 4.4238 × 1007 | 1.7841 × 1006 | 1.7187 × 1009 | 1.1241 × 1006 | |
| F13 | Ave | 2.7718 × 1008 | 8.3133 × 1005 | 2.7489 × 1004 | 2.9417 × 1008 | 1.1212 × 1004 |
| Std | 4.7454 × 1008 | 5.7531 × 1006 | 1.3150 × 1005 | 6.7097 × 1008 | 1.0753 × 1004 | |
| F14 | Ave | 8.4081 × 1005 | 1.6046 × 1006 | 1.2498 × 1006 | 2.6088 × 1006 | 9.1322 × 1005 |
| Std | 8.8546 × 1005 | 1.8701 × 1006 | 1.3323 × 1006 | 2.3320 × 1006 | 9.2958 × 1005 | |
| F15 | Ave | 1.8554 × 1007 | 8.1784 × 1003 | 8.6849 × 1003 | 3.6982 × 1007 | 8.8123 × 1003 |
| Std | 4.5626 × 1007 | 7.5381 × 1003 | 9.0449 × 1003 | 1.4626 × 1008 | 9.2655 × 1003 | |
| F16 | Ave | 3.1143 × 1003 | 2.8244 × 1003 | 2.6633 × 1003 | 3.0309 × 1003 | 2.6426 × 1003 |
| Std | 4.8034 × 1002 | 3.2298 × 1002 | 3.1538 × 1002 | 2.9006 × 1002 | 3.5112 × 1002 | |
| F17 | Ave | 2.2924 × 1003 | 2.3491 × 1003 | 2.1714 × 1003 | 2.4346 × 1003 | 2.1400 × 1003 |
| Std | 2.6367 × 1002 | 2.1885 × 1002 | 2.3330 × 1002 | 2.6166 × 1002 | 2.4677 × 1002 | |
| F18 | Ave | 2.1356 × 1006 | 2.9990 × 1006 | 1.7875 × 1006 | 3.4259 × 1006 | 2.1382 × 1006 |
| Std | 2.3536 × 1006 | 4.4497 × 1006 | 2.7113 × 1006 | 3.6139 × 1006 | 3.2935 × 1006 | |
| F19 | Ave | 1.1452 × 1007 | 9.6457 × 1003 | 7.7706 × 1003 | 1.0082 × 1007 | 1.0154 × 1004 |
| Std | 2.8041 × 1007 | 9.6409 × 1003 | 7.0285 × 1003 | 3.1141 × 1007 | 1.0111 × 1004 | |
| F20 | Ave | 2.6030 × 1003 | 2.5925 × 1003 | 2.4519 × 1003 | 2.6399 × 1003 | 2.3504 × 1003 |
| Std | 2.2812 × 1002 | 2.4554 × 1002 | 2.0489 × 1002 | 2.1367 × 1002 | 1.7585 × 1002 | |
| F21 | Ave | 2.4941 × 1003 | 2.4507 × 1003 | 2.4476 × 1003 | 2.4814 × 1003 | 2.4161 × 1003 |
| Std | 3.6677 × 1001 | 3.6714 × 1001 | 3.5470 × 1001 | 3.2290 × 1001 | 3.1822 × 1001 | |
| F22 | Ave | 5.8895 × 1003 | 4.6699 × 1003 | 4.3228 × 1003 | 5.6522 × 1003 | 3.8092 × 1003 |
| Std | 2.6166 × 1003 | 1.8649 × 1003 | 2.2942 × 1003 | 2.1266 × 1003 | 2.1337 × 1003 | |
| F23 | Ave | 2.8997 × 1003 | 2.8925 × 1003 | 2.8070 × 1003 | 2.9863 × 1003 | 2.7775 × 1003 |
| Std | 4.6097 × 1001 | 8.5296 × 1001 | 4.1910 × 1001 | 1.1897 × 1002 | 3.8988 × 1001 | |
| F24 | Ave | 3.0975 × 1003 | 3.0929 × 1003 | 3.0128 × 1003 | 3.3616 × 1003 | 2.9714 × 1003 |
| Std | 5.7202 × 1001 | 9.9099 × 1001 | 6.4108 × 1001 | 1.8881 × 1002 | 5.0339 × 1001 | |
| F25 | Ave | 3.1982 × 1003 | 3.0288 × 1003 | 2.9148 × 1003 | 3.0772 × 1003 | 2.9022 × 1003 |
| Std | 1.1142 × 1002 | 8.5251 × 1001 | 2.2361 × 1001 | 1.4755 × 1002 | 1.7223 × 1001 | |
| F26 | Ave | 6.1427 × 1003 | 6.2560 × 1003 | 5.2839 × 1003 | 5.6075 × 1003 | 4.7852 × 1003 |
| Std | 6.7740 × 1002 | 9.9379 × 1002 | 1.0448 × 1003 | 1.5807 × 1003 | 7.6806 × 1002 | |
| F27 | Ave | 3.3794 × 1003 | 3.3559 × 1003 | 3.2393 × 1003 | 3.3330 × 1003 | 3.2328 × 1003 |
| Std | 6.8760 × 1001 | 8.4396 × 1001 | 1.2581 × 1001 | 7.5706 × 1001 | 1.1582 × 1001 | |
| F28 | Ave | 3.9168 × 1003 | 3.6032 × 1003 | 3.2889 × 1003 | 3.5823 × 1003 | 3.2635 × 1003 |
| Std | 3.6641 × 1002 | 2.5536 × 1002 | 2.2982 × 1001 | 4.9194 × 1002 | 2.2143 × 1001 | |
| F29 | Ave | 4.3638 × 1003 | 4.1281 × 1003 | 3.7857 × 1003 | 4.1023 × 1003 | 3.6922 × 1003 |
| Std | 2.3958 × 1002 | 3.0785 × 1002 | 1.9756 × 1002 | 2.2164 × 1002 | 2.0932 × 1002 | |
| F30 | Ave | 3.4545 × 1007 | 9.1420 × 1004 | 1.6467 × 1004 | 2.9009 × 1006 | 1.4314 × 1004 |
| Std | 2.9010 × 1007 | 2.5561 × 1005 | 1.0593 × 1004 | 4.0542 × 1006 | 7.9527 × 1003 |
| Function | Metric | GWO | IWOA | AGPSO | HSO | DBO | BPBO | GJO | MGJO |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Ave | 2.8587 × 1009 | 1.8562 × 1006 | 9.5699 × 1008 | 8.3879 × 1003 | 2.4029 × 1008 | 5.1272 × 1008 | 1.3244 × 1010 | 4.1805 × 1003 |
| Std | 1.9458 × 1009 | 1.1626 × 1006 | 1.5751 × 1009 | 7.1732 × 1003 | 1.4977 × 1008 | 2.2170 × 1008 | 5.7246 × 1009 | 3.9175 × 1003 | |
| F2 | Ave | 9.3924 × 1032 | 2.7939 × 1020 | 2.0504 × 1030 | 1.3768 × 1017 | 2.2866 × 1032 | 1.9198 × 1031 | 1.7645 × 1035 | 1.2005 × 1014 |
| Std | 4.3273 × 1033 | 5.3890 × 1020 | 6.3237 × 1030 | 6.7570 × 1017 | 1.0634 × 1033 | 9.3037 × 1031 | 4.9362 × 1035 | 4.0515 × 1014 | |
| F3 | Ave | 6.0705 × 1004 | 1.5353 × 1005 | 8.7115 × 1004 | 4.7849 × 1004 | 9.3870 × 1004 | 6.8247 × 1004 | 6.2327 × 1004 | 8.4737 × 1004 |
| Std | 1.1635 × 1004 | 3.8715 × 1004 | 2.4003 × 1004 | 1.1588 × 1004 | 1.9516 × 1004 | 8.6188 × 1003 | 9.8584 × 1003 | 1.8095 × 1004 | |
| F4 | Ave | 6.4657 × 1002 | 5.3391 × 1002 | 6.3697 × 1002 | 6.9766 × 1002 | 6.7833 × 1002 | 6.8037 × 1002 | 1.1891 × 1003 | 5.1346 × 1002 |
| Std | 1.3296 × 1002 | 3.3118 × 1001 | 1.9760 × 1002 | 9.3288 × 1001 | 1.3805 × 1002 | 6.3945 × 1001 | 4.0519 × 1002 | 2.6729 × 1001 | |
| F5 | Ave | 6.2901 × 1002 | 7.1825 × 1002 | 5.9782 × 1002 | 6.9318 × 1002 | 7.4236 × 1002 | 7.6778 × 1002 | 7.3026 × 1002 | 6.4444 × 1002 |
| Std | 2.8424 × 1001 | 5.2546 × 1001 | 2.5716 × 1001 | 2.5869 × 1001 | 4.5681 × 1001 | 4.2068 × 1001 | 5.6271 × 1001 | 2.5330 × 1001 | |
| F6 | Ave | 6.1185 × 1002 | 6.5630 × 1002 | 6.1126 × 1002 | 6.5217 × 1002 | 6.5132 × 1002 | 6.6112 × 1002 | 6.4144 × 1002 | 6.0006 × 1002 |
| Std | 3.8852 × 1000 | 1.3225 × 1001 | 4.6539 × 1000 | 4.9124 × 1000 | 1.0821 × 1001 | 7.6243 × 1000 | 1.1849 × 1001 | 3.9338 × 10−02 | |
| F7 | Ave | 9.0323 × 1002 | 1.0665 × 1003 | 8.7635 × 1002 | 1.0360 × 1003 | 1.0412 × 1003 | 1.2208 × 1003 | 1.0589 × 1003 | 8.8558 × 1002 |
| Std | 5.2116 × 1001 | 1.0675 × 1002 | 4.6356 × 1001 | 7.2858 × 1001 | 7.8647 × 1001 | 9.1684 × 1001 | 5.4250 × 1001 | 4.3810 × 1001 | |
| F8 | Ave | 9.0326 × 1002 | 9.9943 × 1002 | 9.0543 × 1002 | 1.0364 × 1003 | 1.0460 × 1003 | 1.0096 × 1003 | 9.8746 × 1002 | 9.0705 × 1002 |
| Std | 2.6267 × 1001 | 3.4959 × 1001 | 2.9645 × 1001 | 2.0496 × 1001 | 5.0985 × 1001 | 3.7934 × 1001 | 3.7172 × 1001 | 2.7901 × 1001 | |
| F9 | Ave | 2.7554 × 1003 | 5.1194 × 1003 | 2.6894 × 1003 | 2.4603 × 1003 | 7.0971 × 1003 | 6.9897 × 1003 | 5.5220 × 1003 | 2.2982 × 1003 |
| Std | 1.0419 × 1003 | 1.0454 × 1003 | 1.2678 × 1003 | 7.2450 × 1002 | 1.8701 × 1003 | 2.0065 × 1003 | 1.5915 × 1003 | 1.2869 × 1003 | |
| F10 | Ave | 5.8476 × 1003 | 5.6942 × 1003 | 5.4738 × 1003 | 4.3099 × 1003 | 6.6552 × 1003 | 7.2016 × 1003 | 6.1774 × 1003 | 4.9462 × 1003 |
| Std | 1.9893 × 1003 | 8.0042 × 1002 | 7.2619 × 1002 | 5.4256 × 1002 | 1.3293 × 1003 | 1.2367 × 1003 | 1.3516 × 1003 | 6.8427 × 1002 | |
| F11 | Ave | 2.3487 × 1003 | 1.3924 × 1003 | 1.3576 × 1003 | 1.7803 × 1003 | 1.9510 × 1003 | 1.6641 × 1003 | 3.3628 × 1003 | 1.4763 × 1003 |
| Std | 8.7859 × 1002 | 9.3472 × 1001 | 1.0288 × 1002 | 2.0754 × 1002 | 7.3794 × 1002 | 1.6930 × 1002 | 1.4209 × 1003 | 4.8927 × 1002 | |
| F12 | Ave | 8.7820 × 1007 | 4.5389 × 1006 | 1.2355 × 1008 | 5.5934 × 1005 | 8.4389 × 1007 | 3.7381 × 1007 | 7.7143 × 1008 | 2.0464 × 1006 |
| Std | 8.5028 × 1007 | 3.9906 × 1006 | 3.7092 × 1008 | 6.5551 × 1005 | 1.8851 × 1008 | 2.8545 × 1007 | 6.9451 × 1008 | 1.4525 × 1006 | |
| F13 | Ave | 4.8114 × 1007 | 4.0409 × 1004 | 2.7694 × 1006 | 2.7394 × 1004 | 2.1502 × 1007 | 3.1509 × 1006 | 2.8251 × 1008 | 1.0267 × 1004 |
| Std | 9.6117 × 1007 | 3.5830 × 1004 | 1.3071 × 1007 | 1.8549 × 1004 | 3.7718 × 1007 | 3.5023 × 1006 | 3.4263 × 1008 | 1.0813 × 1004 | |
| F14 | Ave | 5.7297 × 1005 | 2.2773 × 1005 | 7.0773 × 1004 | 1.3045 × 1004 | 2.1921 × 1005 | 7.3482 × 1005 | 1.0858 × 1006 | 8.1641 × 1005 |
| Std | 6.0529 × 1005 | 1.9910 × 1005 | 7.6866 × 1004 | 1.0568 × 1004 | 3.6042 × 1005 | 6.5540 × 1005 | 1.0922 × 1006 | 9.2234 × 1005 | |
| F15 | Ave | 1.2636 × 1006 | 1.0741 × 1004 | 1.5913 × 1004 | 8.7839 × 1003 | 1.0247 × 1005 | 9.8141 × 1004 | 1.4573 × 1007 | 9.1519 × 1003 |
| Std | 1.8713 × 1006 | 1.2041 × 1004 | 1.6669 × 1004 | 3.8447 × 1003 | 1.1228 × 1005 | 1.0401 × 1005 | 2.5383 × 1007 | 8.9950 × 1003 | |
| F16 | Ave | 2.6622 × 1003 | 2.8848 × 1003 | 2.6586 × 1003 | 2.9848 × 1003 | 3.4392 × 1003 | 3.3697 × 1003 | 3.1208 × 1003 | 2.6913 × 1003 |
| Std | 2.7627 × 1002 | 3.4864 × 1002 | 3.0234 × 1002 | 3.3070 × 1002 | 4.7743 × 1002 | 3.6599 × 1002 | 2.8909 × 1002 | 2.9750 × 1002 | |
| F17 | Ave | 2.0425 × 1003 | 2.5122 × 1003 | 2.2104 × 1003 | 2.5545 × 1003 | 2.6511 × 1003 | 2.6071 × 1003 | 2.2896 × 1003 | 2.1777 × 1003 |
| Std | 1.5540 × 1002 | 2.6725 × 1002 | 2.1800 × 1002 | 3.2060 × 1002 | 3.3119 × 1002 | 2.9519 × 1002 | 2.5708 × 1002 | 2.1467 × 1002 | |
| F18 | Ave | 2.0248 × 1006 | 2.8307 × 1006 | 1.6002 × 1006 | 1.2607 × 1005 | 3.2405 × 1006 | 2.4422 × 1006 | 3.6235 × 1006 | 1.3430 × 1006 |
| Std | 2.3149 × 1006 | 3.1961 × 1006 | 1.7270 × 1006 | 8.2646 × 1004 | 3.8582 × 1006 | 2.2565 × 1006 | 5.8186 × 1006 | 2.0981 × 1006 | |
| F19 | Ave | 1.1478 × 1006 | 7.5279 × 1003 | 3.5759 × 1004 | 1.4449 × 1004 | 3.0782 × 1006 | 2.7309 × 1006 | 6.4510 × 1006 | 9.3737 × 1003 |
| Std | 1.3803 × 1006 | 1.0003 × 1004 | 7.9795 × 1004 | 1.7084 × 1004 | 7.2016 × 1006 | 3.3243 × 1006 | 1.1668 × 1007 | 1.1237 × 1004 | |
| F20 | Ave | 2.4838 × 1003 | 2.7435 × 1003 | 2.5174 × 1003 | 2.5551 × 1003 | 2.7188 × 1003 | 2.7472 × 1003 | 2.6782 × 1003 | 2.3669 × 1003 |
| Std | 1.6592 × 1002 | 2.4968 × 1002 | 1.9336 × 1002 | 1.8983 × 1002 | 2.4175 × 1002 | 1.9688 × 1002 | 2.0408 × 1002 | 1.6869 × 1002 | |
| F21 | Ave | 2.4030 × 1003 | 2.5003 × 1003 | 2.4104 × 1003 | 2.5667 × 1003 | 2.5519 × 1003 | 2.4997 × 1003 | 2.4999 × 1003 | 2.4172 × 1003 |
| Std | 2.0699 × 1001 | 4.3511 × 1001 | 3.0560 × 1001 | 1.6294 × 1001 | 5.1257 × 1001 | 4.3093 × 1001 | 5.1069 × 1001 | 3.4323 × 1001 | |
| F22 | Ave | 4.8809 × 1003 | 4.2986 × 1003 | 5.0618 × 1003 | 4.8193 × 1003 | 4.9684 × 1003 | 3.6110 × 1003 | 6.1869 × 1003 | 3.8435 × 1003 |
| Std | 1.8781 × 1003 | 2.3464 × 1003 | 2.1159 × 1003 | 1.5939 × 1003 | 2.4981 × 1003 | 2.2249 × 1003 | 2.3096 × 1003 | 2.1135 × 1003 | |
| F23 | Ave | 2.7842 × 1003 | 2.8797 × 1003 | 2.8785 × 1003 | 2.9091 × 1003 | 3.0026 × 1003 | 2.9595 × 1003 | 2.9265 × 1003 | 2.7787 × 1003 |
| Std | 4.1240 × 1001 | 7.4256 × 1001 | 8.4955 × 1001 | 1.6186 × 1001 | 1.2427 × 1002 | 6.1837 × 1001 | 6.7901 × 1001 | 4.1438 × 1001 | |
| F24 | Ave | 2.9662 × 1003 | 3.0308 × 1003 | 3.1053 × 1003 | 3.0433 × 1003 | 3.1998 × 1003 | 3.0512 × 1003 | 3.1054 × 1003 | 2.9615 × 1003 |
| Std | 6.0541 × 1001 | 7.6090 × 1001 | 9.1501 × 1001 | 1.2406 × 1001 | 9.8925 × 1001 | 5.8957 × 1001 | 6.5715 × 1001 | 5.2031 × 1001 | |
| F25 | Ave | 3.0391 × 1003 | 2.9138 × 1003 | 2.9395 × 1003 | 3.1840 × 1003 | 2.9761 × 1003 | 3.0795 × 1003 | 3.2267 × 1003 | 2.9044 × 1003 |
| Std | 1.2102 × 1002 | 1.6781 × 1001 | 4.6393 × 1001 | 8.6748 × 1001 | 4.1779 × 1001 | 4.5472 × 1001 | 1.2932 × 1002 | 2.2886 × 1001 | |
| F26 | Ave | 5.0335 × 1003 | 5.6594 × 1003 | 5.1083 × 1003 | 5.2881 × 1003 | 7.2851 × 1003 | 6.8372 × 1003 | 6.1636 × 1003 | 4.6601 × 1003 |
| Std | 5.1045 × 1002 | 1.4276 × 1003 | 8.4084 × 1002 | 2.6234 × 1002 | 9.1932 × 1002 | 1.8118 × 1003 | 7.8118 × 1002 | 9.7846 × 1002 | |
| F27 | Ave | 3.2728 × 1003 | 3.4502 × 1003 | 3.2774 × 1003 | 3.3577 × 1003 | 3.3446 × 1003 | 3.4334 × 1003 | 3.3911 × 1003 | 3.2336 × 1003 |
| Std | 3.6129 × 1001 | 1.4546 × 1002 | 3.4694 × 1001 | 7.9813 × 1001 | 5.5498 × 1001 | 9.6239 × 1001 | 7.9391 × 1001 | 1.1126 × 1001 | |
| F28 | Ave | 3.4582 × 1003 | 4.4756 × 1003 | 3.6015 × 1003 | 3.7861 × 1003 | 3.5739 × 1003 | 3.4549 × 1003 | 3.7787 × 1003 | 3.2607 × 1003 |
| Std | 1.4650 × 1002 | 1.0548 × 1003 | 8.4307 × 1002 | 5.6812 × 1002 | 3.9794 × 1002 | 7.9759 × 1001 | 2.3915 × 1002 | 2.4565 × 1001 | |
| F29 | Ave | 3.9170 × 1003 | 4.2740 × 1003 | 3.9372 × 1003 | 4.4687 × 1003 | 4.3476 × 1003 | 4.9087 × 1003 | 4.3690 × 1003 | 3.7215 × 1003 |
| Std | 1.6033 × 1002 | 2.4192 × 1002 | 2.2151 × 1002 | 2.3190 × 1002 | 3.8157 × 1002 | 3.5212 × 1002 | 3.2438 × 1002 | 2.1116 × 1002 | |
| F30 | Ave | 1.3933 × 1007 | 1.2169 × 1005 | 4.0847 × 1005 | 9.5764 × 1004 | 5.7551 × 1006 | 1.3332 × 1007 | 3.8595 × 1007 | 1.1595 × 1004 |
| Std | 1.3980 × 1007 | 2.1137 × 1005 | 1.2051 × 1006 | 1.1256 × 1005 | 7.2456 × 1006 | 8.4294 × 1006 | 3.1914 × 1007 | 3.9623 × 1003 |
| Function | Metric | GWO | IWOA | AGPSO | HSO | DBO | BPBO | GJO | MGJO |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Ave | 5.3510 × 1010 | 8.9745 × 1009 | 2.7509 × 1010 | 3.2404 × 1009 | 8.5312 × 1010 | 5.2731 × 1010 | 1.3279 × 1011 | 2.5979 × 1008 |
| Std | 8.7034 × 1009 | 2.6775 × 1009 | 1.0784 × 1010 | 1.6339 × 1009 | 7.0504 × 1010 | 8.8060 × 1009 | 1.4218 × 1010 | 1.1627 × 1008 | |
| F2 | Ave | 1.2050 × 10135 | 1.2511 × 10133 | 3.5868 × 10139 | 3.1190 × 10201 | 6.1137 × 10163 | 9.3962 × 10154 | 3.1194 × 10149 | 1.3655 × 10101 |
| Std | 6.5262 × 10135 | 6.1838 × 10133 | 1.9620 × 10140 | 6.5535 × 1004 | 6.5535 × 1004 | 6.5535 × 1004 | 1.4435 × 10150 | 5.1024 × 10101 | |
| F3 | Ave | 5.2603 × 1005 | 9.4038 × 1005 | 7.0265 × 1005 | 3.4666 × 1005 | 6.1803 × 1005 | 3.5749 × 1005 | 3.8842 × 1005 | 5.1192 × 1005 |
| Std | 8.9976 × 1004 | 1.0343 × 1005 | 9.5974 × 1004 | 3.4786 × 1004 | 2.4925 × 1005 | 3.0824 × 1004 | 3.5893 × 1004 | 6.3321 × 1004 | |
| F4 | Ave | 6.4441 × 1003 | 1.9157 × 1003 | 5.9269 × 1003 | 3.0318 × 1003 | 1.8998 × 1004 | 7.4066 × 1003 | 2.0314 × 1004 | 1.1419 × 1003 |
| Std | 1.8268 × 1003 | 3.1130 × 1002 | 2.9983 × 1003 | 8.8704 × 1002 | 1.4422 × 1004 | 1.6252 × 1003 | 4.7254 × 1003 | 8.5415 × 1001 | |
| F5 | Ave | 1.2442 × 1003 | 1.4804 × 1003 | 1.3223 × 1003 | 1.6868 × 1003 | 1.6858 × 1003 | 1.7620 × 1003 | 1.5917 × 1003 | 1.3195 × 1003 |
| Std | 7.7468 × 1001 | 6.0703 × 1001 | 9.1677 × 1001 | 8.7948 × 1001 | 2.0586 × 1002 | 6.7735 × 1001 | 1.1573 × 1002 | 1.5512 × 1002 | |
| F6 | Ave | 6.4522 × 1002 | 6.7360 × 1002 | 6.5670 × 1002 | 6.9061 × 1002 | 6.8058 × 1002 | 6.9312 × 1002 | 6.7476 × 1002 | 6.5154 × 1002 |
| Std | 5.0389 × 1000 | 3.2847 × 1000 | 7.7674 × 1000 | 5.1499 × 1000 | 1.1371 × 1001 | 4.0328 × 1000 | 5.9583 × 1000 | 7.1434 × 1000 | |
| F7 | Ave | 2.1978 × 1003 | 3.0995 × 1003 | 3.1326 × 1003 | 4.8226 × 1003 | 3.0094 × 1003 | 3.7014 × 1003 | 2.9671 × 1003 | 2.3527 × 1003 |
| Std | 1.3159 × 1002 | 2.4569 × 1002 | 2.6520 × 1002 | 6.5307 × 1002 | 2.0699 × 1002 | 9.2563 × 1001 | 1.2136 × 1002 | 3.0908 × 1002 | |
| F8 | Ave | 1.5856 × 1003 | 1.9067 × 1003 | 1.6318 × 1003 | 2.0420 × 1003 | 2.1809 × 1003 | 2.2433 × 1003 | 1.9478 × 1003 | 1.6619 × 1003 |
| Std | 1.4423 × 1002 | 6.8833 × 1001 | 1.0815 × 1002 | 7.4633 × 1001 | 2.3425 × 1002 | 7.0908 × 1001 | 1.0835 × 1002 | 1.8880 × 1002 | |
| F9 | Ave | 4.5865 × 1004 | 3.5318 × 1004 | 3.8231 × 1004 | 6.3337 × 1004 | 7.6876 × 1004 | 7.0544 × 1004 | 6.3521 × 1004 | 4.3473 × 1004 |
| Std | 1.3947 × 1004 | 3.8803 × 1003 | 1.0973 × 1004 | 1.6184 × 1004 | 8.5930 × 1003 | 1.0140 × 1004 | 9.0921 × 1003 | 3.6714 × 1003 | |
| F10 | Ave | 1.9070 × 1004 | 1.9403 × 1004 | 2.4635 × 1004 | 2.3683 × 1004 | 2.8480 × 1004 | 2.7304 × 1004 | 2.6966 × 1004 | 2.2392 × 1004 |
| Std | 4.1712 × 1003 | 1.4057 × 1003 | 2.8272 × 1003 | 1.8427 × 1003 | 4.3763 × 1003 | 2.5923 × 1003 | 4.9114 × 1003 | 1.8762 × 1003 | |
| F11 | Ave | 9.2253 × 1004 | 1.5751 × 1005 | 1.0379 × 1005 | 5.7994 × 1004 | 2.4113 × 1005 | 1.4358 × 1005 | 1.0863 × 1005 | 8.3907 × 1004 |
| Std | 1.7735 × 1004 | 5.3303 × 1004 | 3.6954 × 1004 | 2.3412 × 1004 | 6.8023 × 1004 | 2.8041 × 1004 | 2.0842 × 1004 | 2.3945 × 1004 | |
| F12 | Ave | 1.3411 × 1010 | 8.7825 × 1008 | 9.9960 × 1009 | 1.6939 × 1008 | 6.5324 × 1009 | 7.0752 × 1009 | 4.7622 × 1010 | 1.2354 × 1008 |
| Std | 5.3199 × 1009 | 3.4747 × 1008 | 6.2775 × 1009 | 1.0477 × 1008 | 2.1057 × 1009 | 2.0407 × 1009 | 1.0009 × 1010 | 3.4286 × 1007 | |
| F13 | Ave | 1.4569 × 1009 | 7.6721 × 1005 | 1.2596 × 1009 | 7.4976 × 1004 | 3.4423 × 1008 | 2.6518 × 1008 | 9.4564 × 1009 | 1.0271 × 1004 |
| Std | 9.0110 × 1008 | 4.5610 × 1005 | 1.6198 × 1009 | 3.4890 × 1004 | 2.1799 × 1008 | 1.1801 × 1008 | 3.9091 × 1009 | 6.3155 × 1003 | |
| F14 | Ave | 9.0447 × 1006 | 4.2857 × 1006 | 7.9435 × 1006 | 9.7047 × 1005 | 1.6980 × 1007 | 1.4402 × 1007 | 1.7311 × 1007 | 6.9310 × 1006 |
| Std | 5.5295 × 1006 | 1.6898 × 1006 | 6.7914 × 1006 | 6.9679 × 1005 | 1.0376 × 1007 | 5.8969 × 1006 | 1.1189 × 1007 | 2.6292 × 1006 | |
| F15 | Ave | 3.6823 × 1008 | 7.5246 × 1004 | 1.5117 × 1008 | 2.9811 × 1004 | 6.8445 × 1007 | 2.5749 × 1007 | 3.2105 × 1009 | 6.3068 × 1003 |
| Std | 5.6759 × 1008 | 3.6070 × 1004 | 3.4836 × 1008 | 1.0704 × 1004 | 8.9388 × 1007 | 1.7288 × 1007 | 2.4150 × 1009 | 1.1720 × 1004 | |
| F16 | Ave | 6.5838 × 1003 | 6.9150 × 1003 | 7.3807 × 1003 | 7.2401 × 1003 | 9.3081 × 1003 | 1.1244 × 1004 | 9.9269 × 1003 | 5.7588 × 1003 |
| Std | 5.4314 × 1002 | 7.6111 × 1002 | 1.0740 × 1003 | 9.2612 × 1002 | 1.4833 × 1003 | 1.2453 × 1003 | 1.2241 × 1003 | 7.7678 × 1002 | |
| F17 | Ave | 5.5501 × 1003 | 6.3968 × 1003 | 7.5824 × 1003 | 5.6223 × 1003 | 9.1235 × 1003 | 7.9666 × 1003 | 3.1351 × 1004 | 4.9930 × 1003 |
| Std | 9.6950 × 1002 | 6.1720 × 1002 | 3.1625 × 1003 | 4.2981 × 1002 | 1.4514 × 1003 | 7.8680 × 1002 | 5.1530 × 1004 | 6.4923 × 1002 | |
| F18 | Ave | 9.4181 × 1006 | 7.1481 × 1006 | 1.0695 × 1007 | 2.2247 × 1006 | 2.7972 × 1007 | 1.5441 × 1007 | 1.9089 × 1007 | 6.1371 × 1006 |
| Std | 5.2724 × 1006 | 3.5548 × 1006 | 6.7932 × 1006 | 1.7877 × 1006 | 1.5624 × 1007 | 6.1604 × 1006 | 1.0315 × 1007 | 2.9256 × 1006 | |
| F19 | Ave | 3.0200 × 1008 | 5.9721 × 1005 | 2.1440 × 1008 | 2.0822 × 1004 | 7.3010 × 1007 | 3.9518 × 1007 | 2.5227 × 1009 | 5.1664 × 1003 |
| Std | 4.4671 × 1008 | 5.8884 × 1005 | 5.7456 × 1008 | 2.0347 × 1004 | 7.9364 × 1007 | 2.7621 × 1007 | 1.8096 × 1009 | 2.6068 × 1003 | |
| F20 | Ave | 5.6596 × 1003 | 5.9349 × 1003 | 6.3321 × 1003 | 4.8819 × 1003 | 7.3061 × 1003 | 6.4297 × 1003 | 6.4377 × 1003 | 5.8606 × 1003 |
| Std | 1.0939 × 1003 | 5.0468 × 1002 | 6.4152 × 1002 | 4.8240 × 1002 | 7.5312 × 1002 | 6.4935 × 1002 | 1.0003 × 1003 | 1.0923 × 1003 | |
| F21 | Ave | 3.0936 × 1003 | 3.6431 × 1003 | 3.3348 × 1003 | 3.7133 × 1003 | 4.0461 × 1003 | 3.9040 × 1003 | 3.5464 × 1003 | 3.2024 × 1003 |
| Std | 6.6627 × 1001 | 1.8877 × 1002 | 1.2260 × 1002 | 7.0588 × 1001 | 1.4972 × 1002 | 1.6236 × 1002 | 1.2394 × 1002 | 2.1602 × 1002 | |
| F22 | Ave | 2.2917 × 1004 | 2.2472 × 1004 | 2.6821 × 1004 | 2.5741 × 1004 | 2.9813 × 1004 | 3.0436 × 1004 | 2.9424 × 1004 | 2.4632 × 1004 |
| Std | 5.2026 × 1003 | 1.5296 × 1003 | 2.8580 × 1003 | 1.7428 × 1003 | 4.6555 × 1003 | 3.0252 × 1003 | 4.2920 × 1003 | 2.7559 × 1003 | |
| F23 | Ave | 3.7025 × 1003 | 4.1565 × 1003 | 4.5492 × 1003 | 4.0114 × 1003 | 4.8542 × 1003 | 4.5816 × 1003 | 4.5843 × 1003 | 3.4829 × 1003 |
| Std | 6.9705 × 1001 | 1.8345 × 1002 | 2.5633 × 1002 | 5.1409 × 1001 | 1.8344 × 1002 | 2.3162 × 1002 | 2.0724 × 1002 | 2.0993 × 1002 | |
| F24 | Ave | 4.4320 × 1003 | 4.9823 × 1003 | 6.6914 × 1003 | 4.6083 × 1003 | 6.1674 × 1003 | 5.5866 × 1003 | 6.0391 × 1003 | 4.0212 × 1003 |
| Std | 1.7256 × 1002 | 2.7333 × 1002 | 5.7435 × 1002 | 6.4584 × 1001 | 4.1475 × 1002 | 2.6685 × 1002 | 4.4634 × 1002 | 1.6803 × 1002 | |
| F25 | Ave | 7.1507 × 1003 | 4.4340 × 1003 | 6.1216 × 1003 | 6.5600 × 1003 | 8.8138 × 1003 | 7.8050 × 1003 | 1.2755 × 1004 | 3.8202 × 1003 |
| Std | 1.1525 × 1003 | 1.9410 × 1002 | 9.5531 × 1002 | 7.6190 × 1002 | 5.2496 × 1003 | 7.1229 × 1002 | 1.7622 × 1003 | 7.2848 × 1001 | |
| F26 | Ave | 1.7659 × 1004 | 2.2212 × 1004 | 2.5527 × 1004 | 1.9129 × 1004 | 2.6686 × 1004 | 3.2665 × 1004 | 2.8358 × 1004 | 1.6988 × 1004 |
| Std | 1.4143 × 1003 | 4.2171 × 1003 | 4.5872 × 1003 | 1.0966 × 1003 | 3.4511 × 1003 | 3.9829 × 1003 | 2.0930 × 1003 | 2.2942 × 1003 | |
| F27 | Ave | 4.3566 × 1003 | 6.6007 × 1003 | 4.7403 × 1003 | 4.2438 × 1003 | 4.6931 × 1003 | 5.6618 × 1003 | 5.8454 × 1003 | 3.6943 × 1003 |
| Std | 1.9124 × 1002 | 1.5056 × 1003 | 6.2080 × 1002 | 1.9753 × 1002 | 3.8149 × 1002 | 6.2630 × 1002 | 6.0483 × 1002 | 9.3333 × 1001 | |
| F28 | Ave | 9.5038 × 1003 | 1.7317 × 1004 | 1.2574 × 1004 | 1.5498 × 1004 | 1.8865 × 1004 | 1.1127 × 1004 | 1.6434 × 1004 | 4.0417 × 1003 |
| Std | 1.2968 × 1003 | 6.9142 × 1003 | 3.9998 × 1003 | 4.5155 × 1003 | 5.4083 × 1003 | 1.1913 × 1003 | 2.1791 × 1003 | 1.3769 × 1002 | |
| F29 | Ave | 9.4609 × 1003 | 8.4494 × 1003 | 9.2722 × 1003 | 9.5580 × 1003 | 1.2496 × 1004 | 1.4890 × 1004 | 1.5871 × 1004 | 6.7427 × 1003 |
| Std | 8.2399 × 1002 | 7.6366 × 1002 | 8.5661 × 1002 | 7.1012 × 1002 | 3.0845 × 1003 | 1.4930 × 1003 | 4.8154 × 1003 | 5.1538 × 1002 | |
| F30 | Ave | 1.1000 × 1009 | 1.2532 × 1007 | 7.6521 × 1008 | 1.2125 × 1006 | 2.6261 × 1008 | 6.6309 × 1008 | 7.6570 × 1009 | 2.3546 × 1005 |
| Std | 7.4027 × 1008 | 8.9771 × 1006 | 9.5393 × 1008 | 1.0580 × 1006 | 2.3539 × 1008 | 3.1762 × 1008 | 3.4330 × 1009 | 1.2030 × 1005 |
| Function | Metric | GWO | IWOA | AGPSO | HSO | DBO | BPBO | GJO | MGJO |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Ave | 3.5415 × 1003 | 5.8385 × 1002 | 3.0011 × 1002 | 1.3698 × 1003 | 1.9787 × 1003 | 1.0500 × 1003 | 3.3052 × 1003 | 1.2035 × 1003 |
| Std | 2.8924 × 1003 | 2.5780 × 1002 | 4.8818 × 10−01 | 2.0562 × 1002 | 3.2939 × 1003 | 7.1886 × 1002 | 2.3852 × 1003 | 9.4838 × 1002 | |
| F2 | Ave | 4.3341 × 1002 | 4.1967 × 1002 | 4.3021 × 1002 | 4.4484 × 1002 | 4.3446 × 1002 | 4.3632 × 1002 | 4.5063 × 1002 | 4.1308 × 1002 |
| Std | 2.2603 × 1001 | 2.7659 × 1001 | 3.2172 × 1001 | 2.9376 × 1001 | 3.6068 × 1001 | 3.1836 × 1001 | 2.7100 × 1001 | 2.3071 × 1001 | |
| F3 | Ave | 6.0165 × 1002 | 6.1014 × 1002 | 6.0010 × 1002 | 6.1898 × 1002 | 6.1035 × 1002 | 6.2235 × 1002 | 6.0927 × 1002 | 6.0000 × 1002 |
| Std | 2.0177 × 1000 | 6.9742 × 1000 | 3.8896 × 10−01 | 4.1618 × 1000 | 7.1251 × 1000 | 9.9230 × 1000 | 5.4324 × 1000 | 1.8248 × 10−07 | |
| F4 | Ave | 8.1728 × 1002 | 8.3292 × 1002 | 8.1462 × 1002 | 8.3944 × 1002 | 8.3566 × 1002 | 8.2214 × 1002 | 8.3139 × 1002 | 8.1481 × 1002 |
| Std | 8.1755 × 1000 | 1.2004 × 1001 | 7.3628 × 1000 | 4.5694 × 1000 | 1.2153 × 1001 | 7.8466 × 1000 | 9.3321 × 1000 | 7.3113 × 1000 | |
| F5 | Ave | 9.3258 × 1002 | 1.0575 × 1003 | 9.0181 × 1002 | 9.1048 × 1002 | 9.7112 × 1002 | 9.9164 × 1002 | 1.0114 × 1003 | 9.0166 × 1002 |
| Std | 6.0653 × 1001 | 1.9366 × 1002 | 2.8773 × 1000 | 9.5826 × 1000 | 7.5771 × 1001 | 8.6615 × 1001 | 1.1416 × 1002 | 2.9296 × 1000 | |
| F6 | Ave | 5.9301 × 1003 | 2.4035 × 1003 | 4.8602 × 1003 | 2.8979 × 1003 | 5.9127 × 1003 | 4.1557 × 1003 | 1.0893 × 1004 | 3.1694 × 1003 |
| Std | 2.4751 × 1003 | 9.7532 × 1002 | 2.2146 × 1003 | 1.4517 × 1003 | 2.4702 × 1003 | 2.2729 × 1003 | 5.3408 × 1003 | 1.8218 × 1003 | |
| F7 | Ave | 2.0330 × 1003 | 2.0365 × 1003 | 2.0190 × 1003 | 2.0781 × 1003 | 2.0393 × 1003 | 2.0603 × 1003 | 2.0462 × 1003 | 2.0098 × 1003 |
| Std | 1.4634 × 1001 | 1.6189 × 1001 | 6.6032 × 1000 | 2.9937 × 1001 | 2.1218 × 1001 | 1.8419 × 1001 | 2.4871 × 1001 | 9.7780 × 1000 | |
| F8 | Ave | 2.2280 × 1003 | 2.2195 × 1003 | 2.2229 × 1003 | 2.2790 × 1003 | 2.2341 × 1003 | 2.2335 × 1003 | 2.2282 × 1003 | 2.2260 × 1003 |
| Std | 2.2821 × 1001 | 9.5001 × 1000 | 5.0381 × 1000 | 6.7574 × 1001 | 3.3128 × 1001 | 2.0924 × 1001 | 3.1546 × 1000 | 4.8810 × 1000 | |
| F9 | Ave | 2.5692 × 1003 | 2.5487 × 1003 | 2.5342 × 1003 | 2.6927 × 1003 | 2.5552 × 1003 | 2.5749 × 1003 | 2.6032 × 1003 | 2.5293 × 1003 |
| Std | 3.7133 × 1001 | 4.3650 × 1001 | 2.6816 × 1001 | 4.4243 × 1001 | 4.3793 × 1001 | 3.7994 × 1001 | 4.1553 × 1001 | 1.7324 × 10−01 | |
| F10 | Ave | 2.5867 × 1003 | 2.5489 × 1003 | 2.5570 × 1003 | 2.6071 × 1003 | 2.5547 × 1003 | 2.5766 × 1003 | 2.5887 × 1003 | 2.5008 × 1003 |
| Std | 6.2669 × 1001 | 5.6479 × 1001 | 6.1452 × 1001 | 1.1611 × 1002 | 6.6522 × 1001 | 6.3166 × 1001 | 6.3634 × 1001 | 1.8645 × 10−01 | |
| F11 | Ave | 2.8748 × 1003 | 2.7401 × 1003 | 2.8376 × 1003 | 2.9730 × 1003 | 2.7700 × 1003 | 2.7744 × 1003 | 2.9859 × 1003 | 2.6839 × 1003 |
| Std | 2.2466 × 1002 | 1.7449 × 1002 | 1.8726 × 1002 | 2.0572 × 1002 | 1.2654 × 1002 | 1.7069 × 1002 | 2.3982 × 1002 | 9.6289 × 1001 | |
| F12 | Ave | 2.8695 × 1003 | 2.8717 × 1003 | 2.8712 × 1003 | 2.8669 × 1003 | 2.8772 × 1003 | 2.8695 × 1003 | 2.8766 × 1003 | 2.8650 × 1003 |
| Std | 1.1415 × 1001 | 2.0568 × 1000 | 1.7011 × 1001 | 1.0262 × 1001 | 2.3393 × 1001 | 1.2292 × 1001 | 1.5871 × 1001 | 1.0730 × 1001 |
| Function | Metric | GWO | IWOA | AGPSO | HSO | DBO | BPBO | GJO | MGJO |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Ave | 1.6530 × 1004 | 2.0859 × 1004 | 1.2046 × 1004 | 7.8069 × 1003 | 3.4305 × 1004 | 2.3080 × 1004 | 1.6040 × 1004 | 2.1086 × 1004 |
| Std | 5.3662 × 1003 | 6.8295 × 1003 | 7.9329 × 1003 | 4.4438 × 1003 | 1.0268 × 1004 | 8.1011 × 1003 | 5.4810 × 1003 | 9.1187 × 1003 | |
| F2 | Ave | 4.9755 × 1002 | 4.6415 × 1002 | 4.7620 × 1002 | 5.5925 × 1002 | 4.9042 × 1002 | 5.6247 × 1002 | 6.1581 × 1002 | 4.6682 × 1002 |
| Std | 3.9461 × 1001 | 1.7315 × 1001 | 4.3064 × 1001 | 6.3565 × 1001 | 5.1359 × 1001 | 5.3795 × 1001 | 7.3198 × 1001 | 2.6211 × 1001 | |
| F3 | Ave | 6.0711 × 1002 | 6.4070 × 1002 | 6.0446 × 1002 | 6.3690 × 1002 | 6.3486 × 1002 | 6.4817 × 1002 | 6.3112 × 1002 | 6.0000 × 1002 |
| Std | 4.4861 × 1000 | 1.8949 × 1001 | 3.4282 × 1000 | 5.2175 × 1000 | 9.3797 × 1000 | 1.3872 × 1001 | 8.6800 × 1000 | 8.3378 × 10−04 | |
| F4 | Ave | 8.6034 × 1002 | 8.8687 × 1002 | 8.5159 × 1002 | 9.1771 × 1002 | 9.0819 × 1002 | 8.8617 × 1002 | 9.0381 × 1002 | 8.5679 × 1002 |
| Std | 3.0605 × 1001 | 2.2540 × 1001 | 1.8976 × 1001 | 1.1865 × 1001 | 3.0499 × 1001 | 1.2952 × 1001 | 3.1246 × 1001 | 1.8707 × 1001 | |
| F5 | Ave | 1.2909 × 1003 | 2.3854 × 1003 | 1.1391 × 1003 | 1.1600 × 1003 | 2.1677 × 1003 | 2.6117 × 1003 | 1.8898 × 1003 | 1.2240 × 1003 |
| Std | 3.2993 × 1002 | 4.9386 × 1002 | 1.1466 × 1002 | 2.7274 × 1002 | 6.0993 × 1002 | 5.8900 × 1002 | 4.9049 × 1002 | 3.5288 × 1002 | |
| F6 | Ave | 2.9536 × 1006 | 7.1596 × 1003 | 2.0715 × 1005 | 4.7155 × 1003 | 7.2529 × 1005 | 1.5692 × 1005 | 1.9905 × 1007 | 5.3478 × 1003 |
| Std | 1.2837 × 1007 | 6.5420 × 1003 | 5.1192 × 1005 | 3.2456 × 1003 | 1.6150 × 1006 | 2.8491 × 1005 | 3.2789 × 1007 | 3.6362 × 1003 | |
| F7 | Ave | 2.1033 × 1003 | 2.1340 × 1003 | 2.0673 × 1003 | 2.1410 × 1003 | 2.1268 × 1003 | 2.1661 × 1003 | 2.1212 × 1003 | 2.0613 × 1003 |
| Std | 5.1832 × 1001 | 4.1502 × 1001 | 3.6736 × 1001 | 4.9555 × 1001 | 4.6537 × 1001 | 4.5945 × 1001 | 4.1601 × 1001 | 3.1778 × 1001 | |
| F8 | Ave | 2.2723 × 1003 | 2.2514 × 1003 | 2.2457 × 1003 | 2.4639 × 1003 | 2.3381 × 1003 | 2.3025 × 1003 | 2.2658 × 1003 | 2.2389 × 1003 |
| Std | 5.7417 × 1001 | 3.8673 × 1001 | 3.5503 × 1001 | 1.2185 × 1002 | 7.0948 × 1001 | 8.0681 × 1001 | 5.6463 × 1001 | 3.8289 × 1001 | |
| F9 | Ave | 2.5315 × 1003 | 2.4809 × 1003 | 2.4970 × 1003 | 2.6989 × 1003 | 2.5141 × 1003 | 2.5216 × 1003 | 2.5919 × 1003 | 2.4866 × 1003 |
| Std | 3.7290 × 1001 | 1.2906 × 10−01 | 2.4913 × 1001 | 7.6430 × 1001 | 3.2234 × 1001 | 3.0870 × 1001 | 4.6168 × 1001 | 2.6549 × 1000 | |
| F10 | Ave | 3.5982 × 1003 | 2.6964 × 1003 | 2.9915 × 1003 | 3.7925 × 1003 | 3.6767 × 1003 | 4.0409 × 1003 | 4.0490 × 1003 | 2.5828 × 1003 |
| Std | 1.0419 × 1003 | 5.5138 × 1002 | 5.8868 × 1002 | 6.6111 × 1002 | 1.3246 × 1003 | 1.2880 × 1003 | 1.5033 × 1003 | 1.6528 × 1002 | |
| F11 | Ave | 3.5272 × 1003 | 2.9012 × 1003 | 3.4571 × 1003 | 3.5842 × 1003 | 3.1253 × 1003 | 3.2194 × 1003 | 4.4994 × 1003 | 2.8934 × 1003 |
| Std | 2.6310 × 1002 | 1.0844 × 1002 | 4.7210 × 1002 | 2.8166 × 1002 | 1.5453 × 1002 | 1.6347 × 1002 | 6.3837 × 1002 | 1.0808 × 1002 | |
| F12 | Ave | 2.9824 × 1003 | 3.0454 × 1003 | 3.0078 × 1003 | 3.0052 × 1003 | 3.0268 × 1003 | 3.0509 × 1003 | 3.0278 × 1003 | 2.9679 × 1003 |
| Std | 2.7524 × 1001 | 1.6390 × 1001 | 5.0636 × 1001 | 3.8326 × 1001 | 6.9680 × 1001 | 5.1204 × 1001 | 5.9206 × 1001 | 2.3602 × 1001 |
| Statistical Results | GWO | IWOA | AGPSO | HSO | DBO | BPBO | GJO |
|---|---|---|---|---|---|---|---|
| CEC2017 dim = 30 (+/=/−) | (20/0/10) | (27/0/3) | (20/0/10) | (27/0/3) | (29/0/1) | (29/0/1) | 28/0/2) |
| CEC2017 dim = 100 (+/=/−) | (27/0/3) | (28/0/2) | (25/0/5) | (28/0/2) | (29/0/1) | (29/0/1) | (29/0/1) |
| CEC2022 dim = 10 (+/=/−) | (11/0/1) | (10/0/2) | (10/0/2) | (11/0/1) | (8/0/4) | (9/0/3) | (11/0/1) |
| CEC2022 dim = 20 (+/=/−) | (11/0/1) | (12/0/0) | (9/0/3) | (10/0/2) | (12/0/0) | (6/0/6) | (12/0/0) |
| Suites | CEC2017 | CEC2022 | ||||||
|---|---|---|---|---|---|---|---|---|
| Dimensions | 30 | 100 | 10 | 20 | ||||
| Algorithms | ||||||||
| GWO | 3.70 | 3 | 3.47 | 2 | 4.50 | 4 | 4.33 | 4 |
| IWOA | 4.40 | 5 | 3.70 | 4 | 3.08 | 3 | 4.17 | 3 |
| AGPSO | 3.10 | 2 | 4.27 | 5 | 2.50 | 2 | 2.58 | 2 |
| HSO | 4.03 | 4 | 3.60 | 3 | 6.50 | 7 | 5.42 | 6 |
| DBO | 6.00 | 6 | 6.37 | 6 | 5.00 | 5 | 5.25 | 5 |
| BPBO | 6.37 | 7 | 6.43 | 8 | 5.25 | 6 | 6.33 | 8 |
| GJO | 6.50 | 8 | 6.40 | 7 | 6.75 | 8 | 5.92 | 7 |
| MGJO | 1.90 | 1 | 1.77 | 1 | 2.42 | 1 | 2.00 | 1 |
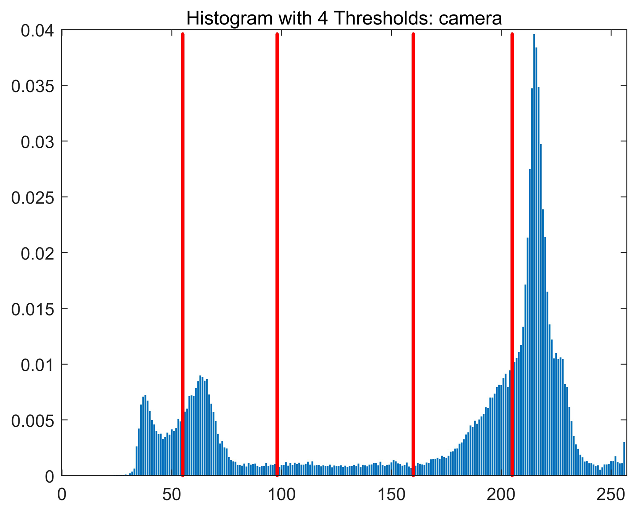
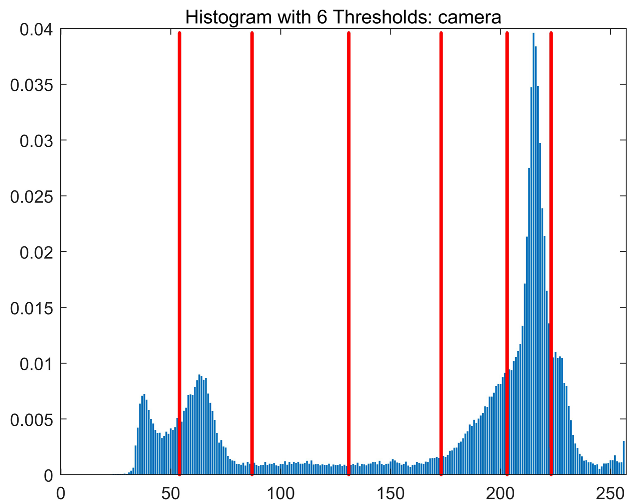
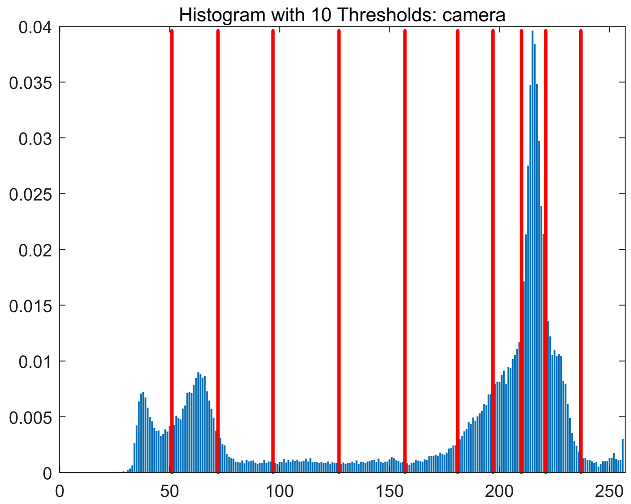
| Images | TH = 4 | TH = 6 | TH = 8 | TH = 10 |
|---|---|---|---|---|
| baboon |  |  | 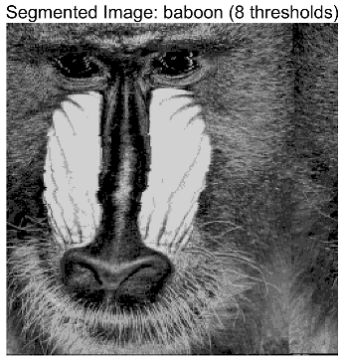 |  |
 |  |  |  | |
| Camera |  |  |  |  |
 |  |  |  | |
| Face |  |  |  |  |
 |  | 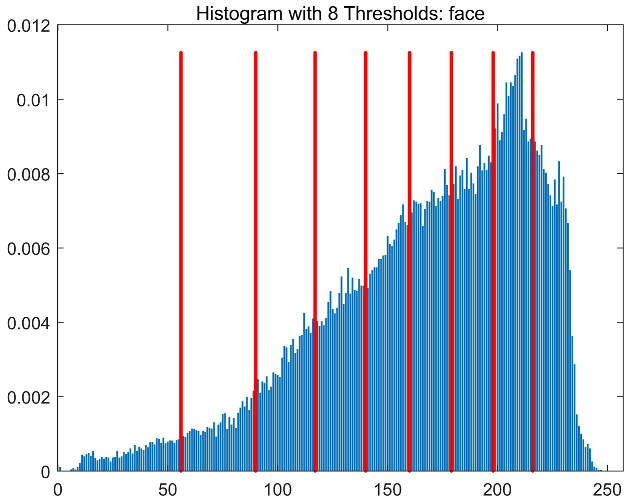 |  | |
| Girl |  |  |  |  |
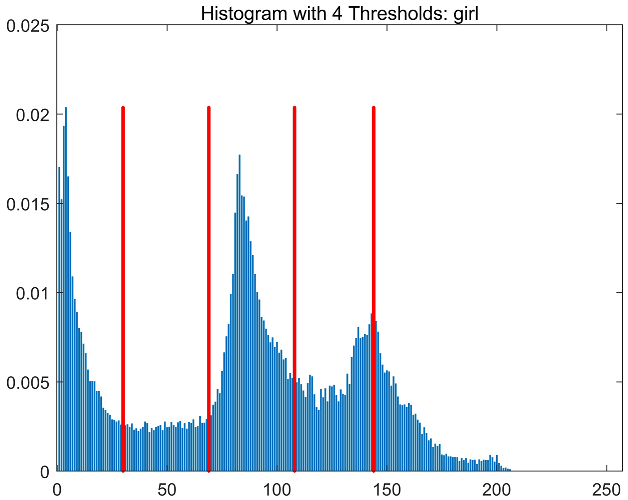 |  | 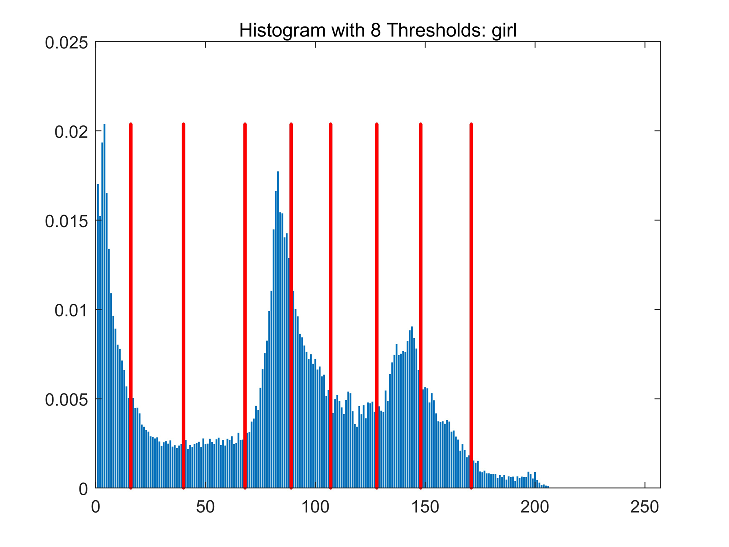 |  | |
| Hunter |  |  |  |  |
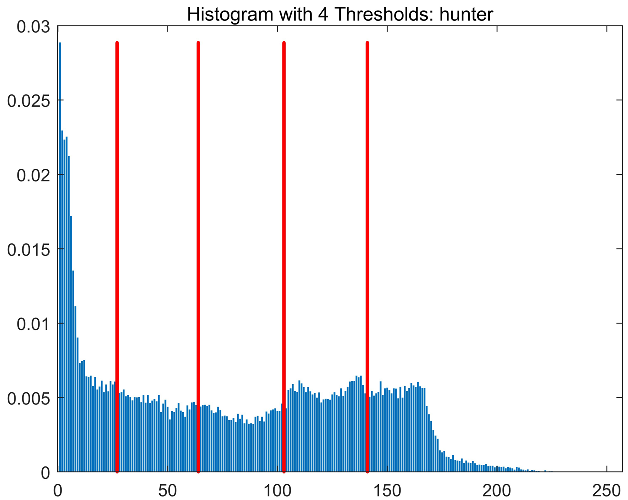 | 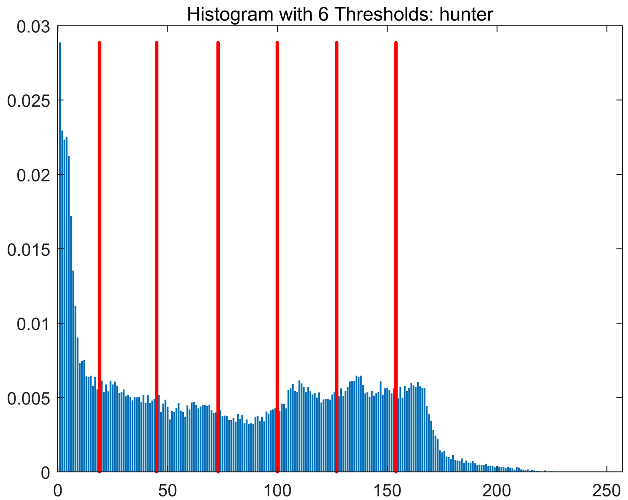 | 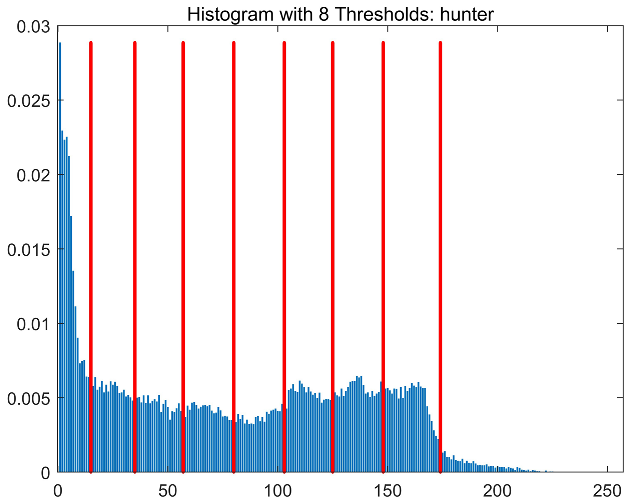 |  | |
| Lena |  |  |  |  |
 | 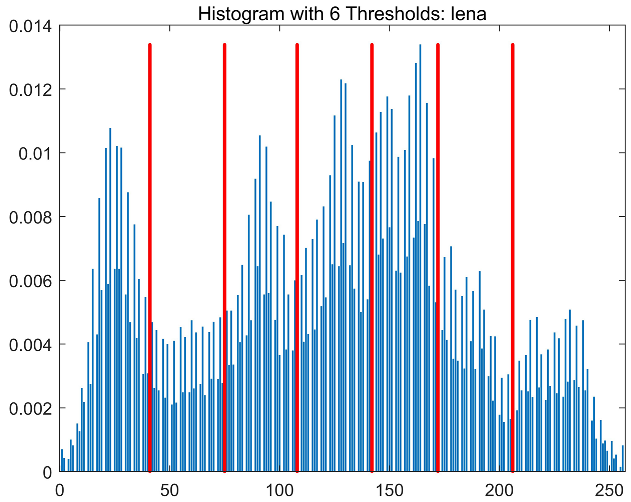 |  |  | |
| Saturn |  |  |  |  |
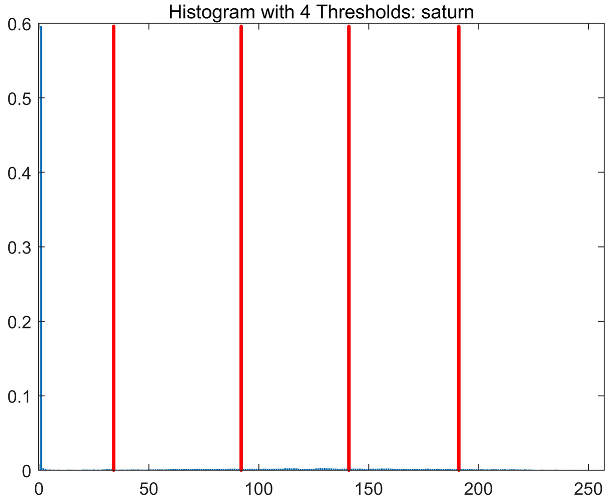 |  |  |  | |
| Terrace |  |  |  |  |
 |  |  |  |
| Images | TH | Metrics | GWO | IWOA | AGPSO | HSO | DBO | BPBO | GJO | MGJO |
|---|---|---|---|---|---|---|---|---|---|---|
| Baboon | 4 | Ave | 3.2985 × 1003 | 3.2958 × 1003 | 3.3001 × 1003 | 3.2652 × 1003 | 3.2993 × 1003 | 3.2945 × 1003 | 3.2933 × 1003 | 3.3008 × 1003 |
| Std | 4.1827 × 1000 | 2.8020 × 1000 | 6.4510 × 10−01 | 1.9685 × 1001 | 1.6491 × 1000 | 4.6041 × 1000 | 6.1253 × 1000 | 3.9126 × 10−02 | ||
| 6 | Ave | 3.3648 × 1003 | 3.3594 × 1003 | 3.3674 × 1003 | 3.3327 × 1003 | 3.3604 × 1003 | 3.3615 × 1003 | 3.3611 × 1003 | 3.3718 × 1003 | |
| Std | 8.5391 × 1000 | 8.3701 × 1000 | 3.3757 × 1000 | 1.0698 × 1001 | 1.1013 × 1001 | 5.4107 × 1000 | 4.8473 × 1000 | 4.9081 × 10−01 | ||
| 8 | Ave | 3.3936 × 1003 | 3.3869 × 1003 | 3.3937 × 1003 | 3.3671 × 1003 | 3.3876 × 1003 | 3.3862 × 1003 | 3.3851 × 1003 | 3.3992 × 1003 | |
| Std | 4.1562 × 1000 | 4.7990 × 1000 | 3.6513 × 1000 | 1.1122 × 1001 | 5.2377 × 1000 | 5.6342 × 1000 | 7.9354 × 1000 | 1.1804 × 1000 | ||
| 10 | Ave | 3.4079 × 1003 | 3.4029 × 1003 | 3.4081 × 1003 | 3.3900 × 1003 | 3.4026 × 1003 | 3.4042 × 1003 | 3.4019 × 1003 | 3.4139 × 1003 | |
| Std | 3.1677 × 1000 | 3.6528 × 1000 | 2.9531 × 1000 | 7.1104 × 1000 | 5.4729 × 1000 | 3.6108 × 1000 | 4.1270 × 1000 | 1.0583 × 1000 | ||
| Camera | 4 | Ave | 4.5975 × 1003 | 4.5975 × 1003 | 4.5990 × 1003 | 4.5836 × 1003 | 4.5983 × 1003 | 4.5968 × 1003 | 4.5950 × 1003 | 4.6001 × 1003 |
| Std | 2.6817 × 1000 | 1.9470 × 1000 | 1.1715 × 1000 | 6.7691 × 1000 | 1.5377 × 1000 | 2.3036 × 1000 | 3.2502 × 1000 | 1.0296 × 1000 | ||
| 6 | Ave | 4.6459 × 1003 | 4.6416 × 1003 | 4.6477 × 1003 | 4.6189 × 1003 | 4.6407 × 1003 | 4.6371 × 1003 | 4.6396 × 1003 | 4.6512 × 1003 | |
| Std | 4.9420 × 1000 | 4.9456 × 1000 | 4.2107 × 1000 | 8.4537 × 1000 | 5.7329 × 1000 | 5.4444 × 1000 | 5.8709 × 1000 | 3.7977 × 10−01 | ||
| 8 | Ave | 4.6603 × 1003 | 4.6605 × 1003 | 4.6648 × 1003 | 4.6416 × 1003 | 4.6567 × 1003 | 4.6597 × 1003 | 4.6587 × 1003 | 4.6690 × 1003 | |
| Std | 6.2075 × 1000 | 3.9347 × 1000 | 2.7189 × 1000 | 9.5247 × 1000 | 5.5192 × 1000 | 5.1934 × 1000 | 4.4859 × 1000 | 1.0893 × 1000 | ||
| 10 | Ave | 4.6739 × 1003 | 4.6706 × 1003 | 4.6739 × 1003 | 4.6527 × 1003 | 4.6669 × 1003 | 4.6688 × 1003 | 4.6692 × 1003 | 4.6791 × 1003 | |
| Std | 3.6129 × 1000 | 2.9887 × 1000 | 1.9996 × 1000 | 8.4757 × 1000 | 4.4742 × 1000 | 3.2907 × 1000 | 3.9017 × 1000 | 9.6454 × 10−01 | ||
| Face | 4 | Ave | 2.1204 × 1003 | 2.1163 × 1003 | 2.1217 × 1003 | 2.0907 × 1003 | 2.1198 × 1003 | 2.1180 × 1003 | 2.1127 × 1003 | 2.1224 × 1003 |
| Std | 2.5080 × 1000 | 4.3746 × 1000 | 1.3134 × 1000 | 1.5501 × 1001 | 3.1669 × 1000 | 3.5967 × 1000 | 1.2110 × 1001 | 8.0498 × 10−02 | ||
| 6 | Ave | 2.1764 × 1003 | 2.1740 × 1003 | 2.1803 × 1003 | 2.1483 × 1003 | 2.1763 × 1003 | 2.1760 × 1003 | 2.1666 × 1003 | 2.1843 × 1003 | |
| Std | 7.3609 × 1000 | 7.4735 × 1000 | 3.2680 × 1000 | 1.2176 × 1001 | 6.8784 × 1000 | 5.4467 × 1000 | 9.2604 × 1000 | 5.6488 × 10−01 | ||
| 8 | Ave | 2.2014 × 1003 | 2.1973 × 1003 | 2.2035 × 1003 | 2.1789 × 1003 | 2.1994 × 1003 | 2.2020 × 1003 | 2.1936 × 1003 | 2.2094 × 1003 | |
| Std | 6.3197 × 1000 | 5.3907 × 1000 | 3.5669 × 1000 | 9.7466 × 1000 | 5.1068 × 1000 | 4.1424 × 1000 | 6.4159 × 1000 | 1.3020 × 1000 | ||
| 10 | Ave | 2.2132 × 1003 | 2.2107 × 1003 | 2.2173 × 1003 | 2.1972 × 1003 | 2.2106 × 1003 | 2.2137 × 1003 | 2.2073 × 1003 | 2.2225 × 1003 | |
| Std | 4.9300 × 1000 | 5.5702 × 1000 | 2.8225 × 1000 | 7.6236 × 1000 | 7.2712 × 1000 | 4.5883 × 1000 | 6.9676 × 1000 | 9.0505 × 10−01 | ||
| Girl | 4 | Ave | 2.5331 × 1003 | 2.5294 × 1003 | 2.5331 × 1003 | 2.5096 × 1003 | 2.5331 × 1003 | 2.5312 × 1003 | 2.5304 × 1003 | 2.5339 × 1003 |
| Std | 2.2156 × 1000 | 3.8668 × 1000 | 2.3908 × 1000 | 1.3297 × 1001 | 1.1515 × 1000 | 3.2110 × 1000 | 3.2500 × 1000 | 9.2841 × 10−03 | ||
| 6 | Ave | 2.5824 × 1003 | 2.5761 × 1003 | 2.5813 × 1003 | 2.5522 × 1003 | 2.5806 × 1003 | 2.5775 × 1003 | 2.5775 × 1003 | 2.5843 × 1003 | |
| Std | 2.3014 × 1000 | 5.6223 × 1000 | 2.7930 × 1000 | 1.2912 × 1001 | 2.6832 × 1000 | 4.1286 × 1000 | 4.1278 × 1000 | 3.5990 × 10−01 | ||
| 8 | Ave | 2.6021 × 1003 | 2.5950 × 1003 | 2.6019 × 1003 | 2.5821 × 1003 | 2.5967 × 1003 | 2.5963 × 1003 | 2.5963 × 1003 | 2.6057 × 1003 | |
| Std | 3.8462 × 1000 | 4.5544 × 1000 | 2.8120 × 1000 | 8.0226 × 1000 | 4.4712 × 1000 | 4.2578 × 1000 | 4.1632 × 1000 | 1.2443 × 1000 | ||
| 10 | Ave | 2.6120 × 1003 | 2.6065 × 1003 | 2.6116 × 1003 | 2.5040 × 1003 | 2.6073 × 1003 | 2.6074 × 1003 | 2.6087 × 1003 | 2.6166 × 1003 | |
| Std | 3.1581 × 1000 | 3.8739 × 1000 | 2.3522 × 1000 | 4.7301 × 1002 | 3.7702 × 1000 | 3.8689 × 1000 | 2.9101 × 1000 | 8.5354 × 10−01 | ||
| Hunter | 4 | Ave | 3.1889 × 1003 | 3.1866 × 1003 | 3.1895 × 1003 | 3.1472 × 1003 | 3.1892 × 1003 | 3.1865 × 1003 | 3.1864 × 1003 | 3.1902 × 1003 |
| Std | 2.1547 × 1000 | 2.5499 × 1000 | 7.3977 × 10−01 | 2.8846 × 1001 | 9.6951 × 10−01 | 4.0963 × 1000 | 2.5061 × 1000 | 1.9189 × 10−01 | ||
| 6 | Ave | 3.2433 × 1003 | 3.2385 × 1003 | 3.2439 × 1003 | 3.2103 × 1003 | 3.2411 × 1003 | 3.2396 × 1003 | 3.2404 × 1003 | 3.2464 × 1003 | |
| Std | 4.4935 × 1000 | 4.3160 × 1000 | 1.4189 × 1000 | 1.6430 × 1001 | 4.7173 × 1000 | 4.9492 × 1000 | 3.6477 × 1000 | 7.5295 × 10−01 | ||
| 8 | Ave | 3.2684 × 1003 | 3.2598 × 1003 | 3.2663 × 1003 | 3.2386 × 1003 | 3.2613 × 1003 | 3.2612 × 1003 | 3.2629 × 1003 | 3.2715 × 1003 | |
| Std | 2.8558 × 1000 | 4.3686 × 1000 | 3.2022 × 1000 | 1.2175 × 1001 | 5.5053 × 1000 | 4.2536 × 1000 | 4.0888 × 1000 | 9.2072 × 10−01 | ||
| 10 | Ave | 3.2787 × 1003 | 3.2728 × 1003 | 3.2777 × 1003 | 3.2506 × 1003 | 3.2725 × 1003 | 3.2734 × 1003 | 3.2742 × 1003 | 3.2836 × 1003 | |
| Std | 3.2829 × 1000 | 4.5857 × 1000 | 3.5896 × 1000 | 1.0999 × 1001 | 4.5371 × 1000 | 4.0687 × 1000 | 3.7927 × 1000 | 8.4336 × 10−01 | ||
| Lena | 4 | Ave | 3.6827 × 1003 | 3.6811 × 1003 | 3.6851 × 1003 | 3.6374 × 1003 | 3.6842 × 1003 | 3.6792 × 1003 | 3.6780 × 1003 | 3.6860 × 1003 |
| Std | 4.3455 × 1000 | 4.8787 × 1000 | 1.5975 × 1000 | 3.3474 × 1001 | 1.9209 × 1000 | 7.4090 × 1000 | 5.3111 × 1000 | 1.1916 × 10−01 | ||
| 6 | Ave | 3.7573 × 1003 | 3.7507 × 1003 | 3.7581 × 1003 | 3.7236 × 1003 | 3.7556 × 1003 | 3.7517 × 1003 | 3.7487 × 1003 | 3.7654 × 1003 | |
| Std | 8.8347 × 1000 | 7.9039 × 1000 | 5.8364 × 1000 | 1.3862 × 1001 | 7.5451 × 1000 | 8.2557 × 1000 | 1.0989 × 1001 | 5.2392 × 10−01 | ||
| 8 | Ave | 3.7870 × 1003 | 3.7825 × 1003 | 3.7896 × 1003 | 3.7610 × 1003 | 3.7840 × 1003 | 3.7823 × 1003 | 3.7790 × 1003 | 3.7946 × 1003 | |
| Std | 4.3173 × 1000 | 5.0347 × 1000 | 3.3579 × 1000 | 1.1018 × 1001 | 6.2895 × 1000 | 5.9568 × 1000 | 6.3455 × 1000 | 1.0259 × 1000 | ||
| 10 | Ave | 3.8035 × 1003 | 3.7996 × 1003 | 3.8053 × 1003 | 3.7832 × 1003 | 3.7985 × 1003 | 3.7992 × 1003 | 3.7967 × 1003 | 3.8118 × 1003 | |
| Std | 5.5683 × 1000 | 3.8848 × 1000 | 3.2966 × 1000 | 7.9172 × 1000 | 5.1814 × 1000 | 5.4822 × 1000 | 4.5858 × 1000 | 1.9341 × 1000 | ||
| Saturn | 4 | Ave | 5.2205 × 1003 | 5.2183 × 1003 | 5.2215 × 1003 | 5.1955 × 1003 | 5.2208 × 1003 | 5.2197 × 1003 | 5.2163 × 1003 | 5.2220 × 1003 |
| Std | 2.7184 × 1000 | 3.2853 × 1000 | 7.1242 × 10−01 | 1.4455 × 1001 | 1.5341 × 1000 | 2.6001 × 1000 | 7.1545 × 1000 | 3.0003 × 10−02 | ||
| 6 | Ave | 5.2692 × 1003 | 5.2659 × 1003 | 5.2713 × 1003 | 5.2475 × 1003 | 5.2686 × 1003 | 5.2665 × 1003 | 5.2660 × 1003 | 5.2726 × 1003 | |
| Std | 3.1010 × 1000 | 3.0999 × 1000 | 1.7429 × 1000 | 9.6328 × 1000 | 3.3621 × 1000 | 3.6739 × 1000 | 3.9684 × 1000 | 4.9814 × 10−01 | ||
| 8 | Ave | 5.2889 × 1003 | 5.2860 × 1003 | 5.2898 × 1003 | 5.2741 × 1003 | 5.2871 × 1003 | 5.2846 × 1003 | 5.2848 × 1003 | 5.2927 × 1003 | |
| Std | 2.5168 × 1000 | 2.4244 × 1000 | 2.0422 × 1000 | 6.7971 × 1000 | 3.3044 × 1000 | 3.3184 × 1000 | 3.6748 × 1000 | 6.0088 × 10−01 | ||
| 10 | Ave | 5.2992 × 1003 | 5.2967 × 1003 | 5.2985 × 1003 | 5.2840 × 1003 | 5.2955 × 1003 | 5.2958 × 1003 | 5.2953 × 1003 | 5.3026 × 1003 | |
| Std | 2.0853 × 1000 | 1.9785 × 1000 | 2.5973 × 1000 | 5.1445 × 1000 | 3.0911 × 1000 | 3.4434 × 1000 | 3.2255 × 1000 | 5.9890 × 10−01 | ||
| Terrace | 4 | Ave | 2.6390 × 1003 | 2.6352 × 1003 | 2.6392 × 1003 | 2.5956 × 1003 | 2.6385 × 1003 | 2.6352 × 1003 | 2.6361 × 1003 | 2.6402 × 1003 |
| Std | 3.3119 × 1000 | 5.8176 × 1000 | 1.1456 × 1000 | 2.2690 × 1001 | 1.9837 × 1000 | 4.7550 × 1000 | 3.1223 × 1000 | 3.7343 × 10−02 | ||
| 6 | Ave | 2.7000 × 1003 | 2.6900 × 1003 | 2.6978 × 1003 | 2.6594 × 1003 | 2.6961 × 1003 | 2.6915 × 1003 | 2.6914 × 1003 | 2.7020 × 1003 | |
| Std | 2.3293 × 1000 | 5.6849 × 1000 | 3.1792 × 1000 | 1.5664 × 1001 | 5.2586 × 1000 | 5.9177 × 1000 | 6.8622 × 1000 | 4.1380 × 10−01 | ||
| 8 | Ave | 2.7248 × 1003 | 2.7156 × 1003 | 2.7224 × 1003 | 2.6972 × 1003 | 2.7195 × 1003 | 2.7198 × 1003 | 2.7190 × 1003 | 2.7284 × 1003 | |
| Std | 4.1674 × 1000 | 5.3877 × 1000 | 3.7844 × 1000 | 9.5988 × 1000 | 5.3308 × 1000 | 3.6885 × 1000 | 3.5037 × 1000 | 1.0277 × 1000 | ||
| 10 | Ave | 2.7384 × 1003 | 2.7316 × 1003 | 2.7359 × 1003 | 2.7091 × 1003 | 2.7335 × 1003 | 2.7315 × 1003 | 2.7325 × 1003 | 2.7419 × 1003 | |
| Std | 2.7462 × 1000 | 4.7626 × 1000 | 2.7346 × 1000 | 1.1469 × 1001 | 4.1832 × 1000 | 4.3540 × 1000 | 3.5022 × 1000 | 1.1363 × 1000 | ||
| Friedman-Rank | 2.73 | 5.70 | 3.49 | 7.93 | 4.30 | 5.32 | 5.37 | 1.18 | ||
| Final-Rank | 2 | 7 | 3 | 8 | 4 | 5 | 6 | 1 | ||
| Images | TH | Metrics | GWO | IWOA | AGPSO | HSO | DBO | BPBO | GJO | MGJO |
|---|---|---|---|---|---|---|---|---|---|---|
| Baboon | 4 | Ave | 18.0952 | 18.2554 | 18.1909 | 17.4612 | 18.1520 | 17.7155 | 18.0750 | 18.2235 |
| Std | 0.2659 | 0.3598 | 0.1669 | 1.0028 | 0.2494 | 0.3909 | 0.4987 | 0.0587 | ||
| 6 | Ave | 21.0145 | 20.9345 | 21.2826 | 19.4113 | 20.7927 | 20.2304 | 20.8563 | 21.3266 | |
| Std | 0.5899 | 0.7698 | 0.3768 | 0.9375 | 0.8806 | 0.6951 | 0.7546 | 0.1942 | ||
| 8 | Ave | 22.9893 | 22.6465 | 23.0175 | 20.9897 | 22.4766 | 21.6938 | 22.6795 | 23.5610 | |
| Std | 0.6046 | 0.7081 | 0.5819 | 0.8642 | 0.8183 | 0.8491 | 0.7449 | 0.3852 | ||
| 10 | Ave | 24.3626 | 24.0177 | 24.4181 | 22.8657 | 24.2954 | 23.3296 | 24.1569 | 25.0596 | |
| Std | 0.6461 | 0.7130 | 0.6644 | 1.0584 | 0.8705 | 0.8327 | 0.8141 | 0.4374 | ||
| Camera | 4 | Ave | 18.3413 | 19.0060 | 18.3878 | 17.5884 | 18.5210 | 18.2794 | 18.2820 | 18.9996 |
| Std | 0.8146 | 1.0353 | 0.7431 | 0.5742 | 0.9090 | 0.8633 | 0.7464 | 0.8982 | ||
| 6 | Ave | 21.1833 | 21.1172 | 21.7305 | 19.8444 | 21.0829 | 20.0684 | 21.1714 | 21.8160 | |
| Std | 1.0512 | 0.9556 | 0.4051 | 1.4722 | 1.0282 | 1.1818 | 0.9735 | 0.1918 | ||
| 8 | Ave | 22.5215 | 22.5343 | 23.0863 | 21.4453 | 22.6065 | 22.0485 | 22.5461 | 23.0673 | |
| Std | 1.0347 | 0.7697 | 0.6265 | 1.5412 | 0.9137 | 0.9112 | 0.8603 | 0.3722 | ||
| 10 | Ave | 23.7482 | 23.5751 | 23.7985 | 22.4346 | 23.8518 | 22.7772 | 23.8941 | 24.0101 | |
| Std | 0.5901 | 1.0687 | 0.8536 | 1.5501 | 1.1107 | 0.8033 | 1.0044 | 0.3680 | ||
| Face | 4 | Ave | 19.6190 | 19.5317 | 19.7119 | 18.7452 | 19.6555 | 19.4749 | 19.4372 | 19.7431 |
| Std | 0.2258 | 0.3417 | 0.1033 | 0.5727 | 0.1728 | 0.3023 | 0.4106 | 0.0407 | ||
| 6 | Ave | 22.1843 | 21.8667 | 22.4044 | 20.9382 | 22.1876 | 22.0046 | 21.7645 | 22.5966 | |
| Std | 0.3766 | 0.7107 | 0.3096 | 0.6649 | 0.5024 | 0.5694 | 0.4976 | 0.1161 | ||
| 8 | Ave | 24.2104 | 23.8621 | 24.2547 | 22.5695 | 24.0278 | 24.0344 | 23.6361 | 24.6478 | |
| Std | 0.4971 | 0.4271 | 0.5197 | 0.7039 | 0.4714 | 0.4733 | 0.4647 | 0.2921 | ||
| 10 | Ave | 25.3571 | 25.0458 | 25.7182 | 23.7160 | 25.1385 | 25.2690 | 24.9027 | 26.4192 | |
| Std | 0.5372 | 0.7170 | 0.3808 | 0.6686 | 0.7911 | 0.6107 | 0.6236 | 0.2050 | ||
| Girl | 4 | Ave | 21.9857 | 21.8110 | 21.9611 | 21.1045 | 22.0105 | 22.1478 | 21.8203 | 21.9595 |
| Std | 0.2566 | 0.3911 | 0.2828 | 0.8421 | 0.1957 | 0.2841 | 0.4064 | 0.0575 | ||
| 6 | Ave | 24.2986 | 23.8934 | 24.2860 | 22.8888 | 24.1695 | 24.2970 | 23.9450 | 24.4533 | |
| Std | 0.4115 | 0.6289 | 0.3916 | 1.1162 | 0.5167 | 0.4098 | 0.5812 | 0.2265 | ||
| 8 | Ave | 26.2020 | 25.4631 | 26.1407 | 24.3075 | 25.6081 | 25.9612 | 25.5383 | 26.3961 | |
| Std | 0.4272 | 0.7363 | 0.4635 | 0.8497 | 0.6244 | 0.5376 | 0.6101 | 0.2812 | ||
| 10 | Ave | 27.5148 | 26.6413 | 27.3021 | 25.1911 | 26.8166 | 27.2625 | 26.7874 | 28.0996 | |
| Std | 0.4306 | 0.6467 | 0.5666 | 1.5980 | 0.6751 | 0.5098 | 0.6573 | 0.2191 | ||
| Hunter | 4 | Ave | 21.9108 | 21.8017 | 21.9201 | 20.8587 | 21.9017 | 21.9194 | 21.7408 | 21.9927 |
| Std | 0.1196 | 0.1763 | 0.0913 | 0.7714 | 0.0954 | 0.1103 | 0.1617 | 0.0288 | ||
| 6 | Ave | 24.4434 | 24.0101 | 24.3554 | 22.6226 | 24.2966 | 24.4141 | 24.1654 | 24.5299 | |
| Std | 0.3119 | 0.3344 | 0.2244 | 0.7563 | 0.3138 | 0.2544 | 0.3551 | 0.2920 | ||
| 8 | Ave | 26.0975 | 25.2994 | 25.8516 | 23.9899 | 25.5459 | 25.8217 | 25.6038 | 26.2694 | |
| Std | 0.2557 | 0.4485 | 0.3325 | 0.7630 | 0.4435 | 0.3720 | 0.3582 | 0.1212 | ||
| 10 | Ave | 27.2447 | 26.5114 | 27.0846 | 24.7966 | 26.6295 | 26.9010 | 26.6213 | 27.8330 | |
| Std | 0.4310 | 0.5125 | 0.4322 | 0.7187 | 0.4018 | 0.4739 | 0.4719 | 0.1634 | ||
| Lena | 4 | Ave | 19.0565 | 19.0102 | 19.0952 | 18.2606 | 19.0721 | 19.0340 | 18.9694 | 19.1212 |
| Std | 0.0888 | 0.1206 | 0.0605 | 0.6663 | 0.0848 | 0.1201 | 0.1461 | 0.0279 | ||
| 6 | Ave | 21.5413 | 21.2753 | 21.5354 | 20.3493 | 21.3816 | 21.2560 | 21.1731 | 21.8512 | |
| Std | 0.3328 | 0.2984 | 0.3216 | 0.5040 | 0.3738 | 0.2894 | 0.4290 | 0.0518 | ||
| 8 | Ave | 23.1264 | 22.8547 | 23.2917 | 21.8235 | 22.8829 | 22.7026 | 22.7378 | 23.6057 | |
| Std | 0.4001 | 0.4382 | 0.3825 | 0.6423 | 0.3833 | 0.4045 | 0.4917 | 0.2887 | ||
| 10 | Ave | 24.2832 | 24.1340 | 24.5612 | 22.9175 | 23.9934 | 23.7670 | 23.8262 | 24.9759 | |
| Std | 0.4871 | 0.4338 | 0.3794 | 0.5785 | 0.5769 | 0.5505 | 0.4946 | 0.3618 | ||
| Saturn | 4 | Ave | 22.2645 | 22.2029 | 22.3277 | 21.4109 | 22.3166 | 22.3655 | 22.1494 | 22.3423 |
| Std | 0.1317 | 0.2373 | 0.0585 | 0.5927 | 0.1163 | 0.1700 | 0.3784 | 0.0270 | ||
| 6 | Ave | 25.0762 | 24.7413 | 25.1943 | 23.5879 | 24.9502 | 25.1228 | 24.7550 | 25.3021 | |
| Std | 0.3315 | 0.3935 | 0.2412 | 0.7636 | 0.3529 | 0.2672 | 0.3721 | 0.0929 | ||
| 8 | Ave | 26.9601 | 26.5835 | 27.0003 | 25.4044 | 26.7132 | 26.6869 | 26.5320 | 27.4439 | |
| Std | 0.3644 | 0.3530 | 0.3017 | 0.7246 | 0.3923 | 0.5373 | 0.3931 | 0.1670 | ||
| 10 | Ave | 28.4526 | 27.9390 | 28.3402 | 26.4258 | 27.8525 | 28.2296 | 27.8216 | 29.0811 | |
| Std | 0.3701 | 0.3439 | 0.4948 | 0.7156 | 0.5970 | 0.4880 | 0.4451 | 0.1862 | ||
| Terrace | 4 | Ave | 21.4487 | 21.3472 | 21.4543 | 20.2352 | 21.4414 | 21.3513 | 21.3498 | 21.4807 |
| Std | 0.0912 | 0.1680 | 0.0446 | 0.5816 | 0.0605 | 0.1477 | 0.1189 | 0.0057 | ||
| 6 | Ave | 23.8957 | 23.4246 | 23.7389 | 22.0499 | 23.6955 | 23.6429 | 23.4807 | 24.0005 | |
| Std | 0.1441 | 0.3004 | 0.2232 | 0.6379 | 0.2887 | 0.2593 | 0.3648 | 0.0381 | ||
| 8 | Ave | 25.5812 | 24.9050 | 25.3399 | 23.7264 | 25.1479 | 25.2346 | 25.1673 | 25.8515 | |
| Std | 0.2904 | 0.4396 | 0.3309 | 0.5738 | 0.4494 | 0.3141 | 0.2904 | 0.0847 | ||
| 10 | Ave | 26.9638 | 26.1866 | 26.6473 | 24.4053 | 26.4007 | 26.3419 | 26.2958 | 27.3360 | |
| Std | 0.3448 | 0.4855 | 0.3269 | 0.8057 | 0.4211 | 0.3865 | 0.3352 | 0.1720 | ||
| Friedman-Rank | 2.82 | 5.52 | 3.74 | 7.94 | 4.33 | 4.71 | 5.40 | 1.54 | ||
| Final-Rank | 2 | 7 | 3 | 8 | 4 | 5 | 6 | 1 | ||
| Images | TH | Metrics | GWO | IWOA | AGPSO | HSO | DBO | BPBO | GJO | MGJO |
|---|---|---|---|---|---|---|---|---|---|---|
| Baboon | 4 | Ave | 0.8176 | 0.8218 | 0.8196 | 0.8040 | 0.8187 | 0.8098 | 0.8184 | 0.8200 |
| Std | 0.0066 | 0.0107 | 0.0046 | 0.0274 | 0.0062 | 0.0088 | 0.0116 | 0.0014 | ||
| 6 | Ave | 0.8795 | 0.8775 | 0.8840 | 0.8459 | 0.8760 | 0.8613 | 0.8755 | 0.8847 | |
| Std | 0.0136 | 0.0209 | 0.0092 | 0.0250 | 0.0224 | 0.0160 | 0.0201 | 0.0042 | ||
| 8 | Ave | 0.9092 | 0.9043 | 0.9092 | 0.8759 | 0.9012 | 0.8846 | 0.9074 | 0.9198 | |
| Std | 0.0140 | 0.0195 | 0.0137 | 0.0207 | 0.0202 | 0.0192 | 0.0186 | 0.0087 | ||
| 10 | Ave | 0.9264 | 0.9230 | 0.9280 | 0.9050 | 0.9295 | 0.9091 | 0.9279 | 0.9363 | |
| Std | 0.0139 | 0.0150 | 0.0141 | 0.0237 | 0.0170 | 0.0161 | 0.0171 | 0.0082 | ||
| Camera | 4 | Ave | 0.8350 | 0.8327 | 0.8361 | 0.8185 | 0.8318 | 0.8311 | 0.8288 | 0.8358 |
| Std | 0.0078 | 0.0085 | 0.0059 | 0.0138 | 0.0084 | 0.0074 | 0.0096 | 0.0044 | ||
| 6 | Ave | 0.8700 | 0.8661 | 0.8746 | 0.8473 | 0.8671 | 0.8624 | 0.8664 | 0.8770 | |
| Std | 0.0088 | 0.0118 | 0.0061 | 0.0150 | 0.0088 | 0.0082 | 0.0133 | 0.0033 | ||
| 8 | Ave | 0.8881 | 0.8868 | 0.8960 | 0.8686 | 0.8864 | 0.8823 | 0.8870 | 0.9006 | |
| Std | 0.0106 | 0.0118 | 0.0073 | 0.0173 | 0.0103 | 0.0106 | 0.0096 | 0.0039 | ||
| 10 | Ave | 0.9077 | 0.9016 | 0.9058 | 0.8823 | 0.9014 | 0.8938 | 0.9037 | 0.9148 | |
| Std | 0.0063 | 0.0113 | 0.0078 | 0.0150 | 0.0100 | 0.0098 | 0.0111 | 0.0040 | ||
| Face | 4 | Ave | 0.7519 | 0.7518 | 0.7536 | 0.7300 | 0.7526 | 0.7541 | 0.7476 | 0.7539 |
| Std | 0.0054 | 0.0059 | 0.0021 | 0.0196 | 0.0043 | 0.0052 | 0.0128 | 0.0009 | ||
| 6 | Ave | 0.8285 | 0.8249 | 0.8363 | 0.7929 | 0.8304 | 0.8321 | 0.8119 | 0.8434 | |
| Std | 0.0132 | 0.0160 | 0.0065 | 0.0223 | 0.0123 | 0.0109 | 0.0162 | 0.0014 | ||
| 8 | Ave | 0.8742 | 0.8648 | 0.8762 | 0.8289 | 0.8700 | 0.8729 | 0.8577 | 0.8912 | |
| Std | 0.0147 | 0.0107 | 0.0092 | 0.0204 | 0.0102 | 0.0108 | 0.0118 | 0.0035 | ||
| 10 | Ave | 0.8936 | 0.8875 | 0.9043 | 0.8602 | 0.8880 | 0.8962 | 0.8829 | 0.9203 | |
| Std | 0.0126 | 0.0149 | 0.0076 | 0.0160 | 0.0205 | 0.0118 | 0.0136 | 0.0036 | ||
| Girl | 4 | Ave | 0.8283 | 0.8255 | 0.8286 | 0.8019 | 0.8278 | 0.8281 | 0.8262 | 0.8295 |
| Std | 0.0039 | 0.0095 | 0.0067 | 0.0141 | 0.0043 | 0.0069 | 0.0067 | 0.0009 | ||
| 6 | Ave | 0.8668 | 0.8612 | 0.8666 | 0.8402 | 0.8678 | 0.8610 | 0.8643 | 0.8691 | |
| Std | 0.0049 | 0.0095 | 0.0053 | 0.0154 | 0.0059 | 0.0072 | 0.0073 | 0.0045 | ||
| 8 | Ave | 0.8979 | 0.8887 | 0.8971 | 0.8629 | 0.8914 | 0.8883 | 0.8906 | 0.9042 | |
| Std | 0.0078 | 0.0080 | 0.0058 | 0.0153 | 0.0085 | 0.0099 | 0.0082 | 0.0024 | ||
| 10 | Ave | 0.9167 | 0.9039 | 0.9155 | 0.8760 | 0.9090 | 0.9070 | 0.9097 | 0.9274 | |
| Std | 0.0065 | 0.0093 | 0.0059 | 0.0212 | 0.0092 | 0.0083 | 0.0073 | 0.0023 | ||
| Hunter | 4 | Ave | 0.8502 | 0.8486 | 0.8508 | 0.8150 | 0.8501 | 0.8466 | 0.8477 | 0.8526 |
| Std | 0.0030 | 0.0036 | 0.0025 | 0.0200 | 0.0030 | 0.0052 | 0.0038 | 0.0009 | ||
| 6 | Ave | 0.9022 | 0.8953 | 0.9028 | 0.8641 | 0.8993 | 0.8969 | 0.8979 | 0.9065 | |
| Std | 0.0060 | 0.0052 | 0.0030 | 0.0169 | 0.0065 | 0.0063 | 0.0047 | 0.0019 | ||
| 8 | Ave | 0.9313 | 0.9193 | 0.9288 | 0.8910 | 0.9215 | 0.9206 | 0.9236 | 0.9364 | |
| Std | 0.0042 | 0.0069 | 0.0052 | 0.0135 | 0.0081 | 0.0065 | 0.0069 | 0.0021 | ||
| 10 | Ave | 0.9440 | 0.9345 | 0.9415 | 0.9037 | 0.9349 | 0.9348 | 0.9377 | 0.9529 | |
| Std | 0.0053 | 0.0082 | 0.0070 | 0.0140 | 0.0070 | 0.0075 | 0.0067 | 0.0024 | ||
| Lena | 4 | Ave | 0.7790 | 0.7792 | 0.7816 | 0.7608 | 0.7802 | 0.7758 | 0.7775 | 0.7800 |
| Std | 0.0032 | 0.0038 | 0.0021 | 0.0197 | 0.0024 | 0.0057 | 0.0051 | 0.0013 | ||
| 6 | Ave | 0.8403 | 0.8346 | 0.8406 | 0.8102 | 0.8367 | 0.8313 | 0.8328 | 0.8486 | |
| Std | 0.0102 | 0.0097 | 0.0102 | 0.0144 | 0.0099 | 0.0093 | 0.0137 | 0.0036 | ||
| 8 | Ave | 0.8705 | 0.8653 | 0.8737 | 0.8409 | 0.8671 | 0.8612 | 0.8627 | 0.8811 | |
| Std | 0.0103 | 0.0116 | 0.0084 | 0.0173 | 0.0087 | 0.0118 | 0.0096 | 0.0050 | ||
| 10 | Ave | 0.8897 | 0.8863 | 0.8934 | 0.8642 | 0.8841 | 0.8817 | 0.8818 | 0.9015 | |
| Std | 0.0092 | 0.0088 | 0.0063 | 0.0154 | 0.0099 | 0.0106 | 0.0116 | 0.0052 | ||
| Saturn | 4 | Ave | 0.8472 | 0.8490 | 0.8482 | 0.8456 | 0.8487 | 0.8507 | 0.8481 | 0.8480 |
| Std | 0.0037 | 0.0062 | 0.0019 | 0.0116 | 0.0035 | 0.0045 | 0.0074 | 0.0005 | ||
| 6 | Ave | 0.8827 | 0.8788 | 0.8840 | 0.8688 | 0.8821 | 0.8847 | 0.8810 | 0.8849 | |
| Std | 0.0049 | 0.0073 | 0.0046 | 0.0130 | 0.0076 | 0.0058 | 0.0071 | 0.0025 | ||
| 8 | Ave | 0.9086 | 0.9049 | 0.9085 | 0.8900 | 0.9047 | 0.9051 | 0.9048 | 0.9126 | |
| Std | 0.0061 | 0.0073 | 0.0046 | 0.0122 | 0.0072 | 0.0070 | 0.0050 | 0.0035 | ||
| 10 | Ave | 0.9258 | 0.9188 | 0.9246 | 0.9031 | 0.9175 | 0.9227 | 0.9173 | 0.9317 | |
| Std | 0.0050 | 0.0056 | 0.0060 | 0.0108 | 0.0076 | 0.0073 | 0.0072 | 0.0021 | ||
| Terrace | 4 | Ave | 0.8433 | 0.8397 | 0.8441 | 0.8064 | 0.8430 | 0.8388 | 0.8410 | 0.8446 |
| Std | 0.0040 | 0.0086 | 0.0023 | 0.0211 | 0.0040 | 0.0071 | 0.0050 | 0.0006 | ||
| 6 | Ave | 0.9016 | 0.8895 | 0.8983 | 0.8561 | 0.8986 | 0.8855 | 0.8922 | 0.9044 | |
| Std | 0.0048 | 0.0107 | 0.0059 | 0.0191 | 0.0067 | 0.0092 | 0.0110 | 0.0020 | ||
| 8 | Ave | 0.9286 | 0.9178 | 0.9264 | 0.8915 | 0.9219 | 0.9170 | 0.9227 | 0.9349 | |
| Std | 0.0100 | 0.0107 | 0.0075 | 0.0151 | 0.0068 | 0.0083 | 0.0083 | 0.0043 | ||
| 10 | Ave | 0.9441 | 0.9367 | 0.9417 | 0.9050 | 0.9367 | 0.9311 | 0.9386 | 0.9534 | |
| Std | 0.0066 | 0.0099 | 0.0066 | 0.0175 | 0.0102 | 0.0103 | 0.0054 | 0.0041 | ||
| Friedman-Rank | 3.29 | 4.96 | 3.68 | 7.72 | 4.21 | 5.62 | 4.60 | 1.93 | ||
| Final-Rank | 2 | 6 | 3 | 8 | 4 | 7 | 5 | 1 | ||
| Images | TH | Metrics | GWO | IWOA | AGPSO | HSO | DBO | BPBO | GJO | MGJO |
|---|---|---|---|---|---|---|---|---|---|---|
| Baboon | 4 | Ave | 0.7189 | 0.7276 | 0.7233 | 0.6908 | 0.7208 | 0.7033 | 0.7174 | 0.7251 |
| Std | 0.0123 | 0.0169 | 0.0084 | 0.0512 | 0.0122 | 0.0182 | 0.0239 | 0.0028 | ||
| 6 | Ave | 0.8238 | 0.8166 | 0.8315 | 0.7672 | 0.8158 | 0.7976 | 0.8168 | 0.8327 | |
| Std | 0.0218 | 0.0289 | 0.0152 | 0.0397 | 0.0355 | 0.0271 | 0.0294 | 0.0081 | ||
| 8 | Ave | 0.8710 | 0.8612 | 0.8717 | 0.8175 | 0.8571 | 0.8368 | 0.8676 | 0.8856 | |
| Std | 0.0195 | 0.0246 | 0.0175 | 0.0302 | 0.0311 | 0.0278 | 0.0247 | 0.0123 | ||
| 10 | Ave | 0.8979 | 0.8901 | 0.8970 | 0.8633 | 0.9011 | 0.8753 | 0.9000 | 0.9088 | |
| Std | 0.0168 | 0.0200 | 0.0185 | 0.0339 | 0.0206 | 0.0229 | 0.0218 | 0.0105 | ||
| Camera | 4 | Ave | 0.6960 | 0.7248 | 0.7008 | 0.6702 | 0.7026 | 0.6940 | 0.6895 | 0.7248 |
| Std | 0.0407 | 0.0442 | 0.0296 | 0.0420 | 0.0387 | 0.0350 | 0.0403 | 0.0344 | ||
| 6 | Ave | 0.7821 | 0.7796 | 0.7987 | 0.7427 | 0.7795 | 0.7466 | 0.7825 | 0.8013 | |
| Std | 0.0303 | 0.0351 | 0.0155 | 0.0612 | 0.0372 | 0.0365 | 0.0371 | 0.0075 | ||
| 8 | Ave | 0.8154 | 0.8117 | 0.8296 | 0.7861 | 0.8198 | 0.8015 | 0.8171 | 0.8311 | |
| Std | 0.0349 | 0.0329 | 0.0216 | 0.0585 | 0.0322 | 0.0278 | 0.0292 | 0.0106 | ||
| 10 | Ave | 0.8404 | 0.8355 | 0.8393 | 0.8183 | 0.8461 | 0.8190 | 0.8457 | 0.8525 | |
| Std | 0.0206 | 0.0320 | 0.0236 | 0.0410 | 0.0277 | 0.0239 | 0.0284 | 0.0093 | ||
| Face | 4 | Ave | 0.7033 | 0.7056 | 0.7064 | 0.6829 | 0.7055 | 0.7075 | 0.7006 | 0.7066 |
| Std | 0.0104 | 0.0121 | 0.0043 | 0.0266 | 0.0093 | 0.0100 | 0.0176 | 0.0019 | ||
| 6 | Ave | 0.7859 | 0.7804 | 0.7930 | 0.7546 | 0.7882 | 0.7903 | 0.7690 | 0.7996 | |
| Std | 0.0131 | 0.0209 | 0.0083 | 0.0294 | 0.0138 | 0.0133 | 0.0190 | 0.0019 | ||
| 8 | Ave | 0.8396 | 0.8284 | 0.8388 | 0.7935 | 0.8340 | 0.8381 | 0.8220 | 0.8537 | |
| Std | 0.0157 | 0.0122 | 0.0100 | 0.0239 | 0.0113 | 0.0114 | 0.0135 | 0.0041 | ||
| 10 | Ave | 0.8617 | 0.8526 | 0.8730 | 0.8281 | 0.8556 | 0.8661 | 0.8503 | 0.8890 | |
| Std | 0.0128 | 0.0182 | 0.0088 | 0.0207 | 0.0236 | 0.0133 | 0.0156 | 0.0047 | ||
| Girl | 4 | Ave | 0.7141 | 0.7136 | 0.7132 | 0.6763 | 0.7128 | 0.7120 | 0.7110 | 0.7141 |
| Std | 0.0036 | 0.0144 | 0.0110 | 0.0272 | 0.0066 | 0.0099 | 0.0097 | 0.0007 | ||
| 6 | Ave | 0.7530 | 0.7512 | 0.7531 | 0.7280 | 0.7652 | 0.7473 | 0.7601 | 0.7566 | |
| Std | 0.0140 | 0.0211 | 0.0165 | 0.0229 | 0.0196 | 0.0138 | 0.0206 | 0.0148 | ||
| 8 | Ave | 0.7973 | 0.7875 | 0.7925 | 0.7499 | 0.8008 | 0.7804 | 0.8034 | 0.8079 | |
| Std | 0.0152 | 0.0178 | 0.0132 | 0.0236 | 0.0165 | 0.0205 | 0.0196 | 0.0106 | ||
| 10 | Ave | 0.8258 | 0.8135 | 0.8217 | 0.7707 | 0.8265 | 0.8016 | 0.8258 | 0.8365 | |
| Std | 0.0164 | 0.0258 | 0.0171 | 0.0322 | 0.0229 | 0.0134 | 0.0157 | 0.0111 | ||
| Hunter | 4 | Ave | 0.6959 | 0.6976 | 0.6963 | 0.6446 | 0.6961 | 0.6856 | 0.6995 | 0.7037 |
| Std | 0.0146 | 0.0158 | 0.0125 | 0.0374 | 0.0167 | 0.0181 | 0.0175 | 0.0064 | ||
| 6 | Ave | 0.7722 | 0.7593 | 0.7722 | 0.7133 | 0.7667 | 0.7643 | 0.7706 | 0.7771 | |
| Std | 0.0170 | 0.0172 | 0.0156 | 0.0358 | 0.0198 | 0.0148 | 0.0128 | 0.0104 | ||
| 8 | Ave | 0.8122 | 0.8005 | 0.8111 | 0.7603 | 0.8106 | 0.7947 | 0.8109 | 0.8228 | |
| Std | 0.0109 | 0.0216 | 0.0128 | 0.0283 | 0.0152 | 0.0197 | 0.0162 | 0.0091 | ||
| 10 | Ave | 0.8411 | 0.8304 | 0.8352 | 0.7806 | 0.8373 | 0.8182 | 0.8410 | 0.8532 | |
| Std | 0.0135 | 0.0167 | 0.0195 | 0.0326 | 0.0239 | 0.0176 | 0.0178 | 0.0100 | ||
| Lena | 4 | Ave | 0.6743 | 0.6738 | 0.6757 | 0.6575 | 0.6759 | 0.6728 | 0.6727 | 0.6756 |
| Std | 0.0044 | 0.0046 | 0.0015 | 0.0242 | 0.0030 | 0.0056 | 0.0057 | 0.0007 | ||
| 6 | Ave | 0.7472 | 0.7458 | 0.7468 | 0.7179 | 0.7417 | 0.7366 | 0.7413 | 0.7568 | |
| Std | 0.0179 | 0.0173 | 0.0142 | 0.0206 | 0.0161 | 0.0133 | 0.0239 | 0.0055 | ||
| 8 | Ave | 0.7930 | 0.7857 | 0.7959 | 0.7624 | 0.7837 | 0.7813 | 0.7893 | 0.8053 | |
| Std | 0.0225 | 0.0223 | 0.0198 | 0.0324 | 0.0162 | 0.0189 | 0.0272 | 0.0158 | ||
| 10 | Ave | 0.8207 | 0.8227 | 0.8303 | 0.7902 | 0.8174 | 0.8059 | 0.8151 | 0.8364 | |
| Std | 0.0197 | 0.0221 | 0.0190 | 0.0269 | 0.0239 | 0.0191 | 0.0286 | 0.0141 | ||
| Saturn | 4 | Ave | 0.8302 | 0.8316 | 0.8316 | 0.8236 | 0.8319 | 0.8343 | 0.8303 | 0.8310 |
| Std | 0.0040 | 0.0076 | 0.0034 | 0.0137 | 0.0049 | 0.0056 | 0.0105 | 0.0007 | ||
| 6 | Ave | 0.8752 | 0.8694 | 0.8783 | 0.8561 | 0.8739 | 0.8748 | 0.8729 | 0.8806 | |
| Std | 0.0060 | 0.0094 | 0.0058 | 0.0162 | 0.0107 | 0.0074 | 0.0076 | 0.0023 | ||
| 8 | Ave | 0.9024 | 0.8981 | 0.9023 | 0.8822 | 0.8983 | 0.8966 | 0.8983 | 0.9069 | |
| Std | 0.0065 | 0.0094 | 0.0054 | 0.0138 | 0.0087 | 0.0090 | 0.0059 | 0.0027 | ||
| 10 | Ave | 0.9213 | 0.9144 | 0.9195 | 0.8978 | 0.9105 | 0.9167 | 0.9119 | 0.9267 | |
| Std | 0.0058 | 0.0057 | 0.0061 | 0.0099 | 0.0092 | 0.0063 | 0.0085 | 0.0025 | ||
| Terrace | 4 | Ave | 0.7184 | 0.7145 | 0.7195 | 0.6644 | 0.7184 | 0.7101 | 0.7139 | 0.7190 |
| Std | 0.0048 | 0.0144 | 0.0053 | 0.0344 | 0.0070 | 0.0155 | 0.0101 | 0.0017 | ||
| 6 | Ave | 0.8010 | 0.7915 | 0.7954 | 0.7296 | 0.8020 | 0.7825 | 0.7955 | 0.8054 | |
| Std | 0.0120 | 0.0244 | 0.0137 | 0.0339 | 0.0142 | 0.0163 | 0.0189 | 0.0053 | ||
| 8 | Ave | 0.8452 | 0.8329 | 0.8393 | 0.7892 | 0.8383 | 0.8232 | 0.8458 | 0.8543 | |
| Std | 0.0166 | 0.0233 | 0.0177 | 0.0300 | 0.0175 | 0.0166 | 0.0173 | 0.0129 | ||
| 10 | Ave | 0.8735 | 0.8659 | 0.8714 | 0.8160 | 0.8661 | 0.8540 | 0.8773 | 0.8894 | |
| Std | 0.0147 | 0.0210 | 0.0160 | 0.0347 | 0.0210 | 0.0194 | 0.0174 | 0.0112 | ||
| Friedman-Rank | 3.58 | 4.48 | 4.14 | 7.55 | 4.06 | 5.58 | 3.97 | 2.65 | ||
| Final-Rank | 2 | 6 | 5 | 8 | 4 | 7 | 3 | 1 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Bao, Z.; Li, X.; Wang, J. Multi-Threshold Art Symmetry Image Segmentation and Numerical Optimization Based on the Modified Golden Jackal Optimization. Symmetry 2025, 17, 2130. https://doi.org/10.3390/sym17122130
Zhang X, Bao Z, Li X, Wang J. Multi-Threshold Art Symmetry Image Segmentation and Numerical Optimization Based on the Modified Golden Jackal Optimization. Symmetry. 2025; 17(12):2130. https://doi.org/10.3390/sym17122130
Chicago/Turabian StyleZhang, Xiaoyan, Zuowen Bao, Xinying Li, and Jianfeng Wang. 2025. "Multi-Threshold Art Symmetry Image Segmentation and Numerical Optimization Based on the Modified Golden Jackal Optimization" Symmetry 17, no. 12: 2130. https://doi.org/10.3390/sym17122130
APA StyleZhang, X., Bao, Z., Li, X., & Wang, J. (2025). Multi-Threshold Art Symmetry Image Segmentation and Numerical Optimization Based on the Modified Golden Jackal Optimization. Symmetry, 17(12), 2130. https://doi.org/10.3390/sym17122130




