A Symmetric Analysis of COVID-19 Transmission Using a Fuzzy Fractional SEIRi–UiHR Model

Abstract

In this research article, we propose a fuzzy fractional-order SEI$R_i{U}_i$HR model to describe the transmission dynamics of COVID-19, comprising susceptible, exposed, infected, reported, unreported, hospitalized, and recovered compartments. The uncertainty in initial conditions is represented using fuzzy numbers, and the fuzzy Laplace transform combined with the Adomian decomposition method is employed to solve nonlinear differential equations and also to derive approximate analytical series of solutions. In addition to fuzzy lower and upper bound solutions, a model is introduced to provide a representative trajectory under uncertainty. A key feature of the proposed model is its inherent symmetry in compartmental transitions and structural formulation, which show the difference in reported and unreported cases. Numerical experiments are conducted to compare fuzzy and normal (non-fuzzy) solutions, supported by 3D visualizations. The results reveal the influence of fractional-order and fuzzy parameters on epidemic progression, demonstrating the model’s capability to capture realistic variability and to provide a flexible framework for analyzing infectious disease dynamics.

1. Introduction

COVID-19, caused by SARS-CoV-2, rapidly escalated into a global pandemic, highlighting the urgent need for accurate epidemic models. Traditional compartmental models often rely on crisp data, yet many infections remain unreported and hospitalization records incomplete, introducing significant uncertainty. Fractional calculus has proven effective in capturing memory effects in disease transmission, while fuzzy logic provides a natural framework for representing imprecise or missing data. From a modeling perspective, COVID-19 progression exhibits biological and structural symmetry, particularly in transitions between symptomatic/asymptomatic and reported/unreported cases. This motivates the use of symmetry-based fuzzy fractional-order models to better capture the complex behavior of viral spread under uncertainty. Our proposed framework integrates these concepts to provide robust analytical tractability and improved interpretability of epidemic dynamics.

However, a significant proportion of infected individuals may remain asymptomatic, posing challenges for disease control and surveillance [1]. Certain factors increase the risk of severe illness and complications from COVID-19, including advanced age, underlying health conditions (such as diabetes, cardiovascular disease, chronic respiratory diseases, and immunosuppression), and socioeconomic disparities. Vulnerable populations, including the elderly, individuals with comorbidities, healthcare workers, and marginalized communities, are at a heightened risk of adverse outcomes [2]. Governments, public health agencies, and communities worldwide have implemented various measures to mitigate the spread of COVID-19, including lockdowns, travel restrictions, social distancing, mask mandates, hand hygiene promotion, widespread testing, contact tracing, quarantine, and vaccination campaigns. However, the effectiveness of these interventions depends on factors such as compliance, healthcare infrastructure, and vaccine distribution. The COVID-19 pandemic continues to pose significant challenges to global health, economies, and societies. Efforts to control the spread of the virus, mitigate its impact on vulnerable populations, and accelerate vaccine distribution remain critical priorities. Collaborative research, data sharing, and evidence-based policymaking are essential in navigating this unprecedented crisis and building resilience against future pandemics [3].

The COVID-19 pandemic has spurred an unprecedented level of mathematical modeling and analysis to understand its spread, predict its trajectory, and guide public health responses. Mathematical models serve as invaluable tools for policymakers, epidemiologists, and healthcare professionals in making informed decisions to mitigate the impact of the virus. By integrating data on transmission dynamics, population demographics, interventions, and other factors, these models provide insights into the complex behavior of the pandemic and help evaluate the effectiveness of control measures. Epidemiological models, such as compartmental models (e.g., SIR, SEIR) and agent-based models, simulate the spread of COVID-19 within populations. These models divide the population into compartments based on disease status (susceptible, exposed, infected, recovered) and simulate the flow of individuals between these compartments over time. By incorporating parameters such as transmission rates, incubation periods, and contact patterns, epidemiological models can estimate key epidemiological metrics like the effective reproduction number ($R_0$), epidemic peaks, and the impact of interventions. The mathematical modeling of COVID-19 relies heavily on real-time data sources, including case reports, testing data, hospitalization rates, and mobility patterns. Statistical techniques such as Bayesian inference, time series analysis, and machine learning are employed to analyze and interpret these data, informing model calibration, validation, and forecasting. Data-driven approaches enable researchers to assess the accuracy of model predictions, identify emerging trends, and adapt strategies accordingly [4]. Mathematical models of COVID-19 are subject to various sources of uncertainty, including parameter variability, model structure, and data quality. Sensitivity analysis techniques assess the impact of these uncertainties on model outcomes, helping to quantify the robustness of predictions and identify critical factors driving the spread of the virus. Uncertainty quantification facilitates risk assessment, scenario planning, and decision-making under uncertainty [5]. Mathematical modeling plays a crucial role in informing policy decisions related to COVID-19, such as social distancing measures, mask mandates, vaccination strategies, and healthcare resource allocation. Models provide policymakers with evidence-based projections of the potential outcomes of different intervention scenarios, allowing them to weigh trade-offs between public health, economic, and societal considerations. Policy evaluations based on modeling results help optimize resource allocation and minimize the overall burden of the pandemic [6]. Mathematical perspectives offer valuable insights into the dynamics of the COVID-19 pandemic, guiding public health responses and policy decisions. By integrating epidemiological principles, data analytics, and computational techniques, mathematical modeling contributes to our understanding of disease transmission, informs proactive interventions, and enhances preparedness for future health emergencies. Fractional differential equations (FDEs) have emerged as powerful tools for modeling complex dynamical systems exhibiting memory, hereditary properties, and anomalous behaviors. Unlike classical differential equations, which describe systems with integer-order derivatives, FDEs involve derivatives of non-integer order, offering a more flexible framework to capture phenomena with long-range dependencies, non-local effects, and fractal geometries. This introduction provides an overview of fractional calculus and its applications in various scientific disciplines, highlighting recent advancements and key research contributions. Fractional calculus generalizes the concept of differentiation and integration to non-integer orders, enabling the manipulation of functions with fractional exponents. The fractional derivative operator is denoted by $D^{\mathsf{\alpha }}$, where $0<\alpha <1$ or captures the memory and long-range interactions inherent in many physical, biological, and engineering systems. Fractional integrals, fractional differential operators, and fractional differential equations constitute the foundational elements of fractional calculus. FDEs find widespread applications in modeling complex phenomena across various domains, including physics, engineering, finance, biology, and control theory. Examples include anomalous diffusion processes, viscoelastic materials, electromagnetic wave propagation in fractal media, fractional-order circuits, and fractional-order control systems. FDEs offer a versatile framework to describe systems with memory effects, non-local interactions, and fractional dynamics, which are often inadequately captured by classical models [7]. Solving FDEs analytically is often challenging due to the non-local nature of fractional derivatives. Numerical methods, such as fractional finite difference methods, fractional Adams–Bashforth schemes, and fractional spectral methods, play a crucial role in approximating solutions to FDEs. Convergence analysis, stability assessment, and error estimation techniques are essential for ensuring the accuracy and reliability of numerical solutions to fractional differential equations [8]. Recent advancements in fractional calculus have led to novel applications and theoretical developments in various fields. Research efforts focus on refining numerical algorithms, investigating the mathematical properties of fractional operators, exploring fractional-order models for real-world phenomena, and advancing interdisciplinary collaborations. Moreover, the integration of fractional calculus with other mathematical frameworks, such as stochastic processes, dynamical systems theory, and machine learning, opens new avenues for interdisciplinary research and innovation.

Fractional differential equations provide a powerful mathematical framework for modeling complex dynamical systems with memory, non-local interactions, and anomalous behaviors. By extending the classical theory of differentiation to non-integer orders, fractional calculus offers a versatile toolkit for addressing challenges in diverse scientific and engineering disciplines. Continued research and interdisciplinary collaborations are essential for unlocking the full potential of fractional calculus and advancing our understanding of complex phenomena in the natural and engineered world [9]. Epidemic modeling plays a crucial role in understanding the dynamics of infectious diseases and guiding public health interventions. Traditional compartmental models, such as the Susceptible–Infectious–Recovered (SIR) model, assume integer-order derivatives and homogeneous mixing among individuals. However, real-world epidemics often exhibit complex behaviors, including non-Markovian dynamics, long-range interactions, and memory effects. Fractional differential equations (FDEs) offer a flexible framework to capture these complexities, providing a more accurate representation of epidemic spread. This review examines recent advancements in epidemic modeling using fractional calculus and highlights key research contributions in this evolving field. Fractional differential equations extend traditional compartmental models by incorporating fractional-order derivatives to capture memory effects and non-local interactions. Fractional epidemiological models introduce fractional derivatives into the equations governing the dynamics of susceptible, infectious, and recovered populations, allowing for the modeling of complex epidemic behaviors such as long-term memory, sub-diffusion, and spatial heterogeneity [10]. Fractional-order epidemiological models offer a more realistic representation of epidemic spread by accounting for phenomena such as sub-diffusion, long-range interactions, and heterogeneous mixing patterns. These models can better capture the effects of interventions such as social distancing, quarantine, and vaccination on disease transmission of dengue dynamics. Moreover, fractional models enable the study of non-Markovian processes and memory effects, which are prevalent in real-world epidemics [11]. Fractional epidemiological models have been applied to various infectious diseases, including influenza, dengue fever, Ebola, and COVID-19. These models have been used to investigate the impact of interventions, forecast epidemic trajectories, and assess the effectiveness of control measures. Case studies demonstrate the utility of fractional modeling in capturing the complexities of epidemic dynamics and providing insights for public health decision-making by Mittag-Leffler functions used [12]. Despite their potential, fractional epidemiological models pose challenges in terms of parameter estimation, model validation, and computational complexity. Future research directions include the development of efficient numerical methods for solving fractional differential equations, the integration of fractional models with data assimilation techniques, and the exploration of multiscale modeling approaches to capture interactions at different spatial and temporal scales [13]. Fractional differential equations provide a compact and powerful framework for capturing memory, non-local effects, and heterogeneous transmission in epidemic systems. In our study, these properties are combined with fuzzy uncertainty to develop a symmetric fractional SEIRi–UiHR model that more realistically characterizes COVID-19 spread under imprecise and evolving conditions.

The main motivation of this study is to develop a modeling framework that can simultaneously capture uncertainty in epidemic data and memory effects in disease transmission while preserving the structural symmetry between reported and unreported cases. Traditional integer-order SEIR models assume crisp parameters and instantaneous transitions, which are inadequate for COVID-19 dynamics where a large proportion of infections remain undetected, hospitalization records are incomplete, and recovery pathways are heterogeneous. To address these limitations, we introduce a fuzzy fractional-order SEIRi–UiHR model as seen in Figure 1. The fuzzy component allows for the incorporation of imprecise or missing information through fuzzy numbers, thereby reflecting realistic variability in initial conditions and parameter estimation. The fractional-order derivative introduces a memory effect, enabling the model to account for long-range dependencies and non-Markovian dynamics that are characteristic of viral spread. The fractional-order parameter ν symmetrically stretches or compresses epidemic trajectories across all compartments, providing deeper insight into the persistence versus rapid clearance of infection. By combining fuzzy logic and fractional calculus within the SEIRi–UiHR framework, the proposed model achieves two essential goals:

• Quantification of uncertainty in reported/unreported cases and hospitalization dynamics.
• Representation of memory-driven transmission effects that classical models overlook.

This dual integration provides a symmetric and comprehensive framework for analyzing COVID-19 dynamics under uncertainty, improving interpretability, robustness, and alignment with real-world epidemic behavior. Hence, the fuzzy fractional-order SEIRi–UiHR model is not only mathematically innovative but also biologically and epidemiologically motivated.

2. The Notations of the Concerned Parameters

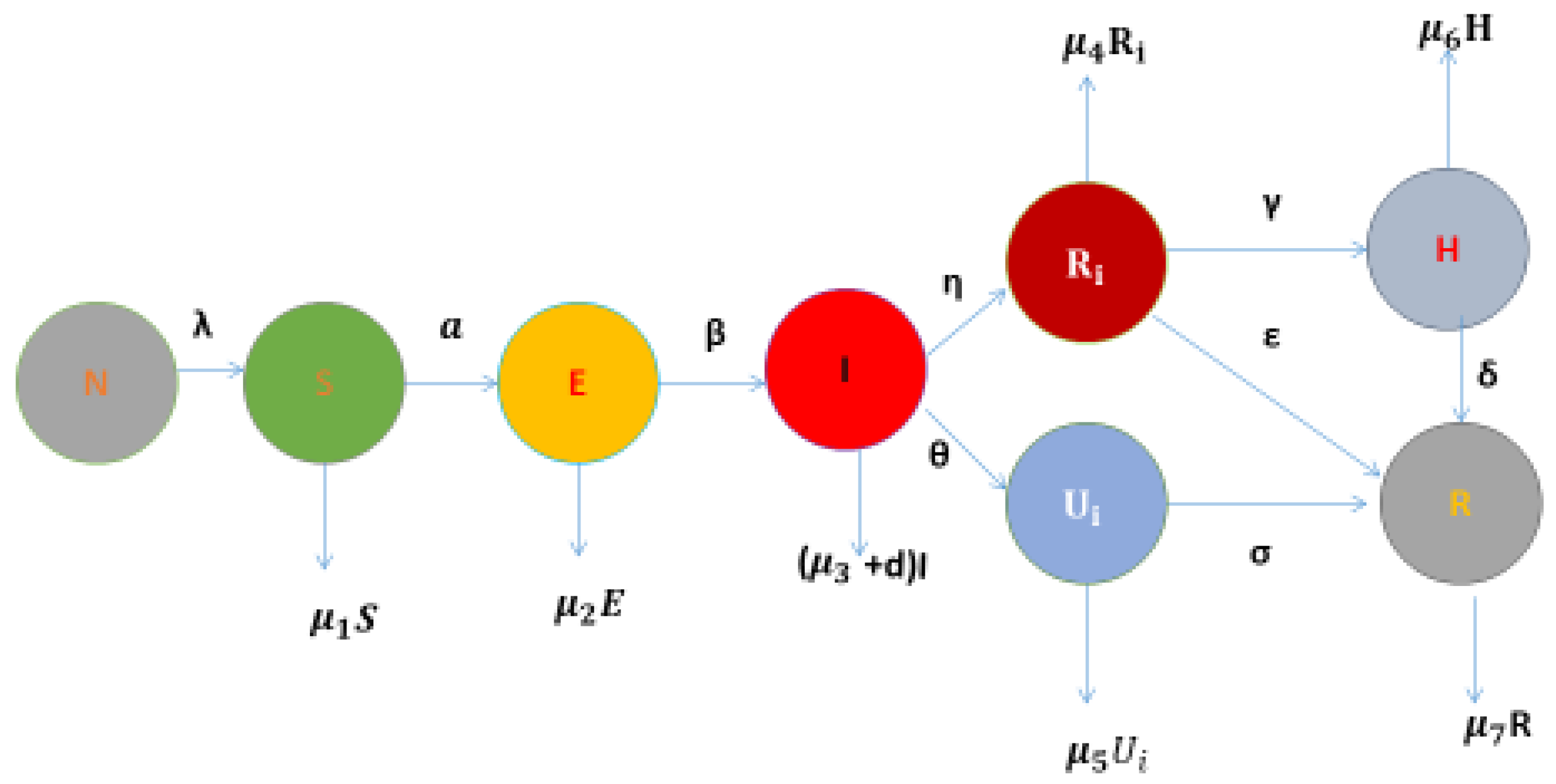
This work was completed by incorporating twenty parameters, and the details of all parameters are provided in

Table 1. Description of parameters used in $SEI{R}_i{U}_{i}HR$ model.

$\mathit{\lambda }$	Expected Population Rate	${\mathit{\mu }}_1,{\mathit{\mu }}_2,{\mathit{\mu }}_3,{\mathit{\mu }}_4,$ ${\mathit{\mu }}_5,{\mathit{\mu }}_6,{\mathit{\mu }}_7$ $\& \mathit{d}$	Mortality and Natural Death (Infection State) Rate in Various Compartments
S	Susceptible Population	$a$	Exposed Rate
E	Exposed Population	$\beta$	Infected Rate
I	Infected Population	$\theta$	Unreported Rate
$R_i$	Reported Population	$\eta$	Reported Rate
$U_i$	Unreported Population	$\gamma$	Hospitalization
$H$	Hospitalized Population	$\epsilon$	Recover Rate
R	Recovered Population	$\delta$	Unreported to Recover Rate

with compartments. This version was modified for better clarity and effectiveness.

Model Structure Explanation ($\mathit{S}\mathit{E}\mathit{I}{\mathit{R}}_{\mathit{i}}{\mathit{U}}_{\mathit{i}}\mathit{H}\mathit{R}$model):

In the proposed $SEI{R}_i{U}_{i}HR$ model (Figure 1), the total population N is divided into seven epidemiological compartments: susceptible (S), exposed (E), infected (I), reported ($R_i$), unreported ($U_i$), hospitalized (H), recovered (R), and removed. Individuals enter the susceptible class at rate $\lambda$ and transition to the exposed class through contact with infection at rate aa. Exposed individuals become infectious at rate $\mathsf{\beta }$, entering the infected compartment. From the infected class, individuals either become reported cases at rate $\eta$ or remain undetected and enter the unreported class at rate $\theta$. Infected individuals also experience mortality or natural death at rate ${\mu }_3+ d$. Reported individuals are removed at rate ${\mu }_4$, while unreported individuals may either be hospitalized at rate $ϵ$, recover directly at rate $\delta$, or be removed at rate ${\mu }_5$. Hospitalized individuals recover at rate $\gamma$ or are removed at rate ${\mu }_6$. Recovered individuals from both pathways are eventually removed at rate ${\mu }_7$. Each transition is governed by a biologically meaningful parameter, as detailed in Table 1, which includes twenty-three parameters covering recruitment, transmission, reporting, reporting, hospitalization, recovery, and mortality dynamics. The model incorporates fuzzy logic to represent uncertainty in detection and hospitalization and fractional calculus to capture memory effects in disease progression. Structural symmetry is embedded in the transitions between reported and unreported compartments, enhancing analytical tractability and interpretability. Based on this, we construct the differential equation $SEI{R}_i{U}_{i}HR$ model

We construct the system of differential equations based on this dynamic system

$$N=S+E+I+R_i+U_i+H+R$$

(1a)

$${\displaystyle \frac{dS}{dt}}=\lambda -\left(a+{\mu }_1\right)S$$

(1b)

$${\displaystyle \frac{dE}{dt}}=aS-\left(\beta +{\mu }_2\right)E$$

(1c)

$${\displaystyle \frac{dI}{dt}}=\beta E-\left(\theta +\eta +d+{\mu }_3\right)I$$

(1d)

$${\displaystyle \frac{d{R}_i}{dt}}=\eta I-\left(\mathsf{\gamma }+\mathsf{\epsilon }+{\mu }_4\right)R_i$$

(1e)

$${\displaystyle \frac{d{\mathrm{U}}_{\mathrm{i}}}{dt}}=\theta \mathrm{I}-\left({\mathsf{\mu }}_5+\mathsf{\sigma }\right){\mathrm{U}}_{\mathrm{i}}$$

(1f)

$${\displaystyle \frac{dH}{dt}}=\gamma R_i-\left({\mu }_6+\delta \right)H$$

(1g)

$${\displaystyle \frac{dR}{dt}}=\sigma {\mathrm{U}}_{\mathrm{i}}+\epsilon R_i+\delta H-{\mu }_{7}R$$

(1h)

The mathematical epidemic model is considered with the initial conditions specified below.

$$S\left(0\right)>0,E\left(0\right)>0,I\left(0\right)>0,R_i\left(0\right)>0,U_i\left(0\right)>0,H\left(0\right)>0,R\left(0\right)>0.$$

In our study, we aim to mathematically analyze the infection system of 2019-nCoV (novel coronavirus) using advanced techniques. Specifically, we employ the fuzzy Laplace transform based on Adomian decomposition to obtain numerical results. This approach offers valuable insights into the dynamical structures governing the physical behavior of 2019-nCoV [14]. To model the outbreak of the coronavirus, we formulate a system of seven equations representing nonlinear fractional-order differential equations (FODEs). These equations depict various stages of the infection process, including susceptible (S), exposed (E), infected (I), reported ($R_i$), unreported ($U_i$), and recovered (R). Each equation captures the interactions and transitions between these compartments, providing a comprehensive framework for understanding the spread and control of the corona virus [15]. Our methodology builds upon previous research on infectious disease modeling and fractional calculus. By applying the fuzzy Laplace transform and Adomian decomposition, we extend the analytical capabilities to address the unique characteristics of 2019-nCoV. The numerical results obtained from this approach offer valuable insights into the complex dynamics of the epidemic, aiding in the development of effective control strategies and public health interventions [16]. This study contributes to the growing body of literature on the mathematical modeling of infectious diseases and provides a novel perspective on the dynamics of 2019-nCoV. The insights of fuzzy fractional functional integral and differential equations gained from this research have implications for epidemic forecasting, healthcare resource allocation, and policy decision-making in response to emerging infectious threats [17].

$$D_t^{\alpha }S\left(t\right)=\lambda -{(\mu }_1+a)S=\lambda -{\mu }_{1}S-aS$$

(2a)

$$D_t^{\alpha }E\left(t\right)=aS-\left({\mu }_2+\beta \right)E=aS-{\mu }_{2}E-\beta E$$

(2b)

$$D_t^{\alpha }I\left(t\right)=\beta E-\left(d+{\mu }_3+\theta +\eta \right)I=\beta E-dI-{\mu }_{3}I-\theta I-\eta I$$

(2c)

$$D_t^{\alpha }{R}_i\left(t\right)=\eta I-\left(\gamma +{\mu }_4+\epsilon \right)R_i=\eta I-{\gamma R}_i-{\mu }_4{R}_i-\epsilon R_i$$

(2d)

$$D_t^{\alpha }{\mathrm{U}}_{\mathrm{i}}\left(t\right)=\theta \mathrm{I}-\left({\mathsf{\mu }}_5+\mathsf{\sigma }\right){\mathrm{U}}_{\mathrm{i}}=\theta \mathrm{I}-{{\mathsf{\mu }}_5\mathrm{U}}_{\mathrm{i}}-\mathsf{\sigma }{\mathrm{U}}_{\mathrm{i}}$$

(2e)

$$D_t^{\alpha }H\left(t\right)=\gamma R_i-\left({\mu }_6+\delta \right)H=\gamma R_i-{\mu }_{6}H-\delta H$$

(2f)

$$D_t^{\alpha }R\left(t\right)=\sigma {\mathrm{U}}_{\mathrm{i}}+\epsilon R_i+\delta H-{\mu }_{7}R$$

(2g)

In recent years, there has been a significant expansion of modern calculus and differential equations (DEs) to encompass fuzzy calculus and fractional-order differential equations (FODEs), respectively. This progression has further extended to fuzzy FODEs, broadening the scope of mathematical modeling to accommodate uncertainty and imprecision [18]. Researchers have extensively studied FODEs and fuzzy integral equations to establish theories regarding the existence and uniqueness of solutions. However, when dealing with fuzzy FODEs, the computation of precise solutions becomes particularly challenging. Consequently, mathematicians have dedicated considerable efforts to developing various solution methods, including perturbation methods, integral transform methods, and spectral techniques. Additionally, a stability analysis of fuzzy DEs has been conducted by some researchers, providing valuable insights into the behavior of these complex systems [19]. In this study, we focus on investigating a model with a fuzzy fractional-order derivative, introducing uncertainty into the initial data. Specifically, we consider the following formulation [20]:

$$D_{fuzzy}^{\alpha } y\left(t\right)=f(t,y\left(t\right))$$

where $0<\alpha \le 1,$ and $D_{fuzzy}^{\alpha }$ represents the fuzzy fractional-order derivative. This investigation builds upon the foundation of fuzzy calculus and fractional calculus, aiming to address the challenges posed by uncertainty in differential equations. By incorporating fuzzy concepts into fractional-order derivatives, we seek to provide a more comprehensive framework for modeling real-world phenomena affected by imprecise or uncertain data [15].

$$D_t^{\alpha }S\left(t\right)=\tilde{\lambda }-(\widetilde{{\mu }_1}+\tilde{a})S=\lambda -\widetilde{{\mu }_1}S-\tilde{a}S$$

(3a)

$${ D}_t^{\alpha }E\left(t\right)=\tilde{a}S-\left(\widetilde{{\mu }_2}+\tilde{\beta }\right)E=\tilde{a}S-\widetilde{{\mu }_2}E-\tilde{\beta }E$$

(3b)

$$D_t^{\alpha }I\left(t\right)=\tilde{\beta }E-\left(\tilde{d}+\widetilde{{\mu }_3}+\tilde{\theta }+\tilde{\eta }\right)I=\tilde{\beta }E-\tilde{d}I-\widetilde{{\mu }_3}I-\tilde{\theta }I-\tilde{\eta }I$$

(3c)

$${ D}_t^{\alpha }{R}_i\left(t\right)=\tilde{\eta }I-\left(\tilde{\gamma }+\widetilde{{\mu }_4}+\tilde{\epsilon }\right)R_i=\tilde{\eta }I-{\tilde{\gamma }R}_i-\widetilde{{\mu }_4}{R}_i-\tilde{\epsilon }{R}_i$$

(3d)

$$D_t^{\alpha }{\mathrm{U}}_{\mathrm{i}}\left(t\right)=\tilde{\theta }{\displaystyle \mathrm{I}}-\left(\widetilde{{\mathsf{\mu }}_5}+\tilde{\mathsf{\sigma }}\right){\mathrm{U}}_{\mathrm{i}}=\tilde{\theta }\mathrm{I}-{\widetilde{{\mathsf{\mu }}_5}\mathrm{U}}_{\mathrm{i}}-\tilde{\mathsf{\sigma }}{\mathrm{U}}_{\mathrm{i}}$$

(3e)

$$D_t^{\alpha }H\left(t\right)=\tilde{\gamma }{R}_i-\left(\widetilde{{\mu }_6}+\tilde{\delta }\right)H=\tilde{\gamma }{R}_i-\widetilde{{\mu }_6}H-\tilde{\delta }H$$

(3f)

$$D_t^{\alpha }R(t)=\tilde{\sigma }{\mathrm{U}}_{\mathrm{i}}+\tilde{\epsilon }{R}_i+\tilde{\delta }H-\widetilde{{\mu }_7}R$$

(3g)

This is associated with the fuzzy initial condition, for α ∈ [0, 1],

$$\tilde{S} \left(0,\alpha \right)=(\underset{\_}{S} \left(0,\alpha \right), \overline{S}\left(0,\alpha \right)), \widetilde{E }\left(0,\alpha \right)=\left(\underset{\_}{E} \left(0,\alpha \right), \overline{E}\left(0,\alpha \right)\right),$$

$$\widetilde{I }\left(0,\alpha \right)=\left(\underset{\_}{I}\left(0,\alpha \right), \overline{I}\left(0,\alpha \right)\right),\widetilde{ R_i}\left(0,\alpha \right)=\left(\underset{\_}{R_i}\left(0,\alpha \right), \overline{R_i}\left(0,\alpha \right)\right),$$

$$\widetilde{{\mathrm{U}}_i}\left(0,\alpha \right)=\left(\underset{\_}{{\mathrm{U}}_{\mathrm{i}}}\left(0,\alpha \right), \overline{{\mathrm{U}}_{\mathrm{i}}}\left(0,\alpha \right)\right),\widetilde{H }\left(0,\alpha \right)=\left(\underset{\_}{H}\left(0,\alpha \right), \overline{H}\left(0,\alpha \right)\right),$$

$$\widetilde{R }\left(0,\alpha \right)=\left(\underset{\_}{R}\left(0,\alpha \right), \overline{R}\left(0,\alpha \right)\right)$$

In response to the current uncertain situation surrounding the COVID-19 pandemic, we were inspired to develop a novel model for coronavirus infection dynamics utilizing concepts from fuzzy fractional calculus. Our motivation stems from the need to better understand and characterize the complex behavior of viral spread, particularly in scenarios where traditional models may fall short in capturing the inherent uncertainty and variability [21]. The proposed model not only incorporates fuzzy fractional calculus but also aims to enhance the representation of the physical behavior exhibited by the COVID-19 infection system. By integrating fuzzy logic and fractional calculus, we strive to create a more realistic framework that closely aligns with the dynamic properties of RNA viruses, such as COVID-19. Our model emphasizes the dynamic interactions between various compartments of the infection system, including susceptible, exposed, infected, reported, unreported, and recovered individuals. Through the incorporation of fuzzy fractional calculus, we account for uncertainties in parameters and initial conditions, thereby improving the model’s ability to reflect real-world complexities [22,23,24].

By leveraging insights from fuzzy mathematics and fractional calculus, our proposed model offers a more nuanced understanding of COVID-19 transmission dynamics. It provides a valuable tool for researchers and policymakers to assess the effectiveness of interventions, forecast epidemic trajectories, and inform public health strategies in the face of evolving uncertainties [25].

3. Preliminaries

This section provides an overview of fundamental concepts relevant to fuzzy fractional calculus, which serve as the foundation for the subsequent discussions.

3.1. Fuzzy Set Theory

Fuzzy set theory, introduced by Zadeh in 1965, extends classical set theory to accommodate degrees of membership rather than strict binary distinctions. Fuzzy sets are characterized by membership functions that assign a degree of membership to each element of the set [26]

$$A=\left\{\left(x,{\mu }_A\left(x\right)\right)\right| x\in X, 0<{\mu }_A\left(x\right)\le 1\}$$

This expression denotes that A consists of ordered pairs $\left(x,{\mu }_A\left(x\right)\right),$ where $x$ belongs to a universe of discourse $X$, and ${\mu }_A\left(x\right)$ represents the degree of membership of $x$ in the fuzzy set $A$. The degree of membership ${\mu }_A\left(x\right)$ varies between 0 and 1, inclusively, reflecting the extent to which $x$ belongs to $A$. This mathematical representation encapsulates the fuzzy nature of the set $A$, allowing for the modeling of uncertainty and vagueness in data.

3.2. Fractional Calculus

Fractional calculus deals with derivatives and integrals of non-integer orders. It provides a mathematical framework for analyzing systems with fractional dynamics, offering insights into phenomena such as anomalous diffusion and viscoelastic behavior [26].

It extends the concepts of traditional calculus to include fractional derivatives and integrals, enabling the analysis of systems with fractional dynamics. Fractional calculus has found applications in various fields such as physics, engineering, biology, and finance. It allows for the modeling of phenomena exhibiting complex behavior, including anomalous diffusion, viscoelasticity, and fractals [27]. A fractional derivative of order α of a function $f(x)$, denoted by $D^{\alpha }f(x)$, is defined as

$$D^{\alpha }f\left(x\right)={\displaystyle \frac{1}{\Gamma \left(n-\alpha \right)}}\left[{\displaystyle \frac{d^n}{d{x}^n}}\underset{a}{\overset{x}{\int }}{\left(x-t\right)}^{n-\alpha -1}f\left(t\right)dt\right]$$

where $n-1<\alpha <n$, $n$ is the smallest integer greater than $\alpha$, and $\Gamma$ is the gamma function [28,29].

3.3. Fuzzy Fractional Calculus

Fuzzy fractional calculus combines fuzzy logic and fractional calculus, allowing for the analysis of systems with uncertain or imprecise data using fractional-order operators with fuzzy parameters [30]. Fuzzy fractional calculus is a mathematical framework that combines concepts from fuzzy set theory and fractional calculus. A fuzzy fractional derivative of order $\alpha$ for a fuzzy-valued function $f\left(x\right)$, denoted by $D_{fuzzy}^{\alpha }f\left(x\right)$, can be defined using fuzzy set theory and fractional calculus principles. One common approach is to extend the fractional derivative definition to incorporate fuzzy membership functions. A possible expression for the fuzzy fractional derivative is as follows:

$$D_{fuzzy}^{\alpha }f\left(x\right)= {\displaystyle \frac{1}{\Gamma \left(n-\alpha \right)}}\left[{\displaystyle \frac{d^n}{d{x}^n}}\underset{a}{\overset{x}{\int }}{\left(x-t\right)}^{n-\alpha -1}\mu \left(t\right)f\left(t\right)dt\right]$$

where $n-1< \alpha <n,$ n is the smallest integer greater than $\alpha , \mu (t)$ is the fuzzy membership function, and $\Gamma$ is the gamma function [29,30,31].

3.4. Fuzzy Fractional Differential Equations (FFDEs)

FFDEs are differential equations involving fuzzy fractional derivatives. These equations provide a framework for modeling systems exhibiting both fractional dynamics and fuzzy uncertainty. Fuzzy fractional differential equations (FFDEs) are differential equations that combine the concepts of fuzzy set theory and fractional calculus. They are used to model dynamic systems where the rate of change of a variable is described by a fractional derivative, and the parameters or initial conditions involve uncertainty captured by fuzzy logic.

A general form of a fuzzy fractional differential equation can be represented as follows:

$$D_{fuzzy}^{\alpha }f\left(x\right)=f\left(t,y(t)\right)$$

where

• $D_{fuzzy}^{\alpha }f\left(x\right)$ represents the fuzzy fractional derivative operator.
• $y(t)$ is an unknown function of time, $f\left(t,y(t)\right)$ is a function describing the relationship between y and its derivatives with respect to $t$, and $0<\alpha \le 1$ denotes the order of the fractional derivative.
• The fuzzy fractional derivative $D_{fuzzy}^{\alpha }y(t)$ incorporates both fuzzy set theory and fractional calculus, allowing for the modeling of systems with uncertain or imprecise dynamics [32,33,34].

3.5. Fuzzy Level Set

Fuzzy level sets are a generalization of traditional level sets to accommodate uncertainty or ambiguity in defining boundaries between regions in images or data. They provide a flexible framework for capturing gradual transitions and uncertain distinctions between objects or features. Let $\Omega$ denote the domain of interest, and consider a fuzzy set A defined over $\Omega$. The fuzzy level set $\varphi (x)$ is defined as a scalar function that represents the degree to which each point $x$ in $\Omega$ belongs to the fuzzy set $A$. Formally, the fuzzy level set $\varphi (x)$ is defined by its membership function ${\mu }_{\varphi }\left(x\right)$ which assigns a degree of membership to each point $x$ in Ω which assigns a degree of membership to each point x, indicating the extent to which $x$ lies within the boundary of the fuzzy set $A$.

The mathematical expression for a fuzzy level set $\varphi (x)$ can be represented as $\varphi (x)$ = ${\mu }_{\varphi }\left(x\right)$.

Here, ${\mu }_{\varphi }\left(x\right)$ is the membership function of the fuzzy level set, indicating the degree of membership of each point $x \mathrm{i}\mathrm{n}$Ω. $A_{\alpha }=\left\{x\in \mathsf{\Omega }\right| {\mu }_A\left(x\right)\ge \alpha \}$, which yields a crisp set representation of the fuzzy boundary [35,36].

3.6. Fuzzy Number

A fuzzy number is a generalization of a crisp (traditional) number, which represents a precise value, to a range of values with associated degrees of membership. In other words, a fuzzy number expresses uncertainty or vagueness regarding the exact value of a quantity. A fuzzy number A is typically defined by a membership function ${\mu }_A(x)$ that assigns a degree of membership to each real number $x$ within a specified interval. The membership function ${\mu }_A(x)$ indicates the degree to which x belongs to the fuzzy number A, with values ranging from 0 (not a member) to 1 (fully a member). Mathematically, the membership function ${\mu }_A(x)$ satisfies the following properties:

(a) 

Non-negativity: ${\mu }_A\left(x\right)\ge 0$ for all $x$

(b) 

Normalization: $Su{p}_x{\mu }_A\left(x\right)=1,$ where sup denotes the supremum.

3.7. Fuzziness

The membership function ${\mu }_A\left(x\right)$ can take any value between 0 and 1, inclusively, as mathematically represented by ${\mu }_A\left(x\right): [\mathrm{a},\mathrm{b}]\to [0 1]$. An expression for a fuzzy number A can be written as follows: $A=\left\{\left(x,{\mu }_A\left(x\right)\right)\right| x\in [a,b]\},$

Here, $[a,b]$ is the interval over which the fuzzy number is defined, and ${\mu }_A\left(x\right)$ is the membership function indicating the degree of membership of each $x$ in the interval. Fuzzy numbers are useful in representing imprecise or uncertain data in various fields, including decision-making, control systems, and optimization.

(a) Boundedness: The boundedness of a fuzzy number $\tilde{A}$ is inherent in its definition within a closed interval [a, b] $supp\left(\tilde{A}\right)=\left\{x\in \mathbb{R}\right|{\mu }_A\left(x\right)\ge 0\}\subseteq [a,b], a,b\in \mathbb{R},a<b$.

(b) Convexity: The convexity of the membership function ${\mu }_A\left(x\right)$ ensures that it monotonically increases from 0 to 1 within the interval [a, b], implying that for any $x_1,x_2$, $x_1<x_2,{\mu }_A\left(x_1\right)\le {\mu }_A\left(x_2\right)$ [30].

3.8. Hausdorff Distance

The Hausdorff distance is a measure of similarity between two sets of points in a metric space. It quantifies how far apart two sets are from each other by considering the maximum distance of a point in one set to the closest point in the other set. Let A and B be two subsets of a metric space X. The Hausdorff distance $d_H(A,B)$ between A and B is defined as follows:

$$d_H\left(A,B\right)=\mathrm{m}\mathrm{a}\mathrm{x}\{{\mathrm{s}\mathrm{u}\mathrm{p}}_{\mathrm{a}\in \mathrm{A}}in{f}_{b\in B }d\left(a,b\right),{\mathrm{s}\mathrm{u}\mathrm{p}}_{\mathrm{b}\in \mathrm{B}}In{f}_{a\in A}d\left(b,a\right)$$

3.9. H-Difference

Let A and B be two fuzzy numbers. The Hukuhara difference (or H-difference) of $\tilde{A}$ and $\tilde{B}$ is the fuzzy number $\tilde{C}$ such that $\tilde{A}=\tilde{B} \oplus \tilde{C}$ where $\oplus$ denotes the Minkowski addition of fuzzy numbers. In terms of α-cuts, they are given by $(\tilde{A} \oplus {\tilde{B})}_{\alpha } =\left[{\underset{\_}{A}}_{\alpha }-{\underset{\_}{B}}_{\alpha }, {\overline{A}}_{\alpha }-{\overline{B}}_{\alpha }\right], {\forall }_{\alpha }\in \left[0, 1\right].$

3.10. Fuzzy Mapping

A fuzzy mapping, also known as a fuzzy function, is a generalization of a traditional (crisp) mapping that allows for the representation of uncertain or vague relationships between elements of two sets. In a fuzzy mapping, each element of the domain set is associated with a fuzzy set of values in the range set, reflecting the degree of membership of each element in the output set. Let X and Y be two sets, and consider a fuzzy mapping f from X to Y. A fuzzy mapping f assigns to each element x in the domain set X a fuzzy set of values in the range set Y, denoted as $f(x)$.

$$f:X\to f\left(Y\right)$$

where $f(Y)$ represents the set of all subsets of Y. For each $x \in X$, the fuzzy set $f(x)$ characterizes the uncertain relationship between x and the elements of Y.

$$f\left(x\right)=\left\{\left(y,{\mu }_{f\left(x\right)}\left(y\right)\right)\right| y\in Y \}$$

where ${\mu }_{f\left(x\right)}\left(y\right)$ is the membership function that assigns a degree of membership to each $y$ in $Y$ for the element $x$ in $X$.

The fuzzy mapping $f$ allows for the representation of imprecise or uncertain relationships between real numbers and linguistic terms, capturing the gradual transitions between different degrees of membership.

3.11. Riemann–Liouville Fractional Integral

The Riemann–Liouville fractional integral is a generalization of the classical integral to non-integer orders. It is defined by a convolution integral involving the original function and a weight function, typically expressed as a power function.

Let $f(x)$ be a real-valued function defined on the interval $[a,b]$, and let $\alpha >0$ be a real number. The Riemann–Liouville fractional integral of order $\alpha$ of $f\left(x\right),$ denoted by $I^{\alpha }f\left(x\right)$, is defined as follows:

$${(I}_a^{\alpha }f)\left(x\right)={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}\underset{\alpha }{\overset{x}{\int }}{\left(x-t\right)}^{\alpha -1}f\left(t\right)dt, \alpha , t \in \left(0,\infty \right) x>a$$

where $\mathit{\Gamma }\left(\alpha \right)$ is the gamma function.

For a fuzzy-valued function $\varphi \left(t\right),$ with parametric form

$${{[I}_a^{\alpha }\varphi \left(t\right)]}_{P }=I_a^{\alpha }\underset{\_}{{\varphi }_p}\left(t\right),I_a^{\alpha }\overline{{\varphi }_p}\left(t\right)], 0\le p\le 1,$$

$$I_a^{\alpha }\underset{\_}{{\varphi }_p}\left(t\right)={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}\underset{\alpha }{\overset{x}{\int }}{\left(x-s\right)}^{\alpha -1}\underset{\_}{{\varphi }_p}\left(s\right)ds, \alpha , t \in (0,\infty )$$

$$I_a^{\alpha }\overline{{\varphi }_p}\left(t\right)={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}\underset{\alpha }{\overset{x}{\int }}{\left(x-s\right)}^{\alpha -1}\overline{{\varphi }_p}\left(s\right)ds, \alpha , t \in (0,\infty )$$

3.12. Fuzzy Fractional Caputo’s Derivative

The fuzzy fractional Caputo’s derivative is a generalization of the traditional Caputo’s derivative to accommodate fractional-order operators with fuzzy parameters. It extends the concept of fuzzy fractional calculus to describe the dynamics of systems with uncertain or imprecise fractional orders.

Mathematical Expression:

The fuzzy fractional Caputo’s derivative of a function $y(t)$ is defined as follows:

$$D_{fuzzy}^{\alpha }y\left(t\right)={\displaystyle \frac{1}{\Gamma \left(1-\alpha \right)}}\left[\underset{\alpha }{\overset{t}{\int }}{\left(t-\tau \right)}^{-\alpha }\mu \left(\tau \right)y^{\prime }\left(\tau \right)d\tau \right]$$

where $0<\alpha \le 1$ is the fractional order, $\Gamma$ is the gamma function, $\mathit{\mu }\left(\mathit{\tau }\right)$ is the fuzzy membership function indicating the degree of membership of $\tau$ in a fuzzy set, and $y^{\prime }\left(\tau \right)$ denotes the derivative of $y(\tau )$ with respect to $\tau$.

3.13. Upper and Lower Bounds in $\mathit{\alpha }$-Cut

Let $\tilde{x}$ be a fuzzy number with membership function ${\mu }_{\tilde{x}}$: $R\to [0, 1]$. For a given $\alpha \in (0, 1]$, the $\alpha$-cut of $\tilde{x}$ is defined as follows:

$${\left[\tilde{x}\right]}_{\alpha }=\left\{x\in R \right|{\mu }_{\tilde{x}}\left(x\right)\ge \alpha \}, 0<\alpha \le 1.$$

This $\alpha$-cut is always a closed and bounded interval: ${\left[\tilde{x}\right]}_{\alpha }=\left[\underset{\_}{x}\left(\alpha \right), \overline{x}(\alpha )\right]$.

$\underset{\_}{x}\left(\alpha \right)$ is the fuzzy lower bound (left endpoint)—a non-decreasing function of α.

$\overline{x}\left(\alpha \right)$ is the fuzzy upper bound (right endpoint)—a non-increasing function of α.

3.14. Symmetric Fuzzy Solution

The solution $U(t)$ is a symmetric fuzzy number if its $\alpha$-cuts, ${\left[U\left(t\right)\right]}^{\alpha }$= [$(\underset{\_}{u}\left(t,\alpha \right), \overline{u}(t,\alpha )$], exhibit mirror symmetry around their center (the crisp solution).

• Fuzzy Laplace Transform

The fuzzy Laplace transform is a mathematical tool used to analyze and solve differential equations involving fuzzy initial conditions or parameters. It extends the classical Laplace transform to accommodate uncertainty or imprecision present in the system.

Given a function $f(t)$ with fuzzy initial conditions or parameters, the fuzzy Laplace transform $F(s)$ is defined as follows:

$$F\left(s\right)= \underset{0}{\overset{\infty }{\int }}{e}^{-st}\mu \left(\tau \right)f(t)dt.$$

where

• $\mu (t)$ is the membership function representing the fuzziness of the initial conditions or parameter.
• $s$ is the complex variable in the Laplace domain, and t is the time variable. The fuzzy Laplace transform $F(s)$ provides a representation of the function $f(t)$ in the Laplace domain, considering the uncertainty encapsulated by the membership function $\mu (t)$.

For $0\le r\le 1,$ the parametric form of $\mathit{\varphi }\left(\mathit{\chi }\right)$ is represented by

$$\underset{0}{\overset{\infty }{\int }}f\left(\chi ,r\right).e^{-s\chi }d\chi =\left[\underset{0}{\overset{\infty }{\int }}\underset{\_}{f}\left(\chi ,r\right).e^{-s\chi }d\chi ,\underset{0}{\overset{\infty }{\int }}\overline{f}\left(\chi ,r\right).e^{-s\chi }d\chi ,\right]$$

$$L\left[f\left(\chi ,r\right)\right]=[L\underset{\_}{f}\left(\chi ,r\right),L\overline{f}\left(\chi ,r\right)]$$

Theorem 1

([34,35,36]). $f\in C^F[0,b]\cap L^F[0,b]$; then for $0\le p\le 1$ and $0<\beta \le 1$ , the Laplace transform of the fuzzy fractional derivative in Caputo’s terms is given by

$$L\left[{\left(D^{\beta }f\left(t\right)\right)}_p\right]=S^{\beta }L\left[f\left(t\right)\right]-S^{\beta -1}L\left[f\left(0\right)\right]$$

3.15. Fixed Point Theory

Let us consider the modified right-hand side of the fuzzy fractional Model (2) using fixed point theory to discuss its existence and uniqueness. Here is a formulation of the modified model:

$$D^{\alpha }u\left(t\right)=F\left(t,u\left(t\right), \mu \right),$$

where $F:\left[a,b\right]\chi X \chi Y\to X$ is a mapping defined on a closed interval [a, b] with $X$ and $Y$ being Banach spaces. The parameter $\mu$ represents the fuzzy parameters that capture uncertainty or imprecision.

To discuss the existence and uniqueness of solutions to this model, we can utilize fixed point theory. Fixed point theory provides conditions under which a mapping has a unique fixed point, which in turn can be related to the existence and uniqueness of solutions to the differential equation.

• Main Results

In the following section, the existence and uniqueness of solutions to the subsequent fuzzy fractional model are discussed, and we provide the procedure for finding a semi-analytic solution of the model by using the fuzzy Laplace transform.

• Existence and Uniqueness

In this section, by the use of fixed point theory, the existence and uniqueness of the subsequent fuzzy fractional model are discussed. Consider the right-hand sides of Model (2):

$$A\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)=\tilde{\lambda }-(\widetilde{{\mu }_1}+\tilde{a})S=\lambda -\widetilde{{\mu }_1}S-\tilde{a}S$$

$$B\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)=\tilde{a}S-\left(\widetilde{{\mu }_2}+\tilde{\beta }\right)E=\tilde{a}S-\widetilde{{\mu }_2}E-\tilde{\beta }E$$

$$C\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)=\tilde{\beta }E-\left(\tilde{d}+\widetilde{{\mu }_3}+\tilde{\theta }+\tilde{\eta }\right)I=\tilde{\beta }E-\tilde{d}I-\widetilde{{\mu }_3}I-\tilde{\theta }I-\tilde{\eta }I$$

$$D\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)=\tilde{\eta }I-\left(\tilde{\gamma }+\widetilde{{\mu }_4}+\tilde{\epsilon }\right)R_i=\tilde{\eta }I-{\tilde{\gamma }R}_i-\widetilde{{\mu }_4}{R}_i-\tilde{\epsilon }{R}_i$$

$$E\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)=\tilde{\theta }\mathrm{I}-\left(\widetilde{{\mathsf{\mu }}_5}+\tilde{\mathsf{\sigma }}\right){\mathrm{U}}_{\mathrm{i}}=\tilde{\theta }\mathrm{I}-{\widetilde{{\mathsf{\mu }}_5}\mathrm{U}}_{\mathrm{i}}-\tilde{\mathsf{\sigma }}{\mathrm{U}}_{\mathrm{i}}$$

$$F\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)=\tilde{\gamma }{R}_i-\left(\widetilde{{\mu }_6}+\tilde{\delta }\right)H=\tilde{\gamma }{R}_i-\widetilde{{\mu }_6}H-\tilde{\delta }H$$

$$G\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)=\tilde{\sigma }{\mathrm{U}}_{\mathrm{i}}+\tilde{\epsilon }{R}_i+\tilde{\delta }H-\widetilde{{\mu }_7}R$$

where A, B, C, D, E, F, and G are fuzzy functions. Thus, for $0< \alpha \le 1$, the given Model (2) can be written as

$$\{\begin{array}{cc}{D}_t^{\alpha }S\left(t\right)=A\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\hfill & \mathrm{(4a)}\hfill \\ D_t^{\alpha }E\left(t\right)=B\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\hfill & \mathrm{(4b)}\hfill \\ D_t^{\alpha }I\left(t\right)=C\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\hfill & \mathrm{(4c)}\hfill \\ D_t^{\alpha }{R}_i\left(t\right)=\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\hfill & \mathrm{(4d)}\hfill \\ D_t^{\alpha }{\mathrm{U}}_{\mathrm{i}}\left(t\right)=E\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\hfill & \mathrm{(4e)}\hfill \\ D_t^{\alpha }H\left(t\right)=F\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\hfill & \mathrm{(4f)}\hfill \\ D_t^{\alpha }R\left(t\right)=G\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\hfill & \mathrm{(4g)}\hfill \end{array}$$

with the following fuzzy initial conditions:

$$\tilde{S}\left(0,\alpha \right)=(\underset{\_}{S}\left(0,\alpha \right), \overline{S}\left(0,\alpha \right)), \widetilde{E }\left(0,\alpha \right)=\left(\underset{\_}{E}\left(0,\alpha \right), \overline{E}\left(0,\alpha \right)\right),$$

$$\tilde{I}\left(0,\alpha \right)=\left(\underset{\_}{I} \left(0,\alpha \right), \overline{I}\left(0,\alpha \right)\right),\widetilde{ R_i}\left(0,\alpha \right)=\left(\underset{\_}{R_i}\left(0,\alpha \right), \overline{R_i}\left(0,\alpha \right)\right),$$

$$\widetilde{{\mathrm{U}}_i}\left(0,\alpha \right)=\left(\underset{\_}{{\mathrm{U}}_{\mathrm{i}}}\left(0,\alpha \right), \overline{{\mathrm{U}}_{\mathrm{i}}}\left(0,\alpha \right)\right),\widetilde{H }\left(0,\alpha \right)=\left(\underset{\_}{H} \left(0,\alpha \right), \overline{H}\left(0,\alpha \right)\right),$$

$$\widetilde{R }\left(0,\alpha \right)=\left(\underset{\_}{R} \left(0,\alpha \right), \overline{R}\left(0,\alpha \right)\right).$$

Now, applying fuzzy fractional integral $I^r$ and using initial conditions, we get

$$\{\begin{array}{cc}{S}_n\left(t\right)=\tilde{S} \left(0,\alpha \right)+{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}\underset{0}{\overset{t}{\int }}{\left(t-\Delta \right)}^{\gamma -1 }A\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)& \mathrm{(5a)}\\ E_n\left(t\right)=\tilde{E} \left(0,\alpha \right)+{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}\underset{0}{\overset{t}{\int }}{\left(t-\Delta \right)}^{\gamma -1 }A\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)& \mathrm{(5b)}\\ I_n\left(t\right)=\tilde{I} \left(0,\alpha \right)+{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}\underset{0}{\overset{t}{\int }}{\left(t-\Delta \right)}^{\gamma -1 }A\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)& \mathrm{(5c)}\\ R_{i_n}\left(t\right)=\widetilde{R_i} \left(0,\alpha \right)+{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}\underset{0}{\overset{t}{\int }}{\left(t-\Delta \right)}^{\gamma -1 }A\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)& \mathrm{(5d)}\\ {U_i}_n\left(t\right)=\widetilde{U_i} \left(0,\alpha \right)+{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}\underset{0}{\overset{t}{\int }}{\left(t-\Delta \right)}^{\gamma -1 }A\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)& \mathrm{(5e)}\\ H_n\left(t\right)=\tilde{H} \left(0,\alpha \right)+{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}\underset{0}{\overset{t}{\int }}{\left(t-\Delta \right)}^{\gamma -1 }A\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)& \mathrm{(5f)}\\ R_n\left(t\right)=\tilde{R} \left(0,\alpha \right)+{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}\underset{0}{\overset{t}{\int }}{\left(t-\Delta \right)}^{\gamma -1 }A\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)& \mathrm{(5g)}\end{array}$$

Let us define a Banach space as $\mathcal{B}={\mathcal{B}}_1\chi {\mathcal{B}}_2\chi {\mathcal{B}}_3\chi {\mathcal{B}}_4\chi {\mathcal{B}}_5\chi {\mathcal{B}}_6\chi {\mathcal{B}}_7$ under the fuzzy norm:

$$\begin{gathered} \left|\left|S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right|\right|= \\ ma{x}_{t\in [0,T]}\left[\left|S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right|\right]. \end{gathered}$$

Thus, the equation is rewritten as

$$\widetilde{g_n}\left(t\right)=\tilde{g}\left(0,\alpha \right)+{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}\underset{0}{\overset{t}{\int }}{\left(t-\Delta \right)}^{\gamma -1 }\Theta \left(\Delta ,\widetilde{g_n}\left(\Delta \right)d\Delta \right),$$

where

$${\tilde{g}}_n\left(t\right)=\left\{\begin{array}{c}{A}_n\left(t\right)\\ B_n\left(t\right)\\ C_n\left(t\right)\\ D_n\left(t\right)\\ E_n\left(t\right)\\ F_n\left(t\right)\\ G_n(t)\end{array}\right.{\tilde{g}}_n\left(0,\alpha \right)=\left\{\begin{array}{c}\tilde{A}\left(0,\alpha \right)\\ \tilde{B}\left(0,\alpha \right)\\ \tilde{C}\left(0,\alpha \right)\\ \tilde{D}\left(0,\alpha \right)\\ \tilde{E}\left(0,\alpha \right)\\ \tilde{F}\left(0,\alpha \right)\\ \tilde{G}\left(0,\alpha \right)\end{array}\right.$$

and

$$\Theta \left(t,\tilde{g}\left(t\right)\right)=\left\{\begin{array}{c}A\left(t,S\left(t\right),E\left(t\right),E(t),I(t),R_i(t),U_i(t),R(t)\right),\\ B\left(t,S\left(t\right),E\left(t\right),E(t),I(t),R_i(t),U_i(t),R(t)\right),\\ C\left(t,S\left(t\right),E\left(t\right),E(t),I(t),R_i(t),U_i(t),R(t)\right),\\ D\left(t,S\left(t\right),E\left(t\right),E(t),I(t),R_i(t),U_i(t),R(t)\right),\\ E\left(t,S\left(t\right),E\left(t\right),E(t),I(t),R_i(t),U_i(t),R(t)\right),\\ F\left(t,S\left(t\right),E\left(t\right),E(t),I(t),R_i(t),U_i(t),R(t)\right),\\ G\left(t,S\left(t\right),E\left(t\right),E(t),I(t),R_i(t),U_i(t),R(t)\right).\end{array}\right.$$

In order to obtain the required results, we consider the following assumptions:

(A1) There exist a constant $P_g>0$ and $Q_g>0 \ni \left|\Theta \left(t,\tilde{g}\left(t\right)\right)\right|<P_g\left|\tilde{g}\left(\mathit{t}\right)\right|+Q_g.$

(A2) There exist a constant $K_g>0$ such that for each ${\tilde{g}}_1\left(\mathit{t}\right),{\tilde{g}}_2\left(\mathit{t}\right)\in B$, we have

$$\left|\Theta \left(t,{\tilde{g}}_1\left(t\right)\right)-\Theta \left(t,{\tilde{g}}_2\left(t\right)\right)\right|\le K_g|{\tilde{g}}_1\left(t\right)-{\tilde{g}}_2\left(t\right)|$$

Theorem 2.

By using Assumption A1, we obtain the prescribed system and at least one solution.

Proof. 

Let $\Omega =\left\{\tilde{g}\left(\mathit{t}\right)\in 𝓑:\left|\left|\tilde{g}\left(\mathit{t}\right)\right|\right|<r\right\}\subset 𝓑$ be a convex and closed fuzzy set. We take the mapping $v: \Omega \to \Omega$ such that

$$v\left\{\tilde{g}\left(t\right)\right\}=\tilde{g}\left(0,r\right)+{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}{\int }_0^t{\left(t-\Delta \right)}^{\gamma -1 }\Theta \left(\Delta ,\tilde{g}\left(\Delta \right)d\Delta \right)$$

For any $\tilde{g}\left(\mathit{t}\right)\in \Omega ,$ one can obtain

$$\begin{array}{c}\left|\left|v\left\{\tilde{g}\left(\mathit{t}\right)\right\}\right|\right|=\underset{t\in \left[0,\mathit{T}\right]}{\max }| \tilde{g}\left(0,r\right)+{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}{\int }_0^t{\left(t-\Delta \right)}^{\gamma -1 }\Theta \left(\Delta ,\tilde{g}\left(\Delta \right)d\Delta \right)|\hfill \\ \le \left|\tilde{g}\left(0,r\right)\right|+{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}{\int }_0^t{\left(t-\Delta \right)}^{\gamma -1 }|\Theta \left(\Delta ,\tilde{g}\left(\Delta \right))|d\Delta \right)\hfill \\ \le \left|\tilde{g}\left(0,r\right)\right|+{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}{\int }_0^t{\left(t-\Delta \right)}^{\gamma -1 }\left[{\mathrm{P}}_g\left|\tilde{g}\left(t\right)\right|+Q_g\right]d\Delta \hfill \\ \le \left|\tilde{g}\left(0,r\right)\right|+{\displaystyle \frac{{\tau }^{\gamma }}{\Gamma \left(\gamma +1\right)}}[{\mathrm{P}}_g\left|\tilde{g}\left(t\right)\right|+Q_g] \hfill \end{array}$$

From the last inequality, we have $\tilde{g}\left(t\right)\subset t,$ which implies that the operator $\tilde{g}$ is bounded. Next we show that the operator ψ is completely continuous. For this, let ${\varphi }_1$,${\varphi }_2$ ∈ [0, T] be such that ${\varphi }_1$<${\varphi }_2$; then

$$\begin{array}{c}|| v (\tilde{g}\left(\mathit{t}\right)){(\varphi }_1)-v (\tilde{g}\left(\mathit{t}\right)){(\varphi }_2)||\hfill \\ =|{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}\underset{0}{\overset{{\varphi }_2}{\int }}{\left({\varphi }_2-\Delta \right)}^{\gamma -1 }\Theta \left(\Delta ,\tilde{g}\left(\Delta \right))d\Delta \right)-{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}\underset{0}{\overset{{\varphi }_2}{\int }}{\left({\varphi }_1-\Delta \right)}^{\gamma -1 }\Theta \left(\Delta ,\tilde{g}\left(\Delta \right))d\Delta \right) |\hfill \\ \le {\displaystyle \frac{\left[{\varphi }_2^{\gamma }-{\varphi }_1^{\gamma }\right]\left[M_g|\tilde{g}\left(t\right)+N_g\right]}{\Gamma \left(\gamma +1\right)}}\hfill \end{array}$$

From the last inequality, we see that the right-hand side goes to zero as ${\varphi }_2\to {\varphi }_1$. Hence

$$\left|\right| v (\tilde{g}\left(\mathit{t}\right)){(\varphi }_1)-v (\tilde{g}\left(\mathit{t}\right)){(\varphi }_2)\left|\right|\to 0 \mathrm{a}\mathrm{s} {\varphi }_2\to {\varphi }_1$$

Thus, the operator $v$ is equicontinuous. By the Arzela–Ascoli theorem, the operator $v$ is completely continuous, and $v$ is bounded as proven earlier. Therefore, System (3) has at least one solution by Schauder’s fixed point theorem. □

Theorem 3.

If Assumption (A-1) holds, then the considered system (3) has a unique solution if ${\varphi }^{\alpha } L_f<\Gamma \left(\gamma +1\right).$

Proof. 

Let ${\tilde{g}}_1\left(t\right),{\tilde{g}}_2\left(t\right)\in 𝓑$; then

$$\begin{array}{c}\left|\left|v\left({\tilde{g}}_{n_1}\left(t\right)\right)-v\left({\tilde{g}}_{n_2}\left(t\right)\right)\right|\right|\hfill \\ =\underset{t\in \left[0, T\right]}{\mathrm{m}\mathrm{a}\mathrm{x}}|{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}\underset{0}{\overset{t}{\int }}{\left(t-\Delta \right)}^{\gamma -1 }\Theta \left(\Delta ,{\tilde{g}}_{n_1}\left(\Delta \right))d\Delta \right)\hfill \\ -{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}\underset{0}{\overset{t}{\int }}{\left(t-\Delta \right)}^{\gamma -1 }\Theta \left(\Delta ,{\tilde{g}}_{n_2}\left(\Delta \right))d\Delta \right)|\left|\left|v\left({\tilde{g}}_{n_1}\left(t\right)\right)-v\left({\tilde{g}}_{n_2}\left(t\right)\right)\right|\right|\hfill \\ =\underset{t\in \left[0, T\right]}{\mathrm{m}\mathrm{a}\mathrm{x}}{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}\left|\underset{0}{\overset{t}{\int }}{\left(t-\Delta \right)}^{\gamma -1 }\Theta \left(\Delta ,{\tilde{g}}_{n_1}\left(\Delta \right))d\Delta \right)-{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}\underset{0}{\overset{t}{\int }}{\left(t-\Delta \right)}^{\gamma -1 }\Theta \left(\Delta ,{\tilde{g}}_{n_2}\left(\Delta \right))d\Delta \right)\right|\hfill \\ \le {\displaystyle \frac{{\tau }^{\gamma }}{\Gamma \left(\gamma +1\right)}}{L}_f|{\tilde{g}}_{n_1}-{\tilde{g}}_{n_2}|\hfill \end{array}$$

Hence $v$ is a contraction. Hence, by the Banach contraction theorem, System (3) has a unique solution. The procedure for this solution is as follows.

Here a general method is provided in order to find the solution of the considered system using the fuzzy Laplace transform (FLT).

Taking the fuzzy Laplace transform of (3) and using initial conditions, we get

$$\begin{array}{c}L\left[D_t^{\alpha }S\left(t\right)\right]=L\left[A\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\right]\\ L\left[D_t^{\alpha }E\left(t\right)\right]=L[ B\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)]\\ L\left[D_t^{\alpha }I\left(t\right)\right]=L\left[C\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\right]\\ L\left[D_t^{\alpha }{R}_i\left(t\right)\right]=L\left[\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\right]\\ L\left[D_t^{\alpha }{\mathrm{U}}_{\mathrm{i}}\left(t\right)\right]=L[ E\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)]\\ L\left[D_t^{\alpha }H\left(t\right)\right]=L\left[F\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\right]\\ L\left[D_t^{\alpha }R\left(t\right)\right]=L[ G\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)]\end{array}$$

$$\begin{array}{c}{s}^{\gamma }\left[S\left(t\right)\right]=s^{\gamma -1}\tilde{S} \left(0,\alpha \right)+{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}{\int }_0^t{\left(t-\Delta \right)}^{\gamma -1 }A\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\\ s^{\gamma }\left[E\left(t\right)\right]=s^{\gamma -1} \tilde{E} \left(0,\alpha \right)+{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}{\int }_0^t{\left(t-\Delta \right)}^{\gamma -1 }B\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\\ s^{\gamma }\left[I\left(t\right)\right]=s^{\gamma -1} \tilde{I} \left(0,\alpha \right)+{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}{\int }_0^t{\left(t-\Delta \right)}^{\gamma -1 }C\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\\ s^{\gamma }{[R}_i\left(t\right)]=s^{\gamma -1} \widetilde{R_i} \left(0,\alpha \right)+{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}{\int }_0^t{\left(t-\Delta \right)}^{\gamma -1 }D\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\\ s^{\gamma }{[U}_i\left(t\right)]=s^{\gamma -1} \widetilde{U_i} \left(0,\alpha \right)+{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}{\int }_0^t{\left(t-\Delta \right)}^{\gamma -1 }E\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\\ s^{\gamma }\left[H\left(t\right)\right]=s^{\gamma -1} \tilde{H} \left(0,\alpha \right)+{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}{\int }_0^t{\left(t-\Delta \right)}^{\gamma -1 }F\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\\ s^{\gamma }\left[R\left(t\right)\right]=s^{\gamma -1}\tilde{R} \left(0,\alpha \right)+{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}{\int }_0^t{\left(t-\Delta \right)}^{\gamma -1 }G\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\end{array}.$$

$$\begin{array}{c}L\left[D_t^{\alpha }S\left(t\right)\right]=s^{\gamma -1}\tilde{S} \left(0,\alpha \right)+{\displaystyle \frac{1}{s^{\gamma }}}L\left[A\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\right]\\ L\left[D_t^{\alpha }E\left(t\right)\right]=s^{\gamma -1} \tilde{E} \left(0,\alpha \right)+{\displaystyle \frac{1}{\Gamma s^{\gamma }}}L\left[B\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\right]\\ L\left[D_t^{\alpha }I\left(t\right)\right]=s^{-1} \tilde{I} \left(0,\alpha \right)+{\displaystyle \frac{1}{s^{\gamma }}}L\left[C\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\right]\\ L\left[D_t^{\alpha }{R}_i\left(t\right)\right]=s^{-1} \widetilde{R_i} \left(0,\alpha \right)+{\displaystyle \frac{1}{s^{\gamma }}}L\left[D\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\right]\\ L\left[D_t^{\alpha }{\mathrm{U}}_{\mathrm{i}}\left(t\right)\right]=s^{-1} \widetilde{U_i} \left(0,\alpha \right)+{\displaystyle \frac{1}{s^{\gamma }}}L\left[F\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\right]\\ L\left[D_t^{\alpha }H\left(t\right)\right]=s^{-1} \tilde{H} \left(0,\alpha \right)+{\displaystyle \frac{1}{s^{\gamma }}}L\left[G\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\right]\\ L\left[D_t^{\alpha }R\left(t\right)\right]=s^{-1}\tilde{R} \left(0,\alpha \right)+{\displaystyle \frac{1}{s^{\gamma }}}L\left[H\left(t,S\left(t\right),E\left(t\right),I\left(t\right),R_i\left(t\right),U_i\left(t\right),H\left(t\right),R\left(t\right)\right)\right]\end{array}$$

The infinite series solution is given by the following:

$$S_k\left(t\right)= \sum _{n=0}^{\infty }{S}_{k_n}(t),{ E}_k\left(t\right)= \sum _{n=0}^{\infty }{E}_{k_n}(t), I_k\left(t\right)= \sum _{n=0}^{\infty }{I}_{k_n}(t),$$

$$R_{i_k}\left(t\right)=\sum _{n=0}^{\infty }{R_i}_{k_n}(t),U_{i_k}\left(t\right)=\sum _{n=0}^{\infty }{U_i}_{k_n}(t),H_k\left(t\right)=\sum _{n=0}^{\infty }{H}_{k_n}\left(t\right),$$

$$R_k\left(t\right)=\sum _{n=0}^{\infty }{R}_{k_n}(t)$$

where $Z_{1,n}$ are Adomian polynomials, representing nonlinear terms.

$$\begin{array}{c}L\left[{\displaystyle \sum _{n=0}^{\infty }}{S}_{kn}\left(t\right)\right]=s^{-1}\tilde{S} \left(0,\alpha \right)+{\displaystyle \frac{1}{s^{\gamma }}}L\left[A\left(t,S_k\left(t\right),E_k\left(t\right),I_k\left(t\right),R_{i_k}\left(t\right),{U_i}_k\left(t\right),H_k\left(t\right),R_k\left(t\right)\right)\right]\\ L\left[{\displaystyle \sum _{n=0}^{\infty }}{E}_{kn}\left(t\right)\right]=s^{-1} \tilde{E} \left(0,\alpha \right)+{\displaystyle \frac{1}{s^{\gamma }}}L\left[B\left(t,S_k\left(t\right),E_k\left(t\right),I_k\left(t\right),R_{i_k}\left(t\right),{U_i}_k\left(t\right),H_k\left(t\right),R_k\left(t\right)\right)\right]\\ L\left[{\displaystyle \sum _{n=0}^{\infty }}{I}_{kn}\left(t\right)\right]=s^{-1} \tilde{I} \left(0,\alpha \right)+{\displaystyle \frac{1}{s^{\gamma }}}L\left[C\left(t,S_k\left(t\right),E_k\left(t\right),I_k\left(t\right),R_{i_k}\left(t\right),{U_i}_k\left(t\right),H_k\left(t\right),R_k\left(t\right)\right)\right]\\ L\left[{\displaystyle \sum _{n=0}^{\infty }}{R_i}_{kn}\left(t\right)\right]=s^{-1} \widetilde{R_i} \left(0,\alpha \right)+{\displaystyle \frac{1}{s^{\gamma }}}L\left[D\left(t,S_k\left(t\right),E_k\left(t\right),I_k\left(t\right),R_{i_k}\left(t\right),{U_i}_k\left(t\right),H_k\left(t\right),R_k\left(t\right)\right)\right]\\ L\left[{\displaystyle \sum _{n=0}^{\infty }}{U_i}_{kn}\left(t\right)\right]=s^{-1} \widetilde{U_i} \left(0,\alpha \right)+{\displaystyle \frac{1}{s^{\gamma }}}L\left[E\left(t,S_k\left(t\right),E_k\left(t\right),I_k\left(t\right),R_{i_k}\left(t\right),{U_i}_k\left(t\right),H_k\left(t\right),R_k\left(t\right)\right)\right]\\ L\left[{\displaystyle \sum _{n=0}^{\infty }}{H}_{kn}\left(t\right)\right]=s^{-1} \tilde{H} \left(0,\alpha \right)+{\displaystyle \frac{1}{s^{\gamma }}}L\left[F\left(t,S_k\left(t\right),E_k\left(t\right),I_k\left(t\right),R_{i_k}\left(t\right),{U_i}_k\left(t\right),H_k\left(t\right),R_k\left(t\right)\right)\right]\\ L\left[{\displaystyle \sum _{n=0}^{\infty }}{R}_{kn}(t)\right]=s^{-1}\tilde{R} \left(0,\alpha \right)+{\displaystyle \frac{1}{s^{\gamma }}}L\left[G\left(t,S_k\left(t\right),E_k\left(t\right),I_k\left(t\right),R_{i_k}\left(t\right),{U_i}_k\left(t\right),H_k\left(t\right),R_k\left(t\right)\right)\right]\end{array}$$

Taking the inverse Laplace transform, we have

$$\begin{array}{c}\left[{\displaystyle \sum _{n=0}^{\infty }}{S}_{kn}\left(t\right)\right]=\tilde{S} \left(0,\alpha \right)+L^{-1}\left[{\displaystyle \frac{1}{s^{\gamma }}}L\left[A\left(t,S_k\left(t\right),E_k\left(t\right),I_k\left(t\right),R_{i_k}\left(t\right),{U_i}_k\left(t\right),H_k\left(t\right),R_k\left(t\right)\right)\right]\right]\\ \left[{\displaystyle \sum _{n=0}^{\infty }}{E}_{kn}\left(t\right)\right]=\tilde{E} \left(0,\alpha \right)+L^{-1}\left[{\displaystyle \frac{1}{s^{\gamma }}}L\left[B\left(t,S_k\left(t\right),E_k\left(t\right),I_k\left(t\right),R_{i_k}\left(t\right),{U_i}_k\left(t\right),H_k\left(t\right),R_k\left(t\right)\right)\right]\right]\\ \left[{\displaystyle \sum _{n=0}^{\infty }}{I}_{kn}\left(t\right)\right]=\tilde{I} \left(0,\alpha \right)+L^{-1}\left[{\displaystyle \frac{1}{s^{\gamma }}}L\left[C\left(t,S_k\left(t\right),E_k\left(t\right),I_k\left(t\right),R_{i_k}\left(t\right),{U_i}_k\left(t\right),H_k\left(t\right),R_k\left(t\right)\right)\right]\right]\\ \left[{\displaystyle \sum _{n=0}^{\infty }}{R_i}_{kn}\left(t\right)\right]=\widetilde{R_i} \left(0,\alpha \right)+L^{-1}\left[{\displaystyle \frac{1}{s^{\gamma }}}L\left[D\left(t,S_k\left(t\right),E_k\left(t\right),I_k\left(t\right),R_{i_k}\left(t\right),{U_i}_k\left(t\right),H_k\left(t\right),R_k\left(t\right)\right)\right]\right]\\ \left[{\displaystyle \sum _{n=0}^{\infty }}{U_i}_{kn}\left(t\right)\right]=\widetilde{U_i} \left(0,\alpha \right)+L^{-1}\left[{\displaystyle \frac{1}{s^{\gamma }}}L\left[E\left(t,S_k\left(t\right),E_k\left(t\right),I_k\left(t\right),R_{i_k}\left(t\right),{U_i}_k\left(t\right),H_k\left(t\right),R_k\left(t\right)\right)\right]\right]\\ \left[{\displaystyle \sum _{n=0}^{\infty }}{H}_{kn}\left(t\right)\right]=\tilde{H} \left(0,\alpha \right)+L^{-1}\left[{\displaystyle \frac{1}{s^{\gamma }}}L\left[F\left(t,S_k\left(t\right),E_k\left(t\right),I_k\left(t\right),R_{i_k}\left(t\right),{U_i}_k\left(t\right),H_k\left(t\right),R_k\left(t\right)\right)\right]\right]\\ \left[{\displaystyle \sum _{n=0}^{\infty }}{R}_{kn}(t)\right]=\tilde{R} \left(0,\alpha \right)+L^{-1}[{\displaystyle \frac{1}{s^{\gamma }}}L[G\left(t,S_k\left(t\right),E_k\left(t\right),I_k\left(t\right),R_{i_k}\left(t\right),{U_i}_k\left(t\right),H_k\left(t\right),R_k\left(t\right)\right)]\end{array}$$

Comparing the terms on both sides, we consider the first two terms of the series

$$\left\{\begin{array}{c} {{\underset{\_}{A}}_n}_0\left(t\right)=\underset{\_}{A}\left(0,\alpha \right), \overline{S_{n0}}\left(t\right)=\overline{A}\left(0,\alpha \right) \\ {{\underset{\_}{B}}_n}_0\left(t\right)=\underset{\_}{B}\left(0,\alpha \right), \overline{E_{n0}}\left(t\right)=\overline{B}\left(0,\alpha \right), \\ {{\underset{\_}{C}}_n}_0\left(t\right)=\underset{\_}{C}\left(0,\alpha \right), \overline{I_{n0}}\left(t\right)=\overline{C}\left(0,\alpha \right), \\ {{\underset{\_}{D}}_n}_0\left(t\right)=\underset{\_}{D}\left(0,\alpha \right), \overline{{R_i}_{n0}}\left(t\right)=\overline{D}\left(0,\alpha \right), \\ {{ \underset{\_}{E}}_n}_0\left(t\right)=\underset{\_}{E}\left(0,\alpha \right), \overline{{U_i}_{n0}}\left(t\right)=\overline{E}\left(0,\alpha \right), \\ {{\underset{\_}{F}}_n}_0\left(t\right)=\underset{\_}{F}\left(0,\alpha \right), \overline{H_{n0}}\left(t\right)=\overline{F}\left(0,\alpha \right),\\ {{\underset{\_}{G}}_n}_0\left(t\right)=\underset{\_}{G}\left(0,\alpha \right), \overline{R_{n0}}\left(t\right)=\overline{G}\left(0,\alpha \right), \\ \end{array}\right.$$

Similarly, we can find the other terms. □

Hence, the series solution of the considered system is given by the initial conditions of all cases.

(a) 

Suspect Population Cases:

$$\left\{\begin{array}{c}{\underset{\_}{S}}_0 \left(t, \alpha \right)=2\alpha -1\\ \overline{S_0}\left(t, \alpha \right)=1-2\alpha \end{array}\right.$$

(6)

$$\left\{\begin{array}{c}{\underset{\_}{S}}_1 \left(t, \alpha \right)=\left[\left[\left( \lambda -{\mu }_1\left(2\alpha -1\right)-a{\left(2\alpha -1\right)}^2\right)\right]{\displaystyle \frac{t^{\gamma }}{\Gamma \left(\gamma +1\right)}}\right]\\ \overline{S_1}\left(t, \alpha \right)=\left[\left[\left( \lambda +{\mu }_1\left(2\alpha -1\right)-a{\left(2\alpha -1\right)}^2\right)\right]{\displaystyle \frac{t^{\gamma }}{\Gamma \left(\gamma +1\right)}}\right]\end{array}\right.$$

(7)

$$\left\{\begin{array}{c}{\underset{\_}{S}}_2 \left(t, \alpha \right)=\left[\begin{array}{c}-(a(I_1(2\alpha -1)-((2\alpha -1)(a{\left(2\alpha -1\right)}^2-\lambda +{\mu }_1\left(2\alpha -1\right))){\displaystyle \frac{t^{\gamma }}{\Gamma \left(\gamma +1\right)}}-\\ ({\mu }_1(a{\left(2\alpha -1\right)}^2-\lambda +{\mu }_1(2\alpha -1)){\displaystyle \frac{t^{\gamma }}{\Gamma \left(\gamma +1\right)}} \end{array}\right]{\displaystyle \frac{t^{2\gamma }}{\Gamma \left(\gamma +1\right)}} \\ \overline{S_2}\left(t, \alpha \right)=\left[\begin{array}{c} (a(I_1(2\alpha -1)+((2\alpha -1)(\lambda -a{\left(2\alpha -1\right)}^2+{\mu }_1\left(2\alpha -1\right))){\displaystyle \frac{t^{\gamma }}{\Gamma \left(\gamma +1\right)}}-\\ ({\mu }_1(\lambda -a{\left(2\alpha -1\right)}^2+{\mu }_1(2\alpha -1)){\displaystyle \frac{t^{\gamma }}{\Gamma \left(\gamma +1\right)}} \end{array}\right]{\displaystyle \frac{t^{2\gamma }}{\Gamma \left(\gamma +1\right)}} \end{array}\right..$$

(8)

Hence, the suspect case population series solution of the system is given by

$$\left\{\begin{array}{c}{\underset{\_}{S}}_n \left(t, \alpha \right)={\underset{\_}{S}}_0 \left(t, \alpha \right)+{\underset{\_}{S}}_1 \left(t, \alpha \right)+{\underset{\_}{S}}_2 \left(t, \alpha \right)+\cdots \\ \overline{S_n}\left(t, \alpha \right)=\overline{S_0}\left(t, \alpha \right)+\overline{S_1}\left(t, \alpha \right)+\overline{S_2}\left(t, \alpha \right)+\cdots \end{array}\right.$$

$$\left\{\begin{array}{c}{\underset{\_}{S}}_n \left(t, \alpha \right)=2\alpha -1+\left[\left[\left( \lambda -{\mu }_1\left(2\alpha -1\right)-a{\left(2\alpha -1\right)}^2\right)\right]{\displaystyle \frac{t^{\gamma }}{\Gamma \left(\gamma +1\right)}}\right]+\\ \left[\begin{array}{c}-(a(I_1(2\alpha -1)-((2\alpha -1)(a{\left(2\alpha -1\right)}^2-\lambda +{\mu }_1\left(2\alpha -1\right))){\displaystyle \frac{t^{\gamma }}{\Gamma \left(\gamma +1\right)}}-\\ ({\mu }_1(a{\left(2\alpha -1\right)}^2-\lambda +{\mu }_1(2\alpha -1)){\displaystyle \frac{t^{\gamma }}{\Gamma \left(\gamma +1\right)}} \end{array}\right]{\displaystyle \frac{t^{2\gamma }}{\Gamma \left(\gamma +1\right)}}+\cdots \\ \overline{S_n}\left(t, \alpha \right)=1-2\alpha +\left[\left[\left( \lambda +{\mu }_1\left(2\alpha -1\right)-a{\left(2\alpha -1\right)}^2\right)\right]{\displaystyle \frac{t^{\gamma }}{\Gamma \left(\gamma +1\right)}}\right]+\\ \left[\begin{array}{c} (a(I_1(2\alpha -1)+((2\alpha -1)(\lambda -a{\left(2\alpha -1\right)}^2+{\mu }_1\left(2\alpha -1\right))){\displaystyle \frac{t^{\gamma }}{\Gamma \left(\gamma +1\right)}}-\\ ({\mu }_1(\lambda -a{\left(2\alpha -1\right)}^2+{\mu }_1(2\alpha -1)){\displaystyle \frac{t^{\gamma }}{\Gamma \left(\gamma +1\right)}} \end{array}\right]{\displaystyle \frac{t^{2\gamma }}{\Gamma \left(\gamma +1\right)}}\end{array}\right.$$

(9)

(b) 

Exposed Population Cases:

$$\left\{\begin{array}{c}{\underset{\_}{E}}_0 \left(t, \alpha \right)=2\alpha -1\\ \overline{E_0}\left(t, \alpha \right)=1-2\alpha \end{array}\right.$$

(10)

$$\left\{\begin{array}{c}{\underset{\_}{E}}_1 \left(t, \alpha \right)=[ a {\left(2 \alpha -1\right)}^2-(2 \alpha -1)(\beta +{\mu }_2)] {\displaystyle \frac{t^{\gamma }}{\Gamma \left(\gamma +1\right)}}\\ \overline{E_1}\left(t, \alpha \right)=[ a {\left(2 \alpha -1\right)}^2+(2 \alpha -1)(\beta +{\mu }_2)] {\displaystyle \frac{t^{\gamma }}{\Gamma \left(\gamma +1\right)}}\end{array}\right.$$

(11)

$$\left\{\begin{array}{c}{\underset{\_}{E}}_2 \left(t, \alpha \right)=\left[-\left(\beta +{\mu }_2\right)\left[ a {\left(2 \alpha -1\right)}^2-\left(2 \alpha -1\right)\left(\beta +{\mu }_2\right)\right]\right] {\displaystyle \frac{t^{2\gamma }}{\Gamma {\left(\gamma +1\right)}^2}} \\ \overline{E_2}\left(t, \alpha \right)=\left[-(\beta +{\mu }_2)[a{\left(2 \alpha -1\right)}^2+(2 \alpha -1) (\beta +{\mu }_2)]{\displaystyle \frac{t^{2\gamma }}{\Gamma {\left(2\gamma +1\right)}^2}}\right]{\displaystyle \frac{t^{2\gamma }}{\Gamma \left(\gamma +1\right)}} \end{array}\right..$$

(12)

Hence, the exposed case population series solution of the system is given by

$$\left\{\begin{array}{c}{\underset{\_}{E}}_n \left(t, \alpha \right)={\underset{\_}{E}}_0 \left(t, \alpha \right)+{\underset{\_}{E}}_1 \left(t, \alpha \right)+{\underset{\_}{E}}_2 \left(t, \alpha \right)+\cdots \\ \overline{E_n}\left(t, \alpha \right)=\overline{E_0}\left(t, \alpha \right)+\overline{E_1}\left(t, \alpha \right)+\overline{E_2}\left(t, \alpha \right)+\cdots \end{array}\right.$$

$$\left\{\begin{array}{c}{\underset{\_}{E}}_n \left(t, \alpha \right)=2\alpha -1+[ a {\left(2 \alpha -1\right)}^2+(2 \alpha -1)(\beta +{\mu }_2)] {\displaystyle \frac{t^{\gamma }}{\Gamma \left(\gamma +1\right)}}+\\ -\left(\beta +{\mu }_2\right)\left[ a {\left(2 \alpha -1\right)}^2-\left(2 \alpha -1\right)\left(\beta +{\mu }_2\right)\right]{\displaystyle \frac{t^{2\gamma }}{\Gamma {\left(\gamma +1\right)}^2}}+\cdots \\ \overline{E_n}\left(t, \alpha \right)=1-2\alpha +[ a {\left(2 \alpha -1\right)}^2+(2 \alpha -1)(\beta +{\mu }_2)] {\displaystyle \frac{t^{\gamma }}{\Gamma \left(\gamma +1\right)}}+\\ \left[-(\beta +{\mu }_2)[ a{\left(2 \alpha -1\right)}^2+(2 \alpha -1) (\beta +{\mu }_2)]{\displaystyle \frac{t^{2\gamma }}{\Gamma {\left(2\gamma +1\right)}^2}}\right]{\displaystyle \frac{t^{2\gamma }}{\Gamma \left(\gamma +1\right)}}\end{array}\right.$$

(13)

(c) 

Infected Population Cases: 

$$\left\{\begin{array}{c}{\underset{\_}{I}}_0 (t, \alpha )=2\alpha -1\\ \overline{I_0}(t, \alpha )=1-2\alpha \end{array}\right.$$

(14)

$$\left\{\begin{array}{c}{\underset{\_}{I}}_1 \left(t, \alpha \right)=-[(2\alpha -1)(\eta -\beta +{\mu }_3)]{\displaystyle \frac{t^{\gamma }}{\Gamma \left( \gamma +1\right)}}\\ \overline{I_1}\left(t, \alpha \right)=(2\alpha -1)(\eta -\beta +{\mu }_3)\left\}{\displaystyle \frac{t^{\gamma }}{\Gamma \left(\gamma +1\right)}}\right\}\end{array}\right.$$

(15)

$$\left\{\begin{array}{c}\begin{array}{c}{\underset{\_}{I}}_2 \left(t, \alpha \right)=\\ \left[\begin{array}{c}{\displaystyle \frac{[(2\alpha -1)(\left(\eta +{\mu }_3\right)\left(\left(2\alpha -1\right)\left(\eta +{\mu }_3 \right)-\beta \left(2\alpha -1\right)\right)+\beta \left(a{\left(2\alpha -1\right)}^2-\left(2\alpha -1\right)\left(\beta +{\mu }_2 \right)\right)]}{\Gamma \left( \gamma +1\right)}}\end{array}{\displaystyle \frac{t^{2\gamma }}{\Gamma \left(2 \gamma +1\right)}} \right]\end{array}\\ \overline{I_2}\left(t, \alpha \right)=\\ \left[\begin{array}{c}-{\displaystyle \frac{[(2\alpha -1)(\left(\eta +{\mu }_3\right)\left(\left(2\alpha -1\right)\left(\eta +{\mu }_3 \right)-\beta \left(2\alpha -1\right)\right)-\beta \left(a{\left(2\alpha -1\right)}^2-\left(2\alpha -1\right)\left(\beta +{\mu }_2 \right)\right)]}{\Gamma \left( \gamma +1\right)}}\end{array}{\displaystyle \frac{t^{2\gamma }}{\Gamma \left(2 \gamma +1\right)}} \right]\end{array}\right..$$

(16)

$$\left\{\begin{array}{c}\begin{array}{c}{\underset{\_}{I}}_n \left(t, \alpha \right)=\left(2\alpha -1\right)+\\ \left[\left[ a {\left(2 \alpha -1\right)}^2-\left(2 \alpha -1\right)\left(\beta +{\mu }_2 \right)\right]{\displaystyle \frac{t^{\gamma }}{\Gamma \left(\gamma +1\right)}}\right]+\\ \left[\begin{array}{c}{\displaystyle \frac{[(2\alpha -1)(\left(\eta +{\mu }_3\right)\left(\left(2\alpha -1\right)\left(\eta +{\mu }_3 \right)-\beta \left(2\alpha -1\right)\right)+\beta \left(a{\left(2\alpha -1\right)}^2-\left(2\alpha -1\right)\left(\beta +{\mu }_2 \right)\right)]}{\Gamma \left( \gamma +1\right)}}\end{array}{\displaystyle \frac{t^{2\gamma }}{\Gamma \left(2 \gamma +1\right)}} \right]\end{array}\\ \overline{I_n}\left(t, \alpha \right)=\left(1-2\alpha \right)+\\ \left[\left(2\alpha -1\right)\left(\eta -\beta +{\mu }_3\right){\displaystyle \frac{t^{\gamma }}{\Gamma \left(\gamma +1\right)}}\right] \\ \left[\begin{array}{c}-{\displaystyle \frac{[(2\alpha -1)(\left(\eta +{\mu }_3\right)\left(\left(2\alpha -1\right)\left(\eta +{\mu }_3 \right)-\beta \left(2\alpha -1\right)\right)-\beta \left(a{\left(2\alpha -1\right)}^2-\left(2\alpha -1\right)\left(\beta +{\mu }_2 \right)\right)]}{\Gamma \left( \gamma +1\right)}}\end{array}{\displaystyle \frac{t^{2\gamma }}{\Gamma \left(2 \gamma +1\right)}} \right]\end{array}\right..$$

(17)

(d) 

Reported Population Cases:

$$\left\{\begin{array}{c}{\underset{\_}{R_i}}_0 (t, \alpha )=2\alpha -1\\ \overline{{R_i}_0}(t, \alpha )=1-2\alpha \end{array}\right.$$

(18)

$$\left\{\begin{array}{c}{\underset{\_}{R_i}}_1 \left(t, \alpha \right)=-\left[\left(\left(2\alpha -1\right)\left(d+\epsilon +{\mu }_4\right)-\eta \left(2\alpha -1\right)\right)\right] {\displaystyle \frac{t^{\gamma }}{\Gamma \left( \gamma +1\right)}} \\ \overline{{R_i}_1}(t, \alpha )=\left[\left(\left(2\alpha -1\right)\left(d+\epsilon +{\mu }_4\right)-\eta \left(2\alpha -1\right)\right)\right] {\displaystyle \frac{t^{\gamma }}{\Gamma \left( \gamma +1\right)}}\end{array}\right.$$

(19)

$$\left\{\begin{array}{c}{\underset{\_}{R_i}}_2 \left(t, \alpha \right)=\left(2\alpha -1\right)\left[ {\left(d+\epsilon +{\mu }_4\right)}^2-\eta \left(d+\epsilon +{\mu }_4\right)-\eta \left(\eta +{\mu }_3-\beta \right)\right]{\displaystyle \frac{t^{2\gamma }}{\Gamma \left( \gamma +1\right)\Gamma \left( 2\gamma +1\right)}} \\ \overline{{R_i}_2}\left(t, \alpha \right)=-\left(2\alpha -1\right)\left[ {\left(d+\epsilon +{\mu }_4\right)}^2-\eta \left(d+\epsilon +{\mu }_4\right)-\eta \left(\eta +{\mu }_3-\beta \right)\right]{\displaystyle \frac{t^{2\gamma }}{\Gamma \left( \gamma +1\right)\Gamma \left( 2\gamma +1\right)}}\end{array}\right.$$

(20)

$$\left\{\begin{array}{c}{\underset{\_}{R_i}}_n \left(t, \alpha \right)=2\alpha -1-\left[\left(\left(2\alpha -1\right)\left(d+\epsilon +{\mu }_4\right)-\eta \left(2\alpha -1\right)\right)\right] {\displaystyle \frac{t^{\gamma }}{\Gamma \left( \gamma +1\right)}}+\\ \left(2\alpha -1\right)\left[ {\left(d+\epsilon +{\mu }_4\right)}^2-\eta \left(d+\epsilon +{\mu }_4\right)-\eta \left(\eta +{\mu }_3-\beta \right)\right]{\displaystyle \frac{t^{2\gamma }}{\Gamma \left( \gamma +1\right)\Gamma \left( 2\gamma +1\right)}} \\ \overline{{R_i}_n}\left(t, \alpha \right)=1-2\alpha +\left[\left(\left(2\alpha -1\right)\left(d+\epsilon +{\mu }_4\right)-\eta \left(2\alpha -1\right)\right)\right] {\displaystyle \frac{t^{\gamma }}{\Gamma \left( \gamma +1\right)}}\\ -\left(2\alpha -1\right)\left[ {\left(d+\epsilon +{\mu }_4\right)}^2-\eta \left(d+\epsilon +{\mu }_4\right)-\eta \left(\eta +{\mu }_3-\beta \right)\right]{\displaystyle \frac{t^{2\gamma }}{\Gamma \left( \gamma +1\right)\Gamma \left( 2\gamma +1\right)}} \end{array}\right.$$

(21)

(e) 

Unreported Population Cases:

$$\left\{\begin{array}{c}{\underset{\_}{U_i}}_0 (t, \alpha )=2\alpha -1\\ \overline{U_0}(t, \alpha )=1-2\alpha \end{array}\right.$$

(22)

$$\left\{\begin{array}{c}{\underset{\_}{U_i}}_1 \left(t, \alpha \right)=\left[\left(2\alpha -1\right)\left( d+{\mu }_5+\sigma -\theta \right)\right]{\displaystyle \frac{t^{\gamma }}{\Gamma \left( \gamma +1\right)}} \\ \overline{U_1}\left(t, \alpha \right)=-\left[\left(2\alpha -1\right)\left( d+{\mu }_5+\sigma -\theta \right)\right]{\displaystyle \frac{t^{\gamma }}{\Gamma \left( \gamma +1\right)}} \end{array}\right.$$

(23)

$$\left\{\begin{array}{c}{\underset{\_}{U_i}}_2 \left(t, \alpha \right)=[[d^2+2d{\mu }_5+2d\sigma -\theta d+{\mu }_5^2+2{\mu }_5\sigma -\theta {\mu }_5+{\sigma }^2-\theta \sigma +\beta \theta -\eta \theta -{\mu }_3\theta ]\\ {\displaystyle \frac{\left( 2\alpha -1\right)t^{2\gamma }}{\Gamma \left( \gamma +1\right)\Gamma \left( 2\gamma +1\right)}}] \\ \overline{U_2}\left(t, \alpha \right)=-[[d^2+2d{\mu }_5+2d\sigma -\theta d+{\mu }_5^2+2{\mu }_5\sigma -\theta {\mu }_5+{\sigma }^2-\theta \sigma +\beta \theta -\eta \theta -{\mu }_3\theta ]\\ {\displaystyle \frac{\left( 2\alpha -1\right)t^{2\gamma }}{\Gamma \left( \gamma +1\right)\Gamma \left( 2\gamma +1\right)}}]\\ \end{array}\right.$$

(24)

$$\left\{\begin{array}{c}{\underset{\_}{U_i}}_n \left(t, \alpha \right)=2\alpha -1\left[+\left(2\alpha -1\right)\left( d+{\mu }_5+\sigma -\theta \right)\right]{\displaystyle \frac{t^{\gamma }}{\Gamma \left( \gamma +1\right)}}+\\ \left[\right[d^2+2d{\mu }_5+2d\sigma -\theta d+{\mu }_5^2+2{\mu }_5\sigma -\theta {\mu }_5+{\sigma }^2-\theta \sigma +\beta \theta -\eta \theta -{\mu }_3\theta )]{\displaystyle \frac{\left( 2\alpha -1\right)t^{2\gamma }}{\Gamma \left( \gamma +1\right)\Gamma \left( 2\gamma +1\right)}}]\\ \overline{{U_i}_n}\left(t, \alpha \right)=1-2\alpha -\left[\left(2\alpha -1\right)\left( d+{\mu }_5+\sigma -\theta \right)\right]{\displaystyle \frac{t^{\gamma }}{\Gamma \left( \gamma +1\right)}}\\ -\left[\right[d^2+2d{\mu }_5+2d\sigma -\theta d+{\mu }_5^2+2{\mu }_5\sigma -\theta {\mu }_5+{\sigma }^2-\theta \sigma +\beta \theta -\eta \theta -{\mu }_3\theta )]{\displaystyle \frac{\left( 2\alpha -1\right)t^{2\gamma }}{\Gamma \left( \gamma +1\right)\Gamma \left( 2\gamma +1\right)}}]\\ \end{array}\right.$$

(25)

(f) 

Hospitalization Population Cases

$$\left\{\begin{array}{c}{\underset{\_}{H}}_0 (t, \alpha )=2\alpha -1\\ \overline{H_0}(t, \alpha )=1-2\alpha \end{array}\right.$$

(26)

$$\left\{\begin{array}{c}{\underset{\_}{H}}_1 \left(t, \alpha \right)=(2\alpha -1)-\left(2\alpha -1\right)\left(d+\delta -g+{\mu }_6\right){\displaystyle \frac{t^{\gamma }}{\Gamma \left( \gamma +1\right)}}+\\ \left(2\alpha -1\right){\left(d+\delta -g+{\mu }_6\right)}^2{\displaystyle \frac{t^{2\gamma }}{\Gamma {\left( \gamma +1\right)}^2\Gamma \left(2 \gamma +1\right)}} \\ \\ \overline{H_1}\left(t, \alpha \right)=\left(2\alpha -1\right)-\left(2\alpha -1\right)\left(d+\delta -g+{\mu }_6\right){\displaystyle \frac{t^{\gamma }}{\Gamma \left( \gamma +1\right)}}+\\ \left(1-2\alpha \right){\left(d+\delta -g+{\mu }_6\right)}^2{\displaystyle \frac{t^{2\gamma }}{\Gamma {\left( \gamma +1\right)}^2\Gamma \left(2 \gamma +1\right)}}\end{array}\right.$$

(27)

$$\left\{\begin{array}{c}{\underset{\_}{H}}_2 \left(t, \alpha \right)=\left[\left(2\alpha -1\right){\left(d+\delta -g+{\mu }_6\right)}^2\right]{\displaystyle \frac{t^{2\gamma }}{\Gamma {\left( \gamma +1\right)}^2\Gamma \left(2 \gamma +1\right)}}\\ \overline{H_2}\left(t, \alpha \right)=-\left[\left(2\alpha -1\right){\left(d+\delta -g+{\mu }_6\right)}^2\right]{\displaystyle \frac{t^{2\gamma }}{\Gamma {\left( \gamma +1\right)}^2\Gamma \left(2 \gamma +1\right)}}\end{array}\right.$$

(28)

$$\left\{\begin{array}{c}{\underset{\_}{H}}_n \left(t, \alpha \right)=2\alpha -1+[\left(2\alpha -1\right)-\left(2\alpha -1\right)\left(d+\delta -g+{\mu }_6\right)]{\displaystyle \frac{t^{\gamma }}{\Gamma \left( \gamma +1\right)}}+\\ \left(2\alpha -1\right){\left(d+\delta -g+{\mu }_6\right)}^2{\displaystyle \frac{t^{2\gamma }}{\Gamma {\left( \gamma +1\right)}^2\Gamma \left(2 \gamma +1\right)}}+\left[\left(2\alpha -1\right){\left(d+\delta -g+{\mu }_6\right)}^2\right]{\displaystyle \frac{t^{2\gamma }}{\Gamma {\left( \gamma +1\right)}^2\Gamma \left(2 \gamma +1\right)}}\\ \\ \overline{H_n}\left(t, \alpha \right)=1-2\alpha +\left[\left(2\alpha -1\right)-\left(2\alpha -1\right)\left(d+\delta -g+{\mu }_6\right)\right]{\displaystyle \frac{t^{\gamma }}{\Gamma \left( \gamma +1\right)}}+\\ \left(1-2\alpha \right){\left(d+\delta -g+{\mu }_6\right)}^2{\displaystyle \frac{t^{2\gamma }}{\Gamma {\left( \gamma +1\right)}^2\Gamma \left(2 \gamma +1\right)}}-\left[\left(2\alpha -1\right){\left(d+\delta -g+{\mu }_6\right)}^2\right]{\displaystyle \frac{t^{2\gamma }}{\Gamma {\left( \gamma +1\right)}^2\Gamma \left(2 \gamma +1\right)}}\end{array}\right.$$

(29)

(g) 

Recovered Population Cases:

$$\left\{\begin{array}{c}{\underset{\_}{R}}_0 (t, \alpha )=2\alpha -1\\ \overline{R_0}(t, \alpha )=1-2\alpha \end{array}\right.$$

(30)

$$\left\{\begin{array}{c}{\underset{\_}{R}}_1 \left(t, \alpha \right)=\left(2\alpha -1\right)\left(\delta +ϵ-{\mu }_7+\sigma \right){\displaystyle \frac{t^{\gamma }}{\Gamma \left( \gamma +1\right)}} \\ \overline{R_1}\left(t, \alpha \right)=-\left[\left(2\alpha -1\right)\left(\delta +ϵ-{\mu }_7+\sigma \right)\right]{\displaystyle \frac{t^{\gamma }}{\Gamma \left( \gamma +1\right)}}\end{array}\right.$$

(31)

$$\left\{\begin{array}{c}{\underset{\_}{R}}_n \left(t, \alpha \right)=2\alpha -1+(2\alpha -1) (\delta +ϵ-{\mu }_7+\sigma ){\displaystyle \frac{t^{\gamma }}{\Gamma \left( \gamma +1\right)}} \\ \overline{R_n}\left(t, \alpha \right)=1-2\alpha -[(2\alpha -1) (\delta +ϵ-{\mu }_7+\sigma )]{\displaystyle \frac{t^{\gamma }}{\Gamma \left( \gamma +1\right)}}\end{array}\right.$$

(32)

4. Numerical Results and Discussion

We examine a tabular representation of the parameters associated with the model. The proposed Model (2) is analyzed with the initial conditions provided in Table 1, which presents a description of the parameters used in the $SEI{R}_i{U}_{i}HR$ model, which were modified to enhance clarity and accuracy and signify the initial values of the primary variables at the start of the simulation or analysis. The corresponding numerical values, which are used for both numerical analysis and graphical representations, are provided in

Table 2. Parameter values used for $SEI{R}_i{U}_{i}HR$ model simulations.

Notation	Parameter Description	Numerical Value
$\lambda$	Expectable	0.1
S	Initial value of susceptible	0.22
E	Initial value of exposed	0.1
I	Initial value of infected	0.015
$R_i$	Initial value of reported	0.05
$U_i$	Initial value of unreported	0.1
H	Initial value of hospitalized	0.3
R	Initial value of recovered	0.2
${\mu }_1$	Mortality rate in suspected cases	0.05
${\mu }_2$	Mortality rate in exposed cases	0.03
${\mu }_3$	Mortality rate in infection cases	0.02
${\mu }_4,$	Mortality rate in reported cases	0.05
${\mu }_5$	Mortality rate in unreported cases	0.02
${\mu }_6$	Mortality rate in hospitalized cases	0.05
${\mu }_7$	Mortality rate in recovered cases	0.02
$a$	Exposed rate	0.1
$\beta$	Infected rate	0.02
$\theta$	Unreported rate	0.03
$\eta$	Reported rate	0.01
$\gamma$	Hospitalization	0.035
$\epsilon$	Recover rate	0.03
$\delta$	Unreported to recover rate	0.02

: Parameter values used for $SEI{R}_i{U}_{i}HR$ model simulations. These values form the basis for examining the system dynamics and evaluating the model outcomes.

• Graphical Interpretation of Normal Solution and Fuzzy Bound Solutions: The graphical interpretation highlights the behavior of the fuzzy lower and upper bound solutions in relation to the normal solution, offering deeper insight into the uncertainty of disease transmission and progression across all compartments. Although the same methodological framework is applied throughout, the results are presented compartment-wise for clarity, with distinct figure numbers assigned to each case.

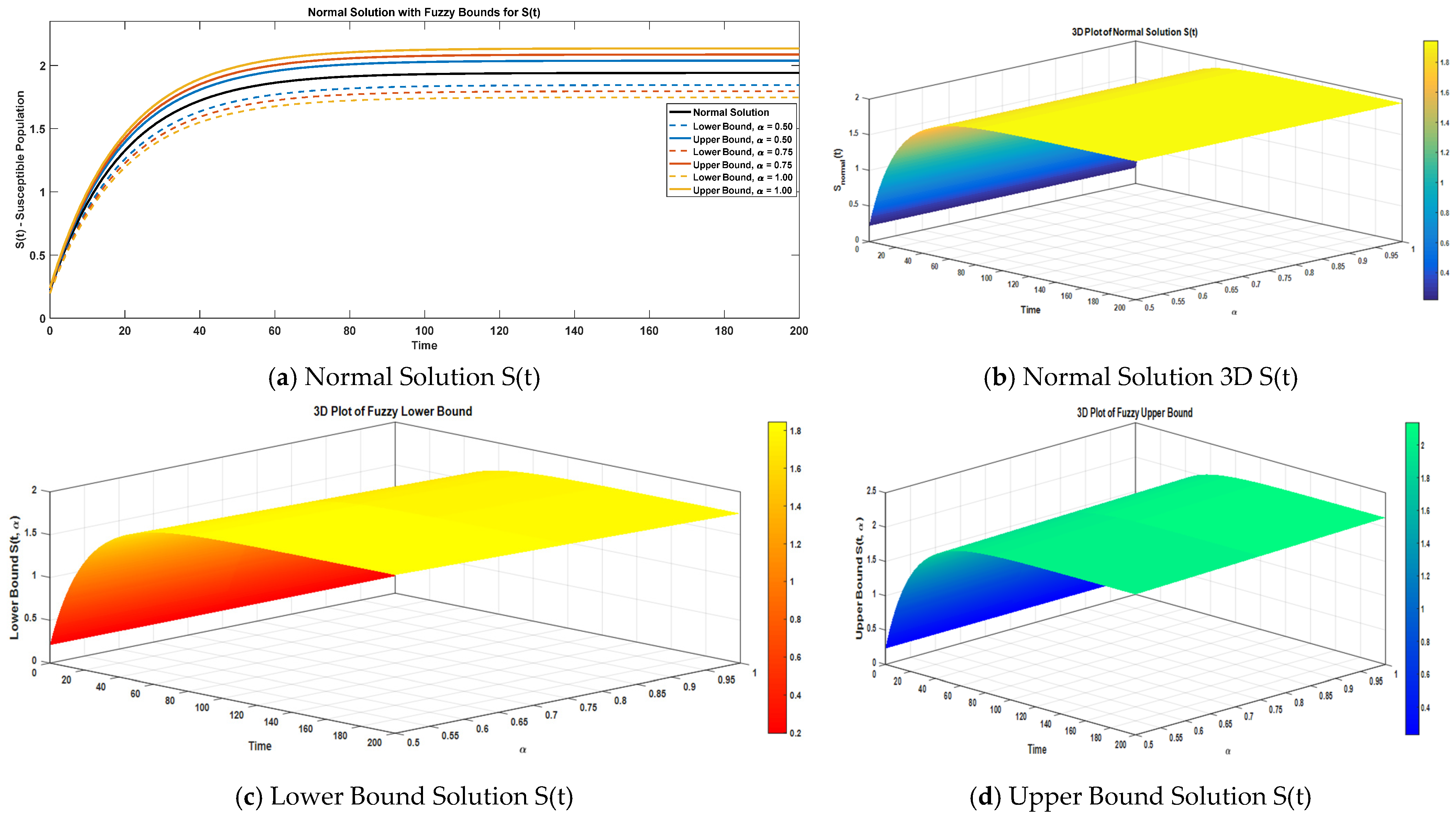
Figure 2a illustrates a two-dimensional plot of the susceptible compartment case under the normal solution. It also presents the variation in fuzzy lower and upper bound solutions corresponding to uncertainty levels α = 0.50, 0.75, and 0.1. Figure 2b, 2c, and 2d, respectively, display the three-dimensional surface plots of the normal solution, fuzzy lower bound solution, and fuzzy upper bound solution for the susceptible compartment. A detailed comparative analysis is carried out between the approximate normal solution and the fuzzy lower and upper bound solutions for the susceptible compartment, based on three-term series expansions under varying fractional orders. This comparison spans the uncertainty domain α ∈ [0, 1], emphasizing the impact of fractional dynamics and fuzzy uncertainty on the evolution of susceptible cases.

The numerical representation of the susceptible compartment is presented in

Table 3. Numerical representation of susceptible cases of normal, lower, and upper solutions with various values of α.

Time (t)	[Normal, Lower, Upper] α = 0.50 Solution	[Normal, Lower, Upper] α = 0.75 Solution	[Normal, Lower, Upper] α = 1 Solution
0	[0.2200, 0.2090, 0.2310]	[0.2200, 0.2035, 0.2365]	[0.2200, 0.1980, 0.2420]
50	[1.8106, 1.7200, 1.9011]	[1.8106, 1.6748, 1.9464]	[1.8106, 1.6295,1.9916]
100	[1.9318, 1.8352, 2.0284]	[1.9318, 1.7869, 2.0766]	[1.9318, 1.7386, 2.1249]
150	[1.9318, 1.8352, 2.0284]	[1.9318, 1.7869,2.0766]	[1.9318, 1.7386, 2.1249]
200	[1.9318, 1.8352, 2.0284]	[1.9318, 1.7869, 2.0766]	[1.9318, 1.7386, 2.1249]

, showing the normal, lower, and upper fuzzy solutions across fractional times t $\in$ {0, 50, 100, 150, 200} at different α levels. A key observation is that although the susceptible population eventually stabilizes around 1.93, the fuzzy bounds systematically widen with increasing α, signifying a corresponding increase in the model’s inherent uncertainty (fuzziness).

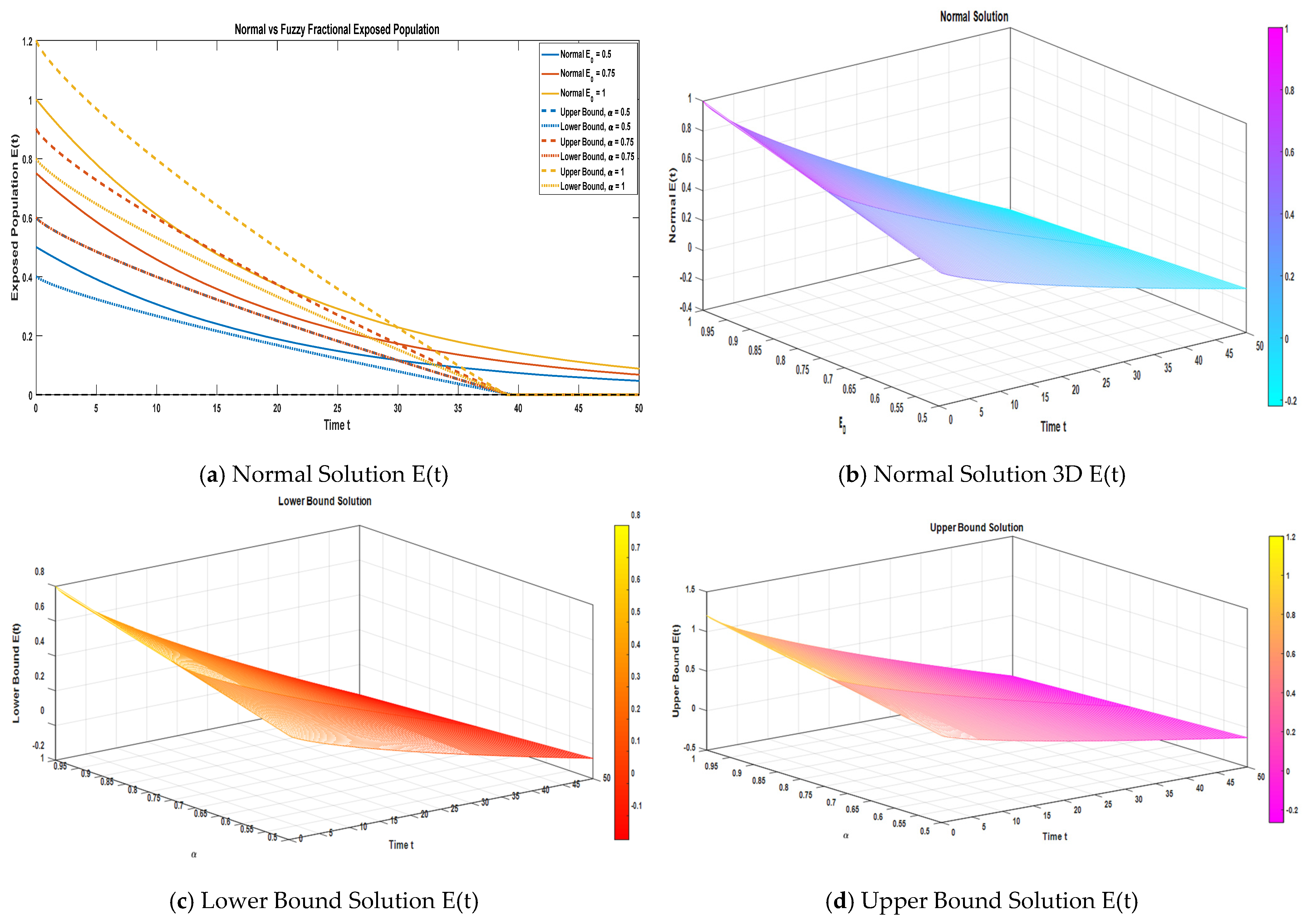
Figure 3a illustrates a two-dimensional plot of the exposed compartment under the normal solution. In addition, it highlights the variations in the fuzzy lower and upper bound solutions corresponding to uncertainty levels α = 0.50, 0.75, and 1. Figure 3b, 3c, and 3d, respectively, present the three-dimensional surface plots of the normal solution, the fuzzy lower bound solution, and the fuzzy upper bound solution for the exposed compartment. A comprehensive comparative analysis is performed between the approximate normal solution and the fuzzy lower and upper bound solutions for the exposed compartment, utilizing three-term series expansions under different fractional orders. This analysis, carried out across the uncertainty domain α ∈ [0, 1], underscores how fractional dynamics and fuzzy uncertainty jointly influence the temporal evolution of the exposed population.

The dynamics of the exposed compartment (E) are numerically represented in

Table 4. Numerical representation of exposed cases of normal, lower, and upper solutions with various values of α.

Time (t)	[Normal, Lower, Upper] α = 0.50 Solution	[Normal, Lower, Upper] α = 0.75 Solution	[Normal, Lower, Upper] α = 1 Solution
10	[0.3315, 0.2657, 0.3974]	[0.4962, 0.3974, 0.5949]	[0.6608, 0.5291, 0.7925]
20	[0.2067, 0.1661, 0.2472]	[0.3080, 0.2472, 0.3689]	[0.4094, 0.3283, 0.4905]
30	[0.0997, 0.0808, 0.1186]	[0.1469, 0.1186, 0.1752]	[0.1940, 0.1563, 0.2318]

, which compares the normal, lower, and upper fuzzy solutions under varying uncertainty levels (α) and fractional orders. The data clearly show a sharp temporal decline in the exposed population, which approaches negligible values within the first t = 30 time units. A critical observation regarding the uncertainty analysis is that the interval between the fuzzy bounds widens proportionally to the increase in α, signifying that the highest uncertainty is associated with the highest degree of fuzziness. The fact that the normal solution is successfully enclosed within these bounds validates the model’s robustness and its ability to incorporate and quantify uncertainty.

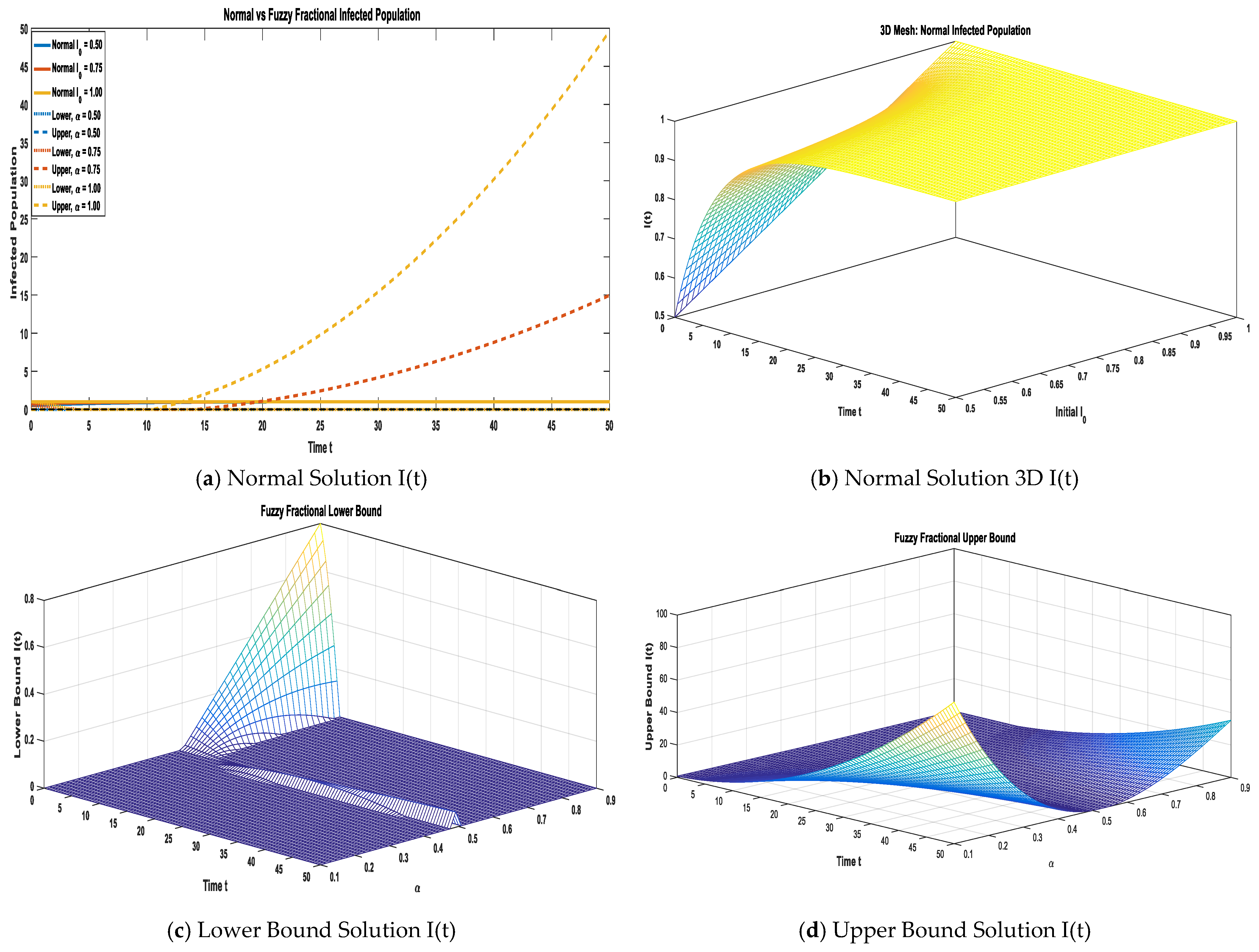
The dynamics of the infected compartment are illustrated in Figure 4a. Specifically, Figure 4a provides a 2D comparison of the normal solution with the fuzzy lower and upper bounds (α = 0.50, 0.75, 1.00), while Figure 4b–d offer complementary 3D surface plots for each solution type. This analysis contrasts the approximate normal solution against the fuzzy bounds under varying fractional orders over α ∈ [0, 1], demonstrating their combined effect on forecasting the infected population. We make a comparison of the approximate normal solution and fuzzy lower and upper bound solutions for the infected compartment for three terms at the given uncertainty values α ∈ [0, 1] against various fractional orders.

Table 5. Numerical representation of infected cases of normal, lower, and upper solutions with various values of α.

Time (t)	[Normal, Lower, Upper] α = 0.50 Solution	[Normal, Lower, Upper] α = 0.75 Solution	[Normal, Lower, Upper] α = 1 Solution
10	[0.3315, 0.2657, 0.3974]	[0.4962, 0.3974, 0.5949]	[0.6608, 0.5291, 0.7925]
20	[0.2067, 0.1661, 0.2472]	[0.3080, 0.2472, 0.3689]	[0.4094, 0.3283, 0.4905]
30	[0.0997, 0.0808, 0.1186]	[0.1469, 0.1186, 0.1752]	[0.1940, 0.1563, 0.2318]

presents a comparison of the approximate normal solution, fuzzy lower bound, and fuzzy upper bound for the infected compartment (I) under varying uncertainty values (α $\in$ [0, 1]). The results show that the infected population initially exhibits moderate values but undergoes a rapid temporal decline across all α-levels, reflecting the diminishing spread of the infection in the model. The analysis of uncertainty reveals a clear trend: at α = 0.50, the fuzzy bounds are the tightest and closely track the normal solution, indicating minimal uncertainty. Conversely, as the α value increases (to 0.75 and 1.00), the bounds widen, effectively capturing the greater uncertainty in the infection dynamics. Crucially, the normal solution consistently lies symmetrically within the lower and upper bounds. This suggests that while the infection spread diminishes consistently over time, the degree of uncertainty in the predicted infected population is highly sensitive to the fuzziness parameter (α).

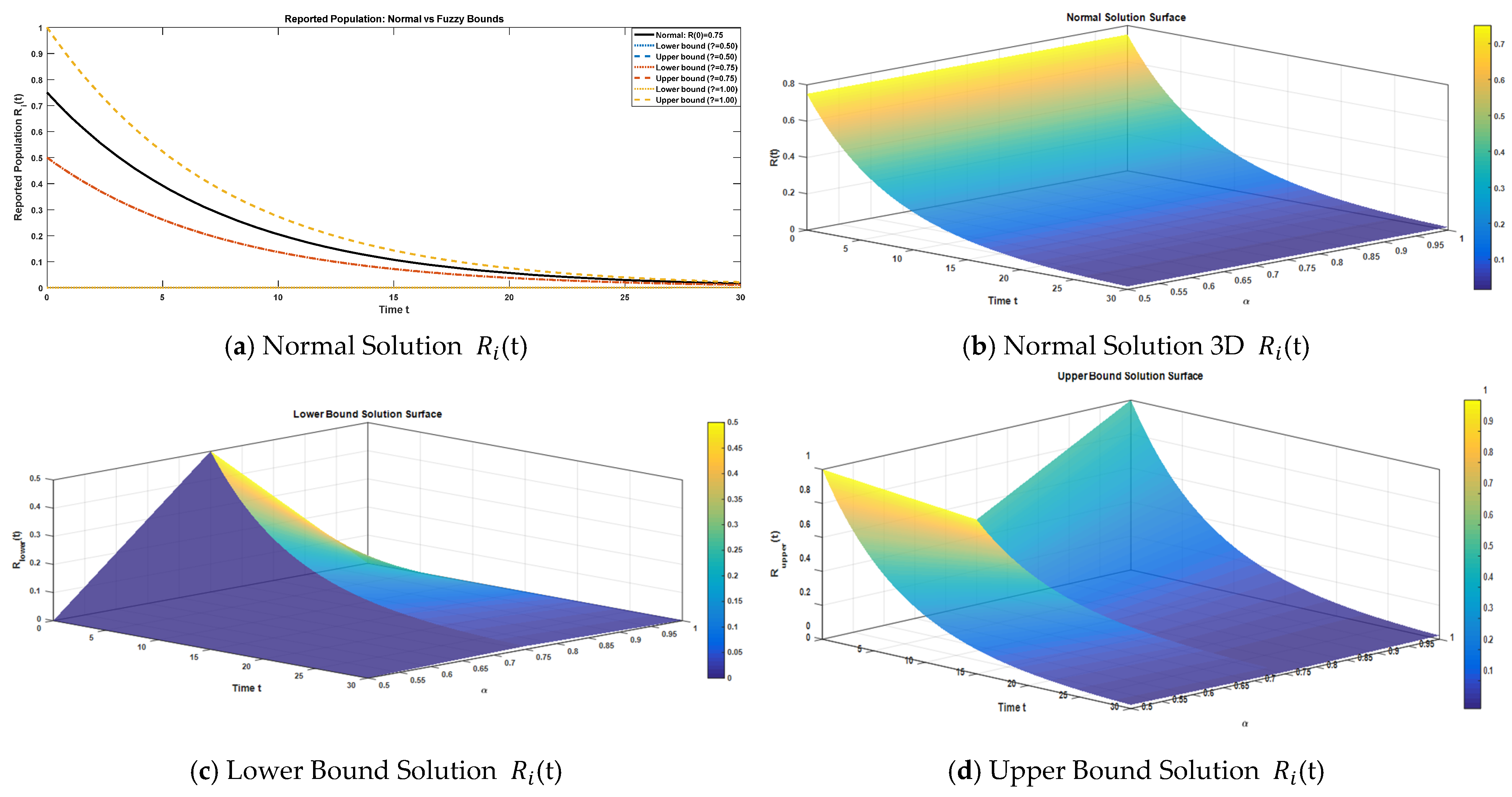
Figure 5a displays a two-dimensional graph for the reported case compartment under the normal and fuzzy bounded solutions (α = 0.50, 0.75, 1.00). The corresponding three-dimensional surfaces for the normal, lower, and upper bound solutions are shown in Figure 5b–d. The system’s response to uncertainty and fractional order was evaluated by comparing these three-term solutions across α ∈ [0, 1], quantifying the sensitivity of reported cases to these parameters. We make a comparison of the approximate normal solution and fuzzy lower and upper bound solutions for the reported compartment for three terms at the given uncertainty values α ∈ [0, 1] against various fractional orders.

The dynamics of the reported compartment ($R_i$) are detailed in

Table 6. Numerical representation of reported cases of normal, lower, and upper solutions with various values of α.

Time (t)	[Normal, Lower, Upper] α = 0.50 Solution	[Normal, Lower, Upper] α = 0.75 Solution	[Normal, Lower, Upper] α = 1 Solution
10	[0.2066, 0.0008, 0.2752]	[0.2066, 0.1380, 0.1380]	[0.2066, 0.0008, 0.2752]
20	[0.0564, 0.0011, 0.0749]	[0.0564, 0.0380, 0.0380]]	[0.0564, 0.0011, 0.0749]
30	[0.0163, 0.0011, 0.0214]	[0.0163, 0.0113, 0.0113]	[0.0163, 0.0011, 0.0214]

, comparing the normal, lower, and upper fuzzy solutions across various α-values. The reported population shows a rapid and consistent decline over time, with values becoming minimal by t = 30. The uncertainty analysis demonstrates that the tightest fuzzy bounds occur at α = 0.75, where the lower and upper solutions converge, signifying a point of minimal uncertainty and high predictive stability for the reported cases. For α = 0.50 and α = 1.00, the bounds are wider, capturing a larger spread of uncertainty. This suggests that the uncertainty inherent in the reported population is highly dependent on the specific degree of fuzziness (α), but the overall normal trajectory remains robustly captured within the fuzzy bounds.

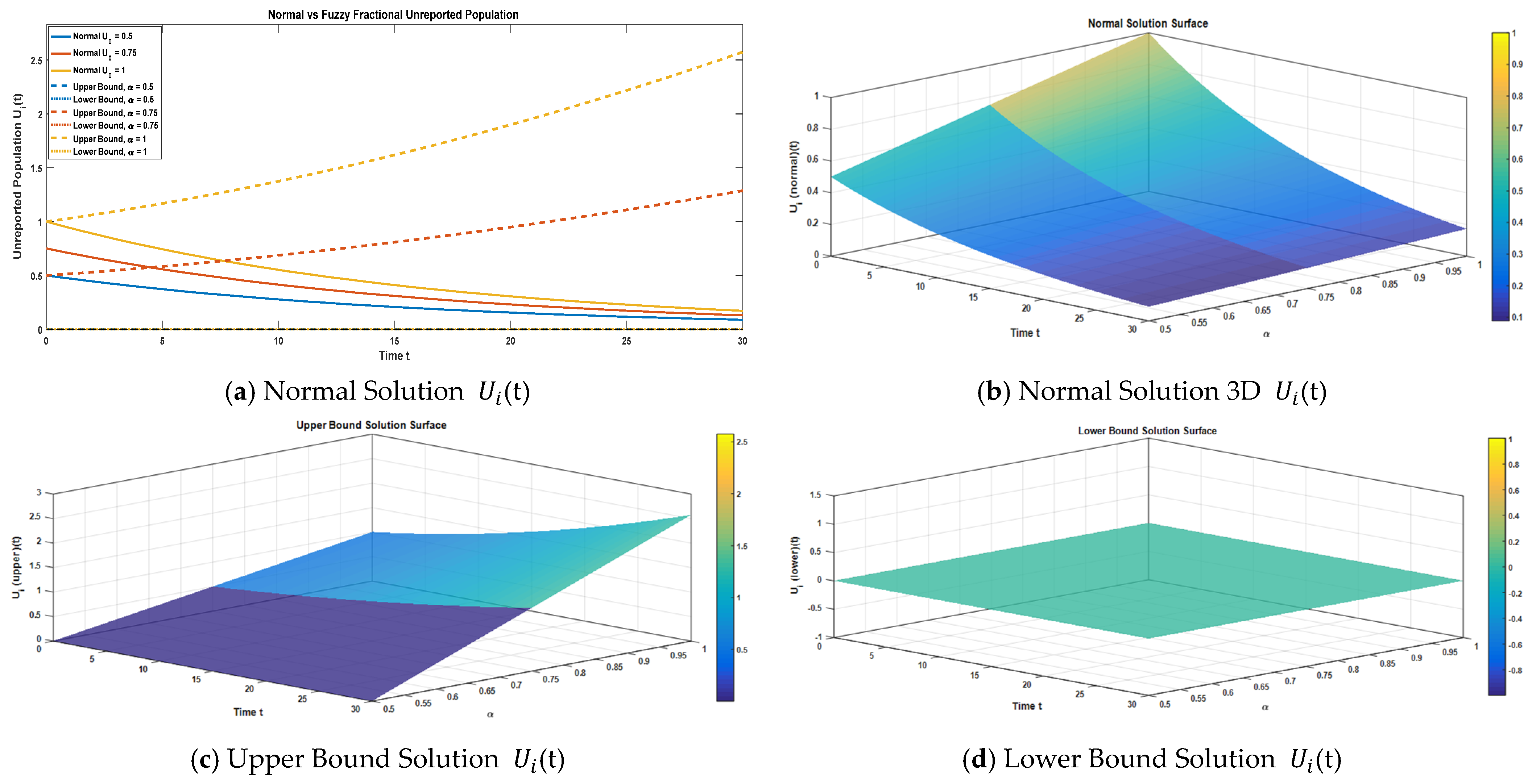
Figure 6a displays a two-dimensional representation of the unreported compartment under the normal solution, along with the fuzzy lower and upper bound solutions for α = 0.50, 0.75, and 1. Figure 6b–d show the three-dimensional surface plots corresponding to the normal solution, fuzzy lower bound solution, and fuzzy upper bound solution. Comparative analysis using three-term series expansions under different fractional orders reveals the significance of fractional dynamics and fuzzy uncertainty in terms of the dynamics of unreported cases within α ∈ [0, 1].

We make a comparison of the approximate normal solution and fuzzy lower and upper bound solutions for the unreported compartment for three terms at the given uncertainty values α ∈ [0, 1] against various fractional orders.

Table 7. Numerical representation of unreported cases of normal, lower, and upper solutions with various values of α.

Time (t)	[Normal, Lower, Upper] α = 0.50 Solution	[Normal, Lower, Upper] α = 0.75 Solution	[Normal, Lower, Upper] α = 1 Solution
10	[0.2066, 0.0008, 0.2752]	[0.2066, 0.1380, 0.1380]	[0.2066, 0.0008, 0.2752]
20	[0.0564, 0.0011, 0.0749]	[0.0564, 0.0380, 0.0380]	[0.0564, 0.0011, 0.0749]
30	[0.0163, 0.0011, 0.0214]	[0.0163, 0.0113, 0.0113]	[0.0163, 0.0011, 0.0214]

presents a comparison of the approximate normal solution, fuzzy lower bound, and fuzzy upper bound for the unreported compartment ($U_i$) under various uncertainty values (α $\in$ [0, 1]). The numerical results demonstrate a sharp temporal decline in the unreported population across all α-levels, with values approaching near zero by t = 30. This indicates that, considering the model parameters, the initial pool of unreported cases quickly dissipates. An analysis of the fuzzy bounds reveals a highly sensitive and non-monotonic uncertainty profile. At the extreme fuzziness levels of α = 0.50 and α = 1.00, the bounds are wider, reflecting a larger interval of uncertainty. However, at the intermediate value of α = 0.75, the fuzzy bounds significantly narrow and converge, often resulting in the lower and upper solutions being identical (e.g., at t = 10, [0.2066, 0.1380, 0.1380]). This behavior suggests that a specific combination of parameters and initial conditions at α = 0.75 leads to minimal uncertainty and a high degree of confidence in the predicted trajectory of the unreported cases. Overall, the results confirm that the unreported compartment diminishes rapidly, and the fuzzy framework effectively captures the compartment’s sensitivity to the degree of fuzziness (α) in the system.

Figure 7a illustrates a two-dimensional plot of the hospitalized compartment under the normal solution, together with fuzzy lower and upper bound variations for α = 0.50, 0.75, and 1. Figure 7b–d display the respective three-dimensional plots of the normal solution, fuzzy lower bound solution, and fuzzy upper bound solution. A comparative evaluation, based on three-term series expansions across different fractional orders, demonstrates how fractional dynamics and fuzzy uncertainty interact to influence hospitalized case trajectories within the uncertainty interval α ∈ [0, 1].

We make a comparison of the approximate normal solution and fuzzy lower and upper bound solutions for the hospitalized compartment for three terms at the given uncertainty values α ∈ [0, 1] against various fractional orders.

Table 8. Numerical representation of hospitalized cases of normal, lower, and upper solutions with various values of α.

Time (t)	[Normal, Lower, Upper] α = 0.50 Solution	[Normal, Lower, Upper] α = 0.75 Solution	[Normal, Lower, Upper] α = 1 Solution
10	[0.3686, 0.5157, 0.5784]	[0.3686, 0.0768, 1.0172]	[0.3686, 0.0000, 1.4561]
20	[0.2172, 0.3337, 0.4576,]	[0.2172, 0.0000, 1.3243]	[0.2172, 0.0000, 2.1911]

presents a comparison of the approximate normal solution, fuzzy lower bound, and fuzzy upper bound for the hospitalized compartment (H) under varying uncertainty values (α $\in$ [0, 1]). The data confirms that the hospitalized population declines consistently over time across all α-levels. However, in stark contrast to the other compartments, the fuzzy bounds exhibit a dramatically wider spread, particularly as the fuzziness parameter α increases (e.g., the upper bound at α = 1.00 is notably large). This phenomenon points to a significantly greater inherent uncertainty in the predicted hospitalization dynamics. The wide bounding interval suggests that the hospitalization parameter (γ) is highly sensitive to parameter uncertainty, making the precise peak and decline in hospitalized cases the most variable prediction in the model. Nevertheless, the normal solution remains successfully contained within the lower and upper bounds for all cases, confirming the overall stability of the fuzzy framework despite the high variability in predicted outcomes.

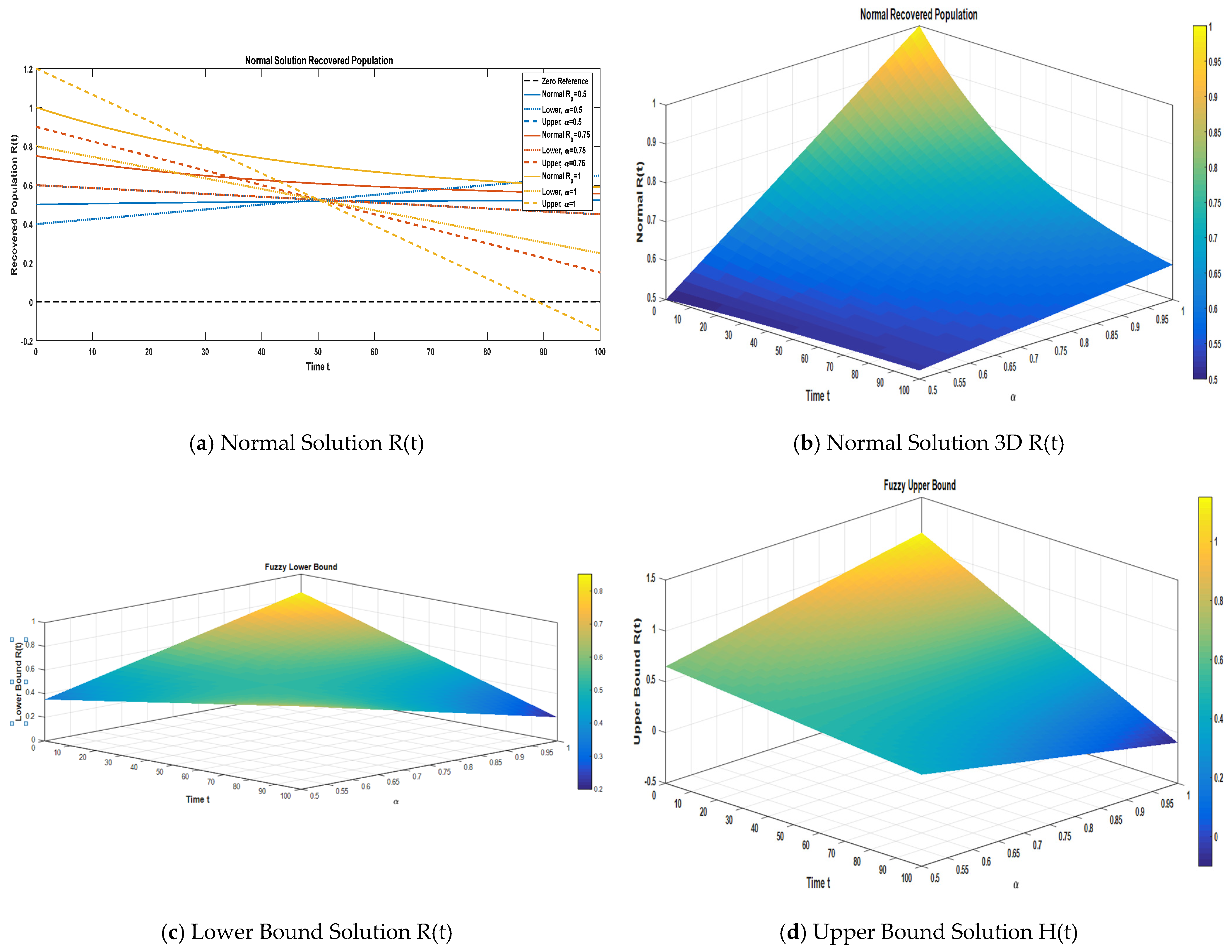
Figure 8a provides a two-dimensional plot of the recovered compartment under the normal solution, in addition to the fuzzy lower and upper bound solutions for α = 0.50, 0.75, and 1. Figure 8b–d present the three-dimensional surface plots corresponding to the normal and fuzzy lower and fuzzy upper bound solutions. The comparative investigation, employing three-term series expansions under varying fractional orders, underscores the role of fractional dynamics and fuzzy uncertainty in governing the recovery trends within α ∈ [0, 1].

In the Figure 8a–d we make a comparison of the approximate normal solution and fuzzy lower and upper bound solutions for the recovered compartment for three terms at the given uncertainty values α ∈ [0, 1] against various fractional orders.

Table 9. Numerical representation of recover cases of normal, lower, and upper solutions with various values of α.

Time (t)	[Normal, Lower, Upper] α = 0.50 Solution	[Normal, Lower, Upper] α = 0.75 Solution	[Normal, Lower, Upper] α = 1 Solution
10	[0.5045, 0.4251, 0.5850]]	[0.7091, 0.5850, 0.8248]	[0.9137, 0.7449, 1.0647]
20	[0.5083, 0.4501, 0.5699]	[0.6757, 0.5699, 0.7497]	[0.8432, 0.6898, 0.9295]
30	[0.5113, 0.4752, 0.5549]	[0.6483, 0.5549, 0.6745]	[0.7854, 0.6347, 0.7942]

presents a comparison of the approximate normal solution, fuzzy lower bound, and fuzzy upper bound for the recovered compartment (R) under various uncertainty values (α $\in$ [0, 1]). The numerical results indicate that the recovered population remains relatively stable over the simulated time period (t = 10 to t = 30). Crucially, the fuzzy bounds widen significantly as the fuzziness parameter (α) increases, confirming that higher uncertainty in the input parameters directly translates to a larger spread in the predicted recovered cases (e.g., compare α = 0.50 to α = 1.00). Conversely, the spread between the bounds narrows as time progresses, suggesting that the uncertainty in the recovered compartment decreases over time. The normal solution consistently lies within the fuzzy boundaries, confirming that the recovered dynamics exhibit moderate sensitivity to parameter fuzziness but maintain a steady, robust trend across all considered α-levels.

5. Sensitivity Analysis of Fractional-Order SEIRi–UiHR Model

Sensitivity analysis plays a crucial role in understanding how model outcomes respond to variations in key parameters, particularly in complex epidemic systems governed by fractional-order dynamics. In the SEIRi–UiHR framework, the fractional order $\nu$ controls the strength of memory effects and non-local interactions, which are fundamental characteristics of real-world infectious disease transmission. By systematically varying $\nu$ and observing its influence on all epidemiological compartments, we assess the robustness of the model and identify how fractional dynamics modify the intensity, timing, and shape of epidemic trajectories. This analysis provides deeper insight into the structural symmetry introduced by fractional calculus and highlights the importance of memory-driven processes in capturing realistic disease progression.

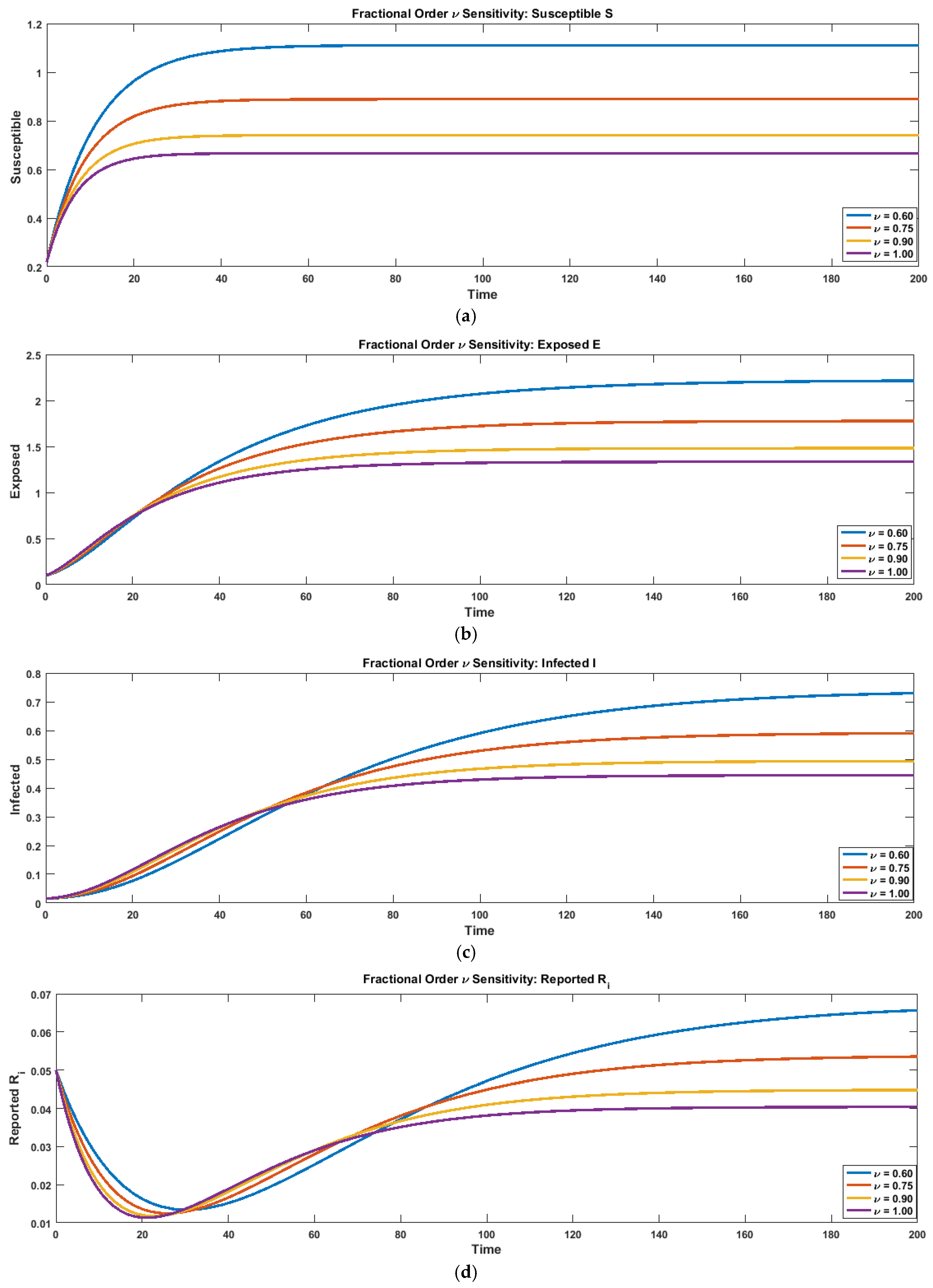
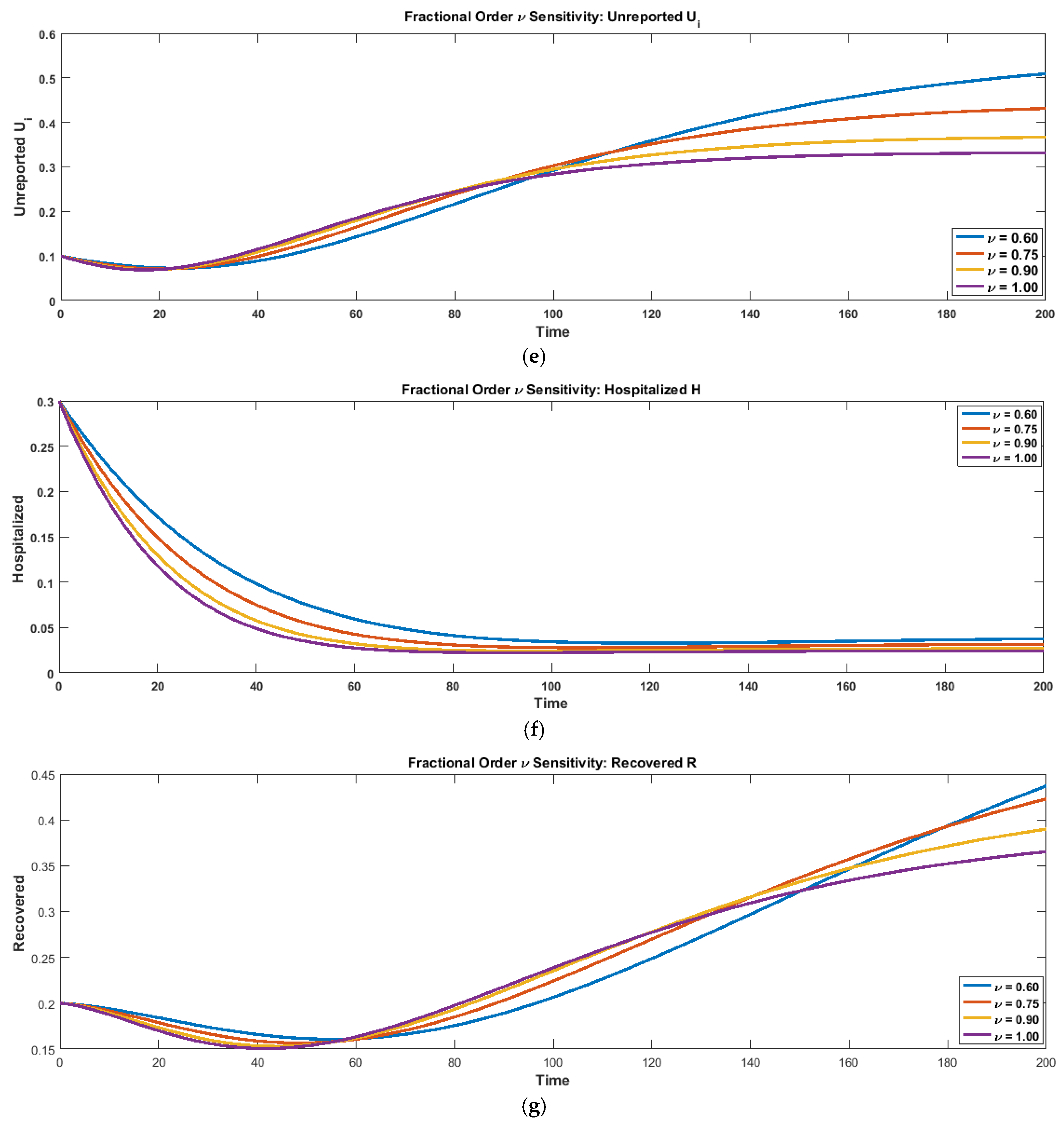
To examine the influence of memory effects, shown in Figure 9a–g, on epidemic dynamics, a fractional-order sensitivity analysis was performed for $\nu =\{0.60, 0.75, 0.90, 1.00\}$. The time-series plots generated for all seven compartments (S, E, I, Ri, Ui, H, R) demonstrate that the fractional order exerts a significant influence on the temporal evolution and peak behavior of the system. For lower values of $\nu$, the trajectories of all compartments become smoother and more delayed, reflecting the stronger non-local memory inherent in fractional operators. In particular, the susceptible and exposed curves decline more slowly for $\nu =0.60$, indicating a reduced rate of progression from susceptibility to exposure. Conversely, higher values of $\nu$ (approaching the classical case $\nu =1$) produce earlier and sharper peaks in the infected, reported, unreported, and hospitalized populations, revealing increased transmission intensity and faster epidemic escalation. This behavior confirms that fractional dynamics effectively modulate the speed and magnitude of disease spread. The numerical results are summarized in a grouped in Figure 9a–g comparing the peak values of S, E, I, Ri, Ui, H, and the final recovered population R across different fractional orders. The analysis reveals a clear trend: peak S and peak E decrease as $\nu$ increases, whereas the peaks of the infectious- and reporting-related states (I, Ri, Ui, H) rise consistently with larger $\nu$. Similarly, the final recovered population shows an increasing trend with higher $\nu$, consistent with faster transition dynamics in the classical model. Overall, the sensitivity analysis confirms that reducing the fractional order smoothens and suppresses outbreak peaks, while increasing $\nu$ amplifies epidemic intensity. These results highlight the crucial role of the fractional-order derivative in capturing memory-driven effects and illustrate how fractional modeling introduces structural symmetry in the temporal evolution of epidemic compartments.

The Figure 10 illustrates how the peak values of all epidemiological compartments, change as the fractional order $\nu$ varies. A lower fractional order ($e.g., \nu =0.6$) corresponds to stronger memory effects, causing slower transitions between compartments. This leads to higher peaks in exposed and infected populations, indicating delayed but intensified disease progression. As $\nu$ increases toward the classical integer-order case ($\nu =1$), memory effects weaken, and the system becomes more responsive. Consequently, the peak values of exposed, infected, reported, and hospitalized populations decrease, reflecting earlier and more controlled epidemic waves. The final size of the recovered population also stabilizes across higher $\nu$ values, showing reduced long-term disease burden. Overall, the bar plot confirms that the fractional parameter $\nu$ plays a significant role in shaping outbreak magnitude: lower $\mathit{\nu }$ amplifies epidemic peaks, whereas higher $\mathit{\nu }$ suppresses them, demonstrating the importance of memory dynamics in the SEIRi–UiHR system.

6. Conclusions

In this study, our main contribution was the establishment of the existence and uniqueness of solutions for the fuzzy fractional-order SEIRi–UiHR model describing COVID-19 transmission dynamics. By employing a systematic procedure that combines the fuzzy Laplace transform with the Adomian decomposition method, we derived approximate analytical solutions and demonstrated their convergence and effectiveness through comparative analyses between fuzzy and classical outcomes. Importantly, the model reveals both structural and graphical symmetry across compartments, particularly in the mirrored transitions between reported and unreported cases and in the recovery and hospitalization dynamics. These symmetrical patterns are preserved under fuzzy initial conditions and fractional-order operators, thereby enhancing the interpretability, robustness, and analytical tractability of the system. The fusion of fuzziness with fractional calculus provides a powerful framework for capturing the global dynamics of epidemic systems under uncertainty. Graphical simulations further confirm symmetry in solution trajectories, with consistent shapes and behaviors across compartments despite parameter fuzziness. This visual consistency supports the analysis of symmetry from a complex systems perspective and reinforces the model’s relevance to real-world infectious disease modeling. Looking ahead, future research may explore formal symmetry analysis using group-theoretic or Lie symmetry methods to characterize invariant properties and reduce model complexity. Extending the framework to incorporate spatial or network-based symmetry could also provide deeper insights into heterogeneous transmission patterns and intervention strategies. Overall, the integration of symmetry principles with fuzzy fractional calculus opens promising avenues for developing robust, interpretable, and scalable epidemic modeling frameworks.