Author Contributions
Conceptualization, B.O. and A.A.; Methodology, F.C.; software, N.D.; validation, B.E.; formal analysis, F.C., N.D. and A.A.; resources, A.A.; data curation, B.E.; writing—original draft, N.D.; writing—review and editing, F.C. and B.O.; supervision, B.O.; project administration, A.A.; funding acquisition, B.E. All authors have read and agreed to the published version of the manuscript.
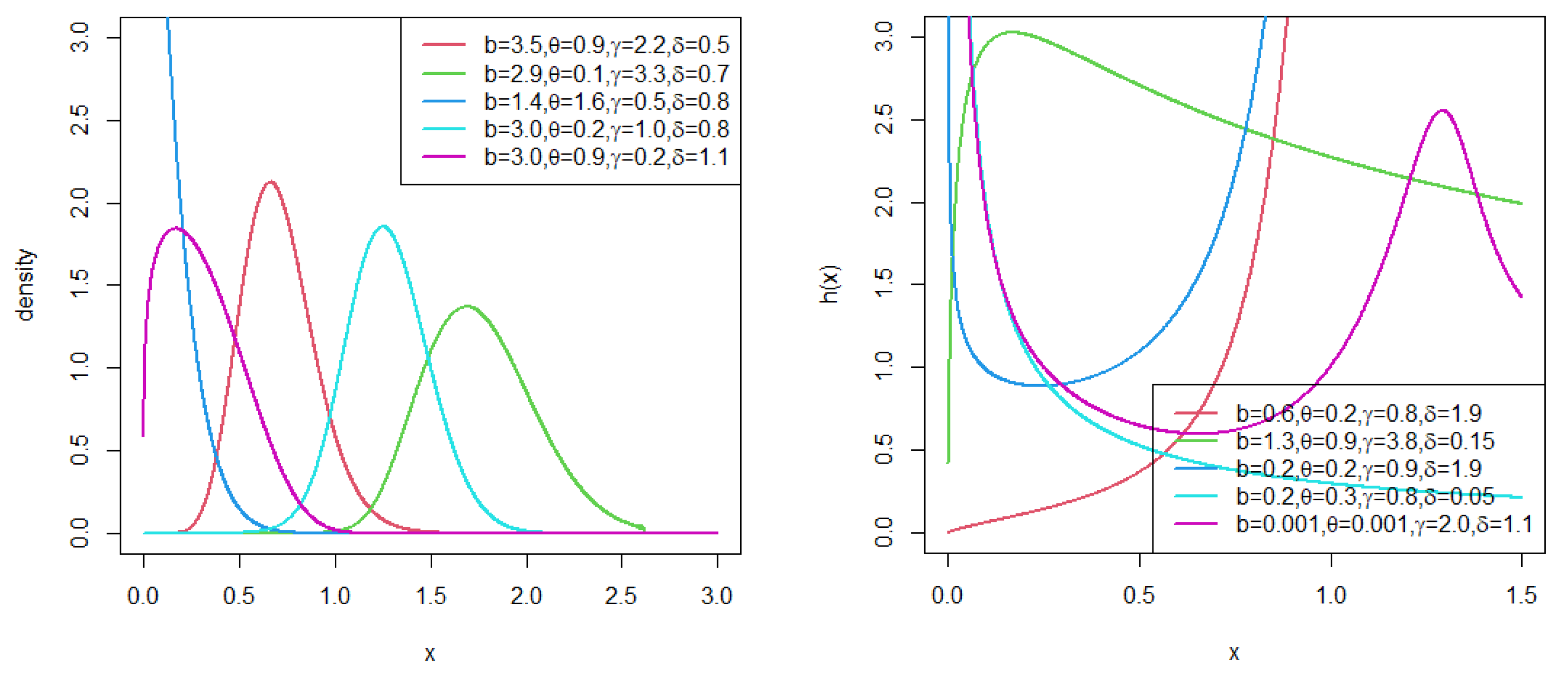
Figure 1.
PDF and HRF plots for TL-HT-OBX-LLoG distribution for selected parameter values.
Figure 1.
PDF and HRF plots for TL-HT-OBX-LLoG distribution for selected parameter values.
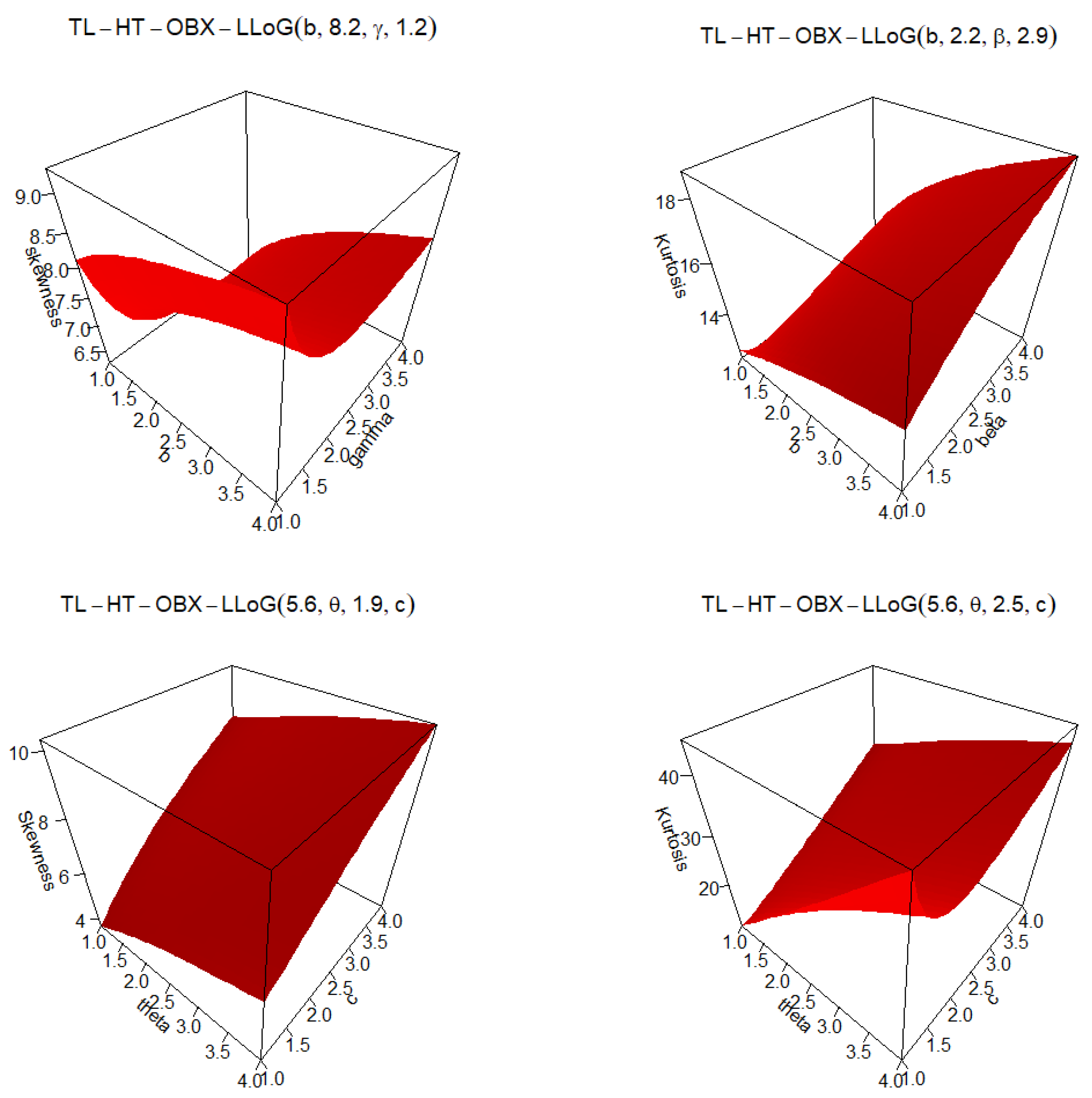
Figure 2.
SK and KT plots for TL-HT-OBX-LLoG distribution for selected parameter values.
Figure 2.
SK and KT plots for TL-HT-OBX-LLoG distribution for selected parameter values.
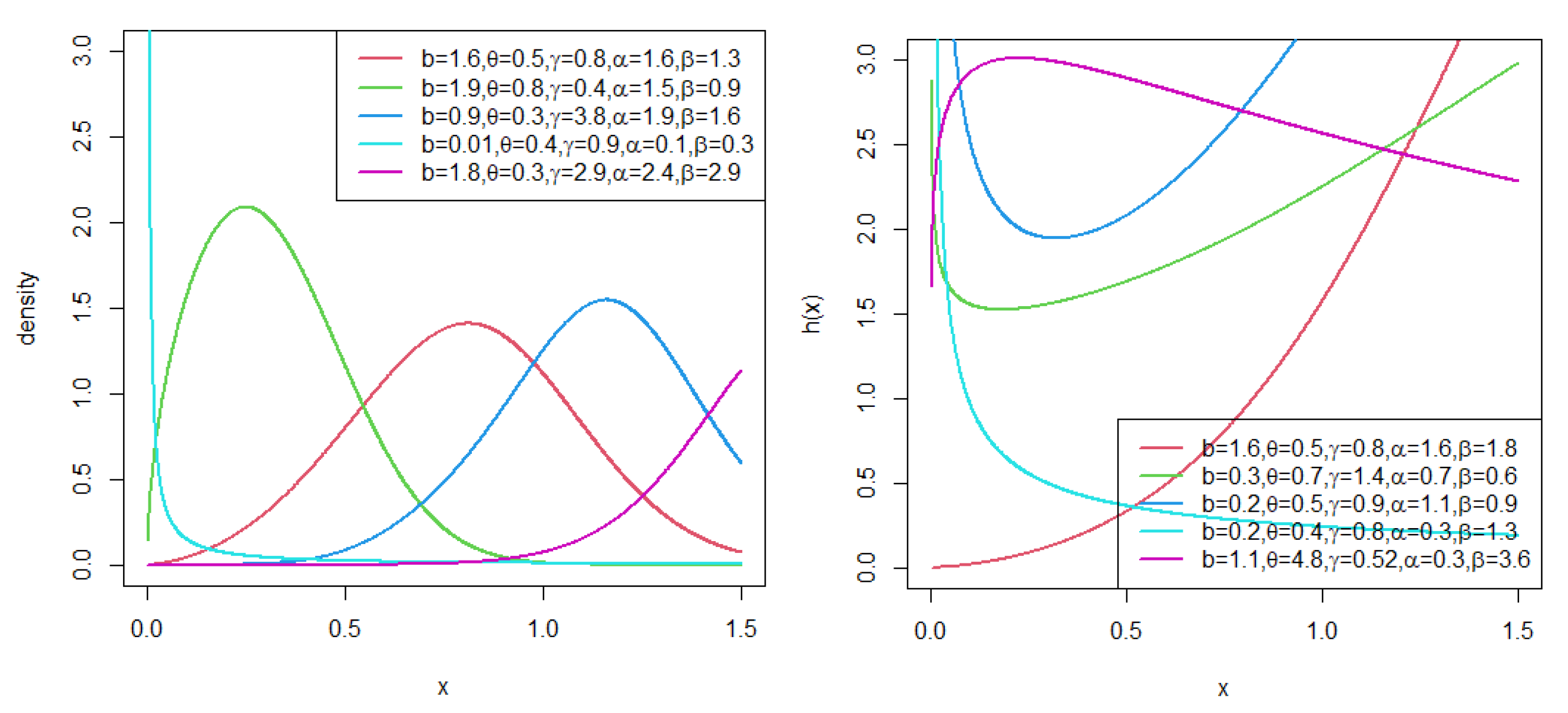
Figure 3.
PDF and HRF plots for TL-HT-OBX-W distribution for selected parameter values.
Figure 3.
PDF and HRF plots for TL-HT-OBX-W distribution for selected parameter values.
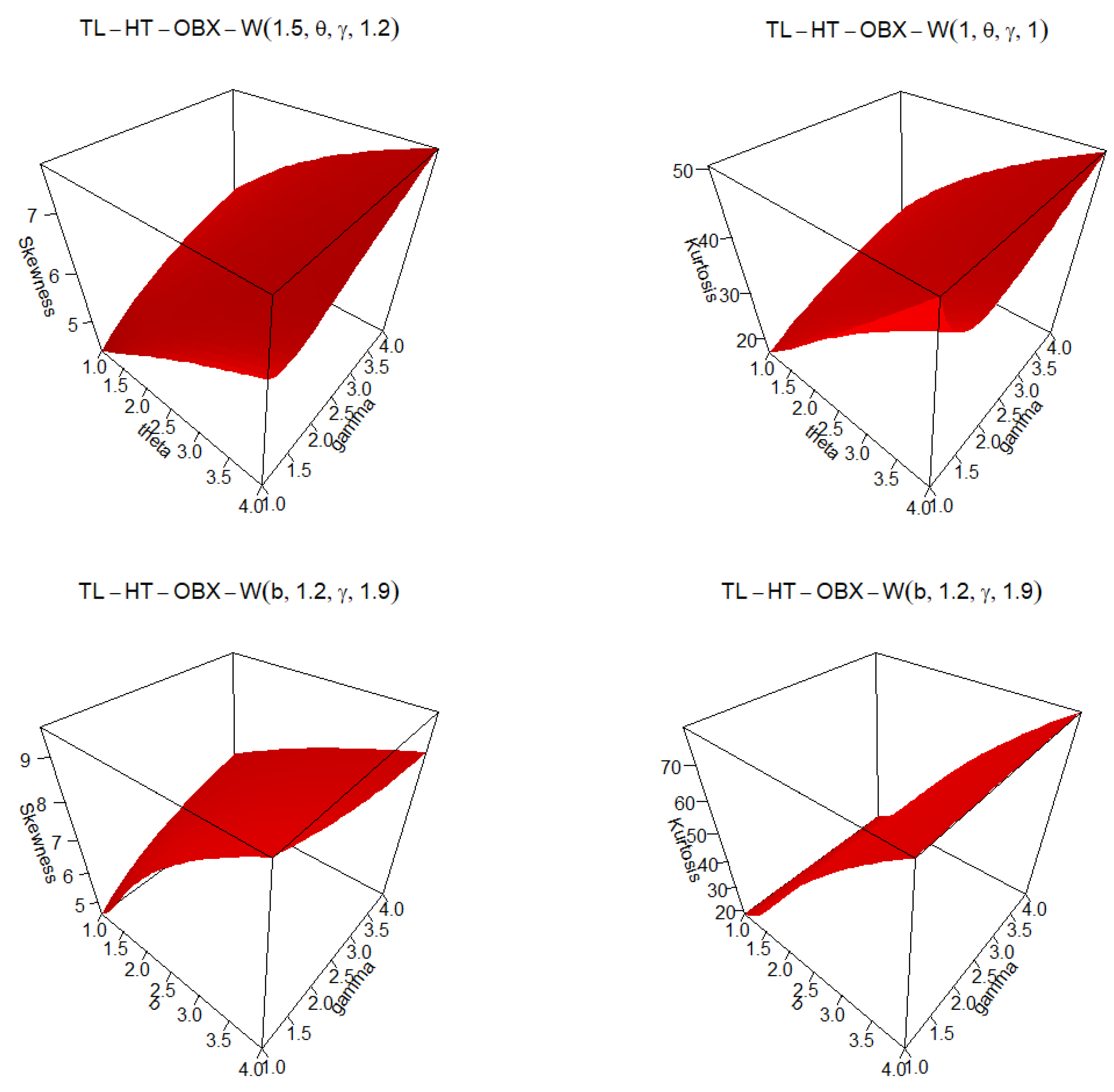
Figure 4.
SK and KT plots for TL-HT-OBX-W distribution for selected parameter values.
Figure 4.
SK and KT plots for TL-HT-OBX-W distribution for selected parameter values.
Figure 5.
Plots of the PDF and HRF for TL-HT-OBX-Lx distribution for selected parameter values.
Figure 5.
Plots of the PDF and HRF for TL-HT-OBX-Lx distribution for selected parameter values.
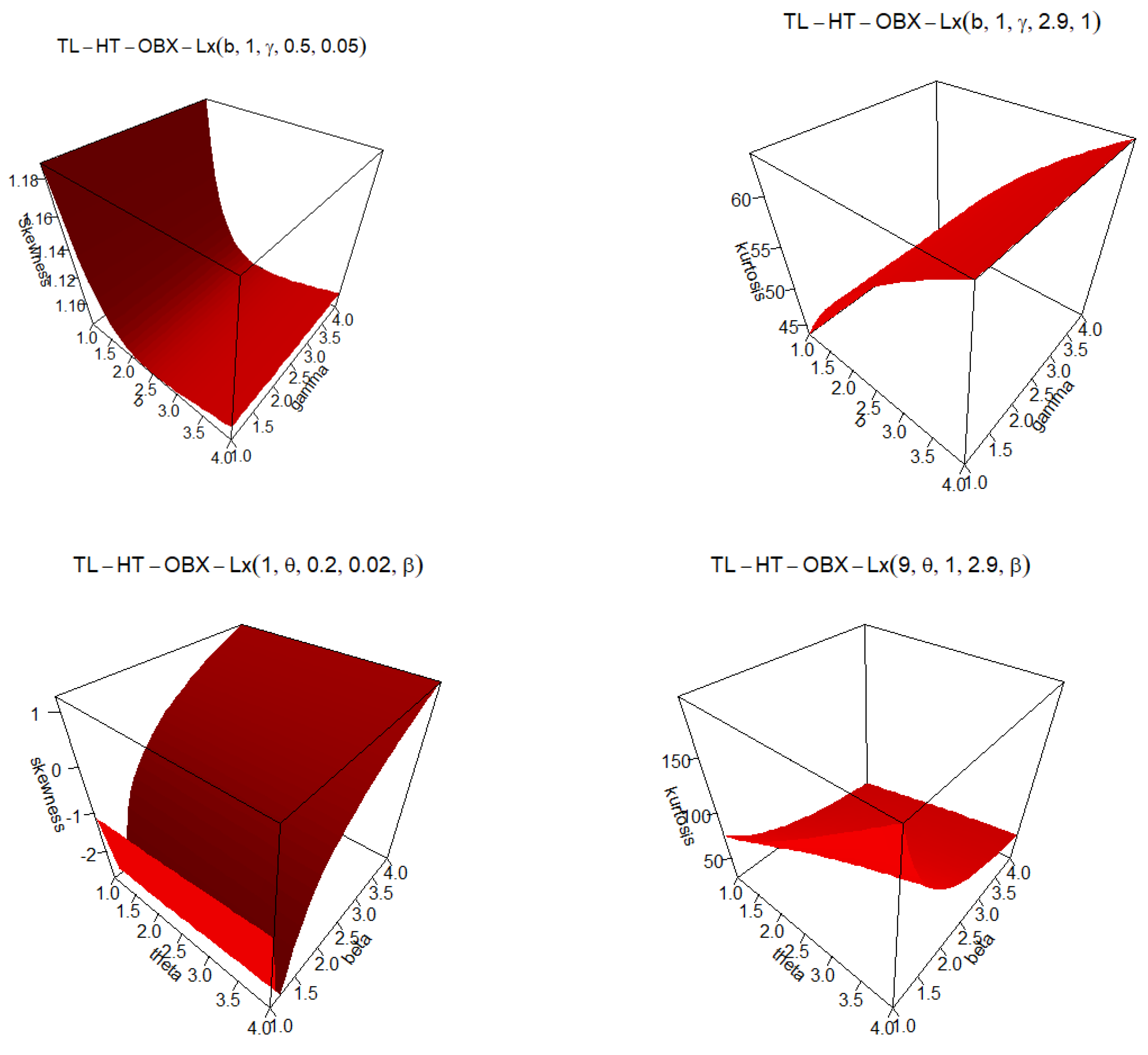
Figure 6.
SK and KT plots for TL-HT-OBX-Lx distribution for selected parameter values.
Figure 6.
SK and KT plots for TL-HT-OBX-Lx distribution for selected parameter values.
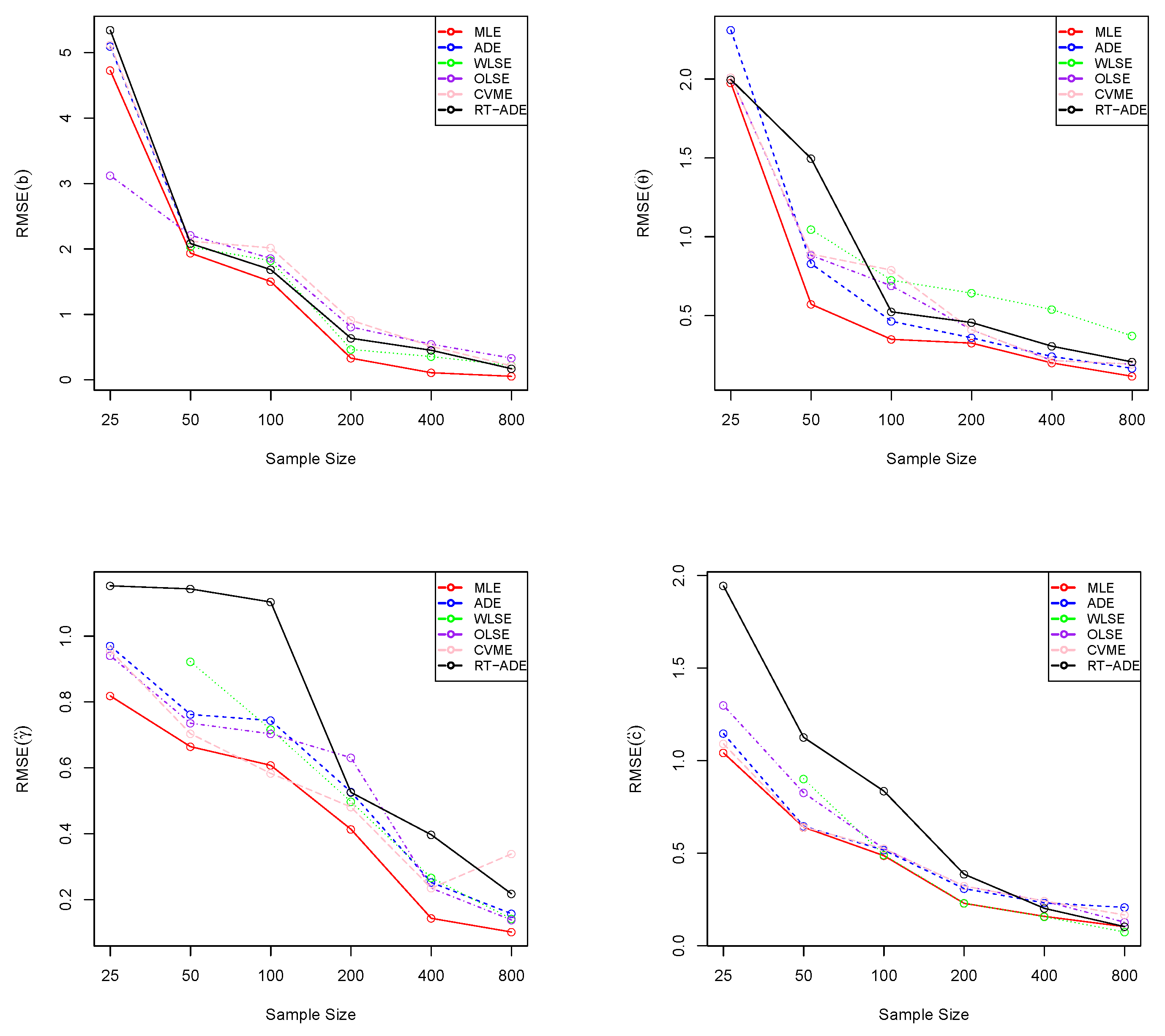
Figure 7.
Plots of RMSEs from
Table 1.
Figure 7.
Plots of RMSEs from
Table 1.
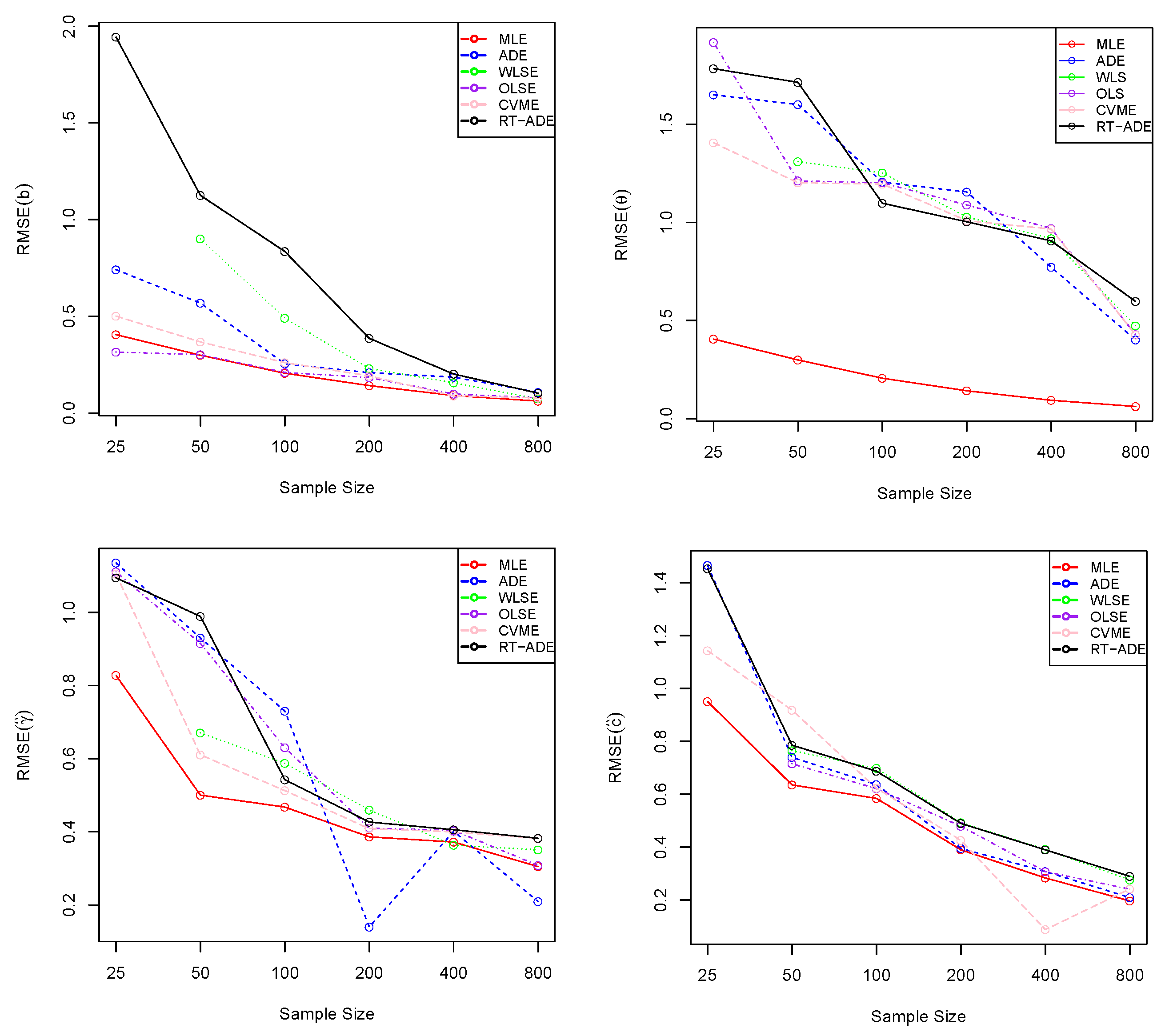
Figure 8.
Plots of RMSEs from
Table 2.
Figure 8.
Plots of RMSEs from
Table 2.
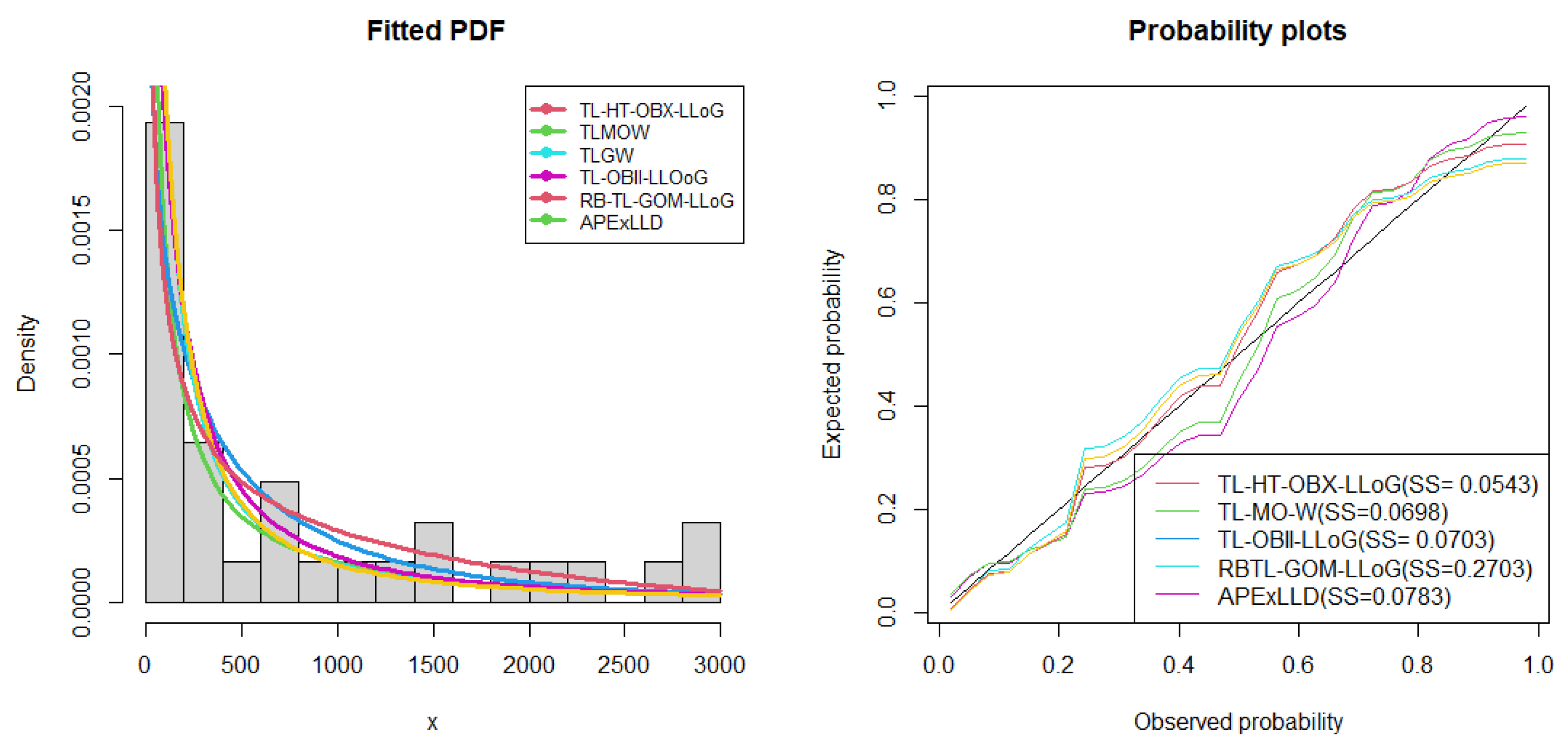
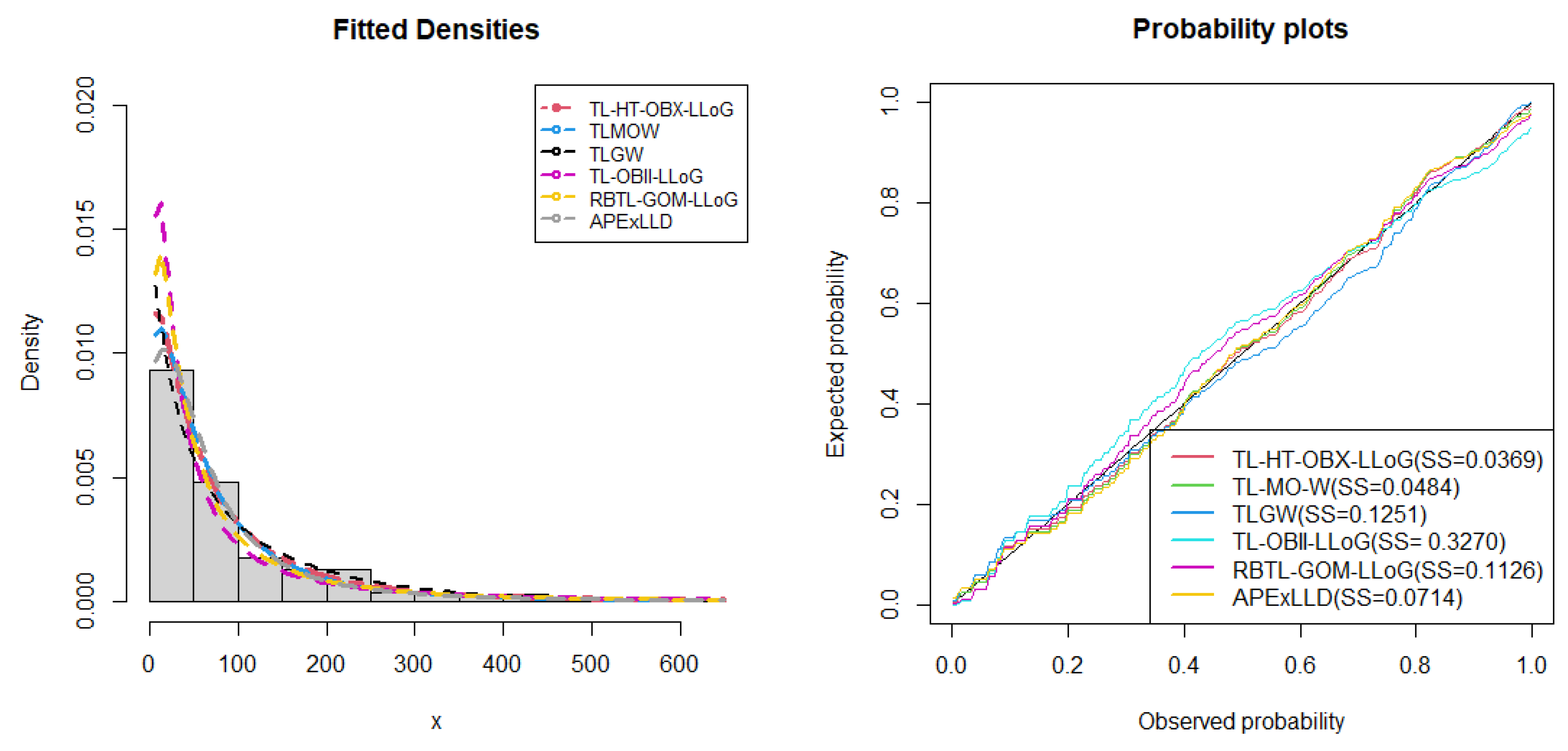
Figure 9.
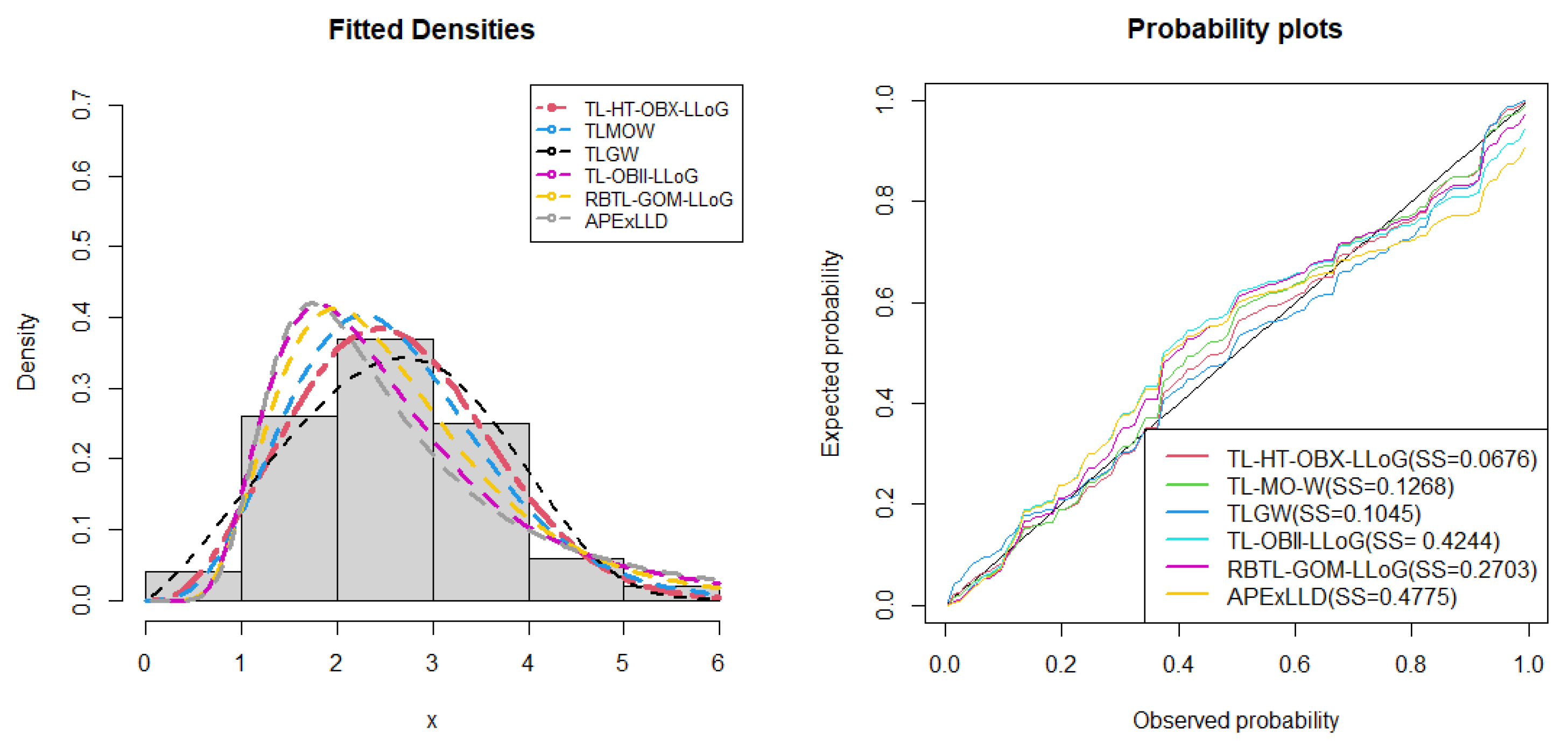
Fitted density superimposed on the histogram and observed probability vs expected probability plots for European COVID-19 data.
Figure 9.
Fitted density superimposed on the histogram and observed probability vs expected probability plots for European COVID-19 data.
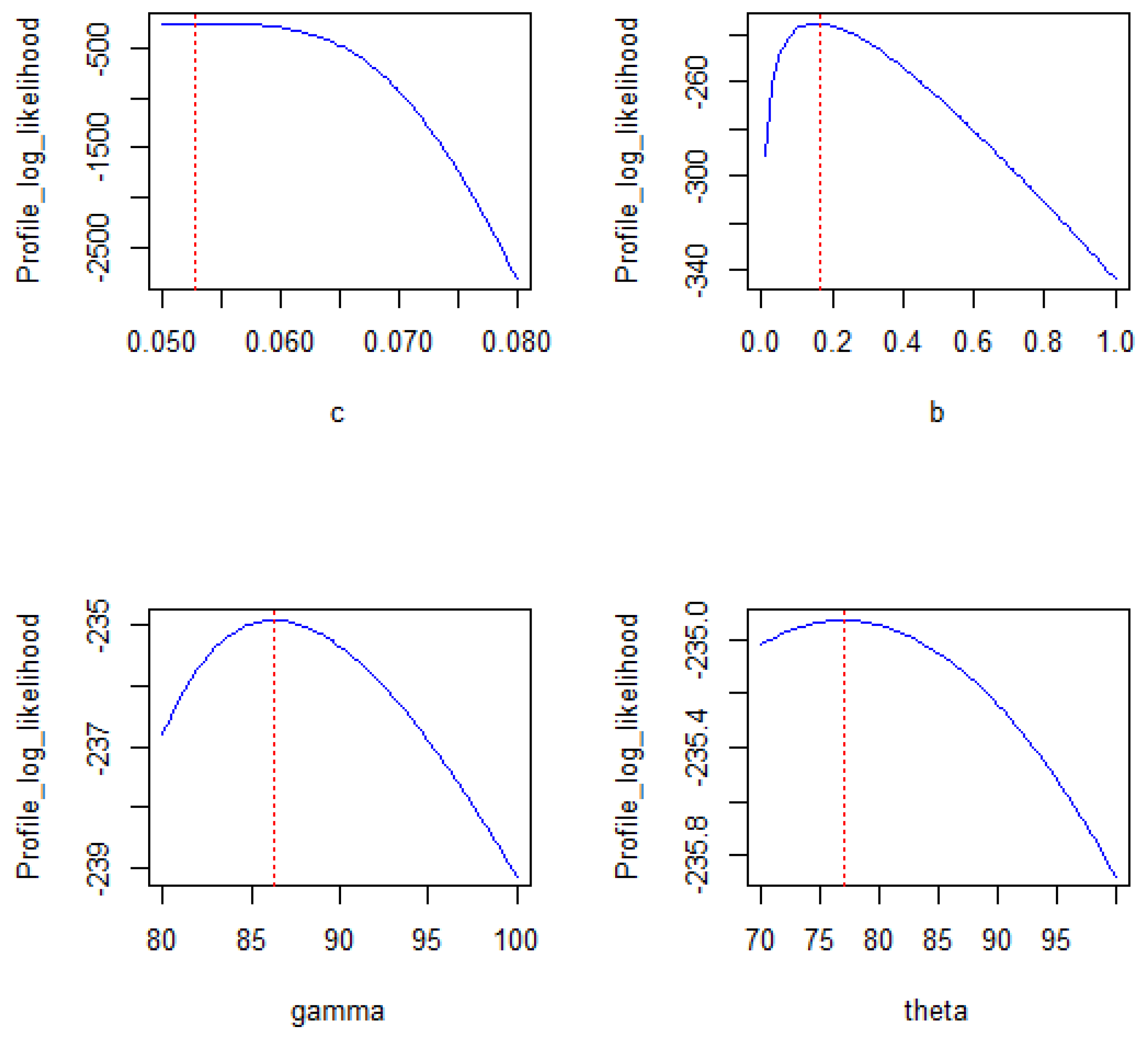
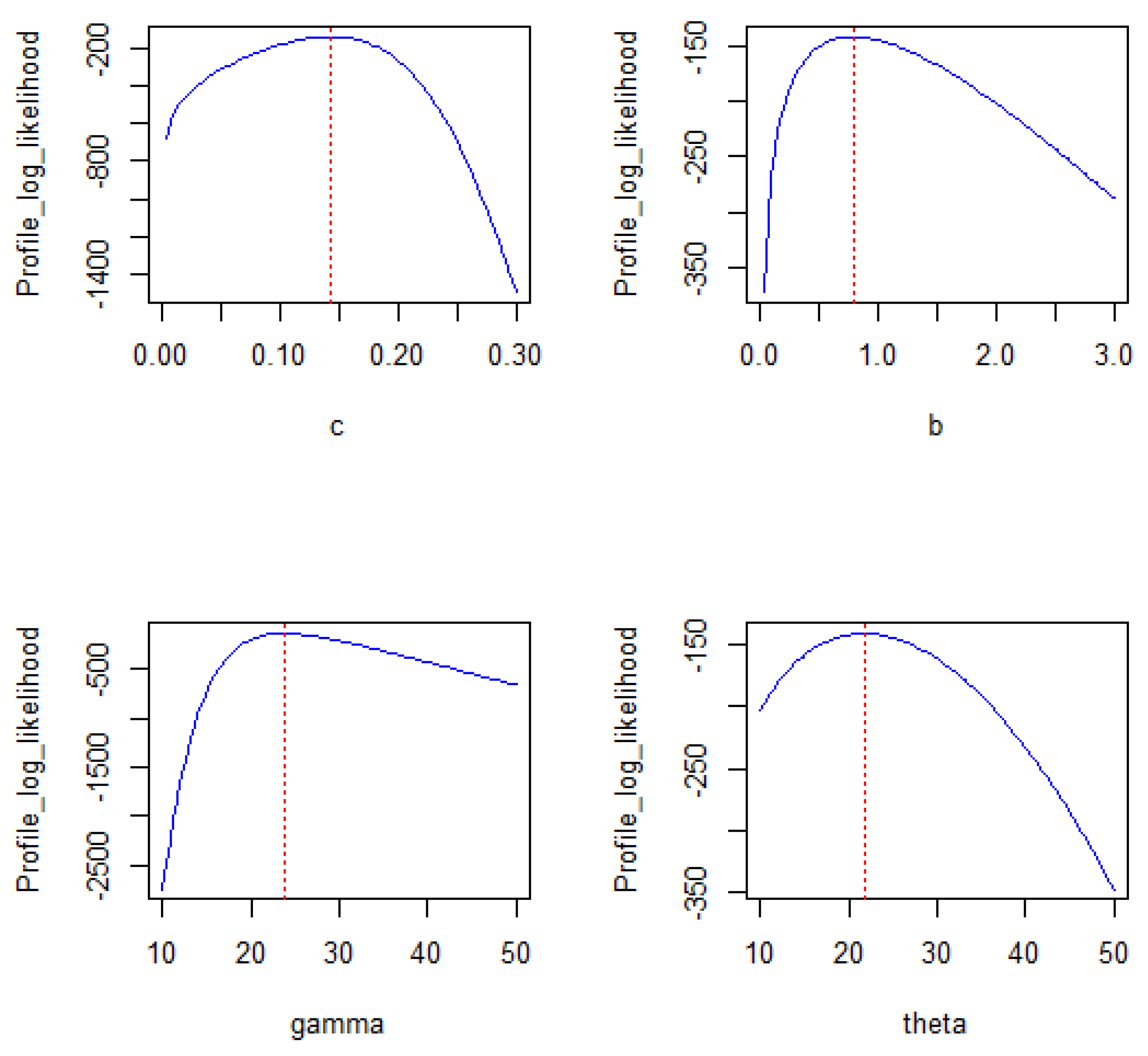
Figure 10.
Profile log-likelihood function plots for the European COVID-19 dataset.
Figure 10.
Profile log-likelihood function plots for the European COVID-19 dataset.
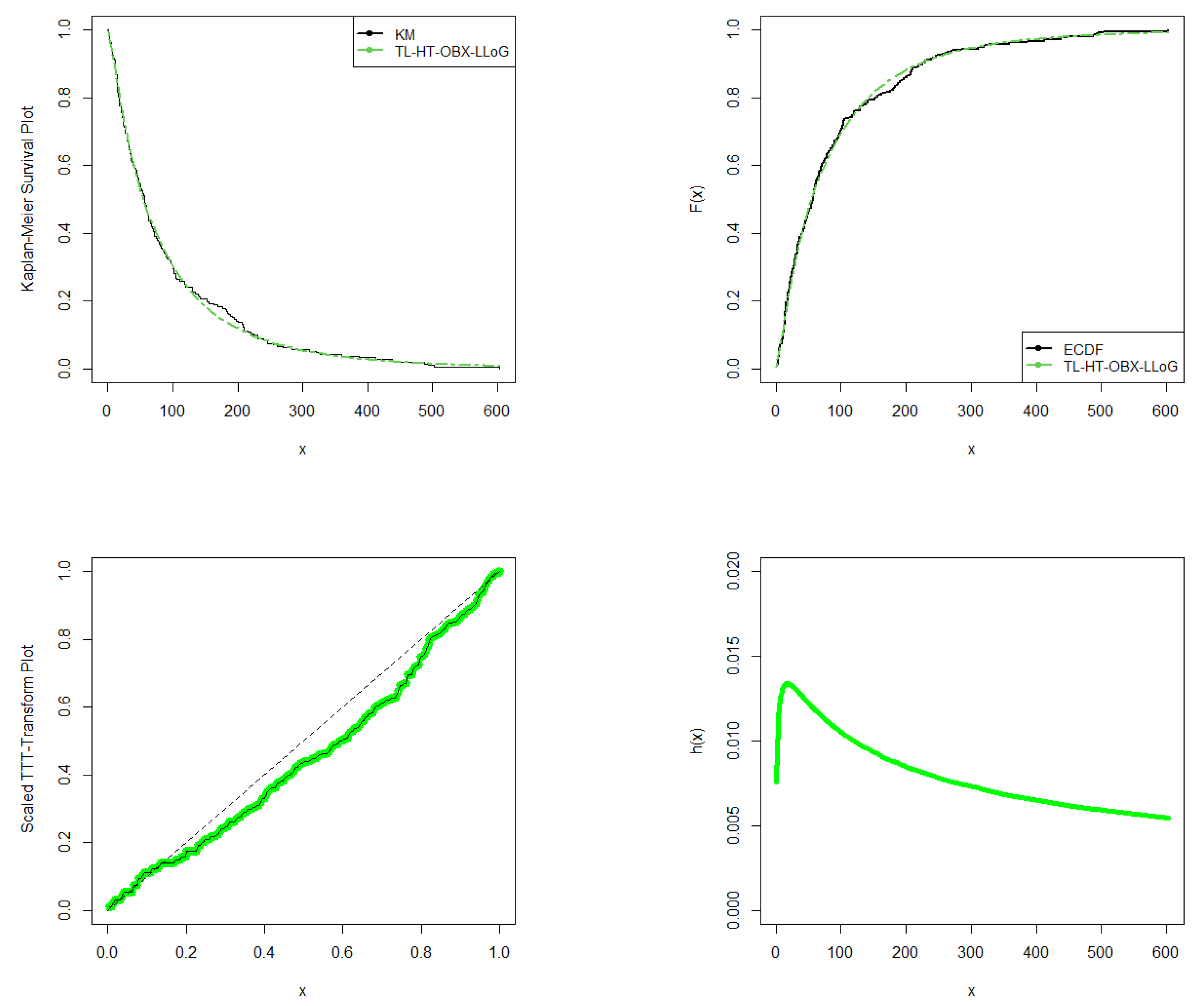
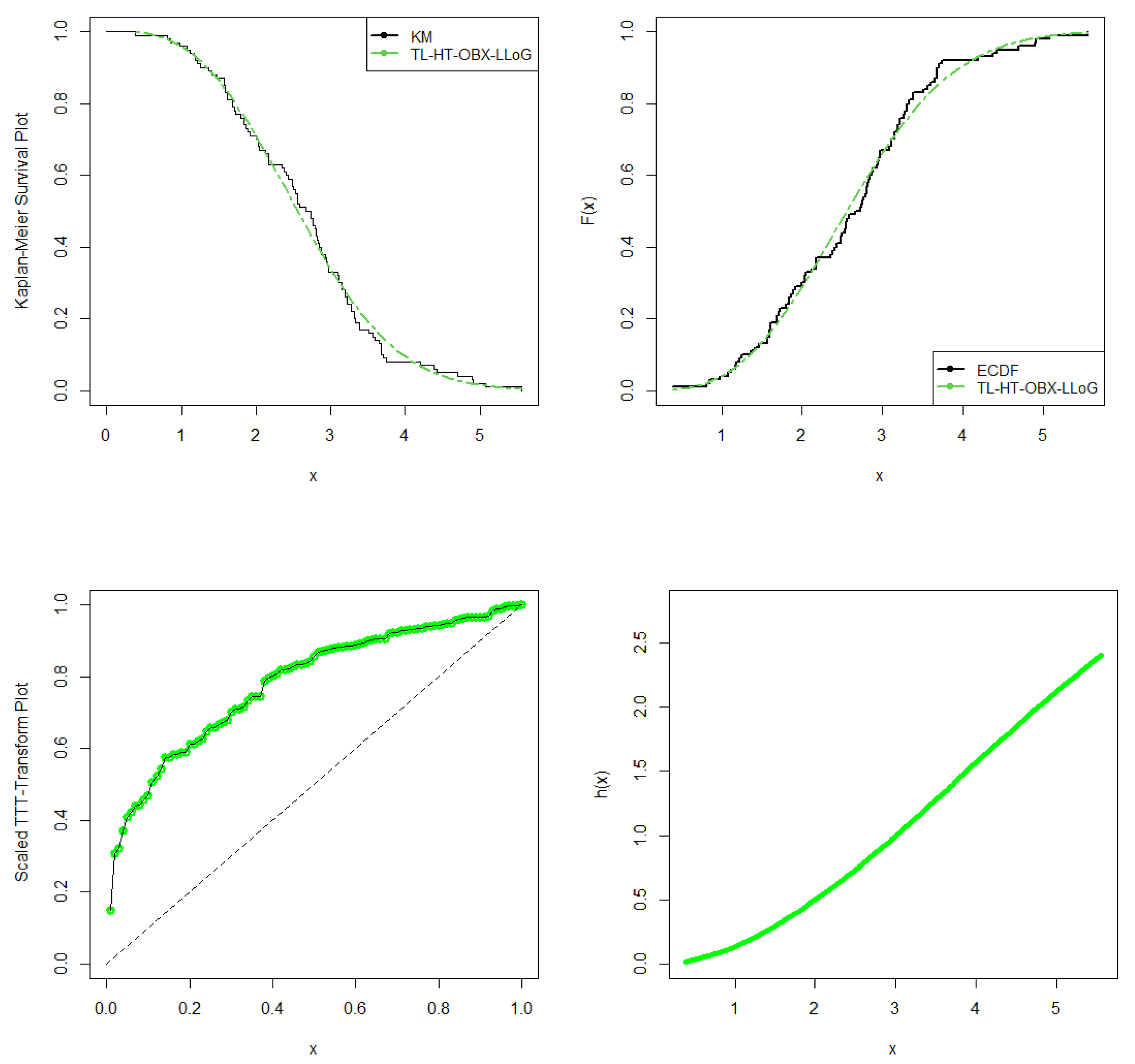
Figure 11.
Fitted K–M, ECDF, TTT, and HRF plots for the European COVID-19 dataset.
Figure 11.
Fitted K–M, ECDF, TTT, and HRF plots for the European COVID-19 dataset.
Figure 12.
Fitted density superimposed on the histogram and observed probability vs expected probability plots for air conditioning system data.
Figure 12.
Fitted density superimposed on the histogram and observed probability vs expected probability plots for air conditioning system data.
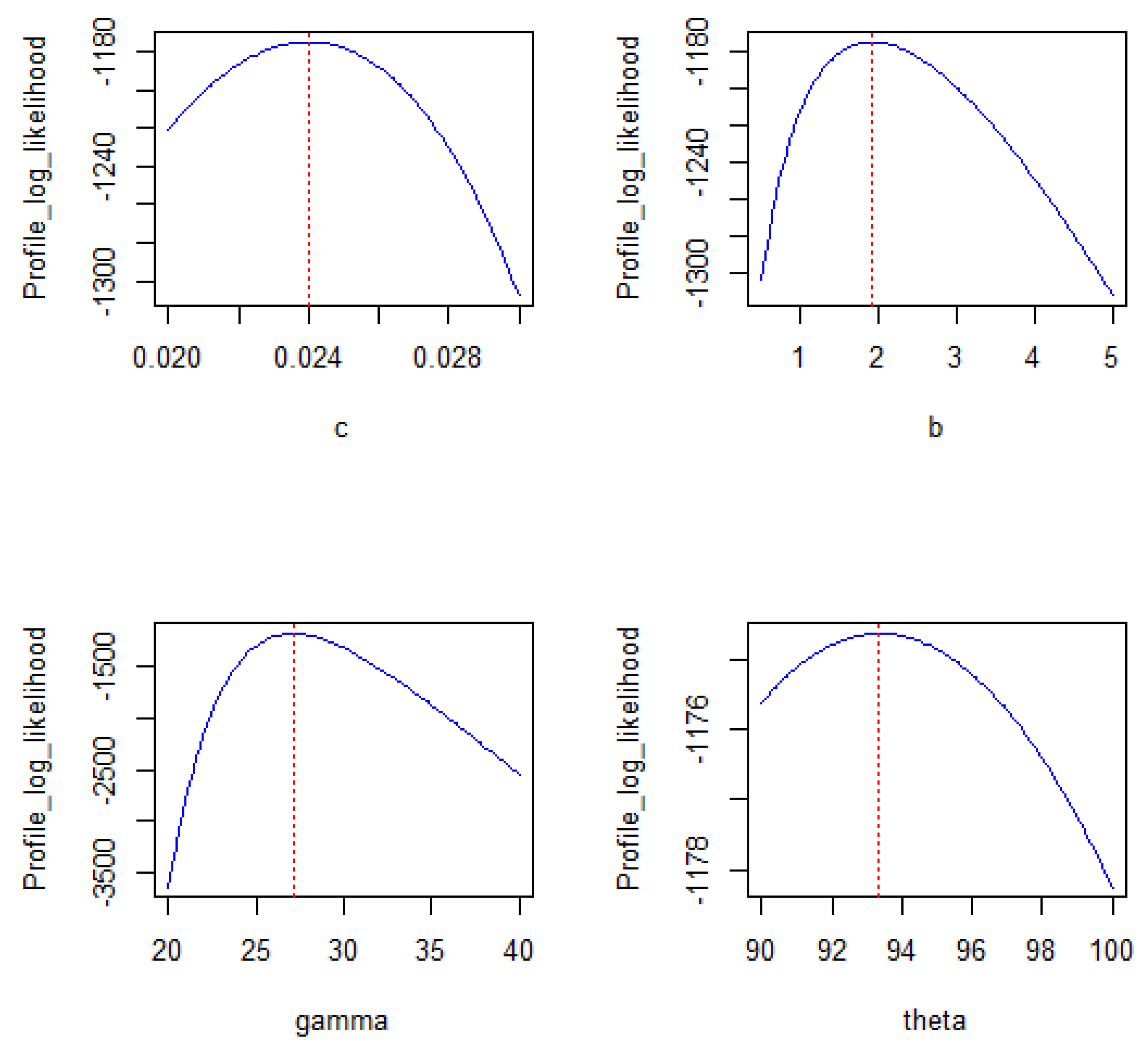
Figure 13.
Plots of the profile log-likelihood function of the parameters of the TL-HT-OBX-LLoG distribution on air conditioning system data.
Figure 13.
Plots of the profile log-likelihood function of the parameters of the TL-HT-OBX-LLoG distribution on air conditioning system data.
Figure 14.
Fitted K-M, ECDF, the TTT, and HRF for air conditioning system data.
Figure 14.
Fitted K-M, ECDF, the TTT, and HRF for air conditioning system data.
Figure 15.
Fitted density superimposed on the histogram and observed probability vs. expected probability plots for carbon fibers data.
Figure 15.
Fitted density superimposed on the histogram and observed probability vs. expected probability plots for carbon fibers data.
Figure 16.
Plots of the profile log-likelihood function of the parameters of the TL-HT-OBX-LLoG distribution on carbon fiber data.
Figure 16.
Plots of the profile log-likelihood function of the parameters of the TL-HT-OBX-LLoG distribution on carbon fiber data.
Figure 17.
Fitted K-M, ECDF, TTT, and HRF plots for carbon fiber data.
Figure 17.
Fitted K-M, ECDF, TTT, and HRF plots for carbon fiber data.
Table 1.
Simulation results for .
Table 1.
Simulation results for .
| | | MLE | OLSE | WLSE | RT-ADE | CVME | ADE |
|---|
| n | Parameter | ABias | RMSE | ABias | RMSE | ABias | RMSE | ABias | RMSE | ABias | RMSE | ABias | RMSE |
|---|
| 25 | b | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | c | | | | | | | | | | | | |
| ∑ ranks | 10 | 27 | 23 | 39 | 33 | 34 |
| 50 | b | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | c | | | | | | | | | | | | |
| ∑ ranks | 8 | 30 | 30 | 41 | 32 | 26 |
| 100 | b | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | c | | | | | | | | | | | | |
| ∑ ranks | 9 | 30 | 33 | 34 | 35 | 27 |
| 200 | b | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | c | | | | | | | | | | | | |
| ∑ ranks | 8 | 36.5 | 31 | 41 | 29.5 | 25 |
| 400 | b | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | c | | | | | | | | | | | | |
| ∑ ranks | 8 | 28 | 33 | 42 | 27 | 27 |
| 800 | b | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | c | | | | | | | | | | | | |
| ∑ ranks | 8 | 25 | 35 | 44 | 27 | 29 |
Table 2.
Simulation results for .
Table 2.
Simulation results for .
| | | MLE | OLSE | WLSE | RT-ADE | CVME | ADE |
|---|
| n | Parameter | ABias | RMSE | ABias | RMSE | ABias | RMSE | ABias | RMSE | ABias | RMSE | ABias | RMSE |
|---|
| 25 | b | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | c | | | | | | | | | | | | |
| ∑ ranks | 10 | 32 | 34 | 32 | 24 | 36 |
| 50 | b | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | c | | | | | | | | | | | | |
| ∑ ranks | 9 | 28 | 26 | 42 | 27 | 36 |
| 100 | b | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | c | | | | | | | | | | | | |
| ∑ ranks | 9 | 28 | 26 | 42 | 27 | 36 |
| 200 | b | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | c | | | | | | | | | | | | |
| ∑ ranks | 8 | 30 | 32 | 32 | 28 | 37 |
| 400 | b | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | c | | | | | | | | | | | | |
| ∑ ranks | 14 | 29 | 30 | 38 | 23 | 34 |
| 800 | b | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| | c | | | | | | | | | | | | |
| ∑ ranks | 8 | 27 | 33 | 38 | 27 | 35 |
Table 3.
Partial and overall ranks.
Table 3.
Partial and overall ranks.
| Parameters | n | MLE | OLSE | WLSE | RT-ADE | CVME | ADE |
|---|
| 25 | 1.0 | 3.0 | 2.0 | 6.0 | 4.0 | 5.0 |
| 50 | 1.0 | 3.5 | 3.5 | 6.0 | 5.0 | 2.0 |
| 100 | 1.0 | 3.0 | 4.0 | 5.0 | 6.0 | 2.0 |
| 200 | 1.0 | 5.0 | 4.0 | 6.0 | 3.0 | 2.0 |
| 400 | 1.0 | 4.0 | 5.0 | 6.0 | 2.5 | 2.5 |
| 800 | 1.0 | 2.0 | 5.0 | 6.0 | 3.0 | 4.0 |
| 25 | 1.0 | 3.5 | 5.0 | 3.5 | 2.0 | 6.0 |
| 50 | 1.0 | 4.0 | 2.0 | 6.0 | 3.0 | 5.0 |
| 100 | 1.0 | 4.0 | 2.0 | 6.0 | 3.0 | 5.0 |
| 200 | 1.0 | 3.0 | 4.5 | 4.5 | 2.0 | 6.0 |
| 400 | 1.0 | 3.0 | 4.0 | 6.0 | 2.0 | 5.0 |
| 800 | 1.0 | 2.5 | 4.0 | 6.0 | 2.5 | 5.0 |
| Sum of Ranks ( ranks) | 12.0 | 40.5 | 45 | 67.0 | 38.0 | 49.5 |
| Overall Rank | 1 | 3 | 4 | 6 | 2 | 5 |
Table 4.
Simulation results of VaR, TVaR, TV and TVP.
Table 4.
Simulation results of VaR, TVaR, TV and TVP.
| Significance Level | | 0.7 | 0.75 | 0.8 | 0.85 | 0.9 | 0.95 |
|---|
| TL-HT-OBX-LLoG () | VaR | 1.0900 | 1.1243 | 1.1629 | 1.2084 | 1.2667 | 1.3550 |
| | TVaR | 2.5753 | 2.8945 | 3.3405 | 4.0218 | 5.2357 | 8.2734 |
| | TV | 6.7601 | 9.0587 | 12.9110 | 20.3024 | 38.2684 | 112.9639 |
| | TVP | 2.1567 | 3.8995 | 6.9882 | 13.2352 | 29.2059 | 99.0422 |
| TL-HT-OBX-LLoG () | VaR | 0.9820 | 1.0197 | 1.0614 | 1.1097 | 1.1701 | 1.2587 |
| | TVaR | 2.2263 | 2.4837 | 2.8363 | 3.3611 | 4.2620 | 6.3805 |
| | TV | 2.2452 | 3.1552 | 4.6563 | 7.4590 | 13.9535 | 38.5016 |
| | TVP | 0.6546 | 0.7173 | 0.8887 | 2.9790 | 8.2961 | 30.1960 |
| TL-HT-OBX-LLoG () | VaR | 0.8637 | 0.9097 | 0.9614 | 1.0223 | 1.0998 | 1.2160 |
| | TVaR | 1.1192 | 1.1643 | 1.2178 | 1.2845 | 1.3754 | 1.5235 |
| | TV | 0.0394 | 0.0606 | 0.0899 | 0.1341 | 0.2109 | 0.3908 |
| | TVP | 1.0916 | 1.1188 | 1.1458 | 1.1705 | 1.1856 | 1.1922 |
| TL-HT-OBX-LLoG () | VaR | 0.7146 | 0.7752 | 0.8446 | 0.9280 | 1.0365 | 1.2036 |
| | TVaR | 1.5786 | 1.7425 | 1.9563 | 2.2540 | 2.7154 | 3.5995 |
| | TV | 0.6999 | 0.9981 | 1.4591 | 2.2374 | 3.7630 | 7.7935 |
| | TVP | 0.7892 | 0.9939 | 0.7890 | 0.3522 | 0.6712 | 3.8042 |
| TL-HT-OBX-LLoG () | VaR | 0.9318 | 0.9879 | 1.0522 | 1.1295 | 1.2303 | 1.3866 |
| | TVaR | 1.1440 | 1.1809 | 1.2213 | 1.2653 | 1.3093 | 1.3178 |
| | TV | 0.0662 | 0.0711 | 0.0806 | 0.0992 | 0.1410 | 0.2664 |
| | TVP | 1.1903 | 1.2343 | 1.2858 | 1.3497 | 1.4363 | 1.5709 |
| APExLLD () | VaR | 0.2286 | 0.2406 | 0.2550 | 0.2736 | 0.3002 | 0.3489 |
| | TVaR | 0.2989 | 0.3118 | 0.3278 | 0.3491 | 0.3807 | 0.4401 |
| | TV | 0.0076 | 0.0081 | 0.0088 | 0.0098 | 0.0116 | 0.0155 |
| | TVP | 0.3042 | 0.3179 | 0.3349 | 0.3575 | 0.3912 | 0.4549 |
| TL-OBIII-LLoG () | VaR | 0.0188 | 0.0244 | 0.0321 | 0.0432 | 0.0610 | 0.0960 |
| | TVaR | 0.0188 | 0.0244 | 0.3212 | 0.0432 | 0.0616 | 0.0960 |
| | TV | 0.0026 | 0.0027 | 0.0029 | 0.0031 | 0.0033 | 0.0035 |
| | TVP | 0.0632 | 0.07146 | 0.
0820 | 0.0964 | 0.1180 | 0.1573 |
Table 5.
MLEs and goodness-of-fit statistics for European COVID-19 data.
Table 5.
MLEs and goodness-of-fit statistics for European COVID-19 data.
| | Estimates | Statistics |
|---|
| Model | | | | | | | | | | | K-S | p-Value |
|---|
| TL-HT-OBX-LLoG | 0.1632 | 77.0570 | 86.2790 | 0.0527 | 469.8573 | 477.8573 | 479.3958 | 483.5933 | 0.0612 | 0.4063 | 0.1395 | 0.8363 |
| | (0.0309) | () | () | (0.0012) | | | | | | | | |
| | b | | | | | | | | | | | |
| TL-MO-W | 1.4593 | 0.8235 | | 0.0644 | 474.6477 | 482.6477 | 484.1862 | 488.3836 | 0.0743 | 0.5126 | 0.1137 | 0.7756 |
| | ( ) | ( ) | ( ) | (3.3077) | | | | | | | | |
| | | | | | | | | | | | | |
| TLGW | 2.1406 | 1.0016 | 0.0009 | 0.3249 | 479.6846 | 487.6843 | 489.2227 | 493.4202 | 0.0594 | 0.432755 | 0.1381 | 0.5492 |
| | (0.6769) | (0.2702 ) | (0.0007 ) | (0.0627) | | | | | | | | |
| | | | b | | | | | | | | | |
| TL-OBIII-LLoG | 23.6880 | 54.3560 | 0.3035 | 0.0218 | 477.9591 | 485.9591 | 487.4976 | 491.6951 | 0.0944 | 0.6608 | 0.1213 | 0.7065 |
| | () | (0.0004) | (0.0838) | (0.0019) | | | | | | | | |
| | | b | | c | | | | | | | | |
| RBTL-GOM-LLoG | 117.5400 | 639.1300 | 0.2550 | 0.03700 | 474.9944 | 482.9944 | 484.5328 | 488.7303 | 0.0684 | 0.4988 | 0.11157 | 0.7949 |
| | () | () | () | () | | | | | | | | |
| | | a | b | c | | | | | | | | |
| APExLLD | 17.7183 | 0.7336 | 2.9073 | 7.3059 | 478.9729 | 486.9729 | 488.5116 | 492.7088 | 0.1020 | 0.7046 | 0.1306 | 0.6188 |
| | (49.5295) | (0.1981) | (31.6092) | (47.4060) | | | | | | | | |
Table 6.
MLEs and goodness-of-fit statistics for air conditioning system data.
Table 6.
MLEs and goodness-of-fit statistics for air conditioning system data.
| | Estimates | Statistics |
|---|
| Model | | | | | | | | | | | K-S | p-Value |
|---|
| TL-HT-OBX-LLoG | 1.9239 | 93.3560 | 27.1493 | 0.0240 | 2349.263 | 2357.263 | 2357.456 | 2370.708 | 0.0361 | 0.2664 | 0.0389 | 0.9032 |
| | (0.9029) | (0.0942) | (2.3284) | (0.0042) | | | | | | | | |
| | b | | | | | | | | | | | |
| TL-MO-W | 1.4593 | | | 10.621 | 2353.468 | 2361.468 | 2361.661 | 2374.913 | 0.0532 | 0.4013 | 0.0424 | 0.8380 |
| | ( ) | ( ) | ( ) | () | | | | | | | | |
| | | | | | | | | | | | | |
| TLGW | | | | 3.3233 | 2351.21 | 2359.209 | 2359.402 | 2372.654 | 0.0933 | 0.5971 | 0.0604 | 0.4188 |
| | () | ( ) | ( ) | (1.0007) | | | | | | | | |
| | | | b | | | | | | | | | |
| TL-OBIII-LLoG | 0.196 | 25.2716 | 0.5054 | 3.3422 | 2380.947 | 2388.947 | 2389.139 | 2402.392 | 0.3176 | 2.1313 | 0.0781 | 0.1478 |
| | (0.0143) | (14.6865) | (0.2935) | (0.0045) | | | | | | | | |
| | | b | | c | | | | | | | | |
| RBTL-GOM-LLoG | 25.1700 | 154.5700 | | | 2360.408 | 2368.407 | 2368.6000 | 2381.8530 | 0.1213 | 0.8643 | 0.0570 | 0.4924 |
| | (5.7056) | (1.2095) | () | () | | | | | | | | |
| | | a | b | c | | | | | | | | |
| APExLLD | 6264.8000 | 1.6330 | 64.4680 | | 2361.203 | 2369.2030 | 2369.3950 | 2382.6480 | 0.1013 | 0.7386 | 0.0433 | 0.8175 |
| | () | () | (19.6270) | () | | | | | | | | |
Table 7.
MLEs and goodness-of-fit statistics for carbon fiber data.
Table 7.
MLEs and goodness-of-fit statistics for carbon fiber data.
| | Estimates | Statistics |
|---|
| Model | | | | | | | | | | | K-S | p-Value |
|---|
| TL-HT-OBX-LLoG | 0.7903 | 21.8224 | 23.7367 | 0.1432 | 282.6951 | 290.6951 | 291.1162 | 301.1158 | 0.0698 | 0.4112 | 0.0646 | 0.7978 |
| | (0.3979) | (0.4300) | (3.8674) | (0.0288) | | | | | | | | |
| | b | | | | | | | | | | | |
| TL-MO-W | 3.3659 | 2.3309 | 1.2030 | 0.4678 | 284.4367 | 292.4367 | 292.8578 | 302.8574 | 0.1171 | 0.5965 | 0.0899 | 0.3933 |
| | (3.6182) | (2.3762) | (0.9359) | (0.8570) | | | | | | | | |
| | | | | | | | | | | | | |
| TLGW | 0.7550 | 0.6563 | 0.2294 | 4.3882 | 287.3756 | 295.3756 | 295.7966 | 305.7962 | 0.0829 | 0.6607 | 0.0808 | 0.5311 |
| | (0.2470) | (0.26670) | (0.0180) | (1.1956) | | | | | | | | |
| | | | b | | | | | | | | | |
| TL-OBIII-LLoG | 110.5900 | 11.4590 | | | 307.5220 | 315.5220 | 315.9431 | 325.9427 | 0.4058 | 2.2273 | 0.1350 | 0.0520 |
| | () | (6.5830) | () | () | | | | | | | | |
| | | b | | c | | | | | | | | |
| RBTL-GOM-LLoG | 111.7200 | 981.5200 | 1.0785 | | 296.4615 | 304.4616 | 304.8826 | 314.8823 | 0.2731 | 1.4586 | 0.1175 | 0.1264 |
| | ( ) | () | () | () | | | | | | | | |
| | | a | b | c | | | | | | | | |
| APExLLD | 897.0300 | 2.3362 | | 321.8300 | 319.9412 | 327.9412 | 328.3623 | 338.3619 | 0.5611 | 3.1168 | 0.1384 | 0.0433 |
| | ) | () | () | () | | | | | | | | |