Double-Swarm Grey Wolf Optimizer with Covariance and Dimension Learning for Engineering Optimization Problems
Abstract
1. Introduction
- (1)
- Chaotic grouping is utilized to generate two sub-swarms of grey wolves. This strategy can improve population diversity of CDL-DGWO algorithm.
- (2)
- Covariance and dimension learning strategies are utilized to improve the hunting behavior of grey wolves, which can enhance the global search capability and algorithm stability.
- (3)
- The performance of the CDL-DGWO algorithm is validated on 23 benchmark problems and the CEC2017 test suite. The results indicate that the CDL-DGWO outperforms the compared swarm intelligence algorithms such as PSO, MFO, and GWO variants in terms of solving optimal solutions and convergence performance. Additionally, the CDL-DGWO is applied to three engineering design problems, which fully demonstrate the practicality of the proposed methodology.
2. Grey Wolf Optimizer (GWO)
| Algorithm 1: Grey Wolf Optimizer (GWO). |
1: Initialize , dimension D, population size N, , ; % and represent the maximum number of function evaluations and the current number of function evaluations respectively. 2: Initialize population of wolves; 3: while 4: Calculate the fitness value of wolves and update ; 5: , and are the first three wolves with the best fitness; 6: for 7: for 8: Updata parameters a, and ; 10: end 11: end 12: end while |
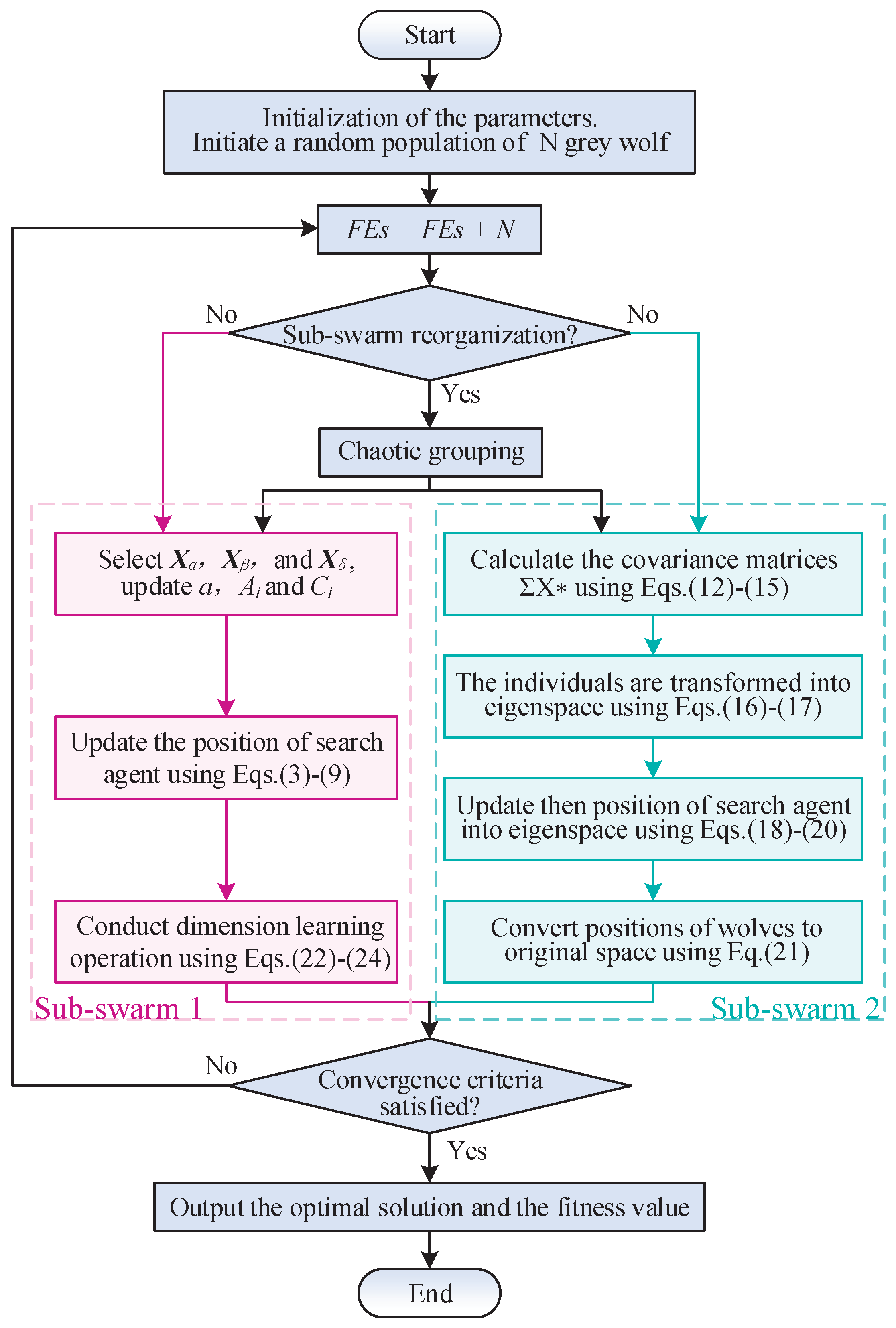
3. Double-Swarm Grey Wolf Optimizer with Covariance and Dimension Learning (CDL-DGWO)
3.1. Chaotic Grouping and Dynamic Regrouping
| Algorithm 2: Chaotic grouping mechanism. |
1: The first chaotic value () is initialized randomly in (0,1); 2: for
3: ; 4: ; 5: end for 6: 7: The grey wolf population is divided into two sub-swarms according to I; |
3.2. Learning Strategies
3.3. Framework of the CDL-DGWO
- Step 1:
- Initialize the system parameters, which include population size N, individual dimension d, random parameters a, and , as well as the maximum number of function evaluations () and the current number of function evaluations ().
- Step 2:
- Generate the initial population of wolves randomly within the defined upper and lower bounds of .
- Step 3:
- Divide the population into two sub-swarms using Algorithm 2.
- Step 4:
- Check the stopping criteria: Determine whether or the best fitness value meets the accuracy requirements. If conditions are met, output the position of as the best approximated optimum, otherwise, proceed to step 5.
- Step 5:
- Calculate and sort the fitness of each individual, updating . Select the top three individuals as , and .
- Step 6:
- Step 7:
- For the Sub-swarm 2, introduce a covariance matrix to enhance information sharing among individual variables, thereby improving the overall performance of the algorithm.
- Step 8:
- Perform dynamic regrouping using Equation (11) and Algorithm 2, then return to Step 4.
- Step 9:
- Return the best solution.
| Algorithm 3: Pseudocode of CDL-DGWO. |
1: Initialize , d, N, , ; 2: Initialize population of wolves; 3: The population is divided into 2 sub-swarms by Algorithm 2; 4: while 5: Calculate the fitness value of wolves, ; 6: , and are the first three wolves with the best fitness; %% The Sub-swarm 1 7: for 8: for 9: Updata parameters a, and ; 11: end 12: end %% The Sub-swarm 2 15: is obtained, which is composed of eigenvectors of , based on eigen decomposition relation Equation (16); 16: The individuals of wolves are transformed into eigenspace based on eigenvector using Equation (17); 17: for 18: for 19: Updata parameters a, and ; 21: end 22: end 23: Convert positions of wolves to original space using Equation (21); 24: If mod(t,)==0 25: Regrouping using Algorithm 2; 26: end 27: end while |
3.4. Computational Complexity of the CDL-DGWO
- (1)
- Fitness Evaluation: .
- (2)
- Standard GWO Operations (population update, leader selection): .
- (3)
- (4)
- (5)
- Chaotic Grouping: The generation and sorting of chaotic sequences incur , but when amortized over all iterations, this becomes negligible.
4. Test Results and Analysis
4.1. Test Suites, Test Methods and Performance Index
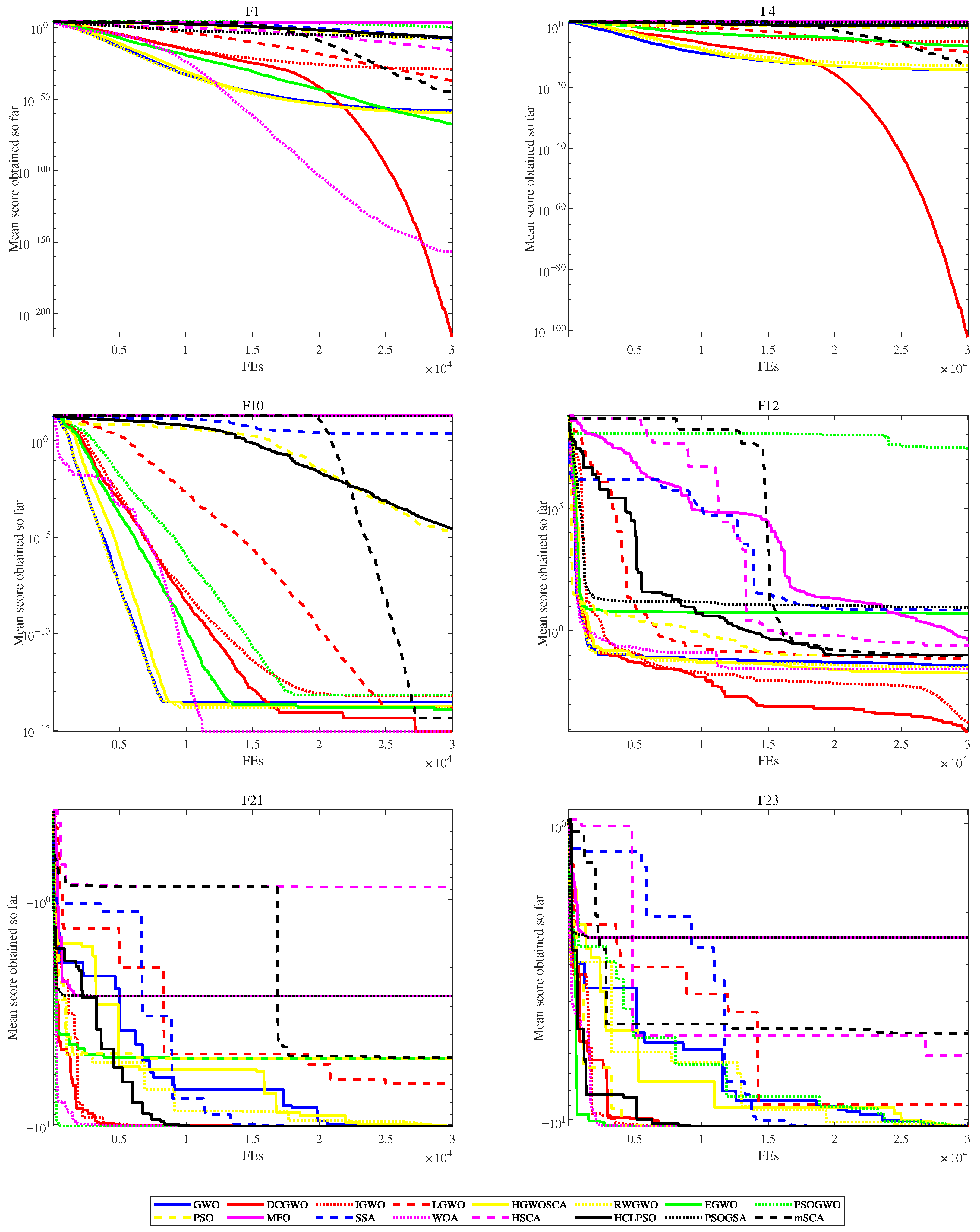
4.2. Effects of Proposed Strategies
4.3. Comparisons on Classical Benchmark Problems
4.4. Comparisons on CEC 2017
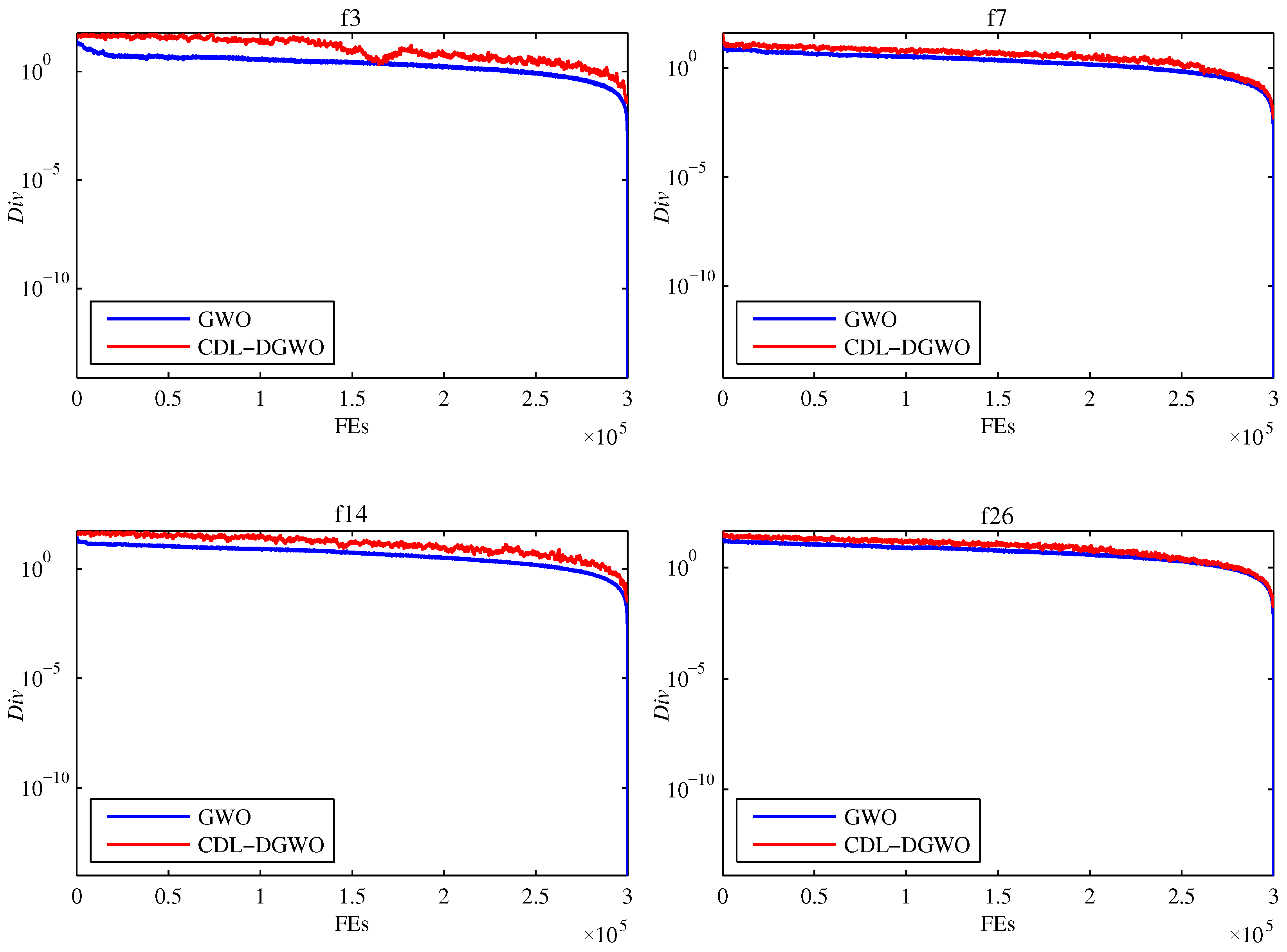
4.5. Analysis of Population Diversity in CDL-DGWO
5. Testing of Engineering Design Problems
5.1. Constrained Problem
5.2. Tension/Compression Spring Design Problem
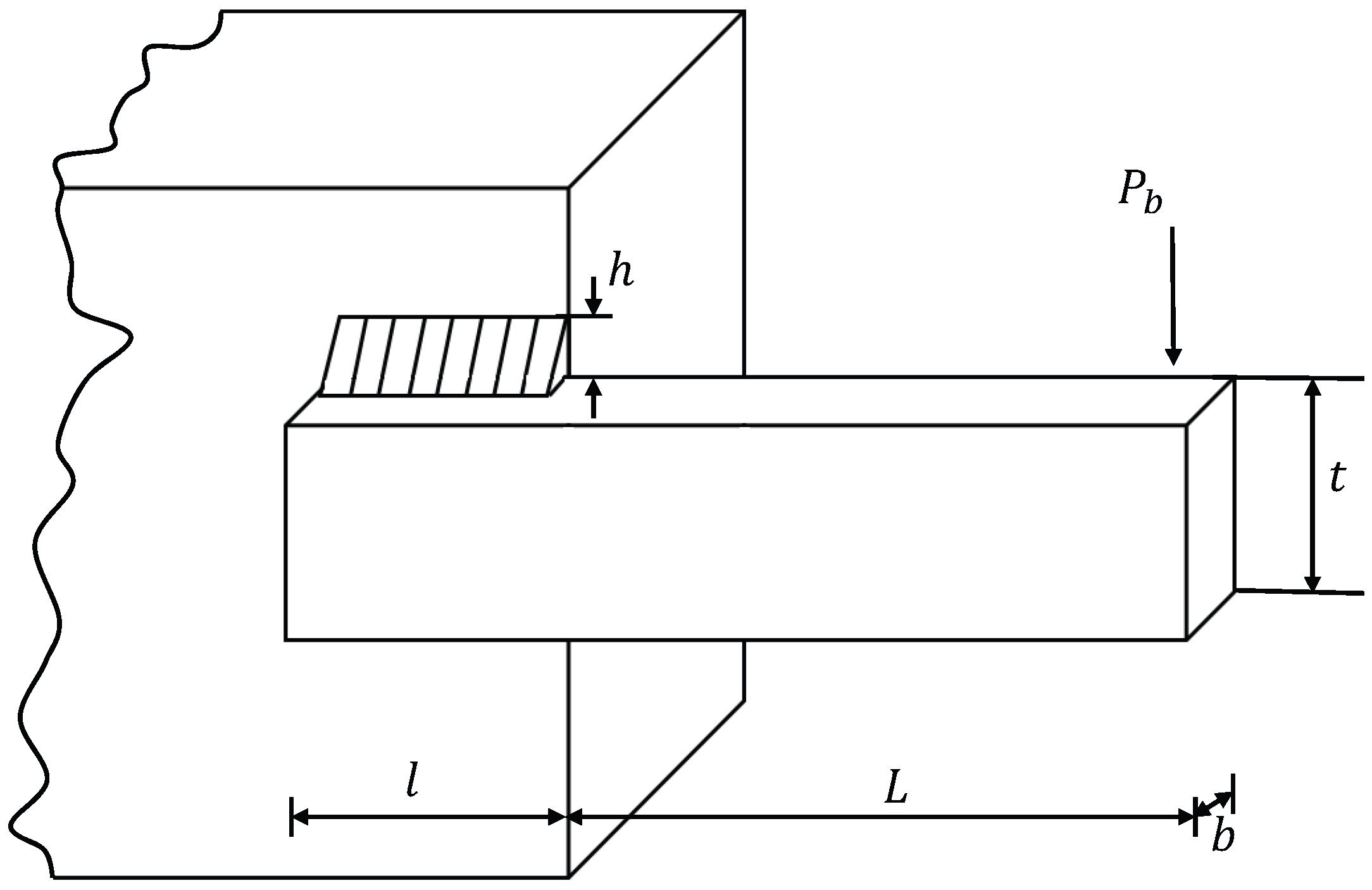
5.3. Welded Beam Design Problem
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Acronyms and Abbreviations | |
| GWO | Grey Wolf Optimizer |
| CDL-DGWO | Double-swarm Grey Wolf Optimizer with Covariance and Dimension Learning |
| PSO | Particle Swarm Optimization |
| MFO | Moth Flame Optimization |
| SMA | Slime Mold Algorithm |
| WOA | Whale Optimization Algorithm |
| MA | Mayfly Algorithm |
| HHO | Harris Hawks Optimization |
| SCA | Sine Cosine Algorithm |
| GSA | Gravitational Search Algorithm |
| LGWO | modified Lévy-embedded Grey Wolf Optimizer |
| RWGWO | Random Walk Grey Wolf Optimizer |
| SOF | Survival Of the Fittest |
| DE | Differential Evolution |
| DI-GWOCD | Discrete version of the Improved Grey Wolf Optimizer |
| IAGWO | Improved multi-strategy adaptive Grey Wolf Optimization |
| IMF | Inverse Multiquadratic Function |
| ACoM-ABC | Artificial Bee Colony Algorithm with Adaptive Covariance Matrix |
| ABC | Artificial Bee Colony |
| CCoM-ABC | Cumulative Covariance Matrix Artificial Bee Colony |
| CMA-GWO | Covariance Matrix Adapted Grey Wolf Optimizer |
| I-GWO | Improved Grey Wolf Optimizer |
| DLH | Dimension Learning-based Hunting |
| MIGWO | Multi-swarm Improved Grey Wolf Optimizer |
| HGWOSCA | Hybrid Grey Wolf Optimizer (GWO)–Sine Cosine Algorithm (SCA) |
| EGWO | Enhanced Grey Wolf Optimizer |
| PSOGWO | Hybrid Particle Swarm Optimization (PSO)Grey Wolf Optimizer (GWO) |
| SSA | Salp Swarm Algorithm |
| HSCA | Hybrid Sine Cosine Algorithm |
| HCLPSO | Heterogeneous Comprehensive Learning Particle Swarm Optimization |
| PSOGSA | Hybrid Particle Swarm Optimization (PSO)–Gravitational Search Algorithm (GSA) |
| mSCA | self-adaptive Sine Cosine Algorithm |
| CEC | Congress on Evolutionary Computation |
| C-GWO | Double-swarm Grey Wolf Optimizer with Covariance |
| D-GWO | Double-swarm Grey Wolf Optimizer with Dimension Learning |
| Mathematical Symbols | |
| t | Current iteration number |
| T | Maximum number of iterations |
| N | Population size (number of wolves) |
| D | Dimensionality of the problem (number of variables) |
| Position vector of a grey wolf | |
| , , | Position vectors of the alpha, beta, and delta wolves (best solutions) |
| Position vector of the prey | |
| , | Coefficient vectors in GWO |
| a | Control parameter that decreases linearly from 2 to 0 |
| Distance vector between a wolf and the prey | |
| Covariance matrix | |
| Orthogonal matrix of eigenvectors | |
| Diagonal matrix of eigenvalues | |
| Position vector in the eigenspace | |
| Neighborhood radius for dimension learning | |
| Neighborhood of the i-th wolf | |
| Candidate solution from dimension learning | |
| Regrouping interval | |
| , | Maximum and minimum values for calculation |
| Maximum number of function evaluations | |
| Current number of function evaluations | |
| Mean value of all solutions in the d-th dimension | |
| Population diversity index | |
References
- Yu, X.; Wu, X. Ensemble grey wolf Optimizer and its application for image segmentation. Expert Syst. Appl. 2022, 209, 118267. [Google Scholar] [CrossRef]
- Tai, T.C.; Lee, C.C.; Kuo, C.C. A hybrid grey wolf optimization algorithm using robust learning mechanism for large scale economic load dispatch with vale-point effect. Appl. Sci. 2023, 13, 2727. [Google Scholar] [CrossRef]
- Pan, H.; Chen, S.; Xiong, H. A high-dimensional feature selection method based on modified Gray Wolf Optimization. Appl. Soft Comput. 2023, 135, 110031. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization: An overview. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Zhang, T.; Zhou, Y.; Zhou, G.; Deng, W.; Luo, Q. Bioinspired bare bones mayfly algorithm for large-scale spherical minimum spanning tree. Front. Bioeng. Biotechnol. 2022, 10, 830037. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Ebrahimi, S.M.; Hasanzadeh, S.; Khatibi, S. Parameter identification of fuel cell using repairable grey wolf optimization algorithm. Appl. Soft Comput. 2023, 147, 110791. [Google Scholar] [CrossRef]
- Yu, X.W.; Huang, L.P.; Liu, Y.; Zhang, K.; Li, P.; Li, Y. WSN node location based on beetle antennae search to improve the gray wolf algorithm. Wirel. Netw. 2022, 28, 539–549. [Google Scholar] [CrossRef]
- Dereli, S. A new modified grey wolf optimization algorithm proposal for a fundamental engineering problem in robotics. Neural Comput. Appl. 2021, 33, 14119–14131. [Google Scholar] [CrossRef]
- Singh, N.; Singh, S. A novel hybrid GWO-SCA approach for optimization problems. Eng. Sci. Technol. Int. J. 2017, 20, 1586–1601. [Google Scholar] [CrossRef]
- Yu, X.; Zhao, Q.; Lin, Q.; Wang, T. A grey wolf optimizer-based chaotic gravitational search algorithm for global optimization. J.·Supercomput. 2023, 79, 2691–2739. [Google Scholar] [CrossRef]
- Keshri, R.; Vidyarthi, D.P. An ML-based task clustering and placement using hybrid Jaya-gray wolf optimization in fog-cloud ecosystem. Concurr. Comput. Pract. Exp. 2024, 36, e8109. [Google Scholar] [CrossRef]
- Heidari, A.A.; Pahlavani, P. An efficient modified grey wolf optimizer with Levy flight for optimization tasks. Appl. Soft Comput. 2017, 60, 115–134. [Google Scholar] [CrossRef]
- Gupta, S.; Deep, K. A novel random walk grey wolf optimizer. Swarm Evol. Comput. 2019, 44, 101–112. [Google Scholar] [CrossRef]
- Wang, J.S.; Li, S.X. An improved grey wolf optimizer based on differential evolution and elimination mechanism. Sci. Rep. 2019, 9, 7181. [Google Scholar] [CrossRef]
- Yao, K.; Sun, J.; Chen, C.; Cao, Y.; Xu, M.; Zhou, X.; Tang, N.; Tian, Y. An information entropy-based grey wolf optimizer. Soft Comput. 2023, 27, 4669–4684. [Google Scholar] [CrossRef]
- Qin, H.; Meng, T.; Cao, Y. Fuzzy strategy grey wolf optimizer for complex multimodal optimization problems. Sensors 2022, 22, 6420. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Moeini, E.; Taghian, S.; Mirjalili, S. Discrete improved grey wolf optimizer for community detection. J. Bionic Eng. 2023, 20, 2331–2358. [Google Scholar] [CrossRef]
- Yu, M.; Xu, J.; Liang, W.; Qiu, Y.; Bao, S.; Tang, L. Improved multi-strategy adaptive Grey Wolf Optimization for practical engineering applications and high-dimensional problem solving. Artif. Intell. Rev. 2024, 57, 277. [Google Scholar] [CrossRef]
- Yang, J.; Cui, J.; Zhang, Y.D. Artificial bee colony algorithm with adaptive covariance matrix for hearing loss detection. Knowl.-Based Syst. 2021, 216, 106792. [Google Scholar] [CrossRef]
- Yang, J.; Xia, X.; Cui, J.; Zhang, Y.D. An artificial bee colony algorithm with a cumulative covariance matrix mechanism and its application in parameter optimization for hearing loss detection models. Expert Syst. Appl. 2023, 229, 120533. [Google Scholar] [CrossRef]
- Dhar, A.R.; Gupta, D.; Roy, S.S.; Lohar, A.K.; Mandal, N. Covariance matrix adapted grey wolf optimizer tuned eXtreme gradient boost for bi-directional modelling of direct metal deposition process. Expert Syst. Appl. 2022, 199, 116971. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Faris, H.; Aljarah, I.; Al-Betar, M.A.; Mirjalili, S. Grey wolf optimizer: A review of recent variants and applications. Neural Comput. Appl. 2018, 30, 413–435. [Google Scholar] [CrossRef]
- Ma, S.; Fang, Y.; Zhao, X.; Liu, Z. Multi-swarm improved Grey Wolf Optimizer with double adaptive weights and dimension learning for global optimization problems. Math. Comput. Simul. 2023, 205, 619–641. [Google Scholar] [CrossRef]
- Chen, K.; Xue, B.; Zhang, M.; Zhou, F. Novel chaotic grouping particle swarm optimization with a dynamic regrouping strategy for solving numerical optimization tasks. Knowl.-Based Syst. 2020, 194, 105568. [Google Scholar] [CrossRef]
- Chen, Y.; Li, L.; Peng, H.; Xiao, J.; Wu, Q. Dynamic multi-swarm differential learning particle swarm optimizer. Swarm Evol. Comput. 2018, 39, 209–221. [Google Scholar] [CrossRef]
- Yao, X.; Liu, Y.; Lin, G. Evolutionary programming made faster. IEEE Trans. Evol. Comput. 1999, 3, 82–102. [Google Scholar] [CrossRef]
- Awad, N.H.; Ali, M.Z.; Suganthan, P.N. Ensemble sinusoidal differential covariance matrix adaptation with Euclidean neighborhood for solving CEC2017 benchmark problems. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 372–379. [Google Scholar]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Augmented grey wolf optimizer for grid-connected PMSG-based wind energy conversion systems. Appl. Soft Comput. 2018, 69, 504–515. [Google Scholar] [CrossRef]
- Şenel, F.A.; Gökçe, F.; Yüksel, A.S.; Yiğit, T. A novel hybrid PSO–GWO algorithm for optimization problems. Eng. Comput. 2019, 35, 1359–1373. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Gupta, S.; Deep, K. A novel hybrid sine cosine algorithm for global optimization and its application to train multilayer perceptrons. Appl. Intell. 2020, 50, 993–1026. [Google Scholar] [CrossRef]
- Lynn, N.; Suganthan, P.N. Heterogeneous comprehensive learning particle swarm optimization with enhanced exploration and exploitation. Swarm Evol. Comput. 2015, 24, 11–24. [Google Scholar] [CrossRef]
- Mirjalili, S.; Hashim, S.Z.M. A new hybrid PSOGSA algorithm for function optimization. In Proceedings of the 2010 International Conference on Computer and Information Application, Tianjin, China, 3–5 December 2010; pp. 374–377. [Google Scholar]
- Gupta, S.; Deep, K. A hybrid self-adaptive sine cosine algorithm with opposition based learning. Expert Syst. Appl. 2019, 119, 210–230. [Google Scholar] [CrossRef]
- Cheng, S.; Shi, Y.; Qin, Q.; Zhang, Q.; Bai, R. Population diversity maintenance in brain storm optimization algorithm. J. Artif. Intell. Soft Comput. Res. 2014, 4, 83–97. [Google Scholar] [CrossRef]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A.; Hamdi, M. Water cycle algorithm—A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012, 110, 151–166. [Google Scholar] [CrossRef]
- Coello, C.A.C. Use of a self-adaptive penalty approach for engineering optimization problems. Comput. Ind. 2000, 41, 113–127. [Google Scholar] [CrossRef]

| Algorithm | Population Size (n) | Parameters | Reference |
|---|---|---|---|
| CDL-DGWO | 30 | ~ | |
| GWO | 30 | [5] | |
| MIGWO | 30 | [30] | |
| IGWO | 30 | [27] | |
| LGWO | 30 | [17] | |
| HGWOSCA | 30 | [14] | |
| RWGWO | 30 | [18] | |
| EGWO | 30 | [35] | |
| PSOGWO | 30 | [36] | |
| PSO | 30 | [37] | |
| MFO | 30 | [6] | |
| SSA | 30 | [38] | |
| WOA | 30 | [8] | |
| HSCA | 30 | a = 2, , , | [39] |
| HCLPSO | 30 | [40] | |
| PSOGSA | 30 | [41] | |
| mSCA | 30 | [42] |
| Algorithm | Chaotic Grouping and Dynamic Regrouping | Covariance | Dimension Learning |
|---|---|---|---|
| GWO | 0 | 0 | 0 |
| C-GWO | 1 | 1 | 0 |
| D-GWO | 1 | 0 | 1 |
| CDL-DGWO | 1 | 1 | 1 |
| GWO | C-GWO | D-GWO | CDL-DGWO | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | St | |
| F1 | ||||||||
| F2 | ||||||||
| F3 | ||||||||
| F4 | ||||||||
| F5 | ||||||||
| F6 | ||||||||
| F7 | ||||||||
| F8 | ||||||||
| F9 | ||||||||
| F10 | ||||||||
| F11 | ||||||||
| F12 | ||||||||
| F13 | ||||||||
| F14 | ||||||||
| F15 | ||||||||
| F16 | ||||||||
| F17 | ||||||||
| F18 | ||||||||
| F19 | ||||||||
| F20 | ||||||||
| F21 | ||||||||
| F22 | ||||||||
| F23 | ||||||||
| CDL-DGWO VS. | + | − | ≈ | R+ | R− | p-Value | a = 0.05 |
|---|---|---|---|---|---|---|---|
| GWO | 22 | 1 | 0 | 267 | 9 | 0.000087 | + |
| C-GWO | 19 | 3 | 1 | 240 | 36 | 0.003302 | + |
| D-GWO | 22 | 1 | 0 | 269 | 7 | 0.000068 | + |
| GWO | C-GWO | D-GWO | CDL-DGWO | |
|---|---|---|---|---|
| Ave | 3.1739 | 2.7609 | 2.8261 | 1.2391 |
| Rank | 4 | 2 | 3 | 1 |
| CDL-DGWO | GWO | IGWO | LGWO | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| F1 | ||||||||
| F2 | ||||||||
| F3 | ||||||||
| F4 | ||||||||
| F5 | ||||||||
| F6 | ||||||||
| F7 | ||||||||
| F8 | ||||||||
| F9 | ||||||||
| F10 | ||||||||
| F11 | ||||||||
| F12 | ||||||||
| F13 | ||||||||
| F14 | ||||||||
| F15 | ||||||||
| F16 | ||||||||
| F17 | ||||||||
| F18 | ||||||||
| F19 | ||||||||
| F20 | ||||||||
| F21 | ||||||||
| F22 | ||||||||
| F23 | ||||||||
| HGWOSCA | RWGWO | EGWO | PSOGWO | |||||
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| F1 | ||||||||
| F2 | ||||||||
| F3 | ||||||||
| F4 | ||||||||
| F5 | ||||||||
| F6 | ||||||||
| F7 | ||||||||
| F8 | ||||||||
| F9 | ||||||||
| F10 | ||||||||
| F11 | ||||||||
| F12 | ||||||||
| F13 | ||||||||
| F14 | ||||||||
| F15 | ||||||||
| F16 | ||||||||
| F17 | ||||||||
| F18 | ||||||||
| F19 | ||||||||
| F20 | ||||||||
| F21 | ||||||||
| F22 | ||||||||
| F23 | ||||||||
| PSO | MFO | SSA | WOA | |||||
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| F1 | ||||||||
| F2 | ||||||||
| F3 | ||||||||
| F4 | ||||||||
| F5 | ||||||||
| F6 | ||||||||
| F7 | ||||||||
| F8 | ||||||||
| F9 | ||||||||
| F10 | ||||||||
| F11 | ||||||||
| F12 | ||||||||
| F13 | ||||||||
| F14 | ||||||||
| F15 | ||||||||
| F16 | ||||||||
| F17 | ||||||||
| F18 | ||||||||
| F19 | ||||||||
| F20 | ||||||||
| F21 | ||||||||
| F22 | ||||||||
| F23 | ||||||||
| HSCA | HCLPSO | PSOGSA | mSCA | |||||
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| F1 | ||||||||
| F2 | ||||||||
| F3 | ||||||||
| F4 | ||||||||
| F5 | ||||||||
| F6 | ||||||||
| F7 | ||||||||
| F8 | ||||||||
| F9 | ||||||||
| F10 | ||||||||
| F11 | ||||||||
| F12 | ||||||||
| F13 | ||||||||
| F14 | ||||||||
| F15 | ||||||||
| F16 | ||||||||
| F17 | ||||||||
| F18 | ||||||||
| F19 | ||||||||
| F20 | ||||||||
| F21 | ||||||||
| F22 | ||||||||
| F23 | ||||||||
| CDL-DGWO VS. | + | − | ≈ | R+ | R− | p-Value | a = 0.05 |
|---|---|---|---|---|---|---|---|
| GWO | 22 | 1 | 0 | 267 | 9 | 0.00009 | + |
| IGWO | 13 | 10 | 0 | 178 | 98 | 0.22376 | ≈ |
| LGWO | 23 | 0 | 0 | 276 | 0 | 0.00003 | + |
| HGWOSCA | 22 | 1 | 0 | 267 | 9 | 0.00009 | + |
| RWGWO | 22 | 1 | 0 | 265 | 11 | 0.00011 | + |
| EGWO | 22 | 1 | 0 | 268 | 8 | 0.00008 | + |
| PSOGWO | 23 | 0 | 0 | 276 | 0 | 0.00003 | + |
| PSO | 16 | 7 | 0 | 240 | 36 | 0.00192 | + |
| MFO | 19 | 4 | 0 | 266 | 10 | 0.00010 | + |
| SSA | 17 | 6 | 0 | 251 | 25 | 0.00059 | + |
| WOA | 21 | 2 | 0 | 249 | 27 | 0.00074 | + |
| HSCA | 23 | 0 | 0 | 276 | 0 | 0.00003 | + |
| HCLPSO | 11 | 12 | 0 | 165 | 111 | 0.41153 | ≈ |
| PSOGSA | 18 | 5 | 0 | 261 | 15 | 0.00018 | + |
| mSCA | 21 | 0 | 2 | 276 | 0 | 0.00006 | + |
| Rank | Ave | Rank | Ave | ||
|---|---|---|---|---|---|
| CDL-DGWO | 1 | 3.2 | PSO | 6 | 7.3 |
| GWO | 8 | 7.7 | MFO | 13 | 11.2 |
| IGWO | 2 | 4.4 | SSA | 11 | 9.7 |
| LGWO | 12 | 10.1 | WOA | 7 | 7.3 |
| HGWOSCA | 5 | 7.3 | HSCA | 15 | 12.4 |
| RWGWO | 4 | 6.5 | HCLPSO | 3 | 5.7 |
| EGWO | 10 | 9.6 | PSOGSA | 14 | 11.9 |
| PSOGWO | 16 | 13.4 | mSCA | 9 | 8.3 |
| CDL-DGWO | GWO | IGWO | LGWO | |||||
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| f1 | ||||||||
| f3 | ||||||||
| f4 | ||||||||
| f5 | ||||||||
| f6 | ||||||||
| f7 | ||||||||
| f8 | ||||||||
| f9 | ||||||||
| f10 | ||||||||
| f11 | ||||||||
| f12 | ||||||||
| f13 | ||||||||
| f14 | ||||||||
| f15 | ||||||||
| f16 | ||||||||
| f17 | ||||||||
| f18 | ||||||||
| f19 | ||||||||
| f20 | ||||||||
| f21 | ||||||||
| f22 | ||||||||
| f23 | ||||||||
| f24 | ||||||||
| f25 | ||||||||
| f26 | ||||||||
| f27 | ||||||||
| f28 | ||||||||
| f29 | ||||||||
| f30 | ||||||||
| HGWOSCA | RWGWO | EGWO | PSOGWO | |||||
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| f1 | ||||||||
| f3 | ||||||||
| f4 | ||||||||
| f5 | ||||||||
| f6 | ||||||||
| f7 | ||||||||
| f8 | ||||||||
| f9 | ||||||||
| f10 | ||||||||
| f11 | ||||||||
| f12 | ||||||||
| f13 | ||||||||
| f14 | ||||||||
| f15 | ||||||||
| f16 | ||||||||
| f17 | ||||||||
| f18 | ||||||||
| f19 | ||||||||
| f20 | ||||||||
| f21 | ||||||||
| f22 | ||||||||
| f23 | ||||||||
| f24 | ||||||||
| f25 | ||||||||
| f26 | ||||||||
| f27 | ||||||||
| f28 | ||||||||
| f29 | ||||||||
| f30 | ||||||||
| MIGWO | PSO | MFO | SSA | |||||
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| f1 | ||||||||
| f3 | ||||||||
| f4 | ||||||||
| f5 | ||||||||
| f6 | ||||||||
| f7 | ||||||||
| f8 | ||||||||
| f9 | ||||||||
| f10 | ||||||||
| f11 | ||||||||
| f12 | ||||||||
| f13 | ||||||||
| f14 | ||||||||
| f15 | ||||||||
| f16 | ||||||||
| f17 | ||||||||
| f18 | ||||||||
| f19 | ||||||||
| f20 | ||||||||
| f21 | ||||||||
| f22 | ||||||||
| f23 | ||||||||
| f24 | ||||||||
| f25 | ||||||||
| f26 | ||||||||
| f27 | ||||||||
| f28 | ||||||||
| f29 | ||||||||
| f30 | ||||||||
| WOA | HSCA | PSOGSA | mSCA | |||||
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| f1 | ||||||||
| f3 | ||||||||
| f4 | ||||||||
| f5 | ||||||||
| f6 | ||||||||
| f7 | ||||||||
| f8 | ||||||||
| f9 | ||||||||
| f10 | ||||||||
| f11 | ||||||||
| f12 | ||||||||
| f13 | ||||||||
| f14 | ||||||||
| f15 | ||||||||
| f16 | ||||||||
| f17 | ||||||||
| f18 | ||||||||
| f19 | ||||||||
| f20 | ||||||||
| f21 | ||||||||
| f22 | ||||||||
| f23 | ||||||||
| f24 | ||||||||
| f25 | ||||||||
| f26 | ||||||||
| f27 | ||||||||
| f28 | ||||||||
| f29 | ||||||||
| f30 | ||||||||
| CDL-DGWO VS. | + | − | ≈ | R+ | R− | p-Value | a = 0.05 |
|---|---|---|---|---|---|---|---|
| GWO | 29 | 0 | 0 | 435 | 0 | 0.00000 | + |
| IGWO | 7 | 22 | 0 | 94 | 341 | 0.00757 | − |
| LGWO | 29 | 0 | 0 | 435 | 0 | 0.00000 | + |
| HGWOSCA | 29 | 0 | 0 | 435 | 0 | 0.00000 | + |
| RWGWO | 21 | 8 | 0 | 347 | 88 | 0.00511 | ≈ |
| EGWO | 29 | 0 | 0 | 435 | 0 | 0.00000 | + |
| PSOGWO | 29 | 0 | 0 | 435 | 0 | 0.00000 | + |
| MIGWO | 23 | 6 | 0 | 369 | 66 | 0.00105 | + |
| PSO | 16 | 13 | 0 | 205 | 230 | 0.78694 | ≈ |
| MFO | 29 | 0 | 0 | 435 | 0 | 0.00000 | + |
| SSA | 21 | 8 | 0 | 293 | 142 | 0.10256 | ≈ |
| WOA | 28 | 1 | 0 | 417 | 18 | 0.00002 | + |
| HSCA | 29 | 0 | 0 | 435 | 0 | 0.00000 | + |
| PSOGSA | 29 | 0 | 0 | 435 | 0 | 0.00000 | + |
| mSCA | 28 | 1 | 0 | 417 | 18 | 0.00002 | + |
| Rank | Ave | Rank | Ave | ||
|---|---|---|---|---|---|
| CDL-DGWO | 2 | 3.03 | MIGWO | 4 | 4.76 |
| GWO | 9 | 8.55 | PSO | 6 | 5.79 |
| IGWO | 1 | 2.21 | MFO | 12 | 12.21 |
| LGWO | 11 | 11.45 | SSA | 7 | 6.45 |
| HGWOSCA | 8 | 7.55 | WOA | 13 | 12.28 |
| RWGWO | 3 | 4.21 | HSCA | 15 | 13.69 |
| EGWO | 16 | 14.66 | PSOGSA | 14 | 13.66 |
| PSOGWO | 10 | 9.93 | mSCA | 5 | 5.59 |
| Mean | Std | Best | Best Values for Variables | |||||
|---|---|---|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | x5 | ||||
| CDL-DGWO | −30,939.86 | 240.84 | −31,453.63 | 58.1663 | 30.2820 | 30.9084 | 46.29 | 42.19 |
| GWO | −30,657.62 | 3.37 | −30,663.58 | 78 | 33 | 30.01993 | 45 | 36.72181 |
| MIGWO | −30,621.15 | 19.16 | −30,652.95 | 78.1843 | 36.3522 | 32.8490 | 35.8049 | 34.0235 |
| IGWO | −30,653.64 | 5.15 | −30,660.87 | 78.0330 | 33.0005 | 30.0320 | 44.9935 | 36.6943 |
| LGWO | −30,514.90 | 84.48 | −30,631.71 | 78 | 33 | 30.5260 | 45 | 35.8899 |
| HGWOSCA | −30,655.91 | 3.64 | −30,662.48 | 78 | 33 | 30.0244 | 45 | 36.7473 |
| RWGWO | −30,659.20 | 3.56 | −30,664.49 | 78 | 33 | 30.0067 | 45 | 36.7748 |
| EGWO | −30,658.42 | 5.88 | −30,664.79 | 78 | 33.0182 | 30.0358 | 45 | 36.6768 |
| PSOGWO | −30,650.96 | 27.82 | −30,665.28 | 78 | 33 | 30.0208 | 44.9763 | 36.7329 |
| MFO | −30,642.89 | 43.32 | −30,665.54 | 78 | 33 | 29.9953 | 45 | 36.7758 |
| SSA | −29,739.53 | −29,739.53 | 78.0427 | 35.6896 | 33.9524 | 41.2558 | 30.1411 | |
| WOA | −29,913.76 | 142.60 | −30,323.91 | 78 | 35.5690 | 33.7554 | 40.9303 | 29.9783 |
| HSCA | −30,280.57 | 188.77 | −30,566.36 | 78 | 33 | 30.4282 | 45 | 36.1814 |
| PSOGSA | −30,660.77 | 19.52 | −30,665.54 | 78 | 33 | 29.9953 | 45 | 36.7758 |
| mSCA | −30,607.12 | 34.17 | −30,647.25 | 78 | 33.1531 | 30.1047 | 44.9989 | 36.5289 |
| Mean | Std | Best | Best Values for Variables | |||
|---|---|---|---|---|---|---|
| x1 | x2 | x3 | ||||
| CDL-DGWO | 0.0127 | 0.0000 | 0.0127 | 0.0519 | 0.3599 | 11.1646 |
| GWO | 0.0128 | 0.0000 | 0.0127 | 0.0546 | 0.4303 | 8.0324 |
| MIGWO | 0.0128 | 0.0000 | 0.0127 | 0.0535 | 0.3814 | 11.7483 |
| IGWO | 0.0127 | 0.0000 | 0.0127 | 0.0517 | 0.3562 | 11.3484 |
| LGWO | 0.0132 | 0.0005 | 0.0128 | 0.0539 | 0.4088 | 9.1575 |
| HGWOSCA | 0.0128 | 0.0002 | 0.0127 | 0.0500 | 0.3172 | 14.0638 |
| RWGWO | 0.0128 | 0.0002 | 0.0127 | 0.0500 | 0.3172 | 14.0646 |
| EGWO | 0.0132 | 0.0005 | 0.0127 | 0.0585 | 0.5413 | 5.2880 |
| PSOGWO | 0.0128 | 0.0001 | 0.0127 | 0.0501 | 0.3187 | 13.9319 |
| MFO | 0.0131 | 0.0008 | 0.0127 | 0.0500 | 0.3174 | 14.0278 |
| SSA | 0.0185 | 0.0777 | 1.3657 | 1.4074 | ||
| WOA | 0.0142 | 0.0011 | 0.0127 | 0.0657 | 0.7960 | 2.6487 |
| HSCA | 0.0139 | 0.0009 | 0.0130 | 0.0500 | 0.3115 | 15.0000 |
| PSOGSA | 0.0135 | 0.0009 | 0.0127 | 0.0528 | 0.3828 | 9.9089 |
| mSCA | 0.0128 | 0.0002 | 0.0127 | 0.0507 | 0.3318 | 12.9811 |
| Mean | Std | Best | Best Values for Variables | ||||
|---|---|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | ||||
| CDL-DGWO | 1.7249 | 1.7249 | 0.2057 | 3.4705 | 9.0366 | 0.2057 | |
| GWO | 1.7295 | 0.0032 | 1.7262 | 0.2046 | 3.4990 | 9.0382 | 0.2058 |
| MIGWO | 1.7410 | 0.0081 | 1.7314 | 0.2351 | 3.2464 | 8.4059 | 0.2436 |
| IGWO | 1.7295 | 0.0015 | 1.7267 | 0.2053 | 3.4809 | 9.0614 | 0.2058 |
| LGWO | 1.8406 | 0.0297 | 1.7622 | 0.2064 | 3.5079 | 9.0255 | 0.2170 |
| HGWOSCA | 1.7302 | 0.0030 | 1.7263 | 0.2056 | 3.4777 | 9.0453 | 0.2060 |
| RWGWO | 1.7290 | 0.0017 | 1.7266 | 0.2039 | 3.5142 | 9.0429 | 0.2057 |
| EGWO | 1.7472 | 0.0404 | 1.7264 | 0.2046 | 3.4962 | 9.0349 | 0.2059 |
| PSOGWO | 1.7444 | 0.0352 | 1.7251 | 0.2054 | 3.6264 | 9.0816 | 0.2088 |
| MFO | 1.8213 | 0.1587 | 1.7249 | 0.3087 | 2.5470 | 7.3754 | 0.3088 |
| SSA | 9.5473 | 9.5473 | 1.1900 | 3.1444 | 3.4581 | 1.6228 | |
| WOA | 4.2099 | 0.9787 | 1.9154 | 0.1654 | 4.1512 | 10.0000 | 0.2050 |
| HSCA | 1.8732 | 0.0489 | 1.7835 | 0.2130 | 4.0698 | 8.7929 | 0.2195 |
| PSOGSA | 2.2723 | 0.2732 | 1.7472 | 0.2990 | 2.6560 | 7.3623 | 0.3099 |
| mSCA | 1.7415 | 0.0111 | 1.7277 | 0.2026 | 3.5556 | 9.0790 | 0.2081 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, S.; Xu, M.; Zhao, X.; Yan, X. Double-Swarm Grey Wolf Optimizer with Covariance and Dimension Learning for Engineering Optimization Problems. Symmetry 2025, 17, 2030. https://doi.org/10.3390/sym17122030
Ma S, Xu M, Zhao X, Yan X. Double-Swarm Grey Wolf Optimizer with Covariance and Dimension Learning for Engineering Optimization Problems. Symmetry. 2025; 17(12):2030. https://doi.org/10.3390/sym17122030
Chicago/Turabian StyleMa, Shuidong, Miao Xu, Xiaodong Zhao, and Xiaodong Yan. 2025. "Double-Swarm Grey Wolf Optimizer with Covariance and Dimension Learning for Engineering Optimization Problems" Symmetry 17, no. 12: 2030. https://doi.org/10.3390/sym17122030
APA StyleMa, S., Xu, M., Zhao, X., & Yan, X. (2025). Double-Swarm Grey Wolf Optimizer with Covariance and Dimension Learning for Engineering Optimization Problems. Symmetry, 17(12), 2030. https://doi.org/10.3390/sym17122030




