Stem Structures and Novel Localized Wave Molecules of the (2+1)-Dimensional pKP-BKP Equation
Abstract
1. Introduction
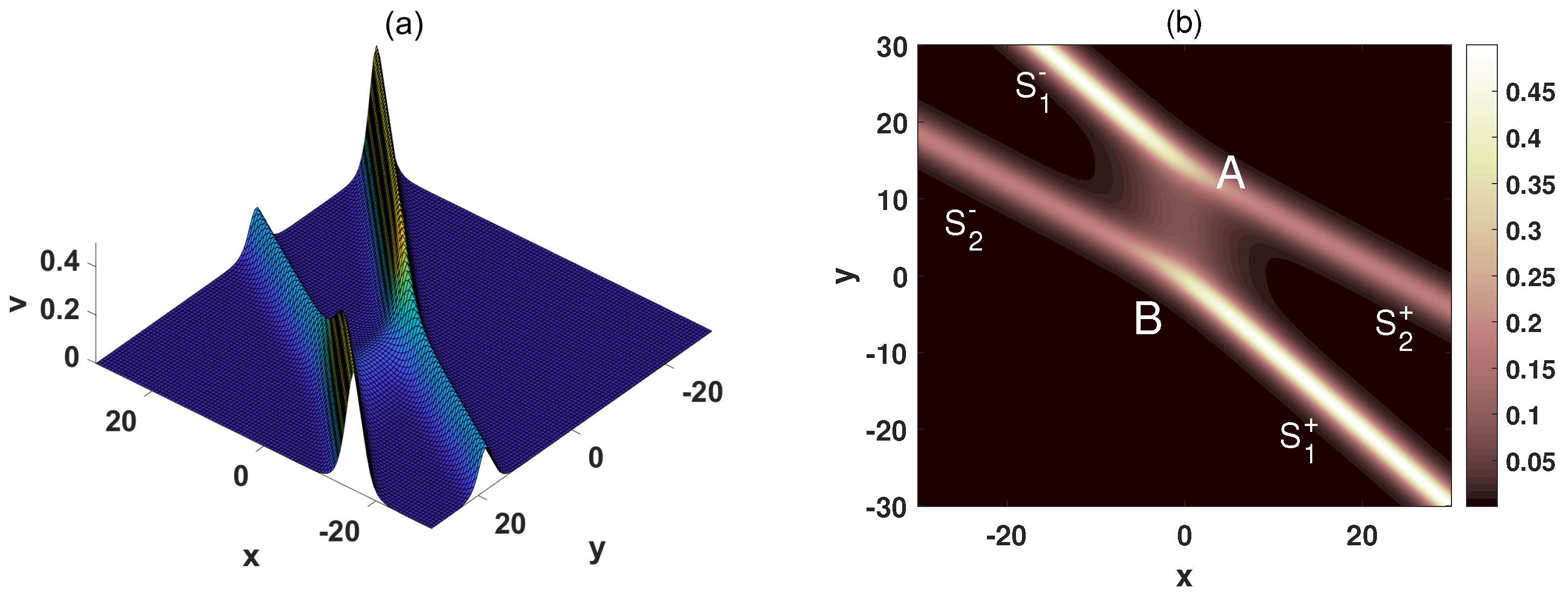
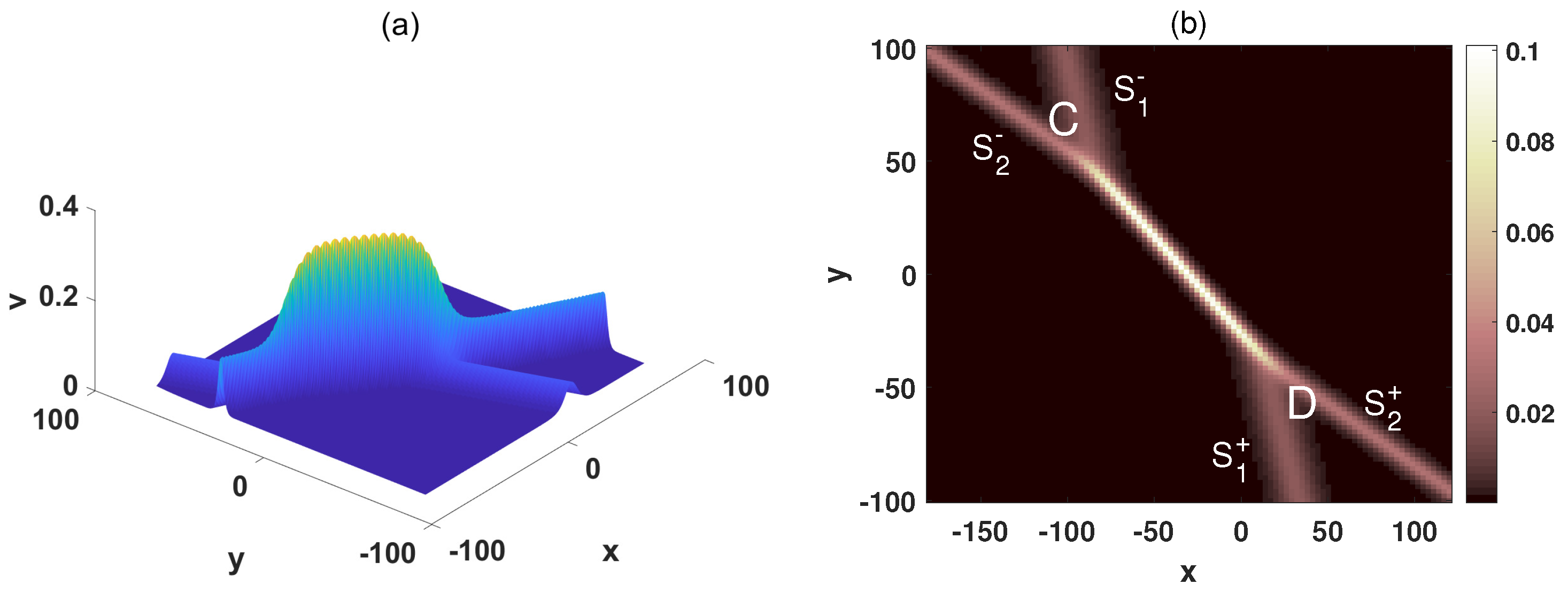
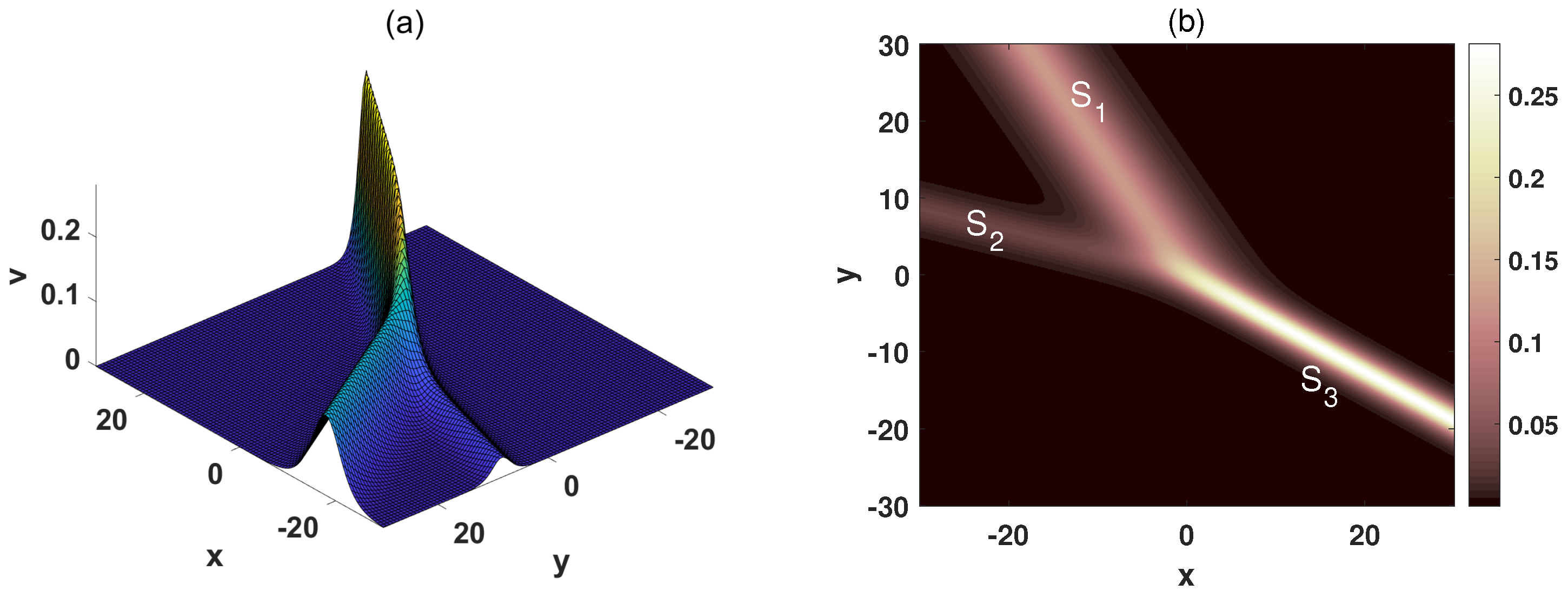
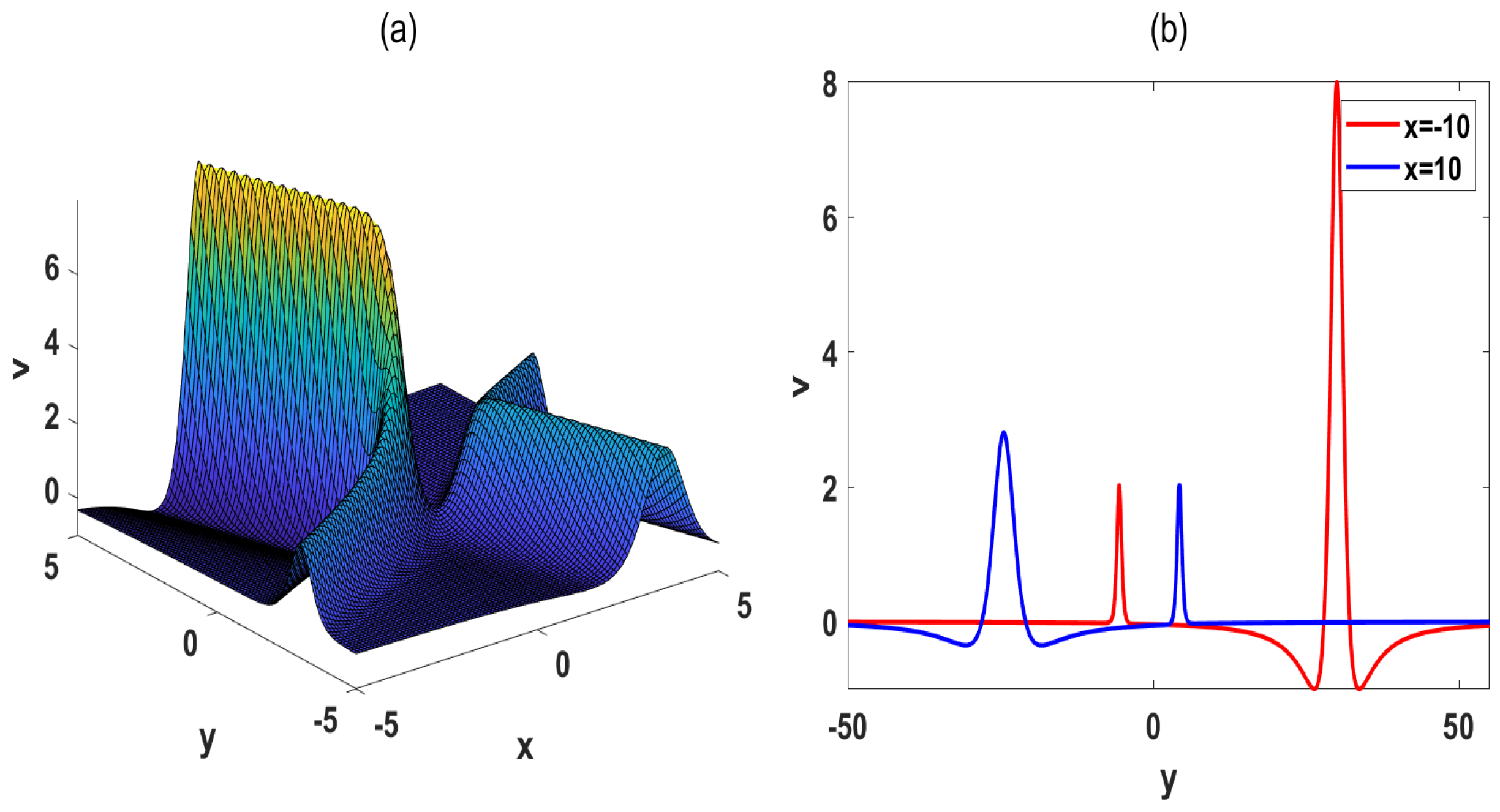
2. Stem Structures of the (2+1)-Dimensional pKP-BKP Equation
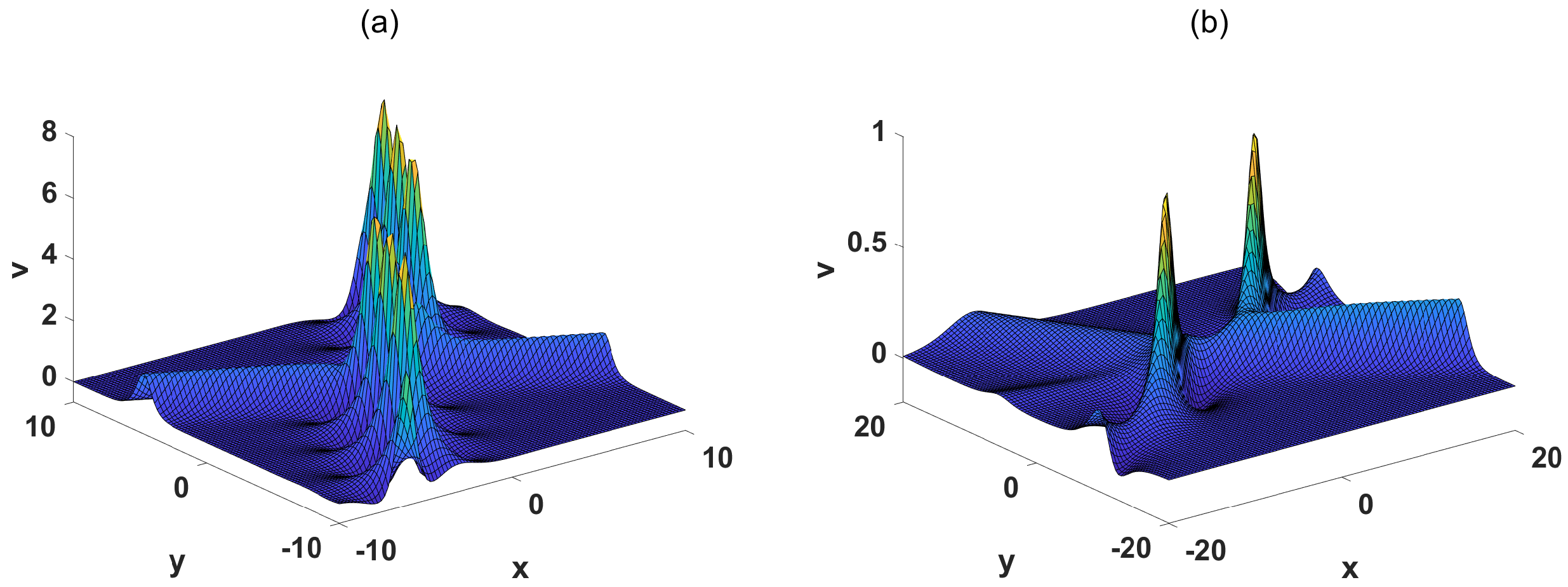
3. Interaction Among Breather Wave, Transformed Wave and Soliton of the (2+1)-Dimensional pKP-BKP Equation
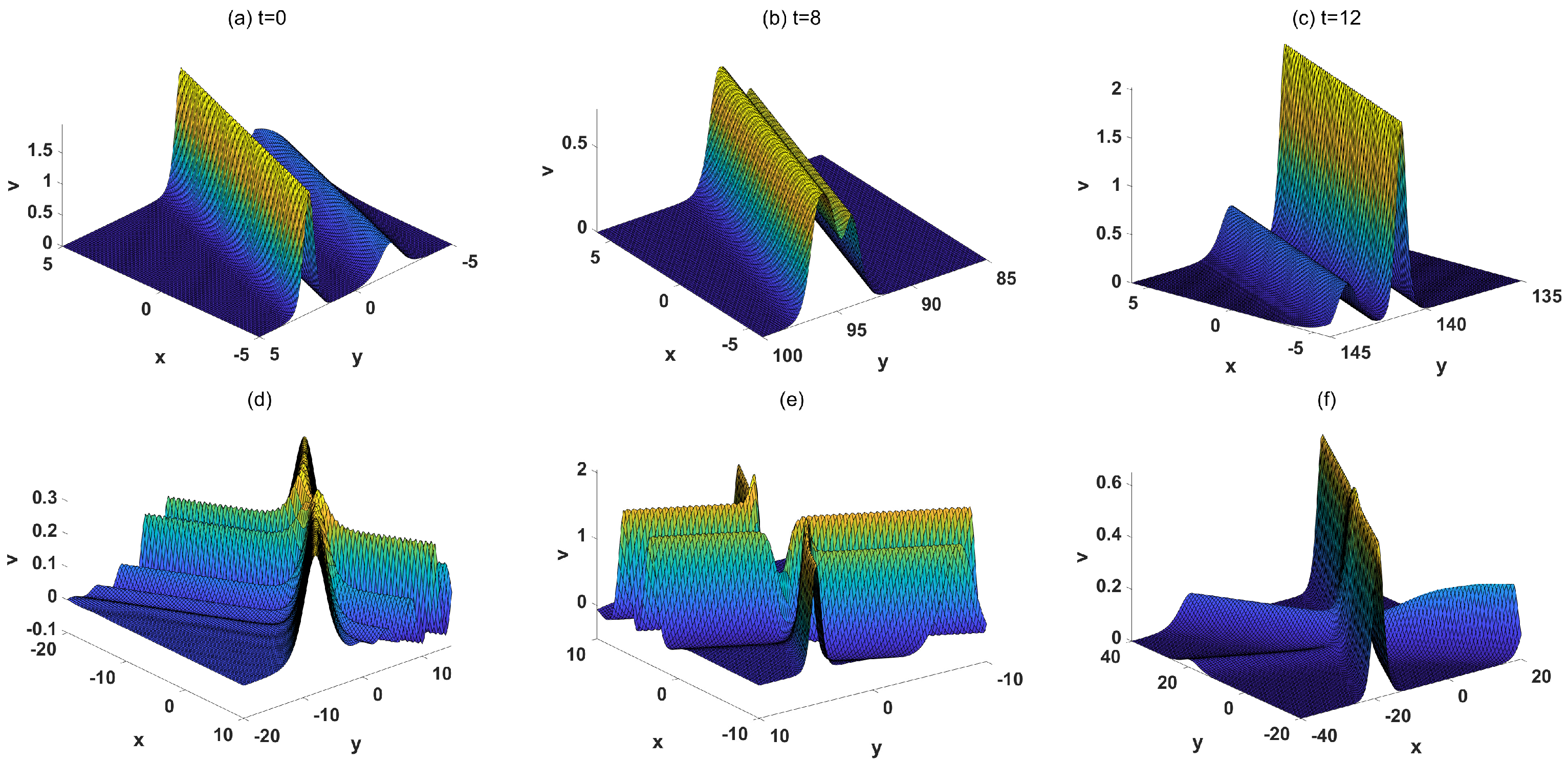
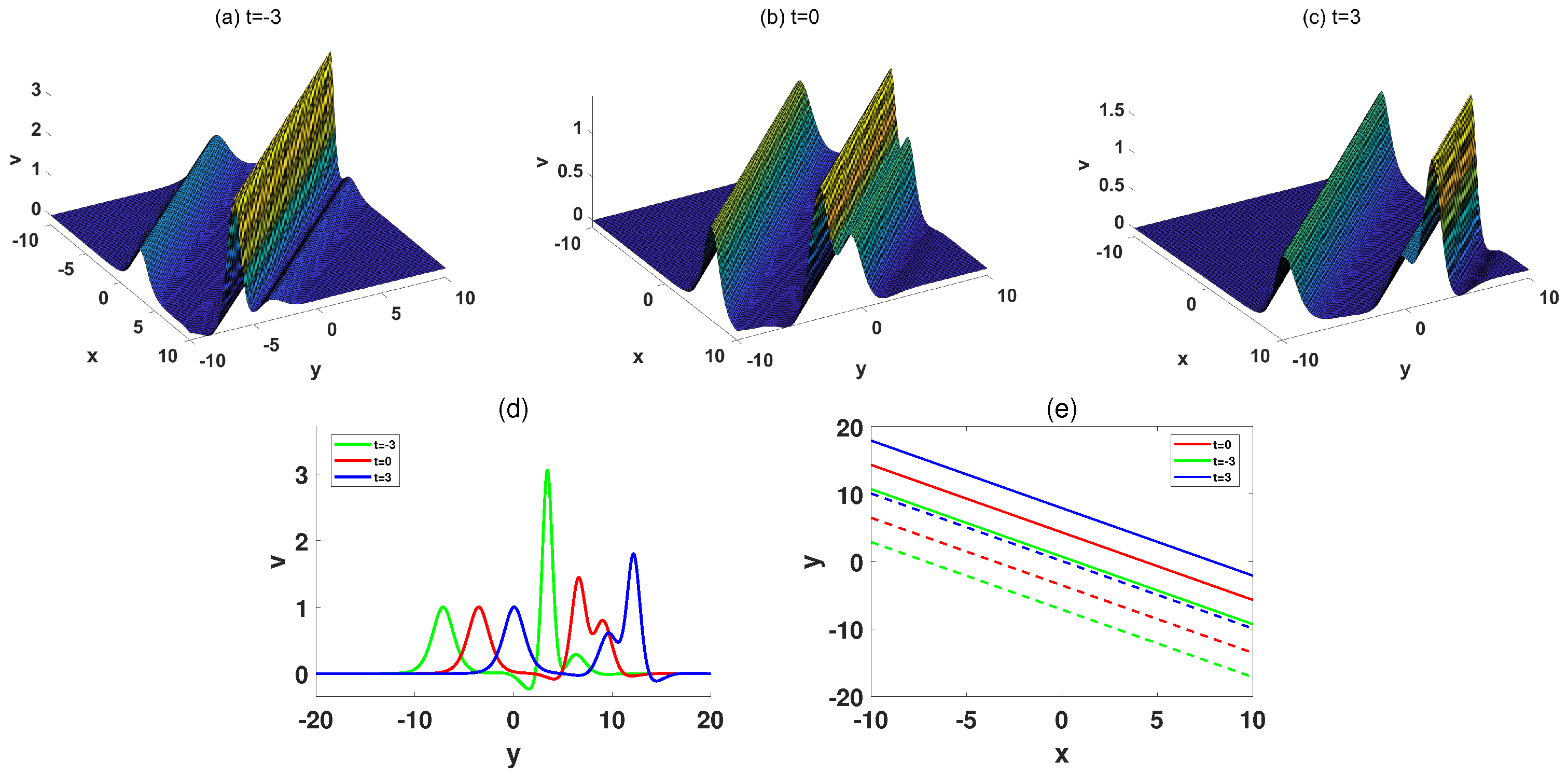
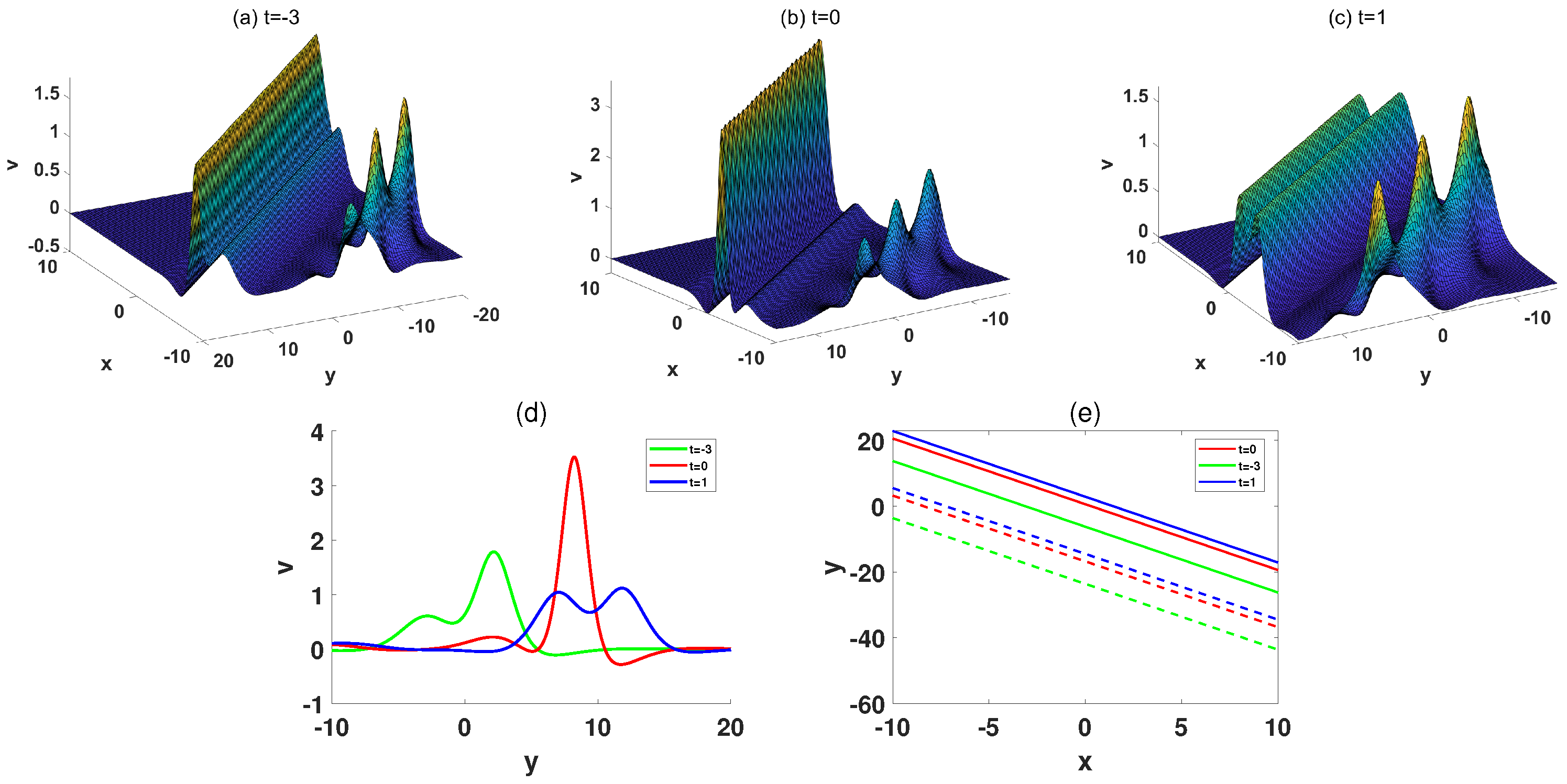
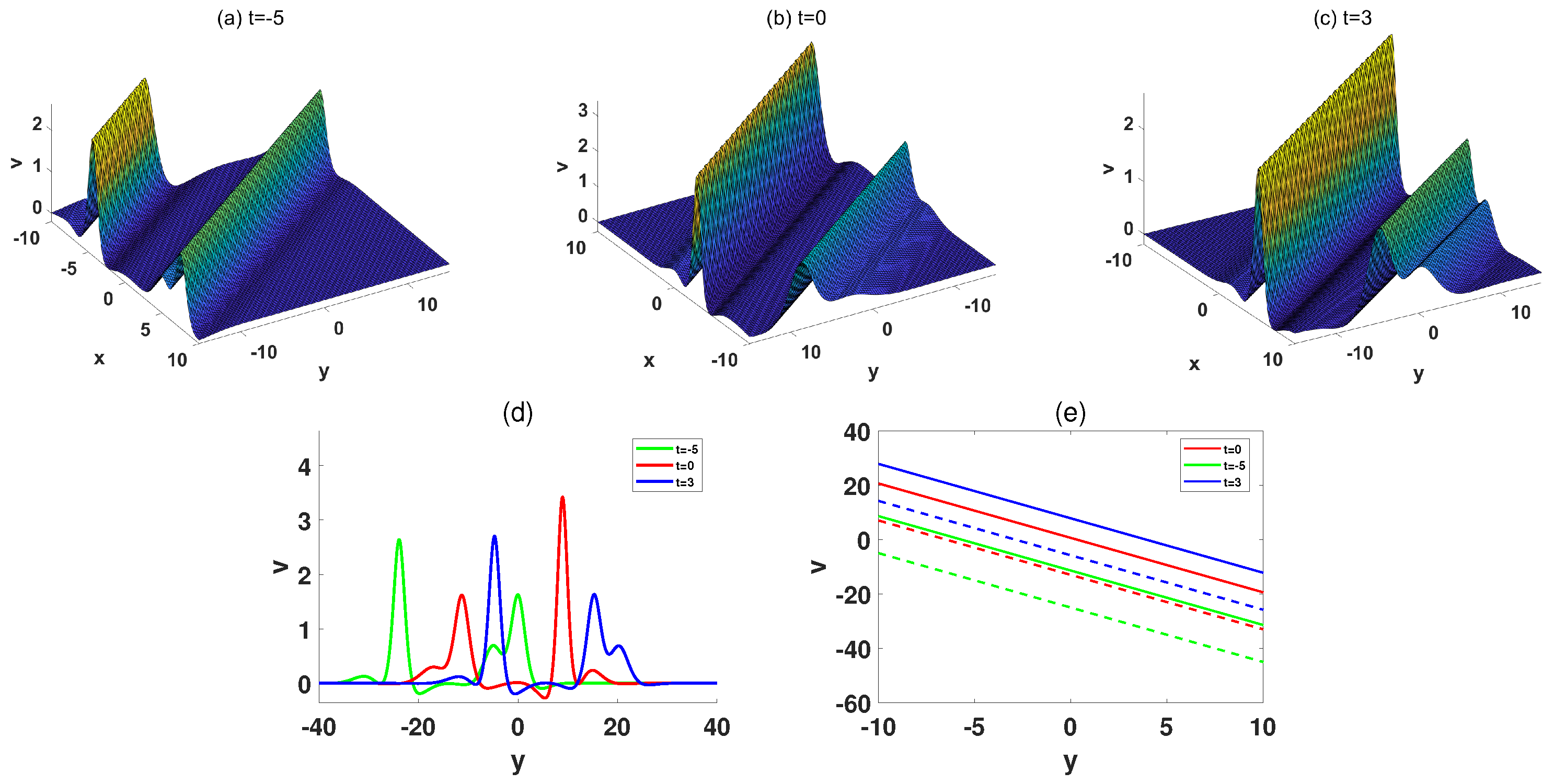
4. Transformed Wave-Soliton Molecule and Transformed Wave Molecule of the (2+1)-Dimensional pKP-BKP Equation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Q.; Mihalache, D.; Belić, M.R.; Lin, J. Mode conversion of various solitons in parabolic and cross-phase potential wells. Opt. Lett. 2024, 49, 1607–1610. [Google Scholar] [CrossRef]
- Yao, X.M.; Zhao, J.F.; Liang, R. State-transition mechanisms for (2+1)-dimensional Sawada-Kotera equation with the variable coefficients in plasma physics and fluid dynamics. Chaos Solitons Fractals 2025, 197, 116485. [Google Scholar] [CrossRef]
- Wang, Q.; Mihalache, D.; Belić, M.R.; Zeng, L.; Lin, J. Spiraling Laguerre-Gaussian solitons and arrays in parabolic potential wells. Opt. Lett. 2023, 48, 4233–4236. [Google Scholar] [CrossRef]
- Mohan, B.; Kumar, S. Generalization and analytic exploration of soliton solutions for nonlinear evolution equations via a novel symbolic approach in fluids and nonlinear sciences. Chin. J. Phys. 2024, 92, 10–21. [Google Scholar] [CrossRef]
- Tanwar, D.V. Lie symmetry reductions and generalized exact solutions of Date-Jimbo Kashiwara-Miwa equation. Chaos Soliton Fractals 2022, 162, 112414. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Kaup, D.J.; Newell, A.C.; Segur, H. The inverse scattering transform-Fourier analysis for nonlinear problems. Stud. Appl. Math. 1974, 53, 249–315. [Google Scholar] [CrossRef]
- Satsuma, J. Hirota bilinear method for nonlinear evolution equations. In Direct and Inverse Methods in Nonlinear Evolution Equations; Springer: Berlin/Heidelberg, Germany, 2003; Volume 632, pp. 171–222. [Google Scholar]
- Kumar, S.; Kumar, A. Lie symmetry reductions and group invariant solutions of (2+1)-dimensional modified veronese web equation. Nonlinear Dyn. 2019, 98, 1891–1903. [Google Scholar] [CrossRef]
- Gu, C.H.; Hu, H.S.; Zhou, Z.S. Darboux Transformations in Integrable Systems: Theory and Their Applications to Geometry; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Taha, T.R.; Ablowitz, M.I. Analytical and numerical aspects of certain nonlinear evolution equations. II. Numerical, nonlinear Schrödinger equation. J. Comput. Phys. 1984, 55, 203–230. [Google Scholar] [CrossRef]
- Ma, W.X. Wronskians, generalized Wronskians and solutions to the Korteweg-de Vries equation. Chaos Solitons Fractals 2004, 19, 163–170. [Google Scholar] [CrossRef]
- Maccari, A. The Kadomtsev-Petviashvili equation as a source of integrable model equations. J. Math. Phys. 1996, 37, 6207–6212. [Google Scholar] [CrossRef]
- Pava, J.A.; Plaza, R.G. Instability theory of kink and anti-kink profiles for the sine-Gordon equation on Josephson tricrystal boundaries. Physica D 2021, 427, 133020. [Google Scholar] [CrossRef]
- Yang, Z.P.; Zhong, W.P. Dark Localized Waves in Shallow Waters: Analysis within an Extended Boussinesq System. Chin. Phys. Lett. 2024, 41, 044201. [Google Scholar] [CrossRef]
- Kath, W.L.; Smyth, N.F. Soliton evolution and radiation loss for the Korteweg-de Vries equation. Phys. Rev. E 1995, 51, 661. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.H.; Porsezian, K.; He, J.S. Breather and rogue wave solutions of a generalized nonlinear Schrödinger equation. Phys. Rev. E 2013, 87, 053202. [Google Scholar] [CrossRef]
- Ma, W.X. Lump solutions to the Kadomtsev-Petviashvili equation. Phys. Lett. A 2015, 379, 1975–1978. [Google Scholar] [CrossRef]
- Kako, F.; Yajima, N. Interaction of ion-acoustic solitons in two-dimensional space. J. Phys. Soc. Jpn. 1980, 49, 2063–2071. [Google Scholar] [CrossRef]
- Ohkuma, K.; Wadati, M. The Kadomtsev-Petviashvili equation: The trace method and the soliton resonances. J. Phys. Soc. Jpn. 1983, 52, 749–760. [Google Scholar] [CrossRef]
- Shen, Y.; Tian, B.; Zhou, T.Y.; Gao, X.T. Shallow-water-wave studies on a (2+1)-dimensional Hirota-Satsuma-Ito system: X-type soliton, resonant Y-type soliton and hybrid solutions. Chaos Solitons Fractals 2022, 157, 111861. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Baldwin, D.E. Nonlinear shallow ocean-wave soliton interactions on flat beaches. Phys. Rev. E 2012, 86, 036305. [Google Scholar] [CrossRef]
- Chowdury, A.; Krolikowski, W. Breather-to-soliton transformation rules in the hierarchy of nonlinear Schrödinger equations. Phys. Rev. E 2017, 95, 062226. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, J.-H.; Wang, Z.-Q.; Liu, C.; Li, M.; Qi, F.-H.; Guo, R. Breather-to-soliton transitions, nonlinear wave interactions, and modulational instability in a higher-order generalized nonlinear Schrödinger equation. Phys. Rev. E 2016, 93, 012214. [Google Scholar] [CrossRef] [PubMed]
- Chowdury, A.; Kedziora, D.J.; Ankiewicz, A.; Akhmediev, N. Breather-to-soliton conversions described by the quintic equation of the nonlinear Schrödinger hierarchy. Phys. Rev. E 2015, 91, 032928. [Google Scholar] [CrossRef] [PubMed]
- Huang, Q.M.; Gao, Y.T.; Hu, L. Breather-to-soliton transition for a sixth-order nonlinear Schrödinger equation in an optical fiber. Appl. Math. Lett. 2018, 75, 135–140. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, L.; Liu, C.; Li, M.; Zhao, Y.-C. High-dimensional nonlinear wave transitions and their mechanisms. Chaos 2020, 30, 113107. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Ren, B. Nonlinear waves and transition mechanisms for (2+1)-dimensional Korteweg-de Vries-Sawada-Kotera-Ramani equation. Wave Motion 2024, 130, 103383. [Google Scholar] [CrossRef]
- Ma, Y.L.; Li, B.Q. Soliton interactions, soliton bifurcations and molecules, breather molecules, breather-to-soliton transitions, and conservation laws for a nonlinear (3+1)-dimensional shallow water wave equation. Nonlinear Dyn. 2024, 112, 2851–2867. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Ren, B. Conversion mechanisms and transformed waves for the (3+1)-dimensional nonlinear equation. Phys. Fluids 2024, 36, 102129. [Google Scholar] [CrossRef]
- Krupa, K.; Nithyanandan, K.; Andral, U.; Tchofo-Dinda, P.; Grelu, P. Real-time observation of internal motion within ultrafast dissipative optical soliton molecules. Phys. Rev. Lett. 2017, 118, 243901. [Google Scholar] [CrossRef]
- Stratmann, M.; Pagel, T.; Mitschke, F. Experimental observation of temporal soliton molecules. Phys. Rev. Lett. 2005, 95, 143902. [Google Scholar] [CrossRef]
- Herink, G.; Kurtz, F.; Jalali, B.; Solli, D.R.; Ropers, C. Real-time spectral interferometry probes the internal dynamics of femtosecond soliton molecules. Science 2017, 356, 50–54. [Google Scholar] [CrossRef]
- Li, B.M. Optical soliton resonances and soliton molecules for the Lakshmanan-Porsezian-Daniel system in nonlinear optics. Nonlinear Dyn. 2023, 111, 6689–6699. [Google Scholar] [CrossRef]
- Lou, S.Y. Soliton molecules and asymmetric solitons in three fifth order systems via velocity resonance. J. Phys. Commun. 2020, 4, 041002. [Google Scholar] [CrossRef]
- Ma, Y.X. Soliton resonances, soliton molecules, soliton oscillations and heterotypic solitons for the nonlinear Maccari system. Nonlinear Dyn. 2023, 111, 18331–18344. [Google Scholar] [CrossRef]
- Ma, W.X. N-soliton solution of a combined pKP-BKP equation. J. Geom. Phys. 2021, 165, 104191. [Google Scholar] [CrossRef]
- Ma, H.C.; Yue, S.P.; Deng, A.P. Lump and interaction solutions for a (2+1)-dimensional combined pKP-BKP equation in fluids. Mod. Phys. Lett. B 2022, 36, 2250069. [Google Scholar] [CrossRef]
- Ma, H.C. Complexiton solutions, kink soliton and breather-wave solutions for the (2+1)-dimensional combined potential Kadomtsev-Petviashvili with B-type Kadomtsev-Petviashvili equation. Phys. Scr. 2023, 98, 095239. [Google Scholar] [CrossRef]
- Zhang, L.H.; Zhao, Z.L.; Zhang, Y.F. Dynamics of transformed nonlinear waves for the (2+1)-dimensional pKP-BKP equation: Interactions and molecular waves. Phys. Scr. 2024, 99, 075220. [Google Scholar] [CrossRef]
- Feng, Y.; Bilige, S. Resonant multi-soliton, M-breather, M-lump and hybrid solutions of a combined pKP-BKP equation. J. Geom. Phys. 2021, 169, 104322. [Google Scholar] [CrossRef]
- Tariq, K.U.; Wazwaz, A.M.; Tufail, R. Lump, periodic and travelling wave solutions to the (2+1)-dimensional pKP-BKP model. Eur. Phys. J. Plus 2022, 137, 1100. [Google Scholar] [CrossRef]
| Soliton | Trajectory | Velocity | Amplitude | Component |
|---|---|---|---|---|
| Soliton | Trajectory | Velocity | Amplitude | Component |
|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.; Zhang, X.; Ren, B. Stem Structures and Novel Localized Wave Molecules of the (2+1)-Dimensional pKP-BKP Equation. Symmetry 2025, 17, 2028. https://doi.org/10.3390/sym17122028
Zhu W, Zhang X, Ren B. Stem Structures and Novel Localized Wave Molecules of the (2+1)-Dimensional pKP-BKP Equation. Symmetry. 2025; 17(12):2028. https://doi.org/10.3390/sym17122028
Chicago/Turabian StyleZhu, Wei, Xueqing Zhang, and Bo Ren. 2025. "Stem Structures and Novel Localized Wave Molecules of the (2+1)-Dimensional pKP-BKP Equation" Symmetry 17, no. 12: 2028. https://doi.org/10.3390/sym17122028
APA StyleZhu, W., Zhang, X., & Ren, B. (2025). Stem Structures and Novel Localized Wave Molecules of the (2+1)-Dimensional pKP-BKP Equation. Symmetry, 17(12), 2028. https://doi.org/10.3390/sym17122028







