APDP-FL: Personalized Federated Learning Based on Adaptive Differential Privacy

Abstract

Frequent gradient exchange and heterogeneous data distribution in federated learning can lead to serious privacy leakage risks. Traditional privacy-preserving strategies fail to meet the personalized privacy needs from different users and may cause a decrease in model accuracy and convergence difficulties. The symmetry of federated learning may lead to the insufficiency of contribution evaluation mechanisms in protecting the privacy of sensitive data holders. However, federated learning avoids the risk of privacy leakage caused by data centralization because the raw data is always stored on the local device during the training process, and only encrypted model parameters or gradient updates are exchanged. To address these issues, this paper proposes an adaptive personalized differential privacy federated learning scheme APDP-FL. First, we propose an adaptive noise addition method that scores each round of training based on the parameters generated during training and dynamically adjusts the noise level for the next round. This method adds larger noise scales in the early stages of training, consuming less privacy budget, and gradually reduces noise addition during training to accelerate model convergence. Second, we design a personalized privacy protection strategy that adds noise tailored to individual needs for participating clients based on their privacy preferences. This solves the problem of insufficient or excessive privacy protection for some participants due to identical privacy budget sets for all clients, achieving personalized privacy protection for clients. Finally, we conduct extensive experimental simulations, comparisons, and analyses on three real federated datasets, MNIST, FMNIST, and CIFAR-10, verifying the advantages of APDP-FL in terms of privacy protection, model accuracy, and convergence speed.

1. Introduction

The development of large language models has led to an explosion in the applications of artificial intelligence. In particular, the branch of machine learning [1] has been widely utilized in areas such as computer vision [2], natural language processing [3], and image generation [4]. Traditional centralized machine learning usually requires collecting a large amount of training data and handing it over to a third party for cleaning and aggregation; then, the model can be trained and published. However, the loss of participants’ control over their own data during the training process, coupled with the increase in the amount of training data, makes the risk of privacy leakage increase, which leads to limitations in the further development of machine learning.

Federated learning [5] (FL), as a distributed machine learning framework, is a breakthrough technology for addressing the privacy protection of machine learning. Federated learning adopts a “data localization and parameter exchange mechanism”, where each participant uses their own data to train the model locally, encrypting only the model parameters (such as gradients or weights) and uploading them to the central server for aggregation, rather than transmitting the original data. This design ensures that the raw data is always kept locally, greatly reducing the risk of data leakage. Currently, federated learning has been widely adopted in domains such as intelligent transportation, healthcare, and energy/power systems [6,7,8].

Although federated learning can realize model training with “data localization” and effectively reduce the risk of privacy leakage (e.g., sensitive information of raw data in machine learning may be leaked through model parameters, gradient updates, or parameter exchange processes), it is not able to completely resist external privacy attacks, and many studies have shown that federated learning strategies still have some privacy leakage and data security problems [9]. First, due to the distributed nature of federated learning, it is difficult to ensure that the local models uploaded by clients are non-malicious, and once a malicious client uploads a malicious model, it will interfere with the global model of federated learning. Second, the model gradient uploaded by the client also contains some information of the local data, and the attacker can reverse launch the client’s original data through the model gradient. Therefore, it is urgent to construct a federated learning scheme that is secure and efficient and ensures data security and privacy.

In order to solve the FL privacy protection problem, researchers have proposed a large number of solutions. The mainstream solutions are mainly based on homomorphic encryption (HE) [10], secure multi-party computation (SMC) [11], and differential privacy (DP) [12]. HE can train and predict models in the ciphertext state, but the encryption and decryption operations and ciphertext transmission will place huge computational and communication pressure on the FL system. SMC can complete model training without disclosing client privacy, but it will introduce huge communication overhead to the FL. DP can provide rigorous mathematical proofs to guarantee the validity of the privacy protection, and it is suitable for various types of data analysis tasks, as well as being able to flexibly balance privacy protection and data availability. In summary, DP has strict mathematical definitions, adjustable privacy budgets, and lightweight computation, making it more suitable for FL distributed environments. However, the application of DP in FL still faces the problems of trade-offs between privacy protection and model performance, poor model accuracy, and inefficient communication, in addition to the challenges exacerbated by the non-independent and identically distributed (non-IID) nature of local data.

The current research on personalized differential privacy in federated learning mainly focuses on dynamic optimization and localized protection. Researchers propose an adaptive noise adjustment mechanism that dynamically optimizes the noise level of each client through the design of a noise scaler under a given privacy budget. At the same time, the direction matrix is used to correct the model’s update direction, effectively alleviating the model drift problem caused by noise introduction. In terms of technical implementation, reparameterization training is used to select personalized client update information, combined with a dynamic adaptive norm control model update range, significantly improving the targeting of noise injection. In terms of cross-domain applications, the privacy budget allocation scheme based on information entropy provides differentiated privacy protection strengths for different users according to the distribution differences of user data, achieving the optimal balance between privacy and utility.

Therefore, in order to explore how to improve FL model training efficiency and accuracy, as well as communication efficiency, under DP protection, we propose a personalized federated learning framework (APDP-FL) based on self-adaptive adapted differential privacy. Our contributions to this work can be summarized as follows:

(1)

This study propose the APDP-FL architecture to solve the three problems of personalized privacy requirements, accuracy reduction, and model convergence difficulties in FL.

(2)

An adaptive noise addition method is proposed to score each parameter for each round of the training process, and then, it dynamically adjusts the size of the added noise for the next round, which consumes less of the privacy budget and speeds up the model’s convergence.

(3)

A personalized privacy protection strategy is designed, which can add noise for the client; it meets its own needs according to the user’s privacy preference, solving the problem of insufficient or excessive privacy protection for some clients due to the same set of privacy budgets, and it realizes the personalized privacy protection of the client.

(4)

Extensive experiments are carried out on three real datasets: MNIST, FMNIST, and CIFAR-10. The results show that APDP-FL is superior to state-of the-art baselines in terms of privacy protection, model accuracy, and convergence speed.

The rest of this paper is organized as follows. In Section 2, we present a literature review of related work. Section 3 describes the background and problem setting, including FL, differential privacy, system model, attack model, and design objectives. Section 4 details the proposed APDP-FL scheme. Section 5 provides the performance analysis of APDP-FL. Section 6 provides the experimental results and analyses. The conclusions are drawn in Section 7.

2. Related Work

Although the “Data Localization” training mode in federated learning can effectively reduce the risk of local data privacy leakage, it is still unable to completely provide protection against privacy attacks. Currently, the academic solutions that address the privacy risk of federated learning are mainly based on homomorphic encryption (HE), secure multi-party computation (SMC), and differential privacy (DP).

2.1. Homomorphic Encryption

HE allows model training and predictions in ciphertext without decrypting data through data encryption, ciphertext computation, model parameter encryption, and secure aggregation. Hu et al. [13] proposed MaskCrypt to balance the trade-off between security and practicality when homomorphic encryption is used. Rather than encrypting model updates in their entirety, MaskCrypt applies an encryption mask to sift out a small portion of the updates for encryption. Kumbhar et al. [14] designed puzzle Archimedes optimization algorithm (PAOA)-based multi-key HE. Healthcare parties utilized noise-free HE to protect sensitive data and enhance communication security. Wang et al. [15] proposed a secure and privacy-preserving medical data federated learning architecture based on Paillier homomorphic encryption; the shared training model of the client is encrypted to ensure security and privacy. Cai et al. [16] proposed a secure and efficient federated learning scheme (SecFed) based on multi-key HE to preserve user privacy and delegated some operations to TEE to improve efficiency while ensuring security. Hu et al. [13] proposed MaskCrypt, a new mechanism designed to balance the trade-off between security and practicality when homomorphic encryption is used. However, the encryption and decryption operations and ciphertext transmission of HE can place huge computational and communication pressure on the FL system and cannot handle complex operations.

2.2. Secure Multi-Party Computation

SMC ensures that all parties in FL work together on model training and prediction without disclosing their private data through secret sharing, obfuscated circuits, homomorphic encryption, and inadvertent transmission. Tan et al. [17] proposed a privacy-preserving personalized federated learning scheme under secure multi-party computation (SMC-PPFL), which preserved privacy while obtaining a local personalized model with high prediction accuracy. Ciucanu et al. [18] proposed three secure protocols relying on secure multi-party computation, which guarantee desirable security properties for the following: input data, intermediate data, and output data. Kalapaaking et al. [19] proposed a convolutional neural network (CNN)-based federated learning framework that combined secure multi-party computation (SMC)-based aggregation and encrypted inference methods, all within the context of 6G and IoMT. Xiao et al. [20] proposed a practical secure federated learning system named PrSeFL, which implemented secure multiparty computation-based secure aggregation in blockchain environments. Tan et al. [17] proposed a privacy-preserving personalized federated learning scheme under secure multi-party computation (SMC-PPFL), which could preserve privacy while obtaining a local personalized model with high prediction accuracy. However, SMC usually involves a large number of data interactions and computations, which incurs a huge communication overhead and may become a performance bottleneck.

2.3. Differential Privacy

DP is able to flexibly balance the privacy and availability of local data by adding random noise to local data or local models, which makes it impossible for an attacker to infer the client’s privacy information from the data analysis results. Lyu et al. [21] proposed a scheme that combines differential privacy with federated learning to realize privacy-preserving outcomes. Tang et al. [22] proposed a novel privacy-preserving FL system (ReFL) that enforced DP and avoided accuracy reductions in global models caused by the excessive DP noise of rogue clients. Fukami et al. [23] proposed a primal–dual DP algorithm with denoising normalization (DP-Norm) for less sensitivity to noise/interference, such as DP diffusion and heterogeneous data allocation. The above schemes perform poorly in FL with complex datasets due to the trade-off between privacy budget and performance. Sun et al. [24] provide a localized differential privacy–federated learning (LDP-FL) solution, solving the problem above, but it still exhibits poor accuracy in large model testing with a small number of users. Bhowmick et al. [25] were the first to combine localized differential privacy with federated learning for deep learning models, proposing a practical approach to large-scale local privacy model training, and this method is suitable for large-scale image classification with almost no decrease in model utility. Xie et al. [26] proposed a federated multitask learning (FedMTL) approach, which was introduced to reformulate the FL model as a multiobjective optimization problem, resulting in a federated multigradient descent algorithm (FedMGDA) with better model personalization against data heterogeneity and Byzantine attacks.

3. Background and Problem Setting

3.1. Federated Learning

The federated learning framework [5] consists of a central server and n clients, each of which has unique access to its private local data $D_k$, where k is a variable and $k\in \{1,2,3,\dots ,n\}$. In each learning round t, the server randomly selects several clients to share the current global model $W_{global}^t$. Each selected client updates its local data at $D_k$ for each local round to obtain a new local model sent to the server at $D_k^{t+1}$. The aggregation process usually uses the federated averaging algorithm to obtain the global model for the next round $D_{global}^{t+1}$ via Equation (1):

$$W_{global}^{t+1}=W_{global}^t+{\displaystyle \frac{\eta }{n}}\sum _{k=1}^n\left(W_k^{t+1}-W_{global}^t\right)$$

(1)

where $\eta$ is the learning rate set by the server when the global model is updated.

There are a total of one server S and n clients in a generic federated learning system, and the server S collaborates with all clients to accomplish the following optimization objectives throughout the federated learning process:

$$\underset{w\in R^d}{\arg \min }f\left(w\right)={\displaystyle \frac{1}{N}}\sum _{n=1}^N{f}_n\left(w\right)$$

(2)

where $f_n$ is the loss function of the client n, w is the local model, and $w\in R^d$ means that the variable w is a d-dimensional real vector. In the neural network, empirical risk minimization with the cross-entropy function is used as its loss function:

$$f_n\left(w\right)={\displaystyle \frac{1}{|D_n|}}\sum _{j=1}^{|D_n|}L\left(x_j,y_j,w\right)$$

(3)

where $|D_n|$ is the total number of samples owned by client n, and $\left(x_j,y_j\right)$ is the j-$th$ sample in client n.

In each training round of federated learning $t\in \left\{1,2,3,\dots ,T\right\}$, the server sends the current global model $W_{global}^t$ to each client. Clients train their own local model $W_k^{t+1}$ locally using their own private data $D_k\in \left\{D_1,D_2,D_3,\dots ,D_K\right\}$. Then, the client computes its own model update gradient as ${\Delta }_k^{t+1}=W_k^{t+1}-W_{global}^t$ and sends it to the server. After the server receives the updates sent by the clients, it aggregates the model’s updates using the aggregation function and then updates the global model using Equations (2)–(4) to obtain the global model $W_{global}^{t+1}$, which is used for the next round of training:

$$W_{global}^{t+1}=W_{global}^t+\eta ·g\left(\left\{{\Delta }^{t+1}\right\}\right)$$

(4)

where $\eta$ is the learning rate of the server in federated learning; $g(·)$ is the aggregation function, which is chosen according to the aggregation strategy; and $\left\{{\Delta }^{t+1}\right\}={\bigcup }_{k\in C_k}{\Delta }_k^{t+1}$. The training process continues until the global model reaches the desired performance metrics on the validation dataset maintained by the server or reaches the maximum number of iteration rounds. All clients keep their private data confidential throughout the training process; for example, the attacker and the server do not have access to the client’s private data.

3.2. Differential Privacy

Differential privacy solves the core contradiction between privacy protection and data availability in the era of big data, providing a verifiable and implementable privacy protection framework for governments, enterprises, and individuals. Especially in the context of the proliferation of sensitive data and the tightening of privacy regulations, its technology has become the cornerstone of data security. Differential privacy is achieved by adding noise to the data that matches a specific distribution; even if a single piece of datum in the dataset is modified, it will not significantly change the statistical results, so it can effectively defend against differential attacks and thus protect personal privacy.

Definition 1

(Differential Privacy in Deep Learning). Let the mechanism of a deep learning algorithm be M. The training dataset is taken as input and trained using gradient descent; the output is the trained model’s parameters; $P_M$ is the set consisting of all possible outputs. Then, for any two neighboring training datasets D and $D^{\prime }$, the parameter distribution of the output satisfies Equation (5):

$$P_M\left[M\left(D\right)\in S_M\right]\le exp\left(\epsilon \right)\times P_M\left[M\left(D^{\prime }\right)\in S_M\right]+\delta$$

(5)

It can be said that the deep learning algorithm mechanism M satisfies $\left(\epsilon ,\delta \right)$-DP (differential privacy), the parameter ε is the privacy-preserving budget, and the size of ε is negatively correlated with the privacy-preserving effect. δ represents the relaxation factor, which represents the probability of violating strict differential privacy. When ε is larger, this means that the added noise is small, and the privacy protection level is low. Conversely, when it is smaller, the added noise is large, and the privacy protection level is high. However, in the limit, the privacy-preserving budget is $\epsilon =0$, which will have the highest privacy-preserving effect, and the difference between the outputs of the algorithm mechanism M on two neighboring datasets will be completely indistinguishable. However, because adding too much noise to the dataset will result in a large amount of interference when using the dataset, rendering the data unusable, it is necessary to control $\epsilon >0$ in practice. δ is called the relaxation term, which indicates the probability of being able to tolerate illegal strict differential privacy, and it is typically set to $\left({\displaystyle \frac{1}{\left|D\right|}}\right)$.

Definition 2

(Rényi Differential Privacy). Rényi differential privacy is obtained by restricting Rényi scattering, For two probability distributions P and Q, the Rényi divergence of order α is defined as follows:

$$D_{\alpha }\left(P\left|\right|Q\right)={\displaystyle \frac{1}{\alpha -1}}log{E}_{x\sim Q}{\left({\displaystyle \frac{P\left(x\right)}{Q\left(x\right)}}\right)}^{\alpha }$$

(6)

where the $P\left(x\right)$ and $Q\left(x\right)$ distributions represent the probability density function of x on the distributions P and Q. And for the mechanism M described in definition 1, let $M\left(D\right)\left(w\right)$ represent the probability density of training on the dataset D to obtain the result w. If the mechanism M satisfies $\left(\alpha ,\epsilon \right)$-RDP for any $\alpha \in \left(1,\infty \right)$, then the mechanism M needs to satisfy the following:

$$D_{\alpha }\left(M\left(D\right)\left|\right|M\left(D^{\prime }\right)\right)\le \epsilon$$

(7)

3.3. System Model

In this paper, the differential privacy federal average algorithm is used to provide different privacy budget levels, and participants can achieve personalized privacy protection by choosing the privacy level that meets their needs. Due to the use of a uniform noise addition strategy throughout the process, this will lead to the addition of excessive noise at the late stage of training, which affects the model accuracy. Therefore, adaptive noise addition technology is also introduced in the scheme, where noise is added adaptively during the training process to minimize the impact on the global model’s accuracy. The framework of the adaptive personalized differential privacy federated learning algorithm is shown in Figure 1.

The system architecture consists of a centralized parameter server and multiple participating clients, achieving a balance between privacy and model performance through “data localization+model collaboration”. Firstly, the server distributes the initialized global model $W_{t-1}$ (including model structure and initial weight parameters) and preset noise parameter ${\sigma }_i$ (such as noise scales in differential privacy, privacy budget $\epsilon$, etc.) to all participating learning clients. After receiving the initial model and noise parameters issued by the server, the client iteratively trains the model using their own private dataset $D_i$ (which is always kept locally and not transmitted externally). After training is completed, the client needs to perform critical local privacy protection processing: Perturb the locally trained model parameters based on their personalized privacy preference $r_i$ and the noisy parameters distributed by the server. After completing noise processing, the client uploads the perturbed model parameters (rather than the original model or local data) to the server. After collecting the encrypted model parameters from all clients, the server performs weighted averaging on the model parameters from different clients to integrate knowledge from all parties and update the weights of the global model. Subsequently, the server uses the reserved validation dataset to evaluate the performance of the aggregated global model, calculates key indicators such as accuracy and loss function values, and dynamically adjusts the denoising coefficient for the next round of training based on the evaluation score. If the model’s performance does not meet expectations, the noise intensity can be appropriately reduced to improve model accuracy. If the privacy risk is high (for example, if it is found through privacy budget monitoring that the consumption of $\epsilon$ is too fast), the amplitude of noise enhancement should be increased to strengthen protection. This dynamic adjustment mechanism achieves the automated optimization of privacy utility trade-off through a feedback loop. Finally, the server distributes the updated global model (which incorporates multi-party knowledge but hides individual data features) and the recalculated new round of denoising coefficients to all participating clients, initiating the next round of federated learning iteration.

3.4. Attack Model

We assume that the central server is honest and curious, will perform the federated learning process strictly and accurately, and return correct results to all clients after the global aggregation of the received intermediate parameters. However, the central server is curious about the private data of participating users and tries to obtain private data by analyzing the model parameters submitted by users. All users adhere to the model training process with respect to the same central server, but they may try to obtain other users’ private information through the global model or public channels. Assuming that there is an active attacker A in the training process with the goal of inferring the private information of users using intermediate parameters or aggregation results, attacker A has the following capabilities:

(1)

The ability to eavesdrop the intermediate parameters of the interaction between the central server and the user through the public channel to infer the private information of the user.

(2)

The ability to hack the central server and use the intermediate parameters or aggregation results of the server to infer the private information of the user.

(3)

The ability to hack into one or more users and use their information to infer private data about other users but not the ability to manipulate all users at once.

3.5. Design Objectives

The proposed scheme should ensure the data privacy of participating users and provide personalized privacy protection for participants, and it should also ensure that the accuracy of the model is not degraded:

(1)

Data Privacy: Ensure that Attacker A cannot directly or indirectly use the local model parameters and the global model aggregated by the central server to infer the private data of users.

(2)

Personalized Privacy Protection: Different users possess different sensitivities to data, and the scheme should ensure that all participants can set their own privacy parameters at the beginning of training to meet their personalized privacy protection needs.

(3)

Model Accuracy: The server needs to provide noise addition coefficients for participating users, and the scheme needs to ensure that the noise added in each round meets privacy protection needs while not affecting the model’s accuracy as much as possible.

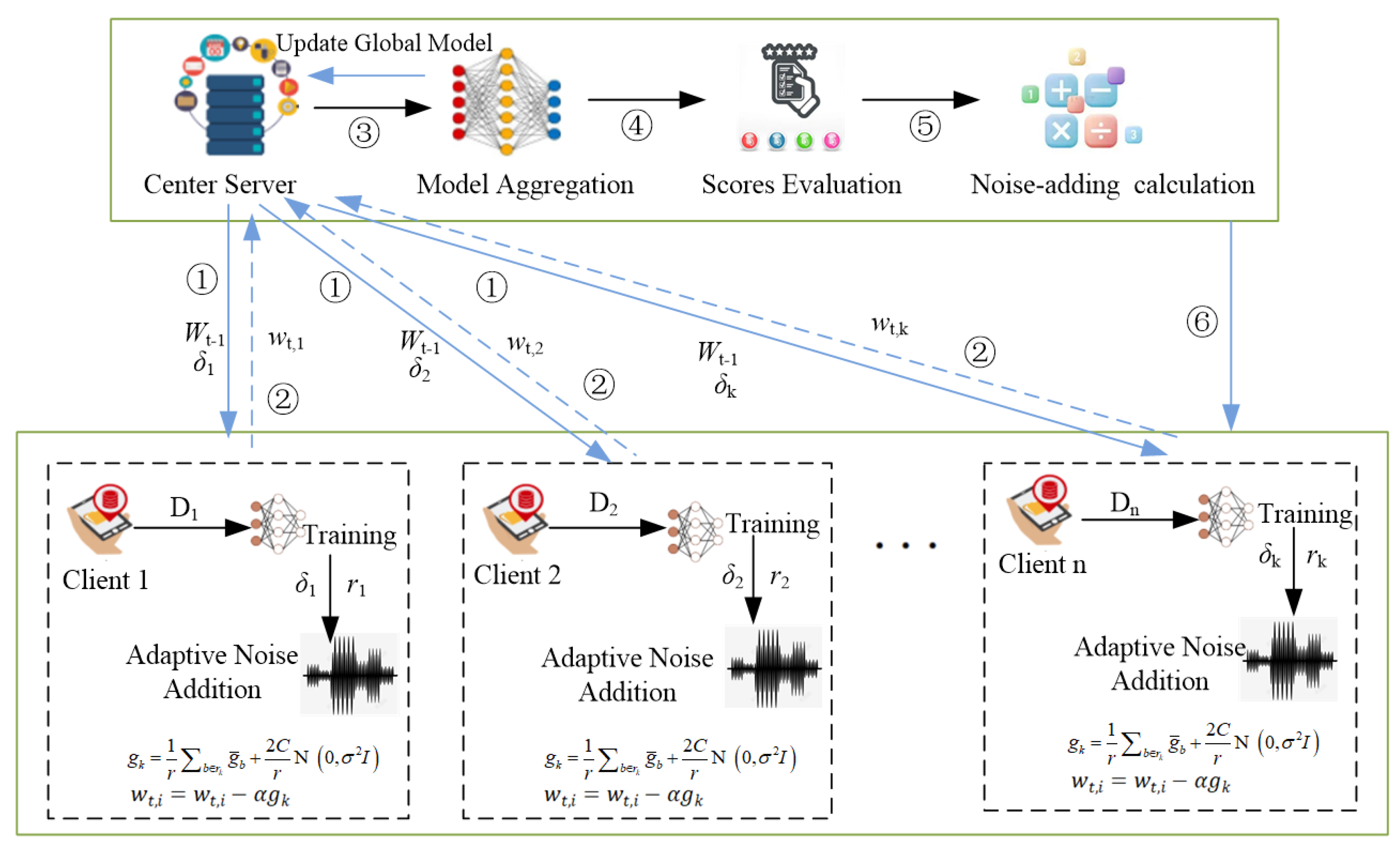
4. Adaptive Personalized Differential Privacy Federated Learning Algorithm (APDP-FL)

APDP-FL mainly consists of two core parts: adaptive noise addition and personalized privacy protection. According to the various parameters generated during the training process to score each round of training and the scoring results that dynamically adjust the size of the next noise-adding round, the client’s local training will be based on their own privacy preferences, adjusting the level of local privacy protection to achieve the personalized privacy protection of the client.

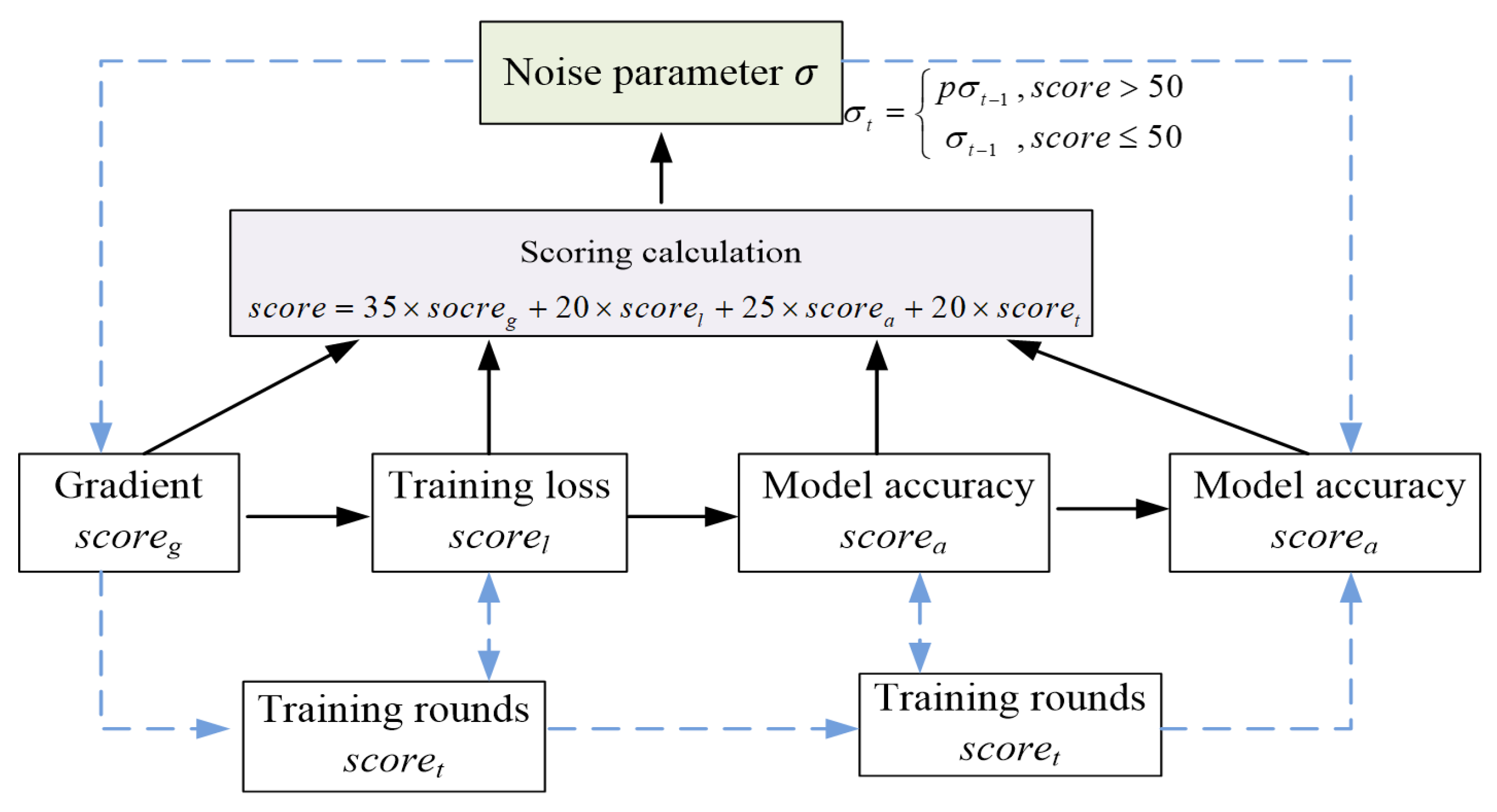
4.1. Adaptive Noise Addition

As training progresses, the gradient of the model uploaded by the client will gradually decrease, and adding noise at the same level as before when the model is about to converge will affect the accuracy of the model. Therefore, adding more noise in the early stage of training and reducing the added noise in the later stage can reduce the impact on the model’s accuracy. In the case of limited privacy budget, the parameter $\sigma$ of adding noise dynamically according to the indexes in the training process can reduce the impact on the model’s accuracy with the same privacy budget.

In order to realize the adaptive addition of noise in FL, this paper fuses four metrics, gradient size, training loss, model accuracy, and training rounds, to design a scoring function. When the score exceeds 50 points, the noise parameter $\sigma$ is reduced to $p\sigma$, where $p\left(0<p<1\right)$ is a constant, and the server calculates the score of the round during the training process and then dynamically adjusts the noise parameter $\sigma$ sent to the client according to the score. Each computational module of the scoring function is as follows:

(1)

Gradient: Let $\left|g_t\right|$ be the gradient biparadigm at the time of global model update in the t-th round of communication, g represents gradient, and let $\left|g_{max}\right|$ be the maximum value of the historical gradient biparadigm. The scoring of ${score}_g$ with the gradient as the scoring criterion is calculated using the following formula:

$${score}_g=min\left\{max\left\{2\left(1-{\displaystyle \frac{2\left|g_t\right|}{\left|g_{max}\right|}}\right),0\right\},1\right\}\times 100\%$$

(8)

To minimize added noise when the global model gradient paradigm is small, the opposite of the ratio of $\left|g_t\right|$ to $\left|g_{max}\right|$ plus 1 was used as the scoring criterion for the gradient, and the size of ${score}_g$ was limited to no more than $100\%$.

When the global model gradient paradigm is small, the model approaches convergence, and noise needs to be reduced to avoid interfering with optimization. Using the inverse of the ratio of the current gradient, two normal forms were used relative to the historical average plus 1 as the score. Dynamic denoising is as follows: The smaller the gradient, the higher the score, and the stronger the denoising. Limit the rating to ≤100% to ensure privacy protection and prevent noise from disappearing.

(2)

Training Loss: Let ${Loss}_t$ be the loss on the test set after the t-th round of communication, and let ${Loss}_{t-1}$ be the loss on the $t-1$ round. This module’s score ${score}_l$ is calculated as follows:

$${score}_l=\left\{\begin{array}{cc}100\%,\hfill & iflos{s}_{t-1}<los{s}_t\hfill \\ 0,\hfill & else\hfill \end{array}\right.$$

(9)

If the training loss of the current round is greater than the training loss of the previous round, this means that the noise added during the training of this round may be too large, so during the next round of training, as little noise as possible should be added.

(3)

Model Accuracy: Let ${Acc}_t$ be the accuracy of the global model on the test set after the t-th round of communication, and let ${Acc}_{t-1}$, ${Acc}_{t-2}$, ${Acc}_{t-3}$, and ${Acc}_{t-4}$ be the accuracy of the model in the first four rounds. The model accuracy module score ${score}_a$ is calculated as follows:

$${score}_a=\left\{\begin{array}{cc}100,\%\hfill & if{\displaystyle \frac{(Ac{c}_t+Ac{c}_{t-1}+Ac{c}_{t-3}+Ac{c}_{t-4})}{5}}>Ac{c}_t\hfill \\ 0,\hfill & else\hfill \end{array}\right.$$

(10)

${score}_a$ is based on the mean value of the model accuracy of the last five times (a represents accuracy). If the model accuracy of the last round is lower than the mean value, this means that the model’s accuracy has shown a downward trend during the training process, so it is necessary to minimize the addition of noise and reduce the interference of added noise on the model’s accuracy.

(4)

Training Rounds: Set $T_m$ as the maximum number of communication rounds set. The training process needs to gradually reduce the addition of noise; thus, the training rounds that prevail in ${score}_t$ are calculated as follows:

$$scor{e}_t=min\left({\displaystyle \frac{2t}{T_m}},1\right)\times 100\%$$

(11)

Combining the above scoring formula and giving different weights to each module, the final scoring calculation method can be derived as follows:

$$score=35\times socr{e}_g+20\times scor{e}_l+25\times scor{e}_a+20\times scor{e}_t$$

(12)

The comprehensive scoring function dynamically adjusts noise intensities by the weighted fusion of individual scores, where the weight coefficients $\alpha =35, \beta =20$, $\gamma =35, \delta =20$, and delta satisfy $\alpha +\beta +\gamma +\delta =100$ and dynamically allocate $\alpha , \beta , \gamma$, and $\delta$ according to task requirements. The coefficients can be dynamically adjusted.

Relying on this scoring function, adaptive noise additions to the model during the training process can be realized, where the details of variations in the noise parameter $\sigma$ are as follows:

$${\sigma }_t=\left\{\begin{array}{cc}p{\sigma }_{t-1},\hfill & score>50\hfill \\ {\sigma }_{t-1},\hfill & score\le 50\hfill \end{array}\right.$$

(13)

where $p\left(0<p<1\right)$ is a constant, representing the proportion of reduced noise addition. The process of calculating noise parameters is shown in Figure 2.

4.2. Personalized Privacy Protection

Personalized privacy protection strategy is added on the basis of adaptive noise addition, which allows participants to add noise that meets their own needs, and this solves the problem of insufficient or excessive privacy protection for some participants due to the same privacy budget set for each client.

The personalized differential privacy strategy works on the basis of the adaptive noise addition strategy, and the server sends Gaussian noise parameters $\sigma$ to the participating users during each round of training, and if all users have the same privacy level, the noise addition process during the training is as follows:

$$g_k={\displaystyle \frac{1}{r}}\sum _{b\in r_k}{\overline{g}}_b+{\displaystyle \frac{2C}{r}}\mathcal{N}(0,{\sigma }^{2}I)$$

(14)

where ${\overline{g}}_b$ is the gradient of the model after gradient clipping, I represents the identity matrix, and $r_k$ is the subset of the client’s k-th round of sampling, while r is the sample size, and C is the gradient clipping factor. The size of the added noise is determined by the Gaussian noise parameter $\sigma$. The larger $\sigma$ is, the more noise is added to the gradient, which is good for privacy protection, but model utilization will be reduced. Therefore, the local privacy protection level can be controlled by controlling the size of the Gaussian noise parameter $\sigma$. Participating users need to quantify their privacy preferences, $R=\left\{R_1,R_2,R_3,\dots ,R_n\right\}$, and set the standard privacy protection level L. During local training, the client needs to adjust the Gaussian noise parameter $\sigma$ according to the set privacy preference $R_i$ and the standard privacy protection level L before adding noise to the model gradient:

$${\sigma }_i={\displaystyle \frac{R_i}{L}}\sigma$$

(15)

It is very difficult to compute the privacy overhead for each client since each client in each round adds a different amount of noise to the model’s gradient. Therefore, after one round of the learning process, this paper calculates the privacy overhead under the standard privacy protection level, and at the same time, since the noise added in each round is dynamic, it is necessary to determine whether the privacy overhead exceeds the privacy budget after the completion of each round of training, and if the privacy budget is consumed in advance, the federated training process needs to be terminated early.

The criteria for the standard privacy protection level L are as follows: The smaller the L value, the greater the strength of privacy protection. The larger the L value, the weaker the privacy protection strength. According to research practice, when $L<0.1$, this provides strong privacy protection. When $L<1$, generally acceptable privacy protection is provided.

4.3. APDP-FL Training Process

4.3.1. Server-Side Training Process

First, the server randomly selects the clients participating in this round of learning and sends the global model $W_{t-1}$ and the noise parameter ${\sigma }_{t-1}$ of this round to the selected clients. The selected clients use the global model for multiple rounds of local training, adding noise to the model according to the locally set privacy preference $R_i$, the standard privacy protection level L, and the Gaussian noise parameter ${\sigma }_{t-1}$ distributed by the server. Finally, the model parameters, ${\tilde{w}}_i^t$, are uploaded. The server receives the model parameters uploaded by the client and completes model aggregation to update the global model with the set learning rate. Then, calculate the baseline privacy overhead ${\epsilon }_t$ for this round and determine whether ${\epsilon }_t$ exceeds the set privacy budget. If the privacy budget reaches the upper limit, the training process needs to be aborted. Test the global model on the test set to obtain the training loss and model accuracy, calculate the training score for this round based on the scoring function, and generate a new noise parameter ${\sigma }^t$ based on the score. Repeat the above steps and stop the federated learning process if the privacy budget is exhausted or the number of training rounds reaches a pre-set value, $T_m$. The algorithm of APDP-FL on the server side is as follows (Algorithm 1).

Algorithm 1 APDP-FL server-side algorithm

Input:  Set of users participating in federated learning N, maximum number of communication rounds $T_m$, user selection rate $\gamma ,\left(0<\gamma <1\right)$, privacy budget $\epsilon$, learning rate $\eta$; Output:  global model W;   1: Initialize the global model $W_0$;   2: for$t=1,2,\dots ,T_m$do   3:      Server randomly selects $\gamma \left|N\right|$ users who will participate in this round of learning $n^t\subset \left[N\right]$;   4:      Server sends model parameter $W_{t-1}$ and noise parameter to client $i\in n^t{\sigma }_{t-1}$;   5:      for$i\in n^t$ do                  ▹ Clients run simultaneously        ▹ Client i executes local learning strategy to get local model for round t and adds noise.   6:    ${\tilde{w}}_{t,i}\leftarrow ClientUpdate(W_{t-1},{\sigma }_{t-1})$;   7:    Client uploads local model ${\tilde{w}}_{t,i}$;   8:      end for   9:      Server collects model from client $w_{t,i}$; 10:      Update the global model $W_t=W_{t-1}+{\displaystyle \frac{\eta }{\gamma \left|N\right|}}{\sum }_{i\in n^t}{\tilde{w}}_{t,i}$; 11:      Calculate the privacy overhead for this round ${\epsilon }_t$; 12:      if${\epsilon }_t>\epsilon$then 13:    End model training; 14:      end if 15:      Calculate the score for this round $score$; 16:      if$socre>50$then 17:    ${\sigma }_t=p{\sigma }_{t-1}$; 18:      end if 19: end for

4.3.2. Client-Side Training Process

First, the client determines the number of local update iterations, E, and downloads the global model $W_{t-1}$ and noise parameters, ${\sigma }_{t-1}$, from the server. Then, the data subset involved in training is obtained by equal sampling the local dataset $D_i$ with the size of d, and the local model is trained, where the local data needs to be partitioned into data subsets, b, according to the batch size; the data subsets are iterated to train the model gradient and perform gradient clipping. Finally, noise is added to the model gradient, and the model is updated according to the local privacy preferences, standard privacy levels, and noise parameters distributed by the server. The updated model is then uploaded to the server. The algorithm of APDP-FL on the client side is as follows (Algorithm 2):

Algorithm 2 APDP-FL client-side algorithm

Input:  local dataset $D_i$, minimum iterative packet size d, number of local trainings E, loss function $\mathcal{L}$, standard privacy protection level L, learning rate $\alpha$, privacy preference $R_i$, global model $W_{t-1}$, noise parameters ${\sigma }_{t-1}$; Output:  local model after noise addition ${\tilde{w}}_{t,i}$;   1: Download the global model from the server $W_{t-1}$;   2: $w_{j,i}=W_{t-1}$;                    ▹Update the local model   3: for$j=1,2,\dots ,E$do   4:       Divide the local dataset $D_i$ into subsets b of size d;   5:       for each batch $b\in D_i$ do   6:             $g_b=\nabla \mathcal{L}\left(w_{j,i};b\right)$;   7:             ${\overline{g}}_b=g_b/max(1,{\Vert g_b\Vert }_2/C)$;            ▹ Perform gradient clipping   8:       end for   9:       ${\sigma }_i={\displaystyle \frac{R_i}{L}}\sigma$; 10:       $g_k={\displaystyle \frac{1}{r}}{\sum }_{x\in r_k}{\overline{g}}_b+{\displaystyle \frac{2C}{r}}\mathcal{N}\left(0,{\sigma }_i^{2}I\right)$;          ▹ add noise to the model gradient 11:       $w_{j,i}=w_{j,i}-\alpha g_k$; 12: end for 13: ${\tilde{w}}_{t,i}=w_{j,i}$; 14: Submit the noisy local model ${\tilde{w}}_{t,i}$ to the server;

5. Performance Analysis

5.1. Privacy Protection

APDP-FL satisfies $\left(\epsilon ,\delta \right)$-DP; the proof is as follows.

Theorem 1.

Given the client’s local data sampling parameter q; the current training round T; the number of clients picked in each training round u; the number of local iterations F; and the Gaussian mechanism $Mf\left(d\right)=f\left(d\right)+N(0,{\sigma }_t^2)$, where ${\sigma }_t$ is the Gaussian noise parameter of the standard privacy-preserving level at the t-th round of training, at $\alpha \ge 2$ if ${\sigma }_t$ is satisfied, we have the following:

$$\sum _{t=1}^T{\epsilon }^{\prime }(\alpha ,{\sigma }_t)+{\displaystyle \frac{log\frac{1}{\delta }}{\alpha -1}}\le \epsilon$$

(16)

Then, APDP-FL satisfies $\left(\epsilon ,\delta \right)$-DP.

Proof of Theorem 1. 

According to the RDP Gaussian mechanism [27], the Gaussian mechanism $Mf\left(d\right)=f\left(d\right)+N\left(0,{\sigma }_t^2\right)$ satisfies $\left(\alpha ,{\displaystyle \frac{\alpha }{2{\sigma }_t^2}}\right)$-RDP when the Gaussian noise parameter is ${\sigma }_t$, which means $\epsilon \left(\alpha ,{\sigma }_t\right)\le {\displaystyle \frac{\alpha }{2{\sigma }_t^2}}$. Also, according to the subsampled mechanism of the RDP algorithm [28], the privacy overhead at each subsampled mechanism during a training session is as follows:

$${\epsilon }_i^{\prime }(\alpha ,{\sigma }_t)\le {\displaystyle \frac{1}{\alpha -1}}log\{1+q^2\left(\begin{array}{c}\alpha \\ 2\end{array}\right)min\{4(e^{{\displaystyle \frac{1}{{\sigma }_t^2}}}-1),e^{{\displaystyle \frac{1}{{\sigma }_t^2}}}min[2,{(e^{\infty }-1)}^2]\}+\sum _{j=3}^{\alpha }{q}^j\left(\begin{array}{c}\alpha \\ j\end{array}\right)e^{{\displaystyle \frac{j(j-1)}{2{\sigma }_t^2}}}min[2,{\left(e^{\infty }-1\right)}^j]\}$$

(17)

Since $e^{\infty }$ has no upper bound, $min\left[\left\{2,{\left(e^{\infty }-1\right)}^2\right\}\right]\to 2$, $min\left[\left\{2,{\left(e^{\infty }-1\right)}^j\right\}\right]\to 2$, and the equation above can be simplified into the following:

$${\epsilon }_i^{\prime }(\alpha ,{\sigma }_t)\le {\displaystyle \frac{1}{\alpha -1}}log\{1+q^2\left(\begin{array}{c}\alpha \\ 2\end{array}\right)min[4(e^{{\displaystyle \frac{1}{{\sigma }_t^2}}}-1),2e^{{\displaystyle \frac{1}{{\sigma }_t^2}}}]+2\sum _{j=3}^{\alpha }{q}^j\left(\begin{array}{c}\alpha \\ j\end{array}\right)e^{{\displaystyle \frac{j(j-1)}{2{\sigma }_t^2}}}\}$$

(18)

Since all subsampled operations satisfy $\left(\alpha ,{\epsilon }_i^{\prime }\left(\alpha ,{\sigma }_t\right)\right)$-RDP, according to the RDP combination theorem, the privacy overhead after F rounds of local training is calculate as follows:

$${\epsilon }_i^{\prime }(\alpha ,{\sigma }_t)\le {\displaystyle \frac{F}{\alpha -1}}log\{1+q^2\left(\begin{array}{c}\alpha \\ 2\end{array}\right)min[4(e^{{\displaystyle \frac{1}{{\sigma }_t^2}}}-1),2e^{{\displaystyle \frac{1}{{\sigma }_t^2}}}]+2\sum _{j=3}^{\alpha }{q}^j\left(\begin{array}{c}\alpha \\ j\end{array}\right)e^{{\displaystyle \frac{j(j-1)}{2{\sigma }_t^2}}}\}$$

(19)

Therefore, when the number of clients is u, the privacy overhead of APDP-FL for one round of communication over the global dataset D is as follows:

$${\epsilon }_i^{\prime }(\alpha ,{\sigma }_t)\le {\displaystyle \frac{F}{\alpha -1}}log\{1+q^2\left(\begin{array}{c}\alpha \\ 2\end{array}\right)min[4(e^{{\displaystyle \frac{1}{{\sigma }_t^2}}}-1),2e^{{\displaystyle \frac{1}{u{\sigma }_t^2}}}]+2\sum _{j=3}^{\alpha }{q}^j\left(\begin{array}{c}\alpha \\ j\end{array}\right)e^{{\displaystyle \frac{j(j-1)}{2u{\sigma }_t^2}}}\}$$

(20)

After the T-round of training, the total privacy budget consumed by the entire global model is as follows:

$$\sum _{t=1}^T{\displaystyle \frac{F}{\alpha -1}}log\{1+q^2\left(\begin{array}{c}\alpha \\ 2\end{array}\right)min[4(e^{{\displaystyle \frac{1}{u{\sigma }_t^2}}}-1),2e^{{\displaystyle \frac{1}{u{\sigma }_t^2}}}]+2\sum _{j=3}^{\alpha }{q}^j\left(\begin{array}{c}\alpha \\ j\end{array}\right)e^{{\displaystyle \frac{j\left(j-1\right)}{2u{\sigma }_t^2}}}\}+{\displaystyle \frac{log\left(\frac{1}{\delta }\right)}{\alpha -1}}\le \epsilon$$

(21)

Let $\left(\alpha ,{\sum }_{t=1}^T{\epsilon }^{\prime }\left(\alpha ,{\sigma }_t\right)\right)$ be represented by DP. If ${\sigma }_t$ satisfies

$$\sum _{t=1}^T{\epsilon }^{\prime }\left(\alpha ,{\sigma }_t\right)+{\displaystyle \frac{log\left(\frac{1}{\delta }\right)}{\alpha -1}}\le \epsilon$$

(22)

then APDP-FL satisfies

$$\left(\sum _{t=1}^T{\epsilon }^{\prime }\left(\alpha ,{\sigma }_t\right)+{\displaystyle \frac{log\left(\frac{1}{\delta }\right)}{\alpha -1}},\delta \right)-\mathrm{DP}$$

(23)

If APDP-FL satisfies $\left(\epsilon ,\delta \right)$-DP, the proof is complete. □

Although it has been proven that the proposed scheme satisfies $(\epsilon ,\delta )-\mathrm{differential}\mathrm{privacy}$, attackers may still launch multiple attacks using model parameters, gradients, or aggregation results. The following is an analysis of the attack model:

(1)

Membership Inference Attack (MIA)

Attackers use model outputs (such as prediction confidence) to determine whether a certain piece of datum participated in training. For example, in medical federated learning, attackers may infer whether a specific patient participated in the training set of a disease study. Differential privacy reduces the success rate of MIA by adding noise to blur data correlations. However, attacks may still infer member identities based on the differences in statistical model outputs.

(2)

Reconstruction Attack

Attackers use model gradients or parameters to infer the original training data. For example, gradient inversion attack utilizes optimization algorithms to reconstruct image data from gradients, and gradient cropping and noise addition can increase the difficulty of reconstruction. But if the noise intensity is insufficient, attackers may still approach the real data through multiple iterations of optimization.

(3)

Model Inversion Attack

Attackers generate adversarial samples by querying the model’s API and inferring the distribution of training data. For example, in medical federated learning, attackers may use GANs to generate fake images that are similar to training data. However, although differential privacy reduces data distinguishability, it cannot completely prevent attackers from using generative models to simulate data distribution.

(4)

Backdoor Attack

The attacker implants specific triggers in the training data, causing the model to output preset results under specific inputs. For example, in image classification, attackers may add tiny markers in the corners of the image, forcing the model to classify it into a specific category. Differential privacy has no direct defense against backdoor attacks, and attackers may bypass noise interference by poisoning data, especially when triggers overlap with normal data distributions.

5.2. Complexity Analysis

Typically, the time complexity of federated learning algorithms is mainly related to several of its main processes, such as communication overhead, model aggregation, and client-side local training. In the APDP-FL proposed in this paper, assume that the communication overhead between the server and each client is $O\left(T\right)$ during each round of learning, the maximum number of training rounds in the training process is R, and the server communicates with $\mu N$ users selected in each round. The time complexity overhead with respect to communication during the whole training process is $O\left(T\times R\times \mu N\right)$. In the process of locally training the client, assume that the amount of training data of each client is D, the number of local number of iterations is F, and the size of the model parameters is M. The time overhead spent with respect to the client local is mainly a result of local training, adding Gaussian noise, and gradient clipping, and the time complexity is $O\left(D\times M\times F\right)$, $O\left(M\right)$, and $O\left(1\right)$ respectively. In the server update model stage, the biparadigm of the model gradient needs to be computed when calculating the score, and its time complexity is proportional to the size of the model parameters, and its time complexity is $O\left(M\times R\right)$. Thus, the total time complexity of the APDP-FL algorithm is $O\left(T\times R\times \mu N\right)+O\left(D\times M\times F\right)+O\left(M\right)+O\left(M\times R\right)$. The time complexity of the algorithm is within the acceptable range and has strong application value.

6. Experiment

The hardware environment for the experiments comprises AMD Ryzen 7 5800H 3.20 GHz, 16.00 RAM, Win11 64-bit, and an NVIDIA GeForce RTX 3050 GPU, and the software environment is as follows: compiled language: Python 3.9 version; IDE: Pycharm2023.3 version; deep learning framework and version: PyTorch1.8.0 and CUDA11.1.

6.1. Experimental Settings

(1)

Dataset Introduction

We set up a federated learning system with multiple clients and a central server for collaborative training until the global model converged; then, training stopped. In this paper, we use three commonly used image classification datasets, MNIST, Fashion-MNIST, and CIFAR-10, for the image classification task. The MNIST dataset consists of 60,000 training samples with 10,000 test samples, the size of each image is $28\times 28$, and the content of the image is handwritten numbers from 0 to 9. Fashion-MNIST similarly consists of 60,000 training samples with 10,000 test samples, the size of each image is $28\times 28$, and the image content includes 10 different kinds of goods. CIFAR-10 includes 60,000 natural images divided into 10 classes, and each image is $3\times 32\times 32$.

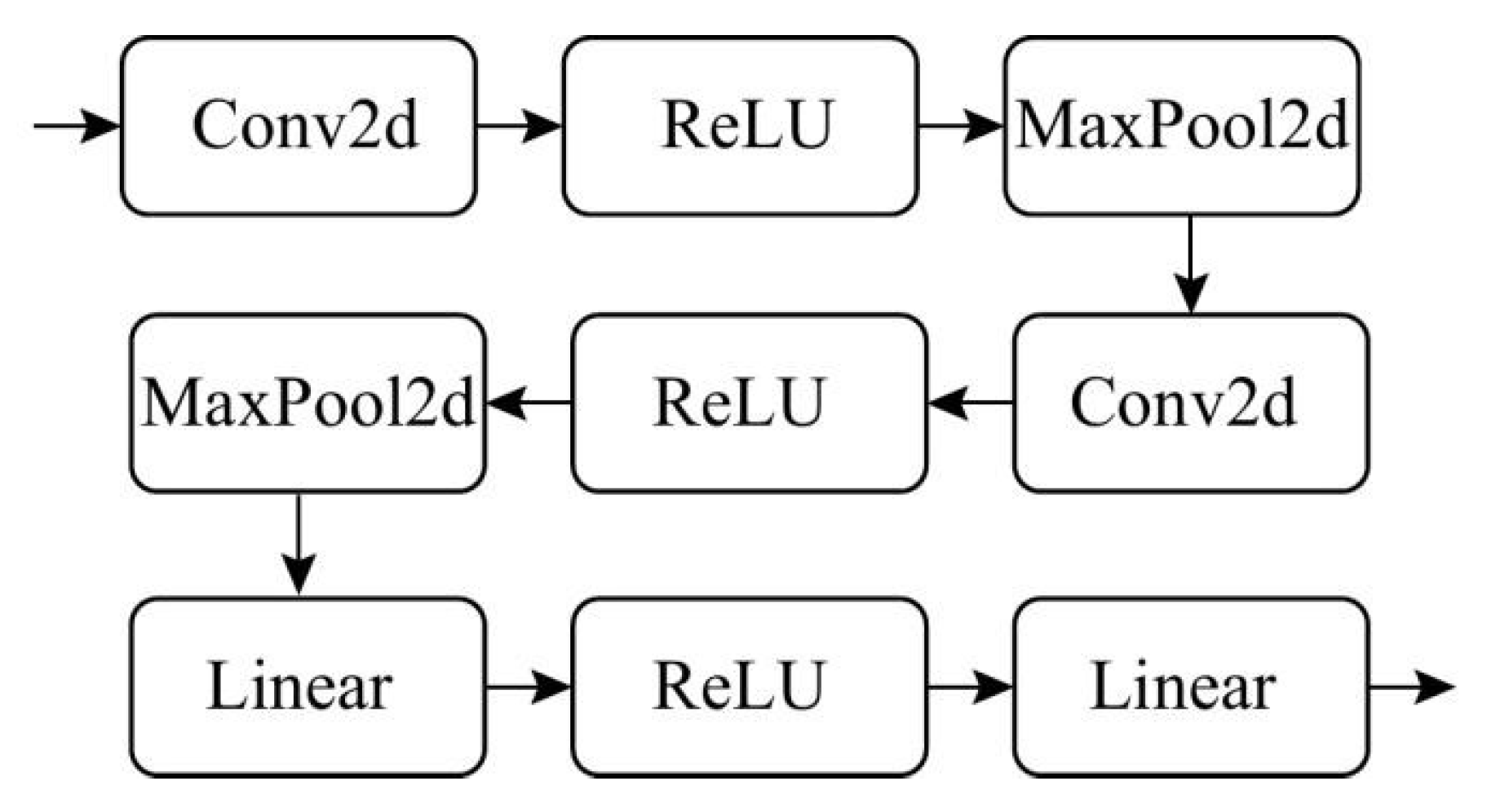
(2)

Neural Network Architecture

The experiment used a two-layer convolutional neural network on both the FMNIST dataset and the CIFAR10 dataset, as shown in Figure 3. The model structures on the two datasets are the same, but due to different inputs and outputs, the number of parameters in the model is slightly different.

(3)

Hyperparameter setting

The privacy preference levels selected by users are set to conform to normal distributions. The initial Gaussian noise parameters, $\sigma$, are 5 and 10; the learning rate $\alpha$ is 0.05; the number of participating users is 100; the noise reduction coefficient q is 0.90/0.94/0.98 (MNIST/Fashion-MNIST/CIFAR-10); the client’s selection rate in each round is 0.1. The maximum number of training rounds is 100, and the number of local training iterations is 5/10/20 (MNIST/Fashion-MNIST/CIFAR-10).

(4)

Test metrics

Accuracy is used as the evaluation index of model utility for comparison, which is calculated as follows:

$$Acc={\displaystyle \frac{Accurat{e}_{num}}{Tota{l}_{num}}}\times 100\%$$

(24)

where $Accurat{e}_{num}$ is the number of correctly predicted samples, and $Tota{l}_{num}$ is the number of samples in the whole test set. In order to visualize the progress of federated learning in the process of privacy budget consumption, this paper stretches the privacy budget consumed by APDP-FL and the comparison scheme to a uniform scale for graphical comparison.

(5)

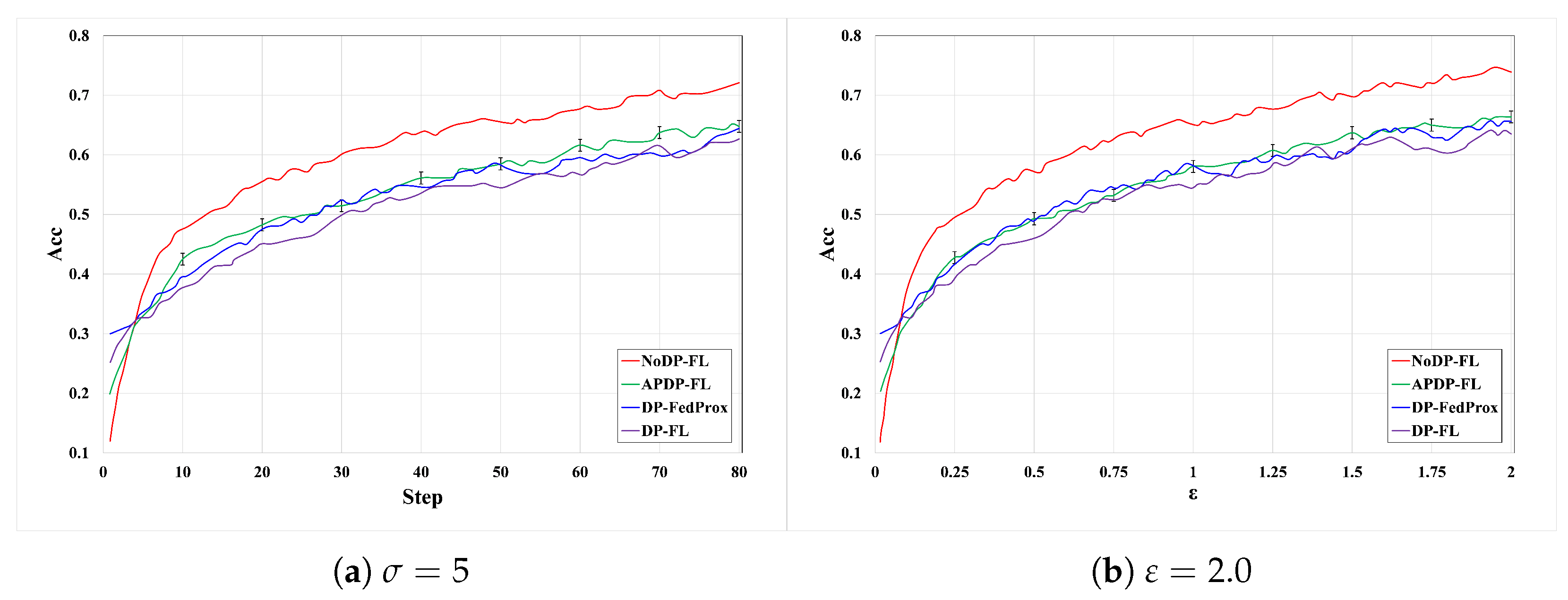
Baselines

The comparison schemes in the experiment include NoDP-FL, DP-FL, and DP-FLProx, where NoDP-FL [29] represents the federated learning scheme without adding noise; NoDP-FL represents no privacy budget consumption; DP-FL [30] represents the generalized federated learning scheme for differential privacy, which adds a unified noise; and DP-FLProx [31] represents the privacy-preserving scheme using differential privacy on FedProx.

(6)

Evaluation Metrics: Main task accuracy (MTA) [32] indicates the accuracy of a model with respect to its main (benign) task, which is used in this experiment to measure the performance of the defense method. The formula is as follows:

$$MTA={\displaystyle \frac{(x,y)\in M_n}{M_n}}\times 100\%$$

(25)

where $(x,y)$ represents the labels that are categorized correctly, and $M_n$ denotes the benign model. The larger the $MTA$, the better the performance of the method.

6.2. Experimental Performance Analysis

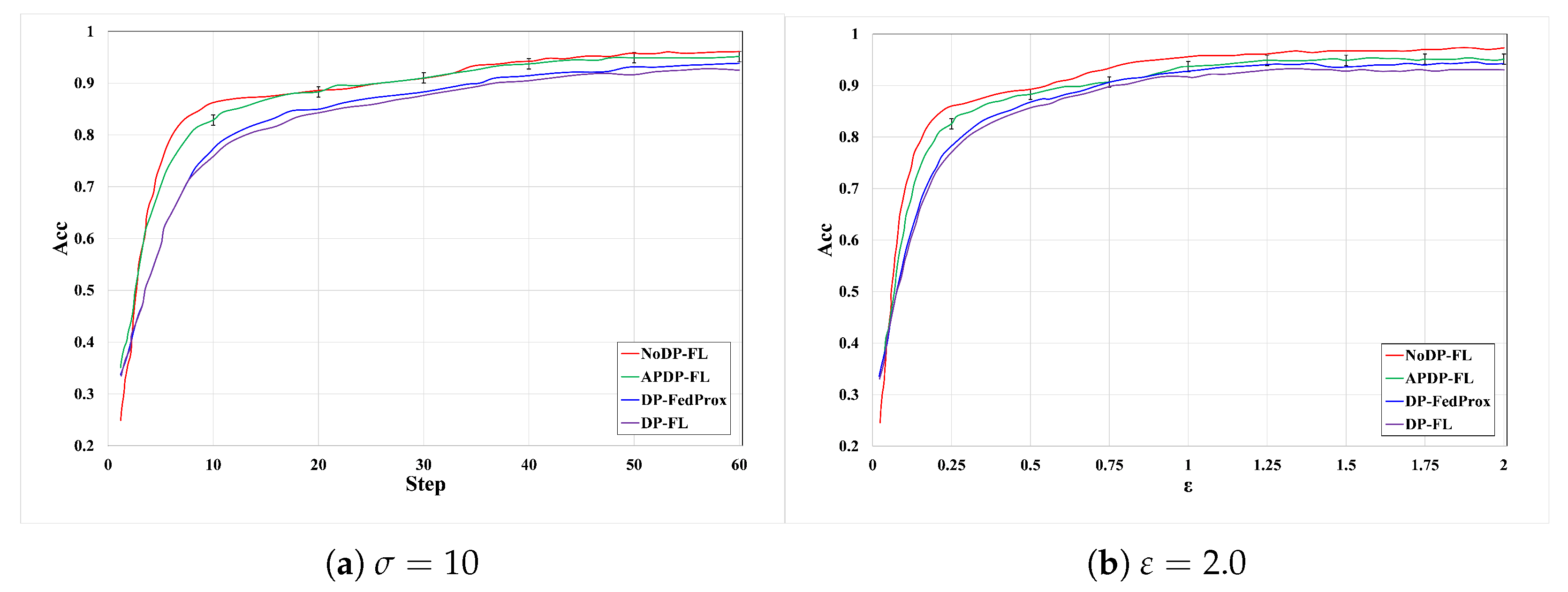
6.2.1. Experiments on the MNIST Dataset

The privacy preference levels selected by users are set to conform to the normal distribution. The initial Gaussian noise parameters, $\sigma$, are 5 and 10; the learning rate $\alpha$ is $0.05$; the number of participating users is 100; the noise reduction coefficient q is $0.90$; the client’s selection rate in each round is $0.1$. The maximum number of training rounds is 100, and the number of local training iterations is 5. The results of the experiments are shown as Figure 4 and Figure 5.

In the MNIST dataset, with the initial Gaussian noise parameter $\sigma$ of 5 and the privacy budget $\epsilon$ of $2.5$, after exhausting the privacy budget, APDP-FL reaches a final model accuracy of $(96.31\pm 0.17)$%, while DP-FL reaches $94.27\%$ and DP-FedProx reaches $95.18\%$. If no noise is added during the training process, the model’s accuracy can eventually reach $97.21\%$ after the model converges. From the communication cost perspective, APDP-FL has a total of 63 rounds of training and achieves $96.31\%$ before exhausting the privacy budget, which is just $0.9\%$ lower than NoDP-FL, which does not add noise and carries out training to make the model converge in its entirety.

With an initial Gaussian noise parameter $\sigma$ of 10 and privacy budget $\epsilon$ of 2, APDP-FL can eventually reach $(95.16\pm 0.14)$% model accuracy after exhausting the privacy budget. DP-FL can eventually reach $93.11\%$ model accuracy after exhausting the privacy budget. DP-FedProx can eventually reach $94.23\%$ model accuracy after exhausting the privacy budget. From the perspective of communication cost, APDP-FL has a total of 76 rounds of training before exhausting the privacy budget and achieves $95.16\%$, which is $2.05\%$ more accurate than the model trained by the DP-FL scheme under the addition of uniform noise during the training process.

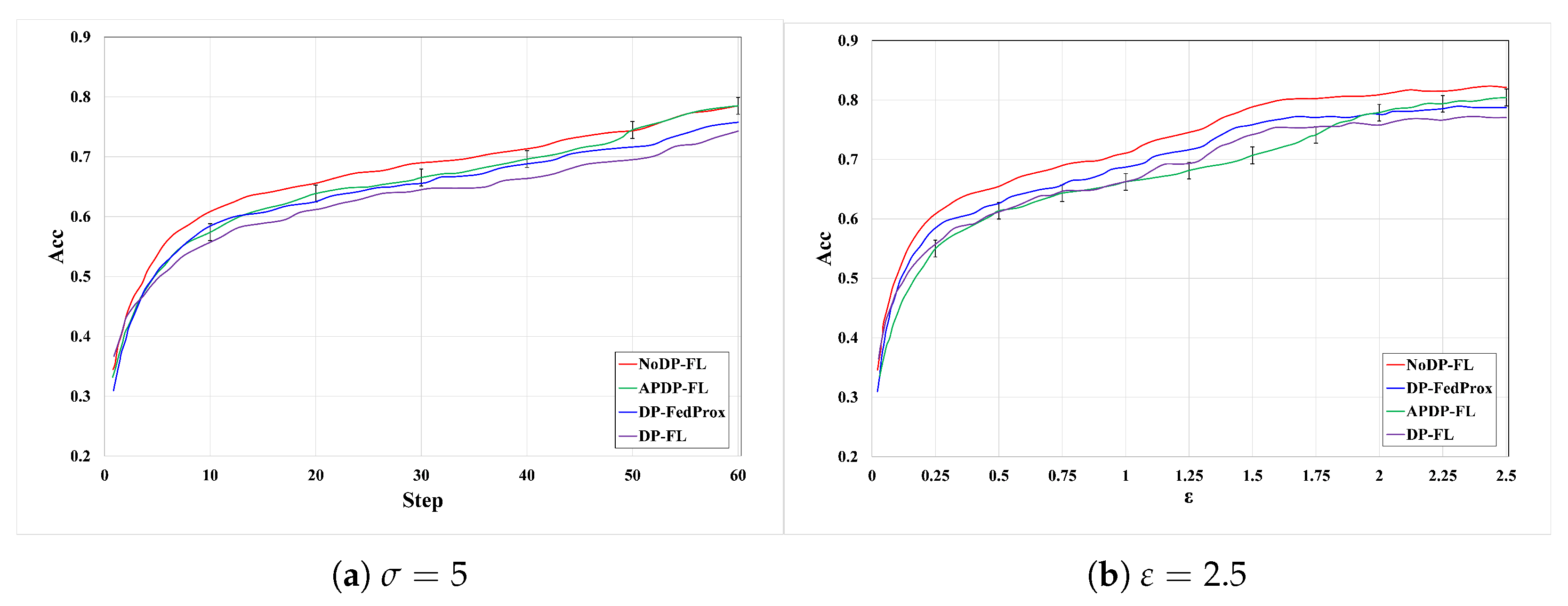
6.2.2. Experiments on the Fashion-MNIST Dataset

The user-selected privacy preference levels are set to conform to the normal distribution. The initial Gaussian noise parameters, $\sigma$, are 5 and 10; the learning rate $\alpha$ is $0.05$; the number of participating users is 100; the noise reduction coefficient q is 0.94; the selection rate of the client in each round is 0.1. The maximum number of training rounds is 100, and the number of local training iterations is 10. The experimental results are shown in Figure 6 and Figure 7.

In the Fashion-MNIST dataset, with the initial Gaussian noise parameter $\sigma$ set to 5 and the privacy budget $\epsilon$ set to 2.5, the model accuracy of APDP-FL can finally reach $(80.39\pm 0.25)$% after exhausting the privacy budget. The model accuracy of DP-FL can finally reach 77.18% after exhausting the privacy budget. The model accuracy of DP-FedProx can finally reach 78.18% after exhausting the privacy budget. Model accuracy can finally reach 78.76%, and if no noise is added during the training process, the model’s accuracy can finally reach 82.17% after the model converges. From a communication cost perspective, APDP-FL has 72 rounds of training and achieves 80.39% before exhausting the privacy budget, which is only 1.78% lower than NoDP-FL; this does not add noise and carries out training so that the model converges in its entirety.

Setting the initial Gaussian noise parameter $\sigma$ as 10 and the privacy budget $\epsilon$ as 2, the model accuracy of APDP-FL can finally reach $(78.55\pm 0.22)$% after exhausting the privacy budget. DP-FL can finally reach 75.92% after exhausting the privacy budget. DP-FedProx can finally reach 77.06% after exhausting the privacy budget. From the perspective of communication cost, APDP-FL performed a total of 80 rounds of training before exhausting the privacy budget and achieved 78.55%, which is 2.63% more accurate than the model trained by the DP-FL scheme under the addition of uniform noise during the training process.

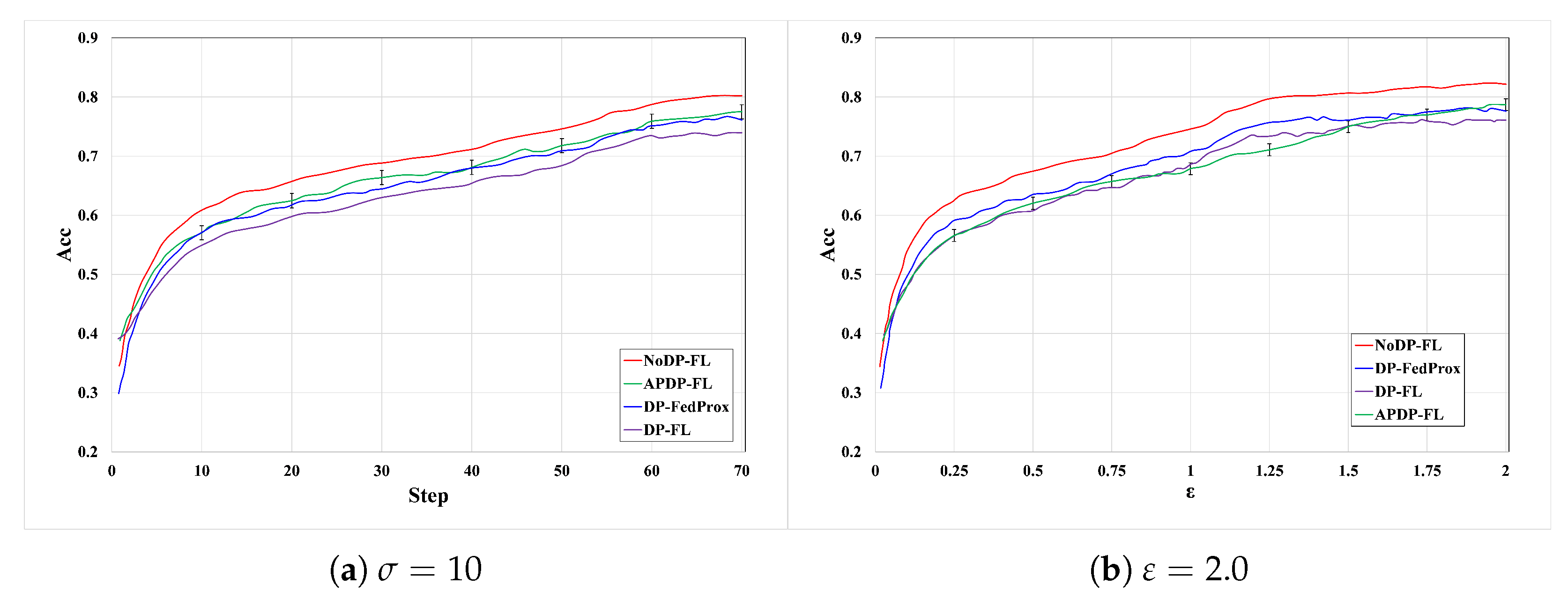
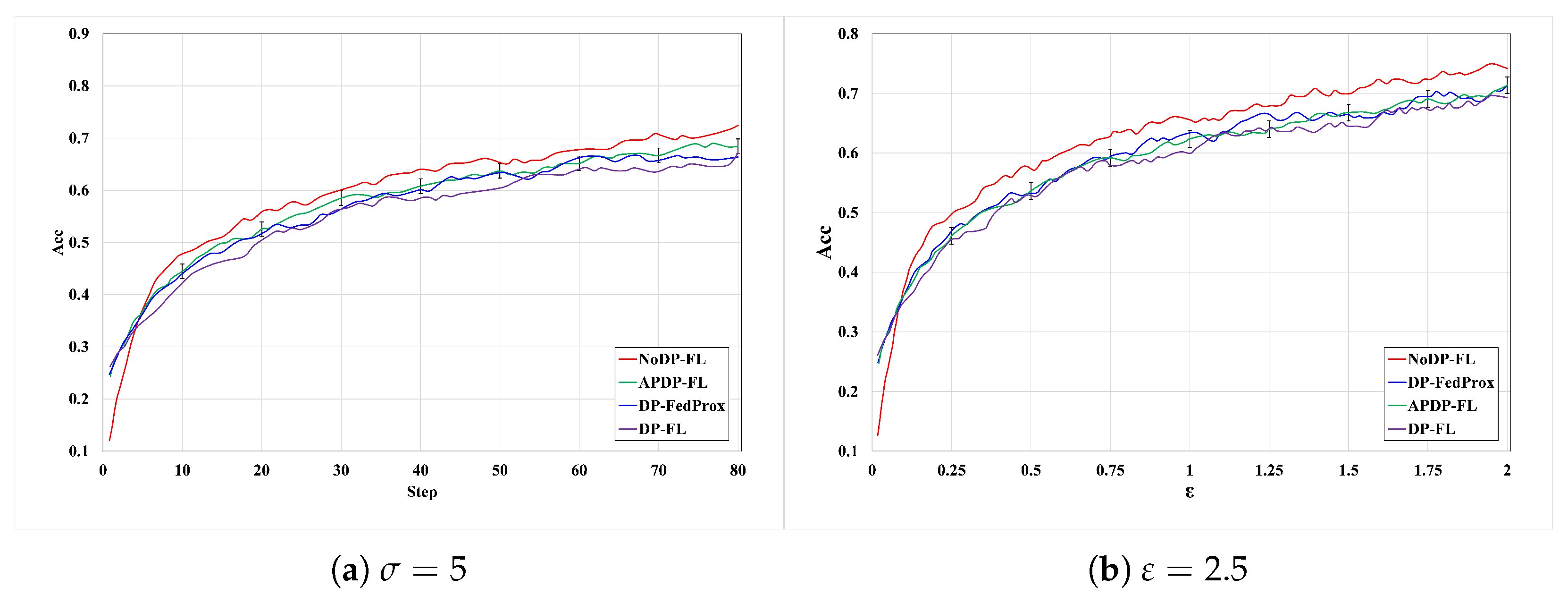
6.2.3. Experiments on the CIFAR-10 Dataset

The privacy preference level selected by users is set to conform to the normal distribution. The initial Gaussian noise parameters, $\sigma$, are 5 and 10; the learning rate $\alpha$ is 0.05; the participating users are 100; the noise reduction coefficient q is 0.98; the selection rate of the clients in each round is 0.1. The maximum number of training rounds is 100, and the number of local training iterations is 20. The results of the experiments are shown in Figure 8 and Figure 9.

In the CIFAR-10 dataset, with the initial Gaussian noise parameter $\sigma$ set to 5 and the privacy budget $\epsilon$ set to 2.5, the model accuracy of APDP-FL can finally reach $(70.74\pm 0.26)$% after exhausting the privacy budget. DP-FL can finally reach 69.11% after exhausting the privacy budget. DP-FedProx can finally reach 70.07% after exhausting the privacy budget, and if no noise is added during the training process, the model accuracy can eventually reach 74.06% after the model converges. From a communication cost perspective, APDP-FL underwent a total of 88 rounds of training and achieved 70.74% before exhausting the privacy budget, only 3.32% lower than NoDP-FL, which was trained without adding noise and converged the model in its entirety.

Setting the initial Gaussian noise parameter $\sigma$ as 10 and the privacy budget $\epsilon$ as 2, APDP-FL can finally reach $(66.32\pm 0.13)$% model accuracy after exhausting the privacy budget (repeat the experiment five runs to obtain the average value and range of values). DP-FL can finally reach 63.53% model accuracy after exhausting the privacy budget. DP-FedProx can finally reach 65.66% model accuracy after exhausting the privacy budget. From a communication cost perspective, APDP-FL has a total of 96 rounds of training before exhausting the privacy budget, and it achieves 66.32%, which is 2.79% more accurate than the model trained by the DP-FL scheme with the addition of a uniform amount of noise during the training process.

We analyze APDP-FL’s experimental results to investigate how Gaussian noise parameter $\sigma$ and the privacy budget $\epsilon$ impact model accuracy across varying levels of data heterogeneity. The experimental results demonstrate certain advantages compared to other similar methods after exhausting the privacy budget $\epsilon$, which is about 2.05–2.79% more accurate than scheme using differential privacy. The specific quantitative of the results are shown in

Table 1. Test accuracy (%) of APDP-FL on different datasets for different initial Gaussian noise parameters, $\sigma$, and privacy budgets, $\epsilon$.

Method	MNIST		Fashion-MNIST		CIFAR-10
	$\mathbf{\sigma }=\mathbf{5},\mathbf{\epsilon }=\mathbf{2.5}$	$\mathbf{\sigma }=\mathbf{10},\mathbf{\epsilon }=\mathbf{2.0}$	$\mathbf{\sigma }=\mathbf{5},\mathbf{\epsilon }=\mathbf{2.5}$	$\mathbf{\sigma }=\mathbf{10},\mathbf{\epsilon }=\mathbf{2.0}$	$\mathbf{\sigma }=\mathbf{5},\mathbf{\epsilon }=\mathbf{2.5}$	$\mathbf{\sigma }=\mathbf{10},\mathbf{\epsilon }=\mathbf{2.0}$
NoDP-FL	97.21	96.08	82.17	79.96	74.06	75.62
DP-FL	94.27	93.11	77.18	75.92	69.11	63.55
DP-FedProx	95.18	94.23	78.18	77.06	70.07	65.66
APDP-FL	$96.31\pm 0.17$	$95.16\pm 0.14$	$80.39\pm 0.25$	$78.55\pm 0.22$	$70.74\pm 0.26$	$66.32\pm 0.13$

.

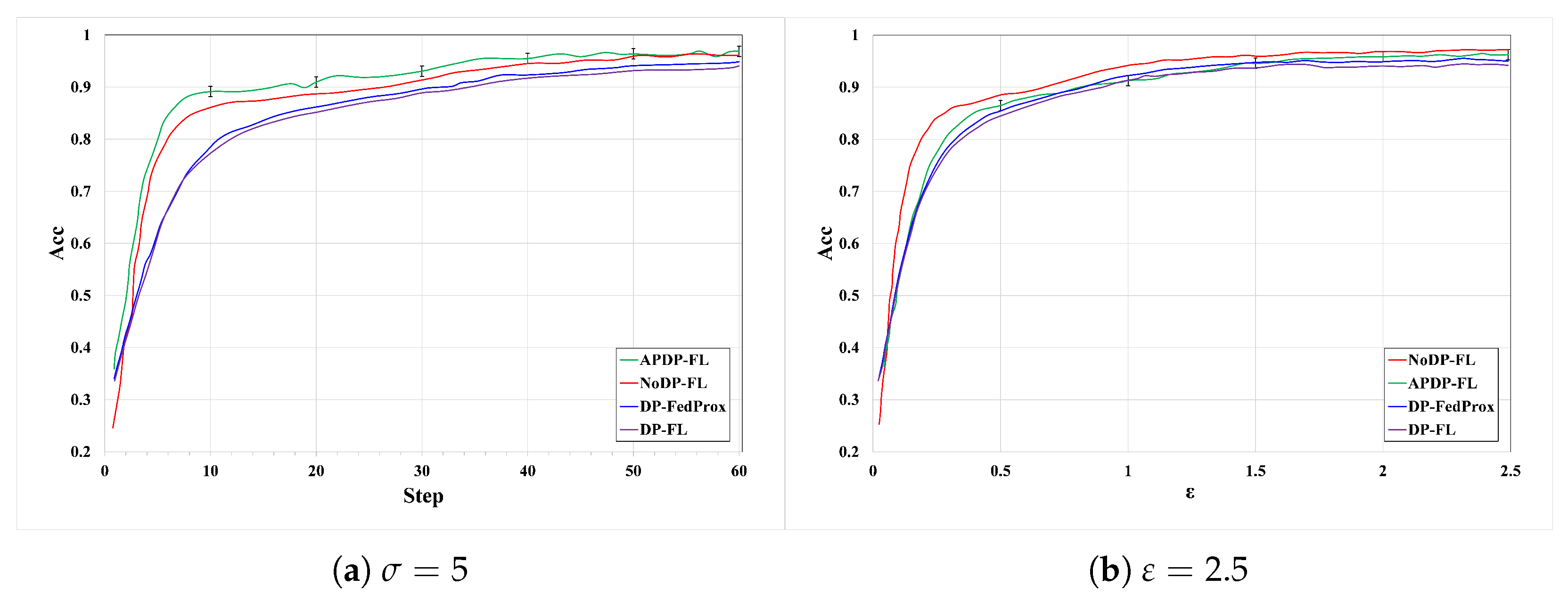
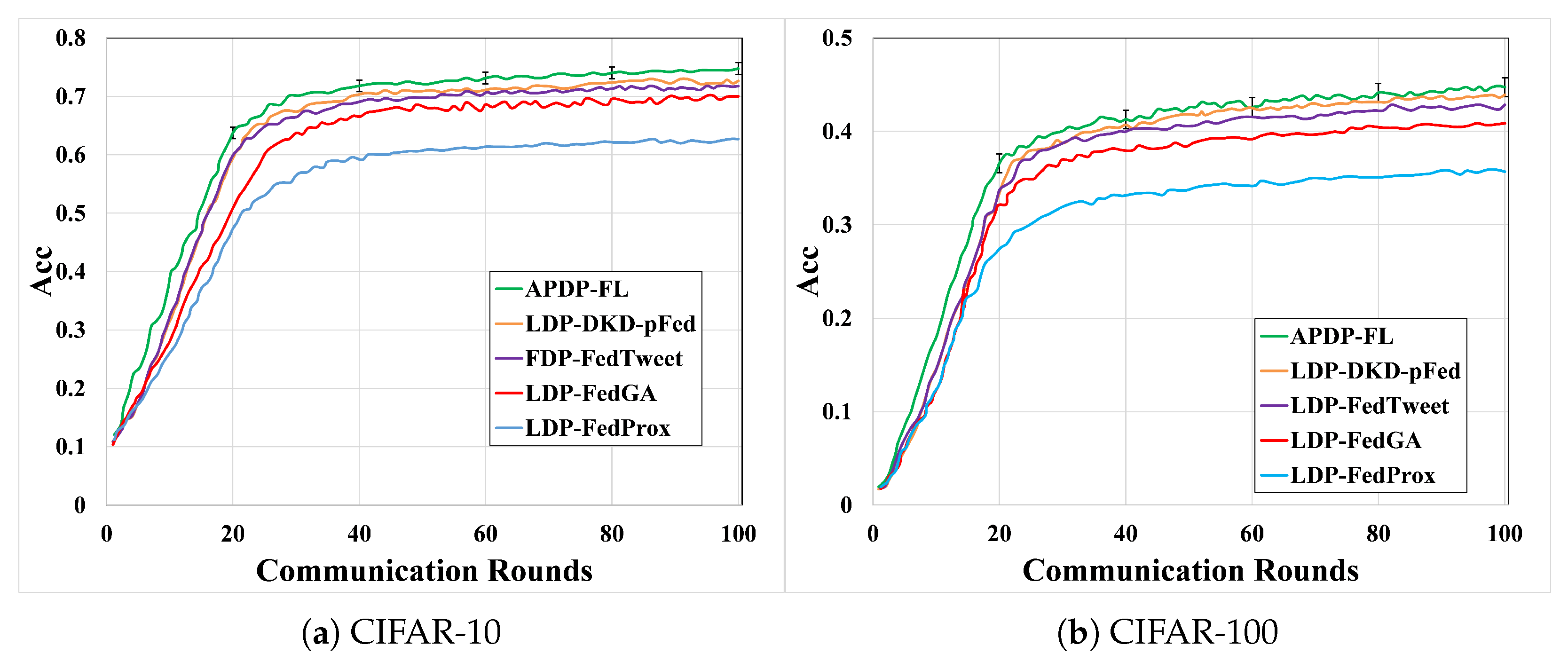
6.2.4. Comparison with Other Methods

This section evaluates the effectiveness of the APDP-FL method by comparing it with existing state-of-the-art approaches. Non-independent identically distributed (non-IID) data are generated on the CIFAR-10 and CIFAR-100 datasets, with data heterogeneity measured using the $\gamma$. The experimental comparison schemes are as follows: (1) LDP-FedProx [31], where FedProx incorporates local differential privacy; (2) LDP-FedGA [33], federated learning of generative adversarial networks with local differential privacy; (3) LDP-FedTweet [34], two-stage knowledge distillation with local differential privacy; (4) LDP-DKD-pFed [35], federated learning of personalized models with differential privacy. CIFAR-10 and CIFAR-100 employ Dirichlet coefficients of 0.05 and 0.1, respectively, to simulate heterogeneous datasets.

The experimental results demonstrate that APDP-FL exhibits a more pronounced advantage in model accuracy (as shown in Figure 10). On the heterogeneous CIFAR-10 dataset, APDP-FL can finally reach $(74.52\pm 0.12)$% model accuracy, and it achieves accuracy improvements ranging from 1.9% to 4.52% compared to other methods. On the heterogeneous CIFAR-100 dataset, APDP-FL can finally reach $(44.98\pm 0.18)$% model accuracy. Its improvement spans 0.89% to 3.96%, while APDP-FL requires significantly fewer communication rounds than alternative approaches. This fully demonstrates that, in a federated learning environment with the same number of communication rounds, APDP-FL achieves higher model accuracy.

Under identical privacy budgets in heterogeneous data scenarios, despite incorporating multiple complex techniques, APDP-FL achieves superior model accuracy due to its optimized adaptive local differential privacy mechanism and the synergistic effects of knowledge distillation and GANs on model training. Regarding computational overhead, while APDP-FL’s technical combination introduces increased computational complexity, its rapid convergence properties ensure that overall time consumption does not significantly increase compared to other methods when processing heterogeneous CIFAR-10 and CIFAR-100 datasets. It even demonstrates advantages in the complex heterogeneous CIFAR-100 training scenario, further highlighting APDP-FL’s comprehensive strengths in heterogeneous data federated learning.

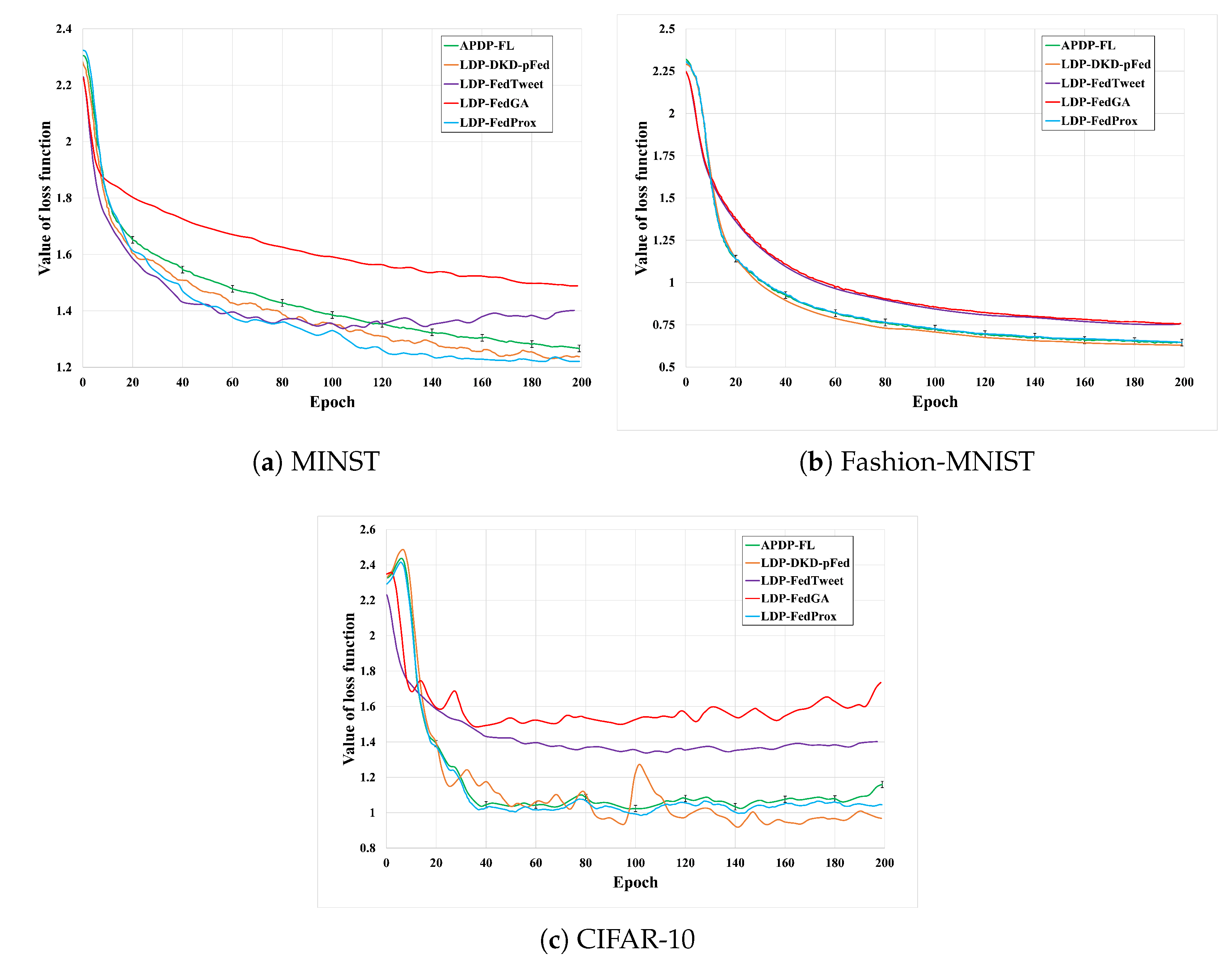
6.2.5. Model Convergence

In order to evaluate the convergence speed and stability of the model during the training process, five methods (APDP-FL, LDP-FedProx, LDP-FedGA, LDP -FedTweet, and LDP-DKD-pFeed) were trained for 200 rounds, and the corresponding loss function values for each round were recorded. The loss curves were plotted, as shown in Figure 11.

The convergence experiment results show that APDP-FL can converge faster and maintain lower final loss values on all three datasets. Compared to methods such as LDP-FedProx and LDP-FedTweet, its training curve is smoother, indicating that this method has better optimization ability and convergence stability.

6.2.6. Computational Overhead and Communication Rounds

(1)

Comparison of computational overhead between APDP-FL and DP-FL

From

Table 2. Comparison of computational overhead under different client numbers (seconds/rounds).

Clients Number	DP-FL	APDP-FL	Overhead Variance Rate
250	12.4	13.1	5.5%
500	10.8	11.3	4.4%
1000	10.4	10.8	3.7%

, it can be seen that, in non-IID data, APDP-FL obtains the global model through local model weighting, and the optimization process requires more local iterations, resulting in slightly higher computational overhead than DP-FL. As the client data size increases (from 250 to 1000 client samples) or the local training epochs increase (from 1 to 10), the efficiency difference between the two methods gradually narrows. For example, when the client data volume is N = 1000, the computational cost of APDP-FL is only about 3–8% higher than that of DP-FL.

(2)

Comparison of communication rounds between baselines

From

Table 3. Comparison of computational overhead under different client numbers (seconds/rounds).

Schemes	Client Upload Data Size	Server Distributed Data Size	Total Communication Cost	Additional Cost Sources
APDP-FL	11.0 MB × 20 = 220 MB	11.0 MB × 20 = 220 MB	440 MB	Personalized noise parameters + model adjustment
FedAvg	10 MB × 20 = 200 MB	10 MB × 20 = 200 MB	400 MB	Model parameter transmission
NoDP-FL	10.5 MB × 20 = 210 MB	10.5 MB × 20 = 210 MB	420 MB	Encryption or redundant parameters
DP-FL	10.5 MB × 20 = 210 MB	10.5 MB × 20 = 210 MB	420 MB	Additional noise parameters

, it can be seen that due to the addition of noise parameters, the communication cost of the privacy scheme is about 5% higher than that of the non-privacy scheme (420 vs. 400 MB). The personalized plan increases costs by approximately 4.8% (440 vs. 420 MB) due to the transmission of more local adjustment information. If personalized needs need to be taken into account, personalized solutions may have slightly higher costs, but privacy protection is more precise.

7. Conclusions

In this paper, the APDP-FL algorithm is proposed to address the problems of reduced model accuracy and inability to meet the personalized privacy requirements of traditional differential privacy techniques in order to protect federated learning. In terms of theoretical contribution, the algorithm first scores each round of training according to the parameters generated during the training process, and then, it automatically adjusts the noise scale added in the next round according to the scoring results. Meanwhile, when the client locally trains, it will adjust the local privacy protection level according to its own privacy preference, which meets the personalized privacy needs of different users, and the usability and superiority of the algorithm are proven through a series of experiments. In terms of technological innovation, the algorithm introduces personalized privacy protection strategies based on adaptive noise mechanisms. By adjusting noise, participants can adjust the Gaussian noise parameters according to their own privacy preferences, solving the problem of insufficient or excessive protection caused by a unified privacy budget setting. The experimental results have shown that this strategy has a 0.9% lower accuracy than the noise free approach on the MNIST dataset (96.31% vs. 97.21%), and the difference is also controlled within 3.32% on the CIFAR-10 dataset.

Although APDP-FL provides different privacy levels, it does not take into account the accurate privacy budget for different users. However, the problem of accurate privacy budgets can be solved through adaptive noise allocation, personalized dynamic adjustment, and optimization strategies such as gradient clipping. Future directions include multidimensional evaluation systems, personalized measurement, cross-data source budget management, graph data privacy allocation, and intelligent dynamic adjustment.

Therefore, future work needs to provide accurate privacy budgets directly to the participating clients and calculate the coefficients to adjust the Gaussian noise parameters to provide more accurate personalized privacy protection services. It is also very important to analyze whether the personalized approach actually achieves the desired, varied levels of privacy protection for different clients as intended.