Strategic Scenario Interaction: A Computational Framework Based on Game-Theoretic and Quantum-Inspired Modeling

Abstract

Strategic foresight often involves navigating deeply uncertain futures through scenario-based reasoning. Traditional methods rely on static narratives or probabilistic models, which fail to capture the dynamic, interacting, and nonexclusive nature of competing futures. This paper introduces a quantum-inspired framework for scenario interaction grounded in the mathematical formalism of superposition, interference, and contextuality. Agents are modeled as epistemic learners who iteratively update their preferences across multiple narrative pathways, which are treated as basis states in a conceptual Hilbert space. The simulation combines reinforcement learning with stochastic imitation, producing emergent distributions that resemble quantum-like collapse under feedback. Central to the model is the emergence of symmetries in the scenario structure and learning dynamics. Agents begin with neutral priors, facing a balanced reward landscape, epistemic and normative symmetry that is gradually broken through adaptive behavior. However, statistical symmetries persist at the ensemble level, as agents maintain partial preferences and oscillate among futures. These layered symmetries reflect both the cognitive realism of foresight practices and the mathematical tractability of quantum-inspired systems. The proposed model bridges strategic foresight, game-theoretic interaction, and quantum cognition, and offers a novel computational lens to study how futures are constructed, selected, and stabilized under uncertainty.

1. Introduction

The discipline of foresight is largely characterized by qualitative methodologies, especially in contexts marked by high uncertainty, ambiguity, and complexity. The qualitative methods in question include scenario building, qualitative interviewing, text and document analysis, workshops, and participatory dialogue among stakeholders. These methods are used to provide insights for understanding future developments through proactive thinking and behavior. Qualitative scenario development and analysis are useful tools for initial exploratory pathways, where the presence of uncertainty and incomplete knowledge does not allow for definite projections and predictions [1]. Given that the future (at any present moment) is an interactive space of possibilities, scenarios enable the coexistence of multiple futures without assigning deterministic probabilities, thereby shifting the focus from prediction to preparedness [2].

While theoretical scenario analysis is undeniably flexible, useful, and insightful for understanding what the future might contain, it has received significant criticism for its weakness in presenting or measuring the quantitative outcomes of the described behaviors and structural changes [3]. Most conventional scenario-based approaches treat narratives as discrete and non-interacting branches, neglecting the systemic interdependencies, feedback loops, and cognitive overlaps that frequently characterize real-world decision environments. Such methodological structures depend on separability assumptions, wherein futures develop along distinct trajectories and actors make selections based on fixed preferences or external criteria. Another point of criticism concerns the difficulties in addressing nonlinearity, narrative entanglement, and preference reversibility, which are key elements of human decision-making processes [4,5].

It should be emphasized that this constitutes a broader issue concerning decision-making within the neoclassical paradigm, rather than one limited to foresight studies. This recognition has, in particular, underscored the necessity of adopting an interdisciplinary perspective for understanding human economic behavior and, by extension, prospective or future behavior [6]. As a result, elements from psychology, sociology, neuropsychology, and other sciences provide a broader lens for assessing problems and developing strategies (see, for example, Simon [7], Kahneman & Tversky [8], Serra [9], et cetera).

In support of an interdisciplinary perspective, this study attempts to connect foresight and physics. Through the lens of physics, the future, like a particle’s state, is not completely unknown but rather undefined prior to its analysis. Both quantum states and future developments in complex systems are governed by intricate dynamics of causality and path dependency. The evolutionary path up to a given point in time constrains and shapes the set of possible future states, rendering both quantum and future outcomes accessible only in probabilistic rather than deterministic terms.

Advancements in quantum cognition and decision theory have introduced novel frameworks for conceptualizing beliefs, preferences, and actions in contexts characterized by ambiguity and contextual dependence [10]. Within this emerging body of literature, mental states are modeled not as discrete choices but as superpositions of potentialities, with decision moments analogous to measurement processes.

Given the limited attention that the issue of scenario and agent interaction has received, as well as the lack of a mathematical framework to estimate the effects of such interaction—which in general stems from the limited quantification of the foresight discipline—this study bridges the gap by introducing a quantum-inspired framework for scenario interaction. If we accept alternative scenarios as potential futures (in the literal sense of their likelihood of being realized), it becomes easier to discern the analogy with the quantum perspective. Specifically, before the systemic and behavioral processes that lead to the future unfold, all the scenarios we have envisioned may contribute to a particular outcome; in that sense, they are all potentially active. However, once a decisive moment of decision-making occurs, the spectrum of possible future scenarios collapses into a single one: the one that actually materializes. Conceptually, this line of thought echoes Schrödinger’s well-known thought experiment, illustrating the coexistence of potential states until observation collapses them into one.

Instead of considering scenarios as mutually exclusive trajectories, we conceptualize them as coexisting narrative states within a shared conceptual space. In this space, agents iteratively adjust their preferences using bounded rationality [7] and social imitation. This framework was operationalized via a multi-agent simulation that utilized reinforcement learning and stochastic choice dynamics. Agents are initialized with neutral priors over a balanced reward landscape, reflecting epistemic and normative symmetry among potential futures. Over time, they update their beliefs based on local experiences and feedback, leading to a probabilistic convergence toward their preferred narratives while maintaining persistent openness to alternative possibilities.

In our model, we assume a finite population of interacting agents who continuously choose among three general directions for the future (Green Tech, Growth First, and Social Equity). Their choice is based on observation, and it is updated through a probabilistic rule that reflects the relative popularity of each option while maintaining a baseline likelihood for all possibilities. Over time, this imitation process generates collective dynamics in which certain scenarios may dominate, coexist, or oscillate depending on social feedback and contextual framing. The model thus combines principles from agent-based social learning with a quantum-inspired formalism, allowing the state of collective foresight to be represented as a superposition of multiple potential futures, influenced by interference effects, contextual dependencies, and entangled interactions among agents’ beliefs.

The proposed framework facilitates the understanding and analysis of those essential characteristics inherent in real-world foresight processes, such as the partial alignment of preferences with normative identity, interference among narratives, and reversibility of commitments under changing conditions. Additionally, it allows for the formal representation of contextual effects, where the order of inquiry or framing influences outcomes, entanglement of beliefs across agents or domains, and dynamic symmetry breaking, wherein initially equivalent futures become differentiated through interactions. The simulation was not intended to predict outcomes but rather to trace the evolution of scenario distributions and preference architectures over time under minimal assumptions regarding agent rationality or system structure. In addition, our approach captures the complexity of real-world systems and human decision-making through a foresight framework, unlike current attempts to quantify future trajectories using forecasting and econometric modeling, which assume linear and deterministic relationships [11].

Our findings indicate that strategic behavior under conditions of uncertainty frequently results in structured pluralism, wherein agents tend to converge on certain potential futures, albeit not excluding others. This emergent pattern embodies both local adaptation and system-wide symmetry, with scenario commitment akin to quantum decoherence—a probabilistic resolution rather than a deterministic selection. These dynamics provide valuable insights for policy design and anticipatory governance [12], suggesting that resilient strategies may arise not from consensus or optimization but from navigating coherent diversity within the future possibility space.

This study advances both theoretical and methodological dimensions by integrating foresight modeling with a quantum-compatible formalism. Theoretically, it enriches the discourse on futures studies, while methodologically, it introduces a versatile simulation framework based on the mathematical principles of interference and superposition. This study paves the way for novel research avenues concerning scenario interaction, learning in ambiguous conditions, and the influence of symmetry in shaping long-term strategic environments.

2. Theoretical Background

2.1. Foresight and Physics: Unfolding the Conceptual Parallels

Foresight refers to the process of anticipating future probabilities and options for action by systematically understanding the future [13]. Scenario planning serves as a foresight tool that enables consideration of multiple future states.

Scenario design involves creating these alternative states and typically encompasses distinct steps [14]. These steps include [15]: (i) setting the purpose and timeline for the scenario exercise; (ii) identifying the forces of change and other “predetermined” uncertainties; (iii) introducing creative uncertainty through the exploration of wild cards and weak signals; (iv) generating approximately four scenarios and placing them within a scenario matrix; and (v) evaluating the produced scenarios along with their implications for the future and policymaking. There is no consensus on the specific steps followed in scenario design, as it largely relies on intuitive logic, trend extrapolation, and, at times, probabilistic modeling through forecasting [16]. This approach utilizes stochastic models to create ensembles of possible futures. These approaches typically presuppose that uncertainties can be categorized, bounded, or at least structured in terms of probability distributions, thereby enabling decision makers to navigate a manageable spectrum of outcomes [14].

Such methods present several limitations: (i) they frequently assume independence among scenario branches, thereby overlooking significant interactions, feedback loops, or emergent dynamics; (ii) the number of scenarios considered is typically limited and is selected more for cognitive manageability than for systemic comprehensiveness; (iii) the selection and framing of scenarios tend to be subjective and nonformalized, introducing biases and inconsistencies; (iv) classical probability frameworks encounter challenges in representing situations involving cognitive paradoxes, incompatible beliefs, or overlapping futures.

Scenarios translate complex notions into narratives about the future and generate futures intelligence for policymaking. Thus, while they are not aimed at exact prediction of the future, their purpose is to foster an environment of proactivity for the changes to come, and this is why foresight is often considered a “social science of the artificial” [17].

Through the philosophical lens, the exploration of future perspectives via foresight is a way to move beyond the limitations of a singular present [18]. Additionally, imagination bridges the present with the future due to the phenomenological structure of the latter [18]. The future, as an envelope of potentialities, leads to its conceptual connection with physics and the understanding of time. Such a connection has been previously explored by Christophilopoulos [19], who sought to expand the futures cone framework by integrating notions from physics to enhance one’s capacity to imagine possible futures and to comprehend the long-term impacts of even small actions.

On another note, for Nakhmanson [20], there are notable analogies between sociology and quantum mechanics: (i) societies (ensembles) can be described as wholes, (ii) actors from different social settings form heterogeneous ensembles, (iii) actors within the same social setting exhibit homogeneous behavior (collective versus anticollective), and (iv) there appears to be a kind of “intention” underlying evolution. Additionally, quantum physics and the future are accompanied by the same complex dynamics regarding causality and path dependency. Essentially, quantum states, just like the future, are only approachable if the (quantum) system’s evolution path is known up to a specific time [21].

This necessitates the exploration of more expressive mathematical frameworks that can effectively encapsulate the ambiguity, contextuality, and plurality of potential futures in a non-reductive manner. In this context, the formalism of quantum theory has emerged as a compelling alternative. Foundational mathematics, encompassing vector spaces, non-commutative operators, and probabilistic amplitudes, provides a more complex structure for representing how potential futures can coexist, interfere, and collapse through interaction [22].

In light of this, we explore the possibilities of an interaction between quantum theory and futures analysis not for predicting the future but for enriching the conceptual and mathematical vocabulary available for scenario analysis and interaction. In this context, the term quantum-inspired does not imply a physical equivalence between social systems and quantum systems; rather, it denotes the use of formal analogies (such as superposition, contextuality, and probabilistic interference) to model ambiguity, coexistence of narratives, and the dynamic interplay of potential futures.

2.2. Decision-Making and Scenario Analysis in a Quantum-Inspired Game Theoretic Context

One of the main shortcomings of neoclassical economics in decision-making processes is the assumption of full rationality, which requires a closed normative system in which individuals are identical, hold stable expectations, and have access to all available information. In this setting, firms and organizations are treated as black boxes, and managers are not differentiated [6]. In real-world applications, individuals differ due to their personal characteristics, experiences, and social environments, which eventually affect their decision-making processes [23]. Such characteristics generate anomalies in the consistency of human behavior.

To address these anomalies, the quantum cognition framework offers a promising approach for modeling human cognitive processes under uncertainty [10]. According to She et al. [24], cognitive and decision-making behavior is easily influenced by situational context, which is highly analogous to particle behavior in physical systems. A similar finding arises from Khrennikova [25], who argues that psychological and quantum experimental data present notable similarities, allowing for the interdisciplinary application of quantum-theoretic formalism. The mathematical framework of quantum mechanics provides a systematic basis for modeling uncertainty in human cognition and decision-making, as quantum cognition has demonstrated its ability to explain deviations from expected utility theory, such as order effects, conjunction and disjunction fallacies, and interference phenomena [24,26].

The fundamental mathematical construct in quantum theory is the state vector, or alternatively the density matrix, which exists in a Hilbert space. This state may be a superposition of multiple basis states, indicating that the system is not confined to a single configuration but exists in a simultaneous amalgamation of possibilities. It is only upon measurement that the system “collapses” into one of these basis states, a process that is inherently probabilistic and context-dependent.

Empirical literature on quantum cognition models and decision-making is relatively recent and focuses on using quantum theory as a generalized probability framework to explain anomalies in human judgment and behavior [27]. Notably, many of these approaches intersect with game theory due to its capacity to bridge neoclassical and behavioral economics. For example, Forno et al. [28] studied dynamics in binary choices when introducing quantum cognition into the Schelling model, distinguishing between context-insensitive agents (compatible choices in the quantum framework) and context-sensitive agents (incompatible choices). Furthermore, Ashtiani and Azgomi [29] constructed a two-stage quantum decision model to account for four game-theoretic empirical studies (the prisoner’s dilemma, splitting money game, the price is right game, and sheriff’s dilemma) and found that it can explain paradoxical behaviors in strategic games. These studies have demonstrated that quantum-like representations can effectively capture intersubjective uncertainty, belief entanglement, and nonclassical correlations in opinion dynamics and policy evaluation [30].

In general, the quantum cognition framework has been extended to include social systems, institutional choices, and collective decision-making under conditions of uncertainty, thereby contributing to the emergence of what is now termed quantum social science [10]. Despite these advancements, applications to foresight and scenario analysis remain limited.

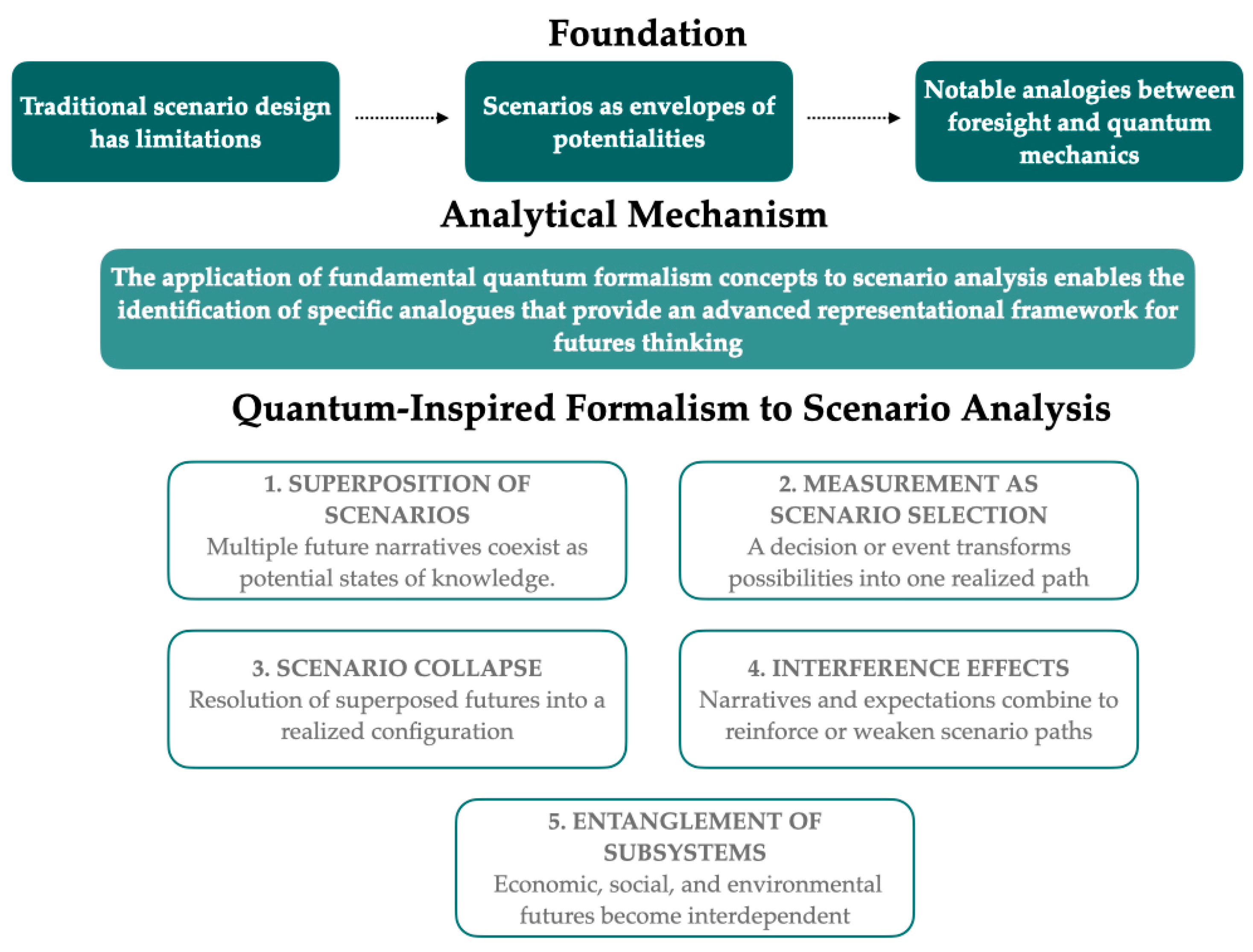
To this end, the application of fundamental quantum-formalism concepts to scenario analysis enables the identification of specific analogues that provide an advanced representational framework for futures thinking. This framework accommodates ambiguity, conflicting beliefs, and systemic interdependence without the need for artificial separation or additivity [31]. It is based on the following principles:

1. 

Superposition of Scenarios

Rather than selecting a single scenario or assigning fixed probabilities to each scenario, we conceptualized the state of knowledge as a superposition:

$$\mid \mathit{\Psi }\rangle ={\alpha }_1\mid {\mathit{s}}_1\rangle +{\alpha }_2\mid {\mathit{s}}_2\rangle +\cdots +{\alpha }_n\mid {\mathit{s}}_{\mathit{n}}\rangle$$

where $\mid {\mathit{s}}_{\mathit{i}}\rangle$ are individual scenario vectors and ${\alpha }_i$ are complex amplitudes encoding intensity, plausibility, or cognitive weight.

2. 

Measurement as Scenario Selection

A decision, event, or policy intervention functions as a measurement operator that projects the state of the scenario onto a singular realized pathway. This process modifies the system itself, similar to the collapse postulate.

3. 

Non-commutativity and Contextuality

The sequence in which questions or interventions are posed is significant; assessing “climate risk” prior to “technological innovation” may result in a different outcome than if the order is reversed. This phenomenon illustrates the noncommutative nature of quantum observables.

4. 

Interference Effects

Similar to the way probability amplitudes can interfere constructively or destructively, narratives, expectations, and policy framing can also influence scenario outcomes. This phenomenon can elucidate paradoxes or preference reversals that are not accounted for by classical logic [26].

5. 

Entanglement of Subsystems

The futures of various subsystems, such as the economy and environment, may become intertwined, resulting in outcomes that are no longer independent, even in the absence of direct causal relationships. This phenomenon encapsulates the interdependence of global phenomena without reducing them to correlations.

At this point, it is important to mention that a few significant studies have investigated quantum-inspired logic for narrative evolution [21] and the employment of quantum models to formalize ambiguity in future expectations [32]; however, to our knowledge, there is currently no comprehensive framework that explicitly models scenarios as quantum states, treats scenario interaction as interference, or facilitates simulation-based exploration of this dynamic space. Therefore, the present study aims to bridge the gap between quantum cognition models and strategic foresight by introducing a formal quantum framework for the representation, manipulation, and resolution of scenarios.

The following Figure 1 presents the conceptual framework of the study.

3. Mathematical Formulation

3.1. Agents and Scenarios

We examine a finite population of decision-making entities, referred to as agents $A=\{\mathrm{1,2},\dots ,N\}$. Each agent may represent a stakeholder, such as an individual, organization, social group, or political actor, engaged in the strategic anticipation of future developments.

The agents operate within a shared strategic environment, wherein they must repeatedly select from a finite set of future pathways or scenarios $\mathcal{S}=\{{\mathit{s}}_1,{\mathit{s}}_2,\dots ,{\mathit{s}}_{\mathit{K}}\}$. Each scenario encapsulates a coherent narrative regarding the potential evolution of society, technology, the economy, and the environment.

In our implementation, we defined the following three scenario archetypes, which reflect widely debated themes in contemporary policy discourse:

• Green Tech: scenarios that prioritize technological innovation and improvements in efficiency to address environmental degradation and climate change.
• Growth First: scenarios that emphasize economic growth, often at the cost of environmental sustainability or equitable distribution.
• Social Equity: scenarios focused on social justice, inclusivity, and the equitable distribution of resources and opportunities.

Each agent $i\in \mathcal{A}$ selects one scenario $s_i^t\in \mathcal{S}$ at each time step $t\in N$, resulting in a system configuration $s^t=\left(s_1^t,s_2^t,\dots ,s_N^t\right)$. These configurations are not fixed; rather, they undergo dynamic evolution as agents interact, revise their beliefs, and react to observed trends within the population.

This setup is positioned within the extensive literature on agent-based models of collective behavior [33], in which simple micro-level rules lead to the emergence of complex macro-level phenomena. The modeling of agent decision-making across alternative scenarios is consistent with research in scenario planning and foresight science, especially within frameworks that highlight scenario co-evolution [34] and strategic alignment dynamics [35]. Notably, our formulation allows agents’ preferences to be endogenous and adaptive, rather than static, which aligns with empirical findings in social psychology and behavioral economics concerning norm-driven and peer-influenced decision-making [36].

To implement these concepts, we developed an agent-based simulation framework that captures both the probabilistic dynamics and semantic interactions among competing futures. This simulation is not intended to predict a singular outcome; rather, it aims to trace the prevalence and resilience of potential scenarios as they arise from decentralized decision-making processes and localized imitation under conditions of uncertainty. The methodology is as follows.

3.2. Stochastic Dynamics

The agents in our model do not function independently of each other. At each discrete time step t, they observe the scenario choices made by others and may subsequently revise their decisions. This process is formalized through a stochastic rule, drawing inspiration from evolutionary dynamics and models of imitation in social learning [37].

Let $s_i^t\in \mathcal{S}$ denote the scenario chosen by agent $i$ at time $t$. At time $t+1$, each agent samples a peer $j \ne i$ uniformly at random from the population and observes their current scenario choice $s_j^t$. The agent subsequently revises their decision based on a probability that is contingent upon the observed distribution of scenario preferences within the population. This reflects the notion that agents are influenced by both their peers and by emergent trends.

The transition probability $\mathrm{P}\left(s_i^{t+1}=s_k∣{\mathit{s}}^{\mathit{t}}\right)$ is modeled as a function of the relative popularity of each scenario in the current population configuration. A simple and tractable formulation is as follows:

$$\mathrm{P}\left(s_i^{t+1}=s_k\right)={\displaystyle \frac{n_k^t+\alpha }{N+K\alpha }}$$

where

• $n_k^t$ is the number of agents choosing scenario $s_k$ at time t;
• $\alpha >0$ is a smoothing parameter (a form of “prior belief”);
• $N$ is the total number of agents;
• $K=\left|\mathcal{S}\right|$ is the number of scenarios.

This rule pertains to a generalized Pólya urn process, wherein scenarios that are more popular are more likely to be emulated; however, all scenarios maintain a fundamental probability of selection, even if they are temporarily less favored than others. The stochastic process is ergodic and guarantees long-term convergence to a stationary distribution under mild regularity conditions [38].

In this context, the stochastic evolution of scenario choices follows a Markov process, which means that agents’ future choices depend only on their current state and not on past trajectories. This formulation is standard for modeling adaptive behavior and allows the system to be represented by a transition matrix that captures the probabilities of moving between scenarios.

A salient characteristic of this formulation is its alignment with the concept of bounded rationality: agents do not engage in optimization over intricate future scenarios but instead respond to limited and imprecise signals, such as the actions of their peers. In this setup, the sampling of a single peer $j$ serves as a local proxy for the overall population trend. The observed scenario $s_j^t$ does not enter the probability expression directly; rather, it informs the agent’s estimation of the aggregate scenario frequencies $n_k^t$, which represent the expected likelihood of encountering each scenario through repeated observations. Thus, imitation operates at the population level, and each agent’s revision is guided by a representative peer observation rather than by direct pairwise copying. This design maintains analytical tractability while capturing the diffusion of preferences through social-learning processes.

The imitation mechanism can be further developed to incorporate elements such as prestige weighting [39], memory depth [40], and focal scenario effects, where certain options gain prominence due to framing or institutional endorsement [41]. In models incorporating memory, the agent’s update rule may rely not only on the current distribution but also on the weighted average of previous rounds. Such “inertial imitation” processes [42] may result in slower adaptation but lead to more robust convergence. These dynamics reflect the dissemination of narratives within real-world strategic foresight, where dominant scenarios may arise not from rational consensus but through feedback loops of attention and repetition, even when initially suboptimal.

Although our current implementation employs a discrete agent-based model characterized by classical transition dynamics, several components exhibit a structure consistent with quantum principles. For instance, the presence of stochastic imitation with smoothing parallels the persistence of nonzero amplitudes across alternative configurations, akin to superposition rather than collapse [10]. The probabilistic nature of agents’ imitation, as opposed to the deterministic selection of the most frequent scenario, introduces a fundamental indeterminacy that aligns with the quantum concepts of non-deterministic evolution [43]. Furthermore, the ergodic nature of the system, where each scenario retains a non-negligible probability of recurrence, reflects the concept of probabilistic recurrence in decoherence models of open quantum systems [44]. These conceptual parallels support our interpretation of the modeling framework as compatible with, and partially inspired by, quantum perspectives on choice, diffusion, and memory.

3.3. Quantum Choice and Interference Structure

In our framework, each scenario is not merely a static attractor but exists as a probabilistic amplitude influenced by the distribution of other agents’ beliefs. When an agent updates its choice, this process does not simply reflect independent probabilities, but is contextually entangled with the local configuration, akin to quantum interference, where the presence of multiple paths alters the final distribution of outcomes [45].

In addition to these structural similarities, it is essential to elucidate the fundamental “unit of action” within our framework. This clarification enhances the analogy with quantum systems and addresses a common inquiry regarding the role of quantum elements in scenario modeling.

In the realm of quantum physics, a quantum is defined as the smallest indivisible unit of action or energy. In our theoretical framework, this role is fulfilled by discrete decision events, through which agents select among various scenarios. Each decision represents a minimal, probabilistic, and context-dependent action, similar to a quantum measurement. These micro-level decision quanta serve as the foundational elements of the system: while each is insignificant in isolation, their cumulative effect across agents and over time gives rise to emergent dynamics, such as convergence, pluralism, and oscillatory switching. This analogy strengthens the conceptual link between quantum-inspired reasoning and scenario interaction, illustrating that continuous systemic evolution is ultimately composed of discrete, indivisible units of decision-making [10].

The application of a smoothing kernel to the local imitation process introduces an effect that is analogous to the off-diagonal elements of the density matrix. This effect encapsulates the notion that beliefs are not simply additive; rather, they can reinforce or suppress one another based on their relative positions within the configuration space. Consequently, our simulation transcends the purely classical Markovian diffusion of preferences, exhibiting a quantum-like interference pattern. Here, the structure of the probabilities is influenced by the geometry of the belief space and its evolution over time.

This interpretation is consistent with broader initiatives in quantum cognition and quantum-like social modeling, wherein decision-making processes are conceptualized as evolving not merely over discrete alternatives but within a Hilbert-like information space. In this space, potentialities, rather than solely actualities, dictate behavior [10]. In this context, the concept of entanglement is epistemic rather than physical; the decisions of agents are interdependent, with outcomes shaped by shared informational fields rather than isolated rationality.

Consequently, although our simulation is based on a classical computational framework, its structural characteristics reflect essential aspects of quantum theoretical reasoning, namely superposition, interference, and contextual dependence. This suggests that quantum-compatible frameworks can be effectively applied to foresight and scenario modeling without necessitating the direct application of quantum mechanics.

In mathematical terms, the interference-like behavior arises from the interaction between the Softmax updating rule and the smoothed imitation kernel, which jointly generate nonlinear cross-dependencies among scenario probabilities. Because the sequence of these updates affects subsequent transition probabilities, the process is order-dependent and, therefore, non-commutative, a property that mirrors contextuality in quantum-like systems.

However, it should be emphasized that the present formulation is quantum-inspired rather than quantum-mechanical in the strict sense. Analogies are employed at a structural and epistemic level to represent contextuality and non-additive interactions between beliefs, rather than as a physical theory of microscopic phenomena. This approach preserves probabilistic consistency within a classical stochastic system while retaining the conceptual richness of quantum reasoning in modeling uncertainty and interdependence.

Therefore, the model consistently maintains a clear distinction between the physical, mathematical, and conceptual applications of the quantum analogy, ensuring that each operates within its appropriate interpretive domain.

4. Materials and Methods

To implement our quantum-inspired scenario framework, we developed a multi-agent simulation in which a limited number of epistemic agents iteratively engage with a series of competing future scenarios. The objective is to investigate the evolution of collective preference structures as agents update their internal models through experience-based feedback, operating under conditions of bounded rationality and incomplete information. This approach integrates concepts from reinforcement learning, evolutionary game theory, and narrative-driven foresight modeling.

The simulation is situated within a stylized foresight exercise that examines the future of national policy in the aftermath of crises such as environmental degradation, economic stagnation, or social unrest. The primary inquiry focuses on how societies prioritize technological sustainability, economic growth, and social equity in long-term strategic planning.

Three competing future scenarios are defined as follows.

• Green Tech: A future characterized by accelerated environmental transitions, decarbonization, and investment in clean technology, potentially at the expense of short-term economic efficiency.
• Growth First: A developmental strategy centered on gross domestic product growth, deregulation, and infrastructure expansion, predicated on the belief that such economic prosperity will ultimately facilitate environmental and social advancements.
• Social Equity: A future focused on redistributive policies, participatory governance, and social justice, which may serve to limit both technological disruption and capital-intensive expansion.

These narratives exemplify real-world policy tensions and serve as an ideal framework for investigating scenario dynamics under conditions of uncertainty and normative divergences. The objective is not to ascertain a preferable future, but rather to analyze how agents with conflicting priorities learn, adapt, and polarize over time, potentially demonstrating how consensus, conflict, or enduring pluralism may arise.

4.1. Agent Architecture and Scenario Space

The model comprises three agents (Green, Growth, and Equity), each embodying a distinct normative orientation or institutional logic. At each discrete time step, the agents select from three predefined scenarios: Green Tech, Growth First, and Social Equity.

In this conceptual scenario space, these options are regarded as basis states, akin to orthogonal vectors within a Hilbert space.

Each agent possesses an internal subjective utility function that evaluates the available scenarios as follows:

$${\mathrm{U}}_i\left(s\right)\hspace{1em}\mathrm{for}\hspace{1em}s\in \mathcal{S}$$

Initially, all values ${\mathrm{U}}_i\left(s\right)=1.0$, reflecting epistemic neutrality.

Agents are modeled as bounded rational learners by combining reinforcement learning with stochastic imitation. This hybrid mechanism provides a realistic yet tractable way to capture adaptation when information is limited and uncertainty is deep [46]. While more sophisticated formulations, such as artificial intelligence-based or Bayesian adaptive agents, could be explored in future research, the present design serves as a first-step approximation that is suitable for investigating emergent collective behavior.

4.2. Choice Mechanism: Softmax Selection Under Uncertainty

Scenario selection is governed by a SoftMax rule, which is extensively utilized in probabilistic decision-making models under conditions of uncertainty. Specifically, agent i selects scenario s with probability

$${\mathrm{P}}_i\left(s\right)={\displaystyle \frac{{\mathrm{e}}^{{\mathrm{U}}_i\left(s\right)/T}}{{\sum }_{s^{\prime }\in \mathcal{S}}{\mathrm{e}}^{{\mathrm{U}}_i\left(s^{\prime }\right)/T}}}$$

Parameter T (temperature) regulates exploration vs. exploitation. As $T\to 0$, agents behave deterministically; as $T\to \mathrm{\infty }$, their behavior approximates random choice.

The Softmax rule translates the relative utilities of agents into choice probabilities through smooth logistic mapping. Higher utility values yield higher selection probabilities, whereas the temperature parameter T controls the degree of randomness in decision-making, from near-deterministic choices at low T to exploratory behavior at high T.

This probabilistic choice rule aligns with quantum amplitude-to-probability mapping, wherein the exponential weights function as analogs of squared amplitudes within a cognitive framework [32].

Although this correspondence draws inspiration from quantum probability theory, the model remains classical in its computational implementation, and no complex-valued amplitudes or Hilbert-space operators are used. The analogy serves to represent the contextual and non-additive aspects of belief updating, rather than replicating the formal machinery of quantum mechanics. In this sense, the Softmax transformation provides a structural analog of the amplitude-to-probability projection, allowing the model to capture interference-like effects in decision-making while preserving mathematical transparency.

In this quantum-inspired context, an “observation” corresponds to an agent’s moment of choice, that is, when a probabilistic preference over multiple potential scenarios becomes a realized selection. This event functions as a conceptual analog of quantum collapse: the latent superposition of alternative futures is reduced to a single observed configuration. The process is not implemented through a physical projection rule (such as a Lüders operator) but through the Softmax sampling of scenario probabilities. Accordingly, the collapse represents a cognitive and informational update within a classical simulation, consistent with the interpretation of the model as quantum-inspired rather than quantum mechanical.

Therefore the “collapse” is not triggered by any probability threshold (e.g., $\mathrm{P}>\mathrm{X}$) but occurs naturally at each iteration when an agent’s probabilistic state is resolved into a concrete scenario through sampling.

In all baseline simulations, the learning rate was set to $a=0.3$ and the Softmax temperature to $T=0.8$, representing a balanced exploration–exploitation regime.

4.3. Feedback and Learning Dynamics

Upon selecting a scenario, the agent receives a context-specific reward that reflects the perceived benefit of the outcome for agent i. Subsequently, agents update their internal utilities by employing an exponential smoothing rule as follows:

$${\mathrm{U}}_i^{\left(t+1\right)}\left(s\right)={\mathrm{U}}_i^{\left(t\right)}\left(s\right)+\alpha \left[{\mathrm{r}}_i\left(s\right)-{\mathrm{U}}_i^{\left(t\right)}\left(s\right)\right]$$

where $\alpha \in \left(0,1\right)$ is the learning rate.

This rule represents a simplified variant of temporal-difference learning that enables agents to update their beliefs adaptively, without requiring comprehensive model knowledge [47].

4.4. Reward Matrix and Inter-Agent Competition

The reward structure was intentionally designed to be asymmetric, thereby introducing a form of narrative competition among the agents.

Table 1. Reward Matrix.

Scenario	Green	Growth	Equity
Green Tech	1.0	0.4	0.6
Growth First	0.3	1.0	0.5
Social Equity	0.5	0.4	1.0

provides a structured overview of the asymmetric reward matrix used to model interactions among the three scenario-oriented agents.

This configuration illustrates the non-universality of scenario desirability, aligning with foresight literature that highlights conflicting stakeholder perspectives [35].

4.5. Simulation Objectives

The simulation is executed using Wolfram Mathematica (version 14.2) and spans a duration of 100 rounds, offering ample temporal scope for the development and stabilization of adaptive learning dynamics. In each round, agents update solely the scenario they have chosen, adhering to a localized experience-based reinforcement rule influenced by Softmax probabilities. This methodology exemplifies how boundedly rational actors refine their preferences through repeated interactions with landscapes of alternative futures.

To address the stochastic characteristics inherent in the learning and selection processes, the model was executed across 1000 independent Monte Carlo iterations. This ensemble approach facilitates the statistical comprehension of systemic tendencies, effectively filtering out artifacts from individual trajectories and enabling robust inferences regarding emergent macro-patterns. Repeated iterations reveal whether convergence occurs toward specific scenarios, whether divergence persists among agents, indicating enduring pluralism, or whether oscillatory patterns emerge, suggesting deeper structural tensions within the scenario space.

The integration of reinforcement learning with scenario dynamics conceptualizes agents not as all-knowing optimizers but as epistemic learners navigating uncertainty. Their adaptive trajectories reflect, in a simplified manner, the practices of foresight professionals who iteratively reassess the plausibility and attractiveness of future narratives in response to new evidence or changing priorities.

Although the model operates within the framework of classical mechanics, it retains conceptual alignment with quantum-informed approaches to futures thinking. Scenario states are considered nonexclusive, permitting overlapping preferences that evolve in a probabilistic rather than deterministic manner. The resulting distributions of choice exhibit interference-like effects, and the feedback-driven stabilization of preferences mirrors the collapse dynamics observed in quantum measurements. This structural analogy offers both a theoretical foundation and cognitive resonance for interpreting agent behavior under conditions of profound uncertainty and narrative multiplicity.

The simulation employs three agents, runs for 100 rounds, with 1000 Monte Carlo iterations, using $a=0.3$ and a Softmax temperature $T=0.8$ as specified in Section 4.2 and Section 4.6.

A complete implementation of the algorithm, including initialization, Softmax sampling, utility updating, and Monte Carlo looping, is provided as Supplementary Material. Figure 2 presents a flowchart offering a concise algorithmic summary of the sequence of operations.

4.6. Sensitivity and Robustness Design

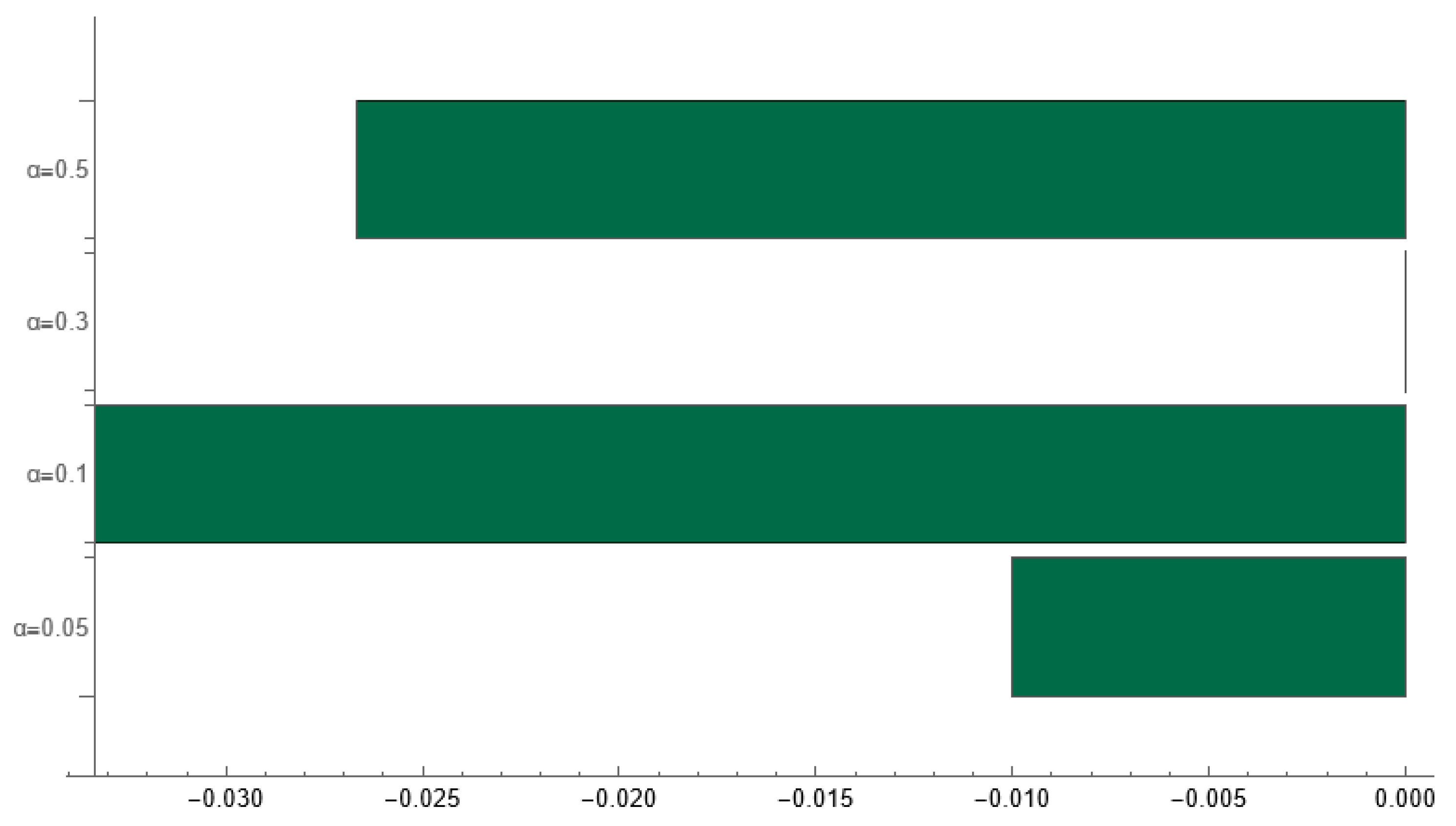
To evaluate the robustness and generalizability of the proposed model, we conducted a systematic sensitivity analysis and supplementary tests employing alternative decision rules. The analysis concentrated on three principal dimensions: (i) the exploration–exploitation balance (Softmax temperature $T$), (ii) the learning rate $\alpha$, and (iii) bounded random perturbations of the reward matrix (±0.1, clipped to [0, 1]). Each configuration was simulated for 100 rounds and replicated 120 times to account for the stochastic variability.

For each grid point, we recorded the final scenario shares, computed Shannon entropy as a compact measure of systemic diversity, and estimated 95% confidence intervals for each scenario’s prevalence using normal approximation. Entropy and confidence intervals provide concise indicators of robustness: entropy captures the persistence of diversity, whereas overlapping confidence intervals signal stable relative shares.

Tornado diagrams were used to visualize the one-at-a-time effects of $T$ and $\alpha$ on scenario prevalence, and additional tests replicated the simulation under ε-greedy and Thompson/Bayesian decision rules to evaluate algorithmic generalizability. Comparative simulations under ε-greedy and Thompson/Bayesian decision rules confirmed that the qualitative outcomes of the model were algorithm-independent.

All sensitivity and comparative analyses were implemented within the same Monte Carlo framework described above, and the results are summarized in Figure A1, Figure A2, Figure A3, Figure A4 and Figure A5 and

Table A1. Entropy vs. T (a = 0.3).

T	0.2	0.5	0.8	1.2	2.0
Entropy	1.09645	1.09755	1.09528	1.09843	1.09836

and

Table A2. Comparison of learning policies: mean entropy and final scenario shares.

Policy	Entropy	Share Green Tech	Share Growth First	Share Social Equity
Softmax	1.09635	0.358	0.304	0.336
egreedy	1.09852	0.327	0.338	0.333
thompson	1.09861	0.333	0.333	0.333

of the Appendix A.

To approximate the degree of epistemic interdependence among agents, we employed system-level diversity metrics derived from their preference distributions. Specifically, the Shannon entropy of the final scenario shares quantifies how strongly the agents’ beliefs remain intertwined rather than collapsing into a single dominant configuration. Higher entropy values indicate persistent mutual influence and overlapping belief states, whereas lower entropy reflects near-independent convergence.

5. Results

The simulation demonstrated discernible patterns in the evolving scenario preferences of agents, despite the inherent stochasticity of individual runs. Across 1000 Monte Carlo iterations of the 100-round learning process, agents tended to gravitate towards scenarios that aligned with their initial dispositions, indicating moderate yet consistent convergence dynamics.

Table 2. Total Agent Selections.

Agent	Green Tech Mean (Std Dev)	Growth First Mean (Std Dev)	Social Equity Mean (Std Dev)
Green	0.457 (0.045)	0.253 (0.041)	0.272 (0.042)
Growth	0.237 (0.039)	0.466 (0.046)	0.297 (0.048)
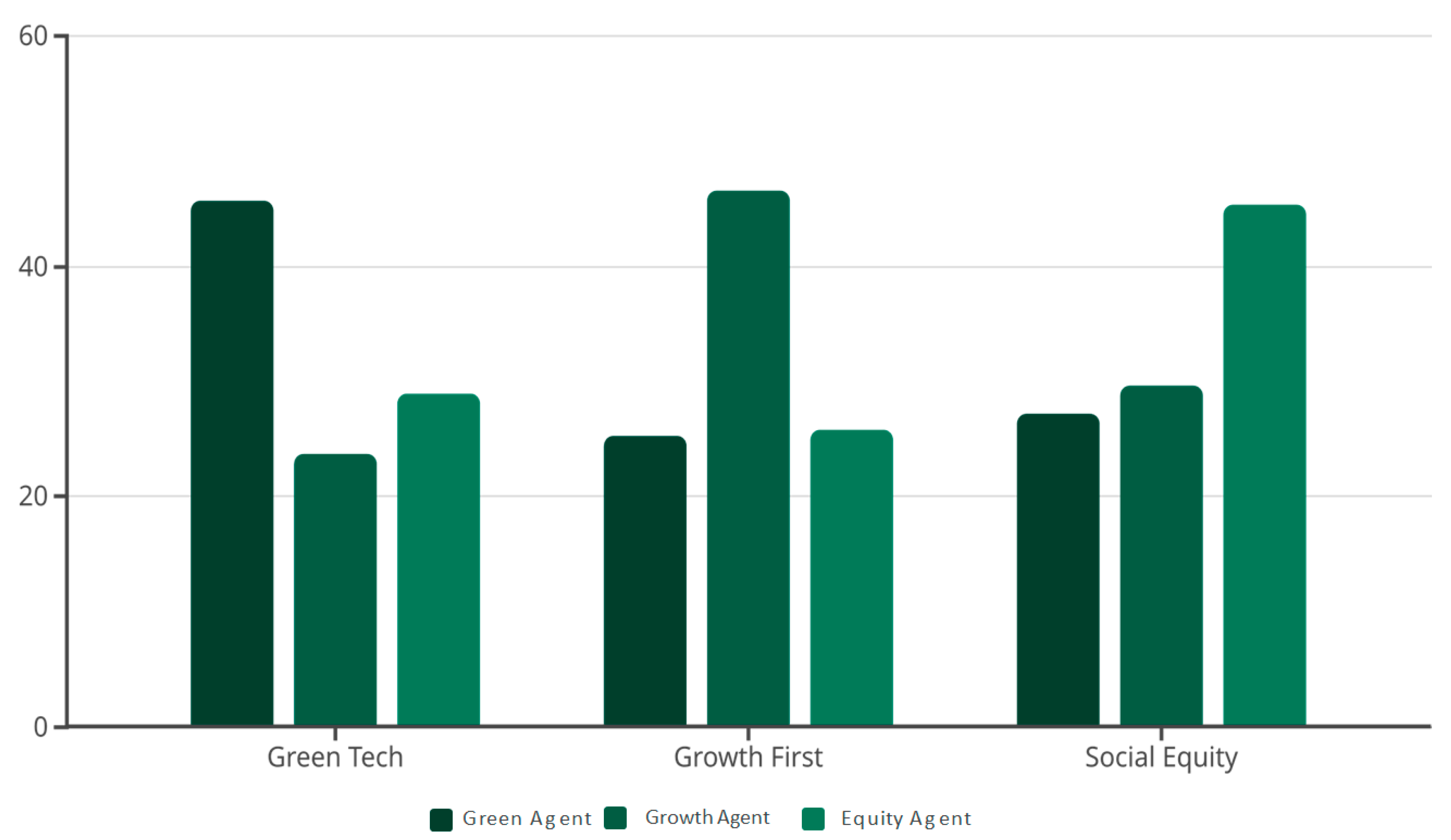
Equity	0.289 (0.042)	0.258 (0.043)	0.453 (0.048)

synthesizes the aggregated selection frequencies observed across the full set of Monte Carlo simulations, capturing the central tendencies and variability in agents’ scenario choices.

Specifically, the Green agent selected the Green Tech scenario in 45.7% of cases (std. dev. 0.045), while choices for Growth First and Social Equity lagged behind at 25.3% and 27.2%, respectively. Conversely, the Growth agent favored the Growth First scenario in 46.6% of rounds (std. dev. 0.046), with lower preference levels for Green Tech (23.7%) and Social Equity (29.7%). Finally, the Equity agent selected the Social Equity scenario most frequently (45.3%, std. dev. 0.048), with roughly equal but lower probabilities for the other two scenarios.

Figure 3 provides a visual summary of these results, illustrating the mean choice proportions for each agent–scenario pairing. Although individual trajectories may exhibit variability, aggregated data indicate that agents tend to develop relatively stable and distinct preference structures over time. Notably, this differentiation is not absolute, because agents occasionally select scenarios that are not aligned with their established preferences. This behavior reflects the influences of exploration, feedback variance, and cross-attraction.

The application of the Monte Carlo simulation ensured that these findings were not merely artifacts of a single random seed or sequence. Rather, they represent robust patterns that emerge across repeated simulations, thereby providing empirical support for discussions on convergence, pluralism, and learning under conditions of deep uncertainty.

In addition to examining aggregate choice proportions, we analyze the underlying transition dynamics using an empirical Markov transition matrix. This matrix encapsulates the probabilities of agents transitioning from one scenario to another across consecutive rounds, averaged over all agents and all Monte Carlo runs.

Table 3. Markov Transition Matrix.

Agent	Green Tech	Growth First	Social Equity
Green	0.376	0.299	0.325
Growth	0.318	0.367	0.315
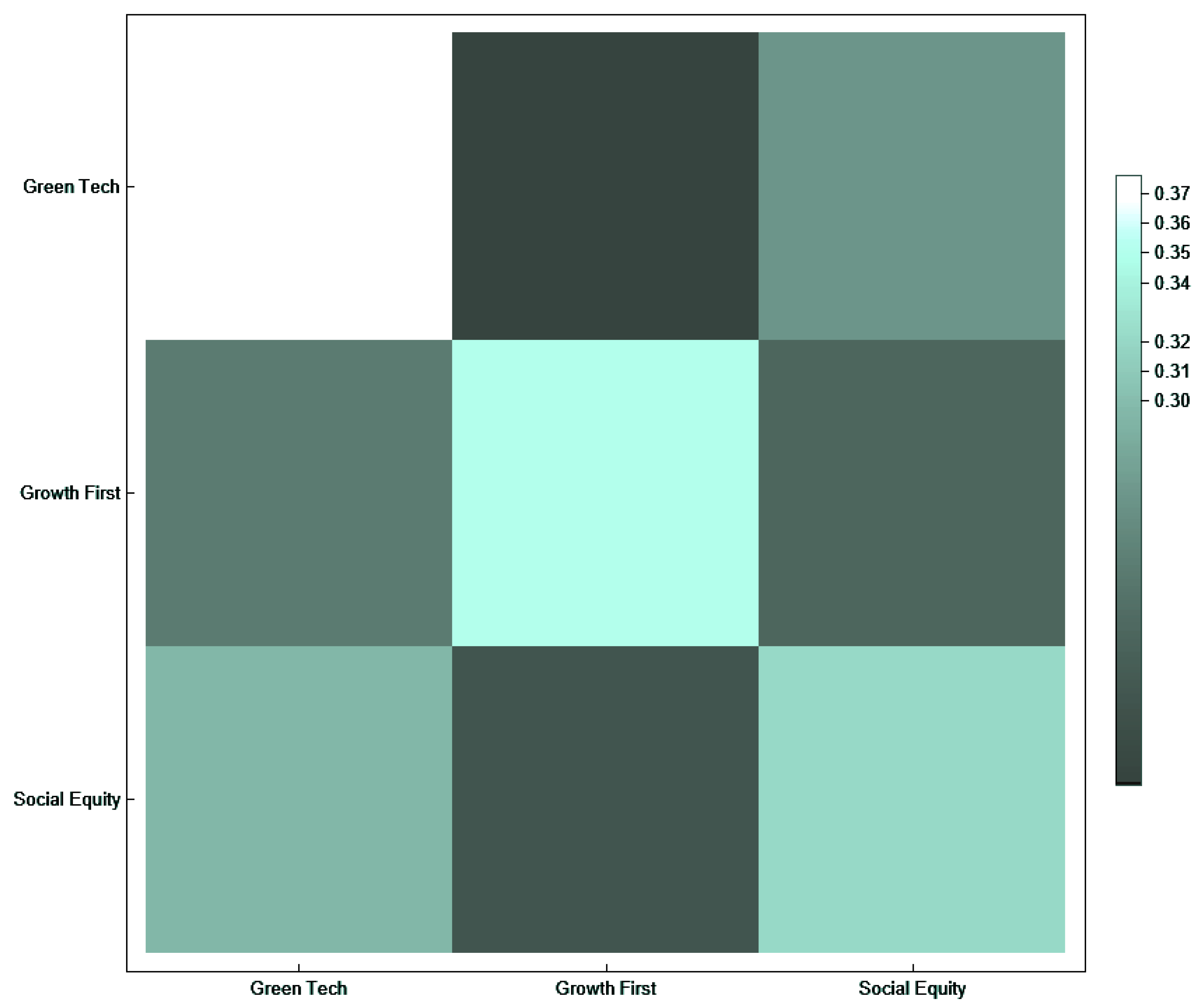
Equity	0.338	0.311	0.351

presents the empirically derived Markov transition matrix that summarizes how agents shift between scenarios from one round to the next.

Each row represents the current scenario, and each column represents a subsequent scenario. For instance, entry 0.315 in the second row and third column indicates that agents who chose Growth First in one round transitioned to Social Equity with a 31.5% probability in the next.

The corresponding heatmap (Figure 4) shows several critical dynamics. Notably, diagonal entries are not predominant, indicating a moderate degree of scenario switching. This observation reflects the exploratory nature of the learning rule and the absence of a firm commitment to a singular scenario. However, the values are not uniform either, suggesting structured tendencies: for example, Green Tech exhibits relatively high outflows to Growth First (38.2%), and Social Equity is the most frequently returned-to scenario from others, especially by the Growth agent.

This pattern of semi-stable transitions supports the interpretation of the model as a system of probabilistic learning under bounded rationality, wherein convergence is not deterministic but is influenced by feedback-dependent adaptation. The Markovian perspective provides a concise and interpretable representation of agent dynamics over time.

To evaluate the long-term stabilization tendencies, we analyzed the final decisions made by each agent across all Monte Carlo simulations. The distribution of these terminal decisions elucidates the scenarios in which agents converge after the complete simulation horizon:

• Green agent: Green Tech (492), Growth First (249), Social Equity (259);
• Growth agent: Growth First (496), Social Equity (287), Green Tech (217);
• Equity agent: Social Equity (492), Green Tech (270), Growth First (238).

These findings indicate that agents frequently revert to their initial scenarios. Specifically, the Green agent opts for Green Tech in nearly half of the simulations, while the Growth agent gravitates towards Growth First, and the Equity agent gravitates towards Social Equity. Nevertheless, the existence of significant minorities selecting alternative scenarios highlights that convergence is not absolute. Cross-scenario learning and partial shifts in alignment are prevalent which is consistent with previous findings on the Markov transitions and choice proportions.

This combination of predominant loyalty and persistent adaptability is emblematic of boundedly rational agents navigating complex and ambiguous futures. Instead of committing to singular narratives, these agents exhibit a preference for certain scenarios while remaining receptive to alternatives, reflecting real-world foresight practices under conditions of uncertainty.

6. Discussion

6.1. Interpretation of Main Results

The simulation results elucidate distinct yet interpretable patterns of agent preferences. Each agent type (Green, Growth, and Equity) demonstrates a tendency to gravitate toward a scenario that most closely aligns with its normative orientation (Figure 3). For example, the Green agent shows the highest average preference for the “Green Tech” scenario (mean 0.457, sd 0.045), whereas the Growth agent prefers “Growth First” (mean 0.466, sd 0.046), and the Equity agent tends toward “Social Equity” (mean 0.453, sd 0.048). This alignment is reflected in the final choice distributions, where the plurality of each agent type selects its anticipated scenario, although not to the exclusion of other options.

This finding demonstrates partial convergence alongside ongoing pluralism. While learning mechanisms guide agents toward their optimal scenarios, the stochastic nature of the process and reward structure allow for a degree of scenario multiplicity. This pluralism reflects cognitive realism: in complex future contexts, actors may develop strong but non-exclusive preferences.

The simulations reported here start from epistemic neutrality ($U_i\left(s_k\right)=1.0$), ensuring that symmetry-breaking arises endogenously. Introducing non-neutral priors, that is, initial utilities favoring one scenario, would act as an external bias analogous to a field in physical symmetry-breaking systems. Stronger priors would accelerate convergence and reduce transient diversity, effectively steering the system toward a biased configuration, whereas moderate asymmetries would merely shorten the time required for spontaneous differentiation to emerge. The qualitative pattern of soft symmetry breaking would remain, but the transition would no longer be purely endogenous to the system.

Notably, the findings indicate that no single scenario prevails universally, and that agents exhibit constrained openness to alternative possibilities. This aligns with the quantum-inspired perspective on scenario selection, wherein futures are conceptualized not as binary outcomes but as superposed states with dynamic amplitudes of plausibility. Consequently, the final choice distributions resemble a “collapse” process—not in a deterministic sense but as a reinforcement-induced decoherence, whereby agents commit to one future narrative while retaining the latent memory of others.

While the classical stochastic formulation describes the diffusion of scenario preferences as a Markov process with well-defined transition probabilities, the quantum-inspired interpretation highlights a different aspect of the same dynamic. In the classical view, uncertainty is purely statistical; each scenario represents a mutually exclusive outcome governed by frequency. In the quantum-collapse analogy, however, uncertainty is epistemic and contextual: before agents commit to a single scenario, multiple potential futures coexist in superposition, influencing each other through interference-like effects. The act of selection, analogous to measurement, reduces this superposition to a realized configuration, yet the latent structure of unobserved alternatives continues to shape subsequent transitions. This interpretation does not alter the numerical results but provides a richer explanatory layer linking probabilistic diffusion to cognitive and narrative entanglement.

In this context, the simulation aligns with interpretive analogies to quantum cognition models [26], wherein decision trajectories are influenced by evolving probabilistic weights, feedback loops, and nonexclusive mental representations. Instead of converging on a classical Nash equilibrium, agents within this system tend to gravitate toward preference attractors, which are defined by iterative learning under conditions of uncertainty.

6.2. Learning Dynamics and Transition Behavior

The temporal evolution of preferences illustrates the influence of reinforcement learning on the decision-making processes of agents. In each round, the agents update their utility estimates solely for the chosen scenario, resulting in a path-dependent dynamic that prioritizes consistency over exploration as the rounds advance. This localized learning rule, in conjunction with the SoftMax selection mechanism, engenders asymmetric adaptation—agents intensify their preferences for scenarios that provide relatively higher short-term rewards while maintaining some openness to alternative options.

The Markov transition matrix (Figure 4), derived from an extensive simulation comprising over 100,000 transitions, reveals a complex pattern of switching behavior. Although diagonal dominance is not absolute, all agents exhibit a moderate propensity to remain in their preferred scenario space. For example, the probability of the Green agent remaining in the “Green Tech” scenario is approximately 38%, whereas the probabilities of transitioning to “Growth First” or “Social Equity” are approximately 30% and 32%, respectively. These dynamics indicate that agents oscillate across scenarios in a manner that is neither random nor rigid, but rather influenced by reward gradients and the stochastic nature of the SoftMax choice.

A multi-metric sensitivity assessment was performed to evaluate the effect of the exploration–exploitation balance ($T$) on model behavior (Figure A1, Figure A2 and Figure A4 of the Appendix A).

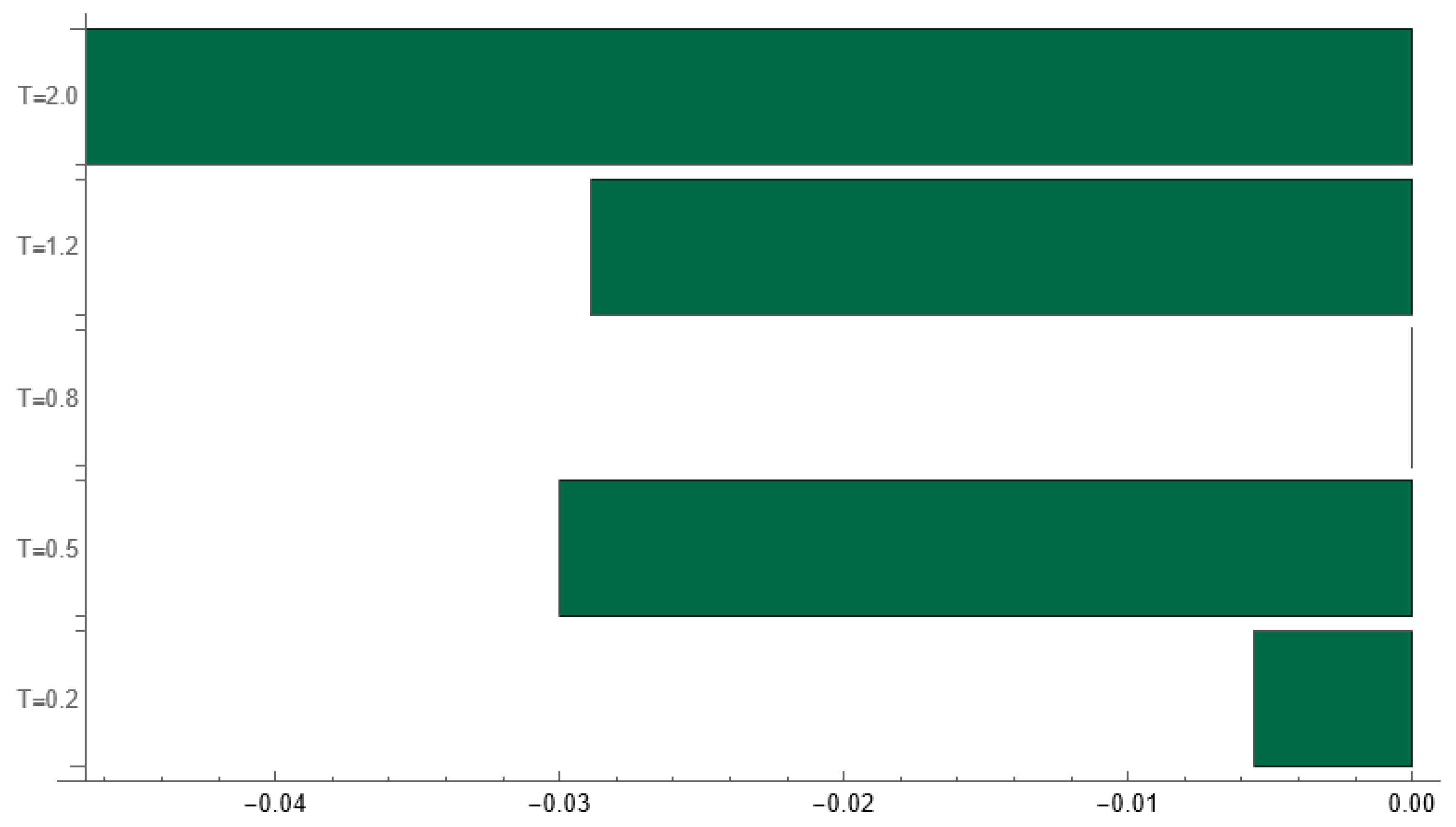
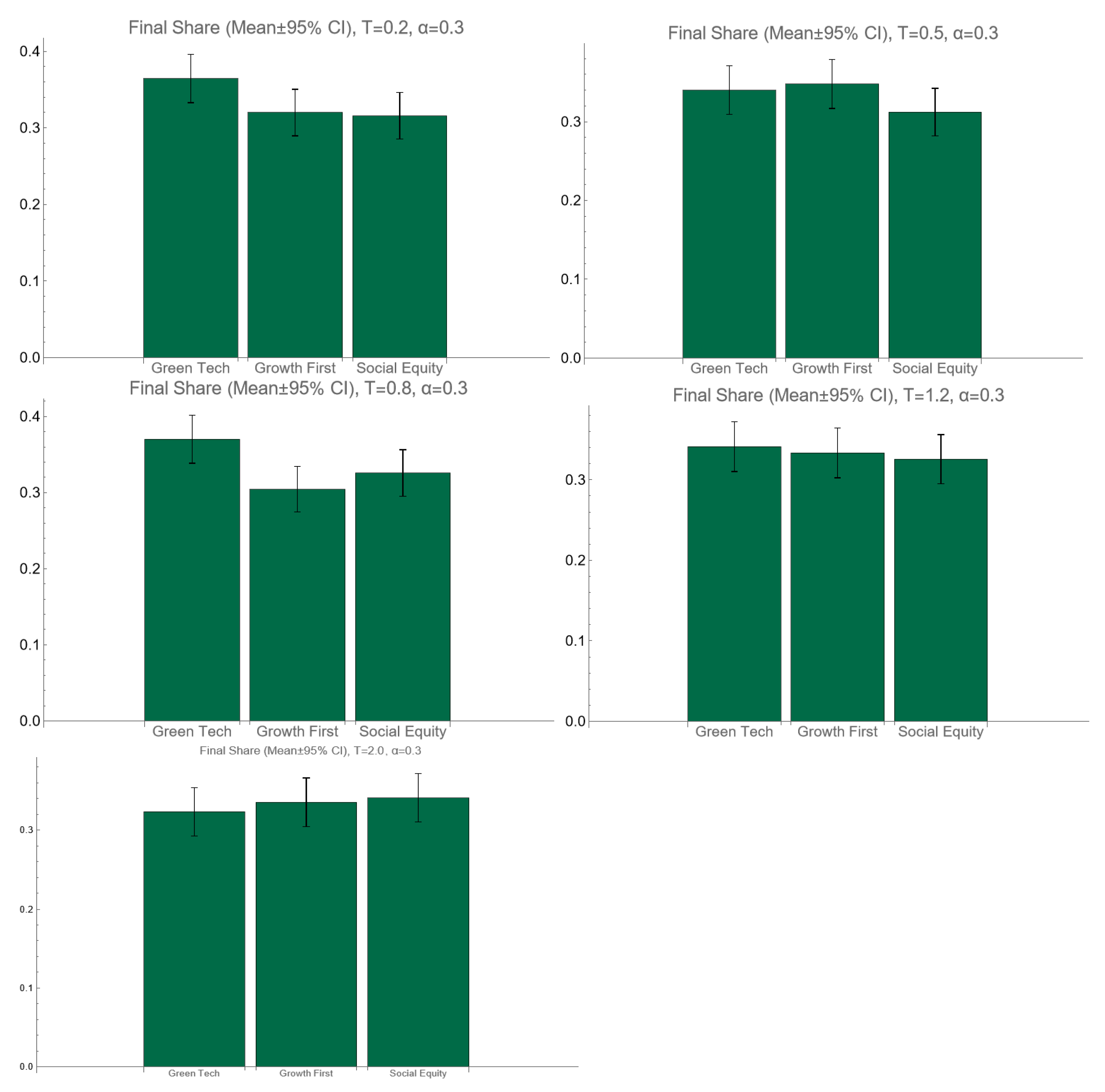
The entropy of the final scenario distribution remains virtually constant (1.095–1.098) across the tested range of $T$ (0.2–2.0, α = 0.3), indicating a high level of systemic robustness and the persistence of diversity in agents’ choices.

The Tornado analysis confirms a mild, monotonic influence of $T$: increasing the temperature reduces the share of the “Green Tech” scenario by roughly 3–5 percentage points relative to the baseline ($T=0.8$), consistent with the expected diffusion of collective focus under higher stochasticity. Complementary 95% confidence intervals (Figure A4 of the Appendix A) overlap substantially for all values of $T$, showing that these small deviations are not statistically significant.

Together, the three indicators (entropy stability, limited directional sensitivity, and overlapping confidence intervals) demonstrate that the model’s qualitative outcome of soft convergence with persistent pluralism is structurally robust to large variations in the exploration parameter.

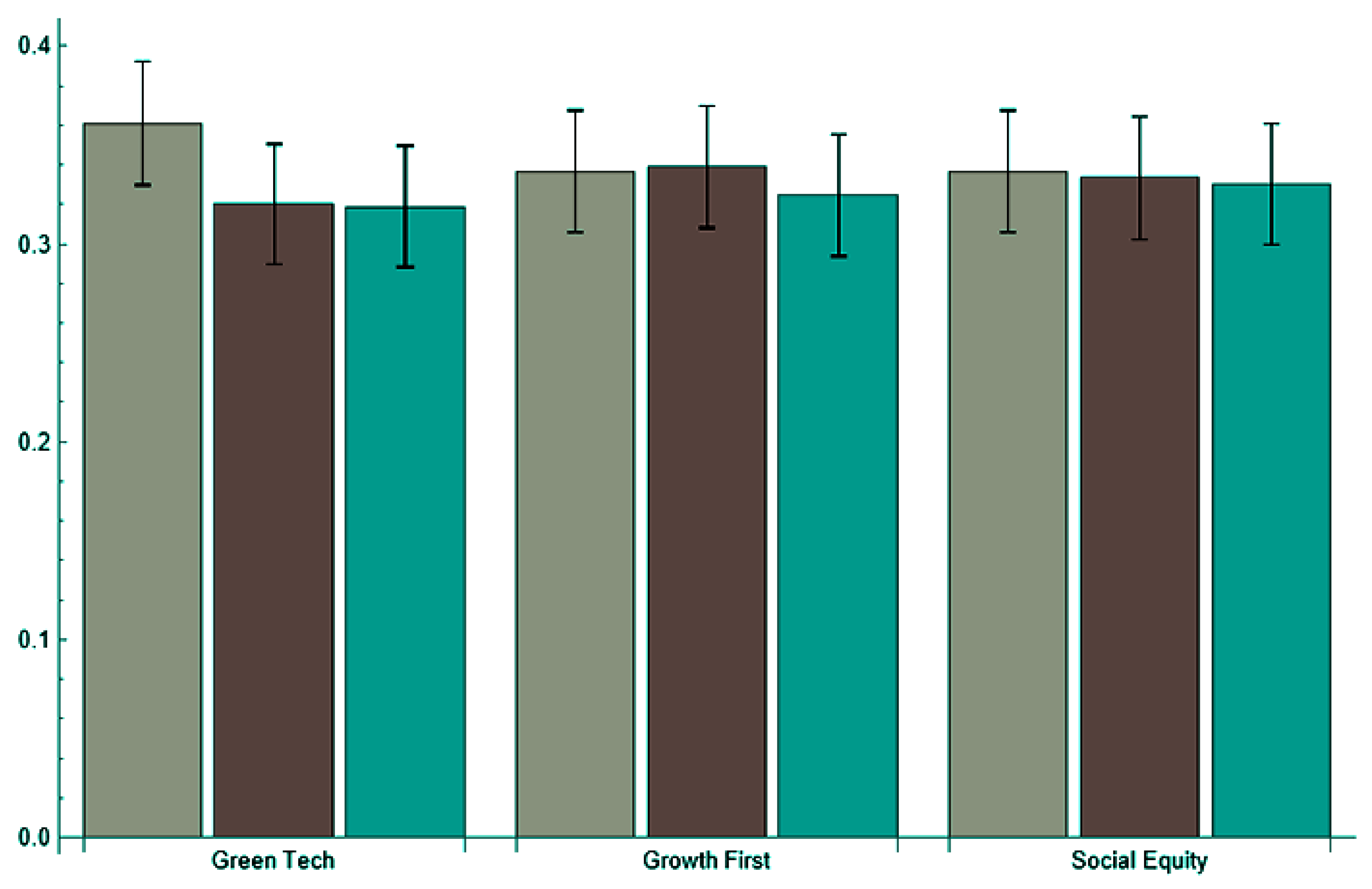
Finally, to test the algorithmic generalizability of the proposed framework, we replicated the simulation under three alternative decision rules: Softmax, ε-greedy, and Thompson/Bayesian updating (Figure A5 of the Appendix A).

The resulting end-state distributions are virtually indistinguishable, with overlapping 95% confidence intervals across all scenarios. Minor differences appear only in convergence speed, not in the composition of the final equilibrium.

This consistency across learning mechanisms demonstrates that the emergent dynamics—soft convergence with persistent pluralism—stem from the model’s structural feedbacks rather than from a particular decision rule. The qualitative outcome is therefore algorithm-independent and robust to the choice of learning policy.

The implications for foresight practice are significant. The selection of scenarios is demonstrated to be sensitive to the historical context, yet it remains reversible; agents may become committed to plausible futures but retain the statistical potential for reassessment. This observation aligns with the notion that scenario commitment is never absolute and that long-term preferences can be influenced by updated feedback, particularly when new rewards or information alter the perceived value landscape.

From a modeling perspective, this transitional behavior emulates the probability amplitude flows observed in quantum decision models, wherein mental states transition not discretely but through evolving probability distributions. Within such models, memory effects, superposition of beliefs, and entangled preference structures can produce similar oscillatory patterns, suggesting that learning in futures contexts may adhere to quantum-like diffusion trajectories rather than linear optimization paths.

6.3. Final Scenario Commitment and Narrative Lock-In

By the conclusion of the simulation, the agents demonstrated distinct yet not entirely stable commitments to specific scenarios. The final distribution of choices indicates that each agent predominantly selects the scenario that aligns with its initial orientation: Green agent gravitates towards “Green Tech,” the Growth agent towards “Growth First,” and the Equity agent towards “Social Equity.” However, in no instance does a single option achieve absolute dominance; each agent maintains a significant minority of selections in alternative futures.

By the conclusion of the simulation, the agents demonstrated distinct, yet not entirely stable, commitments to specific scenarios. The final distribution of choices indicates that each agent predominantly selects the scenario that aligns with its initial orientation: the Green agent gravitates towards “Green Tech,” the Growth agent towards “Growth First,” and the Equity agent towards “Social Equity.” However, in no instance does a single option achieve absolute dominance; each agent maintains a significant minority of selections in alternative futures.

The phenomenon of soft convergence is of significant analytical importance. Instead of yielding a deterministic outcome, the learning process stabilizes into probabilistic attractors, that is, scenarios that are preferred but not exclusive. These patterns reflect a form of narrative lock-in, in which agents gravitate toward familiar futures without entirely eliminating pluralism. This approach balances the dual aims of foresight: anchoring the vision while preserving agility.

Significantly, the findings bolster the interpretive analogy with quantum decoherence: although agents initially exist in a “superposition” of scenario preferences, interaction with the environment (rewards) progressively increases the probability of converging on a single option. Nonetheless, this convergence is statistical rather than absolute, permitting the coexistence of competing narratives even at equilibrium. This supports the proposition that foresight under uncertainty should not aim to eliminate ambiguity but rather to structure it meaningfully through iterative feedback loops.

In practical terms, these findings indicate that scenario processes, when conceptualized as cognitive systems, do not converge towards consensus but rather towards structured diversity, wherein dominant narratives emerge without entirely suppressing alternatives. This phenomenon reflects real-world foresight contexts in which stakeholders may share core perspectives but maintain individualized visions shaped by experience, identity, and strategic objectives.

6.4. Broader Implications for Foresight Practice

The simulation framework delineated in this study provides a cognitively plausible and computationally feasible model for comprehending the evolution of scenario preferences in the contexts of feedback, learning, and bounded rationality. This aligns with contemporary foresight practices in several respects.

The model first emphasizes the significance of adaptive iterations. Instead of perceiving scenario evaluation as a singular judgment, it simulates the process by which preferences are developed and modified over time, and are influenced by partial reinforcement. This approach reflects how practitioners incrementally establish plausibility and commitment through workshops, dialogue, and repeated engagements with uncertain signals.

Second, the development of probabilistic preference structures underscores the importance of non-binary thinking. Scenario analysis frequently encounters challenges in meeting demands for definitive rankings or singular “preferred futures.” In this context, agents do not converge on exclusive choices but rather on weighted patterns of orientation, which more closely resemble the overlapping and occasionally ambivalent visions held by actual stakeholders. Embracing such partial convergence can assist foresight in avoiding premature closure.

Third, the model illustrates how varying epistemic profiles, represented here by agents’ differing reward sensitivities, can produce diverse yet stable outcomes. This finding supports the practice of inclusive, multi-perspective scenario development, in which diversity serves as a catalyst for systemic robustness rather than a threat to coherence.

Overall, the analogy to quantum dynamics serves as a valuable metaphor for enhancing foresight dialogue. Similar to quantum systems that remain indeterminate until observed, future narratives may similarly resist definitive commitment until they are actualized. Embracing, rather than opposing, this indeterminacy may enable practitioners to align scenario work more effectively with the complexities and uncertainties inherent in dynamic environments.

Recent advances in applying game theory to decentralized policy design further support the relevance of this framework [48] demonstrate how game-theoretic coordination can enhance decision-making efficiency in decentralized energy systems. These results parallel the present model’s emphasis on distributed adaptation and local learning under uncertainty, suggesting that quantum- and game-theoretic approaches may provide a unified language for understanding and optimizing collective behavior in complex socio-technical systems such as energy markets and strategic foresight processes.

An additional implication pertains to the performative aspect of policy design, wherein expectations and communication influence systemic dynamics. This perspective is directly linked to the enduring debate on rules versus discretion in policymaking [49]. Rules are associated with stable and predetermined reward structures within which agents learn under fixed parameters. Conversely, discretion allows policy signals to dynamically reshape the reward landscape. Within our framework, even the mere announcement of a policy (such as a green transition program or a redistribution initiative) can influence agents’ subjective utilities prior to any material implementation. Consequently, communication emerges as a systemic variable that alters scenario probabilities and convergence patterns, highlighting the performative power of expectations and narratives [50]. From a foresight perspective, this suggests that both structural incentives (rules) and contextual framing effects (discretion) should be acknowledged as determinants of agent behavior in uncertain environments.

In conclusion, although stylized, the model encourages foresight practitioners to approach learning, uncertainty, and narrative multiplicity not as impediments but as essential design conditions. The application of agent-based simulation represents a step toward formalizing these dynamics, thereby supporting more reflective and adaptive futures thinking.

6.5. Symmetry in Scenario Dynamics

Although the model was not originally designed to prioritize symmetry, a detailed analysis revealed that symmetry is integrated at various levels of its architecture: epistemic, structural, and dynamic. These symmetries not only enhance the internal coherence of the framework, but also conceptually align with recent endeavors to comprehend decision-making and complex systems through symmetry-based analysis [31].

Initially, the model posits epistemic symmetry, wherein all agents commence with identical, unweighted priors over a common scenario space. There is no inherent bias that favors any particular future narrative. The reward matrix was intentionally designed to uphold normative balance, ensuring that each scenario was most appealing to one type of agent while remaining moderately attractive to others. This configuration reflects symmetry in the initial conditions, where agents are structurally equivalent in their capacity to evolve toward any of the futures presented.

As the simulation progresses, these symmetries undergo dynamic disruption. Agents modify their preferences through reinforcement learning and localized feedback, gradually converging on scenarios that align more closely with their normative identities. This phenomenon is analogous to spontaneous symmetry breaking in physical systems, where a system that is initially invariant under transformations selects a specific configuration when subjected to perturbation [51]. In our model, symmetry is neither imposed nor preserved by force but is gently disrupted through stochastic adaptation and the learning dynamics.

Despite this differentiation, a statistical symmetry persists throughout the system. The Monte Carlo ensemble demonstrated that all scenarios retained nonzero probabilities of selection by each agent, even in the later stages of the simulation. Agents occasionally “tunnel” into non-preferred futures, mirroring quantum mechanical behaviors where unlikely transitions remain feasible under specific energy conditions [44]. These transitions contribute to a probabilistic equilibrium that is not sharply peaked but rather distributed across futures, thereby sustaining a degree of pluralism and openness.

Moreover, the structure of the scenario space embodies conceptual symmetry: each of the three principal narratives (Green Tech, Growth First, and Social Equity) aligns with a distinct yet equally valid strategic rationale. The basis vectors representing these futures are considered orthogonal within the Hilbert-like space; however, their interaction through agent learning introduces interference patterns, which are indicative of quantum contextuality and the interplay of symmetry [45].

In conclusion, symmetry within this model transcends its aesthetic role, serving as a generative principle that delineates the initial conditions for framing futures, influences how agents distinguish between them, and regulates the long-term distribution of commitment scenarios. By examining scenario dynamics through the symmetry framework, we attain a more profound understanding of the stability and fluidity inherent in strategic foresight processes. This perspective further bolsters the argument for employing quantum-compatible modeling approaches, wherein symmetry is not merely incidental but is fundamental to representing complex, evolving systems under conditions of uncertainty.

6.6. Limitations and Future Research Directions

This model constitutes an initial endeavor to integrate reinforcement learning with scenario selection under conditions of uncertainty. Although it provides promising insights, it is based on simplified assumptions, such as agent homogeneity and fixed reward structures.

Future research could investigate a broader spectrum of learning styles, integrate social or institutional influences, and facilitate the development or transformation of scenarios over time, thereby enhancing both realism and analytical depth.

In conclusion, the quantum analogy may be further elaborated through more technical advancements, such as quantum-inspired computation or models that more accurately represent the dynamics of superposition and narrative collapse.

The present implementation limits the scenario space to $K=3$ archetypes for clarity of visualization and interpretability. Increasing the number of scenarios would expand the dimensionality of the belief (or “interference”) space from a 3 × 3 to a $K\times K$ transition structure, allowing for more complex superposition patterns, but also introducing combinatorial growth in parameter interactions. Conceptually, higher $K$ would permit richer cross-influences among competing narratives, akin to multi-path interference in quantum systems, while computationally, it would require additional smoothing and normalization steps to maintain stability of the probability matrix. Future work could explore these higher-dimensional extensions using sparse representations or dimensionality reduction techniques to manage the computational complexity.

The present model is intentionally conceptual, designed to demonstrate the feasibility of quantum-inspired representations within a tractable agent-based environment. Scaling the framework to real-world foresight or policy settings, with hundreds of heterogeneous agents and multiple interdependent scenarios, would introduce additional challenges. These include the calibration of reward structures across diverse stakeholders, the management of increased computational complexity, and the interpretation of emergent dynamics in high-dimensional spaces. Future applications could address these issues by coupling the model with empirical data, network-based learning architectures, or reduced-order approximations that preserve the essential features of quantum-inspired contextuality while remaining computationally feasible.

7. Conclusions

This study presents a straightforward yet expressive model for simulating scenario selection under conditions of uncertainty, employing reinforcement learning and SoftMax dynamics to approximate the adaptive convergence or divergence of agents across various potential futures. Through numerous Monte Carlo simulations, distinct preference patterns among agents were observed, along with path-dependent transitions and occasional persistent pluralism. These dynamics reflect essential aspects of foresight practice: the iterative refinement of expectations, the influence of feedback on shaping commitments, and the presence of contingent and, at times, non-exclusive beliefs.

The primary contribution of this study is the introduction of a cognitively plausible and computationally feasible framework that elucidates the evolution of scenario preferences over time. By grounding the model in reinforcement learning and drawing parallels with quantum frameworks, this study offers a novel perspective on how anticipatory systems may explore, update, and ultimately converge on specific futures without necessitating complete rationality or fixed preferences. These conclusions are directly supported by the quantitative outputs presented in Section 5 and by the extended scenario trajectories and sensitivity analyses provided in the Appendix A.

In conclusion, the model encourages further experimentation and indicates that even simple agents operating under minimal assumptions can demonstrate complex dynamics when exploring a landscape of plausible futures. Consequently, it serves as a valuable conceptual and methodological link between decision science, scenario planning, and emerging approaches to future modeling research.