A Symmetry Analysis Method for Teaching Knowledge Graph Evolution Driven by Directed Attributed Graphs

Abstract

Entity symmetry in teaching knowledge graphs is a characteristic of knowledge semantic expression and association, which plays a crucial role in the composition of knowledge structure. However, the evolution of the teaching knowledge graph may disrupt the symmetry of the knowledge structure, leading to the emergence of asymmetric phenomena and resulting in adverse effects on the subsequent search and representation of knowledge. Therefore, this article proposes a symmetry analysis method for the evolution of teaching knowledge graphs driven by directed attributed graphs. Firstly, a teaching knowledge graph model with directed attributed graphs is presented, on which the entity connection symmetry, entity center symmetry, and entity mirror symmetry of the teaching knowledge graph are defined. Then, the addition, replacement, and deletion of entity evolution rules that affect symmetry in the teaching knowledge graph model were characterized, and a teaching knowledge graph evolution algorithm based on directed attributed graph transformation was designed. On this basis, an in-depth analysis was conducted on the symmetry of the evolution of the teaching knowledge graph, which was disrupted and maintained. Finally, experiments verify that preserving or breaking symmetry has a significant impact on the connectivity and path complexity of knowledge graphs. In addition, a case study on the evolution of a Japanese major teaching knowledge graph with both symmetric and asymmetric transformations is provided to validate the feasibility and effectiveness of the proposed directed attributed graph driven symmetry analysis method for educational knowledge graph evolution.

1. Introduction

With the rapid development of emerging technologies such as artificial intelligence, big data, and the Internet of Things, educational informatization is accelerating its evolution towards “smart teaching”. The traditional teaching model centered on teachers and relying solely on textbooks is shifting towards a new teaching paradigm centered on learners and personalized learning paths and supported by intelligent technology. In this process, the teaching knowledge graph [1,2] serves as an important bridge connecting knowledge organization and teaching practice, gradually becoming a key technology to promote the transformation of education towards intelligence, personalization, and systematization. The teaching knowledge graph can not only structure and semantically transform dispersed and fragmented teaching resources but also achieve intelligent functions such as learning path recommendation, learning behavior modeling, and teaching content optimization through knowledge reasoning and graph model analysis, significantly improving teaching efficiency and learning outcomes.

Knowledge graphs, as a graph-structured knowledge representation paradigm, have been widely applied in education in recent years to model disciplinary knowledge systems, generate personalized learning paths, and support intelligent teaching systems [3]. However, current mainstream approaches typically organize knowledge into hierarchical or linear dependency structures, overlooking the prevalent symmetry patterns in educational content. Examples include the mirror correspondence between “linear equations” and “linear inequalities” in both structure and solution methods, the semantic reuse of “commutative law of addition” and “commutative law of multiplication,” and bidirectional prerequisite relationships where two concepts mutually depend on each other. These symmetries are not coincidental; they reflect fundamental cognitive patterns in disciplines and directly influence a knowledge graph’s reasoning capability, path diversity, and pedagogical interpretability. Although research on dynamic knowledge graph evolution has advanced in temporal modeling and cognitive tracing, existing work lacks a formal definition of symmetry, analysis of its evolution dynamics, and quantitative evaluation mechanisms. On one hand, common evolution operations such as unilateral node deletion often unintentionally break symmetric structures, leading to reduced graph connectivity and rigid learning paths. On the other hand, there is little methodological discussion on which symmetries should be preserved or how specific evolution actions affect symmetry properties. Therefore, this paper focuses on which symmetries should be considered in teaching knowledge graphs, how to formally characterize the evolution of teaching knowledge graphs, and how such evolution impacts symmetry. To this end, this paper proposes a directed attributed graph-driven method for analyzing symmetry in the evolution of teaching knowledge graphs. The main contributions are as follows:

(1)

A directed attributed graph-based model for educational knowledge graphs is proposed, and four types of symmetry, namely entity connection symmetry, entity central symmetry, entity mirror symmetry, and structural symmetry, are formally defined based on directed attributed graphs.

(2)

A teaching knowledge graph evolution method based on directed attributed graph transformation is designed. Three graph-based evolution rules—addition, replacement, and deletion of teaching entities—are introduced, and a rule-driven algorithm for evolving teaching knowledge graphs is presented.

(3)

Basic conditions for the preservation and breaking of entity connection symmetry, entity central symmetry, entity mirror symmetry, and structural symmetry in the evolution of educational knowledge graphs based on the directed attributed graph model are provided, and it is experimentally verified that the preservation or breaking of these symmetries has a significant impact on the connectivity and path complexity of knowledge graphs.

The rest of this paper is organized as follows: Section 2 reviews the related work. Section 3 defines symmetries and asymmetries with respect to teaching entities. Section 4 presents the design of evolution operations on teaching knowledge graphs that affect symmetry and asymmetry. Section 5 discusses the conditions under which symmetries in the evolution of teaching knowledge graphs are preserved or disrupted. Section 6 conducts experiments and case studies. Section 7 concludes the paper and outlines future work.

2. Related Work

Currently, research on the application of knowledge graphs in education primarily focuses on constructing disciplinary knowledge systems to support personalized learning, intelligent tutoring, and learning path recommendation. Meanwhile, studies are gradually shifting from static knowledge representation to dynamic evolutionary modeling, emphasizing the updating of knowledge points over time and the evolution of students’ cognitive states. For instance, Gao et al. [4] designed an intelligent system for English teaching that leverages knowledge graphs to achieve personalized and intelligent instruction, enabling knowledge-driven intelligent recommendations and automated assessment to enhance personalized learning pathways. Zhang et al. [5] applied knowledge graphs to digital curriculum reform in engineering disciplines, meeting the demand for student-centered personalized learning and intelligently optimizing instructional content. Guo et al. [6] proposed an educational assessment model that integrates knowledge graphs with convolutional neural networks. By constructing a structured knowledge framework and embedding learner profiles, the model enables personalized learning path recommendation and knowledge mastery prediction. Experiments show that the model significantly improves students’ academic performance and classroom engagement, providing an effective technical approach for intelligent educational evaluation. Ge et al. [7] proposed the DSL-KG algorithm based on dynamic semantic learning, which combines BERT and GNN to achieve automatic construction of English knowledge graphs. Through deep semantic mining and dynamic relationship modeling, the method performs excellently in entity recognition and relation classification, significantly enhancing coverage and efficiency. Experiments and practical applications validate its effectiveness in supporting knowledge recommendation and path planning in intelligent teaching. Wu et al. [8] proposed a knowledge graph-based teaching model for medical mathematical statistics, integrating knowledge graph visualization with the BOPPPS instructional framework to enhance the systematicity and interactivity of instruction. This approach significantly improved students’ learning interest, academic performance, and ability to apply knowledge in course practice, offering a scalable and innovative pathway for reforming medical statistics education. Yang et al. [9] proposed the SGKT model, which constructs thematic knowledge mapping for disciplinary knowledge systems by fully integrating students’ historical interaction data—including problem sequences, difficulty levels, and hierarchical relationships among knowledge concepts. By employing graph convolutional networks to model the cognitive process, the model accurately captures intra-disciplinary knowledge correlations and their influence on learning behaviors. Experiments demonstrate that the model significantly enhances the ability to track students’ knowledge states, providing a more pedagogically grounded solution for personalized learning assessment, among others.

Knowledge graph evolution has emerged as a research hotspot, focusing on the dynamic changes of entities and relations over time. Existing studies aim to model temporal dependencies and capture structural evolution patterns to support reasoning and prediction in dynamic scenarios, attracting significant attention in fields such as event evolution, social networks, and education, thereby advancing the development of temporal knowledge graph representation and updating techniques. For instance, Yang et al. [10] first introduced the problem of entity spatiotemporal evolution summarization. To address the dynamics and incompleteness of knowledge graphs, they proposed a two-stage approach: generating temporal and spatial summaries based on triadic formal concept analysis, followed by constructing spatiotemporal evolution summaries through a fusion strategy. This method effectively integrates multi-source knowledge graph data and supports applications in visualization, data integration, and question answering, offering a novel perspective for dynamic knowledge graph research. Ning et al. [11] proposed the Temporal Contextual Embedding (TCE) model to address the insufficient modeling of temporal dependencies in temporal knowledge graphs, employing a GRU mechanism to capture long-term evolutionary dynamics of relations. By embedding correlations between adjacent timestamps, the model enhances temporal representation capability and significantly improves performance in modeling dynamic relational evolution across multiple benchmark datasets, thus advancing the development of temporal knowledge graph completion techniques. Yang et al. [12] proposed a heterogeneous graph-based spatiotemporal evolution knowledge tracing model (TSKT), which integrates spatial adaptation and temporal assimilation mechanisms to construct a multi-attribute knowledge space and designs a dual update module for spatiotemporal dynamics, effectively characterizing students’ cognitive processes. The method significantly improves prediction performance on three datasets, providing a modeling paradigm for knowledge tracing that more closely aligns with human cognition. Liu et al. [13] proposed the TFCE method, aiming to address the challenges of temporal evolution and data incompleteness in temporal knowledge graphs (TKGs). TFCE comprises a temporal feature module, a complex evolution module, and a temporal embedding decoder, responsible for time encoding, recursive modeling of entity-relation evolution, and handling incomplete data, respectively. Experiments demonstrate that TFCE significantly outperforms existing methods on the ICEWS14, ICEWS05-15, and ICEWS18 datasets, showcasing its superior performance and potential in TKG representation learning, among others. Moreover, research on symmetry in graph-related domains has also made notable progress, particularly in graph neural networks. For instance, Cao et al. [14] proposed the Linear Graph Neural Network (LGNN), which employs symmetric normalization as a preprocessing step to eliminate structural bias and implicitly preserves the topological symmetry of graphs, achieving strong node classification performance with high computational efficiency, especially on sparse networks. Li et al. [15] introduced a graph neural network based multivariate time series forecasting model that utilizes extremely symmetric modal decomposition to extract temporal features across multiple scales, explicitly modeling symmetric structural patterns in time series. By integrating transfer entropy to construct a causal graph, their method effectively fuses symmetry with spatiotemporal dependencies to enhance prediction accuracy. Xu et al. [16] developed a symmetry-aware multi-agent reinforcement learning architecture that leverages group symmetry theory to design permutation-equivariant policy networks and permutation-invariant value networks, thereby reducing the parameter complexity of joint policies and significantly improving sample efficiency and scalability. Drexler et al. [17] proposed mapping planning states into graphs and detecting state symmetries and isomorphisms, revealing that existing GNNs and description logics, limited by the expressive power of C₂, fail to distinguish non-isomorphic states, thus hindering generalized policy learning and underscoring the critical role of symmetry and isomorphism analysis in planning.

In summary, current research focuses on the application of teaching knowledge graphs in education and their dynamic evolution, aiming to support personalized learning, intelligent tutoring, and cognitive tracing. However, existing studies primarily emphasize the temporal evolution and hierarchical organization of knowledge, with insufficient attention given to the symmetry characteristics embedded within teaching knowledge graphs. In fact, symmetrical properties such as concept symmetry and relation symmetry in teaching knowledge graphs can help reveal intrinsic structural patterns of disciplines, enhance the rationality of knowledge organization, and improve the effectiveness of learning transfer. These features represent a significant yet underexplored direction for advancing intelligent educational modeling.

3. Definition of Symmetric and Asymmetric Graph Models for Teaching Entities

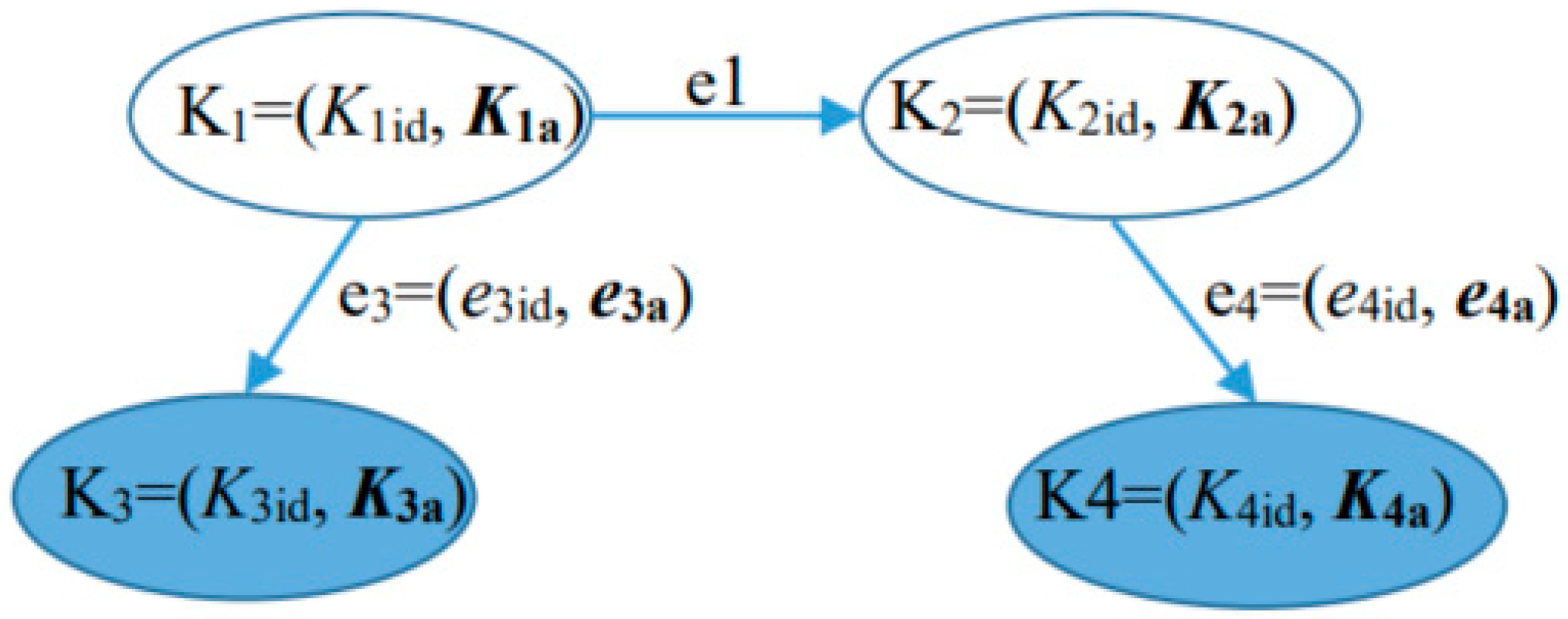
3.1. Definition of Directed Attributed Graph and Graph Transformations

As the foundational model for teaching knowledge graphs, graphs serve core functions in knowledge organization, semantic expression, and relational modeling, providing critical support for knowledge association, reasoning, and application within intelligent teaching systems. A graph model with clear structure and precise semantics can not only effectively represent hierarchical, dependency, and contextual relationships among knowledge points, but also lay a solid technical foundation for pedagogical applications such as personalized learning path recommendation, intelligent tutoring, and learning analytics. Therefore, establishing rigorous formal definitions and structured descriptions of the graph model is a prerequisite for constructing high-quality teaching knowledge graphs. Only with a well-defined graph structure, explicit relationship types, and standardized semantic expressions can the interpretability, scalability, and operability of knowledge graphs in educational contexts be ensured.

Definition 1. (Directed Graph):

 A directed graph is a mathematical structure that represents directed relationships between objects, typically defined as a 2-tuple G = (V, E), where V is a finite and non-empty set of nodes representing the entities described in the graph, and E $\subseteq$ V $\times$ V is a set of edges, with each edge being an ordered pair of nodes from V, indicating a directed connection from one node to another.

Definition 2. (Directed Attributed Graph):

 A directed attributed graph is typically defined as a 6-tuple G_A = (V, E, A_V, A_E, $\varnothing$_A, $\varnothing$_E). Here, V is a finite and non-empty set of nodes representing the entities described in the graph; E $\subseteq$ V $\times$ V is a set of edges, with each edge being an ordered pair of nodes from V, indicating a directed connection from one node to another. A_V is the set of node attributes, containing all attribute types assigned to nodes, where each node v $\in$ V has a corresponding set of attribute values a_v; A_E is the set of edge attributes, containing all attribute types assigned to edges, where each edge e $\in$ E has a corresponding set of attribute values e_v. $\varnothing$_A is a mapping function that assigns attributes to specific nodes, and $\varnothing$_E is a mapping function that assigns attributes to specific edges.

Definition 3. (Directed Attributed Graph Model for Teaching Knowledge Graph):

 The directed attributed graph model for a teaching knowledge graph is typically defined as a 6-tuple G_K = (V, E, A_V, A_E, $\varnothing$_A, $\varnothing$_E). Here, V is a finite and non-empty set of knowledge points, representing the educational concepts described in the knowledge graph; E $\subseteq$ V $\times$ V is a set of relations, with each relation being an ordered pair of knowledge points from V, indicating a directed relationship between two knowledge points; A_V is the set of knowledge point attributes, containing all attribute types assigned to knowledge points, where each knowledge point v $\in$ V has a corresponding set of attribute values a_v; A_E is the set of relation attributes, containing all attribute types assigned to relations, where each relation e $\in$ E has a corresponding set of attribute values e_v; $\varnothing$_A is a mapping function that assigns attributes to specific knowledge points; and $\varnothing$_E is a mapping function that assigns attributes to specific relations.

Definition 4. (Isomorphism of Directed Attributed Graph):

 Suppose there are two directed attributed graphs G_A1 = (V1, E1, A_V1, A_E1, $\varnothing$_A1, $\varnothing$_E1) and G_A2 = (V2, E2, A_V2, A_E2, $\varnothing$_A2, $\varnothing$_E2). If there exists a bijective function f: V1$\to$V2 such that for any (u, v)$\in$E1, we have (f(u), f(v))$\in$E2 indicating edge consistency, and for any v$\in$V1, $\varnothing$_A1(v) = $\varnothing$_A2(f(v)), as well as for any (u, v)$\in$E1, $\varnothing$_A1(u, v) = $\varnothing$_A2(f(u), f(v)) indicating attribute consistency, then the directed attributed graphs G_A1 and G_A2 are considered isomorphic, denoted as G_A1 $\cong$ G_A2.

Definition 5. (Directed Graph Transformation):

 Suppose there is a directed graph G. Under the transformation rule p: L→R, the directed graph G is transformed into $G^{\prime }$, then we say that G is transformed into $G^{\prime }$. Here, L represents the left subgraph of the transformation rule, and R represents the right subgraph of the transformation rule.

Definition 6. (Teaching Knowledge Graph Transformation):

 Suppose there is a teaching knowledge graph G_k. Under the transformation rule p: L→R, the teaching knowledge graph G_k is transformed into $G_k^{\prime }$, then we say that G_k is transformed into $G_k^{\prime }$. Here, L represents the left subgraph of the transformation rule within the context of the teaching knowledge graph, and R represents the right subgraph of the transformation rule within the context of the teaching knowledge graph.

Definition 7. (Teaching Knowledge Graph Evolution):

 Suppose there is a teaching knowledge graph G_k0. Under the effect of n transformation rules p_i: L→R, the teaching knowledge graph G_k0 evolves into G_kn, i.e., G₀$\underset{p_1}{\to }$G₁$\underset{p_2}{\to }$G₂…$\underset{p_n}{\to }$G_n. Then, we say that G_k0 has evolved into G_kn. Here, each p_i: L→R represents an evolution rule, where L is the left subgraph of the transformation rule within the context of the teaching knowledge graph, and R is the right subgraph of the transformation rule within the context of the teaching knowledge graph.

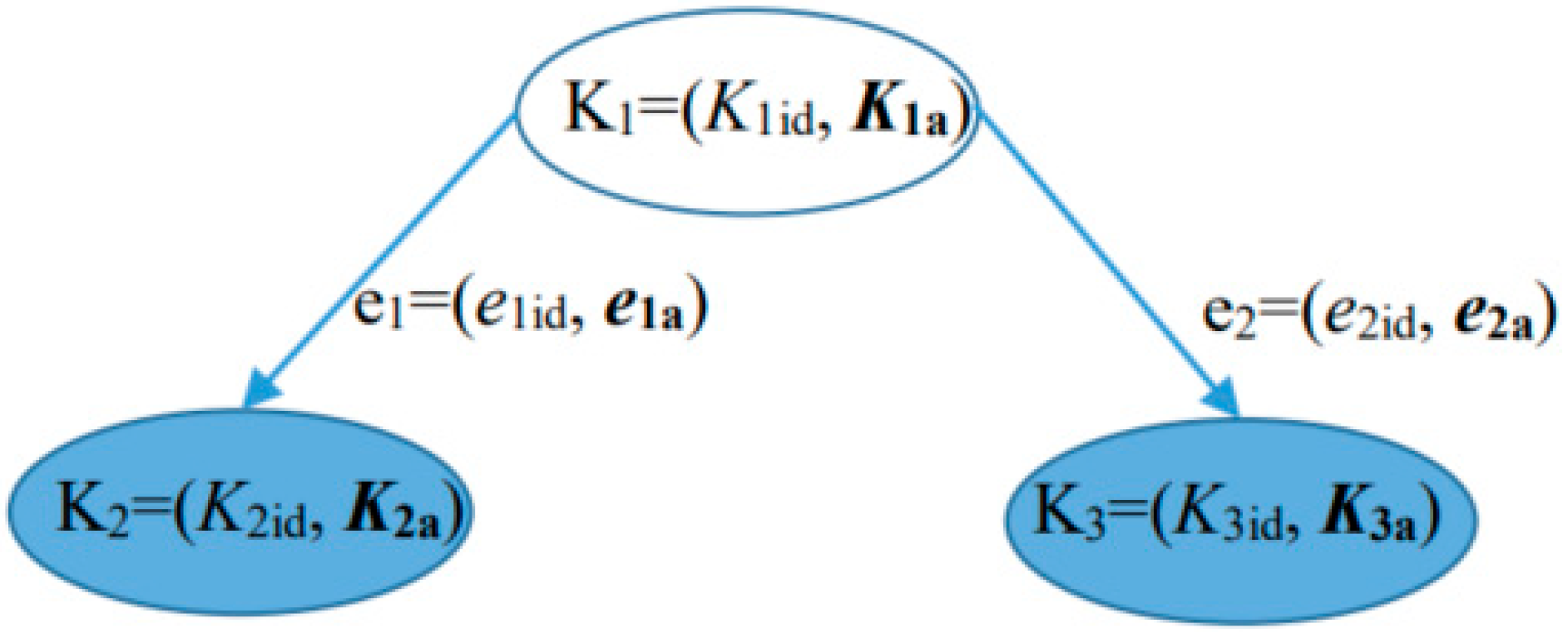
3.2. Definition of Entity Symmetry and Asymmetry

A knowledge graph is fundamentally a knowledge representation formalism based on graph structures, where nodes represent entities or concepts, and edges denote semantic relationships between entities. Symmetry refers to the equivalence or mirror-like property exhibited by certain nodes or relations within the graph, either structurally or semantically. Such symmetric characteristics are commonly observed in relationships such as “synonymy,” “prerequisite reciprocity,” and “bidirectional translation.” Introducing symmetry not only helps to more accurately characterize bidirectional relationships among knowledge elements, but also ensures logical consistency and semantic integrity during the evolution of teaching knowledge graphs. In educational contexts, symmetry is particularly important. For example, in an intelligent tutoring system, if knowledge point A is a prerequisite for knowledge point B, then knowledge point B may represent a subsequent application of A. This mutual dependency reflects semantic symmetry within the graph model. By modeling such symmetric relationships, the system can achieve a more comprehensive understanding of the knowledge structure, thereby improving the accuracy of learning path recommendations. In linguistics and foreign language teaching, symmetry can be used to model semantic mapping between cross-lingual vocabulary, such as “English word A has the same meaning as Chinese word B,” thus supporting the integration and transfer of multilingual knowledge. Therefore, to ensure high-quality and scalable evolution of teaching knowledge graphs, it is essential to rigorously define different types of symmetries.

Definition 8. (Entity Connection Symmetry in Teaching Knowledge Graph):

 In a teaching knowledge graph G_K = (V, E, A_V, A_E, $\varnothing$_A, $\varnothing$_E), consider two entities K₁ = (K_1id, K_1a) $\in$ V and K₂ = (K_2id, K_2a) $\in$ V, where K_1a$\in$A_V and K_2a$\in$A_V. Suppose there exists a connecting relation e₁ = (e_1id, e_1a) $\in$ E, with e_1a $\in$ A_E. If the attribute values of the entities satisfy K_1a = K_2a, then entities are said to exhibit connection symmetry, denoted as K₁$\backsim$K₂. As shown in Figure 1.

Definition 9. (Entity Central Symmetry in Teaching Knowledge Graph):

 In a teaching knowledge graph G_K = (V, E, A_V, A_E, $\varnothing$_A, $\varnothing$_E), consider an entity K₁ = (K_1id, K_1a) $\in$ V that has a connecting relation e₁ = (e_1id, e_1a) with entity K₂ = (K_2id, K_2a) $\in$ V, and another connecting relation e₂ = (e_2id, e_2a) with entity K₃ = (K_3id, K_3a) $\in$ V, where {K_1a, K_2a, K_3a} $\in$ A_V and {e_1a, e_1a} $\in$ A_E. If the attribute values of the entities satisfy K_2a = K_3a and the attribute values of the connecting relations satisfy e_1a = e_2a, then entities K₂ and K₃ are said to exhibit central symmetry, denoted as K₂ $\backsimeq$ K₃. As shown in Figure 2.

Definition 10. (Entity Mirror Symmetry in Teaching Knowledge Graph):

 In a teaching knowledge graph G_K = (V, E, A_V, A_E, $\varnothing$_A, $\varnothing$_E), consider two entities K₁ = (K_1id, K_1a) $\in$ V and K₂ = (K_2id, K_2a) $\in$ V that exhibit connection symmetry. Suppose K₁ has a connecting relation e₃ = (e_3id, e_3a) with entity K₃ = (K_3id, K_3a), and K₂ has a connecting relation e₄ = (e_4id, e_4a) with entity K₄ = (K_4id, K_4a), where {K_1a, K_2a, K_3a, K_4a} $\in$ A_V and {e_3a, e_4a} $\in$ A_E. If the attribute values satisfy K_3a = K_4a and the relation attribute values satisfy e_3a = e_4a, then entities K₃ and K₄ are said to exhibit mirror symmetry, denoted as K₃ $\approxeq$ K₄. As shown in Figure 3.

Definition 11. (Structural Symmetry of Teaching Knowledge Graph):

 Suppose within an educational knowledge graph G_K = (V, E, A_V, A_E, $\varnothing$_A, $\varnothing$_E), there are two sub-knowledge graphs G_K1 = (V1, E1, A_V1, A_E1, $\varnothing$_A1, $\varnothing$_E1) and G_K2 = (V2, E2, A_V2, A_E2, $\varnothing$_V2, $\varnothing$_E2) where G_K1$\subset$G₁ and G_K2$\subset$G_K. If there exists a bijective function f: V1$\to$V2 such that for any (u, v) $\in$ E1, we have (f(u), f(v)) $\in$ E2; and for any v $\in$ V1, $\varnothing$_A1(v) = $\varnothing$_A2(f(v)), as well as for any (u, v) $\in$ E1, $\varnothing$_A1(u, v) = $\varnothing$_A2(f(u), f(v)), making G_K1 and G_K2 isomorphic, then the sub-knowledge graphs G_K1 and G_K2 are said to have structural symmetry.

For example, as shown in Figure 4, within a knowledge graph, G_K1 and G_K2 contain corresponding mappings between edges e₄ and e₆, e₅ and e₇, e₈ and e₉, and between nodes K₃ and K₄, K₅ and K₇, K₆ and K₈, indicating that G_K1 and G_K2 are isomorphic, hence they exhibit structural symmetry.

Definition 12. (Entity Connection Asymmetry in Teaching Knowledge Graph):

 In a teaching knowledge graph G_K = (V, E, A_V, A_E, $\varnothing$_A, $\varnothing$_E), consider two entities K₁ = (K_1id, K_1a) $\in$ V and K₂ = (K_2id, K_2a) $\in$ V, where K_1a $\in$ A_V and K_2a $\in$ A_V. Suppose there exists a connecting relation e₁ = (e_1id, e_1a) $\in$ E, with e_1a $\in$ A_E. If the attribute values of the entities satisfy K_1a ≠ K_2a, then entities are said to exhibit connection asymmetry.

Definition 13. (Entity Central Asymmetry in Teaching Knowledge Graph):

 In a teaching knowledge graph G_K = (V, E, A_V, A_E, $\varnothing$_A, $\varnothing$_E), consider an entity K₁ = (K_1id, K_1a) $\in$ V that has a connecting relation e₁ = (e_1id, e_1a) with entity K₂ = (K_2id, K_2a) $\in$ V, and another connecting relation e₂ = (e_2id, e_2a) with entity K₃ = (K_3id, K_3a) $\in$ V, where {K_1a, K_2a, K_3a} $\in$ A_V and {e_1a, e_1a} $\in$ A_E. If the attribute values of the entities satisfy K_2a ≠ K_3a and the attribute values of the connecting relations satisfy e_1a ≠ e_2a, then entities K₂ and K₃ are said to exhibit central asymmetry.

Definition 14. (Entity Mirror Asymmetry in Teaching Knowledge Graph):

 In a teaching knowledge graph G_K = (V, E, A_V, A_E, $\varnothing$_A, $\varnothing$_E), consider two entities K₁ = (K_1id, K_1a) $\in$ V and K₂ = (K_2id, K_2a) $\in$ V that exhibit connection symmetry. Suppose K₁ has a connecting relation e₃ = (e_3id, e_3a) with entity K₃ = (K_3id, K_3a), and K₂ has a connecting relation e₄ = (e_4id, e_4a) with entity K₄ = (K_4id, K_4a), where {K_1a, K_2a, K_3a, K_4a} $\in$ A_V and {e_3a, e_4a} $\in$ A_E. If the attribute values satisfy K_3a ≠ K_4a and the relation attribute values satisfy e_3a ≠ e_3a, then entities K₃ and K₄ are said to exhibit mirror asymmetry.

4. Directed Attributed Graph-Driven Evolution Rules and Methods for Teaching Knowledge Graph

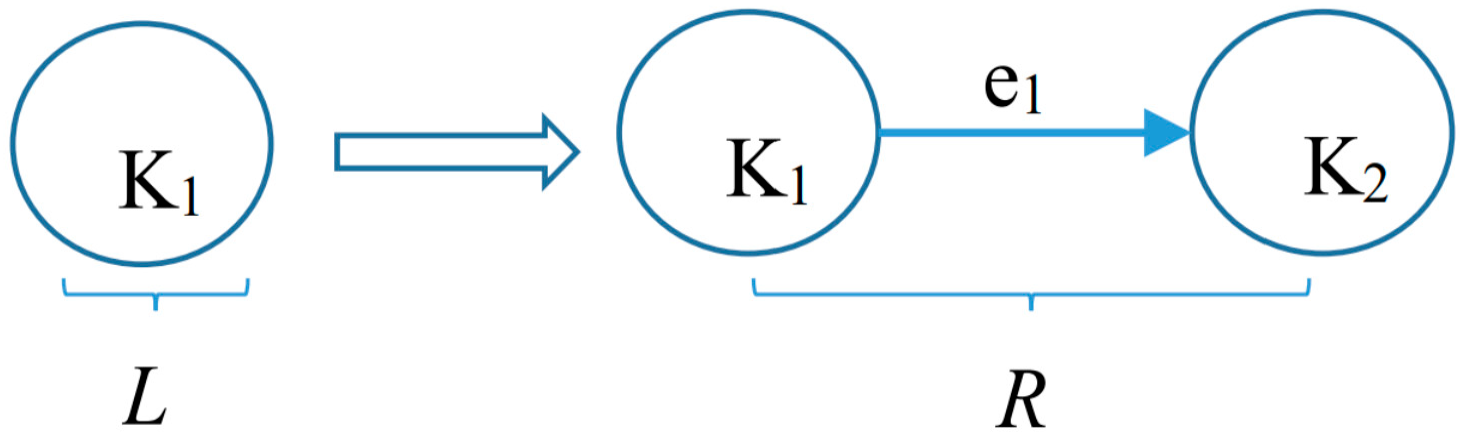
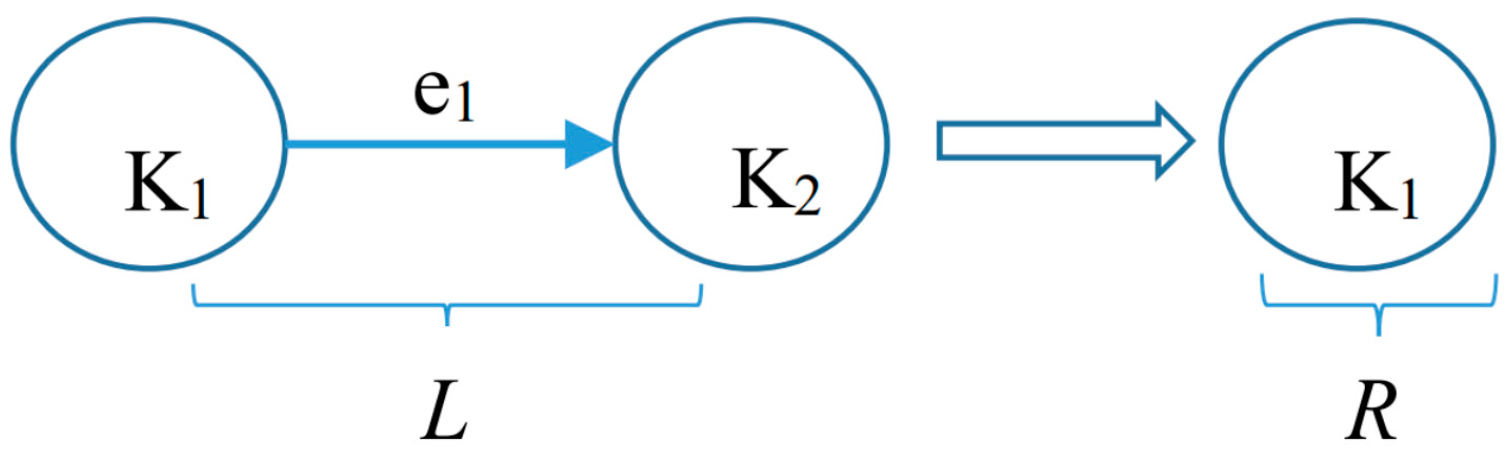
4.1. Teaching Entity Addition Evolution Rule

The teaching knowledge graph G_k is not static after its initial construction. Instead, in the context of intelligent teaching scenarios, new teaching methods, content, objectives, and other knowledge changes often necessitate updates to the knowledge graph, including the addition of new teaching entities. As shown in Figure 5, suppose there is an entity K₁ in the knowledge graph G_k, and a new entity K₂ needs to be added. This addition involves not only incorporating the new entity itself but also establishing a connection relation e₁ between K₁ and K₂. Formally, this can be represented as p₁: K₁→K₁ $\cup$ {K₂, e₁}.

4.2. Teaching Entity Replacement Evolution Rule

In the context of intelligent teaching scenarios, improvements in teaching methods, content, objectives, and other knowledge elements necessitate updates to the knowledge graph, including the replacement of older teaching entities with improved ones. As shown in Figure 6, suppose there are two entities K₁ = (K_1id, K_1a) and K₂ = (K_2id, K_2a) in the knowledge graph G_k. To replace the older teaching entity K₂ with an improved teaching entity K₃ = (K_3id, K_3a), not only must the entity itself be replaced, but the original connection relation e₁ = (e_1id, e_1a) between K₁ and K₂ must also be replaced with a new connection relation e₂ = (e_2id, e_2a). Here, K_2a = K_3a and e_1a = e_2a. Formally, this can be represented as p₂: K₁ $\cup$ {K₂, e₁}→K₁ $\cup$ {K₃, e₂}.

4.3. Teaching Entity Deletion Evolution Rule

In the context of intelligent teaching scenarios, some outdated teaching methods, content, objectives, and other knowledge elements may no longer meet real-world needs and thus need to be eliminated. This necessitates changes to the knowledge graph, including the deletion of older teaching entities. As shown in Figure 7, suppose there are two entities K₁ and K₂ in the knowledge graph G_k. To delete the older teaching entity K₂, not only must the entity itself be removed, but the original connection relation e₁ between K₁ and K₂ must also be deleted. Formally, this can be represented as p₃: K₁ $\cup$ {K₂, e₁}→K₁.

4.4. A Graph Model-Driven Approach to the Evolution of Teaching Knowledge Graph

As indicated by Definition 5, a graph can be transformed into another graph through graph transformation rules, thereby achieving evolutionary updates. Therefore, teaching knowledge graphs can also leverage the evolution rules of directed attributed graphs to evolve one teaching knowledge graph into another. To this end, this paper proposes a directed attributed graph model-driven evolution method for teaching knowledge graphs, as shown in Algorithm 1. Specifically, given a teaching knowledge graph G_k and an evolution rule p_i: L→R, where L represents the left subgraph of the rule and R the right subgraph, the method first retrieves L and then performs subgraph matching within G_k to locate L. If a match is found, L is removed from G_k, and R is subsequently inserted into the corresponding position, resulting in the transformation of the original teaching knowledge graph G_k into a new teaching knowledge graph $G_k^{\prime }$. However, in practical evolution processes, multiple evolution rules often need to be executed concurrently to improve efficiency. Yet, concurrent execution may lead to rule conflicts. For example, a delete-delete conflict occurs when two rules attempt to delete the same entity or edge, which can cause state inconsistency without coordination. Similarly, a delete-preserve conflict arises when one rule intends to delete an entity while another aims to preserve it, also resulting in state inconsistency if executed concurrently. It is evident that concurrent execution is safe only when the two rules operate on disjoint subgraph structures. Therefore, during the execution of Algorithm 1, potential conflicts among concurrently executed rules are always checked first. If a conflict is detected, concurrent execution is prohibited and the process switches to a conflict resolution strategy; otherwise, the rules may be executed concurrently.

The process of evolving from an original teaching knowledge graph to a target teaching knowledge graph under the influence of multiple evolution rules is referred to as the evolution process of the teaching knowledge graph. Suppose there is a teaching knowledge graph G_k0. Under the effect of n evolution rules p_i: L→R, the teaching knowledge graph G_k0 evolves into G_kn, i.e., G_k0$\underset{p_1}{\to }$G_k1$\underset{p_2}{\to }$G_k2…$\underset{p_n}{\to }$G_kn. Here, each p_i: L→R represents an evolution rule where L is the left subgraph and R is the right subgraph of the evolution rule. In practical scenarios, it often requires multiple evolution rules to achieve the desired updates and evolution of the target teaching knowledge graph.

Algorithm 1: Evolution of Teaching Knowledge Graph, ETKG

Input: Teaching Knowledge Graph GK = (V, E, AV, AE, $\varnothing$A, $\varnothing$E), pi: L→R

Output: New Teaching Knowledge Graph $G_k^{\prime }$ = (V, E, AV, AE, $\varnothing$A, $\varnothing$E)

1: F$\leftarrow$Checking_conflict(pi, pj)

2: if (F = true)

3:   Conflict_resolution_strategy(pi, pj)

4: else//Concurrent execution rules

5:  get left_rule L from pi: L→R and pi: L→R

6:  while concurrent traversing nodes not completed do

7:     if L match in GK

8:       cut L in GK

9:       GK$\leftarrow$GK–L

10:       get right_rule R from pi: L→R

11:       paste R in GK

12:       $G_k^{\prime }\leftarrow$GK $\cup$ R

13:       return $G_k^{\prime }$

14:    else if L no match in GK

15:        return No_match_L

5. Symmetry Preservation and Breakage in the Evolution of Teaching Knowledge Graph

Knowledge graphs are not static in practical applications but continuously evolve as new knowledge is introduced and old knowledge is revised or removed. This evolution not only affects the scale and content of the knowledge graph but also significantly impacts its structural properties, especially symmetry. In the early stages of constructing a teaching knowledge graph, due to a relatively complete knowledge system and clearly defined relationships, the graph model often exhibits strong symmetric characteristics, such as mutual prerequisites between knowledge points, bidirectional mappings between concepts, and symmetric distributions of semantic roles. However, as the graph evolves dynamically, newly added knowledge may disrupt the original symmetric structures, leading to increased asymmetry in the graph model. For instance, in a linguistics teaching knowledge graph, the introduction of new grammatical rules or updates to cross-linguistic correspondences may cause originally symmetric syntactic structures to become asymmetric due to semantic drift, thereby undermining the uniformity of knowledge representation and the effectiveness of reasoning. Therefore, throughout the evolution of a teaching knowledge graph, it is crucial to continuously monitor and preserve its symmetric characteristics. When necessary, symmetry should be restored or adjusted through methods such as knowledge reconstruction, relation completion, or graph structure optimization, to ensure the stability, consistency, and reasoning efficiency of the knowledge graph in educational applications. This not only enhances the graph’s interpretability and maintainability but also provides a more solid foundation for downstream tasks such as intelligent tutoring, knowledge transfer, and semantic reasoning. To this end, we will examine how evolution rules affect the preservation or disruption of symmetry during the evolution of teaching knowledge graphs.

Proposition 1. (Symmetry-Preserving Evolution of Teaching Knowledge Graph):

 Suppose there is a teaching knowledge graph G_K = (V, E, A_V, A_E, $\varnothing$_A, $\varnothing$_E). If the replacement evolution rule p₂: K₁  $\cup$ {K₂, e₁}→K₁  $\cup$ {K₃, e₂} are applied to G_k, transforming G_K into $G_K^{\prime }$, where before evolution K₂  $\notin V$ and e₁  $\notin E$ in p₁, and K₃  $\notin V$ and e₂  $\notin E$ in p₂, and K₂ and K₃ have the same mapped attribute relationship, and e₁ and e₂ have the same direction and attribute mapping relationship, then the evolution rules p₁ and p₂ preserve the entity connection symmetry, entity central symmetry, entity mirror symmetry, and structural symmetry during the evolution of the knowledge graph.

Proof. 

Let the initial educational knowledge graph be $G_K^0$ = (V, E, A_V, A_E, $\varnothing$_A, $\varnothing$_E), which possesses entity connection symmetry, central symmetry, mirror symmetry, and structural symmetry. We prove by mathematical induction that these symmetries are preserved after n evolution steps.

(1)

When n = 0, no evolution has been performed, so $G_K^0$ remains the initial educational knowledge graph. By the assumption of the proposition, $G_K^0$ exhibits entity connection symmetry, central symmetry, mirror symmetry, and structural symmetry. Hence, the proposition holds for n = 0.

(2)

When n > 0, assume that after w evolution steps, the knowledge graph $G_K^w$ retains entity connection symmetry, central symmetry, mirror symmetry, and structural symmetry. We now consider the transition from step w to step w + 1. Suppose a replacement rule p₂ is applied to $G_K^w$ to obtain $G_K^{w+1}$. According to the definition of rule p₂, only the local substructure {K₂, e₁} is replaced by {K₃, e₂}, while all other parts remain unchanged. Since A_V(K₂) = A_V(K₃) and A_E(e₂) = A_E(e₃), the new substructure is attribute-wise and connectivity-wise equivalent to the original one, i.e., structurally equivalent. Therefore, $G_K^{w+1}$ also maintains entity connection symmetry, central symmetry, mirror symmetry, and structural symmetry.

Combining (1) and (2), it follows that for any non-negative integer n, the knowledge graph $G_K^n$ preserves entity connection symmetry, central symmetry, mirror symmetry, and structural symmetry. In particular, when n = 1, this corresponds to the single-evolution scenario described in Proposition 1, and the conclusion holds. This completes the proof. □

Proposition 2. (Symmetry-Breaking Evolution of Teaching Knowledge Graph):

 Suppose there is a teaching knowledge graph G_K = (V, E, A_V, A_E, $\varnothing$_A, $\varnothing$_E). If an addition evolution rule p₁: K₁→K₁$\cup${K₂, e₁} is applied to G_K, resulting in an evolved graph $G_K^{\prime }$, where K₂$\notin$V and e₁$\notin$E; or if the deletion evolution rule p₃: K₁$\cup${K₂, e₁}→K₁ is applied to G_K, transforming G_K into $G_K^{\prime }$, where before evolution K₂ is an entity involved in an instance of entity connection symmetry, central symmetry, or mirror symmetry, then the evolution rule p₃ necessarily breaks the entity connection symmetry, central symmetry, mirror symmetry, and structural symmetry in the evolution of the knowledge graph.

Proof. 

We prove Proposition 2 by contradiction. Assume that after applying the deletion rule p₃: K₁$\cup${K₂, e₁}→K₁, the resulting knowledge graph $G_K^{\prime }$ still preserves the original entity connection symmetry, central symmetry, mirror symmetry, and structural symmetry. By the proposition’s assumption, K₂ is a critical entity for at least one type of symmetry before evolution. If K₂ satisfies entity connection symmetry Definition, there exists another entity $K_1^{\prime } \in$V such that $K_1^{\prime }\backsim$K₂; deleting K₂ leaves $K_1^{\prime }$ without a symmetric counterpart, violating Definition. If K₂ is part of a centrally symmetric pair with K₁ $\backsimeq$ K₂ around some center c, its removal breaks the central symmetry since K₁ no longer has a matching counterpart. If K₂ participates in a mirror-symmetric structure K₂ $\approxeq$ K₃, deleting K₂ severs the mirror relationship, invalidating mirror symmetry. Likewise, if K₂ belongs to a symmetric subgraph, its absence causes that subgraph to become non-isomorphic to its original symmetric counterpart, thereby violating structural symmetry. In all cases, $G_K^{\prime }$ cannot retain all four symmetries simultaneously, contradicting the assumption. Hence, the deletion rule p₃ necessarily disrupts the knowledge graph’s symmetry. A similar reasoning applies to the addition rule, and thus the proof is complete. □

6. Evaluation and Illustrative Examples of the Impact of Preserving and Breaking Symmetry in Educational Knowledge Graph Evolution

6.1. Analysis of the Impact of Symmetry Preservation and Breaking in Educational Knowledge Graph Evolution

6.1.1. Evaluation Metrics for Symmetry Preservation and Breaking

To evaluate the impact of symmetry preservation and symmetry breaking on knowledge graphs, we employ two metrics: connectivity and path complexity of the knowledge graph.

The connectivity of the knowledge graph is measured by the Average Shortest Path Length (APL), as shown in Equation (1), which is defined as the average length of the shortest directed paths between all pairs of entity nodes, considering only reachable node pairs.

$$APL\left(GK\right)={\displaystyle \frac{1}{M}}\sum _{\begin{array}{c}u,v\in V\\ u\ne v\\ d\left(u,v\right)<\infty \end{array}}d\left(u,v\right)$$

(1)

where d (u, v) denotes the length of the shortest directed path from node u to node v, and M = |{(u, v)|u$\ne$v, d (u, v) < $\mathrm{\infty }$}| is the number of reachable node pairs. A smaller APL value indicates higher efficiency in knowledge propagation or navigation within the knowledge graph.

The path complexity of the knowledge graph is measured by the Path Diversity Index (PDI), as defined in Equation (2). PDI quantifies whether there exists a single path or multiple alternative paths to reach a target, thereby reflecting the structural flexibility of the knowledge graph.

$$PDI\left(s,t\right)={\displaystyle \frac{\left|P_{s\to t}\right|}{len\left(p_{shortest}\right)}}$$

(2)

where $\left|P_{s\to t}\right|$ is the total number of distinct paths from node s to node t, and len (p_shortest) is the number of edges in the shortest path. A higher PDI value indicates the presence of multiple equivalent paths, reflecting a more robust and flexible graph structure.

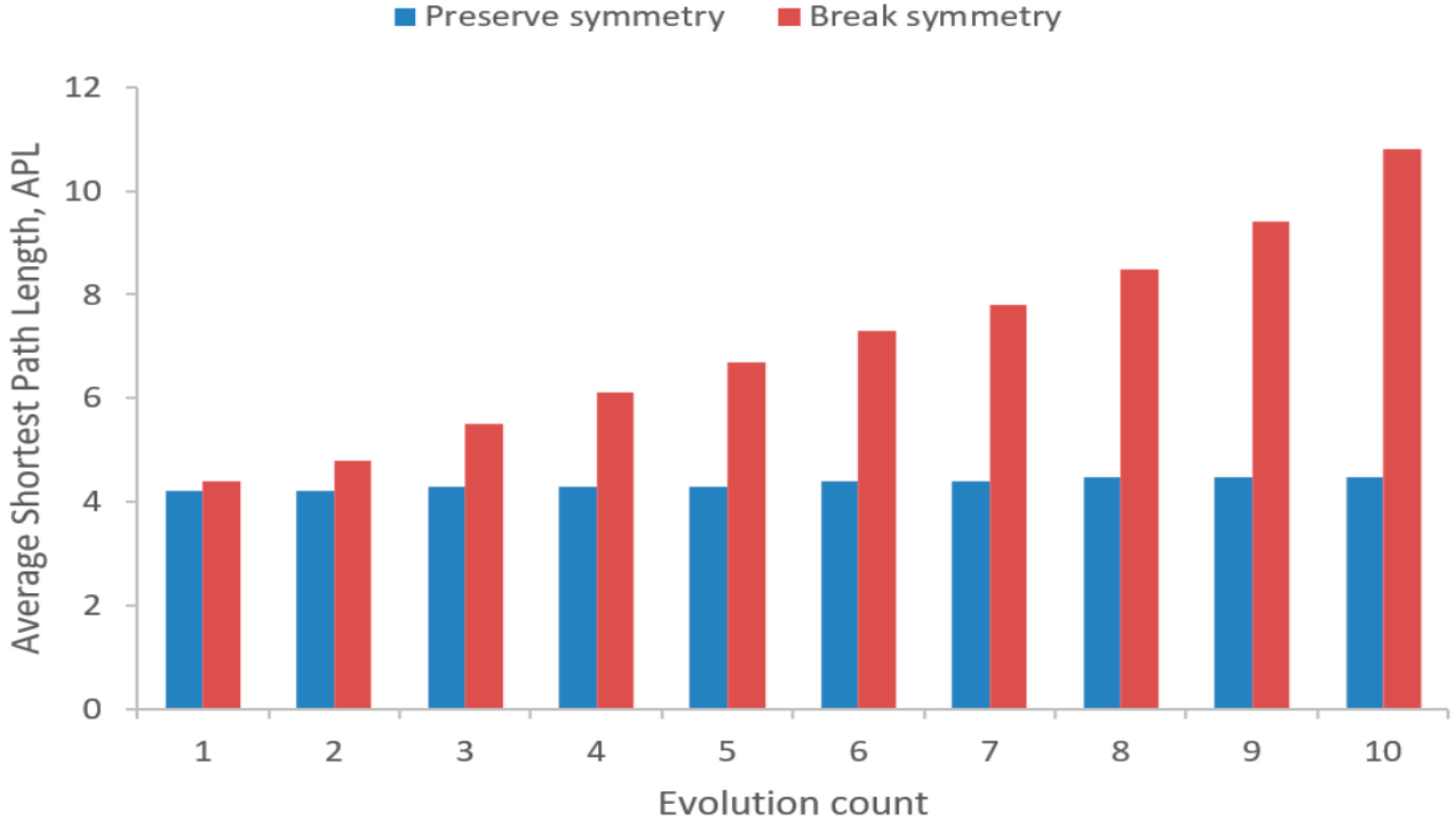
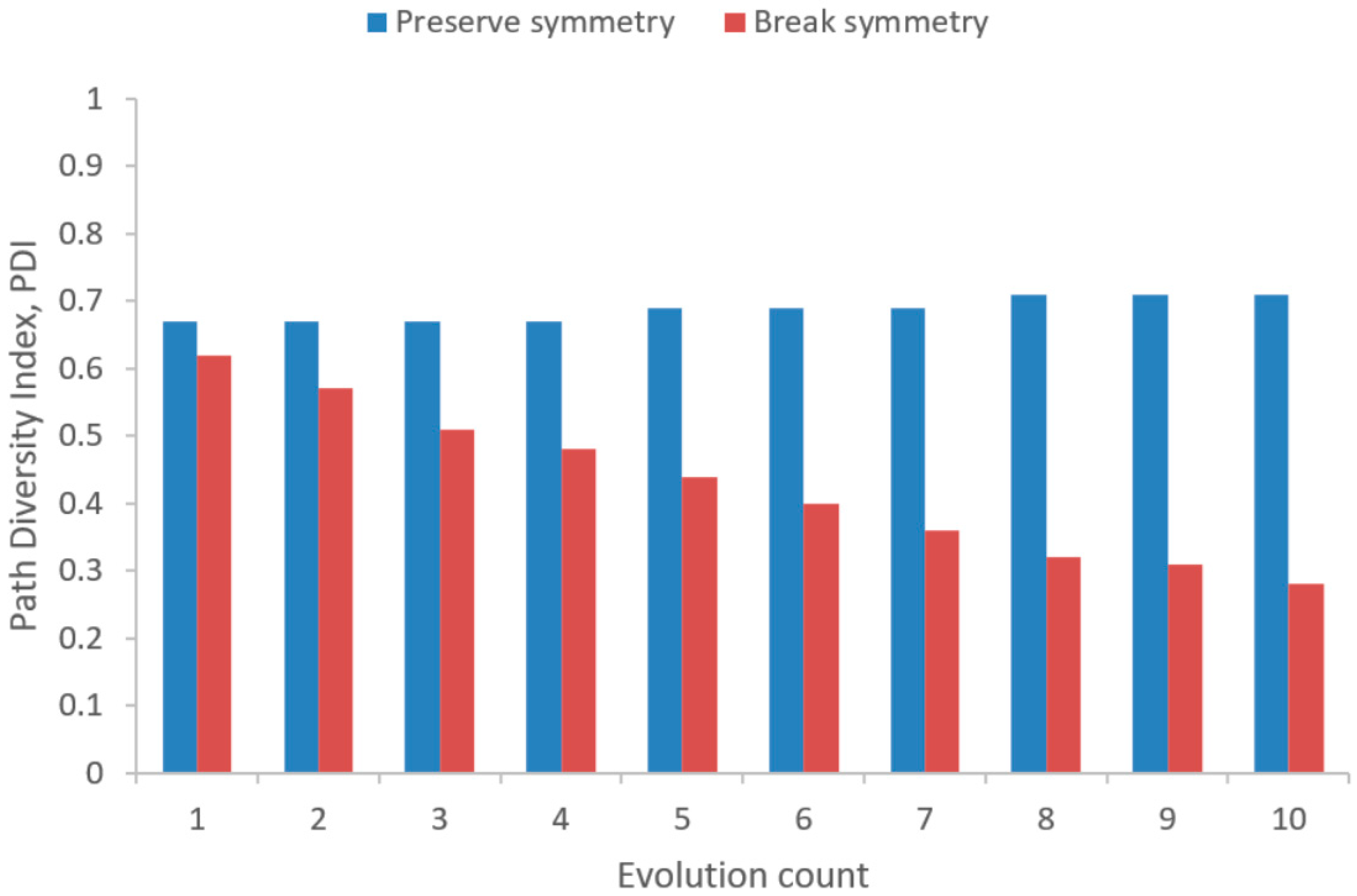
6.1.2. The Impact of Evolution on Connectivity and Path Complexity

To evaluate whether evolution operations that preserve symmetry maintain the structural properties of knowledge graphs better than those that break symmetry, and thus provide a more robust basis for knowledge organization in educational applications, we constructed a simulated educational knowledge graph with 500 nodes. This graph was designed to evenly distribute nodes exhibiting entity connection symmetry, entity central symmetry, entity mirror symmetry, and structural symmetry, ensuring diversity among symmetric node types. We then conducted two groups of experiments: one group applied symmetry-preserving operations and the other applied symmetry-breaking operations. Each group performed 10 rounds of evolution, with each round randomly selecting one type of symmetric node for modification. After each evolution step, we evaluated both the connectivity and the path complexity of the knowledge graph.

As shown in Figure 8, the experimental comparison reveals that symmetry-preserving evolution operations have a smaller impact on the connectivity of the knowledge graph. Specifically, replacement operations that preserve symmetry barely affect connectivity, while addition operations may even enhance connectivity, especially when the symmetric nodes involved are structurally important in the knowledge graph. This suggests that, during the evolution of educational knowledge graphs, symmetry-preserving operations are preferable. In contrast, symmetry-breaking evolution operations significantly degrade connectivity, as deletion operations may remove symmetric nodes that serve as critical hubs, leading to longer and more circuitous paths.

As shown in Figure 9, the experimental comparison shows that symmetry-preserving evolution operations have a relatively small impact on path diversity in the knowledge graph. Replacement operations that maintain symmetry barely affect path diversity, while addition operations may introduce additional paths and lead to a slight increase in path diversity, especially when the symmetric nodes involved are structurally important in the knowledge graph. This further indicates that during the evolution of educational knowledge graphs, symmetry-preserving operations are more desirable. In contrast, symmetry-breaking evolution operations significantly reduce path diversity because deletion operations may remove symmetric nodes that lie on multiple paths, thereby decreasing the number of available traversable routes.

6.2. Symmetric and Asymmetric Case Analysis of Teaching Knowledge Graph Evolution in Japanese Language Major

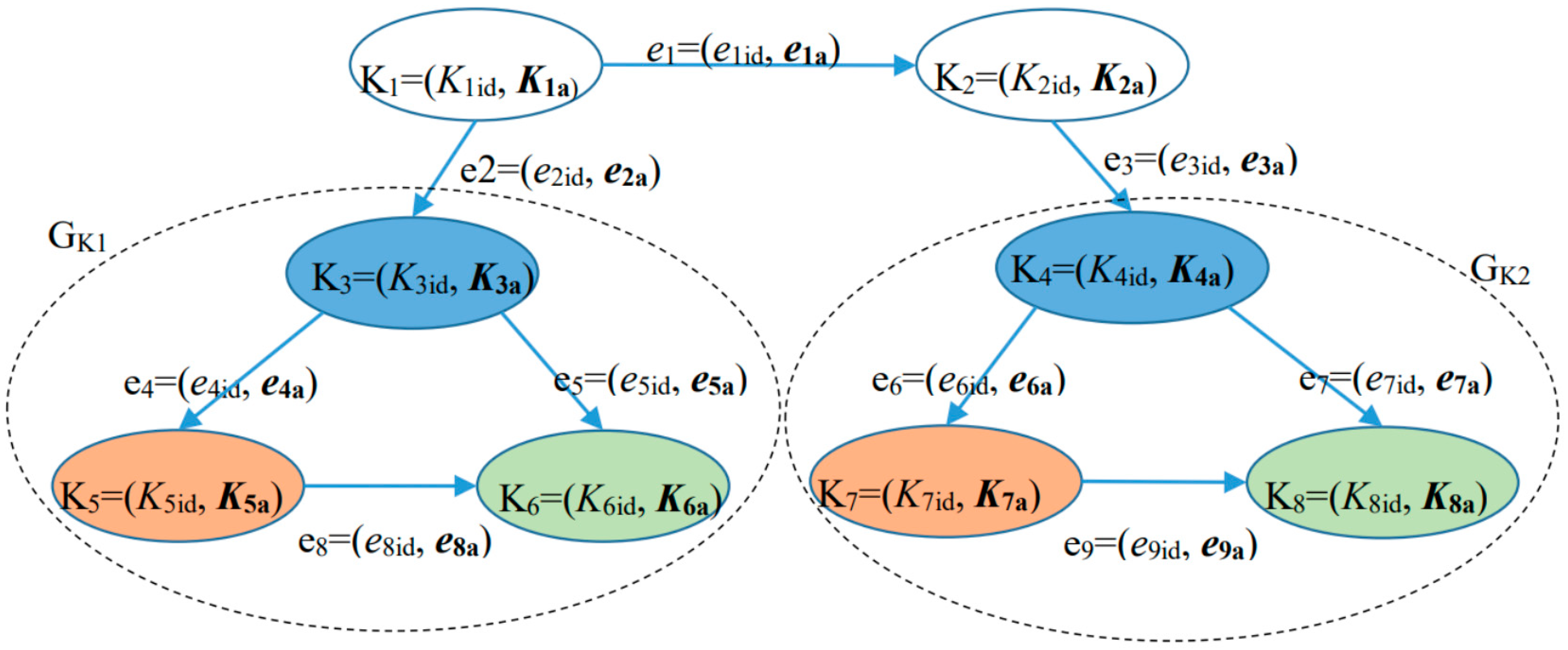
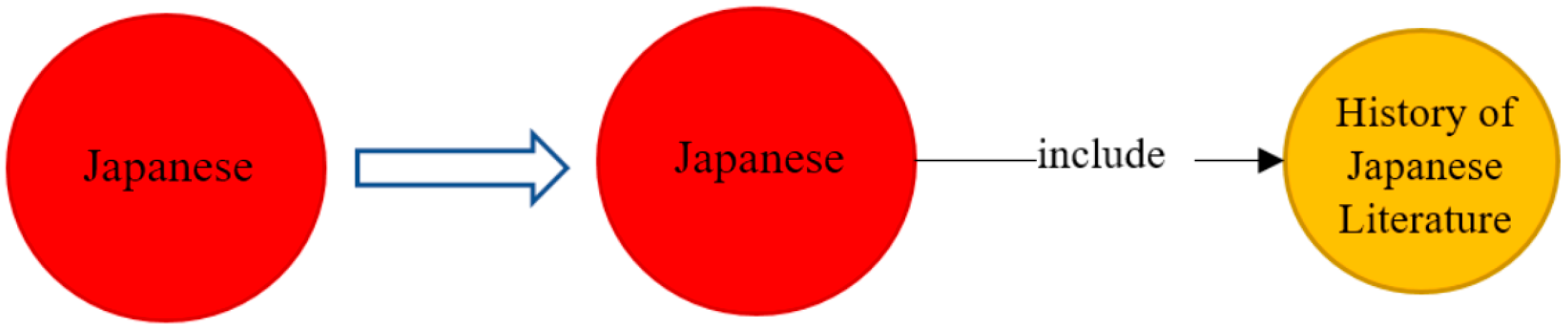
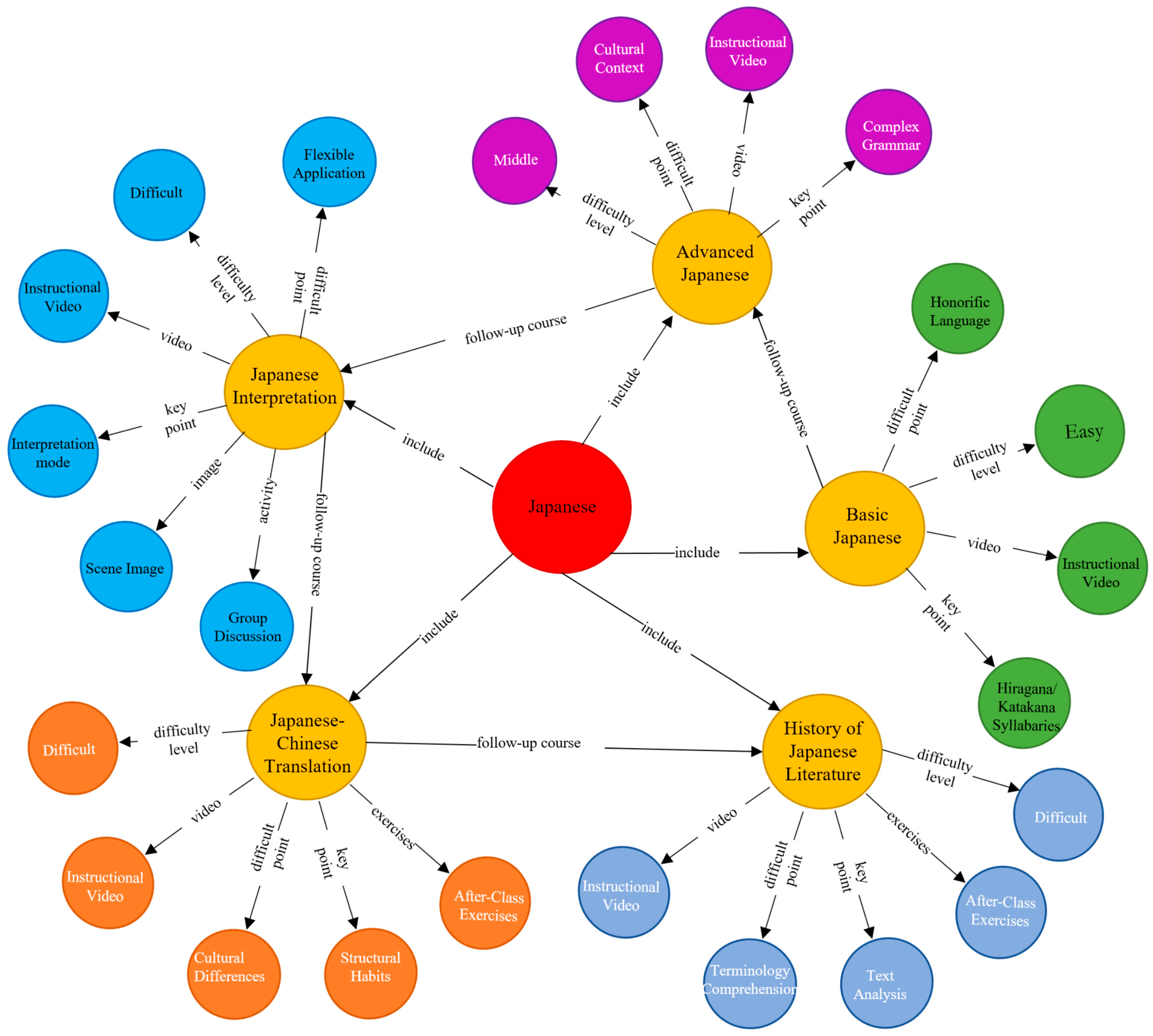
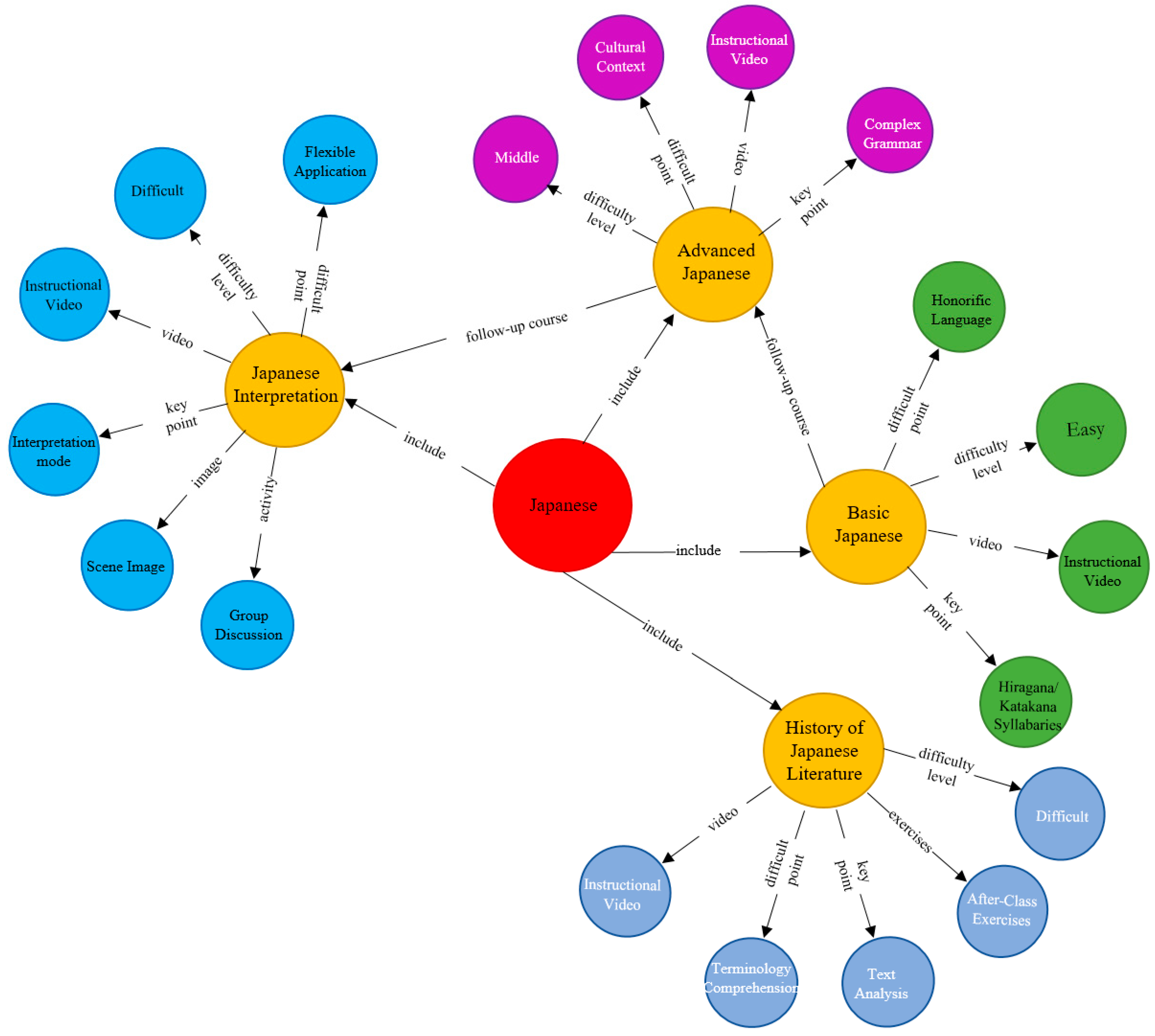
6.2.1. Directed Attributed Graph Model of the Teaching Knowledge Graph for Japanese Language Major

As shown in Figure 10, the teaching knowledge graph for the Japanese Language Major is a directed graph comprising various types of nodes and edges to reflect the teaching relationships within the Japanese language major training system. This graph is a semantic network that organizes Japanese learning content in a structured manner, formally defined as a directed attributed graph G_R0 = (V, E, A_V, A_E, $\varnothing$_A, $\varnothing$_E), where V represents the set of knowledge point nodes such as “Japanese”, “Basic Japanese”, “Honorific System”, etc., and E denotes directed relationships between knowledge points like “include”, “follow-up”, “key point”, etc.; A_V is the set of node attributes used to label different types of teaching entity attributes such as Type I, Type II, Type III, including major, course, course knowledge, etc., while A_E is the set of edge attributes used to label relationship properties between different types of entities, such as relationships between Type I and Type II entities, among Type II entities, and between Type II and Type III entities, including properties like “include”, “sequence”, “type”, etc.; $\varnothing$_A is a node mapping function that assigns attributes to specific nodes, for example, assigning Type I node attributes to the Japanese Language Major node. $\varnothing$_E is an edge mapping function that assigns attributes to specific edges, for example, assigning the “include” attribute to the edge between the Japanese Language Major node and the Basic Japanese node.

This knowledge graph is composed of four major modules: Basic Japanese, Advanced Japanese, Japanese Interpretation, and Japanese-Chinese Translation. The Basic module covers the hiragana/katakana syllabaries and basic grammar, consolidating foundational knowledge through instructional videos. The Advanced module focuses on complex grammar structures and cultural contexts to enhance the flexible use of the language. The Interpretation and Translation modules emphasize differences in language structures between Japanese and Chinese as well as cross-cultural communication, strengthening practical skills through group discussions and interpretation training. This graph not only clearly presents the logical relationships and learning paths between pieces of knowledge but also integrates multimedia resources and teaching activities, supporting personalized learning recommendations and tracking of teaching progress. Through formal modeling, the Japanese teaching knowledge graph achieves systematic, scalable, and intelligent management of teaching content, providing strong support for building an efficient and precise smart foreign language teaching system.

6.2.2. Analysis and Discussion on Symmetry Preservation in the Evolution of the Teaching Knowledge Graph for the Japanese Language Major

The teaching knowledge graph for the Japanese Language Major is not static but continuously evolves in response to changing demands for talent development updated curriculum systems and shifting language usage environments. For example, to meet the need for cultivating well rounded Japanese language professionals the course “History of Japanese Literature” must be incorporated into the curriculum requiring corresponding evolution of the teaching knowledge graph. This evolution must appropriately reflect various knowledge points related to the new course. Such evolution not only involves the addition of nodes and edges but also highlights that a teaching knowledge graph with adaptive capabilities is essential for enabling precise and personalized intelligent foreign language instruction. To achieve this six instances of the addition evolution rule p₁: K₁→K₁ $\cup$ {K₂, e₁} are sequentially applied to add six nodes including “History of Japanese Literature” “Instructional Video” “Terminology Comprehension” “Text Analysis” “Exercises” and “Difficult” as well as eight edges labeled “include” “video” “ difficult point” “key point” “exercises” and “difficulty level”. Figure 11 and Figure 12 illustrate the evolution rules for adding the entities “History of Japanese Literature” and “Instructional Video”, respectively. Due to space limitations the remaining similar evolution rules are not repeated here. Additionally one instance of the replacement evolution rule p₂: K₁ $\cup$ {K₂, e₁}→K₁ $\cup$ {K₃, e₂} is applied replacing the previously empty edge between the nodes “Japanese Chinese Translation” and “History of Japanese Literature” with a “follow up course” edge. As shown in Figure 13, G_R1 is the resulting graph after applying the aforementioned evolution rules to the initial graph G_R0.

Discussion 1.

The teaching knowledge graph G_R0 for the Japanese Language Major is transformed into G_R1 after applying six addition evolution rules and one replacement evolution rule, denoted as $G_{R0}\underset{p_1}{\to }{G}_{R0}\underset{p_1}{\to }{G}_{R0}\underset{p_1}{\to }{G}_{R0}\underset{p_1}{\to }{G}_{R0}\underset{p_1}{\to }{G}_{R0}\underset{p_1}{\to }{G}_{R0}\underset{p_2}{\to }{G}_{R1}$. Since the evolution from G_R0 to G_R1 involves only addition and replacement operations, the resulting graph G_R1 in Figure 13 preserves all instances of entity connection symmetry, central symmetry, and mirror symmetry present in the original graph G_R0 in Figure 10. For example, this includes the connection symmetry between the Basic Japanese and Advanced Japanese entities, the central symmetry of the Japanese Interpretation and Japanese-Chinese Translation entities with respect to the Japanese entity, and the mirror symmetry between the Honorific System and Cultural Context Dependency entities, which both share a “difficulty” relationship with respect to the Advanced Japanese and Basic Japanese entities. This outcome verifies the correctness of Proposition 1, demonstrating that addition and replacement evolution rules enable the teaching knowledge graph for the Japanese Language Major to maintain its original entity connection symmetry, central symmetry, and mirror symmetry.

6.2.3. Analysis and Discussion on Symmetry Breakage in the Evolution of the Teaching Knowledge Graph for the Japanese Language Major

Due to changes in the educational authorities’ requirements for program training, the Japanese major’s educational knowledge graph undergoes curriculum refinement, necessitating adjustments to certain courses in the training plan. Among these, the course “Japanese-Chinese Translation” is prioritized for removal, as it overlaps significantly with content already covered in “Japanese Interpretation” and “Advanced Japanese,” rendering it redundant and unnecessary to offer separately. Consequently, the teaching knowledge graph for the Japanese Language Major must evolve, and all related knowledge points for this course need to be deleted as well. To achieve this, the deletion evolution rule p₃: K₁$\cup${K₂, e₁}→K₁ is applied eight times consecutively to remove six nodes including “Difficult” “Instructional Video” “Cultural Differences between Japanese and Chinese” “Japanese Language Structure Habits” “Exercises” and “Japanese-Chinese Translation” as well as eight edges labeled “include” “video” “difficulty” “focus” “exercises” “difficulty level” “subsequent course”. Figure 14 and Figure 15 illustrate the evolution rules for deleting the entities “Difficult” and “Japanese-Chinese Translation”, respectively while other similar evolution rules are not repeated here due to space limitations. Figure 16 shows the resulting graph G_R2 after the evolution from G_R1.

Discussion 2.

The teaching knowledge graph G_R1 for the Japanese Language Major is transformed into G_R2 after applying eight deletion evolution rules, denoted as$G_{R1}\underset{p_3}{\to }{G}_{R1}\underset{p_3}{\to }{G}_{R1}\underset{p_3}{\to }{G}_{R1}\underset{p_3}{\to }{G}_{R1}\underset{p_3}{\to }{G}_{R1}\underset{p_3}{\to }{G}_{R1}\underset{p_3}{\to }{G}_{R1}\underset{p_8}{\to }{G}_{R2}$. Since the evolution from G_R1 to G_R2 involves only deletion operations, the resulting graph G_R2 in Figure 16 breaks all instances of entity connection symmetry, central symmetry, and mirror symmetry that were present in the original graph G_R1 in Figure 13. For example, this includes the broken connection symmetry between the Japanese Interpretation and Japanese-Chinese Translation entities, the disrupted central symmetry of these two entities with respect to the Japanese entity, and the destroyed mirror symmetry between the Cultural Differences between Japanese and Chinese and Flexible Application entities, which both previously shared a “difficulty” relationship with respect to the Japanese Interpretation and Japanese-Chinese Translation entities. This outcome verifies the correctness of Proposition 2, demonstrating that deletion evolution rules inevitably disrupt the original entity connection symmetry, central symmetry, and mirror symmetry in the teaching knowledge graph for the Japanese Language Major.

7. Conclusions

This paper proposes a symmetry-aware analysis method for the evolution of educational knowledge graphs based on directed attributed graphs. We first formulate a directed attributed graph model for educational knowledge graphs and formally define four types of symmetry on this model: entity connection symmetry, entity central symmetry, mirror symmetry, and structural symmetry. Building upon this foundation, we design graph-based evolution rules for entity addition, replacement, and deletion and describe a rule-driven process for knowledge graph evolution. We then analyze the conditions under which these evolution operations preserve or break symmetry. To evaluate the practical implications, we conduct a simulation experiment comparing the effects of symmetry-preserving versus symmetry-breaking evolutions on graph connectivity and path complexity; the results show that preserving symmetry yields better connectivity and maintains healthier path diversity, thereby supporting more efficient reasoning and enabling richer personalized learning path planning. Furthermore, we present a case study on the evolution of a Japanese-language major knowledge graph to demonstrate the validity and feasibility of our symmetry analysis framework and evolution rules within the directed attributed graph model. Since our approach is grounded in formal graph transformation theory, it is generalizable across different subject domains and educational contexts. Future work will explore using knowledge graph evolution to assess curriculum adaptability, analyze the impact scope of symmetry-breaking operations, and leverage symmetry properties to detect and quantify knowledge redundancy in educational content.