Two Novel Sparse Models for Support Vector Machines
Abstract
1. Introduction
- Two Novel Sparse Models: We propose two novel sparse models: Sparse SVM (SSVM) and Sparse TPMSVM (STPMSVM), with sparsity as a central design objective.
- Symmetry-Driven Sparsification: Sparsity is induced by breaking the rotational symmetry of the -norm through an penalty on the dual variables, a geometric motivation that is then implicitly encoded into the model structure via the KKT conditions.
- Novel KKT-based reformulations transform the traditional QPPs into corresponding LPPs for both models.
- Significant Prediction Efficiency: The LPPs, combined with induced sparsity at the support vector level, allow faster prediction compared with the traditional QPP-based methods.
- Extensive Experimental Validation: Comprehensive experiments on synthetic and benchmark datasets verify that the proposed models achieve an advantageous trade-off among sparsity, prediction speed, and generalization performance.
2. Fundamentals of SVM and TPMSVM Models
2.1. Notations
2.2. SVM Model
2.3. TPMSVM Model
2.4. Geometric Insight: vs. Regularization
3. Two Novel Sparse Models
3.1. SSVM Model
3.2. STPMSVM Model
3.3. Theoretical Analysis
3.4. Sparsity and Symmetry-Breaking Mechanism
3.5. Computational Complexity
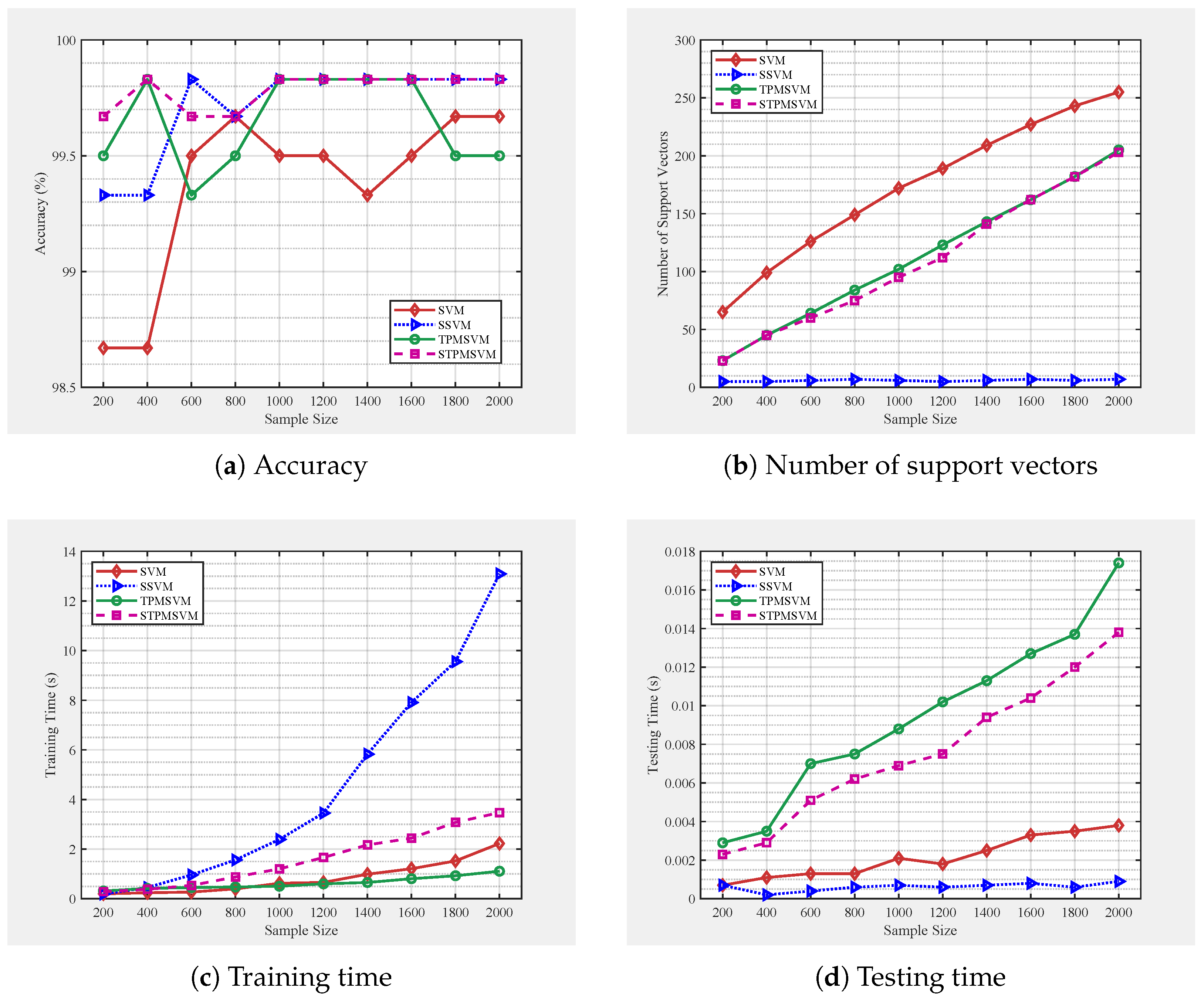
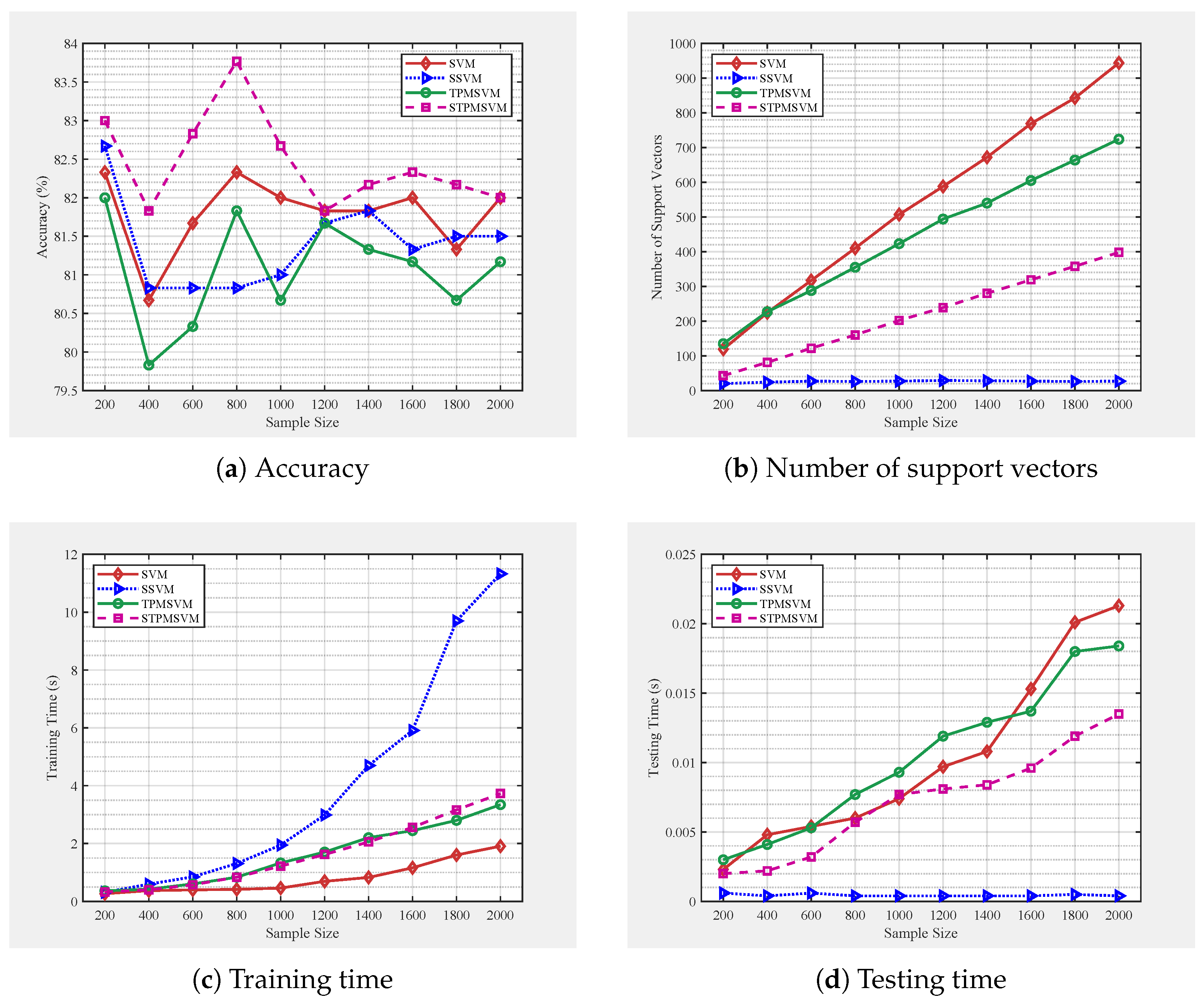
4. Numerical Experiments
4.1. Parameters Setting
4.2. Synthetic Datasets
4.2.1. Example 1
4.2.2. Example 2
- Class +1: , where ,
- Class −1: , , where is Gaussian noise.
4.2.3. Extension of Example 2: Increased Complexity Experiments
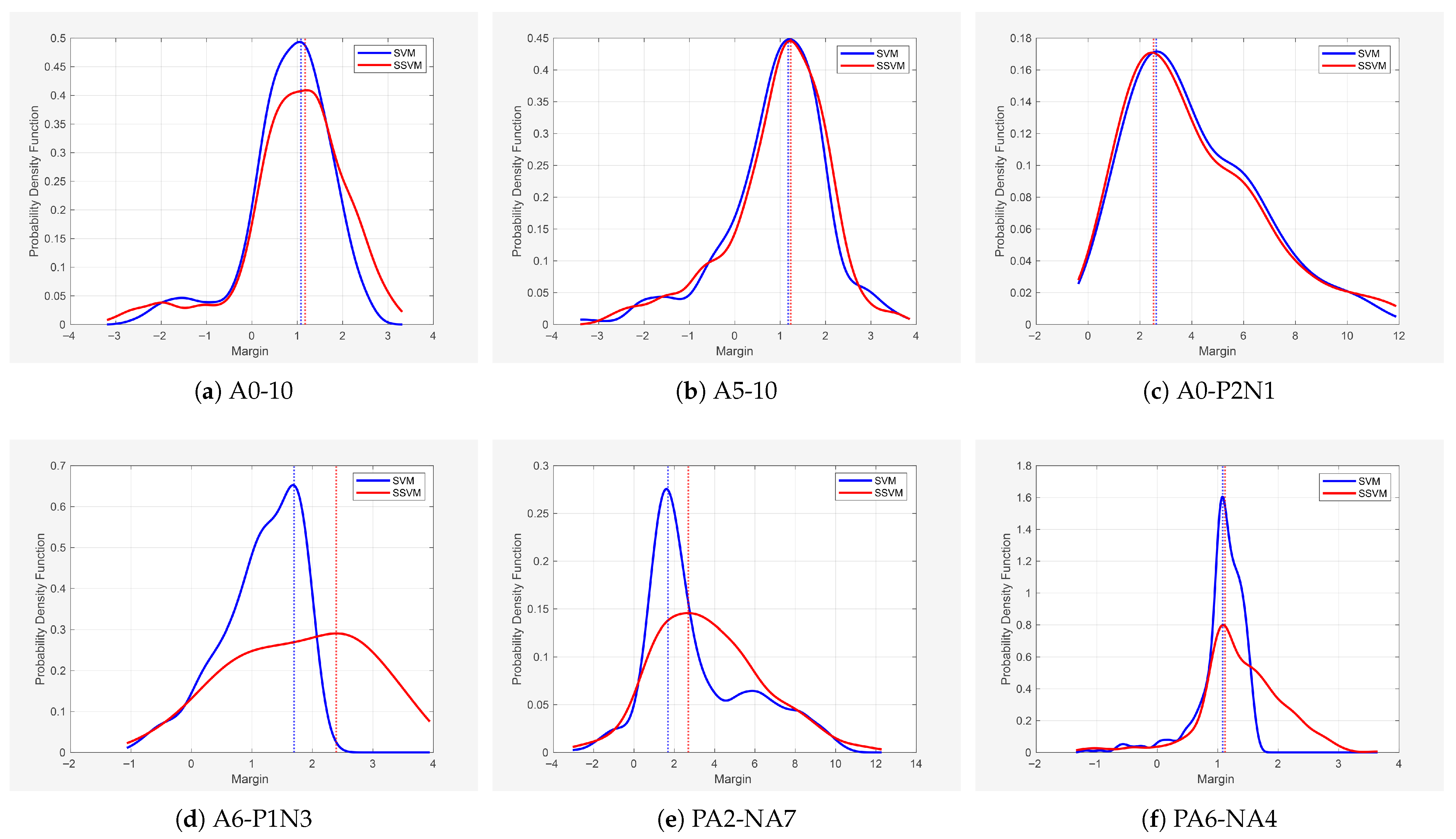
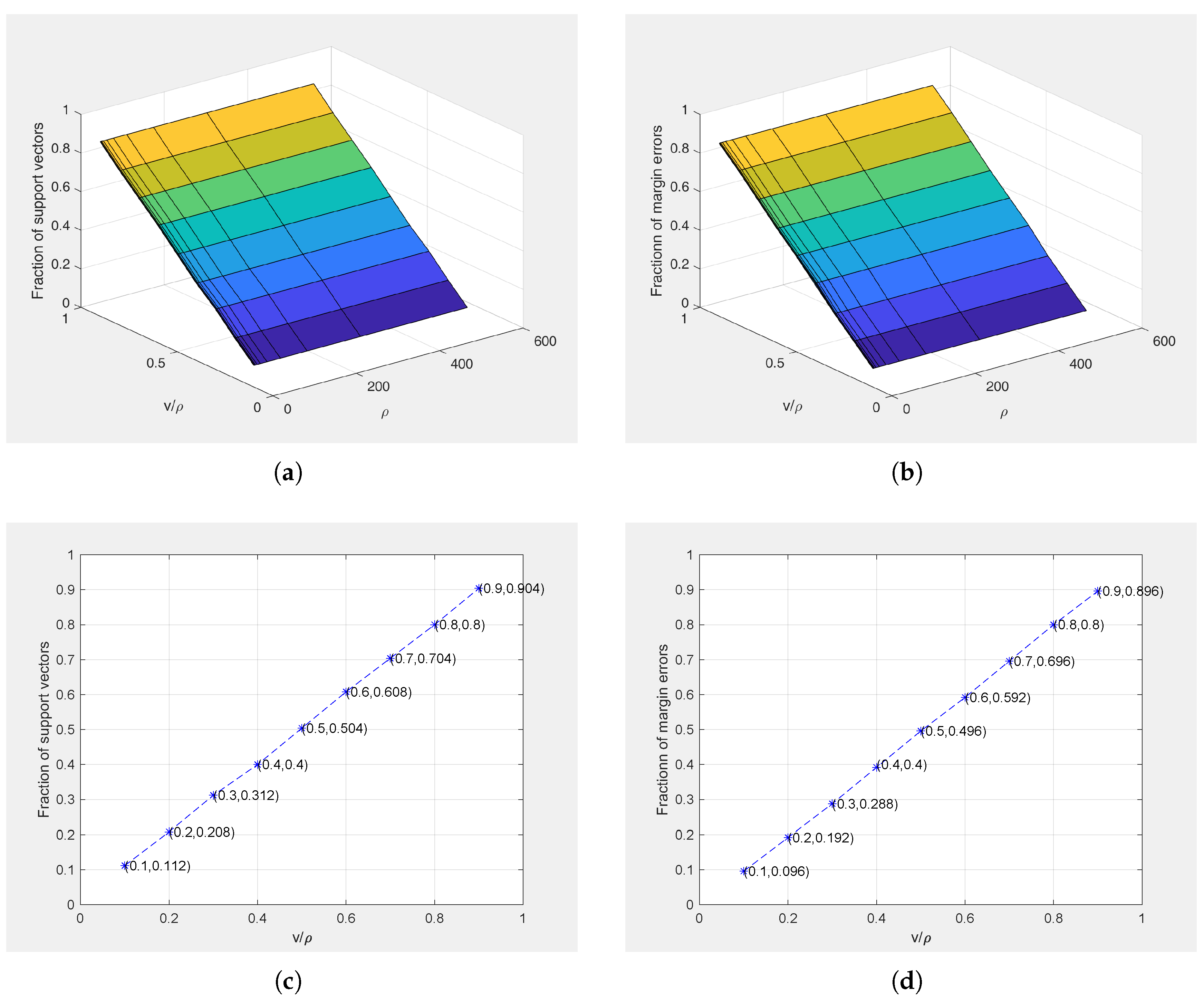
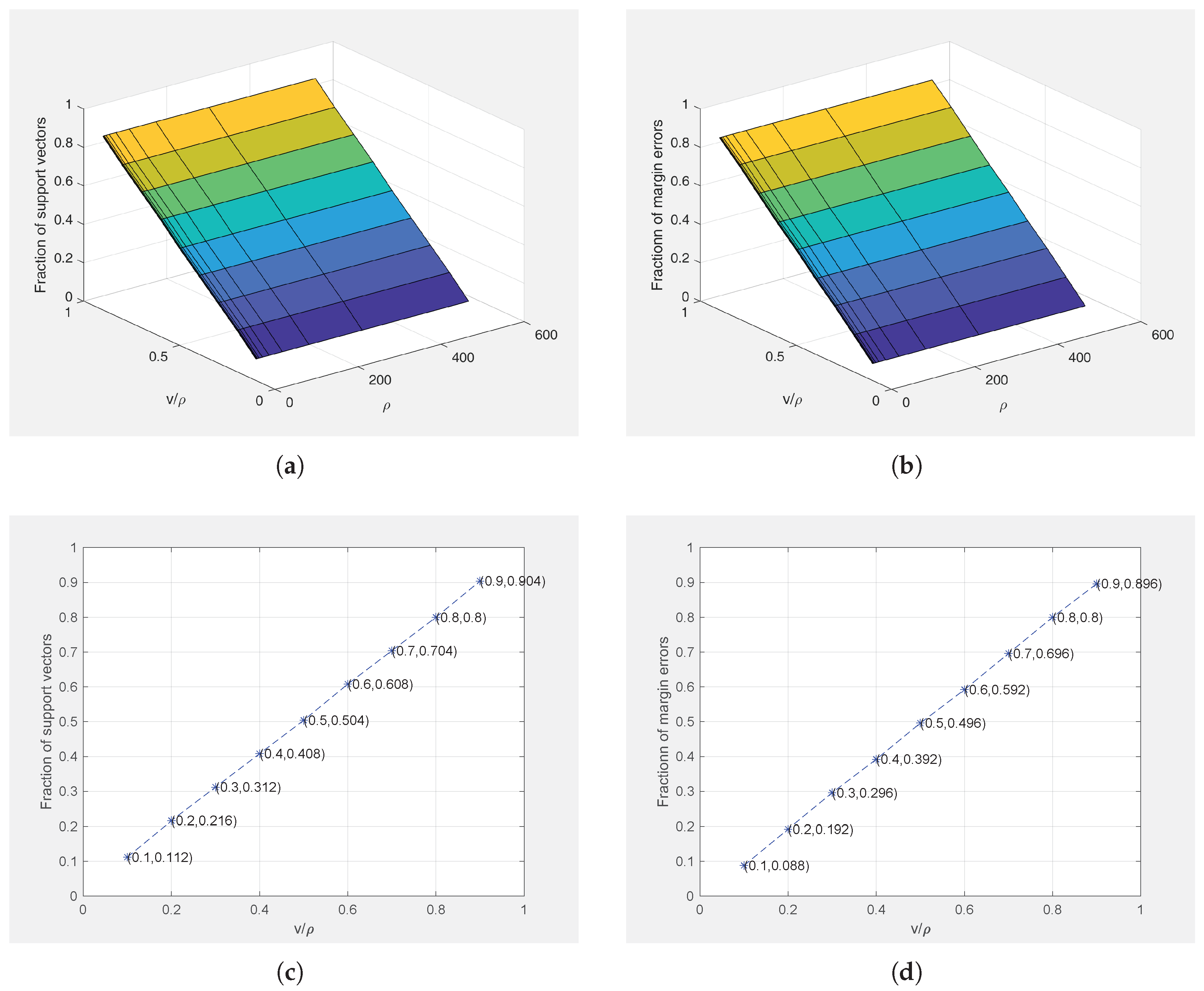
4.2.4. Theorem Verification
4.3. Benchmark Datasets
5. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SVM | Support Vector Machine |
| SSVM | Sparse SVM |
| TPMSVM | Twin Parametric Margin SVM |
| STPMSVM | Sparse TPMSVM |
| KKT | Karush–Kuhn–Tucker |
| QPP | Quadratic programming problem |
| LPP | Linear programming problem |
| Acc. | Accuracy |
| Num-SVs | Number of support vectors |
| Tr-time | Training time |
| Te-time | Testing time |
| Avg. SV-Reduction | Average percentage reduction in the number of support vectors |
| Std | Standard deviation |
| Med | Median |
References
- Shalev-Shwartz, S.; Ben-David, S. Understanding Machine Learning: From Theory to Algorithms; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Shawe-Taylor, J.; Cristianini, N. Kernel Methods for Pattern Analysis; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef]
- Cervantes, J.; Garcia-Lamont, F.; Rodríguez-Mazahua, L.; Lopez, A. A comprehensive survey on support vector machine classification: Applications, challenges and trends. Neurocomputing 2020, 408, 189–215. [Google Scholar] [CrossRef]
- Hao, P.Y. New support vector algorithms with parametric insensitive/margin model. Neural Netw. 2010, 23, 60–73. [Google Scholar] [CrossRef] [PubMed]
- Khemchandani, R.; Jayadeva; Chandra, S. Twin support vector machines for pattern classification. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 905–910. [Google Scholar] [CrossRef]
- Peng, X. TPMSVM: A novel twin parametric-margin support vector machine for pattern recognition. Pattern Recognit. 2011, 44, 2678–2692. [Google Scholar] [CrossRef]
- Tanveer, M.; Rajani, T.; Rastogi, R.; Shao, Y.H.; Ganaie, M.A. Comprehensive review on twin support vector machines. Ann. Oper. Res. 2024, 339, 1223–1268. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, L. Application of support vector machine algorithm in predicting the career development path of college students. Int. J. High Speed Electron. Syst. 2025, 2540230. [Google Scholar] [CrossRef]
- Chandra, M.A.; Bedi, S.S. Survey on SVM and their application in image classification. Int. J. Inf. Technol. 2021, 13, 1–11. [Google Scholar] [CrossRef]
- Zeng, S.; Chen, M.; Li, X.; Wu, Y. A financial distress prediction model based on sparse algorithm and support vector machine. Math. Probl. Eng. 2020, 2020, 5625271. [Google Scholar] [CrossRef]
- Madhu, B.; Rakesh, A.; Rao, K.S. A comparative study of support vector machine and artificial neural network for option price prediction. J. Comput. Commun. 2021, 9, 78–91. [Google Scholar] [CrossRef]
- Kok, Z.H.; Chua, L.S.; Aziz, N.A.; Ismail, W.I.W. Support vector machine in precision agriculture: A review. Comput. Electron. Agric. 2021, 191, 106546. [Google Scholar] [CrossRef]
- Abdullah, D.M.; Abdulazeez, A.M. Machine learning applications based on SVM classification: A review. Qubahan Acad. J. 2021, 1, 81–90. [Google Scholar] [CrossRef]
- Malashin, I.; Tynchenko, V.; Gantimurov, A.; Nelyub, V.; Borodulin, A. Support vector machines in polymer science: A review. Polymers 2025, 17, 491. [Google Scholar] [CrossRef]
- Khyathi, G.; Indumathi, K.P.; Jumana Hasin, A.; Lisa Flavin Jency, M.; Krishnaprakash, G.; Lisa, F.J.M. Support vector machines: A literature review on their application in analyzing mass data for public health. Cureus 2025, 17, e000000. [Google Scholar] [CrossRef]
- Yang, L.; Dong, H. Support vector machine with truncated pinball loss and its application in pattern recognition. Chemom. Intell. Lab. Syst. 2018, 177, 89–99. [Google Scholar] [CrossRef]
- De Leone, R.; Maggioni, F.; Spinelli, A. A multiclass robust twin parametric margin support vector machine with an application to vehicles emissions. In Proceedings of the International Conference on Machine Learning, Optimization, and Data Science, Grasmere, UK, 22–26 September 2023; Springer Nature: Cham, Switzerland, 2023; pp. 299–310. [Google Scholar]
- Wang, H.; Shao, Y. Fast truncated Huber loss SVM for large-scale classification. Knowl.-Based Syst. 2023, 260, 110074. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, H.; Li, W. Sparse and robust support vector machine with capped squared loss for large-scale pattern classification. Pattern Recognit. 2024, 153, 110544. [Google Scholar] [CrossRef]
- Sui, Y.; He, X.; Bai, Y. Implicit regularization in over-parameterized support vector machine. Adv. Neural Inf. Process. Syst. 2023, 36, 31943–31966. [Google Scholar]
- Moosaei, H.; Hladík, M. Sparse solution of least-squares twin multi-class support vector machine using ℓ0 and ℓp-norm for classification and feature selection. Neural Netw. 2023, 166, 471–486. [Google Scholar] [CrossRef]
- Tang, Q.; Li, G. Sparse L0-norm least squares support vector machine with feature selection. Inf. Sci. 2024, 670, 120591. [Google Scholar] [CrossRef]
- Li, N.; Zhang, H.H. Sparse learning with non-convex penalty in multi-classification. J. Data Sci. 2021, 19, 1–20. [Google Scholar] [CrossRef]
- Zhou, S. Sparse SVM for sufficient data reduction. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 5560–5571. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.; Li, Q. A majorization penalty method for SVM with sparse constraint. Optim. Methods Softw. 2023, 38, 474–494. [Google Scholar] [CrossRef]
- Zhu, J.; Rosset, S.; Hastie, T.; Tibshirani, R. 1-norm support vector machines. Adv. Neural Inf. Process. Syst. 2003, 16. [Google Scholar]
- Qu, S.; De Leone, R.; Huang, M. Sparse learning for linear twin parameter-margin support vector machine. In Proceedings of the 3rd Asia Conference on Algorithms, Computing and Machine Learning, Shanghai, China, 22–24 March 2024; pp. 50–55. [Google Scholar]
- Qu, S.; Huang, M.; De Leone, R.; Maggioni, F.; Spinelli, A. An efficient sparse twin parametric insensitive support vector regression model. Mathematics 2025, 13, 2206. [Google Scholar] [CrossRef]
- Wolfe, P. A duality theorem for non-linear programming. Q. Appl. Math. 1961, 19, 239–244. [Google Scholar] [CrossRef]

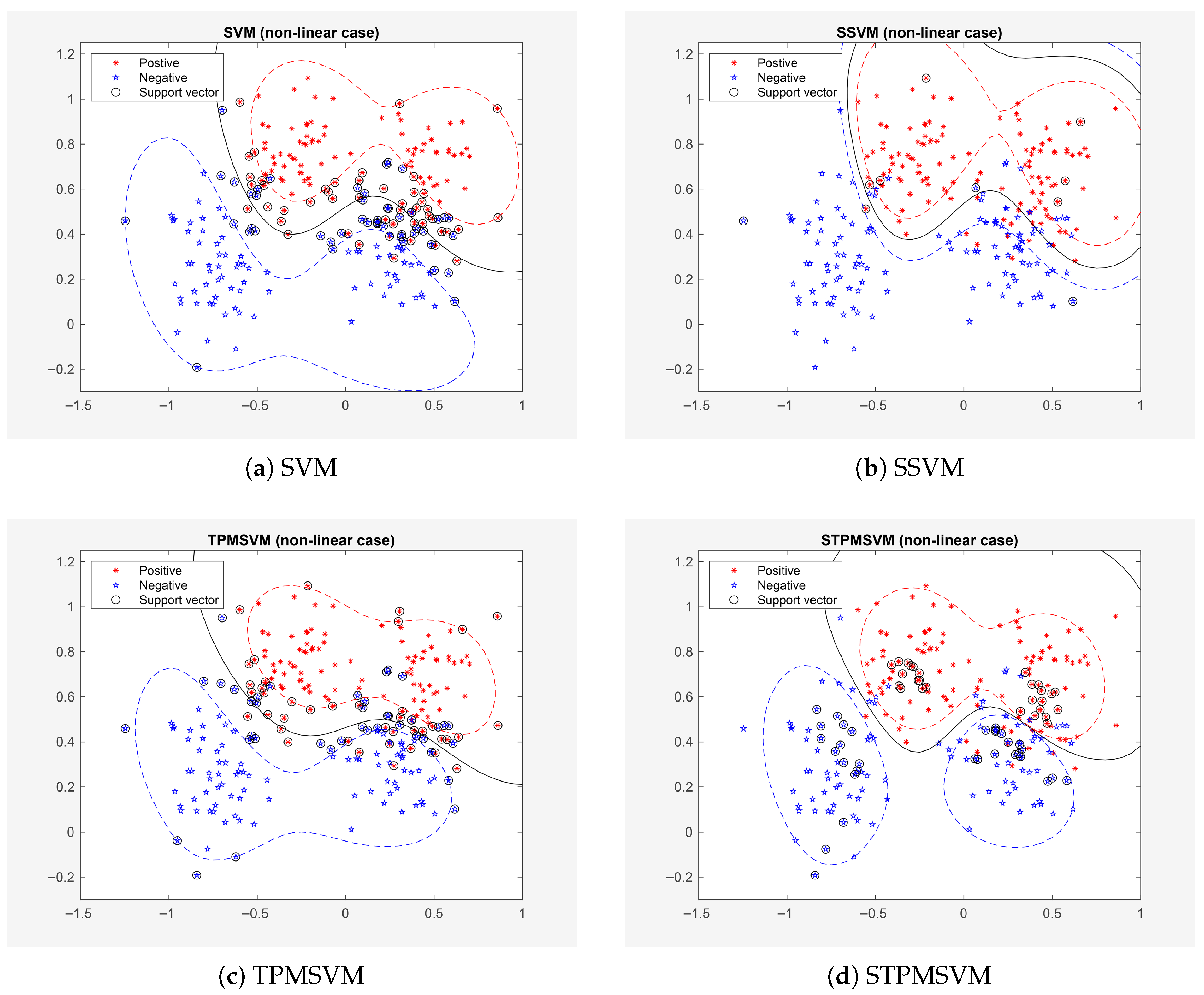


| Model | Variable Penalized | Sparsity Level | Optimization |
|---|---|---|---|
| -norm SVM | Weight vector | Feature level | Single LPP with a objective |
| SSVM | Dual variable | Support vector level | Single LPP with a standard linear objective |
| STPMSVM | Dual variables | Support vector level | Two LPPs with standard linear objectives |
| Notation | Description |
|---|---|
| The number of elements in a index set I | |
| The index set of positive/negative samples, | |
| n | The dimension of samples |
| , the positive samples matrix for the TPMSVM and STPMSVM models | |
| , the negative samples matrix for the TPMSVM and STPMSVM models | |
| e | The vector of opportune dimensions with all components equal to 1 |
| The mapping function from the original input space to the feature space | |
| , the positive samples mapping matrix for the TPMSVM and STPMSVM models | |
| , the negative samples mapping matrix for the TPMSVM and STPMSVM models | |
| The inner product of two vectors |
| Kernel Type | Item | SVM | SSVM | TPMSVM | STPMSVM |
|---|---|---|---|---|---|
| Linear kernel | Acc.(%) | 89.70 | 89.70 | 88.80 | 88.80 |
| Num-SVs | 110 | 14 (↓87.27%) | 83 | 17 (↓79.52%) | |
| Tr-time(s) | 0.2040 | 0.1929 | 0.3296 | 0.3171 | |
| Te-time(s) | 0.0325 | 0.0072 | 0.0744 | 0.0142 | |
| Gaussian kernel | Acc.(%) | 90.40 | 90.60 | 91.20 | 91.40 |
| Num-SVs | 96 | 10 (↓89.58%) | 82 | 57 (↓30.49%) | |
| Tr-time(s) | 0.2316 | 0.2087 | 0.4073 | 0.3140 | |
| Te-time(s) | 0.0261 | 0.0090 | 0.0677 | 0.0509 |
| Dataset | SVM | SSVM | TPMSVM | STPMSVM |
|---|---|---|---|---|
| Acc.(%) | Acc.(%) | Acc.(%) | Acc.(%) | |
| Num-SVs | Num-SVs | Num-SVs | Num-SVs | |
| Tr-Time(s) | Tr-Time(s) | Tr-Time(s) | Tr-Time(s) | |
| Te-Time(s) | Te-Time(s) | Te-Time(s) | Te-Time(s) | |
| A0 | 98.50 ± 2.42 | 98.50 ± 3.37 | 99.50 ± 1.58 | 99.50 ± 0.79 |
| 43.20 ± 0.23 | 16.10 ± 0.74 | 25.20 ± 1.81 | 21.90 ± 1.37 | |
| 0.2312 ± 0.0238 | 0.1949 ± 0.0073 | 0.3808 ±0.0160 | 0.3158 ± 0.0207 | |
| 0.0006 ± 0.0002 | 0.0005 ± 0.0002 | 0.0009 ±0.0004 | 0.0008 ± 0.0003 | |
| A1 | 99.00 ± 2.11 | 99.00 ± 2.11 | 99.50 ± 1.58 | 99.00 ± 2.11 |
| 86.10 ± 1.52 | 27.20 ± 0.92 | 22.10 ± 1.79 | 21.60 ± 1.17 | |
| 0.2189 ± 0.0150 | 0.1893 ± 0.0135 | 0.3169 ± 0.0116 | 0.3169 ± 0.0116 | |
| 0.0009 ± 0.0002 | 0.0003 ± 0.0001 | 0.0010 ±0.0003 | 0.0008 ± 0.0003 | |
| A2 | 99.00 ± 3.16 | 99.00 ± 3.16 | 98.50 ± 3.37 | 99.00 ± 3.16 |
| 118.10 ± 1.85 | 37.90 ± 1.29 | 23.20 ± 2.49 | 22.20 ± 0.92 | |
| 0.2257 ± 0.0113 | 0.1899 ± 0.0062 | 0.3973 ± 0.0925 | 0.3448 ± 0.0325 | |
| 0.0012 ± 0.0002 | 0.0004 ± 0.0003 | 0.0010 ±0.0002 | 0.0009 ± 0.0002 | |
| A3 | 99.00 ± 2.11 | 99.50 ± 1.58 | 99.00 ± 2.11 | 99.00 ± 2.11 |
| 34.60 ± 1.58 | 26.70 ± 0.95 | 24.20 ± 1.81 | 22.80 ± 1.93 | |
| 0.2259 ± 0.0194 | 0.1895 ± 0.0077 | 0.4156 ± 0.0319 | 0.3142 ± 0.0092 | |
| 0.0005 ± 0.0002 | 0.0005 ± 0.0002 | 0.0010 ±0.0003 | 0.0007 ± 0.0002 | |
| A4 | 98.00 ± 2.58 | 98.50 ± 2.42 | 98.50 ± 2.42 | 98.50 ± 2.42 |
| 64.60 ± 1.26 | 24.40 ± 0.70 | 24.60 ± 2.01 | 22.30 ± 1.70 | |
| 0.2277 ± 0.0150 | 0.1917 ± 0.0116 | 0.4100 ± 0.0647 | 0.3230 ± 0.0105 | |
| 0.0006 ± 0.0001 | 0.0004 ± 0.0002 | 0.0011 ±0.0002 | 0.0008 ± 0.0002 | |
| A5 | 96.50 ± 4.12 | 96.50 ± 4.12 | 96.00 ± 5.16 | 96.00 ± 5.16 |
| 122.80 ± 2.04 | 23.90 ± 0.88 | 22.70 ± 0.95 | 20.80 ± 0.63 | |
| 0.2169 ± 0.0133 | 0.1965 ± 0.0125 | 0.3781 ± 0.0200 | 0.3373 ± 0.0453 | |
| 0.0011 ± 0.0001 | 0.0005 ± 0.0002 | 0.0010 ±0.0005 | 0.0007 ± 0.0003 | |
| A6 | 95.50 ± 3.69 | 95.00 ± 6.24 | 93.50 ± 5.80 | 93.50 ± 5.80 |
| 27.60 ± 2.55 | 24.50 ± 1.43 | 25.80 ± 1.32 | 21.60 ± 0.70 | |
| 0.2667 ± 0.0209 | 0.1926 ± 0.0056 | 0.3871 ± 0.0436 | 0.3111 ± 0.0134 | |
| 0.0004 ± 0.0002 | 0.0004 ± 0.0004 | 0.0011 ±0.0003 | 0.0009 ± 0.0002 | |
| A7 | 88.50 ± 9.14 | 86.50 ± 10.01 | 88.50 ± 9.14 | 89.50 ± 7.98 |
| 45.30 ± 3.47 | 33.50 ± 1.27 | 25.50 ± 2.32 | 22.70 ± 1.25 | |
| 0.2401 ± 0.0297 | 0.1936 ± 0.0095 | 0.3878 ± 0.0084 | 0.3860 ± 0.0059 | |
| 0.0005 ± 0.0002 | 0.0005 ± 0.0002 | 0.0010 ±0.0005 | 0.0010 ± 0.0004 | |
| A8 | 80.50 ± 9.26 | 80.50 ± 8.32 | 79.50 ± 6.43 | 80.50 ± 9.56 |
| 130.70 ± 2.26 | 21.50 ± 0.53 | 29.00 ± 2.45 | 26.70 ± 3.56 | |
| 0.2200 ± 0.0148 | 0.2018 ± 0.0175 | 0.3972 ± 0.0212 | 0.3100 ± 0.0130 | |
| 0.0010 ± 0.0002 | 0.0006 ± 0.0002 | 0.0010 ±0.0001 | 0.0009 ± 0.0001 | |
| A9 | 74.00 ± 7.38 | 73.50 ± 8.51 | 74.50 ± 8.32 | 75.50 ± 8.32 |
| 96.10 ± 3.51 | 10.50 ± 0.97 | 70.10 ± 12.00 | 30.10 ± 5.74 | |
| 0.2245 ± 0.0192 | 0.1974 ± 0.0145 | 0.4160 ± 0.0765 | 0.3088 ± 0.0099 | |
| 0.0008 ± 0.0002 | 0.0003 ± 0.0001 | 0.0013 ±0.0008 | 0.0010 ± 0.0002 | |
| Avg. SV-Reduction (%) | — | 57.46 | — | 13.54 |
| p-value/r (Acc.) | a 0.7500/0.1008 | c 0.5313/0.4168 | b 0.1875/0.4168 | |
| p-value/r (Num-SVs) | a,* 0.0488/0.6230 (SSVM < SVM) | c 0.2324/0.3776 | b,* 0.0020/0.9794 (STPMSVM < TPMSVM) | |
| p-value/r (Tr-time) | a,* 0.0488/0.6230 (SSVM < SVM) | c 0.2324/0.3776 | b,* 0.0020/0.9794 (STPMSVM < TPMSVM) | |
| p-value/r (Te-time) | a,* 0.0156/0.7645 (SSVM < SVM) | c,* 0.0020/0.9794 (SSVM < STPMSVM) | b,* 0.0039/0.9125 (STPMSVM < TPMSVM) |
| Dataset | SVM | SSVM | TPMSVM | STPMSVM |
|---|---|---|---|---|
| Acc.(%) | Acc.(%) | Acc.(%) | Acc.(%) | |
| Num-SVs | Num-SVs | Num-SVs | Num-SVs | |
| Tr-Time(s) | Tr-Time(s) | Tr-Time(s) | Tr-Time(s) | |
| Te-Time(s) | Te-Time(s) | Te-Time(s) | Te-Time(s) | |
| A0 | 98.50 ± 2.42 | 98.50 ± 3.37 | 99.50 ± 1.58 | 99.50 ± 0.79 |
| 43.20 ± 0.23 | 16.10 ± 0.74 | 25.20 ± 1.81 | 21.90 ± 1.37 | |
| 0.2312 ± 0.0238 | 0.1949 ± 0.0073 | 0.3808 ±0.0160 | 0.3158 ± 0.0207 | |
| 0.0006 ± 0.0002 | 0.0005 ± 0.0002 | 0.0009 ±0.0004 | 0.0008 ± 0.0003 | |
| 1st | 99.50 ± 1.58 | 98.00 ± 2.58 | 99.50 ± 1.58 | 100.00 ± 0 |
| 48.20 ± 1.03 | 37.50 ± 0.85 | 40.20 ± 1.87 | 25.60 ± 0.70 | |
| 0.2183 ± 0.0092 | 0.1933 ± 0.0107 | 0.3785 ± 0.0260 | 0.2964 ± 0.0107 | |
| 0.0006 ± 0.0003 | 0.0003 ± 0.0002 | 0.0013 ± 0.0007 | 0.0010 ± 0.0002 | |
| 2nd | 99.00 ± 2.11 | 99.50 ± 1.58 | 100.00 ± 0 | 99.50 ± 1.58 |
| 95.70 ± 1.83 | 30.00 ± 1.15 | 25.20 ± 2.66 | 22.30 ± 1.57 | |
| 0.2364 ± 0.0120 | 0.1869 ± 0.0091 | 0.4617 ± 0.0295 | 0.3005 ± 0.0131 | |
| 0.0010 ± 0.0002 | 0.0004 ± 0.0002 | 0.0012 ±0.0004 | 0.0008 ± 0.0003 | |
| 3rd | 100.00 ± 0 | 100.00 ± 0 | 99.00 ± 1.58 | 100.00 ± 0 |
| 86.70 ± 1.89 | 25.40 ± 0.97 | 41.60 ± 0.97 | 22.50 ± 1.51 | |
| 0.2313 ± 0.0151 | 0.1930 ± 0.0134 | 0.3657 ± 0.0078 | 0.2915 ± 0.0120 | |
| 0.0009 ± 0.0002 | 0.0004 ± 0.0001 | 0.0011 ±0.0002 | 0.0009 ± 0.0001 | |
| 4th | 99.00 ± 3.16 | 100.00 ± 0 | 100.00 ± 0 | 100.00 ± 0 |
| 87.80 ± 2.35 | 17.80 ± 0.92 | 26.30 ± 1.95 | 21.20 ± 0.92 | |
| 0.2526 ± 0.0268 | 0.2353 ± 0.0169 | 0.3748 ± 0.0239 | 0.3015 ± 0.0097 | |
| 0.0011 ± 0.0003 | 0.0004 ± 0.0001 | 0.0011 ± 0.0002 | 0.0009 ± 0.0002 | |
| 5th | 98.00 ± 3.50 | 99.00 ± 3.37 | 99.50 ± 1.58 | 99.50 ± 1.58 |
| 87.60 ± 1.96 | 17.40 ± 0.52 | 23.20 ± 1.55 | 22.10 ± 1.37 | |
| 0.2449 ± 0.0187 | 0.2417 ± 0.0177 | 0.3672 ±0.0153 | 0.2975 ± 0.0128 | |
| 0.0010 ± 0.0001 | 0.0005 ± 0.0002 | 0.0010 ±0.0002 | 0.0009 ± 0.0001 | |
| 6th | 99.00 ± 2.11 | 99.50 ± 1.58 | 99.50 ± 1.58 | 99.50 ± 1.58 |
| 23.70 ± 0.67 | 18.60 ± 1.07 | 23.00 ± 2.11 | 22.40 ± 1.26 | |
| 0.2367 ± 0.0145 | 0.2002 ± 0.0090 | 0.3619 ± 0.0094 | 0.2872 ± 0.0101 | |
| 0.0004 ± 0.0003 | 0.0003 ± 0.0002 | 0.0010 ± 0.0002 | 0.0010 ± 0.0002 | |
| 7th | 100.00 ± 0 | 100.00 ± 0 | 100.00 ± 0 | 100.00 ± 0 |
| 32.50 ± 0.85 | 21.20 ± 0.79 | 25.30 ± 3.40 | 22.90 ± 1.10 | |
| 0.2615 ± 0.0506 | 0.1903 ± 0.0088 | 0.3841 ± 0.0569 | 0.2938 ± 0.0115 | |
| 0.0005 ± 0.0002 | 0.0003 ± 0.0001 | 0.0010 ±0.0002 | 0.0008 ± 0.0003 | |
| 8th | 98.00 ± 3.50 | 99.00 ± 3.16 | 98.50 ± 3.37 | 98.50 ± 3.37 |
| 86.50 ± 1.84 | 25.70 ± 1.06 | 23.40 ± 1.07 | 25.60 ± 0.97 | |
| 0.2435 ± 0.0221 | 0.2068 ± 0.0070 | 0.3658 ± 0.0069 | 0.3058 ± 0.0184 | |
| 0.0010 ± 0.0002 | 0.0004 ± 0.0002 | 0.0010 ±0.0004 | 0.0008 ± 0.0002 | |
| 9th | 99.50 ± 1.58 | 99.50 ± 1.58 | 99.50 ± 1.58 | 99.50 ± 1.58 |
| 83.30 ± 1.06 | 25.90 ± 0.74 | 21.80 ± 1.62 | 21.40 ± 1.26 | |
| 0.2432 ± 0.0124 | 0.2219 ± 0.0340 | 0.3911 ± 0.0563 | 0.2975 ± 0.0091 | |
| 0.0010 ± 0.0002 | 0.0004 ± 0.0002 | 0.0011 ±0.0003 | 0.0008 ± 0.0003 | |
| 10th | 97.00 ± 4.83 | 97.00 ± 4.83 | 98.50 ± 2.42 | 98.00 ± 3.50 |
| 72.30 ± 1.89 | 39.00 ± 0.94 | 24.90 ± 1.79 | 22.20 ± 1.93 | |
| 0.2139 ± 0.0092 | 0.2138 ± 0.0120 | 0.3918 ± 0.0479 | 0.3098 ± 0.0169 | |
| 0.0006 ± 0.0001 | 0.0004 ± 0.0002 | 0.0011 ±0.0002 | 0.0006 ± 0.0002 | |
| 11th | 98.00 ± 2.58 | 99.00 ± 2.11 | 99.50 ± 1.58 | 99.50 ± 1.58 |
| 113.60 ± 1.26 | 28.00 ± 0.82 | 27.60 ± 1.58 | 21.50 ± 1.18 | |
| 0.2110 ± 0.0119 | 0.2110 ± 0.0146 | 0.3911 ± 0.0228 | 0.2990 ± 0.0195 | |
| 0.0008 ± 0.0003 | 0.0003 ± 0.0002 | 0.0012 ±0.0003 | 0.0012 ± 0.0003 | |
| 12th | 97.00 ± 4.22 | 98.50 ± 2.42 | 99.00 ± 2.11 | 98.00 ± 2.58 |
| 85.20 ± 1.32 | 25.60 ± 0.97 | 23.10 ± 1.37 | 22.60 ± 1.96 | |
| 0.2194 ± 0.0170 | 0.1961 ± 0.0144 | 0.4142 ± 0.0349 | 0.3030 ± 0.0200 | |
| 0.0007 ± 0.0003 | 0.0004 ± 0.0002 | 0.0011 ±0.0003 | 0.0010 ± 0.0002 | |
| 13th | 97.50 ± 2.64 | 99.50 ± 1.58 | 99.00 ± 2.11 | 98.50 ± 2.42 |
| 94.10 ± 1.66 | 7.70 ± 0.67 | 24.90 ± 1.73 | 21.10 ± 0.88 | |
| 0.2286 ± 0.0183 | 0.2040 ± 0.0125 | 0.4126 ± 0.0307 | 0.3095 ± 0.0226 | |
| 0.0008 ± 0.0002 | 0.0004 ± 0.0002 | 0.0011 ±0.0004 | 0.0009 ± 0.0002 | |
| 14th | 96.00 ± 3.94 | 98.00 ± 2.58 | 99.50 ± 1.58 | 99.00 ± 2.11 |
| 117.60 ± 1.58 | 39.90 ± 0.74 | 57.50 ± 1.43 | 23.10 ± 1.79 | |
| 0.2349 ± 0.0189 | 0.2070 ± 0.0124 | 0.4410 ± 0.0532 | 0.2958 ± 0.0138 | |
| 0.0008 ± 0.0002 | 0.0005 ± 0.0002 | 0.0014 ±0.0009 | 0.0011 ± 0.0002 | |
| 15th | 99.50 ± 1.58 | 100.00 ± 0 | 99.00 ± 3.16 | 99.50 ± 1.58 |
| 90.10 ± 1.52 | 39.90 ± 0.88 | 23.60 ± 2.37 | 23.20 ± 1.48 | |
| 0.2233 ± 0.0141 | 0.1990 ± 0.0048 | 0.4393 ± 0.0446 | 0.3031 ± 0.0110 | |
| 0.0008 ± 0.0003 | 0.0004 ± 0.0002 | 0.0010 ±0.0002 | 0.0010 ± 0.0002 | |
| Mean/Std/Med(Acc.) | 98.47/1.18/98.75 | 99.06/0.87/99.25 | 99.34/0.47/99.50 | 99.28/0.68/99.50 |
| Mean/Std/Med(Num-SVs) | 78.32/27.32/87.15 | 25.98/9.52/25.65 | 28.55/9.65/25.05 | 22.60/1.33/22.35 |
| Mean/Std/Med(Tr-ime) | 0.2332/0.0140/0.2333 | 0.2054/0.0162/0.2021 | 0.3952/0.0303/0.3876 | 0.3000/0.0080/0.2990 |
| Mean/Std/Med(Te-ime) | 0.0008/0.0002/0.0008 | 0.0004/0.0000/0.0004 | 0.0011/0.0001/0.0011 | 0.0009/0.0001/0.0009 |
| Avg. SV-Reduction (%) | — | 61.65 | — | 15.46 |
| p-value/r (Acc.) | a,* 0.0254/0.5589 (SSVM > SVM) | c 0.3086/0.2545 | b 0.7891/0.0669 | |
| p-value/r (Num-SVs) | a,* 0.0004/0.8790 (SSVM < SVM) | c 0.1960/0.3232 | b,* 0.0013/0.8016 (STPMSVM < TPMSVM) | |
| p-value/r (Tr-time) | a,* 0.0001/0.9998 (SSVM < SVM) | c,* 0.0004/0.8790 (SSVM < STPMSVM) | b,* 0.0004/0.8790 (STPMSVM < TPMSVM) | |
| p-value/r (Te-time) | a,* 0.0004/0.8813 (SSVM < SVM) | c,* 0.0004/0.8827 (SSVM < STPMSVM) | b,* 0.0004/0.9171 (STPMSVM < TPMSVM) |
| Dataset | SVM | SSVM | TPMSVM | STPMSVM |
|---|---|---|---|---|
| Acc.(%) | Acc.(%) | Acc.(%) | Acc.(%) | |
| Num-SVs | Num-SVs | Num-SVs | Num-SVs | |
| Tr-Time(s) | Tr-Time(s) | Tr-Time(s) | Tr-Time(s) | |
| Te-Time(s) | Te-Time(s) | Te-Time(s) | Te-Time(s) | |
| A7 | 88.50 ± 9.14 | 86.50 ± 10.01 | 88.50 ± 9.14 | 89.50 ± 7.98 |
| 45.30 ± 3.47 | 33.50 ± 1.27 | 25.50 ± 2.32 | 22.70 ± 1.25 | |
| 0.2401 ± 0.0297 | 0.1936 ± 0.0095 | 0.3878 ± 0.0084 | 0.3860 ± 0.0059 | |
| 0.0005 ± 0.0002 | 0.0005 ± 0.0002 | 0.0010 ±0.0005 | 0.0010 ± 0.0004 | |
| 1st | 92.00 ± 4.83 | 91.00 ± 4.59 | 91.50 ± 4.47 | 92.50 ± 5.40 |
| 92.00 ± 1.94 | 34.40 ± 1.26 | 58.00 ± 1.89 | 39.60 ± 1.07 | |
| 0.2543 ± 0.0177 | 0.1834 ± 0.0077 | 0.3597 ± 0.0149 | 0.2934 ± 0.0068 | |
| 0.0010 ± 0.0003 | 0.0003 ± 0.0002 | 0.0012 ±0.0002 | 0.0010 ± 0.0002 | |
| 2nd | 93.50 ± 6.26 | 92.50 ± 5.89 | 93.50 ± 5.80 | 94.00 ± 6.15 |
| 49.60 ± 1.78 | 29.90 ± 0.74 | 23.50 ± 1.58 | 22.80 ± 0.92 | |
| 0.2548 ± 0.0169 | 0.1870 ± 0.0097 | 0.3804 ± 0.0288 | 0.3768 ± 0.0132 | |
| 0.0007 ± 0.0003 | 0.0002 ± 0.0002 | 0.0010 ±0.0002 | 0.0008 ± 0.0002 | |
| 3rd | 89.00 ± 7.75 | 90.00 ± 6.67 | 89.50 ± 6.43 | 90.00 ± 6.67 |
| 49.10 ± 2.02 | 18.80 ± 0.63 | 24.60 ± 2.17 | 21.50 ± 1.58 | |
| 0.2092 ± 0.0204 | 0.1716 ± 0.0094 | 0.4350 ± 0.0643 | 0.3967 ± 0.0095 | |
| 0.0005 ± 0.0002 | 0.0002 ± 0.0001 | 0.0011 ±0.0003 | 0.0010 ± 0.0003 | |
| 4th | 90.00 ± 6.24 | 90.00 ± 6.24 | 89.00 ± 6.99 | 89.00 ± 5.16 |
| 101.20 ± 2.15 | 6.30 ± 0.67 | 62.60 ± 1.43 | 23.70 ± 2.50 | |
| 0.2095 ± 0.0089 | 0.2002 ± 0.0269 | 0.3652 ± 0.0102 | 0.2950 ± 0.0074 | |
| 0.0008 ± 0.0002 | 0.0004 ± 0.0003 | 0.0012 ±0.0003 | 0.0007 ± 0.0003 | |
| 5th | 88.50 ± 5.80 | 88.00 ± 7.53 | 87.00 ± 5.87 | 87.50 ± 7.17 |
| 50.90 ± 2.85 | 33.30 ± 0.82 | 50.20 ± 2.39 | 24.90 ± 3.00 | |
| 0.2387 ± 0.0179 | 0.1787 ± 0.0065 | 0.3777 ± 0.0313 | 0.3053 ± 0.0219 | |
| 0.0005 ± 0.0002 | 0.0005 ± 0.0002 | 0.0011 ±0.0001 | 0.0010 ± 0.0002 | |
| 6th | 90.00 ± 6.24 | 90.00 ± 5.77 | 89.00 ± 5.68 | 90.50 ± 6.85 |
| 128.50 ± 1.72 | 8.70 ± 0.95 | 23.30 ± 1.89 | 25.30 ± 1.70 | |
| 0.2219 ± 0.0278 | 0.1708 ± 0.0066 | 0.3692 ± 0.0105 | 0.3088 ± 0.0121 | |
| 0.0011 ± 0.0003 | 0.0006 ± 0.0002 | 0.0011 ±0.0002 | 0.0009 ± 0.0003 | |
| 7th | 92.50 ± 5.40 | 91.50 ± 5.80 | 91.00 ± 5.16 | 92.00 ± 5.87 |
| 83.90 ± 2.13 | 19.10 ± 0.57 | 22.80 ± 2.20 | 22.70 ± 1.77 | |
| 0.2237 ± 0.0132 | 0.1772 ± 0.0130 | 0.3944 ± 0.0322 | 0.3794 ± 0.0163 | |
| 0.0007 ± 0.0001 | 0.0005 ± 0.0001 | 0.0010 ±0.0002 | 0.0008 ± 0.0005 | |
| 8th | 89.50 ± 5.99 | 88.00 ± 7.15 | 91.50 ± 5.30 | 91.00 ± 6.15 |
| 103.30 ± 1.83 | 30.30 ± 0.95 | 23.20 ± 1.81 | 23.80 ± 2.15 | |
| 0.2140 ± 0.0152 | 0.1748 ± 0.0126 | 0.3890 ± 0.0305 | 0.3701 ± 0.0404 | |
| 0.0008 ± 0.0002 | 0.0003 ± 0.0002 | 0.0010 ±0.0003 | 0.0008 ± 0.0004 | |
| 9th | 93.00 ± 4.22 | 93.50 ± 4.47 | 92.50 ± 4.25 | 92.00 ± 4.22 |
| 45.30 ± 2.45 | 27.20 ± 1.03 | 25.00 ± 2.31 | 21.70 ± 1.16 | |
| 0.2138 ± 0.0113 | 0.1785 ± 0.0085 | 0.3855 ± 0.0218 | 0.2964 ± 0.0115 | |
| 0.0005 ± 0.0002 | 0.0004 ± 0.0002 | 0.0010 ±0.0003 | 0.0010 ± 0.0001 | |
| 10th | 89.50 ± 9.85 | 88.50 ± 8.18 | 88.50 ± 10.55 | 90.00 ± 9.43 |
| 124.30 ± 2.83 | 15.80 ± 1.14 | 39.50 ± 0.85 | 26.40 ± 4.58 | |
| 0.2131 ± 0.0152 | 0.1769 ± 0.0087 | 0.4439 ± 0.0477 | 0.2923 ± 0.0072 | |
| 0.0010 ± 0.0002 | 0.0003 ± 0.0001 | 0.0012 ±0.0004 | 0.0008 ± 0.0001 | |
| 11th | 91.50 ± 4.12 | 90.50 ± 4.38 | 92.50 ± 4.86 | 91.00 ± 5.16 |
| 115.90 ± 1.29 | 5.40 ± 0.70 | 25.90 ± 1.52 | 22.70 ± 1.83 | |
| 0.2479 ± 0.0158 | 0.1943 ± 0.0334 | 0.3782 ± 0.0163 | 0.2994 ± 0.0228 | |
| 0.0011 ± 0.0002 | 0.0003 ± 0.0002 | 0.0011 ±0.0002 | 0.0011 ± 0.0003 | |
| 12th | 90.00 ± 7.45 | 89.50 ± 7.25 | 88.50 ± 9.44 | 91.00 ± 6.58 |
| 57.00 ± 2.83 | 12.00 ± 0.67 | 29.10 ± 1.45 | 22.60 ± 1.84 | |
| 0.2439 ± 0.0189 | 0.2354 ± 0.0161 | 0.3731 ± 0.0193 | 0.2996 ± 0.0115 | |
| 0.0007 ± 0.0002 | 0.0003 ± 0.0002 | 0.0010 ±0.0002 | 0.0009 ± 0.0002 | |
| 13th | 88.50 ± 5.30 | 87.00 ± 5.37 | 88.50 ± 4.74 | 88.50 ± 4.74 |
| 81.40 ± 2.07 | 9.20 ± 0.92 | 21.90 ± 1.37 | 22.20 ± 1.32 | |
| 0.2224 ± 0.0132 | 0.1848 ± 0.0085 | 0.3605 ± 0.0130 | 0.2977 ± 0.0156 | |
| 0.0007 ± 0.0001 | 0.0003 ± 0.0002 | 0.0011 ±0.0002 | 0.0009 ± 0.0003 | |
| 14th | 88.00 ± 6.32 | 90.50 ± 4.38 | 90.50 ± 4.38 | 88.50 ± 6.69 |
| 48.00 ± 2.75 | 28.70 ± 0.82 | 24.50 ± 1.18 | 22.50 ± 1.08 | |
| 0.2761 ± 0.0282 | 0.1878 ± 0.0081 | 0.3787 ± 0.0312 | 0.3668 ± 0.0620 | |
| 0.0006 ± 0.0003 | 0.0002 ± 0.0001 | 0.0011 ±0.0002 | 0.0010 ± 0.0003 | |
| 15th | 89.50 ± 5.50 | 89.50 ± 8.64 | 89.00 ± 8.43 | 90.00 ± 5.27 |
| 117.90 ± 2.33 | 19.20 ± 1.23 | 40.00 ± 2.40 | 26.40 ± 1.71 | |
| 0.2206 ± 0.0147 | 0.1965 ± 0.0068 | 0.3885 ± 0.0392 | 0.2967 ± 0.0083 | |
| 0.0009 ± 0.0002 | 0.0004 ± 0.0002 | 0.0012 ±0.0002 | 0.0010 ± 0.0002 | |
| Mean/Std/Med(Acc.) | 90.22/1.74/89.75 | 89.78/1.89/90 | 89.91/2.03/89.25 | 90.53/1.64/90.50 |
| Mean/Std/Med(Num-SVs) | 80.85/31.48/82.56 | 20.74/10.39/19.15 | 33.13/13.17/25.70 | 24.47/4.32/22.75 |
| Mean/Std/Med(Tr-ime) | 0.2177/0.0612/0.2228 | 0.1870/0.0157/0.1841 | 0.3855/0.0235/0.3796 | 0.3240/0.03838/0.3025 |
| Mean/Std/Med(Te-ime) | 0.0008/0.0002/0.0007 | 0.0004/0.0001/0.0003 | 0.0010/0.0000/0.0011 | 0.0009/0.0001/0.0010 |
| Avg. SV-Reduction (%) | — | 67.11 | — | 19.67 |
| p-value/r (Acc.) | a 0.0728/0.4228 | c,* 0.0334/0.5015 (STPMSVM > SVM) | b,* 0.0419/0.4797 (STPMSVM > TPMSVM) | |
| p-value/r (Num-SVs) | a,* 0.0004/0.8790 (SSVM < SVM) | c 0.1960/0.3232 | b,* 0.0015/0.7952 (STPMSVM < TPMSVM) | |
| p-value/r (Tr-time) | a,* 0.0033/0.6929 (SSVM < SVM) | c,* 0.0002/0.8770 (SSVM < STPMSVM) | b,* 0.0003/0.8469 (STPMSVM < TPMSVM) | |
| p-value/r (Te-time) | a,* 0.0004/0.9331 (SSVM < SVM) | c,* 0.0001/0.9056 (SSVM < STPMSVM) | b,* 0.0002/0.8713 (STPMSVM < TPMSVM) |
| Dataset | SVM | SSVM | TPMSVM | STPMSVM |
|---|---|---|---|---|
| Acc.(%) | Acc.(%) | Acc.(%) | Acc.(%) | |
| Num-SVs | Num-SVs | Num-SVs | Num-SVs | |
| Tr-Time(s) | Tr-Time(s) | Tr-Time(s) | Tr-Time(s) | |
| Te-Time(s) | Te-Time(s) | Te-Time(s) | Te-Time(s) | |
| A0-00 | 99.75 ± 0.79 | 99.25 ± 1.69 | 99.75 ± 0.79 | 100.00 ± 0.00 |
| 30.00 ± 1.56 | 39.90 ± 0.99 | 42.90 ± 0.88 | 38.60 ± 0.70 | |
| 0.2497 ± 0.0320 | 0.3924 ± 0.0271 | 0.3932 ± 0.0279 | 0.3588 ± 0.0207 | |
| 0.0009 ± 0.0014 | 0.0004 ± 0.0002 | 0.0006 ± 0.0004 | 0.0004 ± 0.0003 | |
| 0.3134 | 0.3169 | 0.3262 | 0.3151 | |
| A0-05 | 94.00 ± 3.37 | 95.00 ± 2.64 | 95.00 ± 2.64 | 95.00 ± 2.64 |
| 104.70 ± 4.67 | 7.00 ± 0.47 | 40.50 ± 1.08 | 39.20 ± 0.92 | |
| 0.2571 ± 0.0289 | 0.4188 ± 0.0205 | 0.3470 ± 0.0283 | 0.3475 ± 0.0133 | |
| 0.0007 ± 0.0004 | 0.0003 ± 0.0002 | 0.0007 ± 0.0002 | 0.0005 ± 0.0001 | |
| 0.3124 | 0.3151 | 0.3158 | 0.3122 | |
| A0-10 | 87.75 ± 5.33 | 88.00 ± 5.11 | 85.00 ± 5.00 | 86.25 ± 5.66 |
| 193.00 ± 1.78 | 22.00 ± 0.82 | 77.20 ± 2.15 | 74.60 ± 0.70 | |
| 0.2073 ± 0.0125 | 0.3631 ± 0.0157 | 0.3354 ± 0.0152 | 0.3407 ± 0.0082 | |
| 0.0006 ± 0.0003 | 0.0004 ± 0.0002 | 0.0006 ± 0.0003 | 0.0004 ± 0.0000 | |
| 0.3119 | 0.3123 | 0.3167 | 0.3131 | |
| A0-15 | 84.25 ± 6.46 | 84.50 ± 6.21 | 83.50 ± 6.99 | 84.50 ± 6.75 |
| 185.30 ± 6.24 | 11.00 ± 0.67 | 78.50 ± 2.88 | 76.10 ± 2.08 | |
| 0.2180 ± 0.0079 | 0.3927 ± 0.0297 | 0.3843 ± 0.0199 | 0.3663 ± 0.0156 | |
| 0.0007 ± 0.0008 | 0.0006 ± 0.0008 | 0.0008 ± 0.0003 | 0.0005 ± 0.0001 | |
| 0.3128 | 0.3119 | 0.3119 | 0.3121 | |
| A5-00 | 94.00 ± 2.93 | 94.50 ± 3.50 | 93.50 ± 2.69 | 94.00 ± 2.93 |
| 48.70 ± 2.93 | 22.10 ± 0.74 | 39.50 ± 0.85 | 39.70 ± 0.82 | |
| 0.2685 ± 0.0326 | 0.3978 ± 0.0200 | 0.3829 ± 0.0394 | 0.3391 ± 0.0151 | |
| 0.0004 ± 0.0002 | 0.0003 ± 0.0001 | 0.0007 ± 0.0006 | 0.0005 ± 0.0001 | |
| 0.3128 | 0.3254 | 0.3121 | 0.3196 | |
| A5-05 | 89.25 ± 2.90 | 90.25 ± 2.49 | 90.00 ± 3.33 | 90.25 ± 2.49 |
| 142.80 ± 3.12 | 31.40 ± 1.5055 | 75.50 ± 0.97 | 73.20 ± 0.79 | |
| 0.2135 ± 0.0220 | 0.3817 ± 0.0292 | 0.3234 ± 0.0164 | 0.3284 ± 0.0180 | |
| 0.0005 ± 0.0003 | 0.0005 ± 0.0003 | 0.0008 ± 0.0007 | 0.0008 ± 0.0001 | |
| 0.3154 | 0.3129 | 0.3150 | 0.3131 | |
| A5-10 | 83.50 ± 6.69 | 83.75 ± 7.19 | 84.25 ± 7.08 | 84.25 ± 6.67 |
| 170.20 ± 9.15 | 10.50 ± 1.35 | 75.60 ± 1.08 | 75.30 ± 1.70 | |
| 0.2245 ± 0.0349 | 0.4521 ± 0.0489 | 0.3356 ± 0.0408 | 0.3610 ± 0.0084 | |
| 0.0005 ± 0.0003 | 0.0002 ± 0.0001 | 0.0010 ± 0.0013 | 0.0006 ± 0.0001 | |
| 0.3132 | 0.3120 | 0.3120 | 0.3125 | |
| A5-15 | 80.25 ± 5.71 | 79.50 ± 6.65 | 79.50 ± 6.85 | 79.75 ± 7.02 |
| 187.30 ± 6.33 | 10.20 ± 1.23 | 151.00 ± 1.15 | 147.30 ± 0.82 | |
| 0.2755 ± 0.0283 | 0.4046 ± 0.0319 | 0.3865 ± 0.0283 | 0.3697 ± 0.0301 | |
| 0.0007 ± 0.0004 | 0.0005 ± 0.0006 | 0.0007 ± 0.0001 | 0.0006 ± 0.0001 | |
| 0.3130 | 0.330 | 0.3237 | 0.3120 | |
| Avg. SV-Reduction (%) | — | 70.50 | — | 3.13 |
| p-value/r (Acc.) | a 0.3281/0.3457 | c 1.0000/0.0000 | b 0.0313/0.7615 | |
| p-value/r (Num-SVs) | a,* 0.0156/0.8547 (SSVM < SVM) | c,* 0.0156/0.8547 (SSVM < STPMSVM) | b,* 0.0973/0.4312 | |
| p-value/r (Tr-time) | a,* 0.0078/0.9405 (SSVM < SVM) | c,* 0.0078/0.9405 (STPMSVM < SSVM) | b 0.4609/0.2607 | |
| p-value/r (Te-time) | a,* 0.0156/0.8547 (SSVM < SVM) | c 0.0938/0.5925 | b,* 0.0156/0.8547 (STPMSVM < TPMSVM) | |
| p-value/r (Brier score) | a 1.0000/0.0000 | c 0.2969/0.3688 | b 0.2422/0.4135 |
| Dataset | SVM | SSVM | TPMSVM | STPMSVM |
|---|---|---|---|---|
| Acc.(%) | Acc.(%) | Acc.(%) | Acc.(%) | |
| Num-SVs | Num-SVs | Num-SVs | Num-SVs | |
| Tr-Time(s) | Tr-Time(s) | Tr-Time(s) | Tr-Time(s) | |
| Te-Time(s) | Te-Time(s) | Te-Time(s) | Te-Time(s) | |
| A0-P1N2 | 99.67 ± 1.05 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 |
| 63.10 ± 3.90 | 30.70 ± 1.06 | 30.60 ± 0.84 | 30.80 ± 0.79 | |
| 0.1993 ± 0.0141 | 0.2710 ± 0.0145 | 0.3370 ± 0.0132 | 0.3751 ± 0.0229 | |
| 0.0005 ± 0.0005 | 0.0004 ± 0.0003 | 0.0009 ± 0.0010 | 0.0006 ± 0.0001 | |
| 0.5288 | 0.5290 | 0.5302 | 0.5303 | |
| A0-P2N1 | 99.00 ± 1.61 | 99.00 ± 1.61 | 99.33 ± 1.41 | 100.00 ± 0.00 |
| 13.60 ± 0.70 | 13.60 ± 0.70 | 30.60 ± 1.43 | 30.10 ± 0.5676 | |
| 0.2945 ± 0.0302 | 0.2678 ± 0.0105 | 0.4815 ± 0.0561 | 0.3661 ± 0.0436 | |
| 0.0007 ± 0.0016 | 0.0005 ± 0.0005 | 0.0010 ± 0.0008 | 0.0010 ± 0.0009 | |
| 0.2405 | 0.2405 | 0.2357 | 0.2355 | |
| A0-P1N3 | 99.75 ± 0.79 | 99.75 ± 0.79 | 100.00 ± 0.00 | 99.75 ± 0.79 |
| 27.50 ± 0.85 | 15.50 ± 0.53 | 39.40 ± 1.08 | 39.90 ± 0.74 | |
| 0.2170 ± 0.0183 | 0.4488 ± 0.0450 | 0.4107 ± 0.0329 | 0.3623 ± 0.0147 | |
| 0.0004 ± 0.0006 | 0.0004 ± 0.0005 | 0.0007 ± 0.0002 | 0.0005 ± 0.0001 | |
| 0.6586 | 0.6580 | 0.6584 | 0.6509 | |
| A0-P3N1 | 99.00 ± 1.29 | 99.00 ± 1.29 | 99.75 ± 0.79 | 99.25 ± 1.21 |
| 29.20 ± 1.81 | 14.20 ± 0.79 | 54.80 ± 2.30 | 51.50 ± 1.84 | |
| 0.2274 ± 0.0332 | 0.4324 ± 0.0308 | 0.5069 ± 0.0355 | 0.4212 ± 0.0165 | |
| 0.0004 ± 0.0003 | 0.0003 ± 0.0002 | 0.0006 ± 0.0001 | 0.0006 ± 0.0001 | |
| 0.2971 | 0.2934 | 0.2935 | 0.2888 | |
| A6-P1N2 | 92.33 ± 4.17 | 93.33 ± 2.90 | 92.67 ± 3.78 | 92.33 ± 3.53 |
| 162.00 ± 2.54 | 56.30 ± 1.83 | 30.80 ± 0.79 | 30.60 ± 0.70 | |
| 0.3924 ± 0.0580 | 0.2463 ± 0.0136 | 0.3292 ± 0.0138 | 0.3315 ± 0.0162 | |
| 0.0006 ± 0.0003 | 0.0005 ± 0.0002 | 0.0006 ± 0.0004 | 0.0004 ± 0.0001 | |
| 0.5436 | 0.5321 | 0.5294 | 0.5292 | |
| A6-P2N1 | 91.67 ± 3.93 | 93.33 ± 4.16 | 91.00 ± 4.73 | 92.67 ± 5.62 |
| 86.30 ± 2.75 | 6.20 ± 0.63 | 34.70 ± 1.25 | 29.90 ± 0.88 | |
| 0.2235 ± 0.0303 | 0.2599 ± 0.0196 | 0.3795 ± 0.0357 | 0.3461 ± 0.0124 | |
| 0.0004 ± 0.0003 | 0.0003 ± 0.0002 | 0.0007 ± 0.0005 | 0.0004 ± 0.0000 | |
| 0.2951 | 0.2670 | 0.2439 | 0.2376 | |
| A6-P1N3 | 93.25 ± 2.90 | 94.00 ± 2.69 | 92.25 ± 3.81 | 93.50 ± 3.57 |
| 127.30 ± 1.70 | 34.30 ± 0.9487 | 146.90 ± 0.57 | 74.70 ± 0.82 | |
| 0.3414 ± 0.0361 | 0.3419 ± 0.0070 | 0.3520 ± 0.0159 | 0.3842 ± 0.0109 | |
| 0.0005 ± 0.0002 | 0.0004 ± 0.0002 | 0.0006 ± 0.0003 | 0.0005 ± 0.0001 | |
| 0.6880 | 0.6758 | 0.6584 | 0.6582 | |
| A6-P3N1 | 93.25 ± 5.66 | 92.25 ± 4.92 | 91.50 ± 4.12 | 92.00 ± 4.97 |
| 73.20 ± 2.94 | 17.70 ± 1.60 | 39.50 ± 0.70 | 39.10 ± 0.74 | |
| 0.2476 ± 0.0212 | 0.3849 ± 0.0188 | 0.2967 ± 0.0090 | 0.4072 ± 0.0138 | |
| 0.0005 ± 0.0005 | 0.0003 ± 0.0002 | 0.0006 ± 0.0002 | 0.0005 ± 0.0001 | |
| 0.3393 | 0.2985 | 0.2893 | 0.2873 | |
| Avg. SV-Reduction (%) | — | 56.66 | — | 8.80 |
| p-value/r (Acc.) | a 0.3750/0.3137 | c 0.5938/0.1886 | b 0.2344/0.4204 | |
| p-value/r (Num-SVs) | a,* 0.0156/0.8547 (SSVM < SVM) | c 0.1094/0.5660 | b 0.1172/0.5539 | |
| p-value/r (Tr-time) | a 0.1953/0.4579 | c 0.1484/0.5109 | b 0.6406/0.1650 | |
| p-value/r (Te-time) | a,* 0.0156/0.8547 (SSVM < SVM) | c,* 0.0391/0.7296 (SSVM < STPMSVM) | b,* 0.0313/0.7615 (STPMSVM < TPMSVM) | |
| p-value/r (Brier score) | a,* 0.0313/0.7615 (SSVM < SVM) | c,* 0.0156/0.8547 (STPMSVM < SSVM) | b,* 0.0156/0.8547 (STPMSVM < TPMSVM) |
| Dataset | SVM | SSVM | TPMSVM | STPMSVM |
|---|---|---|---|---|
| Acc.(%) | Acc.(%) | Acc.(%) | Acc.(%) | |
| Num-SVs | Num-SVs | Num-SVs | Num-SVs | |
| Tr-Time(s) | Tr-Time(s) | Tr-Time(s) | Tr-ime(s) | |
| Te-Time(s) | Te-Time(s) | Te-Time(s) | Te-Time(s) | |
| PA2-NA7 | 95.50 ± 2.30 | 95.75 ± 2.06 | 95.00 ± 1.67 | 95.75 ± 2.06 |
| 53.10 ± 2.02 | 5.80 ± 0.63 | 39.70 ± 1.25 | 39.50 ± 0.53 | |
| 0.2766 ± 0.0194 | 0.4485 ± 0.0511 | 0.3145 ± 0.0347 | 0.3753 ± 0.0118 | |
| 0.0004 ± 0.0003 | 0.0002 ± 0.0000 | 0.0004 ± 0.0001 | 0.0004 ± 0.0001 | |
| 0.3942 | 0.3128 | 0.3181 | 0.3155 | |
| PA7-NA2 | 95.00 ± 4.86 | 95.50 ± 4.22 | 94.25 ± 4.26 | 95.00 ± 4.08 |
| 105.90 ± 4.04 | 5.60 ± 0.52 | 83.60 ± 1.84 | 39.00 ± 0.82 | |
| 0.3463 ± 0.0301 | 0.4598 ± 0.0409 | 0.3882 ± 0.0205 | 0.3663 ± 0.0193 | |
| 0.0004 ± 0.0003 | 0.0003 ± 0.0002 | 0.0008 ± 0.0001 | 0.0005 ± 0.0001 | |
| 0.3209 | 0.3500 | 0.3190 | 0.3133 | |
| PA5-NA7 | 92.50 ± 3.73 | 92.75 ± 3.81 | 91.50 ± 4.74 | 92.25 ± 5.06 |
| 113.40 ± 3.89 | 23.60 ± 0.97 | 39.80 ± 1.40 | 38.80 ± 0.92 | |
| 0.4086 ± 0.0293 | 0.4000 ± 0.0378 | 0.3862 ± 0.0408 | 0.4126 ± 0.0504 | |
| 0.0005 ± 0.0003 | 0.0004 ± 0.0003 | 0.0005 ± 0.0002 | 0.0005 ± 0.0001 | |
| 0.3122 | 0.3248 | 0.3262 | 0.3493 | |
| PA7-NA5 | 93.25 ± 4.09 | 93.00 ± 4.53 | 93.25 ± 5.20 | 93.75 ± 3.95 |
| 72.40 ± 4.86 | 13.20 ± 0.92 | 74.80 ± 1.14 | 38.90 ± 0.88 | |
| 0.2570 ± 0.0169 | 0.4265 ± 0.0408 | 0.3386 ± 0.0208 | 0.3657 ± 0.0246 | |
| 0.0005 ± 0.0001 | 0.0004 ± 0.0002 | 0.0007 ± 0.0003 | 0.0005 ± 0.0001 | |
| 0.3128 | 0.3158 | 0.3147 | 0.3169 | |
| PA3-NA4 | 99.00 ± 1.75 | 99.00 ± 1.75 | 98.75 ± 1.77 | 98.75 ± 1.77 |
| 21.10 ± 1.52 | 5.60 ± 0.70 | 40.40 ± 1.08 | 39.00 ± 0.94 | |
| 0.2548 ± 0.0191 | 0.4187 ± 0.0261 | 0.3336 ± 0.0286 | 0.4510 ± 0.0266 | |
| 0.0003 ± 0.0002 | 0.0002 ± 0.0002 | 0.0007 ± 0.0003 | 0.0007 ± 0.0001 | |
| 0.3220 | 0.3202 | 0.3377 | 0.3597 | |
| PA4-NA3 | 99.00 ± 1.75 | 98.25 ± 2.06 | 98.50 ± 2.11 | 98.50 ± 2.11 |
| 37.10 ± 1.79 | 6.80 ± 0.79 | 42.80 ± 1.75 | 38.70 ± 0.95 | |
| 0.2406 ± 0.0702 | 0.4680 ± 0.0405 | 0.3613 ± 0.0290 | 0.3515 ± 0.0142 | |
| 0.0002 ± 0.0000 | 0.0002 ± 0.0000 | 0.0007 ± 0.0004 | 0.0006 ± 0.0001 | |
| 0.3128 | 0.3476 | 0.3308 | 0.3452 | |
| PA4-NA6 | 97.50 ± 1.67 | 97.25 ± 1.84 | 98.00 ± 1.05 | 97.25 ± 1.42 |
| 61.60 ± 1.51 | 14.80 ± 0.63 | 41.00 ± 1.25 | 38.70 ± 0.48 | |
| 0.2774 ± 0.0475 | 0.3909 ± 0.0217 | 0.2889 ± 0.0217 | 0.3696 ± 0.0412 | |
| 0.0006 ± 0.0008 | 0.0004 ± 0.0002 | 0.0005 ± 0.0001 | 0.0005 ± 0.0001 | |
| 0.3189 | 0.4034 | 0.3194 | 0.3199 | |
| PA6-NA4 | 96.50 ± 2.69 | 96.25 ± 3.39 | 96.50 ± 3.37 | 96.50 ± 3.37 |
| 97.40 ± 3.60 | 54.10 ± 3.45 | 75.50 ± 0.71 | 46.30 ± 0.95 | |
| 0.3877 ± 0.0533 | 0.3907 ± 0.0219 | 0.3275 ± 0.0124 | 0.4362 ± 0.0523 | |
| 0.0005 ± 0.0004 | 0.0004 ± 0.0002 | 0.0005 ± 0.0001 | 0.0004 ± 0.0001 | |
| 0.3168 | 0.3126 | 0.3128 | 0.3138 | |
| Avg. SV-Reduction (%) | — | 77.55 | — | 20.21 |
| p-value/r (Acc.) | a 0.8281/0.0768 | c 0.3750/0.3137 | b 0.9375/0.0277 | |
| p-value/r (Num-SVs) | a,* 0.0078/0.9405 (SSVM < SVM) | c,* 0.0156/0.8547 (SSVM < STPMSVM) | b,* 0.0078/0.9405 (STPMSVM < TPMSVM) | |
| p-value/r (Tr-time) | a,* 0.0234/0.8012 (SVM < SSVM) | c 0.1953/0.4579 | b,* 0.0391/0.7296 (TPMSVM < STPMSVM) | |
| p-value/r (Te-time) | a,* 0.0156/0.8547 (SSVM < SVM) | c,* 0.0156/0.8547 (SSVM < STPMSVM) | b 0.1250/0.5424 | |
| p-value/r (Brier score) | a 0.3828/0.3086 | c 0.9453/0.0243 | b 0.2500/0.4067 |
| Dataset | SVM | SSVM | TPMSVM | STPMSVM |
|---|---|---|---|---|
| A0-10 | 0.8229 ± 0.9187/1.0825 | 0.9811 ± 1.1192/1.1741 | 0.0500 ± 0.0594/0.0456 | 0.0527 ± 0.0608/0.0549 |
| A05-10 | 0.9294 ± 1.1078/1.0825 | 0.9701 ± 1.1046/1.2346 | 0.1948 ± 0.2618/0.1611 | 0.4220 ± 0.4500/0.5962 |
| A0-P2N1 | 4.0523 ± 2.4884/2.6250 | 4.0499 ± 2.6474/2.5210 | 0.1196 ± 0.0781/0.0738 | 0.2084 ± 0.1331/0.1273 |
| A6-P1N3 | 1.1429 ± 0.6519/1.6972 | 1.7837 ± 1.1438/2.3945 | 0.1938 ± 0.1371/0.2466 | 0.1968 ± 0.1386/0.2485 |
| PA2-NA7 | 3.1004 ± 2.5998/1.6863 | 3.7129 ± 2.6712/2.6922 | 0.0659 ± 0.0472/0.0503 | 0.1210 ± 0.0838/0.0951 |
| PA6-NA4 | 1.0556 ± 0.4130/1.0842 | 1.3903 ± 0.6992/1.1200 | 0.3795 ± 0.1600/0.4471 | 0.5223 ± 0.2573/0.5498 |
| Dataset | SVM | SSVM | TPMSVM | STPMSVM |
|---|---|---|---|---|
| Acc.(%) | Acc.(%) | Acc.(%) | Acc.(%) | |
| Num-SVs | Num-SVs | Num-SVs | Num-SVs | |
| Time(s) | Time(s) | Time(s) | Time(s) | |
| B1 | 99.66 ± 0.73 | 98.26 ± 1.15 | 97.23 ± 2.19 | 97.74 ± 1.42 |
| (576×4) | 61.20 ± 2.82 | 54.70 ± 2.11 | 369.30 ± 9.66 | 109.40 ± 1.17 |
| 0.9411 ± 0.0993 | 0.6863 ± 0.0463 | 0.5706 ± 0.0662 | 0.5130 ± 0.0513 | |
| B2 | 89.25 ± 4.72 | 88.25 ± 4.09 | 89.25 ± 5.01 | 89.50 ± 4.97 |
| (400×2) | 93.60 ± 3.98 | 44.20 ± 1.55 | 139.40 ± 4.72 | 76.00 ± 12.91 |
| 0.4390 ± 0.0306 | 0.3759 ± 0.0269 | 0.4523 ± 0.0366 | 0.3831 ± 0.0130 | |
| B3 | 99.93 ± 0.23 | 99.71 ± 0.38 | 96.50 ± 1.68 | 96.50 ± 1.49 |
| (1372×4) | 105.90 ± 1.60 | 62.60 ± 1.35 | 376.60 ± 1.58 | 132.30 ± 2.31 |
| 2.5760 ± 0.2922 | 3.0472 ± 0.1801 | 1.7380 ± 0.1286 | 1.7273 ± 0.1183 | |
| B4 | 96.34 ± 1.58 | 96.49 ± 1.86 | 95.61 ± 2.50 | 96.78 ± 2.44 |
| (683×10) | 177.80 ± 2.44 | 44.70 ± 5.06 | 206.70 ± 3.20 | 111.50 ± 82.20 |
| 1.1613 ± 0.1922 | 0.9509 ± 0.0342 | 0.6623 ± 0.0477 | 0.6107 ± 0.0114 | |
| B5 | 88.57 ± 11.27 | 90.00 ± 11.76 | 90.00 ± 13.55 | 91.43 ± 13.80 |
| (72×19) | 31.20 ± 1.48 | 14.20 ± 1.55 | 23.10 ± 2.13 | 15.40 ± 1.51 |
| 0.1881 ± 0.0159 | 0.1558 ± 0.0171 | 0.3135 ± 0.0081 | 0.2779 ± 0.0212 | |
| B6 | 100.00 ± 0 | 100.00 ± 0 | 100.00 ± 0 | 100.00 ± 0 |
| (88×17) | 51.80 ± 1.23 | 24.30 ± 1.16 | 23.50 ± 3.10 | 13.50 ± 1.43 |
| 0.2037 ± 0.0131 | 0.1558 ± 0.0117 | 0.4003 ± 0.0754 | 0.2913 ± 0.0157 | |
| B7 | 97.65 ± 5.68 | 97.65 ± 5.68 | 97.65 ± 5.68 | 97.65 ± 5.68 |
| (170×54) | 50.50 ± 2.51 | 27.10 ± 0.74 | 26.70 ± 2.41 | 17.90 ± 0.74 |
| 0.2433 ± 0.0232 | 0.1826 ± 0.097 | 0.4075 ± 0.0280 | 0.3000 ± 0.0220 | |
| B8 | 88.00 ± 4.22 | 88.00 ± 4.22 | 74.00 ± 10.75 | 79.00 ± 8.76 |
| (100×9) | 33.40 ± 2.37 | 5.00 ± 0.83 | 32.40 ± 2.07 | 30.40 ± 2.01 |
| 0.1947 ± 0.0185 | 0.1821 ± 0.0417 | 0.3394 ± 0.0130 | 0.2867 ± 0.0048 | |
| B9 | 67.10 ± 14.05 | 66.48 ± 9.12 | 68.57 ± 13.09 | 70.52 ± 10.84 |
| (146×9) | 123.90 ± 1.37 | 74.90 ± 2.23 | 124.90 ± 1.10 | 78.10 ± 2.81 |
| 0.2045 ± 0.0148 | 0.1772 ± 0.0113 | 0.5731 ± 0.0216 | 0.2800 ± 0.0120 | |
| B10 | 82.57 ± 6.59 | 82.57 ± 6.40 | 80.90 ± 7.72 | 77.90 ± 7.85 |
| (299×12) | 138.70 ± 4.14 | 58.90 ± 1.97 | 96.50 ± 3.06 | 47.10 ± 4.65 |
| 0.3627 ± 0.0296 | 0.2649 ± 0.0189 | 0.3965 ± 0.0193 | 0.3494 ± 0.0240 | |
| B11 | 94.58 ± 2.85 | 88.57 ± 11.27 | 90.00 ± 13.55 | 88.75 ± 13.10 |
| (351×34) | 170.70 ± 2.00 | 15.50 ± 1.51 | 23.10 ± 2.13 | 11.80 ± 1.03 |
| 0.4121 ± 0.0563 | 0.3042 ± 0.0130 | 0.4648 ± 0.0270 | 0.3922 ± 0.0270 | |
| B12 | 100.00 ± 0 | 100.00 ± 0 | 100.00 ± 0 | 100.00 ± 0 |
| (100×4) | 43.60 ± 1.07 | 19.10 ± 0.57 | 13.00 ± 0.67 | 11.30 ± 0.95 |
| 0.2200 ± 0.0378 | 0.1790 ± 0.0274 | 0.3397 ± 0.0186 | 0.2822 ± 0.0358 | |
| B13 | 85.50 ± 21.40 | 76.50 ± 23.10 | 86.00 ± 23.19 | 86.00 ± 23.19 |
| (48×90) | 37.40 ± 1.35 | 36.50 ± 1.58 | 43.20 ± 0.42 | 42.70 ± 0.48 |
| 0.1882 ± 0.0114 | 0.1520 ± 0.0063 | 0.3543 ± 0.0204 | 0.2989 ± 0.0414 | |
| B14 | 71.46 ± 1.60 | 71.46 ± 1.60 | 73.10 ± 5.33 | 73.10 ± 5.33 |
| (182×12) | 120.20 ± 1.60 | 11.00 ± 1.54 | 158.60 ± 1.07 | 163.20 ± 0.79 |
| 0.2580 ± 0.0333 | 0.1858 ± 0.0093 | 0.3810 ± 0.0209 | 0.3018 ± 0.0084 | |
| B15 | 94.29 ± 4.52 | 94.29 ± 5.63 | 93.57 ± 5.27 | 93.57 ± 4.05 |
| (140×7) | 39.80 ± 1.81 | 27.60 ± 0.84 | 16.60 ± 0.84 | 17.70 ± 1.34 |
| 0.2174 ± 0.0220 | 0.1728 ± 0.0104 | 0.3379 ± 0.0166 | 0.2915 ± 0.0196 | |
| B16 | 95.35 ± 4.44 | 93.03 ± 4.53 | 94.42 ± 4.86 | 94.44 ± 4.81 |
| (215×5) | 27.80 ± 1.75 | 14.50 ± 1.35 | 62.20 ± 1.23 | 23.30 ± 1.25 |
| 0.2548 ± 0.0170 | 0.2209 ± 0.0209 | 0.4459 ± 0.0158 | 0.3244 ± 0.0175 | |
| B17 | 100.00 ± 0 | 100.00 ± 0 | 100.00 ± 0 | 100.00 ± 0 |
| (146×5) | 50.80 ± 1,23 | 12.00 ± 1.05 | 61.80 ± 6.60 | 20.90 ± 2.38 |
| 0.2136 ± 0.0131 | 0.1863 ± 0.0105 | 0.3505 ± 0.0108 | 0.2872 ± 0.0168 | |
| B18 | 99.90 ± 0.32 | 99.70 ± 0.48 | 99.00 ± 0.82 | 99.50 ± 0.53 |
| (1000×7) | 180.40 ± 2.67 | 81.30 ± 1.06 | 273.6 ± 1.35 | 92.50 ± 1.18 |
| 2.0142 ± 0.2779 | 1.9392 ± 0.2171 | 1.0242 ± 0.1711 | 1.0186 ± 0.0257 | |
| B19 | 98.46 ± 3.24 | 98.46 ± 3.24 | 99.23 ± 2.43 | 99.92 ± 3.97 |
| (130×13) | 59.50 ± 1.72 | 10.80 ± 0.63 | 22.00 ± 1.94 | 17.30 ± 0.95 |
| 0.2180 ± 0.0110 | 0.1819 ± 0.0125 | 0.3818 ± 0.0160 | 0.2880 ± 0.0153 | |
| B20 | 95.44 ± 4.23 | 96.84 ± 3.49 | 89.80 ± 4.37 | 96.13 ± 3.07 |
| (569×30) | 167.00 ± 3.06 | 38.30 ± 1.25 | 316.80 ± 3.22 | 57.30 ± 1.49 |
| 0.8059 ± 0.1276 | 0.5963 ± 0.0114 | 0.5166 ± 0.0571 | 0.4895 ± 0.0165 | |
| Avg. SV-Reduction (%) | — | 56.21 | — | 39.11 |
| p-value/r (Acc.) | a 0.1279/0.3404 | c 0.5349/0.1387 | b 0.1055/0.3620 | |
| p-value/r (Num-SVs) | a,* 0.0001/0.8765 (SSVM < SVM) | c,* 0.0479/0.4424 (SSVM < STPMSVM) | b,* 0.0003/0.8181 (STPMSVM < TPMSVM) | |
| p-value/r (Time) | a,* 0.0015/0.7096 (SSVM < SVM) | c 0.4330/0.1753 | b,* 0.0001/0.8765 (STPMSVM < TPMSVM) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, S.; De Leone, R.; Huang, M. Two Novel Sparse Models for Support Vector Machines. Symmetry 2025, 17, 2004. https://doi.org/10.3390/sym17112004
Qu S, De Leone R, Huang M. Two Novel Sparse Models for Support Vector Machines. Symmetry. 2025; 17(11):2004. https://doi.org/10.3390/sym17112004
Chicago/Turabian StyleQu, Shuanghong, Renato De Leone, and Min Huang. 2025. "Two Novel Sparse Models for Support Vector Machines" Symmetry 17, no. 11: 2004. https://doi.org/10.3390/sym17112004
APA StyleQu, S., De Leone, R., & Huang, M. (2025). Two Novel Sparse Models for Support Vector Machines. Symmetry, 17(11), 2004. https://doi.org/10.3390/sym17112004






