Leveraging the Symmetry Between Active Dual-Steering-Wheel MPC and Passive Air Bearing for Ground-Based Satellite Hovering Tests
Abstract
1. Introduction
1.1. Ground Testing Needs for Satellite Hovering Missions
1.2. The Active Element: MPC for Trajectory and Attitude Tracking
1.2.1. The Extensive Applications of MPC
1.2.2. Theoretical Development in MPC
1.2.3. The Superior Performance of MPC in Trajectory Tracking
1.2.4. Implementation of MPC in This Work
1.3. The Passive Element: Air-Bearing for Micro-Gravity Simulation
1.3.1. Applications of Air-Bearing Motion
1.3.2. Active Actuation Strategy in This Work
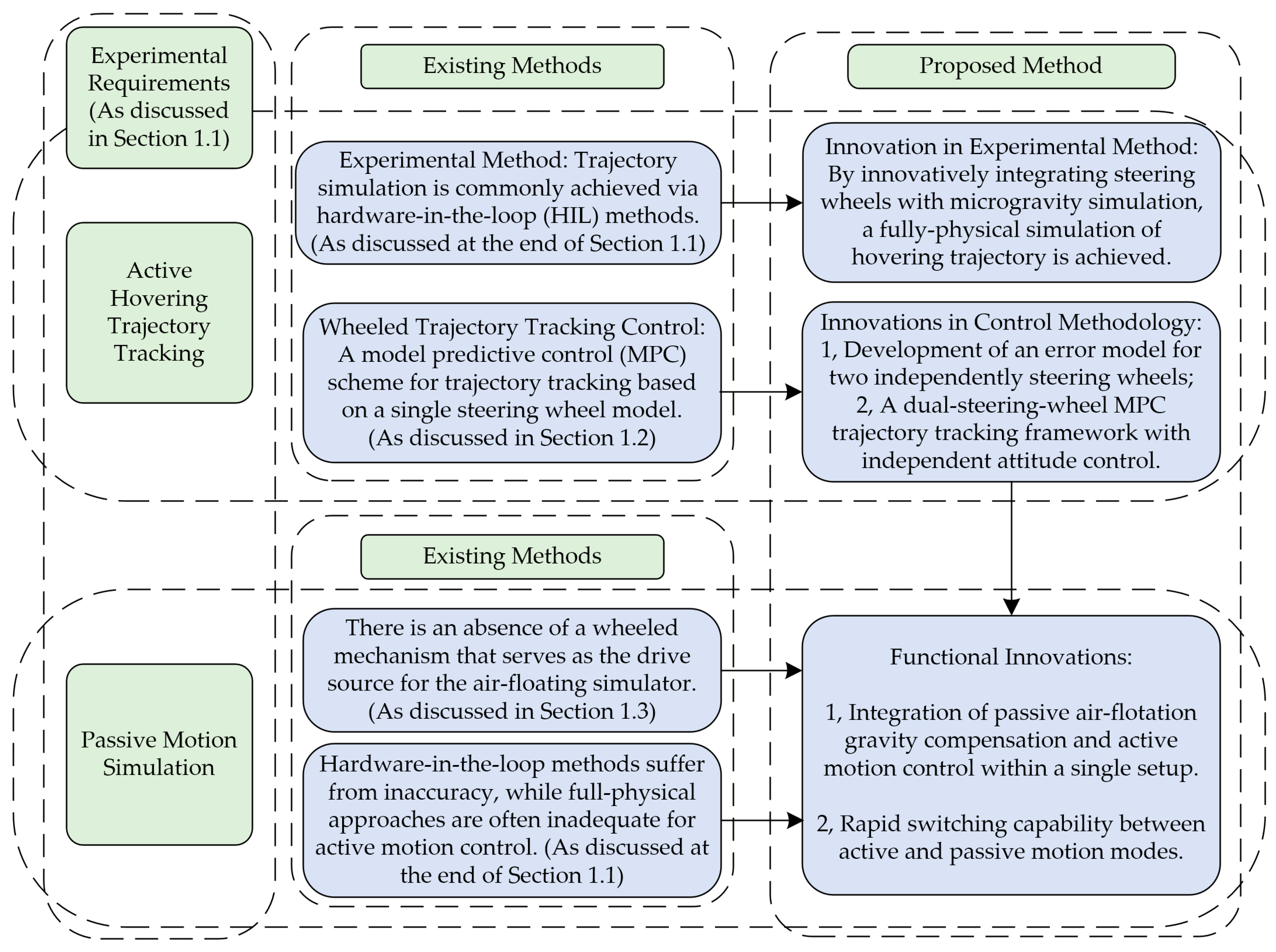
1.4. Contributions and Organization
2. Modeling of Dual-Steering-Wheel Drive and MPC for Hovering Trajectory Tracking
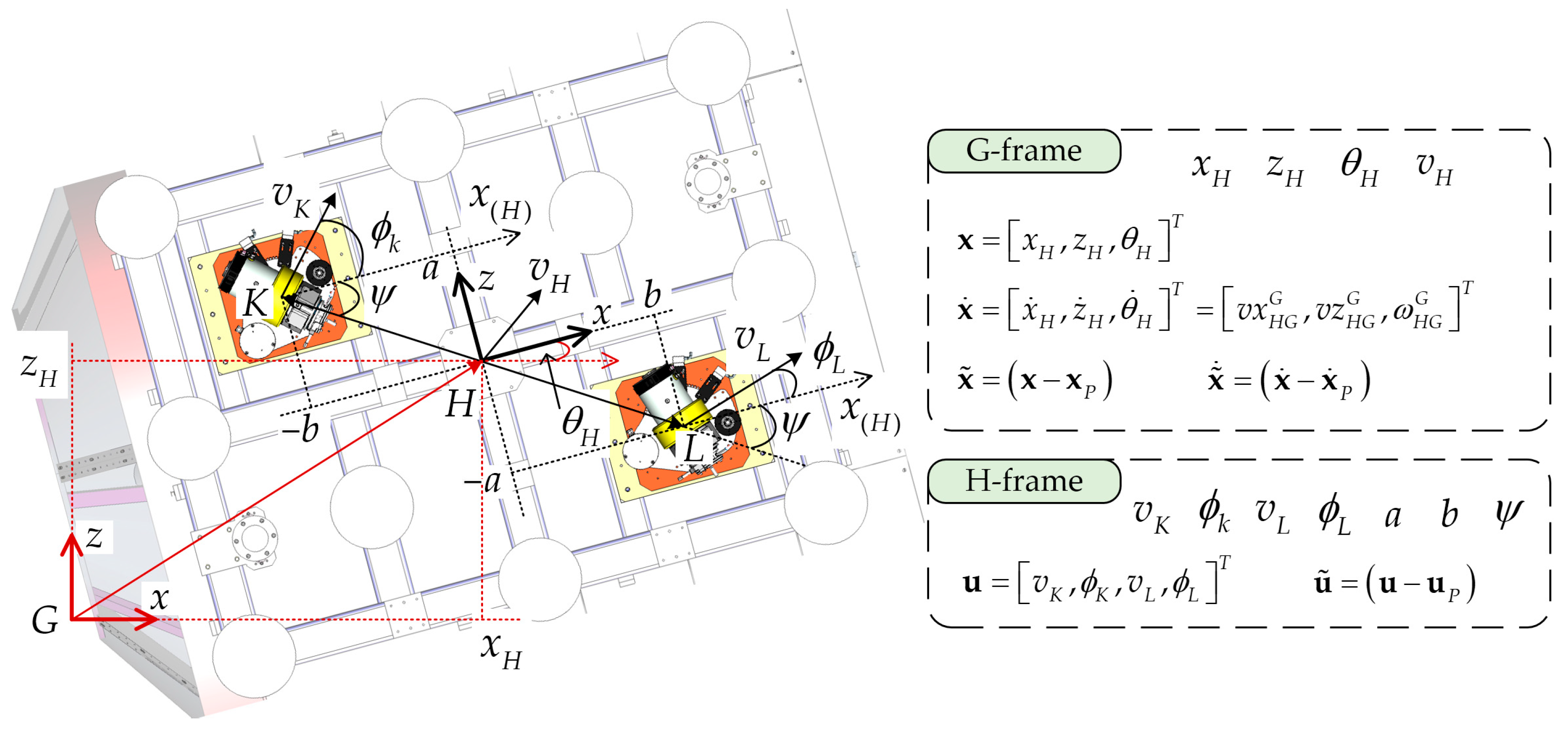
2.1. Modeling of the Dual-Steering-Wheel Drive System
2.2. Formulation of the Pose Tracking Error Model
2.3. MPC Design for Satellite Hovering Trajectory Tracking
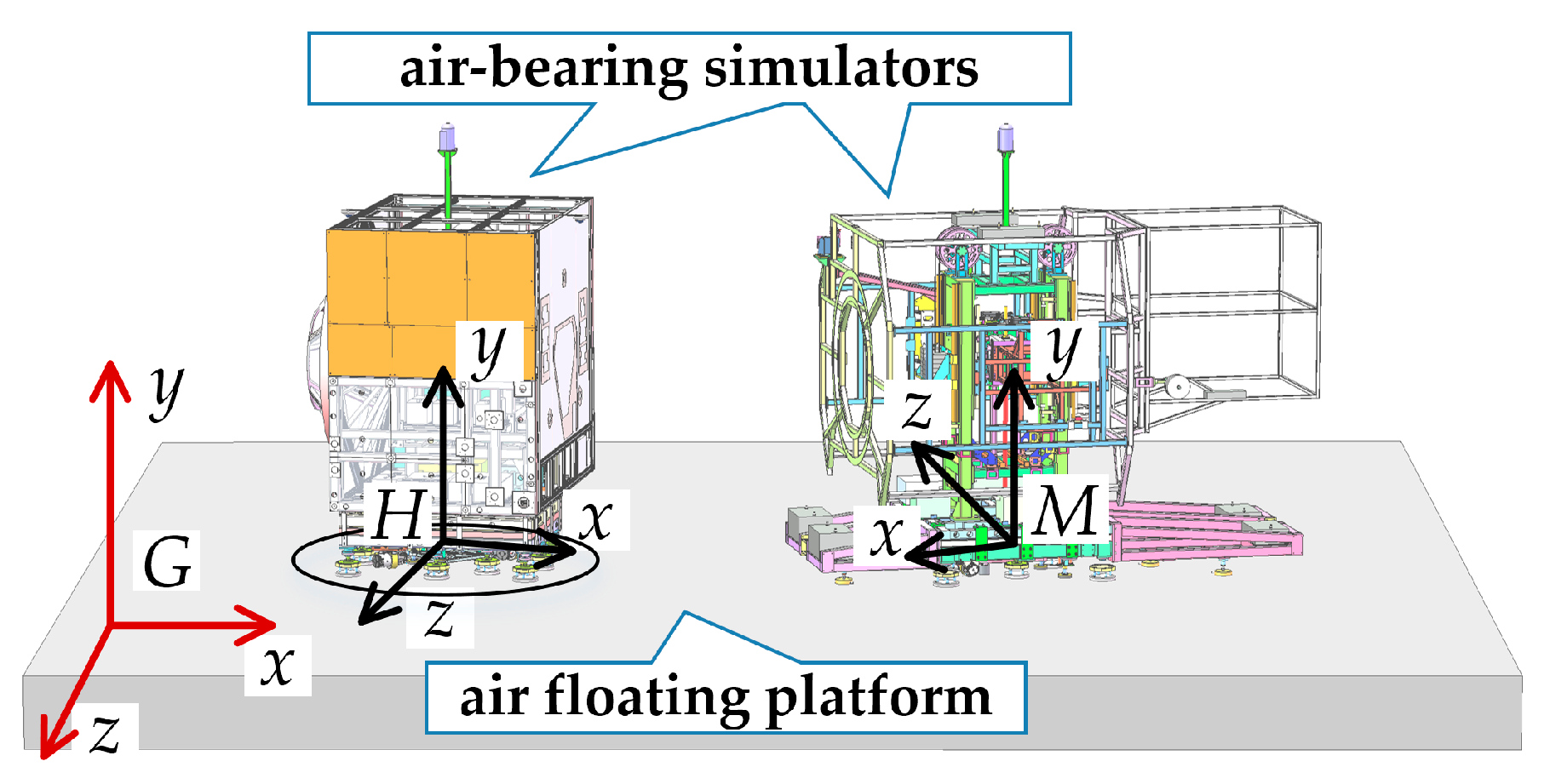
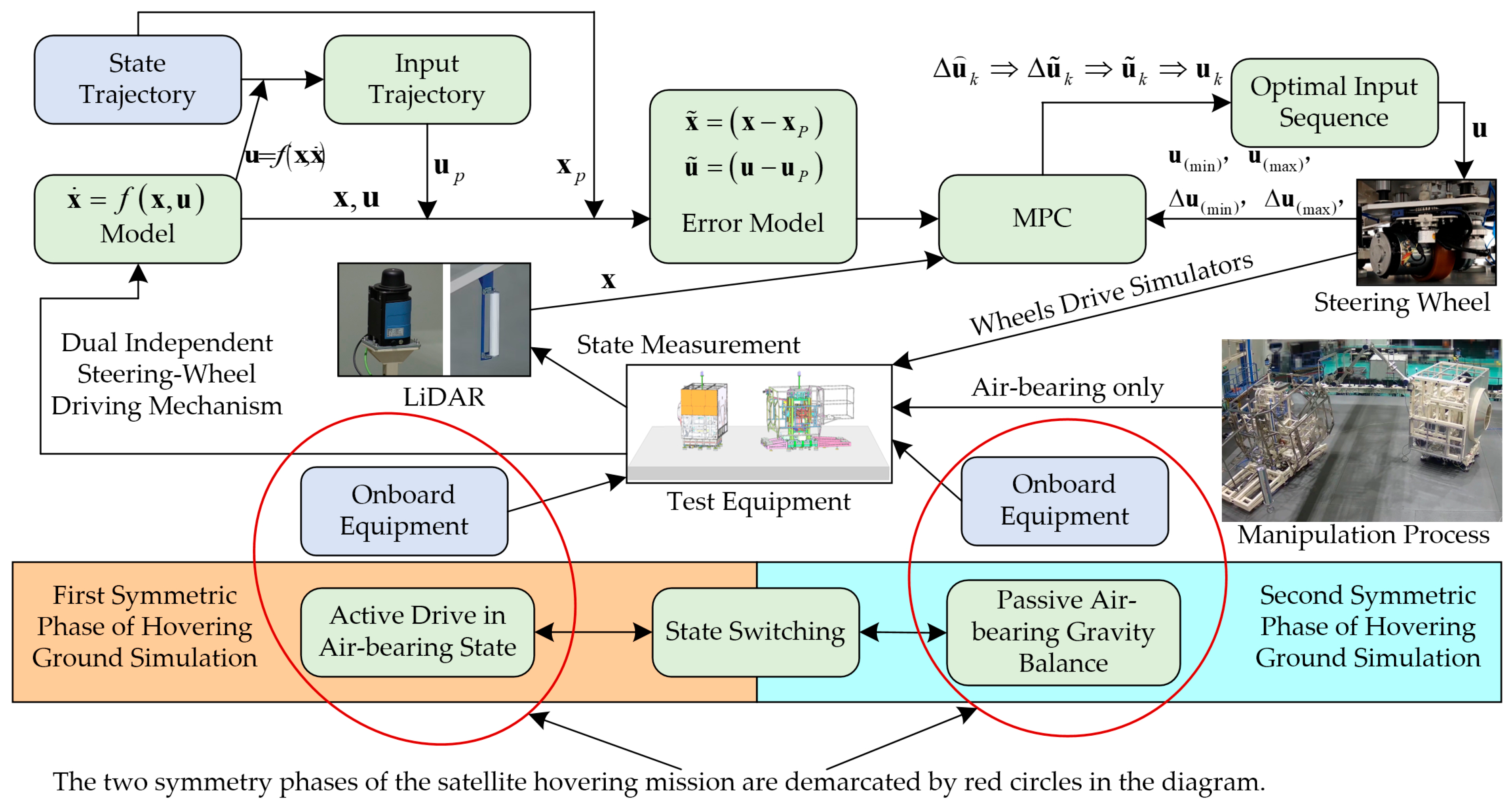
3. A Symmetrical Active-Passive Testing Platform with Full-Physical Air-Bearing
3.1. Emulation of the Micro-Gravity Environment
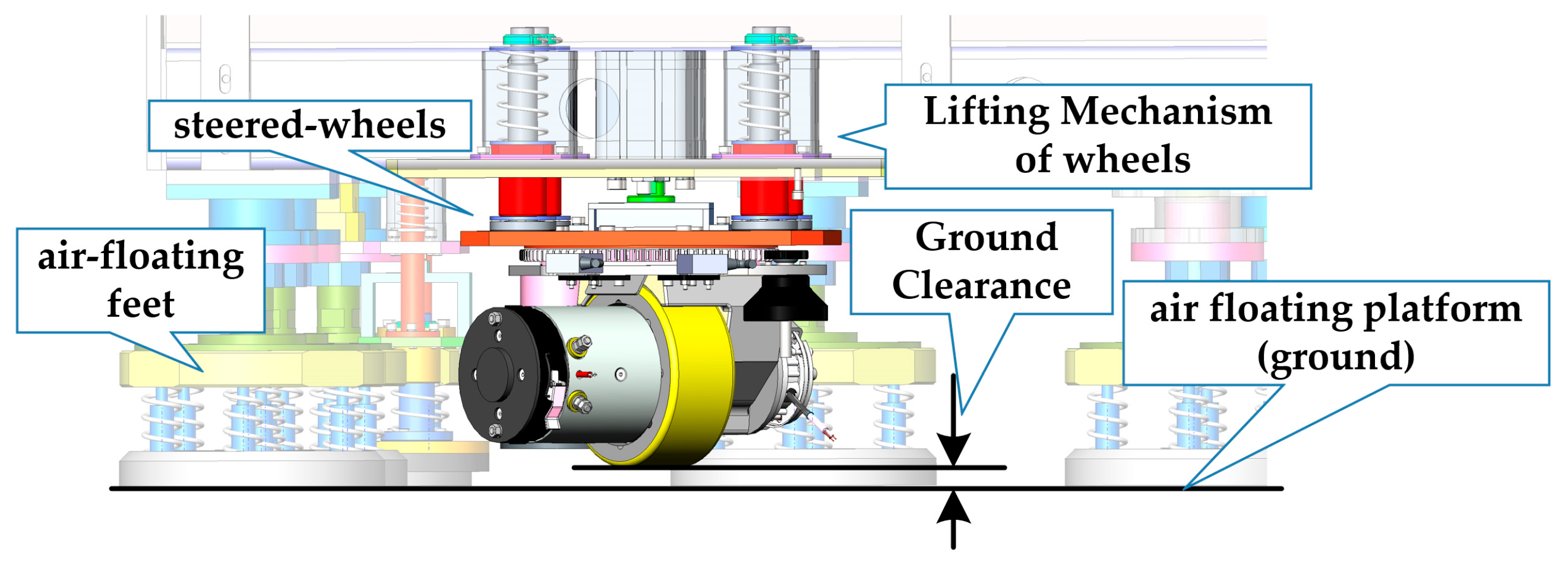
3.2. Implementation of the Active-Passive Symmetry
4. Results
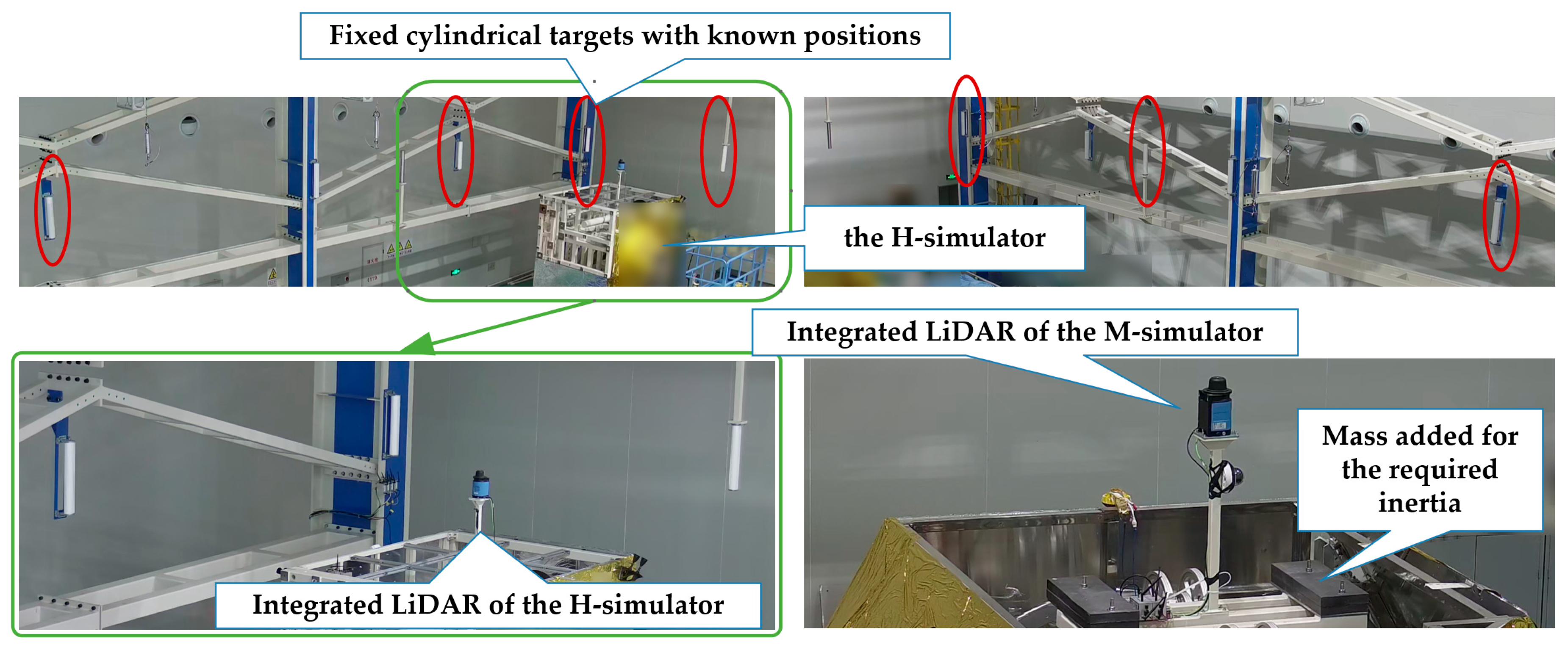
4.1. Key Hardware Components
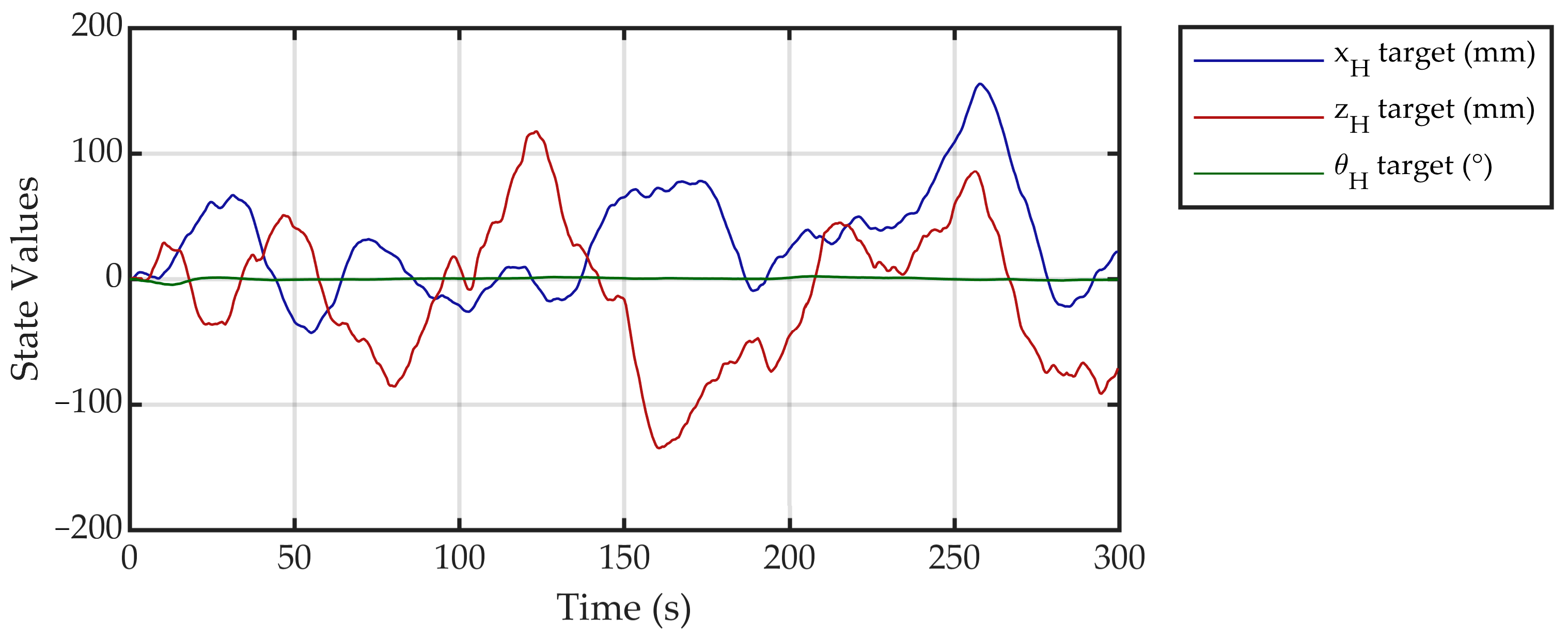
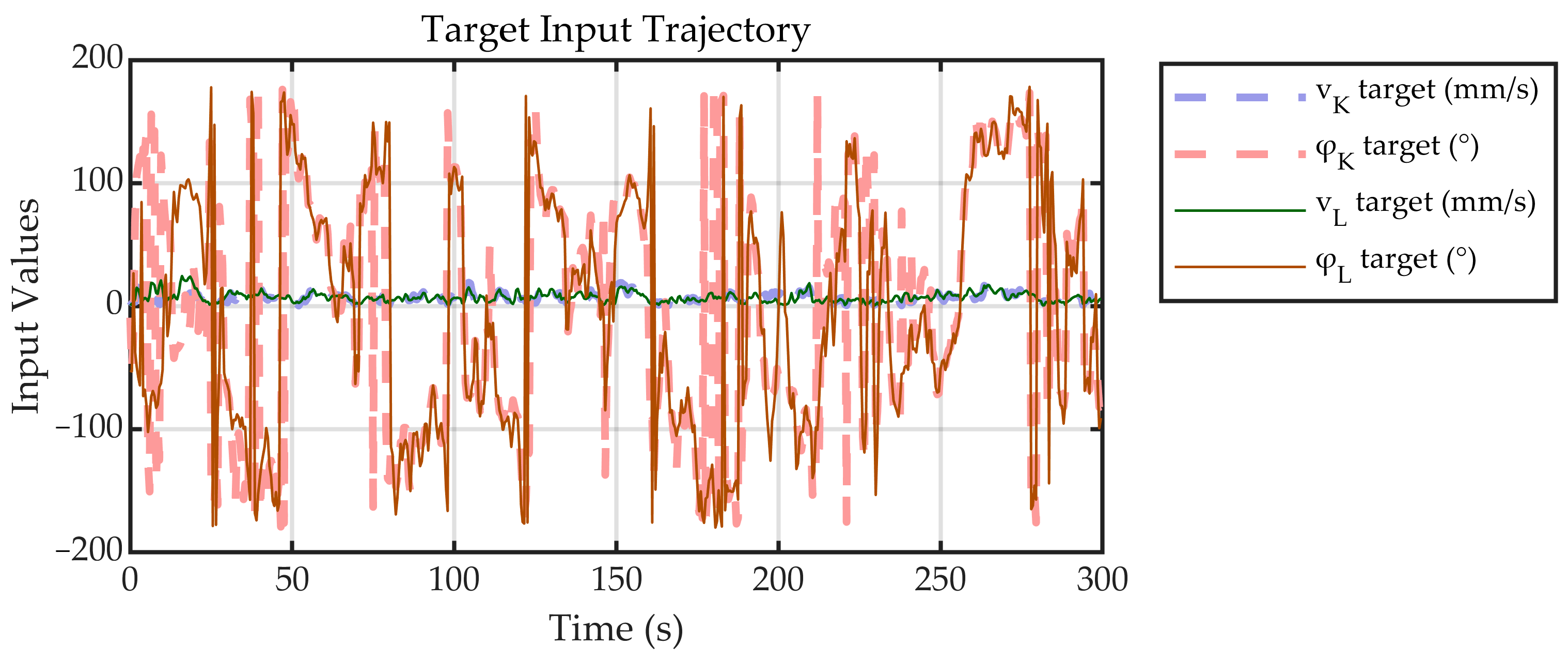
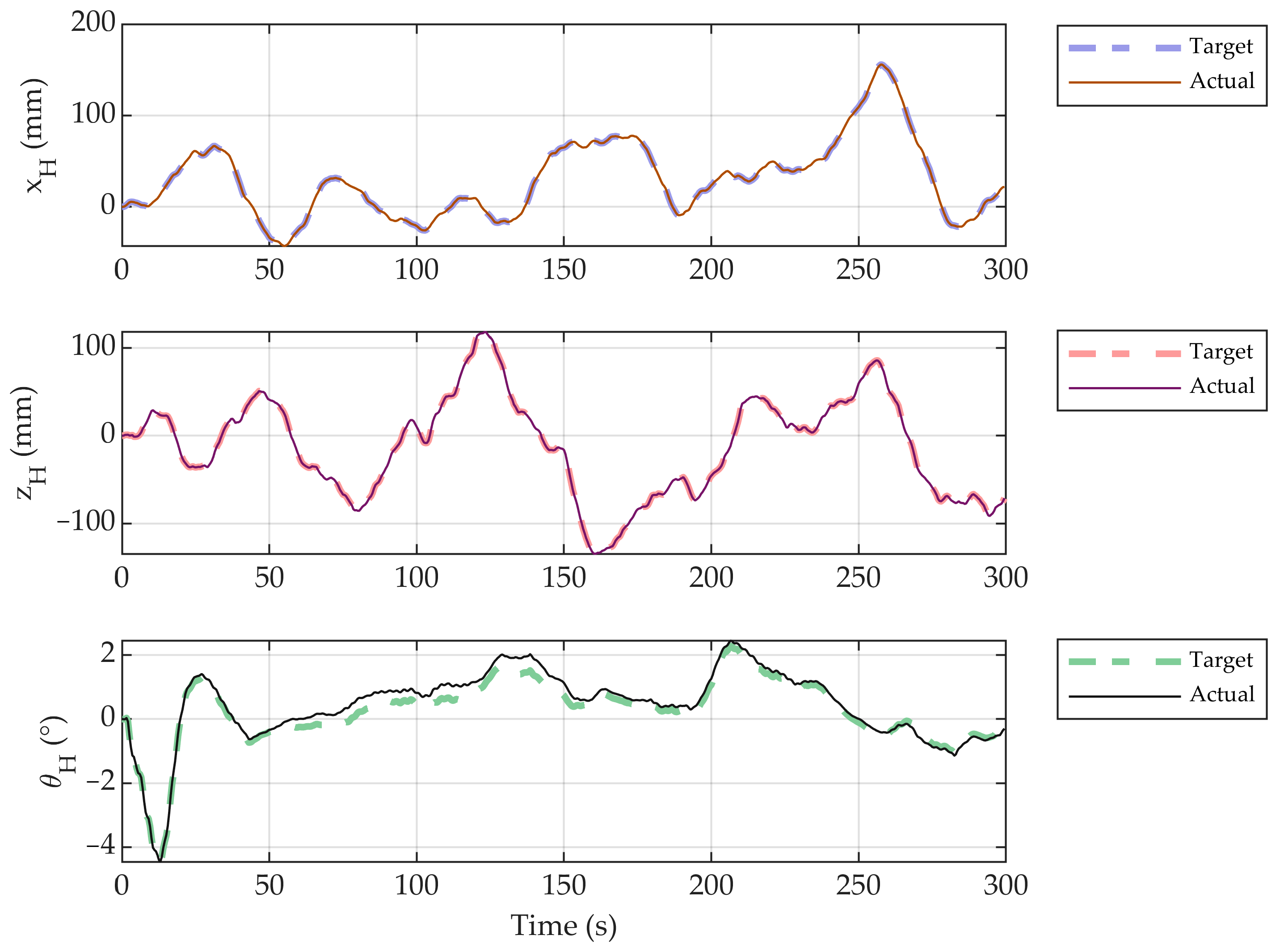
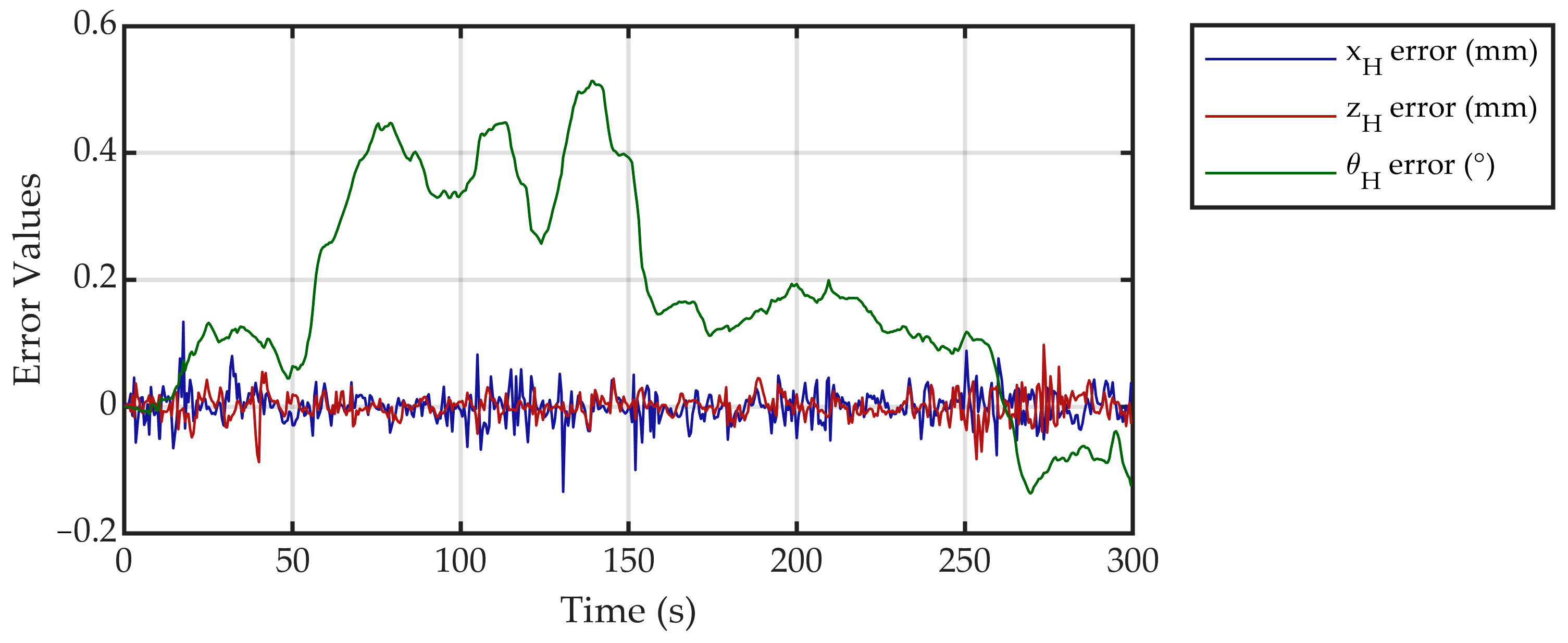
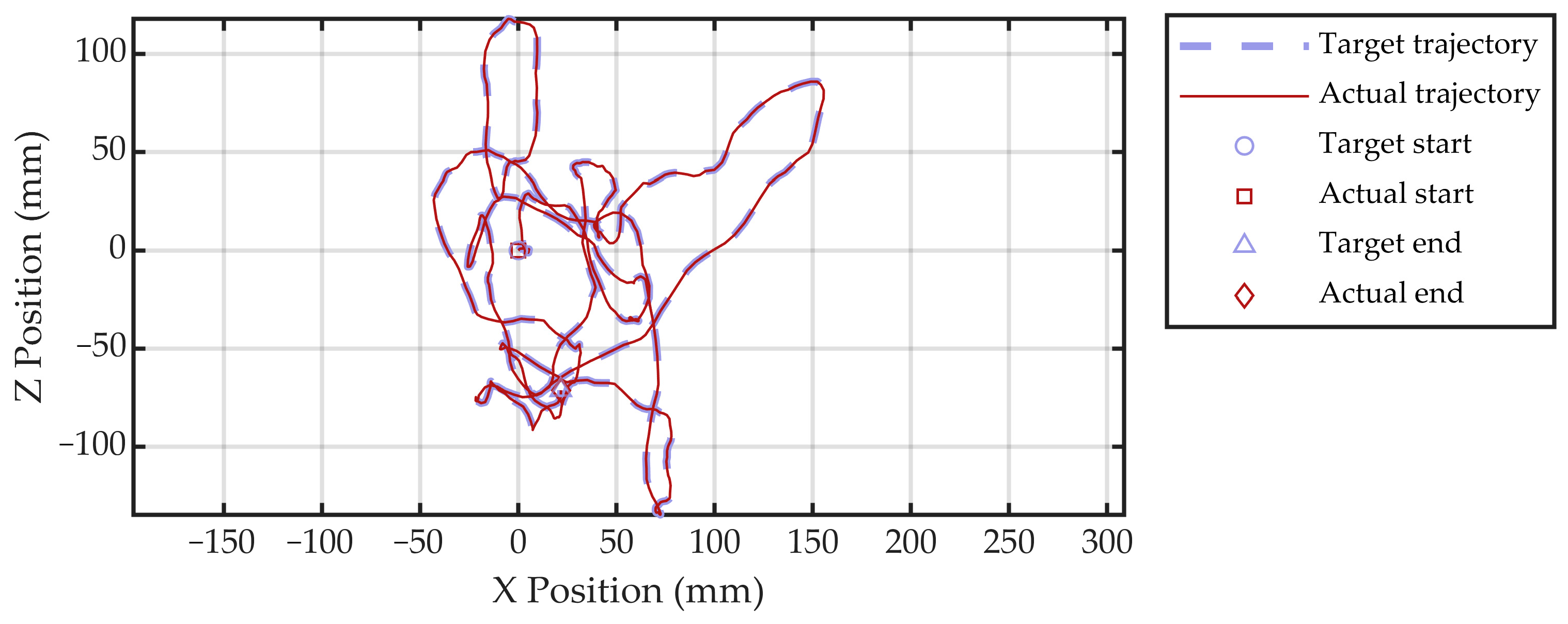
4.2. Active Trajectory Tracking Experimental Results
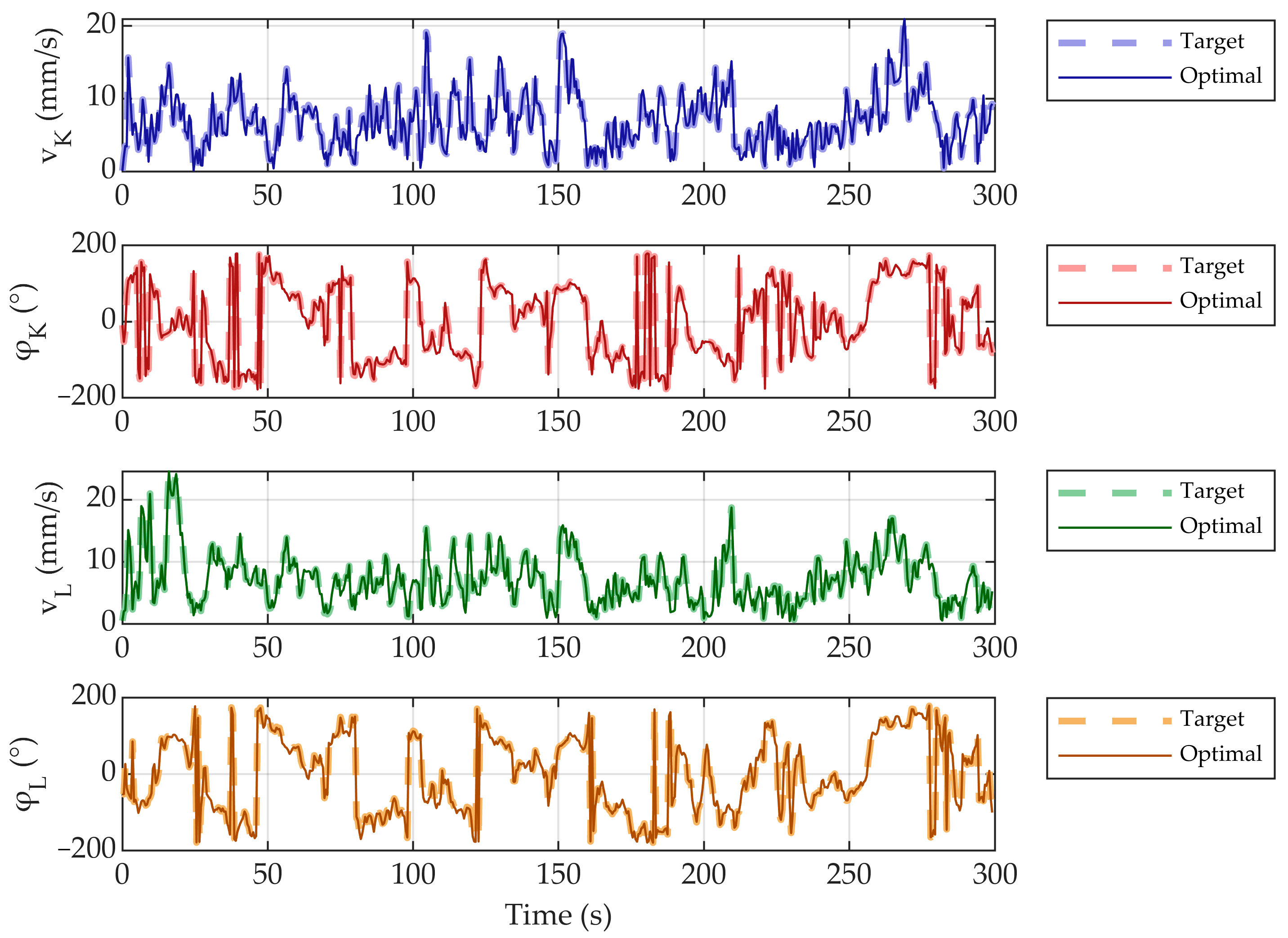
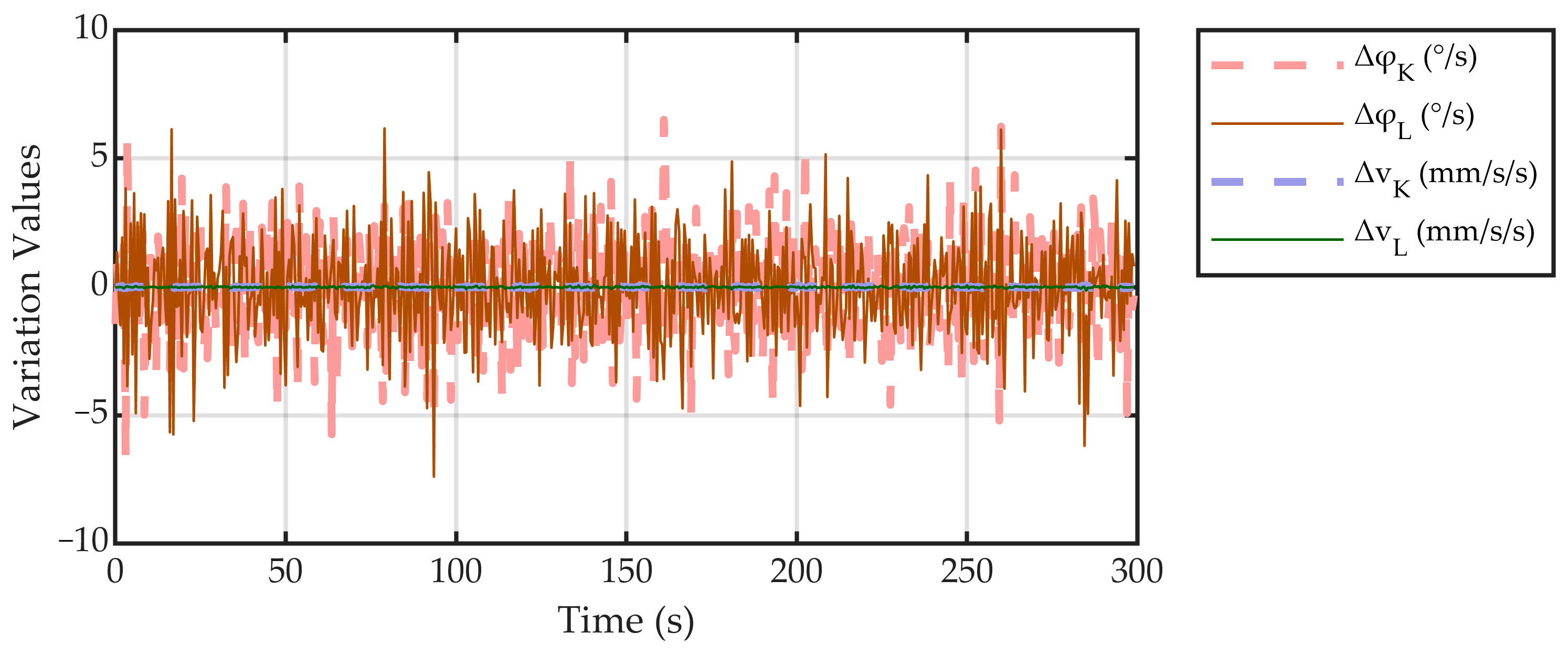
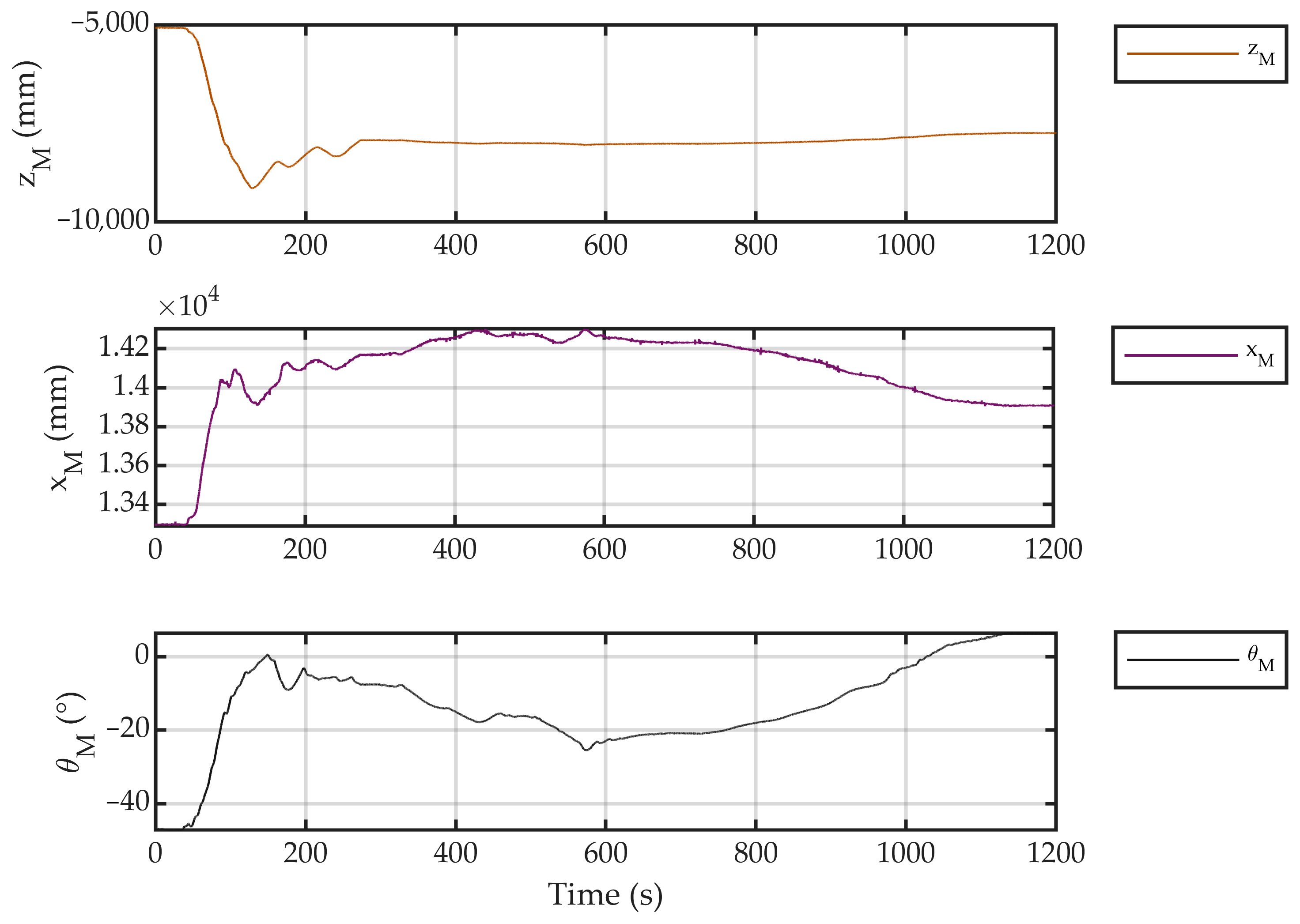
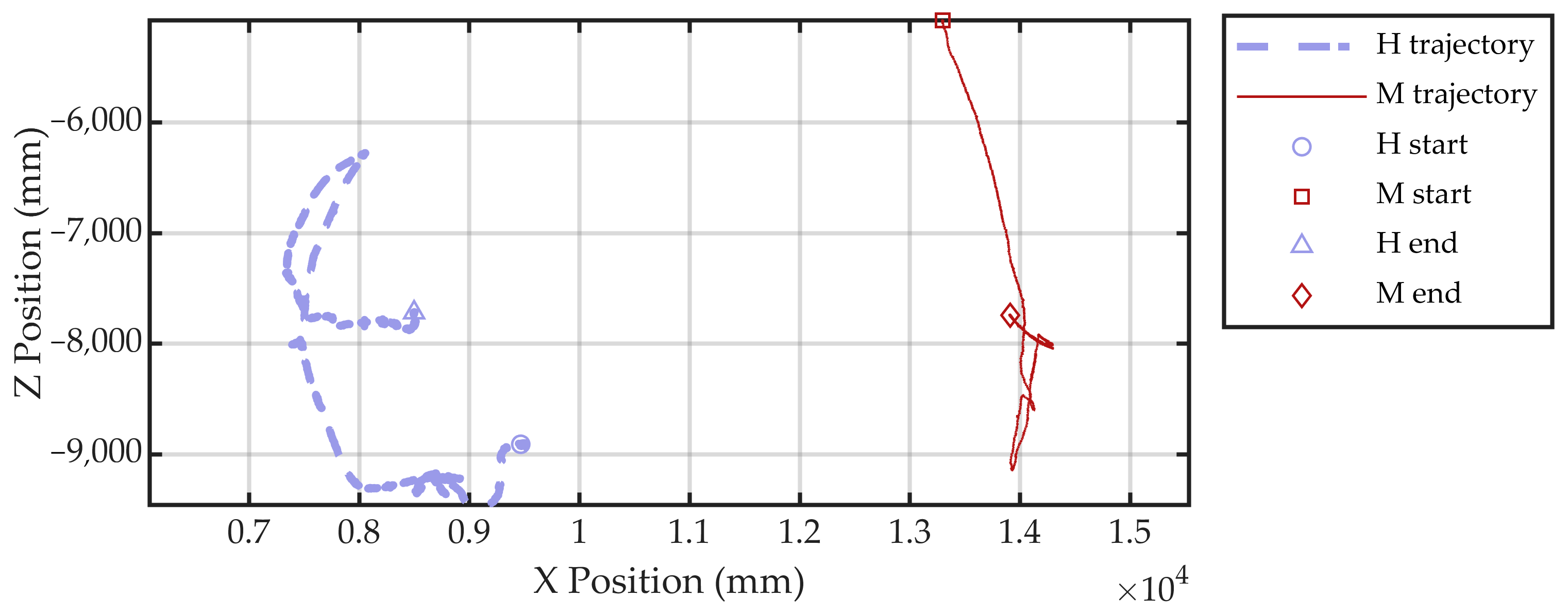
4.3. Passive Air-Bearing Simulation Experimental Results
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MPC | Model Predictive Control |
| NMPC | Nonlinear Model Predictive Control |
References
- Zhao, C.; Maestrini, M.; Di Lizia, P. Low-thrust optimal control of spacecraft hovering for proximity operations. J. Guid. Control Dyn. 2024, 47, 1457–1469. [Google Scholar] [CrossRef]
- Lee, D.; Vukovich, G. Adaptive finite-time control for spacecraft hovering over an asteroid. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1183–1196. [Google Scholar] [CrossRef]
- Ma, X.; Gong, S.; Cheng, L. Autonomous Vision-Based Control for Spacecraft Navigation Around an Asteroid. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 10649–10662. [Google Scholar] [CrossRef]
- Lin, Z.; Wu, B. Image-Based Multispacecraft Feature Tracking Control Under Visibility Constraints with Observer. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 8069–8085. [Google Scholar] [CrossRef]
- Chen, N.; Zhang, Y.; Li, Z.; Cheng, W.; Li, J.; Diao, H.; Wang, W.; Fang, Y. An Improved Sampling-Based Approach for Spacecraft Proximity Operation Path Planning in Near-Circular Orbit. IEEE Access 2020, 8, 41794–41804. [Google Scholar] [CrossRef]
- Lin, Z.; Wu, B.; Wang, D. Specific Tracking Control of Rotating Target Spacecraft Under Safe Motion Constraints. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 2422–2438. [Google Scholar] [CrossRef]
- Shao, J.; Zhou, Q.; Ye, D.; Bernelli-Zazzera, F.; Sun, Z. Feasibility Analysis and Synchronization Control for Underactuated Spacecraft Formation Hovering. IEEE Trans. Control Syst. Technol. 2024, 32, 241–249. [Google Scholar] [CrossRef]
- Shao, J.; Su, B.; Zhou, Q.; Ye, D.; Sun, Z. Formation reconfiguration hovering technique for underactuated satellite. In Proceedings of the 2021 5th Chinese Conference on Swarm Intelligence and Cooperative Control, Shenzhen, China, 19–22 November 2021; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Cao, Y.; Mu, J.; Cheng, X.; Liu, F. Spacecraft-DS: A Spacecraft Dataset for Key Components Detection and Segmentation via Hardware-in-the-Loop Capture. IEEE Sens. J. 2024, 24, 5347–5358. [Google Scholar] [CrossRef]
- Duan, G.; Liu, G.P.; Pang, Z.H. Identification of Unknown Inertia Parameters of Spacecraft and Spacecraft Hovering. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021. [Google Scholar]
- Elmorshedy, M.F.; Xu, W.; El-Sousy, F.F.M.; Islam, R.; Ahmed, A.A. Recent Achievements in Model Predictive Control Techniques for Industrial Motor: A Comprehensive State-of-the-Art. IEEE Access 2021, 9, 58170–58191. [Google Scholar] [CrossRef]
- Huang, X.; Zha, Y.; Lv, X.; Quan, X. Torque Fault-Tolerant Hierarchical Control of 4WID Electric Vehicles Based on Improved MPC and SMC. IEEE Access 2023, 11, 132718–132734. [Google Scholar] [CrossRef]
- Zhao, H.; Yang, H.; Wang, Z.; Xia, Y. Nonlinear MPC on Parallel Parking for Autonomous Vehicles Under State-Dependent Switching. IEEE Trans. Autom. Sci. Eng. 2025, 22, 6377–6387. [Google Scholar] [CrossRef]
- Hassan, A.; Ruiz-Moreno, S.; Frejo, J.R.D.; Maestre, J.M.; Camacho, E.F. Neural-Network Based MPC for Enhanced Lateral Stability in Electric Vehicles. IEEE Access 2024, 12, 23265–23278. [Google Scholar] [CrossRef]
- Tagliabue, A.; How, J.P. Efficient Deep Learning of Robust Policies From MPC Using Imitation and Tube-Guided Data Augmentation. IEEE Trans. Robot. 2024, 40, 4301–4321. [Google Scholar] [CrossRef]
- Hanover, D.; Foehn, P.; Sun, S.; Kaufmann, E.; Scaramuzza, D. Performance, Precision, and Payloads: Adaptive Nonlinear MPC for Quadrotors. IEEE Robot. Autom. Lett. 2022, 7, 690–697. [Google Scholar] [CrossRef]
- Gomaa, M.A.K.; Silva, O.D.; Mann, G.K.I.; Gosine, R.G. Nonlinear MPC Without Terminal Costs or Constraints for Multi-Rotor Aerial Vehicles. IEEE Control Syst. Lett. 2022, 6, 440–445. [Google Scholar] [CrossRef]
- Bauersfeld, L.; Spannagl, L.; Ducard, G.J.J.; Onder, C. MPC Flight Control for a Tilt-Rotor VTOL Aircraft. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2395–2409. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, X.; Chen, X.; Wang, Z.; Wang, P.; Liu, E. Development of HIL—Real vehicle dual steering wheel test platform for automotive SBW system based on variable transmission ratio control. In Proceedings of the International Conference on Electric Vehicle and Vehicle Engineering (CEVVE 2023), Shenzhen, China, 10–12 November 2023. [Google Scholar]
- Quartullo, R.; Bianchini, G.; Garulli, A.; Giannitrapani, A. Robust Output Feedback Variable-Horizon MPC with Adaptive Terminal Constraints. IEEE Control Syst. Lett. 2025, 9, 883–888. [Google Scholar] [CrossRef]
- Chuah, J.; Liang, X.; Ge, S.S. Nonlinear Model Predictive Control of a Dual-Axis Tilting Quadcopter. In Proceedings of the 2023 IEEE International Conference on Cybernetics and Intelligent Systems (CIS) and IEEE Conference on Robotics, Automation and Mechatronics (RAM), Penang, Malaysia, 9–12 June 2023. [Google Scholar]
- Jin, R.; Li, L.; Liang, X.; Zou, X.; Yang, Z.; Ge, S.S.; Huang, H. Energy-efficient design of the powertrain for mechanical-electro-hydraulic equipment via configuring multidimensional controllable variables. Renew. Sustain. Energy Rev. 2024, 201, 114511. [Google Scholar] [CrossRef]
- Singh, V.K.; Tripathi, R.N.; Hanamoto, T. Implementation Strategy for Resource Optimization of FPGA-Based Adaptive Finite Control Set-MPC Using XSG for a VSI System. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 2066–2078. [Google Scholar] [CrossRef]
- Jeong, C.; Brastein, O.M.; Skeie, N.O.; Sharma, R. Hybrid Model Predictive Control Scheme for Controlling Temperature in Building Under Uncertainties. IEEE Access 2023, 11, 116820–116832. [Google Scholar] [CrossRef]
- Domański, P.D.; Ławryńczuk, M. Impact of MPC Embedded Performance Index on Control Quality. IEEE Access 2021, 9, 24787–24795. [Google Scholar] [CrossRef]
- Pang, S.; Zhang, Y.; Huangfu, Y.; Li, X.; Tan, B.; Li, P.; Tian, C.; Quan, S. A Virtual MPC-Based Artificial Neural Network Controller for PMSM Drives in Aircraft Electric Propulsion System. IEEE Trans. Ind. Appl. 2024, 60, 3603–3612. [Google Scholar] [CrossRef]
- Huang, K.; Wei, K.; Li, F.; Yang, C.; Gui, W. LSTM-MPC: A Deep Learning Based Predictive Control Method for Multimode Process Control. IEEE Trans. Ind. Electron. 2023, 70, 11544–11554. [Google Scholar] [CrossRef]
- Zanon, M.; Gros, S. Safe Reinforcement Learning Using Robust MPC. IEEE Trans. Autom. Control 2021, 66, 3638–3652. [Google Scholar] [CrossRef]
- Tsukamoto, H.; Chung, S.J. Neural Contraction Metrics for Robust Estimation and Control: A Convex Optimization Approach. IEEE Control Syst. Lett. 2021, 5, 211–216. [Google Scholar] [CrossRef]
- Najafqolian, M.A.; Alipour, K.; Mousavifard, R.; Tarvirdizadeh, B. Control of Aerial Robots Using Convex QP LMPC and Learning-Based Explicit-MPC. IEEE Trans. Ind. Inform. 2024, 20, 10883–10891. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, W.; Luan, Z.; Wang, C.; Zhou, X.; Wu, H. An Antirollover Control Strategy Based on Time-Varying Nonlinear MPC for Three-Axle Steering/Braking-by-Wire Vehicle. IEEE Trans. Ind. Electron. 2024, 71, 11048–11060. [Google Scholar] [CrossRef]
- You, Y.; Yang, Z.; Zhuo, H.-Z.; Xu, N.; Liao, L.; Jiang, W. Design of an adaptive MPC control system for unmanned ground vehicle based on FP-ADMM and RBFNN. Control Eng. Pract. 2025, 164, 106399. [Google Scholar] [CrossRef]
- Dong, F.; Li, X.; You, K.; Song, S. Standoff Tracking Using DNN-Based MPC with Implementation on FPGA. IEEE Trans. Control Syst. Technol. 2023, 31, 1998–2010. [Google Scholar] [CrossRef]
- Wang, H.; Liu, B.; Ping, X.; An, Q. Path Tracking Control for Autonomous Vehicles Based on an Improved MPC. IEEE Access 2019, 7, 161064–161073. [Google Scholar] [CrossRef]
- Dixit, S.; Montanaro, U.; Dianati, M.; Oxtoby, D.; Mizutani, T.; Mouzakitis, A.; Fallah, S. Trajectory Planning for Autonomous High-Speed Overtaking in Structured Environments Using Robust MPC. IEEE Trans. Intell. Transp. Syst. 2020, 21, 2310–2323. [Google Scholar] [CrossRef]
- Eltrabyly, A.; Ichalal, D.; Mammar, S. Quadcopter Trajectory Tracking in the Presence of 4 Faulty Actuators: A Nonlinear MHE and MPC Approach. IEEE Control Syst. Lett. 2022, 6, 2024–2029. [Google Scholar] [CrossRef]
- Wilde, M.; Clark, C.; Romano, M. Historical survey of kinematic and dynamic spacecraft simulators for laboratory experimentation of on-orbit proximity maneuvers. Prog. Aerosp. Sci. 2019, 110, 100552. [Google Scholar] [CrossRef]
- Chu, M.; Lin, S.; Xu, S.; Wang, G.; Jia, J.; Chang, R. An Omnidirectional Compliant Docking Strategy for Non-Cooperative On-orbit Targets: Principle, Design, Modeling, and Experiment. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 8364–8379. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, C.; Ping, S.; Ren, Y.; Duan, L.; Kang, Q. Similarity Analysis of an Air-bearing Simulator Reproducing Drag-free Control Dynamics. In Proceedings of the 2024 IEEE 25th China Conference on System Simulation Technology and Its Application (CCSSTA), Tianjin, China, 21–23 July 2024. [Google Scholar]
- Mamani, J.G.C.; Wang, X.; Yanyachi, P.R. Automatic Mass Balancing of a Small Spherical Simulator for Attitude Control Verification. IEEE Access 2024, 12, 114465–114479. [Google Scholar] [CrossRef]
- Chen, R.; Wang, J.; Zhou, H.; Bai, Y.; Zhao, Y.; Chen, X. Path Planning and Control for Multiagent Traversing Numerous Obstacles. IEEE Trans. Ind. Electron. 2025, 72, 2938–2947. [Google Scholar] [CrossRef]
- Zhang, D.W.; Liu, G.P. Secure Predictive Control for Networked High-Order Fully Actuated Systems Under Random DoS Attacks. IEEE Trans. Ind. Inform. 2024, 20, 6935–6945. [Google Scholar] [CrossRef]
- Li, Z.; Liu, L.; Xing, X.; Yan, Z.; Liu, Y.; Sun, H. Electromagnetic Characteristics and Modal Analysis of Multi-DOF Motors with Air-Floation. IEEE Access 2022, 10, 53164–53174. [Google Scholar] [CrossRef]
- Li, Z.; Yang, K.; Wang, X. Electromagnetic and Flow Field Analysis of Multi-DOF Motor with Air Bearing Structure. IEEE Trans. Appl. Supercond. 2021, 31, 5204504. [Google Scholar] [CrossRef]
- Zhang, F.; Huang, Q.; Cheng, R.; Zhang, L.; Li, H.; Li, R.; Pan, Q. Development of a Driving and Control System of Large Stroke 3-D Air-Floating Motion Stage with Submicrometer-Scale Positioning Accuracy. IEEE Sens. J. 2024, 24, 2558–2567. [Google Scholar] [CrossRef]
- Zhang, D.W.; Liu, G.P.; Cao, L. Constrained Cooperative Control for High-Order Fully Actuated Multiagent Systems with Application to Air-Bearing Spacecraft Simulators. IEEE/ASME Trans. Mechatron. 2023, 28, 1570–1581. [Google Scholar] [CrossRef]
- Zhang, D.W.; Liu, G.P. Secure Tracking Control of Cyber-Physical Systems Against Hybrid Attacks via FAS Terminal Sliding-Mode Predictive Control. IEEE Trans. Cybern. 2025, 55, 5177–5188. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Gan, H.; Liu, Y.; Luo, Y. Active Disturbance Rejection Fractional-Order Independent Control of Time Delay Systems with Application to Air Floating Motion Platform. IEEE Trans. Instrum. Meas. 2024, 73, 7500410. [Google Scholar] [CrossRef]
- Gao, Y.; Li, W.; Ma, R.; Ma, G.; Xia, H. Spacecraft dynamics full-physical simulator based on air bearing technology. In Proceedings of the IECON 2020 the 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020. [Google Scholar]
- Zhao, M.; Hong, W.; Ma, Y.; Bai, Y.; Zhou, Z. Satellite Simulator for Demonstration of Space Laser Tracking. In Proceedings of the 2022 IEEE 17th Conference on Industrial Electronics and Applications (ICIEA), Chengdu, China, 16–19 December 2022. [Google Scholar]
- Chavan, R.A.; Seigler, T.M.; Hoagg, J.B. Small-Satellite Attitude Control Using Continuous Sinusoids with Strict Amplitude Constraints. IEEE Trans. Control Syst. Technol. 2023, 31, 707–721. [Google Scholar] [CrossRef]
- Jamshidi, S.; Mirzaei, M.; Malekzadeh, M. Applied Optimal Control of Spacecraft Simulator Subject to Failures of Reaction Wheels. Arab. J. Sci. Eng. 2024, 49, 1697–1712. [Google Scholar] [CrossRef]



| Variable Description | Symbol | Value | Units |
|---|---|---|---|
| Max. linear velocity of the simulator | 30 | mm/s | |
| Max. linear acceleration of the simulator | 60 | mm/s2 | |
| Max. angular velocity of the simulator | 1 | °/s | |
| 0.018 | rad/s | ||
| Max. angular acceleration of the simulator | 2 | °/s2 | |
| 0.035 | rad/s2 | ||
| Mass of the simulator | 3000 | kg | |
| Moment of inertia of the simulator | 2000 | kg·m2 | |
| Required max. acceleration force of the simulator | 180 | N | |
| Required max. acceleration torque of the simulator | 70 | Nm | |
| Driving force required per wheel | 140 | N | |
| Contact force per wheel | 1500 | N | |
| Driving force Generated per wheel | 150 | N | |
| Approx. radius of gyration (per wheel) | 700 | mm | |
| Load-fluctuation rate for stable operation | 0.1 | ||
| Friction coefficient | 0.1 |
| Variable Description | Symbol | Value | Units |
|---|---|---|---|
| Required max. velocity per wheel | 43 | mm/s | |
| Required max. acceleration per wheel | 85 | mm/s2 | |
| Velocity limit of the wheel | 50 | mm/s | |
| Acceleration limit of the wheel | 100 | mm/s2 | |
| Steering angle range limit of the wheel | 360 | ° | |
| Steering speed limit of the wheel | 90 | °/s |
| Variable Description | Symbol | Value |
|---|---|---|
| Prediction horizon | 10 | |
| Control horizon | 1 | |
| Sampling time | 0.5 s | |
| State weighting matrix | ||
| Control weighting matrix |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhao, Z.; Jiang, Z.; Xu, Z.; Tian, Y. Leveraging the Symmetry Between Active Dual-Steering-Wheel MPC and Passive Air Bearing for Ground-Based Satellite Hovering Tests. Symmetry 2025, 17, 1990. https://doi.org/10.3390/sym17111990
Zhang X, Zhao Z, Jiang Z, Xu Z, Tian Y. Leveraging the Symmetry Between Active Dual-Steering-Wheel MPC and Passive Air Bearing for Ground-Based Satellite Hovering Tests. Symmetry. 2025; 17(11):1990. https://doi.org/10.3390/sym17111990
Chicago/Turabian StyleZhang, Xiao, Zhen Zhao, Zainan Jiang, Zhigang Xu, and Yonglin Tian. 2025. "Leveraging the Symmetry Between Active Dual-Steering-Wheel MPC and Passive Air Bearing for Ground-Based Satellite Hovering Tests" Symmetry 17, no. 11: 1990. https://doi.org/10.3390/sym17111990
APA StyleZhang, X., Zhao, Z., Jiang, Z., Xu, Z., & Tian, Y. (2025). Leveraging the Symmetry Between Active Dual-Steering-Wheel MPC and Passive Air Bearing for Ground-Based Satellite Hovering Tests. Symmetry, 17(11), 1990. https://doi.org/10.3390/sym17111990







