Settlement Prediction of Preloading Method Based on SSA-BP Neural Network with Consideration of Asymmetric Settlement Behavior
Abstract
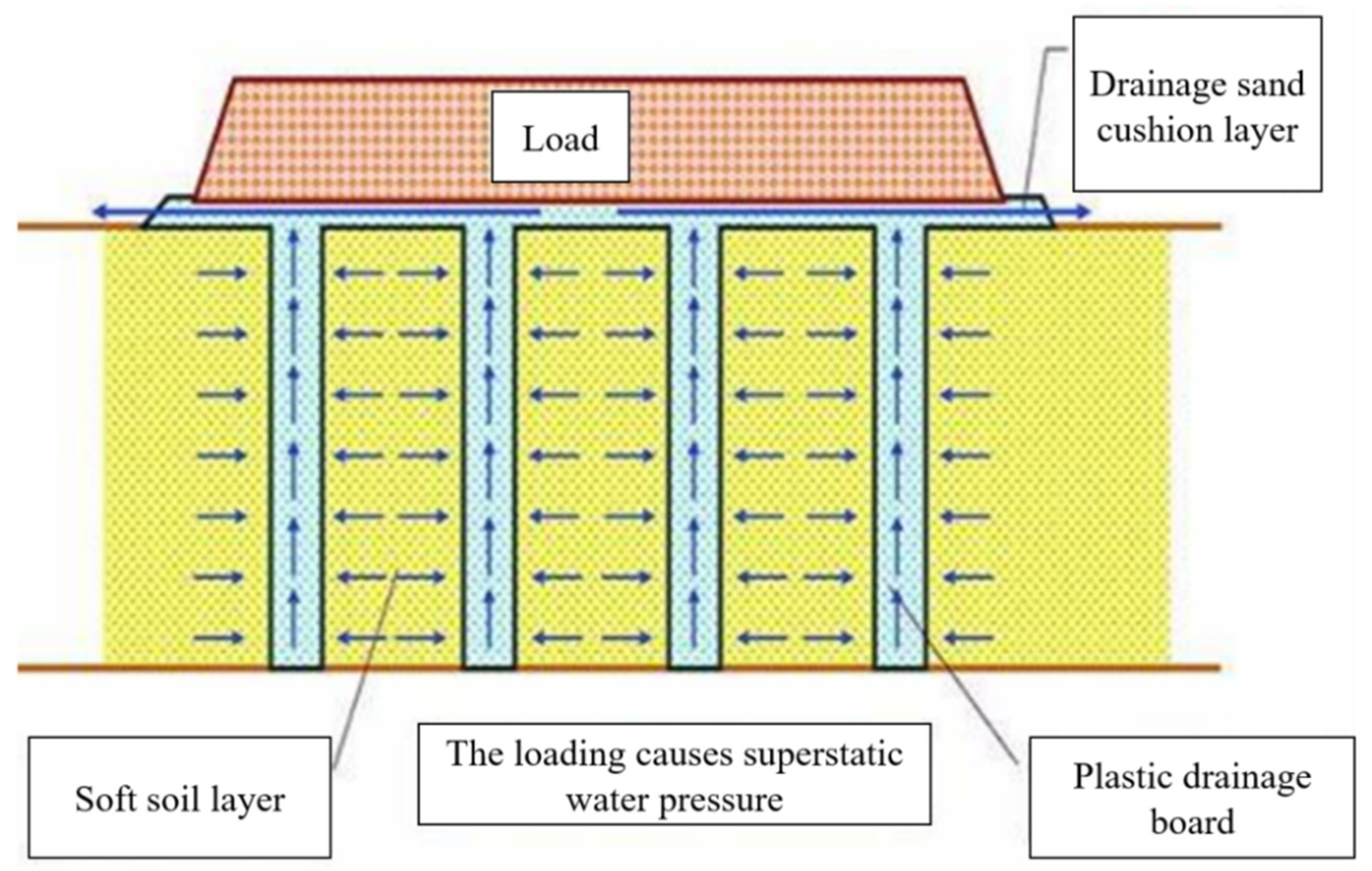
1. Introduction
2. Sparrow Search Algorithm Theory
2.1. Research Status of Sparrow Search Optimization Algorithm
2.2. Principles of Sparrow Search Optimization Algorithm
3. Construction of SSA-BP Model
3.1. SSA-BP Model Evaluation Indicators
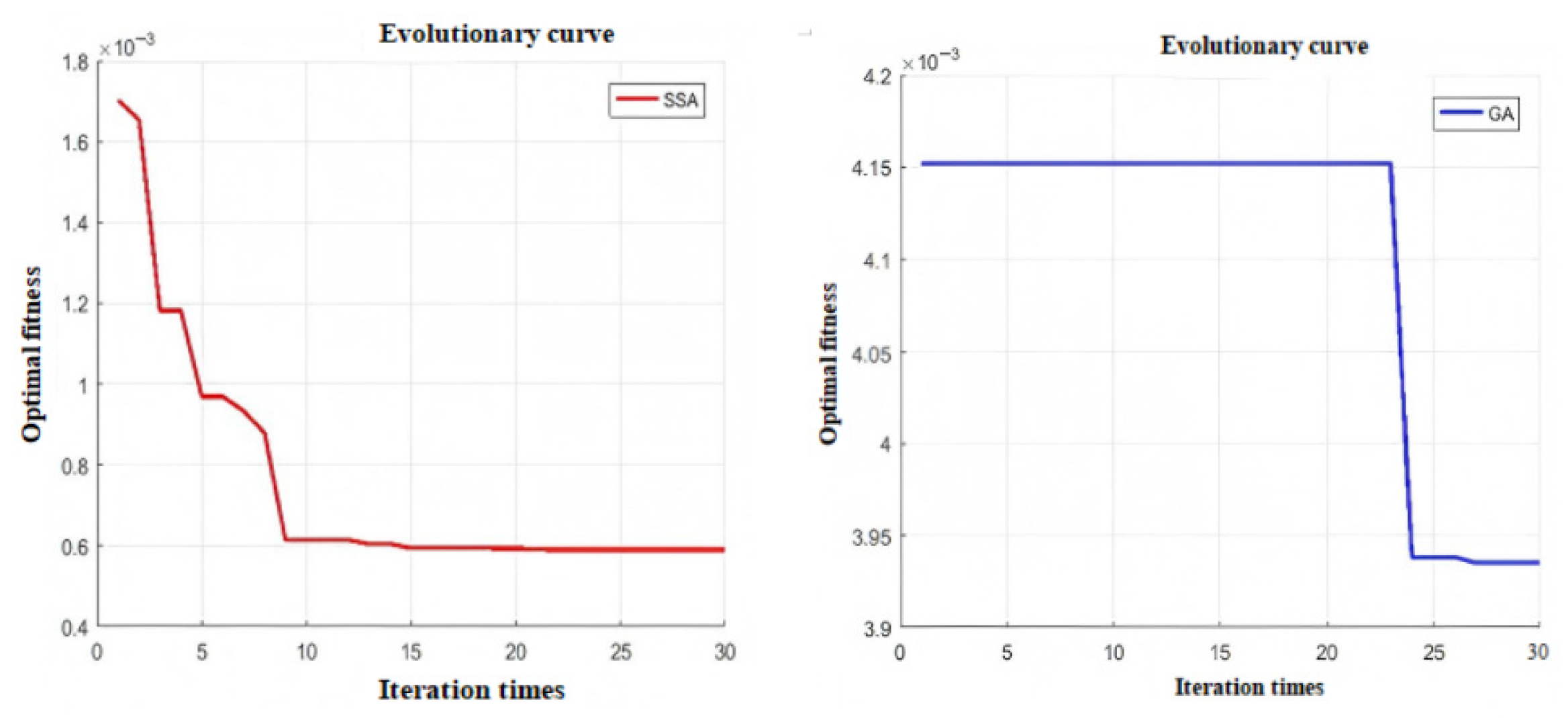
3.2. Algorithm Excellence Test
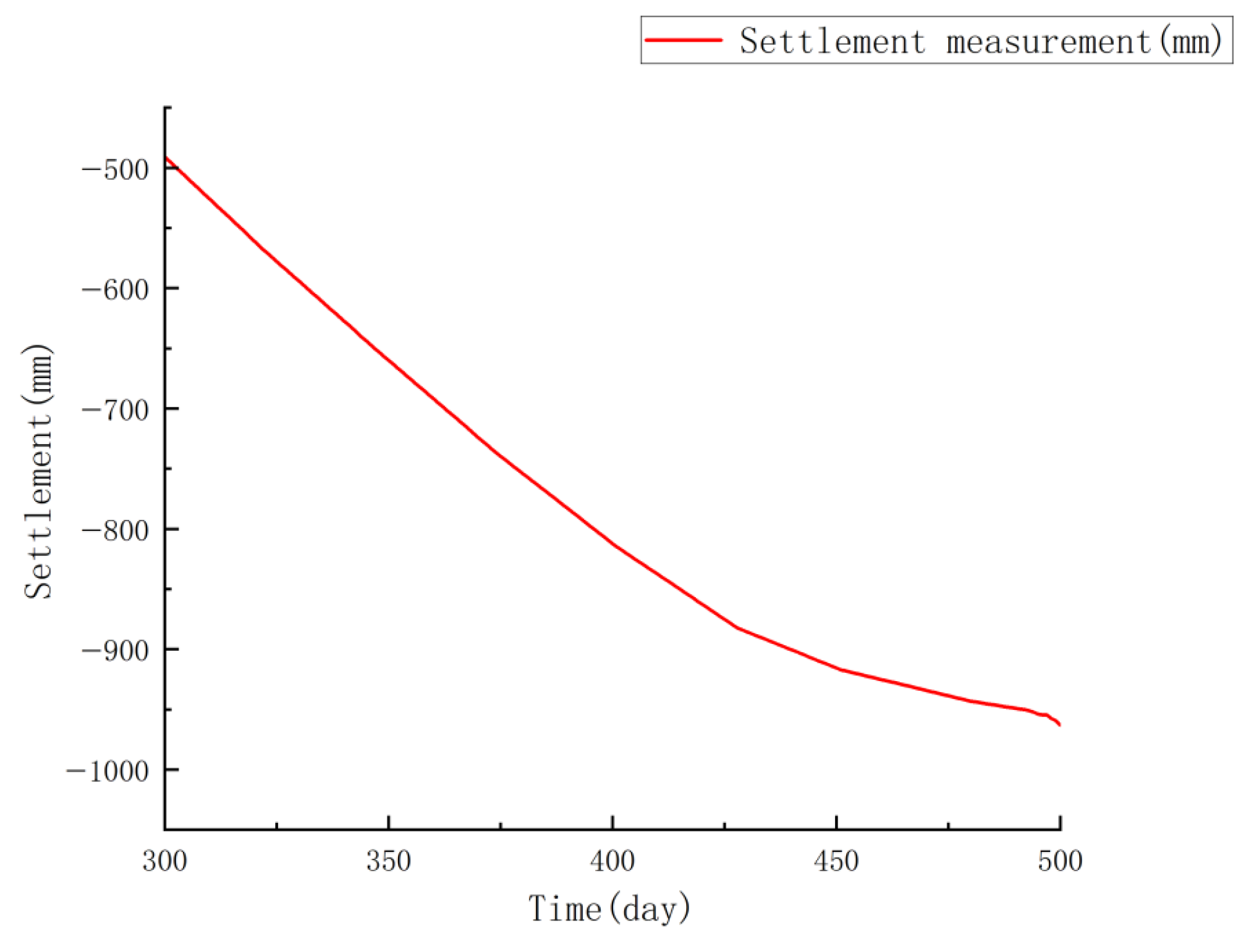
3.3. Comparison of SSA-BP Vertical Settlement Prediction
- ① BP neural network parameter setting
- ② Basic parameter settings for Sparrow Search Algorithm
- ③ Train and predict
4. Comparison of Settlement Prediction
4.1. Three-Point Method
4.2. Hyperbola Method
4.3. Comparison of Calculation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Wu, H. The Application of Plastic Drainage Board Preloading Method in Hydraulic Embankments. Henan Water Conserv. South-North Water Divers. Proj. 2018, 47, 44–45. [Google Scholar]
- She, Q. Application of Surcharge Preload Method in Soft Soil Foundation Treatment of Workshop. Fujian Archit. Constr. 2019, 1, 33–35. [Google Scholar]
- He, P. The Study of Adopting PVD (Plastic Vertical Drain) Preloading Method in Sir Lanka South Railway Subgrade Construction. Constr. Des. For Eng. 2018, 70–73. [Google Scholar] [CrossRef]
- Li, D.; Chen, L.; Chen, Y.; Hu, S.; Chai, Z. Application of artificial solidified crust—PVDs method in ground improvement: A case study. Transp. Geotech. 2023, 39, 100941. [Google Scholar] [CrossRef]
- Yang, S.; Yang, A.; XUF. Vacuum preloading reinforcement of soft dredger soil by modified fiber drainage plate. Rock Soil Mech. 2025, 46, 789–797. [Google Scholar]
- Zhang, C. The Application of Vacuum Combined with Preloading in the Treatment of Municipal Roads on Deep Soft Foundations. Sci. Technol. Innov. 2025, 193–196. [Google Scholar]
- Shao, Z. Plastic Drainage Plate + Preloading Technology in Municipal Road Engineering. North. Build. 2024, 9, 26–29. [Google Scholar]
- Chen, Y.; Chen, Y.; Chen, Z.; Lin, J.; Zhang, M. Research on Innovative Design of Combined Vacuum and Load Preloading Treatment Technology of Composite Plastic Drain Plate. Adhesion 2023, 50, 173–176. [Google Scholar]
- Liu, X. Swirl Enhanced Drainage and Traditional PVC Drain in My Opinion. Sci. Technol. Inf. 2014, 222–223. [Google Scholar]
- Cheng, Z. Study on the Settlement Prediction of Saturated Soft Clay by Plastic Drainage Board Preloading. Master’s Thesis, Zhejiang Sci-Tech University, Hangzhou, China, 2018. [Google Scholar]
- Du, H.; Liu, J.; Yuan, Y.; Zhang, Y.; Song, S.; Xiao, H.; Huang, X. Study on The Methods of Ground Improvement for Widening Expressway on Soft Ground. In Proceedings of the 5th International Conference on Civil Engineering and Transportation 2015, Guangzhou, China, 28–29 November 2015; Atlantis Press: Paris, France, 2016; pp. 840–845. [Google Scholar]
- Pan, Z. Research on the Application of Vacuum Preloading Technology in Soft Soil Foundation. Brick Tile 2025, 152–154. [Google Scholar]
- Hu, X. Application and Discussion of Direct Drainage Method with Plastic Drainage Board Vacuum Preloading Construction Technology. West-China Explor. Eng. 2024, 36, 35–39. [Google Scholar]
- Li, C.; Dias, D. Intelligent prediction and visual optimization of surface settlement induced by earth pressure balance shield tunneling. Tunn. Undergr. Space Technol. 2024, 154, 106138. [Google Scholar] [CrossRef]
- Liao, M.; Wang, K.; Zhou, X.; Tian, L.; Wang, J.; Zhang, H.; Du, Y.; Yang, E. Development of an Intelligent Monitoring System for Settlement Prediction of High-Fill Subgrade. Infrastructures 2025, 10, 220. [Google Scholar] [CrossRef]
- Hu, M.; Zhao, P.; Lu, J.; Wu, B. Mechanism-Driven Intelligent Settlement Prediction for Shield Tunneling Through Areas Without Ground Monitoring. Smart Cities 2025, 8, 6. [Google Scholar] [CrossRef]
- Kovačević, M.; Hadzima-Nyarko, M.; Petronijević, P.; Vasiljević, T.; Radomirović, M. Comparative Analysis of Machine Learning Models for Predicting Interfacial Bond Strength of Fiber-Reinforced Polymer-Concrete. Computation 2025, 13, 17. [Google Scholar] [CrossRef]
- Raju, M.; Shanmugam, K.P.; Shyu, C.R. Application of Machine Learning Predictive Models for Early Detection of Glaucoma Using Real World Data. Appl. Sci. 2023, 13, 2445. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, Q.; Xu, Z. Optimization of Bridge Crane Main Beam Dimensions Based on Sparrow Search Algorithm and Finite Element Analysis. Highlights Sci. Eng. Technol. 2023, 79, 30–38. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A Survey on Sparrow Search Algorithms and Their Applications. Int. J. Syst. Sci. 2024, 55, 814–832. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Y. An Improved Sparrow Search Algorithm for Optimizing Support Vector Machines. IEEE Access 2023, 11, 8199–8206. [Google Scholar] [CrossRef]
- Wang, T.; Zhou, H.; Liu, H. Multi-Label Feature Selection Based on HSIC and Sparrow Search Algorithm. Math. Biosci. Eng. 2023, 20, 14201–14221. [Google Scholar] [CrossRef]
- Shi, G.; Li, R.; Li, F.; Niu, Y.; Yang, L. Depth Sensing with Coding-Free Pattern Based on Topological Constraint. J. Vis. Commun. Image Represent. 2018, 55, 229–242. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, T.; Yang, F.; Yang, Q. A Study of Adaptive Fractional-Order Total Variational Medical Image Denoising. Fractal Fract. 2022, 6, 508. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, Y.; Li, M.; Zhang, Z.; Cao, N.; Shang, J. Multi-UAV Path Planning Based on Fusion of Sparrow Search Algorithm and Improved Bioinspired Neural Network. IEEE Access 2021, 9, 124670–124681. [Google Scholar] [CrossRef]
- Khaleel, M.I. Efficient Job Scheduling Paradigm Based on Hybrid Sparrow Search Algorithm and Differential Evolution Optimization for Heterogeneous Cloud Computing Platforms. Internet Things 2023, 22, 100697. [Google Scholar] [CrossRef]
- Abdulhammed, O.Y. Load Balancing Of Iot Tasks in The Cloud Computing by Using Sparrow Search Algorithm. J. Supercomput. 2022, 78, 3266–3287. [Google Scholar] [CrossRef]
- Jia, H.; Zheng, H.; Huo, S.; Zhou, H.; Zhang, Q. Autonomous Prediction of UAV Launch Parameters Based on SSA-BP Model. In Proceedings of the 2024 WRC Symposium on Advanced Robotics and Automation (WRC SARA), Beijing, China, 23 August 2024. [Google Scholar] [CrossRef]
- Zhang, B.; Tao, X.; Zhang, H.; Yu, J. Study of an SSA-BP Neural Network-Based Strength Prediction Model for Slag–Cement-Stabilized Soil. Materials 2025, 18, 3520. [Google Scholar] [CrossRef]
- Luo, J.; Wang, L.; Xiao, B.; Gao, S.; Li, W.; Deng, J.; Liang, C.; Xia, Y. Bending Prediction Of Bulb Flat Steel By Neural Network Algorithm Based On SSA-BP. In Proceedings of the 2024 IEEE International Conference on Cognitive Computing and Complex Data (ICCD), Qinzhou, China, 28–30 September 2024. [Google Scholar]
- Lee, J.; Kim, K.; Kang, M.; Hong, E.S.; Choi, S. Void Detection for Tunnel Lining Backfill Using Impact-Echo Method Based on Continuous Wavelet Transform and Convolutional Neural Network. Geomech. Eng. 2024, 36, 1–8. [Google Scholar]
- Yan, S.; Liu, W.; Li, X.; Yang, P.; Wu, F.; Yan, Z. Comparative Study and Improvement Analysis of Sparrow Search Algorithm. Wirel. Commun. Mob. Comput. 2022, 2022, 4882521. [Google Scholar] [CrossRef]
- Karakaya, A.-S.; Köhler, K.; Heinovski, J.; Dressler, F.; Bermbach, D. A Realistic Cyclist Model for SUMO Based on the SimRa Dataset. In Proceedings of the 2022 20th Mediterranean Communication and Computer Networking Conference (MedComNet), Pafos, Cyprus, 1–3 June 2022; IEEE Conference Publication: Piscataway, NJ, USA, 2022. [Google Scholar]
- Lawley, C.J.; Gadd, M.G.; Parsa, M.; Lederer, G.W.; Graham, G.E.; Ford, A. Applications of Natural Language Processing to Geoscience Text Data and Prospectivity Modeling. Nat. Resour. Res. 2023, 32, 1503–1527. [Google Scholar] [CrossRef]
- Cang, N.; Qiu, F.; Xue, S.; Jia, Z.; Guo, D.; Zhang, Z.; Li, W. New Discrete-Time Zeroing Neural Network For Solving Time-Dependent Linear Equation with Boundary Constraint. Artif. Intell. Rev. 2024, 57, 140. [Google Scholar]
- Tang, Y.; Xiao, S.; Zhan, Y. Predicting Settlement Along Railway Due to Excavation Using Empirical Method and Neural Networks. Soils Found. 2019, 59, 1037–1051. [Google Scholar] [CrossRef]
- Chung, S.G.; Kweon, H.J. Prediction of Three-Dimensional Consolidation Settlement: Observational Method and Its Applicability. Int. J. Geomech. 2023, 23, 04022308. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, X.; Wang, J. A New Nonlinear Method for Vertical Settlement Prediction of A Single Pile and Pile Groups in Layered Soils. Comput. Geotech. 2012, 45, 118–126. [Google Scholar] [CrossRef]
- Huang, G. Problems and Their Solutions in Predicting Soft Ground Settlement Based on Asaoka’s Method. Rock Soil Mech. 2016, 37, 1061–1065. [Google Scholar]
- Wu, Y. Research on Settlement Monitoring and Prediction of Soft Soil Roadbeds on Highways. Jiangxi Jiancai 2024, 301–303. [Google Scholar]


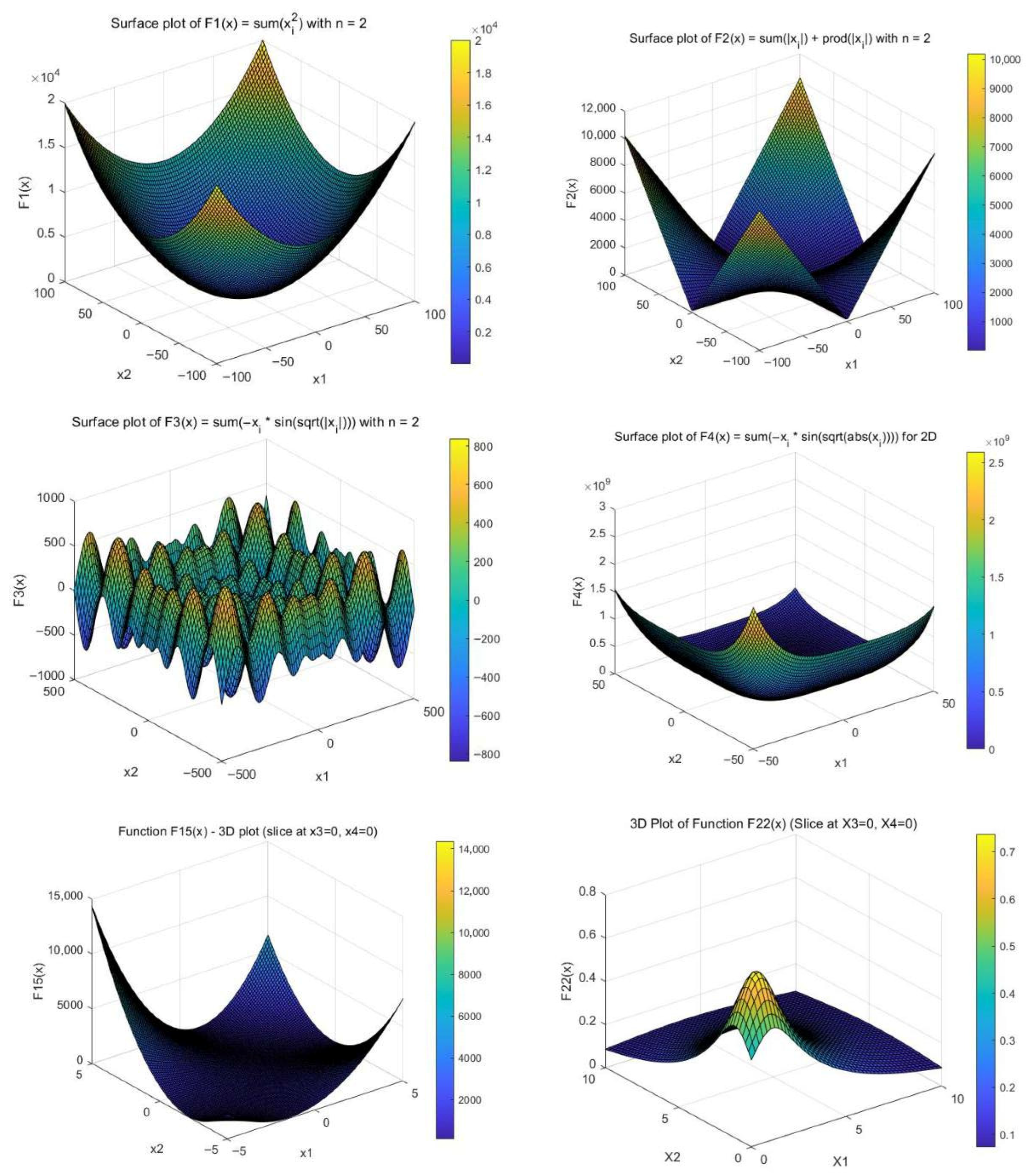







| Algorithm | PSO | DE | GWO | SSA |
|---|---|---|---|---|
| Parameters | c1 = 2 c2 = 2 Wmin = 0.2 Wmax = 0.9 | CR = 0.2 Fmin = 0.2 Fmax = 0.8 | a = (2→0) | ST = 0.8 PD = 0.2 SD = 0.2 |
| Test Function | Dimension | Interval | Minimum Value |
|---|---|---|---|
| 30 | [−100, 100] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−500, 500] | −418.98 × dim | |
| 30 | [−50, 50] | 0 | |
| 4 | [−5, 5] | 0 | |
| 4 | [0, 10] | −10.40 |
| F | Indicators/Algorithms | PSO | DE | GWO | SSA |
|---|---|---|---|---|---|
| Best | 8.93 × 10−6 | 5.55 × 10−14 | 6.31 × 10−28 | 0 | |
| Worst | 8.36 × 10−4 | 4.46 × 104 | 4.66 × 10−25 | 1.37 × 10−67 | |
| F1 | Ave | 1.63 × 10−4 | 3.31 × 103 | 5.25 × 10−26 | 4.58 × 10−69 |
| Std | 2.13 × 10−4 | 1.07 × 104 | 1.13 × 10−25 | 2.51 × 10−68 | |
| Rank | 3 | 4 | 2 | 1 | |
| Best | 4.10 × 10−4 | 5.61 | 1.47 × 10−16 | 0 | |
| Worst | 0.27 | 3.71 × 1013 | 1.61 × 10−15 | 3.45 × 10−40 | |
| F2 | Ave | 0.04 | 1.28 × 1012 | 6.19 × 10−16 | 1.15 × 10−41 |
| Std | 5.50 × 10−2 | 6.77 × 1012 | 3.56 × 10−16 | 6.30 × 10−41 | |
| Rank | 3 | 4 | 2 | 1 | |
| Best | −7203.72 | −12566 | −10562 | −1.26 × 104 | |
| Worst | −2664.29 | −6671.64 | −8506.23 | −9.50 × 103 | |
| F3 | Ave | −5937.33 | −10130.9 | −9321.52 | −1.06 × 104 |
| Std | 1187.28 | 1920.468 | 1570.104 | 2.61 × 103 | |
| Rank | 4 | 2 | 3 | 1 | |
| Best | 5.13 × 10−7 | 3.55 × 10−3 | 6.06 × 10−3 | 1.57 × 10−32 | |
| Worst | 0.114 | 9.25 × 10−2 | 6.53 × 10−2 | 4.18 × 10−8 | |
| F4 | Ave | 3.90 × 10−2 | 2.40 × 10−2 | 2.25 × 10−2 | 2.15 × 10−9 |
| Std | 2.10 × 10−2 | 1.86 × 10−2 | 1.45 × 10−2 | 8.19 × 10−9 | |
| Rank | 4 | 3 | 2 | 1 | |
| Best | 4.10 × 10−3 | 5.608 | 1.47 × 10−16 | 0 | |
| Worst | 2.71 × 10−1 | 3.71 × 1013 | 1.61 × 10−15 | 3.45 × 10−40 | |
| F15 | Ave | 4.03 × 10−2 | 1.28 × 1012 | 6.19 × 10−16 | 1.15 × 10−41 |
| Std | 5.51 × 10−2 | 6.77 × 1012 | 3.56 × 10−16 | 6.30 × 10−41 | |
| Rank | 3 | 4 | 2 | 1 | |
| Best | −10.402 | −6.431 | −10.4 | −10.402 | |
| Worst | −2.752 | −0.528 | −5.09 | −5.088 | |
| F22 | Ave | −8.587 | −1.759 | −9.34 | −9.871 |
| Std | 3.105 | 1.362 | 2.162 | 1.622 | |
| Rank | 3 | 4 | 2 | 1 |
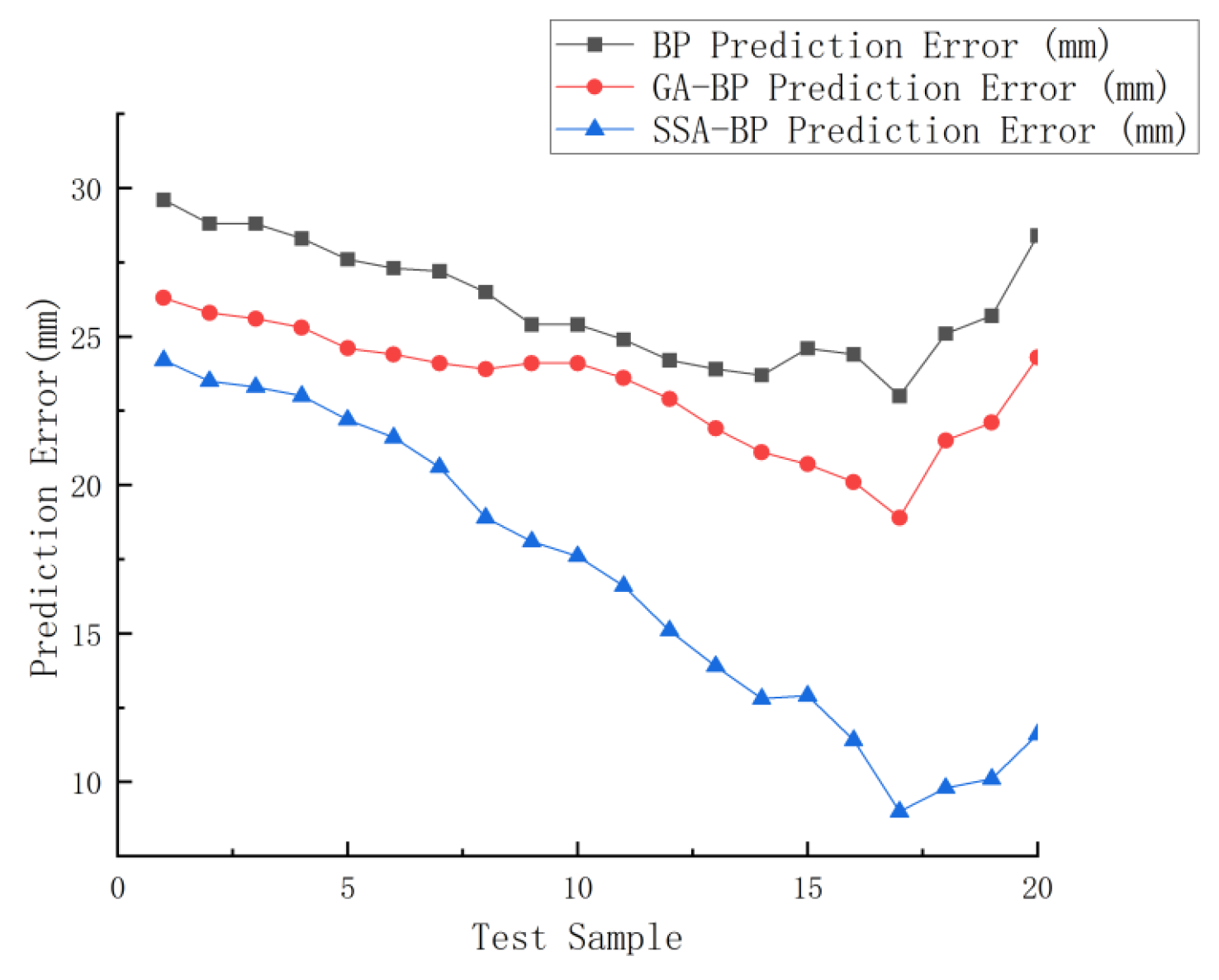
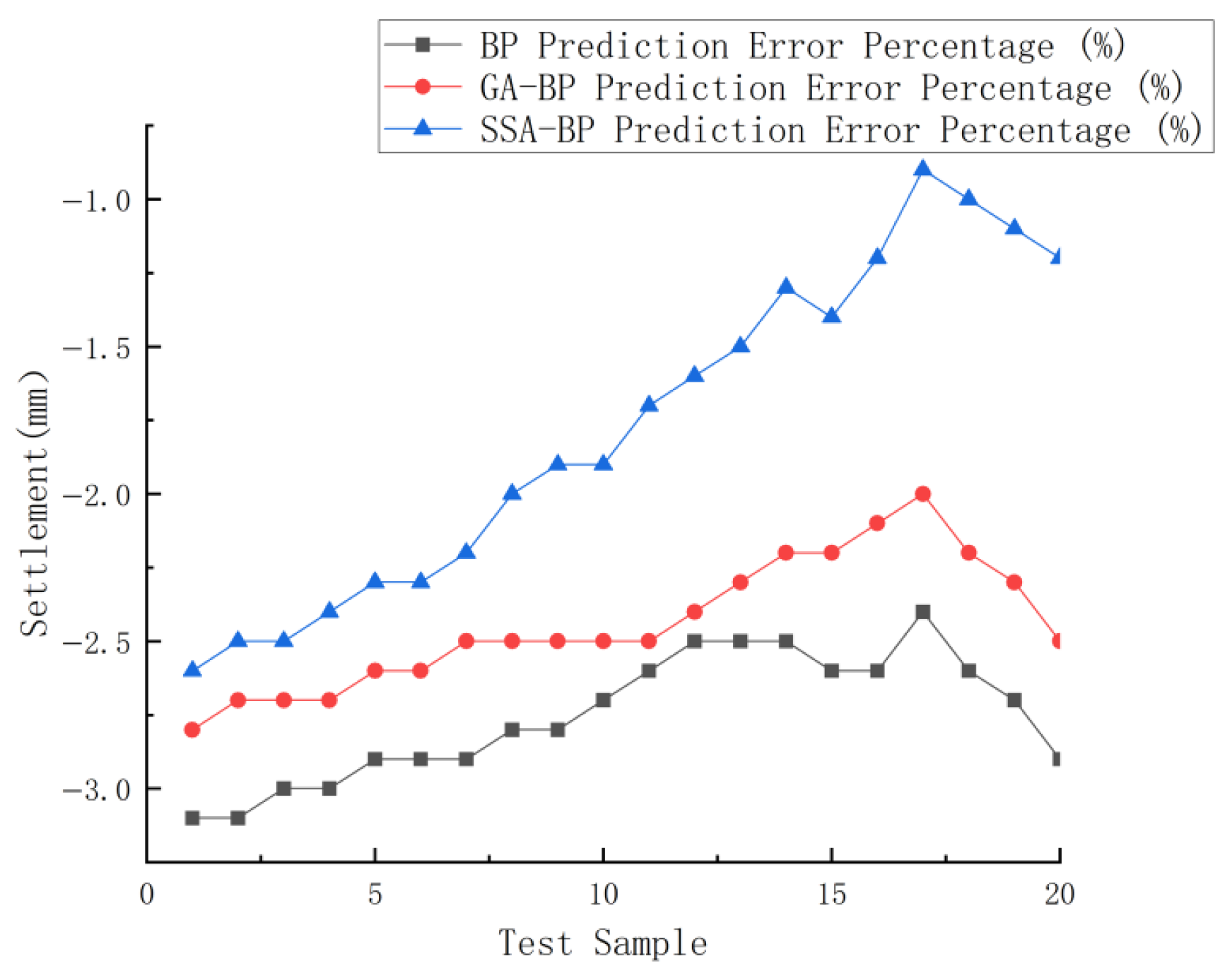
| Period | Actuality (mm) | BP Neural Networks | GA-BP Neural Networks | SSA-BP Neural Networks | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Estimate | Error | Percentage | Estimate | Error | Percentage | Estimate | Error | Percentage | ||
| 1 | −943.8 | −914.2 | 29.6 | −3.1% | −917.5 | 26.3 | −2.8% | −919.6 | 24.2 | −2.6% |
| 2 | −944.0 | −915.2 | 28.8 | −3.1% | −918.2 | 25.8 | −2.7% | −920.5 | 23.5 | −2.5% |
| 3 | −945 | −916.2 | 28.8 | −3.0% | −919.4 | 25.6 | −2.7% | −921.7 | 23.3 | −2.5% |
| 4 | −945.8 | −917.5 | 28.3 | −3.0% | −920.5 | 25.3 | −2.7% | −922.8 | 23 | −2.4% |
| 5 | −946.2 | −918.6 | 27.6 | −2.9% | −921.6 | 24.6 | −2.6% | −924.0 | 22.2 | −2.3% |
| 6 | −946.8 | −919.5 | 27.3 | −2.9% | −922.4 | 24.4 | −2.6% | −925.2 | 21.6 | −2.3% |
| 7 | −947.7 | −920.5 | 27.2 | −2.9% | −923.6 | 24.1 | −2.5% | −927.1 | 20.6 | −2.2% |
| 8 | −948 | −921.5 | 26.5 | −2.8% | −924.1 | 23.9 | −2.5% | −929.1 | 18.9 | −2.0% |
| 9 | −948.6 | −922.4 | 25.4 | −2.8% | −924.5 | 24.1 | −2.5% | −930.5 | 18.1 | −1.9% |
| 10 | −949.2 | −923.8 | 25.4 | −2.7% | −925.1 | 24.1 | −2.5% | −931.6 | 17.6 | −1.9% |
| 11 | −949.8 | −924.9 | 24.9 | −2.6% | −926.2 | 23.6 | −2.5% | −933.2 | 16.6 | −1.7% |
| 12 | −950.2 | −926.0 | 24.2 | −2.5% | −927.3 | 22.9 | −2.4% | −935.1 | 15.1 | −1.6% |
| 13 | −951.1 | −927.2 | 23.9 | −2.5% | −929.2 | 21.9 | −2.3% | −937.2 | 13.9 | −1.5% |
| 14 | −952.3 | −928.6 | 23.7 | −2.5% | −931.2 | 21.1 | −2.2% | −939.5 | 12.8 | −1.3% |
| 15 | −953.9 | −929.3 | 24.6 | −2.6% | −933.2 | 20.7 | −2.2% | −941.0 | 12.9 | −1.4% |
| 16 | −954.6 | −930.2 | 24.4 | −2.6% | −934.5 | 20.1 | −2.1% | −943.2 | 11.4 | −1.2% |
| 17 | −954.5 | −931.5 | 23 | −2.4% | −935.6 | 18.9 | −2.0% | −945.5 | 9 | −0.9% |
| 18 | −957.6 | −932.5 | 25.1 | −2.6% | −936.1 | 21.5 | −2.2% | −947.8 | 9.8 | −1.0% |
| 19 | −959.3 | −933.6 | 25.7 | −2.7% | −937.2 | 22.1 | −2.3% | −949.2 | 10.1 | −1.1% |
| 20 | −962.9 | −934.5 | 28.4 | −2.9% | −938.6 | 24.3 | −2.5% | −951.3 | 11.6 | −1.2% |
| Evaluation | BP | GA-BP | SSA-BP |
|---|---|---|---|
| SSE | 13,781.8 | 10,904.0 | 6158.7 |
| MAE | 26.18 | 23.27 | 16.81 |
| MSE | 689.1 | 545.2 | 307.9 |
| RMSE | 26.25 | 23.35 | 17.55 |
| MAPE | 2.75% | 2.45% | 1.77% |
| R | 0.9119 | 0.9213 | 0.9543 |
| R2 | 0.8315 | 0.8488 | 0.9107 |
| Measuring Point | t1 | (mm) | t2 | (mm) | t3 | (mm) |
|---|---|---|---|---|---|---|
| CJ5 | 380 | −728.2 | 400 | −776.2 | 420 | −812.8 |
| CJ13 | 390 | −782.2 | 410 | −837.6 | 430 | −885.6 |
| CJ17 | 370 | −986.4 | 390 | −1046.3 | 410 | −1087.1 |
| Measuring Point | Predicting Settlement (mm) | Secondary Consolidation Settlement (mm) | (mm) | ||
|---|---|---|---|---|---|
| CJ5 | 37.53 | 0.0136 | −930.3 | 54.4 | −984.7 |
| CJ13 | 5.67 | 0.0071 | −1197.0 | 55.3 | −1252.3 |
| CJ17 | 194.64 | 0.0192 | −1158.9 | 70.5 | −1239.4 |
| Measurement Point | R2 | ||
|---|---|---|---|
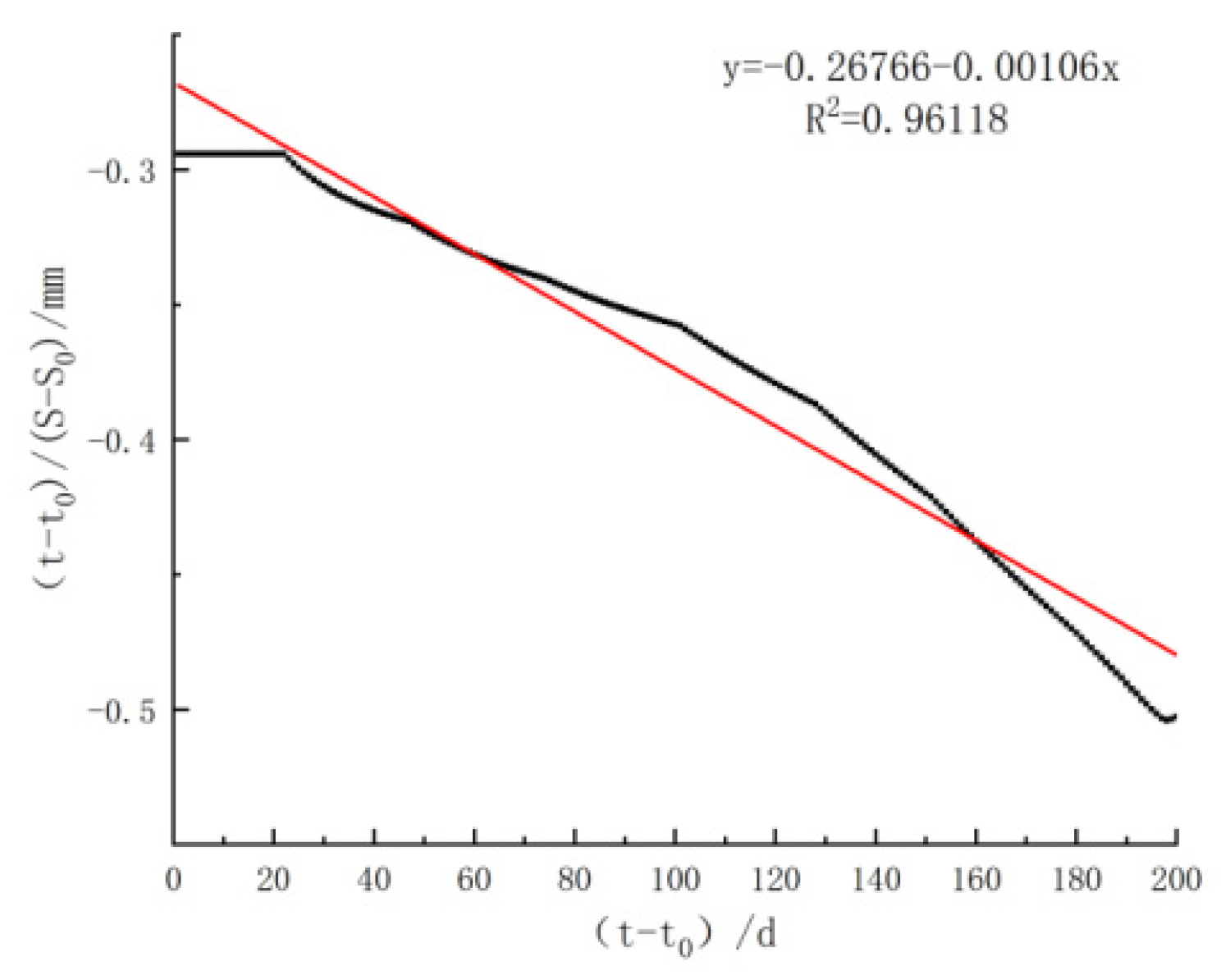
| CJ5 | −0.26766 | −0.00106 | 0.96118 |
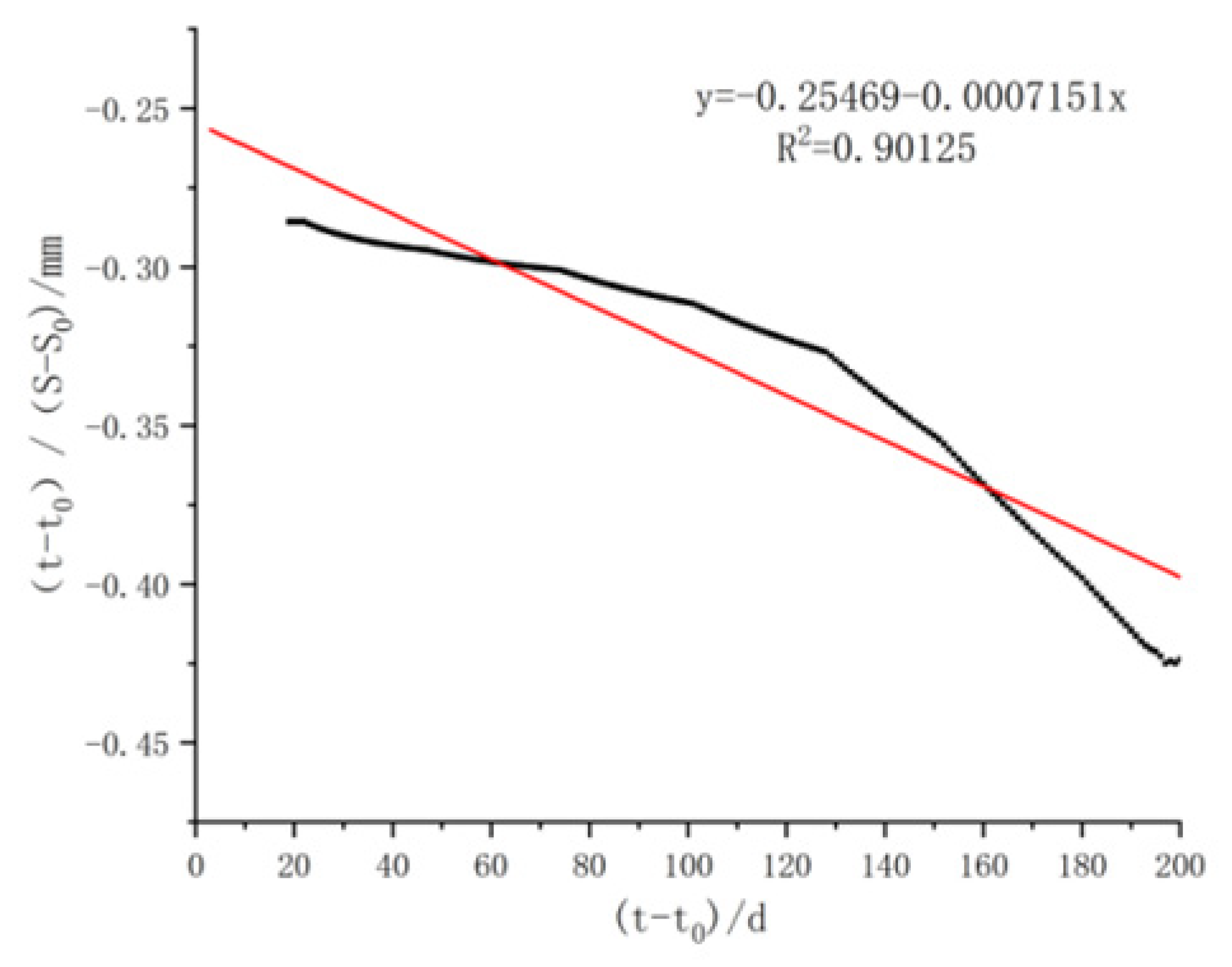
| CJ13 | −0.25469 | −0.00071 | 0.90125 |
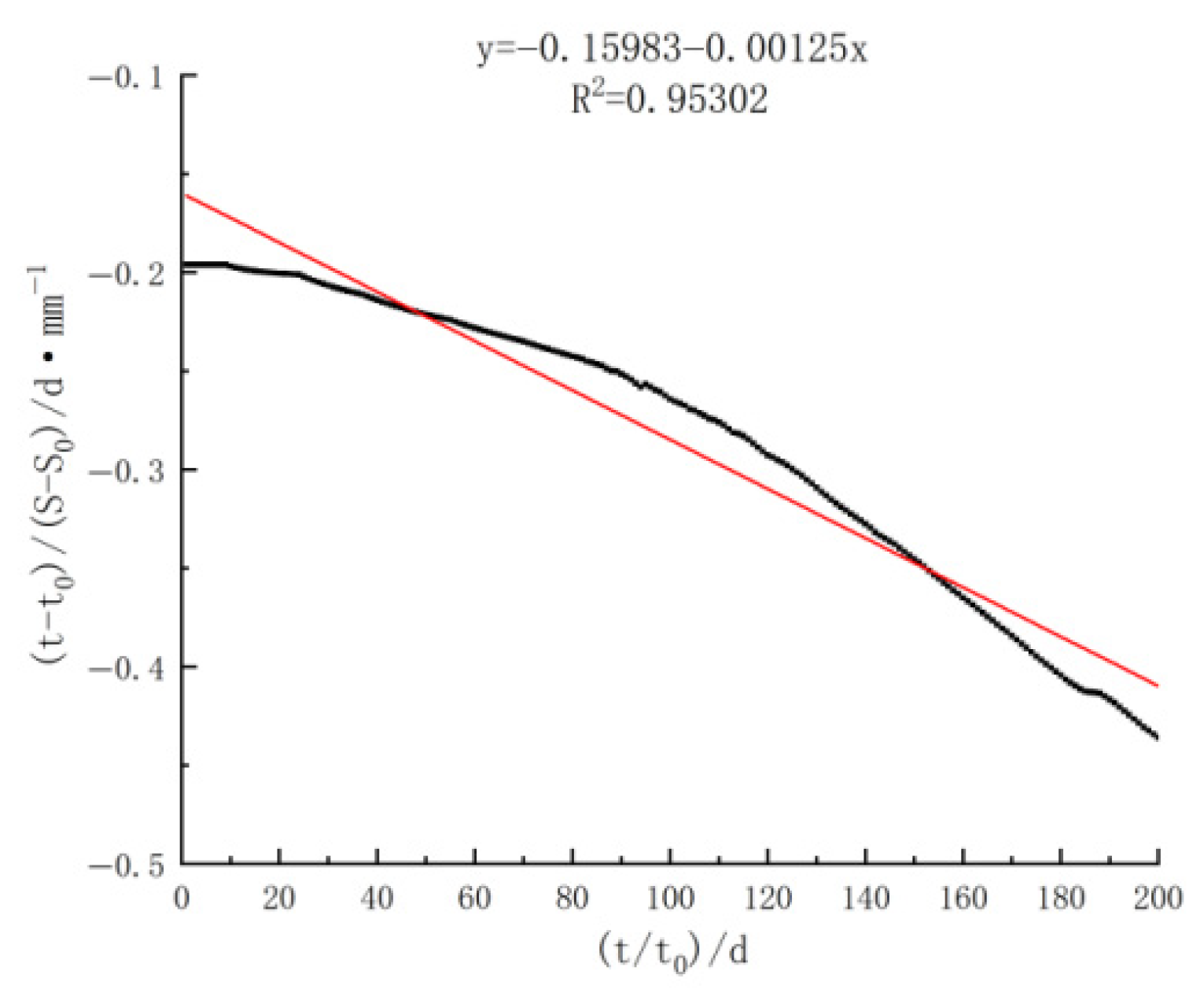
| CJ17 | −0.15983 | −0.00125 | 0.95302 |
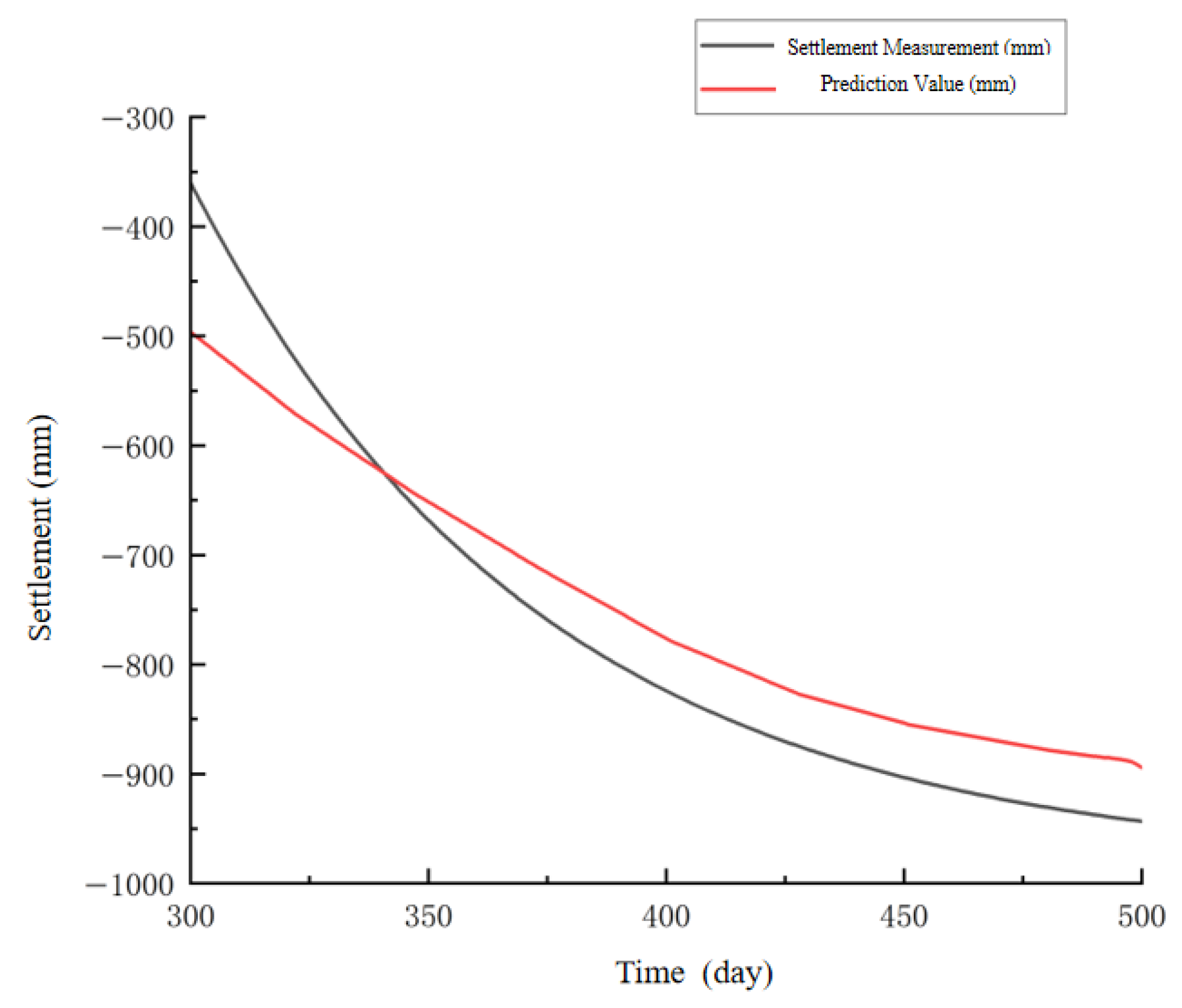
| Monitor Time | Actuality (mm) | Three-Point Method | Hyperbola Method | SSA-BP | |||
|---|---|---|---|---|---|---|---|
| Estimate (mm) | Error | Estimate (mm) | Error | Estimate (mm) | Error | ||
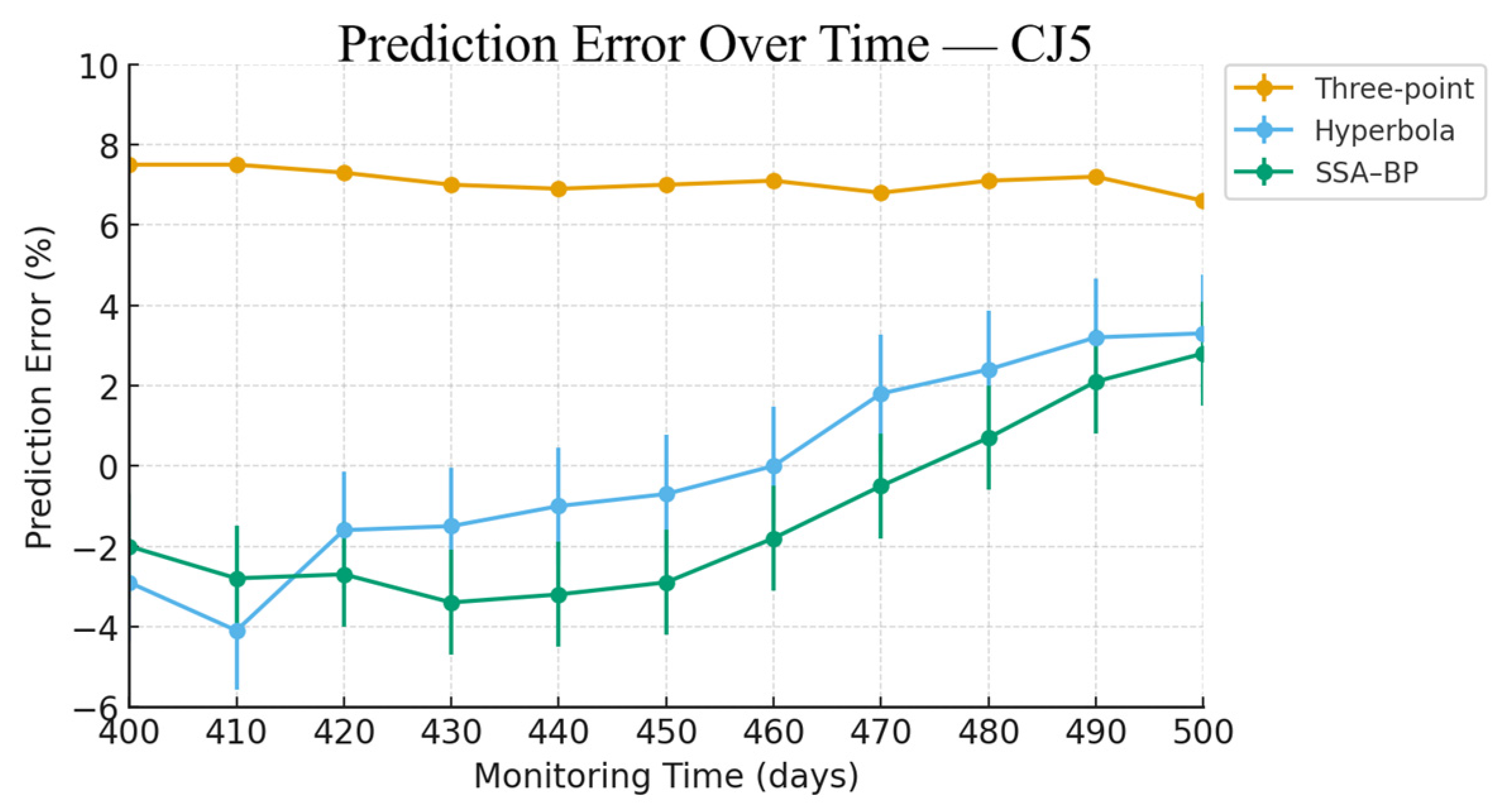
| 400 | −776.2 | −834.1 | 7.5% | −753.9 | −2.9% | −760.5 | −2.0% |
| 410 | −794.8 | −854.5 | 7.5% | −762.6 | −4.1% | −772.5 | −2.8% |
| 420 | −812.8 | −872.3 | 7.3% | −800.2 | −1.6% | −790.5 | −2.7% |
| 430 | −829.6 | −887.8 | 7.0% | −816.9 | −1.5% | −801.2 | −3.4% |
| 440 | −841.6 | −899.3 | 6.9% | −832.8 | −1.0% | −814.5 | −3.2% |
| 450 | −853.6 | −913.2 | 7.0% | −847.9 | −0.7% | −828.8 | −2.9% |
| 460 | −862.5 | −923.5 | 7.1% | −862.2 | 0.0% | −847.2 | −1.8% |
| 470 | −870.0 | −929.5 | 6.8% | −885.9 | 1.8% | −865.6 | −0.5% |
| 480 | −878.0 | −940.4 | 7.1% | −898.9 | 2.4% | −884.0 | 0.7% |
| 490 | −883.4 | −947.3 | 7.2% | −911.4 | 3.2% | −902.3 | 2.1% |
| 500 | −894.2 | −953.3 | 6.6% | −923.3 | 3.3% | −919.2 | 2.8% |
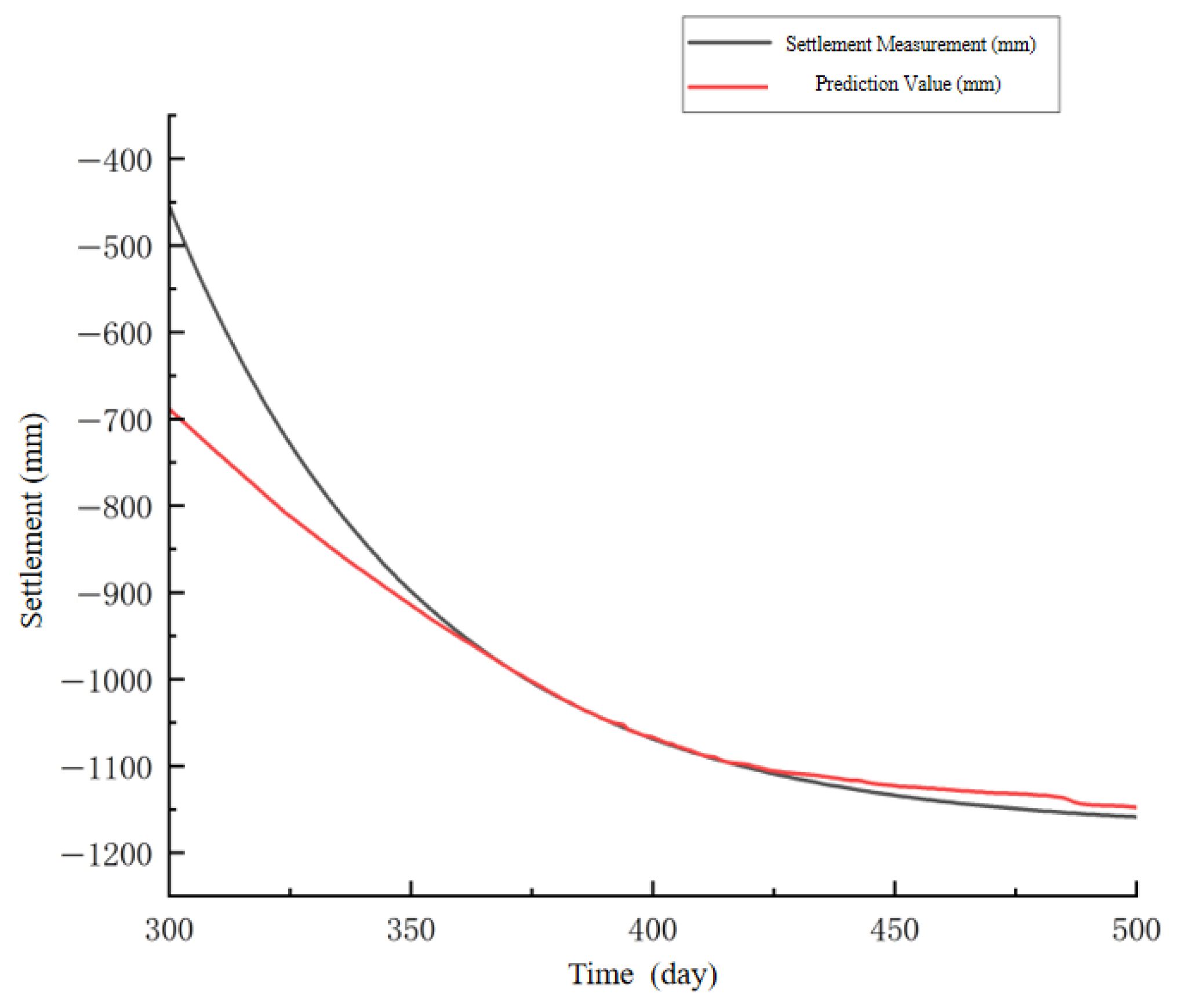
| Monitor Time | Actuality (mm) | Three-Point Method | Hyperbola Method | SSA-BP | |||
|---|---|---|---|---|---|---|---|
| Estimate (mm) | Error | Estimate (mm) | Error | Estimate (mm) | Error | ||
| 400 | −812.2 | −837.4 | 3.1% | −777.9 | −4.2% | −807.1 | −0.6% |
| 410 | −837.6 | −865.9 | 3.4% | −801.4 | −4.3% | −832.8 | −0.6% |
| 420 | −862.6 | −892.4 | 3.5% | −824.0 | −4.5% | −849.2 | −1.6% |
| 430 | −885.6 | −917.0 | 3.5% | −845.6 | −4.5% | −862.5 | −2.6% |
| 440 | −900.6 | −940.0 | 4.4% | −866.3 | −3.8% | −879.5 | −2.3% |
| 450 | −915.6 | −961.4 | 5.0% | −886.2 | −3.2% | −885.6 | −3.3% |
| 460 | −925.3 | −981.4 | 6.1% | −905.3 | −2.2% | −894.7 | −3.3% |
| 470 | −934.2 | −999.9 | 7.0% | −923.8 | −1.1% | −908.5 | −2.8% |
| 480 | −943.2 | −1017.2 | 7.8% | −941.5 | −0.2% | −919.6 | −2.5% |
| 490 | −949.2 | −1034.9 | 9.0% | −958.6 | 1.0% | −931.6 | −1.9% |
| 500 | −962.9 | −1048.3 | 8.9% | −975.1 | 1.3% | −951.3 | −1.2% |
| Monitor Time | Actuality (mm) | Three-Point Method | Hyperbola Method | SSA-BP | |||
|---|---|---|---|---|---|---|---|
| Estimate (mm) | Error | Estimate (mm) | Error | Estimate (mm) | Error | ||
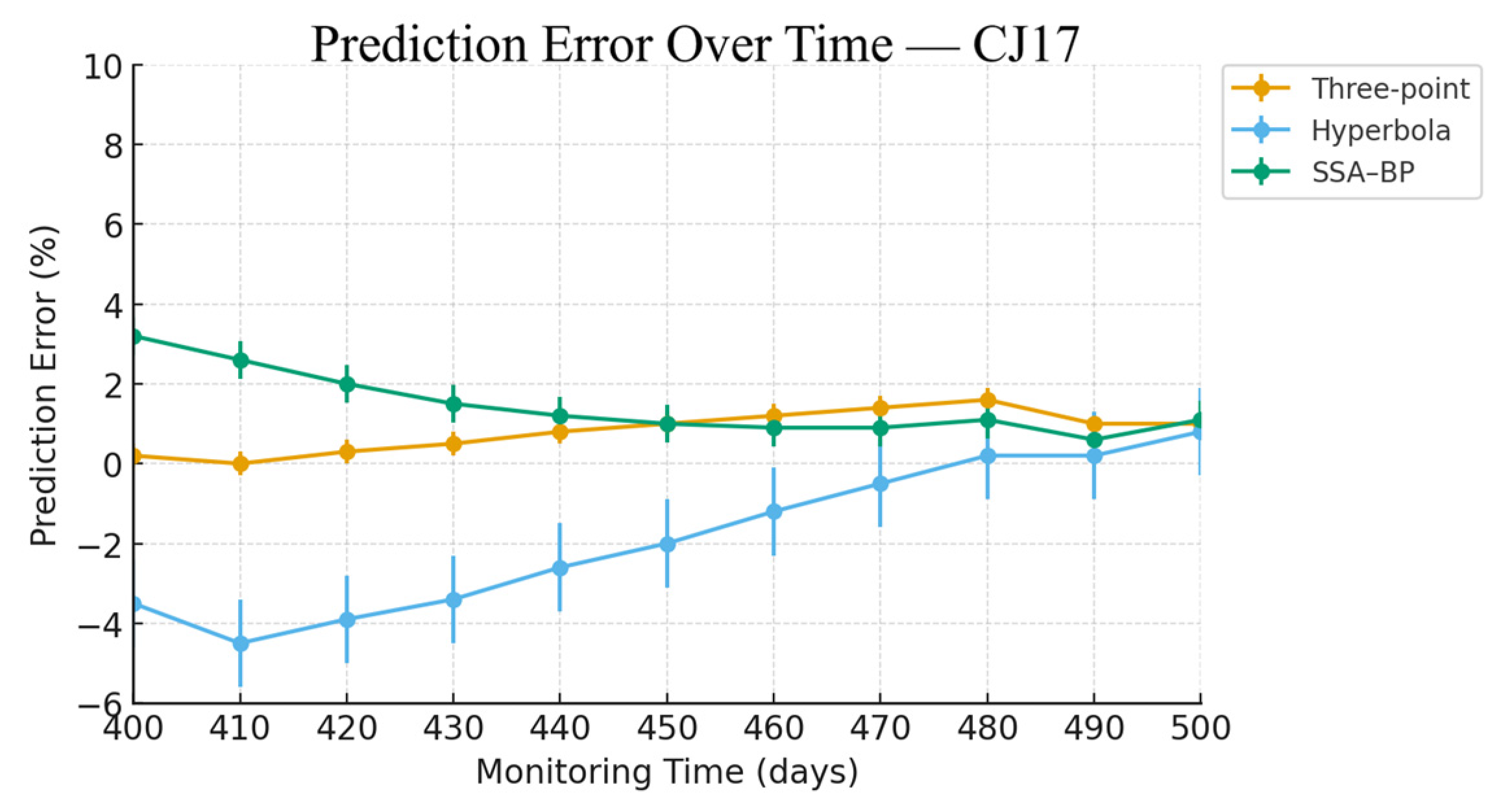
| 400 | −1066.8 | −1068.6 | 0.2% | −1029.5 | −3.5% | −1100.5 | 3.2% |
| 410 | −1087.1 | −1087.1 | 0.0% | −1038.4 | −4.5% | −1115.2 | 2.6% |
| 420 | −1098.5 | −1102.3 | 0.3% | −1055.7 | −3.9% | −1120.5 | 2.0% |
| 430 | −1108.9 | −1114.9 | 0.5% | −1071.7 | −3.4% | −1125.4 | 1.5% |
| 440 | −1115.9 | −1125.3 | 0.8% | −1086.5 | −2.6% | −1129.5 | 1.2% |
| 450 | −1122.8 | −1133.8 | 1.0% | −1100.3 | −2.0% | −1133.9 | 1.0% |
| 460 | −1126.8 | −1140.2 | 1.2% | −1113.1 | −1.2% | −1137.1 | 0.9% |
| 470 | −1130.8 | −1146.2 | 1.4% | −1125.0 | −0.5% | −1141.2 | 0.9% |
| 480 | −1133.6 | −1151.5 | 1.6% | −1136.1 | 0.2% | −1146.6 | 1.1% |
| 490 | −1144.5 | −1155.5 | 1.0% | −1146.6 | 0.2% | −1151.2 | 0.6% |
| 500 | −1147.3 | −1158.8 | 1.0% | −1156.4 | 0.8% | −1159.6 | 1.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Wang, Z.; Duan, H.; Gan, Y.; Chen, S.; Li, M.; Zhao, X.; Xu, E. Settlement Prediction of Preloading Method Based on SSA-BP Neural Network with Consideration of Asymmetric Settlement Behavior. Symmetry 2025, 17, 1989. https://doi.org/10.3390/sym17111989
Wu X, Wang Z, Duan H, Gan Y, Chen S, Li M, Zhao X, Xu E. Settlement Prediction of Preloading Method Based on SSA-BP Neural Network with Consideration of Asymmetric Settlement Behavior. Symmetry. 2025; 17(11):1989. https://doi.org/10.3390/sym17111989
Chicago/Turabian StyleWu, Xinye, Zhiwei Wang, Haixu Duan, Yuxiang Gan, Shenghui Chen, Man Li, Xu Zhao, and Enpu Xu. 2025. "Settlement Prediction of Preloading Method Based on SSA-BP Neural Network with Consideration of Asymmetric Settlement Behavior" Symmetry 17, no. 11: 1989. https://doi.org/10.3390/sym17111989
APA StyleWu, X., Wang, Z., Duan, H., Gan, Y., Chen, S., Li, M., Zhao, X., & Xu, E. (2025). Settlement Prediction of Preloading Method Based on SSA-BP Neural Network with Consideration of Asymmetric Settlement Behavior. Symmetry, 17(11), 1989. https://doi.org/10.3390/sym17111989







