Dynamic Heterogeneous Multi-Agent Inverse Reinforcement Learning Based on Graph Attention Mean Field

Abstract

Multi-agent inverse reinforcement learning (MA-IRL) infers the underlying reward functions or objectives of multiple agents by observing their behavioral data, thereby providing insights into collaboration, competition, or mixed interaction strategies among agents, and addressing the symmetrical ambiguity problem where multiple rewards may correspond to the same strategy. However, most existing algorithms mainly focus on solving cooperative and non-cooperative tasks among homogeneous multi-agent systems, making it difficult to adapt to the dynamic topologies and heterogeneous behavioral strategies of multi-agent systems in real-world applications. This makes it difficult for the algorithm to adapt to scenarios with locally sparse interactions and dynamic heterogeneity, such as autonomous driving, drone swarms, and robot clusters. To address this problem, this study proposes a dynamic heterogeneous multi-agent inverse reinforcement learning framework (GAMF-DHIRL) based on a graph attention mean field (GAMF) to infer the potential reward functions of agents. In GAMF-DHIRL, we introduce a graph attention mean field theory based on adversarial maximum entropy inverse reinforcement learning to dynamically model dependencies between agents and adaptively adjust the influence weights of neighboring nodes through attention mechanisms. Specifically, the GAMF module uses a dynamic adjacency matrix to capture the time-varying characteristics of the interactions among agents. Meanwhile, the typed mean-field approximation reduces computational complexity. Experiments demonstrate that the proposed method can efficiently recover reward functions of heterogeneous agents in collaborative tasks and adversarial environments, and it outperforms traditional MA-IRL methods.

1. Introduction

Inverse reinforcement learning (IRL) aims to infer an underlying reward function from expert demonstrations, thereby enabling agents to learn complex behaviours without explicit reward engineering [1]. However, traditional IRL methods, such as maximum margin planning [2] and Bayesian approaches [3], often struggle with the quality of the expert demonstration data or symmetric reward ambiguity that multiple rewards correspond to the same strategy, because they rely on hand-designed features. To address these limitations, recent advances in deep learning have led to the development of scalable and flexible IRL frameworks. Among these, adversarial inverse reinforcement learning (AIRL) [4] has emerged as a powerful paradigm by integrating generative adversarial networks [5] into the reward learning process. This innovative approach uses a GAN to transform reward learning into a distribution matching problem, which significantly improves the robustness and generalization ability of the reward function [6]. AIRL operates through an adversarial mechanism where a discriminator network distinguishes between expert and learned policies, whereas a policy is optimized by a generator to deceive the discriminator. This mechanism effectively solves the symmetrical ambiguity problems that affect conventional IRL methods.

However, existing AIRL approaches often fail to capture the nuanced relationships between agents that emerge in complex systems, such as urban traffic networks [7], and swarm robotics systems [8]. These challenges have motivated the development of specialized multi-agent AIRL (MA-AIRL) approaches. Recent progress in MA-AIRL can be categorized into three main dimensions: decomposition strategies, opponent modeling, and centralized training with the decentralized execution. Decomposition approaches, such as those proposed by Xue et al. [9], decompose the common task reward into various demonstrations. Opponent modeling techniques, exemplified by the work [10], incorporate predictions of other agents’ policies into each agent’s reward learning process. Centralized training with a decentralized execution paradigm, based on the MADDPG framework [11], has been adapted for MA-AIRL and shows promise in environments requiring coordination. Furthermore, the theoretical understanding of MA-AIRL has improved significantly in recent years. Freihaut et al. conducted a rigorous analysis of feasible reward sets in MA-IRL and addressed these limitations by introducing entropy regularization games, ensuring uniqueness of equilibria and improving interpretability [12]. Concurrently, Golmisheh et al. applied game concepts and IRL algorithms to derive reward functions, and they analyzed the stability and convergence of MA-AIRL algorithms in both cooperative and competitive settings [13].

Despite these advances, significant challenges remain in the development of MA-AIRL methods [14,15]. Generally, multiple agents are considered to be homogeneous. However, in scenarios such as autonomous driving, drone swarms, and robot clusters, the states and objectives of agents may be heterogeneous and subject to dynamic changes. This makes it difficult to guarantee the performance of the algorithm. To address these challenges, we propose a graph attention mean field adversarial dynamic heterogeneous multi-agent inverse reinforcement learning (GAMF-DHIRL). It can capture heterogeneous and dynamic changes in the states and objectives of multiple agents in times, even in scenarios with sparse local interactions and dynamic heterogeneity. In GAMF-DHIRL, building upon AIRL, a graph attention mean field theory is introduced to establish a reward and policy optimization model within a graph network framework. The model uses graph attention mechanisms to capture local dependencies between agents and a typed mean field approximation to propagate the distribution of group policies, achieving global policy coordination.

The main contributions of this study are as follows:

(1)

We proposed a graph attention mean field adversarial dynamic heterogeneous multi-agent inverse reinforcement learning to infer the potential reward functions of agents.

(2)

In the GAMF-DHIRL, the GAMF module uses a dynamic adjacency matrix to capture the time-varying characteristics of the interactions between agents. Meanwhile, the typed mean-field approximation reduces computational complexity.

(3)

The simulation experiments show that this method can efficiently recover the reward functions of heterogeneous agents and significantly outperform traditional MA-IRL methods.

The remainder of this paper is organized as follows. Section 2 reviews the related work on AIRL, adversarial multi-agent IRL, theory of mind, and mean field approximations. Section 3 demonstrates the research background of Markov games and mean field games, AIRL, and mean field IRL. Section 4 details the formal problem formulation and the theoretical foundations of GAMF-DHIRL. Section 5 presents extensive experimental results in simulated environments. Finally, Section 6 concludes the paper, discusses limitations and future directions.

2. Related Works

Adversarial IRL: Integrating adversarial training paradigms into IRL has revolutionized the learning of rewards from expert demonstrations [16,17]. The seminal work by Fu et al. introduced adversarial IRL and established a generative adversarial network-based framework that could robustly recover reward functions [4]. Furthermore, recent theoretical advances have significantly improved our understanding of the AIRL. Liu et al. proposed a travel time estimation method that combines active adversarial IRL and transformers to effectively reduce the cost of sample annotation [18]. Meanwhile, Zhang et al. proposed a new generative adversarial imitation learning model that can automatically learn a difference metric and generate strategies with expert behavior [19]. Song et al. proposed an adaptive generative adversarial maximum entropy IRL algorithm that utilizes updated mixed expert demonstrations to learn rewards and optimize strategies [20].

Multi-agent adversarial IRL: Extending adversarial IRL to multi-agent systems has emerged as a critical research area, driven by applications in autonomous driving, financial markets, and cybersecurity. In recent years, rapid progress has been made in this field in recent years. For example, Yu et al. proposed an effective and scalable multi-agent IRL framework for Markov games with high-dimensional state-action spaces and unknown dynamics [21]. Donge et al. developed a model-based outer-loop inverse optimal control model, and introduced a model-free inverse reinforcement learning algorithm to learn stable rewards [22]. Gruver et al. proposed adversarial IRL and continuous latent variables to learn a shared reward function in scenarios involving varying numbers of agents [23]. Despite significant progress, several fundamental challenges remain in adversarial IRL research, particularly in multi-agent settings, where the joint state-action space grows exponentially with the number of agents [24]. Recent studies have begun to address this issue by developing a mean field and a MoT. However, more fundamental breakthroughs are required [25,26].

IRL based on mean field and MoT: The application of mean field theory to IRL has emerged as a powerful framework for scaling IRL to multi-agents [27]. Classical approaches by Yang et al. established the foundation for mean field IRL by using a mean field distribution to approximate agent interactions and address the curse of dimensionality in multi-agent IRL [28]. Yu et al. proposed a deep latent variable model that learns rewards from demonstrations of different but related tasks in an unsupervised manner, and infers rewards for new, structurally similar tasks from a single demonstration [21]. Mo et al. developed a reinforcement learning algorithm framework that combines fictional game technology to learn the potential cost functions [7]. Chen et al. integrated deep neural networks with mean-field approximations in IRL to learn complex reward structures [29]. Cutting-edge research by Anahtarci et al. proposed the maximum causal entropy IRL under discrete-time stationary mean-field games, introducing a gradient descent algorithm with a guaranteed convergence rate that efficiently computes the optimal solution [30].

Theory of mind (ToM) has revolutionized IRL by allowing agents to reason about the mental states and intentions of others [31]. Remarkable progress has been made in this field in the recent years. For example, Huang et al. studied the effective assessment of human preferences using predictions of small-scale approach-avoidance behaviors in real life within an IRL framework [32]. Tian et al. proposed a new multi-agent IRL framework based on ToM that infers the underlying connections between humans during the learning process [33]. Wu et al. proposed a novel IRL framework that uses ToM reasoning to estimate the posterior distribution of the baseline reward pattern based on the exhibited behavior, and infers a reward function for each agent through distributed equilibrium [34]. Oguntola et al. embedded semantically meaningful beliefs into strategies modeled by deep networks, making them easy to understand [35]. Additionally, Wei et al. used a class of prior distributions to parameterize the accuracy of an agent’s model of the environment, efficiently estimating agent rewards and subjective dynamics in high-dimensional settings [36]. Zhang et al. proposed a multi-agent framework combining ToM and maximum entropy IRL to infer teammates’ reward functions through Bayesian inference [37].

The above researches mainly consider the homogeneous nature of agents. How to combine the advantages of mean field and ToM to improve the performance of algorithms in dynamic heterogeneous environments is a major challenge facing existing adversarial multi-agent IRL.

3. Preliminaries

3.1. Markov Games and Mean Field Games

A Markov game is an extended Markov decision process (MDP) that describes situations where multiple agents interact in a stochastic environment. In this game, each agent has a set of available strategies in each state and chooses an action based on these strategies and the current state [38]. A Markov game in RL is formulated as $\left(\mathcal{S},{\left\{a_i\right\}}_{i=1}^N,{\left\{r_i\right\}}_{i=1}^N,\kappa ,\gamma ,P\right)$, where N is the number of agents, $\mathcal{S}$ represents a set of states, $a_i$ represents the set of actions for an agent i, $r_i:\mathcal{S}\times a_1\times \dots \times a_N\to \mathbb{R}$ is the reward function of an agent i, $\gamma$ represents the discount factor. The function $P\left(s^{t+1}|s^t,a_1,\dots ,a_N\right):\mathcal{S}\times a_1\times \dots \times a_N\to \mathcal{P}\left(\mathcal{S}\right)$ is the state transition distribution, where $\mathcal{P}\left(\mathcal{S}\right)$ indicates the set of probability distributions for the set $\mathcal{S}$. And $\kappa \in \mathcal{P}\left(\mathcal{S}\right)$ indicates the distribution of the initial state. The agents take actions $\left(a_1,a_2,\dots ,a_N\right)$ from the state $s_t$ to the next state $s_{t+1}$ with probability $P\left(s_{t+1}|s_t,a_1,\dots ,a_N\right)$. For convenience, we utilize a wavy line to represent the joint characteristic of variables for all agents. $\tilde{a}=a_1\times \dots \times a_N$ indicates a joint policy for all agents, $\tilde{a}=\left(a_1,\dots ,a_N\right)$ represents a joint policy for an agent, $\tilde{\pi }=\left({\pi }_1,\dots ,{\pi }_N\right)$ represents a joint policy, $\tilde{r}=\left(r_1\left(s,\tilde{a}\right),r_2\left(s,\tilde{a}\right)\dots ,r_N\left(s,\tilde{a}\right)\right)$ denotes a joint reward for all agents. The agent i aims to maximize the expected rewards ${\mathbb{E}}_{\tilde{\pi }}\left[{\sum }_{t=1}^T{\gamma }_t{r}_i\left(s_t,{\tilde{a}}_t\right)|s_0=s,{\tilde{a}}_0=\tilde{a}\right]$, where $\tilde{\pi }$ indicates that the agent selects the joint actions under the $\kappa$ and P. Based on Markov games in RL, suppose that, if we cannot obtain the reward function of the IRL for multiple agents, then a Markov game is formulated as $\left(\mathcal{S},{\left\{a_i\right\}}_{i=1}^N,\kappa ,\gamma ,P\right)$ [39]. Given the demonstrations $\mathcal{D}$, the main objectives of the multi-agent IRL are as follows: (1) the reward function is recovered, and (2) strategy optimization is realized by making the learner’s strategy approach the expert strategy. Let $\left(1,2,\dots ,N\right)$ represent the number of agents. Mean field games simplify the complex interaction problems among multiple agents into an interactive problem between a representative agent and a mean field through an empirical distribution $m\in \mathcal{P}\left(\mathcal{S}\right)$, wherein a mean field is the overall average behavior of the remaining agents. The transition function is defined as $P\left(s^{t+1}|s^t,a_1,\dots ,a_N,m_t\right)$. A mean field flow is composed of $\mathcal{N}+1$ mean fields, that is, $\tilde{m}\triangleq {\left\{m_{\mathfrak{n}}\right\}}_{\mathfrak{n}=0}^{\mathcal{N}}$. Thus, an MDP based on mean field games (MFGs) is defined as $\left(\mathcal{S},{\left\{a_i\right\}}_{i=1}^N,{\left\{r_i\right\}}_{i=1}^N,\kappa ,\gamma ,P,m_0\right)$, where $m_0$ represents the initial mean field. Let $\xi \triangleq {\left\{\left(s_t,a_t\right)\right\}}_{t=0}^T$ to be the expert trajectory. The long-term reward of an agent under the mean field flow $\tilde{m}$ is $R\left(\xi \right)\triangleq {\sum }_{t=0}^{T-1}r\left(s_t,a_t,m_t\right)$. Therefore, an agent’s accumulated rewards are formulated as $J\left(\tilde{m},\tilde{\pi }\right)\triangleq {\mathbb{E}}_{\xi \sim \left(m,\pi \right)}\left[R\left(\xi \right)\right]$, where $s_0\sim m_0$, $a_t\sim {\pi }_t\left(·|s_t\right)$, $s_{t+1}\sim P\left(·|s_t,a_t,m_t\right)$.

3.2. Multi-Agent Adversarial Inverse Reinforcement Learning

To solve the reward functions under demonstrations $\mathcal{D}$, Ziebart et al. [40] innovatively proposed maximum entropy IRL, and expressed constrained optimization problems as maximum entropy models,

$$\begin{array}{cc}\hfill & P\left({\xi }_j|\omega \right)={\displaystyle \frac{1}{z\left(\omega \right)}}{e}^{{\sum }_{s_i\in {\xi }_j}{\omega }^{\mathsf{T}}{\varphi }_{s_i}}{\prod }_{\left(s_i,a_i,s_{i+1}\right)\in {\xi }_j}p\left(s_{i+1}|s_i,a_i\right)\hfill \end{array}$$

(1)

where the vector ${\varphi }_{s_i}$ represents the characteristic function of rewards, and the partition function $z\left(\omega \right)={\sum }_{{\xi }_j}{e}^{{\sum }_{s_i\in {\xi }_j}{\omega }^{\mathsf{T}}{\varphi }_{s_i}}{\prod }_{\left(s_i,a_i,s_{i+1}\right)\in {\xi }_j}p\left(s_{i+1}|s_i,a_i\right)$ is a normalized constant; and $p\left(s_{i+1}|s_i,a_i\right)$ represents the state transition probability. Furthermore, the maximum entropy method is extended to the multi-agent IRL. Under expert demonstrations $\mathcal{D}={\left\{{\xi }_j\right\}}_{j=1}^M$, N multi-agents can obtain the reward function and optimize the strategy by imitating the expert strategy ${\tilde{\pi }}_E=\left({\pi }_{1,E},\dots ,{\pi }_{N,E}\right)$, where ${\xi }_j={\left\{\left(s_{j,t},{\tilde{a}}_{j,t}\right)\right\}}_{t=1}^T$ represents an expert trajectory obtained by sampling $s_0\sim \kappa \left(s\right)$, ${\tilde{a}}_t={\pi }_E\left({\tilde{a}}_t|s_t\right)$, ${\tilde{s}}_{t+1}\sim P\left(s_{t+1}|s_t,{\tilde{a}}_t\right)$. However, in a multi-agent complex dynamic high-dimensional environment, the computation of $z\left(\omega \right)$ is difficult. To solve this problem, multi-agent generative adversarial imitation learning (MA-GAIL) aims to achieve strategy optimization through mimicking expert’s policies directly, as shown in Equation (2),

$$\begin{array}{cc}\hfill & MAGAI{L}_{\eta }\left({\tilde{\pi }}_E\right)=\underset{\stackrel{\sim }{r}}{argmax}-\eta \left(\tilde{r}\right)+\sum _{i=1}^N\left({\mathbb{E}}_{{\tilde{\pi }}_E}\left[r_i\right]\right)-\left(\underset{\tilde{\pi }}{max}\sum _{i=1}^N\left(\lambda H_i\left({\pi }_i\right)+{\mathbb{E}}_{{\pi }_i,{\pi }_{E_{-i}}}\left[r_i\right]\right)\right)\hfill \end{array}$$

(2)

where $H_i\left({\pi }_i\right)={\mathbb{E}}_{{\pi }_i,{\pi }_{E_{-i}}}\left[-log{\pi }_i\left(a_i|s\right)\right]$ indicates the discounted causal entropy of the policy ${\pi }_i$, and $\lambda$ represents the hyperparameter measuring the ability of the entropy regularization term. In Equation (2), the generator controls the policies of all agents in a distributed manner, whereas the discriminator determines whether the behavior of each agent is the corresponding expert behavior. However, MA-GAIL can only mimic expert behaviors and cannot be adapted to new tasks. To solve this problem, MA-AIRL combines a generative adversarial network with the maximum entropy IRL. The goal of MA-AIRL is to maximize the objective function [41],

$$\begin{array}{cc}\hfill & \underset{\theta }{max}J\left(\theta \right)=\underset{\theta }{max}{E}_{\tau \sim D}J\left[log{p}_{\theta }\left(\tau \right)\right]\hfill \end{array}$$

(3)

where the probability distribution is parameterized as $p_{\theta }\left(\tau \right)\propto p\left(s_0\right){\prod }_{t=0}^{T-1}p\left(s_{t+1}|s_t,a_t\right)e^{r_{\theta }\left(s_t,a_t\right)}$. The discriminator aims to minimize the cross-entropy loss between expert demonstrations and generated samples:

$$\begin{array}{cc}\hfill & L\left(\theta \right)={\sum }_{t=0}^T-E_D\left[log{D}_{\theta }\left(s_t,a_t\right)\right]-E_{{\pi }_t}\left[log\left(1-D_{\theta }\left(s_t,a_t\right)\right)\right]\hfill \end{array}$$

(4)

The objective of the policy is to maximize the reward $\widehat{r}\left(s,a\right)$,

$$\begin{array}{cc}\hfill & \widehat{r}\left(s,a\right)=log\left(D_{\theta }\left(s,a\right)\right)-log\left(1-D_{\theta }\left(s,a\right)\right)\hfill \\ \hfill & =f_{\theta }\left(s,a\right)-log\pi \left(a|s\right)\hfill \end{array}$$

(5)

The optimal objective of the discriminator is achieved when $\pi ={\pi }_E$, where $\pi$ is the policy learned through the generator, and ${\pi }_E$ is the expert’s policy. At this point, the optimal output of the discriminator is 0.5, which means that $e^{f_{\theta }\left(s,a\right)}={\pi }_E\left(a|s\right)$.

3.3. Mean Field Inverse Reinforcement Learning

Based on Section 3.2, the adversarial IRL problem based on a mean-field theory (MF-AIRL) is modeled as an MDP based on a mean field, aiming to learn the potential reward function and optimize the policy from expert demonstrations. The optimization problem can be formulated as follows [27]:

$$\left\{\begin{array}{cc}\hfill & \underset{\theta }{min}{D}_{\mathrm{KL}}\left(p_{{\eta }_E,{\pi }_E}\left(\xi \right)\parallel p_{\theta }\left(\xi \right)\right)\hfill \\ \hfill & p_{\theta }\left(\xi \right)={\displaystyle \frac{1}{Z\left(\theta \right)}}\left[\prod _{t=0}^T{m}_{\theta ,t}\left(s_t\right)\right]·e^{{\sum }_{t=0}^T{r}_{\theta }(s_t,a_t,m_{\theta ,t})}\hfill \end{array}\right.$$

(6)

where $r_{\theta }\left(s_t,a_t,m_{\theta ,t}\right)$ is the reward function parameterized with $\theta$, $p_{\theta }$ represents the probability of the generated expert trajectories. MF-AIRL does not model N independent agents but rather models a representative agent while treating the average influence from all neighboring agents as the overall state distribution. The objective with mean field is formulated as follows:

$$\begin{array}{cc}\hfill & J_m\left(\pi \right)=\mathbb{E}\left[\sum _{t=1}^{T}r\left(S_t,A_t,m_t\right)\right]\hfill \end{array}$$

(7)

The mean field ${\left(m_t\right)}_{t\in T}\in M$ induced by some fixed policies $\pi$ is recursively defined as $m_{t+1}\left(s_{t+1}\right)={\sum }_{s\in \mathcal{S}}{m}_t\left(s_t\right){\sum }_{a\in \mathcal{A}}{\pi }_t\left(a_t|s_t\right)p\left(s_{t+1}|s_t,a_t,m_t\right)$, which indicates the space of all mean fields. However, the MF-AIRL, which is based on probabilistic context variables, assumes that multi-agents are homogeneous. This eliminates the need to address graph sparsity and allows the focus to be placed on multi-agent strategy optimization under multi-task scenarios [29]. Existing AIRLs focus on addressing cooperative and non-cooperative tasks for homogeneous multi-agents [15,28]. Consequently, the algorithm cannot consider the heterogeneity of multi-agents, which is a major challenge, making it difficult for the algorithm to adapt to scenarios such as autonomous driving, drone swarms, and robot clusters. These scenarios feature locally sparse interactions and dynamic heterogeneities. This prevents the algorithm from promptly capturing the heterogeneous and dynamic changes in the states and objectives of multi-agents.

4. Graph Attention Mean Field Adversarial Inverse Reinforcement Learning

In scenarios with sparse local interactions and dynamic heterogeneity, we introduce a graph attention mean field theory based on adversarial IRL to establish a reward without a symmetrical ambiguity problem and a strategy optimization model within a graph network framework. The model uses graph attention mechanisms to capture local dependencies between agents, whereas the typed mean-field approximation propagates group strategy distributions to achieve global strategy coordination.

4.1. Problem Description

In dynamic heterogeneous multi-agent systems, let $A=\left\{a_1,\dots ,a_N\right\}$ be a set of agents. Suppose that each agent $a_i$ belongs to a certain type ${\tau }_i^t\in \left\{{\tau }_1,\dots {\tau }_K\right\}$ at time t. The type ${\tau }_i^t$ and strategy ${\pi }_i^t$ may change over time. Therefore, the dynamic heterogeneous multi-agent IRL is modeled as a dynamic heterogeneous graph network $G_t=\left(V_t,E_t\right)$, where the nodes ${\upsilon }_i^t\in V_t$ represent the agents, and the edges $e_{ij}^t\in E_t$ represent the interaction relationships between them. Under expert demonstrations, the main goal is to learn each agent’s strategy ${\pi }_i^t$, maximize long-term cumulative rewards, and adapt to dynamic changes in the type and topology. Actual expert demonstration data can be used as expert demonstrations. Alternatively, we can refer to references [21,27] and use the entropy-regularized MFNE strategy to generate expert demonstration trajectories. Given a joint policy ${\left\{{\pi }_t\left(a_t|s_t\right)\right\}}_{t=1}^T$ generated via the entropy MFNE $\left({\tilde{\mu }}^{\ast },{\tilde{\pi }}^{\ast }\right)$, the entropy regularized MFNE for an $MFG\left(\mathcal{S},A,P,{\mu }_0,r\right)$. Then, $\left({\tilde{\mu }}^{\ast },{\tilde{\pi }}^{\ast }\right)$ is the optimal solution to the optimization problem:

$$\left\{\begin{array}{cc}\hfill & \underset{\mu ,\pi }{min}{D}_{\mathrm{KL}}\left(p_1\left(\xi \right)\parallel p_2\left(\xi \right)\right)\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\mu =\Phi \left(\pi \right)\hfill \end{array}\right.$$

(8)

where $D_{KL}$ indicates the KL divergence, $p_1\left(\tau \right)={\mu }_0\left(s_0\right)·\prod _{t=0}^{T-1}p\left(s_{t+1}|s_t,a_t,{\mu }_t\right)·\prod _{t=0}^T{\pi }_t\left(a_t|s_t\right)$, and $p_2\left(\tau \right)\propto {\mu }_0\left(s_0\right)·\prod _{t=0}^{T-1}p\left(s_{t+1}|s_t,a_t,{\mu }_t\right)·e^{R\left(\xi \right)}$. The trajectory distribution increases exponentially with cumulative rewards without a symmetrical ambiguity problem. Additionally, let ${\tau }_i^t$ be type, ${\pi }_i^t\left(a|s,{\tau }_i^t,m_{{\tau }_i^t}^t\right)$ represent the individual strategy of the type-specific mean field $m_{{\tau }_i^t}^t$, and $m^t={\left\{m_{{\tau }_k}^t\right\}}_{k=1}^K$ be the population distribution, where $m_{{\tau }_k}^t$ is the state-action distribution of type ${\tau }_k$.

4.2. Improved IRL Based on Graph Attention Mean Field

First, we can obtain the expert demonstration trajectories sampled through the entropy regularized MFNE $\left({\tilde{m}}_E,{\tilde{\pi }}_E\right)$. Assuming that these expert demonstration trajectories are optimal, we can maximize the likelihood function of the entropy-regularized MFNE static distribution for the expert trajectories, which is in turn induced by $\omega$-parameterized rewards $r_{\omega }\left(s,a,m\right)$. These expert policies conform to the characteristics of the mean-field Nash equilibrium with some unknown parameterized rewards. $\left({\tilde{m}}_{\omega },{\tilde{\pi }}_{\omega }\right)$ represents the entropy regularized MFNE induced by $\omega$. Then, the learning of rewards can be regarded as an adjustment to $\omega$. The probability of a trajectory $\xi ={\left\{s_t,{\tilde{a}}_t\right\}}_{t=1}^T$ is generated via the entropy regularized MFNE policies with $r_{\omega }$,

$$\begin{array}{cc}\hfill & p_{\omega }\left(\xi \right)={\mu }_0\left(s_0\right)·P\left(s_{t+1}|s_t,{\tilde{a}}_t,m_{\omega ,t}\right)·\prod _{t=0}^T{\tilde{\pi }}_{t,\omega }\left({\tilde{a}}_t|s_t;\tilde{\omega }\right)\hfill \end{array}$$

(9)

where ${\tilde{\pi }}_t\left({\tilde{a}}_t|s_t;\tilde{\omega }\right)$ denotes the stationary joint distributions, $m_0\left(s_0\right)$ is the distribution of the initial mean field flow, and $P\left(s_{t+1}|s_t,{\tilde{a}}_t,m_{\omega ,t}\right)$ represents the state transition probability.

The classical maximum entropy IRL proposed via Ziebart et al. [40] learns the reward function by maximizing the likelihood function of the observed expert demonstration trajectory distribution defined in Equation (1). Inspired by this approach, the learning of the reward function in a dynamic heterogeneous multi-agent IRL is reduced to

$$\begin{array}{cc}\hfill & \underset{\omega }{max}\mathcal{L}\left(\omega \right)\triangleq {\mathbb{E}}_{\xi \sim \left({\mu }_E,{\pi }_E\right)}\left[R_{\omega }\left(\xi \right)+{\sum }_{t=0}^{T-1}logP\left(s_{t+1}|s_t,{\tilde{a}}_t,m_t^{\omega }\right)\right]-log{\mathcal{Z}}_{\omega }\hfill \end{array}$$

(10)

where ${\mathcal{Z}}_{\omega }\triangleq {\sum }_{\xi }{e}^{R_{\omega }\left(\xi \right)}{\prod }_{t=0}^{T-1}logP\left(s_{t+1}|s_t,a_t,m_{t,\omega }\right)$ is the partition function, which is defined as a summation of all expert demonstration trajectories.

However, IRL faces dynamic heterogeneous multi-agents in the process of reward learning and strategy optimization, resulting in large differences in neighboring strategies. This is the main challenge we face in this study. Therefore, we propose a hierarchical graph attention mean-field multi-agent inverse reinforcement learning, which infers implicit reward functions $r_{\psi }\left(s,a,m\right)$ from expert demonstration trajectories through AIRL and learns dynamic heterogeneous policies ${\pi }_{\theta }\left(a|s,\tau ,m\right)$, where m is the mean-field distribution, thereby adapting to dynamic changes in type and topology. First, to capture the dynamic interactions between multiple agents and reduce the computational complexity, we model the latent variables of dynamic heterogeneous multi-agents. Under the expert demonstration trajectory, for the variational encoder VAE $q_{\varphi }$, the input is $\left(s_{i,t},a_{i,t-1}\right)$, and the output latent variable is $z_i^t\in {\mathbb{R}}^d$: $z_i^t\sim q_{\varphi }\left(z|s_i^t,a_i^{t-1},{\tau }_i^{t-1}\right)$. The type ${\tau }_i^t$ of agent i is determined by its latent variable, and the update formula is ${\tau }_i^t=arg{max}_{k}p\left(z_i^t|{\mu }_k\right)$. Thus, we obtain the type probability distribution of agents as follows:

$$\begin{array}{cc}\hfill & p\left({\tau }_i^t={\tau }_k|z_i^t\right)={\displaystyle \frac{e^{-∥z_i^t-{\mu }_k∥}}{{\sum }_{l=1}^K{e}^{-∥z_i^t-{\mu }_l∥}}}\hfill \end{array}$$

(11)

where ${\mu }_k$ is the prototype vector of type ${\tau }_k$, which is updated through the sliding window expectation–maximization (EM) algorithm to ensure the timeliness of type estimation and achieve online clustering.

The pseudocode of the online type inference and clustering via the sliding window EM is shown in Algorithm 1.

Algorithm 1 Online type inference and clustering via sliding window EM

Require:  Sliding window size W, number of types K, type encoder $q_{\varphi }$, current time t. Ensure:  Agent types ${\tau }_i^t$ and updated prototypes $\left\{{\mu }_k\right\}$.  1: Initialize: Maintain a buffer $\mathcal{B}$ of recent latent variables $\left\{(z_i^{t^{\prime }},i)\right\}$ for $t^{\prime }=t-W,...,t$.  2: for each agent $i\in \{1,\dots ,N\}$ do  3:    Encode latent variable: $z_i^t\sim q_{\varphi }(z\mid s_i^t,a_i^{t-1},{\tau }_i^{t-1})$  4:    Add $(z_i^t,i)$ to the buffer $\mathcal{B}$; remove the oldest entries if $\left|\mathcal{B}\right|>W\times N$.  5: end for  6: E-step (Responsibility): For each latent-agent pair $(z,i)\in \mathcal{B}$, compute the responsibility ${\gamma }_{ik}$ that type k has for z: $${\gamma }_{ik}={\displaystyle \frac{exp(-\parallel z-{\mu }_k\parallel )}{{\sum }_{l=1}^{K}exp(-\parallel z-{\mu }_l\parallel )}}(\mathrm{This}\mathrm{is}\mathrm{Equation}(11)\mathrm{in}\mathrm{the}\mathrm{main}\mathrm{paper})$$  7: M-step (Maximization): Update each type prototype ${\mu }_k$: $${\mu }_k\leftarrow {\displaystyle \frac{{\sum }_{(z,i)\in \mathcal{B}}{\gamma }_{ik}·z}{{\sum }_{(z,i)\in \mathcal{B}}{\gamma }_{ik}}}$$  8: for each agent $i\in \{1,\dots ,N\}$ do  9:    Re-assign type based on updated prototypes: ${\tau }_i^t=arg{max}_{k}p(z_i^t\mid {\mu }_k)=arg{min}_k\parallel z_i^t-{\mu }_k\parallel$  10: end for

The process of online type inference and clustering is detailed in Algorithm 1. The core of this process is a sliding window EM algorithm that operates on a fixed-size buffer $\mathcal{B}$ containing the most recent latent variables $z_i$ of all agents. This buffer, with size W, ensures that the type prototypes adapt to recent agent behaviors, providing robustness against non-stationarity.

The algorithm proceeds as follows: First, for each agent, the type encoder $q_{\varphi }$ generates a new latent variable $z_i^t$ based on its current state and previous action (Line 3–4). These new latent variables are added to the sliding window buffer $\mathcal{B}$. The E-step (Line 6) computes the responsibility ${\gamma }_{ik}$, which is the probability that the latent variable z belongs to type k, based on the current prototypes. The M-step (Line 7) then updates each prototype ${\mu }_k$ as the weighted average of all latent variables in the buffer, with weights given by their responsibilities ${\gamma }_{ik}$. Finally, each agent is assigned to the type whose updated prototype is closest to its current latent variable $z_i^t$ (Line 9).

This loop runs at every time step t, allowing the types and their representations to evolve continuously as the agents’ strategies and the environment change. The use of a sliding window prevents the prototypes from being overly influenced by outdated behavior, striking a balance between adaptability and stability.

Then, based on the definition in Section 3.1, the feature of node ${\upsilon }_i^t$ in the heterogeneous dynamic graph $G^t=\left(V^t,E^t\right)$ of the graph attention average field is $h_i^t=\left[s_i^t,z_i^t\right]$, and the neighbor set is $\mathcal{N}\left(i\right)=\left\{j|dist\left(i,j\right)\le r\right\},\left|\mathcal{N}\left(i\right)\right|\le \overline{d}$, where $r_g$ is the interaction radius and $\overline{d}$ is the maximum number of neighbors. To achieve local feature updating, the graph attention network (GAT) is used to update the features of the graph nodes,

$$\begin{array}{cc}\hfill & h_i^t=GAT\left(s_i^t,{\left\{h_j^t\right\}}_{j\in \mathcal{N}\left(i\right)},{\alpha }_{ij}^t\right)\hfill \end{array}$$

(12)

In Equation (12), the coefficient of the attention mechanism is ${\alpha }_{ij}^t=softmax\left(LeakyReLU\right.\left(\right.$ $u_{{\tau }_i^t,{\tau }_j^t}^T\left.\left.\left[W_{\tau }{h}_i^t\right|\left|W_{\tau }{h}_j^t\right]\right)\right)$, where $W_{{\tau }_i}$ and $W_{{\tau }_j}$ are type-specific weight matrices, $u_{{\tau }_i^t,{\tau }_j^t}^T$ is the attention parameter for the type pair $\left({\tau }_i^t,{\tau }_j^t\right)$. For each type ${\tau }_k$, the type mean field $m_{{\tau }_k,\omega }^t$ depends on the strategies ${\pi }_i$ of all agents of the same type, and ${\pi }_i$ is influenced by the reward function through the parameter $\omega$, so the type mean field $m_{{\tau }_k,\omega }^t$ is also influenced by the reward function and thus depends on the parameter $\omega$. The nature of these mean fields (MFs) makes the MF flow and strategy in the entropy regularized MFNE interdependent in Equation (10); therefore, it is not possible to directly obtain the type mean field $m_{{\tau }_k,\omega }^t$. Furthermore, the state transition probabilities in Equation (10) also depend on ${\mu }_{\omega }$ and the dynamic changes in the multi-agent environment. Directly solving the optimization problem in Equation (10) is difficult, which increases the computational complexity of learning rewards and optimizing strategies in a multi-agent dynamic environment. We consider using MLP to map the average of node features to obtain the type mean field $m_{{\tau }_k}^t$,

$$\begin{array}{cc}\hfill & m_{{\tau }_k}^t=m_{{\tau }_k,\omega }^t=MLP\left({\displaystyle \frac{1}{\left|{\mathcal{A}}_{{\tau }_k}^t\right|}}{\sum }_{i\in {\mathcal{A}}_{{\tau }_k}^t}{h}_i^t\right)\hfill \end{array}$$

(13)

where ${\mathcal{A}}_{{\tau }_k}^t=\left\{i|{\tau }_i^t={\tau }_k\right\}$ is a set of agents of type ${\tau }_k$ at time t.

The strategy of agents depends on the type mean field $m_{{\tau }_k}^t$. Therefore, all types of mean fields are aggregated to form global information ${\tilde{m}}_{{\tau }_k}^t$. The dynamic heterogeneous strategy of all agents is calculated as follows:

$$\begin{array}{cc}\hfill & {\tilde{\pi }}_i^t\left(a_i|s_i,{\tau }_i^t,m_{{\tau }_i}^t\right)=softmax\left(f_{\theta }\left(s_i,{\tau }_k^t,{\tilde{m}}_{{\tau }_k}^t\right)\right)\hfill \end{array}$$

(14)

Owing to the overall consistency condition in GAMF-DHIRL (proven in the later sections), the mapping of the average node feature of an agent at each time step matches that of the mean field. Simultaneously, the type mean field $m_{{\tau }_k,\omega }^t$ in Equation (14) makes the transfer function $P\left(s_t,a_t,m_{{\tau }_k,\omega }^t\right)$ depend only on $h_i^t$, thereby decoupling $P\left(s_t,a_t,m_{{\tau }_k,\omega }^t\right)$ from the reward parameter $\omega$. Therefore, in the likelihood function of Equation (10), the reward parameter $\omega$ is omitted, and we obtain the maximum likelihood estimation of GAMF-DHIRL:

$$\begin{array}{cc}\hfill & \underset{\omega }{max}\tilde{\mathcal{L}}\left(\omega ;{\tilde{m}}_{{\tau }_k}^t\right)\triangleq {\mathbb{E}}_{\xi \sim {\mathcal{D}}_E}\left[{\tilde{R}}_{\omega }\left(\xi \right)+{\sum }_{t=0}^{T-1}logP\left(s_{t+1}|s_t,{\tilde{a}}_t,{\tilde{m}}_{{\tau }_k}^t\right)\right]-log{\tilde{\mathcal{Z}}}_{\omega }\hfill \end{array}$$

(15)

where ${\tilde{R}}_{\omega }\left(\tau \right)\triangleq {\sum }_{t=0}^{T-1}{r}_{\omega }\left(s_t,a_t,{\tilde{m}}_{{\tau }_k}^t\right)$ represents the rewards that are dependent on m, and ${\tilde{\mathcal{Z}}}_{\omega }\triangleq {\sum }_{\xi \in {\mathcal{D}}_E}{e}^{{\tilde{\mathcal{R}}}_{\omega }\left(\xi \right)}$ indicates the partition function. Based on the optimization objective of the maximum entropy IRL proposed by Ziebart et al. [40], we can obtain the maximum likelihood estimation objective in Equation (10).

Theorem 1. 

Consider a multi-agent system with dynamic agent types and a graph structure. Let the expert demonstration trajectories ${\tau }_1,\dots {\tau }_j,\dots {\tau }_M$ be independent and identical, which are sampled with MAT-MFNE induced by some unknown rewards. Assume that, for all $s_{i,t}\in {\mathcal{S}}_i$, $a_{i,t}\in A_i$, and $m_{{\tau }_k}^t\in \mathcal{P}\left(\mathcal{S}\right)$, $r_{\omega }\left(s,a,m\right)$ is differentiable with respect to reward parameter ${\omega }_i$. Then, under Assumptions A1–A3, when $M\to \infty$, the equation satisfies ${\nabla }_{\omega }\tilde{\mathcal{L}}\left(\omega ;{\tilde{m}}_{{\tau }_k}^t\right)=0$, which has a root $\tilde{\omega }$ that tends toward the maximum value of the likelihood function in Equation (10).

Assumption 1. 

The mean-field distribution ${\tilde{m}}_{{\tau }_k}^t$ is a consistent estimator of the true empirical distribution $m^t$ for all t, and the error introduced by the typed decomposition $m^t\approx {\prod }_{i=1}^N{\tilde{m}}_{{\tau }_k}^t$ is bounded by $O(1/\sqrt{N})$.

Assumption 2. 

In the dynamic graph ${\mathcal{G}}_t$, the graph diameter is bounded for any time step t, ensuring information propagation in the system. The agent type inference is statistically consistent.

Assumption 3. 

The reward function $r_{\omega }(s,a,m)$ is twice continuously differentiable in ω for all $s\in \mathcal{S}$, $a\in \mathcal{A}$, and $m\in \mathcal{P}\left(\mathcal{S}\right)$, and the Hessian of the log-pseudolikelihood is negative definite in a neighborhood of ${\omega }^{\ast }$.

Proof. 

Consider a standard game with players and a reward function ${\tilde{\mathcal{R}}}_{\omega }={\left\{r_i\left(\tilde{a};{\omega }_i\right)\right\}}_{i=1}^N$. Assume that the expert demonstration $\mathcal{D}=\left({\xi }_1,\dots ,{\xi }_m,\dots ,{\xi }_M\right)$ is generated by $\pi \left(\tilde{a};{\tilde{\omega }}^{\ast }\right)$, where ${\omega }^{\ast }$ represents the true value of the parameter. The pseudolikelihood objective is to maximize Equation (17). Based on Equation (16), the gradient of $\tilde{\mathcal{L}}$ with respect to $\omega$ is as follows:

$$\begin{array}{cc}\hfill & \underset{\omega }{max}\tilde{\mathcal{L}}\left(\omega ;{\tilde{m}}_{{\tau }_k}^t\right)\triangleq {\mathbb{E}}_{\xi \sim {\mathcal{D}}_E}\left[{\tilde{R}}_{\omega }\left(\xi \right)+{\sum }_{t=0}^{T-1}logP\left(s_{t+1}|s_t,{\tilde{a}}_t,{\tilde{m}}_{{\tau }_k}^t\right)\right]-log{\tilde{\mathcal{Z}}}_{\omega }\hfill \end{array}$$

(16)

where ${\tilde{R}}_{\omega }\left(\tau \right)\triangleq {\sum }_{t=0}^{T-1}{r}_{\omega }\left(s_t,a_t,{\tilde{m}}_{{\tau }_k}^t\right)$, and ${\tilde{\mathcal{Z}}}_{\omega }\triangleq {\sum }_{\xi \in {\mathcal{D}}_E}{e}^{{\tilde{\mathcal{R}}}_{\omega }\left(\xi \right)}$. Note that our objective $\tilde{\mathcal{L}}$ depends on the type-based mean-field distribution ${\tilde{m}}_{{\tau }_k}^t$, which is a direct consequence of our MAT-MFNE framework. Under Assumption A1, we can treat ${\tilde{m}}_{{\tau }_k}^t$ as an exogenous input that converges to its true value, allowing us to differentiate $\tilde{\mathcal{L}}$ with respect to $\omega$. The gradient is derived as:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial }{\partial \omega }}\tilde{\mathcal{L}}\left(\omega ;{\tilde{m}}_{{\tau }_k}^t\right)={\displaystyle \frac{\partial }{\partial \omega }}\left({\mathbb{E}}_{\xi \sim {\mathcal{D}}_E}\left[{\tilde{R}}_{\omega }\left(\xi \right)+\sum _{t=0}^{T-1}logP\left(s_{t+1}|s_t,{\tilde{a}}_t,{\tilde{m}}_{{\tau }_k}^t\right)\right]-log{\tilde{\mathcal{Z}}}_{\omega }\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{M}}\sum _{j=1}^M{\displaystyle \frac{\partial }{\partial \omega }}{\tilde{\mathcal{R}}}_{\omega }\left({\xi }_j\right)-{\displaystyle \frac{1}{{\tilde{Z}}_{\omega }}}{\displaystyle \frac{\partial }{\partial \omega }}log{\tilde{Z}}_{\omega }\hfill \\ \hfill & ={\displaystyle \frac{1}{M}}\sum _{j=1}^M{\displaystyle \frac{\partial }{\partial \omega }}{\tilde{\mathcal{R}}}_{\omega }\left({\xi }_j\right)-\sum _{j=1}^M{\displaystyle \frac{e^{{\tilde{\mathcal{R}}}_{\omega }\left({\xi }_j\right)}}{{\tilde{Z}}_{\omega }}}{\displaystyle \frac{\partial }{\partial \omega }}{\tilde{\mathcal{R}}}_{\omega }\left({\xi }_j\right)\hfill \end{array}$$

(17)

Let $p_{{\mathcal{D}}_E}\left(\xi \right)\triangleq {\displaystyle \frac{1}{M}}{\sum }_{j=1}^M{\sum }_{t=0}^T\mathbb{I}\left(s_t^j=s\right)$ represent the empirical expert demonstration trajectory distribution. Based on Equation (17), we can obtain the following equation,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial }{\partial \omega }}\tilde{\mathcal{L}}\left(\omega ;{\tilde{m}}_{{\tau }_k}^t\right)={\displaystyle \frac{\partial }{\partial \omega }}{p}_{{\mathcal{D}}_E}\left(\xi \right){\tilde{R}}_{\omega }\left(\xi \right)-{\sum }_{j=1}^M{\displaystyle \frac{e^{{\tilde{\mathcal{R}}}_{\omega }\left({\xi }_j\right)}}{{\tilde{Z}}_{\omega }}}{\displaystyle \frac{\partial }{\partial \omega }}{\tilde{\mathcal{R}}}_{\omega }\left({\xi }_j\right)\hfill \\ \hfill & ={\displaystyle \frac{\partial }{\partial \omega }}{p}_{{\mathcal{D}}_E}\left(\xi \right){\tilde{R}}_{\omega }\left(\xi \right)-M·p_{{\mathcal{D}}_E}\left(\xi \right){\displaystyle \frac{e^{{\tilde{\mathcal{R}}}_{\omega }\left(\xi \right)}}{{\tilde{Z}}_{\omega }}}{\displaystyle \frac{\partial }{\partial \omega }}{\tilde{\mathcal{R}}}_{\omega }\left(\xi \right)\hfill \\ \hfill & =\left(1-M·{\displaystyle \frac{e^{{\tilde{\mathcal{R}}}_{\omega }\left(\xi \right)}}{{\tilde{Z}}_{\omega }}}\right)p_{{\mathcal{D}}_E}\left({\xi }_j\right){\displaystyle \frac{\partial }{\partial \omega }}{\tilde{\mathcal{R}}}_{\omega }\left(\xi \right)\hfill \end{array}$$

(18)

when $M\to \infty$, by the law of large numbers and the Assumption A1, $p_{{\mathcal{D}}_E}\left(\xi \right)$ tends toward the true trajectory distribution $p\left({\xi }_j\right)$. Let ${\omega }^{\ast }$ be the maximizer of the likelihood objective in Equation (10). Furthermore, under Assumption A2, the dynamic graph and type inference ensure that the model distribution $p_{\omega }$ is well-defined. When the number of expert demonstration samples approaches the limit $M\to \infty$, and optimality $\omega ={\omega }^{\ast }$, we have:

$$\begin{array}{cc}\hfill & M·{\displaystyle \frac{e^{{\tilde{\mathcal{R}}}_{{\omega }^{\ast }}\left(\xi \right)}}{{\tilde{Z}}_{{\omega }^{\ast }}}}=M·{\displaystyle \frac{e^{{\tilde{\mathcal{R}}}_{{\omega }^{\ast }}\left(\xi \right)}}{{\sum }_{\xi \in {\mathcal{D}}_E}{e}^{{\tilde{\mathcal{R}}}_{{\omega }^{\ast }}\left(\xi \right)}}}=1\hfill \end{array}$$

(19)

Substituting the result from Equation (19) into Equation (18), the gradient of Equation (18) is 0.    □

4.3. Graph Attention Mean Field Adversarial IRL

Theorem 1 bridges the gap between the original intractable objective of the MLE in Equation (10) and the tractable empirical objective of the MLE in Equation (16). However, as discussed in Section 3.3, the exact computation of the partition function $Z_{\omega }$ is typically difficult. Similar to the AIRL in [41], we employ importance sampling to estimate the ${\widehat{Z}}_{\omega }$ of the adaptive sampler. Because the policies in MFGs are time-varying, we use a set of T adaptive samplers $\pi \left({\pi }_{{\theta }_0},{\pi }_{{\theta }_1},\dots ,{\pi }_{{\theta }_T}\right)$, where each ${\pi }_{{\theta }_T}$ serves as a parameterized policy. Our proposed GAMF-DHIRL infers implicit reward functions $r_{\psi }\left(s,a,m\right)$ from expert demonstration trajectories ${\pi }_{\theta }\left(s,a,\tau ,m\right)$ and learns strategies that adapt to dynamic heterogeneity, where $m^t$ is the mean field distribution. This framework optimizes rewards and strategies through a game between the generator and discriminator, enabling agents to dynamically adapt to type changes and the non-stationarity of population distributions. The discriminator $D_{\psi }$ is designed to distinguish between expert strategies ${\pi }_E$ and generative strategies ${\pi }_{\theta }$ and can output the estimation for rewards: ${\widehat{D}}_{\omega }\left(s_t,a_t\right)\triangleq {\displaystyle \frac{e^{f_{\omega }\left(s_t,a_t,{\tilde{m}}_{{\tau }_k}^t\right)}}{e^{f_{\omega }\left(s_t,a_t,{\tilde{m}}_{{\tau }_k}^t\right)}+{\pi }_{{\theta }_t}\left(a_t|s_t\right)}}$, where $f_{\psi }\left(s,a,m\right)\approx r_{\psi }\left(s,a,m\right)$ is the reward function. The optimization objective is as follows:

$$\begin{array}{cc}\hfill & \underset{\omega }{max}{\mathbb{E}}_{\xi \sim {\mathcal{D}}_E}\left[{\sum }_{t=0}^{T-1}log{\widehat{D}}_{\omega }\left(s_t,a_t\right)\right]+{\mathbb{E}}_{\xi \sim {\pi }_{\theta }}\left[{\sum }_{t=0}^{T-1}log\left(1-{\widehat{D}}_{\omega }\left(s_t,a_t\right)\right)\right]\hfill \end{array}$$

(20)

The generator can maximize the discriminator reward while satisfying the graph attention mean field game equilibrium:

$$\begin{array}{cc}\hfill & {\pi }_{\theta }=arg{max}_{\pi }{\mathbb{E}}_{\pi }\left({\sum }_{t=0}^T{\gamma }^{t}log{D}_{\psi }\left(s_t,a_t,m_t\right)\right)\hfill \end{array}$$

(21)

The objective of the generator is optimized as follows:

$$\begin{array}{cc}\hfill & \underset{\theta }{max}{\mathbb{E}}_{\tau \sim {\pi }_{\theta }}\left[{\sum }_{t=0}^{T-1}log{\widehat{D}}_{\omega }\left(s_t,a_t\right)-log\left(1-{\widehat{D}}_{\omega }\left(s_t,a_t\right)\right)\right]\hfill \\ \hfill & ={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}\left[{\sum }_{t=0}^{T-1}{f}_{\omega }\left(s_t,a_t,m_{{\tau }_k}^t\right)-{log}_{{\pi }_{{\theta }_t}}\left(a_t|s_t\right)\right]\hfill \end{array}$$

(22)

where the optimization of $D_{\psi }$ is equivalent to estimating the reward function $r_{\psi }$. The policy gradient includes a mean-field term: ${\nabla }_{\theta }J\left(\theta \right)={\mathbb{E}}_{{\pi }_{\theta }}\left[{\nabla }_{\theta }log{\pi }_{\theta }\left(a|s,\tau ,m\right)·Q\left(s,a,m\right)\right]$, where $Q\left(s,a,m\right)=\mathbb{E}\left[{\sum }_{t=0}^{\infty }{\gamma }^t{r}_{\psi }\left(s_t,a_t,m_t\right)\right]$. The update of the policy parameter $\theta$ is interleaved with the update of the reward parameter $\omega$. Intuitively, tuning ${\pi }_{\theta }$ can be viewed as a policy optimization process, that is, finding the GAMF-DHIRL’s policy induced by the current reward parameter to minimize the variance of importance sampling. Training $f_{\omega }$ estimates the reward function by distinguishing between the observed trajectories and those generated by the current adaptive sampler ${\pi }_{\theta }$. We can train ${\pi }_{\theta }$ using backward induction, that is, adjusting ${\pi }_{{\theta }_t}$ based on ${\pi }_{{\theta }_{t+1}},\dots ,{\pi }_{{\theta }_{T-1}}$. In the optimal case, $f_{\omega }$ approximates the latent reward function of GAMF-DHIRL, while $\pi$ approximates the observed policy. The agent achieves efficient and adaptive collaboration with neighboring agents through sparse graph attention, and ensures the statistical consistency of group strategies through typed mean fields. Finally, we obtain the reward model:

$$\begin{array}{cc}\hfill & r_{\theta }\left(s,a,m\right)=f_{\theta }\left(s,a\right)+g_{\theta }\left(m\right)\hfill \end{array}$$

(23)

where $g_{\theta }\left(m\right)$ captures the impact of population distribution.

Theorem 2. 

(Consistency of Adversarial Rewards) Under the AIRL framework [4] and assuming that the expert policy ${\pi }_E$ and the learner’s policy ${\pi }_{\theta }$ induce state-action mean field distributions that are absolutely continuous with respect to each other, the reward function $r_{\psi }$ recovered by the optimally trained discriminator $D_{\psi }$ in the AIRL setting satisfies:

1.

Policy Invariance: At Nash equilibrium, the learned policy ${\pi }_{\theta }$ perfectly recovers the expert policy ${\pi }_E$, and the induced mean field distributions are indistinguishable, i.e., $p_{{\pi }_{\theta }}(s,a,m)=p_{{\pi }_E}(s,a,m)$.

2.

Reward Authenticity: The recovered reward $r_{\psi }(s,a,m)$ is a monotonic transformation of the true underlying reward $r_{\mathrm{true}}(s,a,m)$. Specifically, there exists a strictly increasing function g and a function $\chi (s,m)$ dependent only on the state and mean field such that:

$$r_{\psi }(s,a,m)=g\left(r_{\mathrm{true}}(s,a,m)\right)+\chi (s,m).$$

(24)

Proof. 

The proof follows and extends the theoretical foundations of AIRL [4] to the graph-based mean field multi-agent setting.

The discriminator $D_{\psi }$, parameterized to distinguish expert trajectories from generated ones, is trained to minimize the cross-entropy loss:

$${\mathcal{L}}_D\left(\psi \right)=-{\mathbb{E}}_{(s,a,m)\sim {\pi }_E}[log{D}_{\psi }(s,a,m)]-{\mathbb{E}}_{(s,a,m)\sim {\pi }_{\theta }}[log(1-D_{\psi }(s,a,m))].$$

(25)

For a fixed generator policy ${\pi }_{\theta }$, the optimal discriminator for this objective is known to be:

$$D_{\psi }^{\ast }(s,a,m)={\displaystyle \frac{p_{{\pi }_E}(s,a,m)}{p_{{\pi }_E}(s,a,m)+p_{{\pi }_{\theta }}(s,a,m)}},$$

(26)

where $p_{\pi }(s,a,m)$ is the state-action-mean field distribution induced by policy $\pi$.

Following the AIRL equation [4], we parameterize the discriminator as:

$$D_{\psi }(s,a,m)={\displaystyle \frac{exp\left(f_{\psi }(s,a,m)\right)}{exp\left(f_{\psi }(s,a,m)\right)+{\pi }_{\theta }(a\mid s,m)}},$$

(27)

where $f_{\psi }(s,a,m)$ is a learned function. Substituting this parameterization into the optimal discriminator form in Equation (26) and equating them at equilibrium yields:

$$\begin{array}{cc}\hfill {\displaystyle \frac{exp\left(f_{\psi }^{\ast }(s,a,m)\right)}{exp\left(f_{\psi }^{\ast }(s,a,m)\right)+{\pi }_{\theta }(a\mid s,m)}}& ={\displaystyle \frac{p_{{\pi }_E}(s,a,m)}{p_{{\pi }_E}(s,a,m)+p_{{\pi }_{\theta }}(s,a,m)}}\hfill \\ \hfill \Rightarrow exp\left(f_{\psi }^{\ast }(s,a,m)\right)& ={\displaystyle \frac{p_{{\pi }_E}(s,a,m)}{p_{{\pi }_{\theta }}(s,a,m)}}{\pi }_{\theta }(a\mid s,m).\hfill \end{array}$$

(28)

Taking the logarithm on both sides, we obtain:

$$f_{\psi }^{\ast }(s,a,m)=log{p}_{{\pi }_E}(s,a,m)-log{p}_{{\pi }_{\theta }}(s,a,m)+log{\pi }_{\theta }(a\mid s,m).$$

(29)

Under the maximum entropy policy framework [40], the expert’s trajectory distribution is proportional to the exponential of the cumulative true reward: $p_{{\pi }_E}\left(\tau \right)\propto exp\left({\sum }_t{r}_{\mathrm{true}}(s_t,a_t,m_t)\right)$. This implies that the state-action distribution satisfies $log{p}_{{\pi }_E}(s,a,m)=r_{\mathrm{true}}(s,a,m)+log{p}_E(s,m)-V_E(s,m)$, where $V_E(s,m)$ is a log-partition function that dependents only on the state and mean field. A similar relation holds for ${\pi }_{\theta }$: $log{p}_{{\pi }_{\theta }}(s,a,m)=A_{{\pi }_{\theta }}(s,a,m)+V_{{\pi }_{\theta }}(s,m)$, where A is the advantage function.

Substituting these into Equation (29) and simplifying, we get:

$$\begin{array}{cc}\hfill f_{\psi }^{\ast }(s,a,m)& =\left[r_{\mathrm{true}}(s,a,m)+log{p}_E(s,m)-V_E(s,m)\right]-\left[A_{{\pi }_{\theta }}(s,a,m)+V_{{\pi }_{\theta }}(s,m)\right]+log{\pi }_{\theta }(a\mid s,m)\hfill \\ \hfill & =r_{\mathrm{true}}(s,a,m)-A_{{\pi }_{\theta }}(s,a,m)+\underset{\mathrm{State}-\mathrm{dependent}\mathrm{and}\mathrm{action}-\mathrm{dependent}\mathrm{terms}}{\underbrace{log{\pi }_{\theta }(a\mid s,m)+log{p}_E(s,m)-V_E(s,m)-V_{{\pi }_{\theta }}(s,m)}}.\hfill \end{array}$$

(30)

Crucially, in the single-agent case, AIRL [4] proves that, if $f_{\psi }$ is decomposed as $f_{\psi }(s,a)=r_{\psi }(s,a)+h_{\psi }\left(s\right)$, and the policy is trained with a discount factor $\gamma$, the advantage term $A_{{\pi }_{\theta }}$ cancels out the action-dependent log-policy term, leaving a reward that is state-only. In our multi-agent mean field context, we make a corresponding assumption that the learned function $f_{\psi }$ can recover a reward function $r_{\psi }(s,a,m)$ that is disentangled from the policy. Thus, at convergence (${\pi }_{\theta }\to {\pi }_E$), we have:

$$r_{\psi }(s,a,m)\approx r_{\mathrm{true}}(s,a,m)+\chi (s,m),$$

(31)

where $\chi (s,m)$ is an arbitrary function. This completes the proof, showing that the recovered reward is equivalent to the true reward up to a constant shift dependent only on $(s,m)$, fulfilling the condition for reward authenticity.    □

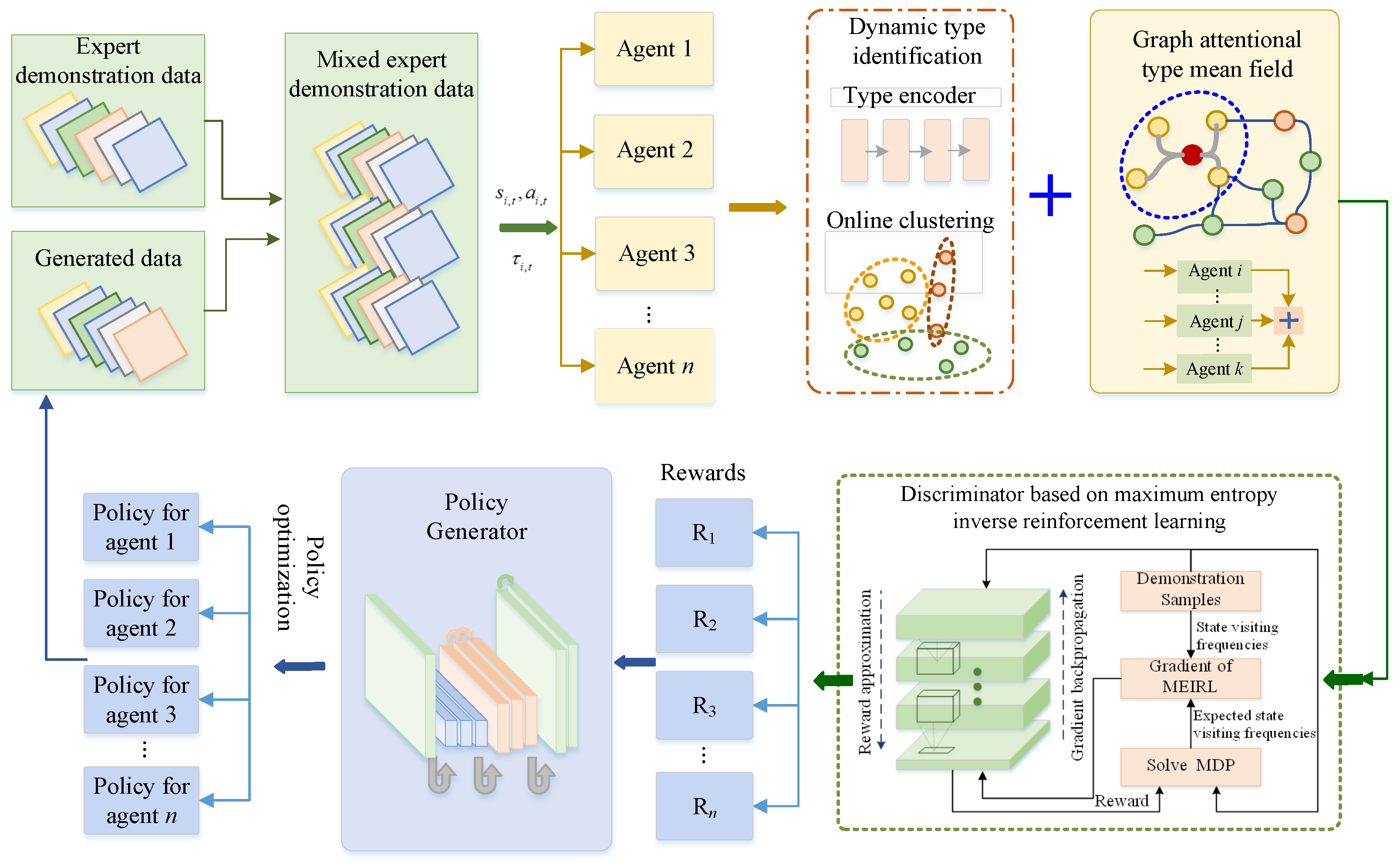
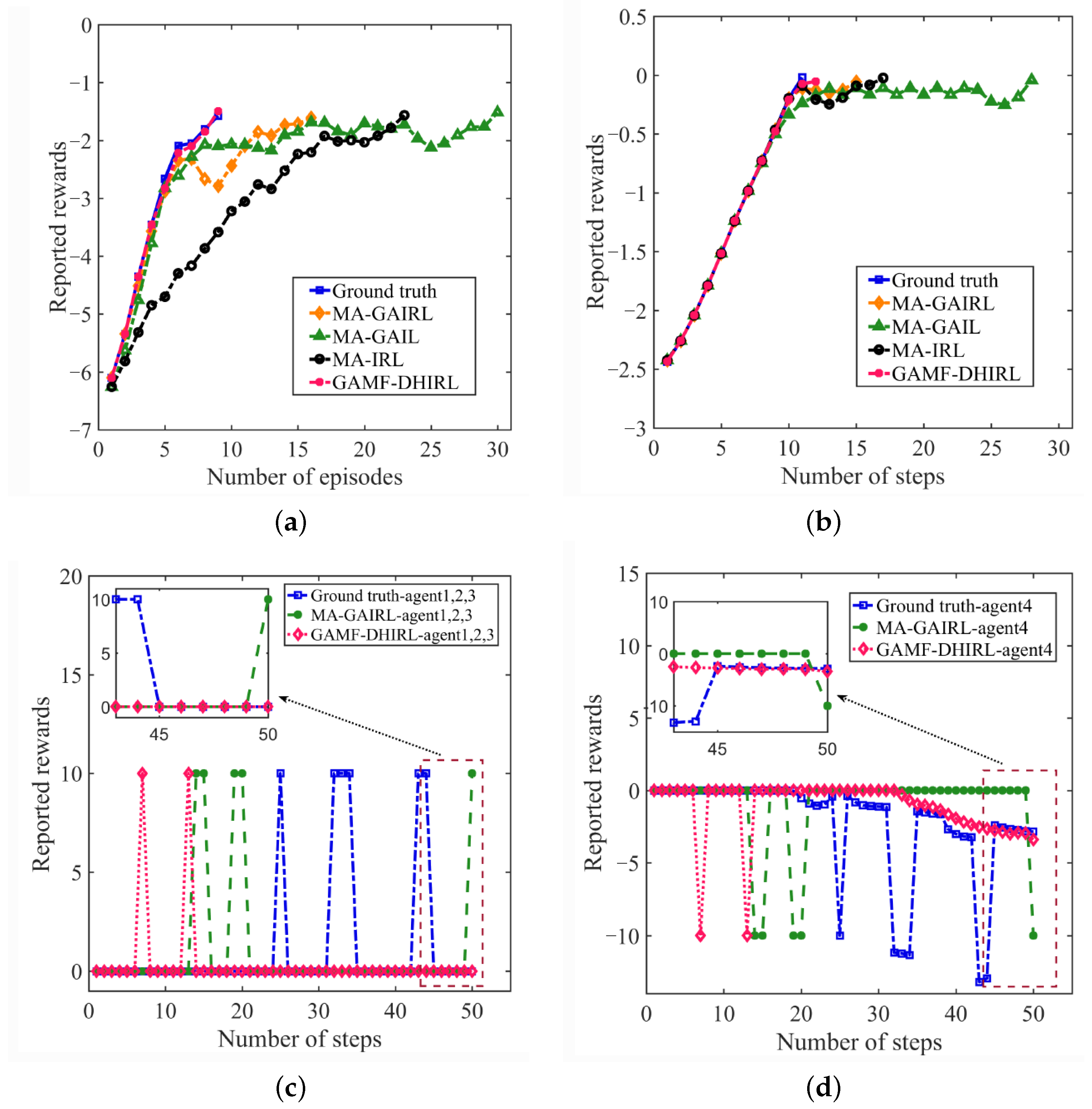
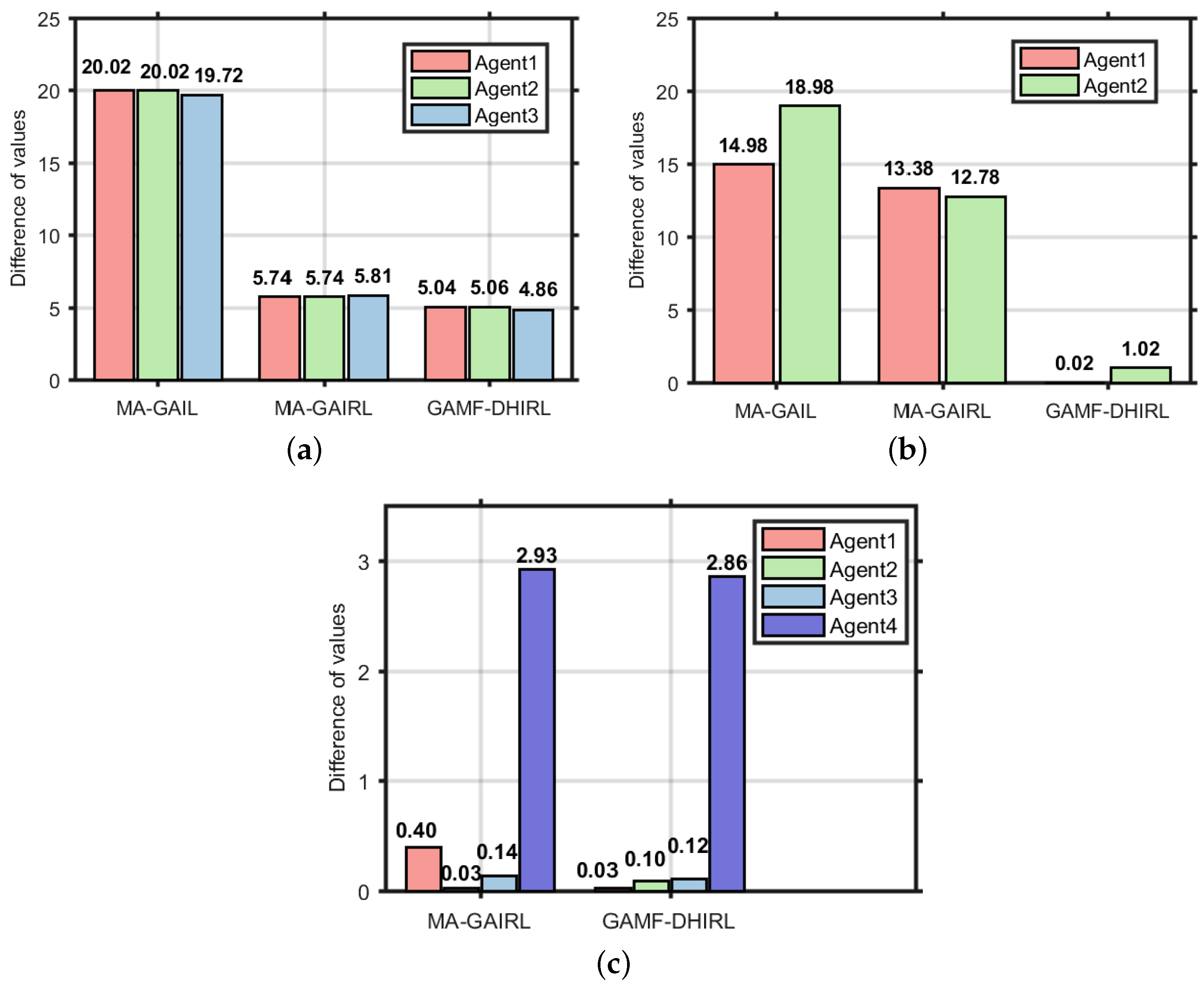
The pseudo-code of the graph attention mean field adversarial inverse reinforcement learning is shown in Algorithm 2. The overall structural framework of graph attention mean field adversarial inverse reinforcement learning is shown in Figure 1. First, we need to obtain mixed expert demonstrations, which consist of the trajectory data (state-action sequences) of one or more experts (or different types of multi-agents) performing tasks in the environment. Under mixed expert demonstrations, the system can achieve cooperation or competition among heterogeneous multi-agent systems, thereby completing dynamic type identification and accurately distinguishing the behavior categories of different agents in the multi-agent system. On this basis, the system further encodes the identified agent types into low-dimensional and computable representation vectors to capture the essential characteristics of agent behaviors. Subsequently, through online clustering methods, the agent behaviors are clustered in real time, and the type labels of the agents are dynamically allocated and updated to continuously optimize the accuracy of type representation. Next, the discriminator based on maximum entropy inverse reinforcement learning uses graph attention networks to calculate the interaction weights between agents, enabling each agent to adaptively aggregate information based on the type encoding of other agents. Simultaneously, the average field theory is used to approximate the complex multi-agent interactions as the interaction between individual and group average behaviors. The main goal of the discriminator is to distinguish as accurately as possible whether a certain trajectory comes from “expert demonstration data” or “generated data”, and gradually learn the implicit reward function without a symmetrical ambiguity problem during this process. Meanwhile, the policy generator continuously adjusts its behavior strategy under the restored reward to generate trajectories that are closer to the expert demonstration. Finally, the system integrates these newly generated high-quality data with the original expert data to form a new generation of hybrid expert demonstration data, thereby continuously expanding and diversifying the scale and diversity of expert data and forming a self-enhancing closed-loop learning process.

Algorithm 2 Graph Attention Mean Field Adversarial Inverse Reinforcement Learning

1: Input: MFG with parameters $\left(\mathcal{S},A,P,m_0\right)$ and observed trajectories ${\mathcal{D}}_E={\left\{{\xi }_j\right\}}_{j=1}^M$, type space $\mathcal{T}$, learning rate $\alpha$, discount factor $\gamma$, number of types K. 2: Initialization: Randomly initialize policy network ${\pi }_{\theta }\left(a\right|s,\tau ,m)$, discriminator $D_{\psi }(s,a,m)$, type encoder $q_{\varphi }\left(z\right|s,a,\tau )$, type prototype $\left\{{\mu }_k\right\}$, and mean field $m_{{\tau }_k}^0=0$ for all ${\tau }_k\in \mathcal{T}$. 3: Estimate the mean field flow ${\tilde{m}}_{{\tau }_k}^t$ from ${\mathcal{D}}_E$. 4: for  $t\in \left\{1,\dots ,T\right\}$do 5:    for each agent $i\in \left\{1,\dots ,N\right\}$ do 6:      Obtain the encoded latent variables $z_i^t\sim q_{\varphi }\left(z\right|s_i^t,a_i^{t-1},{\tau }_i^{t-1})$ 7:      Allocate type: ${\tau }_i^t=arg{max}_{k}p\left(z_i^t\right|{\mu }_k)$, and update the type prototype ${\mu }_k$ 8:      Calculate the neighbor attention weights and update the node features with Equation (12) 9:      Calculate type mean field with Equation (13) 10:      if $tmod\mathrm{update}\_\mathrm{interval}= 0$ or $t=1$ then 11:         Sample expert data batch ${\mathfrak{B}}_E\sim {\mathcal{D}}_E$, and generate policy batch ${\mathfrak{B}}_G\sim {\pi }_{\theta }$ 12:         Update the discriminator and minimize the cross-entropy: $\psi \leftarrow \psi -\alpha {\nabla }_{\psi }\left[{\mathbb{E}}_{{\mathfrak{B}}_E}\left[log{D}_{\psi }\right]+{\mathbb{E}}_{{\mathfrak{B}}_G}\left[log(1-D_{\psi })\right]\right]$ 13:         Update the generator and maximize the rewards: $\theta \leftarrow \theta +\alpha {\nabla }_{\theta }{\mathbb{E}}_{{\mathfrak{B}}_G}\left[log{D}_{\psi }(s,a,m)\right]$ 14:      else 15:         Skip discriminator and generator update for efficiency 16:      end if 17:      if convergence condition is met then 18:         For each type ${\tau }_k$, select the optimal policy using Equation (21) 19:         Update the current policy: ${\pi }_{\theta }\leftarrow {\pi }_{{\tau }_k}^{\ast }$ 20:      else 21:         Continue with current policy ${\pi }_{\theta }$ 22:      end if 23:    end for 24: end for 25: Output: Policy network parameters $\theta$, reward parameters $\psi$, type prototype ${\left\{{\mu }_k\right\}}_{k=1}^K$

4.4. Analysis of Time Complexity

We assume that the number of agents N and the number of types K dynamically change, and $K\ll N$. The state and action dimensions are $d_s,d_a$ respectively, T represents time steps, the latent variable dimension is $d_z$, and the average number of neighbors $\overline{d}$ representing the graph sparsity satisfies $\overline{d}\ll N$.

Theorem 3. 

The complexity of GAMF-DHIRL is $\mathrm{O}\left(TN\left(\overline{d}+C\right)\right)$, where $C=d_z{d}_s+d_h+d_a$.

Proof. 

The proof consists of analyzing the computational cost of each module in GAMF-DHIRL. First, in the dynamic type identification, the type encoder $q_{\varphi }\left(z|s_i,a_i\right)$ is used to calculate latent variables $z_i$, resulting in a complexity of $\mathrm{O}\left(\left(d_s+d_a\right)d_z\right)$ for a single agent and a complexity of $\mathrm{O}\left(N\left(d_s+d_a\right)d_z\right)$ for all agents. Online clustering is then performed using a sliding window EM, requiring a complexity of $\mathrm{O}\left(K{d}_z\right)$ for each update and a total complexity of $\mathrm{O}\left(NK{d}_z\right)$, where K is the number of types ($K\ll N$). Because K and $d_z$ are constants, this term is $\mathrm{O}\left(N\right)$.

Furthermore, in the graph attention average field module, the neighbor aggregation complexity of node feature updates in the GAT layer is $\mathrm{O}\left(\left|\epsilon \right|d_h\right)$, where $\left|\epsilon \right|=N\overline{d}$ is the number of edges, $\overline{d}$ is the average number of neighbors, and the hidden layer dimension $d_h$ is a constant. Therefore, the complexity of the typed average field aggregation is $\mathrm{O}\left(N\overline{d}\right)$.

Finally, during strategy optimization and adversarial training, the policy network ${\pi }_i\left(a_i|s_i,h_i,m_{{\tau }_i}\right)$ has an input dimension of $d_s+d_h+d_a$ and an output dimension of $d_a$, leading to a forward propagation complexity of $\mathrm{O}\left(N\left(d_s+d_h+d_a\right)d_a\right)$. The discriminator $D_{\psi }\left(s,a,m\right)$, which implements the objective in Equation (20), has an input dimension of $d_s+d_a+d_h$ and an output dimension of 1, resulting in a complexity of $\mathrm{O}\left(N\left(d_s+d_a+d_h\right)\right)$.

In summary, the single-step time complexity is ${\mathrm{O}}_{new}=\mathrm{O}\left(N\left(\left(d_s+d_a+K\right)d_z+\overline{d}{d}_h\right.\right.$$\left.\left.+\left(d_h+d_s+d_a\right)d_a\right)\right)$. Under the assumption of constant dimensions, $d_h$, $d_z$, $d_a$, $d_s$, and K are constants, which can be simplified as ${\mathrm{O}}_{new}=\mathrm{O}\left(N\left(\overline{d}+1\right)\right)$. For time steps T, the total complexity is ${\mathrm{O}}_{new}=\mathrm{O}\left(TN\left(\overline{d}+1\right)\right)$. □

5. Experiments and Simulations

We need to answer the following questions: (1) Can our proposed GAMF-DHIRL effectively learn the optimal reward function without the symmetrical ambiguity problem under expert demonstration? (2) Can our proposed GAMF-DHIRL obtain the optimal strategy for each agent based on the learned reward function under expert demonstrations? To enhance the accuracy of the experimental results, all experiments were independently conducted 5 times, and the average values were taken.

5.1. Experimental Setup

To address the two aforementioned issues, we used the classic test environment of multi-agent reinforcement learning with the simulated particle environments to evaluate the performance of the proposed algorithm. Specifically, we used the following three classic scenarios: (1) cooperative navigation: this scenario is primarily used to study how multiple agents cooperate in a two-dimensional space to cover multiple dynamic target points while avoiding collisions and optimizing paths; (2) predator–prey: this scenario is a classic adversarial task in multi-agent reinforcement learning, simulating the dynamic scenario of multiple predators cooperating to hunt one or more prey; and (3) cooperative communication: this scenario is primarily used to study the collaboration, communication, and observation capabilities of multiple agents. Most agents are “dumb” agents that can only observe their local environments. One agent is designated as a “listener” with global observation capabilities. The agents must collaborate in a two-dimensional space to reach a set of dynamic target positions. For all the experiments, we independently conducted them five times and took the average to ensure the accuracy of the results.

The dynamic movement of the target points in the above scenarios involving multiple agents increases the difficulty of the task, which is a multi-task solution problem. The different speeds of the intelligent agents result in their heterogeneity.

In the simulated particle environments, we first obtained expert demonstrations with ground-truth reward functions that could evaluate recovery rewards and optimization strategies. Then, we recovered actual rewards and optimized the policy under expert demonstrations. Our proposed GAMF-DHIRL can use a graph attention mean field to dynamically model dependencies between agents and adaptively adjust the influence weights of neighboring nodes through attention mechanisms. To illustrate the performance of GAMF-DHIRL, we compared GAMF-DHIRL with the following benchmark algorithms and state-of-the-art algorithms:

Multi-agent generative adversarial inverse reinforcement learning (MA-GAIRL) [41]: this algorithm combines generative adversarial models and maximum entropy IRL to learn multi-agent collaborative strategies from expert demonstrations through adversarial training while recovering the underlying reward functions without the symmetrical ambiguity problem.

Generative adversarial imitation learning (MA-GAIL) [42]: Agents learn strategies from expert demonstration data through adversarial training, rather than relying on artificially designed reward functions.

Multi-agent inverse reinforcement learning (MA-IRL) [43]: A distributed data-driven maximum entropy IRL framework for multiagent systems uses state observations to achieve optimal consensus among agents while simultaneously inferring unknown cost functions of all agents.

Multi-agent mean filed inverse reinforcement learning (MF-AIRL) [28]: A novel mean-field adversarial IRL framework based on maximum entropy IRL, which can tackle uncertainties in demonstrations.

The environmental parameter settings used in the experiment are listed in

Table 1. The parameters of the experiment.

Parameters	Values
Batch size	1000
Total timesteps	${10}^7$
Trajectory limitation	200
Discounted factor $\gamma$	0.99
Maximum gradient norm	0.5
Interval of save	100
Coefficient of value function loss	0.5
Coefficient of environment	0.01

.

Both the generator (policy) and discriminator of network architectures in the GAMF-DHIRL are 2-layer multilayer perceptrons (MLPs) with 100 units per hidden layer. The generator (policy network) uses Tanh activation functions and a Softmax output for discrete actions. And the discriminator (discriminator network) uses LeakyReLU (negative slope is 0.2) activations and a Sigmoid output. Optimizer details are as follows: all networks are optimized using the Adam optimizer with a learning rate of $3\times {10}^{-4}$ and betas $\beta =(0.9,0.999)$.

5.2. Evaluation Metrics

To more clearly illustrate the performance of the proposed algorithm, this section provides the definitions and explanations of the evaluation metrics, as follows:

Value loss: The value loss indicates the value of the difference without discount between the predicted value by the critic network and the target value at each step in an episode, which is calculated by ${\mathcal{L}}_{\mathrm{value}}=\mathbb{E}\left[{\displaystyle \frac{1}{Te}}{\sum }_{t=1}^{Te}{\left(V_{\mathrm{critic}}\left(s_{step}\right)-V_{\mathrm{target}}\left(s_{step}\right)\right)}^2\right]$.

Averaged total loss: The total loss is the undiscounted cumulative value of the loss at each timestep, which is calculated by ${\mathcal{L}}_{\mathrm{total}}={\sum }_{\mathrm{episode}=1}^{N_{\mathrm{epi}}}\left({\mathcal{L}}_{\mathrm{value},\mathrm{episode}}\right)$; the averaged total loss is the averaged value of the total loss over the number of timesteps, which is calculated by ${\mathcal{L}}_{\mathrm{avetotal}}={\displaystyle \frac{1}{Te·N_{\mathrm{epi}}}}{\mathcal{L}}_{\mathrm{total}}$.

Explained variance: The explained variance is the average without discount calculated based on all the data collected throughout the entire episodes, which can assess the accuracy of the value function’s prediction and be calculated by $\mathrm{EV}=1-{\displaystyle \frac{\mathrm{Var}\left(G_t-V_{\mathrm{target}}\right)}{\mathrm{Var}\left(G_t\right)}}$, where $G_t={\sum }_{k=t}^{\mathrm{total}\mathrm{timestep}}r(s_k,{\tilde{a}}_k)$ represents the actual rewards starting from time step t, and Var is the variance calculated over all time steps throughout the entire episode.

Q values: The Q values represent the Q value predicted by the critic network for each action at each step in an episode, which is expected cumulative discount value of all future rewards and calculated by $Q_{\mathrm{critic}}={\mathbb{E}}_{\tilde{\pi }}\left[{\sum }_{t=1}^{Te}{\gamma }_t{r}_i(s_t,{\tilde{a}}_t)\mid s_0=s,{\tilde{a}}_0=\tilde{a}\right]$.

Averaged total Q value: The total Q value is the undiscounted cumulative value of the Q values at each time step, which is calculated by $Q_{\mathrm{total}}={\displaystyle \frac{1}{N_{\mathrm{epi}}}}{\sum }_{\mathrm{episode}=1}^{N_{\mathrm{epi}}}\left(Q_{\mathrm{critic},\mathrm{episode}}\right)$; the averaged total Q value is the averaged value of the total Q value over the number of timesteps, which is calculated by $Q_{\mathrm{avetotal}}={\displaystyle \frac{1}{Te·N_{\mathrm{epi}}}}{Q}_{\mathrm{total}}$.

Reported rewards: The reported rewards are the statistically processed reward indicators obtained by the agents when performing tasks in the environment. This value is generally the undiscounted average result obtained from multiple runs, which is calculated by $r_r={\displaystyle \frac{1}{5}}{\sum }_{N=1}^5\left(\tilde{r}\right)$.

5.3. Reward Recovery

To address the first question, we validated the reward learning performance of the proposed GAMF-DHIRL algorithm in three classic scenarios. The total reward function is divided into the distance reward, target reward, and collision reward. The distance reward is generally set as the negative value of the distance between the agent and the target; the target reward is the reward obtained when the agent reaches the target; and the collision reward is the reward obtained from colliding with other agents. A larger reward indicates better reward learning performance of the algorithm. Figure 2a,b show that the recovered rewards of GAMF-DHIRL, MA-GAIRL, MA-GAIL, and MA-IRL under expert demonstration trajectories in the cooperative navigation environment and cooperative communication environment, respectively. Ground truth in the following figures represents the true rewards in the learning environments. From Figure 2a,b, it can be seen that rewards of the proposed GAMF-DHIRL are closer to rewards of the ground truth than those of MA-GAIRL, MA-GAIL, and MA-IRL. Because GAMF-DHIRL uses a dynamic graph attention network to adaptively capture time-varying dependencies between agents and uses mean field approximation to reduce computational complexity, it can learn rewards that are closer to the ground truth.

Figure 2c,d show the recovered rewards of agent 1, agent 2, agent 3, and agent 4 for GAMF-DHIRL and MA-GAIRL in the predator–prey environment. Figure 2a,b show the performances of GAMF-DHIRL and MA-GAIRL are better than those of MA-GAIL and MA-IRL, respectively. Thus, in Figure 2c,d, we compared only the reward learning performances of GAMF-DHIRL and MA-GAIRL. Because the environment is more complex and reward learning is more difficult, GAMF-DHIRL and MA-GAIRL obtained slightly lower reported rewards in the predator–prey environment than in the cooperative navigation and cooperative communication environments. However, owing to the superior performance of the proposed GAMF-DHIRL, even in the predator–prey environment, this algorithm can still obtain rewards closer to the ground truth during the later learning process, compared to MA-GAIRL, MA-GAIL, and MA-IRL.

Figure 3a–c show the difference of values of GAMF-DHIRL, MA-GAIRL, MA-GAIL, and MA-IRL in the cooperative navigation environment, predator-prey environment, and cooperative communication environment, respectively. The difference of values can evaluate the quality of the recovery reward function, and the smaller the value, the better. Figure 3 shows that GAMF-DHIRL has the largest difference of values of all agents, compared with MA-GAIRL, MA-GAIL, and MA-AIRL in these above three environments. Due to the complexity of the predator–prey environment, the number of agent types in this environment is greater than that in the cooperative navigation environment and cooperative communication environment. The value difference of agent 2 for GAMF-DHIRL is higher than that of MA-GAIRL. The value difference of agent 2 for GAMF-DHIRL is 0.03, while the value difference of agent 2 for MA-GAIRL is 0.10. The difference between them is relatively small; therefore, the performance of GAMF-DHIRL is still superior to that of MA-GAIRL.

Figure 4a,b show the changing trend of the difference of rewards during the learning process. During the learning process, it is necessary to make difference of rewards approach zero. From Figure 4, we can know that GAMF-DHIRL offers difference of rewards that are closer to zero, compared with MA-GAIRL, MA-GAIL, and MA-IRL. Therefore, GAMF-DHIRL outperforms MA-GAIRL, MA-GAIL, and MA-IRL.

5.4. Policy Optimization

To answer the first question, in the three classic scenarios, we compared our proposed GAMF-DHIRL with MA-GAIRL and MA-GAIL in terms of optimization.

Table 2. Results of GAMF-DHIRL, MA-GAIRL, and MA-GAIL in the cooperative navigation environment.

Methods	Values Loss	Explained Variance	Q Values	Reported Rewards
MA-GAIL	23.1 ± 0.001	0.426 ± 0.001	−21.5 ± 0.300	0.674 ± 0.001
MA-GAIRL	4.78 ± 0.001	0.398 ± 0.005	−7.34 ± 0.070	0.805 ± 0.002
GAMF-DHIRL	4.77 ± 0.001	0.457 ± 0.008	−6.57 ± 0.180	0.894 ± 0.004

,

Table 3. Results of GAMF-DHIRL, MA-GAIRL, and MA-GAIL in the cooperative communication environment.

Methods	Values Loss	Explained Variance	Q Values	Reported Rewards
MA-GAIL	16.98 ± 2.001	0.30 ± 0.008	−17.00 ± 2.000	0.70 ± 0.001
MA-GAIRL	13.08 ± 0.301	0.52 ± 0.003	−14.60 ± 1.200	0.72 ± 0.002
GAMF-DHIRL	0.56 ± 0.465	0.84 ± 0.017	−5.47 ± 0.103	0.89 ± 0.003

and

Table 4. Results of GAMF-DHIRL, MA-GAIRL, MA-GAIL, and MA-IRL in the predator–prey environment.

Methods	Agents	Averaged Total Loss	Averaged Total Q Value	Reported Rewards
	1	$1.62\times {10}^4$ ± $2.47\times {10}^2$	$-4.44\times {10}^5$ ± $3.70\times {10}^2$	−0.399 ± 0.049
MA-	2	$1.05\times {10}^0$ ± $1.30\times {10}^{-1}$	$-8.38\times {10}^1$ ± $1.40\times {10}^{-1}$	−0.032 ± 0.008
GAIRL	3	$9.15\times {10}^{-1}$ ± $2.30\times {10}^{-2}$	$-3.95\times {10}^1$ ± $2.50\times {10}^{-1}$	−0.139 ± 0.026
	4	$1.77\times {10}^{-1}$ ± $1.50\times {10}^{-2}$	$-3.33\times {10}^0$ ± $4.20\times {10}^{-1}$	0.086 ± 0.010
	1	$\mathbf{1}.\mathbf{61}\times {\mathbf{10}}^{\mathbf{4}}$± $\mathbf{1}.\mathbf{09}\times {\mathbf{10}}^{\mathbf{2}}$	$-\mathbf{8}.\mathbf{66}\times {\mathbf{10}}^{\mathbf{4}}$± $\mathbf{2}.\mathbf{94}\times {\mathbf{10}}^{\mathbf{2}}$	0.134 ± 0.037
GAMF-	2	$\mathbf{6}.\mathbf{93}\times {\mathbf{10}}^{-\mathbf{2}}$± $\mathbf{8}.\mathbf{50}\times {\mathbf{10}}^{-\mathbf{2}}$	$-\mathbf{5}.\mathbf{81}\times {\mathbf{10}}^{\mathbf{0}}$± $\mathbf{1}.\mathbf{60}\times {\mathbf{10}}^{-\mathbf{1}}$	−0.053 ± 0.002
DHIRL	3	$\mathbf{1}.\mathbf{22}\times {\mathbf{10}}^{-\mathbf{1}}$± $\mathbf{1}.\mathbf{06}\times {\mathbf{10}}^{-\mathbf{2}}$	$-\mathbf{1}.\mathbf{11}\times {\mathbf{10}}^{\mathbf{1}}$± $\mathbf{1}.\mathbf{08}\times {\mathbf{10}}^{-\mathbf{1}}$	−0.005 ± 0.001
	4	$\mathbf{1}.\mathbf{48}\times {\mathbf{10}}^{-\mathbf{1}}$± $\mathbf{1}.\mathbf{26}\times {\mathbf{10}}^{-\mathbf{2}}$	$-\mathbf{1}.\mathbf{96}\times {\mathbf{10}}^{\mathbf{0}}$± $\mathbf{1}.\mathbf{00}\times {\mathbf{10}}^{-\mathbf{1}}$	0.217 ± 0.030

show the results of GAMF-DHIRL, MA-GAIRL, and MA-GAIL, respectively. In Table 2 and Table 3, we calculate the value loss, explained variance, Q values, and reported rewards. The greater the explained variance, the more accurate the algorithm’s learning and prediction performance will be. And the Q values and reported rewards should be as large as possible. From Table 2 and Table 3, it can be seen that GAMF-DHIRL has a lower value loss and a higher explained variance, Q values, and reported rewards, compared with MA-GAIRL and MA-GAIL. This is because GAMF-DHIRL can use a dynamic adjacency matrix to capture the time-varying characteristics of the interactions between agents. Therefore, GAMF-DHIRL outperforms MA-GAIRL and MA-GAIL.

Based on the results of value loss, explained variance, Q values, and reported rewards in Table 2 and Table 3, we use the averaged total loss and the averaged total Q value to reflect the performance of the data obtained throughout the training process in a complex predator-prey environment with a greater variety of agents. In Table 4, the total loss is the cumulative total of all losses, and the averaged total loss is the averaged total loss at each time step. The total Q value is the cumulative total of all Q value, and the averaged total Q value is the averaged total Q value at each time step. In this environment, agent 1, agent 2, and agent 3 have a cooperative relationship with each other and compete with agent 4. Therefore, the results of agent 1, agent 2, and agent 3 are similar, whereas they differ from those of agent 4. The results in Table 4 show that the agents of GAMF-DHIRL have a smaller averaged total loss, larger averaged total Q value, and reported rewards, compared to MA-GAIRL. Additionally, throughout the entire training process, the learning curves of the averaged total loss and averaged total Q value are shown in Figure A1a–d.

To verify the impact brought by the graph attention mean field, we conducted ablation experiments. We separately obtained the time taken by the GAMF-DHIRL proposed in this study and the MA-GAIRL without graph attention mean field to complete the total time step, as shown in

Table 5. Running times for GAMF-DHIRL and MA-GAIRL in simulated particle environments.

Environments	Methods	Running Times
Cooperative	MA-GAIRL	72755.91 ± 252.70 s
navigation environment	GAMF-DHIRL	71709.61 ± 518.93 s
	MF-AIRL	72025.85 ± 327.42 s
Predator–prey	MA-GAIRL	46950.76 ± 20.76 s
environment	GAMF-DHIRL	46259.26 ± 97.12 s
	MF-AIRL	46530.34 ± 45.31 s

. In addition, to verify the impact brought by the graph attention, we conducted ablation experiments to separately obtain the time taken by the MF-AIRL. In the cooperative navigation environment, predator–prey environment, and cooperative communication environment, the proposed GAMF-DHIRL had the shorter running time than MA-GAIRL and MF-AIRL, which indicates that the graph attention mean field can reduce the computational complexity of the algorithm.

To further illustrate the impact brought by the graph attention mean field and graph attention, the obtained results of difference of rewards for GAMF-DHIRL, MA-GAIRL, and MF-AIRL are shown in

Table 6. Difference of rewards in the cooperative navigation and predator–prey environments.

Environments	GAMF-DHIRL	MA-GAIRL	MF-AIRL
Cooperative navigation	0.046 ± 0.021	0.985 ± 0.042	0.742 ± 0.083
Predator–prey	0.055 ± 0.006	0.094 ± 0.005	0.083 ± 0.003

throughout the entire training process. The smaller the difference of rewards is, the better the performance of the algorithm will be. From Table 6, we can know that GAMF-DHIRL has the smallest difference of reward than those of MA-GAIRL, and MF-AIRL. Therefore, the GAMF-DHIRL exhibits the best performance.

Additionally, we have investigated the sensitivity of the attention mechanism in GAMF-DHIRL by varying the average neighborhood sizes of 2, 4, 8, and 16. The results are shown in

Table 7. Q values with different average neighborhood sizes in the cooperative navigation and operative communication environments.

Environments	2	4	8	16
Cooperative navigation	−10.86 ± 0.040	−9.23 ± 0.037	−6.83 ± 0.019	−9.72 ± 0.026
Cooperative communication	−10.27 ± 0.300	−7.25 ± 0.204	−5.82 ± 0.105	−8.30 ± 0.190

. From Table 7, it can be known that the optimal average neighborhood size is 8, and GAMF-DHIRL has the best Q values when the average neighborhood size is 8.

6. Conclusions and Future Works

This study proposes a dynamic and heterogeneous multi-agent inverse reinforcement learning framework based on a graph attention mean field. This framework effectively addresses the limitations of traditional inverse reinforcement learning methods in modeling dynamic topologies and heterogeneous behaviors. The model uses a dynamic graph attention network to adaptively capture time-varying dependencies between agents, reducing computational complexity through mean field approximation. This makes the model suitable for large-scale population studies. Experiments demonstrate that this method efficiently recovers the reward functions of heterogeneous agents in collaborative and adversarial scenarios, outperforming traditional IRL methods in terms of performance.

In an extremely large-scale mutation environment, the interference resistance and scalability of the proposed algorithm have not been verified explicitly. Our next research tasks include the following: (1) improving the interference resistance of the proposed algorithm, that is, how to achieve high coverage when some target points are covered or dynamically moving and (2) improving the algorithm’s scalability, that is, whether the algorithm can maintain good performance when the number of agents increases to tens of thousands.