Estimation of the Common Mean of Zero-Inflated Inverse Gaussian Distributions: Application to Road Accident Fatalities in Thailand
Abstract
1. Introduction
2. Mean
3. Common Mean
3.1. Generalized Confidence Interval Approach
| Algorithm 1 GCI approach |
1. Generate from ZIIG distribution with parameters , , and , where and , and compute , , , and 2. Generate and compute using Equation (13) 3. Generate and compute using Equation (14) 4. Generate and compute using Equation (15) 5. Compute using Equation (16) 6. Compute using Equation (17) 7. Compute using Equation (18) 8. Repeat steps 2–7 a total of 1000 times 9. Compute and using Equation (19) |
3.2. Parameter Bootstrap Approach
| Algorithm 2 Parametric bootstrap approach |
1. Generate from ZIIG distribution with parameters , , and , where and 2. Acquire the bootstrap sample from achieved in step 1 and compute and 3. Compute using Equation (20) 4. Compute using Equation (21) 5. Compute using Equation (22) 6. Repeat step 2–5 a total of 1000 times 7. Compute and using Equation (23) |
3.3. Bayesian Approach
| Algorithm 3 Bayesian and HPD approaches |
1. Generate from ZIIG distribution with parameters , , and , where and 2. Specify prior distributions of the parameters as , , and , based on trial hyperparameters 3. Use Metropolis-within-Gibbs sampler in R to obtain posterior samples of ,,: For each parameter, sample from its conditional posterior given the current values of the other parameters. Apply the Metropolis-Hastings step when the conditional posterior is not available in closed form 4. At each iteration, compute derived quantities: using Equation (24), using Equation (25), and using Equation (26) 5.Repeat steps 3–4 for a total of 5000 iterations 6. Discard the first 1000 iterations as burn-in to allow the chain to converge 7. Using the remaining 4000 posterior samples, compute and using Equation (27) and compute and using Equation (28) |
3.4. Highest Posterior Density Approach
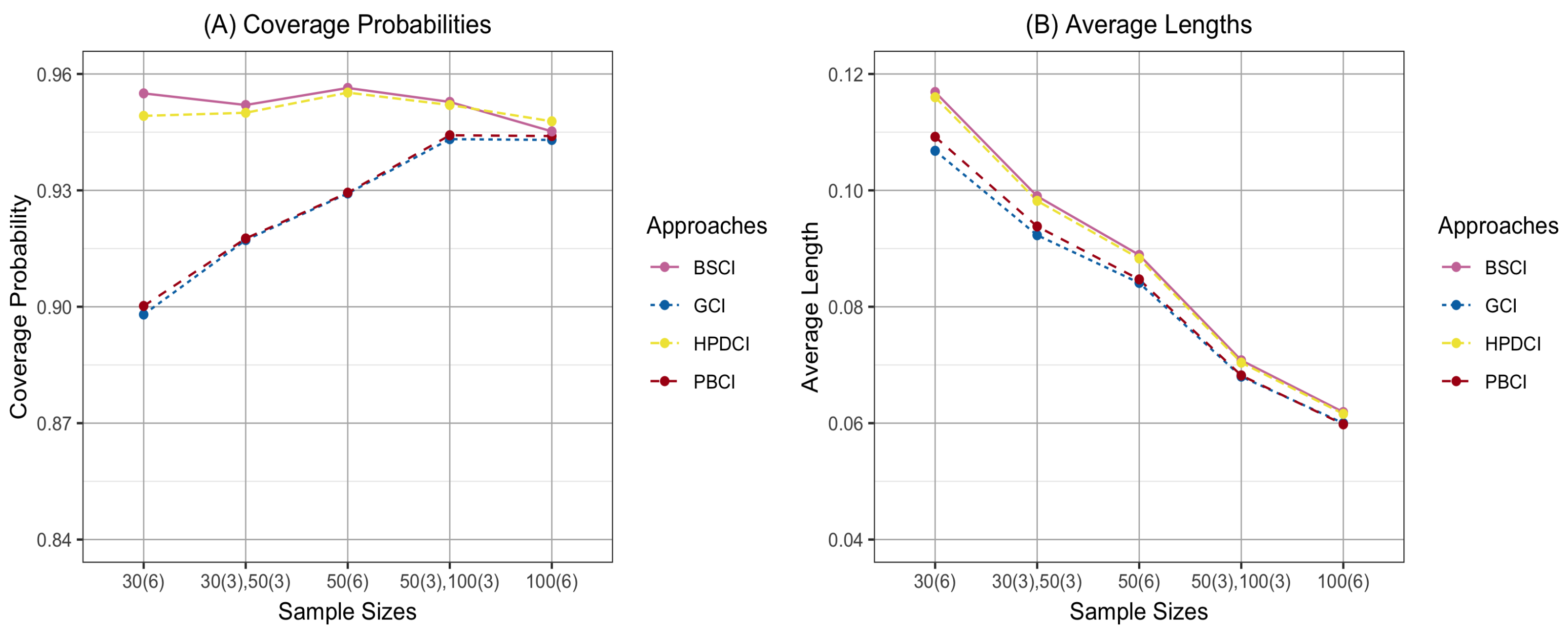
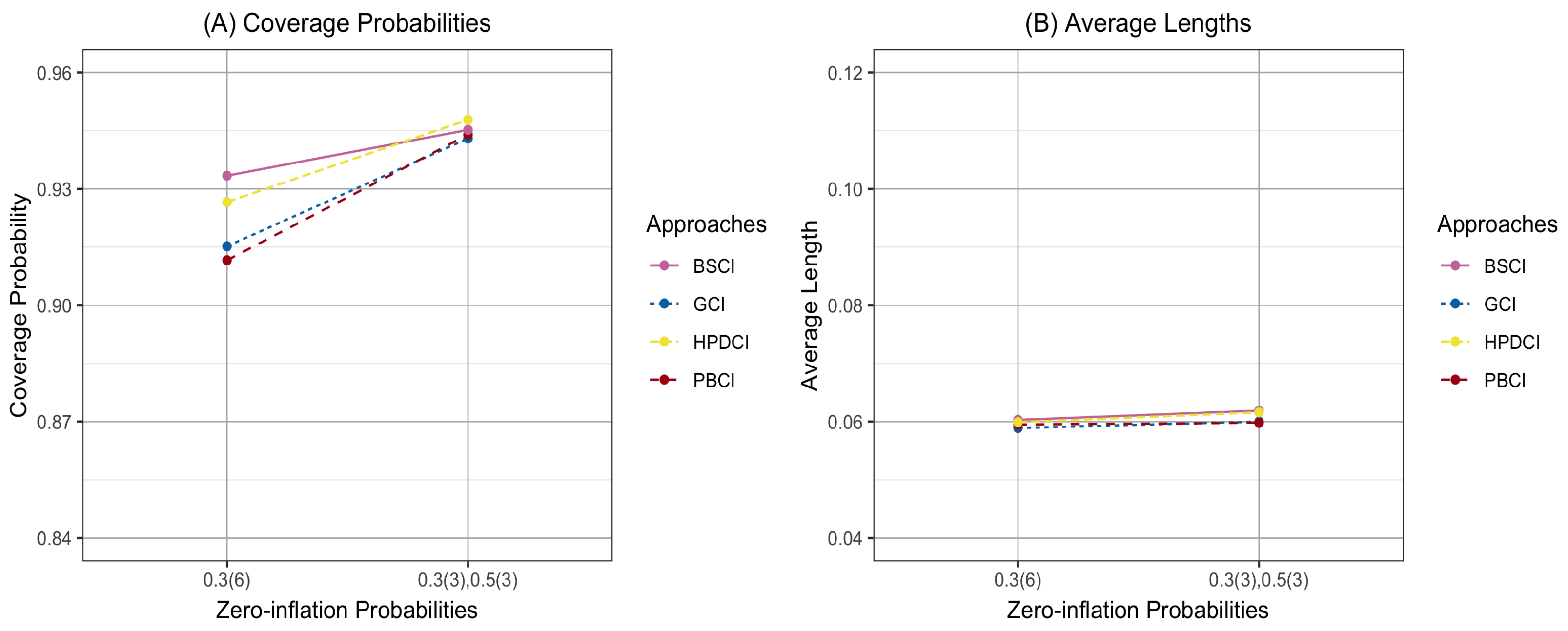
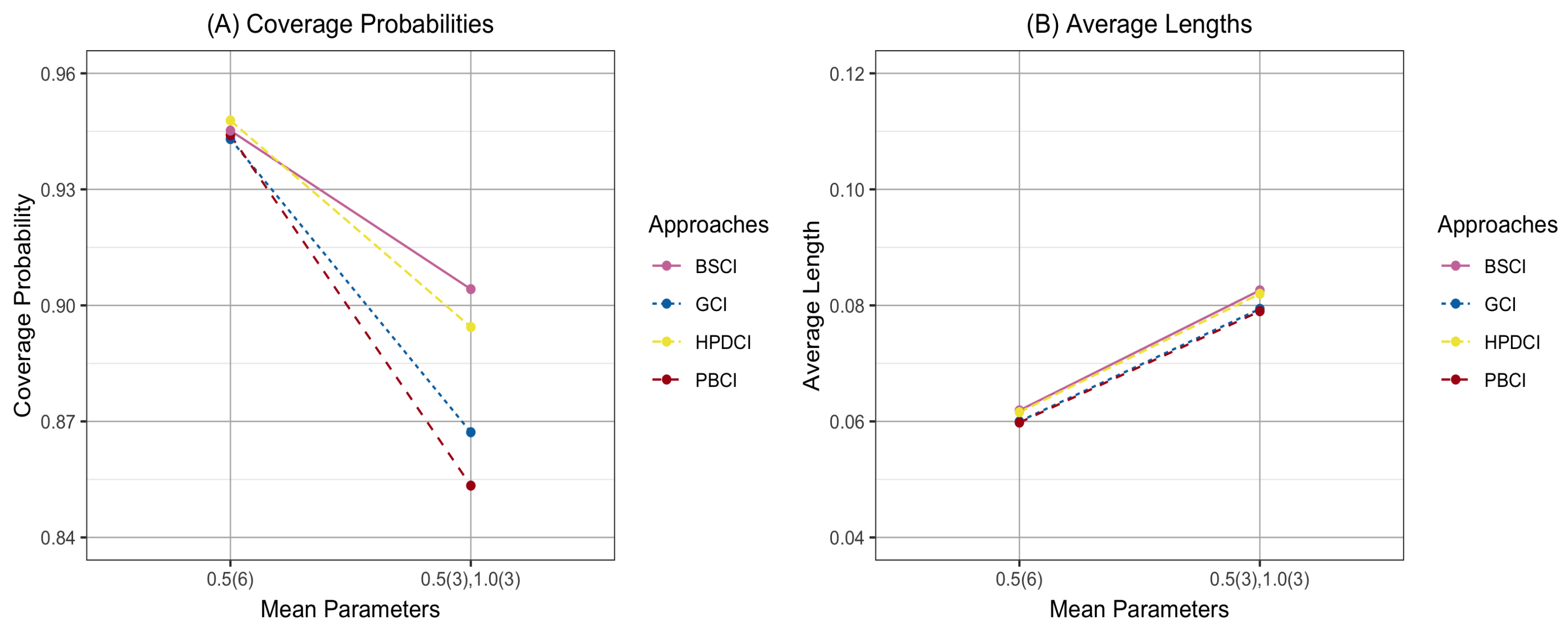
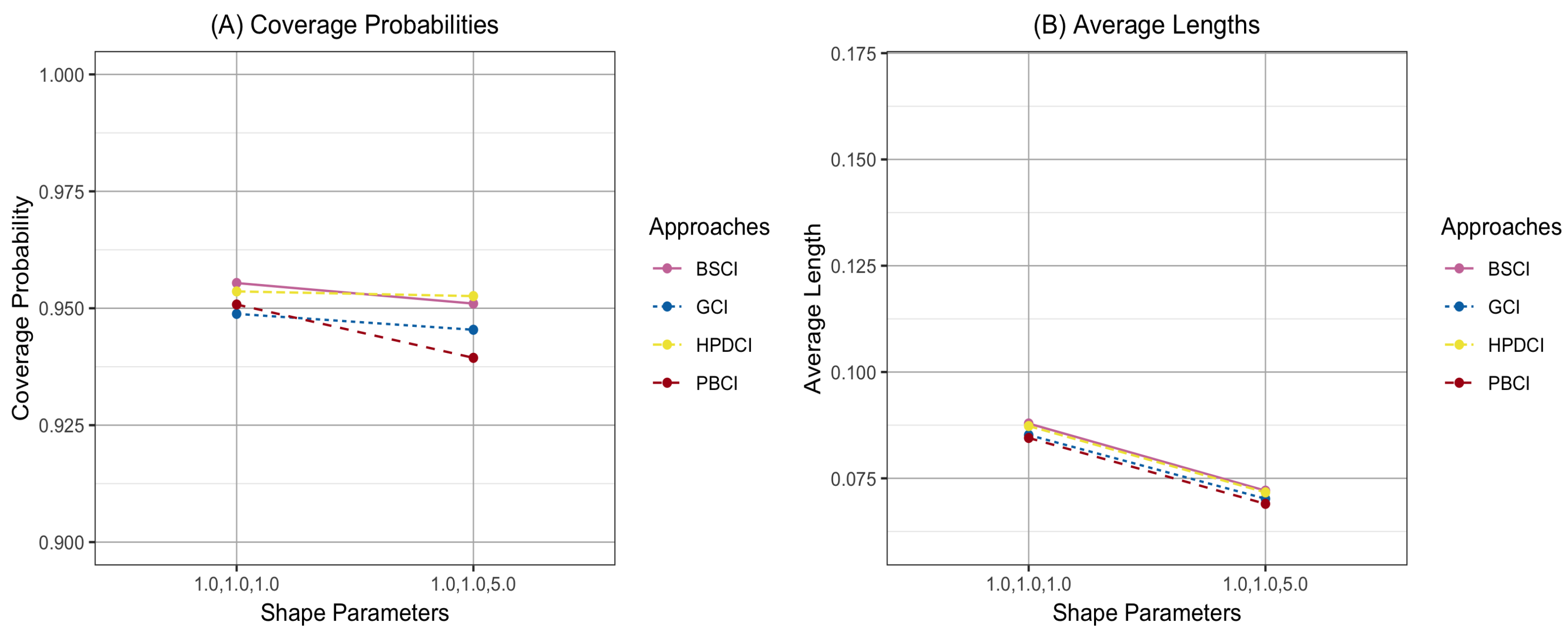
4. Results and Parameter Estimation Effects
| Algorithm 4 CP and AL |
1. Given , , , and 2. Generate sample from ZIIG distributions 3. Compute using Equation (9) 4. Compute using Equation (11) 5. Compute using Equation (12) 6. Use Algorithm 1 to construct 7. Use Algorithm 2 to construct 8. Use Algorithm 3 to construct and 9. If , set 1 else set 0 10. Compute 11. Repeat steps 2 - 10 a total of 5000 times 12. Use the mean of to compute the CPs 13. Use the mean of to compute the ALs |
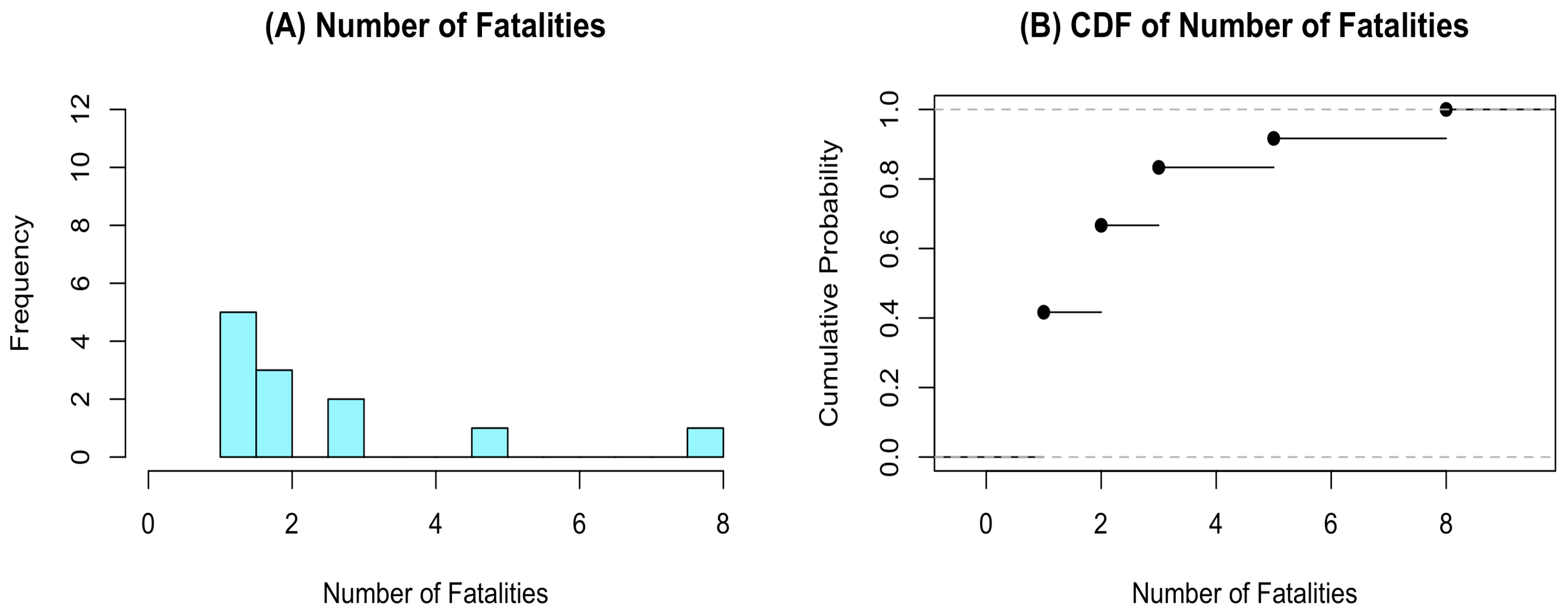
5. An Empirical Application
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Variance Approximation of the ZIIZ Mean Estimator Using the Delta Method
Appendix B. Derivation of the Posterior Distribution for the ZIIG Model
References
- Krishnamoorthy, K.; Tian, L. Inferences on the difference and ratio of the means of two inverse Gaussian distributions. J. Stat. Plan. Inference 2008, 138, 2082–2089. [Google Scholar] [CrossRef]
- Punzo, A. A new look at the inverse Gaussian distribution with applications to insurance and economic data. J. Appl. Stat. 2019, 46, 1260–1287. [Google Scholar] [CrossRef]
- Gelman, A.; Hill, J. Data Analysis Using Regression and Multilevel/Hierarchical Models; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Borenstein, M.; Hedges, L.V.; Higgins, J.P.T.; Rothstein, H.R. Introduction to Meta-Analysis; John Wiley & Sons, Ltd.: Chichester, UK, 2009. [Google Scholar]
- Katahira, K. How hierarchical models improve point estimates of individual-level parameters. J. Math. Psychol. 2016, 73, 37–58. [Google Scholar] [CrossRef]
- Slud, E.V.; Vonta, I.; Kagan, A.M. Combining estimators of a common parameter across samples. Stat. Theory Relat. Fields 2018, 2, 158–171. [Google Scholar] [CrossRef]
- Ye, R.D.; Ma, T.F.; Wang, S.G. Inferences on the common mean of several inverse Gaussian populations. Comput. Stat. Data Anal. 2010, 54, 906–915. [Google Scholar] [CrossRef]
- Bera, S.; Jana, N. On estimating common mean of several inverse Gaussian distributions. Metrika 2022, 85, 115–139. [Google Scholar] [CrossRef]
- Jana, N.; Gautam, M. Confidence intervals of difference and ratio of means for zero-adjusted inverse Gaussian distributions. Commun. Stat. Simul. Comput. 2022, 53, 3302–3326. [Google Scholar] [CrossRef]
- Khumpasee, W.; Niwitpong, S.A.; Niwitpong, S. Confidence intervals for the coefficient of variation in delta-inverse Gaussian distributions. Symmetry 2024, 16, 1488. [Google Scholar] [CrossRef]
- Niwitpong, S.A.; Khumpasee, W.; Niwitpong, S. Confidence intervals for the variance of delta-inverse Gaussian distribution with application to traffic mortality count. J. Phys. Conf. Ser. 2025, 3041, 012009. [Google Scholar] [CrossRef]
- Weerahandi, S. Generalized confidence intervals. J. Am. Stat. Assoc. 1993, 88, 899–905. [Google Scholar] [CrossRef]
- Krishnamoorthy, K.; Lu, Y. Inference on the common means of several normal populations based on the generalized variable method. Biometrics 2003, 59, 237–247. [Google Scholar] [CrossRef]
- Tian, L. Inferences on the common coefficient of variation. Stat. Med. 2005, 24, 2213–2220. [Google Scholar] [CrossRef]
- Chen, Y.H.; Zhou, X.H. Generalized Confidence Intervals for the Ratio or Difference of Two Means for Lognormal Populations with Zeros; UW Biostatistics Working Paper Series; Working Paper 296; Elsevier: Amsterdam, The Netherlands, 2006; pp. 1–26. [Google Scholar]
- Tian, L.; Wu, J. Inferences on the common mean of several log-normal populations: The generalized variable approach. Biometrical J. 2007, 49, 944–951. [Google Scholar] [CrossRef]
- Padgett, W.J.; Tomlinson, M.A. Lower confidence bounds for percentiles of Weibull and Birnbaum-Saunders distributions. J. Stat. Comput. Simul. 2003, 73, 429–443. [Google Scholar] [CrossRef]
- Altunkaynak, B.; Gamgam, H. Bootstrap confidence intervals for the coefficient of quartile variation. Commun. Stat. Simul. Comput. 2019, 48, 2138–2146. [Google Scholar] [CrossRef]
- Zhang, G. A parametric bootstrap approach for one-way ANOVA under unequal variances with unbalanced data. Commun. Stat. Simul. Comput. 2015, 44, 827–832. [Google Scholar] [CrossRef]
- Aizpurua, J.I.; Stewart, B.G.; McArthur, S.D.J.; Penalba, M.; Barrenetxea, M.; Muxika, E.; Ringwood, J.V. Probabilistic forecasting informed failure prognostics framework for improved RUL prediction under uncertainty: A transformer case study. Reliab. Eng. Syst. Saf. 2022, 226, 108676. [Google Scholar] [CrossRef]
- Harvey, J.; van der Merwe, A.J. Bayesian confidence intervals for means and variances of lognormal and bivariate lognormal distributions. J. Stat. Plan. Inference 2012, 142, 1294–1309. [Google Scholar] [CrossRef]
- Rao, K.A.; D’Cunha, J.G. Bayesian inference for median of the lognormal distribution. J. Mod. Appl. Stat. Methods 2016, 15, 526–535. [Google Scholar] [CrossRef]
- Ma, Z.; Chen, G. Bayesian methods for dealing with missing data problems. J. Korean Stat. Soc. 2018, 47, 297–313. [Google Scholar] [CrossRef]
- Wu, W.H.; Hsieh, H.N. Generalized confidence interval estimation for the mean of delta-lognormal distribution: An application to New Zealand trawl survey data. J. Appl. Stat. 2014, 41, 1471–1485. [Google Scholar] [CrossRef]
- Casella, G.; Berger, R.L. Statistical Inference; Duxbury: Bolinas, CA, USA, 2002. [Google Scholar]
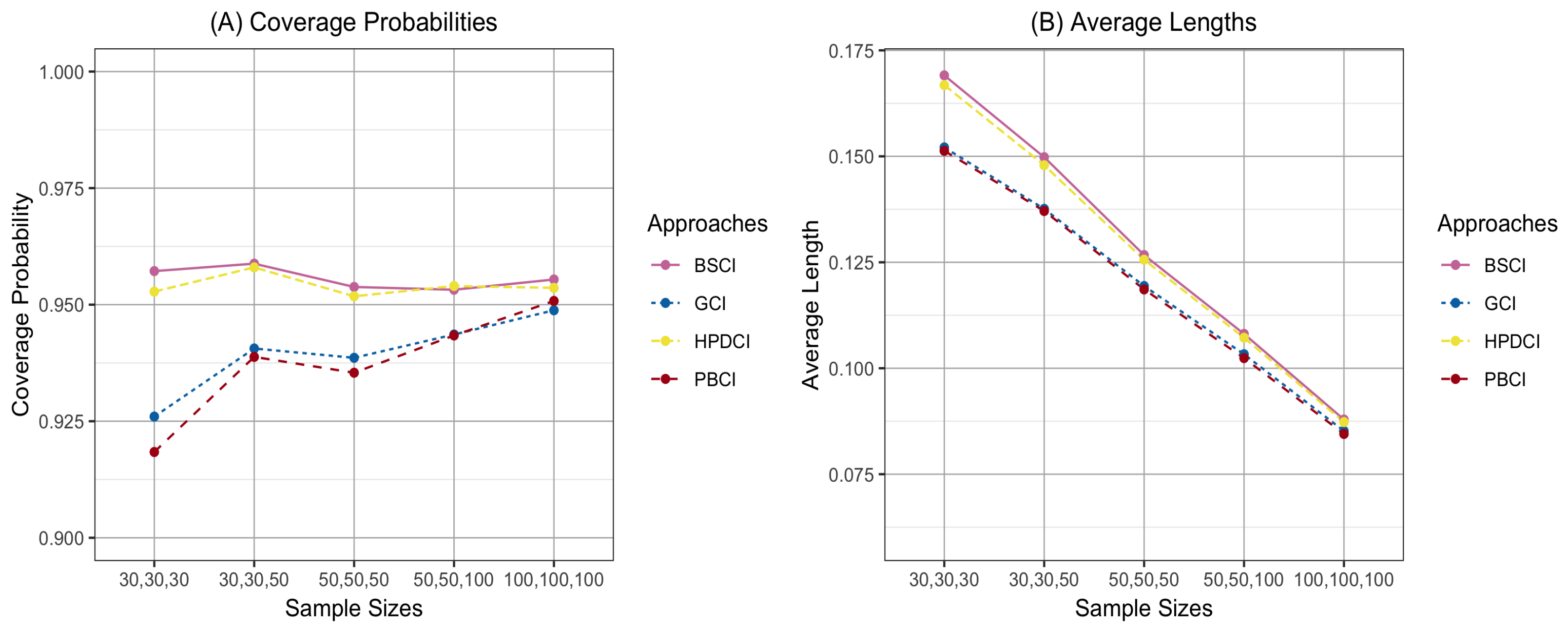

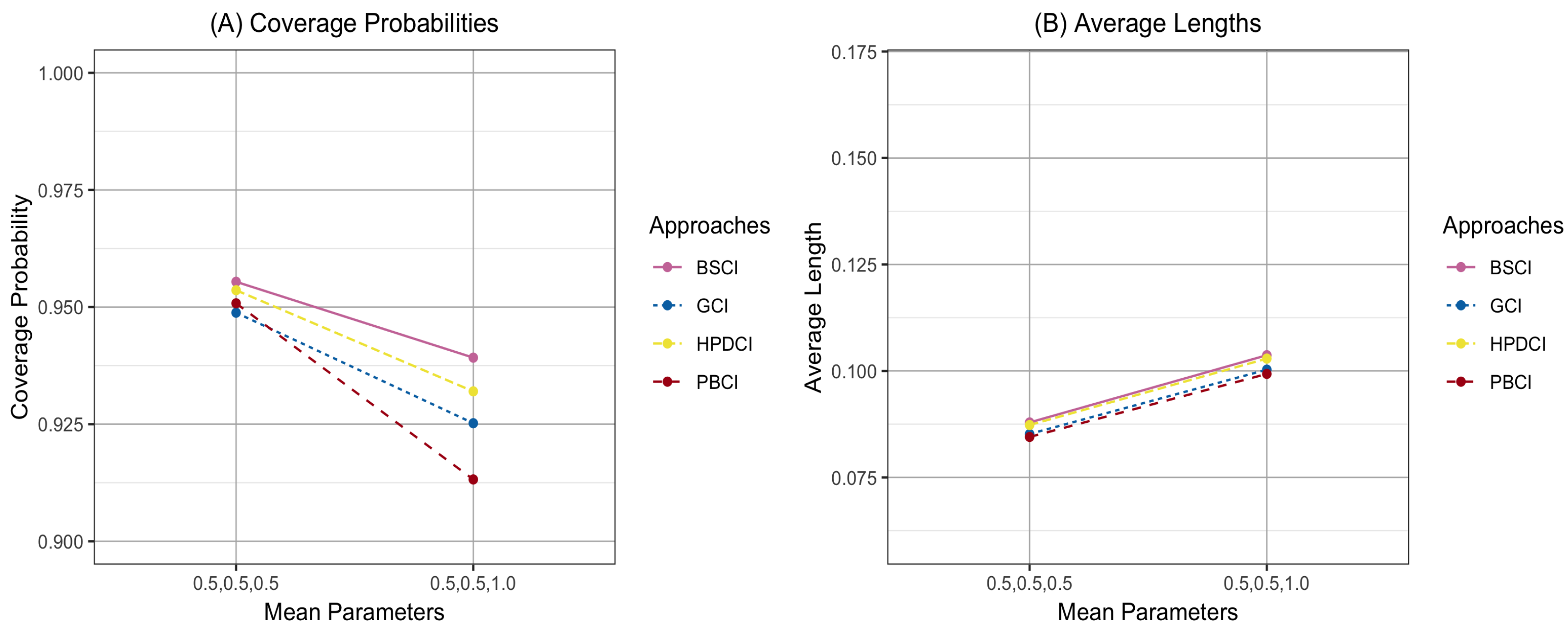

| CP (AL) | |||||||
|---|---|---|---|---|---|---|---|
| 30,30,30 | 0.3,0.3,0.3 | 0.5,0.5,0.5 | 1.0,1.0,1.0 | 0.9086 | 0.8996 | 0.9400 | 0.9274 |
| (0.1496) | (0.1507) | (0.1638) | (0.1616) | ||||
| 0.5,0.5,0.5 | 1.0,1.0,5.0 | 0.9316 | 0.9378 | 0.9558 | 0.9474 | ||
| (0.1314) | (0.1353) | (0.1381) | (0.1371) | ||||
| 0.5,0.5,1.0 | 1.0,1.0,1.0 | 0.9148 | 0.8982 | 0.9482 | 0.9346 | ||
| (0.1872) | (0.1823) | (0.2118) | (0.2074) | ||||
| 0.5,0.5,1.0 | 1.0,1.0,5.0 | 0.9168 | 0.9078 | 0.9386 | 0.9316 | ||
| (0.2041) | (0.2044) | (0.2236) | (0.2192) | ||||
| 0.3,0.3,0.5 | 0.5,0.5,0.5 | 1.0,1.0,1.0 | 0.9260 | 0.9184 | 0.9572 | 0.9528 | |
| (0.1521) | (0.1513) | (0.1691) | (0.1668) | ||||
| 0.5,0.5,0.5 | 1.0,1.0,5.0 | 0.9456 | 0.9434 | 0.9672 | 0.9662 | ||
| (0.1284) | (0.1281) | (0.1391) | (0.1380) | ||||
| 0.5,0.5,1.0 | 1.0,1.0,1.0 | 0.8976 | 0.8714 | 0.9420 | 0.9276 | ||
| (0.1774) | (0.1761) | (0.2007) | (0.1968) | ||||
| 0.5,0.5,1.0 | 1.0,1.0,5.0 | 0.9152 | 0.9024 | 0.9492 | 0.9356 | ||
| (0.1793) | (0.1783) | (0.1986) | (0.1952) | ||||
| 30,30,50 | 0.3,0.3,0.3 | 0.5,0.5,0.5 | 1.0,1.0,1.0 | 0.9112 | 0.8962 | 0.9400 | 0.9304 |
| (0.1356) | (0.1365) | (0.1457) | (0.1440) | ||||
| 0.5,0.5,0.5 | 1.0,1.0,5.0 | 0.9274 | 0.9320 | 0.9468 | 0.9406 | ||
| (0.1146) | (0.1179) | (0.1188) | (0.1181) | ||||
| 0.5,0.5,1.0 | 1.0,1.0,1.0 | 0.9102 | 0.8876 | 0.9442 | 0.9322 | ||
| (0.1903) | (0.1842) | (0.2166) | (0.2123) | ||||
| 0.5,0.5,1.0 | 1.0,1.0,5.0 | 0.9064 | 0.8880 | 0.9366 | 0.9244 | ||
| (0.2046) | (0.2034) | (0.2252) | (0.2214) | ||||
| 0.3,0.3,0.5 | 0.5,0.5,0.5 | 1.0,1.0,1.0 | 0.9406 | 0.9388 | 0.9588 | 0.9580 | |
| (0.1376) | (0.1371) | (0.1498) | (0.1479) | ||||
| 0.5,0.5,0.5 | 1.0,1.0,5.0 | 0.9502 | 0.9482 | 0.9688 | 0.9680 | ||
| (0.1116) | (0.1120) | (0.1184) | (0.1176) | ||||
| 0.5,0.5,1.0 | 1.0,1.0,1.0 | 0.8888 | 0.8616 | 0.9322 | 0.9218 | ||
| (0.1736) | (0.1710) | (0.1957) | (0.1921) | ||||
| 0.5,0.5,1.0 | 1.0,1.0,5.0 | 0.8942 | 0.8746 | 0.9328 | 0.9178 | ||
| (0.1745) | (0.1738) | (0.1919) | (0.1892) | ||||
| 50,50,50 | 0.3,0.3,0.3 | 0.5,0.5,0.5 | 1.0,1.0,1.0 | 0.9218 | 0.9132 | 0.9422 | 0.9330 |
| (0.1171) | (0.1176) | (0.1233) | (0.1221) | ||||
| 0.5,0.5,0.5 | 1.0,1.0,5.0 | 0.9368 | 0.9392 | 0.9506 | 0.9460 | ||
| (0.1027) | (0.1045) | (0.1055) | (0.1049) | ||||
| 0.5,0.5,1.0 | 1.0,1.0,1.0 | 0.9374 | 0.9248 | 0.9564 | 0.9490 | ||
| (0.1489) | (0.1456) | (0.1597) | (0.1577) | ||||
| 0.5,0.5,1.0 | 1.0,1.0,5.0 | 0.9262 | 0.9202 | 0.9422 | 0.9322 | ||
| (0.1604) | (0.1608) | (0.1688) | (0.1666) | ||||
| 0.3,0.3,0.5 | 0.5,0.5,0.5 | 1.0,1.0,1.0 | 0.9386 | 0.9354 | 0.9538 | 0.9518 | |
| (0.1194) | (0.1186) | (0.1267) | (0.1256) | ||||
| 0.5,0.5,0.5 | 1.0,1.0,5.0 | 0.9500 | 0.9486 | 0.9658 | 0.9638 | ||
| (0.0993) | (0.0985) | (0.1043) | (0.1037) | ||||
| 0.5,0.5,1.0 | 1.0,1.0,1.0 | 0.9160 | 0.8948 | 0.9424 | 0.9288 | ||
| (0.1400) | (0.1383) | (0.1499) | (0.1481) | ||||
| 0.5,0.5,1.0 | 1.0,1.0,5.0 | 0.9192 | 0.9064 | 0.9432 | 0.9318 | ||
| (0.1410) | (0.1406) | (0.1491) | (0.1475) | ||||
| 50,50,100 | 0.3,0.3,0.3 | 0.5,0.5,0.5 | 1.0,1.0,1.0 | 0.9316 | 0.9242 | 0.9476 | 0.9410 |
| (0.1020) | (0.1023) | (0.1059) | (0.1051) | ||||
| 0.5,0.5,0.5 | 1.0,1.0,5.0 | 0.9426 | 0.9440 | 0.9522 | 0.9476 | ||
| (0.0842) | (0.0856) | (0.0858) | (0.0854) | ||||
| 0.5,0.5,1.0 | 1.0,1.0,1.0 | 0.9288 | 0.9076 | 0.9492 | 0.9416 | ||
| (0.1524) | (0.1478) | (0.1644) | (0.1623) | ||||
| 0.5,0.5,1.0 | 1.0,1.0,5.0 | 0.9226 | 0.9110 | 0.9420 | 0.9332 | ||
| (0.1627) | (0.1626) | (0.1726) | (0.1707) | ||||
| 0.3,0.3,0.5 | 0.5,0.5,0.5 | 1.0,1.0,1.0 | 0.9436 | 0.9434 | 0.9532 | 0.9540 | |
| (0.1033) | (0.1024) | (0.1081) | (0.1072) | ||||
| 0.5,0.5,0.5 | 1.0,1.0,5.0 | 0.9498 | 0.9448 | 0.9610 | 0.9606 | ||
| (0.0814) | (0.0808) | (0.0842) | (0.0838) | ||||
| 0.5,0.5,1.0 | 1.0,1.0,1.0 | 0.9132 | 0.8910 | 0.9402 | 0.9302 | ||
| (0.1372) | (0.1352) | (0.1466) | (0.1450) | ||||
| 0.5,0.5,1.0 | 1.0,1.0,5.0 | 0.9122 | 0.8918 | 0.9366 | 0.9278 | ||
| (0.1364) | (0.1361) | (0.1437) | (0.1424) | ||||
| 100,100,100 | 0.3,0.3,0.3 | 0.5,0.5,0.5 | 1.0,1.0,1.0 | 0.9388 | 0.9332 | 0.9484 | 0.9458 |
| (0.0837) | (0.0838) | (0.0858) | (0.0852) | ||||
| 0.5,0.5,0.5 | 1.0,1.0,5.0 | 0.9490 | 0.9472 | 0.9536 | 0.9510 | ||
| (0.0729) | (0.0735) | (0.0739) | (0.0735) | ||||
| 0.5,0.5,1.0 | 1.0,1.0,1.0 | 0.9456 | 0.9332 | 0.9524 | 0.9478 | ||
| (0.1071) | (0.1051) | (0.1112) | (0.1103) | ||||
| 0.5,0.5,1.0 | 1.0,1.0,5.0 | 0.9394 | 0.9342 | 0.9468 | 0.9420 | ||
| (0.1150) | (0.1151) | (0.1184) | (0.1173) | ||||
| 0.3,0.3,0.5 | 0.5,0.5,0.5 | 1.0,1.0,1.0 | 0.9488 | 0.9508 | 0.9554 | 0.9536 | |
| (0.0852) | (0.0845) | (0.0879) | (0.0873) | ||||
| 0.5,0.5,0.5 | 1.0,1.0,5.0 | 0.9454 | 0.9394 | 0.9510 | 0.9526 | ||
| (0.0702) | (0.0690) | (0.0721) | (0.0717) | ||||
| 0.5,0.5,1.0 | 1.0,1.0,1.0 | 0.9252 | 0.9132 | 0.9392 | 0.9320 | ||
| (0.1003) | (0.0993) | (0.1037) | (0.1029) | ||||
| 0.5,0.5,1.0 | 1.0,1.0,5.0 | 0.9232 | 0.9156 | 0.9346 | 0.9264 | ||
| (0.1008) | (0.1004) | (0.1036) | (0.1028) | ||||
| CP (AL) | |||||||
|---|---|---|---|---|---|---|---|
| 30,30,30,30,30,30 | 0.3,0.3,0.3,0.3,0.3,0.3 | 0.5,0.5,0.5,0.5,0.5,0.5 | 1.0,1.0,1.0,1.0,1.0,1.0 | 0.8274 | 0.8342 | 0.8876 | 0.8734 |
| (0.1038) | (0.1079) | (0.1121) | (0.1112) | ||||
| 0.5,0.5,0.5,0.5,0.5,0.5 | 1.0,1.0,1.0,5.0,5.0,5.0 | 0.9230 | 0.9420 | 0.9290 | 0.9230 | ||
| (0.0903) | (0.0957) | (0.0926) | (0.0921) | ||||
| 0.5,0.5,0.5,1.0,1.0,1.0 | 1.0,1.0,1.0,1.0,1.0,1.0 | 0.8848 | 0.8670 | 0.9292 | 0.9112 | ||
| (0.1513) | (0.1516) | (0.1698) | (0.1677) | ||||
| 0.5,0.5,0.5,1.0,1.0,1.0 | 1.0,1.0,1.0,5.0,5.0,5.0 | 0.9012 | 0.9010 | 0.9142 | 0.8978 | ||
| (0.1679) | (0.1745) | (0.1803) | (0.1782) | ||||
| 0.3,0.3,0.3,0.5,0.5,0.5 | 0.5,0.5,0.5,0.5,0.5,0.5 | 1.0,1.0,1.0,1.0,1.0,1.0 | 0.8980 | 0.9002 | 0.9550 | 0.9492 | |
| (0.1068) | (0.1092) | (0.1169) | (0.1160) | ||||
| 0.5,0.5,0.5,0.5,0.5,0.5 | 1.0,1.0,1.0,5.0,5.0,5.0 | 0.9514 | 0.9512 | 0.9732 | 0.9714 | ||
| (0.0881) | (0.0890) | (0.0933) | (0.0928) | ||||
| 0.5,0.5,0.5,1.0,1.0,1.0 | 1.0,1.0,1.0,1.0,1.0,1.0 | 0.8034 | 0.7842 | 0.8922 | 0.8716 | ||
| (0.1372) | (0.1408) | (0.1544) | (0.1527) | ||||
| 0.5,0.5,0.5,1.0,1.0,1.0 | 1.0,1.0,1.0,5.0,5.0,5.0 | 0.8550 | 0.8498 | 0.9076 | 0.8898 | ||
| (0.1408) | (0.1442) | (0.1540) | (0.1525) | ||||
| 30,30,30,50,50,50 | 0.3,0.3,0.3,0.3,0.3,0.3 | 0.5,0.5,0.5,0.5,0.5,0.5 | 1.0,1.0,1.0,1.0,1.0,1.0 | 0.8552 | 0.8554 | 0.9002 | 0.8878 |
| (0.0912) | (0.0941) | (0.0966) | (0.0960) | ||||
| 0.5,0.5,0.5,0.5,0.5,0.5 | 1.0,1.0,1.0,5.0,5.0,5.0 | 0.9316 | 0.9446 | 0.9380 | 0.9336 | ||
| (0.0753) | (0.0786) | (0.0767) | (0.0764) | ||||
| 0.5,0.5,0.5,1.0,1.0,1.0 | 1.0,1.0,1.0,1.0,1.0,1.0 | 0.8684 | 0.8412 | 0.9292 | 0.9094 | ||
| (0.1537) | (0.1524) | (0.1733) | (0.1713) | ||||
| 0.5,0.5,0.5,1.0,1.0,1.0 | 1.0,1.0,1.0,5.0,5.0,5.0 | 0.8880 | 0.8750 | 0.9192 | 0.9034 | ||
| (0.1645) | (0.1700) | (0.1782) | (0.1766) | ||||
| 0.3,0.3,0.3,0.5,0.5,0.5 | 0.5,0.5,0.5,0.5,0.5,0.5 | 1.0,1.0,1.0,1.0,1.0,1.0 | 0.9172 | 0.9176 | 0.9520 | 0.9500 | |
| (0.0923) | (0.0938) | (0.0990) | (0.0982) | ||||
| 0.5,0.5,0.5,0.5,0.5,0.5 | 1.0,1.0,1.0,5.0,5.0,5.0 | 0.9470 | 0.9450 | 0.9656 | 0.9638 | ||
| (0.0736) | (0.0745) | (0.0768) | (0.0764) | ||||
| 0.5,0.5,0.5,1.0,1.0,1.0 | 1.0,1.0,1.0,1.0,1.0,1.0 | 0.7894 | 0.7640 | 0.8832 | 0.8652 | ||
| (0.1339) | (0.1353) | (0.1503) | (0.1487) | ||||
| 0.5,0.5,0.5,1.0,1.0,1.0 | 1.0,1.0,1.0,5.0,5.0,5.0 | 0.8358 | 0.8262 | 0.8982 | 0.8824 | ||
| (0.1349) | (0.1384) | (0.1464) | (0.1452) | ||||
| 50,50,50,50,50,50 | 0.3,0.3,0.3,0.3,0.3,0.3 | 0.5,0.5,0.5,0.5,0.5,0.5 | 1.0,1.0,1.0,1.0,1.0,1.0 | 0.8764 | 0.8726 | 0.9132 | 0.9002 |
| (0.0821) | (0.0840) | (0.0859) | (0.0854) | ||||
| 0.5,0.5,0.5, 0.5,0.5,0.5 | 1.0,1.0,1.0,5.0,5.0,5.0 | 0.9432 | 0.9494 | 0.9472 | 0.9438 | ||
| (0.0697) | (0.0721) | (0.0708) | (0.0705) | ||||
| 0.5,0.5,0.5,1.0,1.0,1.0 | .0,1.0,1.0,1.0,1.0,1.0 | 0.9018 | 0.8896 | 0.9334 | 0.9204 | ||
| (0.1215) | (0.1203) | (0.1308) | (0.1296) | ||||
| 0.5,0.5,0.5,1.0,1.0,1.0 | 1.0,1.0,1.0,5.0,5.0,5.0 | 0.9130 | 0.9100 | 0.9230 | 0.9102 | ||
| (0.1330) | (0.1364) | (0.1391) | (0.1378) | ||||
| 0.3,0.3,0.3,0.5,0.5,0.5 | 0.5,0.5,0.5,0.5,0.5,0.5 | 1.0,1.0,1.0,1.0,1.0,1.0 | 0.9292 | 0.9294 | 0.9564 | 0.9552 | |
| (0.0841) | (0.0847) | (0.0889) | (0.0883) | ||||
| 0.5,0.5,0.5,0.5,0.5,0.5 | 1.0,1.0,1.0,5.0,5.0,5.0 | 0.9492 | 0.9424 | 0.9598 | 0.9602 | ||
| (0.0673) | (0.0671) | (0.0701) | (0.0698) | ||||
| 0.5,0.5,0.5,1.0,1.0,1.0 | 1.0,1.0,1.0,1.0,1.0,1.0 | 0.8382 | 0.8188 | 0.8970 | 0.8784 | ||
| (0.1095) | (0.1103) | (0.1177) | (0.1167) | ||||
| 0.5,0.5,0.5,1.0,1.0,1.0 | 1.0,1.0,1.0,5.0,5.0,5.0 | 0.8588 | 0.8520 | 0.8972 | 0.8814 | ||
| (0.1109) | (0.1124) | (0.1169) | (0.1160) | ||||
| 50,50,50,100,100,100 | 0.3,0.3,0.3, 0.3,0.3,0.3 | 0.5,0.5,0.5,0.5,0.5,0.5 | 1.0,1.0,1.0,1.0,1.0,1.0 | 0.9016 | 0.8978 | 0.9272 | 0.9206 |
| (0.0677) | (0.0689) | (0.0699) | (0.0695) | ||||
| 0.5,0.5,0.5,0.5,0.5,0.5 | 1.0,1.0,1.0,5.0,5.0,5.0 | 0.9334 | 0.9432 | 0.9396 | 0.9378 | ||
| (0.0540) | (0.0551) | (0.0546) | (0.0544) | ||||
| 0.5,0.5,0.5,1.0,1.0,1.0 | 1.0,1.0,1.0,1.0,1.0,1.0 | 0.9018 | 0.8750 | 0.9408 | 0.9306 | ||
| (0.1237) | (0.1216) | (0.1336) | (0.1325) | ||||
| 0.5,0.5,0.5,1.0,1.0,1.0 | 1.0,1.0,1.0,5.0,5.0,5.0 | 0.9120 | 0.8938 | 0.9360 | 0.9238 | ||
| (0.1280) | (0.1310) | (0.1350) | (0.1341) | ||||
| 0.3,0.3,0.3,0.5,0.5,0.5 | 0.5,0.5,0.5, 0.5,0.5,0.5 | 1.0,1.0,1.0,1.0,1.0,1.0 | 0.9432 | 0.9442 | 0.9528 | 0.9520 | |
| (0.0680) | (0.0682) | (0.0708) | (0.0704) | ||||
| 0.5,0.5,0.5, 0.5,0.5,0.5 | 1.0,1.0,1.0,5.0,5.0,5.0 | 0.9508 | 0.9394 | 0.9578 | 0.9584 | ||
| (0.0528) | (0.0525) | (0.0542) | (0.0540) | ||||
| 0.5,0.5,0.5,1.0,1.0,1.0 | 1.0,1.0,1.0,1.0,1.0,1.0 | 0.8094 | 0.7808 | 0.8812 | 0.8654 | ||
| (0.1054) | (0.1054) | (0.1129) | (0.1121) | ||||
| 0.5,0.5,0.5,1.0,1.0,1.0 | 1.0,1.0,1.0,5.0,5.0,5.0 | 0.8376 | 0.8172 | 0.8840 | 0.8696 | ||
| (0.1036) | (0.1051) | (0.1085) | (0.1078) | ||||
| 100,100,100,100,100,100 | 0.3,0.3,0.3, 0.3,0.3,0.3 | 0.5,0.5,0.5, 0.5,0.5,0.5 | 1.0,1.0,1.0,1.0,1.0,1.0 | 0.9152 | 0.9116 | 0.9334 | 0.9266 |
| (0.0589) | (0.0595) | (0.0603) | (0.0599) | ||||
| 0.5,0.5,0.5, 0.5,0.5,0.5 | 1.0,1.0,1.0,5.0,5.0,5.0 | 0.9402 | 0.9446 | 0.9432 | 0.9414 | ||
| (0.0491) | (0.0498) | (0.0495) | (0.0493) | ||||
| 0.5,0.5,0.5,1.0,1.0,1.0 | 1.0,1.0,1.0,1.0,1.0,1.0 | 0.9268 | 0.9162 | 0.9412 | 0.9342 | ||
| (0.0884) | (0.0872) | (0.0924) | (0.0917) | ||||
| 0.5,0.5,0.5,1.0,1.0,1.0 | 1.0,1.0,1.0,5.0,5.0,5.0 | 0.9312 | 0.9306 | 0.9366 | 0.9302 | ||
| (0.0955) | (0.0969) | (0.0984) | (0.0977) | ||||
| 0.3,0.3,0.3,0.5,0.5,0.5 | 0.5,0.5,0.5,0.5,0.5,0.5 | 1.0,1.0,1.0,1.0,1.0,1.0 | 0.9430 | 0.9440 | 0.9452 | 0.9478 | |
| (0.0600) | (0.0598) | (0.0619) | (0.0616) | ||||
| 0.5,0.5,0.5,0.5,0.5,0.5 | 1.0,1.0,1.0,5.0,5.0,5.0 | 0.9316 | 0.9160 | 0.9344 | 0.9344 | ||
| (0.0472) | (0.0465) | (0.0484) | (0.0482) | ||||
| 0.5,0.5,0.5,1.0,1.0,1.0 | 1.0,1.0,1.0,1.0,1.0,1.0 | 0.8672 | 0.8534 | 0.9042 | 0.8944 | ||
| (0.0794) | (0.0790) | (0.0826) | (0.0820) | ||||
| 0.5,0.5,0.5,1.0,1.0,1.0 | 1.0,1.0,1.0,5.0,5.0,5.0 | 0.8732 | 0.8644 | 0.9008 | 0.8896 | ||
| (0.0797) | (0.0802) | (0.0820) | (0.0815) | ||||
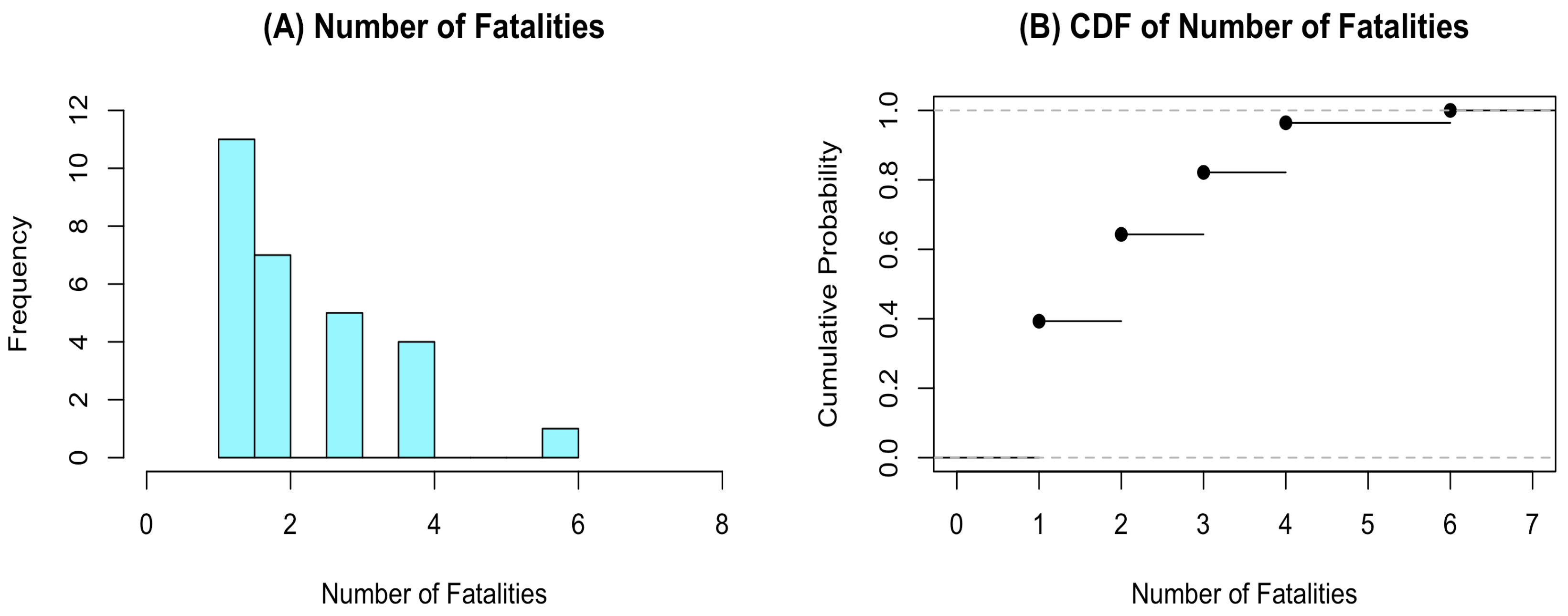
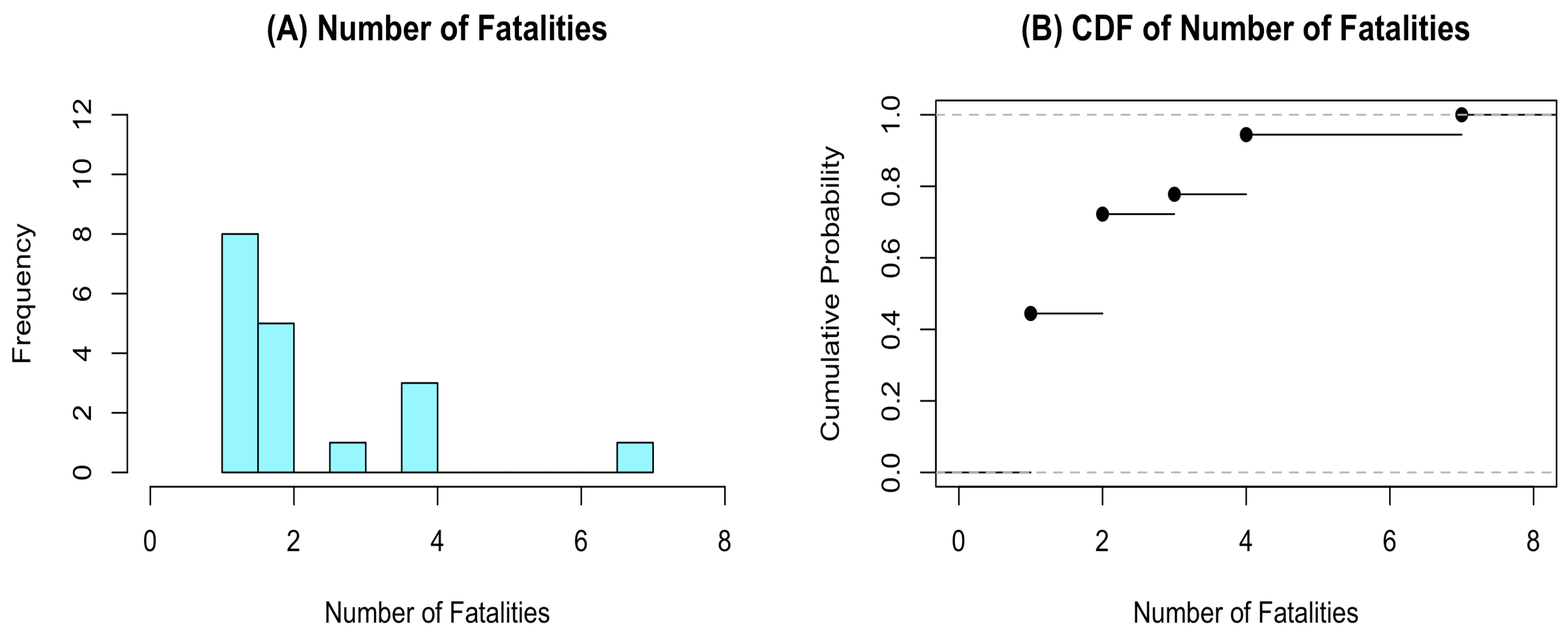
| Provinces | Number of Fatalities | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bangkok | 1 | 1 | 2 | 1 | 4 | 4 | 0 | 0 | 1 | 0 |
| 1 | 2 | 2 | 1 | 0 | 0 | 0 | 1 | 4 | 0 | |
| 0 | 3 | 3 | 1 | 0 | 0 | 0 | 3 | 1 | 0 | |
| 0 | 0 | 0 | 3 | 0 | 2 | 2 | 2 | 4 | 0 | |
| 0 | 2 | 0 | 0 | 0 | 1 | 1 | 6 | 0 | 3 | |
| Nakhon Ratchasima | 0 | 0 | 7 | 0 | 2 | 0 | 1 | 2 | 1 | 1 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 4 | 0 | 0 | |
| 1 | 2 | 4 | 4 | 1 | 2 | 1 | 1 | 0 | 0 | |
| 3 | 2 | 0 | ||||||||
| Chiang Rai | 0 | 2 | 3 | 8 | 0 | 0 | 0 | 2 | 1 | 1 |
| 0 | 5 | 3 | 0 | 0 | 1 | 1 | 1 | 2 | ||
| Distributions | AIC | ||
|---|---|---|---|
| Bangkok | Nakhon Ratchasima Province | Chiang Rai Province | |
| Normal | 97.7922 | 71.6194 | 54.9375 |
| Log-normal | 87.4447 | 58.9964 | 44.5847 |
| Weibull | 90.9186 | 63.5082 | 47.8631 |
| Gamma | 88.9962 | 61.6297 | 46.7522 |
| Exponential | 102.5161 | 66.7463 | 47.9910 |
| Logistic | 97.9099 | 69.8144 | 53.2323 |
| Cauchy | 107.3701 | 70.5189 | 51.7585 |
| Inverse Gaussian | 86.4661 | 58.2498 | 44.0142 |
| Statistics | Bangkok | Nakhon Ratchasima Province | Chiang Rai Province |
|---|---|---|---|
| Total sample size | 50 | 33 | 19 |
| () | |||
| Number of zero observations | 22 | 15 | 7 |
| () | |||
| Number of non-zero observations | 28 | 18 | 12 |
| () | |||
| Estimator of probability of an | 0.4400 | 0.4545 | 0.3684 |
| excess zero parameter () | |||
| Estimator of mean parameter | 2.2143 | 2.2222 | 2.5000 |
| () | |||
| Estimator of scale parameter | 5.9725 | 4.9639 | 4.4582 |
| () | |||
| Estimator for mean | 1.2400 | 1.2121 | 1.5789 |
| () | |||
| Estimator of variance for mean | 0.0635 | 0.1046 | 0.2377 |
| () |
| Confidence Intervals | Lower Limit | Upper Limit | Length |
|---|---|---|---|
| 0.9603 | 1.6190 | 0.6587 | |
| 0.9249 | 1.5557 | 0.6308 | |
| 0.9795 | 1.6552 | 0.6757 | |
| 0.9527 | 1.6035 | 0.6508 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thangjai, W.; Niwitpong, S.-A.; Niwitpong, S. Estimation of the Common Mean of Zero-Inflated Inverse Gaussian Distributions: Application to Road Accident Fatalities in Thailand. Symmetry 2025, 17, 1944. https://doi.org/10.3390/sym17111944
Thangjai W, Niwitpong S-A, Niwitpong S. Estimation of the Common Mean of Zero-Inflated Inverse Gaussian Distributions: Application to Road Accident Fatalities in Thailand. Symmetry. 2025; 17(11):1944. https://doi.org/10.3390/sym17111944
Chicago/Turabian StyleThangjai, Warisa, Sa-Aat Niwitpong, and Suparat Niwitpong. 2025. "Estimation of the Common Mean of Zero-Inflated Inverse Gaussian Distributions: Application to Road Accident Fatalities in Thailand" Symmetry 17, no. 11: 1944. https://doi.org/10.3390/sym17111944
APA StyleThangjai, W., Niwitpong, S.-A., & Niwitpong, S. (2025). Estimation of the Common Mean of Zero-Inflated Inverse Gaussian Distributions: Application to Road Accident Fatalities in Thailand. Symmetry, 17(11), 1944. https://doi.org/10.3390/sym17111944






