Relevance of Inclined Magnetohydrodynamics and Nanoparticle Radius on Tangent-Hyperbolic Flow over a Stretching Sheet: A Symmetric Modeling Perspective with Higher-Order Slip

Abstract

This article investigates the impact of Arrhenius energy and the radius of a nanoparticle subject to an irregular heat source on tangent-hyperbolic nanofluid flow over a stretching sheet with nonlinear radiation. The convective boundary effect, higher-order slip, and micropolarity are all included for a water-based $Cu$ nanofluid. The present study investigates the significance of a nanoparticle’s radius under inclined MHD conditions. The thermally convective flow of the nanofluid is optimized for the heat-transfer rate using the response surface technique. The modeled governing equations are converted into a system of first-order ODEs using the proper similarity transformations, and the BVP5C algorithm—a finite-difference-based solver—is then used to solve these ODEs numerically. Microrotation, thermal boundary-layer thickness, and the skin-friction coefficient all decrease as the nanoparticle radius increases. The thermal layer thickens as the Biot number increases. As the higher-order slip parameter coefficient increases, the results indicate that the skin friction and local Nusselt number fall. Using tables, figures, contour plots, and surface plots, the effects of several influencing factors on the rates of heat and mass transfer, as well as on the skin-friction factor, are demonstrated. The study uses “Response Surface Methodology” (RSM) in conjunction with “Analysis of Variance” (ANOVA) to optimize the most important factors, which are probably the magnetic parameter and the nanoparticle radius that control the flow and heat-transfer properties. Additionally, with a Nusselt number $R^2$ value of $99.96$, indicating an excellent fit, the suggested model exhibits amazing precision. The reliability and efficiency of the estimated model are assessed using the residual versus fitted plot.

1. Introduction

Nanoparticles can be suspended to overcome the limited thermal conductivity of traditional heat-transfer fluids, resulting in nanofluids with much higher thermal conductivity for industrial applications. Increasing thermal conductivity ensures faster heat dissipation, reduces thermal damage, enhances heat-transfer efficiency, and fosters system reliability. By utilizing nanoparticles more effectively in nanofluid applications, thermal and energy system efficiency is improved, energy consumption is reduced, and sustainability is promoted [1]. Ali et al. [2] looked into the impact of varying the radius of copper nanoparticles on the flow of nanofluids under the combined influence of a magnetic field and porous media, aiming to optimize heat-transfer rates by analyzing effects on microrotation, velocity, and temperature profiles. Ref. [3] demonstrated that, while the magnetic field resisted fluid flow, the addition of nanoparticles enhanced heat transfer, and that slip, viscosity variations, and magnetic effects were important factors in regulating thermal conductivity in porous materials. Sachin et al. [4] used a nanofluid consisting of graphene oxide and aluminum oxide nanoparticles to investigate the effects of an inclined magnetic field on fluid flow over a stretching surface. They also analyzed several parameters to determine how they influence physical properties that are important in the biological, physical, and engineering sciences. The importance of mass flux due to a temperature gradient, heat flux resulting from a concentration gradient, and nanoparticle radius in the dynamics of a fluid exposed to an inclined magnetic field was examined by Shah et al. [5]. A magnetic field and thermal radiation were considered in the flow and heat transfer of a nanofluid with fine particles flowing over a stretching surface [6].

Peristalsis of Ree–Eyring non-Newtonian fluid is crucial for researching the rheological properties of biological fluids, such as blood, saliva, intracellular fluids, interstitial fluids, and intravascular fluids [7]. The effects of different variables on fluid temperature and velocity, as well as the influence of thermal radiation and an inclined magnetic field on an MHD boundary layer across an exponentially stretching sheet, were investigated. The findings were consistent with previous similar studies [8]. Srinivasulu et al. [9] numerically examined the influence of an aligned magnetic field on Williamson nanofluid flow across a stretching surface with convective boundary conditions. Hayat et al. [10] explored the effects of heat transfer and an inclined magnetic field on the flow of a third-grade fluid across an exponentially stretching surface. The impact of heat transfer and an inclined magnetic field on a stretching sheet with elastic deformation was also studied [11]. For both Newtonian and non-Newtonian fluids, the study demonstrated that velocity profiles increased with Casson and stretching ratio parameters but decreased with increasing magnetic field parameters. In both fluid types, temperature profiles rose as the magnetic parameter, Prandtl number, and Eckert number increased [12].

Using numerical techniques to assess velocity, temperature, skin friction, and the Nusselt number, Sudais [13] examined the effects of a heat source and variable thermal conductivity on steady radiative MHD flow adjacent to a stagnation point over a nonconducting stretching sheet. The effects of radiation and different heat fluxes on EMHD nanofluid flow across a stretching sheet were investigated in the study by Ali et al. [14]. In addition to improving the temperature field, the radiation parameter also improved the flow characteristics by increasing the velocity.

The mathematical model of entropy generation in convective magnetohydrodynamic flow of a Williamson nanofluid over a stretching sheet with suction and Cattaneo–Christov heat flux was numerically analyzed [15]. With thermal radiation incorporated in the energy equation, the flow and heat transfer properties of a viscous nanofluid across a nonlinearly stretching sheet have been explored in the presence of thermal radiation and changeable wall temperature [16]. A stretching surface with variable viscosity and convective conditions was used in the study by Mabood et al. [17] to investigate the effects of thermal radiation and slip on MHD Casson nanofluid flow. Over a flat plate with convective heat flux and a non-uniform heat source/sink, the study evaluated the impact of temperature-dependent characteristics, partial slip, and thermal radiation on hydromagnetic flow and heat transfer [18]. Anagandula et al. [19] investigated velocity- and thermal-slip-affected Williamson fluid flow across a stretching sheet with radiation and an inclined magnetic field, and they discovered that greater radiation increased the temperature. Multiple slip effects on unsteady MHD flow with heat and mass transfer over a stretching sheet were examined by Mabood et al. [20]. The research takes into account non-uniform sheet velocity, the Soret effect, thermal radiation, and a time-dependent magnetic field.

The study of convective magnetohydrodynamic (MHD) biofluid transport through a non-uniform duct is of interest because of its applications in biomedical devices and equipment [21]. The peristaltic flow of a Jeffrey nanofluid along a vertical diverging channel under the influence of activation energy, heat generation, thermal radiation, and an inclined magnetic field has been analyzed [22]. The study examined the impacts of cobalt ferrite, magnetic fields, and slip effects on the flow of a specific magnetic fluid over a stretching or shrinking surface, as well as their influence on heat transfer, flow stability, and friction [23]. The effects of radiation, multiple slip, and an inclined magnetic field on the flow of a Williamson fluid over a stretching sheet were examined by Srinu et al. [24]. The effects of velocity and thermal slip in MHD hybrid-nanofluid flow across a permeable, exponentially stretching or shrinking sheet were investigated by Patel et al. [25], and it was demonstrated that these factors enhanced heat transfer and supported sustainable energy. The fluid velocity and boundary-layer thickness were affected by the Deborah number and velocity slip in the MHD flow and heat transfer of a Jeffrey nanoliquid over a stretching sheet [26]. The slip-flow nanofluid over a permeable stretching sheet under magnetohydrodynamic forces was examined by Adel et al. [27]. It was found that while the thermal boundary-layer thickness increased with higher slip velocity and magnetic parameters, the velocity boundary-layer thickness decreased. Using an RSM technique to optimize the heat-transfer properties of Casson hybrid-nanofluid flow across a porous, exponentially stretching surface [28]. Baithalu et al. [29] conducted a thorough RSM–ANOVA study to optimize shear and coupling stress analysis for magnetomicropolar dissipative nanofluid flow over a stretching surface.

The previously mentioned literature is still pertinent to research examining the significance of the nanoparticle radius under the simultaneous effects of a magnetic field and nonlinear thermal radiation. An exponential heat source and a higher-order boundary condition are also considered in the flow of a water-based $Cu$ tangent-hyperbolic fluid over a stretching sheet. The controlling partial differential equations were reduced using a similarity transformation, followed by their conversion into a set of nonlinear ordinary differential equations and their numerical solution using MATLAB (2021)’s BVP5C method.

The current study presents a novel aspect by using Response Surface Methodology (RSM)-based CCD design to optimize the thermal transmission rate. Systems employing micropolar hybrid nanofluids are optimized in the study’s results, which could be applied to various industrial and technical operations. Furthermore, combining RSM with ANOVA demonstrates an effective approach for clarifying the optimization of heat transfer when multiple components are involved. Tables and graphs illustrate the effects of various physical parameters on skin friction, temperature profiles, microrotation, dimensionless velocities, and the Nusselt number. Important information on the fluid’s flow properties and thermal behavior under different conditions is provided by the analysis results. In engineering applications where fluid dynamics and heat transfer are important, these findings can help optimize operations.

2. Model Description

This work investigates a two-dimensional, incompressible, viscous flow of a tangent-hyperbolic nanofluid over a stretching sheet with second-order slip and convective boundary conditions. The stretching surface, with a stretching velocity, runs along the x-axis. The transport phenomena of nonlinear convective and radiative micropolar nanofluid flow with varying nanoparticle radii have been taken into consideration. Additionally, the effects of an exponential heat source, inclined MHD, hydrodynamic slip, passive control of nanoparticles, and Arrhenius activation energy are taken into consideration. The sheet stretches linearly with the velocity $U_w=ax$, where a is a constant, while keeping the origin stationary [Figure 1]. The fluid is a water-based $Cu$ nanofluid. The controlling boundary-layer equations are developed using the boundary-layer approximations.

Figure 1. Physical flow diagram.

Refs. [30,31,32,33]

$$\begin{array}{c}\left({\displaystyle \frac{\partial v}{\partial y}}+{\displaystyle \frac{\partial u}{\partial x}}\right)=0.\end{array}$$

(1)

$$\begin{array}{c}\left(v.{\displaystyle \frac{\partial u}{\partial y}}+u.{\displaystyle \frac{\partial u}{\partial x}}\right)={\displaystyle \frac{1}{{\rho }_{nf}}}({\mu }_{nf}(1-n)+k){\displaystyle \frac{.{\partial }^{2}u}{\partial y^2}}+\surd 2n\Gamma {\displaystyle \frac{{\mu }_{nf}}{{\rho }_{nf}}}\left({\displaystyle \frac{\partial u}{\partial y}}\right){\displaystyle \frac{{\partial }^{2}u}{\partial y^2}}+{\displaystyle \frac{k}{{\rho }_{nf}}}{\displaystyle \frac{\partial N}{\partial y}}-{\displaystyle \frac{{\sigma }_{nf}si{n}^2\left(\gamma \right){\left(B_o\right)}^2}{{\rho }_{nf}}}u\end{array}$$

(2)

$$\begin{array}{c}v{\displaystyle \frac{\partial N}{\partial y}}+u{\displaystyle \frac{\partial N}{\partial x}}={\displaystyle \frac{{\gamma }_{nf}}{\left({\rho }_{nf}\right)j}}{\displaystyle \frac{{\partial }^{2}N}{\partial y^2}}-{\displaystyle \frac{\kappa }{\left({\rho }_{nf}\right)j}}({\displaystyle \frac{\partial N}{\partial y}}+2N)\end{array}$$

(3)

$$\begin{array}{c}\left(v{\displaystyle \frac{\partial T}{\partial y}}+u{\displaystyle \frac{\partial T}{\partial x}}\right)={\displaystyle \frac{{\kappa }_{nf}}{{\left(\rho c_p\right)}_{nf}}}{\displaystyle \frac{{\partial }^{2}T}{\partial y^2}}+{\displaystyle \frac{16{\sigma }^{*}}{3m^{*}{\left(\rho C_p\right)}_{nf}}}{\displaystyle \frac{\partial }{\partial y}}\left(T^3{\displaystyle \frac{\partial T}{\partial y}}\right)+{\displaystyle \frac{Q_t}{{\left(\rho C_p\right)}_{nf}}}(T-T_{\infty })+Q_e(T_f-T_{\infty })e^{-mz\sqrt{{\displaystyle \frac{ax}{{\nu }_f}}}}\end{array}$$

(4)

$$\begin{array}{c}u{\displaystyle \frac{\partial C}{\partial x}}+v{\displaystyle \frac{\partial C}{\partial y}}=D_B{\displaystyle \frac{{\partial }^{2}C}{\partial y^2}}-kr(C-C_{\infty })exp\left({\displaystyle \frac{-E}{k^{*}T}}\right){\left({\displaystyle \frac{T}{T_{\infty }}}\right)}^n\end{array}$$

(5)

The problem mentioned above has a couple of boundary conditions [34,35]:

$$\begin{array}{c}u=ax+L_1{\displaystyle \frac{\partial u}{\partial y}}+L_2{\displaystyle \frac{{\partial }^{2}u}{\partial y^2}},v=0,N=-r^{*}{\displaystyle \frac{\partial u}{\partial y}},{\kappa }_{nf}{\displaystyle \frac{\partial T}{\partial r}}=h_{f1}(T-T_f),D_m{\displaystyle \frac{\partial C}{\partial r}}=h_{f2}(C-C_w),aty=0.\\ u⟶0,N⟶0,T⟶0,C⟶0aty⟶\infty \end{array}$$

(6)

The acronyms listed below stand for the following terms: The effective heat capacity of the nanofluid is indicated by ${\left(\rho c\right)}_p$. $Q_e$ is the material parameter representing the heat source coefficient, which depends on the exponential spatial. ${\gamma }_{nf}={\mu }_{nf}(j+{\displaystyle \frac{k}{2}}j)$ denotes the spin gradient’s viscosity. The symbols used to represent fluid density, angular velocity (microrotation vector), micro-inertia, and viscosity vortex are $\kappa ,j,\rho ,$ and N. The Brownian diffusion coefficient is denoted by $D_B$. The heat transfer coefficient is denoted by $h_f$; the reaction rate is denoted by $k_r$; activation energy is denoted by $E_a$; the exponential index is denoted by n; the fitted rate constant is denoted by m; ${{\kappa }_r}^2\left({\displaystyle \frac{T}{T_{\infty }}}\right)$ is the heat sink coefficient that is thermally dependent $Q_T$; and $e^{-{\displaystyle \frac{E_a}{K^{*}T}}}$ is the Arrhenius function. $0\le r^{*}\le 1$ is the value of the parameter $r^{*}$ for the boundary constant. The antisymmetric portion of the stress tensor vanishes at $r^{*}=0.5$, and turbulent boundary-layer flows occur at $r^{*}=1$. N = 0 occurs at the surface when $r^{*}=0$, where the microelements are unable to spin. The subsequent correspondence transforms can be utilized to alter Equations (2) to (6) in a set of differential equations [36]:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \Phi =\sqrt{\left(a{\nu }_f\right)}f\left(\xi \right)x,\theta (T_{\infty }-T_f)=(T_{\infty }-T),\xi =y\sqrt{{\displaystyle \frac{a}{{\nu }_f}}},\\ \hfill u={\displaystyle \frac{\partial \Phi }{\partial x}}=ax{f}^{\prime }\left(\xi \right),\beta ={\displaystyle \frac{N}{ax}}\sqrt{{\displaystyle \frac{a}{{\nu }_f}}},\phi (C_{\infty }-C_f)=(C_{\infty }-C)\end{array}\end{array}$$

$\xi$ represents the dimensionless coordinate.

$$\begin{array}{c}{\displaystyle \frac{1}{R_1}}((n-1)+R_{1}K+nW{f}^{″}\left(\xi \right))f^{‴}\left(\xi \right)-R_2(-f\left(\xi \right)f^{″}\left(\xi \right)+{\left(f^{\prime }\left(\xi \right)\right)}^2)+K{\beta }^{\prime }\left(\xi \right)-R_{3}Msi{n}^2\left(\gamma \right)f^{\prime }\left(\xi \right)=0\end{array}$$

(7)

$$\begin{array}{c}{\displaystyle \frac{(2+K{R}_1)}{2R_1}}{\beta }^{″}\left(\xi \right)+R_2(f{\beta }^{\prime }\left(\xi \right)-f^{\prime }\left(\xi \right)\beta \left(\xi \right)-K(f^{″}\left(\xi \right)+2\beta \left(\xi \right))=0\end{array}$$

(8)

$$\begin{array}{c}{\displaystyle \frac{R_4}{R_5}}{\displaystyle \frac{1}{Pr}}{\theta }^{″}\left(\xi \right)+{\displaystyle \frac{4Rd}{R_{5}Pr}}{(({\theta }_m-1)\theta +1)}^2({\theta }_m-1){\left({\theta }^{\prime }\left(\xi \right)\right)}^2-f{\theta }^{\prime }\left(\xi \right)+{\displaystyle \frac{Qt}{R_5}}\theta \\ +{\displaystyle \frac{4Rd}{3R_{5}Pr}}{(({\theta }_m-1)\theta +1)}^3{\theta }^{″}\left(\xi \right)+{\displaystyle \frac{Qe}{A_5}}{e}^{-m\xi }=0\end{array}$$

(9)

$$\begin{array}{c}{\psi }^{″}\left(\xi \right)-Scf{\psi }^{\prime }\left(\xi \right)-{Kr}^{2}Sc{(1+\theta \delta )}^n{e}^{{\displaystyle \frac{E_a}{(1+\delta \theta )}}}\psi =0\end{array}$$

(10)

together with various boundary conditions:

$$\begin{array}{c}f\left(\xi \right)=1+{\alpha }_1{f}^{\prime }\left(\xi \right)+{\alpha }_2{f}^{″}\left(\xi \right),f^{\prime }\left(\xi \right)=0,\beta \left(\xi \right)=-r\ast f^{\prime }\left(\xi \right),{\theta }^{\prime }\left(\xi \right)=-B{i}_t\{1-\theta \left(\xi \right)\},\\ {\psi }^{\prime }\left(\xi \right)=-B{i}_c\{1-\psi \left(\xi \right)\},at\xi =0f^{\prime }\left(\xi \right)⟶0,\beta ⟶0,\theta \left(\xi \right)⟶0,\psi \left(\xi \right)⟶0,at\xi ⟶\infty .\end{array}$$

(11)

The resulting connection between the dynamic viscosities of the base fluid and the nanofluid was established by Gosukonda et al. [37] and Graham [38]:

$${\displaystyle \frac{{\mu }_{nf}}{{\mu }_{bf}}}=1+{\displaystyle \frac{5}{2}}\varphi +\left[{\displaystyle \frac{1}{{\displaystyle \frac{H}{D_p}}\left({\displaystyle \frac{H}{D_p}}+2\right){\left({\displaystyle \frac{H}{D_p}}+2\right)}^2}}\right]$$

(12)

The nanoparticle radius is denoted by the term $D_p$, the inter-particle spacing is denoted by H, the Prandtl number is denoted by $Pr$, the Biot number is denoted by $Bi$, and the rendition parameter is denoted by $R_d$. The magnetic parameter is denoted by M, the similarity variable is denoted by $\xi$, the Schmidt number is denoted by $S_c$, the exponential space-dependent heat source parameter is denoted by $Q_E$, the thermal heat source is denoted by $Q_T$, the temperature ratio parameter is denoted by $\delta$, the reaction parameter is denoted by $K_r$, the dimensionless activation energy is denoted by $E_A$, the Weissenberg number is denoted by W, the material parameter is denoted by K and nanofluid’s thermophysical characteristics are shown in Table 1.

$$\begin{array}{c}M={\displaystyle \frac{{\sigma }_f{B_O}^2}{{\rho }_{f}ax}},Pr={\displaystyle \frac{{\left(\mu c_p\right)}_f}{{\kappa }_f}},W=\Gamma x\sqrt{{\displaystyle \frac{2a^3}{{\nu }_f}}},K={\displaystyle \frac{{\kappa }_f}{{\nu }_f}},R_d={\displaystyle \frac{4\sigma \ast {T_{\infty }}^3}{\kappa \ast {\kappa }_f}}\\ {\theta }_m={\displaystyle \frac{T_f}{T_{\infty }}},K_r={\displaystyle \frac{{k_r}^2}{ax}}\\ Bi={\displaystyle \frac{h_f}{{\kappa }_f}}\sqrt{{\displaystyle \frac{{\nu }_f}{a}}},Q_E={\displaystyle \frac{Q_e}{{\left(\rho c_p\right)}_{f}ax}},E_A={\displaystyle \frac{E_a}{K{T}_{\infty }}},Q_T={\displaystyle \frac{Q_t}{{\left(\rho c_p\right)}_{f}ax}},S_c={\displaystyle \frac{{\nu }_f}{D_B}},\delta ={\displaystyle \frac{T_w-T_{\infty }}{T_{\infty }}},\end{array}$$

Table 1. The nanofluid’s thermophysical characteristics.

Properties	Nanofluid
Viscosity $\left(\mu \right)$	$R_1={\displaystyle \frac{{\mu }_{nf}}{{\mu }_{bf}}}=1+{\displaystyle \frac{5}{2}}\varphi +\left[{\displaystyle \frac{1}{{\displaystyle \frac{H}{D_p}}\left({\displaystyle \frac{H}{D_p}}+2\right){\left({\displaystyle \frac{H}{D_p}}+2\right)}^2}}\right]$
Density $\left(\rho \right)$	$R_2={\displaystyle \frac{{\rho }_{nf}}{{\rho }_f}}=(1-\varphi )+{\displaystyle \frac{{\rho }_s}{{\rho }_f}}\varphi$
Electrical conductivity $\left(\sigma \right)$	$R_3={\displaystyle \frac{{\sigma }_{nf}}{{\sigma }_f}}=1+3{\displaystyle \frac{\left({\displaystyle \frac{{\sigma }_s}{{\sigma }_f}}-1\right)\varphi }{\left({\displaystyle \frac{{\sigma }_s}{{\sigma }_f}}+2\right)-\left({\displaystyle \frac{{\sigma }_s}{{\sigma }_f}}-1\right)\varphi }},$
The thermal conductivity	$R_4={\displaystyle \frac{k_{bf}}{k_f}}={\displaystyle \frac{-2\varphi ({\kappa }_f-{\kappa }_s)+2{\kappa }_f+{\kappa }_s}{2{\kappa }_f+{\kappa }_s+\varphi ({\kappa }_f-{\kappa }_s)}}$
Heat capacity of the nanofluid $\left(\rho C_p\right)$	$R_5={\displaystyle \frac{{\left(\rho C_p\right)}_{nf}}{{\left(\rho C_p\right)}_f}}={\displaystyle \frac{{\left(\rho c_p\right)}_s}{{\left(\rho c_p\right)}_f}}\varphi +{\left(\rho c_p\right)}_f(1-\varphi )$

3. Engineering Quantities

The specifications of the skin-friction coefficient ($C{f}_x$) and Nusselt number ($N{u}_x$) are

$$C{f}_x={\displaystyle \frac{{\tau }_w^{\prime }}{u_w{\rho }_f}}{\displaystyle \frac{\partial u}{\partial y}},N{u}_x=-{\displaystyle \frac{x{q}_w^{\prime }}{{\kappa }_f\left(T_{\infty }-T_f\right)}}$$

where $q_w^{\prime }$ and ${\tau }_w^{\prime }$ stand for heat flux and shear stress, respectively. The friction drag coefficient $C{f}_x$ and dimensionless Nusselt number $N{u}_x$ are

$${\displaystyle \frac{1}{2}}\sqrt{R{e}_x}C{f}_x={\displaystyle \frac{R_1}{R_2}}(1-n)f^{″}\left(0\right)+{\displaystyle \frac{R_1}{R_2}}{\displaystyle \frac{n}{2}}W{f}^{″}\left(0\right),\sqrt{R{e}_x}=-\left\{R_4+{\displaystyle \frac{4Rd}{3}}{\left[\left({\theta }_m-1\right)\theta +1\right]}^3\right\}{\theta }^{\prime }\left(0\right)$$

where $\sqrt{R{e}_x}={\displaystyle \frac{\sqrt{a}x}{\sqrt{{\nu }_f}}}$ is the Reynolds number.

4. Methodology and Validation

The highly nonlinear coupled ODE system with boundary condition (11) and Equations (7)–(10) can be solved using the BVP5C method function in the MATLAB solver. The BVP5C technique is often used to solve ODEs when the problem’s details are unknown in advance, and a flexible approach is needed to strike a compromise between accuracy and efficiency.

The following is the first guess strategy and solver setup:

For every dependent variable—$f^{\prime }\left(\xi \right),\theta \left(\xi \right),\psi \left(\xi \right),\beta \left(\xi \right)$—over the computational domain, an initial mesh of 500 equally spaced points is generated for $0<\xi <{\xi }_{\infty }$. The BVP5C solver refines the guesses iteratively until the residuals fall within the specified tolerance. The hypotheses are built on physically expected trends, such as exponential decline for temperature, concentration, and motile microbe density, and linear variation for velocity.

Tolerance and convergence criteria are as follows:

The solver iteratively updates the solution until the largest residual norm, $\left|R\right(\xi \left)\right|$, is less than ${10}^{-9}$ over the entire domain. This ensures high numerical precision by setting the relative and absolute error tolerances to ${10}^{-9}$, confirming that further mesh refinement (up to 500 points) results in changes of less than 0.01 in the key output parameters—the skin-friction coefficient, Nusselt number, and Sherwood number.

Following sensitivity tests in which ${\xi }_{\infty }$ was varied from 6 to 9, the far-field boundary of ${\xi }_{\infty }$ = 7 was selected. It was found that, with minimal variation (${10}^{-9}$) in the calculated findings, the velocity, temperature, and concentration profiles all reached their asymptotic ambient values ($T_{\infty },C_{\infty }$) beyond $\xi =7$. This guarantees computational efficiency without compromising accuracy. Plotting the profiles and increasing ${\xi }_{\infty }$ until no discernible difference in the curves was seen allowed us to confirm the asymptotic nature of the profiles.

Now we set $f=y_1,f^{\prime }=y_2,f^{″}=y_3,\beta =y_4,{\beta }^{\prime }=y_5,\theta =y_6,{\theta }^{\prime }=y_7,\psi =y_8,{\psi }^{\prime }=y_9$.

Accordingly, we have

$$\begin{array}{c}{y_1}^{\prime }=y_2\end{array}$$

(13)

$$\begin{array}{c}{y_2}^{\prime }=y_3\end{array}$$

(14)

$$\begin{array}{c}{y_3}^{\prime }={\displaystyle \frac{R_1}{\left[\left(1-n\right)+K{R}_1+nW{y}_3\right]}}\left[R_{3}Msi{n}^2\left(\gamma \right)y_2-K{y}_5+R_2\left(y_2{y}_2-y_1{y}_3\right)\right]\end{array}$$

(15)

$$\begin{array}{c}{y_4}^{\prime }=y_5\end{array}$$

(16)

$$\begin{array}{c}{y_5}^{\prime }={\displaystyle \frac{-2R_1}{\left[\left(2+K{R}_1\right)\right]}}\left[R_2(y_1{y}_5-y_2{y}_4)+K\left(y_3+2y_4\right)\right]\end{array}$$

(17)

$$\begin{array}{c}{y_6}^{\prime }=y_7\\ {y_7}^{\prime }={\displaystyle \frac{-Pr}{\left[R_4+\frac{4Rd}{3}{\left(\left({\theta }_m-1\right)y_6+1\right)}^3\right]}}\left[R_5{y}_1{y}_7-Q_T{y}_6-Q_E{e}^{-m\xi }-{\displaystyle \frac{4Rd}{3}}{\left(\left({\theta }_m-1\right)y_6+1\right)}^2\left({\theta }_m-1\right){y_7}^2\right]\end{array}$$

(18)

$$\begin{array}{c}{y_8}^{\prime }=y_9\end{array}$$

(19)

$$\begin{array}{c}{y_9}^{\prime }=S_c\left(y_1{y}_9\right)+K_r{S}_c{\left(1+\delta y_6\right)}^{n1}{y}_8{e}^{{\displaystyle \frac{E_A}{\left(1+\delta y_6\right)}}}\end{array}$$

(20)

The boundary conditions as

$$\begin{array}{c}{y}_1=1+{\alpha }_1{y}_2+{\alpha }_2{y}_3,y_2=0y_4+r_{*}{y}_2{R}_4{y}_7-B{i}_t{y}_6+B{i}_t=0,y_9-B{i}_c{y}_8+B{i}_c=0\\ y_2=0,y_4=0,y_6=0,y_8=0\end{array}$$

(21)

The final solution is obtained by calculating the variable values across the domain, and the level of accuracy is verified in Table 2.

Table 2. Evaluation of $(-{\theta }^{\prime }\left(0\right))$.

(Pr)	Hamad [39]	Reddy et al. [40]	Khan et al. [41]	Present Result
000.07	00.06630	0.06560	00.0656	0.0662700
000.02	00.16910	0.1691	00.16909	0.1690970
000.70	00.45390	00.5349	000.45391	0.4539290
002.08	00.91130	0.9114	00.91136	0.911340
07.00	01.89540	1.89050	001.89540	1.895490
0020.00	03.35390	003.3539	003.35390	3.353930
070.00	06.46220	006.4622	006.46220	6.462033

5. Concluding Results

The figures depict the effects of several important parameters on the velocity $\left(f^{\prime }\left(\xi \right)\right)$, microrotation $\beta \left(\xi \right)$, temperature $\theta \left(\xi \right)$, and concentration profiles in the presence of stimulating influences from inclined MHD and the nanoparticle radius $D_p$.

Table 3 displays the variation of the skin-friction coefficient for different values of the velocity ratio parameter $\left(W\right)$, permeability parameter $\left(K\right)$, velocity slip, ${\alpha }_1$ and ${\alpha }_2$, and the inclination angle $\gamma$ for two distinct particle diameters, $D_p=1.5$ and $D_p=2.5$. The results demonstrate that $C_f$ increases as W and K increase, suggesting that increased permeability and stronger stretching worsen surface shear stress. Conversely, greater values of the velocity slip parameter ${\alpha }_1$ result in a drop in $C_f$, indicating that microrotational effects reduce wall shear and counteract fluid motion. The sensitivity of friction to microrotation coupling is also demonstrated by the fact that a larger negative ${\alpha }_2$ raises Cf. Additionally, as the magnetic field inclination angle $\gamma$ increases from 45 to 90, cf decreases for all parameter combinations because the magnetic damping effect is stronger at higher inclinations. The higher particle diameter, $D_p=2.5$, yields considerably higher Cf values than $D_p=1.5$ because larger particles have a thicker boundary layer and stronger momentum interaction.

Table 3. The skin local drag $C{f}_x$ for different values of $W,K,{\alpha }_1,{\alpha }_2$ at $D_p=1.5,D_P=2.5$.

${\mathit{D}}_{\mathit{p}}$	W	K	${\mathit{\alpha }}_1$	${\mathit{\alpha }}_2$	$\mathit{\gamma }={45}^{\circ }$	$\mathit{\gamma }={60}^{\circ }$	$\mathit{\gamma }={90}^{\circ }$
						${\mathit{C}\mathit{f}}_{\mathit{x}}{\mathit{R}{\mathit{e}}_{\mathit{x}}}^{-\mathbf{1}/\mathbf{2}}$
0.5	1	0.2	0.3	−0.2	0.171403	0.164388	0.157900
-	2	-	-	-	0.178299	0.170096	0.162549
-	3	-	-	-	0.182826	0.173244	0.164507
-	1	0.1	-	-	0.171403	0.164388	0.157900
-	-	0.3	-	-	0.180127	0.173679	0.167681
-	-	0.5	-	-	0.187215	0.176356	0.175605
-	-	-	0.2	-	0.161218	0.154174	0.147726
-	-	-	0.4	-	0.144643	0.137570	0.131204
-	-	-	0.6	-	0.131651	0.124581	0.118308
-	-	-	-	−0.1	0.185657	0.179809	0.174352
-	-	-	-	−0.3	0.160349	0.152581	0.145462
-	-	-	-	−0.5	0.143806	0.135125	0.127294
2.5	1	0.2	0.3	−0.2	0.635614	0.624038	0.613040
-	2	-	-	-	0.645480	0.632598	0.620323
-	3	-	-	-	0.653447	0.638875	0.624930
-	1	0.1	-	-	0.635614	0.624038	0.613040
-	-	0.3	-	-	0.652255	0.642415	0.633078
-	-	0.5	-	-	0.661703	0.652785	0.644332
-	-	-	0.2	-	0.603732	0.591008	0.579044
-	-	-	0.4	-	0.550961	0.536536	0.523183
-	-	-	0.6	-	0.508685	0.4930860	0.4788178
-	-	-	-	−0.1	0.653815	0.644263	0.635207
-	-	-	-	−0.3	0.619106	0.605816	0.593201
-	-	-	-	−0.5	0.590125	0.574080	0.558918

The Table 4 shows that the local Nusselt number $N{u}_x$ changes for two particle diameter ratios ($D_p=1.5$ and $D_p=2.5$) for different values of W, $Rd$, ${\alpha }_1$, $B{i}_t$, and n. Given that $N{u}_x$ rises with increasing radiation parameter $Rd$ and Biot number $B{i}_t$, the results indicate enhanced heat transfer due to stronger radiative and convective effects. In contrast, when the power-law index n or the microrotation parameter ${\alpha }_1$ rises, $N{u}_x$ falls, signifying a drop in temperature. Moreover, when the inclination angle $\gamma$ increases from 45 to 90, $N{u}_x$ decreases. Figure 2a–d illustrate that the magnitude of the velocity distribution increases as the radius of the nanoparticle $\left(D_p\right)$ increases from $D_p=0.5$ to $D_p=2.5$. Consequently, the interphase and the nanoparticles are affected by the nanoparticle radius. In these nanofluids, the velocity increases as viscosity decreases with particle size. This explains why the velocity of the current transport phenomena increases with the radius of $Cu$. The impact of an increasing external magnetic flux, which is directly proportional to the angle ($\gamma$), is also observed. According to Figure 2a–d, lower velocities in the transport phenomena are achieved with increasing magnetic strength.

Table 4. The Nusselt number $N{u}_x$ for different values of $W,Rd,{\alpha }_1,n,B{i}_t$ at $D_p=1.5,D_p=2.5$.

${\mathit{D}}_{\mathit{p}}$	W	$\mathit{R}\mathit{d}$	${\mathit{\alpha }}_1$	${\mathit{B}\mathit{i}}_{\mathit{t}}$	n	$\mathit{\gamma }={45}^{\circ }$	$\mathit{\gamma }={60}^{\circ }$	$\mathit{\gamma }={90}^{\circ }$
							${\mathit{N}\mathit{u}}_{\mathit{x}}{\mathit{R}{\mathit{e}}_{\mathit{x}}}^{-\mathbf{1}/\mathbf{2}}$
0.5	1	0.3	0.3	0.4	0.1	0.340775	0.333676	0.325730
-	2	-	-	-	-	0.336437	0.327900	0.318076
-	3	-	-	-	-	0.330744	0.3200993	0.307367
-	-	0.2	-	-	-	0.276113	0.270680	0.264769
-	-	0.5	-	-	-	0.372445	0.364310	0.355064
-	-	0.8	-	-	-	0.464338	0.452047	0.4373610
-	-	-	0.2	-	-	0.334765	0.326346	0.316736
-	-	-	0.4	-	-	0.322603	0.3109522	0.296955
-	-	-	0.6	-	-	0.310003	0.294070	0.273516
-	-	-	-	0.1	-	0.129783	0.128227	0.126461
-	-	-	-	0.3	-	0.340775	0.333676	0.325730
-	-	-	-	0.5	-	0.500608	0.486400	0.470715
-	-	-	-	-	0.2	0.336605	0.328256	0.318675
-	-	-	-	-	0.3	0.324084	0.311148	0.294880
-	-	-	-	-	0.4	0.298521	0.270927	0.223660
2.5	1	0.3	0.3	0.4	0.1	0.367723	0.365959	0.364185
-	2	-	-	-	-	0.366845	0.364900	0.362930
-	3	-	-	-	-	0.365774	0.363589	0.361355
-	-	0.2	-	-	-	0.297977	0.296502	0.2950280
-	-	0.5	-	-	-	0.402407	0.400476	0.3985308
-	-	0.8	-	-	-	0.505571	0.503045	0.500479
-	-	-	0.2	-	-	0.3646806	0.3625965	0.360498
-	-	-	0.4	-	-	0.3588739	0.356124	0.353344
-	-	-	0.6	-	-	0.353333	0.349879	0.346364
-	-	-	-	0.1	-	0.135507	0.135139	0.134769
-	-	-	-	0.3	-	0.367723	0.365959	0.364185
-	-	-	-	0.5	-	0.556278	0.552552	0.548818
-	-	-	-	-	0.2	0.366664	0.364733	0.362782
-	-	-	-	-	0.3	0.363809	0.361383	0.358900
-	-	-	-	-	0.4	0.359020	0.355597	0.352000

Figure 2. (a–d) Fluctuation in velocity profile $f\left(\xi \right)$ with $D_p$ and inclined MHD at various values of W, K, ${\alpha }_1$ and ${\alpha }_2$.

The impact of the Weissenberg number W on the velocity field is shown in Figure 2a. The velocity profile slightly decreases with increasing W. The Weissenberg number is physically defined as the ratio of the fluid relaxation time to the characteristic process time. A decrease in the velocity field occurs due to the increasing resistance to fluid motion caused by a longer relaxation time as the Weissenberg number increases.

The relationship between the material parameter and the velocity profile is depicted in Figure 2b. It is observed that the velocity profile decreases as a function of K for nanoparticle radii $(D_p=0.5)$ and $(D_p=2.5)$. Higher K values are physically associated with lower viscosity and weaker rotation of the fluid’s particle moments. The material behavior changes without structural alteration due to its intrinsic properties. With higher K values, it is evident that the fluid moves at a higher velocity near the wall and slows down as it moves away from it. Figure 2c,d illustrate the effects of the first- and second-order slip parameters on the velocity field. The hydrodynamic boundary-layer thickness decreases, and the velocity field becomes smaller as the absolute values of ${\alpha }_1$ and ${\alpha }_2$ increase. In physical terms, an increase in the slip parameters decreases the thickness of the flow field and the velocity boundary layer because of the increased resistance to fluid motion.

Figure 3a–d show that the microrotation distribution decreases as the radius of $Cu$ nanoparticles increases from $D_p=0.5$ to $D_p=2.5$, while the distribution pattern indicates enhanced fluid-layer activity with an increase in $\gamma$ from $\pi /6$ to $\pi /2$ in each profile. By increasing frictional heating between the fluid layers, the Lorentz drag physically releases energy as heat. This leads to a thickening of the thermal boundary layer. Additionally, the profile thickens as W and K increase, whereas the first-order and second-order slip parameters exhibit the opposite behavior.

Figure 3. (a–d) Deviation in the microrotation velocity profile, $\beta \left(\xi \right)$, with $D_p$ and inclined MHD at various values of W, K, ${\alpha }_1$, and ${\alpha }_2$.

Figure 4a–d show that as the particle radius $D_p$ increases, the thermal boundary-layer thickness decreases. For $D_p=2.5$, the thermal boundary layer is significantly reduced, indicating a decline in the fluid-layer thermal properties with increasing $Cu$ nanoparticle radius. However, the thermal layer thickens as $\gamma$ increases due to the parallel influence of MHD. Additionally, it is found that the fluid layers associated with $Rd$ and $B{i}_t$ exhibit a rapidly growing thermal boundary layer. The temperature gradient increases as a result of stronger convective heating at the sheet, which is physically correlated with a larger $B{i}_t$. With a greater temperature difference, the thermal influence can penetrate further into the quiescent fluid. As the fluid temperature increases with the Biot number, convective heat transfer is enhanced and the sheet’s thermal resistance decreases. The thermal boundary layer is found to be a highly significant increasing feature of the fluid layers for $Qt$ and $Qe$.

Figure 4. (a–d) Variation in $\theta \left(\xi \right)$ with $D_p$ and inclined MHD at various values of $Rd$, $B{i}_t$, $Qt$, and $Qe$.

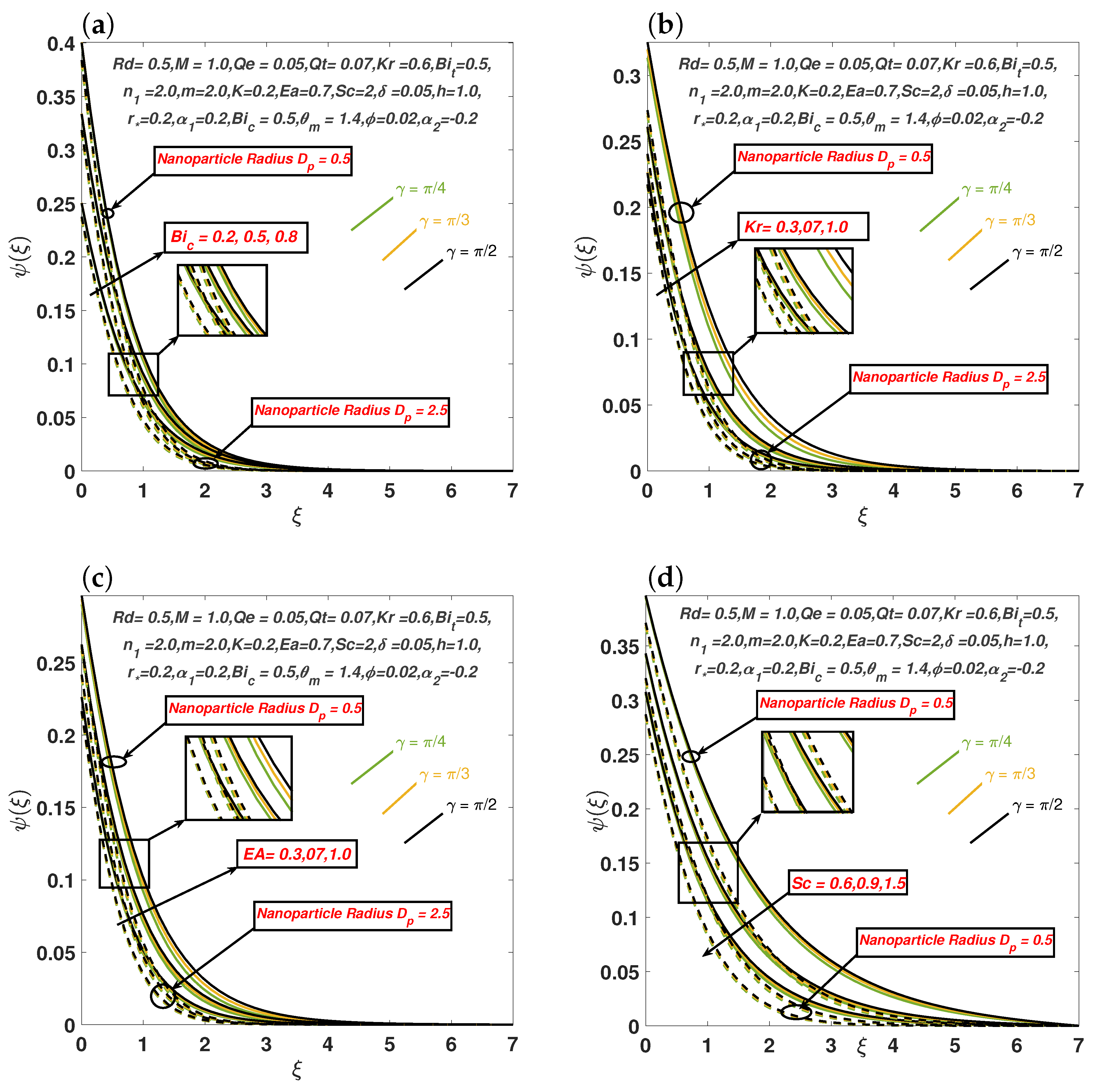
Figure 5a,b illustrate how the concentration Biot number, chemical-reaction parameter $K_r$, nanoparticle radius $D_p$, and the stimulating influence of inclined MHD affect the concentration profile. The relationship between the Schmidt number ($Sc$) and the activation-energy parameter ($E_a$) with the concentration profile is shown in Figure 5c,d. The $Ea$ increases the profile, while a notable decrease is observed with $Sc$. Physically, the activation-energy parameter provides atoms or molecules with greater energy to interact, thereby intensifying the chemical reaction and enhancing the concentration profile.

Figure 5. (a–d) Deviation in the concentration profile $\psi \left(\xi \right)$ with $D_p$ and the inclined MHD at various values of $B{i}_c$, $Kr$, $EA$, and $Sc$.

6. Response Surface Methodology (RSM)

The interaction between pertinent attributes and the response variable is statistically investigated using RSM. RSM uses data from the central composite design to estimate the model for the dependent variable (Mahanthesh et al. [42]). The heat transport of the $\{Cu/H_{2}O\}$ nanoliquid, represented as $\left\{N{u}_{x}R{e}_x^{(-1/2)}\right\}$, is selected as the dependent variable in this problem, and the independent variables are the magnetic parameter $(0.3\le M\le 0.7)$, the nanoparticle radius $(0.5\le D_P\le 2.5)$, the magnetic parameter $(0.1\le M\le 0.9)$, and the radiation parameter $(0.2\le Rd\le 0.6)$. Table 5 displays the effective parameters and their levels. A generic model for the response variable, including interactive, quadratic, and linear terms, is expressed as follows:

$$\begin{array}{c}\hfill Response=X_1{A}_1+X_2{B}_1+X_3{C}_1+X_4{A}_1{B}_1+X_5{B}_1{C}_1+X_6{A}_1{C}_1+X_7{A_1}^2+X_8{B_1}^2+X_9{C_1}^2+X_{1}0\end{array}$$

(22)

Regression coefficients are represented by $X_i$ (i = 1 to 10). According to the CCD, the experimental plan and responses for the 20 runs are shown in Table 6.

Table 5. Levels of effective parameters.

Parameter	Symbol	Levels
		(Low)(−1)	(Median)(0)	(High)(1)
M	$A_1$	0.3	0.5	0.7
$D_p$	$B_1$	0.5	1.5	2.5
$Rd$	$C_1$	0.4	0.4	0.6

Table 6. Response-based experimental design.

$\mathit{R}\mathit{u}\mathit{n}$	${\mathit{A}}_1$	${\mathit{B}}_1$	${\mathit{C}}_1$	M	${\mathit{D}}_{\mathit{p}}$	$\mathit{R}\mathit{d}$	${\mathit{N}\mathit{u}}_{\mathit{x}}{\mathit{R}\mathit{e}}_{\mathit{x}}^{-1/2}$
1	−1	−1	−1	0.3	0.5	0.2	0.277591
2	1	−1	−1	0.7	0.5	0.2	0.264769
3	−1	1	−1	0.3	2.5	0.2	0.298398
4	1	1	−1	0.7	2.5	0.2	0.295028
5	−1	−1	1	0.3	0.5	0.6	0.406078
6	1	−1	1	0.7	0.5	0.6	0.383514
7	−1	1	1	0.3	2.5	0.6	0.43755
8	1	1	1	0.7	2.5	0.6	0.432702
9	−1	0	0	0.3	1.5	0.4	0.358964
10	1	0	1	0.7	1.5	0.4	0.35728
11	0	−1	0	0.5	0.5	0.4	0.334737
12	0	1	0	0.5	2.5	0.4	0.366211
13	0	0	−1	0.5	1.5	0.2	0.287633
14	0	0	1	0.5	1.5	0.6	0.421811
15	0	0	0	0.5	1.5	0.4	0.355221
16	0	0	0	0.5	1.5	0.4	0.355221
17	0	0	0	0.5	1.5	0.4	0.355221
18	0	0	0	0.5	1.5	0.4	0.355221
19	0	0	0	0.5	1.5	0.4	0.355221
20	0	0	0	0.5	1.5	0.4	0.355221

The estimated model’s efficiency is detailed in the ANOVA table (Table 7). A parameter is deemed significant if its associated p-value is less than 0.05 and its related F-value is larger than 1. See Areekara et al. [43]. The quadratic terms in M and $D_p$, as well as the interaction term $M\ast D_p$, are found to be meaningless. These terms are, therefore, removed from the model. With a coefficient of determination ($R^2$) of 99.96, the model’s accuracy is increased. The uncoded version of the fitted quadratic model for $N{u}_x/\sqrt{R{e}_x}$ is provided by

$$\begin{array}{c}N{u}_x/\sqrt{R{e}_x}=0.21763-0.0755M+0.01841D_p+0.3538Rd+0.0414M\ast M-0.00599D_P*D_p\\ -0.0436Rd\ast Rd+0.01698M\ast D_p-0.0351M\ast Rd+0.01850D_p\ast Rd\end{array}$$

(23)

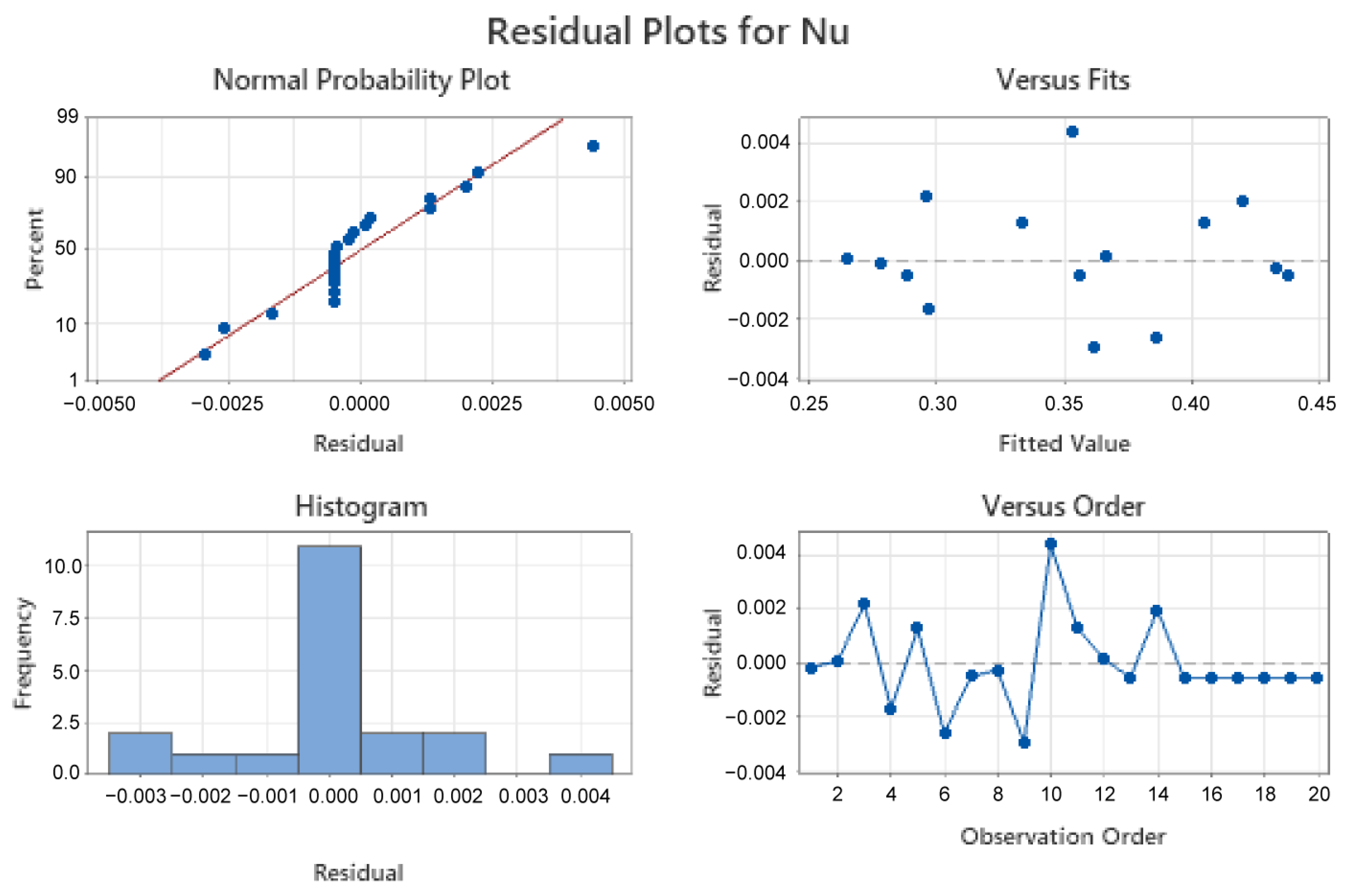
The residual versus fitted plot shown in Figure 6 is used to evaluate the estimated model’s dependability. The model’s accuracy is further increased by the fitted versus residual plot, which displays a maximum error of 0.010. By putting the third variable at the midpoint, Figure 7 (contour plots) and Figure 8 (surface plots) demonstrate that two independent factors can have an impact on the dependent variable simultaneously and make it clear that higher values of Rd and $D_p$ and a lower M, result in greater heat transfer.

Table 7. ANOVA table.

Source	Deg.	Adj. Sum	Adj. Mean	F-Value	p-Value
	of Freedom	of Squares	Squares
Model	9	0.046608	0.005179	986.76	0.000
Linear	3	0.046196	0.015399	2934.12	0.000
M	1	0.000205	0.000205	39.08	0.000
$D_p$	1	0.002663	0.002663	507.50	0.000
Rd	1	0.043327	0.043327	8255.78	0.000
Square	3	0.000194	0.000065	12.33	0.001
$M\ast M$	1	0.000008	0.000008	1.44	0.258
$D_p\ast D_p$	1	0.000099	0.000099	18.81	0.001
$Rd\ast Rd$	1	0.000008	0.000008	1.59	0.236
2-Way Interaction	3	0.000217	0.000072	13.81	0.001
$M\ast D_p$	1	0.000092	0.000092	17.58	0.002
$M\ast Rd$	1	0.000016	0.000016	3.00	0.114
$D_p\ast Rd$	1	0.000109	0.000109	20.86	0.001
Error	10	0.000052	0.000005
Lack-of-Fit	5	0.000052	0.000010	*	*
Pure Error	5	0.000000	0.000000
Total	19	0.046660

* p-value is less than 0.05 and F-value is larger than 1.

Figure 6. Residuals Plots for $N{u}_x{\left(R{e}_x\right)}^{-1/2}$.

Figure 7. Contour plots for $N{u}_x{\left(R{e}_x\right)}^{-1/2}$.

Figure 8. Surface plots for $N{u}_x{\left(R{e}_x\right)}^{-1/2}$.

7. Conclusions

For tangent-hyperbolic, water-based $Cu$ nanofluid flows, the significance of the $Cu$ nanoparticle radius and the effects of various parameters on the temperature distribution, skin friction, velocity profile, microrotation, and Nusselt number—along with micropolar effects, the convective boundary condition, nonlinear thermal radiation, and an exponential heat source—are currently being studied. Using the BVP5C approach, the effects of MHD on the flow over a stretching sheet are determined. Additionally, the graphical depictions illustrate the variations in temperature, velocity, and microrotation caused by various interacting parameters. The influences of inclined MHD, nanoparticle radius, and thermal radiation on the rate of heat transfer are statistically analyzed using RSM. The complex interaction among the variables governed by these parameters leads to the following noteworthy findings from this study:

(1)

The ANOVA table and the residual vs. fitted plot are used to evaluate the efficacy and reliability of the estimated model, respectively, based on the radius and velocity of motion of the nanoparticles.

(2)

Increasing the nanoparticle radius leads to a decrease in microrotational velocity, whereas increasing the $\gamma$ and K parameters enhances the relative fluid layers.

(3)

Temperature increases with augmentations in exponential heat sources, nonlinear radiation, and the Biot number, but decreases with increasing nanoparticle radius.

(4)

The skin-friction coefficient decreases as the slip parameter, Weissenberg number, magnetic field (M), and nanoparticle radius. Despite this, the Nusselt number exhibits the reverse pattern with respect to the nanoparticle radius.

(5)

The concentration of the nanofluid is enhanced by activation energy.

(6)

The thickness of the hydrodynamic boundary layer strengthens with the radius of the nanoparticle and the inclined MHD ($\gamma$). It reduces as the second slip parameters increase, but it responds in a different way when the thermal field is included.

(7)

The fitted quadratic regression model is perfect for the given range of involved parameters. $$\begin{gathered} N{u}_x/\sqrt{R{e}_x}=0.21763-0.0755M+0.01841D_p+0.3538Rd+0.0414M*M- \\ 0.00599D_p\ast D_p-0.0436Rd\ast Rd+0.01698M\ast D_p-0.0351M\ast Rd+0.01850D_p\ast Rd \end{gathered}$$.