Symmetry, Conservation Law, Uniqueness and Stability of Optimal Control and Inverse Problems for Burgers’ Equation
Abstract
1. Introduction
- Theoretical framework. We prove the existence of a minimizer using the direct method in calculating variations and establish necessary first-order optimality conditions via an adjoint equation. Under strict convexity of the regularized cost function, we further show the uniqueness of the control pair and continuous dependence on perturbations in the data and source term.
- Energy-consistent discretization. Motivated by the physical energy conservation law [25] of Burgers’ equation, we derive a discrete energy balance that equates the spatial change im the time-integrated squared state to the combined contributions of the source forcing and diffusion dissipation. Our detailed error analysis decomposes the conservation law error into two distinct sources: state variable error propagation () and energy discretization truncation error, yielding a total bound of . This explains why observation noise limits conservation accuracy even with extreme grid refinement. Among them, represents all the errors generated during the discretization process, and represents the errors generated during the iterative process. These two types of errors can be studied separately. This makes the sources of errors in our numerical experiments clearer.
- Efficient two-stage optimization with physical guidance. To accelerate convergence and improve robustness against noise, we introduce a two-stage procedure: an initial coarse grid search guided by physical priors, followed by a nested, gradient-based optimization (interior-point then SQP) that refines boundary shape and diffusion coefficient. Our error analysis demonstrates that this approach effectively minimizes both error components. Numerical experiments on synthetic noisy data demonstrate that the method recovers g, u, the full state , and the effective source term with relative errors below 1–2%, even under moderate observation noise, validating our theoretical error bounds.
2. Optimal Control Theory
2.1. Lie Group Symmetries of Burgers’ Equation
- 1.
- Time translation:
- 2.
- Scaling symmetry:
- 3.
- Galilean transformation:
2.2. Optimal Control
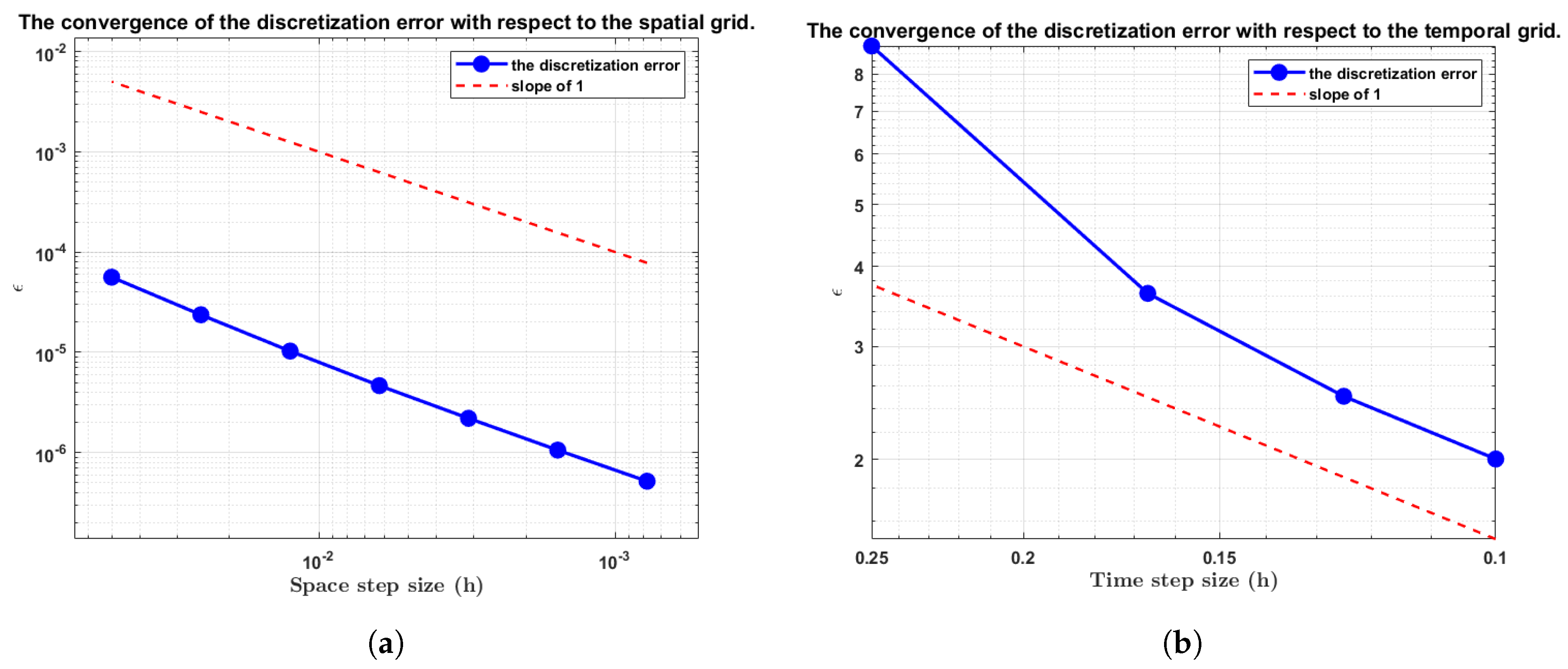
- (Discretization Error): Errors arising from spatial-temporal grid discretization, bounded by .
- (Iterative Error): Errors from algorithmic convergence and data perturbations, bounded by where is the perturbation level.
3. Energy Conservation Law
4. Numerical Experiments
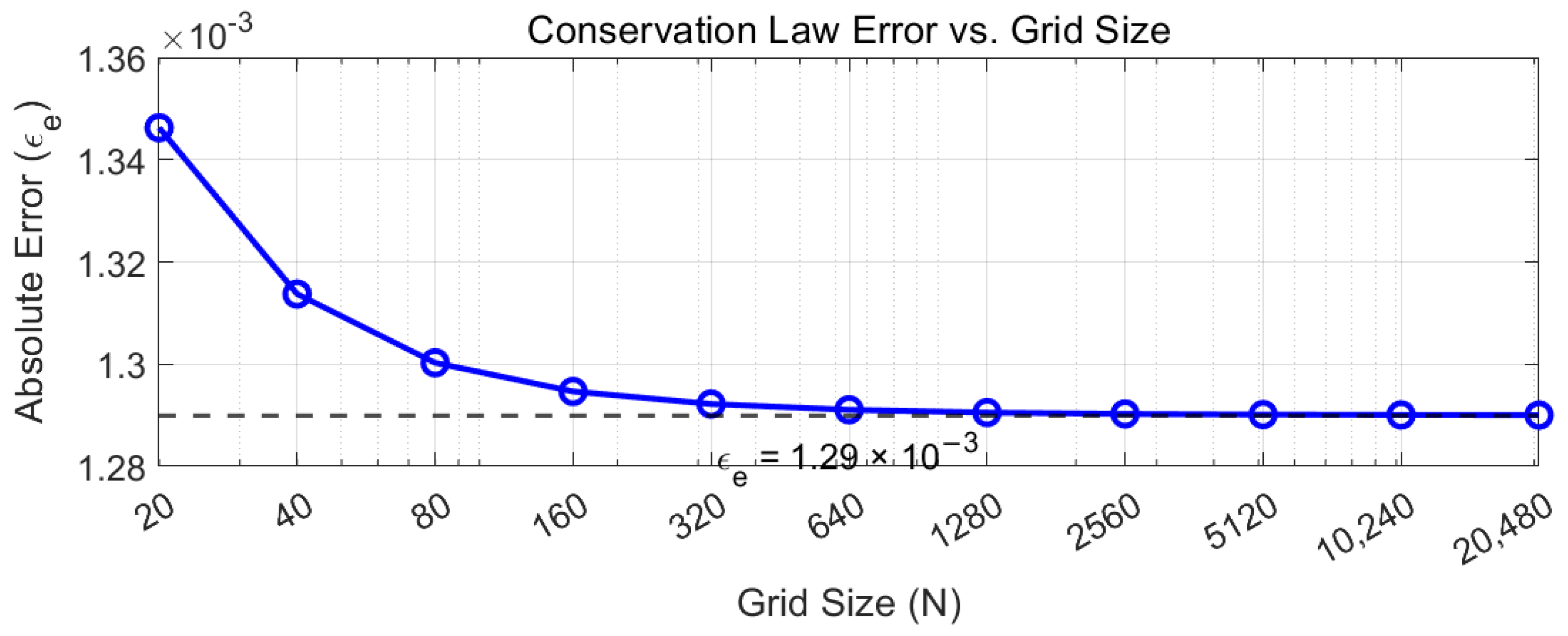
4.1. Verification of the Conservation Law
4.1.1. Iterative Error Analysis
4.1.2. Discretization Error Analysis
4.1.3. Error Plateau Sensitivity Analysis
- Initial conditions (9 variants, ±200% variation): Plateau range .
- Time steps (): Plateau variation ±2.3%.
- Boundary types (Dirichlet/Neumann/Robin): 10–29% difference.
- Monte Carlo (100 runs): 6.7% coefficient of variation.
4.2. Multi-Scale Adaptive Algorithm for Solving the Inverse Problem
| Algorithm 1 Dual-Functional Descent Method (DFDM) |
|
4.2.1. Algorithm Steps and Important Parameters
- Coarse-grid search guided by prior knowledge. Parameterize the boundary condition respecting the equation’s symmetry properties based on the Gaussian-modulated sine function, and use a three-dimensional grid search to determine the parameters preliminarily.
- Two-layer gradient optimization. First, optimize the boundary shape based on terminal fitting. Then, jointly optimize the boundary condition and the source term (Algorithm 1), ensuring that the optimization process preserves the fundamental symmetries of the problem, and use the interior-point method and the SQP (Sequential Quadratic Programming [30]) algorithm for iteration. The final optimization results are , , , , , .
- In the low-x region accuracy. We use a non-uniform grid for spatial discretization to improve the calculation accuracy in the low-x region,The minimum step size of the spatial grid information is 0.002162, and the maximum step size is 0.009618.
4.2.2. Error Analysis
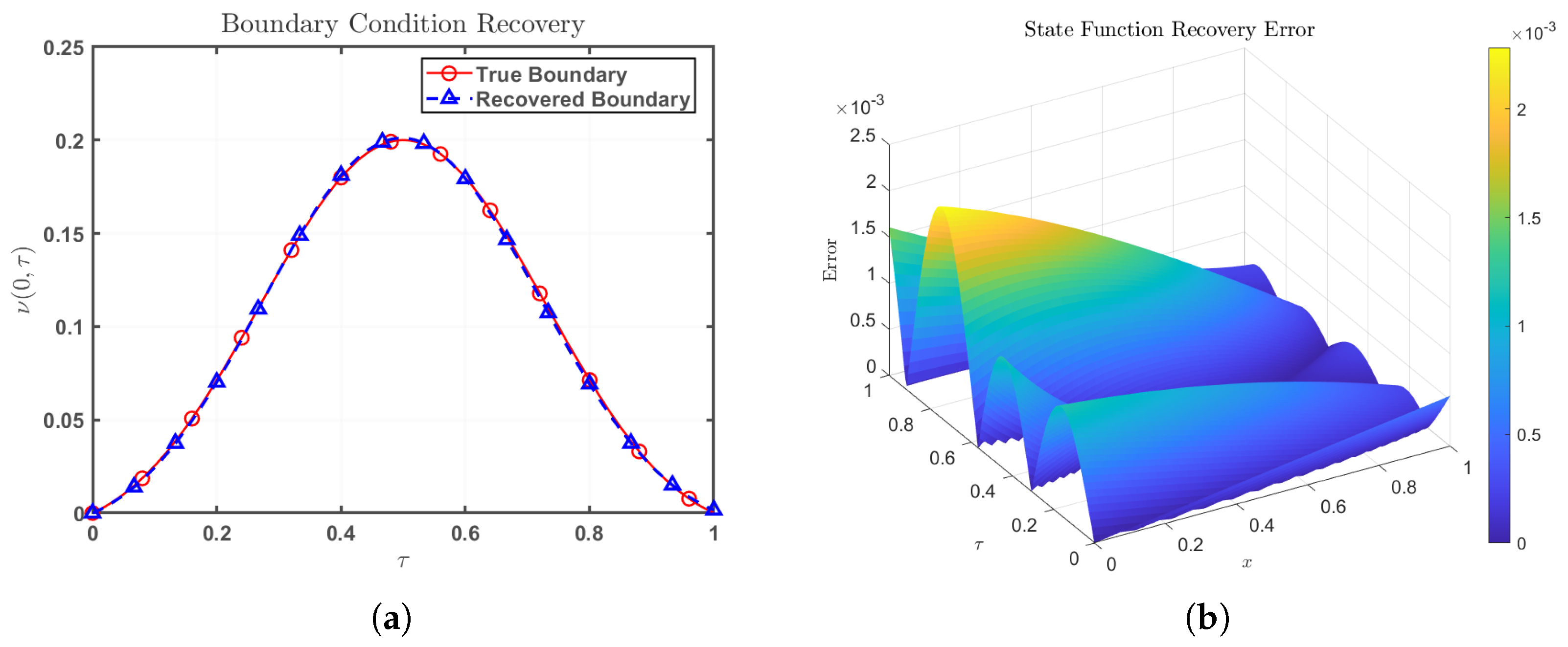
4.3. Perturbation Stability Analysis
- Linear error growth with confirms the theoretical bound .
- Constant extracted from slope analysis.
- Maximum perturbation yields errors , well within theoretical predictions.
| () | 0 | 0.5 | 1 | 1.5 | 2 |
|---|---|---|---|---|---|
| Boundary | 0.0117932 | 0.0104257 | 0.00992636 | 0.0095675 | 0.00919247 |
| State Function | 0.0111091 | 0.009895 | 0.0093705 | 0.009 | 0.0086289 |
5. Conclusions
- Theoretical framework and methodological synergy: Proved the existence, uniqueness, and stability of solutions against data perturbations using optimal control theory. Integrated regularization and conservation laws to provide a theoretically rigorous and practically viable solution for inverse problems in Burgers’ equation.
- Error analysis: Revealed the internal correlation of dual error sources in inverse problems—iterative error (dominated by observation noise) and discretization error (governed by grid accuracy).
- Iterative error (): Originated from observation data perturbation (), with a theoretical bound of , setting a lower limit for solution accuracy.
- Discretization error (): Stemmed from grid discretization (), bounded by , determining noise-free convergence rate.
Total error bound: , linking accuracy to both noise and grid precision. - Algorithm design: Developed an energy-consistent discrete scheme that respected the equation’s symmetry properties and a two-stage adaptive strategy to balance computational efficiency and accuracy. Theoretically, could converge to first-order (), though current equipment limits large-scale grid iterations. The preservation of symmetry properties enhanced the physical consistency of the recovered solutions.
- Numerical validation: Achieved boundary error < 1% and energy conservation error 0.13% under moderate noise, with linear robustness to noise perturbations, aligning with theoretical predictions.
5.1. Future Research Directions
- Extension to Higher-Dimensional Cases: Adapting the symmetry-aware framework to 2D/3D Burgers’ equations with complex boundary geometries.
- Nonlinear Regularization: Incorporating total variation regularization while preserving symmetry properties.
- Adaptive Mesh Refinement: Developing symmetry-guided adaptive mesh strategies for complex flow scenarios.
- Machine Learning Integration: Combining physics-informed neural networks with our theoretical framework.
5.2. Comparison with Related Studies
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liao, W.; Dehghan, M.; Mohebbi, A. Direct numerical method for an inverse problem of a parabolic partial differential equation. J. Comput. Appl. Math. 2009, 232, 351–360. [Google Scholar] [CrossRef]
- Thomas, B.; Pascal, F.; Mohamed, I.; Olivier, B.; Abdel-Malek, Z.; Christophe, D. Identification of partial differential equations in structural mechanics theory through k-space analysis and design. Compos. Struct. 2023, 304, 116297. [Google Scholar]
- Meysam, J.; Hassan, S.; Hossein, N.P. Satellite attitude PDE-based controller design considering fluid fuel sloshing in planar maneuver. Aerosp. Sci. Technol. 2022, 122, 107366. [Google Scholar] [CrossRef]
- Omar, S.; Mirjam, F. On the use of Fourier Features-Physics Informed Neural Networks (FF-PINN) for forward and inverse fluid mechanics problems. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2023, 237, 846–866. [Google Scholar]
- Ashurov, R.R.; Saparbayev, R.A. Forward and Inverse Problems for Fractional Telegraph Equation. Lobachevskii J. Math. 2024, 45, 4459–4478. [Google Scholar] [CrossRef]
- Karnakov, P.; Litvinov, S.; Koumoutsakos, P. Solving inverse problems in physics by optimizing a discrete loss: Fast and accurate learning without neural networks. Proc. Natl. Acad. Sci. USA Nexus 2024, 3, pgae005. [Google Scholar] [CrossRef] [PubMed]
- Keller, J.B. Inverse Problems. Am. Math. Mon. 1976, 83, 107–118. [Google Scholar] [CrossRef]
- Hadamard, J. Lectures on Cauchy’s Problem in Partial Differential Equations; Courier Corporation: North Chelmsford, MA, USA, 1923. [Google Scholar]
- Burgers, J. A Mathematical Model Illustrating the Theory of Turbulence. Adv. Appl. Mech. 1948, 1, 171–199. [Google Scholar]
- Li, Y.; Zong, X.; Zhang, J.; Li, X. High-order schemes with mass and energy conservation for solving the one-dimensional Zakharov system. J. Phys. Conf. Ser. 2025, 2964, 012089. [Google Scholar] [CrossRef]
- Bai, G.; Hu, J.; Li, B. High-Order Mass- and Energy-Conserving Methods for the Nonlinear Schrödinger Equation. SIAM J. Sci. Comput. 2024, 46, A1026–A1046. [Google Scholar] [CrossRef]
- Yang, S.; Xiong, X. A Fractional Tikhonov Regularisation Method for Finding Source Terms in a Time-Fractional Radial Heat Equation. East Asian J. Appl. Math. 2019, 9, 386–408. [Google Scholar] [CrossRef]
- Saouli, N.; Zouyed, F. A modified Tikhonov regularization method for a class of inverse parabolic problems. Analele Univ. Ovidius Constanta-Ser. Mat. 2020, 28, 181–204. [Google Scholar] [CrossRef]
- Denisov, A.M. Integral equations related to the study of an inverse coefficient problem for a system of partial differential equations. Differ. Equ. 2016, 52, 1142–1149. [Google Scholar] [CrossRef]
- Huntul, M.J.; Abbas, M. An inverse problem of fourth-order partial differential equation with nonlocal integral condition. Adv. Contin. Discret. Model. 2022, 2022, 55. [Google Scholar] [CrossRef]
- Zhang, Z.; Jin, Q. Heuristic rule for non-stationary iterated Tikhonov regularization in Banach spaces. Inverse Probl. 2018, 34, 115002. [Google Scholar] [CrossRef]
- Andrey, B. On the uniqueness of solutions in inverse problems for Burgers’ equation under a transverse diffusion. J. Inverse Ill-Posed Probl. 2023, 31, 595–609. [Google Scholar]
- Zhang, Y.X.; Jia, J.; Yan, L. Bayesian approach to a nonlinear inverse problem for a time-space fractional diffusion equation. Inverse Probl. 2018, 34, 125002. [Google Scholar] [CrossRef]
- Yi, S.; Sun, H. A Hybrided Trapezoidal-Difference Scheme for Nonlinear Time-Fractional Fourth-Order Advection-Dispersion Equation Based on Chebyshev Spectral Collocation Method. Adv. Appl. Math. Mech. 2019, 11, 595–609. [Google Scholar] [CrossRef]
- Wang, Y.; Yi, S. A Compact Difference-Galerkin Spectral Method of the Fourth-Order Equation with a Time-Fractional Derivative. Fractal Fract. 2025, 9, 155. [Google Scholar] [CrossRef]
- Yi, S.; Yao, L. A steady barycentric Lagrange interpolation method for the 2D higher-order time-fractional telegraph equation with nonlocal boundary condition with error analysis. Numer. Methods Partial. Differ. Equ. 2019, 35, 595–609. [Google Scholar] [CrossRef]
- Molina, E.; Rapaport, A. Optimal synthesis for a class of L∞ optimal control problems in the plane with L1 constraint on the input. Optimization 2025, 74, 1197–1216. [Google Scholar] [CrossRef]
- Pinho, M.; Ferreira, M.; Smirnov, G. Optimal control problem with nonregular mixed constraints via penalty functions. Syst. Control Lett. 2025, 196, 106010. [Google Scholar] [CrossRef]
- Yi, X.; Gong, Z.; Liu, C.; Cheong, H.T.; Teo, K.L.; Wang, S. A control parameterization method for solving combined fractional optimal parameter selection and optimal control problems. Commun. Nonlinear Sci. Numer. Simul. 2025, 141, 108462. [Google Scholar] [CrossRef]
- Li, S.; Wang, H. Non-self-similar solutions containing delta shock waves for nonhomogeneous zero-pressure gas dynamics with energy conservation law by the viscosity method. Math. Methods Appl. Sci. 2024, 48, 5278–5299. [Google Scholar] [CrossRef]
- Giv, H.H. Proving the Banach-Alaoglu Theorem via the Existence of the Stone-Čech Compactification. Am. Math. Mon. 2014, 121, 167–169. [Google Scholar]
- Kolagar, S.M.; Afrouzi, G.A.; Graef, J.R. Variational analysis for Dirichlet impulsive fractional differential inclusions involving the p-Laplacian. Appl. Anal. Discret. Math. 2019, 13, 111–130. [Google Scholar] [CrossRef]
- Xue, W.; Sci, W.L. A Multidimensional Filter SQP Algorithm for Nonlinear Programming. J. Comput. Math. 2020, 38, 661–682. [Google Scholar] [CrossRef]
- Lashkarian, E.; Hejazi, S.R.; Habibi, N.; Motamednezhad, A. Symmetry properties, conservation laws, reduction and numerical approximations of time-fractional cylindrical-Burgers equation. Commun. Nonlinear Sci. Numer. Simul. 2019, 67, 176–191. [Google Scholar] [CrossRef]
- Zhu, X.; Yu, C.; Teo, K.L. Sequential adaptive switching time optimization technique for optimal control problems. Automatica 2022, 146, 110565. [Google Scholar] [CrossRef]
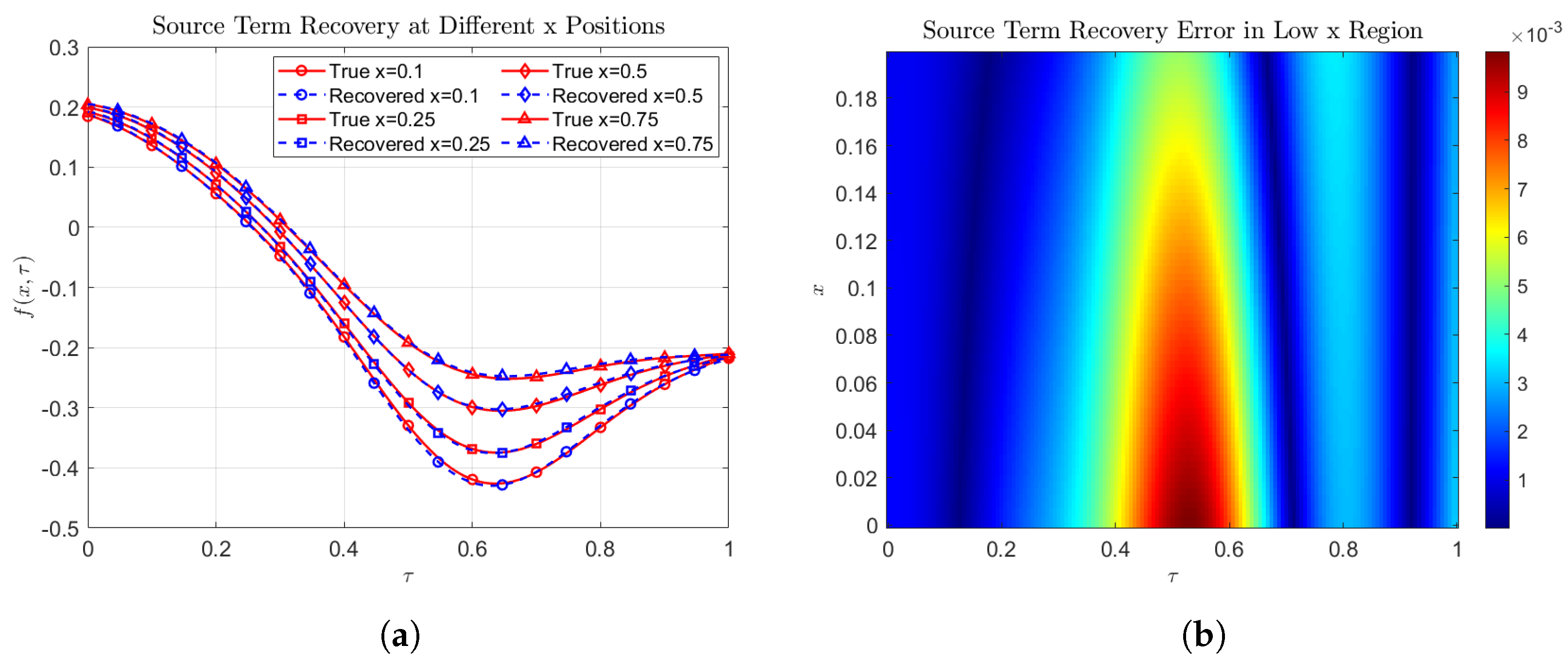
| Interval | |||||
|---|---|---|---|---|---|
| Error |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Y.; Qin, J.; Yi, S. Symmetry, Conservation Law, Uniqueness and Stability of Optimal Control and Inverse Problems for Burgers’ Equation. Symmetry 2025, 17, 1927. https://doi.org/10.3390/sym17111927
Qin Y, Qin J, Yi S. Symmetry, Conservation Law, Uniqueness and Stability of Optimal Control and Inverse Problems for Burgers’ Equation. Symmetry. 2025; 17(11):1927. https://doi.org/10.3390/sym17111927
Chicago/Turabian StyleQin, Yifan, Jiale Qin, and Shichao Yi. 2025. "Symmetry, Conservation Law, Uniqueness and Stability of Optimal Control and Inverse Problems for Burgers’ Equation" Symmetry 17, no. 11: 1927. https://doi.org/10.3390/sym17111927
APA StyleQin, Y., Qin, J., & Yi, S. (2025). Symmetry, Conservation Law, Uniqueness and Stability of Optimal Control and Inverse Problems for Burgers’ Equation. Symmetry, 17(11), 1927. https://doi.org/10.3390/sym17111927







