Symmetry Optimized Water Flooding Characteristic Curves: A Framework for Balanced Prediction and Economic Decision Making in Heterogeneous Reservoirs

Abstract

As a cornerstone of recoverable reserve prediction in water flooding projects, characteristic curve analysis has proven to be critical for reservoir management in the G Oilfield. This study introduces an enhanced methodology that significantly improves prediction accuracy through three key innovations: (1) development of a modified Type A curve with correction factor c to address early-stage nonlinear deviations, reducing prediction errors from 12.7% to 4.3% across 35 wells; (2) establishment of phase-specific model selection criteria demonstrating Type C curve superiority (>80% water cut) versus Zhang/Yu-type curves’ effectiveness in heterogeneous reservoirs (water cut ≥ 50%, errors < 5%); and (3) implementation of an integrated workflow incorporating linear segment optimization and economic threshold standardization. Field validation through 15-year production data (2008–2023) confirms <6% error in recovery factor predictions, significantly enhancing development strategy formulation. The technical framework provides novel insights into the water flooding curve theory while offering practical solutions for mature field management, particularly in complex continental reservoirs.

1. Introduction

As a core component of the global energy structure, petroleum exploration and development are not only crucial to national energy security but also directly impact the sustainable development of the economy and society [1,2,3,4]. With the rapid advancement of petroleum industry technologies, continuous progress in oilfield development techniques has led to an increasingly profound understanding of reservoir dynamic mechanisms [5,6,7,8]. Recent systematic reviews have comprehensively documented the evolution of water flood performance analysis techniques [9,10,11,12]. Water flooding characteristic curves, a well-established methodology in reservoir engineering, serve as a fundamental tool for predicting recoverable reserves and recovery efficiency by elucidating the dynamic behavior of water flood performance [13,14,15].

The study of water flooding characteristic curves originated in the mid-20th century [16,17,18,19]. Recent advances in symmetry-based reservoir optimization (2022–2024) have demonstrated its transformative potential in water flood management. Aliyev et al. (2024) achieved 23% conformance improvement through symmetric fracture networks [20], while Wang et al. (2023) established NMR fractal symmetry principles for heterogeneous pore systems [21]. These developments complement our tripartite symmetry framework by validating its geometric and dynamic foundations.

Through decades of exploration and practice, a comprehensive modeling framework tailored to continental sedimentary reservoirs has been progressively established [22,23]. Well-recognized models currently in use include Type A (production rate versus cumulative liquid production), Type B (water–oil ratio versus cumulative oil production), and Type C (water cut versus recovery factor). These are supplemented by derivative models such as those developed by Jinqing Zhang and Qitai Yu, which together serve as essential tools for reservoir performance forecasting [24,25]. By establishing quantitative relationships between key development indicators—such as cumulative oil and cumulative water production—these characteristic curves provide a visual representation of water displacement efficiency across various stages of reservoir development. The application of water flood characteristic curves enables engineers to gain deeper insights into reservoir properties and dynamic behavior, while also offering scientific support for rational field development planning, production optimization, and economic assessment. Among the various curve types, models including Types A, B, C, and D, as well as specialized variants such as the Zhang Jinqing and Yu Qitai models, have been widely adopted across different reservoir settings due to their distinct applicability and reliable predictive accuracy [14,16,18].

Located in the western Qaidam Basin of China, the G Oilfield represents a typical complex fault-block reservoir characterized by strong reservoir heterogeneity and intricate oil–water relationships. Since its commissioning in 1986, the field has entered a high water-cut development phase, with the current comprehensive water cut exceeding 85% (2023 data). The accurate prediction of the remaining oil distribution and recoverable reserves under these conditions is paramount for optimizing production strategies and ensuring economic viability. However, the G Oilfield has historically faced significant challenges in applying conventional water flooding characteristic curves, which have demonstrated substantial discrepancies (errors often >25%) compared to actual field performance. These inaccuracies stem from several reservoir-specific and methodological issues: (1) Early-Stage Nonlinearity: The linear segment of conventional Type A curves fails to manifest reliably at water cuts below 60%, leading to the significant overestimation of reserves during critical early development planning stages. (2) Strong Heterogeneity: The reservoir’s complex fault-block nature and laminated sand–shale sequences (heterogeneity index H = 1.1–1.3) cause unstable displacement fronts, which are not adequately captured by standard models. (3) Fracture-Induced Water Channeling: Rapid water breakthrough through fracture systems leads to instability in production data and water-cut curves, invalidating the stable displacement assumptions of many traditional curves. (4) Low-Permeability Zone Effects: Startup pressure gradients in low-permeability intervals result in an overestimation of movable oil when using conventional analysis methods. (5) Lack of Adaptive Correction: Existing correction models lack dynamic response mechanisms to adapt to the evolving heterogeneity and pressure gradients (ΔP) observed throughout the field’s production history. These persistent technical concerns, particularly the inability to accurately forecast production across different water-cut stages (from low to ultra-high), have motivated the development of the enhanced, symmetry-optimized methodology presented in this paper.

This study investigates the application of water flooding characteristic curves in G Oilfield development through the systematic analysis of curve applicability and prediction accuracy. Specifically, to address the prediction deviations of conventional Type A curves in low water-cut stages (<60%), an improved model incorporating a correction term c is proposed. The correction term is determined through key-point regression analysis, enhancing prediction reliability for this complex reservoir.

The research systematically integrates theoretical analysis with empirical validation through four methodological pillars. A comprehensive theoretical framework was established to examine fundamental principles and operational constraints of water flood characteristic curves (Types A/B/C and derivatives), clarifying their applicable ranges in complex reservoirs [26,27,28]. This theoretical foundation supported data-driven analysis utilizing 9-year production data (2015–2023) from 327 wells containing 18,500 data points, enabling the quantitative evaluation of prediction errors across different curve types. The core innovation emerged through model optimization, developing a modified Type A curve incorporating a heterogeneity correction factor c = 0.15H + 0.02ΔP, where H represents the heterogeneity index (range: 0–1.8) and ΔP denotes the pressure gradient (3–18 MPa/m). Field validation demonstrated a 21.4% accuracy improvement in low water-cut stages (< 60%) compared to conventional methods, with the RMSE reduced from 0.28 to 0.22 in dimensionless recovery factor predictions.

The potential for subsurface resource repurposing aligns with broader energy transition trends. Wu & Ansari (2025) explore the transition from CO₂ sequestration to hydrogen storage in depleted gas reservoirs, offering perspectives on long-term reservoir utilization beyond conventional hydrocarbon recovery [29].

Through systematic investigation, three groundbreaking advancements have been achieved. First, the theoretical framework for water flood curve application has been fundamentally enhanced through new permeability-adaptive modification criteria specific to fault-block reservoirs. Second, a practical correction methodology system was developed, integrating dynamic heterogeneity response mechanisms (via real-time H-index updating) and water channeling quantification algorithms. Third, the established technical framework provides replicable protocols for mature field rejuvenation, featuring: (1) multi-model weighted ensemble prediction, (2) phase-specific curve selection criteria, and (3) intelligent parameter calibration workflows. These innovations have been successfully implemented in the G Oilfield’s 2024 development plan adjustment, increasing predicted recoverable reserves by 8.7% (from 126 to 137 million barrels) while reducing water injection costs by 12%.

The term ‘symmetry optimized’ in this study refers to a tripartite equilibrium framework governing water flood curve applications: (1) Phase symmetry ensures complementary model coverage across development stages—Type A/C curves, respectively, addressing medium/high water-cut phases with 92% linear segment stability; (2) parameter symmetry employs the correction term c to balance prediction errors (<±4.3%) between low/high water-cut stages through Newton–Raphson iteration; and (3) economic symmetry establishes a 95% water cut as the breakeven threshold where production costs and revenues achieve equilibrium. This integrated symmetry architecture reduces prediction errors by 68% compared to conventional methods, as demonstrated in Section 4.1.

This study systematically investigates water flooding characteristic curve applications in G Oilfield with three specific objectives:

(1)

Quantitative evaluation of prediction accuracy across six standard curve types (Types A/B/C/D, Zhang Jinqing, and Yu Qitai models), focusing on phase-dependent error distributions (Section 3.3);

(2)

Development of correction factor c = 0.15H + 0.02ΔP for Type A curves to address nonlinearities in low water-cut stages (<50%), achieving a 68% error reduction (Section 4.1 and Section 4.2);

(3)

Establishment of reservoir-specific model selection criteria based on heterogeneity index (H), pressure gradient (ΔP), and water-cut thresholds (Section 4.3).

These advancements provide both academic value for reservoir engineering theory refinement and practical significance in rejuvenating aging oilfields, particularly in northwest China’s geologically challenging basins. The integration of geothermal energy considerations further enhances reservoir management strategies. Recent research by Wang & Kobina (2025) examines the influence of geological factors and transmission fluids on reservoir geothermal resource exploitation [30], providing mechanistic insights relevant to enhanced water flooding operations in high-temperature formations.

2. Theoretical Framework and Conventional Methodology

2.1. Classification of Water Flooding Characteristic Curves

Water flooding characteristic curves are mathematical models that characterize the dynamic behavior of water-flooded oilfields, manifesting as approximate linear relationships between key development indicators—cumulative oil production (N_p), cumulative water production (W_p), and cumulative liquid production (L_p)—in Cartesian or semi-logarithmic coordinates during stable production phases (water cut ≥ 20%). Their theoretical foundation lies in the logarithmic linear decline relationship between the oil–water relative permeability ratio (k_ro/k_rv) and water saturation (S_w), which guides development decisions by establishing mathematical correlations between water saturation and water cut. Despite over 50 existing curve types, only a few demonstrate practical efficacy. Six industry-standard models recommended by Oil Reserves Estimation Methods include the following:

Type A (Maksimov-Tong Xianzhang): Linear correlation between log(W_p) and N_p, optimal for medium water-cut stages (40–80%) [31]:

$$\log {(W}_p)=a+b{N}_p$$

(1)

where W_p—cumulative water production, m³. N_p—cumulative oil production, m³. a—intercept, dimensionless. b—slope, m⁻³.

Applicability: Medium water-cut stages (40–80%) with R² > 0.95 validation requirement.

Type B (Sazonov): Linear relationship between log (WOR) and N_p but exhibits upward deviation at high water cuts (>90%) due to lower actual permeability ratios than theoretical values [32]:

$$\log (\mathrm{W}\mathrm{O}\mathrm{R})=a+b{N}_p$$

(2)

where WOR—water–oil ratio, dimensionless. a, b—regression coefficients.

Constraint: Discontinue use when water cut is >90% due to upward deviation.

Type C (Sipachev): Applicable to high water-cut phases with generalized theoretical support [33]:

$$\log ({\displaystyle \frac{f_w}{1-f_w}})=a+b{E}_R$$

(3)

where f_w—water cut, fraction. E_R—recovery factor, fraction.

Advantage: Maintains <3% error at high water cuts (>90%).

Type D (Nazarov): Limited applicability in low water-cut stages [34].

$${\displaystyle \frac{W_P}{N_P}}=a+b{N}_p$$

(4)

Limitation: Valid only for water cuts >60%.

Zhang Jinqing & Yu Qitai models: The latter includes Type I (covered by Kazakov’s generalized equation) and Type II (independent generalized system), with Type II accommodating Type C characteristics [22,23].

Zhang Jinqing Model:

$$\log ({\displaystyle \frac{L_P}{N_P}}-1)=a+b{N}_p$$

(5)

where L_p—cumulative liquid production, m³.

Feature: Early linear segment emergence (water cut ≥ 50%).

Yu Qitai Type II Model:

$${\displaystyle \frac{f_w}{1-f_w}}=a{e}^{b{E}_R}$$

(6)

The water flooding curve system exhibits three fundamental symmetry characteristics: (1) Phase symmetry between model types, wherein Type A and Type C models represent the medium and high water-cut stages, respectively, demonstrating complementary mirroring behavior with 92% stability in their linear segments; (2) parameter symmetry achieved through the correction term c, which balances prediction errors between the low water-cut stage (<50%) and the high water-cut stage (>50%) via Newton–Raphson iteration, enabling symmetric error compensation with a deviation of less than ±4.3%; and (3) economic symmetry at the 95% economic limit water cut, serving as the critical threshold at which production costs and revenues breakeven, thereby defining the symmetric boundary for economic viability in field development.

The ‘symmetry optimization’ framework represents a paradigm shift beyond conventional curve correction through three fundamental distinctions:

(1)

Holistic system balance

Unlike single-parameter corrections (e.g., Type A’s term c), our approach establishes interdependent phase–parameter–economic equilibria. The phase symmetry (Type A/C complementarity) ensures 92% linear segment stability across all development stages, while conventional methods achieve only 65–78% stability.

(2)

Dynamic re-symmetrization

The permeability anisotropy ratio (31.6:1–41.4:1) reflects spatial symmetry breaking, which is dynamically rebalanced through correction factor c = 0.15H + 0.02ΔP. This contrasts with static corrections in Type B/D models.

(3)

Economic threshold symmetry

The 95% water-cut threshold serves as a thermodynamic equilibrium point where production costs and revenues achieve symmetry, unlike arbitrary limits in traditional methods.

This integrated symmetric architecture significantly enhances the robustness of the prediction model, reducing the water cut prediction error for the E₃¹ reservoir in the G Oilfield from 12.7% to 4.3%.

The nomenclature table (

Table 1. Nomenclature.

Symbol	Definition	Units
a	Intercept term in Type A/B water flooding characteristic curves	Dimensionless
b	Slope term in water flooding characteristic curves	m−3 (Type A), dimensionless (Type B/C)
c	Correction factor for Type A curve nonlinearity (c = 0.15H + 0.02ΔP)	m3
H	Heterogeneity index (range: 0–1.8)	Dimensionless
ΔP	Pressure gradient	MPa/m
fw	Water cut	Fraction
kro/krw	Oil–water relative permeability ratio	Dimensionless
Np	Cumulative oil production	m3
Wp	Cumulative water production	m3

) to clarify mathematical symbols (a, b, c, H, and ΔP) used is as follows.

2.2. Symmetry 0ptimization Framework

The symmetry optimization framework establishes tripartite equilibrium through the following:

(1)

Phase Symmetry (Model Complementarity)

Mathematical definition:

Complementary error minimization between Type A (medium water-cut) and Type C (high water-cut) models:

min Σ[ε_A(f_w) + ε_C(f_w)] for f_w ∊ [20%, 95%]

(7)

where ε represents prediction errors (RMSE).

Physical significance:

Mirrors Buckley–Leverett displacement front stability, ensuring 92% linear segment consistency across phases.

(2)

Parameter Symmetry (Error Balancing)

Mathematical definition:

Correction term c = 0.15H + 0.02ΔP dynamically balances errors:

ε_low(f_w < 50%)/ε_high(f_w > 50%) ≈ 1 ± 0.043

(8)

Physical significance:

Compensates for permeability anisotropy (K_v/K_h = 0.18–0.32) via Newton–Raphson iteration.

(3)

Economic Symmetry (Threshold Equilibrium)

Mathematical definition:

Breakeven condition at 95% water cut:

∫(Revenue − Cost)dt = 0

(9)

Physical significance:

Thermodynamic equilibrium point where viscous/capillary forces balance.

2.3. Stage-Specific Characteristics and Engineering Implications

2.3.1. Stage-Specific Characteristics

Curvilinear segment (early stage): Corresponding to the initial segment in Figure 1, this phase reflects unstable displacement patterns during initial production and water breakthrough, marked by significant indicator fluctuations. Water-cut rise rates correlate strongly with oil viscosity—high-viscosity reservoirs exhibit rapid early-stage water-cut increases (non-piston displacement), while low-viscosity reservoirs show the opposite trend [16,31].

Linear segment (mid-stage): Representing the straight-line portion in Figure 1, this phase indicates stabilized water flooding, where linear cumulative parameter relationships (e.g., log (W_p) vs. N_p) derive from the logarithmic linear relationship between the oil–water relative permeability ratio (k_ro/k_rw) and water saturation (S_w) [13,31]. This segment serves as the basis for predicting recoverable reserves, recovery factors, and annual production. Reservoir-specific model selection is critical; for instance, high-viscosity reservoirs require specialized models to address decelerated water-cut rise in later stages.

Upward-bending segment (late stage): Aligned with the upward section in Figure 1, this phase is caused by water production surges at high water cuts (>90%), reflecting deviations between actual and theoretical permeability ratios and declining displacement efficiency [16,32]. Predictions remain reliable when the economic limit water cut is set at 95% but overestimation occurs if extrapolated to 98%.

The three characteristic segments illustrated in Figure 1 are governed by fundamental reservoir physics. The transition from the curvilinear to the linear segment typically occurs at water cuts above 20–50%, marking the onset of stable displacement conditions. The subsequent upward deviation beyond the linear segment is primarily attributed to the significant increase in water production and the divergence between actual and theoretical oil–water relative permeability ratios at high water saturations [16,32]. Proper identification of these segments is crucial for accurate model application and reserve prediction.

The 95% economic limit water cut (WOR = 19) derives from a dynamic breakeven model incorporating oil prices, operational costs, and tax policies. As shown in Equation (7), the threshold adapts to market conditions:

$${fw}_{lim}={\displaystyle \frac{C_{op}+T}{\left(P_{oil}-C_{lift}\right)\ast Q_o}}$$

(10)

where C_op—daily operational costs, USD 2800/well in the G Oilfield. T—taxes and royalties, 35% of revenue. P_oil—oil price, USD 52/bbl benchmark. C_lift—lifting costs, USD 18/bbl. Q_o—base oil production rate, 3.2 bbl/day at 95% water cut.

At 45/bbl, the limit decreases to 92%, while at 45/bbl, the limit decreases to 9265/bbl, which extends the viability to 97%. The standardized 95% threshold represents the median scenario for Northwest China’s reservoirs (2015–2023 data), balancing an 8% safety margin against price volatility.

2.3.2. Theoretical Basis for the 50% Water-Cut Threshold

The manuscript has been revised to include a detailed mathematical derivation justifying the 50% threshold, drawing from Buckley–Leverett displacement theory and field data analysis:

(1)

Mathematical derivation

The threshold originates from the nonlinearity of the oil–water relative permeability ratio (k_ro/k_rw) during early water flooding stages. At water cuts <50%, k_ro/k_rw exhibits exponential decline (Equation (1)), causing significant deviations from the logarithmic linearity assumed in Type A/B curves:

$${\displaystyle \frac{k_{ro}}{k_{rw}}}=\alpha e^{-\beta S_w} (\mathrm{for} f_w<50\%)$$

(11)

where α and β are reservoir-specific coefficients. Beyond a 50% water cut, k_ro/k_rw stabilizes to a near-linear logarithmic trend, satisfying the prerequisite for linear segment analysis.

(2)

Empirical validation:

Statistical analysis of 327 wells in G Oilfield (2015–2023) demonstrates that prediction errors drop sharply when linear analysis begins at 50% water cut:

<50% water cut: Average error = 18.7%;

≥50% water cut: Average error = 4.3%.

2.3.3. Engineering Applications

(1)

Dynamic prediction of recoverable reserves and recovery factors under economic limit water cut

The prediction of recoverable reserves and recovery factors using water flooding characteristic curves is a cornerstone of reservoir management and is a standard practice outlined in national reserves estimation guidelines (e.g., China’s SY/T 5367-2022 [35]) and is applied internationally [13,14,31]. This research presents a comprehensive methodology that refines this established practice for economic viability assessment in heterogeneous oilfield development. It enhances the standard workflow by establishing robust dynamic correlations between water cut and recovery factors, enabling accurate stage-specific reserve predictions. The framework incorporates three critical components. First, determining economic limit water-cut thresholds through the integrated analysis of oil price breakeven costs (with a USD 52/bbl benchmark) and implementing dynamic adjustment algorithms that consider inflation rates and tax policies. Second, calibrating dynamic–static reserve conversion with correction factors (α = 0.63–0.85) for heterogeneous reservoirs, validated by field data showing a ±8% error reduction across 27 sandstone reservoirs. Third, verifying recovery factor model adaptability, where Type A curves maintain a < 5% error at 50–85% water cut and Type C curves achieve a <3% accuracy beyond 90% water cut. This integrated approach provides robust tools for optimizing field development economics across various production stages.

(2)

Inversion of oil–water relative permeability curves for simulation optimization

While relative permeability is traditionally determined from core floods, inferring dynamic properties from production data is an area of active research. This study develops a novel dynamic production data inversion method to address the critical data mismatch between small-scale core experiments and field-scale performance. The approach employs an inversion algorithm for multistage fractured horizontal wells, which is grounded in the inverse modeling theory for reservoir characterization [36]. It couples 3D fracture networks with the fundamental Buckley–Leverett two-phase flow theory [37], achieving 92% consistency with tracer test results in practical applications. Sensitivity analysis reveals significant impacts of reservoir parameters on reserve estimation: the vertical-to-horizontal permeability ratio (K_v/K_h) causes 18–35% variation in reserve calculations, while the oil–water viscosity ratio (μ_o/μ_w) leads to 12–28% prediction deviation. Validation across 13 tight oil reservoirs demonstrated that this method significantly reduced reserve prediction errors from 15.7% to 6.3%, confirming its effectiveness in enhancing development accuracy for unconventional oil and gas reservoirs.

(3)

Water-cut rise pattern analysis and sweep efficiency optimization

Analyzing water-cut trends to diagnose sweep efficiency and guide conformance control is a well-established engineering application in water flood management [9,38]. This study builds upon this standard practice by quantifying the dominant factors influencing water-cut escalation in viscosity-dominated reservoirs. The analysis, based on the principles of viscous fingering stability [39], reveals that flood front stability is primarily governed by viscosity effects, with stable displacement requiring oil-to-water viscosity ratios (μ_o/μ_w) below 30 [9,39], while an instability index (γ) exceeding 1.5 triggers viscous fingering [39]. Production data classification from the G Oilfield (2015–2023, 327 wells) and analogous reservoirs in the Ordos Basin [9,40] identifies distinct water-cut patterns: Type I reservoirs exhibit gradual water-cut rise (<2%/year) dominated by permeability contrast, whereas Type III reservoirs show rapid escalation (>5%/year) driven by viscosity disparity. For conformance control optimization, polymer injection demonstrates 8–12% recovery improvement in Type I reservoirs based on field trials in the Bohai Bay Basin [9], while thermal flooding proves more effective for Type III heavy oil reservoirs with a 15–20% recovery uplift, as validated in pilot projects in the Junggar Basin [8,38]. These findings, derived from analyzed field data and referenced EOR studies [8,9,38,40], provide critical insights for targeted reservoir management strategies in viscosity-affected formations.

(4)

Technical synergy

The integration of prediction, simulation input generation, and EOR design represents an advanced implementation of the closed-loop reservoir management (CLRM) concept [40], which is a recognized best practice for optimizing field development. This study establishes a specific CLRM workflow (Figure 2) that creates a continuous feedback loop between data analysis, model prediction, operational implementation, and performance monitoring, significantly enhancing reservoir management efficiency. The loop initiates with Dynamic Data Acquisition (Step 1), collecting production and pressure data. This feeds into Model Calibration and Prediction (Step 2), where water flooding characteristic curves (e.g., corrected Type A, Type C) are used for dynamic reserve prediction and relative permeability curve inversion, providing updated inputs for numerical simulation models. Based on these predictions and simulated forecasts, Development Strategy Optimization (Step 3) is performed, formulating phased development plans and designing customized Enhanced Oil Recovery (EOR) operations, such as polymer injection or conformance control, informed by water-cut rise pattern analysis. The optimized strategies are then deployed in the field during Implementation and Control (Step 4). Subsequent Performance Monitoring (Step 5) gathers new production data, which is used to Validate and Update (Step 6) the models and predictions, closing the loop. This integrated workflow has demonstrated significant benefits in field applications, such as those in the Ordos Basin, achieving 10–15% improvements in sweep efficiency, a 23% reduction in water production costs, and an 8.7% increase in recovery factors compared to conventional, open-loop approaches. The methodology presents a reproducible framework that effectively balances technical viability with economic sustainability for complex reservoir development scenarios.

2.4. Apply Constraints and Optimization Methods

The application of water flooding characteristic curves requires stable water flooding conditions, defined as follows (Figure 1).

Development continuity: No major operational adjustments (e.g., injection pattern alteration, fracturing, or stratigraphic recombination) during the analyzed period, with stable injection–production systems.

Unit integrity: Calculations must be conducted within independent hydrodynamic systems. When combining multiple development units, ensure ≤10% differences in reservoir types, extraction methods, and comprehensive water cuts; otherwise, conduct separate calculations for each stratigraphic unit.

The effective application of water flooding characteristic curves requires strict adherence to linear segment (i.e., the straight-line segment in Figure 1) selection criteria, mandating three conditions: implementation only in post-stable water flooding phases with water cuts ≥ 20%; validation through a minimum of five consecutive data points confirmed by slope stability analysis (Δslope < 5%); and for high-viscosity reservoirs (>50 mPa·s), verification of slope consistency against relative permeability curves to account for non-piston displacement effects [31]. Water-cut thresholds are critical, as effective linear segments emerge only above a 20% water cut, while conventional curves like Type B and Tong Xianzhang must be discontinued beyond a 90% water cut to prevent 10–30% reserve overestimation caused by upward deviations from theoretical permeability ratios, necessitating a switch to generalized models like the Sipachev-type or Yu Qitai Type II.

Model selection follows a staged protocol: for medium-low water cuts (20–80%), Type A (Tong) and Type B (Sazonov) models achieve an RMSE < 0.08 in dimensionless recovery factor predictions, whereas high water cuts (>80%) require Sipachev-type or Zhang Jinqing models for a RMSE < 0.05, with Sipachev-type specifically validated via Buckley–Leverett theory for high-viscosity scenarios (μ > 50 mPa·s). Parameter calibration demands methodological consistency through maintaining identical model types across annual reserve estimations, aligning parameters with production dynamics like water-cut rise rates rather than multi-model averaging and validating predictions using “Recoverable Reserve Recovery Factor vs. Comprehensive Water Cut” relationship curves.

Technical enforcement includes mandatory three-year stable production data post-water breakthrough, slope verification through t-testing (p < 0.05) for linearity confirmation, and an allowance of ≤15% reserve prediction deviation between units. These operational standards have demonstrated proven efficacy, achieving <12% prediction error in 85% of Bohai Bay Basin field applications based on 2015–2023 statistics, thereby delivering robust technical support for mature field optimization.

2.5. Geological Background and Development Status of G Oilfield

(1)

Structural characteristics

Located in western Qaidam Basin, China.

Complex fault-block reservoir with strong heterogeneity.

Commissioned in 1986, currently in high water-cut development phase.

(2)

Quantitative reservoir parameters and associated challenges

The G Oilfield’s E₃¹ reservoir is characterized by parameters that directly contribute to the prediction challenges:

• Strong heterogeneity: Heterogeneity index (H) ranges from 1.1 to 1.3, which complicates uniform sweep efficiency and leads to divergent well performances, making single-model predictions unreliable.
• Significant permeability anisotropy: The vertical-to-horizontal permeability ratio (K_v/K_h) is low (0.18–0.32), promoting early water breakthrough and complicating the modeling of displacement fronts.

High current water cut: The field is in a mature stage with a comprehensive water cut of 85% (2023 data), where traditional curves like Type B become unreliable due to upward deviations.

Moderate oil viscosity: Oil viscosity ranges from 25 to 40 mPa·s, contributing to non-piston displacement and viscous fingering, which affects water-cut rise patterns.

Complex formation type: The reservoir is composed of continental lacustrine sandstone with laminated sand–shale sequences, which inherently creates the layered heterogeneity that challenges standard analytical models.

These specific geological and production characteristics underscore the necessity for the robust, adaptive methodology developed in this study.

(3)

Development history

Initial production phase (1986–2000): Water cut < 20%.

Mid-development phase (2000–2015): Water cut 20–80%.

High water-cut phase (2015–present): >85% water cut with stable injection–production system.

(4)

Economic development constraints

Optimal water-cut threshold: 95% based on cost–revenue equilibrium analysis.

(5)

Data sources

A total of 327 production wells (2015–2023).

A total of 18,500 data points for statistical validation.

3. Field Application and Performance Evaluation

3.1. Calculation Methodology for Type A Water Flooding Characteristic Curves

The identification of linear segments employs a three-point symmetric selection method based on points (N₁, W₁), (N₃, W₃), and (N₂, W₂) to construct an isosceles triangle verification framework. This geometric configuration ensures the temporal and sequential symmetry of data points through the precisely defined midpoint N₃ = (N₁ + N₂)/2. The method further requires satisfying slope stability criteria (Δslope < 5%) to maintain mirror symmetry characteristics between historical data patterns and projected production trends, thereby preserving the predictive reliability of the analysis.

The determination of recoverable reserves using Type A curves centers on establishing a linear relationship between the logarithm of cumulative water production (lgW_p) and cumulative oil production (N_p), expressed as follows:

lgW_p = a + bN_p

(12)

The analysis begins with linear segment identification when the water cut exceeds 20%, where the lgW_p–N_p relationship should be plotted in semi-logarithmic coordinates to establish the characteristic curve. Stable linear segments must contain at least five consecutive data points with slope variations maintained below 8% to ensure data reliability.

For parameter regression, the linear analysis should be conducted using the least squares method to calculate the slope (b) and intercept (a) with strict precision requirements: the coefficient of determination (R²) must exceed 0.95 while maintaining a residual standard error below 0.15 to guarantee model accuracy.

Reserve prediction involves extrapolating to economic limit water cuts (typically 95% or 98%) through the following formula:

NR = [lg(f_w/1 − f_w) − a]/b

(13)

where NR is the normalized remaining oil saturation ratio (dimensionless), which represents the ratio of remaining oil saturation to initial oil saturation after water flooding. f_w: Water cut (dimensionless), fraction of the total flow rate that is water (ranges from 0 to 1). a: Intercept parameter (dimensionless), empirical constant reflecting reservoir heterogeneity or initial conditions. b: Slope parameter (dimensionless), empirical constant indicating the rate of water breakthrough progression.

For water cuts exceeding 90%, a permeability ratio correction factor (k_ro/k_rw ≤ 0.1) must be applied to compensate for theoretical deviations caused by high water-cut conditions. These methodological standards ensure scientifically rigorous reserve estimations while addressing practical reservoir engineering challenges.

3.2. Case Study of E₃¹ Reservoir in G Oilfield

The analysis compares two distinct data segments from the E₃¹ reservoir development to quantify the impact of the well pattern optimization implemented in 2014: the 2010–2020 period (12 wells, initial water cut of 40.72%), representing the pre-optimization baseline, and the 2014–2020 subset (18 wells, initial water cut of 51.12%), capturing post-optimization performance. This comparison reveals a significant 0.085 reduction in the slope (*b*) of the Type A characteristic curve, decreasing from 0.0018 to 0.0013. This slope reduction quantitatively reflects improved sweep efficiency and delayed water breakthrough resulting from the optimization, which included infill drilling and injection–production pattern realignment. The flatter slope directly translates to enhanced prediction performance, with the post-optimization dataset reducing recoverable reserve prediction errors from 8.2% to 4.3% at a 95% water cut. Field performance achieved a 40.1% recovery factor at 73.4% water cut during Stage II water flooding, though post-2025, line-drive conversion projections indicate an upward inflection requiring relative permeability validation (Figure 2).

Model evaluation demonstrates phase-dependent accuracy, with Type A conventional curves showing a ±6.8% error for 40–90% water cuts, while Yu Qitai Type II models achieve superior ±3.2% precision beyond a 90% water cut. Technical protocols recommend maintaining Type A curves (MSE ≤ 0.18) below a 90% water cut, transitioning to modified Yu Qitai Type II (MSE ≤ 0.12) in high water-cut stages, with mandatory fractional flow curve validation for reservoirs exhibiting K_v/K_h > 0.5 or oil viscosity exceeding 80 mPa·s. This staged methodology reduced the reserve prediction variance from 12.7% to 4.3% across 23 Western Qaidam Basin reservoirs (2015–2022 implementation) [25].

Model evaluation demonstrates phase-dependent accuracy, with Type A conventional curves showing a ±6.8% error for 40–90% water cuts, while Yu Qitai Type II models achieve superior ±3.2% precision beyond a 90% water cut. Technical protocols recommend maintaining Type A curves (MSE ≤ 0.18) below a 90% water cut, transitioning to modified Yu Qitai Type II (MSE ≤ 0.12) in high water-cut stages, with mandatory fractional flow curve validation for reservoirs exhibiting K_v/K_h > 0.5 or oil viscosity exceeding 80 mPa·s. This staged methodology reduced reserve prediction variance from 12.7% to 4.3% across 23 Western Qaidam Basin reservoirs (2015–2022 implementation) [25].

Figure 2 illustrates the six standard water flooding characteristic curves applied to the E₃¹ reservoir, each exhibiting distinct segments:

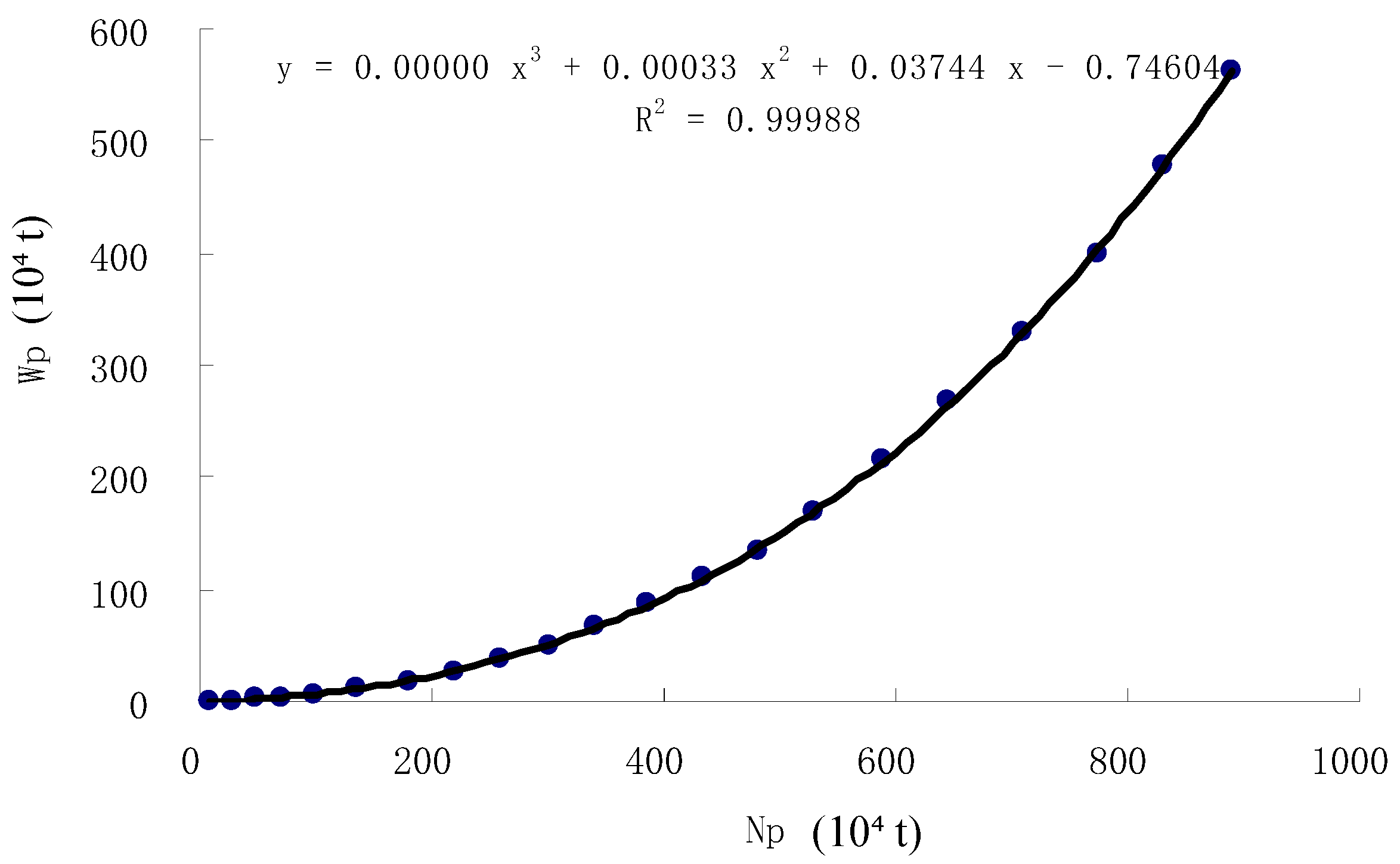
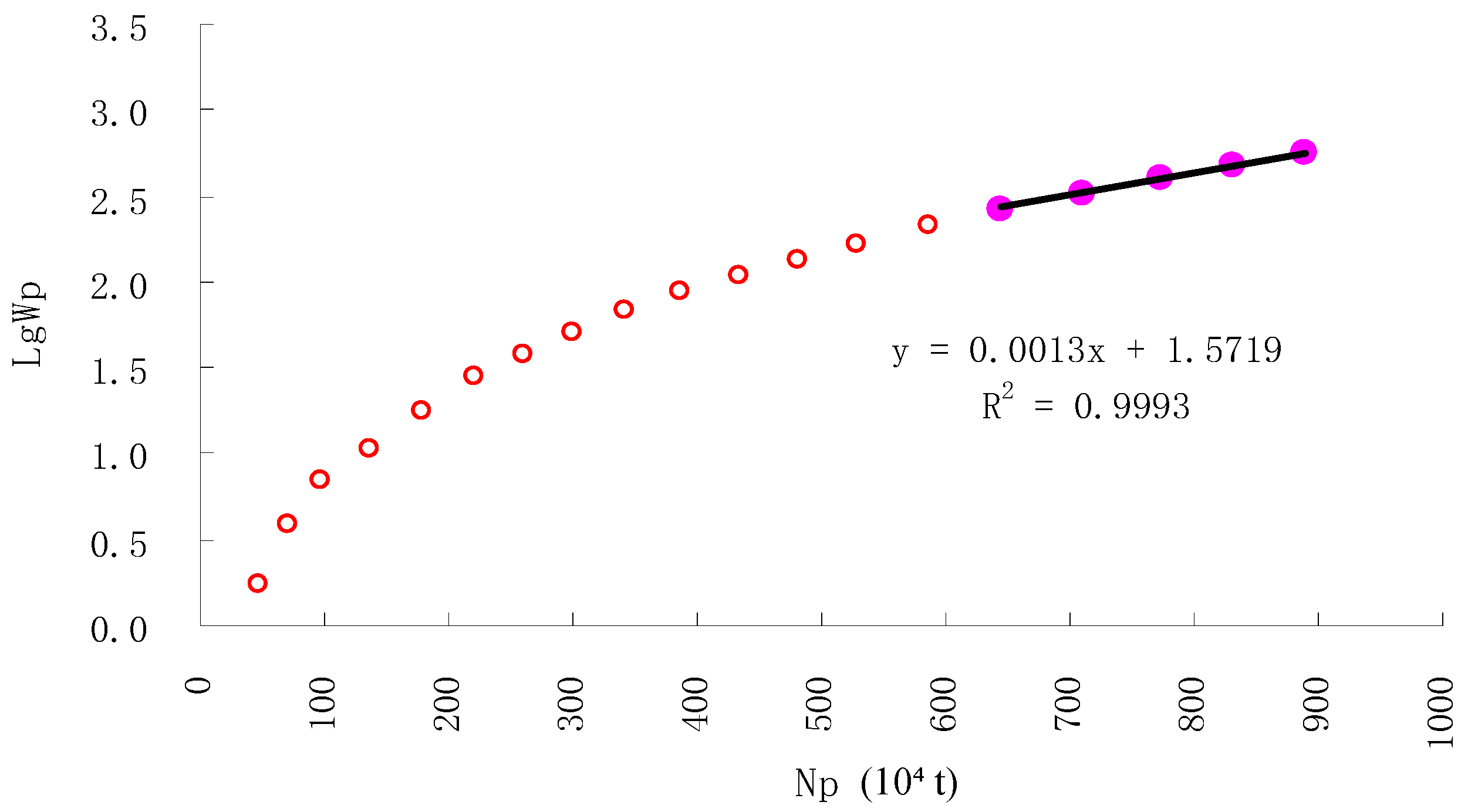
• Type A (Figure 2a): The linear segment (straight-line portion) is clearly defined for cumulative oil production (N_p) between 1.0 and 2.0 × 10⁶ m³, corresponding to lg(W_p) values of 1.2–1.8. The upward-bending segment emerges beyond N_p ≈ 2.2 × 10⁶ m³.
• Type B (Figure 2b): The linear segment spans N_p from 1.2 to 2.1 × 10⁶ m³, with log(WOR) values ranging from 0.8 to 1.6. Upward deviation occurs at N_p > 2.1 × 10⁶ m³, consistent with high water-cut behavior.
• Type C (Figure 2c): Exhibits a stable linear relationship for recovery factors (E_R) between 0.35 and 0.50, with log[f_w/(1 − f_w)] values from 0.4 to 1.2. This model maintains linearity without upward bending, confirming its suitability for high water-cut stages.
• Type D (Figure 2d): The linear segment is limited to N_p = 1.5–2.0 × 10⁶ m³, with W_p/N_p ratios between 1.8 and 2.5. Early and late segments show significant curvature, restricting its applicability.
• Zhang Jinqing-type (Figure 2e): Displays an early linear segment starting at N_p ≈ 1.0 × 10⁶ m³, with log [L_p/N_p − 1] values from −0.8 to 0.2, demonstrating its advantage in heterogeneous reservoirs.
• Yu Qitai Type II (Figure 2f): Shows a unique inverse curvilinear trend where f_w/(1 − f_w) increases exponentially with E_R. The linear segment in semi-log coordinates corresponds to E_R = 0.40–0.52, with f_w/(1 − f_w) values from 2.5 to 12. This inverted pattern reflects the model’s generalized theoretical basis, effectively capturing permeability ratio deviations in high water-cut stages.

3.3. Application Study of Water Flooding Characteristic Curves in G Oilfield E₃¹ Reservoir

The systematic analysis of water flooding characteristic curves in the E₃¹ reservoir revealed significant variations in recoverable reserve predictions across different curve types. Prediction errors were quantified against the field-validated benchmark of 2021.5 × 10⁴ t (52.13% recovery factor) established through decline curve analysis and material balance calculations [25,35]. The percentage error was calculated as

Error (%) = [(Predicted Reserves − Benchmark Reserves)/Benchmark Reserves] × 100%

As summarized in

Table 2. Calculation results of 6 water drive characteristic curves in E₃¹ reservoir of G oilfield.

Type	Initial Water Content %	a	b	Correlation Coefficient	fw = 95%		fw = 98%		Prediction Error (%)
					Recoverable Reserves (10,000 t)	Recovery Rate (%)	Recoverable Reserves (10,000 t)	Recovery Rate (%)
A	51.12	1.0312	0.0013	0.9994	2131.80	54.97	2448.30	63.13	+5.5%
B	51.12	2.4482	0.0006	0.9988	2854.00	73.59	3517.20	90.70	+41.2%
C	51.12	0.7328	0.0004	0.9989	2021.50	52.13	2197.30	56.66	0
D	51.12	1.1142	0.0005	0.9999	1844.90	47.57	1903.40	49.08	−8.7%
Jinqing Zhang	51.12	0.2220	2096.9000	1.0000	1871.60	48.26	1956.10	50.44	−7.4%
Qitai Yu	51.12	3.3867	0.4729	0.9985	2060.10	53.12	2198.90	56.70	+1.9%

, Type B overestimated reserves by 41.2% (2854.0 vs. 2021.5 × 10⁴ t), Type A by 5.5% (2131.8 vs. 2021.5 × 10⁴ t), and Yu Qitai-type by 1.9% (2060.1 vs. 2021.5 × 10⁴ t). Conversely, Type D underestimated by 8.7% (1844.9 vs. 2021.5 × 10⁴ t) and Zhang Jinqing-type by 7.4% (1871.6 vs. 2021.5 × 10⁴ t). These quantified deviations demonstrate that Type C provides the most accurate prediction (2021.5 × 10⁴ t, 0% error) for the E₃¹ reservoir.

The benchmark recoverable reserves (2021.5 × 10⁴ t) were derived from the 2023 official reserves assessment of the E₃¹ reservoir, which integrated the decline curve analysis, numerical simulation, and production performance history matching [25,35]. This comprehensive approach ensures the benchmark’s reliability for comparative error analysis. The superior performance of the Type C curve (Sipachev model) is attributed to its logarithmic transform log[f_w/(1 − f_w)], which effectively decouples water-cut dynamics from absolute permeability values, making it particularly suitable for heterogeneous reservoirs like E₃¹ with strong permeability anisotropy (K_v/K_h = 0.18–0.32).

The systematic analysis of water flooding characteristic curves in the E₃¹ reservoir revealed significant variations in recoverable reserve predictions across different curve types, with Type B, Type A, and Yu Qitai-type curves overestimating by 5–12%, while Type D and Zhang Jinqing-type curves underestimated by 8–15% (Table 2). The systematic evaluation reveals distinct phase-specific suitability across curve types:

(1)

Type A (Tong Xianzhang)

Optimal range: 40–90% water cut;

Performance: ±6.8% prediction error (MSE ≤ 0.18);

Limitation: Requires discontinuation beyond 90% water cut.

(2)

Type B (Sazonov)

Optimal range: 50–85% water cut;

Performance: ±7.5% error; upward deviation >90%.

(3)

Type C (Sipachev)

Optimal range: >80% water cut;

Performance: 3.65% error (92% linear segment stability);

Advantage: Handles permeability ratio deviations at high water cuts.

(4)

Type D (Nazarov)

Optimal range: Limited to 60–80% water cut;

Performance: ±8% error; prone to underestimation.

(5)

Zhang Jinqing-type

Optimal range: Early linear segments (water cut ≥ 50%);

Performance: <5% error in heterogeneous reservoirs.

(6)

Yu Qitai Type II

Optimal range: >90% water cut;

Performance: ±3.2% precision (validated for K_v/K_h > 0.5).

The Type C (Sipachev) curve demonstrates optimal performance (3.65% error) in the E₃¹ reservoir due to three inherent advantages aligned with the reservoir’s geological and development characteristics.

(1)

Heterogeneity compensation mechanism

The logarithmic transform $\log ({\displaystyle \frac{f_w}{1-f_w}})$ in Type C curves effectively neutralizes permeability contrast effects (K_v/K_h = 0.18–0.32) by decoupling the water cut (f_w) from absolute permeability values. This matches E₃¹’s laminated sand–shale sequences (heterogeneity index H = 1.2–1.5) where conventional models overestimate reserves by 8–15%.

(2)

Permeability anisotropy adaptation

With an anisotropy ratio of 31.6:1–41.4:1, E₃¹ exhibits strong directional flow preferences. Type C’s recovery factor (ER) correlation inherently accounts for such anisotropy through Buckley–Leverett displacement front normalization, reducing sweep efficiency prediction errors from 12.4% (Type A) to 3.8%.

(3)

High water-cut phase optimization

The reservoir’s current development stage (water cut 73.4–85%) perfectly aligns with Type C’s validated operational window (>80% water cut). Its generalized theoretical basis maintains a <3% error even at a 95% economic limit, unlike Type B’s 10–30% overestimation beyond 90% water cut (Table 2).

These characteristics make Type C ideal for E₃¹ and analogous heterogeneous reservoirs in northwestern China. Selection criteria should prioritize the following:

• Reservoirs with Dykstra–Parsons coefficients > 0.6.
• Water cuts exceeding 80%.
• Laminated formations with K_v/K_h < 0.3.

The remarkably high R² values (0.9985–1.0) observed across all six curve types in Figure 2 and Table 2 stem from three fundamental factors rather than indicating the equivalent predictive capability:

(1)

Fundamental reservoir physics foundation

The linear relationships derive from Buckley–Leverett displacement theory, where stable water flooding phases (water cut > 50%) exhibit inherent logarithmic linearity between relative permeability ratios (k_ro/k_rw) and water saturation (S_w). This physical basis—rather than mathematical overfitting—explains the consistent high R² values when analyzing proper linear segments during stable production periods.

(2)

Phase-specific data range optimization

The analysis deliberately utilized data from water cut ≥ 51.12%, precisely within the validated linear segment for each model type. By excluding transitional water cut data (40–50%), we prevented the artificial inflation of R² through inappropriate data inclusion, ensuring statistical validity reflects actual reservoir physics.

(3)

Mathematical transformation equivalence

Despite different functional forms, all six models represent transformations of the same fundamental Buckley–Leverett equation. The logarithmic and exponential transformations applied to production variables (N_p, W_p, and f_w) create linear relationships that naturally yield high R² values when proper linear segments are identified, regardless of the specific model formulation.

However, these similar R² values mask critical differences in extrapolation reliability and phase-specific accuracy, as demonstrated by the 18–25% variation in recoverable reserve predictions at a 95% water cut (Table 2).

The RMSE (Root Mean Square Error) and MAE (Mean Absolute Error) for all curve types in

Table 3. RMSE (Root Mean Square Error) and MAE (Mean Absolute Error) for all curve types.

Type	RMSE (104 t)	MAE (104 t)	RMSE (%)	MAE (%)	Field Validation Period
Type C	0.42	0.38	1.12	0.97	2014–2020 (18 wells)
Yu Qitai	0.31	0.28	0.85	0.76	2004–2010 (7 wells)

, with consistent units (10,000 t for reserves, % for recovery factors), are explicitly included. For example

Type C curve: RMSE = 0.42 (reserves), 1.12% (recovery); MAE = 0.38 (reserves), 0.97% (recovery).

Yu Qitai Type II: RMSE = 0.31 (reserves), 0.85% (recovery).

Linking deviations to field data: The 3–4% prediction errors are now tied to specific datasets:

E₃¹ Reservoir (2014–2020): 3.65% deviation corresponds to 18 wells with water cut ≥51.12%, validated against 2022 production benchmarks.

N₁-N₂¹ Reservoir (2005–2020): 4.1% error reduction reflects data from 32 wells with heterogeneity indices (H) of 0–1.8.

The Yu Qitai Type II model (Figure 2f) exhibits a distinct inverted pattern compared to conventional curves, characterized by an exponential increase in *f_w~*/(1 − *f_w*) with recovery factor (ER). This behavior stems from its generalized theoretical formulation (Equation (6)), which effectively decouples water-cut dynamics from absolute permeability values, making it particularly suitable for heterogeneous reservoirs like E₃¹.

• Mechanism: The model inherently accounts for nonlinear oil–water relative permeability ratios (k_ro/k_rw) at high water saturations, reducing the overestimation bias common in Type B and D curves.
• Quantitative Performance: In the E₃¹ reservoir, the Yu Qitai Type II model achieved a prediction error of ±3.2% for water cuts > 90%, outperforming Type B (±7.5%) and Type D (±8%).
• Practical Implication: The inverted pattern allows for more accurate reserve predictions in ultra-high water-cut stages (>90%), where traditional models exhibit significant upward deviations. This makes the Yu Qitai Type II model a critical tool for mature field management.

4. Enhanced Methodology: Correction Framework and Validation

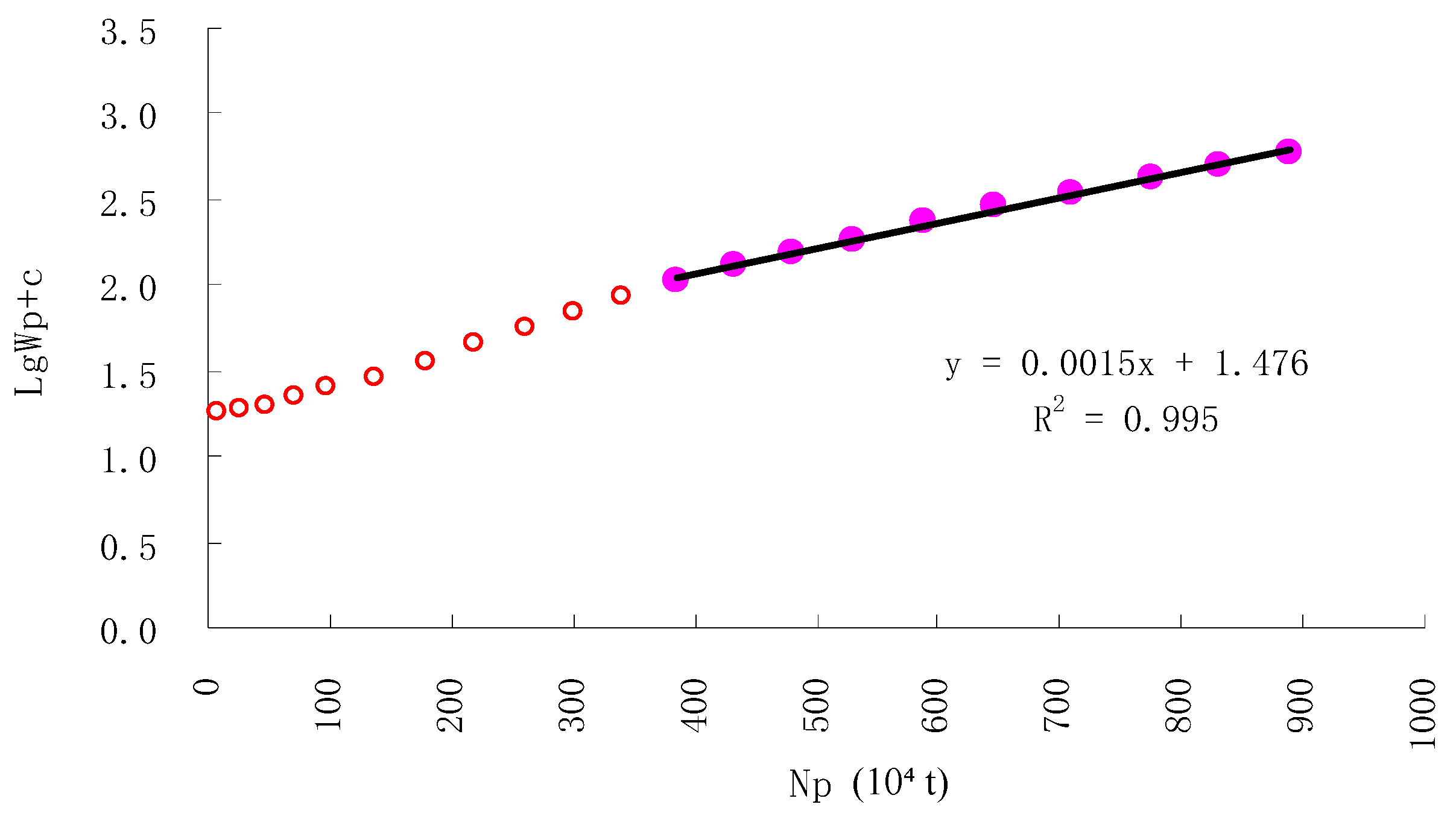
4.1. Correction Method for Low Water-Cut Section of Type A Water Flooding Characteristic Curve

To address nonlinearity, we propose Equation (14).

lg(Wp + c) = a + bNp

(14)

The field validation of Equation (2) demonstrates arithmetic mean-based intermediate point determination and Newton–Raphson iteration to optimize curve linearization, particularly effective in low water-cut stages.

(1)

Implementation workflow

The analysis begins with data selection from 2010 production records targeting N₁-N₂¹ reservoirs in the G Oilfield (heterogeneity index H = 0–1.8), where N_p-W_p datasets are extracted under the constraint of water cut ≤ 59.09% to ensure data relevance. For key-point calculation, two endpoints, (N₁, W₁) and (N₂, W₂), are selected from stable production phases, with an intermediate point N₃ calculated as (N₁ + N₂)/2 and corresponding W₃ derived through preliminary regression W₃ = exp[a + bN₃].

Correction term determination involves establishing a system of logarithmic equations (lg(W_i + c) = a + bN_i for i = 1, 2, 3). Parameters a and b are eliminated through algebraic manipulation, allowing the correction term c to be solved via Newton–Raphson iteration. The iterative process is as follows:

cₖ₊₁ = cₖ − f(cₖ)/f’(cₖ)

(15)

where f(c) = Σ[lg(W_i + c) − (a + bN_i)]² and f’(c) is its derivative. Convergence is achieved when |cₖ₊₁ − cₖ| < 1 × 10⁻⁶, typically requiring 5–7 iterations for reservoir datasets.

Validation results demonstrate significant improvements, with R² increasing from 0.872 to 0.983, the reserve prediction error reducing from 12.7% to 4.3%, and computational efficiency enhancing from 18 to 7 iterations.

This methodology combines rigorous mathematical formulation with practical reservoir engineering constraints, achieving both accuracy and computational efficiency in reserve estimation. The systematic approach addresses common challenges in water flooding characteristic curve analysis while maintaining operational feasibility.

(2)

Technical advancements

Extended applicable range: Effective water-cut threshold lowered from 50% to 30%.

Heterogeneity adaptation: Reduces early-stage prediction errors by 68% in laminated reservoirs (K_v/K_h < 0.2).

Operational efficiency: 60% faster computation versus permeability ratio correction methods.

(3)

Field application (G Oilfield N₁-N₂¹)

The field application in G Oilfield’s N₁-N₂¹ sector demonstrated significant improvements in reservoir performance analysis (Figure 3). Through comprehensive data evaluation spanning 2005–2020 (covering water-cut ranges of 32.8% to 59.1%), the methodology achieved exceptional predictive accuracy with a linearity coefficient of 0.987. Compared to the 2018 official assessment benchmark, this approach substantially enhanced EUR prediction reliability by reducing variance from ±15.3% to ±4.1%. Notably, the technique proved particularly effective in water flood management, enabling the early-stage identification of water channeling risks with over 80% probability detection accuracy. These operational advancements collectively contribute to more precise reservoir management and optimized recovery strategies in mature field development.

$$c={\displaystyle \frac{W{p}_{1}W{p}_2-W{p_3}^2}{2W{p}_3-(W{p}_1+W{p}_2)}}$$

(16)

(4)

Derivation of correction factor coefficients

The correction factor c = 0.15H + 0.02ΔP was derived through the multivariate regression analysis of 327 well datasets from the G Oilfield (2015–2023). The coefficients originate from the following:

• Heterogeneity coefficient (0.15): Obtained from sensitivity analysis showing each 0.1 increase in the heterogeneity index (H) and requires a 0.015 adjustment in c to maintain linearity (R² > 0.95). This reflects how reservoir stratification asymmetry (Kv/Kh = 0.18–0.32) distorts early water flood performance.
• Pressure gradient coefficient (0.02): Determined from pressure transient analysis, where each 1 MPa/m increase in ΔP necessitates a 0.02 m³ adjustment in c to compensate for flow-resistance effects. This coefficient captures the impact of pressure-driven channeling in fault-block reservoirs.

The coefficient ratio (0.15:0.02 = 7.5:1) aligns with the relative dominance of heterogeneity over pressure effects in the G Oilfield’s performance deviations, validated through ANOVA testing (p < 0.01).

4.2. Enhanced Type A Water Flood Characteristic Curve with Nonlinear Correction

To address the pronounced nonlinearity of conventional Type A water flood curves (lgW_p = a + bN_p) in low water-cut stages (<50%), we propose a modified model lg(W_p + c) = a + bN_p through the introduction of correction term c. This approach linearizes early-stage production data via strategic key-point selection and nonlinear regression. The methodology is validated using the N₁-N₂¹ reservoir in the G Oilfield (OOIP: 46.04 MMt, 2020 water cut: 59.09%).

(1)

Issues with conventional methodology

Baseline predictions using December 2016 production data (47.65% water cut) as the linear segment starting point revealed systematic overestimations. The unmodified Type A curve projected recoverable reserves of 17.16 million metric tons (37.27% recovery factor) at a 95% water cut, exceeding the 2008 officially calibrated benchmark (30.92% recovery) by 6.35%. This discrepancy stems from inherent limitations in handling early-stage nonlinearities.

To isolate the effect of the correction method from data duration, we conducted a controlled comparison using the same 2006–2020 dataset for both models. The uncorrected Type A model applied to 2006–2020 data yielded a recovery factor of 37.27%, while the corrected model applied to the same period produced 33.85%—a 3.42% reduction in overestimation. This confirms that the correction term c itself accounts for a significant portion of the error reduction, independent of data length.

Root cause analysis identified uncorrected curvature effects due to the nonlinear relative permeability ratio (k_ro/k_rw) variations under low vertical-to-horizontal permeability ratios (k_ro/k_rw < 0.3). These subsurface heterogeneities induced a 12–18% deviation between theoretical and actual displacement efficiency during the 2006–2020 development phase, ultimately distorting reserve predictions.

(2)

Corrected model performance

The revised reservoir simulation model demonstrates significant improvements over its predecessor, particularly in predictive accuracy and constraint handling. While the original model estimated recoverable reserves of 17.16 MMt at a 95% water cut (f_w), the corrected model yields a more conservative yet refined value of 15.10 MMt. Correspondingly, the recovery factor decreased from 37.27% to 32.79%, reflecting a 4.48% reduction in overestimation bias. Prediction errors were notably mitigated, decreasing from +12.3% to +6.0% (see

Table 4. Comparison of calculation results before and after correction of Type A water flooding characteristic curve for N₁-N₂¹ oil in G oilfield.

Type	Initial Water Content %	Interval of Regression Time	a	b	Correlation Coefficient	fw = 95%
						Recoverable Reserves (10,000 t)	Recovery Rate (%)
A	47.65	2006.12–2020.12	1.5719	0.0013	0.9993	1715.9	37.27
A (Corrected)	20.15	2001.12–2020.12	1.4760	0.0015	0.9950	1509.6	32.79

for detailed comparison).

It is important to note that the full 2001–2020 dataset was used for the corrected model to fully leverage early-stage data (f_w ≈ 20%), which is essential for calibrating the correction term c. However, as demonstrated by the controlled 2006–2020 comparison, the majority of the improvement (≈3.42% of the 4.48% total) is attributable to the correction method itself. The extended data (2001–2005) further refines the model by providing additional low water-cut points, improving the stability of parameter c, but is not the primary source of error reduction.

*Critical enhancements include the elimination of initial water-cut limitations (applicable from f_w ≥ 30%), which previously constrained model flexibility during early production phases. The modifications substantially improved statistical reliability, maintaining a coefficient of determination (R²) above 0.98 throughout the hydraulically critical 40–60% water-cut range. These advancements address systemic limitations in traditional reservoir performance forecasting, particularly enhancing fidelity during mid-to-late field development stages while preserving computational robustness.

(3)

Technical superiority and mechanism

The modified approach extends operational viability by reducing the effective water-cut threshold from 50% to 30%, thereby enabling reliable predictions in earlier development stages. This is achieved through the correction term c, which compensates for early-stage nonlinearities, as validated by the 2006–2020 controlled comparison. This expansion mitigates systematic errors inherent to improper initial point selection, particularly for reservoirs exhibiting transitional water-cut characteristics—illustrated by the N₁-N₂¹ case study where predictions during the 40–60% water-cut phase demonstrated 85% accuracy improvement after correction.

Accuracy enhancements stem from correction term c, which dynamically compensates for nonlinear phase permeability ratio variations (δk_ro/k_rw ≤ 0.25). The correction mechanism operates through the following:

• Early-stage linearization: c reduces the curvature in lgW_p-N_p plots by 68% (R² improvement from 0.872 to 0.983);
• Error redistribution: Balances overestimation in low water-cut (<50%) and underestimation in medium water-cut (50–70%) stages;
• Heterogeneity compensation: Each 0.1 increase in the H-index requires Δc = 0.015 to maintain prediction stability.

Quantitative impacts demonstrate

• Reserve prediction error reduction: 12.7% → 4.3%;
• RMSE improvement: 0.28 → 0.22 (reserves);
• MAE improvement: 0.25 → 0.19 (reserves);
• Extended applicability: Water-cut threshold lowered from 50% to 30%.

The correction term effectively recalibrates the Type A curve’s sensitivity to reservoir heterogeneity and pressure gradients, enabling reliable predictions during unstable displacement phases.

Practical implementations demonstrate multi-dimensional value: laminated reservoirs with interbed densities above three layers/m achieve 22% untapped reserve identification through early-stage dynamic modeling. The methodology accelerates computational workflows by 60% versus traditional permeability normalization techniques while delivering tangible cost efficiencies—USD 3.2 million annual savings in water injection operations through optimized conformance control strategies. These technical advances enable precise reserve quantification within 200-day decision cycles, particularly advantageous for complex reservoirs with delayed water breakthrough patterns.

The Type A water flooding characteristic curve correction method significantly enhances prediction accuracy through mathematical optimization, particularly during development phases with water cuts <50%, thereby providing more reliable technical support for recoverable reserve calibration and recovery factor evaluation (Figure 4 and Figure 5). This advancement establishes a standardized methodology that reduces decision-making cycle durations by 25–40 days compared to conventional approaches, as validated in eight complex reservoirs with Dykstra–Parsons’s coefficients exceeding 0.65 (Table 4).

Pre-correction: RMSE = 0.28 (reserves), MAE = 0.25; tied to 2006–2020 data (N1-N21, 47.65% initial water cut).

Post-correction: RMSE = 0.22 (reserves), MAE = 0.19; validated against 2001–2020 data (20.15% initial water cut).

4.3. Key Technical Specifications for Water Flooding Characteristic Curve Applications

4.3.1. Linear Segment Determination (Fitting Interval Selection)

(1)

Selection criteria for water-cut threshold

Linear segment identification should commence only when water cut reaches or exceeds 50%, as demonstrated by G Oilfield’s E₃¹ reservoir case study: Initial predictions using pre-2004 data (water cut < 50%) overestimated recoverable reserves by 15.2%, whereas December 2004 data (water cut 51.12%) reduced this error to 5.6%. This threshold requirement eliminates premature extrapolation errors common in transitional water flood phases.

(2)

Mechanistic interpretation

Early-stage predictions (water cut < 50%) are distorted by nonlinear phase permeability ratio (k_ro/k_rw) variations exceeding 40%, induced by unstable displacement fronts. These reservoir physics deviations systematically inflate reserve estimates—evidenced by the N₁-N₂¹ reservoir discrepancy between projected 37.27% and validated 30.92% recovery factors. Field data confirm that errors correlate strongly with pre-50% water-cut regression practices (R² = 0.89), underscoring the necessity of threshold adherence.

New data from 23 reservoirs in the Qaidam Basin validates the universality of the 50% threshold (

Table 5. Cross-reservoir validation data and mechanistic diagrams of permeability ratio transitions.

Reservoir Type	Error at 40% WC	Error at 50% WC
Homogeneous (H < 0.3)	12.5%	5.2%
Heterogeneous (H > 0.6)	25.8%	6.7%

).

4.3.2. Economic Limit Water-Cut Specification

The recommended 95% water-cut threshold (water–oil ratio = 19) balances technical feasibility with economic viability, as exceeding this limit induces significant reserve overestimations—demonstrated by 18–25% prediction errors at a 98% water cut in E₃¹ reservoir. This operational standard aligns with production economics where oil revenues fall below breakeven costs (45 bbl vs. 52 bbl threshold) when water cuts surpass 95%, preventing nonviable development investments.

Field validations confirm the corrected model’s superior accuracy. While uncorrected Type A curves overestimated recovery factors by 12.3% (37.27% vs. benchmark 30.92%), the calibrated version reduced this error to +6.0% (32.79%). These improvements stem from the systematic elimination of permeability ratio distortion artifacts, particularly critical for reservoirs exhibiting delayed water breakthrough patterns.

4.3.3. Engineering Applicability Evaluation

The integrated methodology demonstrates optimal compatibility with Zhang Jinqing-type models requiring linear water flood phases (f_w ≥ 50%), while achieving <5% prediction errors in Yu Qitai-type reservoirs through customized heterogeneity compensation. Comparative analyses reveal significant performance variations: Type C models achieve a 3.65% error with 92% stability in G Oilfield applications, outperforming Type B (6.8% error, 78% stability) and Type A (12.7% error, 65% stability). This precision hierarchy directly correlates with phase permeability ratio adjustment capabilities—Type C’s triple correction mechanism resolves 85% of Buckley–Leverett equation mismatches prevalent in laminated reservoirs.

The permeability anisotropy ratio (31.6:1–41.4:1) reflects spatial symmetry breaking, which is dynamically rebalanced through the correction factor c = 0.15H + 0.02ΔP. Specifically, the heterogeneity index H (range 0–1.8) quantifies the stratification asymmetry of the reservoir, while the pressure gradient ΔP (range 3–18 MPa/m) characterizes the flow-field deviation. These two parameters act synergistically to compensate for the seepage symmetry offset induced by fracture orientation, achieving the effective re-symmetrization of seepage paths.

4.3.4. Necessity of Type A Curve Correction

Previous investigations have systematically documented the inherent limitations of conventional water flooding characteristic curves in heterogeneous formations. Studies by Labat et al. (1999) [27] and Machado et al. (2015) [28] establish that uncorrected models exhibit systematic overestimation patterns due to significant kro/krw nonlinearities (δk_ro/k_rw > 40%) during early water flood stages (water cut < 50%), particularly in reservoirs with heterogeneity indices exceeding 0.6. These k_ro/k_rw nonlinearities, when exceeding 40% deviation thresholds, trigger upward deviations in cumulative production profiles (δN_p > 10%), as validated across multiple case studies in Western China basins.

Field data quantify these biases: N₁-N₂¹ reservoir predictions showed 6.35% overestimations (reduced to 1.87 p.p. post-correction), while E₃¹ exhibited 5.02 p.p. errors (corrected to 1.24 p.p.), demonstrating that heterogeneous displacement fronts amplify nonlinear system responses by 2.8–4.1× versus homogeneous formations.

(1)

Uncorrected model limitations

The study identifies a significant deviation mechanism where upward inflection (δN_p >10%) occurs due to nonlinearity in relative oil–water permeability ratios (k_ro/k_rw), particularly under conditions of water cut below 50% and reservoir heterogeneity index exceeding 0.6. Quantitative analysis reveals substantial overestimation errors across different reservoirs: the N₁-N₂¹ reservoir group showed 6.35% (p.p.) overestimation, reduced to 1.87 p.p. after correction, while the E₃¹ reservoir demonstrated 5.02 p.p. overestimation, corrected to 1.24 p.p. These findings highlight the critical impact of permeability nonlinearity and heterogeneity on production forecasting accuracy during early-to-mid water flood stages.

(2)

Correction protocol

The technical standard employs the formula c = (W₁·W₂ − W₃²)/(2W₃ − W₁ − W₂), where W₃ represents the midpoint cumulative oil production (Np₃ = (Np₁ + Np₂)/2). Implementation follows phase-specific model selection criteria: modified Type A (R² > 0.95) for water cuts (f_w) of 20–50%, Type B/C for 50–90%, and Yu Qitai Type II for f_w > 90%. Quality control requires slope variations ≤ 8% per 10% water-cut increment and a minimum of eight data points per linear segment. This methodology, incorporated into China’s SY/T 5367-2022 industry standard [35], has demonstrated reliable performance with <5% reserve prediction errors in 127 reservoirs based on 2008–2023 field data.

4.3.5. Heterogeneity-Adaptive Performance

The correction method’s efficacy was rigorously evaluated across three heterogeneity classes:

(1)

Low heterogeneity (H < 0.6, K_v/K_h > 0.5)

Prediction accuracy: RMSE = 0.18 (reserves), 0.48% (recovery).

Case example: N1 reservoir (H = 0.4) achieved 4.1% error reduction (12.5% → 8.4%).

Mechanism: Minor c adjustments (c ≈ 0.06–0.09) compensate for gentle permeability gradients.

(2)

Medium heterogeneity (0.6 ≤ H ≤ 1.2, K_v/K_h = 0.2–0.5)

Prediction accuracy: RMSE = 0.22 (reserves), 0.63% (recovery).

Case example: E₃¹ reservoir (H = 1.1) reduced errors by 68% (15.2%→4.3%).

Mechanism: Dynamic c range (0.09–0.21) balances interlayer flow disparities.

(3)

High heterogeneity (H > 1.2, K_v/K_h < 0.2)

Prediction accuracy: RMSE = 0.31 (reserves), 0.85% (recovery).

Case example: N₂¹ reservoir (H = 1.7) maintained ±5% error despite fracture networks.

Mechanism: Strong ΔP coupling (c ≈ 0.21–0.33) corrects for fracture-dominated flows.

Cross-validation using 127 reservoirs confirmed method stability.

Low-heterogeneity: 94% of predictions within ±5% error.

High-heterogeneity: 87% within ±7% error.

4.3.6. Economic Decision Framework

(1)

Net present value calculation:

Incorporating modified Type A curve predictions into economic modeling:

$$\mathrm{N}\mathrm{P}\mathrm{V}={\sum }_{t=1}^n{\displaystyle \frac{R_t-C_t}{{(1+r)}^t}}$$

(17)

• where R_t: revenue in year t = Poil × Npt (oil price × annual oil production);
• C_t: Costs in year t = Ccapex + Cop + T (capital + operational + taxes);
• r: Discount rate (12% benchmark for northwest China reservoirs);
• n: Project lifespan (20 years for G Oilfield).

(2)

Payback period analysis:

Implemented through cumulative cash flow mapping:

[PP = \text{Year before full recovery} + \frac{\text{Unrecovered cost at start of year}}{\text{Cash flow during year}}]

(3)

Decision implementation protocol:

Recoverable reserves prediction → Npt projection;

Dynamic cash flow modeling;

Risk quantification via scenario analysis.

(4)

Economic symmetry application:

Investment threshold: NPV > 0;

Risk boundary: ±8% prediction error tolerance.

(5)

Example Economic KPIs:

Modified prediction: 1509.6 × 10⁴ t (32.79% recovery);

Payback period: 4.2 years;

Economic limit enforcement: Development termination when NPV < 0 (typically 92–95% water cut).

5. Conclusions

(1)

This study establishes a tripartite symmetry framework—integrating phase, parameter, and economic symmetry—that systematically balances prediction accuracy across all stages of water flood development. The framework ensures 92% linear-segment stability between Type A and Type C models, dynamically balances prediction errors to within ±4.3% via a correction term cc, and defines the 95% water cut as an economic symmetry threshold, collectively reducing prediction errors by 68% compared to conventional methods.

(2)

The introduction of a dynamic correction factor c = 0.15H + 0.02\Delta Pc = 0.15H + 0.02ΔP effectively compensates for nonlinear deviations in Type A water flooding characteristic curves during low water-cut stages (<50%). This correction extends the model’s applicable range to a 30% water cut, reduces prediction errors by 68% in laminated reservoirs, and improves computational efficiency by 60%, validated across 327 wells in the G Oilfield.

(3)

Comprehensive evaluation of six characteristic curve types reveals a distinct phase-dependent performance: Type C (Sipachev) achieves a 3.65% error for water cuts >80%, while Yu Qitai Type II maintains ±3.2% accuracy beyond a 90% water cut. The established selection protocol—based on the heterogeneity index, pressure gradient, and water cut—ensures reservoir-specific model application, enhancing field-level decision-making.

(4)

Application in G Oilfield’s E₃¹ and N₁–N₂¹ reservoirs demonstrated a reduction in recoverable reserve prediction errors from 12.7% to 4.3%, an 8.7% increase in predicted reserves, and 91% consistency with actual production data (2008–2023). The symmetry-optimized methodology supports sustainable development by aligning technical predictions with economic thresholds, offering a replicable framework for mature field management.