FLAC3D Modeling of Shear Failure and Fracture of Anchor Bolts in Surrounding Rock: A Study on Stress-Bearing Ring Reinforcement
Abstract
1. Introduction
2. Modification and Implementation Process of PILE Structural Elements
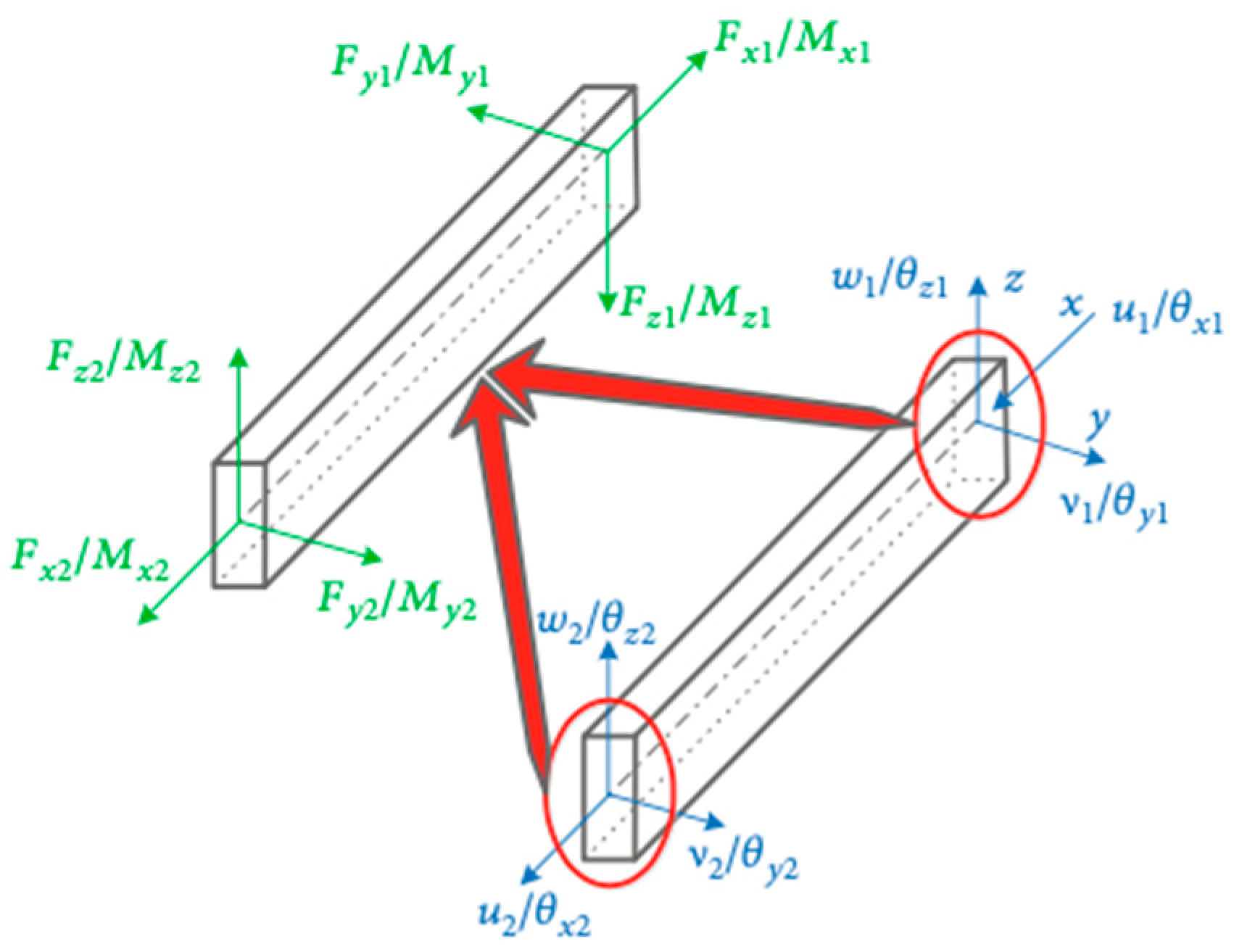
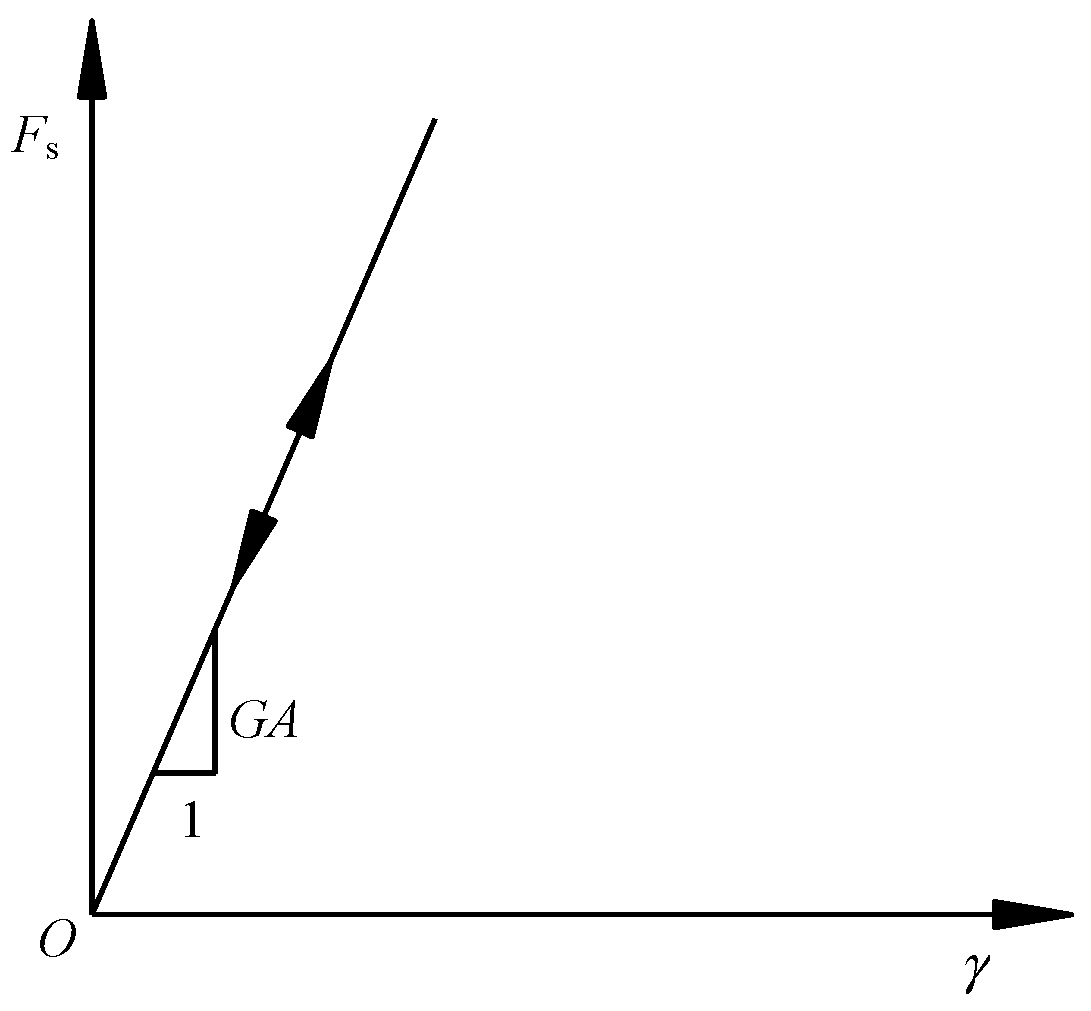
2.1. Existing PILE Structural Element Models in FLAC3D and Their Associated Issues
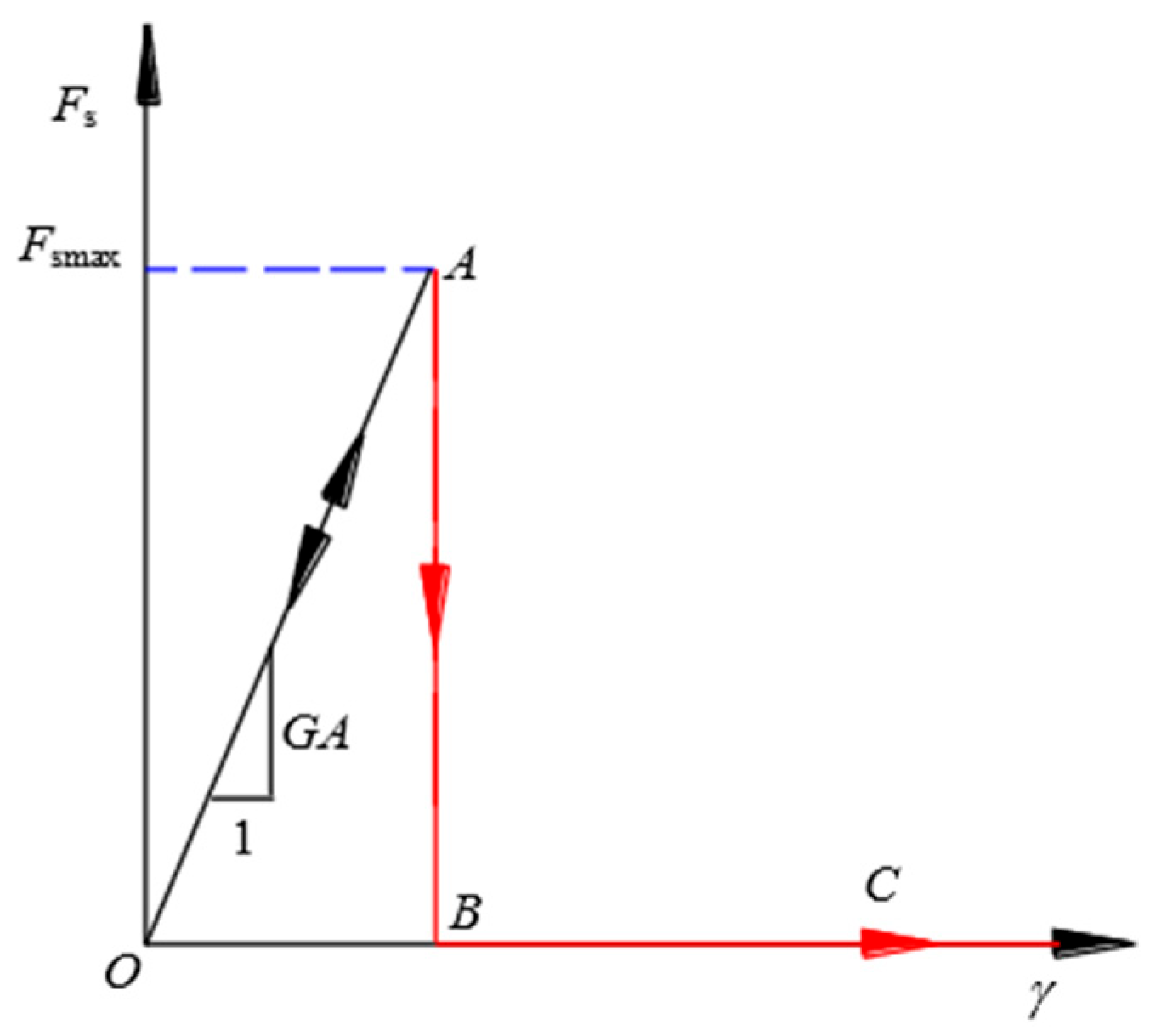
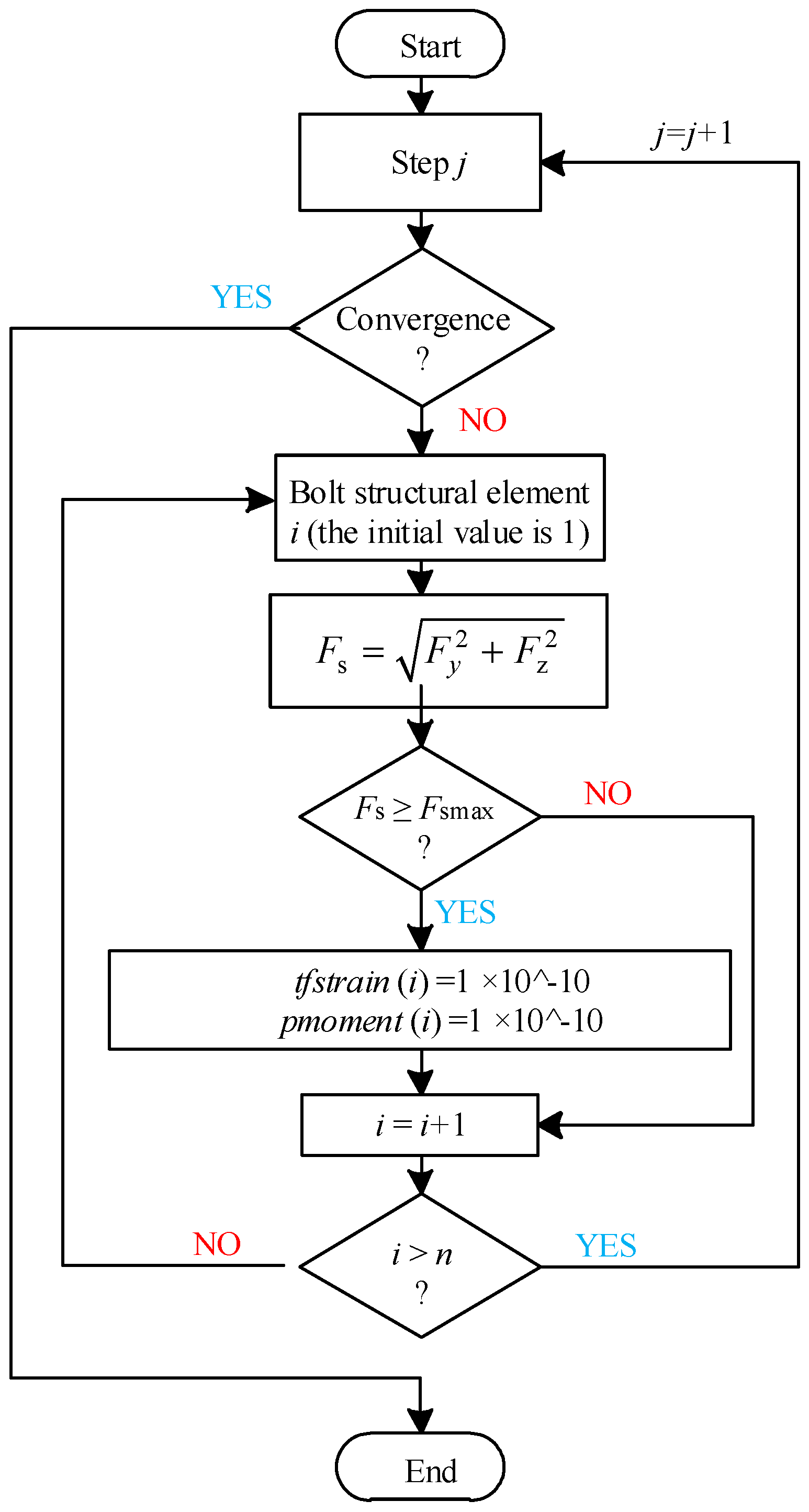
2.2. The Revised Model of PILE Structural Elements and the Implementation Process of Its Modification Program
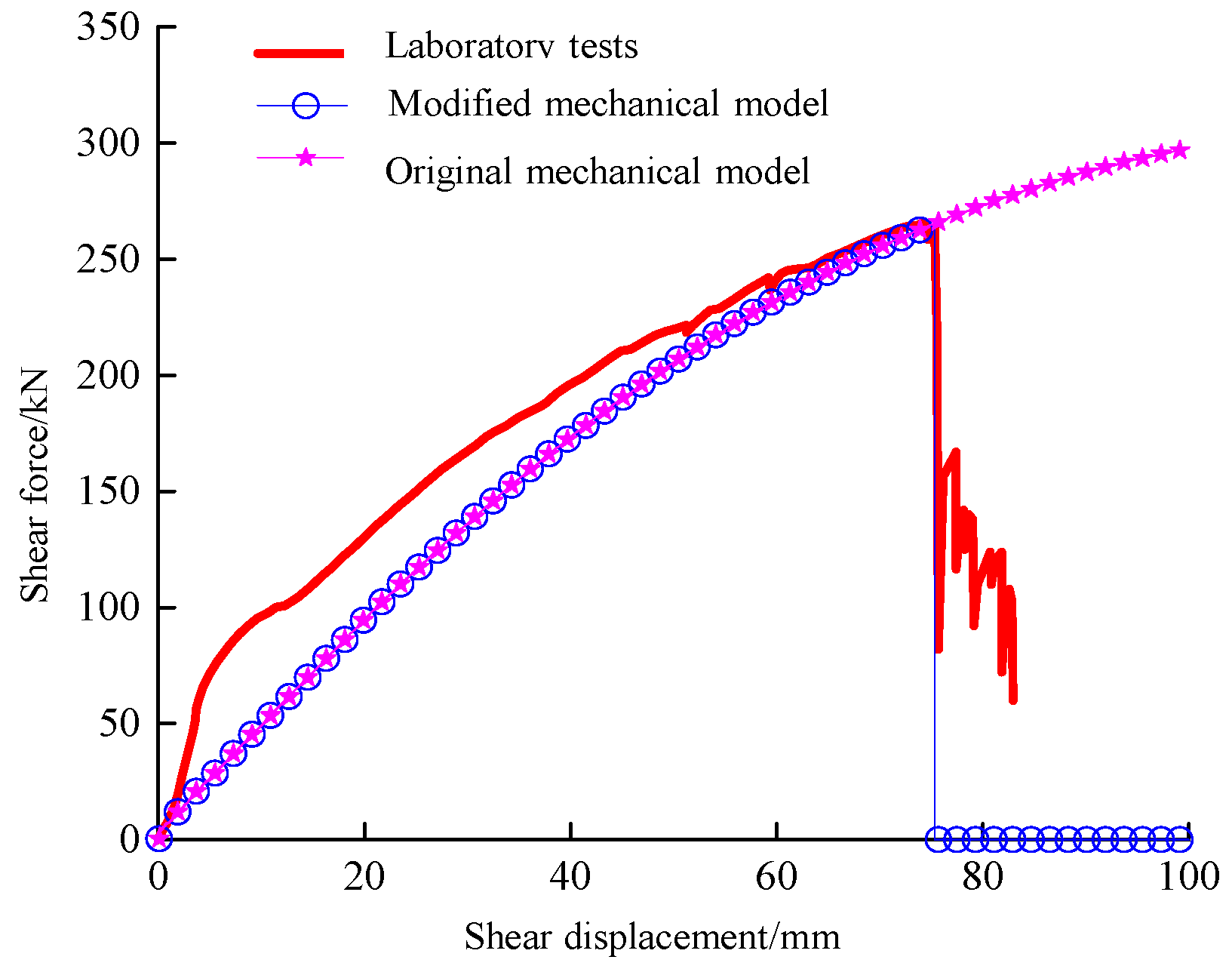
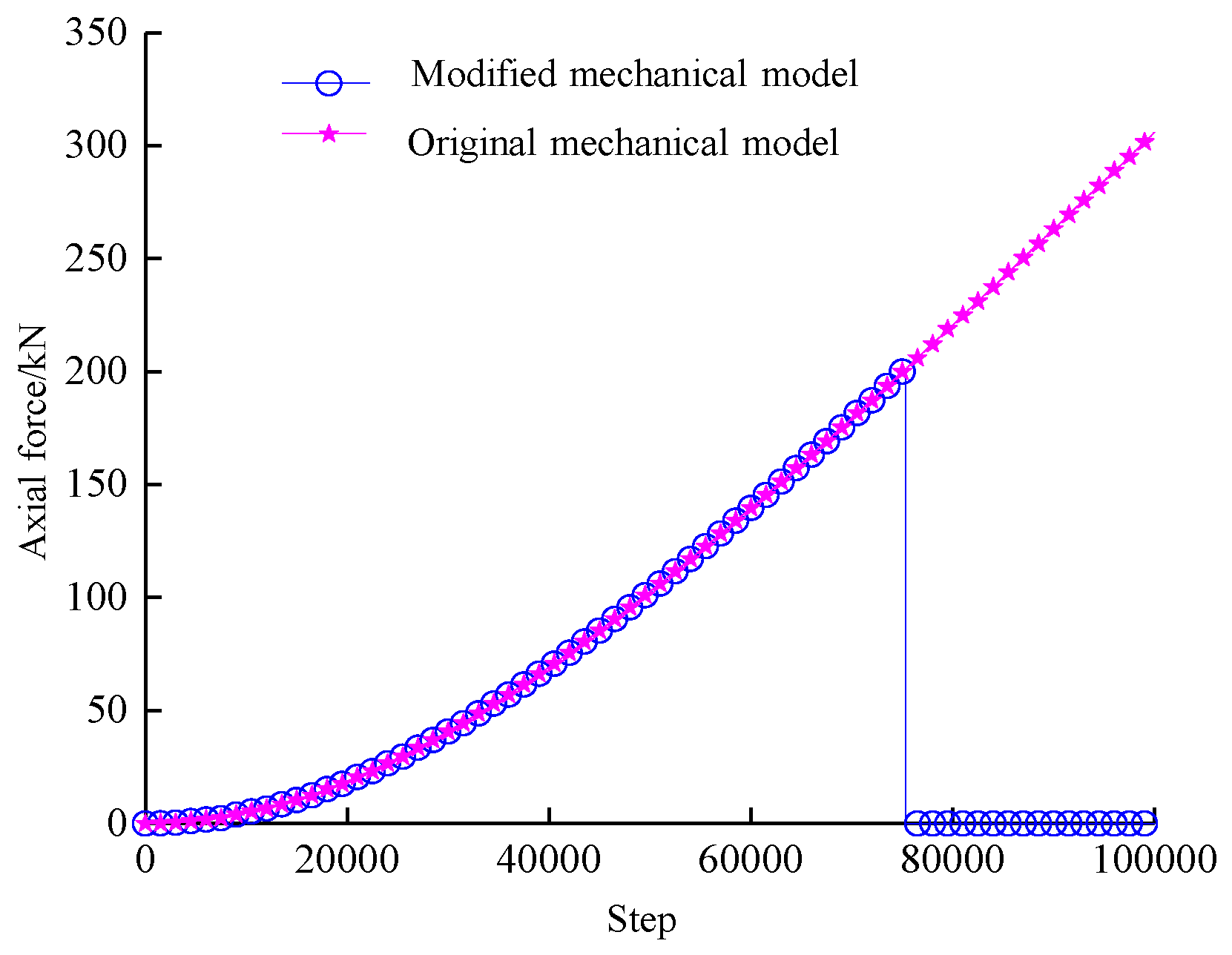
2.3. Verification and Application of the Revised PILE Structural Element Model
3. Mechanism of Action of the Revised PILE Structural Element on the Surrounding Rock of Roadway
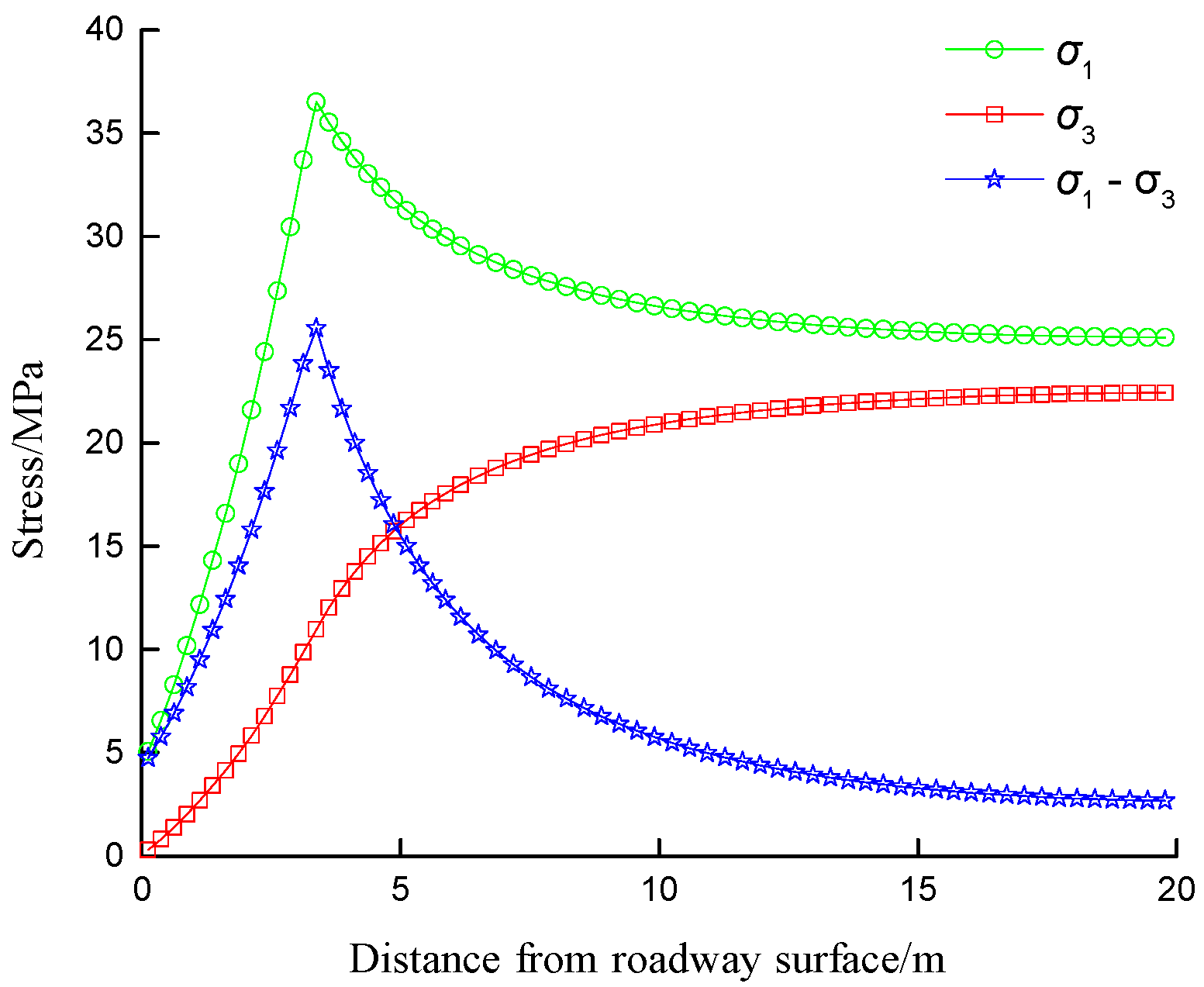
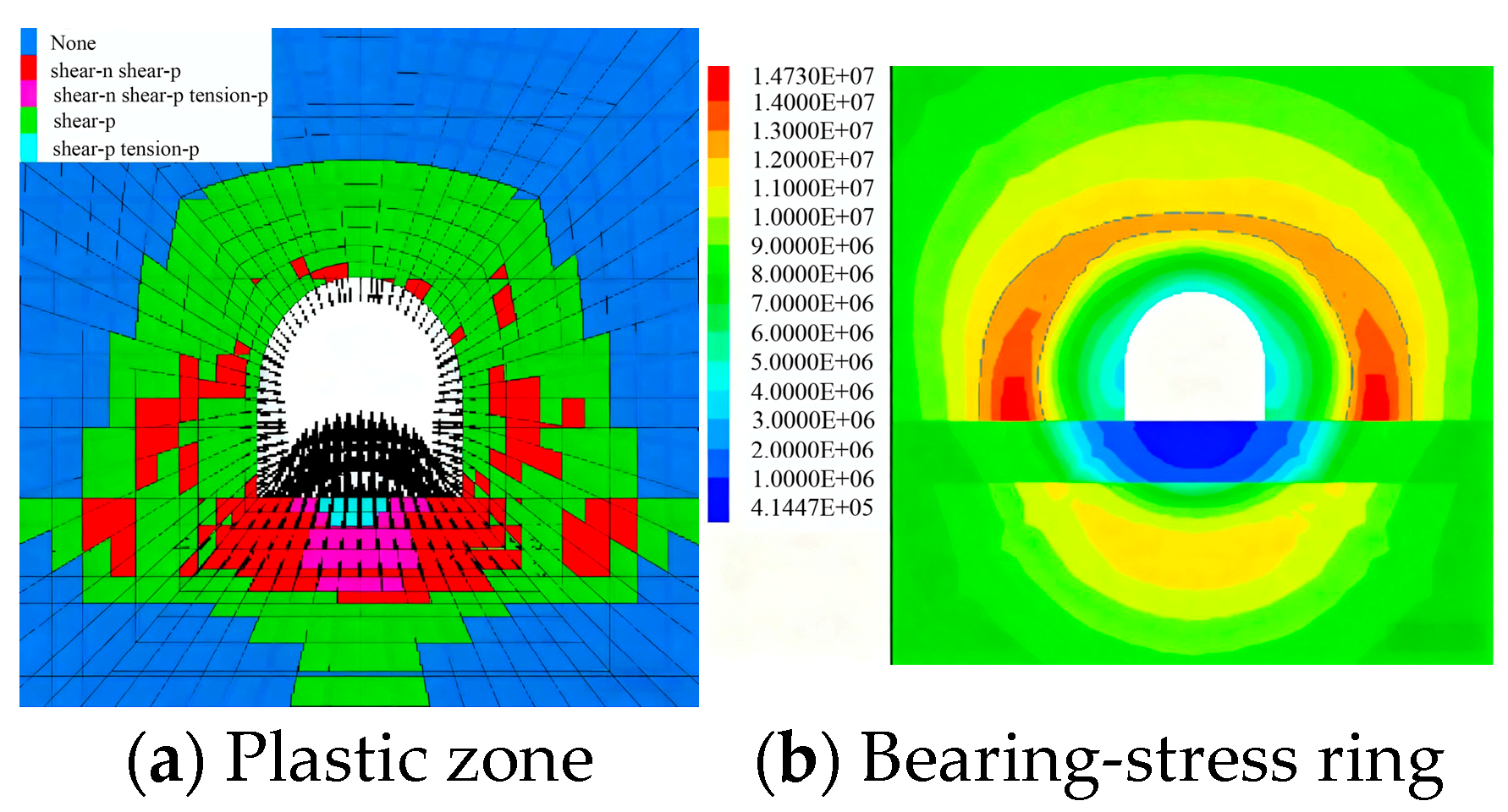
3.1. Proposal of the Concept of Surrounding Rock Stress-Bearing Ring
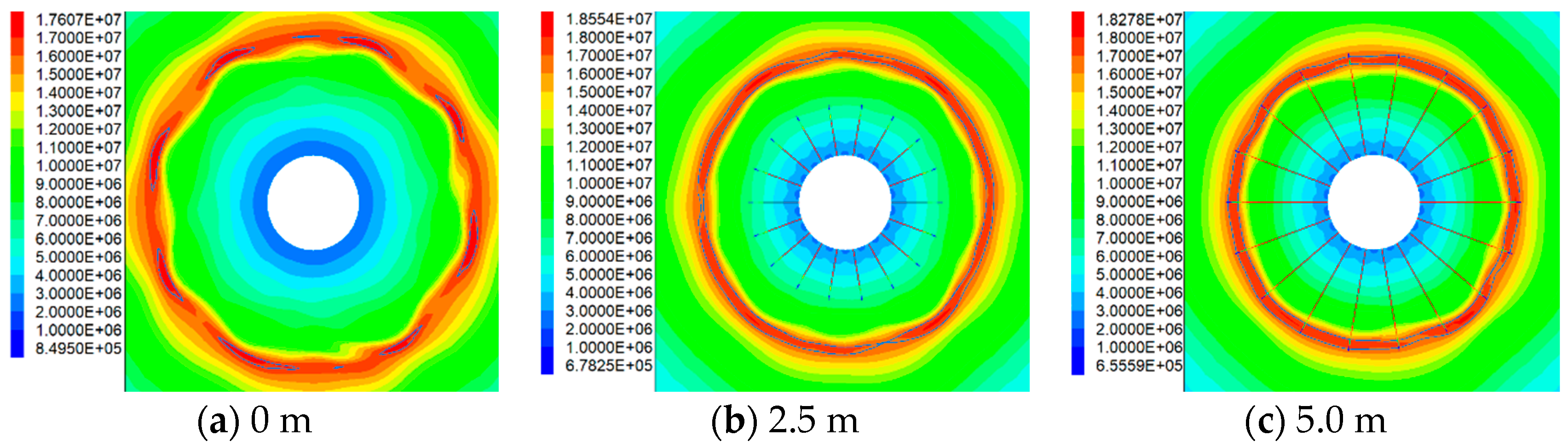
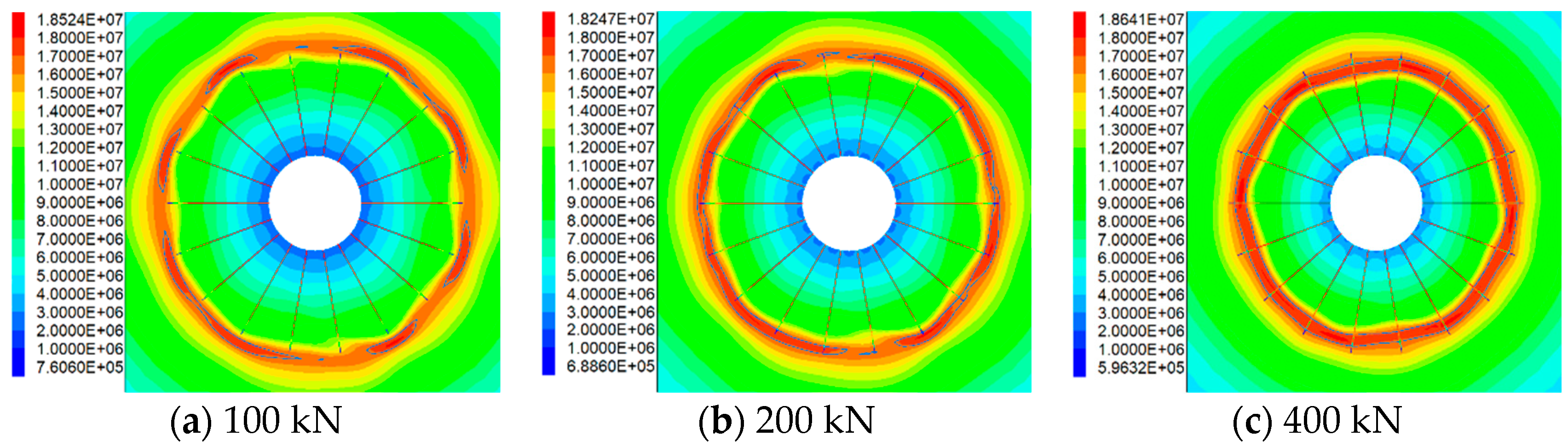
3.2. The Influence of Anchor Bolt Parameters on the Stress-Bearing Ring of Surrounding Rock
4. Practical Reinforcement Effects of Rock Bolt Support on the Stress-Bearing Ring of Surrounding Rock
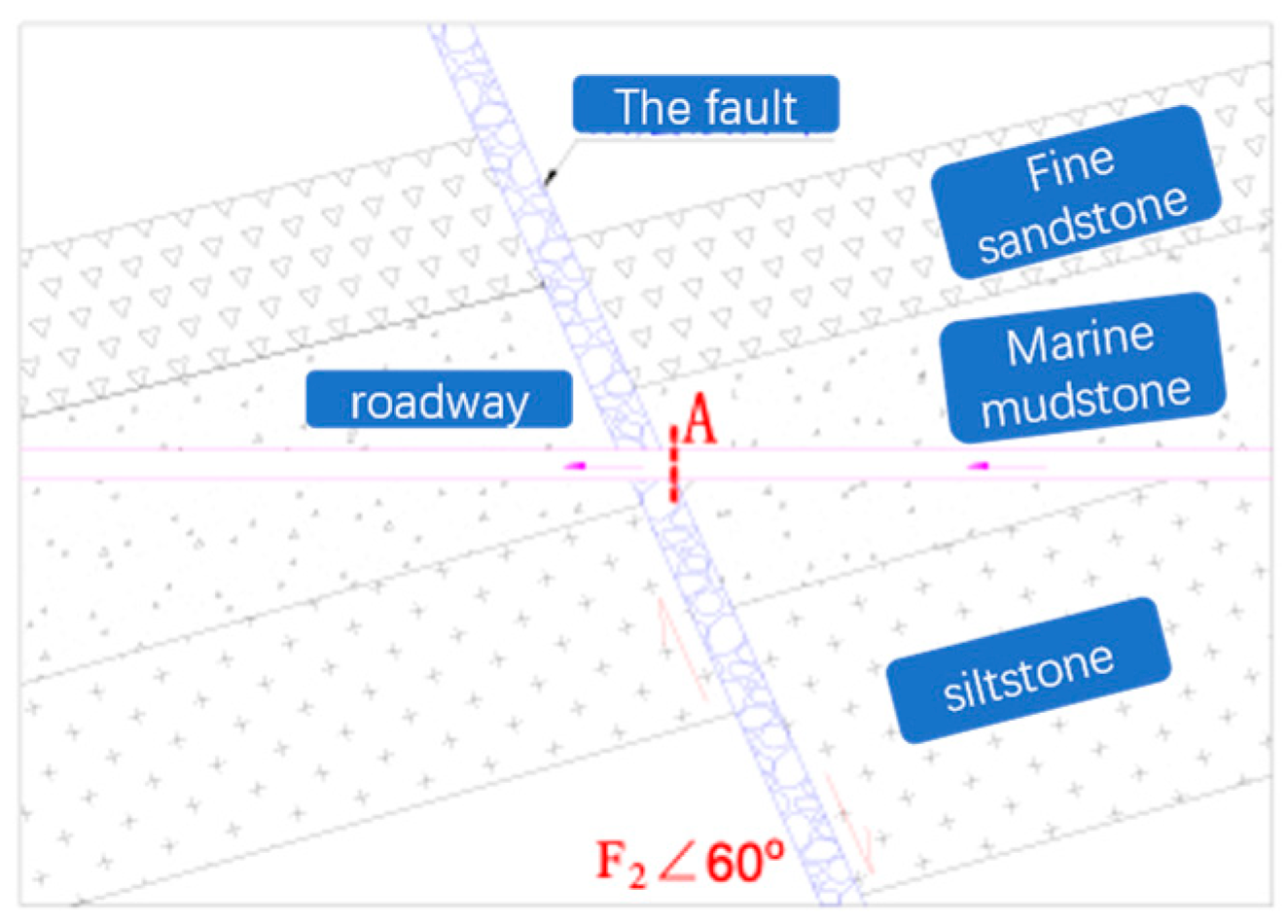
4.1. Overview of the Target Roadway and Characteristics of Surrounding Rock Deformation
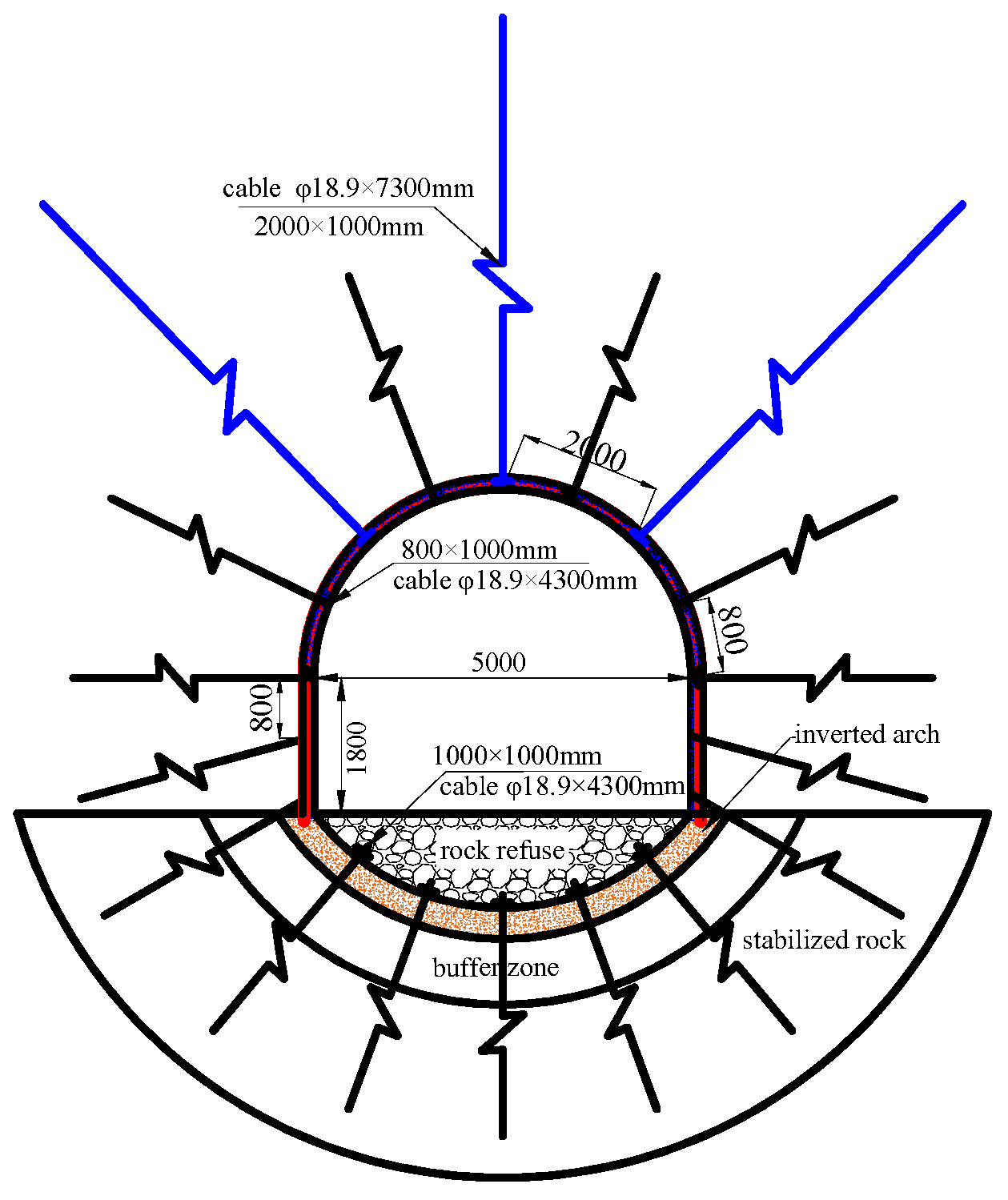
4.2. Control Mechanism and Technical Scheme for Controlling the Target Main Roadway
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kang, H.P. Sixty years development and prospects of rock bolting technology for underground coal mine roadways in China. J. China Univ. Min. Technol. 2016, 45, 1071–1081. [Google Scholar]
- Kang, H.P. Seventy years development and prospects of strata control technologies for coal mine roadways in China. Chin. J. Rock Mech. Eng. 2021, 40, 1–30. [Google Scholar]
- Kang, H.P. Development and prospects of support and reinforcement materials for coal mine roadways. Coal Sci. Technol. 2021, 49, 1–11. [Google Scholar]
- Li, W.; Zhang, C.; Tu, S.; Chen, W.; Ma, M. Face stability analysis of a shield roadway excavated along inclined strata. Undergr. Space 2023, 13, 183–204. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, T.; Du, Y.; Zhang, H.; Ran, J.; Li, W.; Zhang, S. Failure and stability analysis of deep soft rock roadways based on true triaxial geomechanical model tests. Eng. Fail. Anal. 2022, 137, 106255. [Google Scholar] [CrossRef]
- Tu, S.; Li, W.; Zhang, C.; Chen, W. Effect of inclined layered soils on face stability in shield roadwaying based on limit analysis. Tunn. Undergr. Space Technol. 2023, 131, 104773. [Google Scholar] [CrossRef]
- Wu, W.; Wang, T.; Bai, J.; Liu, J.; Wang, X.; Xu, H.; Feng, G. Failure characteristics and cooperative control strategies for gob-side entry driving near an advancing working face: A case study. Processes 2024, 12, 1398. [Google Scholar] [CrossRef]
- Li, W.T.; Wang, L.Y.; Zhang, C.A.; Yang, X.Z.; Mei, Y.C.; Shao, X.; Sun, B.J. Numerical investigation study on tensile-shear failure behavior of rock bolts in inclined strata mining roadways. Eng. Fail. Anal. 2024, 162, 108393. [Google Scholar] [CrossRef]
- Jiang, R.; Dai, F.; Liu, Y.; Li, A. Fast Marching Method for Micro-seismic Source Location in Cavern-Containing Rockmass: Performance Analysis and Engineering Application. Engineering 2021, 7, 1023–1034. [Google Scholar] [CrossRef]
- Li, A.; Liu, Y.; Dai, F.; Liu, K.; Wei, M. Continuum analysis of the structurally controlled displacements for large-scale underground caverns in bedded rock masses. Tunn. Undergr. Space Technol. 2020, 97, 103288. [Google Scholar] [CrossRef]
- Xu, S.; Liu, J.; Yang, X. Pseudo-dynamic analysis of a 3D roadway face in inclined weak strata. Undergr. Space 2023, 12, 156–166. [Google Scholar] [CrossRef]
- Li, W.T.; Yang, N.; Li, T.C.; Zhang, Y.H.; Wang, G. A new approach to simulate the supporting arch in a roadway based on improvement of the beam element in FLAC3D. J. Zhejiang Univ.-Sci. A (Appl. Phys. Eng.) 2018, 18, 179–193. [Google Scholar] [CrossRef]
- Wu, W.D.; Bai, J.B.; Feng, G.R.; Wang, X.Y. Investigation on the mechanism and control methods for roof collapse caused by cable bolt shear rupture. Eng. Fail. Anal. 2021, 130, 105724. [Google Scholar] [CrossRef]
- Meng, Q.B.; Xin, X.K.; Song, Z.M.; Cheng, Z.M.; Song, Y. Theoretical analysis and numerical simulation of energy absorption and control effect of bolt support. J. Cent. South Univ. (Sci. Technol.) 2024, 55, 3426–3440. [Google Scholar]
- Wu, Y.Z.; Kang, H.P. Failure mechanism study on tail of high strength bolt. J. China Coal Soc. 2013, 38, 1537–1541. [Google Scholar]
- Hao, D.; Wu, Y.; Chen, H.; Chu, X.; Li, Y. Instability mechanism and prevention technology of roadway in close distance and extra thick coal seam under goaf. J. China Coal Soc. 2019, 44, 2682–2690. [Google Scholar]
- Zhang, Y.; Su, G.; Li, Y.; Wei, M.; Liu, B. Displacement back-analysis of rock mass parameters for underground caverns using a novel intelligent optimization method. Int. J. Geomech. 2020, 20, 04020035. [Google Scholar] [CrossRef]
- Si, L.; Lou, J.; Yang, J.; Yuan, G. Deformation and stress characteristics of anchor bolt under axial impact. J. China Coal Soc. 2022, 47, 3645–3653. [Google Scholar]
- Si, L.P. Experimental study on mechanical properties of rock bolts under tension and shear loads. J. Min. Strat. Control. Eng. 2022, 4, 033038. [Google Scholar]
- Song, Y.B.; Yan, S.; Bai, J.B.; Hao, S.B.; Chen, Y. Implementation of shear broken failure of bolts in FLAC3D and its application. Chin. J. Rock Mech. Eng. 2017, 36, 1899–1909. [Google Scholar]
- Lou, J.; Lu, Z.; Dong, S.; Fu, Y.; Peng, X.; Li, J.; Yang, L. Dynamic response characteristics of rock bolt support system under low-energycyclic impact: Experimental study. J. Min. Strat. Control. Eng. 2024, 6, 053037. [Google Scholar]
- Tu, M.; Guo, F.; Zhang, X.; Wang, C. Axial force-breaking energy accumulation and dissipation evolution and energy absorption protection mechanism of anchor cable wire. J. China Coal Soc. 2024, 49, 3353–3365. [Google Scholar]
- Chen, S.; Feng, F.; Li, X.; Wang, C.; Li, D.; Rostami, J.; Zhu, Y. Research progress and key issues of laboratory test and numerical simulation for slabbing failure in hard rock under complex mining conditions. J. China Univ. Min. Technol. 2023, 52, 868–888. [Google Scholar]
- Yang, N.; Li, W.T.; Xuan, C.; Zhang, Y.; Li, D.; Li, T.; Wang, G. Improvement of breakable anchor bolt element in FLAC3D and its application in deep coal roadway. J. Min. Saf. Eng. 2017, 34, 251–258. [Google Scholar]
- Li, X.; Aziz, N.; Mirzaghorbanali, A.; Nemcik, J. Behavior of fiber glass bolts, rock bolts and cable bolts in shear. Rock Mech. Rock Eng. 2016, 49, 2723–2735. [Google Scholar] [CrossRef]








| The Name of the Function | Changeability | Purposes |
|---|---|---|
| sp_force(sp_pnt, 1, 2) | no | Monitoring unit shear force in the y-direction |
| sp_force(sp_pnt, 1, 3) | no | Monitoring unit shear force in the z-direction |
| sp_tfstr(sp_pnt) | yes | Element tensile failure strain assignment |
| sp_pmom(sp_pnt) | yes | Element plastic moment assignment |
| Elastic Modulus/GPa | Poisson’s Ratio | Rod Area /m2 | Moment of Inertia in the y-Direction/m4 | Moment of Inertia in the z-Direction/m4 | Polar Moment of Inertia /m4 | Pull Breakage Strain | Plastic Bending Moment /(N·m) |
|---|---|---|---|---|---|---|---|
| 200 | 0.3 | 6.16 × 10−4 | 3.02 × 10−8 | 3.02 × 10−8 | 6.03 × 10−8 | – | – |
| Anchor Solid | Circumference/mm | Tangential Cohesion /MPa | Tangential Internal Friction Angle/(°) | Tangential Stiffness /(N·m−2) | Normal Cohesion /MPa | Normal Internal Friction Angle/(°) | Normal Stiffness /(N·m−2) |
|---|---|---|---|---|---|---|---|
| Free section | 91 | 0 | 0 | 0 | 200 | 0 | 1.0 × 1010 |
| Anchoring section | 91 | 2.0 | 45 | 2.0 × 107 | 200 | 0 | 1.0 × 1010 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Zhang, W.; Bai, J.; Wang, H.; Zhang, Q. FLAC3D Modeling of Shear Failure and Fracture of Anchor Bolts in Surrounding Rock: A Study on Stress-Bearing Ring Reinforcement. Symmetry 2025, 17, 1885. https://doi.org/10.3390/sym17111885
Wang R, Zhang W, Bai J, Wang H, Zhang Q. FLAC3D Modeling of Shear Failure and Fracture of Anchor Bolts in Surrounding Rock: A Study on Stress-Bearing Ring Reinforcement. Symmetry. 2025; 17(11):1885. https://doi.org/10.3390/sym17111885
Chicago/Turabian StyleWang, Rui, Weiguang Zhang, Jianbiao Bai, Haosen Wang, and Qiang Zhang. 2025. "FLAC3D Modeling of Shear Failure and Fracture of Anchor Bolts in Surrounding Rock: A Study on Stress-Bearing Ring Reinforcement" Symmetry 17, no. 11: 1885. https://doi.org/10.3390/sym17111885
APA StyleWang, R., Zhang, W., Bai, J., Wang, H., & Zhang, Q. (2025). FLAC3D Modeling of Shear Failure and Fracture of Anchor Bolts in Surrounding Rock: A Study on Stress-Bearing Ring Reinforcement. Symmetry, 17(11), 1885. https://doi.org/10.3390/sym17111885







