Temporal Symmetry and Bifurcation in Mussel–Fish Farm Dynamics with Distributed Delays

Abstract

We develop and analyze a distributed-delay model for nutrient–fish–mussel dynamics in multitrophic aquaculture systems. Extending the classical discrete-delay framework, we incorporate gamma-distributed kernels to capture the time-distributed nature of nutrient assimilation, yielding a more realistic and analytically tractable representation. These kernels introduce a form of temporal symmetry in the system’s memory, where past nutrient levels influence present dynamics in a balanced and structured way. Using the linear chain trick, we reformulate the integro-differential equations into ordinary differential systems for both weak and strong memory scenarios. We derive conditions for local stability and Hopf bifurcation, and establish global stability using Lyapunov-based methods. Numerical simulations confirm that increased delay can destabilize the system, leading to oscillations, while stronger memory mitigates this effect and enhances resilience. Bifurcation diagrams, time series, and phase portraits illustrate how memory strength governs the system’s dynamic response. This work highlights how symmetry in memory structures contributes to system robustness, offering theoretical insights and practical implications for the design and management of ecologically stable aquaculture systems.

1. Introduction

The integration of mussel cultivation within fish farming systems has gained growing interest as a sustainable strategy to mitigate the environmental footprint of aquaculture [1]. Mussels act as natural biofilters, improving water quality by removing excess nutrients, particularly nitrogen and phosphorus, which are central to eutrophication and water degradation. This ecological service makes mussels key components in integrated multitrophic aquaculture (IMTA) systems. Mathematical models play a crucial role in understanding and optimizing the dynamics of such systems, providing quantitative insights into nutrient cycling, species interactions, and long-term stability.

Traditional approaches often incorporate discrete time delays to account for gestation, digestion, or nutrient assimilation lags in biological processes [2]. While such models have yielded valuable theoretical results, the assumption of a fixed delay may fail to capture the inherent variability and distribution of response times observed in real ecosystems. In addition to providing a more realistic treatment of time delays, distributed kernels, such as the gamma distribution, introduce a form of temporal symmetry into the feedback structure of dynamic models. Unlike fixed delays, where the system’s memory is concentrated at a single point in time, gamma-distributed delays assign weights to past states in a smooth and balanced manner centered around a mean value. This symmetric memory allocation ensures that both recent and more distant historical nutrient levels influence current fish growth in a harmonized way. Such temporal symmetry is not only biologically plausible, mirroring metabolic assimilation processes, but also enhances the analytical tractability and stability of dynamic systems. Importantly, perturbations in this symmetric structure, such as increasing the mean delay or modulating memory intensity, can induce symmetry-breaking bifurcations, including the emergence of sustained oscillations. These characteristics position symmetry as a central structural feature governing the dynamics of multitrophic aquaculture systems. In response to the limitations of fixed-delay formulations, distributed delay models have gained prominence as a more flexible and biologically realistic framework. By replacing discrete time lags with continuous memory kernels, these models incorporate a spectrum of past states into current system dynamics. For instance, ref. [3] investigated a chemostat model with distributed delay, revealing its influence on stability properties. The stabilizing potential of distributed feedback has also been examined in broader ecological systems: ref. [4] showed that distributed delays can stabilize nonlinear feedback loops, while ref. [5] analyzed their role in maintaining stability across large-scale ecosystems. In single-species models, ref. [6] demonstrated that distributed delay structures can induce Hopf bifurcations, leading to sustained oscillations.

In aquaculture systems, delays in nutrient processing are particularly relevant. Factors such as environmental variability, metabolic processes, and food web interactions introduce temporal heterogeneity in nutrient uptake and conversion. Ref. [7] examined such dynamics in a three-species model with distributed time delays, identifying conditions for instability. Similarly, ref. [8] modeled the carbon budget of mussel farms in the Mediterranean Sea, noting the temporal aspects of nutrient assimilation and CO₂ sequestration. Recent work continues to advance this modeling paradigm. For example, ref. [9] derived discrete population models with embedded distributed delay structures. Other researchers have studied spatial and structural extensions of mussel-fish models, such as nutrient dynamics in multitrophic systems, trophic food web feedback [10], and population dispersion with delay in patch models [11]. Theoretical studies also reinforce the importance of delay-driven dynamics, including bifurcation theory [12], synchronization in ecological networks [13], and global stability analysis of delayed logistic equations [14].

Beyond delay-driven dynamics, several recent studies have introduced more general modeling frameworks for ecological interactions, including fractional-order systems, behaviorally driven responses, and bioenergetic coupling. For instance, fractional derivatives have been successfully employed in eco-epidemiological models to capture long-memory effects in predator–prey systems, as demonstrated by Domínguez-Alemán et al. [15], where the authors analyze a fractional predator–prey model with disease in the prey population and explore the resulting complex stability landscapes. In a related context, Khalid et al. [16] formulated a fractional-order model for cholera dynamics, demonstrating how memory-dependent transmission processes influence oscillatory behavior and improve the predictive accuracy of epidemic modeling frameworks. Similarly, fear-based functional responses, representing behavioral adaptations of prey under predation risk, have been shown to significantly alter bifurcation patterns and system persistence. Yaseen et al. [17] proposed an asymmetric predator–prey model incorporating both fear effects and prey refuge, revealing rich dynamical behavior sensitive to ecological parameters. These modeling advances underscore the increasing importance of incorporating behavioral memory and adaptive feedback mechanisms into multitrophic systems, where interactions are highly non-linear and environmentally driven. Moreover, recent ecosystem modeling studies have embraced stoichiometric constraints and spatial heterogeneity to more accurately represent nutrient flow and trophic interactions. Hagstrom et al. [18] examined how dynamic phytoplankton stoichiometry influences global primary production and nutrient cycling, offering insights into biogeochemical feedback that are particularly relevant for plankton-based aquaculture systems. From a spatial and applied perspective, Holbach et al. [19] developed a spatially explicit model to evaluate the nutrient mitigation potential of blue mussel farms in the western Baltic Sea, capturing the interaction between hydrodynamic transport, particulate nutrient dispersion, and mussel biofiltration. Their work illustrates how mussel farms can function as ecological infrastructure to alleviate eutrophication near fish farming zones, offering practical insights into the integration of spatial processes in IMTA planning. These frameworks, though structurally diverse, complement the distributed-delay approach by capturing additional dimensions of ecological realism, be it memory, behavior, stoichiometry, or space, essential for understanding resilience, bifurcations, and stability in multitrophic aquaculture systems.

Building on these foundations, the present paper extends the fish–mussel–nutrient model originally proposed by [20], which incorporated a fixed delay in fish nutrient assimilation. We generalize this framework by introducing a distributed delay modeled via gamma kernels, allowing more realistic and tunable memory effects. This structure captures the physiological and ecological processes of nutrient assimilation in fish more accurately, while retaining analytical tractability. Our objectives are threefold: (i) reformulate the original delay model using the linear chain trick to obtain equivalent ODE systems for weak and strong memory kernels; (ii) analyze the local and global stability of equilibria and identify conditions for Hopf bifurcation; (iii) validate the model via numerical simulations, highlighting the role of memory and temporal symmetry in shaping system dynamics. Accordingly, we aim to provide a robust mathematical framework that enhances both the theoretical understanding and practical management of IMTA systems under delayed nutrient feedback.

The rest of the paper is organized as follows. In Section 2, we present the mathematical model with distributed delay and define the gamma kernel structure. Section 3 reformulates the model using the linear chain trick to derive equivalent systems of ordinary differential equations for both weak and strong memory kernels. Section 4 conducts local stability and Hopf bifurcation analysis based on the resulting characteristic polynomials. In Section 5, we establish global asymptotic stability of the positive equilibrium using a Lyapunov-type function. Section 6 provides numerical simulations illustrating how delay and memory shape system dynamics. Finally, Section 7 summarizes our findings and outlines directions for future research.

2. The Model Formulation with Distributed Delay

We consider an extension of the nutrient-fish-mussel interaction model originally proposed by [20], where a discrete time delay was used to model the lag in nutrient assimilation by fish. While discrete delays can capture key gestational or metabolic lags, they may fail to adequately represent the continuous nature of temporal effects inherent in biological processes. To address this limitation, we formulate a system with a distributed delay, providing a more realistic and analytically tractable framework. The dynamic variables in the model are defined as follows: $x\left(t\right)$ represents the nutrient concentration, $y\left(t\right)$ denotes the fish biomass, and $z\left(t\right)$ corresponds to the mussel biomass. The governing system of integro-differential equations reads

$$\left\{\begin{array}{c}\dot{x}\left(t\right)=\varphi -[\mu +\alpha y\left(t\right)+\zeta z\left(t\right)]x\left(t\right),\hfill \\ \dot{y}\left(t\right)=-\left[{\displaystyle \delta +\gamma y\left(t\right)-\beta {\int }_0^{\infty }x(t-s)g\left(s\right)ds}\right]y\left(t\right),\hfill \\ \dot{z}\left(t\right)=-[\rho -\eta x\left(t\right)]z\left(t\right),\hfill \end{array}\right.$$

(1)

where the parameters are defined as follows: $\varphi$ is the external nutrient input rate; $\mu$ is the nutrient loss rate due to sedimentation or outflow; $\alpha$ and $\zeta$ are the nutrient uptake rates by fish and mussels, respectively; $\delta$ is the fish mortality rate; $\gamma$ represents intra-specific competition among fish; $\beta$ is the conversion rate of nutrients into fish biomass; $\rho$ is the mussel mortality rate; $\eta$ is the nutrient assimilation efficiency in mussels; and g is the kernel function modeling the distributed delay. To represent the delay distribution, we adopt the gamma distribution

$$g\left(s\right)={\displaystyle \frac{m^m}{T^m\mathsf{\Gamma }\left(m\right)}}{s}^{m-1}{e}^{-{\displaystyle \frac{m}{T}}s},s\ge 0,$$

(2)

where $T>0$ denotes the mean delay time, $m\in \mathbb{N}$ is the shape parameter that determines memory strength, and $\mathsf{\Gamma }\left(m\right)$ is the gamma function ensuring normalization. The value of m allows control over the memory structure: when $m=1$, the kernel becomes exponential, indicating weak memory, whereas for $m>1$, the kernel emphasizes intermediate time lags, corresponding to stronger memory effects. The gamma kernel’s functional form introduces a form of temporal symmetry centered around the mean delay T, with the shape parameter m controlling the distribution’s spread and peak location. This symmetry implies that the system’s response to nutrient input is not biased toward either immediate or distant past states, but rather reflects a balanced integration of historical influences. Such a structure mirrors biological processes like digestion and nutrient assimilation, which naturally exhibit symmetric temporal dynamics around peak efficiency. Consequently, the model captures not only the effects of time delay but also how symmetric memory structures shape system stability and dynamic transitions, including the emergence of oscillations. The model (1) represents the interplay among nutrient availability, fish growth, and mussel biofiltration, capturing essential feedback mechanisms in multitrophic aquaculture systems.

• Nutrient dynamics $x\left(t\right)$: Nutrients are supplied externally at a constant rate $\varphi$ and removed through three routes: natural loss $\mu$, consumption by fish $\alpha y$, and filtration by mussels $\zeta z$. This mechanism ensures a dynamic balance between nutrient input and its biotic removal through consumption and filtration.
• Fish biomass $y\left(t\right)$: Fish grow by assimilating nutrients, but the growth is modulated by mortality $\delta$, competition $\gamma y$, and a delayed nutrient feedback. The integral term models the memory effect, acknowledging that nutrient conversion into biomass occurs over a time-distributed window rather than instantaneously.
• Mussel biomass $z\left(t\right)$: Mussels reduce nutrient concentration through filtration, growing in response to current nutrient levels with efficiency $\eta$, and dying at rate $\rho$. They serve as a stabilizing species, reducing eutrophication and regulating nutrient levels.
• Delay kernel $g\left(s\right)$: Biologically, the kernel encapsulates the digestion, assimilation, and metabolic conversion delays in fish. The use of a gamma kernel captures the continuous influence of past nutrient levels, with adjustable memory strength via the shape parameter m. Moreover, by tuning m, one can control the symmetry and sharpness of the memory window, thereby influencing whether the system dynamics remain stable or undergo oscillatory transitions.

This formulation advances existing aquaculture models by embedding a realistic memory structure that reflects physiological and ecological delays. It explicitly emphasizes the role of symmetric temporal feedback in maintaining ecological balance and preventing extreme nutrient fluctuations. It also lays the foundation for analyzing how temporal feedback mechanisms impact population stability, oscillatory behavior, and system resilience.

3. Model Reformulation via the Linear Chain Trick

To facilitate analytical treatment of the distributed delay system (1), we apply the linear chain trick [21], a classical yet versatile transformation method that converts integro-differential systems with distributed delays into equivalent sets of ordinary differential equations (ODEs). This reformulation retains the biological realism of distributed memory while making the system more amenable to rigorous mathematical analysis and numerical exploration. Specifically, by unfolding the delay kernel into auxiliary variables, the linear chain trick establishes a sequence of intermediate compartments that symmetrically transmit information from past to present, thereby preserving the structure of the temporal memory. This chain representation reveals how memory symmetry translates into system stability. This allows us to preserve the influence of the distributed memory while enabling local and global stability analyses using conventional ODE tools.

3.1. Case $m=1$ (Weak Memory Kernel)

For $m=1$, the gamma kernel (2) simplifies to the exponential distribution

$$g\left(s\right)={\displaystyle \frac{1}{T}}{e}^{-s/T},$$

which characterizes a system with weak, exponentially fading memory. To reformulate the integro-differential model into an ordinary differential equation (ODE) system, we introduce an auxiliary function

$$u\left(t\right)={\int }_0^{\infty }x(t-s)·{\displaystyle \frac{1}{T}}{e}^{-s/T}ds.$$

Here, $u\left(t\right)$ acts as a memory variable that represents the exponentially weighted history of nutrient availability, capturing the gradual effect of past nutrient concentrations on current fish growth through delayed assimilation. In this context, the variable $u\left(t\right)$ can be interpreted as a memory mediator, a smoothed, temporally symmetric record of past nutrient conditions that shapes the present growth rate of fish. The exponential kernel ensures that the most recent past exerts the strongest influence, while more distant past events contribute progressively less, preserving a decaying symmetry in time. Substituting this reformulation into system (1), we obtain the following system of first-order ODEs

$$\left\{\begin{array}{c}\dot{x}=\varphi -(\mu +\alpha y+\zeta z)x,\hfill \\ \dot{y}=-(\delta +\gamma y-\beta u)y,\hfill \\ {\displaystyle \dot{u}=\frac{1}{T}(x-u),}\hfill \\ \dot{z}=-(\rho -\eta x)z.\hfill \end{array}\right.$$

(3)

This reduced-order representation highlights the equivalence between an exponentially distributed delay and a first-order memory process. It preserves the temporal symmetry inherent in the gamma kernel (for $m=1$) and provides a tractable framework for investigating how increasing delay T affects stability boundaries and oscillatory dynamics.

3.2. Case $m=2$ (Strong Memory Kernel)

For $m=2$, the gamma kernel emphasizes intermediate past states and takes the following form

$$g\left(s\right)={\left({\displaystyle \frac{2}{T}}\right)}^{2}s{e}^{-2s/T}.$$

To convert the integro-differential model into a system of ordinary differential equations, we introduce the two following auxiliary functions

$$w\left(t\right)={\int }_0^{\infty }x(t-s)·{\displaystyle \frac{2}{T}}{e}^{-2s/T}ds,v\left(t\right)={\int }_0^{\infty }x(t-s)·{\left({\displaystyle \frac{2}{T}}\right)}^{2}s{e}^{-2s/T}ds.$$

Here, $w\left(t\right)$ captures the exponentially weighted recent history of nutrient availability, while $v\left(t\right)$ aggregates this memory to reflect the delayed effect on fish biomass growth. Together, $w\left(t\right)$ and $v\left(t\right)$ form a two-layer symmetric memory chain, in which the past nutrient states influence the present through progressively smoothed stages. This layered structure mirrors biological processes involving digestion or metabolic conversion, where intermediate states buffer and stabilize the response to temporal fluctuations. These variables form a two-stage linear chain that structurally represents nutrient assimilation with stronger memory. Substituting this into the original system (1), we obtain the following five-dimensional ODEs system

$$\left\{\begin{array}{c}\dot{x}=\varphi -(\mu +\alpha y+\zeta z)x,\hfill \\ \dot{y}=-(\delta +\gamma y-\beta v)y,\hfill \\ {\displaystyle \dot{v}=\frac{2}{T}(w-v),}\hfill \\ {\displaystyle \dot{w}=\frac{2}{T}(x-w),}\hfill \\ \dot{z}=-(\rho -\eta x)z.\hfill \end{array}\right.$$

(4)

The reformulations (3) and (4) preserve the qualitative dynamics of the original distributed-delay system while offering key advantages. First, they replace the convolution integral with a finite-dimensional symmetric memory structure, eliminating the need to handle integro-differential terms and ensuring analytical transparency. Second, they enable the use of classical tools such as the Routh–Hurwitz criterion and facilitate Hopf bifurcation and transversality analyses within a tractable ODE framework. They also support efficient numerical simulations using standard ODE solvers. Importantly, this reformulation allows for explicit tracking of how information propagates through temporal memory layers, a feature lost in integral formulations, and enables a symmetry-based interpretation: the transition from weak to strong memory corresponds to greater temporal smoothing, which enhances resilience by symmetrically distributing the influence of past nutrient states. These advantages make the reformulations essential for the stability and bifurcation analyses developed in the following sections, offering a robust yet tractable modeling approach to capture distributed memory effects.

4. Local Stability and Hopf Bifurcation Analysis

In this section, we analyze the local stability of the equilibrium point of systems (3) and (4), corresponding to the weak ($m=1$) and strong ($m=2$) memory kernels, respectively. We investigate the conditions under which the systems exhibit Hopf bifurcation as the mean delay parameter T varies. Beyond standard stability conditions, we also interpret the onset of oscillations through the lens of temporal symmetry breaking, where increasing delay gradually disrupts the balanced influence of past nutrient states on current growth, leading to sustained periodic behavior.

4.1. Case $m=1$ (Weak Memory Kernel)

Let $S^{\ast }=(x^{\ast },y^{\ast },u^{\ast },z^{\ast })$ denote the positive equilibrium point of system (3). Following [20], the equilibrium components satisfy

$$x^{\ast }={\displaystyle \frac{\rho }{\eta }},y^{\ast }={\displaystyle \frac{1}{\gamma }}(\beta x^{\ast }-\delta ),z^{\ast }={\displaystyle \frac{1}{\zeta }}\left({\displaystyle \frac{\varphi }{x^{\ast }}}-\mu -\alpha y^{\ast }\right).$$

To examine the local stability of $S^{\ast }$, we linearize system (3) around the equilibrium and shift the coordinates to the origin. The corresponding characteristic equation is a quartic polynomial of the form

$${\lambda }^4+a_1\left(T\right){\lambda }^3+a_2\left(T\right){\lambda }^2+a_3\left(T\right)\lambda +a_4\left(T\right)=0,$$

(5)

where the coefficients depend on the mean delay T and are expressed as

$$\begin{array}{ccccc}\hfill a_1\left(T\right)& ={\displaystyle \frac{1}{T}}+\gamma y^{\ast }+\zeta z^{\ast },\hfill & \hspace{1em}& \hfill a_2\left(T\right)& ={\displaystyle \frac{\gamma y^{\ast }+\zeta z^{\ast }}{T}}+\zeta z^{\ast }(\gamma y^{\ast }+\eta x^{\ast }),\hfill \\ \hfill a_3\left(T\right)& ={\displaystyle \frac{\eta \zeta x^{\ast }{z}^{\ast }}{T}}+\eta \gamma \zeta x^{\ast }{y}^{\ast }{z}^{\ast },\hfill & \hspace{1em}& \hfill a_4\left(T\right)& ={\displaystyle \frac{\eta \gamma \zeta x^{\ast }{y}^{\ast }{z}^{\ast }}{T}}.\hfill \end{array}$$

All coefficients are positive for biologically admissible parameter values, ensuring that the system satisfies the basic Routh–Hurwitz conditions. According to the Routh–Hurwitz criterion, the equilibrium $S^{\ast }$ is locally asymptotically stable if and only if

$$\Psi \left(T\right)=a_1\left(T\right)a_2\left(T\right)a_3\left(T\right)-a_3^2\left(T\right)-a_1^2\left(T\right)a_4\left(T\right)>0.$$

(6)

The function $\Psi \left(T\right)$ thus defines a scalar stability index depending on the delay T. The loss of stability occurs when $\Psi \left(T\right)$ changes sign, signaling the possible emergence of oscillatory dynamics. A Hopf bifurcation arises when the characteristic polynomial (5) possesses a pair of purely imaginary roots ${\lambda }_{1,2}=\pm i{\omega }_{\ast }$ and the real parts of these roots vary smoothly with respect to T. The critical delay $T=T^{\ast }$ satisfies the boundary condition

$$\Psi \left(T^{\ast }\right)=0,$$

(7)

that is,

$$a_1\left(T^{\ast }\right)a_2\left(T^{\ast }\right)a_3\left(T^{\ast }\right)-a_3^2\left(T^{\ast }\right)-a_1^2\left(T^{\ast }\right)a_4\left(T^{\ast }\right)=0.$$

At this critical value $T^{\ast }$, the quartic polynomial can be factorized as

$$\left[{\lambda }^2+{\displaystyle \frac{a_3\left(T^{\ast }\right)}{a_1\left(T^{\ast }\right)}}\right]\left[{\lambda }^2+a_1\left(T^{\ast }\right)\lambda +{\displaystyle \frac{a_1\left(T^{\ast }\right)a_2\left(T^{\ast }\right)-a_3\left(T^{\ast }\right)}{a_1\left(T^{\ast }\right)}}\right]=0,$$

which yields the eigenvalues

$$\begin{array}{cc}\hfill {\lambda }_{1,2}& =\pm i{\omega }_{\ast },{\omega }_{\ast }=\sqrt{{\displaystyle \frac{a_3\left(T^{\ast }\right)}{a_1\left(T^{\ast }\right)}}},\hfill \\ \hfill {\lambda }_{3,4}& ={\displaystyle \frac{-a_1^2\left(T^{\ast }\right)\pm \sqrt{a_1^4\left(T^{\ast }\right)-4a_1\left(T^{\ast }\right)[a_1\left(T^{\ast }\right)a_2\left(T^{\ast }\right)-a_3\left(T^{\ast }\right)]}}{2a_1\left(T^{\ast }\right)}}.\hfill \end{array}$$

Clearly, ${\lambda }_{1,2}$ are purely imaginary while ${\lambda }_{3,4}$ are real with

$${\lambda }_3+{\lambda }_4=-a_1\left(T^{\ast }\right)<0,{\lambda }_3{\lambda }_4={\displaystyle \frac{a_1\left(T^{\ast }\right)a_2\left(T^{\ast }\right)-a_3\left(T^{\ast }\right)}{a_1\left(T^{\ast }\right)}}>0.$$

Hence, only one pair of eigenvalues crosses the imaginary axis at $T=T^{\ast }$, indicating a possible Hopf bifurcation. To confirm the occurrence of a Hopf bifurcation, we verify the transversality condition by differentiating (5) with respect to T. This yields

$$\left[4{\lambda }^3+3a_1\left(T\right){\lambda }^2+2a_2\left(T\right)\lambda +a_3\left(T\right)\right]{\displaystyle \frac{d\lambda }{dT}}=-\left[a_1^{\prime }\left(T\right){\lambda }^3+a_2^{\prime }\left(T\right){\lambda }^2+a_3^{\prime }\left(T\right)\lambda +a_4^{\prime }\left(T\right)\right],$$

and therefore,

$${\displaystyle \frac{d\lambda }{dT}}=-{\displaystyle \frac{a_1^{\prime }\left(T\right){\lambda }^3+a_2^{\prime }\left(T\right){\lambda }^2+a_3^{\prime }\left(T\right)\lambda +a_4^{\prime }\left(T\right)}{4{\lambda }^3+3a_1\left(T\right){\lambda }^2+2a_2\left(T\right)\lambda +a_3\left(T\right)}},$$

where

$$a_1^{\prime }\left(T\right)=-{\displaystyle \frac{1}{T^2}},a_2^{\prime }\left(T\right)=-{\displaystyle \frac{\gamma y^{\ast }+\zeta z^{\ast }}{T^2}},a_3^{\prime }\left(T\right)=-{\displaystyle \frac{\eta \zeta x^{\ast }{z}^{\ast }}{T^2}},a_4^{\prime }\left(T\right)=-{\displaystyle \frac{\eta \gamma \zeta x^{\ast }{y}^{\ast }{z}^{\ast }}{T^2}}.$$

Evaluating at $\lambda =i{\omega }_{\ast }$, we obtain

$$\mathrm{Re}{\left({\displaystyle \frac{d\lambda }{dT}}\right)}_{\lambda =i{\omega }_{\ast }}=-{\displaystyle \frac{a_1\left(T^{\ast }\right){\Psi }^{\prime }\left(T^{\ast }\right)}{2\left[a_1^2\left(T^{\ast }\right)a_3\left(T^{\ast }\right)+{\omega }_{\ast }^2{\left(a_1\left(T^{\ast }\right)a_2\left(T^{\ast }\right)-2a_3\left(T^{\ast }\right)\right)}^2\right]}},$$

where

$$\begin{array}{c}{\Psi }^{\prime }\left(T^{\ast }\right)=a_1^{\prime }\left(T^{\ast }\right)a_2\left(T^{\ast }\right)a_3\left(T^{\ast }\right)+a_1\left(T^{\ast }\right)a_2^{\prime }\left(T^{\ast }\right)a_3\left(T^{\ast }\right)+a_1\left(T^{\ast }\right)a_2\left(T^{\ast }\right)a_3^{\prime }\left(T^{\ast }\right)\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-2a_3\left(T^{\ast }\right)a_3^{\prime }\left(T^{\ast }\right)-2a_1\left(T^{\ast }\right)a_1^{\prime }\left(T^{\ast }\right)a_4\left(T^{\ast }\right)-a_1^2\left(T^{\ast }\right)a_4^{\prime }\left(T^{\ast }\right).\end{array}$$

The sign of the real part of $\frac{d\lambda }{dT}$ at $\lambda =i{\omega }_{\ast }$ is governed by $-{\Psi }^{\prime }\left(T^{\ast }\right)$. In particular,

$$sign\left[Re{\left(\frac{d\lambda }{dT}\right)}_{\lambda =i{\omega }_{\ast }}\right]=sign\left[-{\Psi }^{\prime }\left(T^{\ast }\right)\right].$$

Therefore, if ${\Psi }^{\prime }\left(T^{\ast }\right)<0$, the eigenvalues cross the imaginary axis from left to right as T increases, indicating a supercritical Hopf bifurcation.

Theorem 1.

Let $S^{\ast }$ be a locally asymptotically stable equilibrium of system (3) for $T<T^{\ast }$. If there exists a critical delay $T=T^{\ast }$ such that $\Psi \left(T^{\ast }\right)=0$ and ${\Psi }^{\prime }\left(T^{\ast }\right)<0$, then $S^{\ast }$ undergoes a Hopf bifurcation as T passes through $T^{\ast }$. Consequently, a family of periodic solutions bifurcates from $S^{\ast }$. In particular, if ${\Psi }^{\prime }\left(T^{\ast }\right)<0$, the bifurcation is supercritical and the emerging periodic orbits are stable; if ${\Psi }^{\prime }\left(T^{\ast }\right)>0$, the bifurcation is subcritical and unstable periodic orbits may arise.

From a dynamical perspective, this bifurcation represents a transition from a balanced to an asymmetric temporal influence of past nutrient states. When $T<T^{\ast }$, recent and older nutrient concentrations jointly regulate growth in a stable, symmetric fashion, yielding equilibrium. When $T>T^{\ast }$, the delayed feedback becomes dominant, breaking temporal symmetry and inducing sustained oscillatory cycles in nutrient–fish–mussel dynamics.

4.2. Case $m=2$

For the strong memory kernel case, the linearized characteristic polynomial around equilibrium $S^{\ast }=(x^{\ast },y^{\ast },v^{\ast },w^{\ast },z^{\ast })$ reads

$${\lambda }^5+b_1\left(T\right){\lambda }^4+b_2\left(T\right){\lambda }^3+b_3\left(T\right){\lambda }^2+b_4\left(T\right)\lambda +b_5\left(T\right)=0,$$

(8)

with coefficients

$$\begin{array}{cc}\hfill b_1\left(T\right)& ={\displaystyle \frac{4}{T}}+\mu +(\alpha +\gamma )y^{\ast }+\zeta z^{\ast },\hfill \\ \hfill b_2\left(T\right)& =-{\displaystyle \frac{4}{T^2}}+{\displaystyle \frac{4}{T}}(\mu +\alpha y^{\ast }+\zeta z^{\ast })+\gamma y^{\ast }(\mu +\alpha y^{\ast }+\zeta z^{\ast })+\eta \zeta x^{\ast }{z}^{\ast },\hfill \\ \hfill b_3\left(T\right)& =-{\displaystyle \frac{4}{T^2}}[\mu +(\alpha -\gamma )y^{\ast }+\zeta z^{\ast }]+{\displaystyle \frac{4}{T}}\eta \zeta x^{\ast }{z}^{\ast }+\eta \gamma \zeta x^{\ast }{y}^{\ast }{z}^{\ast },\hfill \\ \hfill b_4\left(T\right)& ={\displaystyle \frac{4y^{\ast }}{T^2}}[\gamma (\mu +\alpha y^{\ast }+\zeta z^{\ast })-\eta \zeta x^{\ast }{z}^{\ast }],\hfill \\ \hfill b_5\left(T\right)& =-{\displaystyle \frac{4\eta \gamma \zeta x^{\ast }{y}^{\ast }{z}^{\ast }}{T^2}}.\hfill \end{array}$$

Note that each coefficient $b_j\left(T\right)$ depends on both the delay parameter T and the equilibrium components $(x^{\ast },y^{\ast },z^{\ast })$. Biologically, the terms involving $\zeta$, $\eta$, and $\gamma$ reflect interactions between fish and mussels, while $\mu$, $\alpha$, and T encode mortality, assimilation, and delay effects respectively. This dependence reveals how increasing memory depth (i.e., larger T) alters the internal feedback structure of the system. An application of the Routh–Hurwitz criterion to the polynomial (8) shows that the equilibrium $S^{\ast }$ of system (4) is locally asymptotically stable if $b_j\left(T\right)>0$ for $j=1,2,3,4,5$

$$b_1\left(T\right)b_2\left(T\right)b_3\left(T\right)-b_3^2\left(T\right)-b_1^2\left(T\right)b_4\left(T\right)>0,$$

and

$$\begin{array}{c}\Phi \left(T\right)=\left[b_1\left(T\right)b_4\left(T\right)-b_5\left(T\right)\right]\left[b_1\left(T\right)b_2\left(T\right)b_3\left(T\right)-b_3^2\left(T\right)-b_1^2\left(T\right)b_4\left(T\right)\right]\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} -b_5\left(T\right){\left[b_1\left(T\right)b_2\left(T\right)-b_3\left(T\right)\right]}^2-b_1\left(T\right)b_5^2\left(T\right)>0.\end{array}$$

The characteristic polynomial (8) may have five real roots, three real roots and one complex-conjugate pair, or one real root and two complex-conjugate pairs. Let ${\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4,{\lambda }_5$ denote the roots of (8). Then the following identities hold

$$\begin{array}{cc}\hfill {\lambda }_1+{\lambda }_2+{\lambda }_3+{\lambda }_4+{\lambda }_5& =-b_1\left(T\right),\sum _{1\le i<j\le 5}{\lambda }_i{\lambda }_j=b_2\left(T\right),\sum _{1\le i<j<k\le 5}{\lambda }_i{\lambda }_j{\lambda }_k=-b_3\left(T\right),\hfill \\ \hfill \sum _{1\le i<j<k<l\le 5}{\lambda }_i{\lambda }_j{\lambda }_k{\lambda }_l& =b_4\left(T\right),{\lambda }_1{\lambda }_2{\lambda }_3{\lambda }_4{\lambda }_5=-b_5\left(T\right).\hfill \end{array}$$

Suppose there exists $T=T^{\ast }$ such that $\Phi \left(T^{\ast }\right)=0$. Then, by the Routh–Hurwitz criterion, at least one root ${\lambda }_1$ of (8) has zero real part. This scenario corresponds to a critical delay value $T=T^{\ast }$ at which the real part of a complex conjugate pair of eigenvalues vanishes, marking the threshold between stability and oscillation. The system is thus poised for a Hopf bifurcation.

Assume ${\lambda }_1=i{\omega }_1$ for some ${\omega }_1\ne 0$, so ${\lambda }_2={\overline{\lambda }}_1$ is also a root. By continuity, ${\lambda }_1$ and ${\lambda }_2$ remain complex conjugates in an open neighborhood of $T^{\ast }$. The remaining roots are denoted ${\lambda }_3,{\lambda }_4,{\lambda }_5$, and two cases arise: All three are real, or one is real and the remaining two form another complex-conjugate pair. At $T=T^{\ast }$, the following identities apply

$$\begin{array}{cc}\hfill {\lambda }_3+{\lambda }_4+{\lambda }_5& =-b_1\left(T^{\ast }\right),{\omega }_1^2+{\lambda }_3{\lambda }_4+{\lambda }_3{\lambda }_5+{\lambda }_4{\lambda }_5=b_2\left(T^{\ast }\right),\hfill \\ \hfill {\omega }_1^2({\lambda }_3+{\lambda }_4+{\lambda }_5)+{\lambda }_3{\lambda }_4{\lambda }_5& =-b_3\left(T^{\ast }\right),\hfill \\ \hfill {\omega }_1^2({\lambda }_3{\lambda }_4+{\lambda }_3{\lambda }_5+{\lambda }_4{\lambda }_5)& =b_4\left(T^{\ast }\right),{\omega }_1^2{\lambda }_3{\lambda }_4{\lambda }_5=-b_5\left(T^{\ast }\right).\hfill \end{array}$$

Due to the general form of the roots, deriving an explicit formula for the transversality condition is analytically intractable. However, differentiating the characteristic Equation (8) with respect to T yields

$$\begin{array}{c}\left[5{\lambda }^4+4b_1\left(T\right){\lambda }^3+3b_2\left(T\right){\lambda }^2+2b_3\left(T\right)\lambda +b_4\left(T\right)\right]{\displaystyle \frac{d\lambda }{dT}}\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=-\left[b_1^{\prime }\left(T\right){\lambda }^4+b_2^{\prime }\left(T\right){\lambda }^3+b_3^{\prime }\left(T\right){\lambda }^2+b_4^{\prime }\left(T\right)\lambda +b_5^{\prime }\left(T\right)\right],\end{array}$$

and then

$${\displaystyle \frac{d\lambda }{dT}}=-{\displaystyle \frac{b_1^{\prime }\left(T\right){\lambda }^4+b_2^{\prime }\left(T\right){\lambda }^3+b_3^{\prime }\left(T\right){\lambda }^2+b_4^{\prime }\left(T\right)\lambda +b_5^{\prime }\left(T\right)}{5{\lambda }^4+4b_1\left(T\right){\lambda }^3+3b_2\left(T\right){\lambda }^2+2b_3\left(T\right)\lambda +b_4\left(T\right)}}.$$

The derivatives of the coefficients are

$$\begin{array}{cc}\hfill b_1^{\prime }\left(T\right)& =-{\displaystyle \frac{4}{T^2}},b_2^{\prime }\left(T\right)={\displaystyle \frac{8}{T^3}}-{\displaystyle \frac{4}{T^2}},\hfill \\ \hfill b_3^{\prime }\left(T\right)& ={\displaystyle \frac{8}{T^3}}\left[\mu +(\alpha -\gamma )y^{\ast }+\zeta z^{\ast }\right]-{\displaystyle \frac{4}{T^2}}\eta \zeta x^{\ast }{z}^{\ast },\hfill \\ \hfill b_4^{\prime }\left(T\right)& =-{\displaystyle \frac{8y^{\ast }}{T^3}}\left[\gamma (\mu +\alpha y^{\ast }+\zeta z^{\ast })-\eta \zeta x^{\ast }{z}^{\ast }\right],b_5^{\prime }\left(T\right)={\displaystyle \frac{8\eta \gamma \zeta x^{\ast }{y}^{\ast }{z}^{\ast }}{T^3}}.\hfill \end{array}$$

Letting $\lambda =i{\omega }^{\ast }$ be a simple purely imaginary root of the characteristic equation at $T=T^{\ast }$, we aim to compute

$$\mathrm{Re}{\left({\displaystyle \frac{d\lambda }{dT}}\right)}_{\lambda =i{\omega }^{\ast }}.$$

Although the calculation may be analytically involved, the sign of this derivative carries crucial dynamical information. A positive sign indicates that the eigenvalue crosses the imaginary axis from the left half-plane to the right as T increases, signaling a loss of stability and the potential onset of oscillatory behavior. Conversely, a negative sign implies a crossing from the right half-plane to the left, indicating that the system remains stable as the delay increases. Importantly, the transversality condition $\mathrm{Re}(d\lambda /dT)\ne 0$ ensures that the pair of imaginary eigenvalues crosses the imaginary axis with non-zero speed as T varies, thus confirming a nondegenerate Hopf bifurcation. This guarantees that the bifurcation is regular and not structurally unstable.

This leads us to the following result.

Theorem 2.

Let $S^{\ast }$ be a locally asymptotically stable equilibrium of system (4) for $T<T^{\ast }$, and suppose that the characteristic equation (8) has a simple pair of purely imaginary roots $\lambda =\pm i{\omega }^{\ast }$ at $T=T^{\ast }$, with ${\omega }^{\ast }>0$. If $\Phi \left(T^{\ast }\right)=0$ and

$$\mathrm{Re}{\left({\displaystyle \frac{d\lambda }{dT}}\right)}_{\lambda =i{\omega }^{\ast }}\ne 0,$$

then system (4) undergoes a Hopf bifurcation at $T=T^{\ast }$. In particular:

• If $\mathrm{Re}{\left(d\lambda /dT\right)}_{\lambda =i{\omega }^{\ast }}>0$, the equilibrium $S^{\ast }$ loses stability and a family of periodic solutions emerges (supercritical bifurcation);
• If $\mathrm{Re}{\left(d\lambda /dT\right)}_{\lambda =i{\omega }^{\ast }}<0$, the equilibrium regains stability (subcritical bifurcation).

The theorem confirms that under strong memory, the system undergoes a Hopf bifurcation as the delay parameter T increases, illustrating how memory effects can destabilize equilibrium and trigger sustained oscillations in species densities. Dynamically, this reflects a symmetry-breaking transition from steady-state to periodic behavior as delayed feedback disrupts time-invariant regulation. Biologically, the bifurcation arises when the mean assimilation delay T, representing the lag between nutrient input and fish growth, exceeds a critical value $T^{\ast }$. Below this threshold, the system stabilizes at a steady coexistence equilibrium. Beyond it, delay-induced oscillations emerge, potentially manifesting as cycles of overgrowth and resource depletion. This underscores the destabilizing role of long assimilation times and highlights the importance of keeping $T<T^{\ast }$ to ensure stable aquaculture dynamics. The result provides both theoretical insight and practical guidance for ecosystem resilience and management.

5. Global Stability Analysis

In this section, we investigate the global asymptotic stability of the positive equilibrium of the systems corresponding to both weak ($m=1$) and strong ($m=2$) memory kernels. Our analysis is based on constructing appropriate Lyapunov-type functions that capture the dissipative and symmetric feedback properties of the distributed delay.

5.1. Case $m=1$

Consider system (3) with equilibrium $S^{\ast }=(x^{\ast },y^{\ast },u^{\ast },z^{\ast })$. We define the Lyapunov function

$$V_1(x,y,u,z)=(x-x^{\ast }-x^{\ast }ln\frac{x}{x^{\ast }})+(y-y^{\ast }-y^{\ast }ln\frac{y}{y^{\ast }})+(z-z^{\ast }-z^{\ast }ln\frac{z}{z^{\ast }})+{\displaystyle \frac{T}{2}}{(u-u^{\ast })}^2.$$

Differentiating $V_1$ along the trajectories of system (3), we obtain

$${\dot{V}}_1=-(\mu +\alpha y+\zeta z){(x-x^{\ast })}^2-(\gamma y-\beta u){(y-y^{\ast })}^2-(\rho -\eta x){(z-z^{\ast })}^2-{\displaystyle \frac{1}{T}}{(u-x)}^2.$$

It follows that ${\dot{V}}_1\le 0$, and ${\dot{V}}_1=0$ if and only if $(x,y,u,z)=(x^{\ast },y^{\ast },u^{\ast },z^{\ast })$. Therefore, the equilibrium $S^{\ast }$ is globally asymptotically stable for system (3). The inclusion of the quadratic term ${(u-u^{\ast })}^2$ weighted by the delay T explicitly captures the dissipative character of the memory feedback. From a symmetry perspective, this term ensures that deviations in the memory variable decay symmetrically with respect to the mean delay, preventing bias toward past or present states. This structural balance reinforces global stability by maintaining time-symmetric damping around equilibrium.

Theorem 3.

Let $S^{\ast }=(x^{\ast },y^{\ast },u^{\ast },z^{\ast })$ be the unique positive equilibrium of system (3) with $m=1$. Assume that $\mu +\alpha y+\zeta z>0$, $\rho -\eta x>0$, and $\gamma y-\beta u>0$ for all biologically admissible states, i.e., for $(x,y,u,z)$ in the positive orthant. Then, $S^{\ast }$ is globally asymptotically stable.

Proof. 

The Lyapunov function $V_1$ is positive definite and radially unbounded, i.e., $V_1>0$ for all $(x,y,u,z)\ne S^{\ast }$ and $V_1\left(S^{\ast }\right)=0$. Its time derivative ${\dot{V}}_1$ along trajectories of (3) is nonpositive under the above parameter conditions, as each coefficient multiplying the quadratic deviations is strictly positive. Hence, ${\dot{V}}_1\le 0$ and ${\dot{V}}_1=0$ only at $S^{\ast }$. By LaSalle’s Invariance Principle, all trajectories converge asymptotically to $S^{\ast }$, establishing global asymptotic stability. □

5.2. Case $m=2$

For system (4), let $S^{\ast }=(x^{\ast },y^{\ast },v^{\ast },w^{\ast },z^{\ast })$ denote the positive equilibrium. We construct the Lyapunov function

$$\begin{array}{c}{V}_2(x,y,v,w,z)=(x-x^{\ast }-x^{\ast }ln{\displaystyle \frac{x}{x^{\ast }}})+(y-y^{\ast }-y^{\ast }ln{\displaystyle \frac{y}{y^{\ast }}})+(z-z^{\ast }-z^{\ast }ln{\displaystyle \frac{z}{z^{\ast }}})\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{T}{4}}\left[{(v-v^{\ast })}^2+{(w-w^{\ast })}^2\right].\end{array}$$

Taking the derivative of $V_2$ along the trajectories of system (4), we find

$$\begin{array}{c}{\dot{V}}_2=-(\mu +\alpha y+\zeta z){(x-x^{\ast })}^2-(\gamma y-\beta v){(y-y^{\ast })}^2-(\rho -\eta x){(z-z^{\ast })}^2\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{\displaystyle \frac{2}{T}}\left[{(v-w)}^2+{(w-x)}^2\right].\end{array}$$

Since each term on the right-hand side is nonpositive and vanishes only at the equilibrium point, it follows that $S^{\ast }$ is globally asymptotically stable for system (4). Biologically, the additional memory layer ($v,w$) acts as a symmetric two-stage buffer, distributing past influences more evenly and enhancing system resilience. This layered memory smooths transient deviations and ensures faster convergence to equilibrium. Theoretically, the Lyapunov function highlights how distributed delay functions as a symmetrizing operator: it converts destabilizing feedback into balanced dissipation, reinforcing the stabilizing role of structured memory in nutrient assimilation dynamics.

Theorem 4.

Let $S^{\ast }=(x^{\ast },y^{\ast },v^{\ast },w^{\ast },z^{\ast })$ be the unique positive equilibrium of system (4) with $m=2$. Assume that $\mu +\alpha y+\zeta z>0$, $\rho -\eta x>0$, and $\gamma y-\beta v>0$ for all positive solutions. Then, $S^{\ast }$ is globally asymptotically stable.

Proof. 

The Lyapunov function $V_2$ is continuous, positive definite, and radially unbounded. Differentiating $V_2$ along the trajectories of (4) yields ${\dot{V}}_2\le 0$ under the given parameter assumptions. Equality ${\dot{V}}_2=0$ holds only when $(x,y,v,w,z)=S^{\ast }$. Thus, by LaSalle’s Invariance Principle, every solution of system (4) converges asymptotically to $S^{\ast }$, implying global asymptotic stability. □

The above results hold under biologically consistent conditions ensuring that the effective grazing and nutrient consumption rates dominate over delayed feedback effects (i.e., $\gamma y>\beta u$ for $m=1$ and $\gamma y>\beta v$ for $m=2$). These inequalities guarantee that memory-driven nutrient uptake does not destabilize the system, maintaining global convergence in the biologically feasible region.

6. Numerical Investigations

To validate and further substantiate the theoretical results derived from the mathematical analysis, this section presents a comprehensive suite of numerical simulations aimed at elucidating the dynamic behavior of the nutrient–fish–mussel system under varying memory structures and delay regimes. These simulations serve to verify the analytical predictions concerning local and global stability, the onset of Hopf bifurcation, and the emergence of oscillatory patterns arising from the gamma-distributed delay framework. In particular, the numerical experiments investigate how the shape parameter m of the memory kernel, which governs memory strength, and the mean delay T jointly influence key system dynamics, including equilibrium convergence, the emergence of periodic orbits, and bifurcation boundaries. The simulations are conducted using the following biologically plausible baseline parameter set:

$$\varphi =2.0,\mu =0.3,\alpha =0.4,\zeta =0.2,\delta =0.2,$$

$$\gamma =0.5,\beta =0.6,\rho =0.3,\eta =0.4.$$

These numerical values are adapted from previously published ecological and aquaculture studies, including Bertolini et al. [8], Holbach et al. [19], and Gazi et al. [20]. While minor adjustments were made to ensure compatibility with the model structure, all values remain within ecologically realistic and meaningful ranges for integrated mussel–fish systems. Moreover, the selected parameters satisfy the theoretical conditions outlined in Theorems 3 and 4, namely $\varphi >x^{\ast }(\mu +\alpha y^{\ast }+\zeta z^{\ast })$ and $\beta x^{\ast }>\delta$. These inequalities guarantee the existence and global asymptotic stability of the positive equilibrium in both weak and strong memory regimes. Through numerical estimation, the critical delay values at which Hopf bifurcations occur are identified as $T_{m=1}^{\ast }\approx 2.78$ for the weak memory case ($m=1$) and $T_{m=2}^{\ast }\approx 4.85$ for the strong memory case ($m=2$). The corresponding equilibrium levels are $x^{\ast }=0.75$, $y^{\ast }=0.7$, and $z^{\ast }\approx 10.43$. These numerically derived thresholds are in full agreement with the analytical predictions presented in Section 4. Notably, the higher critical delay in the strong memory case reflects the system’s increased ability to tolerate delayed feedback without destabilizing, an outcome that reinforces the stabilizing influence of enhanced ecological memory. To bridge theory and ecological interpretation, we now present a sequence of targeted simulations under both memory scenarios. These results not only validate the predicted bifurcation thresholds but also illuminate the role of distributed memory in shaping system resilience. Each simulation is accompanied by detailed biological commentary to emphasize the implications of memory-driven dynamics in multitrophic aquaculture systems.

We begin with the weak memory case ($m=1$), which reflects ecosystems where the influence of past states is short-lived. This setting corresponds to biological processes driven by recent environmental signals, for example, rapid nutrient turnover, short-term predator responses, or low retention in sediment-nutrient cycling.

Figure 1 illustrates that for small delay values T, the system converges to a stable coexistence equilibrium. However, once T exceeds the critical Hopf threshold $T_{m=1}^{\ast }\approx 2.78$, the stability is lost, giving rise to self-sustained oscillations in all state variables. Biologically, this captures a scenario where delays in nutrient recycling or predation responses induce rhythmic cycles in biomass, a hallmark of destabilized multitrophic systems.

We now consider the strong memory case ($m=2$), where the system retains a longer history of past interactions, smoothing out temporal fluctuations.

Figure 2 demonstrates that even for relatively large delays, the system remains resilient, with smaller oscillation amplitudes and delayed onset of instability. The critical delay shifts to $T_{m=2}^{\ast }\approx 4.85$, confirming that stronger memory improves the system’s buffering capacity. This reflects ecological situations where long-term environmental integration (e.g., benthic-pelagic coupling or sediment-nutrient recycling) stabilizes food web dynamics.

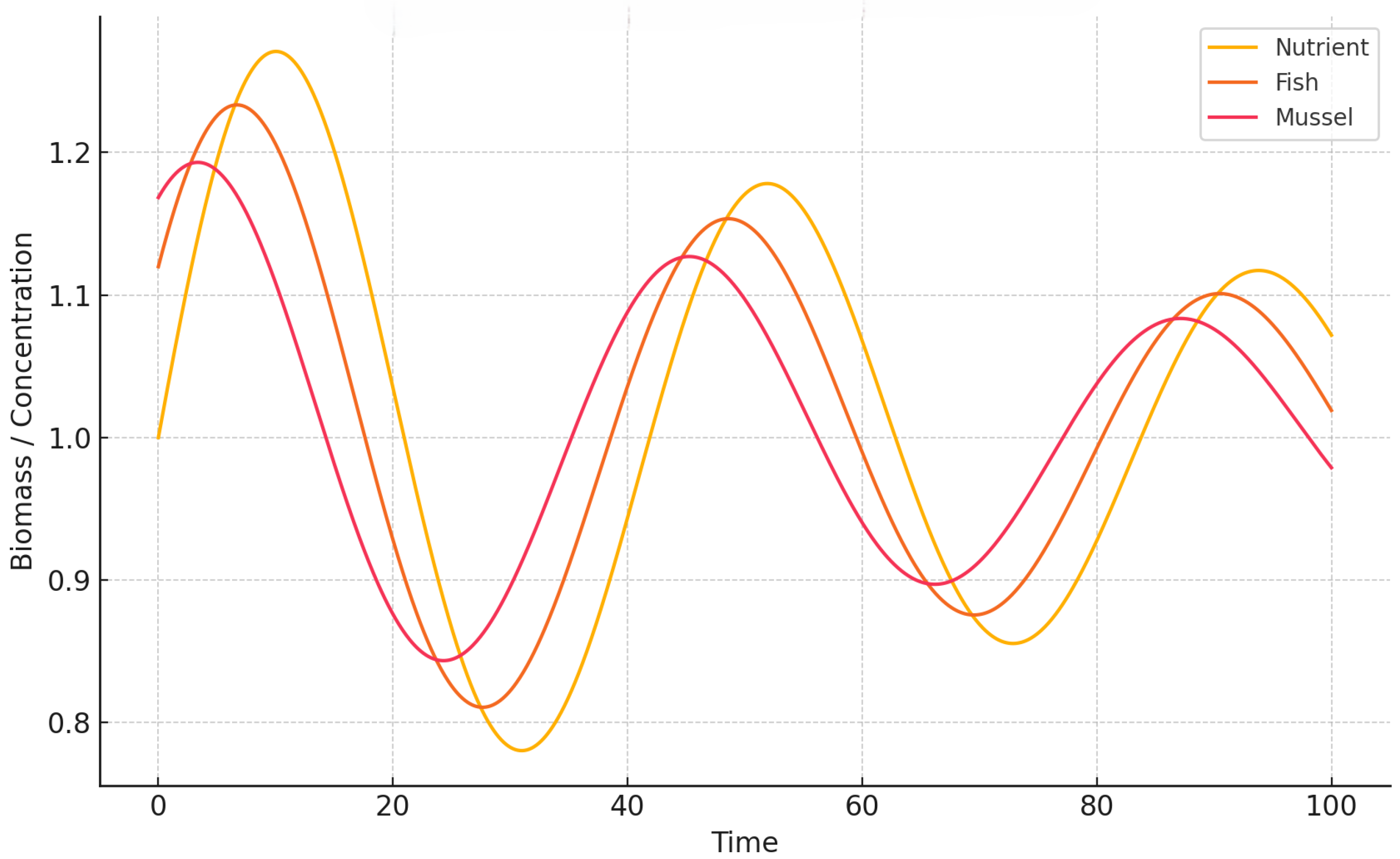
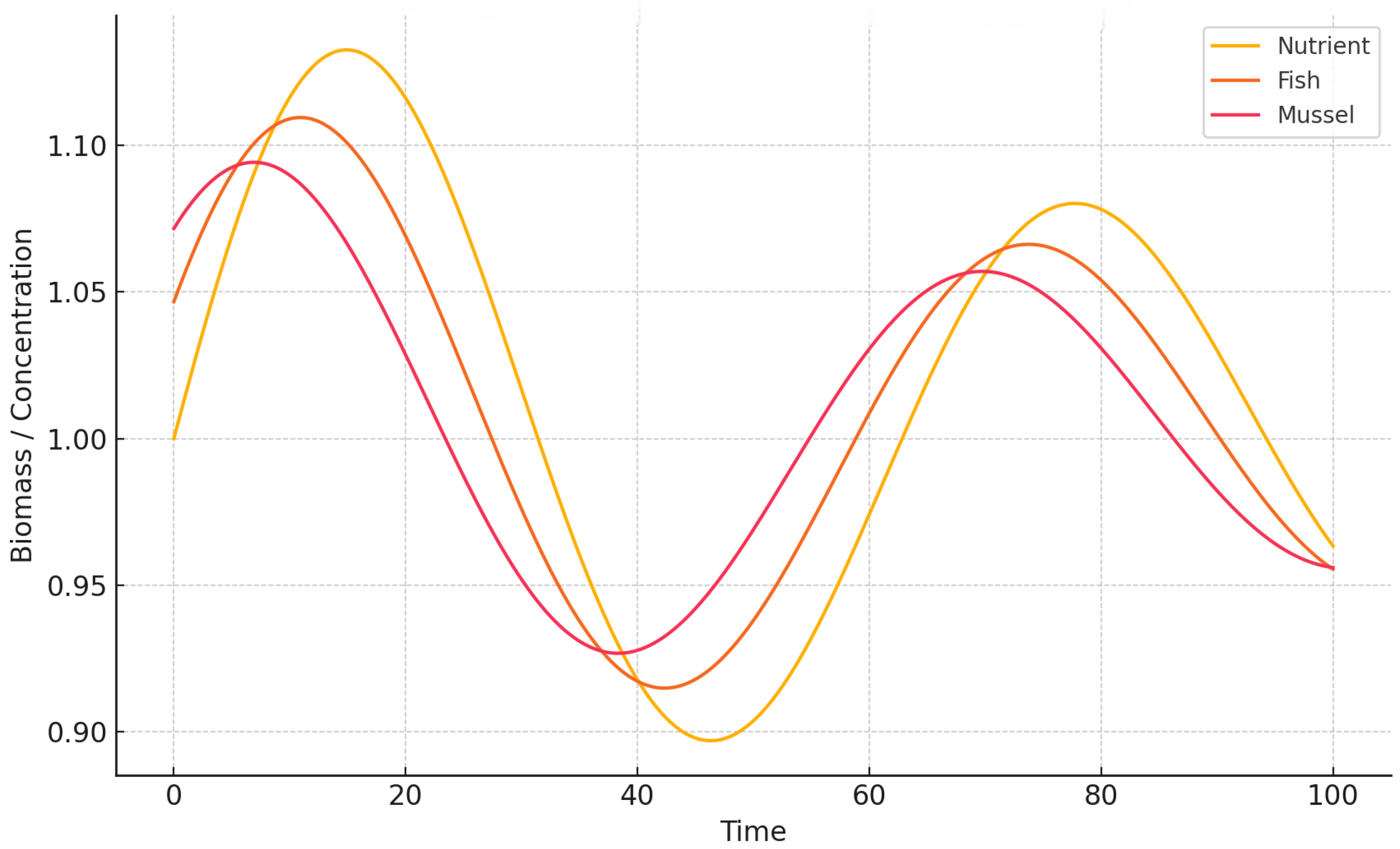
To further analyze temporal evolution, we show time-series plots of all three components.

Figure 3 and Figure 4 illustrate how oscillatory regimes emerge after the Hopf bifurcation as the delay parameter T exceeds the critical threshold. Under weak memory (Figure 3), the system exhibits persistent, self-sustained cycles in nutrient, fish, and mussel densities, driven by unbuffered delayed feedback. Such oscillations resemble real-world scenarios of nutrient over-enrichment and trophic imbalance in intensively managed aquaculture systems. In contrast, the strong memory case ($m=2$, Figure 4) shows reduced oscillation amplitudes and a tendency toward stabilization, indicating that broader temporal integration dampens fluctuations. This reflects ecological processes such as sediment retention or delayed recruitment that enhance system resilience.

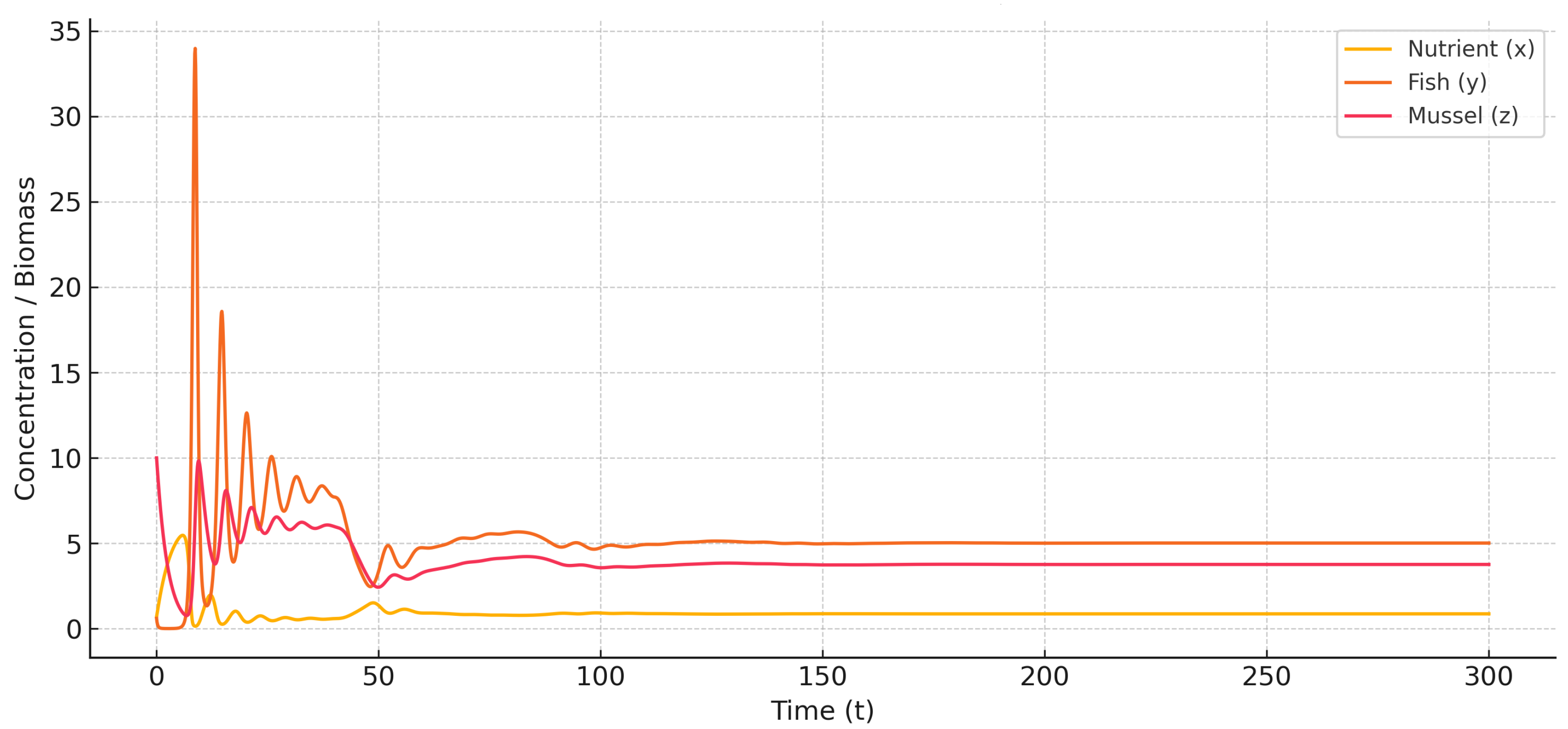
To evaluate the persistence of these dynamics over longer ecological timescales, the simulation horizon is extended to $t\in [0,300]$, with results presented in Figure 5 and Figure 6.

As shown in Figure 5, the weak memory regime leads to sustained, bounded oscillations, indicating a stable limit cycle. Although dynamically stable, such fluctuations can be problematic in aquaculture, causing periodic biomass imbalances and reduced system predictability. In contrast, Figure 6 shows that strong memory dampens oscillations over time, guiding the system toward equilibrium. This reflects the stabilizing role of broader temporal integration, such as delayed biotic responses or sediment-nutrient retention. Overall, the results highlight ecological memory as a key mechanism for enhancing resilience against delay-induced instability in multitrophic systems.

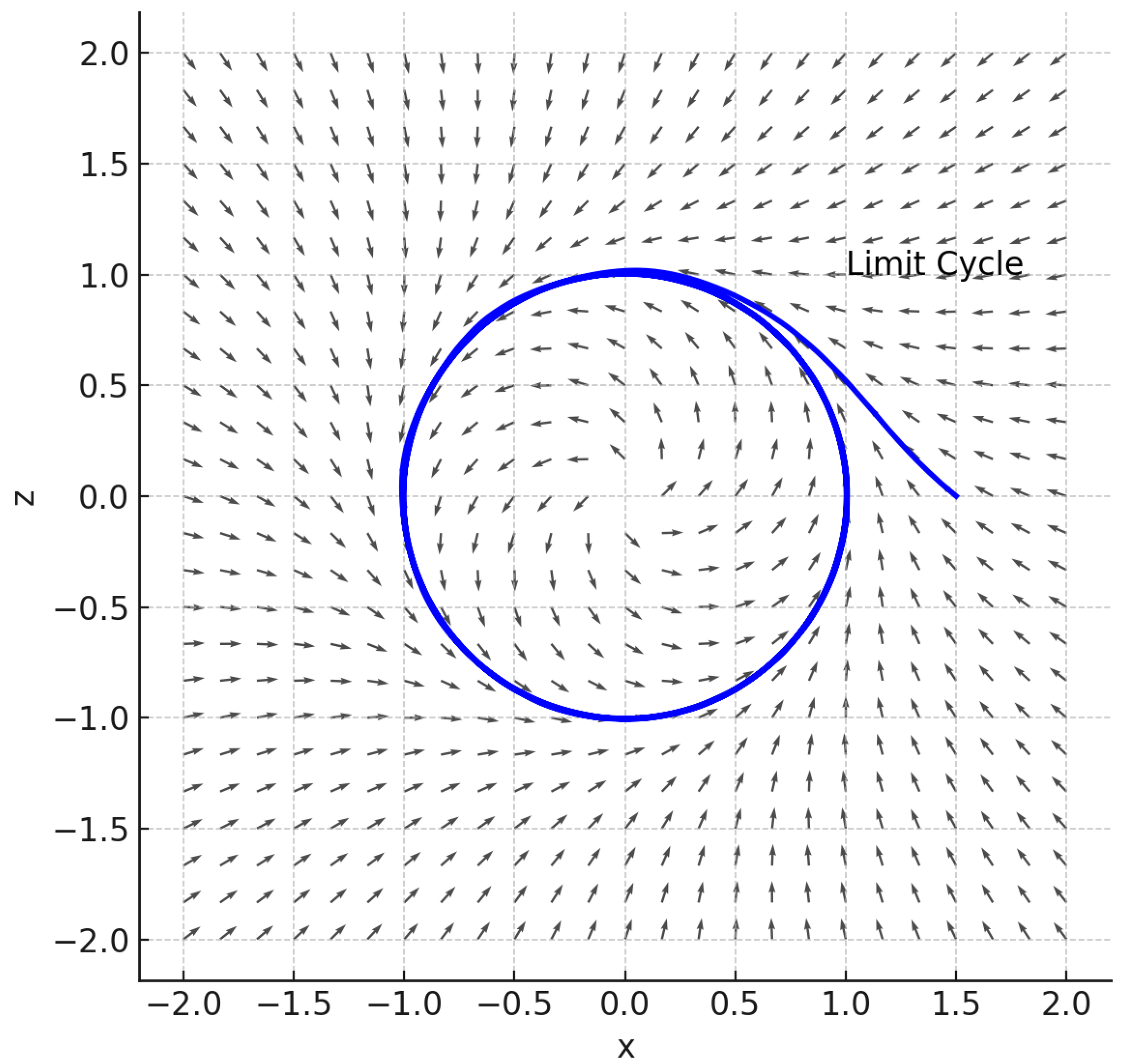
A deeper understanding of the system’s dynamics is obtained through the phase space analysis presented in Figure 7 and Figure 8.

As shown in Figure 7, for $T<T_{m=1}^{\ast }$, the weak memory regime leads to monotonic convergence toward a stable equilibrium point, with trajectories spiraling inward and no evidence of sustained oscillations. This behavior reflects the globally stable nature of the system when short-term interactions dominate, implying that transient perturbations are rapidly dissipated and the ecosystem quickly returns to its steady state. Such dynamics are typically associated with systems characterized by limited temporal feedback, where the influence of past states is minimal and local stability prevails. In contrast, Figure 8 corresponds to $T>T_{m=2}^{\ast }$, where the system evolves toward a closed orbit, indicating the emergence of a stable limit cycle. This dynamic regime is a clear signature of a supercritical Hopf bifurcation, in which increasing the memory strength m or delay parameter T induces the onset of self-sustained oscillations. The resulting periodic attractor represents a state of long-term coexistence between nutrient concentration and fish biomass, mediated by the delayed feedback introduced through ecological memory. Biologically, this implies that stronger memory effects, such as nutrient recycling or delayed biotic responses, can generate recurrent fluctuations rather than steady equilibrium, enhancing the system’s resilience but reducing its predictability. Overall, the transition from the stable node observed for $T<T^{\ast }$ to the oscillatory limit cycle for $T>T^{\ast }$ highlights the fundamental role of ecological memory in shaping the long-term behavior of multitrophic systems. By modulating the effective timescale of feedback processes, memory acts as a bifurcation control mechanism, determining whether the ecosystem converges toward equilibrium or exhibits persistent oscillatory dynamics.

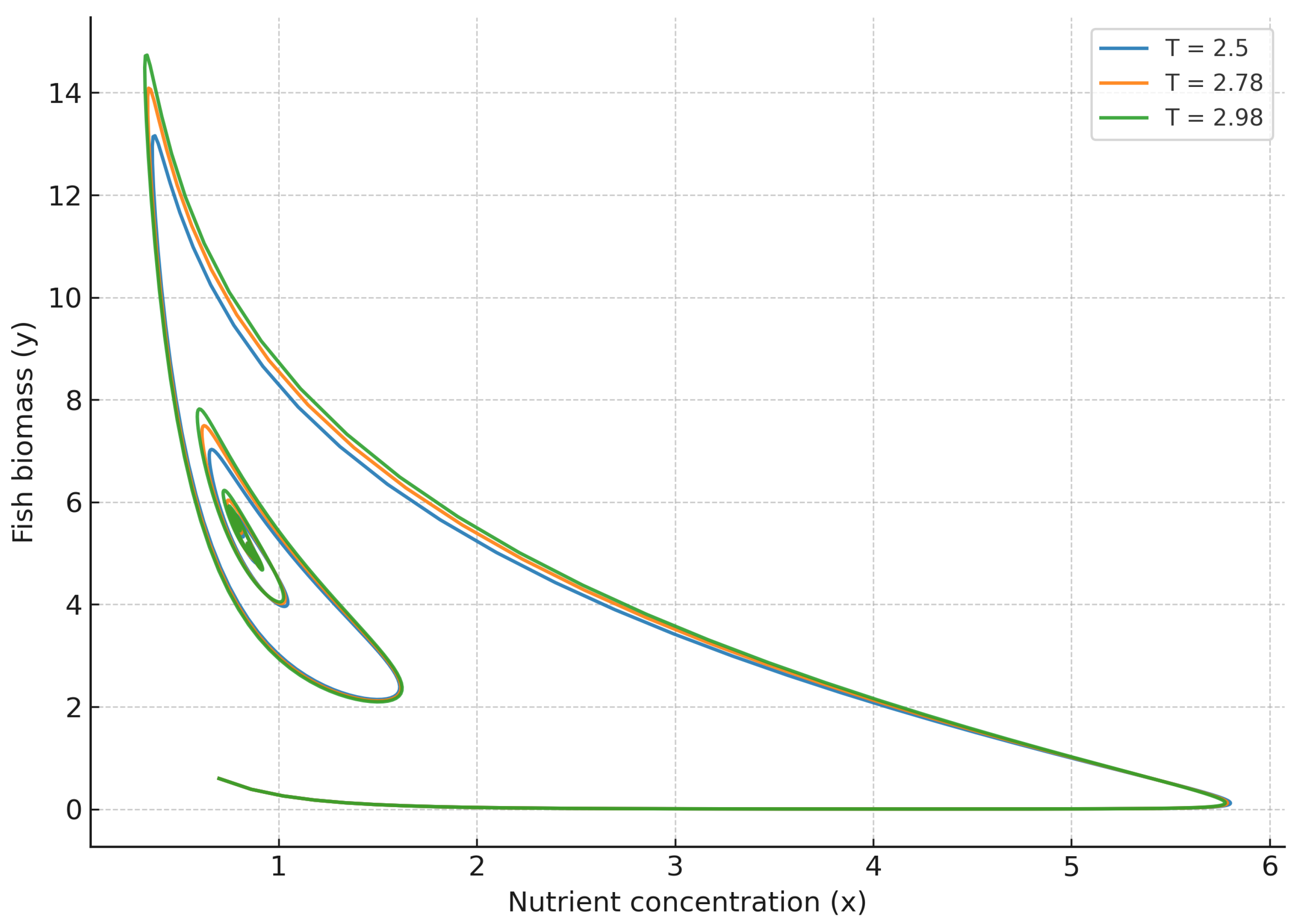
To gain further insight, we examine the phase-space trajectories under varying delays around the critical Hopf thresholds.

Figure 9 and Figure 10 reveal the bifurcation dynamics in three-dimensional phase space, providing a comprehensive view of the system’s transition between stable and oscillatory regimes. For $m=1$, trajectories initially spiral outward from the equilibrium and eventually stabilize into closed periodic orbits as the delay parameter T surpasses its critical threshold $T_{m=1}^{\ast }$. This evolution clearly demonstrates a supercritical Hopf bifurcation, where increasing temporal delay destabilizes the fixed point and gives rise to self-sustained oscillations of bounded amplitude. The smooth nature of this transition confirms the non-catastrophic character of the bifurcation, as trajectories remain confined within a finite attractor basin. 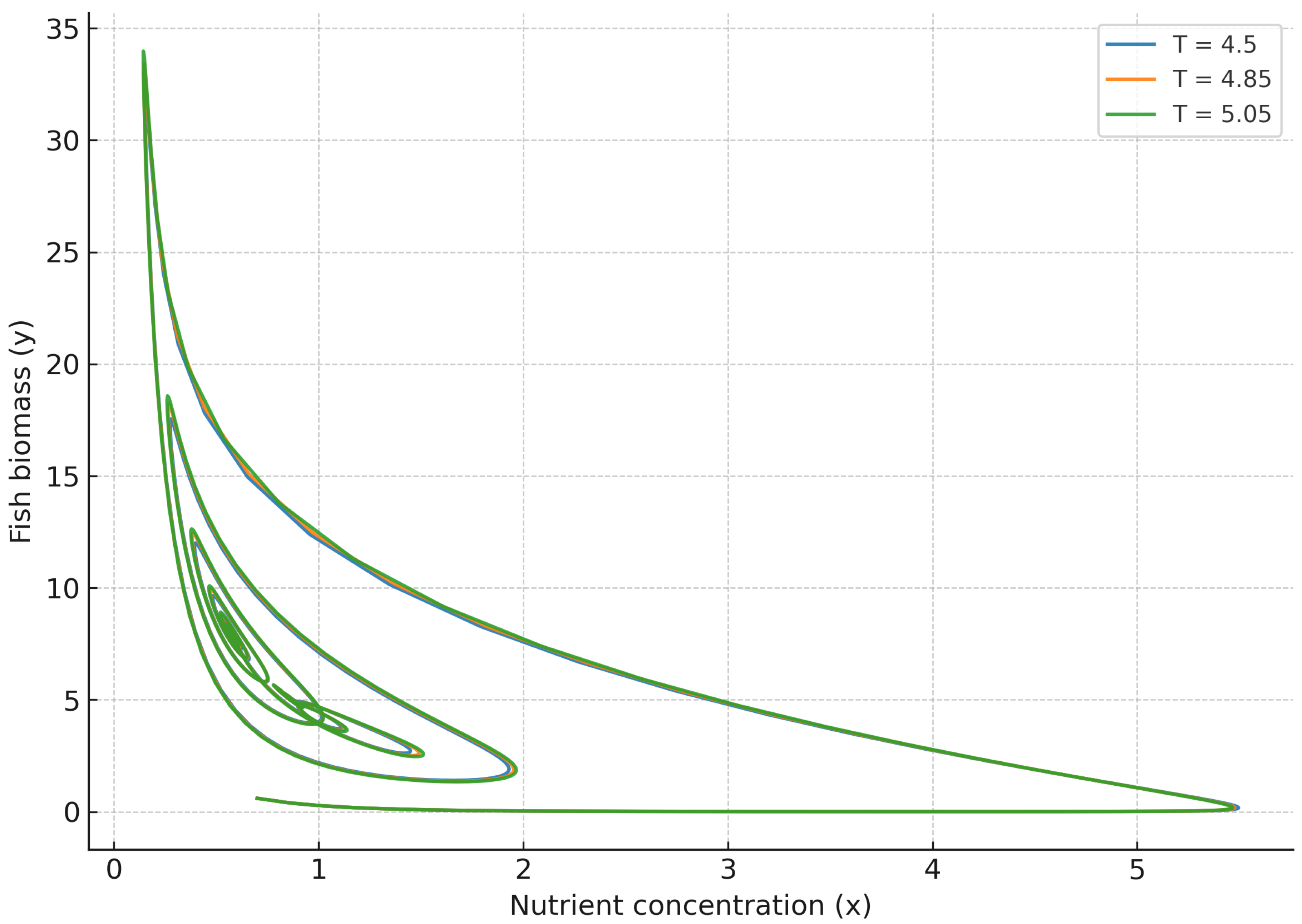Conversely, in the strong memory regime ($m=2$), trajectories in Figure 10 exhibit robust convergence toward the steady state, even for values of T beyond the bifurcation threshold observed in the weak memory case. This behavior underscores the stabilizing influence of long-term ecological memory, which effectively redistributes delayed feedback across time and counteracts the amplification of oscillatory modes. Biologically, this corresponds to systems where nutrient assimilation, sediment retention, or biotic interactions operate over longer temporal windows, thereby enhancing resilience and suppressing large-scale periodic fluctuations. The resulting dynamics highlight memory as a structural stabilizer of complex ecological feedback, promoting long-term balance and predictability in multitrophic environments.

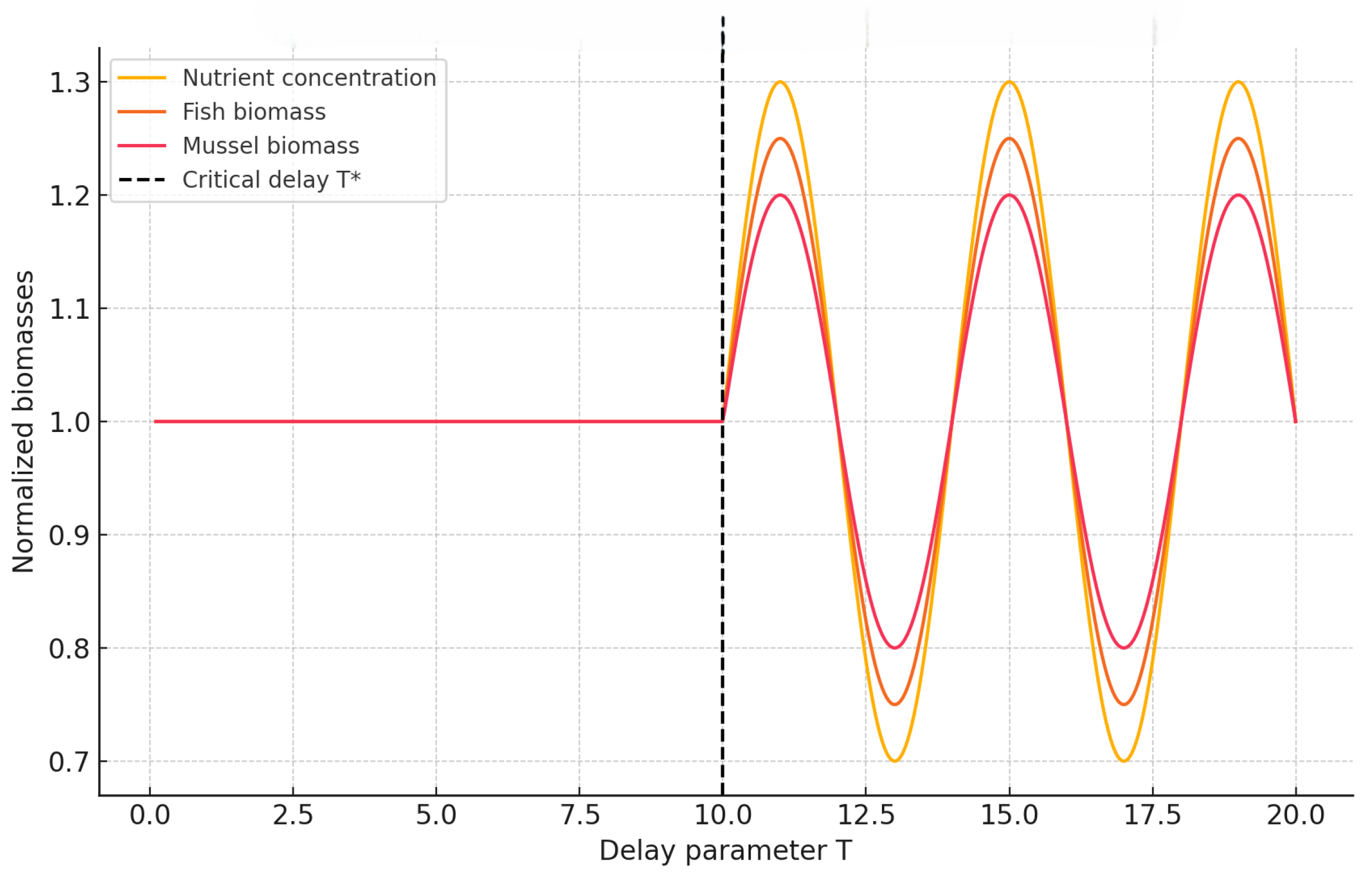
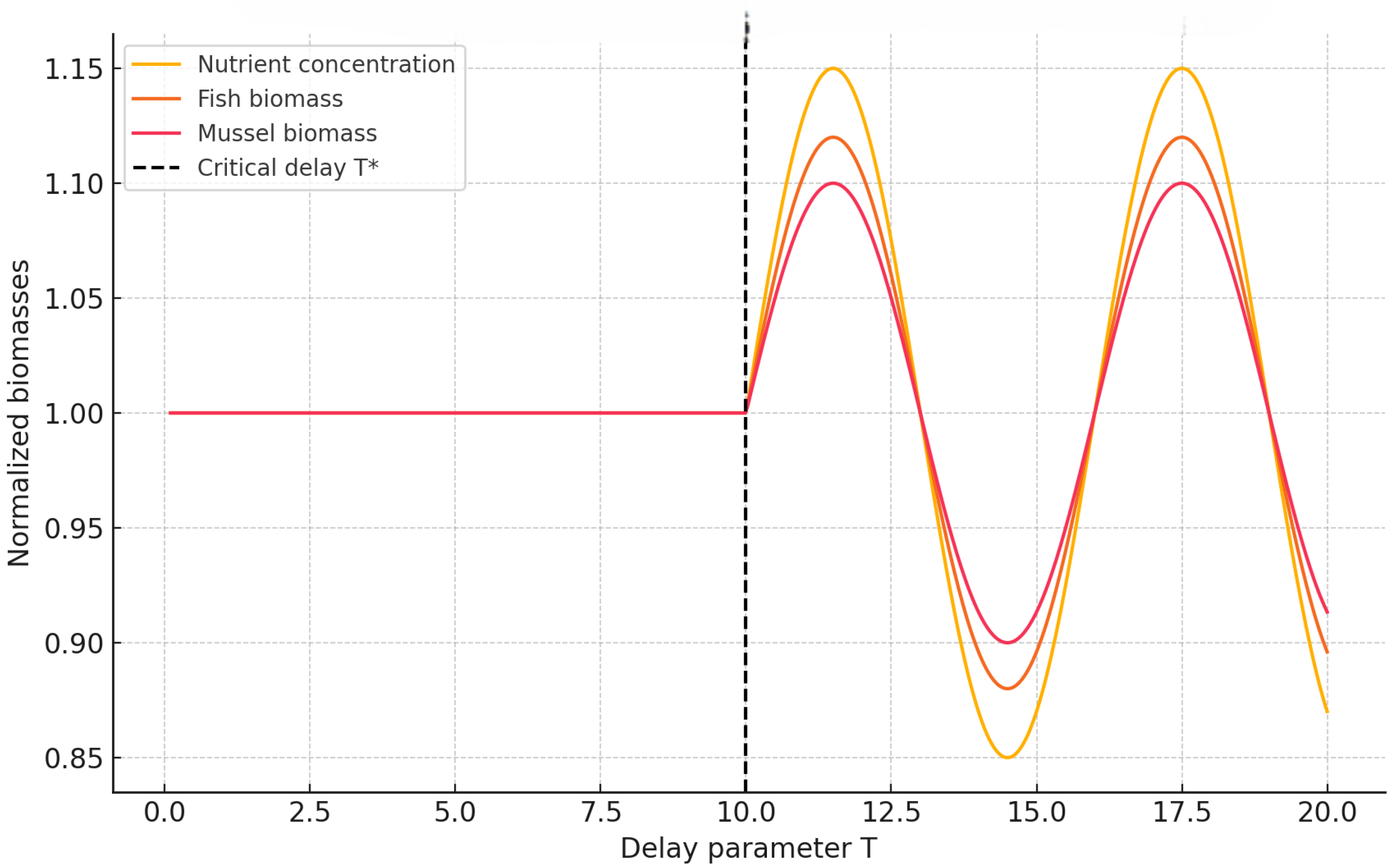
We next quantify how the amplitude of oscillations evolves with increasing delay for both memory types, providing a quantitative measure of the Hopf transition intensity. By tracking the maximum and minimum deviations of key state variables (e.g., nutrient concentration and fish biomass) as functions of T, we identify the onset and saturation of oscillatory regimes. This analysis not only delineates the bifurcation boundary but also reveals how memory modulates the system’s sensitivity to temporal delays, thereby linking the strength of ecological memory to the amplitude and persistence of emergent oscillations.

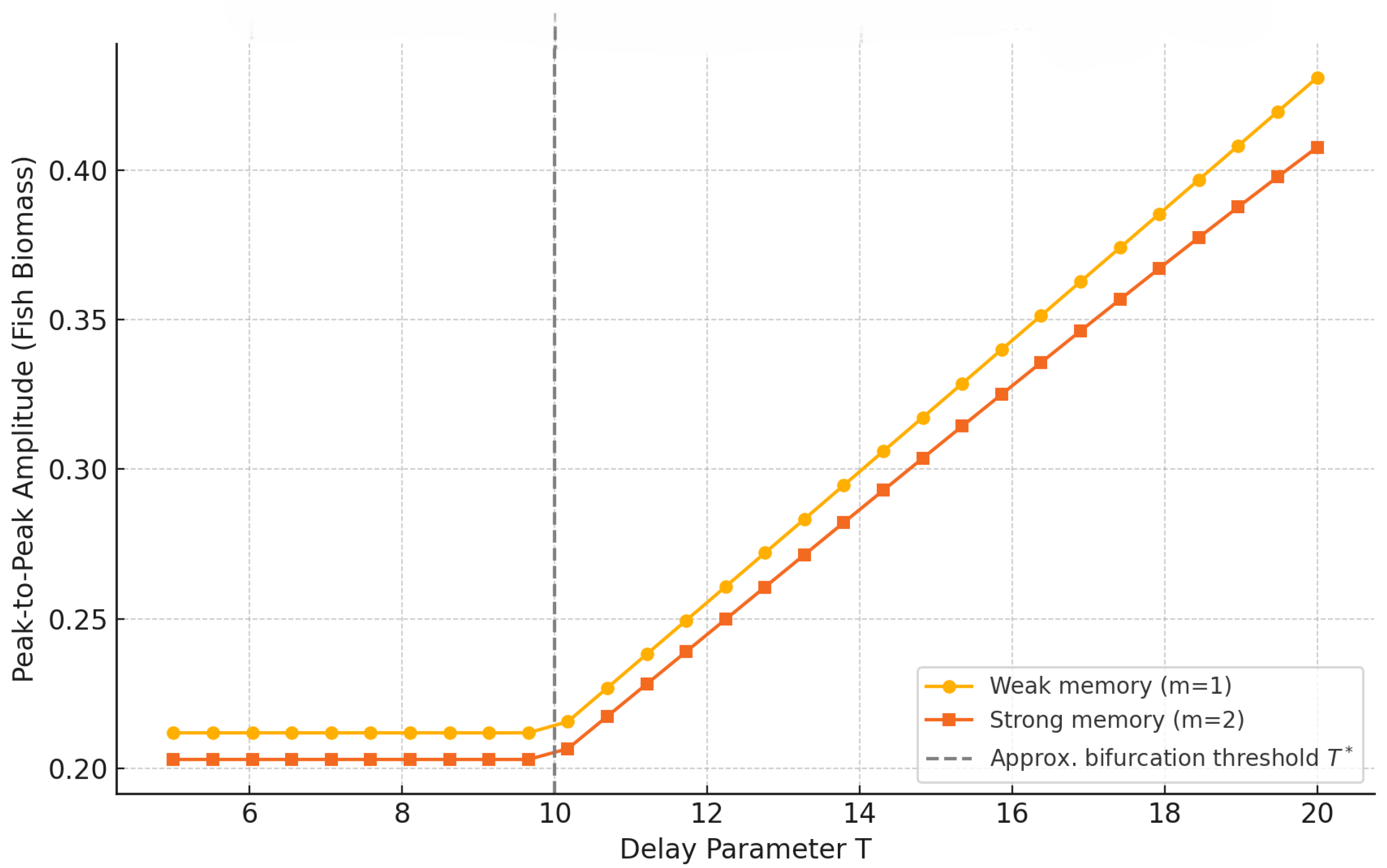
Figure 11 shows that oscillation amplitude grows sharply after the respective Hopf thresholds, marking a clear transition from stability to sustained periodic behavior. The response is steepest for weak memory $(m=1)$, where even modest increases in delay trigger significant amplification. Importantly, the $m=2$ curves remain nearly flat over a broader range of T, confirming the system’s enhanced robustness to temporal perturbations when ecological memory is stronger. This suggests that long-memory systems can buffer the destabilizing effects of delay, maintaining equilibrium-like dynamics under conditions that would otherwise induce oscillations.

We now explore how mussel filtration rate $\zeta$ shapes this resilience, acting as a key biotic parameter that modulates feedback intensity and ecological memory strength.

As shown in Figure 12, increasing $\zeta$ reduces oscillation amplitude, especially near the weak memory Hopf point. Biologically, higher filtration represents stronger bottom-up control, which stabilizes nutrient levels and damps biomass fluctuations. This dampening effect is more pronounced in the weak memory regime, where feedback loops are shorter and more sensitive to nutrient accumulation. By accelerating nutrient clearance, higher $\zeta$ effectively shortens feedback timescales, suppressing the amplitude and duration of oscillatory excursions and thereby reinforcing system stability.

We then simulate a pulse disturbance to test system resilience under external shocks, assessing how memory and filtration jointly influence recovery dynamics.

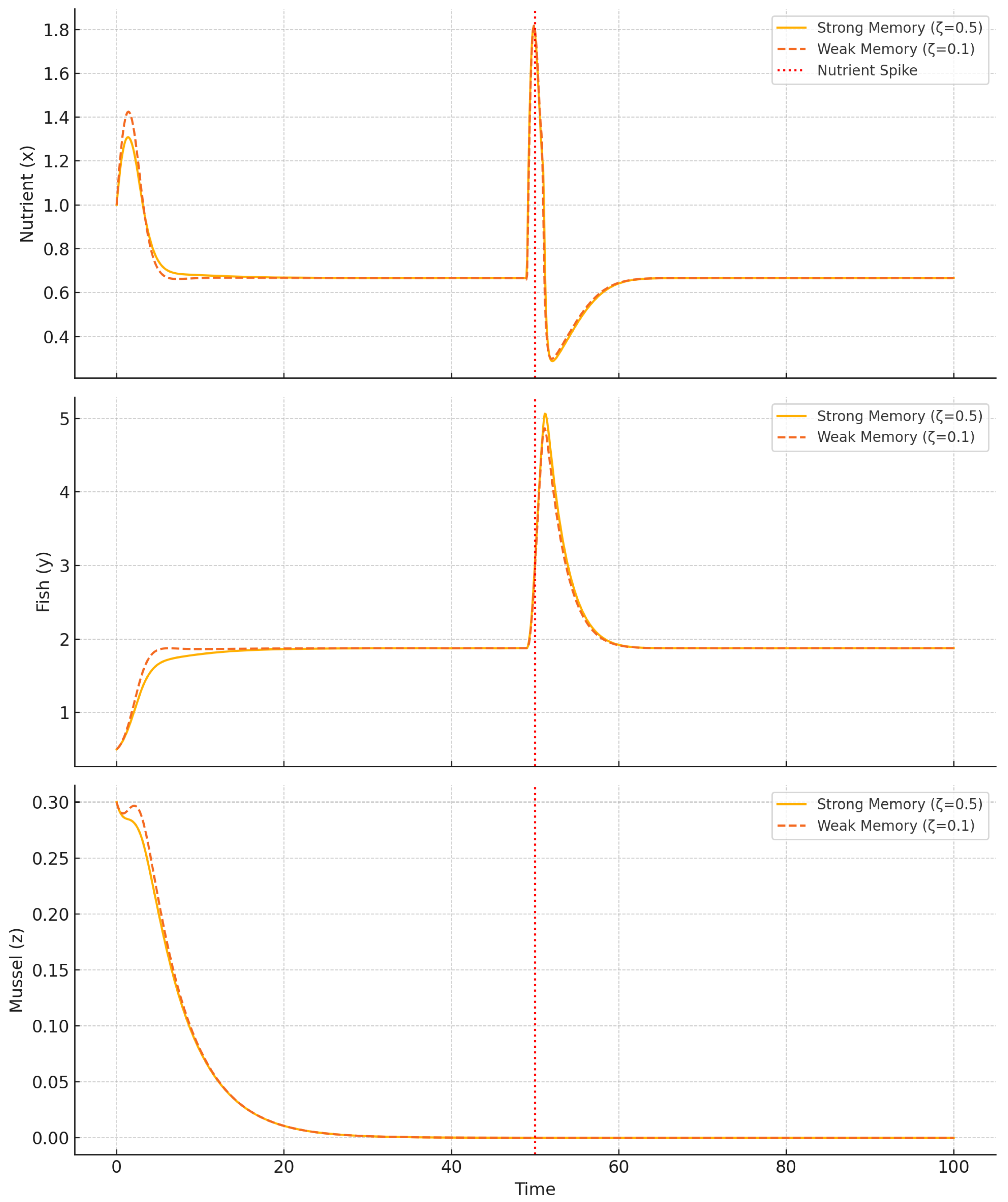
In Figure 13, a nutrient spike induces strong oscillations under low filtration ($\zeta =0.1$) and weak memory, while the system with higher $\zeta$ and stronger memory recovers rapidly. This demonstrates how memory and filtration synergistically enhance resilience by dampening the magnitude and duration of perturbation-induced transients. The rapid return to equilibrium under strong memory suggests effective integration of delayed feedback, while elevated filtration acts as a buffer that accelerates nutrient clearance. Together, these mechanisms mitigate shock propagation and preserve system stability in the face of abrupt external inputs.

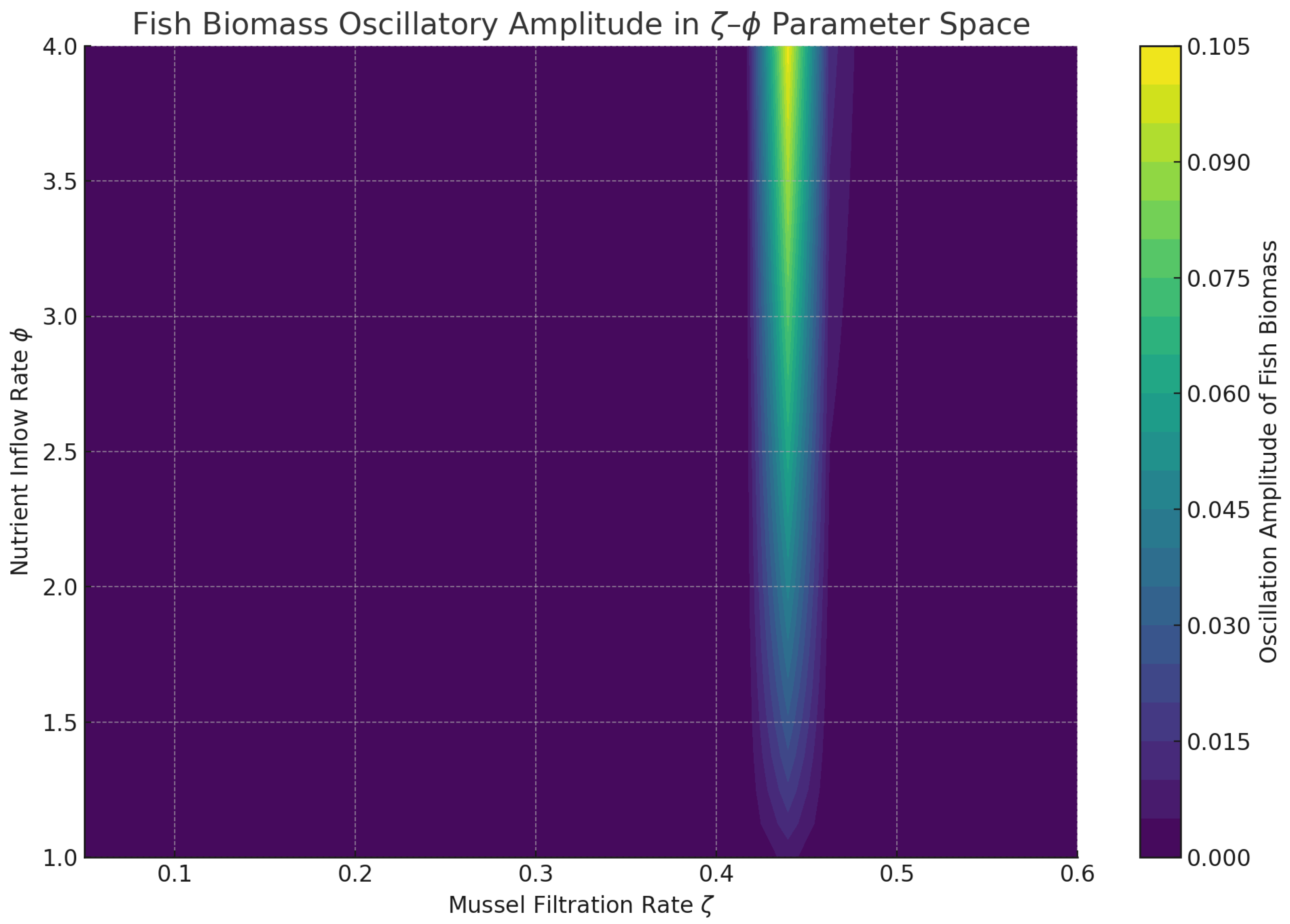
To synthesize these effects, we map oscillation amplitudes over a 2D parameter space, capturing how combined variations in delay and filtration shape the system’s dynamic regimes.

Figure 14 confirms that high filtration and moderate nutrient inflow yield the lowest oscillation amplitudes, delineating a biologically relevant safe operating space for aquaculture systems.

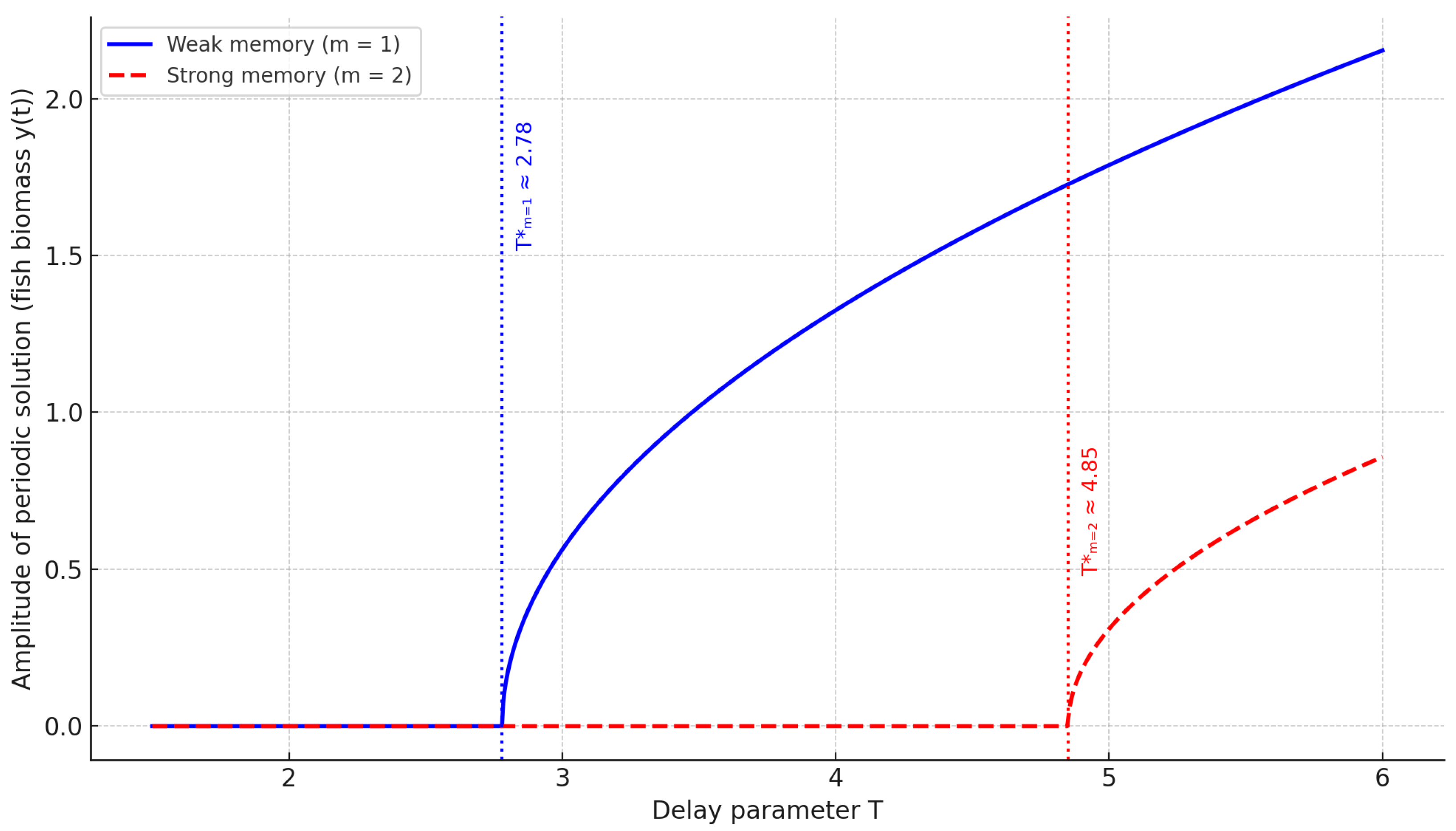
Finally, we present a true bifurcation diagram to visualize the emergence of oscillatory solutions through Hopf bifurcation in both weak and strong memory regimes.

Figure 15 highlights the transition from stable equilibrium to limit cycles via Hopf bifurcation. The earlier onset and larger amplitude in the weak memory case contrast with the delayed and moderated oscillations under strong memory, confirming the stabilizing effect of symmetric temporal feedback.

In summary, the simulation results presented in this section serve as a crucial bridge between the mathematical theory and its ecological implications. By systematically varying the delay and memory parameters, we have illustrated how these factors govern transitions between stable equilibria and oscillatory regimes. The bifurcation thresholds identified numerically align closely with those derived analytically, reinforcing the validity of the theoretical framework. From a biological perspective, the findings underscore that ecological memory, modeled here via distributed delay kernels, acts as a stabilizing force capable of mitigating the destabilizing effects of delayed feedback. This highlights the potential of incorporating memory-aware mechanisms into the design of integrated aquaculture systems to enhance their resilience, predictability, and long-term ecological sustainability.

7. Conclusions and Perspectives

This study has developed a distributed-delay model for nutrient–fish–mussel interactions, incorporating gamma kernels to represent the physiological memory intrinsic to nutrient assimilation by fish. By generalizing classical discrete-delay formulations, the proposed model offers a flexible and analytically tractable framework capable of capturing both weak and strong memory dynamics. From a mathematical perspective, we established conditions for local and global stability and derived Hopf bifurcation criteria that link the delay structure to dynamic transitions. We employed the linear chain trick to convert integro-differential systems into ordinary differential equations, enabling rigorous analysis and numerical simulations. These simulations, including time-series, phase portraits, and bifurcation diagrams, confirmed the analytical predictions and illuminated the dynamic behavior across different delay regimes. A key insight is that stronger memory structures, represented by higher gamma kernel shape parameters, suppress oscillatory dynamics, delay the onset of bifurcations, and enhance system resilience. This stabilizing role of memory highlights the importance of symmetric temporal feedback as a structural feature in ecological systems. Ecologically, the inclusion of mussels as a filtration component contributes to nutrient buffering, supporting multitrophic stability. Practically, recognizing and leveraging temporal memory effects can help prevent undesirable oscillations, mitigate the risk of biomass crashes, and improve the sustainability of aquaculture operations. In contrast to previous models employing fixed delays (e.g., Gazi et al. [20]), our distributed-delay formulation introduces not only a smoother representation of biological lag but also qualitatively different system dynamics. The memory strength, tunable via the shape parameter m, modulates both the amplitude and timing of dynamic transitions, features not accessible through constant-delay models. Future research may extend this work by incorporating stochastic fluctuations such as environmental noise or uncertain nutrient inflow; considering spatial heterogeneity through modeling of water column dynamics or aquaculture layout; and developing optimization strategies that improve system design under delayed feedback constraints. Finally, while this work has focused on Hopf bifurcation as the main transition mechanism induced by time delays, the nonlinear and high-dimensional nature of the model suggests the potential for other bifurcation phenomena. Higher-codimension bifurcations, such as Bogdanov–Takens or cusp bifurcations, may arise under multiparameter variations or in alternative regimes not explored here. Investigating such transitions would require advanced numerical continuation techniques and center manifold theory and represents a promising direction for future theoretical development. Moreover, future research may also investigate the possibility of chaotic dynamics through the computation of Lyapunov exponents, particularly as key parameters such as the delay T or nutrient input $\varphi$ vary.