Distinguishing Strongly Interacting Dark Matter Spikes via EMRI Gravitational Waves
Abstract
1. Introduction
2. Self-Interacting Dark Matter Models
Lagrangians for Self-Interacting Dark Matter
- 1.
- Scalar SIDM with quartic self-interaction (2→2 scattering):
- 2.
- SIMP-like scalar with cubic and higher-order interactions (3→2 and scattering):
- 3.
- SIDM with a light mediator (Yukawa-type interactions):
- 4.
- Multi-component SIDM with discrete symmetries:
- 5.
- General effective interactions:
3. Dark Matter Spike Models
3.1. Classical Spike Model
3.2. Spike Model with Dark Matter Annihilation 2 to 0
3.3. Spike Models with 2-to-2 and 3-to-2 Processes
3.4. Dark Matter Dissolution Effects from Number Changing Processes
3.5. Characteristic Radii: Dissolution and Cutoff
3.6. Dissolution Radius for General DM Number Changing Processes
Special Cases
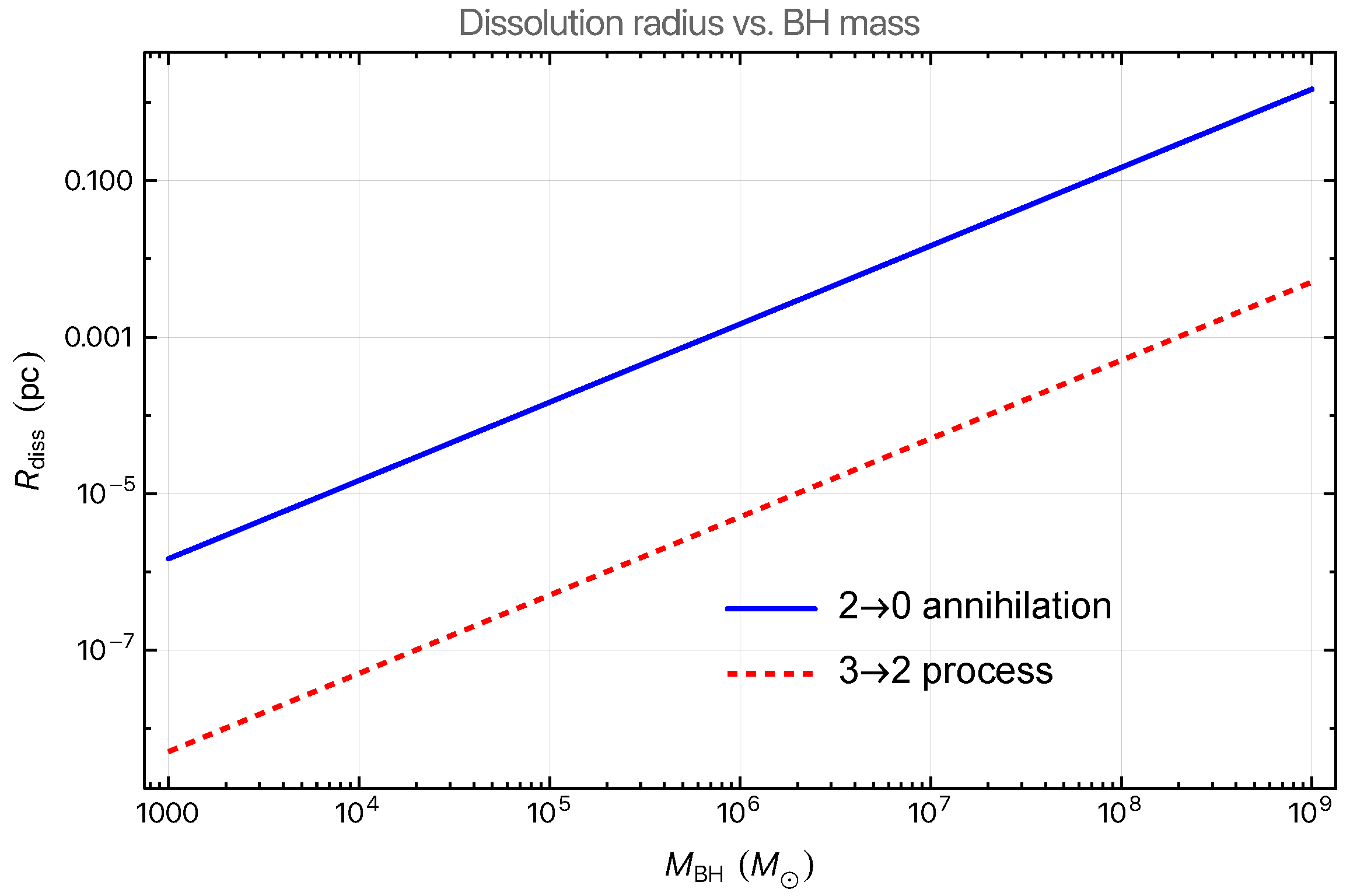
3.7. Relation Between Dissolution Radius and Black Hole Mass
4. Waveform Modeling and Orbital Dynamics
4.1. Equation of Motion for the Stellar-Mass Compact Object
4.2. Orbital Frequency and Circular Orbit Condition
4.3. Energy Balance and Orbital Evolution
4.4. Gravitational Waveform
5. Gravitational Wave Signal and Phase Shift
6. Summary and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bullock, J.S.; Boylan-Kolchin, M. Small-Scale Challenges to the ΛCDM Paradigm. Ann. Rev. Astron. Astrophys. 2017, 55, 343–387. [Google Scholar] [CrossRef]
- Tulin, S.; Yu, H.-B. Dark Matter Self-interactions and Small Scale Structure. Phys. Rep. 2018, 730, 1–57. [Google Scholar] [CrossRef]
- Hochberg, Y.; Kuflik, E.; Volansky, T.; Wacker, J.G. Mechanism for Thermal Relic Dark Matter of Strongly Interacting Massive Particles. Phys. Rev. Lett. 2014, 113, 171301. [Google Scholar] [CrossRef]
- Hochberg, Y.; Kuflik, E.; Murayama, H.; Volansky, T.; Wacker, J.G. Model for Thermal Relic Dark Matter of Strongly Interacting Massive Particles. Phys. Rev. Lett. 2015, 115, 021301. [Google Scholar] [CrossRef] [PubMed]
- Gondolo, P.; Silk, J. Dark Matter Annihilation at the Galactic Center. Phys. Rev. Lett. 1999, 83, 1719. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Paschalidis, V. Self-interacting dark matter cusps around massive black holes. Phys. Rev. D 2014, 89, 023506. [Google Scholar] [CrossRef]
- Alvarez, G.; Yu, H.-B. Density spikes near black holes in self-interacting dark matter halos and indirect detection constraints. Phys. Rev. D 2021, 104, 043013. [Google Scholar] [CrossRef]
- Gao, Z.-F.; Li, B.-P.; de Andrade, L.C.G.; Yang, X.-F. On the Theoretical Properties and Experimental Detection of Dark Matter Axions. Astron. Nachrichten 2025, 346, e70031. [Google Scholar] [CrossRef]
- Gao, Z.-F.; Li, B.-P.; de Andrade, L.C.G. Dark photons and tachyonic instability induced by Barbero-Immirzi parameter and axion-torsion transmutation. Eur. Phys. J. C 2025, 85, 433. [Google Scholar] [CrossRef]
- Gao, Z.-F.; Li, B.-P.; de Andrade, L.C.G. Is there a chiral dark dynamo in the universe induced by quantum correction, Nieh–Yan gravity and Barbero–Immirzi field? arXiv 2025, arXiv:2502.04727. [Google Scholar] [CrossRef]
- Gao, Z.-F.; Xing, C.-C.; Na, W. The scattering of Dirac spinors in rotating spheroids. Eur. Phys. J. C 2020, 80, 582. [Google Scholar] [CrossRef]
- Gao, Z.-F.; Zhao, X.-J.; Yang, X.-F.; Ma, W.-Q.; Hu, Z.-R. Modified Field Equation With Gauss–Bonnet Gravity. Astron. Nachrichten 2025, 346, e20250027. [Google Scholar] [CrossRef]
- Amaro-Seoane, P.; Gair, J.R.; Freitag, M.; Coleman Miller, M.; Mandel, I.; Cutler, C.J.; Babak, S. Intermediate and Extreme Mass-Ratio Inspirals—Astrophysics, Science Applications and Detection Using LISA. Class. Quantum Grav. 2007, 24, R113–R169. [Google Scholar] [CrossRef]
- Babak, S.; Gair, J.; Sesana, A.; Barausse, E.; Sopuerta, C.F.; Berry, C.P.; Klein, A. Science with the Space-Based Interferometer LISA. V. Extreme Mass-Ratio Inspirals. Phys. Rev. D 2017, 95, 103012. [Google Scholar] [CrossRef]
- Eda, K.; Itoh, Y.; Kuroyanagi, S.; Silk, J. New Probe of Dark-Matter Properties: Gravitational Waves from an Intermediate-Mass Black Hole Embedded in a Dark-Matter Minispike. Phys. Rev. Lett. 2013, 110, 221101. [Google Scholar] [CrossRef]
- Yue, X.; Han, W.-B. Gravitational Waves from Extreme Mass Ratio Inspirals in Dark Matter Spikes: A Numerical Study. Phys. Rev. D 2018, 97, 064003. [Google Scholar] [CrossRef]
- Wang, Y.; Han, W.; Wu, X.; Liang, E. Gravitational wave imprints of dark matter annihilation: Probing halo structures through EMRI signals. Class. Quantum Grav. 2025, 42, 175007. [Google Scholar] [CrossRef]
- Li, B.-P.; Gao, Z.-F.; Ma, W.-Q.; Cheng, Q. Braking index of PSR J1846-0258: A model of magnetic inclination evolution and its gravitational-wave implication. Front. Astron. Space Sci. 2025, 12, 1625459. [Google Scholar] [CrossRef]
- Hochberg, Y.; Kuflik, E.; Volansky, T.; Wacker, J.G. The SIMP Miracle. arXiv 2014, arXiv:1402.5143. [Google Scholar] [CrossRef]
- Bernal, N.; Chu, X. Z2 SIMP Dark Matter. JCAP 2015, 1510, 027. [Google Scholar]
- Choi, S.M.; Kim, J.; Ko, P.; Li, J. A multi-component SIMP model with U(1)X → Z2 × Z3. arXiv 2021, arXiv:2103.05956. [Google Scholar] [CrossRef]
- Blinnikov, S.I.; Khlopov, M.Y. On possible effects of ’mirror’ particles. Sov. J. Nucl. Phys. 1982, 36, 472. [Google Scholar]
- Berezhiani, Z.G.; Dolgov, A.D.; Mohapatra, R.N. Asymmetric inflationary reheating and the nature of mirror universe. Phys. Lett. B 1996, 375, 26. [Google Scholar] [CrossRef]
- Mohapatra, R.N.; Okada, N. Matter-dark matter coincidence and the mirror world. Phys. Rev. D 2025, 111, 123510. [Google Scholar] [CrossRef]
- Mohapatra, R.N.; Nussinov, S. Neutron-Mirror Neutron Oscillation Constraints. Phys. Lett. B 2017, 769, 247. [Google Scholar]
- Ciarcelluti, P.; Wallemacq, S. Cosmological constraints on mirror dark matter. Int. J. Mod. Phys. D 2014, 23, 1450013. [Google Scholar]
- Ciarcelluti, P.; Foot, R. Mirror dark matter and the DAMA/Libra signal. Phys. Lett. B 2008, 679, 278. [Google Scholar] [CrossRef]
- Beylin, V.A.; Bikbaev, T.E.; Khlopov, M.Y.; Mayorov, A.G.; Sopin, D.O. Dark Atoms of Nuclear Interacting Dark Matter. Universe 2024, 10, 368. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Phys. Rept. 2005, 405, 279. [Google Scholar] [CrossRef]
- Spergel, D.N.; Steinhardt, P.J. Observational evidence for self-interacting cold dark matter. Phys. Rev. Lett. 2000, 84, 3760. [Google Scholar] [CrossRef]
- Chu, X.; Dekker, A.; Pradler, J. Self-heating dark matter via semi-annihilation. JCAP 2019, 12, 034. [Google Scholar]
- Abazajian, K.N.; Horiuchi, S.; Kaplinghat, M.; Keeley, R.E.; Macias, O. Strong constraints on thermal relic dark matter from Fermi-LAT observations of the Galactic Center. Phys. Rev. D 2020, 102, 043012. [Google Scholar] [CrossRef]
- Kamenetskaia, B.B.; Fujiwara, M.; Ibarra, A.; Toma, T. Dark matter spikes with strongly self-interacting particles. arXiv 2025, arXiv:2506.12642. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Structure of Cold Dark Matter Halos. Astrophys. J. 1996, 462, 563. [Google Scholar] [CrossRef]
- Hopman, C.; Alexander, T. The Effect of Mass Segregation on Gravitational Wave Sources near Massive Black Holes. Astrophys. J. 2005, 629, 362–372. [Google Scholar] [CrossRef]
- Barausse, E.; Cardoso, V.; Pani, P. Environmental Effects for Gravitational-Wave Astrophysics. Phys. Rev. D 2014, 89, 104059. [Google Scholar] [CrossRef]
- Linial, I.; Metzger, B.D. Environmental Perturbations on EMRI Evolution in Galactic Nuclei. Mon. Not. R. Astron. Soc. 2023, 520, 1234–1245. [Google Scholar]
- Gnedin, O.Y.; Primack, J.R. Dark Matter Profile in the Galactic Center. Phys. Rev. Lett. 2004, 93, 061302. [Google Scholar] [CrossRef] [PubMed]
- Merritt, D.; Milosavljevic, M.; Verde, L.; Jimenez, R. Dark Matter Spikes and Annihilation Radiation from the Galactic Center. Astrophys. J. 2002, 569, 51–61. [Google Scholar] [CrossRef]
- Peng, X.; Chen, Y. Impact of Gas and Stellar Background on EMRI Gravitational Waveforms. Astrophys. J. Lett. 2025, 940, L12. [Google Scholar]
- Eda, K.; Itoh, Y.; Kuroyanagi, S.; Silk, J. Gravitational waves as a probe of dark matter minispikes. Phys. Rev. D 2015, 91, 044045. [Google Scholar] [CrossRef]
- Peters, P.C.; Mathews, J. Gravitational radiation from point masses in a Keplerian orbit. Phys. Rev. 1963, 131, 435. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Dynamical friction. I. General considerations: The coefficient of dynamical friction. Astrophys. J. 1943, 97, 255. [Google Scholar] [CrossRef]
- Barack, L.; Cutler, C. LISA Capture Sources: Approximate Waveforms, Signal-to-Noise Ratios, and Parameter Estimation Accuracy. Phys. Rev. D 2004, 69, 082005. [Google Scholar] [CrossRef]
- Bonga, B.; Yang, H.; Hughes, S.A. Tidal resonance in extreme mass-ratio inspirals. Phys. Rev. Lett. 2019, 123, 101103. [Google Scholar] [CrossRef] [PubMed]



| Process | Reaction | Typical Framework | DM Mass Scale | of Final State DM |
|---|---|---|---|---|
| Standard annihilation | Model dependent | None (all energy to SM) | ||
| Semi-annihilation (requires light SM particle, e.g., , ) | Model dependent | |||
| Elastic self-scattering | Model dependent | (energy redistributed) | ||
| SIMP (Strongly Interacting Massive Particle) | ||||
| SIMP framework (self-conjugate DM: real scalar, Majorana fermion, sterile neutrino) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Tang, R.; Han, W.; Liang, E. Distinguishing Strongly Interacting Dark Matter Spikes via EMRI Gravitational Waves. Symmetry 2025, 17, 1878. https://doi.org/10.3390/sym17111878
Wang Y, Tang R, Han W, Liang E. Distinguishing Strongly Interacting Dark Matter Spikes via EMRI Gravitational Waves. Symmetry. 2025; 17(11):1878. https://doi.org/10.3390/sym17111878
Chicago/Turabian StyleWang, Yu, Rundong Tang, Wenbiao Han, and Enwei Liang. 2025. "Distinguishing Strongly Interacting Dark Matter Spikes via EMRI Gravitational Waves" Symmetry 17, no. 11: 1878. https://doi.org/10.3390/sym17111878
APA StyleWang, Y., Tang, R., Han, W., & Liang, E. (2025). Distinguishing Strongly Interacting Dark Matter Spikes via EMRI Gravitational Waves. Symmetry, 17(11), 1878. https://doi.org/10.3390/sym17111878





