UMEAD: Unsupervised Multimodal Entity Alignment for Equipment Knowledge Graphs via Dual-Space Embedding

Abstract

The symmetry between different representation spaces plays a crucial role in effectively modeling complex multimodal data. To address the challenge of equipment knowledge graphs containing hierarchical relationships that cannot be fully represented in a single space, this study proposes UMEAD, an unsupervised multimodal entity alignment method based on dual-space embeddings. The method simultaneously learns graph embeddings in both Euclidean and hyperbolic spaces, forming a structural symmetry where the Euclidean space captures local regularities and the hyperbolic space models global hierarchies. Their complementarity achieves a balanced and symmetric representation of multimodal knowledge. An adaptive feature fusion strategy is further employed to dynamically weight semantic and visual modalities, enhancing the symmetry and complementarity between different modalities. To reduce reliance on scarce pre-aligned data, pseudo seed instances are generated from multimodal features, and an iterative constraint mechanism progressively enlarges the training set, enabling unsupervised alignment. Experiments on public datasets, including EMMEAD, FB15K-DB15K, and FB15K-YAGO15K, demonstrate that the combination of dual-space embeddings, adaptive fusion, and iterative constraints significantly improves alignment accuracy. In summary, the proposed method reduces dependence on pre-aligned data, strengthens multimodal and structural alignment, and its symmetric embedding and fusion design offers a promising approach for the construction and application of multimodal knowledge graphs in the equipment domain.

1. Introduction

In the construction and application of knowledge graphs within the equipment domain, multimodal data offers abundant representational features that facilitate the alignment of entities, enabling more accurate identification and matching of the same entities across different knowledge graphs. Nevertheless, the inherent complexity of equipment knowledge graphs and the challenges of data annotation limit the applicability of traditional supervised entity alignment methods in practice. Specifically, equipment systems exhibit complex relational hierarchies, where the multi-level structure among systems, subsystems, and individual equipment requires alignment methods to account not only for the attributes of individual entities but also for their positions and interrelations within the hierarchical framework [1]. Moreover, the multimodal nature of equipment data renders manual annotation both challenging and error-prone, thereby compromising the quality of labeled data [2]. Consequently, given the limitations of supervised approaches, the development of efficient unsupervised entity alignment methods has become a key research direction in multimodal entity alignment.

1.1. Entity Alignment in Knowledge Graphs

Entity alignment (EA) has long been studied as a means to integrate heterogeneous knowledge graphs. Early embedding-based methods projected entities into a unified vector space and aligned them by similarity. Translation-based models such as MTransE [3] and iterative bootstrapping approaches [4,5] achieved notable progress, but they typically rely on large amounts of labeled alignment seeds, which are costly to obtain in practice. Later works began to leverage graph neural networks (GNNs) for alignment, capturing richer neighborhood structures and relational dependencies [6]. These approaches improved performance under low-resource scenarios but still exhibited sensitivity to seed quality and graph heterogeneity. Recent surveys [7] also highlight that while embedding-based EA has evolved substantially, scalability and robustness remain persistent issues.

1.2. Multimodal Knowledge Graphs and Alignment

To reduce reliance on structural information alone, multimodal knowledge graphs (MMKGs) have been proposed, integrating entities with textual descriptions, images, and attributes. The MMKG dataset [8] has supported a series of multimodal alignment methods that incorporate visual and textual features into entity matching [9,10]. Beyond MMKGs, other multimodal benchmarks have been introduced, where side information such as entity descriptions, category labels, or cross-lingual anchors is leveraged to enhance alignment [11,12]. These works demonstrate that auxiliary modalities can substantially improve alignment accuracy compared to structure-only baselines. Nevertheless, challenges persist: image information is often incomplete or noisy, textual descriptions vary greatly in length and quality, and different modalities may contribute unequally to the final decision. Recent approaches attempt to use contrastive learning or transformer-based fusion [9,10], but achieving adaptive and reliable fusion across modalities remains an open problem.

1.3. Hierarchical and Geometric Representations

Many real-world graphs, particularly in the equipment domain, exhibit hierarchical and tree-like structures. Euclidean embeddings are often insufficient to represent such hierarchies. To address this, researchers have introduced hyperbolic geometry (e.g., Poincaré embeddings [13]) and hyperbolic graph neural networks [14] to capture hierarchical relations with low distortion. Building upon these foundations, several studies have attempted to integrate hyperbolic and Euclidean embeddings to simultaneously model local and global structures [15,16]. Such dual-space or hybrid embedding strategies show promise for hierarchical tasks, but their application in multimodal entity alignment remains limited. In the context of equipment knowledge graphs, where entities are often organized in complex system–subsystem hierarchies, the need for effective hierarchical modeling becomes even more critical. However, most prior multimodal EA models continue to rely solely on Euclidean representations, leaving a gap for methods that can jointly exploit both geometric spaces.

Although prior studies have advanced entity alignment, several challenges remain:

• Seed scarcity and reliability: Existing methods require many labeled seeds, yet obtaining reliable alignment supervision in multimodal equipment KGs is costly and prone to errors.
• Insufficient hierarchical modeling: Euclidean embeddings capture local neighborhood structure but struggle with global hierarchies inherent in equipment systems.
• Static multimodal fusion: Current multimodal alignment methods often use fixed fusion schemes, which cannot adaptively balance the varying quality of different modalities.
• Error propagation in iterative alignment: Bootstrapping and pseudo-labeling approaches risk accumulating noise without robust filtering and validation mechanisms.

To overcome the above challenges, this paper proposes an unsupervised multimodal entity alignment method for equipment knowledge graphs via dual-space embedding (UMEAD). We summarize representative methods in

Table 1. Comparison of UMEAD with representative multimodal entity alignment (EA) methods.

Method	Embedding Space	Modality Fusion	Supervision	Iterative Mechanism
GCN-Align	Euclidean	Structural only	Supervised	–
HGCN	Hyperbolic	Structural only	Supervised	–
DSEA	Euclidean	Static multimodal	Supervised	–
BootEA-M	Euclidean	Static multimodal	Semi-supervised	✔
MMEA	Euclidean	Transformer-based multimodal fusion	Supervised	–
UMAEA	Euclidean	Adaptive multimodal	Unsupervised	–
UMEAD	Euclidean + Hyperbolic	Adaptive multimodal	Unsupervised	✔

, including structural, hierarchical, and multimodal approaches. As shown in the table, most existing models rely on single Euclidean embedding spaces and static or transformer-based fusion strategies, which cannot simultaneously capture local structural similarity and global hierarchical patterns. In contrast, UMEAD jointly employs dual-space embeddings (Euclidean + Hyperbolic), adaptive multimodal fusion, and iterative pseudo-seed expansion to achieve fully unsupervised alignment with improved robustness and generalization.

As summarized in Table 1, UMEAD differs fundamentally from prior multimodal EA models by integrating dual-space representation learning and adaptive multimodal fusion within a fully unsupervised iterative framework. This combination enables UMEAD to simultaneously model local relational dependencies and global hierarchical semantics, while dynamically balancing multiple modalities to ensure robust alignment across heterogeneous equipment knowledge graphs. The main contributions are summarized as follows:

• We design a pseudo-seed generation framework that integrates semantic and visual features to automatically construct high-confidence alignment seeds, providing effective supervision without manual annotation.
• We propose a dual-space embedding strategy that jointly represents equipment knowledge graphs in Euclidean and hyperbolic spaces, enabling the model to capture both fine-grained local relationships and global hierarchical structures.
• We introduce an adaptive feature fusion mechanism that dynamically balances structural, semantic, relational, attribute, and visual features, thereby producing comprehensive and robust entity representations.
• We develop an iterative constraint mechanism combining bidirectional matching, threshold filtering, and delayed confirmation, which reduces error propagation and ensures the reliability of incremental seed expansion.

In summary, the above four contributions jointly define the novelty of UMEAD. Compared with previous multimodal entity alignment methods, UMEAD introduces a distinctive geometric innovation by establishing a dual-space embedding framework that unifies Euclidean and hyperbolic geometries, enabling simultaneous modeling of local regularities and hierarchical relations that single-space models cannot adequately capture. In addition, the adaptive feature fusion module is presented as a geometry-aware, dynamically weighted extension of prior multimodal fusion ideas rather than a brand-new mechanism: it is redesigned to predict modality weights under the dual-space representation and to balance structural, semantic, relational, attribute, and visual signals in a data-dependent manner.

In contrast, components such as pseudo-seed generation and iterative refinement are inspired by prior literature but are reworked with reliability controls to support a fully unsupervised multimodal setting. Hence, UMEAD is not a simple juxtaposition of existing modules but a purpose-built integration of geometry, modality, and self-supervision tailored for equipment knowledge graphs.The effectiveness of the proposed dual-space and adaptive fusion designs is further validated through the ablation results discussed in Section 3.6.

2. Methods

The proposed unsupervised multimodal equipment entity alignment model employs a dual-space embedding strategy to effectively capture the complex relational hierarchies and semantic information inherent in multimodal data from equipment knowledge graphs, thereby enabling unsupervised entity alignment. First, a pseudo-seed generation module is utilized to compute similarities across visual and textual features, automatically constructing initial aligned entity pairs. During the iterative process, the seed set is progressively expanded with high-confidence pairs, thereby reducing reliance on manually annotated data. Second, embedding learning is performed in both Euclidean and hyperbolic spaces. In Euclidean space, a graph attention network aggregates neighborhood information to capture local structural relationships among entities. In contrast, hyperbolic embedding leverages its negative curvature to accurately model hierarchical structures and global distribution patterns. Finally, an information fusion mechanism dynamically integrates embeddings from both spaces through weighted combination, while a tailored loss function enforces closeness of representations for the same entity across spaces and maintains sufficient separability between different entities. The overall framework of the model is illustrated in Figure 1. To further improve readability,

Table 2. Summary of Modules in UMEAD Framework.

Module	Main Inputs	Main Outputs	Key Innovations/Functions
Pseudo-seed Generation Module	Textual descriptions, equipment images	High-confidence pseudo seed pairs	Combines semantic features (Pairwise BERT) and visual features (VGG-16) for unsupervised seed initialization; introduces confidence filtering and delayed confirmation to improve seed reliability.
Dual-space Embedding Module	Structural information from knowledge graphs	Euclidean and hyperbolic embeddings of entities	Jointly models Euclidean and hyperbolic geometries to capture both local and hierarchical relations; enforces consistency between spaces via contrastive learning.
Relation & Attribute Embedding Submodule	Relation triples and attribute triples	Relation embeddings and attribute embeddings	Uses bag-of-words encoding to represent relation and attribute information, enriching structural representations and complementing multimodal features.
Adaptive Feature Fusion Module	Semantic, visual, structural, relation, and attribute embeddings	Unified multimodal representation for each entity	Introduces a geometry-aware dynamic weighting mechanism using a two-layer fully connected network with ReLU, Sigmoid, and Softmax normalization; balances multimodal contributions under the dual-space representation.
Iterative Constraint Mechanism	Initial pseudo-seeds and learned embeddings	Expanded reliable alignment pairs	Employs bidirectional matching, similarity threshold filtering, and delayed confirmation to iteratively refine the pseudo-seed set and reduce noise propagation.

summarizes the inputs, outputs, and core innovations of each module, complementing Figure 1 by providing a concise overview of how semantic, visual, structural, relational, and attribute information are successively processed and fused through the dual-space embedding pipeline.

2.1. Pseudo-Seed Generation Module

In unsupervised multimodal equipment entity alignment, the absence of manually annotated ground-truth aligned pairs necessitates the use of pseudo-seeds to initialize the alignment process. Pseudo-seeds refer to collections of high-confidence aligned entity pairs that provide reliable supervisory signals for subsequent iterative optimization. Most existing approaches generate pseudo-seed sets primarily from visual information; however, visual features are highly sensitive to image quality, and issues such as low resolution or occlusion can undermine the reliability of similarity estimation.

To address this limitation, we propose a pseudo-seed generation method that leverages Pairwise BERT [17] for semantic feature extraction and VGG-16 [18] for visual feature extraction, integrating both modalities to construct high-quality pseudo-seed sets. The selection of VGG-16 and Pairwise BERT as visual and semantic feature extractors is motivated by their demonstrated stability and compatibility in multimodal alignment tasks. VGG-16 provides robust low- and mid-level visual representations that effectively capture structural and texture-based similarities between entities, while Pairwise BERT directly models semantic relationships between paired textual descriptions, enabling precise estimation of contextual similarity. Both models have been extensively validated in prior cross-modal retrieval and entity alignment studies, ensuring reliable and transferable representations for the pseudo-seed generation stage.

Furthermore, the integration of semantic and visual modalities allows the pseudo-seed generation process to exploit complementary information sources. This multimodal fusion enhances the confidence and diversity of selected pairs, thereby providing a more stable supervisory signal for subsequent iterative optimization.

(1)

Semantic Feature Extraction

In equipment entity alignment tasks, textual information (e.g., equipment descriptions) is an important source of semantic representation. To obtain semantic embeddings of entities, we employ Pairwise BERT. Specifically, let $e_i$ denote an entity and $T_i$ textual description. The text is encoded with Pairwise BERT as $h_i^t=BERT\left(T_i\right)$, where $h_i^t$ represents the semantic embedding vector of $e_i$. The semantic similarity between two entities and is then measured using cosine similarity, as defined in Equation  (1):

$$S_t(e_i,e_j)={\displaystyle \frac{h_i^t·h_j^t}{\parallel h_i^t\parallel \parallel h_j^t\parallel }}$$

(1)

By computing the similarity among all equipment pairs, the semantic similarity matrix $M_t$ is obtained, as defined in Equation (2):

$$M_t=\left\{S_t\left(e_i,e_j\right)\mid e_i\in G_1,e_j\in G_2\right\}$$

(2)

where $G_1$ and $G_2$ denote two different knowledge graphs, and $e_1$ and $e_2$ represent entities from $G_1$ and $G_2$, respectively.

(2)

Visual Feature Extraction

Entities are often associated with rich image information. To obtain their visual features, we employ the VGG-16 neural network to generate image embeddings. Let the image corresponding to entity $e_i$ be denoted as $x_i$. Using a pretrained VGG-16 model, the image features are extracted, and the visual representation vector $h_i^v$ for $e_i$ is derived according to Equation (3). Analogous to the semantic features, visual similarity is measured using cosine similarity, as defined in Equation (4):

$$h_i^v=W_i·\mathrm{VGG}\left(x_i\right)+b_i$$

(3)

$$S_v(e_i,e_j)={\displaystyle \frac{h_i^v·h_j^v}{\parallel h_i^v\parallel \parallel h_j^v\parallel }}$$

(4)

By computing the similarity among all entity pairs, the visual similarity matrix $M_v$ is obtained, as shown in Equation (5).

$$M_v=\left\{S_v\left(e_i,e_j\right)\mid e_i\in G_1,e_j\in G_2\right\}$$

(5)

To effectively integrate semantic and visual information, $M_t$ and $M_v$ are fused through weighted combination to form the final multimodal similarity matrix:

$$M=\lambda M_t+(1-\lambda )M_v,\lambda \in [0,1]$$

(6)

where $\lambda$ is a hyperparameter that controls the relative contribution of semantic and visual information.

Based on the multimodal similarity matrix M, entity pairs are iteratively selected in descending order of similarity. Once a pair is selected, any other associations involving these two entities are discarded, thereby ensuring uniqueness among the selected pairs. This procedure continues until the $top-k$ entity pairs, representing the most similar pairs between $G_1$ and $G_2$ in both semantic and visual features, are obtained. Finally, the automatically generated list of unique, high-similarity entity pairs is used to initiate the iterative process, progressively expanding the seed set and providing reliable initial data support for subsequent model training.

2.2. Dual-Space Embedding Module

In equipment knowledge graphs, entities often exhibit complex hierarchical structures and diverse relational patterns. Traditional single-space embedding methods (e.g., Euclidean) are effective in capturing local information but are often insufficient for modeling global hierarchical structures. By contrast, hyperbolic space, with its unique geometric properties, is well-suited for representing relational hierarchies and tree-like structures.

To accurately represent the multi-level hierarchy and complex local relations in equipment knowledge graphs, we employ a dual-space embedding strategy. The Euclidean space focuses on modeling local interactions between closely related entities, such as components within the same subsystem. In contrast, the hyperbolic space provides an efficient representation of global hierarchies, reflecting the tree-like organization of systems and subsystems. Combining the two spaces yields complementary representations: Euclidean embeddings ensure precise local similarity, while hyperbolic embeddings preserve long-range hierarchical consistency. This dual-space design maintains a geometric symmetry between local and global structures, which is particularly beneficial for the hierarchical characteristics of equipment knowledge graphs.

The dual-space embedding module performs joint representation learning in both Euclidean and hyperbolic spaces. Specifically, neighborhood aggregation is first conducted in Euclidean space to capture fine-grained local relations among equipment entities. The resulting representations are then mapped into hyperbolic space through exponential and logarithmic transformations to preserve global hierarchical information. This parallel embedding process ensures that both local and hierarchical structural cues are encoded consistently. By integrating the learned embeddings from the two spaces, the model achieves robust and geometry-aware representations that enhance entity alignment performance.

(1)

Euclidean Space Embedding

Consider a knowledge graph $G=(V,E)$, where V denotes the set of entities and E denotes the edges representing relations among them. The embedding of each entity $e_i\in \lambda$ in Euclidean space is learned using a GAT, as defined in Equation (7):

$$h_i = {\parallel }_{k=1}^K\sigma \left(\sum _{j\in \mathcal{N}\left(i\right)}{\alpha }_{ij}^{\left(k\right)}{W}^{\left(k\right)}{h}_j\right)$$

(7)

where $N\left(i\right)$ denotes the neighbor set of entity $e_i$; $\sigma (.)$ is a nonlinear activation function; K is the number of attention heads; ${\alpha }_{ij}^k$ and $W^k$ denote the attention coefficients and weight matrix of the $k-th$ head, respectively; $h_j$ is the feature vector of a neighbor; and $h_i$ is the embedding representation of entity $e_i$ in Euclidean space.

The graph attention network (GAT) assigns different weights based on the feature similarity between nodes, giving Euclidean embeddings the following properties:

• Adaptivity: Through the attention mechanism, the model adaptively aggregates task-relevant neighbor information, thereby improving the discriminative power of the embeddings.
• Locality: Euclidean embeddings primarily capture neighborhood-level information, making them well-suited for modeling compact local structures among entities.

(2)

Hyperbolic Space Embedding

Hyperbolic space, with its negative curvature, is particularly suitable for representing relational hierarchies and tree-like structures in data. In equipment knowledge graphs, the hierarchical relations between components and the whole often exhibit a distinct tree-like structure. Consequently, employing hyperbolic embeddings enables more effective modeling of global hierarchical structures.

To map embeddings from Euclidean space to hyperbolic space, we employ exponential and logarithmic mappings. Let the Euclidean embedding be $h_i\in R^d$. Its mapping to the Poincaré ball model is given by Equation (8):

$${exp}_0^c\left(h_i\right)=tanh\left(\sqrt{c}\parallel h_i\parallel \right){\displaystyle \frac{h_i}{\sqrt{c}\parallel h_i\parallel }}$$

(8)

When $h_i=0$, we define $ex{p}_0^c\left(0\right)=0$. Conversely, the logarithmic mapping from hyperbolic space back to Euclidean space is given in Equation (9).

$${log}_0^c\left(y_i\right)={\displaystyle \frac{1}{\sqrt{c}}}{tanh}^{-1}\left(\sqrt{c}\parallel y_i\parallel \right){\displaystyle \frac{y_i}{\parallel y_i\parallel }}$$

(9)

With these two mappings, bidirectional conversion between Euclidean and hyperbolic embeddings is enabled, thereby preserving consistency of information. In this paper, we adopt the HGCN model to capture the hierarchical structures of graphs in hyperbolic space. Specifically, the Euclidean embedding $h_i$ is mapped to hyperbolic space using the exponential mapping, as expressed in Equation (10):

$${\mathbf{z}}_i={exp}_o^c\left(h_i\right)$$

(10)

Here, $z_i\in H^{(d,c)}$ denotes the initial embedding $z_i^0$ in hyperbolic space. For the l-th layer, the subsequent hyperbolic embedding is derived via hyperbolic feature aggregation, as defined in Equation (11):

$${\mathbf{z}}_i^{l+1}={exp}_o^c\left(\sigma \left(A{log}_o^c\left({\mathbf{z}}_i^l\right)W_l\right)\right)$$

(11)

where A denotes the symmetrically normalized adjacency matrix, $\sigma$ represents the $ReLU(.)$ activation function, and $W_l$ is a trainable weight matrix. Finally, the output $z_i$ represents the final embedding of entity $e_i$ in hyperbolic space.

Implementation details. In the Poincaré ball model, the curvature parameter c is fixed to $1.0$ throughout training for stable optimization, following established practice in prior hyperbolic embedding studies [13,19]. To ensure numerical stability during the exponential and logarithmic mappings, the norm of each Euclidean vector $\parallel h_i\parallel$ is restricted to remain below $1-ϵ$ ($ϵ=1\times {10}^{-5}$), and the outputs of the tanh and ${tanh}^{-1}$ functions are clipped near the manifold boundary to prevent overflow. Gradient clipping within the range $[-5,5]$ is applied during backpropagation to avoid exploding updates, and all computations are performed in 32-bit floating-point precision. These stabilization techniques guarantee smooth optimization and reproducibility of the dual-space embedding process without altering the overall model architecture.

(3)

Loss Function

To preserve the structural properties of Euclidean embeddings without distortion, we employ contrastive learning to enforce consistency between Euclidean and hyperbolic embeddings.

$$L_{c,i}^{(G^E,G^H)}=-log{\displaystyle \frac{exp\left(\langle {\mathbf{z}}_i·{\mathbf{h}}_i\rangle \right)}{{\sum }_{k\in E}exp\left(\langle {\mathbf{z}}_i·{\mathbf{h}}_i\rangle \right)}}$$

(12)

$$L_1=\sum _{n=\{1,2\}}{\displaystyle \frac{1}{2|{\mathcal{E}}_n|}}\sum _{i\in {\mathcal{E}}_n}\left(L_{c,i}^{({\tilde{G}}_n^E,{\tilde{G}}_n^H)}+L_{c,i}^{({\tilde{G}}_n^H,{\tilde{G}}_n^E)}\right)$$

(13)

Equation (12) is used to compute the contrastive loss of a single entity $e_i$ between its Euclidean embedding $h_i$ and hyperbolic embedding $z_i$. The numerator $exp\left(\langle z_i·h_i\rangle \right)$ measures the similarity between the two embeddings of the current entity, while the denominator ${\sum }_{k\in E}exp\left(\langle z_i·h_i\rangle \right)$ represents the total similarity between the Euclidean and hyperbolic embeddings of all entities. By taking the logarithm and the negative sign, the equation ensures that the higher the similarity of the two embeddings for the current entity, the smaller the loss. In Equation (12), the denominator iterates over all candidate Euclidean embeddings $h_k$ with $k\in \mathcal{E}$, where $\mathcal{E}$ denotes the set of all entities in the current knowledge graph (or mini-batch). The term $exp\left(\langle z_i,h_i\rangle \right)$ in the numerator corresponds to the positive pairof the same entity $e_i$, while all other terms $exp\left(\langle z_i,h_k\rangle \right)$, $k\ne i$, represent negative pairs. This contrastive formulation encourages the Euclidean and hyperbolic embeddings of the same entity to be close, while pushing apart embeddings of different entities.

Equation (13) calculates the contrastive loss between two knowledge graphs (e.g., the source graph $G_1$ and the target graph $G_2$). Here, ${\sum }_{n=\{1,2\}}$ denotes the summation over the two graphs, $\frac{1}{2|{\mathcal{E}}_n|}$ is a normalization factor, and $|{\mathcal{E}}_n|$ represents the number of entities in knowledge graph n. The term ${\sum }_{i\in {\mathcal{E}}_n}$ computes the loss for each entity $e_i$ in graph n. The expressions $L_{c,i}^{({\tilde{G}}_n^E,{\tilde{G}}_n^H)}+L_{c,i}^{({\tilde{G}}_n^H,{\tilde{G}}_n^E)}$ represent the contrastive losses of entity $e_i$ under different embedding space combinations. By accumulating these losses, $L_1$ quantifies the overall consistency of all entities between Euclidean and hyperbolic embeddings across the two knowledge graphs.

2.3. Adaptive Feature Fusion Module

In multimodal knowledge graph entity alignment tasks, each modality of information (e.g., textual descriptions, images, structural features, relations, and attributes) has its own characteristics. The key challenge lies in effectively fusing these modalities. Traditional feature fusion methods often adopt simple weighted summation or concatenation, while ignoring interdependencies among modalities, which results in low information utilization. To address this issue, this chapter proposes a feature fusion method based on fully connected (FC) networks and gating mechanisms. The method dynamically adjusts the weights of different modalities and generates a unified embedding representation for each entity.

Before feature fusion, it is necessary to extract features from each modality. For each entity $e_i$, the following representations are obtained:

Structural information: Graph Attention Networks (GATs) are used to extract structural information, yielding the structural embedding $h_i^g$.

Semantic information: The pre-trained Pairwise BERT model is employed to encode textual descriptions, resulting in the semantic embedding $h_i^t$.

Relational and attribute information: The bag-of-words model is applied to obtain the relational embedding $h_i^r$ and attribute embedding $h_i^a$.

Visual information: The VGG-16 convolutional neural network is used to extract image features, producing the visual embedding $h_i^v$.

Since the importance of each modality may vary under different circumstances, a dynamic weighting mechanism is required. In this work, a two-layer fully connected network with ReLU activation is applied to perform nonlinear mapping and generate weight scores for each modality, as shown in Equation (14):

$$w_i=\sigma \left(W_2\mathrm{ReLU}\left(W_1{x}_i+b_1\right)+b_2\right)$$

(14)

Here, $x_i=[h_i^g,h_i^t,h_i^r,h_i^a,h_i^v]$ denotes the concatenated feature vector; $W_1$ and $W_2$ are learnable parameter matrices; $b_1$ and $b_2$ are bias terms; and $\sigma (.)$ denotes the sigmoid function, which ensures that the weight values lie within the interval $(0,1)$. In this way, a score vector $w_i=[w_i^g,w_i^t,w_i^r,w_i^a,w_i^v]$ that assigns weights to all modalities is obtained.

Since directly adopting $w_i$ may result in scale inconsistency among modality features, softmax normalization is applied to guarantee that the weights across all modalities sum to 1, thereby preventing any particular modality from dominating or being neglected, as shown in Equation (15):

$${\alpha }_i^m={\displaystyle \frac{exp\left(w_i^m\right)}{{\sum }_{m^{\prime }}exp\left(w_i^{m^{\prime }}\right)}},m\in \{g,t,r,a,v\}$$

(15)

Here, ${\alpha }_i^m$ denotes the normalized weight of modality m. After obtaining the weights of all modalities, the modality features are combined through weighted concatenation to derive the final representation of entity e, as shown in Equation (16):

$$h_i^u=\underset{m\in \{g,f,r,a,v\}}{⨁}{\alpha }_i^m{h}_i^m$$

(16)

In our design, the adaptive fusion network adopts a two-layer fully connected structure, as defined in Equation (14), to model nonlinear interactions among different modality features. The first fully connected (FC) layer transforms the concatenated modality vector into a hidden representation with 512 dimensions, followed by a ReLU activation to introduce nonlinearity. The second FC layer maps this hidden representation to five scalar values corresponding to the five modality types (structural, textual, relational, attribute, and visual). A sigmoid function is then applied to constrain the outputs to the range (0, 1), and a subsequent softmax normalization (Equation (15)) ensures that the modality weights sum to one. Dropout with a rate of 0.2 is applied after the ReLU activation to improve generalization.

This configuration is lightweight yet expressive enough to capture inter-modality dependencies without introducing excessive parameters. We found that a single-layer version failed to adequately model nonlinear correlations, while deeper fusion networks (three or more layers) led to slight overfitting and unstable convergence. The empirical comparison in Section 3.8 further supports that the two-layer configuration achieves the best balance between performance and stability.

2.4. Iterative Constraint Mechanism

In multimodal entity alignment tasks, particularly in equipment-related scenarios, the complexity of the data and the incompleteness of multimodal information make it challenging to directly obtain large-scale, high-quality annotated alignment seeds. To address this, an iterative strategy is introduced. Its core idea is to use a small number of initially generated pseudo-seed pairs as the starting point, and then, through model training and updating, iteratively extract new high-confidence alignment pairs from the unaligned entities. This gradually expands the seed set while simultaneously enhancing the embedding representations of the model. The process is repeated until the number of newly generated entity pairs falls below a predefined threshold, at which point the iteration terminates.

The rationale for introducing the iterative constraint mechanism is to provide a stable and progressive learning framework in the absence of sufficient supervision. Instead of relying solely on a limited initial seed set, the iterative process allows the model to continuously refine alignment quality while controlling error propagation through constraint strategies.

Nevertheless, during the iterative process, erroneous entity pairs may be mistakenly incorporated into the seed set and subsequently propagated during training, leading to the accumulation of errors and a decline in alignment accuracy. To mitigate this, a refined filtering strategy is required to ensure the reliability of newly aligned pairs. This chapter introduces constraint strategies including bidirectional nearest neighbor, similarity threshold filtering, and delayed confirmation, thereby constructing a robust iterative optimization framework.

(1)

Bidirectional Nearest Neighbor Constraint.

In equipment knowledge graph alignment, each entity ideally corresponds to a unique match. However, due to heterogeneous data sources and varying entity descriptions, direct similarity-based matching can lead to mismatches. To mitigate this, a bidirectional nearest neighbor constraint is applied.

For each entity $e_i\in G_1$, its most similar entity in $G_2$ is identified as:

$$e_j^{*}=arg\underset{e_j\in G_2}{max}s(e_i,e_j),$$

(17)

and vice versa for $e_j\in G_2$:

$$e_i^{*}=arg\underset{e_i\in G_1}{max}s(e_i,e_j).$$

(18)

Only when $(e_i,e_j)$ are mutual nearest neighbors, i.e.,

$$e_j^{*}=e_j\mathrm{and}{e}_i^{*}=e_i,$$

(19)

is the pair regarded as a reliable alignment candidate. This constraint effectively filters asymmetric matches and reduces noise propagation.

(2)

Similarity Threshold Filtering.

Even if $(e_i,e_j)$ are mutual nearest neighbors, low-similarity pairs may still be erroneous. To improve confidence, we apply a similarity threshold ${\gamma }_k$, retaining only those pairs that exceed this threshold:

$$S_k^{\prime }=\{(e_i,e_j)\mid e_i\in G_1,e_j\in G_2,s(e_i,e_j)\ge {\gamma }_k\}.$$

(20)

(3)

Delayed Confirmation Mechanism.

To further prevent the accumulation of alignment errors, a delayed confirmation strategy is introduced. Instead of immediately adding newly filtered pairs $(e_i,e_j)\in S_k^{\prime }$ to the next iteration’s seed set, they are first placed into a candidate pool $C_k$. If a pair remains consistent with both the bidirectional constraint and the similarity threshold over n consecutive iterations, it is then promoted into the official seed set $S_{k+1}$. This mechanism effectively mitigates the impact of transient noise and improves the reliability of incremental learning.

(4)

Overall Algorithm.

The entire iterative constraint process is summarized in Algorithm 1, which integrates all aforementioned steps into a reproducible procedure. This explicit pseudocode ensures clarity and replicability for future studies.

Algorithm 1 Iterative Constraint Mechanism for Pseudo-Seed Expansion

Require:  $G_1,G_2,S_0,{\gamma }_k,n,T$ Ensure:  $S_T$   1: for $k=1$ to T do   2:        Step 1: Train model using $S_{k-1}$ to update embeddings of $G_1,G_2$.   3:        Step 2: For each $e_i\in G_1$ find nearest $e_j^{*}$ in $G_2$; for each $e_j\in G_2$ find nearest $e_i^{*}$ in $G_1$.   4:          $M_k\leftarrow \{(e_i,e_j)\mid e_j^{*}=e_j\wedge e_i^{*}=e_i\}$.   5:        Step 3: $S_k^{\prime }\leftarrow \{(e_i,e_j)\in M_k\mid s(e_i,e_j)\ge {\gamma }_k\}$.   6:        Step 4: Add $S_k^{\prime }$ to candidate pool $C_k$. Promote pairs that are valid for n consecutive iterations to $S_k$.   7:         if $|S_k-S_{k-1}|<S_{\min }$ then   8:              break   9:        end if  10: end for  11: return  $S_T$

It is worth noting that all backbone networks, including VGG-16, Pairwise BERT, and GAT, are employed in their standard forms without structural modification. This design choice ensures reproducibility and fair comparison with existing multimodal alignment methods. The main contribution of UMEAD lies in the integration of these components through the dual-space embedding and iterative constraint mechanisms, rather than altering their internal architectures.

2.5. Model Alignment Loss

The model’s loss function consists of two parts: (1) the contrastive loss for aligning Euclidean and hyperbolic space embeddings, and (2) the margin-based alignment loss for the entity alignment task.

The contrastive loss for aligning Euclidean and hyperbolic space embeddings is derived from Equation (13). The margin-based alignment loss is calculated as shown in Equation (21):

$$L_2=\sum _{(e_1,e_2)\in S}\sum _{(e_1^{\prime },e_2^{\prime })\in S^{\prime }}{\left[d\left(e_1,e_2\right)-d\left(e_1^{\prime },e_2^{\prime }\right)+\gamma \right]}_{+}$$

(21)

where ${\left[x\right]}_{+}$ represents the positive part of x, i.e., $max(x,0)$; $d(e_1,e_2)=\parallel h_{e_1}^u-h_{e_2}^u\parallel$; $e_1$ is an entity from $G_1$; $e_2$ is an entity from $G_2$; $h_{e_1}^u$ is the composite embedding representation of $e_1$; $h_{e_2}^u$ is the composite embedding representation of $e_2$; $\gamma >0$ is the margin parameter that defines the distance between positive and negative samples; and S and $S^{\prime }$ are the sets of positive and negative samples, respectively, with $S^{\prime }$ being the set of negative samples generated through a nearest-neighbor sampling approach.

By combining these two losses, the final training objective is achieved, as shown in Equation (22):

$$L={\lambda }^{\prime }{L}_1+(1-{\lambda }^{\prime })L_2$$

(22)

where ${\lambda }^{\prime }\in [0,1]$ is a hyperparameter used to balance the impact of the two losses on the overall optimization objective.

3. Experiment

3.1. Datasets

To comprehensively evaluate the proposed UMEAD framework, we conduct experiments on both the Encyclopedia Media Multimodal Entity Alignment Dataset (EMMEAD) and the public multimodal benchmark MMKG [8].

Proprietary dataset (EMMEAD). The EMMEAD dataset is constructed to capture multimodal and hierarchical characteristics of equipment-related knowledge. It contains three main categories of entities:

• Ships: 4 major categories and 28 subcategories, including passenger ships (e.g., high-speed passenger ships, tourist ships), cargo ships (e.g., dry cargo, container, roll-on/roll-off), auxiliary transport ships (e.g., supply ships, hospital ships), and special-purpose ships (e.g., tugboats, research ships).
• Aircraft: 15 categories, including cargo aircraft, passenger aircraft, medical rescue aircraft, business jets, survey aircraft, and others.
• Other related entity types: 11 categories, such as countries/regions, manufacturers, institutions, enterprises, airports, ports, electronic equipment, logistics facilities, and air routes.

The dataset integrates relational triples, attribute triples, and visual data (images). It also contains SameAs links between the encyclopedia and media sources to support entity alignment. Due to the sensitivity of military-related information, this dataset is not publicly available. Its statistics are summarized in

Table 3. Statistics of the datasets used in our experiments.

Dataset	Entities	Relational Triples	Attribute Triples	Images	SameAs
EMMEAD (Encyclopedia)	10,612	50,533	60,341	9453	-
EMMEAD (Media)	9512	40,381	45,354	9810	6500
FB15K	14,951	592,213	29,395	13,444	-
DB15K	14,777	9028	46,121	12,841	12,846
YAGO15K	15,283	122,886	48,405	11,194	11,199

.

Public datasets (MMKG). We also evaluate on the multimodal entity alignment dataset MMKG [8], which combines three widely used knowledge bases: Freebase [20], DBpedia [21], and YAGO [22]. Specifically, FB15K-DB15K is constructed from FB15K (a subset of Freebase) and DB15K (a subset of DBpedia), while FB15K-YAGO15K is derived from FB15K and YAGO15K (a subset of YAGO).

Since many original image links in MMKG are outdated or invalid, entity-related images are supplemented through controlled web retrieval from publicly accessible sources (e.g., Wikipedia, Wikimedia Commons, and major search engines), following the protocols of prior multimodal alignment studies [9,23]. All collected images are de-duplicated via perceptual hashing and manually screened to remove irrelevant content, ensuring that only representative and non-redundant samples are used. To avoid data leakage and maintain fair comparison, the retrieved images are used solely for experimental evaluation. This practice ensures that the dataset remains consistent with the MMKG benchmark while mitigating the impact of missing modalities.

3.2. Evaluation Metrics

To evaluate the alignment performance, we adopt two widely used metrics: Hits@k and Mean Reciprocal Rank (MRR). These metrics are standard in knowledge graph alignment and information retrieval, as they jointly measure both ranking quality and retrieval accuracy.

Hits@k. Hits@k (with $k=1,10$ in our experiments) calculates the proportion of correctly aligned entities that appear within the top-k candidates. It reflects the model’s ability to rank the true counterpart among the most relevant predictions. Formally:

$$\mathrm{Hits}@k={\displaystyle \frac{1}{\left|S\right|}}\sum _{i=1}^{\left|S\right|}\mathsf{\Pi }(r_i,k),$$

(23)

where $\left|S\right|$ denotes the number of test entities, $r_i$ is the rank of the correct counterpart for the i-th entity, and $\mathsf{\Pi }(·)$ is an indicator function:

$$\mathsf{\Pi }(r_i\le k)=\left\{\begin{array}{cc}1,\hfill & r_i\le k,\hfill \\ 0,\hfill & r_i>k.\hfill \end{array}\right.$$

(24)

Mean Reciprocal Rank (MRR). MRR measures the average reciprocal rank of the true counterparts across all test entities, thus providing a more fine-grained evaluation of ranking performance:

$$\mathrm{MRR}={\displaystyle \frac{1}{\left|S\right|}}\sum _{i=1}^{\left|S\right|}{\displaystyle \frac{1}{r_i}}.$$

(25)

Higher values of Hits@k and MRR indicate better alignment performance.

Statistical reliability. To ensure the robustness and reproducibility of the reported results, all experiments are conducted over multiple independent runs with different random seeds. This procedure mitigates the influence of random initialization and sampling variations, providing statistically reliable estimates of model performance.

In addition, to verify the significance of improvements over strong baselines such as UMAEA and MCLEA, paired significance tests (two-tailed t-test and Wilcoxon signed-rank test) are performed on the per-run results. Performance differences reaching the 0.05 significance level are considered statistically significant, though not explicitly annotated in the result tables for clarity. This evaluation protocol follows standard practices in recent alignment studies and ensures that the reported gains reflect consistent algorithmic advantages rather than random fluctuations.

3.3. Experimental Setup

In this experiment, the hidden layer size of the GAT is set to 300, the output dimension of the VGG-16 model is 4096, and the encoding dimension for relationships and attributes is set to 1000. During training, two configurations are considered: the purely unsupervised setting (UMEAD) and a semi-supervised variant (UMEAD-s) for controlled comparison. Both configurations rely entirely on automatically generated pseudo-seeds rather than manually annotated alignment pairs.

In the unsupervised UMEAD configuration, the model starts with a small set of high-confidence pseudo-aligned entity pairs automatically produced by the pseudo-seed generation module; no ground-truth seeds are used at any stage. The “alignment seed ratio” reported in

Table 4. Experimental Parameter Settings (values correspond to unsupervised UMEAD unless otherwise noted).

Parameter	Value
Learning rate	0.001
Weight decay	0.01
Number of epochs	1000
Batch size	512
Embedding dimension	100
Alignment seed ratio (%)	20 1
Iteration similarity threshold ${\gamma }_k$	0.8
Delayed confirmation period n	3
Loss balance parameter ${\lambda }^{\prime }$	0.1

¹ The “alignment seed ratio” denotes the proportion of automatically generated pseudo-seeds; no human-labeled alignments are used.

refers to the proportion of pseudo-seeds relative to the total number of candidate alignments at initialization, rather than human-labeled seeds. For consistency, the same parameter settings are used when comparing the semi-supervised UMEAD-s variant, where a subset of gold alignments (20%) is provided only for reference comparison in certain ablation scenarios.

The pseudo-seed generation weight parameter is set to $\lambda =0.35$, and the number of pseudo-seeds is $k=3000$. Other parameters are listed in Table 4, and the experimental environment is summarized in

Table 5. Experimental Environment.

Configuration	Specification
CPU	Intel(R) Xeon(R) Platinum 8358P
GPU	RTX3090 × 2
RAM	64GB
Operating System	Ubuntu-20.04.5
Python Version	3.7
PyTorch Version	2.0.1

.

To ensure clarity, all subsequent tables explicitly specify whether the results correspond to UMEAD (unsupervised, 0% gold seeds) or UMEAD-s (semi-supervised, with a small proportion of gold seeds for controlled comparison).

The hyperparameters listed in Table 4 were chosen to balance empirical validation and established practice, and their final defaults were confirmed by the sensitivity analysis reported in Section 3.8. In practice we proceeded as follows: for core fusion and loss weights ($\lambda$, ${\lambda }^{\prime }$) we performed small-scale grid-style tuning on a held-out validation split (evaluating coarse candidate values) and selected values that offered the best trade-off between multimodal fusion quality and alignment stability; this yielded $\lambda =0.35$ and ${\lambda }^{\prime }=0.10$. The pseudo-seed related parameters (initial seed count k and similarity threshold ${\gamma }_k$) were set after preliminary experiments that examined the balance between seed diversity and noise—$k=3000$ provides sufficient coverage while ${\gamma }_k=0.8$ effectively filters low-confidence pairs. Architectural and optimizer defaults (embedding dimension, GAT hidden size, VGG output dimension, relation/attribute encoding size, learning rate, weight decay, batch size, and number of epochs) follow commonly used settings in recent EA and multimodal works and were verified to converge stably on our datasets; specifically, embedding dimension = 100 and GAT hidden size = 300 were adopted for a good trade-off between representation capacity and computational cost. The delayed confirmation period n was set conservatively to 3 to reduce transient errors during iterative expansion. We refer readers to Section 3.8 for the full sensitivity plots and brief discussion demonstrating that model performance is relatively stable within nearby parameter ranges.

3.4. Comparative Experiments

To comprehensively evaluate the performance of the proposed unsupervised multimodal entity alignment model (UMEAD) and its semi-supervised variant (UMEAD-s), we compare them with a series of representative baseline methods across three datasets: FB15K-DB15K, FB15K-YAGO15K, and EMMEAD. UMEAD-s serves as a semi-supervised version of UMEAD, where the pseudo-seed generation module is replaced with a small set of pre-aligned seed pairs that are iteratively expanded during training.

Baseline methods. The selected baselines span three main categories:

• Structure-based method:MTransE [3] extends the TransE framework to cross-graph settings by jointly learning entity and relation embeddings across different knowledge graphs. It serves as a fundamental and widely used baseline for structure-only alignment.
• GNN-based methods: GCN-Align [24] employs Graph Convolutional Networks to capture neighborhood information for alignment; RDGCN [25] models interactions between the entity graph and its relational dual graph; HGCN [19] jointly learns entity and relation embeddings without pre-aligned relation seeds; and DSEA [26] integrates multimodal features through self-attention to enhance entity matching.
• Semi-supervised methods: BootEA [4] adopts a bootstrapping framework to iteratively label new aligned pairs; NAEA [27] employs neighborhood-aware attention to capture structural dependencies; SEA [28] leverages semi-supervised adversarial training to mitigate degree distribution bias; and RNM [29] enhances alignment via relation-aware neighborhood matching.
• Unsupervised methods: IMUSE [30] jointly considers relation and attribute triples for alignment; MCLEA [9] applies multimodal contrastive learning to generate pseudo-seeds; SelfKG [31] adopts self-supervised negative sampling; and UMAEA [23] addresses missing visual modalities for robust multimodal alignment, and MMEA [32] performs joint visual–textual embedding learning with static multimodal fusion for entity matching.

For all baseline models, we reproduced the reported results on our datasets using the authors’ official implementations and the hyperparameter settings provided in their papers. All experiments were conducted under the same data partitions, preprocessing procedures, and evaluation metrics as UMEAD, ensuring consistent experimental conditions across methods.

Results of UMEAD-s.

Table 6. Entity alignment performance comparison results (%) of UMEAD-s model.

Model	FB15K-DB15K			FB15K-YAGO15K			EMMEAD
	Hits@1	Hits@10	MRR	Hits@1	Hits@10	MRR	Hits@1	Hits@10	MRR
Structure-based alignment method
MTransE	5.12	16.32	9.70	4.83	17.45	10.11	4.25	15.84	8.93
GNN-based alignment methods
GCN-align	6.30	18.60	11.50	6.55	19.81	12.60	5.30	18.25	9.86
RDGCN	13.34	23.10	15.33	11.61	25.32	18.08	11.06	24.57	15.20
HGCN	14.32	28.45	18.21	13.35	29.12	19.33	15.61	29.89	20.45
DSEA	26.71	40.88	31.60	21.05	37.12	26.33	18.41	32.35	22.16
Semi-supervised alignment methods
BootEA	11.35	23.10	15.85	13.41	25.52	16.91	10.24	23.13	15.15
NAEA	13.87	27.36	18.15	16.55	29.89	18.46	15.68	30.37	18.48
SEA	16.43	32.10	20.55	17.20	31.45	21.88	15.33	28.10	18.63
RNM	24.30	42.15	30.40	25.67	44.20	32.15	22.10	38.45	27.33
Proposed method
UMEAD-s	25.28	48.62	35.20	31.45	50.33	37.12	34.85	52.10	36.50

reports the performance of UMEAD-s against GNN-based and semi-supervised methods. Traditional GNN baselines (e.g., GCN-Align, RDGCN) achieve low accuracy since they primarily exploit structural information while ignoring multimodal cues. HGCN shows some improvements by incorporating hyperbolic embeddings, but its performance remains limited. DSEA outperforms other GNN-based models due to its adaptive self-attention mechanism. Among semi-supervised methods, RNM performs the strongest, confirming the benefit of relation-aware neighborhood modeling. However, UMEAD-s consistently achieves higher performance across FB15K-YAGO15K and EMMEAD, with Hits@1 values of 31.45% and 34.85%, respectively. This demonstrates the effectiveness of combining dual-space embeddings with multimodal pseudo-seeds, even under limited supervision. This improvement stems from the joint learning of Euclidean and hyperbolic spaces, which enables UMEAD-s to capture both local relational similarity and global hierarchical semantics that structure-based, GNN-based, and semi-supervised baselines fail to represent effectively. By integrating graph topology with multimodal cues, UMEAD-s achieves richer feature interactions and more comprehensive representation learning than models that rely solely on structural or unimodal information. Moreover, the multimodal pseudo-seed generation reduces noise during iterative expansion, resulting in more reliable alignment pairs even under limited supervision.

Results of UMEAD.

Table 7. Entity alignment performance comparison results (%) of UMEAD model.

Model	FB15K-DB15K			FB15K-YAGO15K			EMMEAD
	Hits@1	Hits@10	MRR	Hits@1	Hits@10	MRR	Hits@1	Hits@10	MRR
Unsupervised alignment methods
IMUSE	18.64	45.10	27.85	16.10	41.27	25.60	15.33	40.12	24.55
SelfKG	22.43	48.55	30.22	19.38	44.20	28.71	18.25	43.67	27.80
MCLEA	40.88	60.14	45.93	30.15	57.62	38.53	25.15	51.20	35.40
MMEA	37.25	60.48	44.33	31.52	55.17	39.10	30.18	57.68	42.02
UMAEA	48.30	65.89	57.20	43.30	63.63	53.05	35.20	58.45	45.10
Proposed method
UMEAD	45.22	66.20	55.22	44.86	65.96	54.12	41.25	65.80	53.90

presents the comparison of UMEAD with unsupervised baselines. IMUSE and SelfKG underperform across all datasets, with Hits@1 values below 23%, highlighting the limitations of relying solely on structural and attribute triples. MCLEA achieves stronger results by leveraging multimodal contrastive learning, yet still struggles to capture complex hierarchical patterns. UMAEA performs best among baselines, particularly under scenarios of incomplete visual modalities. Nevertheless, UMEAD consistently surpasses UMAEA on FB15K-YAGO15K and EMMEAD, with Hits@1 improvements of 1.56% and 6.05%, respectively. This demonstrates that dual-space embeddings combined with iterative pseudo-seed expansion yield superior performance, especially in equipment-oriented multimodal KGs where both local and global structures are critical. This superiority can be attributed to the dual-space embedding mechanism, which provides geometric complementarity between Euclidean and hyperbolic spaces and enhances the model’s capacity to integrate multimodal information. While the Euclidean component preserves local neighborhood consistency, the hyperbolic space captures hierarchical dependencies, leading to a balanced and expressive representation. Additionally, the iterative constraint mechanism filters low-confidence pairs, preventing error accumulation during unsupervised training and further improving robustness compared with existing multimodal and unimodal baselines.

Summary. Overall, UMEAD and UMEAD-s demonstrate superior alignment accuracy compared with representative baselines. The results highlight three key findings: (1) multimodal information provides substantial benefits over structure-only baselines; (2) dual-space embeddings effectively model both local neighborhood and global hierarchical features; and (3) iterative pseudo-seed expansion enhances the robustness of alignment, reducing the dependency on manual labels while maintaining a high performance in real-world multimodal equipment knowledge graphs. In particular, the integration of geometry-aware embeddings and adaptive fusion enables UMEAD to align entities with higher semantic precision, which explains its consistent performance gains across different datasets.

Further Analysis of Results. Beyond the overall performance comparison, we further analyze the results from three perspectives. First, the clear gap between UMEAD(-s) and traditional embedding-based methods such as MTransE confirms that incorporating multimodal information effectively mitigates the structural sparsity problem in equipment knowledge graphs. In addition, UMEAD(-s) consistently outperforms GNN-based models (e.g., GCN-Align, RDGCN, HGCN), indicating that multimodal cues provide complementary information beyond structural connections. Second, while advanced multimodal methods such as MMEA and other contrastive or fusion-based approaches achieve strong results through visual—textual integration, UMEAD surpasses them by introducing a dual-space embedding mechanism that simultaneously captures local relational regularities and global hierarchical semantics, particularly on FB15K-YAGO15K where hierarchical relations are dominant. Third, compared with semi-supervised and unsupervised competitors, the iterative pseudo-seed mechanism enhances robustness by filtering noisy alignments during training, which ensures stable convergence and prevents overfitting on small seed sets. These analyses collectively demonstrate that the improvement of UMEAD is not incidental but arises from its architectural innovations and adaptive learning mechanisms.

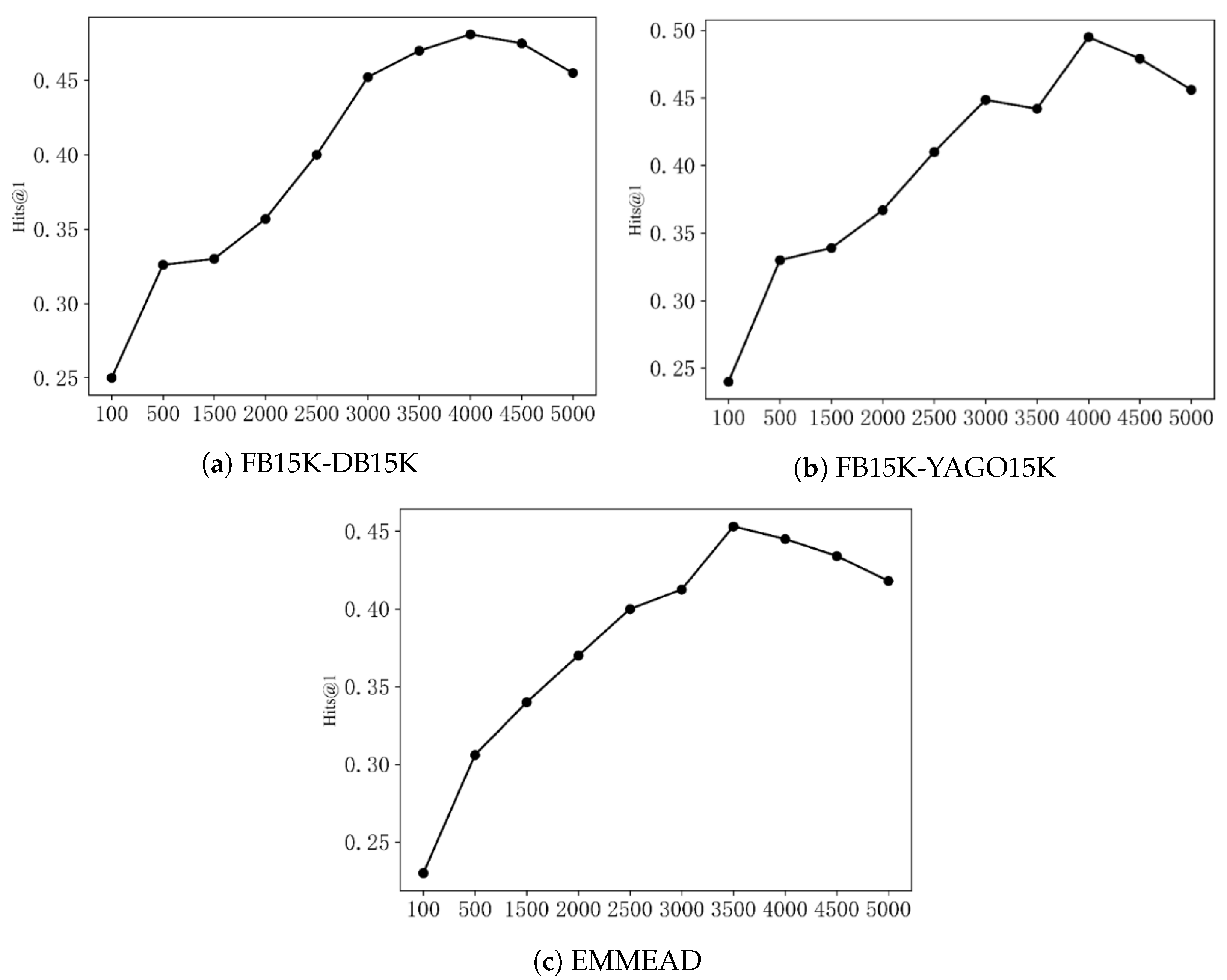
3.5. Experiments on the Number of Pseudo-Seeds

To examine the sensitivity of UMEAD to the size of the initial pseudo-seed set, we varied the threshold parameter k in the pseudo-seed generation module, thereby generating seed sets of different scales. Figure 2 summarizes the results on the three datasets.

The overall trend shows that increasing the number of pseudo-seeds initially improves alignment performance, but performance declines once the seed set grows beyond an optimal scale. Specifically, the best Hits@1 values are observed when the number of pseudo-seeds reaches approximately 3500 on EMMEAD and around 4000 on both FB15K-DB15K and FB15K-YAGO15K. Notably, even with as few as 500 pseudo-seeds, Hits@1 remains above 30% on all datasets, demonstrating the robustness of UMEAD under low-resource conditions.

The decline observed at larger seed sizes is likely due to noise introduced during pseudo-seed expansion. While a moderate number of pseudo-seeds effectively capture key multimodal features (e.g., text and image cues of naval vessels), excessive expansion increases the probability of including low-quality or noisy pairs, which can obscure fine-grained structural distinctions and degrade performance.

In summary, these experiments confirm that UMEAD achieves stable alignment with relatively few pseudo-seeds, and that carefully controlling the scale of the pseudo-seed set is critical to balancing informativeness and noise in multimodal equipment knowledge graph alignment.

3.6. Ablation Study

To comprehensively evaluate the contribution of each functional module in UMEAD, a series of ablation experiments were conducted to isolate the effects of three core components introduced in Section 2: (1) the pseudo-seed generation framework (which integrates multimodal feature extraction and adaptive feature fusion), (2) the dual-space embedding strategy (combining Euclidean and hyperbolic representations), and (3) the iterative constraint mechanism for progressive alignment refinement. Each ablation variant was designed to disable or simplify one or more of these components while keeping the remaining parts intact, ensuring a complete and interpretable module-level evaluation.

Four ablation variants were constructed, namely UMEAD(-se), UMEAD(-v), UMEAD(-il), and UMEAD(-h). UMEAD(-se) excludes semantic information and uses only visual features to generate pseudo-seeds, while UMEAD(-v) removes visual information and relies solely on textual semantics. Together, these two variants reveal the effect of the multimodal pseudo-seed generation and adaptive feature fusion modules, since removing either modality prevents the fusion mechanism from functioning effectively. UMEAD(-il) disables the iterative constraint mechanism for seed expansion, while UMEAD(-h) removes hyperbolic space embedding, using only Euclidean embeddings for entity representation. The performance of these variants was compared against the complete UMEAD model.

As shown in

Table 8. Ablation study results of UMEAD model on entity alignment.

Model	FB15K-DB15K			FB15K-YAGO15K			EMMEAD
	Hits@1	Hits@10	MRR	Hits@1	Hits@10	MRR	Hits@1	Hits@10	MRR
UMEAD(-se)	35.20	54.16	47.67	37.42	51.88	42.17	30.47	56.57	40.89
UMEAD(-v)	31.87	53.76	41.51	35.65	52.32	40.91	25.62	52.24	42.32
UMEAD(-il)	36.72	51.51	47.26	35.41	53.68	43.20	27.37	54.46	44.19
UMEAD(-h)	35.86	55.13	45.23	32.38	56.76	41.03	34.12	57.34	44.76
UMEAD	45.22	66.20	55.22	44.86	65.96	50.12	41.25	65.80	53.90

, the exclusion of visual information in UMEAD(-v) results in the largest performance drop. On the EMMEAD dataset, Hits@1 decreases by 15.63% compared with the complete model, indicating that visual information plays a decisive role in distinguishing equipment entities, as image features contain unique structural and appearance cues that complement textual semantics. Conversely, UMEAD(-se), which removes semantic features, also suffers a notable performance degradation, with MRR values reduced by 13.01% on FB15K-DB15K. This demonstrates the essential role of semantic information in capturing naming variations, textual descriptions, and hierarchical relationships that visual information alone cannot represent effectively. Together, these results highlight the necessity of multimodal integration. When both modalities are used jointly, the adaptive fusion mechanism dynamically balances their contributions, leading to significantly higher alignment reliability and robustness.

Although the adaptive feature fusion mechanism is not independently ablated, its contribution is implicitly reflected in the performance gap between UMEAD(-se)/UMEAD(-v) and the complete UMEAD model. These single-modality variants represent extreme cases where adaptive fusion cannot operate. The consistent performance improvement of the full model thus verifies the fusion mechanism’s effectiveness in mitigating modality bias and enhancing multimodal complementarity.

In the case of UMEAD(-il), where the iterative constraint mechanism is disabled, Hits@1 decreases by more than 8.0% on average across all datasets. Without iterative refinement, error propagation from noisy seeds cannot be effectively mitigated, and the alignment process becomes vulnerable to compounding inaccuracies. The iterative mechanism helps eliminate low-quality pairs and progressively refines the pseudo-seed pool with more reliable alignments, demonstrating its critical role in ensuring stability and robustness.

For UMEAD(-h), removing the hyperbolic space embedding leads to consistent performance declines across all datasets, with the largest drop observed on FB15K-YAGO15K, where Hits@1 decreases by 12.48%. This result clearly validates the critical role of hyperbolic geometry in modeling hierarchical structures. Equipment knowledge graphs often exhibit tree-like and multi-level dependencies that are difficult to represent effectively in Euclidean space. Beyond quantitative evidence, the superiority of the dual-space embedding arises from its geometric and representational complementarity. Euclidean space preserves local neighborhood similarity, enabling fine-grained relational learning, but suffers from distortion when encoding large hierarchical or tree-like patterns. Hyperbolic space, in contrast, provides exponentially increasing representational capacity, allowing entities at different hierarchical depths to be arranged with minimal overlap and preserving global consistency. By jointly optimizing embeddings in both Euclidean and hyperbolic geometries, UMEAD captures fine-grained local regularities and coarse-grained hierarchical dependencies simultaneously. This complementary design not only mitigates structural information loss but also stabilizes alignment under incomplete or noisy multimodal conditions—an advantage that single-space approaches fail to achieve.

In summary, the ablation results confirm that each component of UMEAD contributes indispensably to the overall performance. The pseudo-seed generation (including multimodal fusion) provides strong initial alignment cues, the iterative constraint mechanism enhances reliability through progressive filtering, and the dual-space embedding with hyperbolic geometry preserves global hierarchical consistency. These modules collectively ensure that UMEAD achieves a consistently superior performance across heterogeneous multimodal datasets.

Computational cost and failure analysis. To provide additional practical context, we analyze the computational efficiency and qualitative failure patterns of UMEAD and its ablated variants. All experiments were conducted on an NVIDIA RTX3090 ×2 GPU platform (as detailed in Table 5). On average, the complete UMEAD model required approximately 1.2× the training time of the simplest variant (UMEAD(-h)), primarily due to the additional optimization in hyperbolic space and the iterative constraint mechanism. Parameter counts ranged from 38.2 M for UMEAD(-h) to 46.1M for the complete model, indicating that the observed performance gains stem mainly from architectural design rather than increased model size.

From a qualitative perspective, removing the visual modality (UMEAD(-v)) most severely affects classes of entities with distinctive appearance patterns—such as surface ships and aircraft — where structural cues play a crucial role in disambiguation. In contrast, removing semantic information (UMEAD(-se)) primarily impacts entities with visually similar forms but different operational functions, such as electronic equipment. This observation highlights the complementary strengths of visual and semantic modalities: visual cues enhance local discriminability, whereas textual semantics contribute functional and contextual differentiation. Such insights further illustrate why adaptive fusion and multimodal integration are essential for reliable alignment in complex equipment knowledge graphs.

3.7. Qualitative Case Analysis

To further understand the behavior of UMEAD beyond overall quantitative metrics, we conducted a case-level analysis of representative best and worst alignment results. The goal is to illustrate in which situations the model performs reliably and where it still encounters difficulties.

Selection and evaluation. For each dataset, we selected several aligned entity pairs from the test set with the highest and lowest final similarity scores $s(e_i,e_j)$. The high-confidence pairs represent cases where UMEAD achieved correct and stable alignment, while the low-confidence pairs correspond to mismatches or uncertain predictions. Each case is analyzed according to the available modality combinations (structure, relation, attribute, text, or visual embeddings) and its neighborhood consistency in the knowledge graph.

Observations. The analysis reveals several consistent patterns. High-confidence (best) cases usually occur when: (1) multiple modalities provide mutually consistent evidence (e.g., structural and relational embeddings reinforce each other); (2) entities have dense graph connections that yield reliable contextual aggregation; or (3) pseudo-seeds from similar categories help guide the alignment process. In contrast, low-confidence (worst) cases often arise when: (1) some modalities are missing or incomplete, leading to insufficient cross-modal signals; (2) attributes or relations are sparsely connected, causing structural ambiguity; or (3) pseudo-seeds contain residual noise that misleads the iterative alignment expansion.

Insights and implications. These qualitative findings align with the quantitative results reported earlier: the model performs most robustly when multimodal signals are complementary and structurally consistent, but its reliability decreases under sparse or noisy modality conditions. Such insights suggest two potential directions for improvement: (1) introducing uncertainty-aware fusion weights to down-weight unreliable modalities, and (2) enhancing the pseudo-seed refinement strategy to further suppress noise during iterative updates. Overall, this analysis provides a clearer understanding of UMEAD’s strengths and remaining challenges in complex multimodal alignment scenarios.

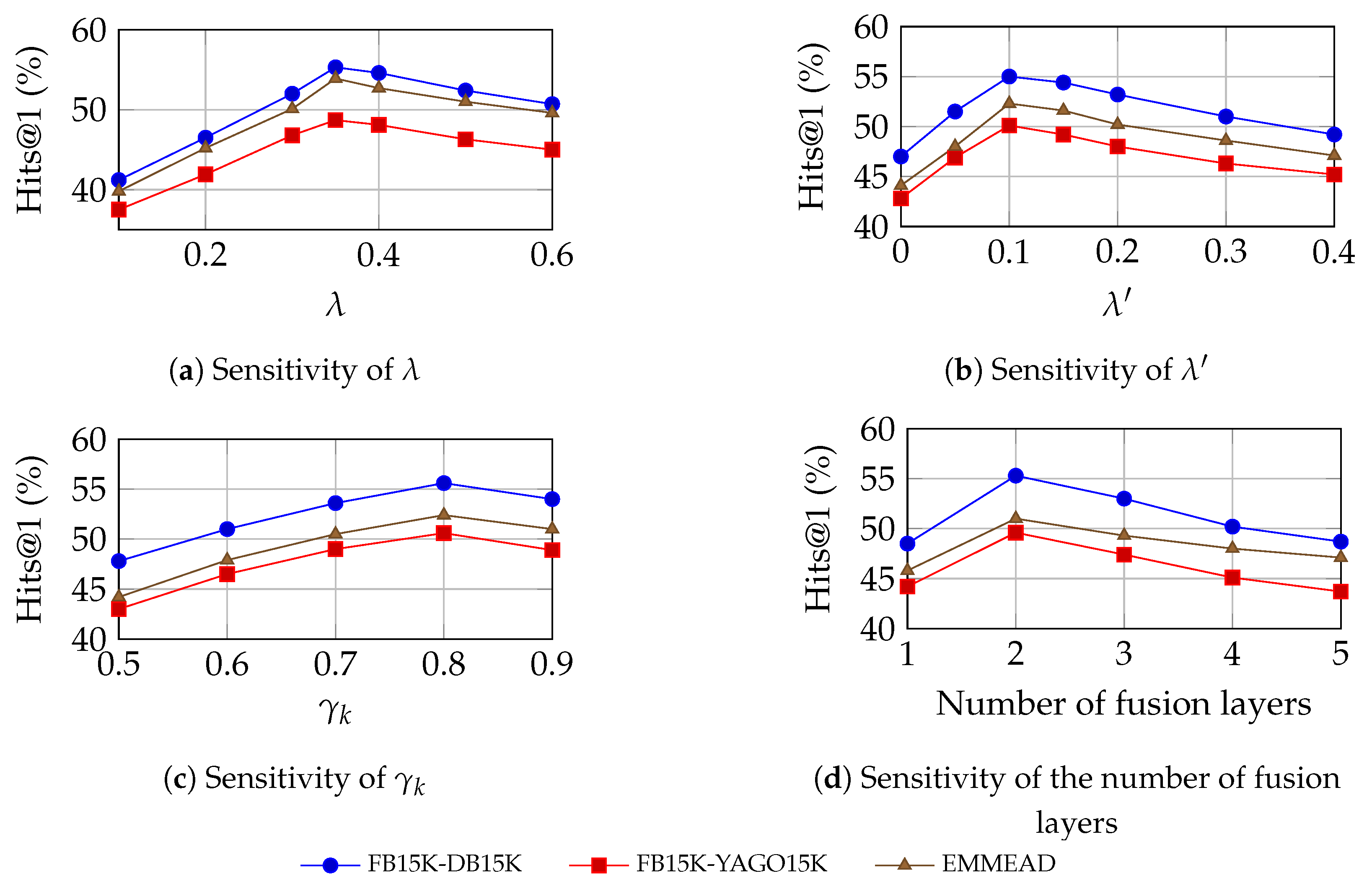
3.8. Hyperparameter Sensitivity Analysis

To evaluate the robustness of UMEAD with respect to key hyperparameters, we conducted sensitivity experiments on $\lambda$, ${\lambda }^{\prime }$, ${\gamma }_k$, and the number of fusion layers. Figure 3 illustrate the variation of Hits@1 on the FB15K-DB15K, FB15K-YAGO15K, and EMMEAD datasets when each parameter is adjusted while keeping the others fixed at their default values.

As shown in the figures, the performance of UMEAD remains stable across datasets within a broad range of hyperparameter settings. The optimal configuration is achieved when $\lambda =0.35$, ${\lambda }^{\prime }=0.1$, ${\gamma }_k=0.8$, and the number of fusion layers is two.

Across all datasets, the model shows consistent sensitivity trends. When $\lambda$ varies within [0.3, 0.4], Hits@1 remains stable, indicating that the pseudo-seed fusion weight has a moderate but consistent influence on alignment quality. For ${\lambda }^{\prime }$, which controls the balance between alignment loss and contrastive loss, performance peaks around 0.1 across datasets and declines slightly when the contrastive loss becomes dominant. The iteration similarity threshold ${\gamma }_k$ exhibits optimal performance near 0.8, confirming that a stricter filtering criterion effectively removes noisy candidate pairs while maintaining sufficient positive matches. Regarding the number of fusion layers, using two fully connected layers achieves the best trade-off between feature interaction and overfitting, while deeper networks tend to slightly reduce performance.

Overall, these results demonstrate that UMEAD remains robust and dataset-agnostic across a broad range of key hyperparameter settings. The chosen default settings ($\lambda =0.35$, ${\lambda }^{\prime }=0.1$, ${\gamma }_k=0.8$, two fusion layers) provide a stable and well-balanced configuration for multimodal entity alignment across heterogeneous datasets.

4. Conclusions

This paper presents UMEAD, an unsupervised multimodal entity alignment framework for equipment knowledge graphs, which integrates four key modules: a pseudo-seed generation strategy that jointly leverages semantic and visual information, a dual-space embedding mechanism that combines Euclidean and hyperbolic spaces to capture both local neighborhood and global hierarchical structures, an adaptive feature fusion module that dynamically balances multimodal contributions, and an iterative constraint mechanism that progressively refines seed quality. Experiments on both public benchmarks and the proprietary EMMEAD dataset confirm the effectiveness and robustness of UMEAD over a range of baselines. In addition, consistent improvements observed on the public MMKG datasets (FB15K-DB15K and FB15K-YAGO15K) demonstrate that UMEAD’s advantages are not limited to hierarchical equipment data, highlighting the generalizability of the proposed approach.

4.1. Complexity Analysis

To clarify scalability and computational feasibility, we provide a concise complexity analysis of UMEAD. Per iteration, the main computational costs arise from three components: (1) representation learning via GAT-based message passing, which scales approximately as $\mathcal{O}\left(\right|E|·d)$, where $\left|E\right|$ is the number of edges and d the embedding dimension; (2) nearest-neighbor search for bidirectional matching, which in a naive implementation requires $\mathcal{O}\left(\right|V{|}^2·d)$ pairwise comparisons and becomes the dominant cost for large graphs; and (3) Euclidean–hyperbolic mappings and geometric operations, which cost $\mathcal{O}\left(\right|V|·d)$ per round. With R denoting the number of iterative rounds, the overall time complexity is therefore:

$$\mathcal{O}\left(R·\left(\right|E|·d+T_{\mathrm{NN}}+|V|·d)\right),$$

where $T_{\mathrm{NN}}$ denotes the nearest-neighbor search cost. In practice, $T_{\mathrm{NN}}$ can be substantially reduced using approximate nearest-neighbor (ANN) search libraries such as FAISS or HNSW, yielding an empirical complexity near $\mathcal{O}\left(\right|V|log|V|·d)$. Hence, the dominant per-iteration cost reduces to $\mathcal{O}\left(\right|E|·d+|V|log|V|·d)$, and the overall cost remains tractable for large-scale graphs. The space complexity is mainly $\mathcal{O}\left(\right|V|·d+|E\left|\right)$ for embedding and graph storage, plus minor overhead for ANN indices. Accordingly, UMEAD is feasible for moderate-to-large graphs when combined with standard engineering measures such as ANN indexing, mini-batch sampling, parallelization, and early stopping in the iterative process.

4.2. Limitations and Future Work

Despite the overall effectiveness of UMEAD, several limitations remain. First, the method is still sensitive to the scale and noise of pseudo-seeds: noisy initial alignments can propagate errors during iterative expansion, which may limit performance under extremely sparse or heterogeneous graph conditions. Second, the quality of multimodal fusion depends on the completeness of available modalities; when one or more modalities are missing or corrupted, the adaptive weighting mechanism may be less reliable. Third, the computational complexity of the dual-space embedding framework (combining Euclidean and hyperbolic representations) can restrict scalability when applied to ultra-large graphs. Lastly, although the framework has demonstrated adaptability across equipment-oriented and general multimodal datasets, it has not yet been extensively validated in open-domain or streaming environments.

Future work will address these limitations along several directions. (1) Noise-robust pseudo-seed generation: incorporating denoising strategies and confidence-based filtering to reduce error propagation. (2) Uncertainty-aware modality fusion: introducing confidence estimation in the fusion network to down-weight unreliable or missing modalities dynamically. (3) Scalable optimization: improving training efficiency through lightweight dual-space projection and distributed contrastive learning. (4) Interpretability and human-in-the-loop refinement: integrating attention visualization and expert feedback to enhance transparency and trustworthiness. (5) Integration of advanced multimodal encoders: replacing backbone extractors with modern vision–language models such as CLIP or ViT to better capture semantic–visual alignment. Together, these directions aim to strengthen UMEAD’s robustness, scalability, and generalization in real-world multimodal knowledge graph alignment tasks.