Nonlinear Influence of Chamber Pressure on the Asymmetric Dynamic Response of a Rifle Muzzle Under Continuous Firing Conditions

Abstract

The symmetry-breaking vibrational response of a gun muzzle, induced by the thermo–mechanical coupling effect under continuous firing, is a critical factor degrading shooting accuracy. This study investigates the nonlinear influence of chamber pressure variation on this asymmetric dynamic response. A thermo–mechanically coupled interaction model between a 5.8 mm bullet and its barrel is established using nonlinear finite element methods, incorporating experimentally measured pressure data. The kinematic state of the muzzle under a heated barrel condition (after 90 rounds) is systematically analyzed across five chamber pressure levels (90% to 110% of standard). The results reveal a highly nonlinear relationship between chamber pressure and muzzle vibration. Surprisingly, the maximum values for comprehensive radial displacement (10.601 × 10⁻³ mm), velocity (0.327 m/s), acceleration (11.083 m/s²), swing angle (0.192 mrad), and swing angular velocity (9.166 rad/s) occurred at the 100% standard pressure, not the highest pressure. Reducing the pressure to 90% of the standard effectively suppressed these asymmetric vibrations, with magnitudes declining by 84.28% to 95.49%. This indicates that the symmetry of the muzzle’s dynamic state is disrupted under thermal effects, and strategically lowering chamber pressure can restore a more symmetric and stable launch attitude, thereby enhancing accuracy. This study elucidates the nonlinear correlation mechanism between pressure and thermally induced asymmetric vibration, providing a novel perspective for optimizing the accuracy of rapid-fire weapons based on symmetry principles.

1. Introduction

The pursuit of superior firing accuracy is inherently a problem of controlling initial disturbances and symmetry. For a projectile to strike its target precisely, its muzzle exit velocity and attitude are the decisive factors. Chamber pressure directly influences the projectile’s velocity, while the muzzle’s vibrational characteristics—often exhibiting asymmetric patterns due to gravity—can alter the forces acting on the projectile during the critical exit phase. This leads to variations in the initial conditions of the external trajectory, thereby compromising firing accuracy.

The influence of peak chamber pressure on the amplitude of muzzle initial disturbance is well-known. While this effect might be limited under controlled, ambient temperature conditions, it becomes profoundly exacerbated during rapid firing. The heat accumulation raises the barrel temperature, inducing changes in material properties and generating a pronounced thermo–mechanical coupling effect. This thermal input breaks the thermodynamic and mechanical symmetry of the barrel system, leading to a complex, nonlinear dynamic response where the influence of chamber pressure on muzzle vibration becomes more intense and unpredictable.

Scholarly investigations into interior ballistics have systematically examined the interplay between chamber pressure dynamics, shock wave behavior, bullet–barrel interactions, and thermal effects on weapon performance. Research developments reveal three interconnected domains of advancement: in interior ballistics and pressure management, studies by Degirmenci [1] and Verberne [2] established fundamental relationships between propellant characteristics and combustion dynamics, while Chen [3] demonstrated active pressure control through segmented chamber designs. Qiu’s [4] symmetric venting mechanism achieved optimal recoil reduction (31.80%) with minimal velocity loss (1.30%), with Guo [5] providing critical insights into abnormal pressure conditions. The projectile–barrel interaction research has identified gravity-induced vibrations (Liu [6]) and rifling wear effects (Shen [7]) as primary factors affecting exit symmetry. Advanced diagnostic methods developed by Zhang [8] enabled direct in-bore observation, while Hruschka [9] and Doig [10] characterized complex transonic aerodynamics during muzzle exit. Thermodynamic studies consistently identify heat accumulation as the fundamental constraint on sustained firing performance. Dai [11], Yang [12], and Chen [13] documented thermal degradation mechanisms ranging from barrel softening to projectile material phase changes, while Hussain’s team [14,15,16] developed predictive thermal models. Complementary research by Huang [17], Gai [18], Chen [19], and Xu [20] quantified thermo–mechanical coupling effects, with Wei [21] and Hua [22] providing structural performance benchmarks under thermal loading.

Although these studies have provided valuable insights, they have often overlooked the nonlinear coupling effect of chamber pressure on muzzle vibration during the in-bore motion and its consequent impact on projectile attitude symmetry. Furthermore, the specific influence of chamber pressure variation on the asymmetric vibrational response of a heated barrel remains scarcely explored. The muzzle vibration at the moment of exit is undoubtedly a critical factor that disrupts the symmetry of the projectile’s launch attitude and thus degrades accuracy.

Therefore, studying this coupling mechanism is imperative. Based on the aforementioned considerations, this study employs a 5.8 mm rifle to establish a thermo–mechanically coupled bullet–barrel interaction model using the nonlinear finite element method. By integrating actual pressure data, we aim to decipher the nonlinear correlation between chamber pressure and the symmetry-breaking vibrational response of the muzzle under continuous firing conditions. The findings are expected to provide new theoretical insights into accuracy degradation and a novel optimization strategy based on controlling dynamic asymmetry.

2. Chamber Pressure Test Experiment

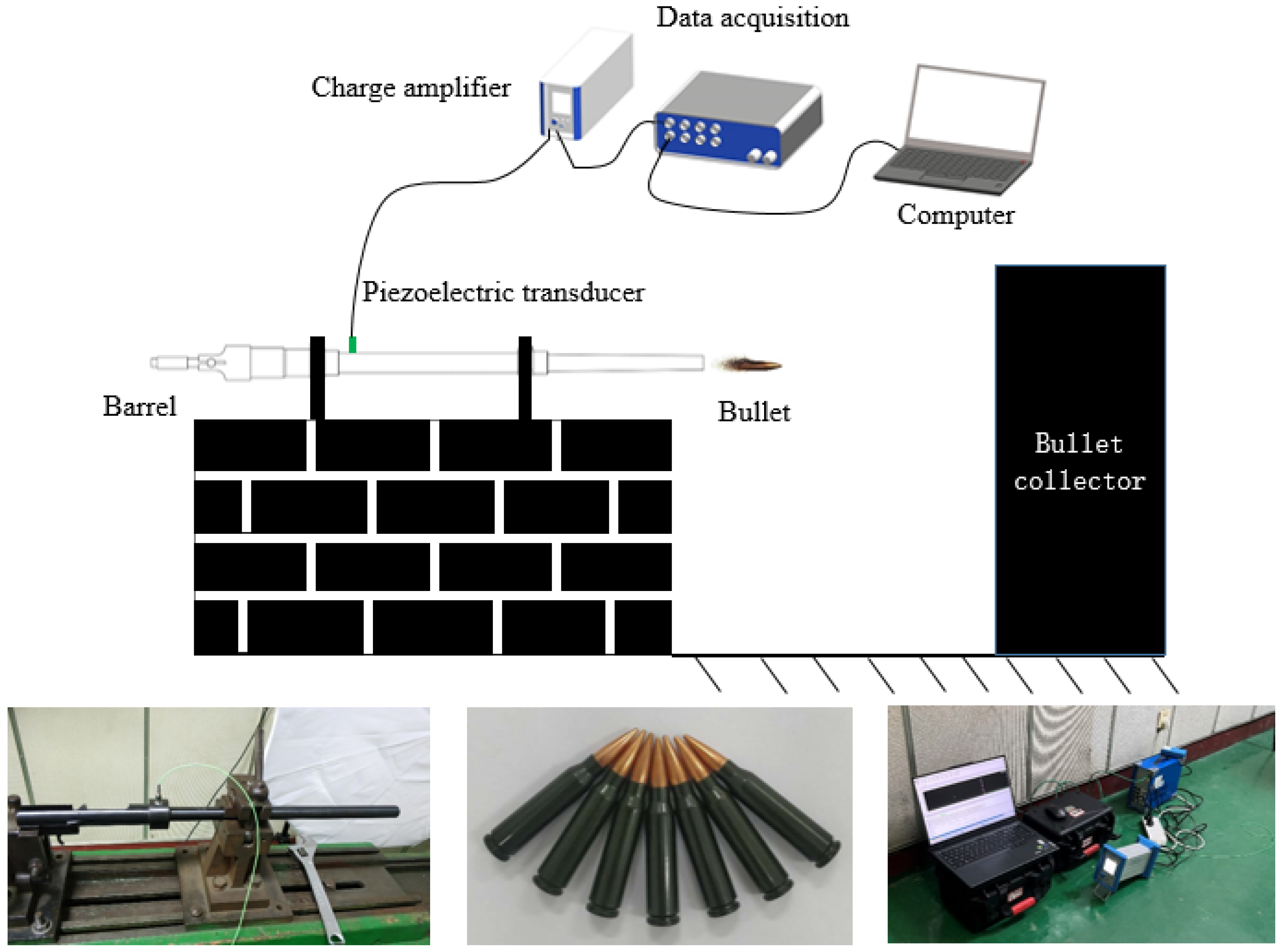
The chamber pressure is measured directly using a piezoelectric system. The experimental setup, schematized in Figure 1, is equipped with a piezoelectric sensor, a charge amplifier, a data acquisition card, and a computer. In this configuration, the pressure signal is first converted to a charge signal by the sensor, then transformed into a voltage signal via the charge amplifier, and finally recorded by the data acquisition card. All experiments are conducted using a 5.8 mm ballistic rifle and standard 5.8 mm general-purpose ammunition.

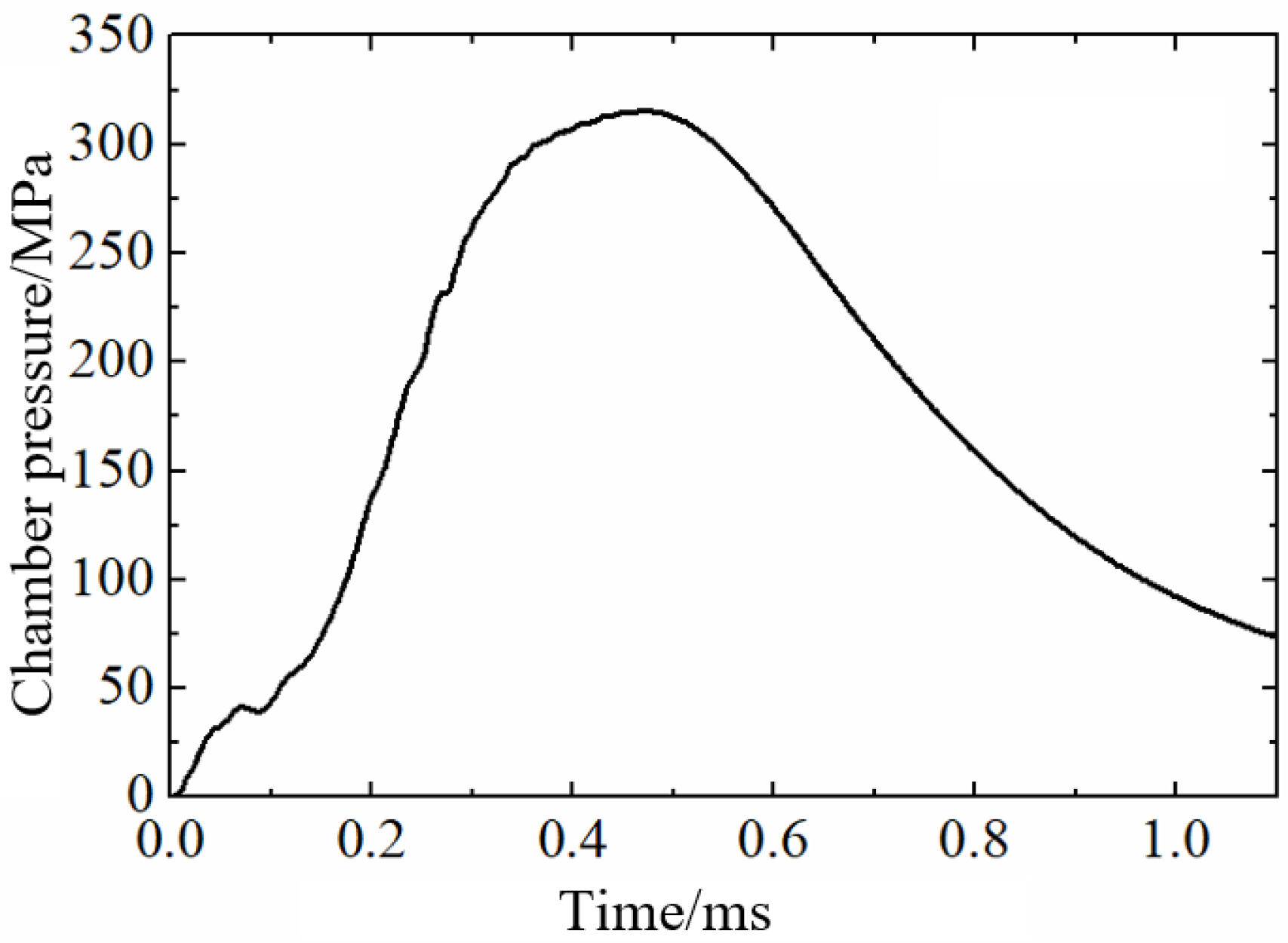
The measured chamber pressure curve is shown in Figure 2. The peak pressure is recorded as 320 MPa. This curve will be converted to obtain the pressure curve acting on boattail. It will serve as the driving force for the projectile’s in-bore motion.

3. Thermo–Mechanical Coupling Modeling Method

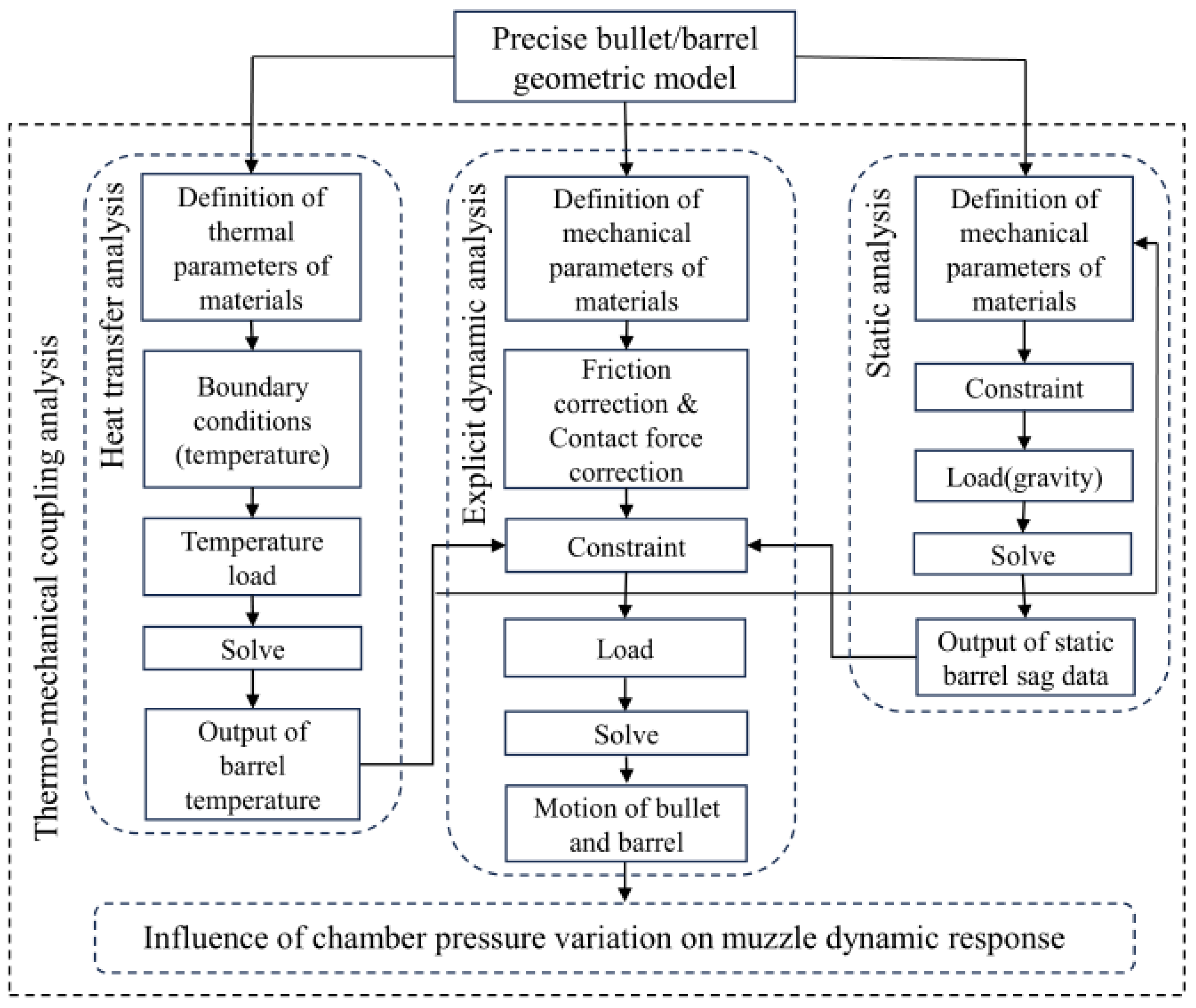
To accurately simulate projectile motion and barrel dynamic response, a partitioned coupling numerical method is adopted. A thermo–mechanical coupled dynamic interaction model between the bullet and the barrel is established using the Abaqus simulation platform. The analysis process is shown in Figure 3. It consists of three interrelated computational modules:

(1)

Transient Heat Transfer Analysis Module

A barrel temperature evolution model is developed based on heat conduction theory. Thermal accumulation during continuous firing is considered. Material thermal properties (thermal conductivity, specific heat capacity) and thermal boundary conditions are defined. The temperature field of the barrel under continuous firing conditions is computed.

(2)

Static Structural Analysis Module

Considering the combined effects of the temperature and gravity, the static sag data of the barrel is output by defining material parameters, temperature and motion boundary conditions, and applying gravity loads.

(3)

Explicit Dynamics Module

Results from the previous two modules are integrated as constraints. Friction and contact force models are modified. The motion of the projectile in a heated barrel is simulated, and the projectile trajectory and muzzle vibration characteristics are analyzed.

3.1. Geometric Modeling and Meshing

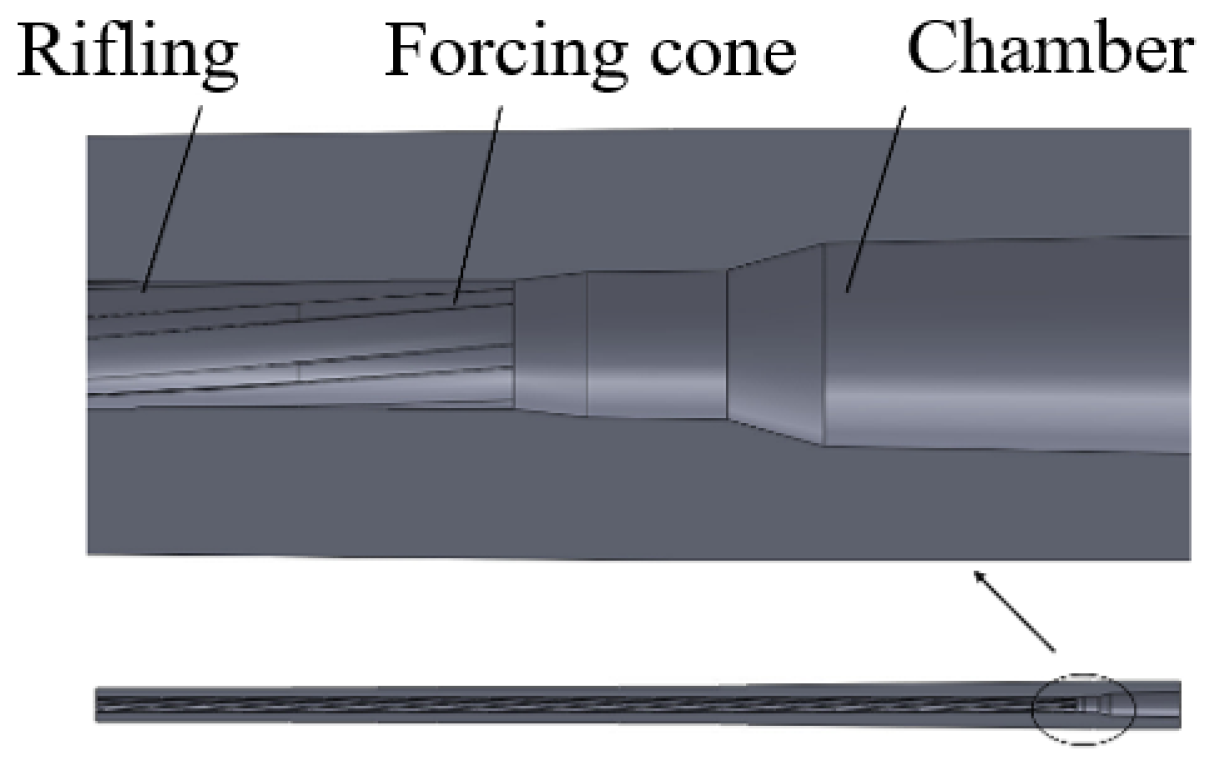
The study objects consist of a 5.8 mm general-purpose cartridge and a 5.8 mm automatic rifle. Cross-sectional schematic diagrams of their geometric models are shown in Figure 4 and Figure 5.

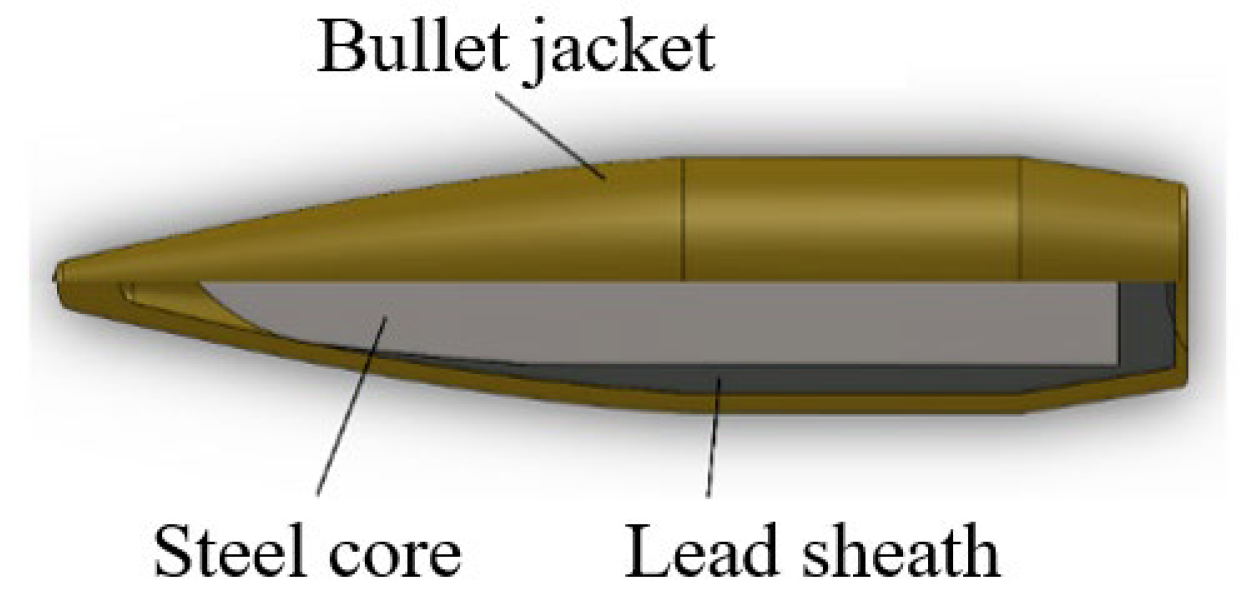
The projectile is designed with a typical three-component structure (copper jacket/lead sheath/steel core). The barrel model retains key features (rifling, forcing cone, etc.). Non-essential structures (threads, barrel bands, etc.) are simplified.

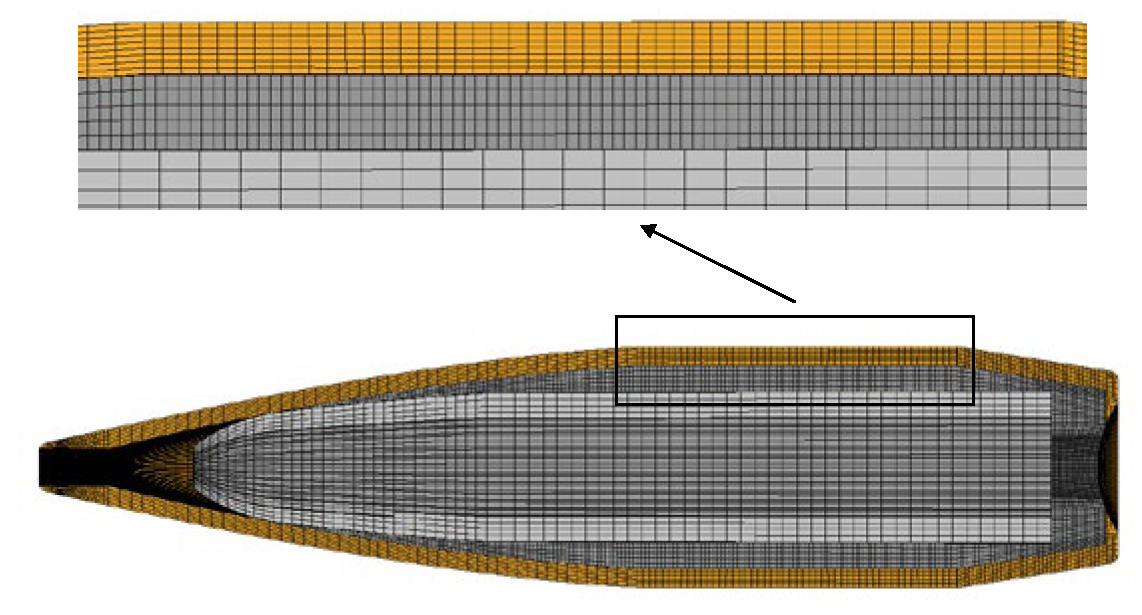
Preprocessing is performed using HyperMesh. Discretization is mainly carried out with C3D8RT elements (8-node thermally coupled hexahedral elements). Sectional mesh diagrams of the bullet and barrel are shown in Figure 6 and Figure 7.

3.2. Basic Assumption

To simplify the computational model, the following reasonable assumptions are made:

(1)

The material is assumed to be isotropic, and its thermophysical parameters (specific heat capacity, thermal conductivity, elastic modulus, and Poisson’s ratio, etc.) are considered to be temperature-dependent;

(2)

Frictional heating and heat conduction effects are taken into account;

(3)

Initial deformation caused by the self-weight of the barrel is considered;

(4)

The influence of air resistance in front of the projectile is neglected.

3.3. Material Constitutive Model

During its in-bore motion, the projectile is subjected to instantaneous high-temperature and high-pressure gas. The jacket undergoes high strain rates, material temperature rise, thermal softening, and strain hardening. These nonlinear mechanical states are experienced. The copper jacket material is specified as H90. The barrel material is designated as 30CrMnSiMoVA. Temperature-dependent material parameters are adopted for the barrel. The Johnson–Cook constitutive model is selected for the jacket material. It is used to describe the thermoviscoplastic behavior. The material parameters are provided in

Table 1. Mechanical and thermodynamic parameters of H90.

Parameter Type	Value
Elastic and thermal	E/GPa	$\mu$	ρ/(kg·m−3)	c/(J·kg−1·K−1)		λ/(W·m−1·K−1)
	112	0.31	8730	375		110
Plastic	A/MPa	B/MPa	C	n	m	Tm/K	${\dot{\epsilon }}_0/s^{-1}$
	112	505	0.09	0.42	1.68	1082	1
Damage failure	D1	D2	D3	D4		D5
	0.54	4.89	−3.03	0.014		1.12

,

Table 2. Mechanical and thermodynamic parameters of lead sheath.

Parameter Type	Value
Elastic and thermal	E/GPa	$\mu$	ρ/(kg·m−3)	c/(J·kg−1·K−1)		λ/(W·m−1·K−1)
	17	0.42	11,340	130		207
Plastic	A/MPa	B/MPa	C	n	m	Tm/K	${\dot{\epsilon }}_0/s^{-1}$
	8	110	0.09	0.52	1.1	760	1

and

Table 3. Mechanical and thermodynamic parameters of 30CrMnSiMoV2A.

Temperature/°C	E/GPa	$\mathit{\mu }$	λ/(W·m−1·K−1)	c/(J·kg−1·K−1)	$\mathit{\alpha }$
16	211	0.27	48	523	1.7 × 10−5
200	202	0.295	42	567
400	190	0.303	36	611
600	180	0.311	30	779
800	162	0.344	24	946

, respectively.

The Johnson–Cook constitutive model can be expressed as follows:

$$\sigma =(A+B{\epsilon }^n)\left[1+C\ln (\dot{\epsilon }/{\dot{\epsilon }}_0)\right](1-T^{\ast m})$$

(1)

where $\sigma$ is the equivalent stress, $\epsilon$ is the equivalent plastic strain, $\dot{\epsilon }$ is the equivalent plastic strain rate; A is the yield stress; B is the hardening modulus; C is the strain rate sensitivity coefficient; m is the thermal softening exponent; n is the work hardening exponent; ${\dot{\epsilon }}_0$ is the reference strain rate; T* is the homologous temperature.

$$T^{\ast }={\displaystyle \frac{T-T_{\mathrm{room}}}{T_{\mathrm{melt}}-T_{\mathrm{room}}}}$$

(2)

where T_room is the reference temperature, T_melt is the melting temperature of the material.

In Table 1, Table 2 and Table 3, E is the elastic modulus, $\mu$ is Poisson’s ratio, $\rho$ is the material density, c is the specific heat capacity, $\lambda$ is the thermal conductivity, $\alpha$ is the coefficient of thermal expansion.

The Johnson–Cook failure criterion describes the damage degree through the damage parameter D, which can be expressed as:

$$D={\displaystyle \sum \frac{\Delta {\epsilon }_{\mathrm{p}}}{{\epsilon }_{\mathrm{f}}}}$$

(3)

where ∆ε_p is the equivalent plastic strain increment; ε_f is the material failure strain.

The material failure strain ε_f can be expressed as follows:

$${\epsilon }_{\mathrm{f}}=\left[D_1+D_2{\mathrm{e}}^{D_3{\sigma }^{\ast }}\right]\left[1+D_4\ln \left({\displaystyle \frac{{\dot{\epsilon }}_{\mathrm{p}}}{{\dot{\epsilon }}_0}}\right)\right]\left(1+D_5{T}^{\ast }\right)$$

(4)

where D₁~D₅ are the damage parameters; σ^* is the ratio of pressure to equivalent stress σ_eff.

$${\sigma }^{\ast }={\displaystyle \frac{p}{{\sigma }_{\mathrm{eff}}}}$$

(5)

The failure model characterizes material degradation through accumulated damage, describing the reduction in material stiffness. The element damage is defined as follows:

$$D\left(\epsilon \right)={\displaystyle \sum \frac{\Delta {\overline{\epsilon }}_{\mathrm{p}}}{{\epsilon }_{\mathrm{f}}}}$$

(6)

where D is the damage parameter, its value ranges from 0 to 1, Initially, D = 0, Material failure occurs when D = 1; ∆ε_p is the plastic strain increment within a single time step.

3.4. Boundary Condition

The boundary conditions of the thermo–mechanically coupled bullet/barrel dynamic response model include constraints, thermal boundary conditions, and loads.

3.4.1. Constraint

To accurately simulate the actual constraints of the weapon system, the following treatments are applied in the model: the breech end of the barrel is rigidly connected to a ground reference point using multipoint constraints (MPC). Initial sagging deformation due to gravity is retained. These approaches ensure both the rationality of the constraints and accurately capture the initial stress state of the barrel before firing.

3.4.2. Thermal Boundary Condition

During the model construction process, the thermo–mechanical coupling effect under actual firing conditions is fully considered. First, the three-dimensional temperature distribution field of the barrel after 90 rounds of continuous firing is obtained through numerical simulation (as shown in Figure 8). This temperature field is imported as an initial condition into the finite element model.

3.4.3. Loads

The driving force for projectile motion in this thermo–mechanical coupled bullet–barrel interaction model is derived from measured chamber pressure converted using Equation (7). The variation in measured chamber pressure over time is shown in Figure 2.

$$p_d={\displaystyle \frac{p}{1+\frac{1}{4}\times \frac{M_{\omega }}{{\phi }_{1}M}}}$$

(7)

where $M_{\omega }$ is the propellant mass, M is the projectile mass, ${\phi }_1$ is the secondary work coefficient.

3.5. Contact

To address the complex contact issues in the thermo–mechanical coupling of the bullet–barrel system, a finite element model is developed based on the Abaqus general contact algorithm. The model primarily handles three key contact pairs: lead sheath–jacket, steel core–lead sheath, and jacket–barrel inner wall. For contact parameters, the normal behavior is defined using a hard contact criterion to describe pressure–overclosure relationships. The tangential behavior is modeled with a penalty friction formulation. To accurately simulate thermo–mechanical coupling effects, a thermal contact algorithm is incorporated. The frictional heat generation coefficient is set to 0.9 to quantify heat generation from friction. Contact thermal resistance parameters are configured to characterize heat transfer between dissimilar materials. This integrated modeling approach, considering both mechanical and thermal coupling, significantly improves the simulation accuracy of bullet–barrel interaction under high temperature and pressure conditions.

3.6. Grid Independence Verification

The thermo–mechanical coupled bullet/barrel interaction finite element model is discretized using hexahedral elements, which generally provide superior quality metrics compared to tetrahedral elements. To ensure a balance between computational efficiency and numerical accuracy, three mesh densities are applied to the barrel for grid independence verification. The mesh sizes are determined based on the minimum geometric feature size of the barrel structure to adequately resolve critical regions.

As shown in

Table 4. Grid independence verification.

Element Type	Barrel Element Numbers/Million	Initial Velocity/m·s−1	Simulation Time/h
C3D8RT	0.87	875.9 (0.5%)	7.8
	1.74	880.2	15.6
	3.48	881.4 (0.1%)	31.5

, the computation time increased significantly with higher mesh density, while a clear loss of accuracy is observed when coarse mesh is used. When the mesh is refined from 0.87 million to 1.74 million elements, the calculated initial velocity increases noticeably from 875.9 m/s to 880.2 m/s. Further refinement to 3.48 million elements resulted in only a 0.1% change in velocity, indicating convergence of the solution. However, the simulation time more than doubled. Therefore, a mesh scheme with 1.74 million elements for the barrel is adopted. This approach effectively reduced computation time while maintaining numerical accuracy.

4. Model Verification

To validate the thermo–mechanical coupled bullet/barrel interaction finite element model, the in-bore travel distance, muzzle velocity, and surface morphology of the projectile are numerically calculated and compared with experimental results.

Due to the extremely short duration and difficulty in direct observation of the bullet/barrel interaction process, direct validation of the model is challenging. However, muzzle velocity and recovered projectile markings can reflect energy conversion and dynamic behavior during firing. Accurate prediction of these two parameters by the finite element model will indicate high reliability in simulating the actual firing dynamics. Although not comprehensive, this approach remains an effective method for model validation [12,17].

The experimental setup for muzzle velocity measurement and projectile soft recovery is shown in Figure 9.

A 5.8 mm automatic rifle and 5.8 mm general-purpose ammunition are used. The muzzle velocity is measured using a system composed of light screens, a timer, and a power supply. Polyurethane foam blocks are employed as the recovery medium. The distance between the light screens is set to 2 m, and the recovery device is placed 10 m from the muzzle. Shooting is performed handheld.

For this projectile muzzle velocity test, a total of 20 rounds of 5.8 mm general-purpose ammunition are fired continuously. The test is conducted with 20 rounds, which is in accordance with the group size specified for rifle and machine gun cartridges in the national military standard. The arithmetic mean of the projectile muzzle velocities is calculated, resulting in an average experimental muzzle velocity of 899.8 m/s. Through the thermo–mechanical coupled finite element analysis, the in-bore motion time is determined to be 0.973 ms, the total travel distance is 435 mm, and the computed muzzle velocity is 880.2 m/s. Compared with the experimental average velocity of 899.8 m/s, the error is 2.2%. These results demonstrate the accuracy of the thermo–mechanical coupled model in simulating the in-bore motion of the projectile. This minor discrepancy is well within the expected range for such complex simulations. This error can be attributed to several potential sources. Firstly, the simulation employed experimentally measured chamber pressure data as the driving force input. It is possible that limitations in the pressure measurement instrumentation or methodology led to a slight underestimation of the actual pressure. This would result in a marginally lower propelling force in the model, consequently contributing to the lower computed muzzle velocity. Secondly, a slight overestimation of the barrel-projectile friction coefficient in the simulation could have increased the frictional energy loss. The close agreement, despite these potential minor deviations, confirms the model’s strong predictive capability.

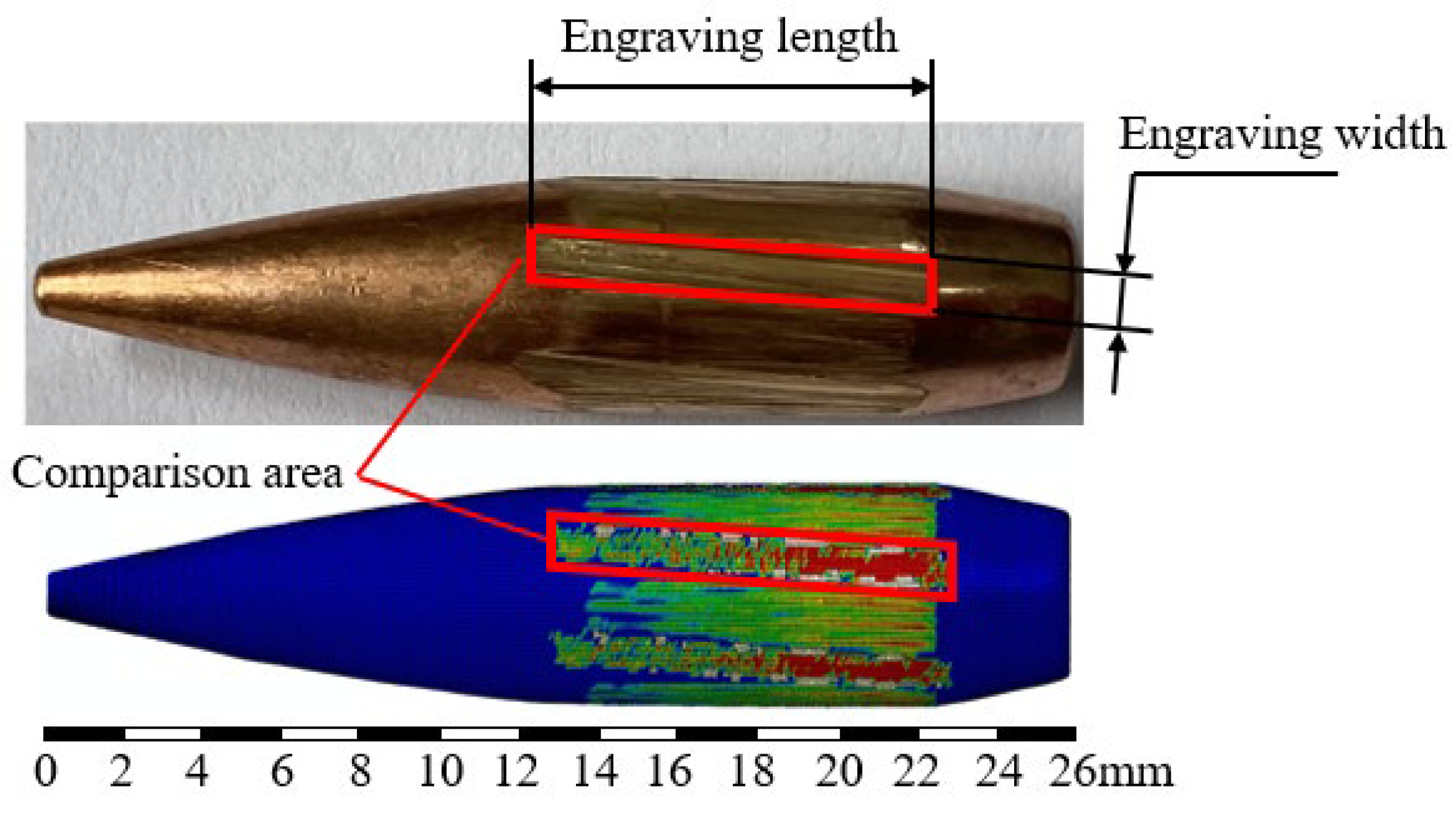
The projectiles recovered in the soft recovery test show no surface scratches and no deformation. A comparison between the scratches on the projectile surface at muzzle exit simulated by the thermo–mechanical coupled bullet–barrel interaction finite element model and the actual surface morphology obtained from the test is shown in Figure 10. The comparisons of scratch length and width are presented in

Table 5. Comparison of soft recovery projectile denting with simulation results.

Value	Average of Experiment Results	Calculation Results	Error/%
Length/mm	9.98	9.92	0.6
Width/mm	0.95	0.92	3.2

. The errors in scratch dimensions are all less than 5%.

In summary, the comparison between the calculated results (projectile muzzle velocity and surface engraving characteristics) and experimental data demonstrates that the thermal–structural coupled bullet–barrel interaction finite element model is accurate and reliable, and can correctly represent the projectile’s travel and behavior within the barrel.

5. Influence of Chamber Pressure Variation on Muzzle Dynamic Response

Chamber pressure serves as the driving force for the projectile’s in-bore motion and plays a critical role in both the projectile movement and barrel dynamics. During actual firing, variations in propellant charge and ambient temperature can cause significant changes in the pressure curve. Changes in chamber pressure not only alter the projectile’s in-bore motion but also affect the movement of the barrel, particularly at the muzzle, further influencing firing accuracy.

This section investigates the influence of different chamber pressures on the muzzle motion state under the condition of a barrel temperature resulting from continuously firing 90 rounds. The chamber pressure of a barrel when firing a standard projectile with a standard propellant charge and according to standard firing specifications is defined as the standard chamber pressure. Based on the standard pressure, cases with 90%, 95%, 100%, 105%, and 110% of standard pressure are investigated at intervals of 5%. The muzzle motion during projectile travel is analyzed under these pressure conditions. A coordinate system is established to clearly describe the muzzle movement [23].

5.1. Influence of Chamber Pressure Variation on Bullet Velocity

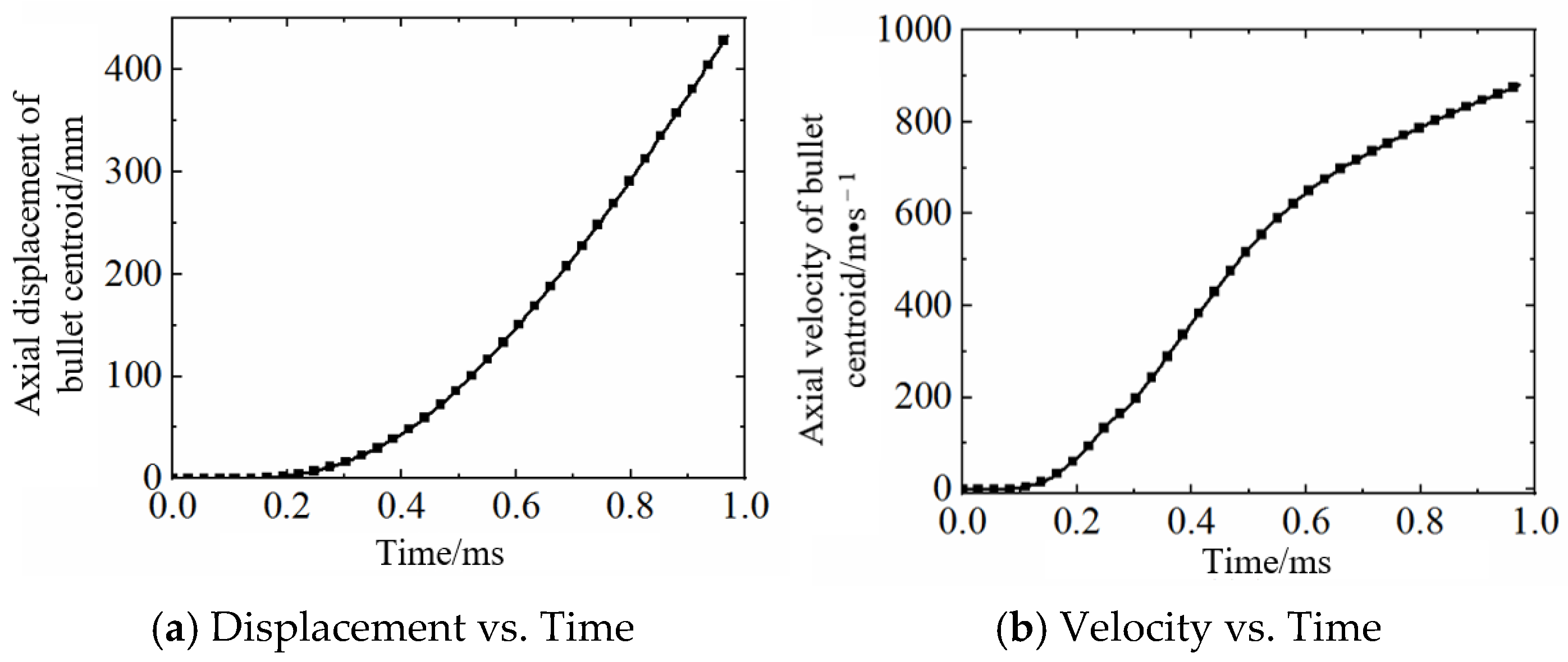
Through analysis using this thermo–mechanical coupled bullet/barrel interaction dynamic response model, the axial displacement and velocity of the projectile’s center of mass during in-bore motion under 100% standard chamber pressure are obtained. The results are shown in Figure 11. The calculated interior ballistic duration is 0.973 ms. The total in-bore travel distance of the projectile is 435 mm. The muzzle velocity is computed as 880.2 m/s. Compared with the experimentally measured average muzzle velocity of 899.8 m/s, the error is 2.2%.

The calculated muzzle velocities of the projectile under five different chamber pressures are shown in

Table 6. Bullet initial velocity at varying chamber pressures.

Group	Time/ms	Initial Velocity/m·s−1
90%	1.034	806.6
95%	1.001	843.7
100%	0.973	880.2
105%	0.946	916.4
110%	0.924	952.7

. A significant positive correlation between chamber pressure and muzzle velocity can be observed. The in-bore motion time of the projectile decreases with increasing pressure. This is consistent with the description of the relationship between chamber pressure and projectile initial velocity in the literature [3].

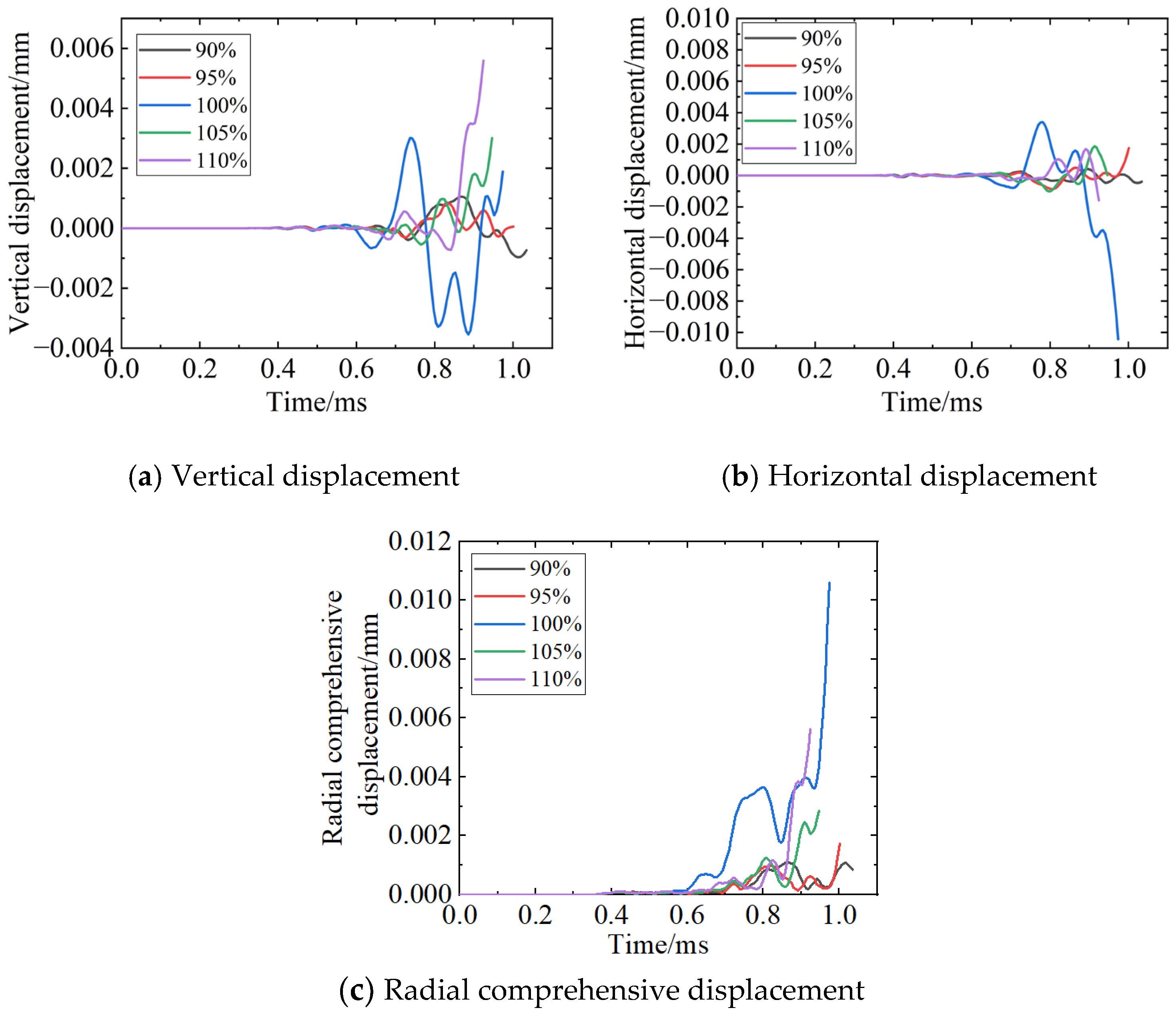
5.2. Influence of Chamber Pressure Variation on Muzzle Center Displacement

The temperature field of the barrel is under the condition of continuously firing 90 rounds. The curves of the muzzle center displacement (vertical, horizontal, and radial) over time under different chamber pressures are shown in Figure 12, and the displacement values of the muzzle center at the moment when the projectile exits the muzzle are given in

Table 7. Displacement of muzzle center at the moment of bullet exit barrel.

Group	Time of Bullet Exit/ms	Vertical Displacement of Muzzle Center/×10−3 mm	Horizontal Displacement of Muzzle Center/×10−3 mm	Radial Comprehensive Displacement of Muzzle Center/×10−3 mm
90%	1.034	−0.727	−0.399	0.829
95%	1.001	0.053	1.758	1.759
100%	0.973	1.894	−10.43	10.601
105%	0.946	3.014	0.003	3.014
110%	0.924	5.600	1.585	5.819

.

As can be seen from Figure 12, the displacement of the muzzle center hardly changes during the first 0.6 ms of the projectile’s engraving, after which it moves upward and to the right. An increase in chamber pressure amplifies the vertical displacement of the muzzle center, as the heightened pressure reduces the effect of gravity on the vertical movement of the muzzle center.

As can be seen from Figure 12 and Table 7, under the condition of a heated barrel with continuous firing of 90 projectiles, the maximum radial displacement at the center of the muzzle at the moment of projectile exit occurs at 100% standard chamber pressure (10.601 μm). And the horizontal displacement dominates in the radial composite displacement. In contrast, the minimum radial displacement at the center of the muzzle at the moment of projectile exit is observed at 90% standard chamber pressure (0.829 μm).

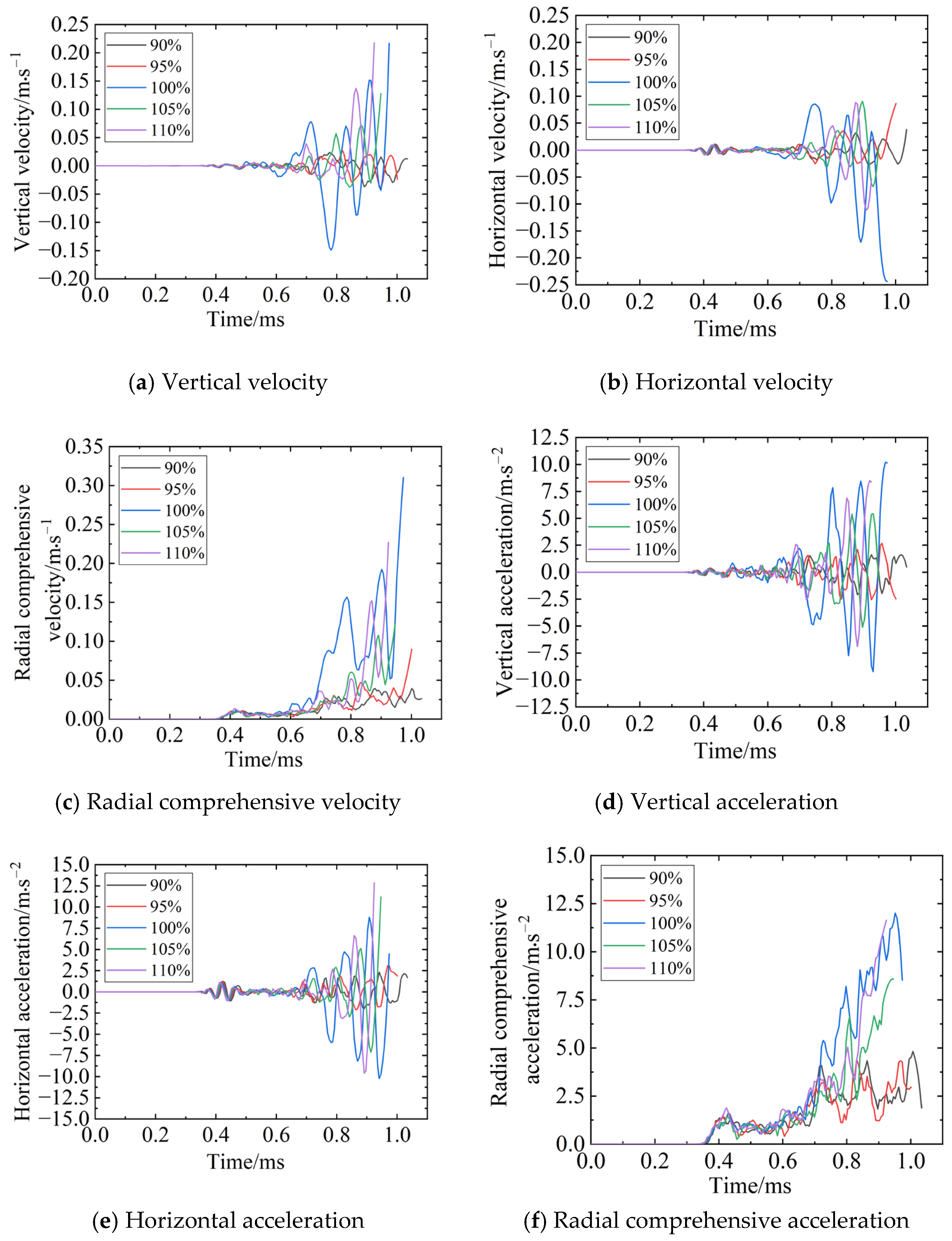
5.3. Influence of Chamber Pressure Variation on Muzzle Center Velocity and Acceleration

Figure 13 shows the time-varying curves of the muzzle center velocity and acceleration (vertical, horizontal, and radial) under different chamber pressures after continuously firing 90 rounds. The muzzle center velocity and acceleration values at the moment of projectile exit are listed in

Table 8. Velocity and acceleration of muzzle center at the moment of bullet exit barrel.

Group	Time of Bullet Exit/ms	Velocity of Muzzle Center/m·s−1			Acceleration of Muzzle Center/m·s−2
		Vertical	Horizontal	Comprehensive	Vertical	Horizontal	Comprehensive
90%	1.034	0.012	0.038	0.040	0.480	1.675	1.742
95%	1.001	−0.024	0.087	0.090	−2.485	1.856	3.102
100%	0.973	0.217	−0.244	0.327	10.134	4.486	11.083
105%	0.946	0.128	0.006	0.128	−0.627	11.210	11.228
110%	0.924	0.217	−0.054	0.224	8.371	12.864	15.348

.

As can be seen from Figure 13 and Table 8, under the heated barrel condition after 90 consecutive rounds, the maximum comprehensive radial velocity of the muzzle center at projectile exit (0.327 m/s) occurred at 100% standard chamber pressure. The minimum comprehensive radial velocity and acceleration (0.04 m/s and 1.742 m/s²) are observed at 90% standard chamber pressure. It can be concluded from Table 8 that as the chamber pressure increases, the horizontal acceleration of the muzzle center at projectile exit increases, as does the comprehensive radial acceleration.

5.4. Influence of Chamber Pressure Variation on Muzzle Plane Swing Angle and Angular Velocity

The temperature field of the barrel is under the condition of continuously firing 90 rounds. The time-varying curves of the muzzle plane swing angle and angular velocity (vertical, lateral, and comprehensive) under different chamber pressures are shown in Figure 14. The values of the muzzle plane swing angle and angular velocity at the moment of projectile exit are listed in

Table 9. Swing angle and angular velocity of muzzle plane at the moment of bullet exit muzzle.

Group	Time of Bullet Exit/ms	Swing angle of Muzzle Plane/mrad			Swing Angle Velocity of Muzzle Plane/rad·s−1
		Vertical	Horizontal	Comprehensive	Vertical	Horizontal	Comprehensive
90%	1.034	0.018	0.013	0.022	0.413	0.013	0.413
95%	1.001	0.006	0.021	0.022	−0.415	2.279	2.316
100%	0.973	−0.107	−0.159	0.192	−3.333	−8.539	9.166
105%	0.946	−0.078	0.078	0.110	−3.636	−2.049	4.174
110%	0.924	−0.139	0.084	0.162	−3.565	−4.229	5.531

.

As shown in Figure 14 and Table 9, under the heated barrel condition after continuously firing 90 projectiles; the maximum muzzle plane swing angle and angular velocity at projectile exit (0.192 mrad and 9.166 rad/s) are observed at 100% standard chamber pressure; and the minimum values (0.022 mrad and 0.413 rad/s) are recorded at 90% standard chamber pressure.

6. Discussion

6.1. Key Findings and Analysis

This study quantifies a critical anomalous phenomenon: under the thermal accumulation conditions induced by continuous firing, the standard (100%) chamber pressure elicits the most intense asymmetric muzzle vibration, rather than the higher (110% standard chamber pressure). This finding challenges the traditional linear perception framework, which typically assumes a monotonic relationship between load amplitude and structural response.

The performance degradation observed in this study closely correlates with several thermally activated mechanisms reported in the literature, thereby validating the reliability of our model. For instance, barrel material softening due to elevated temperatures [13], thermal stripping of the copper jacket [12], and degradation in the projectile jacket’s dynamic response [17] are all documented factors contributing to accuracy loss under heat accumulation. However, the key advancement of this study lies in moving beyond these previously emphasized static or quasi-static degradation phenomena. We systematically reveal, for the first time, the nonlinear regulatory mechanism of pressure on dynamic symmetry under thermo–mechanical coupling conditions. By capturing the transient nonlinear dynamic interaction, we elucidate why the maximum disturbance occurs at a specific pressure level rather than at the peak pressure.

We postulate that this counterintuitive phenomenon stems from a nonlinear dynamic interaction between the pressure load and the barrel’s structural response. Under 100% standard chamber pressure conditions, the spectral characteristics of the pressure pulse likely couple with a specific natural frequency of the heated barrel, thereby exciting a strong resonant response. In contrast, under 110% of standard pressure conditions, the altered temporal characteristics of the pressure pulse shift the dominant excitation frequencies away from this critical resonance range. Furthermore, the increased pressure may enhance local structural stiffness variations or nonlinearities at key interfaces (e.g., projectile and rifling), consequently suppressing resonance to some extent or altering the energy transfer path. This confirms that the maximum dynamic response is not determined solely by the peak load amplitude but rather by a complex synergy between the load’s temporal-spectral characteristics and the structure’s inherent dynamic properties.

Another significant finding is that reducing the chamber pressure from 100% to 90% resulted in a dramatic reduction in muzzle motion parameters by 84% to 95%, as detailed in

Table 10. Kinematic state comparison when bullet exit muzzle under varying chamber pressures.

Parameters	100% Standard Chamber Pressure	90% Standard Chamber Pressure	Decline
Radial comprehensive displacement of muzzle center/×10−3 mm	10.601	0.829	92.18%
Radial comprehensive velocity/m·s−1	0.327	0.040	87.76%
Radial comprehensive acceleration/m·s−2	11.083	1.742	84.28%
Swing angle of muzzle plane/mrad	0.192	0.022	88.54%
Swing angular velocity of muzzle plane/rad·s−1	9.166	0.413	95.49%

. According to muzzle dynamics theory [22], such pronounced suppression of muzzle disturbance directly contributes to improved shooting accuracy. This clearly demonstrates that under thermally compromised barrel conditions, lowering the chamber pressure can effectively mitigate nonlinear muzzle vibrations and enhance accuracy.

The traditional paradigm in army weapon design has long focused on maximizing kinetic energy advantage by increasing muzzle velocity and rate of fire. This study reveals a complementary, and in specific scenarios potentially superior, new pathway: prioritizing dynamic stability through pressure management to restore and maintain shooting accuracy under thermal stress. This signifies a paradigm shift from “energy priority” to “accuracy priority.” For example, in sustained firing scenarios for infantry fighting vehicles or fixed machine guns, compared to solutions requiring hardware modifications such as barrel cooling [14] or material enhancement [16], our strategy provides an immediate solution based on intelligent ballistic control without altering the mechanical structure, demonstrating significant practicality and cost-effectiveness.

6.2. Limitations and Future Research Directions

The primary limitation of this approach is the inherent trade-off with muzzle velocity, which may impact terminal ballistics and effective range. Furthermore, the conclusions are based on a model of a specific 5.8 mm caliber rifle, and their generalizability requires further validation across different weapon platforms.

Based on the findings of this study, we propose two key future research directions:

(1)

Development of “Smart Adaptive” Interior Ballistic Systems: Aiming to achieve real-time dynamic adjustment of the pressure curve based on barrel temperature, realizing the paradigm shift from static design to dynamic control.

(2)

Multi-Objective Optimization for System-Level Design: Conducting research on the trade-off between muzzle velocity and dynamic stability to seek Pareto optimal solutions, thereby systematically addressing the velocity-accuracy trade-off inherent in this approach and promoting the advancement of weapon design methodology.

7. Conclusions

This study reveals the nonlinear and asymmetric nature of the muzzle’s dynamic response under the thermo–mechanical coupling conditions of continuous firing. The key finding is that heat accumulation severely disrupts dynamic symmetry, and contrary to simple linear intuition, the maximum asymmetric vibration is excited by the standard (100%) chamber pressure, not the highest pressure.

Quantitative analysis demonstrates that strategically reducing the chamber pressure to 90% of the standard value can effectively suppress nonlinear vibrations, leading to a dramatic 84% to 95% reduction across all key kinematic parameters, thereby restoring the muzzle to a more symmetric and stable dynamic state.

In summary, this research not only quantifies and elucidates the intrinsic nonlinear correlation mechanism between chamber pressure and thermally induced asymmetric vibration but also demonstrates that “strategic pressure reduction” is an effective method for managing symmetry-breaking vibrations in a heated barrel. Ultimately, this work provides a new paradigm based on dynamic symmetry control for optimizing the accuracy of rapid-fire weapons, shifting the design focus from solely maximizing kinetic energy to the precise regulation of the symmetry of the launch event itself.