A Generalized Nonlinear Extension of Quantum Mechanics

Abstract

We construct the most general form of our previously proposed nonlinear extension of quantum mechanics that possesses three basic properties. Unlike the simpler model, the new version is not completely integrable, but it has an underlying Hamiltonian structure. We analyze a particular solution in detail, and we used a natural extension of the Born rule to compute particle trajectories. We find that closed particle orbits are possible.

1. Introduction of the Model

In a previous paper [1], we proposed a nonlinear extension of quantum mechanics and studied some of its consequences. Our motivations were various: partly, in the spirit of [2,3,4], we simply wanted to see what a particular nonlinear extension of quantum mechanics might look like, and to deduce some of its consequences.

But we also had in mind the question of whether, as others have speculated [5,6,7], the union of gravity with quantum mechanics is best achieved not only by producing a fully quantum version of general relativity, as is contemplated for example in string theory or loop quantum gravity, but also by some other means, such as the coupling of quantum mechanics to a classical version of gravity, as in the work of Oppenheim and collaborators [8], or indeed by the modification of quantum mechanics itself.

In the model we introduced in [1,9], a given system is described by two state vectors, $|\psi >$ and $|\varphi >$, in Hilbert space, in contrast to the single state vector to which ordinary quantum mechanics limits itself. Our procedure is heuristic, that is, we do not impose a prior rationale for introducing two state vectors but instead look ahead to what the consequences are. In that sense, we follow the grand tradition of quantum mechanics, in which everybody knows how to calculate, but nobody knows what it all really means. Our approach affords us the opportunity to generalize quantum mechanics in what we consider to be an interesting way. In our first paper, we presented the minimal realization of this idea, which, surprisingly, allowed us to completely determine the effects of the nonlinearity independently of the dynamics of the underlying quantum mechanical system. This simplicity, however, overly restricted the evolution possibilities. The nonlinearity in that model is proportional to the inner product $\gamma =<\varphi |\psi >$. One finds that $\gamma \to 0$ for large times, so that the effect of the nonlinearity vanishes in the far future and the far past.

In this paper, we retain the same principles but allow for a greater range of dynamical effects at the cost of no longer being able to solve the system of equations exactly. Rather than speculate about the meaning of the second state vector, we study the effects it produces, thereby, hoping to gain information on what meaning it might have. One line of investigation, which we began to consider in [9], is that the additional dynamics have something to do with gravity. In other words, perhaps gravity is, at least in part, a manifestation of the nonlinear aspects of quantum mechanics that we introduced. The fact that our nonlinear modification is universal, i.e., independent of the Hamiltonian of the underlying system, may be relevant in this regard. In Section 3, we define a trajectory function, which describes how a particle would move under the influence of the nonlinear terms, and compute it in a simple case.

If we define

$$|\Psi >=\left(\begin{array}{c}|\psi >\\ |\varphi >\end{array}\right)$$

(1)

and

$$\mathcal{H}=\left(\begin{array}{cc}H& 0\\ 0& H\end{array}\right)$$

(2)

where H is the Hamiltonian of the underlying system, then the equations of motion of the model in reference [1] are:

$$i{\displaystyle \frac{\partial |\Psi >}{\partial t}}=\mathcal{H}|\Psi >+\mathcal{M}|\Psi >$$

(3)

where $\mathcal{M}$ is the Hermitian matrix:

$$\mathcal{M}=\left(\begin{array}{cc}0& g<\varphi |\psi >\\ g^{*}<\psi |\varphi >& 0\end{array}\right)$$

(4)

and the coupling constant $g=a+ib$ is in general complex ($b\ne 0)$.

We replace this $\mathcal{M}$ with a more general one, subject to the following conditions, all of which are obeyed by our original model:

(I)

Each element of $\mathcal{M}$ should depend linearly on the inner products $<\psi |\psi >$, $<\varphi |\psi >$, $<\psi |\varphi >$, and $<\varphi |\varphi >$, and should depend on time only through them.

(II)

The equations of motion should imply that $<\psi |\psi >+<\varphi |\varphi >=N=\mathit{const}.$

(III)

The equations of motion should be invariant under the separate constant phase transformations $|\psi >\to e^{i{\theta }_1}|\psi >$ and $|\varphi >\to e^{i{\theta }_2}|\varphi >$.

The reason for condition I is that it encapsulates the philosophy behind our nonlinear extension of quantum mechanics. There are infinitely many ways to try to extend quantum mechanics. The procedure we choose is to introduce a second state vector, and then to have the relevant inner products govern the dynamics of the nonlinear extension. That is the content of condition I. Condition II is important for two reasons: it is the appropriate generalization of the usual rule that the norm of the state vector remains constant and it ensures that the evolution of the state vectors will remain bounded despite the presence of complex coupling coefficients. Condition III is a consequence of Occam’s razor. It is a symmetry that significantly restricts the number of allowed terms in the equations of motion.

To implement condition II, it is sufficient for $\mathcal{M}$ to be Hermitian, but it is not necessary. $\mathcal{M}$ can have an anti-Hermitian part of the form:

$${\mathcal{M}}^{\prime }=\left(\begin{array}{cc}i\mu <\varphi |\varphi >& \lambda <\varphi |\psi >\\ -\lambda <\psi |\varphi >& -i\mu <\psi |\psi >\end{array}\right),$$

(5)

where $\mu$ and $\lambda$ are real constants. Then the most general $\mathcal{M}$ satisfying conditions (I)–(III) is:

$$\mathcal{M}={\mathcal{M}}_0+{\mathcal{M}}^{\prime }$$

(6)

where

$${\mathcal{M}}_0={\mathcal{M}}_0^{†}=\left(\begin{array}{cc}{\alpha }_1<\psi |\psi >+{\alpha }_2<\varphi |\varphi >& g<\varphi |\psi >\\ g^{*}<\psi |\varphi >& {\beta }_1<\psi |\psi >+{\beta }_2<\varphi |\varphi >\end{array}\right)$$

(7)

where ${\alpha }_i$ and ${\beta }_i$ are real constants, and $g=a+ib$ was defined above. In total, there are eight real parameters, as compared to two in the original model.

The $\tau$-$\delta$ System of Equations

If $\mathcal{M}=0$, all the inner products would be constant. Hence, the inner products obey evolution equations that are independent of $H.$ In these equations, we find that most of the above parameters play no role. With $\gamma =<\varphi |\psi >,$ we define $\delta ={\left|\gamma \right|}^2$, and let

$$\tau =<\psi |\psi >-<\varphi |\varphi >.$$

(8)

The following differential equations for $\tau$ and $\delta$ are a direct consequence of the equations of motion, Equation (3),with the replacement $\mathcal{M}\to {\mathcal{M}}_0+{\mathcal{M}}^{\prime }$:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d\tau }{dt}}& & =\mu \left(N^2-{\tau }^2\right)+4b\delta ,\hfill \\ \hfill {\displaystyle \frac{d\delta }{dt}}& & =-2(b+\mu )\tau \delta .\hfill \end{array}$$

(9)

The analogous equations for the original model are recovered for $\mu =0$. To gain some preliminary insight, we note that we can easily integrate Equation (9) in three special cases: (1) $\mu =0$; (2) $b+\mu =0;$ (3) $b=0$.

Case (1) is just the original model, for which we have that $\tau \left(t\right)$ and $\delta \left(t\right)$ are given by the following equations:

$$\tau \left(t\right)=2{\omega }_{0}tanh2{\omega }_{0}bt,\delta \left(t\right)={\displaystyle \frac{{\omega }_0^2}{{cosh}^{2}2{\omega }_{0}bt}},$$

(10)

where ${\omega }_0$ is a constant of integration. In general, we expect the solution of these two equations to depend on one constant of integration in addition to the freedom to redefine the origin of time, $t\to t-t_0,$, which we do not explicitly indicate.

Case (2): we find $\tau =-2{\omega }_{0}tanh2{\omega }_{0}bt$ and $\delta ={\displaystyle \frac{N^2}{4}}-{\omega }_0^2$.

Case (3): we find $\tau =Ntanh\mu Nt$ and $\delta ={\displaystyle \frac{{\delta }_0}{{cosh}^2\mu Nt}}$. In this case, the constant of integration does not appear in the argument of the tanh function, but only in the normalization of $\delta$.

Noting that in all three special cases $\tau$ is a hyperbolic tangent, we can make the ansatz:

$$\tau ={\alpha }^{\prime }tanh{\beta }^{\prime }t,$$

(11)

where ${\alpha }^{\prime }$ and ${\beta }^{\prime }$ are constants to be determined, and plug this into the full equations for $\tau$ and $\delta$. We indeed find a solution:

$$\tau =Ntanh(b+\mu )Nt$$

(12)

and

$$\delta ={\displaystyle \frac{N^2}{4}}{\left[cosh(b+\mu )Nt\right]}^{-2}.$$

(13)

This is definitely not the general solution, because ${\alpha }^{\prime }$ and ${\beta }^{\prime }$ are fixed by the equations, so there is no free constant of integration. Indeed, if we go through the special cases that we solved above, we find that our solution to the general equations corresponds to a specific choice for the constant of integration: Case (1), ${\omega }_0={\displaystyle \frac{N}{2}}$; Case (2), ${\omega }_0=0$; and Case (3), ${\delta }_0={\displaystyle \frac{N^2}{4}}.$

2. Hamiltonian Formulation of the $\mathbf{\tau }$-$\mathbf{\delta }$ System of Equations

In this section, we want to show that the differential equations for $\tau$ and $\kappa =ln\delta$ can be cast into a Hamiltonian framework, so that a conserved energy can be identified. In terms of the variables $\kappa =ln\delta ,$ and $\Omega ={\tau }^2$, we find:

$${\displaystyle \frac{d\kappa }{dt}}=-2(b+\mu )\tau$$

(14)

and, therefore

$${\displaystyle \frac{d\tau }{dt}}={\displaystyle \frac{d\tau }{d\kappa }}{\displaystyle \frac{d\kappa }{dt}}=-(b+\mu ){\displaystyle \frac{d\Omega }{d\kappa }}=\mu \left(N^2-\Omega \right)+4b{e}^{\kappa }.$$

(15)

This is a first-order linear differential equation for $\Omega$ as a function of $\kappa$, and can be integrated exactly:

$$\Omega ={\tau }^2=N^2-4e^{\kappa }-c{e}^{{\displaystyle \frac{\mu \kappa }{b+\mu }}}=N^2-4\delta -c{\delta }^{{\displaystyle \frac{\mu }{b+\mu }}}$$

(16)

where c is a constant of integration. In the original model, $\mu =0,$ and $c=N^2-4{\omega }_0^2$. The relation above is the generalization of ${\omega }_0^2={\displaystyle \frac{{\tau }^2}{4}}+\delta$ (Equation (2.15) of [1]) in the original model. Since

$$N^2-{\tau }^2-4\delta =4\mathcal{S},$$

(17)

where

$$\mathcal{S}=<\psi |\psi ><\varphi |\varphi >-<\psi |\varphi ><\varphi |\psi >$$

(18)

is the Schwarz parameter, the relation can also be expressed as:

$$4\mathcal{S}=c{\delta }^{{\displaystyle \frac{\mu }{b+\mu }}}.$$

In the original model, $\mathcal{S}$ is a constant, but in this more general case, it apparently will not be.

To solve these equations completely, we would need to substitute the relation between $\tau$ and $\delta$ back into the equations for ${\displaystyle \frac{d\tau }{dt}}$ and ${\displaystyle \frac{d\delta }{dt}}$ and perform one more integration.

To simplify the subsequent discussion, we adopt a slightly different notation. As evolution parameter, we choose $s=-(b+\mu )t$, and define $p={\displaystyle \frac{\mu }{(b+\mu )}}$. [Note that this requires $b+\mu \ne 0,$ so Case 2 above is not covered by this analysis.] The equations of motion for $\tau$ and $\kappa$ are then:

$${\displaystyle \frac{d\kappa }{ds}}=2\tau$$

(19)

and

$${\displaystyle \frac{d\tau }{ds}}=-4e^{\kappa }-pc{e}^{p\kappa },$$

(20)

with the additional relation

$$N^2=h\equiv {\tau }^2+4e^{\kappa }+c{e}^{p\kappa }.$$

(21)

We recognize that $h(\kappa ,\tau )$ serves as the Hamiltonian for this system, with $\kappa$ playing the role of the coordinate and $\tau$ the role of the momentum. In fact the first order equations for $\kappa$ and $\tau$ are just Hamilton’s equations:

$${\displaystyle \frac{d\kappa }{ds}}={\displaystyle \frac{\partial h}{\partial \tau }}$$

(22)

and

$${\displaystyle \frac{d\tau }{ds}}=-{\displaystyle \frac{\partial h}{\partial \kappa }}$$

(23)

So $\kappa$ behaves like the position x of a particle in 1-D, moving in the potential $V\left(\kappa \right)=4e^{\kappa }+c{e}^{p\kappa }$. This explains in a more general way why in the original model $\delta ={\left|\gamma \right|}^2\to 0$ for large times. In the original model, $p=0,$ so $V\left(\kappa \right)$ tends to infinity for large positive $\kappa$, but for large negative $\kappa$ the potential tends smoothly to a constant. Therefore, $\kappa$ escapes to minus infinity, and $\delta =e^{\kappa }$ tends to zero.

If $p>0,V\left(\kappa \right)=4e^{\kappa }+c{e}^{p\kappa }$ will have the same general behavior as in the $p=0$ case. (The parameter c is constrained to be positive because of the relation $c{e}^{p\kappa }=4\mathcal{S}).$ But if $p<0$, $V\left(\kappa \right)$ will tend to infinity both for large positive and negative $\kappa$, insuring that $\delta$ stays bounded away from either zero or infinity as time evolves. In terms of the original parameters, assuming $b>0$, this means $-b<\mu <0$. This is the range of parameters we shall consider going forward.

It is not known to us whether the problem of a classical 1-D particle moving in a potential $V\left(\kappa \right)=4e^{\kappa }+c{e}^{p\kappa }$ with $c>0$ and $p<0$ can be solved exactly. Below we present the general solution for a particular choice of parameters, and another particular solution that is valid for all choices of the parameters.

Energy conservation leads to:

$$E=N^2={\tau }^2+4e^{\kappa }+c{e}^{p\kappa },$$

(24)

where from Hamilton’s equations:

$$2\tau ={\displaystyle \frac{d\kappa }{ds}},$$

(25)

$$N^2={\displaystyle \frac{1}{4}}{\left({\displaystyle \frac{d\kappa }{ds}}\right)}^2+V\left(\kappa \right),$$

(26)

and

$$ds=\pm {\displaystyle \frac{d\kappa }{2\sqrt{N^2-V\left(\kappa \right)}}}.$$

(27)

2.1. The Case $p=-1$

If we choose $\mu =-{\displaystyle \frac{b}{2}}$, then $p=-1$. This also leads to $b+\mu ={\displaystyle \frac{b}{2}}$. so that $s=-{\displaystyle \frac{b}{2}}t$ Furthermore, we can translate the coordinate: $\kappa =\eta +{\eta }_0$, where ${\eta }_0={\displaystyle \frac{1}{2}}ln{\displaystyle \frac{c}{4}}$, so that the potential becomes $V\left(\eta \right)=4\sqrt{c}cosh\eta$.

The potential problem we want to solve is:

$${\displaystyle \frac{d^2\eta }{d{s}^2}}=-{\displaystyle \frac{dV}{d\eta }}=-4\sqrt{c}sinh\left(\eta \right).$$

(28)

The solution is:

$$\eta =\pm 2i\mathrm{am}\left({\displaystyle \frac{1}{2}}\sqrt{\left(8\sqrt{c}-c_1\right){(s+c_2)}^2}|-{\displaystyle \frac{16\sqrt{c}}{c_1-8\sqrt{c}}}\right),$$

(29)

where $\mathrm{am}\left(u\right|m)$ is the Jacobi amplitude which is the inverse of the incomplete elliptic integral of the first kind $F\left(u\right|m)$. Note that to obtain this symmetric potential, we needed to choose $\mu =-b/2$ so that the parameter $s=-{\displaystyle \frac{bt}{2}}$, where t is the actual time.

Utilizing Energy conservation Equation (24), we determine these constants. In particular, one has for the + sign in Equation (27)

$$s=-{\displaystyle \frac{iF\left(\frac{i\eta }{2}|\frac{8\sqrt{c}}{4\sqrt{c}-N^2}\right)}{\sqrt{N^2-4.\sqrt{c}}}}.$$

(30)

Inverting t his equation one obtains:

$$\eta =-2i\mathrm{am}\left(i\sqrt{N^2-4\sqrt{c}}s|{\displaystyle \frac{8\sqrt{c}}{4\sqrt{c}-N^2}}\right)$$

(31)

If we choose $c=4$, then ${\eta }_0=0$. so that $\kappa =\eta$. We plot $\kappa \left(s\right)$ in Figure 1 for $c=4,N^2=25$.

From $\kappa$, we can determine $\tau$

$$\tau \left(s\right)={\displaystyle \frac{1}{2}}{\displaystyle \frac{d\kappa }{ds}}=\sqrt{N^2-4\sqrt{c}}\mathrm{dn}\left(i\sqrt{N^2-4\sqrt{c}}s|{\displaystyle \frac{8\sqrt{c}}{4\sqrt{c}-N^2}}\right)$$

(32)

where $\mathrm{dn}\left(u\right|m)$ is the delta amplitude, satisfying the relationship

$$\mathrm{dn}\left(u\right|m)={\displaystyle \frac{d}{du}}\mathrm{am}\left(u\right|m).$$

When $N^2=25$ and $c=4$, we get the behavior for $\tau \left(s\right)$ as shown in Figure 2.

For the same parameters, we find that $\delta \left(s\right)=e^{\kappa \left(s\right)}$ has the behavior as shown in Figure 3.

In the above figures the parameter $s=-(b+\mu )t=-{\displaystyle \frac{1}{2}}bt$ and $N^2=25,c=4$.

2.2. A Simple Solution When the “Momentum” $\tau$ Is Zero

Given the shape of the potential, there is one obvious, simple, and surprisingly non-trivial solution, when the particle sits at the bottom of the potential with zero momentum $\tau$.

From the equations above, the conditions for this solution are:

$${\displaystyle \frac{d\tau }{ds}}=-4e^{\kappa }-pc{e}^{p\kappa }=0$$

(33)

and $N^2=4e^{\kappa }+c{e}^{p\kappa }$. These two conditions determine c and $e^{\kappa }=\delta$. In particular, we find from Equation (15) and the fact $\Omega =0$ that

$$\delta =\left({\displaystyle \frac{-\mu }{4b}}\right)N^2.$$

(34)

(as discussed earlier, $\mu <0$, so $\delta >0$ as it must be.) Also, since $\tau =0$, we have

$$<\psi |\psi >=<\varphi |\varphi >={\displaystyle \frac{N}{2}}.$$

From the original equations of motion, we find that

$$i{\displaystyle \frac{d\gamma }{dt}}=\left[\lambda N-(g+i\mu )\tau +{\displaystyle \frac{1}{2}}\left({\alpha }_1-{\beta }_1\right)(N+\tau )+{\displaystyle \frac{1}{2}}\left({\alpha }_2-{\beta }_2\right)(N-\tau )\right]\gamma ,$$

(35)

which in our case reduces to

$$i{\displaystyle \frac{d\gamma }{dt}}={\displaystyle \frac{N}{2}}[2\lambda +\alpha -\beta ]\gamma ,$$

(36)

where we have abbreviated ${\alpha }_1+{\alpha }_2=\alpha$ and ${\beta }_1+{\beta }_2=\beta$. Defining $\theta ={\displaystyle \frac{N}{2}}[2\lambda +\alpha -\beta ]$ we have

$$\gamma ={\gamma }_0{e}^{-i\theta t}$$

(37)

with ${{\gamma }_0}^2=\delta =\left({\displaystyle \frac{-\mu }{4b}}\right)N^2$. (In principle, $\gamma$ also contains an overall constant phase, which we neglected here.)

With $\gamma$ in hand, we proceed to the equations of motion for the state vectors, which in the current case become:

$$i{\displaystyle \frac{d|\psi >}{dt}}=H|\psi >+{\displaystyle \frac{N}{2}}(\alpha +i\mu )|\psi >+(g+\lambda )\gamma |\varphi >$$

(38)

and

$$i{\displaystyle \frac{d|\varphi >}{dt}}=H|\varphi >+{\displaystyle \frac{N}{2}}(\beta -i\mu )|\varphi >+\left(g^{*}-\lambda \right){\gamma }^{*}|\psi >.$$

(39)

It might be thought that, once one has solved the nonlinear tau-delta equations, the remaining problem of solving for the state vectors has been reduced to a linear one, since Equations (38) and (39) are linear. This is misleading, however, because after solving these equations, one still must impose the nonlinear conditions that $<\psi |\psi >+<\varphi |\varphi >=N$; $<\psi |\psi >-<\varphi |\varphi >=\tau$ and $<\varphi |\psi >=\gamma$. For the case at hand, we shall carry out this explicitly below.

It is convenient to expand both state vectors in eigenstates of H (assuming a discrete spectrum for notational convenience):

$$|\psi >=\sum _n{\psi }_n{e}^{-i{(E}_n+q)t}|n>$$

(40)

and

$$|\varphi >=\sum _n{\varphi }_n{e}^{-i{(E}_n+q^{\prime })t}|n>$$

(41)

where $q={\displaystyle \frac{N}{2}}(\alpha +i\mu )$ and $q^{\prime }={\displaystyle \frac{N}{2}}(\beta -i\mu )$. We expect that the imaginary parts of q and $q^{\prime }$ will cancel in the final expressions for $|\psi >$ and $|\varphi >$.

We have

$$i{\dot{\psi }}_n=(g+\lambda ){\gamma }_0{e}^{-i{\theta }^{\prime }t}{\varphi }_n$$

(42)

and

$$i{\dot{\varphi }}_n=\left(g^{*}-\lambda \right){\gamma }_0{e}^{i{\theta }^{\prime }t}{\psi }_n,$$

(43)

with ${\theta }^{\prime }=N(\lambda -i\mu )$.

We can decouple these equations by taking another time derivative:

$${\ddot{\psi }}_n+iN(\lambda -i\mu ){\dot{\psi }}_n+(g+\lambda )\left(g^{*}-\lambda \right){{\gamma }_0}^2{\psi }_n=0.$$

(44)

This has solutions of the form ${\psi }_n=K_n{e}^{\nu t}$, where $\nu$ satisfies

$${\nu }^2+iN(\lambda -i\mu )\nu +(g+\lambda )\left(g^{*}-\lambda \right){{\gamma }_0}^2=0.$$

(45)

The two solutions for $\nu$ are:

$${\nu }_{\pm }=-{\displaystyle \frac{\mu N}{2}}+i{\chi }_{\pm },$$

(46)

where ${\chi }_{\pm }=-{\displaystyle \frac{\lambda N}{2}}\pm {\displaystyle \frac{N}{2}}\left|\sqrt{{{\displaystyle \frac{\mu }{b}}{a}^2+\mu }^2\left(1+{\displaystyle \frac{b}{\mu }}\right)-{\lambda }^2\left(1+{\displaystyle \frac{\mu }{b}}\right)}\right|\equiv -{\displaystyle \frac{\lambda N}{2}}\pm \sigma$.

With our choice of parameters, $-b<\mu <0$, all three terms under the radical are negative. Therefore, one can obtain the following (we will need this later):

$${\sigma }^2={\displaystyle \frac{N^2}{4}}\left(-{\displaystyle \frac{\mu }{b}}{a}^2-{\mu }^2\left(1+{\displaystyle \frac{b}{\mu }}\right)+{\lambda }^2\left(1+{\displaystyle \frac{\mu }{b}}\right)\right).$$

(47)

With these inputs, we find:

$$|\psi >=\sum _n{e}^{-i(E_n+{\displaystyle \frac{N}{2}}\alpha +\lambda {\displaystyle \frac{N}{2}})t}\left[K_n^{(+)}{e}^{i\sigma t}+K_n^{(-)}{e}^{-i\sigma t}\right]|n>$$

(48)

and

$$|\varphi >=\sum _n{e}^{-i(E_n+{\displaystyle \frac{N}{2}}\beta -\lambda {\displaystyle \frac{N}{2}})t}\left[K_n^{\prime (+)}{e}^{i\sigma t}+K_n^{\prime (-)}{e}^{-i\sigma t}\right]|n>.$$

(49)

To solve the equations of motion, we must impose the relation between $K_n$ and $K_n^{\prime }$:

$$K_n^{\prime (\pm )}={\displaystyle \frac{i{\nu }_{\pm }}{(g+\lambda ){\gamma }_0}}{K}_n^{(\pm )}.$$

(50)

We see that this proportionality factor does not depend on n.

The $K_n^{(\pm )}$ are not completely arbitrary, because we must insure that

$$<\psi |\psi >=<\varphi |\varphi >={\displaystyle \frac{N}{2}}$$

(51)

and

$$<\varphi |\psi >={\gamma }_0{e}^{-i\theta t},$$

(52)

where $\theta ={\displaystyle \frac{N}{2}}[2\lambda +\alpha -\beta ]$. As we shall see, these are four real conditions for only two variables, so it needs to be checked that they can indeed be satisfied.

In evaluating these conditions, there will be time-dependent cross terms that can be eliminated by imposing:

$$\sum _n{K}_n^{(-)\ast }{K}_n^{(+)}=\sum _n{K}_n^{(+)\ast }{K}_n^{(-)}=0.$$

(53)

This equation also implies:

$$\sum _n{K}_n^{\prime (-)\ast }{K}_n^{\prime (+)}=\sum _n{K}_n^{\prime (+)\ast }{K}_n^{\prime (-)}=0.$$

(54)

Define $S_{\pm }={\sum }_n{K}_n^{(\pm )\ast }{K}_n^{(\pm )}$. Then, the following conditions exist:

$$<\psi |\psi >={\displaystyle \frac{N}{2}}⟹S_{+}+S_{-}={\displaystyle \frac{N}{2}},$$

(55)

$$<\varphi |\varphi >={\displaystyle \frac{N}{2}}⟹{\left|{\nu }_{+}\right|}^2{S}_{+}+{\left|{\nu }_{-}\right|}^2{S}_{-}={\displaystyle \frac{N}{2}}(g^{*}+\lambda )(g+\lambda ){{\gamma }_0}^2,$$

(56)

and

$$<\varphi |\psi >=\gamma ⟹{\nu }_{+}^{*}{S}_{+}+{\nu }_{-}^{*}{S}_{-}=i{{\gamma }_0}^2(g^{*}+\lambda ).$$

(57)

These are four real equations for the two unknowns, $S_{+}$ and $S_{-}$. We can dispose one of these equations immediately. The real parts of ${\nu }_{+}^{*}$ and ${\nu }_{-}^{*}$ are both $-{\displaystyle \frac{\mu N}{2}}$, and the real part of the right-hand side of Equation (57) (using ${{\gamma }_0}^2=\left({\displaystyle \frac{-\mu }{4b}}\right)N^2$) is $\left({\displaystyle \frac{-\mu }{4}}\right)N^2$, so the real part of that equation is obeyed.

The imaginary part of that equation yields an expression for $S_{+}-S_{-}$ as follows:

$$S_{+}-S_{-}={\displaystyle \frac{N^2}{4\sigma }}\left[\lambda \left(1+{\displaystyle \frac{\mu }{b}}\right)+a{\displaystyle \frac{\mu }{b}}\right].$$

(58)

We can obtain another expression for $S_{+}-S_{-}$ from Equation (56) as:

$$S_{+}-S_{-}={\displaystyle \frac{1}{4\lambda \sigma }}\left[{\displaystyle \frac{N^2}{2}}\left({\mu }^2+{\lambda }^2\right)+2{\sigma }^2+{\displaystyle \frac{N^2}{2}}{\displaystyle \frac{\mu }{b}}\left(a^2+b^2+2\lambda a+{\lambda }^2\right)\right].$$

(59)

Using the expression above for ${\sigma }^2$ and some algebra, one can show that these are the same, allowing for a consistent solution for $|\psi >$ and $|\varphi >.$

One remaining consistency check is that, by definition, $S_{+}$ and $S_{-}$ must both be positive, which requires $\left|S_{+}-S_{-}\right|<{\displaystyle \frac{N}{2}}$. From Equation (58), this amounts to

$${\displaystyle \frac{4}{N^2}}{\sigma }^2-{\left[\lambda \left(1+{\displaystyle \frac{\mu }{b}}\right)+a{\displaystyle \frac{\mu }{b}}\right]}^2>0.$$

(60)

Simplifying the expression on the left-hand side of this equation using the formula for ${\sigma }^2$ given above, we find that it is equal to

$$-{\displaystyle \frac{\mu }{b}}\left(1+{\displaystyle \frac{\mu }{b}}\right){(a+\lambda )}^2-\mu (\mu +b),$$

(61)

which is manifestly positive because $-b<\mu <0$.

We can define two vectors that evolve according to H, independently of the nonlinear terms:

$$|A>=\sum _n{K}_n^{(+)}{e}^{-i{E}_{n}t}|n>$$

(62)

and

$$|B>=\sum _n{K}_n^{(-)}{e}^{-i{E}_{n}t}|n>,$$

(63)

and then write

$$|\psi >=e^{-i{\displaystyle \frac{N}{2}}(\alpha +\lambda )t}\left\{e^{i\sigma t}|A>+e^{-i\sigma t}|B>\right\}$$

(64)

and

$$|\varphi >={\displaystyle \frac{i}{(g+\lambda ){\gamma }_0}}{e}^{-i{\displaystyle \frac{N}{2}}(\beta -\lambda )t}\left\{{\nu }_{+}{e}^{i\sigma t}|A>+{\nu }_{-}{e}^{-i\sigma t}|B>\right\}.$$

(65)

$|A>$ and $|B>$ must obey the normalization and orthogonality conditions:

$$<A|A>+<B|B>={\displaystyle \frac{N}{2}};<A|A>-<B|B>={\displaystyle \frac{N^2}{4\sigma }}\left[\lambda \left(1+{\displaystyle \frac{\mu }{b}}\right)+a{\displaystyle \frac{\mu }{b}}\right]$$

(66)

and $<A|B>=0.$

These equations express the general solution for $|\psi >$ and $|\varphi >$, for the particular solution of the $(\tau ,\delta )$ problem that we have considered ($\tau =0,\delta =const.$). The fact that $|\psi >$ is expressed more simply than $|\varphi >$ is an artifact of the order in which we solved the equations and is not a basic property of the system.

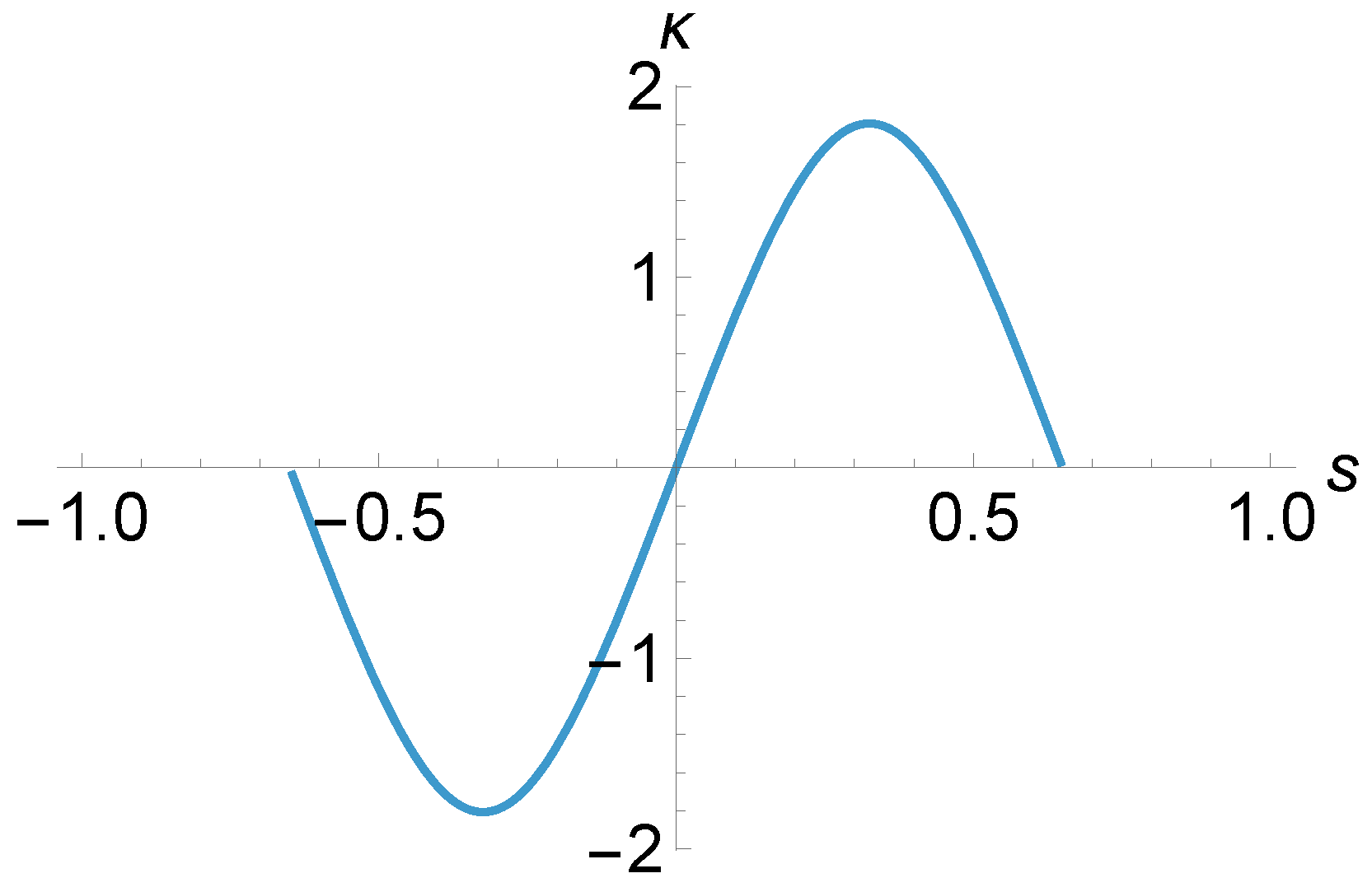
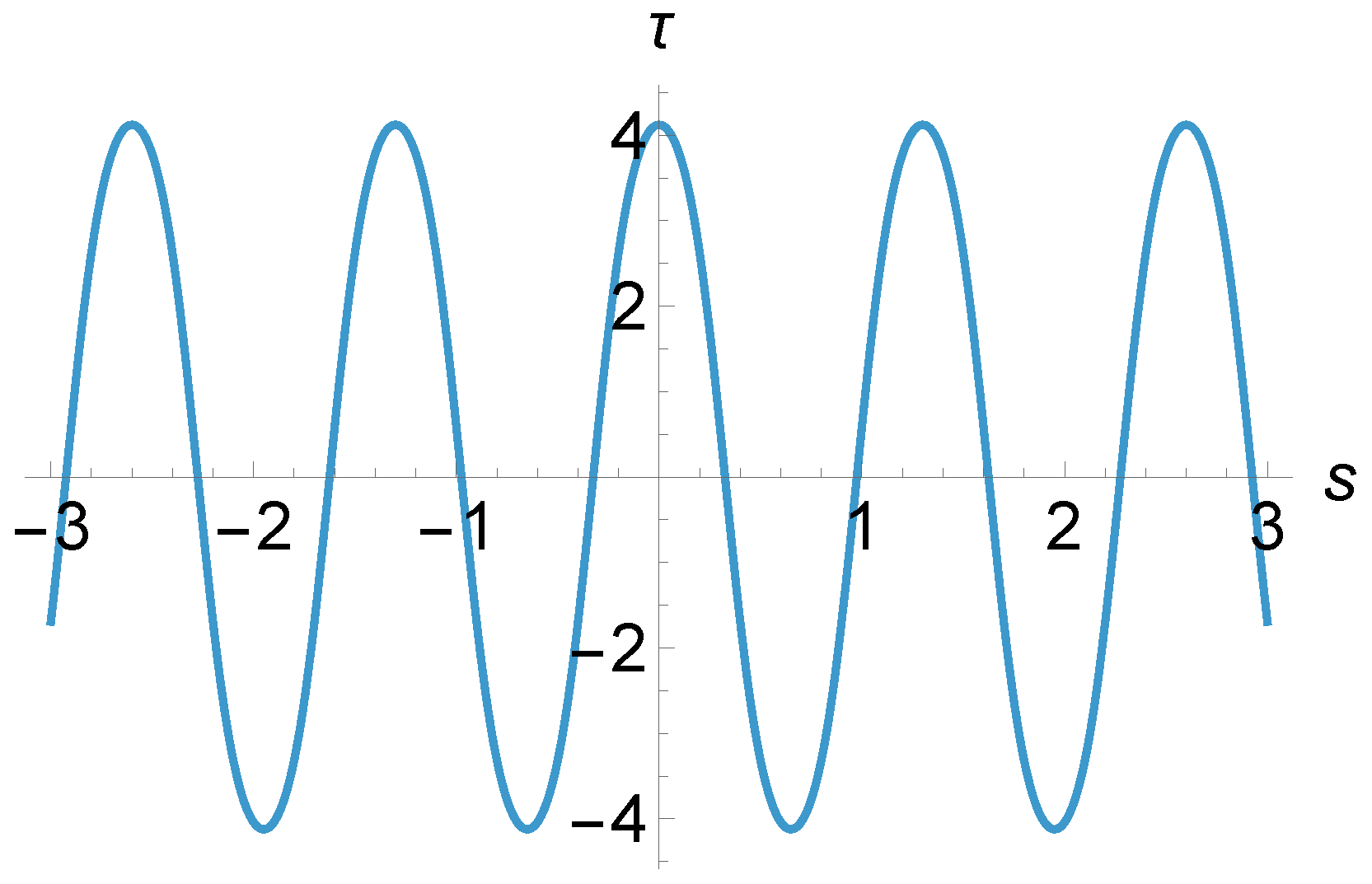
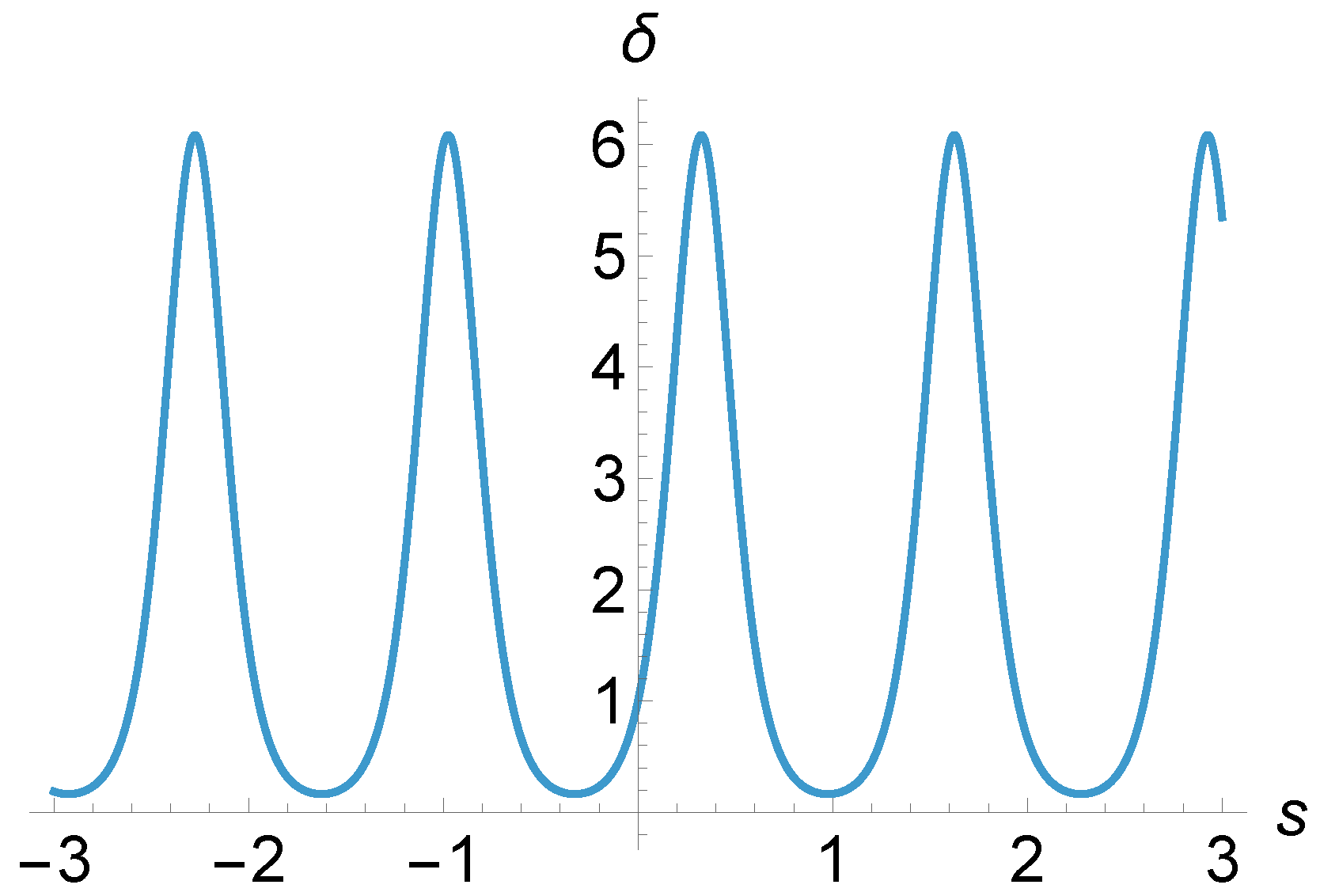
3. Properties of the Density Matrix and the Trajectory Function

In Ref. [1], we defined the density matrix, with its trace properly normalized to one,

$$\rho ={\displaystyle \frac{1}{N}}\left[|\psi ><\psi |+|\varphi ><\varphi |\right],$$

(67)

and observed that it obeys the equation $i\dot{\rho }=[H,\rho ]$, i.e., all the nonlinear effects disappear from $\rho$. This raises a problem, because the most natural extension of the Born rule to our model is to use $\rho$ to define the probability. However, the effects of the nonlinearity would not then be manifest in physical quantities.

Is the same true in the extended model? Using the full equations of motion for $|\psi >$ and $|\varphi >$, we find:

$$\begin{array}{ccc}\hfill i\dot{\rho }& & =[H,\rho ]+2i\mu \left[\left|\psi ><\varphi |\varphi ><\psi \right|-|\varphi ><\psi |\psi ><\varphi |\right]\hfill \\ & & +2\lambda \left[\left|\varphi ><\varphi |\psi ><\psi \right|-|\psi ><\psi |\varphi ><\varphi |\right].\hfill \end{array}$$

(68)

In the case at hand, this becomes

$$i\dot{\rho }=[H,\rho ]+i\mu N\left[|\psi ><\psi |-|\varphi ><\varphi |\right]+2\lambda \left[\gamma |\varphi ><\psi |-{\gamma }^{*}|\psi ><\varphi |\right].$$

(69)

We also have

$$Tr{\rho }^2=1-{\displaystyle \frac{2\mathcal{S}}{N^2}}=1-{\displaystyle \frac{c}{{2N}^2}}{\delta }^{{\displaystyle \frac{\mu }{b+\mu }}}.$$

(70)

In conventional quantum mechanics, the deviation of the trace of ${\rho }^2$ from one is a measure of a lack of purity of the state. Here, we see that this quantity is both generally less than one and dependent on time. It is only equal to one if $c=0$, a limit in which $|\psi >$ and $|\varphi >$ are proportional (because $\mathcal{S}=0$).

Since $\rho$ now includes effects of the nonlinearity, it makes sense to define the expectation value of an operator X as

$$<X\left(t\right)>=Tr\rho \left(t\right)X={\displaystyle \frac{1}{N}}\left[<\psi \left(t\right)|X\left|\psi \left(t\right)>+<\varphi \left(t\right)\right|X|\varphi \left(t\right)>\right].$$

(71)

In what follows, we shall be especially interested in the case where $<X\left(t\right)>$ represents a trajectory, i.e., where X is the position operator for some system. In a somewhat different context, we pursued the idea of using trajectories of this type to investigate the classical effects of the nonlinearity in Ref. [9].

To isolate the effects of the nonlinearity, we want the system to move as an otherwise free particle. We therefore take the Hamiltonian H to be a function of P only, where P is the momentum conjugate to X. It follows that for any two vectors $|{\psi }_1>$ and $|{\psi }_2>$ that evolve according to

$$\left|{\psi }_i\left(t\right)>=e^{-iHt}\right|{\psi }_i>,i=1,2$$

(72)

we have

$${\displaystyle \frac{d^2}{d{t}^2}}<{\psi }_2\left|X\right|{\psi }_1>=0$$

(73)

and, therefore,

$$<{\psi }_2\left|X\right|{\psi }_1>=c_{1}t+c_2.$$

(74)

If ${|\psi }_1>=|{\psi }_2>$, $c_1$ and $c_2$ must be real constants. Otherwise, they can be complex.

3.1. Trajectory Function for the Simple Solution

We would like to calculate the trajectory for the case of the “simple solution” we have obtained above. We consider a position operator in three dimensions, $X_i$, $i=1,2,3.$ The quantities $<A\left|X_i\right|A>,<A\left|X_i\right|B>$ and $<B\left|X_i\right|B>$ will all be linear functions of time. We are interested in the closed orbit of the particle, not in the overall motion of the system through space (the analogy might be that we are interested in the orbit of Earth around the sun, not the motion of the solar system through space). Hence, we take these matrix elements to be constants.

Using the explicit formulas for $|\psi >$ and $|\varphi >$, we can express $<\overrightarrow{X}\left(t\right)>$ as

$$<\overrightarrow{X^{\prime }}\left(t\right)>=<\overrightarrow{X}\left(t\right)>-{\overrightarrow{X}}_0=\overrightarrow{V}cos2\sigma t+\overrightarrow{W}sin2\sigma t$$

(75)

where ${\overrightarrow{X}}_0$, $\overrightarrow{V}$ and $\overrightarrow{W}$ are real constant vectors depending on the values we choose for $<A\left|X_i\right|A>,<A\left|X_i\right|B>$ and $<B\left|X_i\right|B>$. Thus, the particle moves in the plane spanned by $\overrightarrow{V}$ and $\overrightarrow{W}$. Calling the coordinates in this plane $X_1^{\prime }$ and $X_2^{\prime }$, we can orient the axes so that the equation for the orbit can be written in the following form:

$${\displaystyle \frac{{X_1^{\prime }}^{\mathbf{2}}}{{R_1}^{\mathbf{2}}}}+{\displaystyle \frac{{X_2^{\prime }}^{\mathbf{2}}}{{R_2}^{\mathbf{2}}}}=1,$$

(76)

i.e., the equation of an ellipse. However, this is not a Keplerian ellipse. The particle moves harmonically about the center of the ellipse with frequency 2$\sigma$, and does not sweep out equal areas in equal times as measured from one of the foci.

We expect, however, that for more general solutions to the tau-delta problem, the trajectory motion will be less symmetrical, because the potential itself is asymmetric (except for $p=-1$).

3.2. General Formalism

Following the same strategy as for the simple solution where $\kappa$ is a constant, in this section we derive the equations that will be satisfied in the general case, although of course we do not (yet) have solutions for these equations.

The first step is to solve the “tau-delta” problem, i.e., the pair of coupled, nonlinear equations

$${\displaystyle \frac{d\kappa }{ds}}=2\tau$$

(77)

and

$${\displaystyle \frac{d\tau }{ds}}=-4e^{\kappa }-pc{e}^{p\kappa },$$

(78)

together with the constraint

$$N^2=h\equiv {\tau }^2+4e^{\kappa }+c{e}^{p\kappa }$$

(79)

where $s=-(b+\mu )t$ and h is the Hamiltonian as follows:

$${\displaystyle \frac{d\kappa }{ds}}={\displaystyle \frac{\partial h}{\partial \tau }}$$

(80)

and

$${\displaystyle \frac{d\tau }{ds}}=-{\displaystyle \frac{\partial h}{\partial \kappa }}.$$

(81)

The equation for $<\varphi |\psi >=\gamma$ is:

$$i{\displaystyle \frac{d\gamma }{dt}}=\left[\lambda N-(g+i\mu )\tau +{\displaystyle \frac{1}{2}}\left({\alpha }_1-{\beta }_1\right)(N+\tau )+{\displaystyle \frac{1}{2}}\left({\alpha }_2-{\beta }_2\right)(N-\tau )\right]\gamma ,$$

(82)

which can be solved exactly. We define ${\alpha }_1+{\alpha }_2=\alpha$, ${\beta }_1+{\beta }_2=\beta$, ${\alpha }_1-{\alpha }_2={\alpha }^{\prime },$ and ${\beta }_1-{\beta }_2={\beta }^{\prime }$. The solution is

$$\gamma =e^{{\displaystyle \frac{\kappa }{2}}}{e}^{-i(\Lambda +{\theta }_0)},$$

(83)

where $\Lambda =N\left[\lambda +{\displaystyle \frac{1}{2}}(\alpha -\beta )\right]t+{\displaystyle \frac{\kappa }{2(b+\mu )}}\left[a-{\displaystyle \frac{1}{2}}({\alpha }^{\prime }-{\beta }^{\prime })\right]$, and ${\theta }_0$ is an arbitrary real constant. We shall suppress ${\theta }_0$ in the following analysis. The equations for the state vectors are

$$i{\displaystyle \frac{d|\psi >}{dt}}=\left[H+{\displaystyle \frac{N}{2}}((\alpha +i\mu )+{\displaystyle \frac{\tau }{2}}({\alpha }^{\prime }-i\mu )\right]\left|\psi >+(g+\lambda )\gamma \right|\varphi >$$

(84)

and

$$i{\displaystyle \frac{d|\varphi >}{dt}}=\left[H+{\displaystyle \frac{N}{2}}((\beta -i\mu )+{\displaystyle \frac{\tau }{2}}({\beta }^{\prime }-i\mu )\right]\left|\varphi >+\left(g^{*}-\lambda \right){\gamma }^{*}\right|\psi >.$$

(85)

We introduce the kets $|{\psi }^{\prime }>,|{\varphi }^{\prime }>$ via

$$|\psi >=e^{{\displaystyle \frac{\mu Nt}{2}}+{\displaystyle \frac{\mu \kappa }{4(b+\mu )}}}{e}^{-i{\theta }_{\psi }}|{\psi }^{\prime }>,$$

(86)

where ${\theta }_{\psi }=\left[H+{\displaystyle \frac{N}{2}}\alpha \right]t-{\displaystyle \frac{\kappa {\alpha }^{\prime }}{4(b+\mu )}}$, and

$$|\varphi >=e^{{\displaystyle \frac{-\mu Nt}{2}}+{\displaystyle \frac{\mu \kappa }{4(b+\mu )}}}{e}^{-i{\theta }_{\varphi }}{|\varphi }^{\prime }>,$$

(87)

where ${\theta }_{\varphi }=\left[H+{\displaystyle \frac{N}{2}}\beta \right]t-{\displaystyle \frac{\kappa {\beta }^{\prime }}{4(b+\mu )}}$. Then we find the coupled equations

$$i{\displaystyle \frac{d|{\psi }^{\prime }>}{dt}}=e^f(g+\lambda )|{\varphi }^{\prime }>$$

(88)

and

$$i{\displaystyle \frac{d|{\varphi }^{\prime }>}{dt}}=e^{\kappa -f}\left(g^{*}-\lambda \right)|{\psi }^{\prime }>,$$

(89)

where $f={\displaystyle \frac{\kappa }{2}}-\mu Nt-i\left(\lambda Nt+{\displaystyle \frac{a\kappa }{2(b+\mu )}}\right)\equiv {\displaystyle \frac{\kappa }{2}}-\mu Nt-i{\theta }_f$. Note that ${\theta }_{\varphi }-{\theta }_{\psi }-{\theta }_f+\Lambda =0.$

We can decouple these by taking another derivative:

$${\displaystyle \frac{d^2|{\psi }^{\prime }>}{d{t}^2}}-{\displaystyle \frac{df}{dt}}{\displaystyle \frac{d|{\psi }^{\prime }>}{dt}}+(g+\lambda )\left(g^{*}-\lambda \right)e^{\kappa }|{\psi }^{\prime }>=0.$$

(90)

We obtain a similar equation for ${\displaystyle \frac{d^2|{\varphi }^{\prime }>}{d{t}^2}}$, in which f is replaced by $f^{\prime }=\kappa -f$. When $\kappa =const.,$ we find agreement with Equation (44) above. If we assume a solution of the form

$$|{\psi }^{\prime }>=F\left(t\right)|{\psi }_0>$$

(91)

where $|{\psi }_0>$ is a constant vector, then $F\left(t\right)$ obeys:

$${\displaystyle \frac{d^{2}F}{d{t}^2}}-{\displaystyle \frac{df}{dt}}{\displaystyle \frac{dF}{dt}}+(g+\lambda )\left(g^{*}-\lambda \right)e^{\kappa }F=0.$$

(92)

This is a second-order linear differential equation, so it has two linearly independent solutions, $F_1$ and $F_2$. The general solution for $|{\psi }^{\prime }>$ is then

$$|{\psi }^{\prime }>=F_1\left(t\right)|{\psi }_1>+F_2\left(t\right)|{\psi }_2>,$$

(93)

where the $|{\psi }_i>$ are arbitrary constant vectors. It follows that

$$|{\varphi }^{\prime }>={\displaystyle \frac{e^{-f}}{(g+\lambda )}}i\left[{\displaystyle \frac{d{F}_1}{dt}}|{\psi }_1>+{\displaystyle \frac{d{F}_2}{dt}}|{\psi }_2>\right].$$

(94)

The Wronskian of $F_1$ and $F_2$ has a simple form:

$$W\left(F_1,F_2\right)\equiv \dot{F_1}{F}_2-F_1\dot{F_2}=c_0{e}^f,$$

(95)

where $c_0$ is a constant of integration. To recover $|\psi >$ and $|\varphi >$ we first define

$$|{\psi }_i\left(t\right)>=e^{-iHt}|{\psi }_i>,i=1,2.$$

(96)

The $|{\psi }_i\left(t\right)>$ are two ket vectors that evolve according to the original Hamiltonian H. We then have

$$|\psi >=e^{-i{\displaystyle \frac{N}{2}}(\alpha +i\mu )t}{e}^{{\displaystyle \frac{i\kappa }{4}}{\displaystyle \frac{({\alpha }^{\prime }-i\mu )}{(b+\mu )}}}\left[F_1\left(t\right)|{\psi }_1\left(t\right)>+F_2\left(t\right)|{\psi }_2\left(t\right)>\right]$$

(97)

and

$$|\varphi >=e^{-i{\displaystyle \frac{N}{2}}(\beta -i\mu )t}{e}^{{\displaystyle \frac{i\kappa }{4}}{\displaystyle \frac{({\beta }^{\prime }-i\mu )}{(b+\mu )}}}{\displaystyle \frac{e^{-f}}{(g+\lambda )}}i\left[{\displaystyle \frac{d{F}_1}{dt}}|{\psi }_1\left(t\right)>+{\displaystyle \frac{d{F}_2}{dt}}|{\psi }_2\left(t\right)>\right].$$

(98)

If we can integrate (exactly or approximately) the tau-delta equations and also the equations for the $F_i$, the remaining steps to achieving a full solution would then be to impose the following conditions:

$$<\psi |\psi >+<\varphi |\varphi >=N;<\psi |\psi >-<\varphi |\varphi >=\tau ;$$

(99)

and

$$<\varphi |\psi >=\gamma .$$

(100)

4. Conclusions and Outlook

In a previous paper [1], we began an exploration of a particular form of nonlinear extension of quantum mechanics. The extension could be applied to any underlying dynamical system, and featured the introduction of two state vectors instead of the usual single state vector in ordinary quantum mechanics. The model was simple, and the effects of the nonlinearity could be determined completely, although the meaning of the second state vector remained uncertain. An analogy was noted with the two-state formalism of Aharonov and Vaidman [10] which is a time-symmetric formulation of ordinary quantum mechanics, based on earlier work by Aharonov, Bergmann and Lebowitz [11,12]. Our original model possessed a time-reversal symmetry, involving the interchange of $|\psi >$ and $|\varphi >$. In the present extended model, this symmetry is apparently broken by the parameter $\lambda$, as we explain in Appendix A.

Because of our previous model’s simplicity, the dynamics it incorporated was limited. In particular, the effects of the nonlinearity persisted for only a finite duration, decaying exponentially for large times. In addition, the natural extension of the Born rule to the model failed to encompass any of the nonlinear behavior. Therefore, in this paper, we have constructed an expanded version, finding the most general such model consistent with three defining principles that were characteristic of the earlier work. Although we are not yet able to solve this new model completely, we can already see, by studying some simple examples, that the time dependence of the state vectors is much richer than that allowed by the earlier model. In particular, closed orbits exist for a range of parameters, which was not possible when the nonlinearity only persisted for a finite time. Previous attempts to make quantum mechanics nonlinear, such as that of Weinberg, were shown to permit superluminal communication [13,14]. That is, if two widely separated observers, Alice and Bob, were each in possession of a piece of an entangled state, Alice’s measurement would instantaneously collapse the wave function describing Bob’s piece. In ordinary quantum mechanics, however, Bob could not deduce from the collapse what measurement Alice made. In many nonlinear extensions, though, this is no longer true, so Bob can obtain information from Alice instantaneously, violating the so-called no-signaling condition. Traditionally, this has been taken to be a fatal disease. The rationale given in one paper [15] is: “The no-signaling condition states that one cannot send information faster than the speed of light, and is a cornerstone of the special theory of relativity. The community regards this condition as being inviolable.”

We do not yet know whether our model allows this kind of superluminal communication, but if so, we do not regard it as fatal, or even necessarily detrimental. The effect will undoubtedly be hard to observe, and its discovery would reveal an interesting property of nature. We stress that physics is not determined by a vote of “the community”, but rather by the results of reliable experiments.

Our work so far suggests two approximations that may be useful in making further progress. In this paper, we showed that, for a suitably chosen range of parameters, the evolution of $\kappa ={ln\left|\gamma \right|}^2$ is governed by a Hamiltonian whose potential,

$$V\left(\kappa \right)=4e^{\kappa }+c{e}^{p\kappa }$$

(101)

rises exponentially for $\left|\kappa \right|\to \infty$. We solved for the state vectors in the case that $\kappa$ remains stationary at the minimum of the potential. Building on this solution, we can study small oscillations of $\kappa$ about the minimum, to see how this affects the dynamics of the state vectors themselves, i.e., we set

$$\kappa ={\kappa }_0+\delta \kappa$$

(102)

where $e^{{\kappa }_0}=\left({\displaystyle \frac{-\mu }{4b}}\right)N^2$ is the minimum of the potential, and work to lowest order in $\delta \kappa$.

Clearly, this approximation requires $\kappa$ to remain close to the bottom of the potential. A complementary approximation, which should be better the farther $\kappa$ gets from the bottom, is to replace the true potential $V\left(\kappa \right)$ with:

$$\tilde{V}\left(\kappa \right)=4e^{\kappa }\theta \left(\kappa -{\kappa }_1\right)+c{e}^{p\kappa }\theta \left({\kappa }_1-\kappa \right)$$

(103)

where ${\kappa }_1$ is defined by $4e^{{\kappa }_1}=c{e}^{p{\kappa }_1}$, so that $\tilde{V}$ is continuous (this is not the same as the minimum of the potential, unless $p=-1).$ The motivations for this approximation are, first, that in each of the two regions $\kappa >{\kappa }_1$ and $\kappa <{\kappa }_1$ the difference between $V\left(\kappa \right)$ and $\tilde{V}\left(\kappa \right)$ is an exponential tail that grows smaller the larger $\left|\kappa \right|$ becomes; and second, in each region the problem is solvable, because the potential is given by a single exponential, which is just the case considered in our first paper. We anticipate implementing both these approximations in future work.

Our point of view is rather unconventional. Our first goal is to see whether the nonlinearities of our model can account for some or all of the classical behavior of gravity. Whether or not that hope is realized, further analysis of the extension of quantum mechanics that we have proposed may yield valuable insight into the as yet unsolved problem of what quantum mechanics is really all about.