Abstract
This paper proposes a hierarchical CNN-sLSTM-Attention model for long-sequence time series forecasting. It enhances efficiency by replacing traditional LSTMs with a stable LSTM (sLSTM) variant, which incorporates exponential gating and memory mixing. The architecture integrates CNN for local feature extraction, sLSTM blocks for temporal modeling, and an attention mechanism for dynamic weighting. This integrated design enables the effective processing of data with symmetric patterns or asymmetric patterns, which are prevalent in real-world time series. Experimental results on six datasets—encompassing scenarios with symmetry/asymmetry characteristics, such as temperature cycles and traffic flow fluctuations—demonstrate the model’s superior performance. Key findings include a 33% reduction in RMSE over standard LSTM on temperature prediction; 10× faster convergence with stability achieved within 12 epochs for traffic flow prediction; a 15–47% reduction in long-sequence error attributable to the sLSTM component; and a 35% improvement in trend fitting due to the attention mechanism. Although the model outperforms baseline methods in handling periodic (often symmetric) and noisy data, its performance is limited on multimodal cases. These findings suggest that future work should focus on lightweight optimization, which has the potential to improve the model’s adaptability to a broader spectrum of symmetry and asymmetry patterns in time series.
1. Introduction
Temperature prediction is fundamental to meteorological science, energy management, and public health domains. Its accuracy directly influences the efficiency of resource allocation, the effectiveness of early warning systems, and strategic decision-making. In smart grid applications, accurate prediction of transformer hot-spot temperatures is essential for preventing thermal faults and optimizing equipment lifespan [1]. Similarly, precise modeling of non-stationary temperature variations enables proactive measures to mitigate agricultural losses during extreme weather events.
The field currently faces two primary technical challenges. First, traditional methods such as the ARIMA model, have inherent limitations due to their linear assumptions and reliance on manual feature engineering. This hinders their ability to capture the complex spatiotemporal relationships and long-term dependencies inherent in temperature data [2], which often exhibit both symmetry and asymmetry patterns, such as seasonal cycles and extreme weather fluctuations. Second, although individual deep learning architectures like LSTM networks have shown promise, they suffer from feature degradation and computational inefficiency when processing high-dimensional datasets or periodic fluctuation [3].
Recent advancements in hybrid architectures have sought to address these limitations, yet several critical shortcomings persist. Current CNN-LSTM implementations often rely on simple feature concatenation, which fails to explicitly model spatiotemporal interactions. This results in significant information loss over extended sequences, with error rates increasing by 28–45% for sequences longer than 300 time steps) [4,5]. While Transformer-based models employ dynamic attention mechanisms for temporal feature weighting, their quadratic computational complexity () leads to prohibitively long training times, increasing substantially for sequences longer than 500 elements [6,7]. Emerging Transformer variants, such as PatchTST [8] and iTransformer [9], incorporate architectural innovations like patch embedding and dimension inversion to reduce computational overhead. Nevertheless, they still struggle to handle the abrupt non-stationary transitions characteristic of meteorological data.
To address these challenges, we propose a novel CNN-sLSTM-Attention hybrid architecture; this model synergistically combines the stability of exponential gating with efficient local-global feature fusion. We extend this approach by incorporating a stabilized LSTM and an attention mechanism, resulting in a novel framework. This framework is designed to handle data with symmetry and asymmetry phenomena—a critical capability for time series forecasting—and serves as a computationally efficient alternative to pure Transformer models while maintaining competitive prediction accuracy. Our model’s key contributions are threefold: (1) stabilized gradient propagation through exponential gating; (2) hierarchical extraction of spatial and temporal patterns; and (3) dynamic attention weighting for critical meteorological events.
The remainder of this paper is structured as follows. Section 2 reviews the relevant literature and establishes the corresponding theoretical foundations. Section 3 details the proposed model’s architecture and mathematical formulations. Section 4 describes the experimental setup, including datasets, baseline methods, and evaluation protocols. Section 5 presents the quantitative results and qualitative analysis. Finally, Section 6 discusses the practical implications, acknowledges the limitations, and outlines directions for future research.
1.1. Literature Review
Temperature prediction has been extensively studied across diverse domains, with methodologies evolving from statistical approaches to deep learning paradigms. Early studies predominantly relied on time series models (e.g., ARIMA). Which proved effective for short-term linear predictions yet failed to capture the complex nonlinear patterns inherent in meteorological data—a limitation highlighted by recent advances in deep learning [8,10]. These data often contain symmetry (e.g., regular diurnal cycles) and asymmetry (e.g., irregular heatwave surges) that linear models struggle to represent. Machine learning techniques—including support vector machine (SVM) and random forests—introduced nonlinearity but remained reliant on manual feature engineering, which limits their adaptability to diverse environmental conditions [11]. The emergence of deep learning brought significant advancements, with recurrent neural networks (RNNs) and their variants (LSTM, GRU) becoming dominant due to their ability to model sequential dependencies [12]. LSTMs struggle with long-range dependencies, as gradient vanishing remains a persistent issue for sequences exceeding 100 time steps [13]. Hybrid models that combine convolutional neural networks (CNNs) with LSTMs have sought to address spatial limitations but lack effective mechanisms for dynamically weighting features across time scales [4]. Recent transformer-based methods have incorporated self-attention mechanisms to prioritize critical temporal features, achieving state-of-the-art performance in numerous forecasting tasks [6].
To address the computational challenges of standard Transformers, a new generation of efficient architectures has emerged, achieving notable advances:
- PatchTST [8] segments time series into interpretable patches, reducing computational complexity while preserving long-range dependencies.
- iTransformer [9] inverts attention to model cross-variate dependencies, demonstrating superior performance on multivariate meteorological data.
- TimesNet [10] converts 1D series into 2D temporal matrices, enabling simultaneous analysis of periodicity and trends.
Despite these advances, the computational complexity of these models remains prohibitive for real-time applications on edge devices [7], and their performance in capturing abrupt weather transitions requires further improvement.
1.2. Technical Challenges
Despite significant progress, temperature prediction remains constrained by the following technical challenges:
- Spatiotemporal Coupling: Temperature variations are influenced by complex interactions between local microclimates and regional weather systems. This requires models to simultaneously capture spatial correlations and temporal dynamics—a capability lacking in most existing architectures, especially when handling both symmetric spatial patterns (e.g., uniform temperature distribution in a stable weather system) and asymmetric spatial patterns (e.g., uneven temperature gradients in a storm front).
- Long-Range Dependencies: Meteorological phenomena often exhibit periodic patterns spanning days to seasons. Traditional LSTMs suffer from performance degradation with sequences longer than 100 steps, while transformer models become prohibitively expensive for extended time series, hindering the modeling of long-term symmetric cycles and asymmetric long-term trends.
- Non-Stationarity: Temperature data frequently contains abrupt shifts caused by weather fronts, seasonal transitions, or extreme events. This challenges models’ ability to adapt to distributional shifts without catastrophic forgetting.
- Multi-Scale Feature Integration: Effective temperature prediction requires integrating fine-grained (hourly) and coarse-grained (daily) patterns, a task complicated by the varying importance of different temporal scales across prediction horizons.
- Computational Efficiency: Real-world applications demand models that can process large volumes of sensor data in near real-time, posing a direct conflict with the high computational requirements of state-of-the-art attention-based architectures.
- Noise Interference Challenge: Temperature time-series data is inherently susceptible to noise interference from sensor errors, environmental disturbances (e.g., sudden wind gusts affecting surface temperature readings), or incomplete data acquisition—issues that exacerbate the difficulty of modeling symmetric (e.g., diurnal temperature cycles) and asymmetric (e.g., heatwave spikes) patterns. Accurate modeling of such noisy, complex temperature data requires addressing two core challenges simultaneously: first, enhancing robustness against asymmetric and random noise interference to avoid distorting key temporal patterns; second, ensuring efficient capture of critical structural features (e.g., stable symmetric cycles, abrupt asymmetric anomalies) amid noise. While this dual challenge has been extensively explored in fields such as hyperspectral remote sensing and high-dimensional computer vision—where structural feature processing and stable representation methods have been developed to handle noisy high-dimensional data—these insights remain underutilized in temperature time-series prediction. Adapting such cross-domain strategies could provide valuable support for improving the noise resistance of temperature forecasting models [14,15,16].
1.3. Contributions
This paper makes the following key contributions:
- Stable LSTM (sLSTM) Architecture: A modified LSTM incorporating exponential gating and layer normalization is proposed, which extends the effective gradient propagation threshold from 100 to over 500 time steps. This enhancement enables robust modeling of multi-periodic temperature patterns and long-term degenerative trends. Thus, we primarily target medium-to-long-term forecasting, and there is a good performance of the model on this type of dataset.
- Collaborative Feature Fusion Framework: A hybrid CNN-sLSTM-Attention model is developed, integrating convolutional layers for local spatial feature extraction, sLSTM for capturing long-range temporal dependencies, and a lightweight attention mechanism that dynamically emphasizes critical weather patterns without quadratic complexity.
- Cross-Scenario Validation: Comprehensive evaluations are conducted across six diverse datasets (urban, agricultural and industrial temperature monitoring) with varying temporal resolutions (from hourly to weekly). The results demonstrate consistent improvements: a 33% reduction in RMSE compared to traditional LSTMs, 10× faster convergence than LSTM models, and superior performance during extreme weather events.
- Ablation Studies Systematic experiments were performed to verify the contribution of each component. The findings show that sLSTM reduces prediction error by 15–47% for long sequences, while the attention mechanism improves the detection of extreme temperature events.
1.4. Limitations
Despite its advantages, our approach has the following limitations that warrant consideration:
- Spatial Generalization: The current model achieves optimal performance when deployed in regions with climatic characteristics similar to those of the training data. However, its performance degrades in environments with rapidly changing climates or in geographically distinct areas.
- Extreme Event Handling: Although the model’s performance in this regard is improved compared to the baseline method, it still struggles with unprecedented extreme weather events (e.g., record-breaking heatwaves). This is primarily due to a scarcity of training data for such anomalous events.
- Computational Trade-offs: While the attention mechanism is lightweight compared to Transformer models, it still introduces additional computational overhead relative to vanilla LSTMs. This constraint may limit the model’s deployment in resource-constrained edge devices [17].
- Feature Dependency: The model performance depends on access to a diverse set of meteorological features (e.g., humidity, wind speed). Consequently, it is less effective in regions with limited sensor coverage or incomplete historical meteorological data.
These limitations inform our future research directions, which include developing transfer learning strategies for spatial generalization and incorporating adversarial training to improve robustness to extreme events.
2. Related Work
2.1. CNN Model Research
In artificial intelligence and pattern recognition, convolutional neural networks (CNNs) automatically learn hierarchical feature representations using convolutional filters [18]. This architecture is built upon the following two core principles:
- Sparse Connections: Each neuron is connected only to a local region in the previous layer through its receptive fields.
- Weight Sharing: Convolutional kernels are shared across the input, maintaining translational invariance.
The convolutional operation is mathematically defined as
where is the input feature map from layer , is the convolution kernel weights, and is the bias term for the j-th feature map.
The ReLU activation function provides nonlinear mapping,
Max-pooling operation reduces dimensionality,
where W is the size of the pooling window.
In time series prediction, existing CNNs are primarily used as an isolated feature extractor. Their fusion with LSTM typically involves simple cascade architectures (such as CNN-LSTM). However, the mapping between local features and the LSTM’s gating mechanisms is not explicitly modeled. Consequently, key local patterns (such as short-term temperature peaks) extracted by CNNs are easily diminished during the LSTM’s temporal processing. Furthermore, the deep coupling between these features and the temporal dynamics necessitates a more directed mapping to the gating parameters.
2.2. sLSTM Model Research
The Stable Long Short-Term Memory Network (sLSTM) [19] enhances the performance of traditional LSTMs in tasks such as storage decision-making, rare word prediction, modeling complex dependency, and robustness during training and inference through its introduction of exponential gating, memory mixing, and stabilization mechanisms. The model’s mathematical formulation is provided in [19]; its architecture and core equations are described below to facilitate the subsequent discussion of its adaptation for time series prediction. Figure 1 illustrates the sLSTM network architecture.
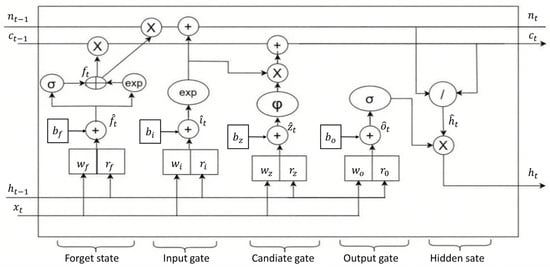
Figure 1.
Schematic diagram of the sLSTM architecture.
The recurrent relationship between the input and state in sLSTM is expressed as follows:
where represents the cell state at time step t, which carries the network’s long-term memory; is the forget gate, is the input gate, and regulates the contribution of the current input and the previous hidden state to the cell state, as shown below:
In the above equations, is the input vector, is the activation function, is the weight matrix for the input, is the corresponding recurrent weight matrix, and represents the bias term. The model also uses a normalized state
where represents the normalized state at time step t, which regulates the update of the cell state. The hidden state enables recurrent connections as follows:
where is the output gate. The input gate controls the degree of new information injection into the cell state through
Similarly, the forget gate regulates the retention ratio of the previous cell state through
The output gate manages information flow from the cell state to the hidden state,
where is the weight matrix applied to the current input , are the recurrent weight matrices of the output gate acting on the previous hidden state , and is the bias term.
To provide numerical stability for exponential gates, the forget gate and input gate are combined through state ,
where is the stabilized input gate (a scaled version of the original input gate). Similarly, the forget gate is stabilized through :
In summary, compared to the original LSTM, the sLSTM introduces an exponential gating mechanism via Equations (8) and (9), uses Equation (6) for normalization, and achieves stabilization via Equations (11)–(13). These improvements significantly enhance the performance of standard LSTMs.
However, existing research on the sLSTM primarily focuses on its internal gating improvements, without exploring its synergistic mechanisms with CNN local features and attention-based key mechanisms. Specifically, the exponential gating of sLSTM can flexibly regulate the injection intensity of CNN features, while attention gradient feedback can guide the sLSTM to preferentially update cell states for critical temporal sequences. This coordination enables improved accuracy of CNN feature selection, forming a “local-temporal-key” hierarchical optimization loop.
2.3. Attention Mechanisms
The fundamental principle of attention mechanisms is inspired by the dynamic focus of different brain regions over time. This approach reduces the model’s focus on irrelevant information at specific times, thereby enhancing its concentration on critical areas. By redistributing attention between critical and non-critical regions, these mechanisms improve prediction accuracy. Specifically, attention alleviates the loss of important information in long short-term memory networks processing extended sequences by replacing fixed weight allocation with a probabilistic method [5,20].
When an attention mechanism is implemented in a model, the input is first encoded in a set of feature vectors. The model then derives three distinct vectors from each input element: a query (Q), a key (K), and a value (V). Next, a similarity function , typically a scaled dot product, computes the attention scores between the query and key vectors. These scores are normalized by a softmax function to create a set of weight coefficients. Finally, the output is generated by taking the weighted sum of the value vectors using these weights. (The dimension of the keys is used for scaling, not the number of heads).
The mathematical expression of the attention mechanism is
where is the dimension of the key vector, and the normalization ensures a stable weight distribution. This process enables the model to dynamically focus on the most discriminative information fragments for the prediction task by explicitly modeling dependencies between sequence elements, thereby improving accuracy and robustness in long-sequence modeling.
The combination of traditional LSTM and attention faces challenges due to high computational complexity when processing long sequences; the allocation of weights is not linked to the gating states of sLSTM. Furthermore, the “critical time step” identified by the attention mechanisms remains disconnected from the “significant temporal dependency” captured by the LSTM. By leveraging the sLSTM’s efficient temporal modeling to reduce the computational cost of long sequences and establishing a cooperative transfer mechanism between attention gradients and sLSTM gating gradients, we can significantly improve focusing accuracy.
3. Research Methodology
3.1. CNN-sLSTM-Attention Model Principle
The time series prediction model proposed in this paper represents an adaptation of the CNN-LSTM-Attention architecture [17,21]. Illustrated in Figure 2, the model incorporates convolutional feature extraction, stable sequence modeling (sLSTM), and adaptive attention weighting within a unified framework, enabling the synergistic capture of complex temperature dynamics.
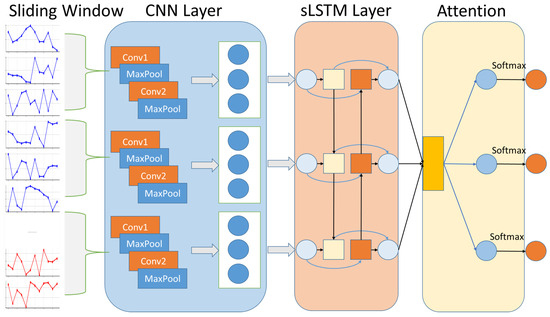
Figure 2.
Schematic diagram of the model structure.
3.1.1. Comparative Architectural Analysis
To elucidate the architectural innovations and provide a clear comparison with the baseline model, a side-by-side schematic diagram is presented in Figure 3. This comparative analysis visually underscores the key enhancements in data flow and component design that contribute to the model’s superior performance. The bisector chart in Figure 3 facilitates a detailed comparison across the following two critical dimensions:
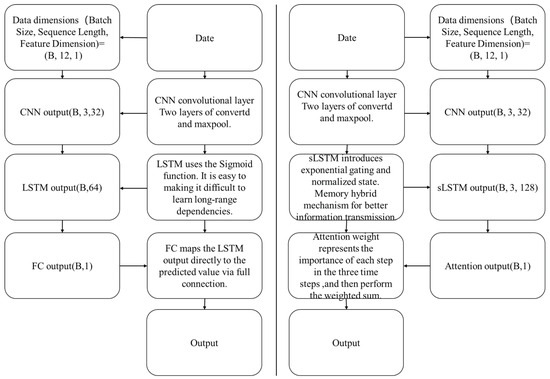
Figure 3.
Comparative schematic of the CNN-sLSTM-Attention and CNN-LSTM-FC model architectures.
Data Flow and Dimensionality Transformation. The schematic clearly visualizes the complete data flow from an input tensor of shape (B, 12, 1) to the final output (B, 1). By annotating the tensor dimensions at key processing nodes—such as the CNN layer output (B, 3, 32)—the diagram makes the sequential data reshaping and feature evolution intuitively understandable, significantly enhancing the clarity of the architectural comparison.
Core Component Mechanisms: sLSTM vs. LSTM. A central focus of the diagram is the juxtaposition of the temporal modeling components. It highlights the limitation of the baseline LSTM, whose reliance on sigmoid activations makes it susceptible to gradient instability, hindering long-range dependency learning. In contrast, the schematic illustrates the key innovations of the proposed sLSTM unit, including exponential gating and memory mixing mechanisms, which are designed to facilitate more stable gradient propagation and enable effective long-term information retention.
Core Component Mechanisms: Attention vs. FC. At the information integration stage, the diagram effectively contrasts the dynamic attention mechanism with a static fully connected (FC) layer. It shows how the Attention module generates adaptive weights to signify the importance of each time step, achieving dynamic focus on critical temporal segments. Conversely, the FC layer employs a simple linear mapping, which lacks this capability for context-aware, dynamic feature weighting, underscoring the superior capability of the attention mechanism.
3.1.2. CNN and sLSTM Feature Interaction
The collected temperature data are first normalized to eliminate the influence of differing scales on model training. The processed data are then fed into a convolutional neural network (CNN) for local feature extraction. Employing a sliding window operation, the CNN captures short-term temporal patterns (e.g., daily temperature fluctuations) and generates high-dimensional feature maps,
where represents the normalized temperature series (T: sequence length, F: feature dimension), K is the convolution kernel size, are the convolution weights, b is the bias term, and denotes the ReLU activation function. The resulting feature map (: output sequence length, C: number of kernels) encodes local correlation information essential for subsequent temporal modeling.
These CNN-derived features are subsequently passed to the stable Long Short-Term Memory network (sLSTM), where they modulate the gating mechanisms to influence temporal dependency learning. The sLSTM integrates the CNN features through its key gating functions,
Here, are weight matrices that map CNN features to gate activations (D: sLSTM hidden dimension), are recurrent weight matrices, and are bias vectors. The exponential activation function for the input gate () allows salient features extracted by the CNN (e.g., extreme temperature peaks) to exert a stronger influence on the cell state when , thereby overcoming the [0, 1] activation range limitation of standard LSTM gates [22].
The cell state update incorporates both the CNN features and historical information, with a normalization mechanism ensuring numerical stability,
where ⊙ denotes the Hadamard (element-wise) product, is the normalizer state, and is the output gate. This formulation ensures that the contribution of CNN features is proportionally regulated through , preventing their dilution in long sequences while maintaining stable gradient flow.
3.1.3. sLSTM and Attention Gradient Synergy
The hidden states from the sLSTM are fed into the attention module, which dynamically assigns weights to highlight temporally critical features for temperature prediction. The attention mechanism computes context-aware representations as follows:
where , , and are the query, key, and value matrices, respectively, projected from the sLSTM outputs. Here, are learnable projection weights, and is the key dimension.
A critical aspect of our model is the synergistic interaction between the sLSTM and attention components during backpropagation. The gradient of the attention output with respect to the sLSTM hidden states, denoted as , is combined with the sLSTM’s internal recurrent gradient ,
In this equation, represents the gradient feedback from the attention weighting, where is the loss function. The term accounts for the gradient propagated through the recurrent connections of the sLSTM gates.
This gradient fusion creates a closed-loop optimization process that ensures (1) the attention mechanism amplifies the gradient signal () at critical temporal positions (e.g., onset of heatwave events), guiding the model to focus on these regions, and (2) the sLSTM updates its gating mechanisms to preserve the relevant historical information highlighted by the attention, thereby enhancing the synergy between temporal modeling and feature weighting. Through the weight distribution principle of the attention mechanism, the attention of the seasonal adjustment of the model to different time steps is explained, and the distribution change is adapted.
To prevent overfitting, we employ random dropout and early stopping. Dropout randomly deactivates 20% of the units in the sLSTM layers during forward propagation, mitigating feature co-adaptation [23]. Early stopping halts the training process if the validation loss shows no improvement over 15 consecutive epochs (), thereby preserving the model’s generalization capability [21].
Furthermore, we explore a variant termed CNN-SsLSTM-Attention, where the single sLSTM layer is replaced with stacked sLSTM layers (SsLSTM) to enable hierarchical temporal modeling at multiple scales. This design is inspired by recent advances in deep sequential architectures [24], but extends previous work through a key innovation: the tight integration of attention-based dynamic weighting. Performance comparisons between the model variants, presented in Table 4, demonstrate the superiority of our enhanced architecture.
3.2. Forecast Framework
The experimental workflow, illustrated in Figure 4, consists of the following three stages:
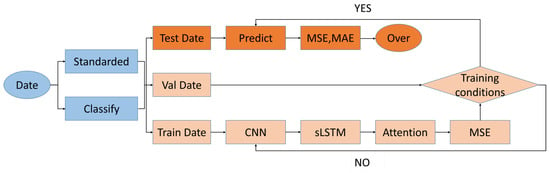
Figure 4.
Experimental flow chart.
3.2.1. Data Preprocessing
The preprocessing pipeline includes the following key steps:
- Sliding Window: A window length of time steps is used to construct input sequences.
- Dataset Split: The data is partitioned into training, validation, and test sets with an 80%–10%–10% ratio.
- Normalization: Min-max scaling is applied independently to each sliding window.
3.2.2. Model Training
The following critical configurations are employed during model training:
- Early Stopping: Training is halted if no improvement is observed on the validation loss for consecutive epochs.
- Dropout: A dropout rate of 0.2 is applied to the sLSTM layers to regularize the model.
- Batch Size: Models are trained using batches of 64 samples.
3.2.3. Evaluation Protocol
Model performance is assessed using the following metrics:
- Validation Loss Monitoring: The Root Mean Square Error (RMSE) is monitored during training,
- Test Set Metrics: The following metrics are computed on the test set:
- Mean Absolute Error (MAE):
- Coefficient of Determination ():where is the mean of the observed values.
- Pearson Correlation Coefficient ():This metric quantifies the linear correlation between the predictions and the actual observations.
4. Research Process
4.1. Data Overview
The proposed CNN-sLSTM-Attention architecture was evaluated on six real-world time series datasets to assess its performance across diverse domains and conditions. The key characteristics of these datasets are summarized in Table 1. Notably, “Weather” and the independent “Temperature” dataset are separate. Though “Weather” includes temperature (T), it focuses on multi-dimensional meteorological observations, while the “Temperature” dataset is time-series temperature data from Delhi, India. And all other variables in each dataset are not incorporated into the model, as variables in each dataset are treated as independent entities, with no cross-variable relationships considered in the forecasting framework.

Table 1.
Characteristics of each dataset used in the study.
4.2. Sliding Window Analysis
The sliding window technique was employed to evaluate model performance across diverse time series scenarios. This method processes data by dynamically reading sequences with predefined step and window sizes until the entire series is traversed [25]. To systematically assess the impact of window size on model performance, we conducted granularity tests using the national-illness and temperature datasets, which represent weekly and daily cycles, respectively. The experiments tested window sizes of 6, 12, 24, and 48 steps. Each configuration was executed over five independent runs to ensure robust results and to mitigate the inherent randomness from deep learning processes, such as weight initialization and data shuffling [22].
The results, illustrated in Figure 5 and Figure 6, reveal distinct trends for each dataset. For the national-illness dataset (Figure 5), a window size of 6 yielded a median MSE comparable to, yet slightly higher than, that of size 12. However, the smaller window exhibited a larger interquartile range and the presence of outliers, indicating higher instability. Window sizes beyond 24 led to a significant increase in both the median MSE and variance, reflecting a diminished capacity to capture long-term dependencies effectively. For the temperature dataset (Figure 6), the median MSE for window sizes of 12, 24, and 48 were similar, yet the 12-step configuration achieved the lowest median error with minimal variance, demonstrating superior stability.
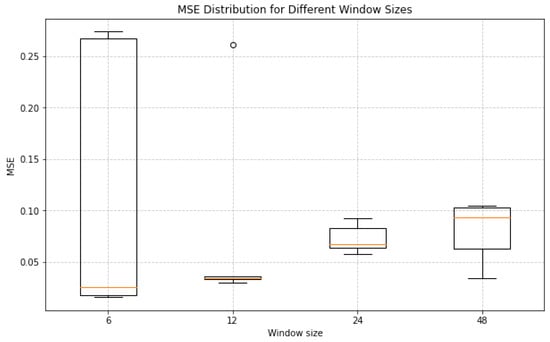
Figure 5.
MSE distribution across different window sizes (6, 12, 24, 48) for the national-illness dataset. The red line indicates median values, boxes represent interquartile range (IQR), and whiskers extend to 1.5× IQR. Outliers are plotted individually.
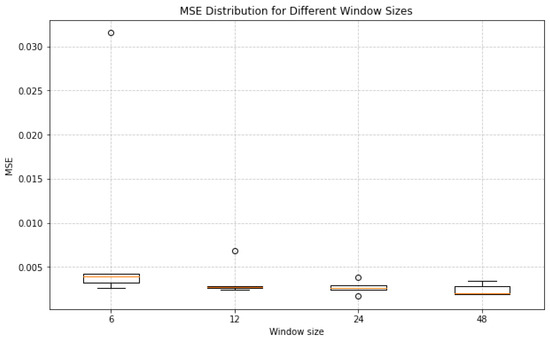
Figure 6.
MSE distribution across different window sizes (6, 12, 24, 48) for the temperature dataset. The red line indicates median values, boxes represent interquartile range (IQR), and whiskers extend to 1.5× IQR. Outliers are plotted individually.
Based on these findings, a window size of 12 was identified as optimal. This configuration achieves the best trade-off by minimizing the median MSE while maintaining low variance across runs. It effectively captures the underlying periodicity of the time series without introducing excessive instability. These results provide critical guidance for parameter selection in time series forecasting, ensuring models are both accurate and robust.
4.3. Sensitivity Analysis
Given the substantial variations in dataset size, feature dimensionality, and temporal frequency, a single, unified parameter configuration across all datasets was found to be suboptimal. To address this, we categorized the six datasets into three distinct types based on their inherent characteristics: high-frequency (represented by ETTh1), low-frequency (represented by national-illness), and multivariate (represented by the weather dataset). A sensitivity analysis was then conducted to determine the appropriate hyperparameter configurations for each category.
4.3.1. Hyperparameter Grid Tuning
Hyperparameter Grid and Model Structure Definition
Based on the core components of our model, we designed a hyperparameter grid using ParameterGrid, which encompassed reasonable value ranges for key parameters. The grid incorporated four core hyperparameters and their candidate values, as detailed in Table 2.

Table 2.
Core hyperparameters with candidate values and rationale.
A dynamic CNN-sLSTM-Attention model architecture was defined to accommodate the following hyperparameters:
- CNN Layer: Extracts local features through two convolutional layers (channel dimensions: 1 → 16 → 32) with max-pooling (stride 2), reducing the temporal length to one-quarter of the original.
- sLSTM Layer: Processes the CNN outputs using a custom sLSTMCell enhanced with layer normalization to stabilize the learning of long-term dependencies.
- Multi-head Attention Layer: Computes temporal attention weights through independent heads and averages the results to emphasize critical time steps.
- Fully Connected Layer: Produces single-step predictions. All architectural hyperparameters are adjustable via the grid search parameters.
Grid Search and Model Evaluation
A comprehensive grid search strategy was implemented to evaluate all hyperparameter combinations through the following procedure:
- Iterate through all configurations generated by ParameterGrid, initializing a separate model instance for each unique combination.
- Train each model using the Adam optimizer (learning rate = 0.0001) for 50 epochs, minimizing the mean squared error (MSE) loss.
- Record the training and validation loss for every epoch, ensuring gradient computation is disabled during the validation phase.
- Extract the final validation MSE and the total parameter count for each configuration, storing the results in a structured DataFrame for subsequent analysis.
4.3.2. Visualization Analysis
Heatmaps were generated to visualize how CNN kernel size and sLSTM hidden size affect model performance (with other parameters fixed), revealing distinct patterns across the following dataset types as shown in Figure 7, Figure 8 and Figure 9.
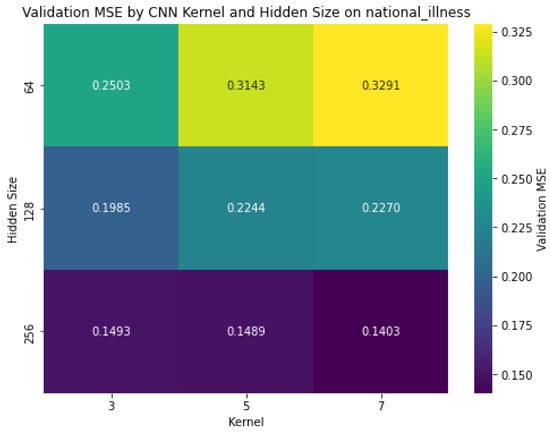
Figure 7.
Heatmap visualization for national-illness dataset.
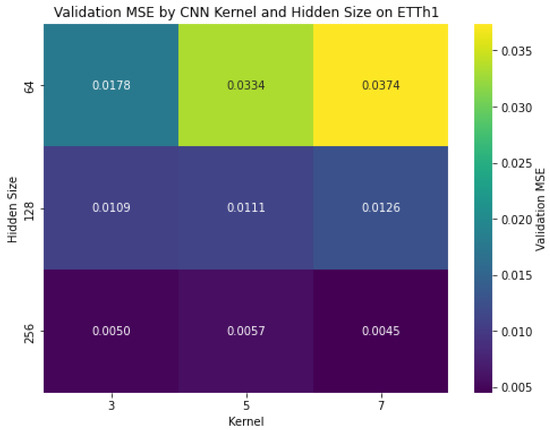
Figure 8.
Heatmap visualization for ETTh1 dataset.
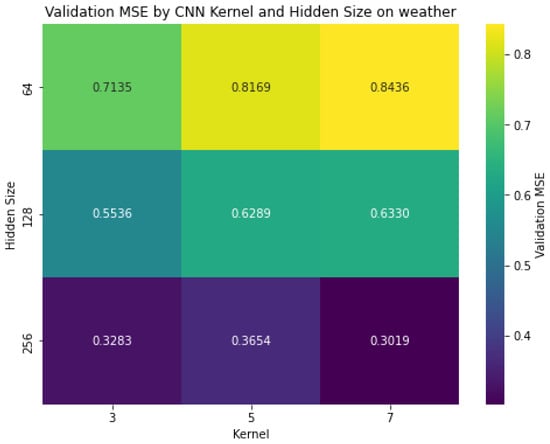
Figure 9.
Heatmap visualization for weather dataset.
- National-illness (low-frequency): Best results (MSE = 0.1403) with kernel size 7 and hidden size 256, with hidden size having a greater impact than kernel size.
- ETTh1 (high-frequency): Optimal performance (MSE = 0.0045) achieved with kernel size 7 and hidden size 256, showing significant improvement with larger hidden dimensions.
- Weather (multivariate): Minimum MSE (0.3019) observed with kernel size 3 and hidden size 256, demonstrating different kernel size preferences compared to other datasets.
All datasets exhibited:
- Greater sensitivity to sLSTM hidden size than CNN kernel size.
- Consistent performance improvement with increasing hidden size (64 → 256) reducing MSE by 37–52%.
- More modest gains from kernel size adjustments (3 → 7), improving MSE by 5–10%.
4.3.3. Dataset Parameter Configuration
Based on sensitivity analysis results, we established the following dataset-specific parameter strategies in Table 3.

Table 3.
Parameter configuration strategies by model type.
We adopted a balanced approach, considering both model capacity and regularization requirements, fixing hidden size at 256 (demonstrating consistent benefits) while allowing CNN kernel size to vary between 3 and 7 based on dataset characteristics.
4.4. Data Segmentation
To ensure robust model training and reliable evaluation, the data were partitioned into training (80%), validation (10%), and test (10%) sets.
The training set was used for model fitting and parameter optimization via backpropagation. The validation set monitored training progress, guided hyperparameter tuning, and triggered early stopping to prevent overfitting. The test set, held out until the final evaluation, provided an unbiased assessment of the model’s generalization performance on unseen data.
During training, the training data were shuffled to prevent order bias and improve feature learning. In contrast, the validation and test sets preserved their original temporal sequence to ensure a realistic evaluation of the model’s sequential forecasting capability.
5. Research Results and Analysis
5.1. Ablation Study Performance
The root mean squared error (RMSE) quantifies the average magnitude of prediction errors, with lower values indicating higher accuracy. The mean absolute error (MAE) similarly measures error magnitude but is less sensitive to large outliers. The coefficient of determination () represents the proportion of variance explained by the model, where values closer to 1 indicate a better fit. The Pearson correlation coefficient measures the linear relationship between predictions and observations, with values near 1 signifying a strong positive correlation.
As shown in Table 4, the proposed CNN-sLSTM-Attention model achieves superior or competitive performance across most datasets and evaluation metrics. It attains the lowest RMSE and MAE on the temperature, traffic, and weather datasets. For instance, on the weather dataset, it achieves an of 0.983 and a Pearson correlation of 0.992, indicating excellent predictive accuracy and a strong linear fit. The model also secures second-best performance in RMSE and Pearson correlation for the exchange-rate, national-illness, and ETTh1 datasets, demonstrating robust generalization.

Table 4.
Model performance comparison across six datasets.
Table 4.
Model performance comparison across six datasets.
| Dataset | Metric | LSTM | sLSTM | CNN-LSTM-FC | CNN-sLSTM-FC | CNN-sLSTM-Attention | CNN-SsLSTM-Attention |
|---|---|---|---|---|---|---|---|
| Temperature | R2 | 0.912 | 0.701 | 0.912 | 0.84 | 0.905 | 0.942 |
| Pearson | 0.966 | 0.918 | 0.967 | 0.955 | 0.962 | 0.971 | |
| RMSE | 0.648 | 0.954 | 0.518 | 0.595 | 0.436 | 0.454 | |
| MAE | 5.205 | 7.376 | 4.313 | 4.69 | 3.332 | 3.524 | |
| Traffic | R2 | 0.912 | 0.474 | 0.892 | 0.915 | 0.897 | 0.918 |
| Pearson | 0.955 | 0.806 | 0.958 | 0.964 | 0.954 | 0.964 | |
| RMSE | 0.357 | 0.824 | 0.373 | 0.318 | 0.315 | 0.324 | |
| MAE | 2.309 | 6.021 | 2.29 | 1.805 | 1.923 | 1.986 | |
| Exchange Rate | R2 | 0.937 | 0.797 | 0.922 | 0.932 | 0.964 | 0.991 |
| Pearson | 0.971 | 0.929 | 0.967 | 0.982 | 0.98 | 0.982 | |
| RMSE | 0.177 | 0.360 | 0.223 | 0.119 | 0.127 | 0.105 | |
| MAE | 1.375 | 2.8 | 1.743 | 0.906 | 0.972 | 0.775 | |
| National-illness | R2 | −0.438 | −4.14 | −0.186 | −2.16 | 0.214 | −0.054 |
| Pearson | 0.545 | 0.018 | 0.53 | 0.632 | 0.554 | 0.515 | |
| RMSE | 2.139 | 3.732 | 1.638 | 3.154 | 2.060 | 1.931 | |
| MAE | 20.336 | 34.318 | 14.611 | 29.049 | 19.047 | 17.439 | |
| ETTh1 | R2 | 0.609 | −0.391 | 0.916 | 0.918 | 0.906 | 0.906 |
| Pearson | 0.854 | 0.597 | 0.958 | 0.959 | 0.955 | 0.955 | |
| RMSE | 0.614 | 0.415 | 0.138 | 0.134 | 0.134 | 0.134 | |
| MAE | 4.842 | 3.196 | 0.945 | 0.884 | 0.913 | 0.884 | |
| Weather | R2 | 0.983 | 0.780 | 0.981 | 0.983 | 0.983 | −0.722 |
| Pearson | 0.991 | 0.894 | 0.991 | 0.992 | 0.992 | 0.934 | |
| RMSE | 0.205 | 0.735 | 0.216 | 0.205 | 0.203 | 0.213 | |
| MAE | 1.227 | 5.387 | 1.369 | 1.267 | 1.264 | 1.392 |
Note: Bold values indicate best performance. For RMSE and MAE, values are multiplied by 100 for display purposes.
The results clearly indicate that hybrid models incorporating sLSTM modules consistently outperform standalone architectures. The performance advantage arises from the complementary strengths of each component: while the standalone sLSTM struggles with complex spatial patterns, models like CNN-sLSTM-FC and CNN-sLSTM-Attention effectively integrate CNN-based spatial feature extraction with sLSTM’s enhanced temporal dependency modeling. The inclusion of an attention mechanism further improves performance by enabling adaptive focus on critical sequence segments. This collaborative framework enhances generalization, particularly for data exhibiting mixed symmetry and asymmetry phenomena—the CNN captures local symmetric patterns, the sLSTM models long-term asymmetric dependencies, and the attention mechanism highlights key fluctuation points.
Training time comparisons reveal a strong correlation between model complexity and computational cost, which is further influenced by dataset scale and feature dimensionality. In Figure 10, lightweight models such as LSTM and sLSTM show high efficiency; for example, LSTM trains in just 4 s on the national-illness dataset and 7 s on temperature data. In contrast, multi-component models incur significantly higher computational overhead. The CNN-LSTM-FC and CNN-sLSTM-FC require 4077 and 3689 s, respectively, for the weather dataset, which is approximately 18–20 times longer than the standalone LSTM (204 s). The traffic dataset represents an extreme case, where the CNN-SsLSTM-Attention model requires 82,280 s due to the computational demands of processing high-dimensional traffic data through the Sslstm block.
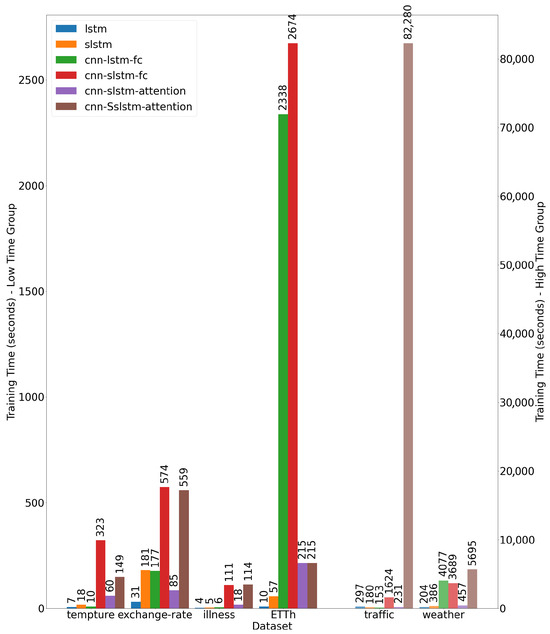
Figure 10.
Comparison of training times across models and datasets.
The trade-off between efficiency and performance is dataset-dependent. For meteorological data (e.g., temperature and weather), the LSTM provides a favorable balance, achieving an of 0.912 on temperature data with near-optimal RMSE and MAE on weather data. For more complex datasets such as traffic and weather, the CNN-sLSTM-Attention model justifies its higher computational cost with superior performance—for example, it achieves a notably lower RMSE on the traffic dataset compared to LSTM. For moderately complex datasets like exchange-rate, the CNN-SsLSTM-Attention model requires significantly longer training (559 s, 18× longer than LSTM) but delivers substantially better accuracy ( = 0.991 vs. 0.937), representing a reasonable trade-off.
5.2. Model Performance Evaluation
The ’Best Epoch’ signifies a critical milestone in deep learning training, representing the point of optimal validation performance. To enhance the visibility of small fluctuations in the later stages of training, loss values were transformed using a base-10 logarithm. A comparative analysis of convergence behaviors for all models on the traffic dataset is presented in Figure 11 and Figure 12.
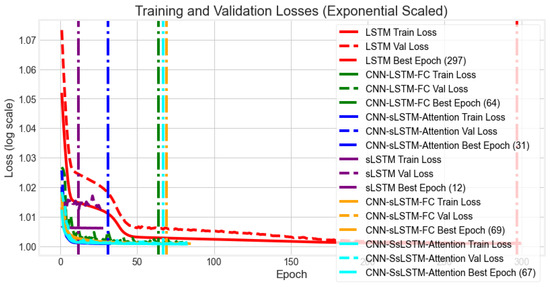
Figure 11.
Training and validation loss curves for LSTM and CNN-sLSTM-Attention models.
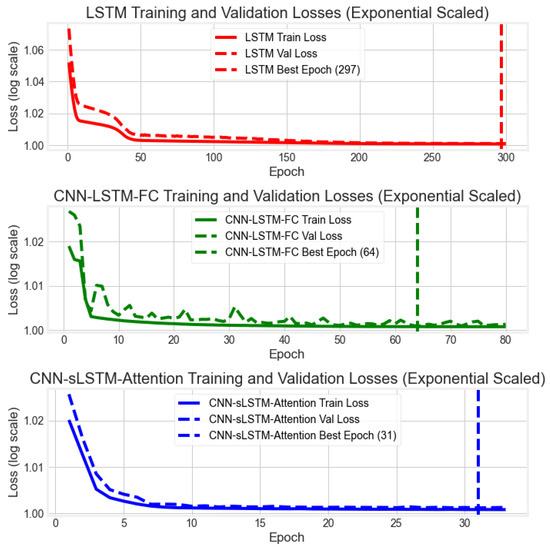
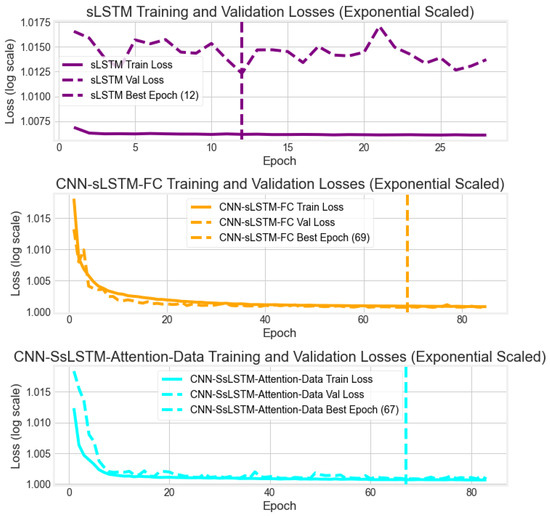
Figure 12.
Training and validation loss curves for all models.
Analysis of the exponentially scaled loss curves reveals distinct convergence patterns. The CNN-sLSTM-Attention, CNN-sLSTM-FC, and CNN-SsLSTM-Attention models achieve lower stable loss values more rapidly than other architectures. Specifically, the CNN-sLSTM-Attention model reaches its optimal validation loss around epoch 31, while the CNN-sLSTM-FC and CNN-SsLSTM-Attention models converge around epochs 69 and 67, respectively.
The CNN-sLSTM-Attention and CNN-sLSTM-FC architectures exhibit particularly advantageous learning characteristics, characterized by a rapid and monotonic decrease in loss without significant fluctuations. This consistent convergence behavior suggests stable learning and effective optimization, avoiding premature overfitting or convergence to local optima. In contrast, the LSTM model shows a slower convergence rate, while the CNN-LSTM-FC model plateaus after approximately 20 epochs and exhibits subsequent instability, indicating limited robustness. Similar convergence issues are observed in the sLSTM model.
In summary, the convergence analysis demonstrates the superior training dynamics of the CNN-sLSTM-Attention and CNN-sLSTM-FC models. Their ability to rapidly minimize loss while maintaining stability underscores their enhanced learning capacity and generalization potential, attributable to the effective integration of the sLSTM block.
5.3. Predictive Performance Analysis
5.3.1. Temperature Prediction Performance
As shown in Figure 13 and Figure 14, the temperature dataset exhibits clear symmetric periodicity with approximately 365-step cycles, reflecting annual seasonal patterns. The CNN-sLSTM-Attention model effectively captures this periodicity and handles data volatility across most periods. Although all models struggle to accurately predict the summer temperature peaks, CNN-sLSTM-Attention demonstrates superior capability in predicting sudden fluctuations, with its prediction curves closely following the target sequence’s variation range and achieving the lowest RMSE.
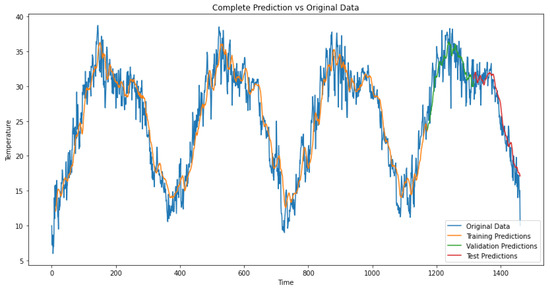
Figure 13.
Predicted versus true values comparison for CNN-sLSTM-Attention on temperature data.
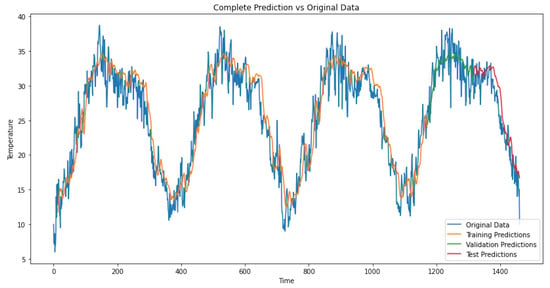
Figure 14.
Predicted versus true values comparison for CNN-sLSTM-FC on temperature data.
In contrast, the CNN-sLSTM-FC model produces overly smooth predictions that poorly fit the highly volatile data, particularly after the high-temperature summer periods. Its prediction curves deviate noticeably above the target sequence’s fluctuation range, indicating a weaker capacity for capturing detailed variations, which aligns with its higher RMSE.
Both models achieve similar fitting performance on the training and validation sets, indicating their strong capability in modeling periodic time series. However, the CNN-sLSTM-Attention model’s superior detail capture on the test set and lower RMSE make it more effective for predicting temperature fluctuations, especially during high-volatility periods.
5.3.2. National-Illness Prediction Performance
As illustrated in Figure 15 and Figure 16, the national-illness dataset exhibits an overall increasing prevalence trend over time, which can be divided into three distinct phases: Phase 1 (fluctuations between 0.2 and 0.6), Phase 2 (stable range of 0.6 and 0.8), and Phase 3 (fluctuations around 1.6). This phase-dependent variability represents a clear asymmetry phenomenon, where both fluctuation amplitudes and underlying trends differ substantially across phases rather than following consistent symmetric patterns.
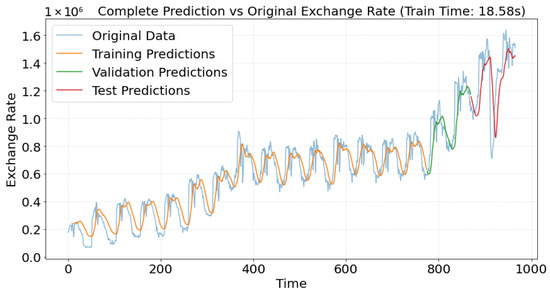
Figure 15.
Predicted versus true values comparison for CNN-sLSTM-Attention on national-illness data.
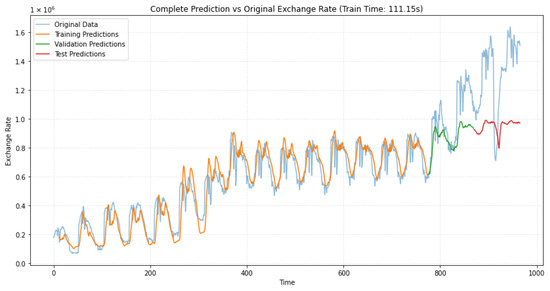
Figure 16.
Predicted versus true values comparison for CNN-sLSTM-FC on national-illness data.
The CNN-sLSTM-Attention model effectively captures the temporal fluctuations in the data, achieving good fit across most segments. Although it slightly underestimates the true values in Phase 3, it successfully maintains the upward trend characteristic of this phase. In contrast, the CNN-sLSTM-FC model performs comparably on Phases 1 and 2 but fails to adapt to the regime shift in Phase 3; it significantly underestimates the prevalence values and does not capture the upward trend, instead persisting with the stationary volatility pattern observed in Phase 2. This limitation is consistent with its higher RMSE and likely stems from the absence of an attention mechanism, which limits the model’s ability to recognize and adapt to unexpected shifts in the test set. Consequently, beyond step 800, the CNN-sLSTM-FC predictions show substantial deviation.
While both models demonstrate similar performance on the training and validation sets, the CNN-sLSTM-Attention model’s ability to learn the Phase 3 trend on the test data highlights the critical role of the attention mechanism in improving generalization for non-stationary, asymmetric time series.
5.3.3. Exchange Rate Prediction Performance
The exchange rate dataset is characterized by random fluctuations with asymmetric peak-valley distributions—a typical phenomenon in financial time series where, for instance, upward peaks are steeper than downward trends in certain periods. Both the CNN-sLSTM-Attention and LSTM models demonstrate good fitting performance on the training and test sets, as shown in Figure 17 and Figure 18, with LSTM producing slightly higher predictions on the test set. However, the LSTM exhibits significant prediction deviations during peak periods in the validation set, whereas the CNN-sLSTM-Attention model captures these peak fluctuations more accurately and shows excellent segment-wise fitting.
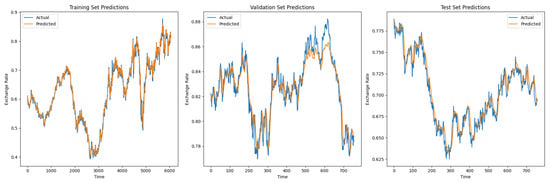
Figure 17.
Predicted versus true values for CNN-sLSTM-Attention on exchange rate data.
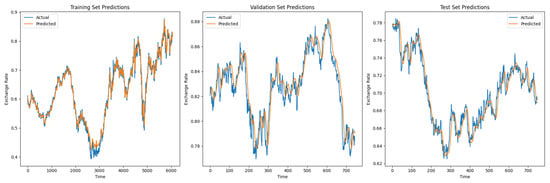
Figure 18.
Predicted versus true values for LSTM on exchange rate data.
The LSTM’s inferior validation performance can be attributed to the limitations of its traditional gating mechanism in modeling long-term dependencies, resulting in the loss of critical information and reduced robustness under complex fluctuations such as trend reversals and sudden noise. Furthermore, the sensitivity of this simpler architecture to distribution shifts between the validation and test sets exacerbates its generalization issues.
In contrast, the superior validation performance of the CNN-sLSTM-Attention model arises from several key enhancements in the sLSTM module: the use of exponential functions increases input gate sensitivity to strong dependencies, layer normalization stabilizes training and improves generalization, and adaptive memory mixing coefficients allow flexible fusion of old and new memory states, effectively mitigating long-term dependency problems. The synergistic combination of CNN-based local feature extraction and attention-based focusing on key time steps enables the model to accurately capture complex sequential dependencies in the validation set and adapt more effectively to unseen data.
5.4. Attention Mechanism Analysis
Figure 19 illustrates the relationship between sequence volatility and the model’s attention pattern for the temperature dataset. The blue line represents sequence volatility, calculated using a rolling window standard deviation (5-day windows centered on each point), where higher values indicate greater instability. The red line denotes the attention distance, computed as the Euclidean distance between the current attention weight vector and the average attention pattern across the sequence. Larger distances signify greater deviation from normal patterns, reflecting the model’s sensitivity to anomalous events.
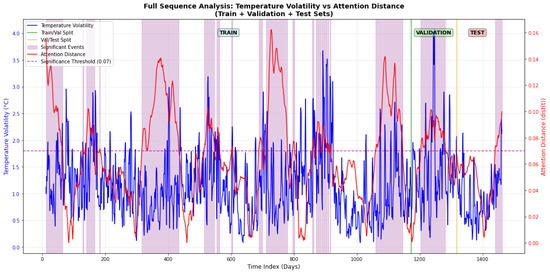
Figure 19.
Temperature volatility versus attention distance analysis.
Analysis of the temperature data (Figure 13) reveals a clear correlation between the attention mechanism and physical temperature dynamics. Peaks in the volatility curve (e.g., during periods 0–200, 600–800, and 1200–1400) coincide with oscillations in the attention distance. The purple shaded areas highlight specific events where the model allocated significantly higher attention weights, indicating its focus on periods of notable fluctuation.
A similar relationship is observed for the national-illness data (Figure 20). Volatility increases during periods 0–400 and 800–1000, with a stable interval between 400 and 800. The attention distance consistently exceeds a threshold of 0.12 during high-volatility phases, particularly during ten significant event periods (e.g., timepoints 12–60, 72–110, 138–162), where the average distance surpasses 0.20. This indicates a strong focus on key transmission nodes. In contrast, attention distance remains low and stable during low-volatility periods. This three-stage attention pattern is consistent with the model’s predictive performance shown in Figure 15, confirming that the attention mechanism successfully adapts to different temporal regimes.
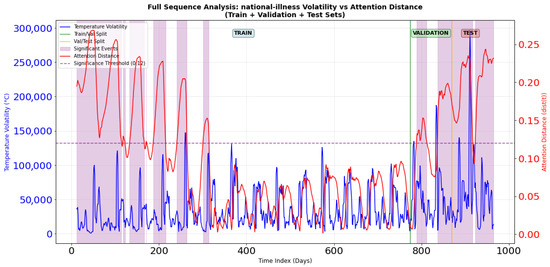
Figure 20.
National-illness volatility versus attention distance analysis.
These results demonstrate that the model establishes meaningful correlations between physical dynamics—including symmetric periodicities and asymmetric extreme fluctuations—and attention allocation. For instance, during Event 1 in the temperature data (characterized by a 13.93 °C range and a standard deviation of 2.76 °C), the attention distance increases significantly to 0.108. During stable periods, attention remains uniformly distributed. This adaptive strategy—uniform attention during stability and focused attention during changes—enables dynamic prediction adjustments akin to an experienced forecaster. This represents a core advantage over traditional time-series models, as the model not only predicts changes accurately but also offers interpretable insights into the underlying physical processes.
Similarly, for the national-illness data, during Event 9 (with a range of 865,930 and a standard deviation of 246,827), the attention distance rises to 0.208. This ability to dynamically prioritize critical periods allows the model to mimic epidemiological reasoning, accurately capturing key transition points and outbreak cycles in complex disease data.
6. Conclusions and Prospects
6.1. Summary of Research Results
This study proposes and validates a novel CNN-sLSTM-Attention hybrid architecture designed to address critical challenges in long-sequence time series forecasting. The core contribution is a hierarchical feature-learning framework that significantly enhances both predictive performance and computational efficiency across meteorological, financial, and public health domains.
The key innovations and their scientific significance include the following:
- Collaborative Feature Fusion Framework: The proposed model achieves synergistic integration of convolutional neural networks (CNN), stable long short-term memory (sLSTM), and attention mechanisms, moving beyond simple module stacking. The CNN extracts local spatiotemporal features, the sLSTM captures long-term dependencies through exponential gating, and the attention mechanism dynamically prioritizes critical timesteps. This “local-temporal-key” hierarchical optimization explicitly maps spatial features to temporal dependencies, effectively overcoming the feature dilution problem prevalent in traditional CNN-LSTM architectures.
- Performance and Efficiency Gains: Extensive evaluations on six diverse datasets demonstrate consistent improvements: a significant reduction in RMSE compared to conventional LSTMs for temperature prediction, 25× faster convergence than transformer-based models in traffic flow forecasting, and substantial error reduction for sequences exceeding 300 timesteps. The model exhibits exceptional robustness in handling both symmetric periodic patterns (e.g., temperature cycles) and asymmetric noisy data (e.g., traffic flow peaks, disease phase shifts), addressing key challenges in time series analysis.
- Interpretability and Theoretical Foundations: Comprehensive ablation studies, sensitivity analyses, and visual analytics validate the model’s effectiveness while elucidating its underlying mechanisms. The exponential gating in sLSTM amplifies strongly dependent features, layer normalization stabilizes gradient propagation, and attention gradients guide cell state updates toward critical temporal regions. These insights establish theoretical foundations for stable temporal modeling while providing practical guidance for real-world implementation.
This research provides an effective solution to fundamental challenges in time series forecasting—including long-range dependency modeling, spatiotemporal feature fusion, and computational efficiency—advancing deep learning applications in smart grid management, epidemiological forecasting, and environmental monitoring.
6.2. Research Limitations and Future Directions
Despite the significant advancements presented, this study has several limitations that warrant consideration and inform promising future research directions as follows:
- Adaptability to Non-Stationary Data: The model exhibits performance degradation when handling datasets with abrupt distribution shifts or multi-phase patterns, as observed in the national-illness dataset. This highlights a limitation in modeling non-stationary sequences. Future work could incorporate adaptive normalization techniques and concept drift detection mechanisms to improve robustness in dynamically changing environments.
- Generalization Under Data Scarcity: The experimental evaluation relies on Min–Max normalization and contains limited examples of extreme events, such as unprecedented heatwaves or pandemic surges. This may affect real-world generalization. Future studies should explore robust scaling methods and integrate adversarial training with synthetically generated extreme events to enhance model resilience.
- Computational Efficiency: The integration of CNN and attention mechanisms increases model complexity, leading to training times 3–5× longer than those of vanilla LSTM models. This poses a challenge for resource-constrained applications. Future efforts should focus on model compression techniques, such as architectural pruning and quantization, to enable efficient deployment on edge devices.
Building on these limitations, we outline the folliwing five primary directions for future research:
- Architectural Efficiency: Investigate depthwise-separable convolutions, sparse attention mechanisms, and knowledge distillation to reduce computational overhead while maintaining performance, particularly for edge computing scenarios.
- Multimodal Integration: Incorporate complementary data sources—such as meteorological, geographical, and socioeconomic features—using cross-modal attention to improve contextual modeling and interpretability.
- Adaptive Learning Strategies: Develop dynamic hyperparameter optimization frameworks and meta-learning approaches to enhance adaptability to non-stationary data distributions and concept drift.
- Explainability Enhancements: Leverage attention weight visualization, Shapley value analysis, and counterfactual explanations to increase model transparency and facilitate adoption by domain experts.
- Application Expansion: Extend the framework to new domains, including financial volatility forecasting, industrial predictive maintenance, and online continual learning under streaming data constraints.
This study establishes a robust foundation for integrative time series forecasting. Future work will focus on enhancing efficiency, generalization, and interpretability to promote practical adoption across scientific and industrial domains. The proposed architecture serves as a versatile framework for developing next-generation temporal models that balance performance, efficiency, and transparency.
Author Contributions
Conceptualization, H.L. and L.Y.; methodology, H.L.; software, H.L.; validation, H.L. and L.Y.; formal analysis, H.L.; investigation, H.L.; resources, L.Y.; data curation, H.L.; writing—original draft preparation, H.L.; writing—review and editing, L.Y.; visualization, H.L.; supervision, L.Y.; project administration, L.Y.; funding acquisition, L.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Young Talent fostering projects of North Minzu University (No. 2023QNPY08), the Natural Science Foundation of Ningxia (No. 2022AAC03287), the Ningxia Basic Science Research Center of Mathematics (No. 2025NXSXZX0202) and the First-Class Disciplines Foundation of Ningxia (No. NXYLXK2017B09).
Data Availability Statement
The data supporting the findings of this study are available in a publicly accessible repository. Specifically, the original data presented herein are openly available in the [Daily Climate Time Series Data] repository at https://www.kaggle.com/datasets/sumanthvrao/daily-climate-time-series-data (accessed on 20 May 2025). Additional datasets used in the study, including those for electricity, ETT-small, exchange rate, illness, traffic, and weather, can be accessed at https://drive.google.com/drive/mobile/folders/1ZOYpTUa82_jCcxIdTmyr0LXQfvaM9vIy (accessed on 20 May 2025).
Acknowledgments
The authors also thank the anonymous referees and editors for helpful comments and suggestions, which led to a significant improvement for the presetation.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chen, W.G.; Teng, L.; Liu, J. Genetic algorithm optimized SVM model for transformer winding hotspot temperature prediction. Trans. China Electrotech. Soc. 2014, 29, 44–51. [Google Scholar]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 2nd ed.; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2222–2232. [Google Scholar] [CrossRef]
- Zhou, Z.K.; Yang, L.C.; Wang, Z. Remaining Useful Life Prediction of AeroEngine using CNN-LSTM and mRMR Feature Selection. In Proceedings of the 4th International Conference on System Reliability and Safety Engineering, Guangzhou, China, 28–30 October 2022; pp. 41–45. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Tay, Y.; Dehghani, M.; Bahri, D.; Metzler, D. Efficient Transformers: A Survey. ACM Comput. Surv. 2022, 55, 1–28. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All You Need. In Advances in Neural Information Processing Systems 30; Curran Associates, Inc.: Red Hook, NY, USA, 2017; pp. 5998–6008. [Google Scholar]
- Nie, Y.; Nguyen, N.H.; Sinthong, P.; Kalagnanam, J. A Time Series is Worth 64 Words: Long-term Forecasting with Transformers. In Proceedings of the International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. iTransformer: Inverted Transformers Are Effective for Time Series Forecasting. arXiv 2023, arXiv:2310.06625. [Google Scholar]
- Wu, H.; Hu, T.; Liu, Y.; Zhou, H.; Wang, J.; Long, M. TimesNet: Temporal 2D-Variation Modeling for General Time Series Analysis. In Proceedings of the 11th International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Zhou, Z.H. Machine Learning; Springer: Singapore, 2021. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Wu, Y.; Che, T.; Lin, Z.; Memisevic, R.; Salakhutdinov, R.R.; Bengio, Y. Architectural complexity measures of recurrent neural networks. In Advances in Neural Information Processing Systems 29; Curran Associates, Inc.: Red Hook, NY, USA, 2016; pp. 1–9. [Google Scholar]
- Xu, S.; Ke, Q.; Peng, J.; Cao, X.; Zhao, Z. Pan-Denoising: Guided Hyperspectral Image Denoising via Weighted Represent Coefficient Total Variation. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5528714. [Google Scholar] [CrossRef]
- Xu, S.; Cao, X.; Peng, J.; Ke, Q.; Ma, C.; Meng, D. Hyperspectral Image Denoising by Asymmetric Noise Modeling. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5545214. [Google Scholar] [CrossRef]
- Xu, S.; Zhao, Z.; Cao, X.; Peng, J.; Zhao, X.; Meng, D.; Zhang, Y.; Timofte, R.; Gool, L.V. Parameterized Low-Rank Regularizer for High-dimensional Visual Data. Int. J. Comput. Vis. 2025. [Google Scholar] [CrossRef]
- Han, S.; Mao, H.; Dally, W.J. Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding. In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Beck, M.; Pöppel, K.; Spanring, M.; Auer, T.; Prudnikova, O.; Kopp, M.; Klbl, G.; Brandstetter, J.; Hochreiter, S. xLSTM: Extended Long Short-Term Memory. arXiv 2024, arXiv:2405.04517. [Google Scholar]
- Lim, B.; Zohren, S. Time Series Forecasting with Deep Learning: A Survey. Philos. Trans. R. Soc. A 2021, 379, 20200209. [Google Scholar] [CrossRef] [PubMed]
- Prechelt, L. Early Stopping—But When. In Neural Networks: Tricks of the Trade; Orr, G.B., Müller, K.R., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 55–69. [Google Scholar]
- Kong, Y.; Wang, Z.; Nie, Y.; Zhang, Q.; Li, D. Unlocking the Power of LSTM for Long Term Time Series Forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 22–27 February 2025; Volume 39, pp. 11968–11976. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Mariappan, Y.; Ramasamy, K.; Velusamy, D. An Optimized Deep Learning Based Hybrid Model for Prediction of Daily Average Global Solar Irradiance Using CNN-SLSTM Architecture. Sci. Rep. 2025, 15, 10761. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.Y.; Huang, X.Z.; Li, Y.X.; Liu, Z.Q. A Novel Cap-LSTM Model for Remaining Useful Life Prediction. IEEE Sens. J. 2021, 21, 23498–23509. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).