Development of an Efficient CUSUM Control Chart for Monitoring the Scale Parameter of the Inverse Maxwell Distribution in Asymmetric, Non-Normal Process Monitoring with Industrial Applications
Abstract
1. Introduction
- (i)
- Better capturing of long tails and extreme values;
- (ii)
- Improved fit for lifetime and reliability data;
- (iii)
- More appropriate control limits for skewed processes;
- (iv)
- Higher sensitivity to sudden shifts and outliers.
2. Materials and Procedures
2.1. IM Distribution and Its Parameters
2.2. IMEWMA Control Chart
- (i)
- is known;
- (ii)
- is not known.
3. Formation of the Postulated CUSUM Control Chart for IM Distribution
4. Assessment of the IMCUSUM Control Chart’s Performance
- For both the IMCUSUM and IMEWMA charts, the ARL0 values are approximately 370 across all subgroup sizes ( = 1, 3, 6, 9). This indicates that, under IC conditions, both charts produce an out-of-control signal, on average, at every 370th plotted point, which aligns with the nominal ARL0 target.
- As the size of the shift increases, the ARL values for both charts decrease significantly. This demonstrates that both charts are effective in recognizing process shifts, with the IMCUSUM chart generally showing lower ARL values compared to the IMEWMA chart for the same shift magnitudes. For example:
- i
- For = 1.10, the IMCUSUM chart achieves ARL values ranging from 47.35 to 140.6, while the IMEWMA chart achieves ARL values ranging from 72.6 to 184.
- ii
- For smaller shifts (e.g., 1.01 to 1.05), the IMCUSUM chart consistently outperforms the IMEWMA chart, even for larger subgroup sizes ( = 6, 9).
- The IMCUSUM chart demonstrates greater sensitivity to small and moderate shifts compared to the IMEWMA chart. For instance:
- i
- At = 1.02, the IMCUSUM chart achieves ARL values of 242.6 to 301.3, while the IMEWMA chart achieves ARL values of 256 to 321.
- ii
- This trend is consistent across all subgroup sizes, indicating that the IMCUSUM chart is better suited for detecting smaller shifts in the process.
- One of the primary goals of this study is to demonstrate that the IMCUSUM chart excels with small practical and meaningful subgroup sizes typical of real-world manufacturing and testing environments. The results fully bear witness in support of this intention:
- i
- When = 1, the ARL of the IMCUSUM chart is 140.6 with = 1.10 against 184 with the IMEWMA chart. This indicates that the IMCUSUM chart will detect shifts 31% faster relative to the IMEWMA chart with small subgroup sizes.
- ii
- With the smaller i.e., = 1.02, the IMCUSUM has an ARL of 301.3 with n = 1 and the IMEWMA has an ARL of 321. This further highlights the better small-shift detection of the IMCUSUM with minimal data.
- SDRL reduces with an increase in the shift magnitude in the two plots. The SDRL of the IMCUSUM plot tends to be lower compared to the SDRL of the IMEWMA plot and signifies a more stable detection of shifts. For instance:
- i
- When the = 1.10 has been applied, the SDRL of the IMCUSUM will be between 24.4 and 133.2 and that of the IMEWMA will be between 69.5 and 182.
- MRL also diminishes with a larger shift size, and the smaller MRL of the IMCUSUM relative to the IMEWMA further confirms the better detection of shifts by the IMCUSUM chart. For example:
- i
- With a = 1.10, the IMCUSUM plot reaches the values of the MRL between 42 and 99 and the IMEWMA plot reaches the values of the MRL between 52 and 128.5.
- Increasing the two-chart subgroup size () increases the detection power with smaller values of the ARL, SDRL, and the MRL with a larger . The behavior of the IMCUSUM with small subgroup sizes of = 1 and 3 are of particular interest; with a = 1.05, the IMCUSUM has an ARL of 106.3 to 221.4 and the IMEWMA has an ARL of 155 to 255.
- i
- This emphasizes the necessity of an adequate if the highest possible performance of the chart has to be maximized, with the IMCUSUM chart also turning out to be superior with small samples.
- Table 3 and Table 4 present the percentiles of the both charts’ run lengths (P25, P50, P75, and P90) demonstrate that the IMCUSUM chart detects shifts earlier and with a higher consistency than the IMEWMA chart. For example:
- i
- When = 1.10 the 90th percentile of the IMCUSUM plot ranges between 79 and 314.1 and that of the IMEWMA plot ranges between 212 and 546.05.
- ii
- Thus, the IMCUSUM chart will be capable of detecting shifts with fewer samples than the IMEWMA chart.
5. Simulation Results and Discussion
- i
- A sample of observations is generated from T~Gamma (3/2, 2.
- ii
- A predetermined sample of size is chosen for every random sample.
- iii
- The sample is converted by implementing the square root transformation to T, resulting in a sample drawn from the Maxwell distributed random variable x.
- iv
- A sample of size from the random variable R of the IM is derived by taking R = 1/x.
- v
- The IMCUSUM statistic, and , are computed for each sample.
- vi
- Steps 1–5 are repeated as far as the desired number of samples are achieved.
- vii
- Control limits are computed as outlined in the preceding section.
- viii
- All values of the and statistics are plotted against the control limits.
- ix
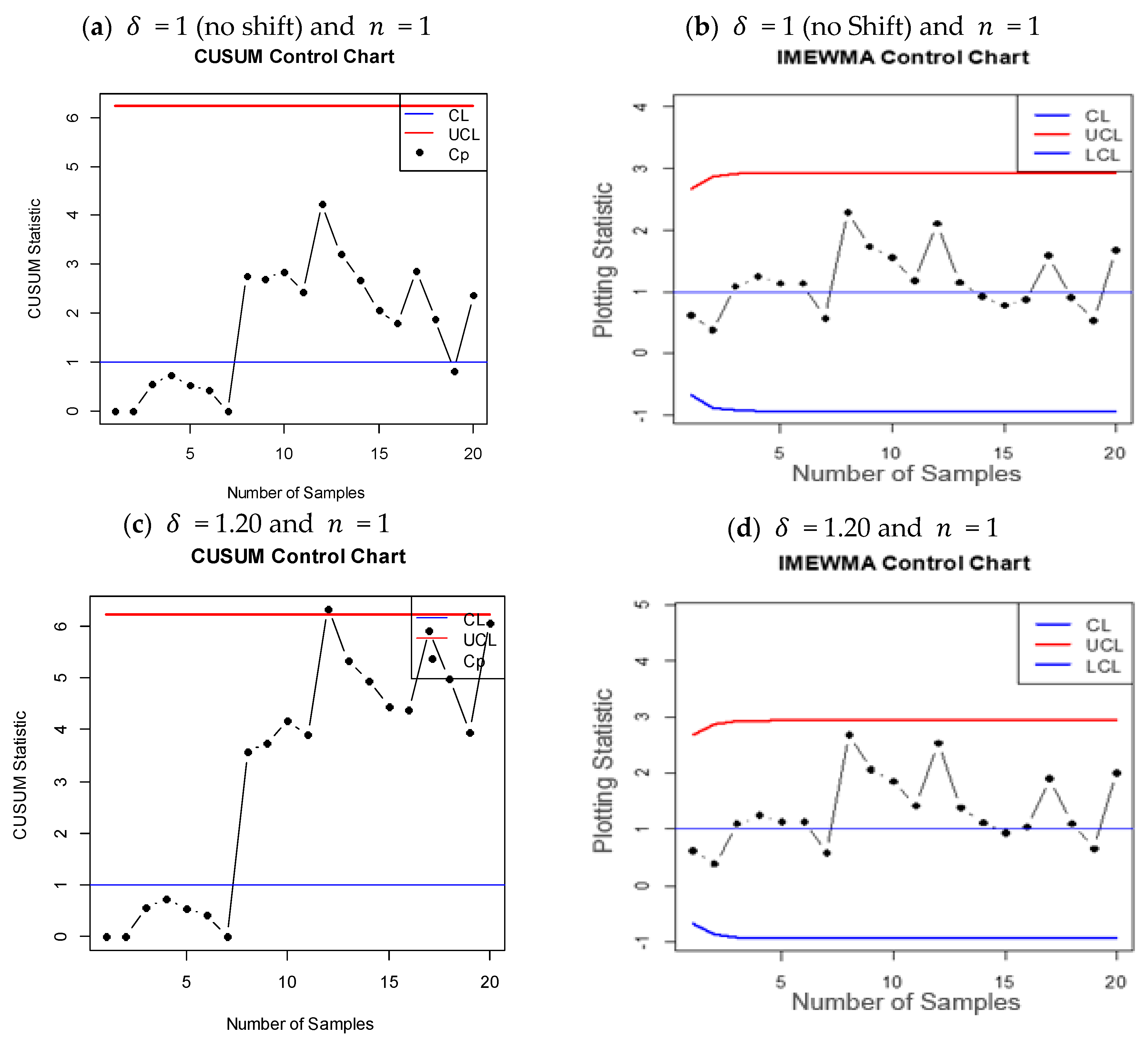
- Data is generated from the IM distribution using = 1, and 60 sample observations are created.
- x
- The Kolmogorov–Smirnov (K–S) test is used to verify that the data conforms to the IM distribution. The null hypothesis is not rejected, confirming that the data follows the IM distribution.
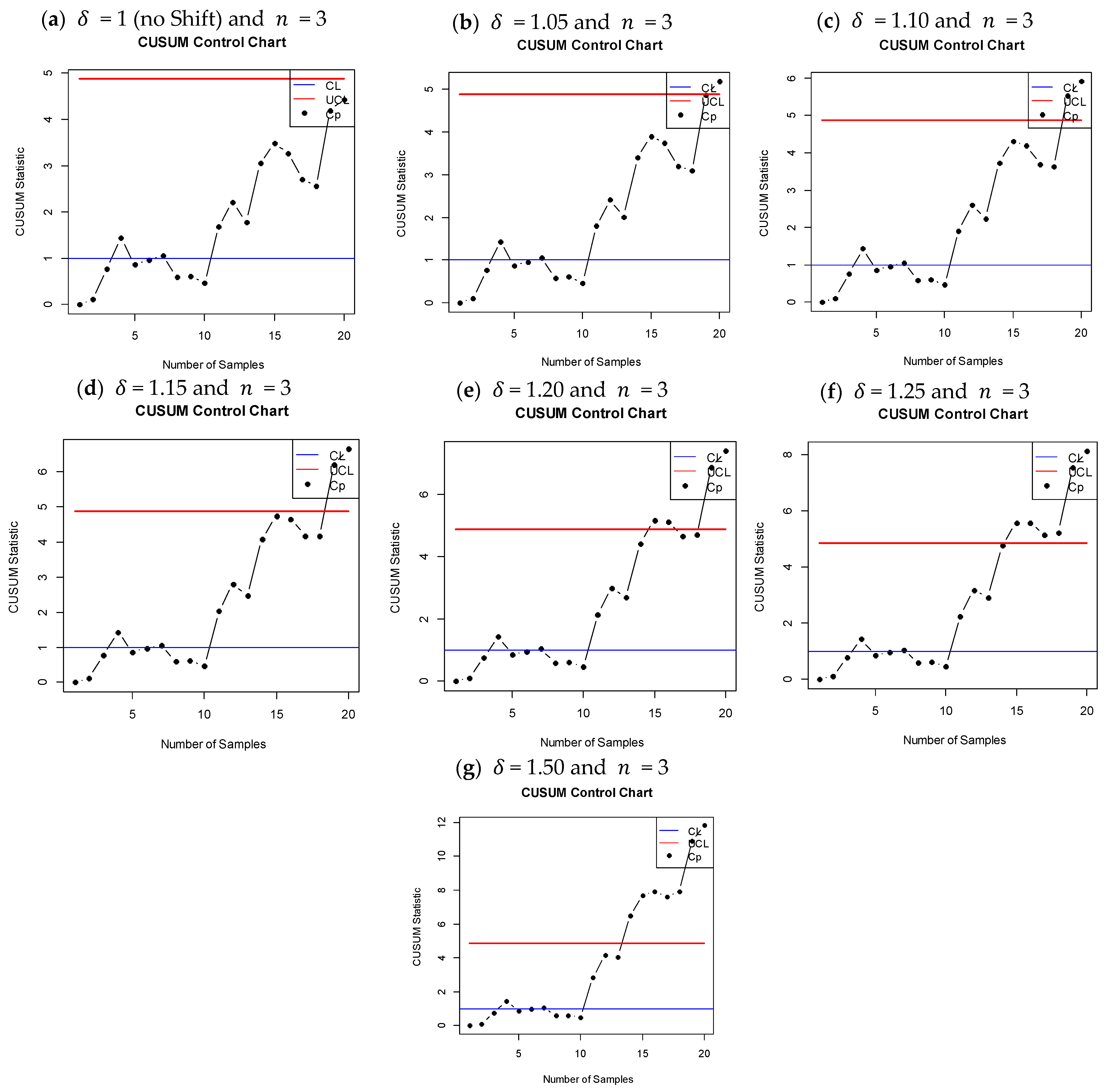
- xi
- For graphical representation, the design parameters are set as = 3, k = 0.5, and ARL0 = 370.
- xii
- To evaluate the chart’s capability to observe process variations, shifts in the process scale parameter are introduced at 5%, 10%, 15%, 20%, 25%, and 50% after the 10th sample.
- xiii
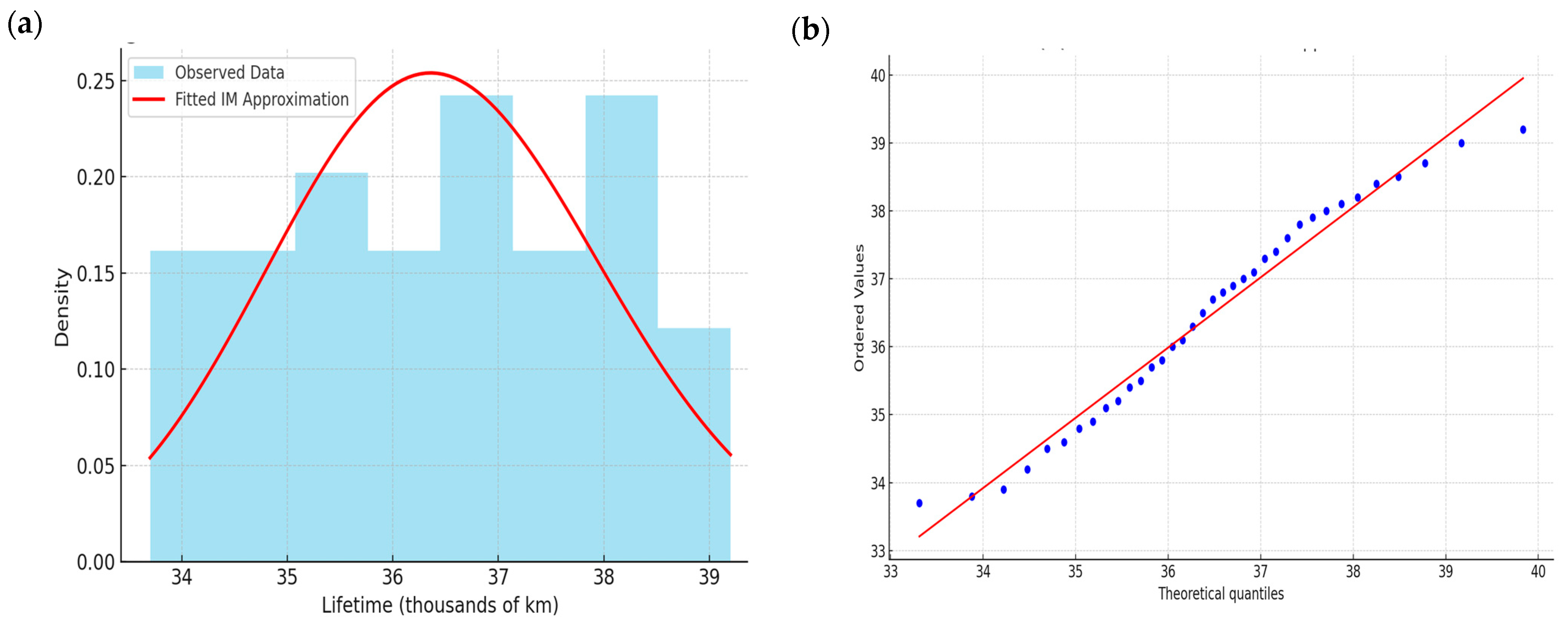
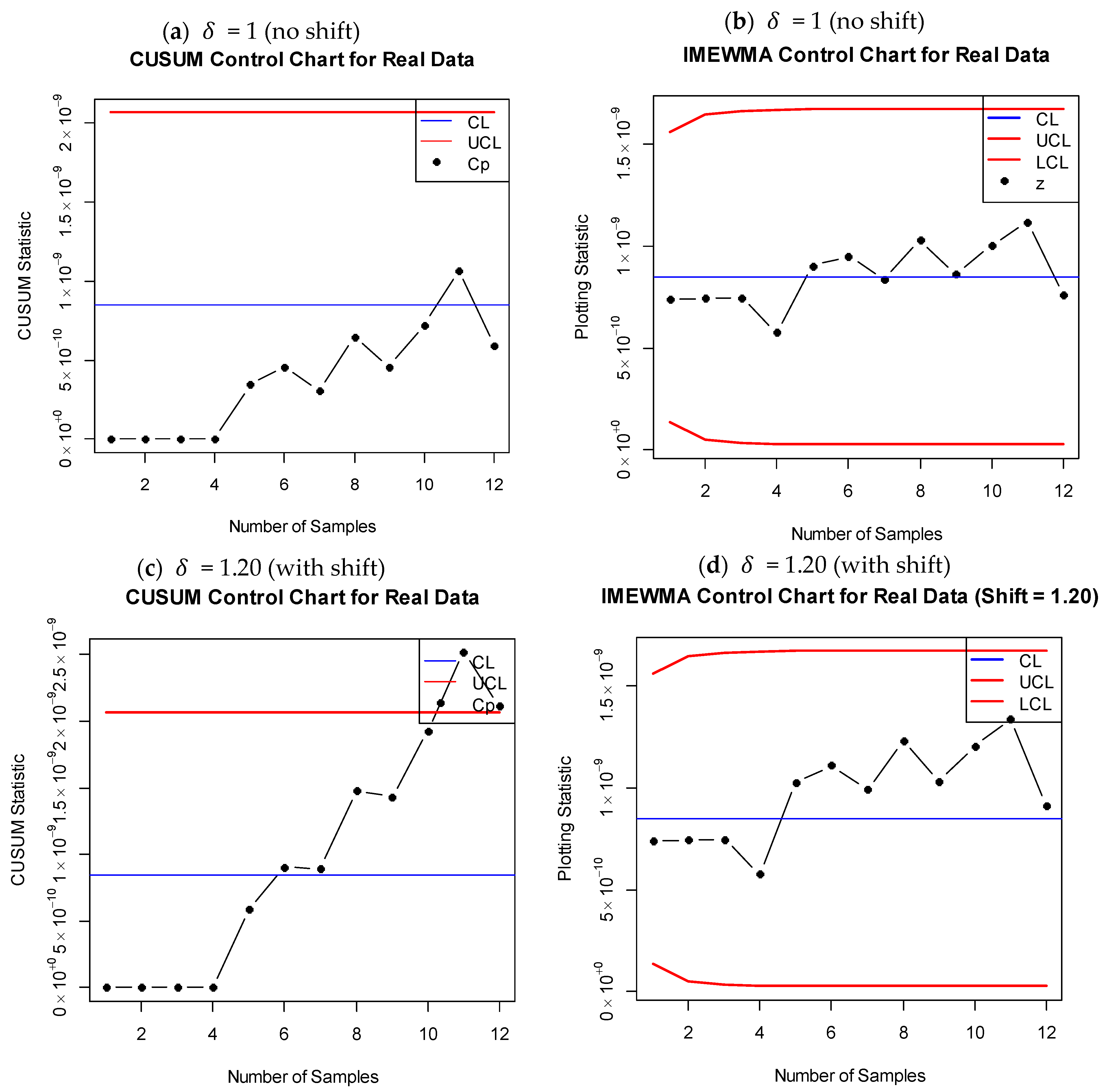
6. Real Life Application
7. Conclusions
8. Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shewhart, W.A. Statistical method from an engineering viewpoint. J. Am. Stat. Assoc. 1931, 26, 262–269. [Google Scholar] [CrossRef]
- Page, E.S. Continuous inspection schemes. Biometrika 1954, 41, 100–115. [Google Scholar] [CrossRef]
- Roberts, S.W. Control chart tests based on geometric moving averages. Technometrics 1959, 1, 239–250. [Google Scholar] [CrossRef]
- Reynolds, M.R., Jr.; Stoumbos, Z.G. Robust CUSUM charts for monitoring the process mean and variance. Qual. Reliab. Eng. Int. 2010, 26, 453–473. [Google Scholar] [CrossRef]
- Gan, F.F. Monitoring Poisson observations using modified exponentially weighted moving average control charts. Commun. Stat.-Simul. Comput. 1990, 19, 103–124. [Google Scholar] [CrossRef]
- Abbasi, S.A.; Riaz, M.; Miller, A.; Ahmad, S.; Nazir, H.Z. EWMA dispersion control charts for normal and non-normal processes. Qual. Reliab. Eng. Int. 2015, 31, 1691–1704. [Google Scholar] [CrossRef]
- Borror, C.M.; Montgomery, D.C.; Runger, G.C. Robustness of the EWMA control chart to non-normality. J. Qual. Technol. 1999, 31, 309–316. [Google Scholar] [CrossRef]
- Jones-Farmer, L.A.; Woodall, W.H.; Steiner, S.H.; Champ, C.W. An overview of Phase I analysis for process improvement and monitoring. J. Qual. Technol. 2014, 46, 265–280. [Google Scholar] [CrossRef]
- Zwetsloot, I.M.; Jones-Farmer, L.A.; Woodall, W.H. Monitoring univariate processes using control charts: Some practical issues and advice. Qual. Eng. 2024, 36, 487–499. [Google Scholar] [CrossRef]
- Acosta-Mejia, C.A.; Pignatiello, J.J.; Rao, B.V. A comparison of control charting procedures for monitoring process dispersion. IIE Trans. 1999, 31, 569–579. [Google Scholar] [CrossRef]
- Sanusi, R.A.; Abbas, N.; Riaz, M. On efficient CUSUM-type location control charts using auxiliary information. Qual. Technol. Quant. Manag. 2018, 15, 87–105. [Google Scholar] [CrossRef]
- Tran, K.P.; Castagliola, P.; Celano, G. Monitoring the ratio of population means of a bivariate normal distribution using CUSUM type control charts. Stat. Pap. 2018, 59, 387–413. [Google Scholar] [CrossRef]
- Huang, W.; Shu, L.; Jiang, W.; Tsui, K.L. Evaluation of run-length distribution for CUSUM charts under gamma distributions. IIE Trans. 2013, 45, 981–994. [Google Scholar] [CrossRef]
- Celano, G.; Castagliola, P.; Trovato, E. The economic performance of a CUSUM t control chart for monitoring short production runs. Qual. Technol. Quant. Manag. 2012, 9, 329–354. [Google Scholar] [CrossRef]
- Ryu, J.H.; Wan, G.; Kim, S. Optimal design of a CUSUM chart for a mean shift of unknown size. J. Qual. Technol. 2010, 42, 311–326. [Google Scholar] [CrossRef]
- Hossain, M.P.; Sanusi, R.A.; Omar, M.H.; Riaz, M. On designing Maxwell CUSUM control chart: An efficient way to monitor failure rates in boring processes. Int. J. Adv. Manuf. Technol. 2019, 100, 1923–1930. [Google Scholar] [CrossRef]
- Sato, S.; Inoue, J. Inverse gaussian distribution and its application. Electron. Commun. Jpn. (Part III Fundam. Electron. Sci.) 1994, 77, 32–42. [Google Scholar] [CrossRef]
- Krishna, H.; Malik, M. Reliability estimation in Maxwell distribution with progressively Type-II censored data. J. Stat. Comput. Simul. 2012, 82, 623–641. [Google Scholar] [CrossRef]
- Tomer, S.K.; Panwar, M.S. Estimation procedures for Maxwell distribution under type-I progressive hybrid censoring scheme. J. Stat. Comput. Simul. 2015, 85, 339–356. [Google Scholar] [CrossRef]
- Brilliantov, N.V.; Pöschel, T. Deviation from Maxwell distribution in granular gases with constant restitution coefficient. Phys. Rev. E 2000, 61, 2809–2812. [Google Scholar] [CrossRef][Green Version]
- Kazmi, S.M.A.; Aslam, M.; Ali, S. On the bayesian estimation for two component mixture of Maxwell distribution, assuming type I censored data. Int. J. Appl. Sci. Technol. 2012, 2, 197–218. [Google Scholar][Green Version]
- Kazmi, S.M.A.; Aslam, M.; Ali, S. Note on the maximum likelihood estimators for the mixture of Maxwell distributions using type-I censored scheme. Open Stat. Probab. J. 2011, 3, 31–35. [Google Scholar] [CrossRef]
- Singh, K.L.; Srivastava, R.S. Inverse Maxwell distribution as a survival model, genesis and parameter estimation. Res. J. Math. Stat. Sci. 2014, 2, 23–28. [Google Scholar]
- Karlis, D.; Santourian, A. Model-based clustering with non-elliptically contoured distributions. Stat. Comput. 2009, 19, 73–83. [Google Scholar] [CrossRef]
- Singh, K.L.; Srivastava, R.S. Estimation of the parameter in the size-biased Inverse Maxwell distribution. Int. J. Stat. Math. 2014, 10, 52–55. [Google Scholar]
- Singh, K.L.; Srivastava, R.S. Bayesian estimation of parameter of Inverse Maxwell distribution via size-biased sampling. Int. J. Sci. Res. 2014, 3, 1835–1839. [Google Scholar]
- Loganathan, A.; Chelvi, S.M.; Uma, M. Bayes estimation of parameter in Inverse Maxwell distribution under weighted quadratic loss function. Int. J. Sci. Res. Math. Stat. Sci. 2017, 4, 13–16. [Google Scholar] [CrossRef]
- Arafat, S.Y.; Hossain, M.P.; Ajadi, J.O.; Riaz, M. On the development of EWMA control chart for inverse Maxwell distribution. J. Test. Eval. 2021, 49, 1086–1103. [Google Scholar] [CrossRef]
- Omar, M.H.; Arafat, S.Y.; Hossain, M.P.; Riaz, M. Inverse Maxwell distribution and statistical process control: An efficient approach for monitoring positively skewed process. Symmetry 2021, 13, 189. [Google Scholar] [CrossRef]
- Maqsood, M.; Sanaullah, A.; Mahmood, Y.; Al-Rezami, A.Y.; Abdalla, M.Z.M. Efficient control chart-based monitoring of scale parameter for a process with heavy-tailed non-normal distribution. AIMS Math. 2023, 8, 30075–30101. [Google Scholar] [CrossRef]
- Rao, N.; Farid, M.; Jha, N.K. Szász-integral operators linking general-Appell polynomials and approximation. AIMS Math. 2025, 10, 13836–13854. [Google Scholar] [CrossRef]
- Ayman-Mursaleen, M.; Nasiruzzaman, M.; Rao, N. On the Approximation of Szász-Jakimovski-Leviatan Beta Type Integral Operators Enhanced by Appell Polynomials. Iran. J. Sci. 2025, 49, 1013–1022. [Google Scholar] [CrossRef]
- Xie, M.; Goh, T.N.; Kuralmani, V. Statistical Models and Control Charts for High-Quality Processes; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Lucas, J.M.; Saccucci, M.S. Exponentially weighted moving average control schemes: Properties and enhancements. Technometrics 1990, 32, 981–994. [Google Scholar] [CrossRef] [PubMed]
- Domangue, R.; Patch, S.C. Some omnibus exponentially weighted moving average statistical process monitoring schemes. Technometrics 1991, 33, 299–313. [Google Scholar] [CrossRef]
- Lucas, J.M. Combined Shewhart-CUSUM quality control schemes. J. Qual. Technol. 1982, 14, 51–59. [Google Scholar] [CrossRef]
- Gupta, S.C.; Kapoor, V.K. Fundamentals of Mathematical Statistics; Sultan Chand & Sons: New Delhi, India, 2020. [Google Scholar]

| = 13.21 | = 30.991 | = 52.86 | = 71.35 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ARL | SDRL | MRL | ARL | SDRL | MRL | ARL | SDRL | MRL | ARL | SDRL | MRL | |
| 1 | 370.9 | 362.3 | 255 | 369.8 | 345 | 264 | 370.1 | 332.4 | 266 | 370.5 | 329.5 | 269 |
| 1.01 | 330 | 320 | 232 | 333 | 308.3 | 240 | 328.6 | 293.4 | 242 | 311.8 | 276.3 | 266 |
| 1.02 | 301.3 | 286.3 | 214 | 297 | 273.6 | 214 | 271.8 | 237 | 201 | 242.6 | 199.9 | 183 |
| 1.03 | 273.9 | 265.8 | 191 | 252.4 | 230.7 | 183 | 210.3 | 180.6 | 155 | 179.5 | 142.6 | 137 |
| 1.04 | 242.5 | 235 | 170 | 215.7 | 193.5 | 156 | 167 | 135.7 | 127 | 135.2 | 101.2 | 106 |
| 1.05 | 221.4 | 214 | 155 | 181.5 | 164.3 | 133 | 132.6 | 103.5 | 102 | 106.3 | 74.41 | 86 |
| 1.10 | 140.6 | 133.2 | 99 | 87.55 | 69.53 | 67 | 58.46 | 35.46 | 50 | 47.35 | 24.4 | 42 |
| 1.15 | 95.35 | 86.69 | 69 | 51.94 | 36.27 | 43 | 36.46 | 18.54 | 33 | 30.32 | 12.82 | 28 |
| 1.16 | 90.3 | 82.97 | 65 | 47.71 | 31.77 | 39 | 33.58 | 16.51 | 30 | 28.34 | 11.79 | 26 |
| 1.17 | 83.12 | 74.92 | 60 | 44.28 | 29.16 | 37 | 31.49 | 15.38 | 28 | 26.45 | 10.45 | 25 |
| 1.18 | 78.17 | 70.6 | 58 | 41.14 | 26.82 | 34 | 29.28 | 13.83 | 27 | 24.79 | 9.81 | 23 |
| 1.19 | 72.79 | 64.96 | 53 | 38.65 | 24.49 | 33 | 27.64 | 12.73 | 25 | 23.47 | 9.11 | 22 |
| = 1, λ = 0.5 and L = 4.110 | = 3, λ = 0.5 and L = 3.558 | = 6, λ = 0.5 and L = 3.321 | = 9, λ = 0.5 and L = 3.214 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ARL | SDRL | MRL | ARL | SDRL | MRL | ARL | SDRL | MRL | ARL | SDRL | MRL | |
| 1 | 371 | 371 | 261 | 366.46 | 356 | 252 | 369.2 | 364 | 257 | 371 | 369.9 | 259.5 |
| 1.01 | 343 | 347 | 240 | 338.28 | 337 | 235 | 333.2 | 332 | 233 | 316 | 311.3 | 217 |
| 1.02 | 321 | 315 | 227 | 301.1 | 303 | 205 | 275.1 | 268 | 194 | 256 | 251.8 | 179 |
| 1.03 | 296 | 298 | 203.5 | 265.55 | 265 | 187 | 232.8 | 230 | 162 | 214 | 207.7 | 151 |
| 1.04 | 272 | 267 | 193 | 234.08 | 234 | 163 | 201.9 | 199 | 140 | 174 | 174.7 | 120 |
| 1.05 | 255 | 252 | 176 | 212.14 | 215 | 147 | 172.1 | 172 | 119 | 155 | 153 | 107 |
| 1.10 | 184 | 182 | 128.5 | 210.09 | 213 | 146 | 90.32 | 87.8 | 62 | 72.6 | 69.5 | 52 |
| 1.15 | 136 | 136 | 94 | 214.91 | 213 | 105 | 51.77 | 50.3 | 37 | 38 | 36.36 | 27 |
| 1.16 | 125 | 128 | 85 | 77.56 | 76.5 | 53 | 45.59 | 43.8 | 32 | 34.2 | 33.37 | 24 |
| 1.17 | 121 | 119 | 85 | 69.14 | 69 | 48 | 42.21 | 40.3 | 30 | 31 | 29.6 | 22 |
| 1.18 | 113 | 112 | 78 | 64.89 | 62.4 | 46 | 37.65 | 36.4 | 27 | 27.2 | 25.08 | 19 |
| 1.19 | 105 | 106 | 71 | 60.51 | 59.9 | 42 | 35.03 | 33.9 | 24 | 24.8 | 23.28 | 18 |
| = 13.21 | = 30.991 | = 52.86 | = 71.35 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P25 | P50 | P75 | P90 | P25 | P50 | P75 | P90 | P25 | P50 | P75 | P90 | P25 | P50 | P75 | P90 | |
| 1 | 114 | 255 | 510 | 1100 | 123 | 264 | 508 | 820 | 131 | 266 | 504 | 821 | 141 | 269 | 493 | 798 |
| 1.01 | 102 | 231.5 | 455 | 748 | 113 | 240 | 452 | 735 | 122 | 242 | 439 | 703 | 120 | 226 | 419 | 669 |
| 1.02 | 94 | 214 | 420 | 681 | 102 | 214 | 403 | 649 | 103 | 201 | 366 | 577 | 101 | 183 | 326 | 507 |
| 1.03 | 87 | 191 | 375 | 621.1 | 89 | 183 | 344 | 549 | 83 | 155 | 280 | 443 | 79 | 137 | 236 | 367 |
| 1.04 | 77 | 170 | 333 | 544.1 | 78 | 156 | 294 | 471 | 72 | 127 | 219 | 344 | 64 | 106 | 175 | 266 |
| 1.05 | 70 | 155 | 304 | 491.1 | 66 | 133 | 243 | 393 | 60 | 102 | 174 | 270 | 54 | 86 | 137 | 203 |
| 1.10 | 46 | 99 | 192 | 314.1 | 39 | 67 | 114 | 178 | 33 | 50 | 74 | 106 | 30 | 42 | 59 | 79 |
| 1.15 | 34 | 69 | 129 | 209 | 27 | 43 | 67 | 99 | 23 | 33 | 46 | 61 | 21 | 28 | 37 | 47 |
| 1.16 | 32 | 65 | 122 | 197 | 25 | 39 | 61 | 90 | 22 | 30 | 42 | 55 | 20 | 26 | 34 | 44 |
| 1.17 | 30 | 60 | 113 | 182 | 24 | 37 | 56 | 81 | 20 | 28 | 39 | 52 | 19 | 25 | 32 | 41 |
| 1.18 | 29 | 58 | 105 | 169 | 22 | 34 | 52 | 76 | 20 | 27 | 36 | 47 | 18 | 23 | 30 | 37 |
| 1.19 | 27 | 53 | 98 | 156 | 21 | 33 | 49 | 70 | 19 | 25 | 34 | 44 | 17 | 22 | 28 | 35 |
| = 1, λ = 0.5 and L = 4.110 | = 3, λ = 0.5 and L = 3.558 | = 6, λ = 0.5 and L = 3.321 | = 9, λ = 0.5 and L = 3.214 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P25 | P50 | P75 | P90 | P25 | P50 | P75 | P90 | P25 | P50 | P75 | P90 | P25 | P50 | P75 | P90 | |
| 1 | 110 | 261 | 509.3 | 1125 | 108 | 252 | 505 | 3340 | 106 | 257 | 515 | 1107 | 108.8 | 260 | 513 | 1109 |
| 1.01 | 98 | 240 | 467 | 1025.2 | 99 | 235 | 461 | 1016 | 97 | 233 | 459 | 994.2 | 93 | 217 | 439.3 | 955.1 |
| 1.02 | 96 | 227 | 443.3 | 952.05 | 86 | 205 | 412 | 930 | 82 | 194 | 377.3 | 830 | 74 | 179 | 358.3 | 764 |
| 1.03 | 82 | 204 | 412.3 | 906 | 78 | 187 | 359 | 791 | 66 | 162 | 325 | 695 | 63 | 151 | 297 | 639 |
| 1.04 | 82 | 193 | 376 | 810 | 69 | 163 | 325.3 | 687 | 60 | 140 | 280 | 600.1 | 50 | 120 | 245 | 512 |
| 1.05 | 73 | 176 | 356.3 | 764.05 | 61 | 147 | 289 | 2162 | 51 | 119 | 239 | 494.1 | 46 | 107 | 214.3 | 463 |
| 1.10 | 55 | 129 | 257 | 546.05 | 61 | 146 | 289 | 626 | 27 | 62 | 125 | 271 | 22 | 52 | 101 | 212 |
| 1.15 | 39 | 94 | 190 | 404 | 63 | 105 | 299 | 634 | 16 | 37 | 72 | 153 | 12 | 27 | 52 | 112 |
| 1.16 | 35 | 85 | 174 | 376 | 23 | 53 | 107 | 234 | 14 | 32 | 62 | 133 | 11 | 24 | 46 | 100 |
| 1.17 | 36 | 85 | 165 | 370 | 21 | 48 | 95 | 203 | 13 | 30 | 57 | 122 | 10 | 22 | 42 | 89 |
| 1.18 | 33 | 78 | 157 | 338 | 20 | 46 | 89 | 189 | 12 | 27 | 51 | 111 | 9 | 19 | 37 | 77 |
| 1.19 | 31 | 71 | 143 | 316 | 18 | 42 | 83 | 178 | 11 | 24 | 48 | 106 | 8 | 18 | 33.25 | 72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nisa, G.; Abdelwahab, M.M.; Sanaullah, A.; Maqsood, M.; Abdelkawy, M.A.; Hasaballah, M.M. Development of an Efficient CUSUM Control Chart for Monitoring the Scale Parameter of the Inverse Maxwell Distribution in Asymmetric, Non-Normal Process Monitoring with Industrial Applications. Symmetry 2025, 17, 1819. https://doi.org/10.3390/sym17111819
Nisa G, Abdelwahab MM, Sanaullah A, Maqsood M, Abdelkawy MA, Hasaballah MM. Development of an Efficient CUSUM Control Chart for Monitoring the Scale Parameter of the Inverse Maxwell Distribution in Asymmetric, Non-Normal Process Monitoring with Industrial Applications. Symmetry. 2025; 17(11):1819. https://doi.org/10.3390/sym17111819
Chicago/Turabian StyleNisa, Gul, Mahmoud M. Abdelwahab, Aamir Sanaullah, Mediha Maqsood, Mohamed A. Abdelkawy, and Mustafa M. Hasaballah. 2025. "Development of an Efficient CUSUM Control Chart for Monitoring the Scale Parameter of the Inverse Maxwell Distribution in Asymmetric, Non-Normal Process Monitoring with Industrial Applications" Symmetry 17, no. 11: 1819. https://doi.org/10.3390/sym17111819
APA StyleNisa, G., Abdelwahab, M. M., Sanaullah, A., Maqsood, M., Abdelkawy, M. A., & Hasaballah, M. M. (2025). Development of an Efficient CUSUM Control Chart for Monitoring the Scale Parameter of the Inverse Maxwell Distribution in Asymmetric, Non-Normal Process Monitoring with Industrial Applications. Symmetry, 17(11), 1819. https://doi.org/10.3390/sym17111819








