Multi-Objective Emergency Path Planning Based on Improved Nondominant Sorting Genetic Algorithm

Abstract

Three-dimensional path planning in emergency logistics is a complex optimization problem, particularly challenging because it requires considering conflicting objectives such as flight time, energy consumption, and obstacle avoidance. Unlike most urban logistics research, this study examines emergency delivery path planning in mountainous environments during natural disasters. One of the most effective approaches to this problem is to employ multi-objective evolutionary algorithms. However, while multi-objective genetic algorithms can handle multiple conflicting objectives, they struggle when dealing with complex constraints. This paper proposes a multi-objective genetic optimization method, Adaptive Crossover-Mutation Multi-Objective Genetic Optimization (ACM-NSGA-II), based on the classic NSGA-II framework. Inspired by the principle of symmetry, this method dynamically adjusts the mutation and crossover rates based on population diversity to maintain a balanced exploration–exploitation trade-off. When population diversity is low, the mutation rate is increased to promote exploration of the solution space; when population diversity is high, the crossover rate is increased to promote better information exchange. The algorithm maintains symmetry by gradually adjusting the step size, balancing adaptability and stability. To address the obstacle avoidance problem, we introduced a dynamic path repair strategy that respects the symmetry of no-fly zone boundaries and terrain features, ensuring the safety and efficiency of Unmanned Aerial Vehicles. This algorithm jointly optimizes three objectives: safety cost, flight time, and energy consumption. The algorithm was tested in a mountainous environment model simulating a remote area. In experiments, ACM-NSGA-II was compared with several mainstream evolutionary algorithms. The Pareto set and hypervolume metrics of each method were recorded and statistically analyzed at a 5% significance level. The results show that ACM-NSGA-II outperforms the baseline algorithms in terms of diversity, convergence, and feasibility. Specifically, compared with the traditional NSGA-II, ACM-NSGA-II improved the average hypervolume metric by 53.39% and reduced the average flight time by 24.26%. ACM-NSGA-II also demonstrated significant advantages over other popular standard algorithms. Experimental results show that it can effectively solve the path planning challenge of emergency logistics Unmanned Aerial Vehicles in mountainous environments.

1. Introduction

With the frequent occurrence of natural disasters and public health emergencies, traditional emergency logistics systems are facing significant challenges [1]. Traffic disruptions, limited communications, and road congestion often hinder the timely and reliable transportation of materials [2]. In such scenarios, unmanned aerial vehicles (UAVs) provide a flexible, miniaturized solution with long-range flight capabilities and strong endurance, making them an ideal tool for emergency logistics [3]. However, deploying UAVs in complex environments, such as mountainous terrain, presents unique challenges due to the need for efficient path planning.

In recent years, the application of drone path planning in emergency logistics has received widespread attention. Various models and algorithms have been proposed to optimize the flight paths of drones, aiming to minimize time and energy consumption, and avoid obstacles and no-fly zones. For example, Murray et al. [4] first proposed a mixed integer programming model for truck-drone collaborative delivery in 2015, with the goal of minimizing the total delivery time; Agatz et al. [5] formalized it as a traveling salesman problem for drones and proposed a heuristic algorithm based on local search and dynamic programming. In addition, companies such as JD.com, SF Express, DHL, and Amazon [6] have successfully integrated drones into their logistics systems, mainly in urban environments. Although more and more research has focused on drone path planning for urban logistics and has made progress [7,8,9], research on path optimization in mountainous areas is still limited, especially in remote mountainous areas (especially emergency logistics) under harsh environments or natural disasters. Drone path planning is still in its infancy. This study aims to remedy this deficiency by applying the improved unstructured genetic algorithm-II (NSGA-II) algorithm (ACM-NSGA-II) to emergency logistics, especially to UAV path planning in complex mountainous environments.

The UAV path planning problem in emergency logistics is inherently complex because it requires optimizing multiple conflicting objectives, such as flight time, energy consumption, and safety. While precise optimization methods can guarantee an optimal solution, they are computationally expensive, especially when dealing with large problem instances or complex terrain, where the computation time increases exponentially. These methods are not suitable for real-time applications where fast decision-making is crucial. In contrast, approximate methods such as genetic algorithms (GAs) and other metaheuristic algorithms have been developed for decades, and the emergence of multi-objective evolutionary algorithms (MOEAs) [10] overcomes the problem that traditional single-objective optimization algorithms are generally unable to effectively solve these conflicting objectives. MOEAs can provide approximate optimal solutions within a reasonable time frame, thereby better handling such complex problems [11,12], making them particularly suitable for real-time UAV path planning.

The NSGA-II algorithm, proposed by Deb (2002), is one of the most representative multi-objective evolutionary algorithms [13]. NSGA-II utilizes a non-dominated sorting and crowding distance mechanism, excelling in solution diversity and convergence, and is capable of handling problems with multiple conflicting objectives [14]. Deb’s work provides new insights into solving multi-objective optimization problems and promotes the application of evolutionary algorithms to complex engineering problems. Compared to earlier multi-objective evolutionary algorithms, NSGA-II exhibits improved convergence and can effectively search for optimal or near-optimal solutions [15]. Given the complexity and dynamic nature of UAV path planning in emergency logistics, where multiple conflicting objectives such as minimizing flight time, energy consumption, and ensuring safety must be optimized simultaneously, the NSGA-II algorithm offers a suitable framework. Numerous studies have demonstrated that NSGA-II can find high-quality solutions in a short computational time, making it particularly suitable for solving large-scale problems [16]. Furthermore, NSGA-II is independent of the specific nature of the problem, making it widely applicable to various multi-objective optimization problems, including drone path planning and production scheduling [17]. Given its proven ability to handle complex optimization tasks, NSGA-II provides a robust solution to the multi-objective path planning challenges posed by emergency logistics. In addition, NSGA-II can also be combined with other algorithms, such as particle swarm optimization (PSO) or simulated annealing (SA), to further improve its performance in specific applications [18]. This ability to adapt and integrate with other methods is crucial for improving the efficiency and effectiveness of UAV path planning in challenging environments.

However, NSGA-II does have some limitations. Although NSGA-II incorporates a crowding distance mechanism to maintain solution diversity, it can still become trapped in local optima in certain situations [19]. This is particularly true when the solution space is complex and contains multiple local extremes, causing NSGA-II to miss the global optimal solution. Furthermore, a major limitation of NSGA-II is its lack of an effective adaptive mechanism. While the algorithm can search the solution space using non-dominated sorting and crowding distance, it exhibits poor adaptability in dynamic environments, such as those with changing constraints or objective functions [20].

In the context of UAV path planning for emergency logistics, particularly in complex mountainous environments, these limitations pose a significant challenge. The need for UAVs to adapt to rapidly changing conditions, such as no-fly zones, obstacles, and fluctuating terrain, makes the use of traditional NSGA-II inadequate for real-time applications. To address these challenges, this paper aims to improve NSGA-II by proposing a variant that can handle complex constraints and dynamic changes in the environment, specifically applied to UAV path planning in emergency logistics. The motivation behind using NSGA-II is rooted in its proven ability to handle multi-objective optimization problems, such as minimizing flight time, energy consumption, and ensuring safety, which are essential in UAV path planning. However, in its standard form, NSGA-II struggles in dynamic, real-time environments where constraints and objectives change unpredictably. To enhance its performance in these challenging scenarios, we propose a multi-objective genetic algorithm, ACM-NSGA-II, with the following key contributions:

First, we propose an adaptive crossover and mutation strategy (ACM) that dynamically adjusts the crossover and mutation probabilities based on the population’s diversity and evolutionary progress. The motivation behind this adjustment is to overcome the issue of premature convergence, which is common in traditional multi-objective evolutionary algorithms, where the population becomes trapped in local optima early in the search process. This issue is particularly problematic in dynamic environments like UAV path planning for emergency logistics, where the search space is complex and evolving. By dynamically modifying the genetic operators based on the population’s state, ACM increases the exploration capability, particularly in the later stages of the search, when the algorithm needs to balance between exploiting known good solutions and exploring new areas. This strategy draws inspiration from the balance between exploration and exploitation in evolutionary search, ensuring a well-rounded exploration of the solution space without sacrificing convergence [21].

Furthermore, we propose an adaptive elite retention strategy that archives the best solutions in each generation, merges them with the current population, and performs non-dominated sorting and deduplication to ensure that the best historical solutions are retained. This innovation is motivated by the realization that traditional multi-objective algorithms that only consider the best solutions in the current generation may miss valuable solutions from previous generations. In dynamic, real-world problems such as drone path planning in emergency logistics, the environment is constantly changing (e.g., obstacles or no-fly zones), so retaining high-quality solutions from previous generations is crucial to maintaining diversity and solution quality. By retaining these elite solutions, we can avoid the gradual loss of diversity and ensure that the best solutions found earlier in the search process are not discarded, which would hinder the algorithm’s ability to adapt to changing conditions [22].

Furthermore, we introduce a dynamic path repair strategy that calculates the relationship between each point on the path and the terrain and no-fly zones, and dynamically adjusts the UAV’s trajectory to avoid these constraints. The motivation behind this strategy is to improve the traditional penalty-based approach, which statically handles constraints, resulting in suboptimal solutions. In real-world UAV path planning, especially in emergency logistics, the environment is constantly changing, and static constraints such as no-fly zones or terrain features must be handled dynamically. Dynamic path repair ensures that the path remains safe, feasible, and efficient by continuously adjusting these constraints during the search process. This innovation goes beyond the rigid penalty function and enables the algorithm to handle constraints more naturally and adaptively to match the dynamic characteristics of UAVs operating in complex environments such as mountainous terrain [23].

Finally, we introduce a dynamic injection and population diversity maintenance strategy. This adaptive injection strategy allows for the introduction of new exploration directions when the population becomes crowded, ensuring that the search does not stagnate. This approach is motivated by the fact that traditional algorithms often suffer from insufficient diversity when the population converges to a local optimum. This lack of diversity can be detrimental because it reduces the algorithm’s ability to explore new, potentially better solutions. By assessing the population’s crowding level and selectively injecting new individuals, we are able to maintain healthy levels of diversity and exploration, preventing the algorithm from getting stuck in local optima and continuously improving the quality of solutions throughout the search.

The remainder of this paper is organized as follows: First, Section 2 introduces the environment modeling and problem description. Then, Section 3 explains the overall framework and core components of the proposed ACM-NSGA-II. Next, Section 4 describes the experimental setup, and presents the empirical study. Finally, Section 5 pro-vides conclusions and prospects for future work.

2. Related Work

2.1. Problem Description

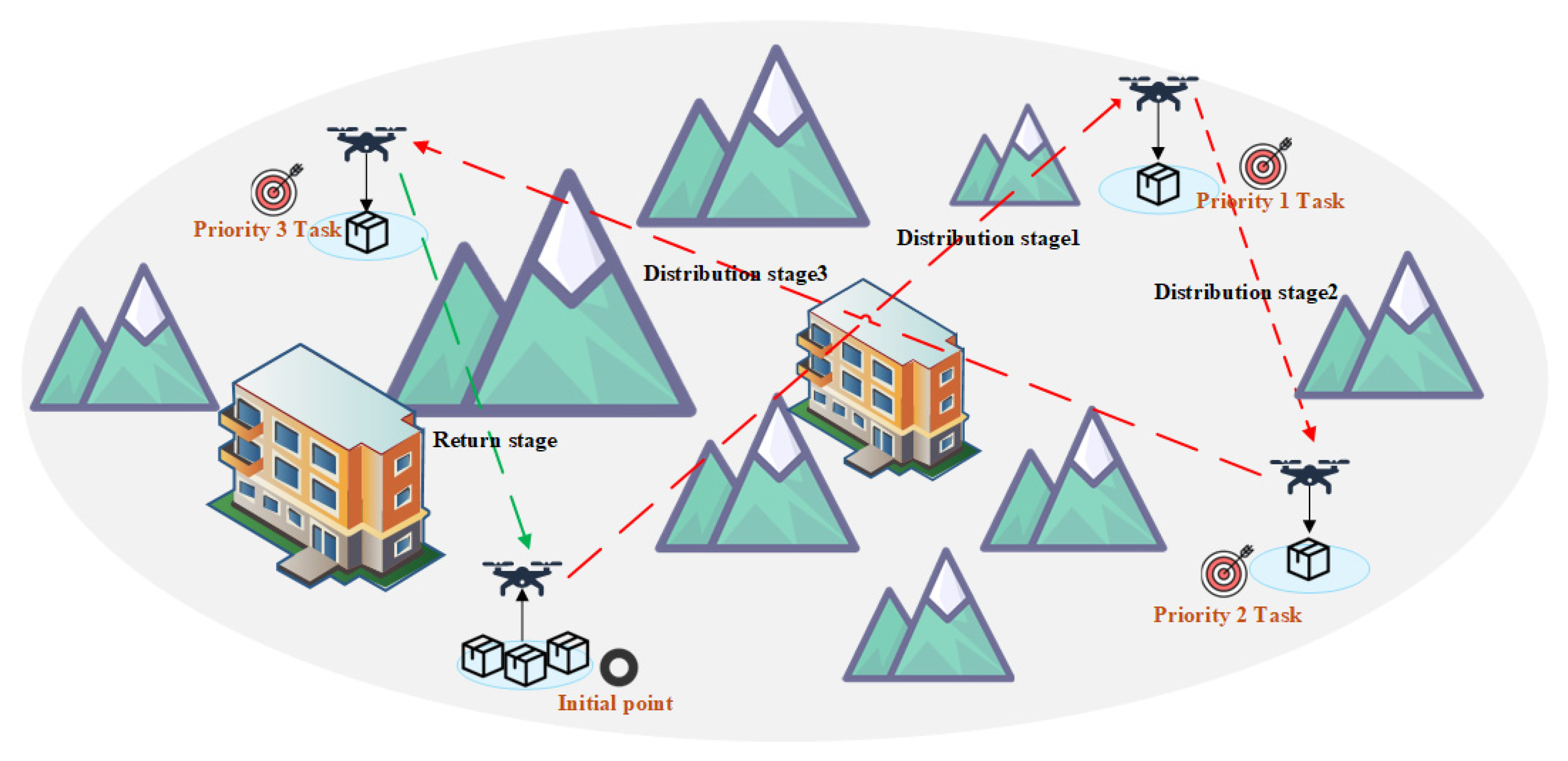
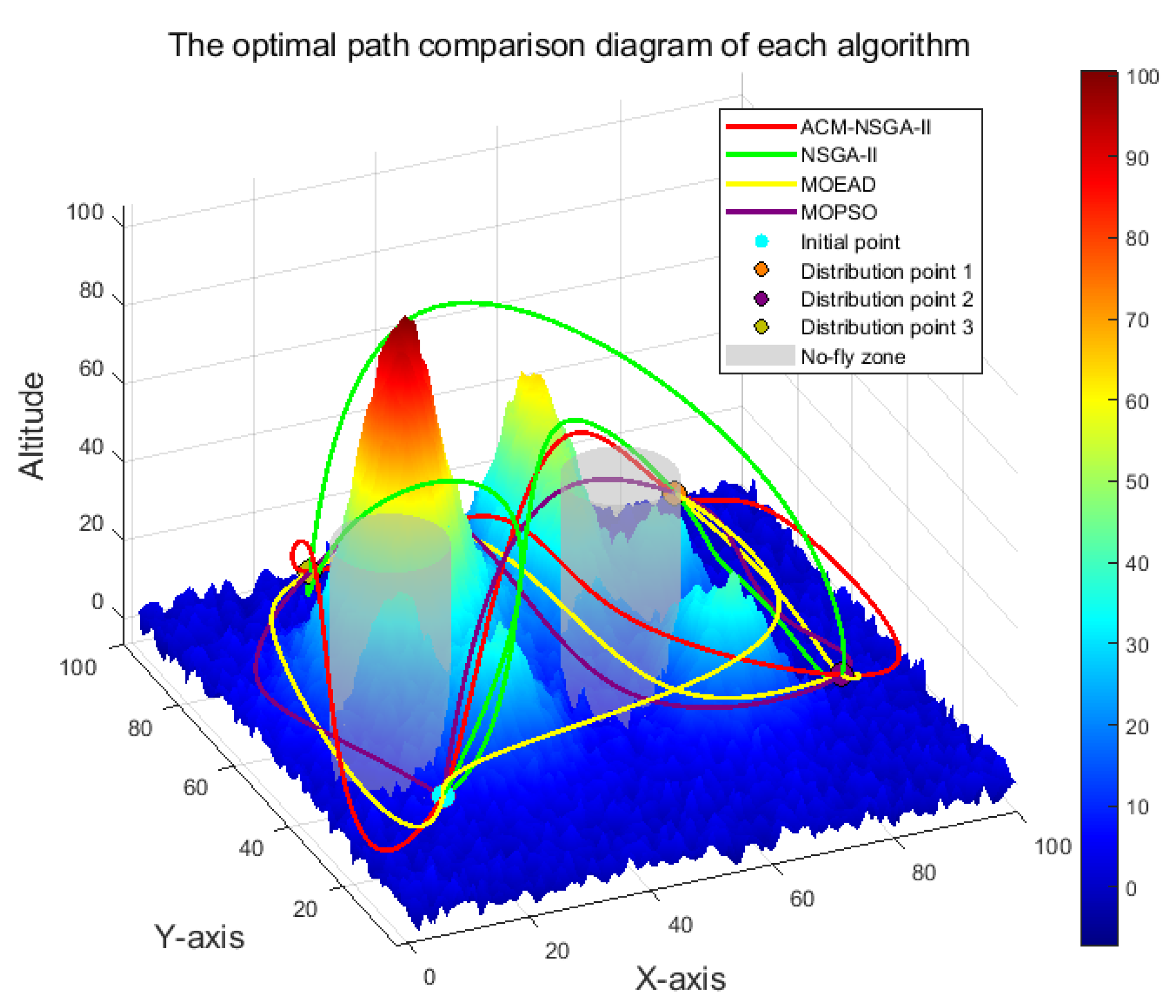
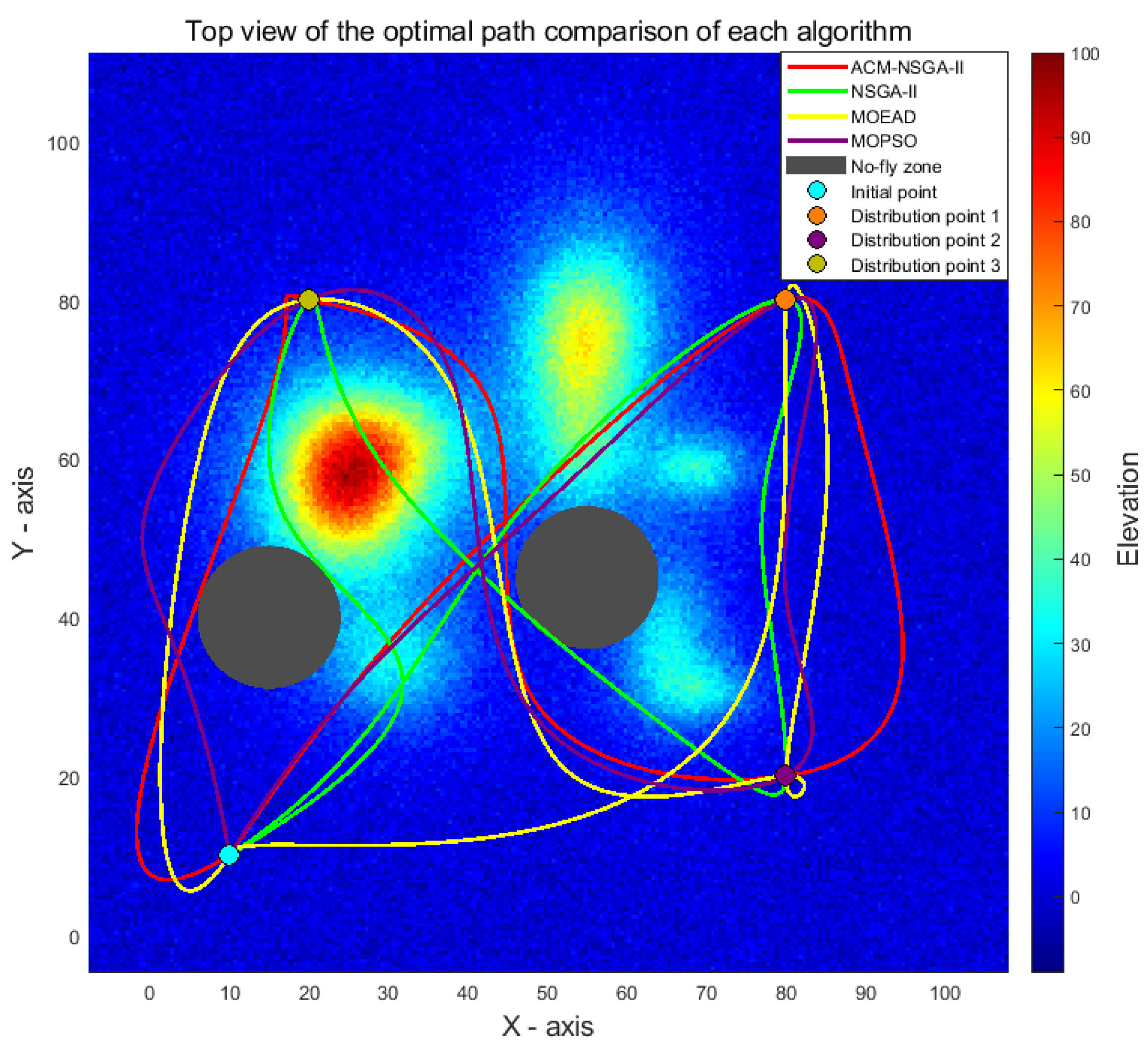
After a natural disaster, road congestion often hinders the timely delivery of relief supplies. This study considers a post-disaster scenario in a mountainous area, where a rechargeable electric drone is deployed from a logistics hub (departure point) to deliver relief supplies. Departing from the hub, the drone navigates complex three-dimensional terrain, avoiding natural obstacles (such as mountains) and restricted areas (such as military airspace and village buildings). It delivers supplies to three designated destinations based on priority and then returns to the logistics hub (departure point) to complete its mission. This paper draws a schematic diagram of the drone delivery mission as shown in Figure 1 for readers to understand.

As shown in Figure 1, a drone takes off from a starting point, carrying emergency supplies, and first flies to a priority 1 area to drop the supplies. The drone then flies to priority 2 and priority 3 destinations. After completing the delivery mission, the drone returns to the starting point from the last destination. This research model is based on the following assumptions:

• The unmanned aerial vehicle meets all technical requirements for the task;
• The locations of the logistics distribution points and each receiving point are known;
• The drone departs with a full charge, the flight speed is pre-set, and no new mission arrangements are accepted after departure;
• It can perform real-time obstacle avoidance, while weather and emergencies are not considered.

To conduct experiments under ideal conditions, this study used a drone with performance that could fully handle the delivery requirements of the mission, minimizing the impact of objective factors such as drone performance on the research.

Table 1. Unmanned aerial vehicle performance parameter setting table.

Parameter	Value
Maximum Payload (dual-battery mode)	30 kg
Maximum Payload (single-battery mode)	40 kg
Max Flight Range (30 kg, dual battery)	16 km
Max Flight Time (30 kg, dual battery)	18 min
Max Horizontal Flight Speed	20 m/s
Maximum Turning Angle	30°

lists the drone’s performance characteristics derived from the mission requirements, including a maximum payload of 30 kg in dual-battery mode and 40 kg in single-battery mode. With a 30 kg payload, the drone has a flight range of 16 km, an endurance of 18 min, a cruising speed of 20 m/s, and a maximum turning angle of 30°.

2.2. Symbols and Paraments

In this article, we have created a symbol alphabet to clearly and accurately represent the various variables and their relationships within the path planning algorithm. This alphabet not only provides detailed descriptions of the key variables involved in the formulas but also clarifies the physical meaning and mathematical background of each symbol. This alphabet symbol helps readers more intuitively understand the role and interrelationships of each variable within the algorithm, avoiding misunderstandings caused by unclear symbols or vague definitions.

2.3. Environment Modeling

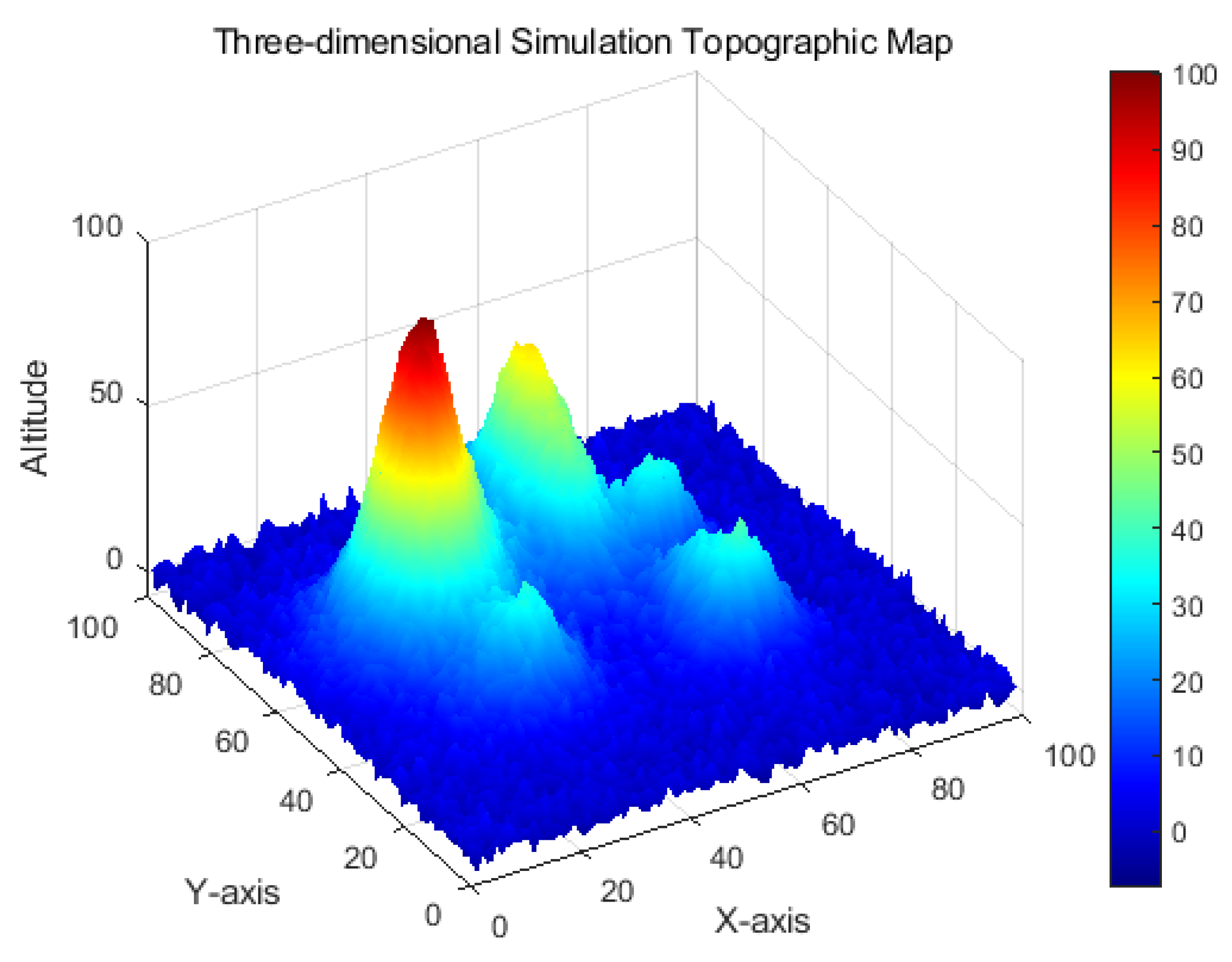
Terrain modeling is a critical component in drone path planning, as flight paths must be planned based on real terrain to ensure the drone avoids collisions with ground obstacles or other elevated objects. The goal of terrain modeling is to generate a virtual Three-dimensional environment using a digital elevation model (DEM) or similar technology [24], allowing accurate simulation of the aircraft’s movements within that environment. Terrain modeling is not limited to the ground surface but can also include topographic features such as buildings, peaks, and canyons. Typically, terrain models must accurately reflect the ground’s Three-dimensional spatial structure, which is crucial for flight path planning. To simulate complex Three-dimensional terrain, various modeling methods can be utilized, such as peak information generation, fractal noise generation, and texture mapping. These methods can effectively generate terrain maps that meet practical requirements, providing sufficient environmental data support for path planning.

The terrain model in this study is generated using peak information and fractal noise. We first simulate the elevation variations of the terrain by generating random peak information. Each peak is described by three parameters: its center, range, and height. Based on this, fractal noise is used to further adjust the randomness of the terrain, making it more similar to natural terrain.

In the specific modeling process, the height of the terrain Z (x, y) is composed of multiple peaks and noise, which can be expressed as:

$$Z (x, y) = {\sum }_{i = 1}^{N_m}{h}_i·\mathit{exp}\left(- {\left({\displaystyle \frac{x-x_i}{2{ \sigma }_{x_i}^2}}\right)}^2-{\left({\displaystyle \frac{y -{ y}_i}{2{ \sigma }_{y_i}^2}}\right)}^2\right) + \eta \left(x, y\right)$$

(1)

Here, h_i is the height of the i peak, ($x_i$, $y_i$) are the center coordinates of the peak, ${\sigma }_{x_i}$, ${\sigma }_{y_i}$ is the horizontal extension of the peak, η (x, y) and is the fractal noise term. $N_m$ is the number of peaks. The definitions of variables in all formulas are shown in

Table 2. Symbol and parameter table.

Symbols and Paraments	Description
$i$	The index of the task or waypoint
j	The index of a task or waypoint that is different from i
$r$	No-fly zone radius
$v$	Flight speed
$\alpha$	Adjusted altitude-energy coefficient.
$T$	Total flight time
$E$	Total energy expenditure
C	Security costs of the path
M	Total mass of the drone
$\eta (x, y)$	Fractal noise or disturbance term
$N_m$	Number of peaks
$x_i$	The x-axis coordinate of the i-th path point
$y_i$	The y-axis coordinate of the i-th path point
$z_i$	The z-axis coordinate of the i-th path point
zterrain	The altitude of the terrain at a certain coordinate
$h_i$	The altitude of the i-th waypoint
$x_c$	x-axis coordinate of the center of the no-fly zone
$y_c$	y-axis coordinate of the center of the no-fly zone
$z_c$	z-axis coordinate of the center of the no-fly zone
$N_p$	Total number of points in the path
$M_0$	Unmanned Aerial Vehicle’s empty mass
$m{D}_i$	Payload mass at the i-th delivery point
$d_i$	The length of path segment i
$f_i$	Workload coefficient of the i-th stage
θi	The angle between the velocity vectors of the i-th point
ci	Minimum vertical distance
$C_{col}$	A constant indicating the severity of the collision penalty
$w_{\mathit{stage}}$	The mass of the i-th flight phase
ηi	Efficiency coefficient of the i-th flight phase
Eflight	Total flight energy consumption
Pi,j	Euclidean distance between the i-th and j-th waypoints
Pnfz,i,j	Penalty when the i-th and j-th waypoints enter the no-fly zone
$C_{\mathit{nfz}}$	Constant for the severity coefficient of the no-fly zone penalty
${\delta }_{i, j}^2$	Distance measurement between waypoints and no-fly zones
$E_{\mathit{hover},i}$	Hovering energy consumption of the i-th delivery point
$t_{\mathit{hover}}$	The hovering time of the i-th delivery point
${\dot{E}}_{\mathit{hover}}$	Energy consumption rate when hovering
$w_i$	The Unmanned Aerial Vehicle’s mission load at this point
Ptime, i	Time window penalty for the i-th delivery point
αi	i-th Penalty weight coefficient of delivery point
Td,i	The actual time to arrive at the i-th delivery point
Wi	The time window of the i-th delivery point
${\sigma }_{x_i}$	The horizontal standard deviations of the i-th peak
${\sigma }_{y_i}$	The vertical standard deviations of the i-th peak
$P_{\theta , i}^{\left(1\right)}$	Angle squared penalty
$P_{\theta , i}^{\left(2\right)}$	Energy-based penalty
Pcoll, i	Collision penalty for point i

.

A no-fly zone is typically considered a cylindrical area, defined by its center, radius, and height. We define a no-fly zone as a cylinder in three-dimensional space. During path planning, the constraints on the cylinder ensure that the aircraft does not enter the no-fly zone by modifying the path.

The geometric constraints of the no-fly zone can be expressed as:

$$\mathit{Distance}\mathit{to}\mathit{No-Fly} \mathit{Zone} \mathit{Boundary} = \sqrt{{\left(x - x_c\right)}^2 + {\left(y - y_c\right)}^2 }\le r$$

(2)

where $\left(x_c, y_c\right)$ is the center coordinate of the no-fly zone, and r is the radius of the no-fly zone. Under these constraints, when the flight path enters the no-fly zone, the algorithm adjusts the flight path through a path repair mechanism to ensure the safety of the aircraft.

2.4. Mathematical Modeling of UAV Path Planning

In mountainous emergency logistics, UAVs encounter significant challenges due to complex terrain, obstacle interference, and the urgency of disaster response. The key task is to deliver relief supplies to target locations efficiently and safely under these constraints. To address this, a comprehensive mathematical model is developed, incorporating five practical constraints: payload capacity, energy limits, turning penalties, obstacle avoidance costs, and penalties related to hovering and time windows. These factors are embedded into a composite fitness function to evaluate path feasibility.

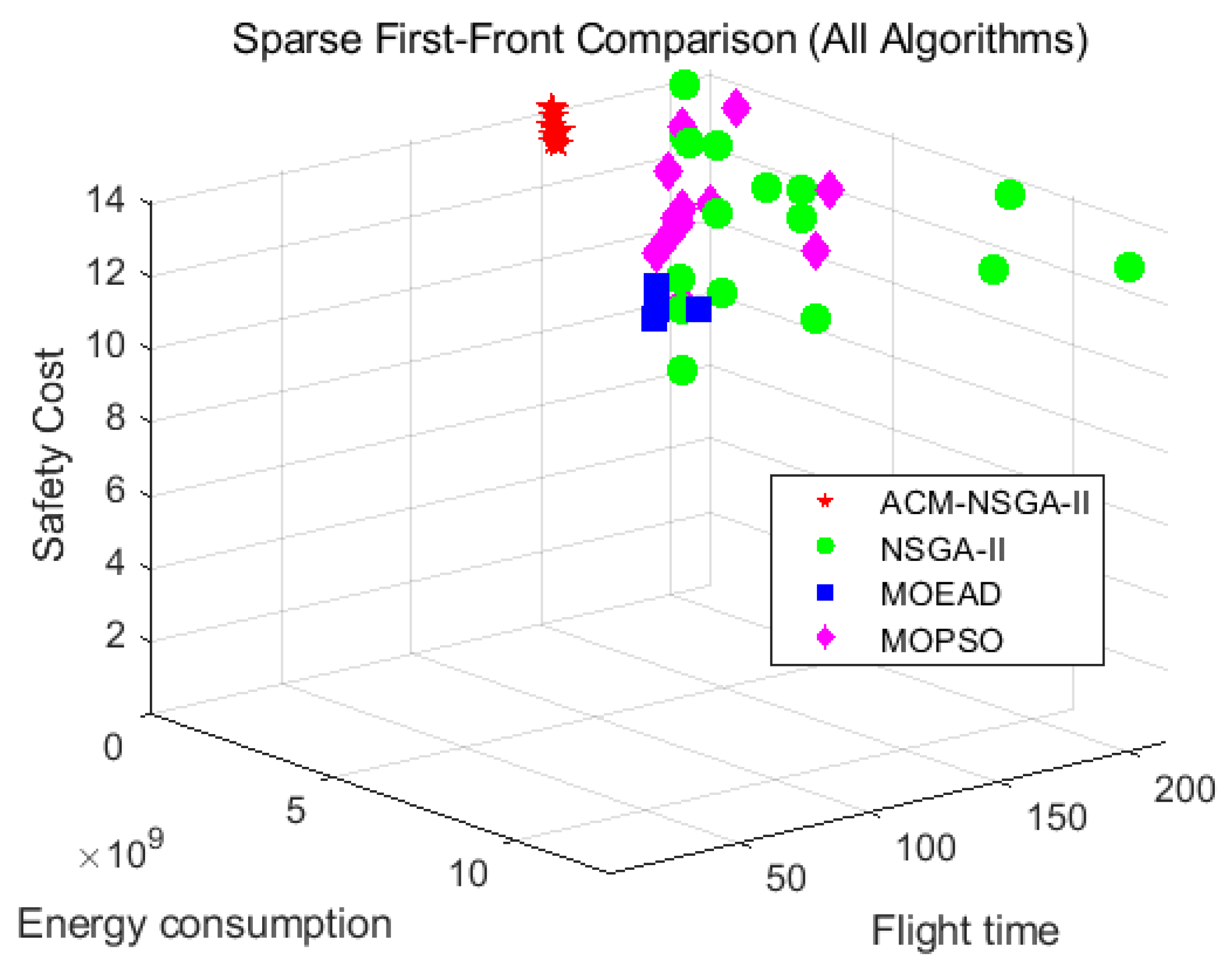
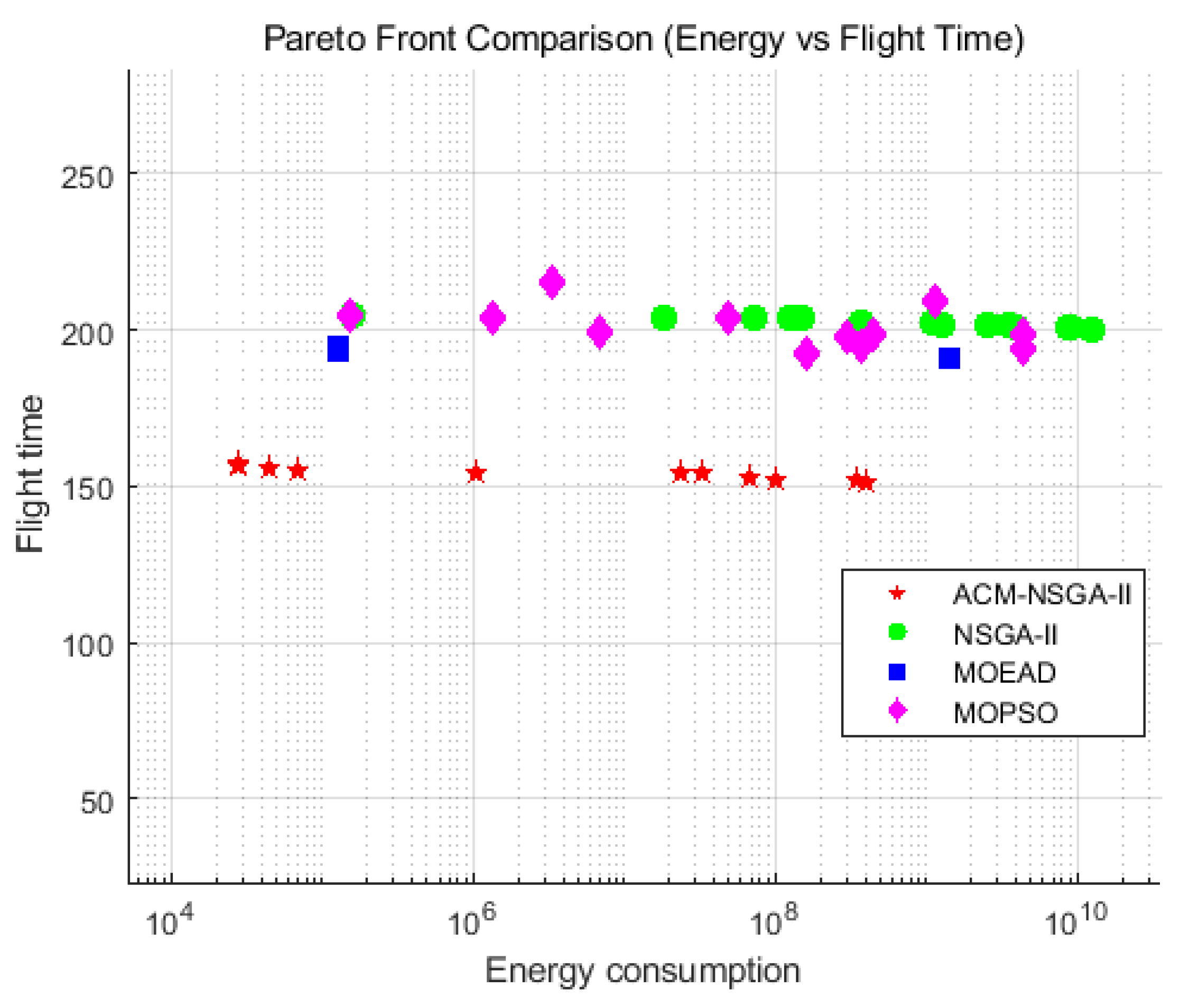
The model aims to simultaneously optimize three conflicting objectives:

• Minimize total flight time to ensure timely delivery;
• Minimize energy consumption to improve endurance;
• Minimize safety cost (i.e., distance from terrain obstacles and no-fly zones) to ensure route safety.

By framing the problem as a multi-objective optimization task, this study offers a robust and adaptable solution for UAV-based logistics in complex, high-risk mountainous environments.

2.4.1. Optimization Goal Definition

In disasters or emergencies, every minute of delay can result in unforeseen losses or harm, making flight time a crucial consideration. Furthermore, extending flight time allows drones to perform more missions without requiring frequent recharging, reducing the need for logistical support and improving mission efficiency. Finally, drone flight safety must be considered to ensure the safety of supplies during transportation and avoid further danger to affected areas or personnel. With these considerations in mind, this study primarily considered three optimization objectives: flight time, energy consumption, and safety costs.

1. Flight Time

The flight time [25] is the time required for the drone to fly from the starting point to each delivery point, assuming that the Unmanned Aerial Vehicle flies at a constant speed. The formula is:

$$T = {\sum }_{i = 1}^{N_p-1} {\displaystyle \frac{d_i}{v}}$$

(3)

In the formula, T indicates the total flight time of the unmanned aerial vehicle, $N_p$ indicates the number of points (nodes) in the path, $d_i$ indicates the distance between consecutive waypoints or delivery points, $v$ indicates the constant speed of the unmanned aerial vehicle.

This formula calculates the total flight time by summing up the distances between consecutive points and dividing them by the drone’s constant speed.

2. Energy Consumption

Energy consumption [26] is estimated based on the flight time, flight distance, altitude difference, load, and possible climb or descent of the path. In this model, energy consumption varies with flight distance and altitude during flight. The formula is:

$$E = {\sum }_{i = 1}^{ N_p- 1} d_i \left(1 + \alpha \left|h_{i + 1} - h_i\right|\right)$$

(4)

E indicates the total energy consumption of the unmanned aerial vehicle, α indicates the coefficient representing how much the altitude difference affects the energy consumption, $h_i$, $h_{i + 1}$ indicates the altitude of the current and next waypoint.

In this formula, energy consumption is proportional to the flight distance and altitude difference. Changes in altitude (such as climbing or descending) increase energy consumption, especially when there is vertical movement during flight. In addition, a penalty term is generated based on the collision of the path with terrain or no-fly zones.

3. Safety Costs

Safety cost [27] is a core concept in drone path planning. It quantifies the degree to which a path (or a point on a path) is close to obstacles or other dangerous areas, ensuring that the drone avoids collisions during flight. Its main goal is to guide the planning algorithm to generate paths that avoid potential dangers.

$$C=\begin{array}{c}{N}_p\\ \mathit{min}\\ i=1\end{array}(z_i-z_{\mathit{terrain}}(x_i,y_i)),$$

(5)

C indicates the safety cost of the path, z_i indicates the z-axis coordinate of the i-th path point, z_terrain (x_i, y_i) indicates the altitude of the terrain at the (x_i, y_i) coordinates (from the terrain map).

In this study, safety cost is considered as part of the cost function (flight time and energy consumption are optimized together). The closer to the danger, the higher the safety cost; the safer (farther) the danger, the lower the safety cost (usually approaching zero).

2.4.2. Constraint Definitions

1. Load and mass constraints

The total mass of the drone M is composed of the empty mass M₀ and the payload at each delivery point mD_i. Flight path planning must ensure that the total mass does not exceed the maximum allowable mass M_max. The formula is:

$$M = M_0 + {\sum }_{i = 1}^3 m{D}_i$$

(6)

2. Energy Consumption Constraints

Because the mission requires flying to three distribution points, delivering supplies, and returning, it is divided into four phases. Since the drone’s payload decreases after arriving at a distribution point to perform a drop, each phase corresponds to a different mass $w_{\mathit{stage}}$. Furthermore, the energy consumption of each phase is related to the aircraft’s altitude difference, air density, and efficiency factor. The energy consumption formula takes into account climb/descent penalties and propulsion efficiency. The total energy of the flight is the cumulative energy consumption of each phase ∆E_i. The energy consumption of each phase is calculated using the following formula:

$$\Delta E_i = d_i·f_i·\left({\displaystyle \frac{w_{\mathit{stage}}}{25}}\right)·{\eta }_i,$$

(7)

$$E_{\mathit{flight}}={\sum }_{i=1}^4 \Delta E_i$$

(8)

3. Turning penalty

For continuous velocity vectors v₁ and v₂, a turning penalty θ_i is calculated and applied. The turning penalty includes an angle squared penalty and an energy-based penalty, which together affect energy consumption. The formula is:

$$P_{\theta , i}^{\left(1\right)}= k_{\theta } {\theta }_i^2, p_{\theta , i}^{\left(2\right)}= \left(1 + 0.2{\theta }_i\right){ ‖v_1‖}^2,$$

(9)

$$P_{\theta }={\sum }_i \left(P_{\theta , i}^{\left(1\right)}+{ P}_{\theta , i}^{\left(2\right)}\right)$$

(10)

4. Obstacle and No-Fly Zone Penalties

The aircraft must maintain a certain safe distance from the ground at every point along its path. If the aircraft’s distance from the ground falls below the set minimum safe altitude, a collision penalty is incurred. The formula is:

$$P_{\mathit{coll},i}=C_{\mathit{col}}{(5-c_i)}^2,$$

(11)

$$P_{\mathit{coll}}={\sum }_i{P}_{\mathit{coll}, i}$$

(12)

No-fly zone: If the path enters the no-fly zone, an obstacle avoidance penalty is imposed. The formula is:

$$P_{i,j} = \sqrt{{\left(x_i - x_j\right)}^2 + {\left(y_i - y_j\right)}^2}, P_{\mathit{nfz},i,j} = C_{\mathit{nfz}} {\delta }_{i, j}^2$$

(13)

5. Hovering and Time Window Penalty

Hovering Energy Consumption: The drone will hover over each drop point during the delivery process, and this hovering consumes additional energy, as shown in the following formula:

$$E_{\mathit{hover},i} = t_{\mathit{hover}} {\dot{E}}_{\mathit{hover}} {\displaystyle \frac{w_i}{25}}$$

(14)

Time window penalty [28]: If the time required for the drone to reach the delivery point exceeds the preset time window, an overdue penalty will be incurred. This penalty is also intended to ensure that the drone completes the emergency material delivery task as promptly as possible, in line with the timeliness requirements of emergency logistics. The formula is:

$$P_{\mathit{time},i} = {\alpha }_i (T_{d,i}-W_i)$$

(15)

These constraints ensure the physical feasibility of the flight path and the efficiency of the mission requirements by incorporating multiple factors, including mass, energy consumption, turning penalties, obstacle and no-fly zone penalties, hovering, and time window penalties. In the code, these constraints are dynamically calculated and adjusted across each step of the path to ensure the drone achieves optimal performance in a multi-objective optimization.

3. Proposed Algorithm

In this section, we first introduce the overall framework of the proposed ACM-NSGA-II algorithm. Then, we further explain its key components, namely the adaptive crossover mutation strategy, the dynamic path repair strategy, the dynamic injection and population diversity maintenance strategy.

3.1. General Framework

This section describes the overall process of the proposed ACM-NSGA-II algorithm. The inputs include the population size N and the feature dimension D, and the output is the optimized non-dominated path set NextPop. The overall framework is shown in the pseudocode of Algorithm 1. The algorithm first initializes the population and then enters the main program, performing fitness evaluation, non-dominated sorting, and tournament selection. Crossover and mutation operations are then performed based on population diversity and algebraic decay, adjusting the probabilities of crossover and mutation to generate the next generation of paths (as shown in Algorithm 2). Dynamic path modification is then performed. During path repair, the path is dynamically adjusted based on the distance from the no-fly zone to ensure that the path does not collide with the no-fly zone or terrain (as shown in Algorithm 3). During the environmental selection phase, the current optimal solution is saved and elite selection is performed (as shown in Algorithm 4). Adaptive random injection is then performed. When the population crowding is too low, random individuals are injected to enhance diversity (as shown in Algorithm 5). N representative individuals are then selected as the next generation population using non-dominated sorting and crowding distance. When the termination condition is met (for example, the maximum number of iterations is reached), the algorithm outputs the final set of non-dominated paths.

Algorithm 1. General Framework (N, D)

Input: Population size N, Feature dimension D; Output: Final population FinalPop;

1: CurrentPop ← Randomly generate N initial solutions; //Initialize the population

2: Gen ← 0; //Generation Counter

3: CurrentArc ← Φ //Archive set

4: While Gen < MaxGen do;

5:   EvaluateFitness (CurrentPop); // Fitness evaluation

6:   [Fronts, Crowding] ← NonDominatedSortAndCrowding (CurrentPop); // Non-dominated sort- ing and crowding distance

7:   Parents ← CheampionshipSelection (CurrentPop, Fronts, Crowding); // Tournament Se lection

8:    Offspring ← AdaptiveCrossoverMutation (Parents); //Adaptive crossover and muta- tion by Algorithm 2

9:   Offspring’← DynamicPathRepair (Offspring); // Dynamic path repair by Algorithm 3

10:   [NextPop, CurrentArc, ArchiveUpdated ← UpdateArchive (CurrentPop, Offspring’, CurrentArc)]; // ArchiveUpdate by Algorithm 4

11:  if ArchiveUpdated then

12:   NextPop ← AdaptiveRandomInjection (NextPop, CurrentArc,K); // Adaptive random injection by Algorithm 5

13:   end if

14: End while

15: FinalPop ← NextPop;// Set final population

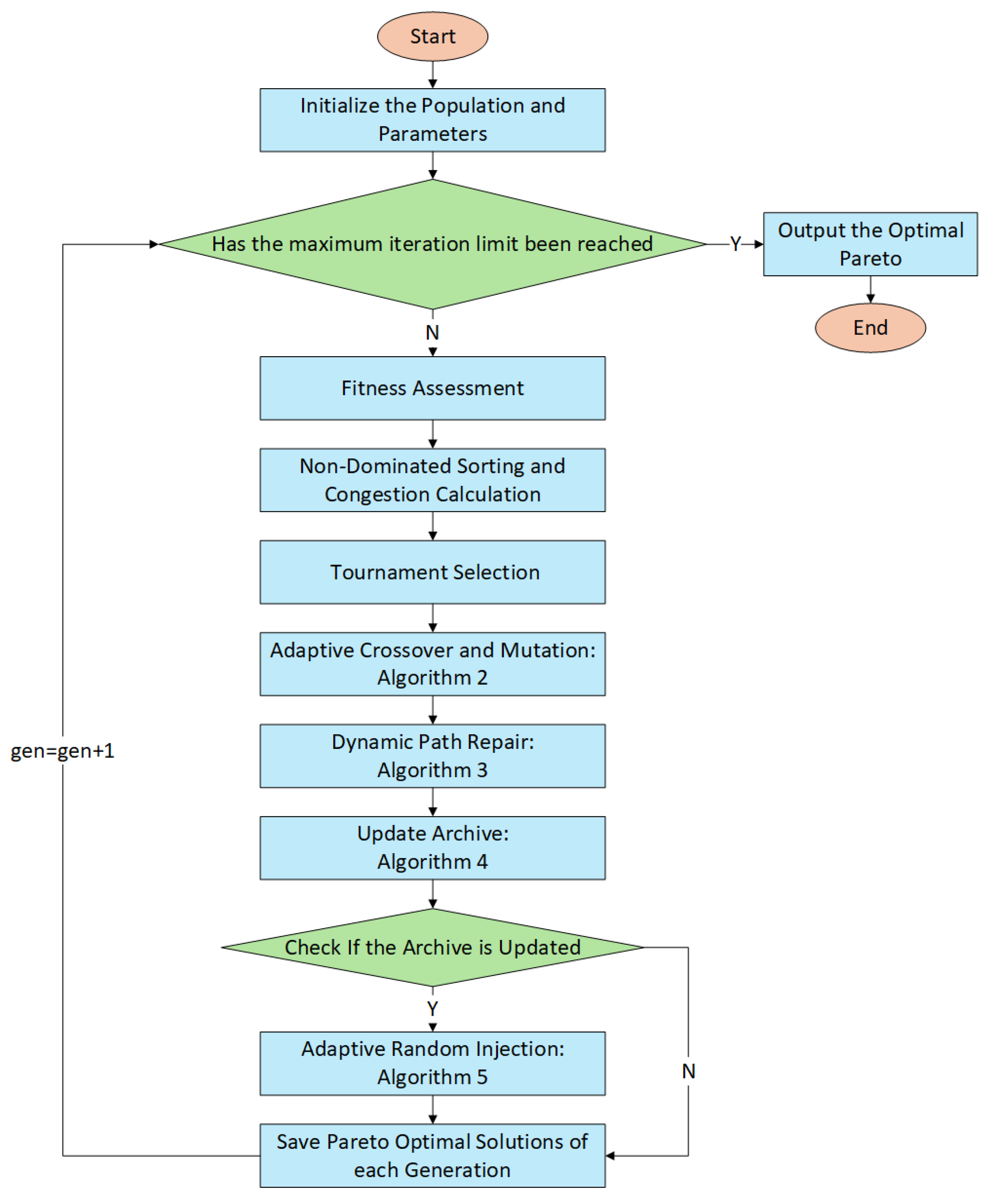
The overall process is shown in Figure 2, which clearly demonstrates the key steps such as population initialization, iterative update, adaptive crossover and mutation, dynamic path repair and elite retention, and demonstrates the algorithm’s adaptive ability in multi-objective optimization under complex constraints:

Step 1: Build the algorithm environment and configure basic flight information for the Unmanned Aerial Vehicle.

Step 2: Initialize the population and set all relevant parameter values.

Step 3: Check if the maximum number of iterations has been reached.

Step 4: Evaluate the population’s fitness.

Step 5: Non-dominated sorting and crowding distance calculation.

Step 6: Tournament selection mechanism.

Step 7: Adaptive crossover and mutation (Algorithm 2).

Step 8: Dynamic path repair (Algorithm 3).

Step 9: Update the external archive (Algorithm 4).

Step 10: Check if the archive is updated.

Step 11: Adaptive random injection (Algorithm 5).

Step 12: Save Pareto optimal solutions for each generation.

Step 13: Output the final Pareto optimal solutions.

3.2. Adaptive Crossover and Mutation

Traditional crossover and mutation rates are pre-set and cannot be adjusted based on the current population diversity. This can lead to insufficient exploration and, in turn, limit optimization effectiveness. Furthermore, traditional crossover and mutation methods often over-rely on global search and overlook the potential of local search. Local optimization may be effective in the early stages, but when the solution space has already entered a favorable region, excessive crossover and mutation operations can disrupt existing good solutions.

Compared to traditional crossover and mutation methods, adaptive crossover and mutation [29] effectively avoid premature convergence in the early stages by adjusting the crossover and mutation probabilities based on population diversity and generational decay. This process utilizes symmetry principles to ensure balanced exploration and exploitation, adjusting the crossover and mutation rates in such a way that prevents the algorithm from converging too early and allows for a more efficient global search. Furthermore, by adjusting the crossover and mutation ratios based on population diversity, adaptive crossover and mutation maintains population diversity throughout the search process, preventing regression into local optima while improving solution accuracy and quality. This approach has been shown to be more effective for complex optimization problems.

Specifically, as shown in Algorithm 2, this study adopted an adaptive segmented crossover [30] and smooth mutation strategy. Traditional crossover methods may introduce some unreasonable structures in the path (for example, the path may collide with a no-fly zone or terrain after crossing). Segmented crossover, on the other hand, reduces the risk of path unreasonableness by limiting the crossover operation to specific areas of the path. Segmented operations can handle highly nonlinear and complex constraints, thereby providing better optimization solutions. The advantage of smooth mutation is that it can adjust certain points in the path through interpolation and small perturbations, rather than directly changing the entire path. This approach ensures that the mutated path does not deviate significantly from the original path, helping to maintain the smoothness and feasibility of the path. Compared with traditional mutation methods, smooth mutation can avoid drastic changes in the path, reduce the risk of path unreasonableness, and improve the refinement and stability of the optimization process.

Algorithm 2. Adaptive Crossover Mutation (Parents, Gen, MaxGen, CR, MU)

Input: Parents Parents, Current Algebra Gen, Max generations MaxGen, Initial crossover rate CR, Initial mutation rate MU; Output: Offspring Offspring;

1: Offspring ← Φ; // Initialize offspring collection

2: R ←AdjustCrossoverRate(Gen, MaxGen, CR);// Adjust crossover rate

3: Pm ←AdjustMutationRate(Gen, MaxGen, MU); // Adjust mutation rate

4: for each pair (P1, P2) from Parents do;

5:   if rand() < R then

6:     [c1, c2]← Crossover (P1, P2); // Perform crossover

7:   end if

8:   c1 ← Mutate (c1, Pm); // Mutate first offspring

9:   c2 ← Mutate (c2, Pm); // Mutate second offspring

10:   Offspring. add (c1); // Add c1 to offspring collection

11:   Offspring. add (c2); // Add c2 to offspring collection

12: end for

13: return Offspring;

3.3. Dynamic Path Repair

In traditional NSGA-II algorithms, the feasibility of path generation typically relies on satisfying constraints, but there is typically no dedicated mechanism to handle conflicts between the path and the environment (no-fly zones, terrain). Failure to meet these constraints can result in unsafe paths, impacting the algorithm’s overall performance. Unlike traditional NSGA-II, dynamic path repair not only optimizes objective functions (such as flight time and energy consumption) but also performs real-time repairs after each generated path based on environmental changes (such as no-fly zones and terrain changes), ensuring that the path consistently meets safety constraints during the optimization process. This ensures that the path planning process does not cross no-fly zones or fall below terrain altitude, thus ensuring flight safety.

The local search strategy in dynamic path repair is a significant difference from traditional NSGA-II. Specifically, local search utilizes two common path optimization methods—1-opt and 2-opt—to perform refined optimization during the path repair process. 1-opt optimizes the total path length by swapping the positions of adjacent points in the path, making it suitable for rapid adjustments and local improvements. 2-opt, on the other hand, eliminates intersections by swapping the connections between two non-adjacent path segments, further optimizing the path structure and achieving more optimal path adjustments. Whenever a conflict occurs during path repair, the algorithm applies both methods simultaneously and selects the optimal optimization result by comparing fitness (e.g., path length, flight time, energy consumption, etc.).

The advantage of the local search method lies in its ability to select the appropriate repair strategy for different types of path conflicts. When applying 1-opt and 2-opt, the algorithm not only considers local optimization but also selects the optimal path to minimize flight time and energy consumption. For example, if a path has large turns, the 1-opt method quickly smooths the path by swapping the order of adjacent nodes. If a path has significant intersections, the 2-opt method can eliminate intersections by adjusting the order of path segments, further optimizing the path structure. Through this local optimization approach, dynamic path repair effectively improves path quality while avoiding over-adjustments and maintaining path integrity.

Furthermore, dynamic path repair employs a symmetry strategy, taking into account the symmetry of environmental constraints during the path repair process. If the terrain or no-fly zone is symmetrical, the repair algorithm attempts to symmetrically adjust both sides of the path to reduce duplicate repairs and over-corrections, further improving computational efficiency. This symmetry strategy not only reduces unnecessary computation but also ensures balanced adjustments on both sides of the path, avoiding over-repairing on one side and under-repairing on the other. This approach enables the algorithm to more efficiently optimize paths in complex environments, ensuring consistency and efficiency during the path repair process.

Dynamic path repair is an incremental repair process that does not require replanning the entire path each time. Each repair only targets the problematic portion of the path, significantly reducing computational overhead and improving algorithmic efficiency. Symmetry ensures that if one part of the path requires adjustment, the other part can be modified in a similar manner, avoiding recalculation and preserving the overall path structure. Specifically, in Algorithm 3, the code implementation uses the RepairPath function to examine each point on the path, calculate the minimum safety margin between the path and the terrain, and make adjustments as needed. When the path approaches a no-fly zone or terrain obstacle, the repair process uses methods such as horizontal push-off and vertical lift to ensure that the path does not collide with the obstacle. By applying a symmetric strategy when possible and making effective adjustments to both sides of the path, the repair process can better adapt to complex environments and optimize the path, considering both local and global constraints.

However, repair operations are limited to localized repairs of the path; they are triggered only when the path collides with an obstacle, such as a no-fly zone or terrain. This avoids unnecessary computation and improves the computational efficiency of the path planning algorithm. Furthermore, by adjusting only the portion of the path that conflicts with an obstacle or no-fly zone, unnecessary over-repairs are avoided, preserving the path’s original structural consistency as much as possible, which helps reduce flight time and energy consumption. A symmetry strategy also plays a role in the repair process, ensuring that adjustments on one side of the path are symmetrical with the other, resulting in a more optimized overall repair process.

Algorithm 3. Dynamic Path Repair (Offspring)

Input: Offspring Offspring; Output: Repaired offspring Offspring’;

1: Offspring’ ← Φ // Initialize the repaired offspring collection

2: for each x in Offspring do;

3:    if not IsFeasible(x) then;

4:     x ← RepairByHeuristic (x); // Apply heuristic repair

5:   end if;

6:   if LocalImprovementEnabled then;

7:     bestSolution ← x; // Start with the current solution

8:     newSolution1Opt ← Apply1Opt(x); // Apply 1-opt local search

9:     newSolution2Opt ← Apply2Opt(x); // Apply 2-opt local search

10:     if Fitness(newSolution1Opt) < Fitness(bestSolution) then

11:      bestSolution ← newSolution1Opt; // Update best solution if 1-opt is better

12:     end if;

13:     if Fitness(newSolution2Opt) < Fitness(bestSolution) then

14:       bestSolution ← newSolution2Opt; // Update best solution if 2-opt is better

15:     end if;

16:     x ← bestSolution; // Choose the best solution

17:   end if;

18:   Offspring’.add(x); // Add repaired x to the repaired offspring collection

19: end for;

20: Offspring’ ← RemoveDuplicatedAnd Clamp (Offspring); // Remove duplication and maintain boundaries

21: return Offspring’;

3.4. Update Archive and Environmental Selection

Traditional elite retention mechanisms often select individuals based on crowding calculations, which can lead to a loss of diversity among individuals. This is especially true when NSGA-II handles multiple objectives. Crowding can lead to an over-concentration of individuals in certain target areas, neglecting other potentially high-quality solutions. Furthermore, if the environment changes during path planning, traditional elite retention mechanisms cannot effectively update the elite solution set, resulting in some paths that are no longer valid or do not meet the new environmental constraints remaining in the solution set and failing to be updated in a timely manner.

In this study, in Algorithm 4, the elite retention mechanism introduces environmental adaptability updates [31]. When the environment (such as no-fly zones or terrain) changes, the algorithm not only updates the paths but also dynamically updates the elite solution set to ensure that the paths adapt to the new environmental conditions. This dynamic adaptability enables the elite solutions to respond to environmental changes in real time. Path planning not only considers the objective function but also adjusts the paths based on new environmental constraints, ensuring that the paths in the elite solution set always meet environmental requirements. Furthermore, in traditional NSGA-II, elite solutions are typically retained based on the non-dominated ordering of the current generation, without considering past solutions. This algorithm, by retaining historically excellent solutions, aggregates the experience gained throughout the optimization process into a global Pareto set. This allows the algorithm to draw upon historically excellent paths throughout the optimization process, maintaining global search capabilities. By retaining historically excellent solutions, the elite retention mechanism can integrate high-quality solutions from multiple generations, rather than simply the best solution from the current generation. This approach effectively improves the diversity and robustness of the population, helping to find a wider range of optimal solutions within the search space.

Algorithm 4. UpdateArchive (CurrentPop, Offspring’, CurrentArc, N)

Input: Current population CurrentPop, Repaired offspring Offspring’, Current Archive CurrentArc, population size N; Output: Final population FinalPop, Updated archive UpdateArc, Flag indicating if archive is updated ArchiveUpdated;

1: U ← CurrentPop ∪ Offspring’; // Combine parent and offspring

2: EvaluateFitness (U); // Evaluate fitness of the combined population

3: Fronts ← FastNonDominatedSort(U); // Non-dominated sorting

4: NewArc ← CurrentArc ∪ {All solutions in U at the first level}; // Add new non-dominated solutions to archive

5: NewArc ← NonDominatedFilter (NewArc); // Remove redundancy and preserve diver- sity

6:  if |NewArc| > ArchiveSizeLimit then;

7:    NewArc ← TruncateByCrowding (NewArc, ArchiveSizeLimit);

8:  end if;

9: i ← 1

10:   while |FinalPop| + |Fronts [i]| ≤ N do;

11:    FinalPop ← FinalPop ∪ Fronts [i]; // Add front solutions to the next generation

12:     i ← i + 1

13:   end while;

14: Remain ←N − |FinalPop|; // Remaining space in population

15:   if Remain > 0 then;

16:    Sorted ← SortBuCrowdingDescending (Fronts [i]); // Sort by crowding

17:    FinalPop ← FinalPop ∪ Sorted [1: Remain]; // Add remaining solutions

18:   end if;

19: ArchiveUpdated ← (NewArc ≠ CurrentArc); // Check if the archive is updated

20: CurrentArc ← NewArc; // Update the archive

21:   if ArchiveUpdated then;

22:    Call AdaptiveRandomInjection(FinalPop, CurrentArc, K); // Algorithm 5

23:   end if;

24: return FinalPop, CurrentArc, ArchiveUpdated;

3.5. Adaptive Random Injection

The traditional NSGA-II algorithm, based on population selection and crossover mutation during the search process, may over-search within known areas and overlook other potentially high-quality solutions. The lack of a mechanism to force the introduction of new solutions limits the search space during optimization, potentially missing out on better solutions. Especially in no-fly zones and when terrain constraints are complex, once the population converges on a local area, the optimization process stalls and fails to effectively explore uncovered areas.

Adaptive random injection promotes a broader exploration of the solution space. The introduction of new individuals provides the algorithm with more possible solution paths, helping the optimization process to move beyond the current solution space and into un-explored areas. This maintains population stability and avoids over-reliance on local solutions. Incorporating symmetrical patterns in the injected solutions can further enhance this effect, allowing the algorithm to explore solutions that reflect similar characteristics in different parts of the search space, thus improving overall search efficiency. Adaptive random injection effectively avoids premature convergence by continuously injecting new random solutions. The addition of new solutions provides the algorithm with more opportunities for global exploration, making the optimization process more resilient and enabling it to escape the trap of local optimal solutions.

The adaptive random injection is divided into two parts: guided injection and random injection. The guided injection process selects individuals from the archive and perturbs them, introducing high-quality, archive-based variants to explore different regions of the solution space. This method constitutes about 60% of the injected individuals, with their variations guided by previously discovered solutions. The remaining 40% of individuals are generated randomly to increase exploration, promoting diversity and preventing the optimization process from getting stuck in local optima.

This approach leverages the synergy between archive-based guidance and random injection to improve the algorithm’s capability to explore diverse areas in the search space. This mechanism ensures that when population diversity is low, the algorithm increases the number of randomly injected solutions, providing more opportunities for the exploration of new paths. On the other hand, when diversity is high, the algorithm relies more on archive-based solutions, focusing on fine-tuning the population around high-quality regions. This adaptive mechanism helps in maintaining a balance between exploration and exploitation, preventing premature convergence while ensuring path feasibility and security in dynamic environments.

In this study, in Algorithm 5, the number of randomly injected individuals is related to the population crowding level. When diversity is insufficient, the number of injected individuals is increased accordingly. This adaptive mechanism effectively improves the diversity of the population. This approach effectively avoids the limitations of traditional NSGA-II, improving population diversity, preventing premature convergence, enhancing global search capabilities, and better maintaining path security and feasibility in dynamic environments, while leveraging symmetry to ensure a more balanced exploration.

Algorithm 5. AdaptiveRandomInjection (CurrentPop, CurrentArc, K)

Input: Current population CurrentPop, Current Archive CurrentArc, Injection number K; Output: Final population FinalPop;

1: Candidates ← SelectCandidatesForReplacement (CurrentPop); // Select K permutations

2: n_guided ← ceil (k * 0.6); // 60% generated by archive reorganization

3: n_guided ← k − n_guided; // 40% generated randomly

4: NewSols ← Φ

5: for i = 1 to n_guided do;

6:  a ←SampleFromArchive (CurrentArc); // Sample high-quality individuals from archive

7:  b ←Perturb (a); // Apply perturbation

8:  NewSols.add (RepairIfNeeded (b)); // Apply repair if necessary 9: end if

10: for i = 1 to n_random do;

11:  r ← RandomInit (1); // Generate random individuals

12:  NewSols. add (r); // Add random individuals to NewSols

13: end for;

14: FinalPop ← Replace (CurrentPop, Candidates [1: k], NewSols); // Replace candidates with new solu-tions

15: return FinalPop; // Return the updated population

3.6. More Discussions

This section provides a theoretical analysis of several commonly used crossover operator combinations in genetic algorithms proposed in the recent literature [32]. These combinations include PMX + PBX, PMX + OX2, PMX + OX1, and PBX + OX2. These combinations will be explored in the context of emergency path planning for drones. This path planning involves optimizing multiple objectives, such as flight time, energy consumption, and safety costs, while also adhering to constraints such as terrain restrictions, no-fly zones, and altitude requirements.

1. PMX + PBX

PMX (Partially Mapped Crossover) ensures that the offspring maintains a feasible order of waypoints, preventing duplication. PBX (Position-Based Crossover), on the other hand, focuses on preserving relative positions of genes in the offspring, which is useful for maintaining critical point sequences like delivery points and start/end locations.

Application to UAV Path Planning: This combination can be effective in maintaining sequence integrity while also adjusting intermediate waypoints. By preserving the order and positions of critical waypoints, this combination can help generate valid and optimized flight paths while reducing energy consumption and flight time.

2. PMX + OX2

PMX prevents duplication of waypoints, while OX2 (Two-Point Order Crossover) ensures that the order of genes between the two crossover points is maintained. This allows for better exploration of the search space while maintaining the overall order of the path.

Application to UAV Path Planning: This combination may be particularly useful when the path sequence is highly important, such as ensuring that a drone follows a specific delivery sequence while avoiding obstacles or no-fly zones. It can optimize the path length while respecting the flight constraints.

3. PMX + OX1

Similarly to PMX + OX2, OX1 focuses on the order of the sequence by crossing paths at a single point, while PMX ensures that the resulting offspring maintains a valid order without duplication.

Application to UAV Path Planning: In scenarios where sequence preservation is crucial (e.g., delivery points), this combination allows for the generation of diverse offspring while maintaining path legality. It can effectively optimize flight time and energy consumption by adjusting the non-fixed segments of the path.

4. PBX + OX2

PBX preserves the relative positions of genes, while OX2 maintains the order between crossover points, allowing for more global exploration of the search space without disturbing critical waypoints.

Application to UAV Path Planning: This combination might be particularly useful in cases where there are multiple delivery points to be visited, but the overall order of visit matters more than the exact path taken. It allows exploration while preserving feasibility with respect to key constraints like no-fly zones and terrain limitations.

Each crossover combination presents distinct theoretical advantages depending on the nature of the UAV path planning problem. By selecting the appropriate crossover method, it is possible to explore the solution space more effectively while maintaining feasible paths that satisfy the problem’s constraints. In future work, we will test these combinations in UAV path planning experiments to evaluate their effectiveness in optimizing for multiple objectives, including flight time, energy consumption, and safety margin.

4. Experimental Design and Result Analysis

4.1. Experimental Setups

The experimental scenario is set in a three-dimensional terrain space of size [100, 100, 100]. The terrain is generated using a simulated mountain environment based on Equation (1). The pure terrain map is shown in Figure 3. The logistics distribution center, serving as the departure and return point, is located at coordinates (10, 10, 20) and is marked by a cyan circle. The three distribution points corresponding to the disaster relief areas are located at (80, 80, 20), (80, 20, 20), and (20, 80, 20), represented by orange, purple, and olive circles, respectively. The two restricted areas represent military control zones or no-fly zones and are modeled as cylinders with a radius of 9 and a maximum height of 60, with centers at (15, 40) and (55, 45), respectively.

Key parameters in the ACM-NSGA-II algorithm include the population size (N), the number of iterations (Gen), the initial crossover rate (CR), and the initial mutation rate (MU). Although this paper employs an adaptive crossover and mutation process, both the initial crossover rate and the initial mutation rate have specific values, and their impact on the algorithm’s optimization performance must be considered. For smaller problems, genetic algorithms typically use a population size of 100 or less and approximately 100 iterations. The crossover rate is typically set between 0.6 and 0.9, and the mutation rate is typically set between 0.01 and 0.1 [33]. Due to the large number of parameters, this paper uses the Taguchi experimental method to determine the optimal parameter combination and designs corresponding orthogonal experiments [34]. The corresponding levels of each parameter are shown in

Table 3. Parameter level setting.

Parameter	Parameter Number
	1	2	3
N	20	40	60
Gen	50	100	150
CR	0.7	0.8	0.9
MU	0.03	0.06	0.09

.

The Taguchi method avoids repeated testing of certain parameter combinations. Through orthogonal design, a wider range of experimental conditions can be covered, resulting in nine combinations. However, the ODS (Optimization Result Performance Index) index can fluctuate due to factors such as the randomness of the genetic algorithm. Therefore, three calculations were performed on each combination to obtain the average ODS value, as shown in

Table 4. Taguchi orthogonal array.

Parameter	Parameter Number				ODS
	N	Gen	CR	MU
1	1	1	1	1	0.91686
2	1	2	2	2	0.91868
3	1	3	3	3	0.91914
4	2	1	2	3	0.91967
5	2	2	3	1	0.92078
6	2	3	1	2	0.92002
7	3	1	3	2	0.92054
8	3	2	1	3	0.92158
9	3	3	2	1	0.91973

.

We analyze the average ODS value for each group and plot the parameter results in a line chart, as shown in Figure 4. This chart shows the impact of different parameter combinations on the optimization results. By observing the average ODS value for each parameter (N, Gen, CR, MU), we can select the optimal parameter combination. The higher the ODS, the better the optimization results. Therefore, when selecting parameters, it is generally recommended to choose a combination with a higher ODS value, as this indicates that the algorithm performs better with that parameter combination and is more likely to achieve the optimization goal. From the trend of the line in the experimental results, we can also see that increasing the population size has a positive effect on the optimization in the specific scenario of this study. However, considering the low complexity of the task model and the small scale of the problem, in order to save computing resources and time while ensuring the optimization effect, I chose a relatively small population size parameter. This choice can not only obtain sufficient optimization results within a reasonable time range, but also effectively reduce the computing cost and avoid unnecessary computing overhead caused by an overly large population. Therefore, no experimental discussion on a larger population was conducted.

Based on the above parameter settings, the optimal recommended parameter combination is: N = 60, Gen = 100, CR = 0.9, and MU = 0.09. This combination ensures good results while optimizing the algorithm’s convergence speed. Furthermore, we found that the default parameter settings of 0.03MU and 0.9CR (the most common predefined combination) did not achieve optimal results for this experimental model. Therefore, we believe that using these default crossover and mutation rates is not optimal from the perspective of solution quality and time complexity. Reasonable parameter selection should be made based on the actual application scenario and task model.

In addition to some internal algorithm parameters, some model framework parameters also need to be set. To simulate mountainous terrain, the number of peaks is set to 10, and the coordinates of the starting point, release point, and no-fly zone are set as shown in

Table 5. Algorithm model initialization parameter setting table.

Parameter Name	Value	Parameter Name	Value
Population size	60	Start and end point	[10, 10, 20]
Number of iterations	100	Delivery point	[80, 80, 20; 80, 20, 20; 20, 80, 20]
Initial crossover rate	0.9	Center of No-fly zone	[15, 40; 55, 45]
Initial mutation rate	0.09	Number of peaks	10

.

To comprehensively evaluate the performance improvements of the proposed method, we selected three representative multi-objective optimization algorithms: standard NSGA-II, MOPSO, and MOEA/D as baselines. For fairness and consistency, all four algorithms were run under the same experimental conditions. To ensure statistical significance, each algorithm was independently run 30 times under the same environment settings.

4.2. Analysis of Experimental Results

To provide a comprehensive assessment of the performance advantages of the proposed ACM-NSGA-II algorithm for unmanned aerial vehicle path planning in complex mountainous environments, this section presents an in-depth analysis from four key perspectives: path visualization, Pareto solution distribution, hypervolume (HV) metric, and statistical significance testing. The proposed algorithm is compared with three classic multi-objective optimization algorithms: standard NSGA-II, MOPSO, and MOEA/D. To ensure the objectivity and robustness of the evaluation, each algorithm was independently executed 30 times.

4.2.1. Path Visualization

Figure 5 illustrates the global optimal paths generated by the four algorithms in a representative run. The ACM-NSGA-II route (red line) and those of NSGA-II (green), MOEA/D (yellow), and MOPSO (purple) all successfully navigate through the three designated delivery points while avoiding prohibited areas.

The no-fly zones are rendered in a nearly transparent color to facilitate visual inspection of the drone’s flight path when flying behind them, avoiding blind spots. In order to provide a more comprehensive presentation, Figure 6 shows the global optimal paths generated by the four algorithms in a typical run from a top view. In the top-down view, the no-fly zones are darker in color because, from a bird’s-eye view, the nearly transparent no-fly zones are difficult to distinguish from the surrounding terrain. Therefore, the darker color was chosen to distinguish them. However, Figure 5 and Figure 6 show the same no-fly zone.

Figure 5 and Figure 6 shows the UAV paths generated by different algorithms under the same complex terrain, obstacle, and no-fly zone configuration. Among all methods, the ACM-NSGA-II algorithm generates the most reasonable path. The path closely follows the terrain contours, maintains a safe altitude margin, and generates the smoothest and most coherent route based on flight inertia. This minimizes energy consumption and flight time while avoiding collisions with obstacles, meeting the objectives of emergency logistics. This path demonstrates good flexibility and stability when traversing narrow feasible corridors and bypassing complex obstacles. The generated trajectory is smooth and continuous, with high search accuracy and adaptability to constraints. In contrast, the path generated by the standard NSGA-II algorithm is overly conservative, maintaining a large distance from obstacles and no-fly zones. While ensuring feasibility, this increases path length and energy consumption, resulting in reduced planning efficiency. The path generated by the MOPSO algorithm also exhibits some fluctuations, with some sections slightly winding, while others are overly conservative, maintaining a large distance from obstacles and no-fly zones, resulting in reduced planning efficiency. The trajectory generated by the MOEA/D algorithm exhibits significant fluctuations, large turns, and frequent vertical deviations, resulting in an unstable path structure, which may affect the continuity and dynamic feasibility required for practical UAV flight control.

In summary, ACM-NSGA-II outperforms the other three algorithms in terms of path planning accuracy, constraint handling capabilities, and trade-offs between optimization objectives. The generated paths not only meet the feasibility requirements for UAV flight but also minimize flight time and energy consumption, demonstrating the robustness and practicality of the proposed method in complex environments.

4.2.2. Pareto Solution Distribution

To further compare the solution distribution characteristics of the proposed algorithm with those of mainstream multi-objective optimization methods, Figure 7 shows the Pareto first-level solutions obtained by ACM-NSGA-II, MOPSO, MOEA/D, and NSGA-II in a single independent run. The three optimization objectives are safety cost, flight time, and energy consumption with a penalty term.

As shown in Figure 7, the solution generated by ACM-NSGA-II lacks a safety cost advantage. This is because emergency logistics prioritizes timeliness, and drones often choose riskier routes to deliver emergency supplies more quickly. However, it does have significant advantages in terms of energy consumption and flight time. However, the energy consumption and flight time comparisons between the four algorithms in the figure are unclear. To more clearly demonstrate the differences in energy consumption and flight time between ACM-NSGA-II and the standard NSGA-II, MOPSO, and MOEA/D algorithms, Figure 8 plots the two-dimensional optimization objective diagram.

In Figure 8, flight time is used directly as the vertical axis because the magnitude differences between the algorithms are relatively small. The differences in flight time can be clearly observed in the figure. According to statistical data, ACM-NSGA-II reduces flight time by 18.24% compared to MOEAD, and ACM-NSGA-II reduces flight time by 20.61% compared to MOPSO.ACM-NSGA-II reduces flight time by 24.26% compared to NSGA-II.

However, due to the significant differences in energy consumption between the algorithms, the horizontal axis data has been logarithmically transformed. Scaling large values can reduce significant differences between data points, thereby enhancing the visualization of algorithm characteristics. While the energy consumption penalty factor is included, the numerical range is relatively wide. However, it is clear that the ACM-NSGA-II algorithm reduces energy consumption by at least one to two orders of magnitude compared to the other algorithms.

As shown in Figure 8, the ACM-NSGA-II algorithm significantly outperforms the other three algorithms in terms of energy consumption and flight time, demonstrating its excellent global search capability within the effective solution domain and highlighting its strong potential in emergency logistics scenarios.

4.2.3. Hypervolume Metric

To comprehensively evaluate the performance of various algorithms for multi-objective optimization in path planning problems, this study used the hypervolume (HV) metric as the primary evaluation criterion. Hypervolume not only measures the convergence of a solution set but also reflects its diversity, and is therefore widely considered one of the most representative performance metrics in multi-objective optimization.

Figure 9 shows the normalized hypervolume evolution curves of each algorithm in a single representative run. The ACM-NSGA-II curve (red) generally outperforms NSGA-II (green), MOEA/D (blue), and MOPSO (magenta). Overall, the SCM-NSGA-II algorithm exhibits excellent convergence from the very beginning and quickly stabilizes within approximately 20 iterations. Around iteration 30, the convergence results shift slightly upward, ultimately stabilizing the hypervolume value at around 0.67. This result significantly outperforms the other three algorithms, demonstrating its superior performance in terms of solution accuracy and breadth of distribution. In contrast, the standard NSGA-II algorithm showed a convergence trend initially, but gradually plateaued with increasing iterations, with the optimal hypervolume value stabilizing at around 0.43. This reflects its susceptibility to local optima and limited optimization capabilities. The MOPSO algorithm also exhibited rapid convergence early on, but plateaued after approximately 20 generations, ultimately stabilizing its hypervolume value at around 0.44. The MOEA/D algorithm also exhibited early convergence, reaching a plateau at approximately 20 generations and rising slightly at approximately 30 generations.

To minimize the impact of random errors on the experimental data, each algorithm was independently run 30 times with the same parameter settings, and the normalized hypervolume values were recorded. The statistical results are shown in

Table 6. Comparison of average hypervolume and standard deviation for each algorithm.

Algorithm	Average Hypervolume Value	Standard Deviation
ACM-NSGA-II	0.6797	0.0133
NSGA-II	0.4431	0.0288
MOPSO	0.4573	0.0154
MOEA/D	0.4245	0.0243

. As can be seen from the table, the proposed ACM-NSGA-II outperforms all other compared algorithms in terms of average hypervolume value. Specifically, its average hypervolume reached 0.6797, an improvement of 53.39% over NSGA-II, 48.61% over MOPSO, and 60.11% over MOEA/D. Therefore, ACM-NSGA-II demonstrates significant advantages in both solution quality and stability. Furthermore, its standard deviation is the smallest compared to the other algorithms, indicating less performance volatility and strong robustness across multiple runs.

Comparing experimental results, we found that the proposed algorithm significantly outperformed other algorithms in terms of the hypervolume metric. This demonstrates that the solution set generated by our algorithm not only exhibits outstanding convergence in multi-objective optimization but also exhibits significant advantages in solution diversity. The higher hypervolume value reflects our algorithm’s ability to more comprehensively explore the objective space and find more optimal solutions, demonstrating its superior performance in path planning problems.

4.2.4. Statistical Significance Testing

A statistical significance test is a statistical method used to assess whether sample data supports a hypothesis. This test can determine whether an observed effect or difference in the sample data is likely due to chance, or whether there is sufficient evidence to support the existence of the effect or difference. To further evaluate the statistical significance of the performance advantage of the proposed ACM-NSGA-II algorithm, this study conducted two-sample t-tests and Mann–Whitney U tests on the normalized hypervolume values obtained from 30 independent runs at a 5% significance level. Furthermore, this study used boxplots to visualize the distribution of algorithm performance, as shown in Figure 10. The blue box used in the figure represents the outer frame of the box plot, and the red line represents the median of the data. The shape of the blue box shows the interquartile range of the data, and the black horizontal line represents the extreme values of the data.

As can be seen from Figure 10, the median of the MOEA/D algorithm is relatively low, approximately 0.45, and there are obvious outliers. The slightly larger interval width indicates that the performance of this algorithm fluctuated to some extent across the 30 experiments. MOPSO also has a lower median, but compared to MOEA/D, its results are more consistent, with a narrower box and less fluctuation, meaning its performance is more stable. NSGA-II has a higher median than both MOEAD and MOPSO, indicating better overall performance. However, the wider box width indicates that the performance of this algorithm fluctuates significantly. ACM-NSGA-II has the highest median, close to 0.68, and performs significantly better than the other three algorithms. Its narrow interval indicates stable results, excellent performance, and the best overall performance. The distribution of hypervolume values is the smallest, making it the most effective of the four algorithms.

In this study, we used a nonparametric statistical test, the Wilcoxon signed-rank test, to compare the performance of the proposed algorithm with the baseline algorithm. Compared to parametric tests (such as the t-test), this method does not require the performance difference data to follow a normal distribution, making it more robust and applicable. The null hypothesis (H₀) is that the median performance difference between the two algorithms is zero. By calculating the performance difference for all paired samples and performing a rank test based on their absolute values, we can determine whether the observed performance advantage is significantly greater than that explained by random chance.

Statistical analysis results show that the p-values obtained from the Wilcoxon signed-rank test for the proposed algorithm ACM-NSGA-II and the other standard algorithms MOEAD, MOPSO, and NSGA-II in the mountain model are all less than 0.05 (p < 0.05 is generally considered the standard for rejecting the null hypothesis and indicating statistical significance). This result strongly confirms that the proposed algorithm achieves statistically significant performance improvement over the baseline algorithm. To more intuitively present the pairwise comparison results for all algorithms, a table of exact p-values is provided in

Table 7. p-value analysis of significant differences between different algorithms.

Algorithm Pair	p-Value
ACM-NSGA-II vs. MOEAD	3.0142 × 10−11
ACM-NSGA-II vs. MOPSO	3.0085 × 10−11
ACM-NSGA-II vs. NSGA-II	3.0104 × 10−11

. The table clearly shows the significant differences between the improved algorithm and the other algorithms.

The table shows the comparison results between ACM-NSGA-II and three algorithms (MOEAD, MOPSO, and NSGA-II). The p-values for all algorithm comparisons are well below 0.05. Specifically, the p-values for ACM-NSGA-II versus MOEAD, MOPSO, and NSGA-II are 3.0142 × 10⁻¹¹, 3.0085 × 10⁻¹¹, and 3.0104 × 10⁻¹¹, respectively. This indicates that the differences between ACM-NSGA-II and the other algorithms are highly statistically significant, far exceeding the typical significance level (p < 0.05), further demonstrating the superiority of ACM-NSGA-II in optimization performance.

Overall, both the box plot visualization and statistical test results indicate that the proposed improved algorithm not only provides higher solution quality for multi-objective Unmanned Aerial Vehicle path planning but also exhibits superior stability and optimization capabilities compared with the classical method.

5. Conclusions

In summary, the ACM-NSGA-II algorithm has made significant progress in multi-objective optimization for last-mile drone delivery in mountainous areas. By integrating innovative features such as an adaptive crossover and mutation strategy, dynamic path repair, and dynamic injection, this approach achieves superior performance in minimizing flight time and energy consumption. Specifically, compared to the traditional NSGA-II, ACM-NSGA-II improves the average overcapacity index by 53.39% and reduces the average flight time by 24.26%. The algorithm’s superior global search capabilities and ability to efficiently overcome complex environmental constraints demonstrate its potential for practical application in emergency logistics. We also found that the preset parameter settings of 0.03MU and 0.9CR (the most common predefined combination) did not achieve optimal results for this experimental model. Therefore, we believe that using this preset crossover and mutation rate is suboptimal from the perspective of solution quality and time complexity.

Future work will focus on applying this algorithm to real-world scenarios, including integrating it with drone swarms for collaborative delivery and exploring synergies with 6G networks to enhance long-distance logistics capabilities. These advances aim to further enhance the system’s robustness, scalability, and real-time adaptability in dynamic, heterogeneous environments. Additionally, we plan to include a comparative analysis of different crossover operator combinations (such as PMX + PBX + OX2 + OX1) within the UAV path planning framework. These advances aim to further enhance the system’s robustness, scalability, and real-time adaptability in complex, heterogeneous environments.