Development of an Efficient CUSUM Control Chart for Monitoring the Scale Parameter of the Inverse Maxwell Distribution in Asymmetric, Non-Normal Process Monitoring with Industrial Applications

Abstract

Control charts are commonly practical as diagnostic tools in statistical applications to recognize probable changes in a process. Control charts find general use as diagnostic tools in statistics in the detection of probable shifts in a process. Among the variety of methods of detection of smaller shifts in processes, the cumulative sum (CUSUM) chart is the most useful in general use. The standard CUSUM chart is often based on the normal distribution, an assumption that does not often align with the quality characters of the majority of real processes. However, many real-world processes exhibit asymmetric and heavy-tailed behavior, which limits the performance of traditional symmetric control chart models. This study presents a new CUSUM control chart based on the inverse Maxwell (IM) distribution and terms it the IMCUSUM chart. The proposed chart’s performance is assessed based on run-length (RL) metrics, which comprise the RL average, the standard deviation of RL, and the median RL. Comparison with the existing IM exponentially weighted moving average (IMEWMA) chart is performed. The results reveal that the proposed IMCUSUM chart performs better compared with the existing IMEWMA chart, especially in the detection of small and moderate shifts in processes. The practical application of the proposed IMCUSUM chart is demonstrated with the application of the proposed and existing control charts in the survival analysis of the lifetimes of brake pads of cars. This real application example highlights the practical application of the proposed IMCUSUM chart in real processes.

1. Introduction

Statistical process control (SPC) encompasses the use of statistical methods to perform process monitoring and Statistical control. SPC commences at the planning of a product or a service, wherein the definition and critical attributes are decided. The use of control charts, initially developed by Shewhart in 1931 [1], remains an integral part of SPC. However, the effectiveness of these charts largely depends on the underlying assumptions about the process data. In practice, these assumptions are often violated. For example, many industrial processes produce data that deviate from normality, exhibit skewness, or contain outliers. Such deviations from normality lead to asymmetric data patterns, where traditional symmetric control chart models fail to adequately represent process behavior. In such cases, traditional control charts designed for normally distributed data can fail to detect shifts effectively. Robustness of the system improves if the design of the control charts becomes independent of strict assumptions. The application of the use of control charts also varies with the nature of the variation and the scale of the variation that has to be detected and the characteristics of the process. Broadly, control charts can be categorized into two types: memoryless charts, such as Shewhart charts, and memory-type charts, such as the cumulative sum (CUSUM) chart by Page [2] and the exponentially weighted moving average (EWMA) chart by Roberts [3]. Memoryless charts are simple but struggle to detect small or moderate process shifts. In contrast, memory-type charts accumulate past information, making them more sensitive to gradual or subtle changes in process parameters. Reynolds and Stoumbos [4] described that CUSUM control charts can robustly monitor the mean and dispersion of a process when the assumption of normality is not fulfilled. Gan [5] applied an EWMA control chart to monitor both binomial and Poisson processes. Abbasi et al. [6] examined EWMA control charts for both normal and non-normal distributions like the logistic and Student’s t distributions. This makes CUSUM and EWMA charts particularly effective for handling challenges like non-normality and outliers. This accumulation of information provides a way to detect departures from symmetry in the process behavior more effectively.

Phase I focuses on retrospective analysis, where the aim is to estimate process parameters and establish the in-control state of the process (Borror [7]). Since parameter estimation introduces uncertainty, it can significantly influence Phase II performance metrics such as the average run length (ARL). Prior studies (Jones-Farmer et al. and Zwetsloot et al. [8,9]) emphasize that inaccurate parameter estimation in Phase I often leads to inflated false alarm rates or delayed detection in Phase II. While the present work assumes parameters are known or accurately estimated, we acknowledge that estimation effects can impact run length performance, and addressing this issue remains an important direction for future research.

Early work on CUSUM charts assumed normally distributed data. For example, Acosta-Mejia et al. [10] compared dispersion charts under normality and showed that CUSUM performed best in terms of average run length (ARL). Sanusi et al. [11] developed CUSUM-based methods for early detection of dispersion changes, and Tran et al. [12] studied the impact of parameter estimation, noting that even small errors could substantially affect ARL. These studies reinforce the strength of CUSUM charts but also highlight the limitations of normality-based assumptions. This has motivated the development of control charts for non-normal distributions. For example, Huang et al. [13] considered the gamma distribution, Celano et al. [14] applied CUSUM to the t-distribution, and Ryu et al. [15] studied heavy-tailed double exponential distributions. Hossain et al. [16] extended CUSUM methodology to the Maxwell distribution. These works demonstrate the importance of tailoring CUSUM control chart-based techniques to the underlying distribution of process data.

In many applications of engineering, agriculture, and industrial sectors, process data often deviate from normality (Sato & Inoue [17]). In such cases, alternative families of distributions, including inverse counterparts of well-known models, become useful tools for capturing actual data behavior more accurately. These inverse families are particularly important because they account for asymmetry and heavy-tailedness in practical processes, capturing deviations that symmetric models fail to describe.

The Maxwell distribution, originally derived from statistical mechanics, has found applications in lifetime modeling, reliability studies, chemistry, and physics (Krishna & Malik [18]; Tomer & Panwar [19]; Brilliantov & Poschel [20]; Kazmi et al. [21]). Its family has been extended to discrete and mixture forms (Kazmi et al. [22]; Hossain et al. [16]). To address its limitations in modeling heavy-tailed behavior, Singh and Srivastava [23] introduced the Inverse Maxwell (IM) distribution. This positively skewed distribution exhibits heavier tails than the Maxwell distribution, representing an asymmetric structure that better captures the variability and irregularity present in practical processes. It is well suited to lifetime and reliability data where extreme values are important (Karlis & Santourian [24]. Singh and Srivastava [25,26]) studied its statistical properties such as survival functions, moments, and parameter estimation, while Loganathan et al. [27] considered Bayesian estimation under different loss functions.

The IM distribution has since been applied in SPC, though only in a limited number of studies. Arafat et al. [28] proposed an IMEWMA control chart, showing its effectiveness in detecting small to moderate shifts in the scale parameter, with applications to brake pad lifetimes and breast cancer survival data. Omar et al. [29] developed a Shewhart-type chart (VIM) for IM data, deriving control limits and demonstrating its superiority over Weibull and Gamma charts when the true process followed IM; they also illustrated its performance with car brake pad lifetimes. More recently, Maqsood et al. [30] proposed an extended IMEWMA chart (IMEEWMA) that improved sensitivity to small shifts, validated through simulations and applications to reliability data such as the lifetimes of brake pads. Recent works, such as Rao et al. [31] and Ayman-Mursaleen et al. [32], emphasize advanced mathematical tools for process modeling, inspiring the development of control charts for specialized distributions like IM. These studies collectively underline the necessity of exploring alternative asymmetrical probabilistic models through heavy-tailed distributions to improve detection precision and robustness.

These studies confirm the relevance of the IM distribution in quality control, especially for heavy-tailed asymmetric processes. Its advantages include the following:

(i)

Better capturing of long tails and extreme values;

(ii)

Improved fit for lifetime and reliability data;

(iii)

More appropriate control limits for skewed processes;

(iv)

Higher sensitivity to sudden shifts and outliers.

Despite these advantages, the IM distribution remains underexplored in the field of SPC. The only available contributions on IM distribution-based control charts so far are a few types, namely the VIM, IMEWMA, and IMEEWMA charts, which have shown good performance in detecting small to moderate shifts. However, CUSUM schemes are widely recognized as powerful alternatives, often offering greater sensitivity to small-moderate shifts, particularly when calibrated for specific distributions. The existing work lacks the availability or development of a CUSUM control chart for the IM distribution, particularly for monitoring its scale parameter. This gap is significant because extending methodology from the Maxwell to the IM distribution is not straightforward; the heavier tails and distinct asymmetrical nature of the IM distribution require new calibrations and performance assessments. Thus, this study develops a novel IMCUSUM chart to address asymmetry in process behavior and improve monitoring performance in non-normal environments. The proposed chart provides a complementary alternative to IMEWMA, offering a robust and sensitive tool for monitoring asymmetric, heavy-tailed processes, thereby extending the scope of memory-type control charts in non-normal settings.

Section 2 reviews the IM distribution and the existing IMEWMA control chart. In Section 3, the formation of the proposed IMCUSUM chart is described. Section 4 discusses performance measures, while Section 5 presents a simulation-based comparison between the IMCUSUM and IMEWMA charts. In Section 6 a real-world illustrative example is presented to demonstrate the chart’s practical applications. Finally, Section 7 presents a comprehensive discussion of the findings.

2. Materials and Procedures

To estimate the parameters and performance of the proposed control chart, we introduce the methodology and its development in the following sections. Section 2.1 introduces the heavy-tailed IM distribution and its key properties. In Section 2.2, we revisit the EWMA control chart tailored for the IM distribution to facilitate comparison.

2.1. IM Distribution and Its Parameters

A continuous random variable X is said to follow the Maxwell distribution with a single scale parameter σ if its probability density function (PDF) is expressed as

$$\mathrm{f}\left(\mathrm{x},\sigma \right)=\sqrt{{\displaystyle \frac{2}{\pi }}}{\sigma }^{-3}{\mathrm{x}}^2{\mathrm{e}}^{\left({\displaystyle \frac{{-\mathrm{x}}^2}{2{\sigma }^2}}\right)};\mathrm{x}>0.$$

Defining $\mathrm{Y}={\mathrm{X}}^{-1}$ as the inverse Maxwell random variable, the PDF of the IM distribution with scale parameter σ is expressed as

$$\mathrm{f}\left(\mathrm{y},\sigma \right)=\sqrt{{\displaystyle \frac{2}{\pi }}}{\sigma }^{-3}{\mathrm{y}}^{-4}{\mathrm{e}}^{\left({\displaystyle \frac{-1}{2{\mathrm{y}}^2{\sigma }^2}}\right)}, \mathrm{for} \mathrm{y}>0.$$

The maximum likelihood estimator (MLE) of σ is computed by

$$\widehat{\sigma }=\sqrt{3{\mathrm{n}}^{-1}{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\displaystyle \frac{1}{{\mathrm{y}}_{\mathrm{i}}^2}}}.$$

2.2. IMEWMA Control Chart

Roberts [3] first proposed the EWMA control chart, which assumes normality. However, Arafat et al. [28] adapted the EWMA method for non-normal distributions, specifically for the IM distribution, leading to the development of the IMEWMA chart. The plotting statistic for the IMEWMA chart is expressed as

$${\mathrm{Z}}_{\mathrm{i}}=\lambda {\mathrm{V}}_{\mathrm{I}\mathrm{M}\mathrm{i}}+(1-\lambda ){\mathrm{Z}}_{\mathrm{i}-1},$$

where ${\mathrm{V}}_{\mathrm{I}\mathrm{M}\mathrm{i}}$ is based on the current value for *(i = 1, 2, 3, …), ${\mathrm{Z}}_{\mathrm{i}-1}$ shows the previous result of the statistic, and $\lambda$ [0, 1] is a smoothing constant. The starting value ${\mathrm{Z}}_0$ is set equal to ${\sigma }_0^2$. The Phase I sample is used to estimate the scale parameter if it is unknown.

For the IMEWMA statistics the mean and variance obtained are given below,

$$\mathrm{E}\left({\mathrm{Z}}_{\mathrm{i}}\right)={\sigma }^2\mathrm{and} * \mathrm{V}\mathrm{a}\mathrm{r}\left({\mathrm{Z}}_{\mathrm{i}}\right)={\displaystyle \frac{2{\sigma }^4}{3\mathrm{n}}}\{{\displaystyle \frac{\lambda }{2-\lambda }}(1-{(1-\lambda )}^{2\mathrm{i}})\}.$$

Here, ${\sigma }^2$ is the square of the parameter of IM distribution. The lower and upper control limits of the statistic of the control chart of IMEWMA are defined as follows:

$$\mathrm{L}\mathrm{C}\mathrm{L}={\sigma }^2[1-\mathrm{L}\sqrt{{\displaystyle \frac{2}{3\mathrm{n}}}\times {\displaystyle \frac{\lambda }{2-\lambda }}(1-{(1-\lambda )}^{2\mathrm{i}})}], \mathrm{C}\mathrm{L}={\sigma }^2$$

and

$$\mathrm{U}\mathrm{C}\mathrm{L}={\sigma }^2[1+\mathrm{L}\sqrt{{\displaystyle \frac{2}{3\mathrm{n}}}\times {\displaystyle \frac{\lambda }{2-\lambda }}(1-{(1-\lambda )}^{2\mathrm{i}})}].$$

Two scenarios may arise for monitoring the scale parameter of the IM distribution:

(i)

${\sigma }^2$ is known;

(ii)

${\sigma }^2$ is not known.

For the situation where ${\sigma }^2$ is unknown, the corresponding control limits are provided below.

$$\mathrm{L}\mathrm{C}\mathrm{L}=\overline{{\mathrm{V}}_{\mathrm{I}\mathrm{M}}}[1-\mathrm{L}\sqrt{{\displaystyle \frac{2}{3\mathrm{n}}}\times {\displaystyle \frac{\lambda }{2-\lambda }}(1-{(1-\lambda )}^{2\mathrm{i}})}], \mathrm{C}\mathrm{L}=\overline{{\mathrm{V}}_{\mathrm{I}\mathrm{M}}}$$

and

$$\mathrm{U}\mathrm{C}\mathrm{L}=\overline{{\mathrm{V}}_{\mathrm{I}\mathrm{M}}}[1+\mathrm{L}\sqrt{{\displaystyle \frac{2}{3\mathrm{n}}}\times {\displaystyle \frac{\lambda }{2-\lambda }}(1-{(1-\lambda )}^{2\mathrm{i}})}].$$

The process is considered to be out of control if any data point falls above the upper control limit (UCL) or falls below the lower control limit (LCL). If all data points stay within these limits, the system is deemed in control.

3. Formation of the Postulated CUSUM Control Chart for IM Distribution

The CUSUM chart is a memory-type control chart widely used to detect small to medium shifts in process monitoring. In this study, we introduce a CUSUM chart for the non-normal IM distribution, referred to as the IMCUSUM chart. The necessary calculations for designing the IMCUSUM chart are outlined below. Consider $\mathrm{p}={\displaystyle \frac{1}{2{\mathrm{y}}^2{\sigma }^2}}$ from the PDF of the IM distribution.

After simplification, we obtain $\mathrm{y}=\sqrt{{\displaystyle \frac{1}{2\mathrm{p}{\sigma }^2}}}$. Using the Jacobian transformation the PDF of p is derived as

$$\mathrm{j}=\left|{\displaystyle \frac{\mathrm{d}\mathrm{y}}{\mathrm{d}\mathrm{p}}}\right|={\displaystyle \frac{1}{2\sqrt{2}\sigma {\mathrm{p}}^{3/2}}.}$$

The PDF of IM distribution becomes

$$\mathrm{f}(\mathrm{p},\sigma )={\displaystyle \frac{\sqrt{2}}{\sqrt{\pi }}}{\displaystyle \frac{1}{{\sigma }^3}}{\left(\sqrt{{\displaystyle \frac{1}{2\mathrm{p}{\sigma }^2}}}\right)}^4{\mathrm{e}}^{-\mathrm{p}}{\displaystyle \frac{1}{2\sqrt{2}\sigma {\mathrm{p}}^{3/2}}.}$$

After simplification, it is

$$\mathrm{f}\left(\mathrm{p},\sigma \right)={\displaystyle \frac{2}{\sqrt{\pi }}}{\mathrm{p}}^{1/2}{\mathrm{e}}^{-\mathrm{p}},$$

which can also be written as

$$\mathrm{f}\left(\mathrm{p},\sigma \right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\frac{3}{2}\right)}}{\mathrm{p}}^{{\displaystyle \frac{3}{2}}-1}{\mathrm{e}}^{-\mathrm{p}}.$$

This represents a gamma distribution with location parameter ${\displaystyle \frac{3}{2}}$ and scale parameter 1, denoted as ${\left(2{\mathrm{y}}^2{\sigma }^2\right)}^{-1}$∼Gamma (${\displaystyle \frac{3}{2}}$, 1). By utilizing the additive property of the gamma distribution, the total of independent and identically distributed IM variates are given by ${\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{p}}_{\mathrm{i}}$~gamma (${\displaystyle \frac{3\mathrm{n}}{2}}$, 1). Let ${\mathrm{V}}_{\mathrm{I}\mathrm{M}}=3{\mathrm{n}}^{-1}{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\displaystyle \frac{1}{{\mathrm{y}}_{\mathrm{i}}^2}}$, which equals the square of the MLE of σ. The pivotal quantity $\mathrm{Q}$ = ${\displaystyle \frac{3\mathrm{n}{\mathrm{V}}_{\mathrm{I}\mathrm{M}}}{2{\sigma }^2}}$ assumes a gamma distribution with the same mean and variance ${\displaystyle \frac{3\mathrm{n}}{2}}$. Thus, ${\mathrm{V}}_{\mathrm{I}\mathrm{M}}$ has the mean and variance given below,

$$\mathrm{E}\left({\mathrm{V}}_{\mathrm{I}\mathrm{M}}\right)={\sigma }^2,$$

and

$$\mathrm{V}\mathrm{a}\mathrm{r}\left({\mathrm{V}}_{\mathrm{I}\mathrm{M}}\right)={\displaystyle \frac{2{\sigma }^4}{3\mathrm{n}}}.$$

The CUSUM plotting statistic for the IM distribution when ${\sigma }^2$ is known is written as

$${\mathrm{C}}_{\mathrm{i}}^{+}=\mathrm{m}\mathrm{a}\mathrm{x}(0,{\mathrm{V}}_{\mathrm{I}\mathrm{M}\mathrm{i}}-\mathrm{K}+{\mathrm{C}}_{\mathrm{i}-1}^{+}-1)$$

and

$${\mathrm{C}}_{\mathrm{i}}^{-}=\mathrm{m}\mathrm{a}\mathrm{x}(0,{\mathrm{V}}_{\mathrm{I}\mathrm{M}\mathrm{i}}-\mathrm{K}+{\mathrm{C}}_{\mathrm{i}-1}^{-}-1),$$

where ${\mathrm{C}}_{\mathrm{i}}^{+}$ and ${\mathrm{C}}_{\mathrm{i}}^{-}$ represent the upper and lower CUSUM statistics, with ${\mathrm{C}}_0^{+}$ = ${\mathrm{C}}_0^{-}$ = 0, and K denotes the reference value and is determined as $\mathrm{K}=\mathrm{k}{\displaystyle \frac{{\sigma }^2\sqrt{2}}{\sqrt{3\mathrm{n}}}}$ and $\mathrm{k} = {\displaystyle \frac{\mathsf{\delta }}{2}}$, where δ denotes the shift expressed relative to the process standard deviation (σ). In this study, we used σ = 1 (i.e., δ is measured in units of one standard deviation), therefore k = 0.5 and n is the sample size. For the postulated statistic, ${\mathrm{V}}_{\mathrm{I}\mathrm{M}\mathrm{i}}$ is the current observations for (i = 1, 2, 3, …) and ${\mathrm{C}}_{\mathrm{i}-1}^{+}$, ${\mathrm{C}}_{\mathrm{i}-1}^{-}$ denote the previous values of the statistic. The values of ${\mathrm{C}}_{\mathrm{i}}^{+}$ and ${\mathrm{C}}_{\mathrm{i}}^{-}$ are computed for every sample, and then these values are visualized against the control limit H $=\mathrm{h}{\displaystyle \frac{{\sigma }^2\sqrt{2}}{\sqrt{3\mathrm{n}}}}$. The value of h is selected to obtain the expected average run length.

When ${\sigma }^2$ is unknown, ${\mathrm{V}}_{\mathrm{I}\mathrm{M}}$ is estimated and the CUSUM statistics are adjusted as follows,

$${\mathrm{C}}_{\mathrm{i}}^{+}=\mathrm{m}\mathrm{a}\mathrm{x}(0,{\overline{\mathrm{V}}}_{\mathrm{I}\mathrm{M}\mathrm{i}}-\mathrm{K}+{\mathrm{C}}_{\mathrm{i}-1}^{+}-1)$$

and

$${\mathrm{C}}_{\mathrm{i}}^{-}=\mathrm{m}\mathrm{a}\mathrm{x}(0,{\overline{\mathrm{V}}}_{\mathrm{I}\mathrm{M}\mathrm{i}}-\mathrm{K}+{\mathrm{C}}_{\mathrm{i}-1}^{-}-1).$$

The hypothesis for testing the performance of the scale parameter in the IM distribution is given below:

$${\mathrm{H}}_0={\sigma }^2={\sigma }_0^2, \mathrm{with} \mathsf{\delta }= 1, \mathrm{versus} {\mathrm{H}}_1={\sigma }^2={\sigma }_1^2=\mathsf{\delta }{\sigma }_0^2, \mathrm{with} \mathsf{\delta } > 1.$$

Here, $\mathsf{\delta }\ne$1 identifies that the process has shifted.

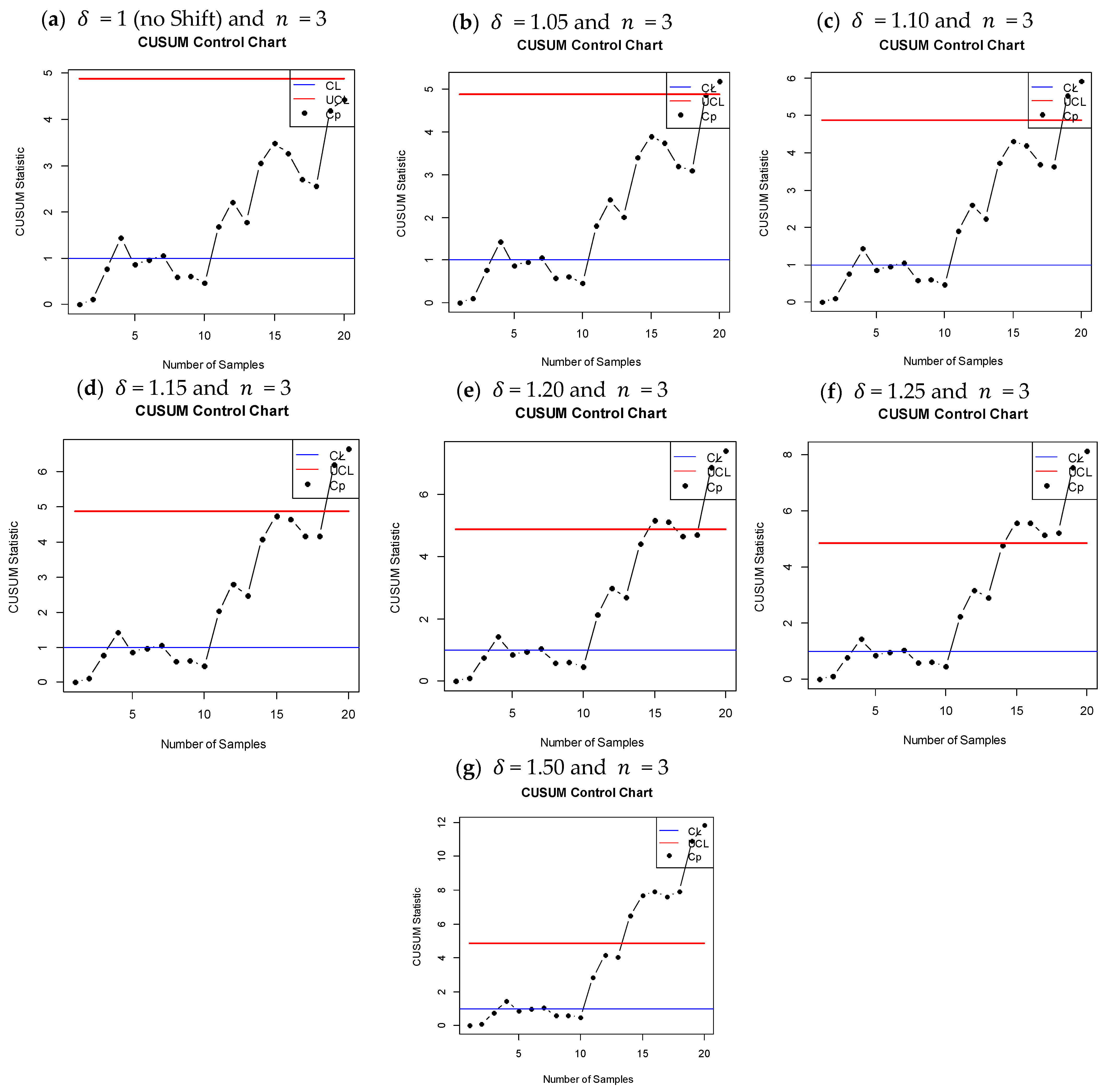
4. Assessment of the IMCUSUM Control Chart’s Performance

The effectiveness of a control chart is conventionally assessed using metrics such as the average run length (ARL), standard deviation of run length (SDRL), and median run length (MRL). These measures are widely recognized as benchmarks for evaluating the performance of several control charts in terms of detection ability. The run length (RL) refers to the count of sample points observed before detecting the first out-of-control (OOC) signal. ARL captures the mean of the RL, and the SDRL captures the variability of the RL. A larger in-control (IC) ARL (ARL₀) relative to ARL₁ (OOC ARL) indicates effective performance, with smaller ARL₁ values reflecting faster detection of shifts (Xie et al. [33].

Several methods are available for evaluating control chart performance, including the integral equation method, Markov chain method (Lucas & Saccucci [34]), and Monte Carlo simulation (Domangue & Patch [35]). In this study, ARL, SDRL, MRL, and quantiles are computed using Monte Carlo simulation (10,000 replications) in R version 4.4.1. The control chart coefficients for both the IMCUSUM and IMEWMA charts are calibrated such that ARL₀ ≈ 370 is approximated, ensuring a fair baseline for comparison.

Table 1. Performance of the IMCUSUM chart across various subgroup sizes using ARL₀ = 370.

$\delta$	$\mathit{n}$$= 1 \mathbf{and} \mathit{h}$ = 13.21			$\mathit{n}$$= 3 \mathbf{and} \mathit{h}$ = 30.991			$\mathit{n}$$= 6 \mathbf{and} \mathit{h}$ = 52.86			$\mathit{n}$$= 9 \mathbf{and} \mathit{h}$ = 71.35
	ARL	SDRL	MRL	ARL	SDRL	MRL	ARL	SDRL	MRL	ARL	SDRL	MRL
1	370.9	362.3	255	369.8	345	264	370.1	332.4	266	370.5	329.5	269
1.01	330	320	232	333	308.3	240	328.6	293.4	242	311.8	276.3	266
1.02	301.3	286.3	214	297	273.6	214	271.8	237	201	242.6	199.9	183
1.03	273.9	265.8	191	252.4	230.7	183	210.3	180.6	155	179.5	142.6	137
1.04	242.5	235	170	215.7	193.5	156	167	135.7	127	135.2	101.2	106
1.05	221.4	214	155	181.5	164.3	133	132.6	103.5	102	106.3	74.41	86
1.10	140.6	133.2	99	87.55	69.53	67	58.46	35.46	50	47.35	24.4	42
1.15	95.35	86.69	69	51.94	36.27	43	36.46	18.54	33	30.32	12.82	28
1.16	90.3	82.97	65	47.71	31.77	39	33.58	16.51	30	28.34	11.79	26
1.17	83.12	74.92	60	44.28	29.16	37	31.49	15.38	28	26.45	10.45	25
1.18	78.17	70.6	58	41.14	26.82	34	29.28	13.83	27	24.79	9.81	23
1.19	72.79	64.96	53	38.65	24.49	33	27.64	12.73	25	23.47	9.11	22

and

Table 2. Performance of the IMEWMA chart across various subgroup sizes using ARL₀ = 370.

$\delta$	$\mathit{n}$ = 1, λ = 0.5 and L = 4.110			$\mathit{n}$ = 3, λ = 0.5 and L = 3.558			$\mathit{n}$ = 6, λ = 0.5 and L = 3.321			$\mathit{n}$ = 9, λ = 0.5 and L = 3.214
	ARL	SDRL	MRL	ARL	SDRL	MRL	ARL	SDRL	MRL	ARL	SDRL	MRL
1	371	371	261	366.46	356	252	369.2	364	257	371	369.9	259.5
1.01	343	347	240	338.28	337	235	333.2	332	233	316	311.3	217
1.02	321	315	227	301.1	303	205	275.1	268	194	256	251.8	179
1.03	296	298	203.5	265.55	265	187	232.8	230	162	214	207.7	151
1.04	272	267	193	234.08	234	163	201.9	199	140	174	174.7	120
1.05	255	252	176	212.14	215	147	172.1	172	119	155	153	107
1.10	184	182	128.5	210.09	213	146	90.32	87.8	62	72.6	69.5	52
1.15	136	136	94	214.91	213	105	51.77	50.3	37	38	36.36	27
1.16	125	128	85	77.56	76.5	53	45.59	43.8	32	34.2	33.37	24
1.17	121	119	85	69.14	69	48	42.21	40.3	30	31	29.6	22
1.18	113	112	78	64.89	62.4	46	37.65	36.4	27	27.2	25.08	19
1.19	105	106	71	60.51	59.9	42	35.03	33.9	24	24.8	23.28	18

present the performance metrics of the postulated IMCUSUM chart and the present IMEWMA chart, respectively, across various subgroup sizes and shift magnitudes. Shifts ranging from 1.01 to 1.50 times the scale parameter are selected to represent very small to moderate process changes, which are the most challenging for control charts to detect. Such fine-grained shifts are commonly considered in SPC simulation studies (see Lucas [36]; Abbasi et al. [6]) because they allow for careful evaluation of chart sensitivity. The results were evaluated using ARL, SDRL, and MRL. The following key observations were made:

• For both the IMCUSUM and IMEWMA charts, the ARL₀ values are approximately 370 across all subgroup sizes ($n$ = 1, 3, 6, 9). This indicates that, under IC conditions, both charts produce an out-of-control signal, on average, at every 370th plotted point, which aligns with the nominal ARL₀ target.
• As the size of the shift increases, the ARL values for both charts decrease significantly. This demonstrates that both charts are effective in recognizing process shifts, with the IMCUSUM chart generally showing lower ARL values compared to the IMEWMA chart for the same shift magnitudes. For example:

  i

  For $\mathsf{\delta }$ = 1.10, the IMCUSUM chart achieves ARL values ranging from 47.35 to 140.6, while the IMEWMA chart achieves ARL values ranging from 72.6 to 184.

  ii

  For smaller shifts (e.g., 1.01 to 1.05), the IMCUSUM chart consistently outperforms the IMEWMA chart, even for larger subgroup sizes ($n$ = 6, 9).

• The IMCUSUM chart demonstrates greater sensitivity to small and moderate shifts compared to the IMEWMA chart. For instance:

  i

  At $\mathsf{\delta }$ = 1.02, the IMCUSUM chart achieves ARL values of 242.6 to 301.3, while the IMEWMA chart achieves ARL values of 256 to 321.

  ii

  This trend is consistent across all subgroup sizes, indicating that the IMCUSUM chart is better suited for detecting smaller shifts in the process.

• One of the primary goals of this study is to demonstrate that the IMCUSUM chart excels with small practical and meaningful subgroup sizes typical of real-world manufacturing and testing environments. The results fully bear witness in support of this intention:

  i

  When $n$ = 1, the ARL of the IMCUSUM chart is 140.6 with $\mathsf{\delta }$ = 1.10 against 184 with the IMEWMA chart. This indicates that the IMCUSUM chart will detect shifts 31% faster relative to the IMEWMA chart with small subgroup sizes.

  ii

  With the smaller i.e., $\mathsf{\delta }$ = 1.02, the IMCUSUM has an ARL of 301.3 with n = 1 and the IMEWMA has an ARL of 321. This further highlights the better small-shift detection of the IMCUSUM with minimal data.

• SDRL reduces with an increase in the shift magnitude in the two plots. The SDRL of the IMCUSUM plot tends to be lower compared to the SDRL of the IMEWMA plot and signifies a more stable detection of shifts. For instance:

  i

  When the $\mathsf{\delta }$ = 1.10 has been applied, the SDRL of the IMCUSUM will be between 24.4 and 133.2 and that of the IMEWMA will be between 69.5 and 182.

• MRL also diminishes with a larger shift size, and the smaller MRL of the IMCUSUM relative to the IMEWMA further confirms the better detection of shifts by the IMCUSUM chart. For example:

  i

  With a $\mathsf{\delta }$ = 1.10, the IMCUSUM plot reaches the values of the MRL between 42 and 99 and the IMEWMA plot reaches the values of the MRL between 52 and 128.5.

• Increasing the two-chart subgroup size ($n$) increases the detection power with smaller values of the ARL, SDRL, and the MRL with a larger $n$. The behavior of the IMCUSUM with small subgroup sizes of $n$= 1 and 3 are of particular interest; with a $\mathsf{\delta }$ = 1.05, the IMCUSUM has an ARL of 106.3 to 221.4 and the IMEWMA has an ARL of 155 to 255.

  i

  This emphasizes the necessity of an adequate $n$ if the highest possible performance of the chart has to be maximized, with the IMCUSUM chart also turning out to be superior with small samples.

• Table 3. Percentiles of RL for IMCUSUM chart.

  $\delta$	$\mathit{n}$$= 1 \mathbf{and} \mathit{h}$ = 13.21				$\mathit{n}$$= 3 \mathbf{and} \mathit{h}$ = 30.991				$\mathit{n}$$= 6 \mathbf{and} \mathit{h}$ = 52.86				$\mathit{n}$$= 9 \mathbf{and} \mathit{h}$ = 71.35
  	P25	P50	P75	P90	P25	P50	P75	P90	P25	P50	P75	P90	P25	P50	P75	P90
  1	114	255	510	1100	123	264	508	820	131	266	504	821	141	269	493	798
  1.01	102	231.5	455	748	113	240	452	735	122	242	439	703	120	226	419	669
  1.02	94	214	420	681	102	214	403	649	103	201	366	577	101	183	326	507
  1.03	87	191	375	621.1	89	183	344	549	83	155	280	443	79	137	236	367
  1.04	77	170	333	544.1	78	156	294	471	72	127	219	344	64	106	175	266
  1.05	70	155	304	491.1	66	133	243	393	60	102	174	270	54	86	137	203
  1.10	46	99	192	314.1	39	67	114	178	33	50	74	106	30	42	59	79
  1.15	34	69	129	209	27	43	67	99	23	33	46	61	21	28	37	47
  1.16	32	65	122	197	25	39	61	90	22	30	42	55	20	26	34	44
  1.17	30	60	113	182	24	37	56	81	20	28	39	52	19	25	32	41
  1.18	29	58	105	169	22	34	52	76	20	27	36	47	18	23	30	37
  1.19	27	53	98	156	21	33	49	70	19	25	34	44	17	22	28	35

  and

  Table 4. Percentiles of RL for IMEWMA chart.

  $\delta$	$\mathit{n}$ = 1, λ = 0.5 and L = 4.110				$\mathit{n}$ = 3, λ = 0.5 and L = 3.558				$\mathit{n}$ = 6, λ = 0.5 and L = 3.321				$\mathit{n}$ = 9, λ = 0.5 and L = 3.214
  	P25	P50	P75	P90	P25	P50	P75	P90	P25	P50	P75	P90	P25	P50	P75	P90
  1	110	261	509.3	1125	108	252	505	3340	106	257	515	1107	108.8	260	513	1109
  1.01	98	240	467	1025.2	99	235	461	1016	97	233	459	994.2	93	217	439.3	955.1
  1.02	96	227	443.3	952.05	86	205	412	930	82	194	377.3	830	74	179	358.3	764
  1.03	82	204	412.3	906	78	187	359	791	66	162	325	695	63	151	297	639
  1.04	82	193	376	810	69	163	325.3	687	60	140	280	600.1	50	120	245	512
  1.05	73	176	356.3	764.05	61	147	289	2162	51	119	239	494.1	46	107	214.3	463
  1.10	55	129	257	546.05	61	146	289	626	27	62	125	271	22	52	101	212
  1.15	39	94	190	404	63	105	299	634	16	37	72	153	12	27	52	112
  1.16	35	85	174	376	23	53	107	234	14	32	62	133	11	24	46	100
  1.17	36	85	165	370	21	48	95	203	13	30	57	122	10	22	42	89
  1.18	33	78	157	338	20	46	89	189	12	27	51	111	9	19	37	77
  1.19	31	71	143	316	18	42	83	178	11	24	48	106	8	18	33.25	72

  present the percentiles of the both charts’ run lengths (P25, P50, P75, and P90) demonstrate that the IMCUSUM chart detects shifts earlier and with a higher consistency than the IMEWMA chart. For example:

  i

  When $\mathsf{\delta }$ = 1.10 the 90th percentile of the IMCUSUM plot ranges between 79 and 314.1 and that of the IMEWMA plot ranges between 212 and 546.05.

  ii

  Thus, the IMCUSUM chart will be capable of detecting shifts with fewer samples than the IMEWMA chart.

These findings demonstrate that the IMCUSUM chart has superior detection of small- and middle-sized shifts relative to the IMEWMA chart, particularly with small $n$ that are practical and meaningful in real life manufacturing and testing environments. The smaller values of the ARL, SDRL, and MRL of the IMCUSUM chart demonstrate that it will detect shifts faster. The percentiles of the run length also demonstrate that the IMCUSUM chart will detect shifts at an earlier interval and thus it will be a superior option in the detection of processes that follow heavy-tailed and non-normal distributions and with the testing of small $n$.

5. Simulation Results and Discussion

Random data has been applied in this simulation analysis in an effort to reflect real life and project the performance of the proposed IMCUSUM chart against the conventional IMEWMA chart. The simulation process includes the following steps:

i

A sample of $n$ observations is generated from T~Gamma (3/2, 2${\sigma }_0^2)$.

ii

A predetermined sample of size $n$ is chosen for every random sample.

iii

The sample is converted by implementing the square root transformation to T, resulting in a sample drawn from the Maxwell distributed random variable x.

iv

A sample of size $n$ from the random variable R of the IM is derived by taking R = 1/x.

v

The IMCUSUM statistic, $C_i^{+}$ and $C_i^{-}$, are computed for each sample.

vi

Steps 1–5 are repeated as far as the desired number of samples are achieved.

vii

Control limits are computed as outlined in the preceding section.

viii

All values of the $C_i^{+}$ and $C_i^{-}$ statistics are plotted against the control limits.

ix

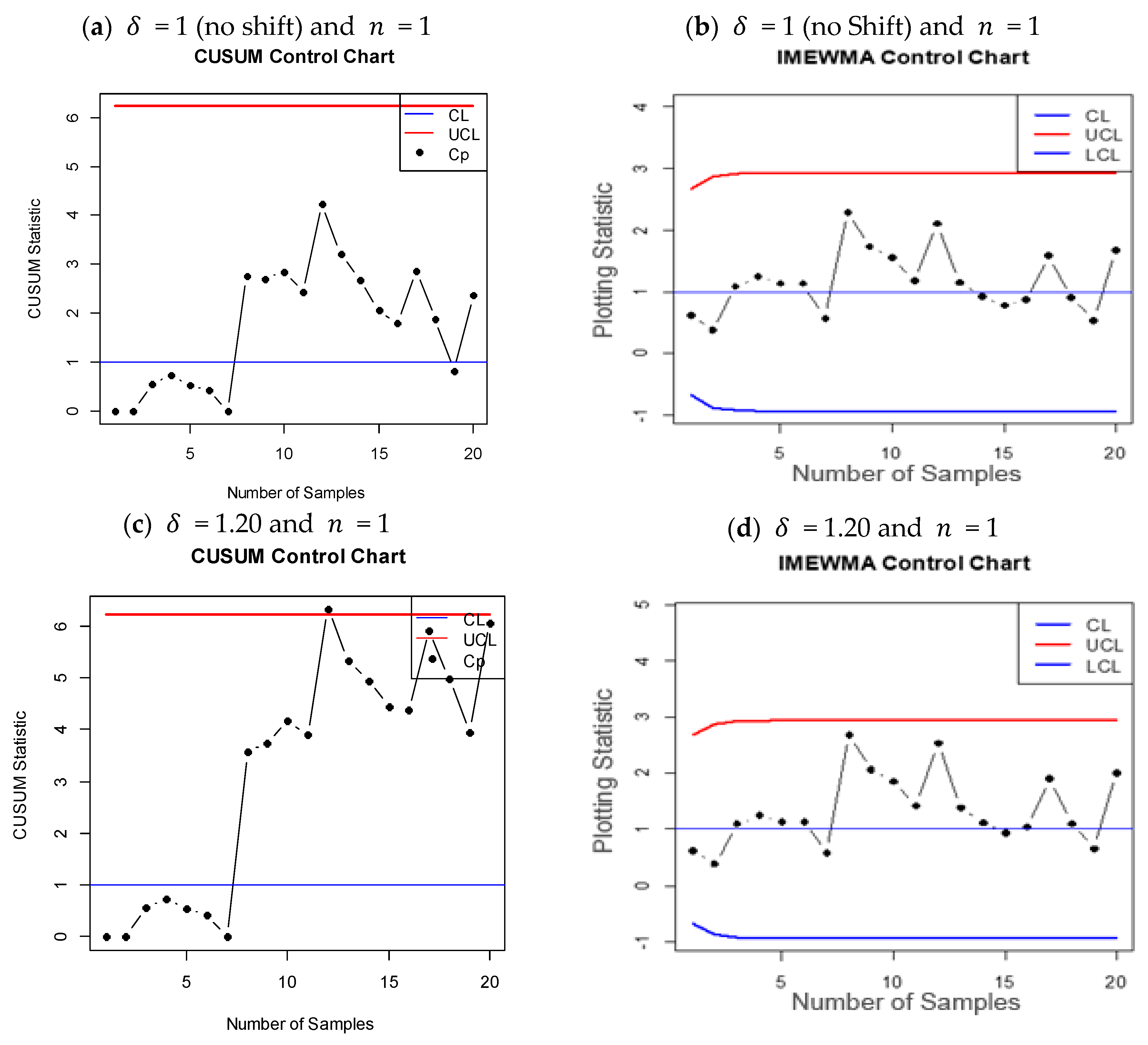
Data is generated from the IM distribution using ${\sigma }_0$ = 1, and 60 sample observations are created.

x

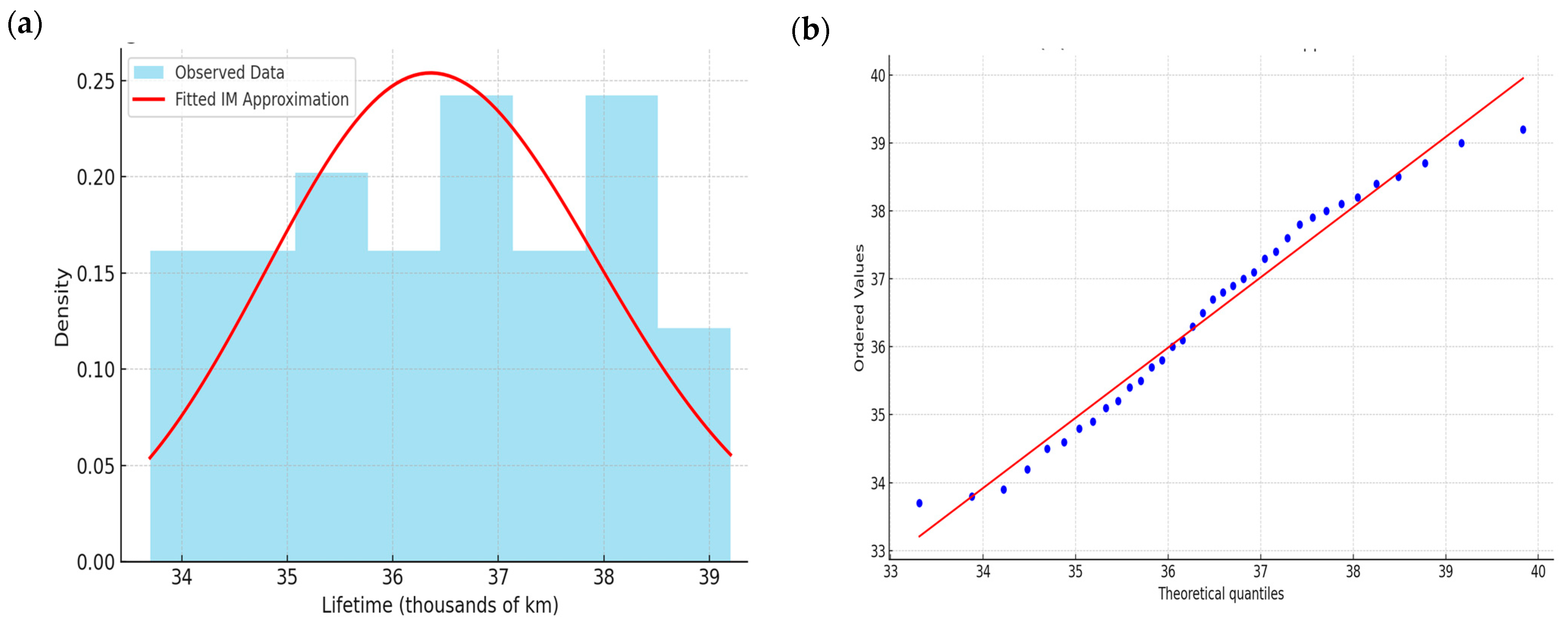
The Kolmogorov–Smirnov (K–S) test is used to verify that the data conforms to the IM distribution. The null hypothesis is not rejected, confirming that the data follows the IM distribution.

xi

For graphical representation, the design parameters are set as $n$ = 3, k = 0.5, and ARL₀ = 370.

xii

To evaluate the chart’s capability to observe process variations, shifts in the process scale parameter are introduced at 5%, 10%, 15%, 20%, 25%, and 50% after the 10th sample.

xiii

The effectiveness of the IMCUSUM chart is compared with the existing IMEWMA chart (Figure 1 and Figure 2).

The simulation outcomes demonstrate the superior performance of the IMCUSUM chart in detecting process shifts, especially for small to moderate shifts and small subgroup sizes. The following observations highlight the supremacy of the IMCUSUM chart over the IMEWMA chart.

In the case of small shifts, the IMCUSUM chart exhibits greater sensitivity and effectiveness. For instance, with a 5% increment in the scale parameter, the IMEWMA chart fails to signal an OOC condition, while the IMCUSUM chart detects an OOC signal after the 18th data point. Equivalently, the IMCUSUM also displays an OOC status at the 15th sample during a 15% shift and the IMEWMA at the 18th sample. The results highlight the detection of small shifts at an earlier interval with the aid of the IMCUSUM compared with the IMEWMA chart.

In the situation of moderate shifts, the IMCUSUM plot still has an edge over the IMEWMA plot. Under a 20% scale increment, the IMCUSUM plot declares an OOC condition at the 14th observation and the IMEWMA plot at the 18th observation. Under a 25% increment, the IMCUSUM plot declares an OOC condition at the 13th observation and the IMEWMA plot at the 18th observation. The findings indicate the IMCUSUM plot more quickly detects moderate shifts and further illustrate the IMCUSUM plot’s predominance.

Both plots perform equally with large shifts, although the IMCUSUM plot has an added benefit. Under a 50% increment in shift, the IMCUSUM plot detects an OOC at the 13th observation and the IMEWMA plot at the 15th observation. The difference becomes smaller with larger shifts, although the IMCUSUM plot correctly identifies shifts at an earlier period of observation, confirming the plot’s consistency with a large set of shifts of varied amplitudes. This example verifies the effectiveness of the IMCUSUM with small subgroup sizes that are practical and useful in real-world manufacturing and testing environments. The findings categorically confirm this intention. For instance, with $n$ = 1 and $\mathsf{\delta }$= 1.20, the IMCUSUM raises an OOC alarm at the 7th sample point and the IMEWMA does not trigger any OOC alarm. This highlights the better performance of the IMCUSUM with small $n$, making it a practical and useful option in real-world environments, in which small samples prevail.

The visual comparison of the IMCUSUM and the IMEWMA plots further confirms the findings. The visual comparison of the two plots for different shifts of different magnitudes has been provided in Figure 1a–g and Figure 2a–g. The figures demonstrate that the IMCUSUM plot consistently yields OOC signals earlier and at a larger scale compared to the IMEWMA plot. Figure 3a–d also demonstrates the behavior of the IMCUSUM plot with $n$ = 1 and how it effectively identifies shifts with small $n$. The visual plots emphasize the strength and effectiveness of the IMCUSUM plot in real-time environments.

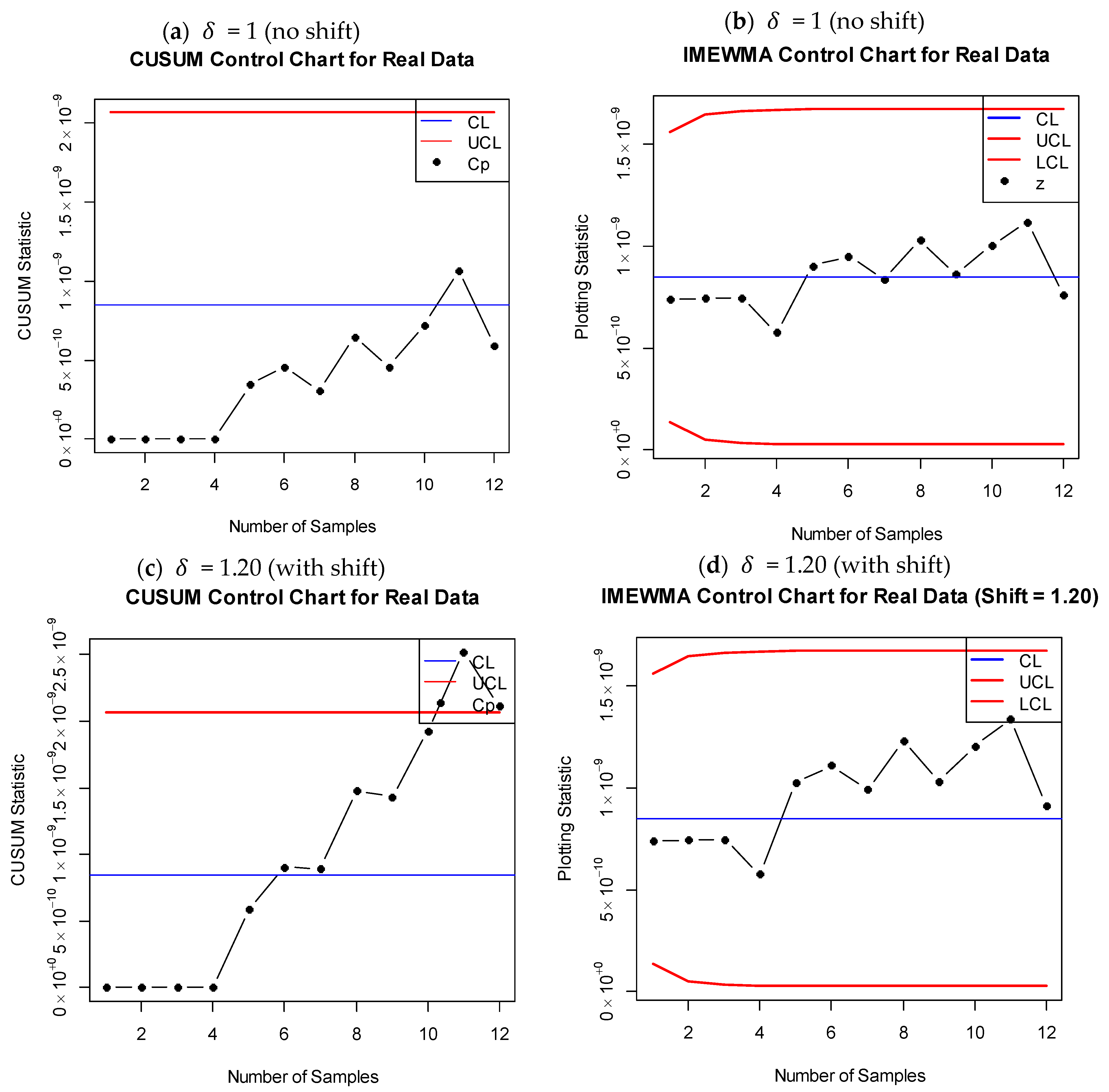
6. Real Life Application

To assess the effectiveness of the proposed IMCUSUM chart, a real-world data set consisting of the lifetimes of brake pads from 36 vehicles was considered. Lifetime was measured by the distance traveled while the brake pads remain in use. The data were organized into 12 subgroups of size 3 each. These subgroups were used to construct and analyze the control charts. The MLE for the scale parameter was calculated as ${\overline{V}}_{IM}$ = 8.47869 × 10⁻¹⁰. The Kolmogorov–Smirnov (K–S) test statistic of 0.261 with a corresponding p-value of 0.4745 showed that the null hypothesis was not rejected, confirming that the data adequately followed the IM distribution. The suitability of the IM distribution for modeling automotive brake pad lifetimes has been supported in earlier studies (Arafat et al. [28]; Omar et al. [29]; Maqsood et al. [30]), and in this study its appropriateness was further validated using the histogram and Q-Q plot in Figure 4a,b. To construct dynamic control limits for the IMCUSUM and IMEWMA charts, the coefficients $h$ and L for $n$ = 3 were employed, as provided in Table 1 and Table 2, respectively.

According to Gupta and Kapoor [37], there are different principles for identifying a lack of control, including a point beyond the control limits, a sequence of seven or more consecutive points, points exceeding certain secondary limits, points clustering too closely around the central line, the presence of trends, and the presence of cycles. Since none of these criteria can be observed in Figure 5a,b, we determined that the process was IC.

Figure 5c,d presents the IMCUSUM and IMEWMA charts for the brake pad lifetime data, respectively, considering $\mathsf{\delta }=1.20$ after the 4th sample observation. Although there was a 20% increment in the shift, the IMEWMA chart showed that the process remained IC. However, the IMCUSUM chart detected an OOC condition, as the 11th point went outside the control limit. The lifetime data demonstrates the IMCUSUM chart’s superior ability to identify small to medium shifts in real-world applications.

Based on the lifetime data, the proposed IMCUSUM control chart demonstrates superior shift detection capability compared to the IMEWMA chart. The IMCUSUM chart effectively detects small to moderate shifts, such as the 20% shift introduced in the data set, while the IMEWMA chart was not able to observe the same shift. This highlights the limitations of the IMEWMA chart in identifying smaller process deviations and confirms the IMCUSUM chart’s practical applicability in real-world scenarios.

Figure 5a–d illustrates the superior detection capabilities of the IMCUSUM chart compared with the IMEWMA chart visually. The results affirm that the IMCUSUM chart is a superior tool for process control in the case of small and moderate shifts.

7. Conclusions

This study develops an IMCUSUM control chart tailored to processes following the inverse Maxwell (IM) distribution, with a focus on monitoring its scale parameter. Maximum likelihood estimation was employed for parameter estimation, and the chart’s performance was assessed using standard run-length metrics including ARL, SDRL, and MRL.

Simulation results demonstrated that the IMCUSUM chart performed particularly well in detecting small and moderate shifts, especially with small subgroup sizes. This property is critical, as small subgroups are common in practical manufacturing and quality-control contexts. Compared to the existing IMEWMA chart, the IMCUSUM chart exhibited greater sensitivity to small shifts, while both approaches performed similarly for larger deviations. These findings highlight the strength of the IMCUSUM chart in enhancing early detection of process changes. The real-data application to automotive brake pad lifetimes further validates the chart’s effectiveness. The IMCUSUM chart successfully signals even subtle out-of-control conditions where the IMEWMA chart does not, underscoring its practical value in reliability and industrial monitoring scenarios.

By explicitly incorporating the asymmetric characteristics of the inverse Maxwell distribution, the proposed IMCUSUM chart captures real-world process behaviors more accurately than symmetric, normality-based approaches. This enables more balanced detection of shifts in skewed or heavy-tailed environments, thereby improving reliability in decision-making.

Overall, the IMCUSUM chart offers a robust and sensitive tool for detecting shifts in IM-distributed processes, complementing existing IM-based methods. Its design, grounded in asymmetric distributional behavior, extends the conventional scope of symmetric control chart frameworks, making it a valuable addition to modern statistical process control methods.

8. Limitations and Future Work

The present study focuses on developing and evaluating the IMCUSUM chart for monitoring the scale parameter of the inverse Maxwell distribution. While the results demonstrate strong detection capability, especially for small and moderate shifts, some natural limitations in the study’s scope should be acknowledged. The study emphasizes simulation-based evaluation and illustrates the application through a reliability data set.

Although this provides a strong proof of concept, future research may extend the analysis to a wider range of data sets from the engineering, agriculture, and biomedical domains to further assess practical utility. In addition, extending the comparison of IMCUSUM charts with other distribution-specific or distribution-free methods offers an interesting direction for broadening its benchmarking. Another valuable avenue is incorporating Phase I estimation variability into the design, which would provide more realistic performance assessments. Finally, adaptive and hybrid memory-type schemes may be investigated to enhance detection capability under dynamic process conditions.